Egzamin dla Aktuariuszy z 6 kwietnia 2009 r.
Matematyka Finansowa
Zadanie 1
Strategię tworzymy tak by:
X
X
1 +
2
= PV
t
t
1
2
1
,
1
1
,
1
gdzie
X 1 ⋅ + X
t
2
1
⋅ t 2 = PV ⋅
D
t
t
1
2
1
,
1
1
,
1
PV = 1000( a + a + a 10
12
15 )
PV ⋅ D = 1000(
2
10
2
12
2
15
v + 2 v + ... + 10 v + v + 2 v + ... + 12 v + v + 2 v + ... + 15 v ) podstawiamy i wychodzi odpowiedź E) czyli t = ,
4 t = ,
8 X = 1866 ,
9 X = 16748
1
2
1
2
Zadanie 2
PoŜyczamy 100 z krótkiej sprzedaŜy akcji, będziemy musieli zwrócić cenę akcji po 6
miesiącach – ile zarobimy?
Zysk arbitraŜowy będzie jeŜeli zawsze zarobimy więcej niŜ cena akcji po 6 miesiącach Inwestujemy 100:
X – cena akcji po 6 miesiącach
a – tyle inwestujemy w aktywa wolne od ryzyka b – tyle inwestujemy w opcje kupna
c – tyle inwestujemy w opcje sprzedaŜy a+b+c=100 gdzie a jest nieujemne b,c – mogą być ujemne 0,07⋅0,5
b
c
ZYSK = ae
+
max( X − 95 0
; ) +
max 9
( 5 − X 0
; ) − X
1 ,
1 4
,
5 6
I. X < 95
0,07⋅0,5
c
ZYSK = ae
+
9
( 5 − X ) − X chcemy by ZYSK>0 i nzl od X
,
5 6
c
czyli −
−1 = 0 → c = − ,
5 6
,
5 6
II tak samo dla X>95
b
b
0,07 0,5
ZYSK =
⋅
ae
+
( X − 9 )
5 − X →
−1 = 0 → b = 1 ,
1 4
1 ,
1 4
1 ,
1 4
wtedy ZYSK(I)=ZYSK(II)=
0,07 0
⋅ ,5
ae
− 95
a = 100 − b − c = 100 −1 , 1 4 + ,
5 6 = 9 ,
4 2
ODP = (9 ,
4 2 0,035
e
− 95) −0,035
⋅ e
= 9 ,
4 2 − 95 −0,035
e
≈ ,
2 47
S (0) ≡ 7 → F
GDZIE ⊗ - zbiór pusty
0 = { ,
0
}
Ω
F
jest generowane przez rozbicie Ω na zbiory S ) 1
(
1
− 1
( 1
)
i S )
1
(
1
− (4) czyli na zbiory
1
{ w , w , w , w → F = ,
⊗ ,
Ω w , w , w , w czyli (i) TAK
1
2 } {
3
4 }
1
{
{ 1 2} { 3 4}
1
1
13
10
23
dla w , w E S t =
F =
⋅ + ⋅ =
+
=
=
1
2
( ( 2) 1) 13
10
11 5
,
2
2
2
2
2
1
1
dla w , w E S t =
F = ⋅
+ ⋅ =
3
4
( ( 2) 1) 6
2
4
2
2
czyli (ii) NIE (iii) TAK
(iv) chcemy, by
− r
S t
( ) e był martyngałem:
E( S )
1
(
− r
e
F =
p +
− r
p e
=
0 )
(11
4
1
2 )
7
E(
r
−
x
x e
S (2) r
e
F
1 )
(13 1 +10 2 ) − =
=
11
(6
r
y
y e
1 + 2
2 ) −
= 4
niezaleŜne układy równań:
11 p
p
er
13 x
x
er
6 y
y
er
1 + 2
2 = 4
1 + 10
2 = 11
1 + 4
2 = 7
I
.
II
.
III
.
p
p
x
x
y
y
1 +
2 = 1
1 +
2 = 1
1 +
2 = 1
rozwiązując I:
1 (
1 1 − p +
=
2 )
r
4 p
7 e
2
11
11
9
,
4 7
0 < p =
− r
e < 1 musi być z tego r < ln
≈
2
7
7
11
II analogicznie:
13
8
,
1 3
2
r < ln
≈
<
11
11
11
2
czyli dla r >
nie istnieje miara martyngałowa
11
Zadanie 4
t
t
1
a( s, t) = exp ∫δ ( s, w) dw =
ex
p ∫
dw
s
w 1
s
+ +
s
t∫ 1
1
dw = [ln 1
( + s + w)] t
+ s + t
ln 1
(
s
t)
ln 1
(
s
s)
ln
s =
+ + −
+ + =
1 + s + w
1 + 2 s
s
1 + s + t
a( s, t) =
1 + 2 s
1 + 2 + 5
8
a(
)
5
,
2
=
=
1 + 2 ⋅ 2
5
1 + 2 + 3
6
a(
)
3
,
2
=
=
1 + 2 ⋅ 2
5
1 + 3 + 5
9
a
)
5
,
3
(
=
=
1 + 2 ⋅ 3
7
8
6 9
56 − 54
2
ODP =
−
=
=
5
5 7
35
35
Zadanie 5
To, Ŝe u(s) znane i d(2) znane oznacza, Ŝe jeśli chcielibyśmy osiągnąć zysk arbitraŜowy to tylko kupując obligację dwuletnią tzn po okresie 2
Badamy granicę w nieskończoności więc interesuje nas zachowanie: P( , 0 2) P( ,
2 ∞)
T
T −
T −
Wiemy: 0 1,
0,2
e
= e (1+ R( ,
2 T )) 2 → (1 + R( ,
2 T )) 2
0 1
, T −0,2
= e
I
T −
T −
Ale: ( 1
,
1 − d (2))(1 + R( ,
2 T )) 2 = ( 1
,
1 − d ( T )) 1
Podstawiając z I:
(
T −
T −
1
,
1 − d (2)) 0 1, 0,2
e
= ( 1,
1 − d ( T )) 1
(
0 1
, T
0,2
1
−
1
,
1 − d (2))
1 T
−
T 1
−
T 1
− e
e
= 1,
1 − d ( T )
→exp(0 )
1
,
1
1
→
→
6 4
4 7 4
4 8
4
6
4
7 86 4
4 7 4
4 8
1
T
d ( T ) = 1
,
1 − ( 1
,
1 − d (2))
1
,
0
,
0 2
T 1
− exp
exp −
→ 1
,
1
0 1
,
− e ≈ 0
T −1
T −1
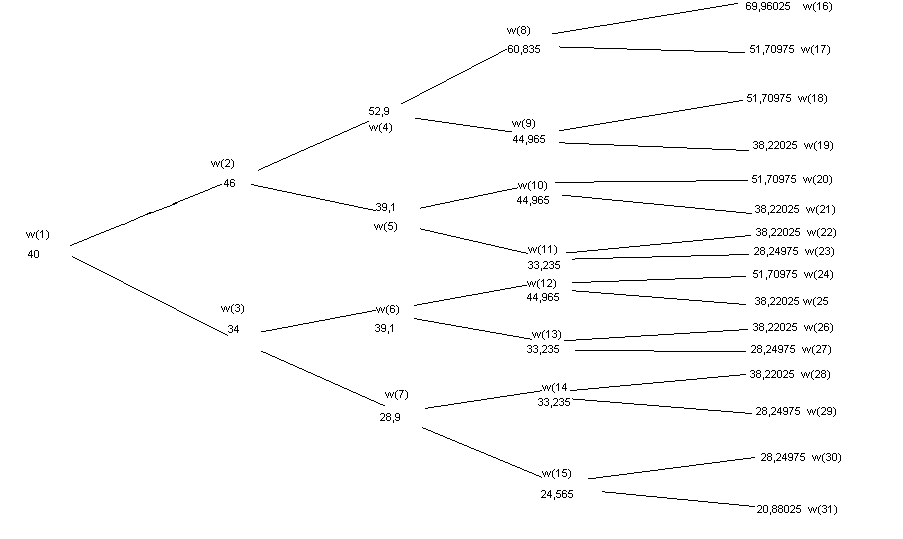
Zadanie 6
p
- prawdopodobieństwo wzrostu ceny akcji 1
p
- prawdopodobieństwo spadku ceny akcji 2
c(i) – cena opcji w węźle i
z braku arbitraŜu mamy:
1
10
17
p
,
1 05
1
12
46 p
34 p
40
,
1 05
3
6
1 +
2 =
⋅(
)
1 =
( ) −
12
→
1
23
10
p
p
1
1 +
2 =
p
,
1 05
2 =
−
( )
12
6
3
wyceniamy od prawej strony:
c(18)=c(17)=c(20)=c(24)=51,70975-44=7,70975
c(16)=69,96025-44=25,96025
c(31)=c(30)=c(29)=c(28)=c(27)=c(26)=c(25)=c(23)=c(22)=c(21)=c(19)=0
−
c )
8
(
= [ p c 1
( 6) + p c 1
( 7) ,
1 05
1
2
]( ) 112
1
−12
c 9
( ) = p c 1
(
)
8 ( ,
1 0 )
5
1
1
−12
c 1
( 0) = p c(20)( ,
1 0 )
5
1
1
−12
c 1
( 2) = p c(24)( ,
1 0 )
5
1
c 1
( )
1 = c 1
( )
3 = c 1
( 4) = c 1
(
)
5 = 0
−
c(4) = [ p c )
8
(
+ p c 9
( )
,
1
( 0 )
5
1
2
]
1
12
1
−12
c )
5
(
= p c 1
( 0)( ,
1 0 )
5
1
1
−12
c(6) = p c 1
( 2)( ,
1 0 )
5
1
c(7)=0
−
c(2) = [ p c(4) + p c ) 5
(
,
1
( 0 )
5
1
2
]
1
12
1
−12
c )
3
(
= p c( )
6 ( ,
1 0 )
5
1
1
1
2
2
c )
1
(
=
−12
p c(2)( ,
1 0 )
5
p c )
3
( ( ,
1 0 )
5
p c(4)
p p c )
5
(
,
1
( 0 )
5
p p c(6)( ,
1 0 )
5
1
+
−12
2
= [ 21
+ 1 2
]
−12 +
−12
1
2
=
3
3
3
= [ 3
p c )
8
(
p p c 9
( ) ,
1
( 0 )
5
p p c 1
( 0)( ,
1 0 )
5
p p c 1
( 2)( ,
1 0 )
5
1
+ 21 2
]
−12 +
−
2
12
1
2
+
−
2
12
1
2
=
4
4
4
4
= [ 4
p c 1
( 6)
p p c 1
( 7) ,
1
( 0 )
5
p p c 1
(
)
8 ( ,
1 0 )
5
p p c(20)( ,
1 0 )
5
p p c(24)( ,
1 0 )
5
1
+ 31 2
]
−12 +
−
3
12
1
2
+
−
3
12
1
2
+
−
3
12
1
2
=
= [
1
−
4
p ⋅ 25 9
, 6025
3
+ p p ⋅ 7,70975
3
+ p p ⋅ 7,70975
3
+ p p ⋅ 7,70975
3
+ p p ⋅ 7,70975
≈
1
1
2
1
2
1
2
1
2
] ,1(0 )5 3 8,
3
Zadanie 7
10
1
300000 = 1
R ⋅ a
+ R 2
a
10;0,07
10;0,09
0
,
1 7
dług po 15 latach:
DL 1
( )
5 = R 2 ⋅ a
5;0,09
( )
5 = R 3 ⋅ a
10;0,08
odsetki spłacone w 7 i 14 racie:
4
3
1
1
OD(7) = 1
R − 1
R ⋅ a
+
R 2 ⋅ a
− 1
R ⋅ a
−
R 2 ⋅ a
4;0,07
,
1 07
10;0,09
3;0,07
,
1 07
10;0,09
OD 1
(
)
4 = R 2 − [ R 2 ⋅ a
− R 2 ⋅ a
7;0,09
6;0,09 ]
10
10
1
1
1 −
−
10 1
0
,
1 7
1
0
,
1 9
I 3
. 00000 = 1
R
+ R 2
0
,
0 7
0
,
1 7
0
,
0 9
4
3
1
1
1 −
1 −
,
1 07
,
1 07
II. R 1⋅ 1 −
+
+
,
0 07
,
0 07
1
4
4
4
4
4
2
4
4
4
4
4
3
A
7
6
10
10
1
1
1
1
1 −
1 −
−
−
4 1
3 1
,
1 09
,
1 09
1
,
1 09
1
,
1 09
+ R 2 1−
+
−
+
= 3162 ,160
,
0 09
,
0 09
,
1 07
,
0 09
,
1 07
,
0 09
1
4
4
4
4
4
4
4
4
4
4
4
4
4
4
2
4
4
4
4
4
4
4
4
4
4
4
4
4
4
3
B
10
1
−
10 1
1
,
1 09
300000 − R 2
,
0 07
,
1 07
,
0 09
I → 1
R =
10
1
1 −
,
1 07
wstawiamy do II:
10
1
10 1 −
300000 ⋅ ,
0 07
,
0 07
1
,
1 09
−
⋅ R 2 ⋅ A + R 2 ⋅ B = 3162 , 1 6 →
10
10
1
1 ,
1 07
,
0 09
1 −
1 −
,
1 07
,
1 07
1
4
4
4
4
4
4
2
4
4
4
4
4
4
3
C
300000 ⋅
3162 ,
1 6 −
,
0 07 ⋅ A
1 10
1 −
,
1 07
→ R 2 =
B − A ⋅ C
5
1
1 −
,
1 09
100000 + R 2
,
0 08
,
0 09
R 3 =
10
1
1 −
,
1 08
10
1
1 −
,
1 08
ODP = R 3 ⋅10 − R 3
≈ 108800
,
0 08
Zadanie 8
15
1
1 −
1
,
1
10000
100000 = Ra = R
→ R =
15
15
1
,
0
1
1 −
1
,
1
spłacony kapitał w (K+1) racie = KAP
KAP = R( a
− a
= Rv 15−
15− K
14−
)
K
K
dług po wpłaceniu KAP:
15− K
DLUG( KAP) = Ra
− Rv
= Ra
15− K
14− K
czyli po operacji będzie spłacał o 1 rok krócej OD – odsetki bez dodatkowej wpłaty
OD
- odsetki gdy wpłacona dodatkowa kwota KAP
OD=15R-100000
OD
= 14
15
R +
− K
Rv
KAP
−100000
15 R −100000 −14
15
R −
− K
Rv
+100000 = 701 ,
4 03
15− K
150000
140000
10000
1
−
−
= 701 ,
4 03
15
15
15
1
,
1
1
1
1
1 −
1 −
1 −
1
,
1
1
,
1
1
,
1
15− K
10000
1
1
−
=
03
,
7014
15
1
,
1
1
1 −
1
,
1
15
1
701 ,
4 031
−
15− K
1
,
1
1
1 −
=
1
,
1
10000
15
1
701 ,
4 031
−
1
,
1
K −
1
,
1
15 = 1−
10000
15
1
701 ,
4 031 −
1
,
1
( K −1 )
5 ln 1
,
1 = ln1 −
10000
15
1
701 ,
4 031
−
1
,
1
ln 1
−
10000
K =
+15 ≈ 7
ln 1
,
1
Zadanie 9
a – kwota na obligację
P – cena obligacji
N(I), N(II) – nominał
N(III) – kwota wypłacana dla obligacji III N 1
N 2
v
P( I ) =
P( II ) = N 2 ⋅ , 0 05 a
+
P( III ) = N 3
= 20 N 3
,
1
( 0 )
5 15
20
,
1
( 0 )
5 20
1 − v
15
a
1
b
2
20
20 2
LICZ =
1
5 N 1
+
,
0 05 N 2( v + 2 v + ... + 20 v ) N
c
+
+
20
[ N (3 Ia)]
P( I )
,
1 05
P( II )
,
1
( 0 )
5
P( III )
MIAN=a+b+c=1
a
− 20 21
v
b ⋅ ,
0 05 N 2 20
+ 20 N 2 ⋅ 20
v
cN 3 ⋅ ,
1 05
15 aN 1
,
1
( 0 )
5 15
1 − v
2
LICZ =
+
+
,
0 05
=
,
1
( 0 )
5 15
N 1
,
0 05 N 2 ⋅ a + N 2 ⋅ 20
v
20 N 3
20
,
1 0 (
5 a
− 20 v 21
20
)+ 20 v 20
= 15 a + b ⋅
+ 2 c
1 =
20
,
0 05 a
+ v
20
,
1 05 a
− 20 v 20 + 20 v 20
,
1 05 a
= 15 a + b
20
+ 2 c
1 = 15 a
20
+
b + 2 c
1
,
0 05 a
+ v 20
,
0 05 a
+ v 20
20
20
I poniewaŜ a+b+c=1 to LICZ=17,5
15 a + 21 c = 20
a + c
czyli
,
1 05 a
15 a +
20
b + 21 c = 17 5
,
20
,
0 05 a
+ v
20
15 a + 21 c = 20 a + 20 c
1 (
5 a + b + c) =
15
,
1 05 a
3 c +
20
b + 21 c = 17 5
,
,
0 05 a
+ 20
v
20
3 c +15 b + 15 c = 15
z II 18c=15-15b
czyli:
0
,
1 5 a
20 − 20
20
b +
b = 17 5
,
0
,
0 5
20
a
+ v
20
5
,
2
b =
≈ 3 %
6
0
,
1 5 a
20
20
− 0,
0 5
20
a
+ v
20
Zadanie 10
SPOSÓB I:
Na koniec kaŜdego roku mamy 0,1
Z II Funduszu mamy:
Na koniec 2 roku – 0,1*0,07
Na koniec i-tego roku : 0,1*(i-1)*0,07
WYPŁATA z III Funduszu:
13
12
1
,
0 ⋅ ,
0 07 ⋅ ,
1 08 + 1
,
0 ⋅ 2 ⋅ ,
0 07 ⋅ ,
1 08
+ ... + 1
,
0 ⋅14 ⋅ ,
0 07 = 1
,
0 ⋅ ,
0 07(
13
12
0
,
1 08 + 2 ⋅ ,
1 08
+ ... +14 ⋅ ,
1 08 )
I = ,
1 0813 + 2 ⋅ ,
1 0812 + ... + 14
I ⋅ ,
1 08 = ,
1 0814 + 2 ⋅ ,
1 0813 + ... + 14 ⋅ ,
1 08
−
−
14
1
,
1 0814
13
,
1 0 (
8 ,
1 0814
)1
I ,
1
( 08 − )
1 = ,
1 08 + ,
1 08 + ... + ,
1 08 −14 = ,
1 08
−14 =
−14
1 − ,
1 08
,
0 08
,
1 0 (
8 ,
1 0814 − )
1
14
I =
−
,
0 082
,
0 08
0
,
1
(8 0,
1 814 − )
1
14
WYPLAT (
A I ) = 1 + 15 ⋅ 1
,
0 + 1
,
0 ⋅ 0
,
0 7
−
2
0
,
0 8
0
,
0 8
SPOSÓB II
Odsetki z Funduszu 1 na koniec 2 roku = 1
,
1 ⋅ 1
,
0
W Funduszu 1 zostaje: 1,1
Odsetki z Funduszu 1 na koniec 4 roku = 1
,
1 2 ⋅ 1
,
0
W Funduszu 1 zostaje
2
1
,
1
Itd.
Odsetki na koniec 14 roku z Funduszu 1 = 1
,
1 7 ⋅ 1
,
0
W Funduszu 1 zostaje:
7
1
,
1
Czyli z Funduszu 1 na koniec mamy 8
1
,
1
WYPŁATA Z II FUNDUSZU:
7
1
1 −
1
,
1
2
,
1 07
13
2
11
7
13
1
,
1 ⋅ 1
,
0 ⋅ ,
1 07
+ 1
,
1
⋅ 1
,
0 ⋅ ,
1 07 + ... + 1
,
1
⋅ 1
,
0 ⋅ ,
1 07 = 1
,
0 ⋅ 1
,
1 ⋅ ,
1 07
1
1 − 1
,
1
2
,
1 07
7
1
,
1
1 −
2
,
1 07
8
13
WYPLAT (
A II ) = 1
,
1
+ 1
,
0 ⋅ 1
,
1 ⋅ ,
1 07
1
,
1
1 −
2
,
1 07
1
1
j = [ WYPLAT (
A I )]15 −1
1
j 2 = [ WYPLAT (
A II )]15 −1
j 2 − 1
j ≈ ,
0 45% ≈ 5
,
0 %