
Egzamin dla Aktuariuszy z 30 listopada 2009 r.
Matematyka Finansowa
Zadanie 1
( )
( )
( )
0
0
0
,
,
,
t
r
V
t
r
V
t
r
f
L
A
−
=
muszą być spełnione warunki:
(
)
(
)
0
,
.
2
0
,
.
1
0
0
0
0
=
=
t
r
dr
df
t
r
f
( )
r
r
r
r
r
r
t
r
V
L
15
10
5
0
)
1
(
1
1200
)
1
(
1
1200
)
1
(
1
1200
,
−
−
−
+
−
+
+
−
+
+
−
⋅
=
(
)
72
,
21049
,
0
0
≈
t
r
V
L
[
]
[
]
+
+
−
−
+
−
+
+
−
−
+
−
=
−
−
−
−
11
2
6
2
)
1
(
10
...
)
1
(
1200
)
1
(
5
...
)
1
(
1200
r
r
r
r
dr
dV
L
[
]
→
−
−
+
−
−
+
−
−
−
=
+
−
−
+
−
+
−
−
i
v
i
v
i
v
i
v
i
v
i
v
v
r
r
16
15
11
10
6
5
16
2
10
1
10
1
5
1
1200
)
1
(
15
...
)
1
(
1200
(
)
54
,
98594
,
0
0
−
≈
→
t
r
dr
dV
L
( )
(
)
(
)
2
1
1
1
,
2
1
0
t
t
A
r
X
r
X
t
r
V
−
−
+
+
+
=
( )
(
)
1
2
2
1
1
1
0
2
1
)
1
(
1
,
−
−
−
−
+
−
+
−
=
t
t
A
r
X
t
r
X
t
dr
t
r
dV
sprawdzamy:
(
)
0
0
, t
r
V
A
21050
)
),
),
26733
)
21050
)
≈
≈
≈
e
d
c
b
a
z tego b) odpada
sprawdzamy:
(
)
0
0
, t
r
dr
dV
A
114250
)
95394
)
84391
)
127613
)
−
≈
−
≈
−
≈
−
≈
e
d
c
a
z tego najbliżej odpowiedź d)

Zadanie 2
(
)
(
)
+
⋅
+
⋅
+
⋅
+
⋅
=
2
07
,
1
1
50000
25
,
0
5000
75
,
0
8
,
0
07
,
1
1
50000
2
,
0
5000
8
,
0
ODP
(
)
=
⋅
+
⋅
⋅
+
3
07
,
1
1
50000
35
,
0
105000
65
,
0
75
,
0
8
,
0
66437
07
,
1
1
51450
07
,
1
1
13000
07
,
1
1
14000
3
2
≈
⋅
+
⋅
+
⋅
=
Zadanie 3
Do funduszu wpłacamy tyle by na koniec mieć 200 000 czyli:
[
]
1
)
1
(
200000
200000
1
...
)
1
(
.
5
4
−
+
=
→
=
+
+
+
r
r
X
r
X
I
odsetki skumulowane w funduszu:
1
)
1
(
1000000
200000
5
200000
)
(
5
−
+
−
=
−
=
r
r
X
F
OD
Odsetki zapłacone:
100000
5
200000
1
,
0
)
(
=
⋅
⋅
=
Z
OD
[
]
1
)
1
(
200000
200000
1
...
)
1
(
.
10
9
−
+
=
→
=
+
+
+
r
r
Y
r
Y
II
1
)
1
(
2000000
200000
10
200000
)
(
10
−
+
−
=
−
=
r
r
Y
F
OD
200000
)
(
=
Z
OD
16876575
,
0
1
)
1
(
75
,
68765
100000
1
)
1
(
1000000
.
1
5
5
=
−
+
→
=
−
−
+
r
r
r
r
41
,
134815
1
)
1
(
1
1
)
1
(
2000000
41
,
134815
1
)
1
(
2000000
.
2
5
5
10
=
+
+
−
+
→
=
−
+
r
r
r
r
r
Z tego:
[
]
%
5
,
8
1
)
1
(
41
,
134815
16876575
,
0
2000000
5
≈
→
−
+
=
⋅
r
r
Zadanie 4
OD(6)=12-KAP(6)
OD(12)=14-KAP(12)
KAP(6)=DŁ(5)-DŁ(6)
KAP(12)=DŁ(11)-DŁ(12)
10
7
6
5
2
5
...
14
17
20
...
14
12
)
5
(
v
v
v
v
v
v
DL
+
+
+
+
+
+
+
=
9
6
5
4
2
5
...
14
17
20
...
16
14
)
6
(
v
v
v
v
v
v
DL
+
+
+
+
+
+
+
=
4
3
2
5
8
11
14
)
11
(
v
v
v
v
DL
+
+
+
=
3
2
5
8
11
)
12
(
v
v
v
DL
+
+
=

−
−
−
−
−
+
+
+
+
+
+
+
=
4
2
10
7
6
5
2
20
...
16
14
5
...
14
17
20
...
14
12
)
6
(
v
v
v
v
v
v
v
v
v
KAP
10
9
8
7
6
5
4
3
2
9
6
5
5
3
3
3
3
3
2
2
2
2
5
...
14
17
v
v
v
v
v
v
v
v
v
v
v
v
v
+
+
+
+
+
+
−
−
−
−
=
−
−
−
−
4
3
2
3
2
4
3
2
5
3
3
3
5
8
11
5
8
11
14
)
12
(
v
v
v
v
v
v
v
v
v
v
v
KAP
+
+
+
=
−
−
−
+
+
+
=
=
−
−
−
−
−
−
−
+
+
+
+
=
−
=
2
5
3
3
3
3
3
2
2
2
2
12
)
12
(
)
6
(
10
9
8
7
6
5
4
3
2
v
v
v
v
v
v
v
v
v
v
OD
OD
ODP
=
→
−
=
camy))
przeksztal
dalej
formalnie
ale
)
(
B
w
tylko
3v
-
E,
i
B
w
tylko
wystepuje
5
9
10
B
v
=
−
−
−
−
−
−
−
+
−
+
+
+
+
=
2
5
3
3
3
3
3
3
3
4
2
2
2
3
10
9
8
7
6
5
5
5
5
5
4
3
2
4
v
v
v
v
v
v
a
v
a
v
v
v
v
v
a
=
−
−
−
−
−
−
−
+
−
−
+
+
=
2
5
3
3
3
3
3
3
3
2
2
2
3
10
9
8
7
6
5
5
5
5
5
5
4
5
4
v
v
v
v
v
v
a
v
a
v
v
v
a
a
(
)
=
−
−
−
−
−
−
−
+
+
+
+
+
−
+
−
+
=
2
5
3
3
3
3
3
3
3
3
3
3
2
2
3
2
3
10
9
8
7
6
5
10
9
8
7
6
5
4
5
5
4
v
v
v
v
v
v
v
v
v
v
v
v
v
a
v
a
(
)
2
2
5
2
3
2
3
10
5
4
5
5
4
−
−
−
+
−
+
=
v
v
v
a
v
a
Zadanie 5
X – rata w 1 okresie
Y – rata w 2 okresie
K – kredyt
Z – niewiadoma = ODP
K
Y
X
B
A
=
+
+
+
+
+
+
4
4
4
4
8
4
4
4
4
7
6
4
4
4
4
4
8
4
4
4
4
4
7
6
12
24
24
6
3
03
,
1
1
...
03
,
1
1
03
,
1
1
03
,
1
1
...
03
,
1
1
03
,
1
1
.
1
K
YB
XA
Y
X
K
Y
X
=
+
+
+
=
−
+
2
,
1
9
,
0
.
3
100000
3
2
12
8
.
2
z 2: 6X+9Y=100000+K
Y
K
YB
XA
K
YB
XA
A
B
2
X
0,2YB
0,1XA
stronami
odejmujemy
2
,
1
9
,
0
=
→
=
→
=
+
=
+
wstawiamy do 2:
BY
Y
Y
A
B
3
100000
9
12
+
=
+
AB
A
B
A
B
A
B
Y
3
9
12
100000
3
9
12
100000
−
+
=
−
+
=
AB
A
B
AB
K
AB
A
B
B
X
3
9
12
300000
,
3
9
12
200000
−
+
=
−
+
=
C
AB
A
B
AB
Z
Z
XA
c
)
3
9
12
(
100000
03
,
1
1
...
03
,
1
1
03
,
1
1
03
,
1
1
12
6
3
24
−
+
=
→
+
+
+
+
4
4
4
4
4
4
3
4
4
4
4
4
4
2
1
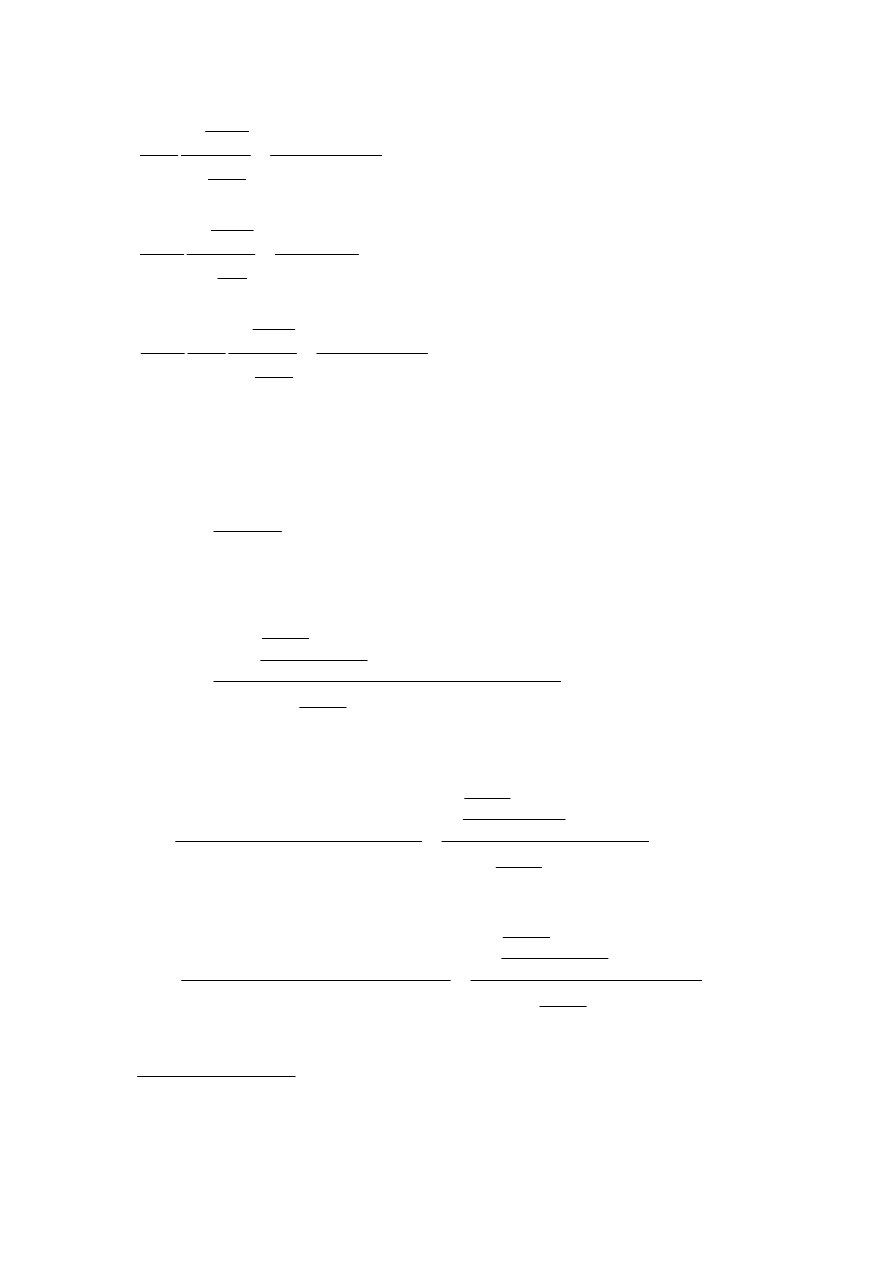
(
)
1
03
,
1
03
,
1
1
03
,
1
03
,
1
1
1
03
,
1
1
1
03
,
1
1
3
24
24
3
24
3
−
−
=
−
−
=
A
03
,
0
03
,
1
1
03
,
1
03
,
1
1
1
03
,
1
1
1
03
,
1
1
36
12
12
25
⋅
−
=
−
−
=
B
(
)
1
03
,
1
03
,
1
1
03
,
1
03
,
1
1
1
03
,
1
1
1
03
,
1
1
03
,
1
1
3
36
12
3
12
3
24
−
−
=
−
−
=
C
Z tego:
61400
≈
ODP
Zadanie 6
Obliczamy duration zobowiązań:
)
(
)
(
)
(
ZOB
M
ZOB
L
ZOB
DUR
=
(
)
15
10
20
2
1500000
500000
20
...
2
10000
)
(
v
v
v
v
v
ZOB
L
+
+
+
+
+
=
(
)
15
10
20
2
100000
50000
...
10000
)
(
v
v
v
v
v
ZOB
M
+
+
+
+
+
=
15
10
20
15
10
21
20
100000
50000
1
10000
1500000
500000
1
20
1
10000
)
(
v
v
i
v
v
v
v
v
i
v
ZOB
DUR
+
+
−
+
+
−
−
−
=
ODP=x
Duration 1 obligacji:
(
)
(
)
10
10
10
11
10
10
10
2
10
10
2
1000
1
50
10000
1
10
1
50
1000
...
50
10000
10
...
2
50
)
(
v
i
v
v
v
v
i
v
v
v
v
v
v
v
v
v
I
dur
+
−
+
−
−
−
=
+
+
+
+
+
+
+
+
=
Duration 2 obligacji:
(
)
(
)
20
20
20
21
20
20
20
2
20
20
2
5000
1
250
100000
1
20
1
250
5000
...
250
100000
20
...
2
250
)
(
v
i
v
v
v
v
i
v
v
v
v
v
v
v
v
v
II
dur
+
−
+
−
−
−
=
+
+
+
+
+
+
+
+
=
)
(
)
(
)
1
(
)
(
ZOB
DUR
II
dur
x
I
dur
x
=
−
+
⋅
%
52
)
(
)
(
)
(
)
(
≈
−
−
=
II
dur
I
dur
II
dur
ZOB
DUR
x

Zadanie 7
N – nominał obligacji
=
+
+
+
+
⋅
⋅
=
20
20
20
20
2
2
05
,
1
99
,
0
03
,
0
05
,
1
99
,
0
...
05
,
1
1
99
,
0
05
,
1
1
99
,
0
650
N
N
C
N
N
C
650
35
33
03
,
0
35
33
1
35
33
1
35
33
20
20
=
→
⋅
+
⋅
−
−
=
4
4
4
4
4
3
4
4
4
4
4
2
1
C
N
S
650000
1000
=
=
743000
02
,
1
650000
7
,
0
3
≈
⋅
=
C
X
Zadanie 8
∑
∞
=
−
=
1
3
)
1
(
1
k
k
k
v
v
a
można wiele strumieni
k
a utworzyć np:
2
10
3
)
1
(
1
)
1
(
1
1
v
v
a
a
v
v
v
a
a
a
k
−
=
=
→
−
=
−
⋅
→
=
2 przykład:
3
10
10
3
10
10
10
)
1
(
1
)
1
(
1
10
dla
0
0
v
v
a
v
v
a
k
a
a
k
−
=
→
−
=
⋅
→
≠
=
>
z tego wynika, że (E) jest prawidłową odpowiedzią
Zadanie 9
w=wartość opcji = wartość wewnętrzna + time value
p – prawdopodobieństwo wzrostu ceny
7
,
0
04
,
1
110
)
1
(
9
,
0
110
1
,
1
110
=
⋅
=
−
⋅
+
⋅
p
p
p
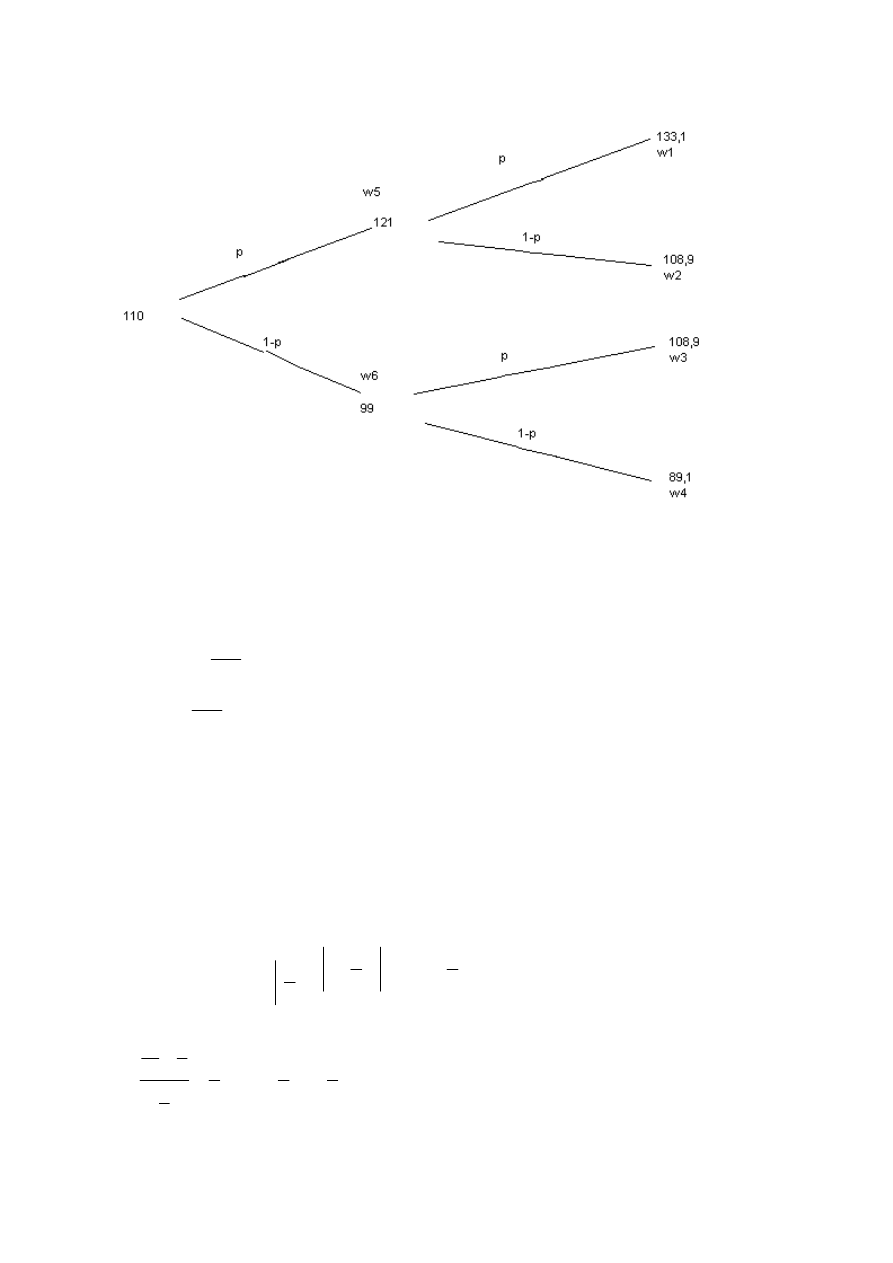
w1=33,1
w2=8,9
w3=8,9
w4=0
(
)
84
,
24
9
,
8
3
,
0
1
,
33
7
,
0
04
,
1
1
;
21
max
5
≈
⋅
+
⋅
=
w
04
,
1
1
9
,
8
6
⋅
=
p
w
(
)
[
]
45
,
18
10
;
6
)
1
(
5
max
≈
⋅
−
+
=
v
w
p
pw
w
45
,
8
10
45
,
18
=
−
=
ODP
Zadanie 10
Brak arbitrażu więc:
1
ale
5
,
0
2
05
,
1
2
4
6
,
2
=
+
+
=
+
=
q
p
qv
pv
qv
pv
9
,
0
3
4
2
,
1
3
4
3
4
5
,
0
5
,
1
05
,
1
2
2
6
,
2
=
→
=
→
−
→
⋅
+
=
+
=
→
v
v
II
I
v
pv
v
pv
8
,
1
8
,
1
6
,
2
+
=
p
9
5
,
9
4
9
4
5
9
5
9
5
13
=
=
→
=
−
=
q
p
p

Wyszukiwarka
Podobne podstrony:
2009.11.30 matematyka finansowa
1 2009 10 05 matematyka finansowaid 8924
1 2009.04.06 matematyka finansowa
2009 11 30 rachunek i statystykaid 26677
1 2009.10.05 matematyka finansowa
1 2009 04 06 matematyka finansowaid 8923
2004 10 11 matematyka finansowaid 25165
Matematyka finansowa, Wyklad 11 F
2009 11 08 5 Finanse NBP,BFG, PBid 26674 ppt
Egzamin 2003.10.11, rozwiazania zadań aktuarialnych matematyka finansowa
2004.10.11 matematyka finansowa
Matematyka finansowa Wyklad 11 F
2003 10 11 matematyka finansowaid 21704
2009 11 08 6 Finanse BANKI KOMid 26675 ppt
11-16 (ROZWIAZANIA DO ZADAN) matma, uczelnia, matematyka finansowa
więcej podobnych podstron