Egzamin dla Aktuariuszy z 11 października 2004 r.
Matematyka Finansowa
Zadanie 1
[
]
[
]
X
K
K
K
=
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ë
é
−
÷
ø
ö
ç
è
æ
−
⋅
+
−
÷
ø
ö
ç
è
æ
−
⋅
⋅
=
=
⋅
⋅
+
+
⋅
+
⋅
+
+
+
⋅
⋅
+
+
⋅
⋅
+
⋅
003
,
1
002
,
1
1
003
,
1
002
,
1
1
002
,
1
003
,
1
2000
05
,
0
003
,
1
002
,
1
1
003
,
1
002
,
1
1
003
,
1
2000
100
002
,
1
003
,
1
2000
...
002
,
1
003
,
1
2000
002
,
1
003
,
1
2000
100
5
003
,
1
002
,
1
2000
...
003
,
1
002
,
1
2000
003
,
1
2000
100
180
180
380
360
360
359
181
179
180
180
181
179
359
360
11
1500
0015
,
0
;
180
≈
→
=
K
a
X
Zadanie 2
25
2
18
7
5
2
2
23
7
5
5500
1
1
500
1000
)
1
(
...
5500
...
1500
1000
v
v
v
v
v
v
I
Iv
v
v
v
I
−
−
−
+
=
−
=
+
+
+
=
[
]
2640
1
5500
1
1
500
1000
10
2
5500
1000
1
)
1
(
5500
...
)
1
(
1500
)
1
(
1000
1
550
...
200
150
100
)
7
(
...
)
21
(
)
23
(
)
25
(
2
25
2
18
7
5
30
23
7
5
30
23
30
9
30
7
30
5
30
550
200
150
100
≈
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ë
é
−
−
−
−
+
−
+
=
=
−
+
+
−
+
−
=
+
+
+
+
=
=
+
+
+
+
=
v
v
v
v
v
v
a
v
v
v
a
a
a
a
a
a
a
a
a
ZAD
ZAD
ZAD
ZAD
ODP
Zadanie 3
25
5
,
0
2
)
50
(
−
=
+
−
S
S
S
[
]
[
]
35
,
5
1
,
1
25
50
9
,
0
2
,
1
5
,
0
4
,
0
6
,
0
3
25
50
2
,
1
5
,
0
6
,
0
:
3
2
2
3
3
≈
−
⋅
⋅
⋅
+
−
⋅
ODP
NAJBLI
ś
EJ A

Zadanie 4
A+B+C=1000000
Wypłata:
(
]
ï
î
ï
í
ì
+
>
−
+
∈
≤
)
5
,
0
1
(
1000000
15000
)
10000
(
100
1000000
15000
;
10000
1000000
10000
k
ind
ind
k
ind
ind
Zabezpieczenie:
ï
ï
ï
î
ï
ï
ï
í
ì
⋅
+
−
+
−
⋅
+
−
⋅
III
12
,
1
)
15000
(
200
)
10000
(
1200
A
II
12
,
1
)
10000
(
1200
A
I
12
,
1
C
ind
B
ind
C
ind
C
1000000
12
,
1
10000
>
⋅
→
≤
C
ind
gdy
Szukamy maksymalnego k wi
ę
c w wy
ż
szych przedziałach trzeba maksymalizowa
ć
A+B bo
A+B s
ą
wieksze od C dla du
ż
ych ind
Z tego wynika,
ż
e:
12
,
1
1000000
=
C
(
]
ï
ï
î
ïï
í
ì
⋅
>
−
+
−
∈
−
>
−
k
ind
B
ind
A
ind
k
ind
A
5
,
0
1000000
)
15000
(
200
)
10000
(
1200
0
10000;1500
ind
dla
)
10000
(
100
)
10000
(
1200
Trzeba zmaksymalizowa
ć
A z II przedziału ale jednocze
ś
nie funkcja A/1200*ind+B/200*ind
musi by
ć
rosn
ą
ca bo inaczej mo
ż
e by
ć
nieograniczona strata
St
ą
d
0
6
0
200
1200
)
(
)
12
,
1
1
1
(
1000000
>
+
→
>
+
=
′
−
=
+
B
A
B
A
ind
f
i
B
A
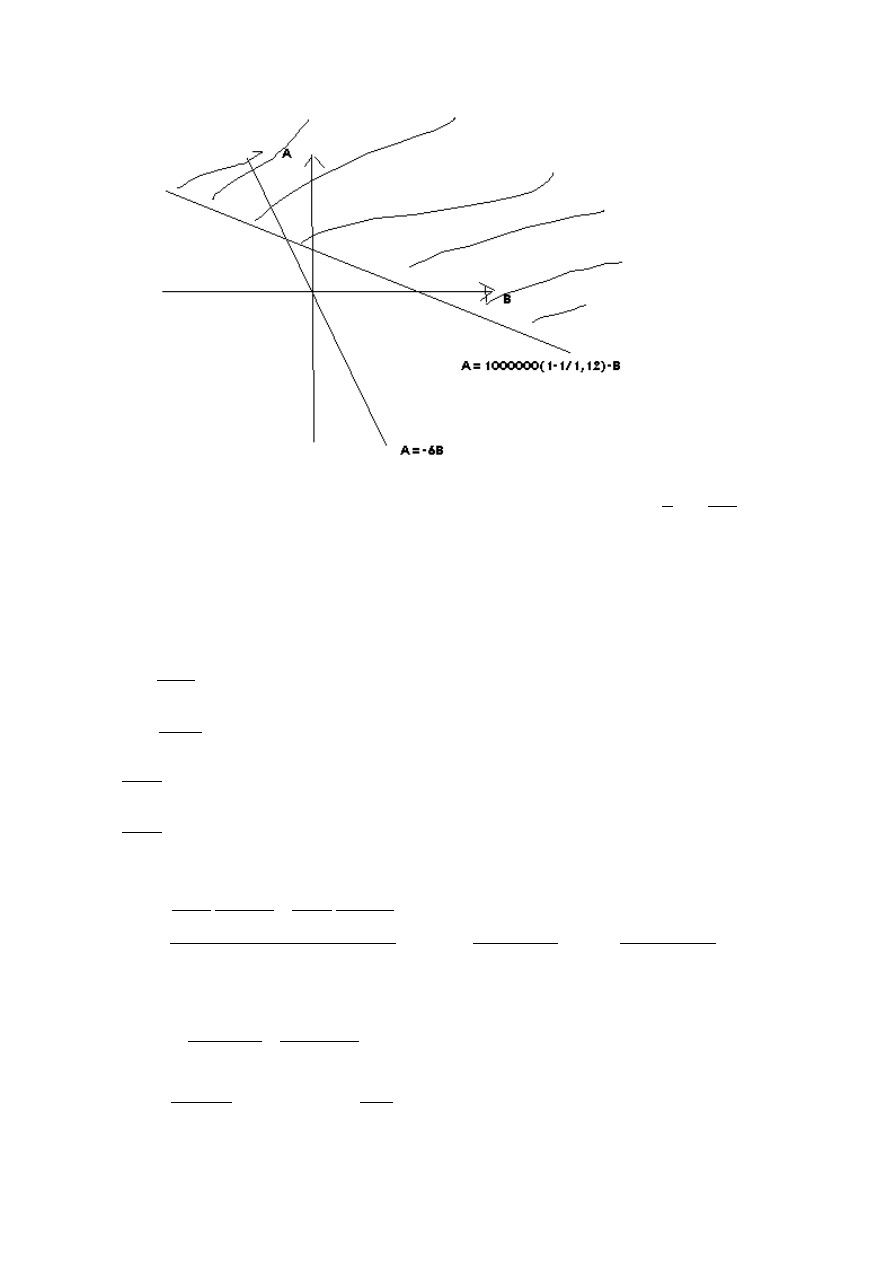
Szukamy max A i takiego
ż
eby le
ż
ał na prostej A+B=.....
)
12
,
1
1
1
)(
5
1
1
(
1000000
−
+
=
→
A
Wstawiamy A do II nierówno
ś
ci i st
ą
d k<=1,07
Zadanie 5
X - kapitał
10
2
2
5
1
1
05
,
1
05
,
1
N
C
N
C
=
=
1
5
,
0
C
X
- ilo
ść
obl. 1
2
5
,
0
C
X
- ilo
ść
obl. 2
1.
ú
ú
û
ù
ê
ê
ë
é
−
+
⋅
+
+
⋅
=
=
ú
ú
û
ù
ê
ê
ë
é
−
+
+
+
=
ú
ú
ú
ú
ú
û
ù
ê
ê
ê
ê
ê
ë
é
−
+
+
+
1
)
1
(
05
,
1
5
,
0
)
1
(
05
,
1
5
,
0
1
)
1
(
05
,
1
5
,
0
05
,
1
)
1
(
5
,
0
1
)
1
(
5
,
0
)
1
(
5
,
0
9
10
4
5
9
2
10
2
5
4
1
1
9
2
2
4
1
1
r
r
E
r
N
N
r
N
N
E
X
r
N
C
X
r
N
C
X
E
2.
ò
−
+
=
÷
÷
ø
ö
ç
ç
è
æ
+
07
,
0
02
,
0
4
4
05
,
0
1
)
1
(
)
1
(
1
dr
r
r
E
Z 1 i 2 wychodzi około 8,9%

Zadanie 6
[
]
å
å
å
å
∞
=
∞
=
∞
=
∞
=
=
−
=
→
+
⋅
=
1
1
1
1
1
)
(
)
(
)
(
)
(
k
k
k
k
k
k
k
k
i
v
v
kv
i
a
X
i
f
v
i
f
k
i
a
X
÷
ø
ö
ç
è
æ
−
=
å
∞
=
1
)
(
)
(
k
k
kv
i
a
X
i
i
f
gdzie sum
ę
oznaczamy przez N
2
3
2
2
)
1
)(
(
1
1
)
(
...
)
(
2
)
(
...
)
(
2
)
(
i
i
i
a
i
i
i
i
a
N
v
i
a
v
i
a
Nv
v
i
a
v
i
a
N
+
=
+
=
+
+
=
+
+
=
ú
û
ù
ê
ë
é
+
−
=
úû
ù
êë
é
+
−
=
4
2
2
)
1
(
)
1
)(
(
)
(
i
i
X
i
i
i
i
a
X
i
i
f
Dalej łatwo przekształci
ć
do postaci: (5)
I łatwo wykaza
ć
ż
e wszystkie inne s
ą
nierówne (5)
Zadanie 7
Korzystamy z ró
ż
niczkowania logarytmicznego:
( )
[
]
0
)
2
,
0
ln(
ln
100
)
(
ln
1
)
2
,
0
ln(
=
+
=
′
÷
ø
ö
ç
è
æ
′
+
′
=
′
−
−
t
t
t
t
S
u
u
v
u
v
u
u
t
v
v
5
t
dla
min
5
1
2
,
0
2
=
=
→
=
t
t
Cena obligacji: =
2
1
07
,
1
;
4
07
,
1
100
3
5
,
0
+
−
a
151600
5
5
6000
1000
≈
⋅
+
⋅
=
CENAOBL
ODP
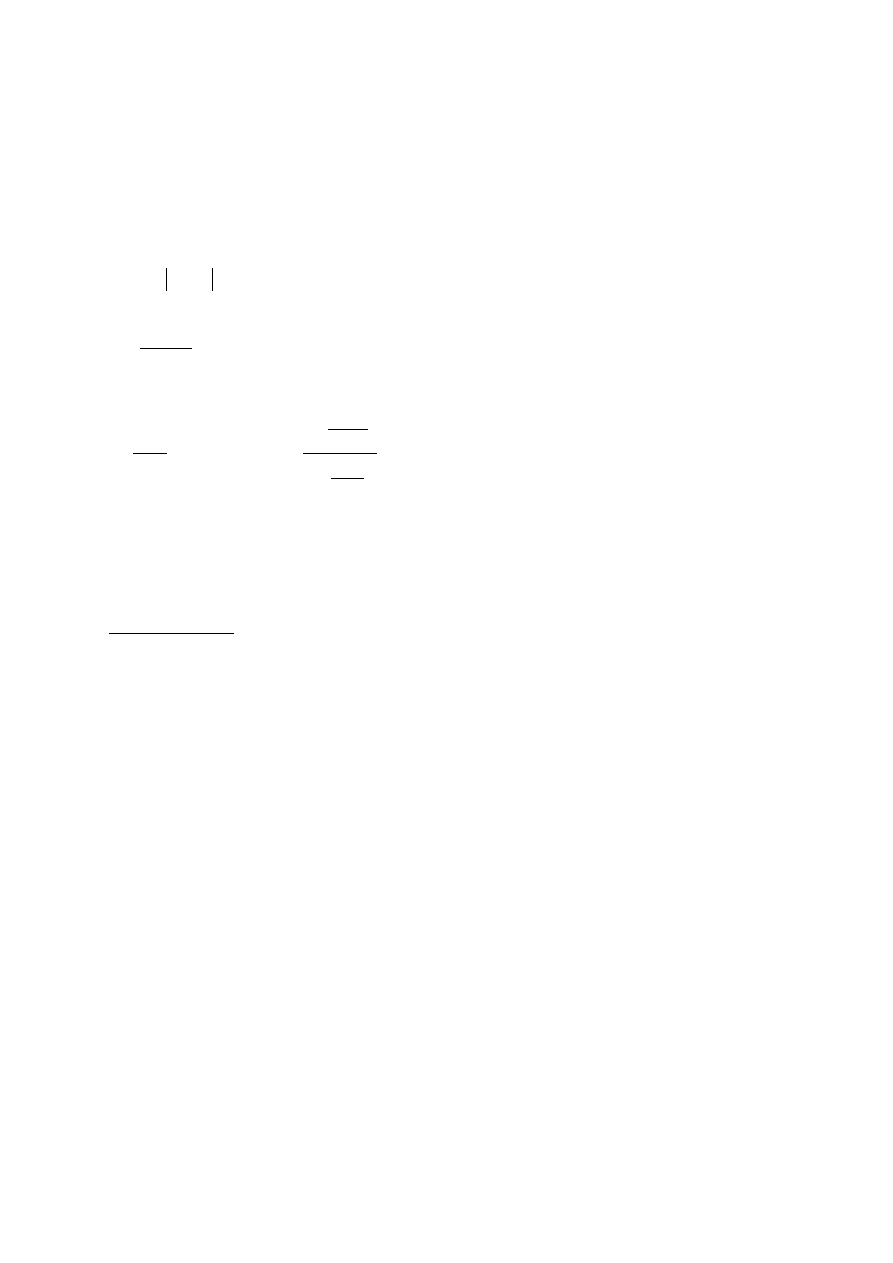
Zadanie 8
ych
nieparzyst
k
dla
)
3
)(
2
(
...
3
6
5
1
4
3
2
2
3
2
1
→
ï
ï
î
ï
ï
í
ì
+
+
=
⋅
⋅
=
⋅
⋅
=
k
k
k
r
r
r
k
19
17
15
13
11
9
7
5
3
166782
109820
68850
40560
22022
10692
4410
1400
270
12
1
,
0
v
v
v
v
v
v
v
v
v
v
i
WOR
+
+
+
+
+
+
+
+
+
+
=
=
=
obliczamy
1
12
0957
,
0
1
12
r
r
→
+
=
÷
ø
ö
ç
è
æ
+
400
19
22
21
17
20
19
2
2
20
19
18
17
+
⋅
⋅
+
⋅
⋅
=
+
+
+
=
r
r
r
r
X
dane
o
wszystk
3
,
11
1
1
ln
ln
1
1
*
*
≈
÷
ø
ö
ç
è
æ
+
÷
ø
ö
ç
è
æ
=
→
=
÷
ø
ö
ç
è
æ
+
r
X
WOR
t
WOR
r
X
t
Zadanie 9
Liczymy na piechot
ę
w miar
ę
szybko:
6153
,
218
)
7
(
28
)
7
(
58547003
,
6
)
7
(
20085
,
197
)
7
(
...
...
109
)
1
(
4
)
1
(
5
100
02
,
0
3
)
1
(
110
)
1
(
100
K(0)
≈
=
=
≈
=
=
=
⋅
+
=
=
=
STANK
W
K
STANP
STANK
W
K
P
STAN
STAN
8
233,476919
STANK(8)
0
W(8)
ja)
przekracza
(tu
7
)
8
(
4769
,
240
)
8
(
=
=
=
≈
K
STANP
4
,
307
7
1
,
1
7
1
,
1
36
1
,
1
)
8
(
2
≈
−
⋅
−
⋅
+
⋅
=
STANK
ODP

Zadanie 10
r - rata kredytu a)
3
1
105000
35000
)
3
(
3
2
105000
35000
)
2
(
1
105000
35000
)
1
(
⋅
+
=
⋅
⋅
+
=
⋅
⋅
+
=
r
RATA
r
RATA
r
RATA
0,125
Er
y
jednostajn
)
15
,
0
;
1
,
0
(
=
≅
J
r
105000
2
)
(
⋅
=
r
A
OD
)
2
,
0
4
,
0
;
1
,
0
5
,
3
(
/
5
,
3
0
i
i
K
USD
K
i
+
+
≅
=
KWOTA KREDYTU =
105000
30000
0
=
K
3
1
30000
05
,
0
10000
)
3
(
3
2
30000
05
,
0
10000
)
2
(
1
30000
05
,
0
10000
)
1
(
3
3
2
2
1
1
K
K
RATA
K
K
RATA
K
K
RATA
⋅
+
=
⋅
+
=
⋅
⋅
+
=
105000
10500
11000
11500
)
(
3
2
1
−
+
+
=
K
K
K
B
OD
26250
125
,
0
210000
)
(
=
⋅
=
=
A
A
E
17000
105000
8
,
3
10500
7
,
3
11000
6
,
3
11500
=
−
⋅
+
⋅
+
⋅
=
B
65
,
0
≈
A
B
Wyszukiwarka
Podobne podstrony:
2004.10.11 matematyka finansowa
2003 10 11 matematyka finansowaid 21704
2004 10 11 prawdopodobie stwo i statystykaid 25166
1 2006 10 09 matematyka finansowaid 8919
1 2009 10 05 matematyka finansowaid 8924
2002 10 12 matematyka finansowaid 21647
2007.10.08 matematyka finansowa
2008.10.06 matematyka finansowa
2004.10.11 prawdopodobie stwo i statystyka
2004 10 11 pra
mat fiz 2004 10 11 id 282351 Nieznany
1 2009.10.05 matematyka finansowa
1 2006.10.09 matematyka finansowa
2010.10.04 matematyka finansowa
dodawanie (10-11), matematyka
2010 10 04 matematyka finansowaid 27009
więcej podobnych podstron