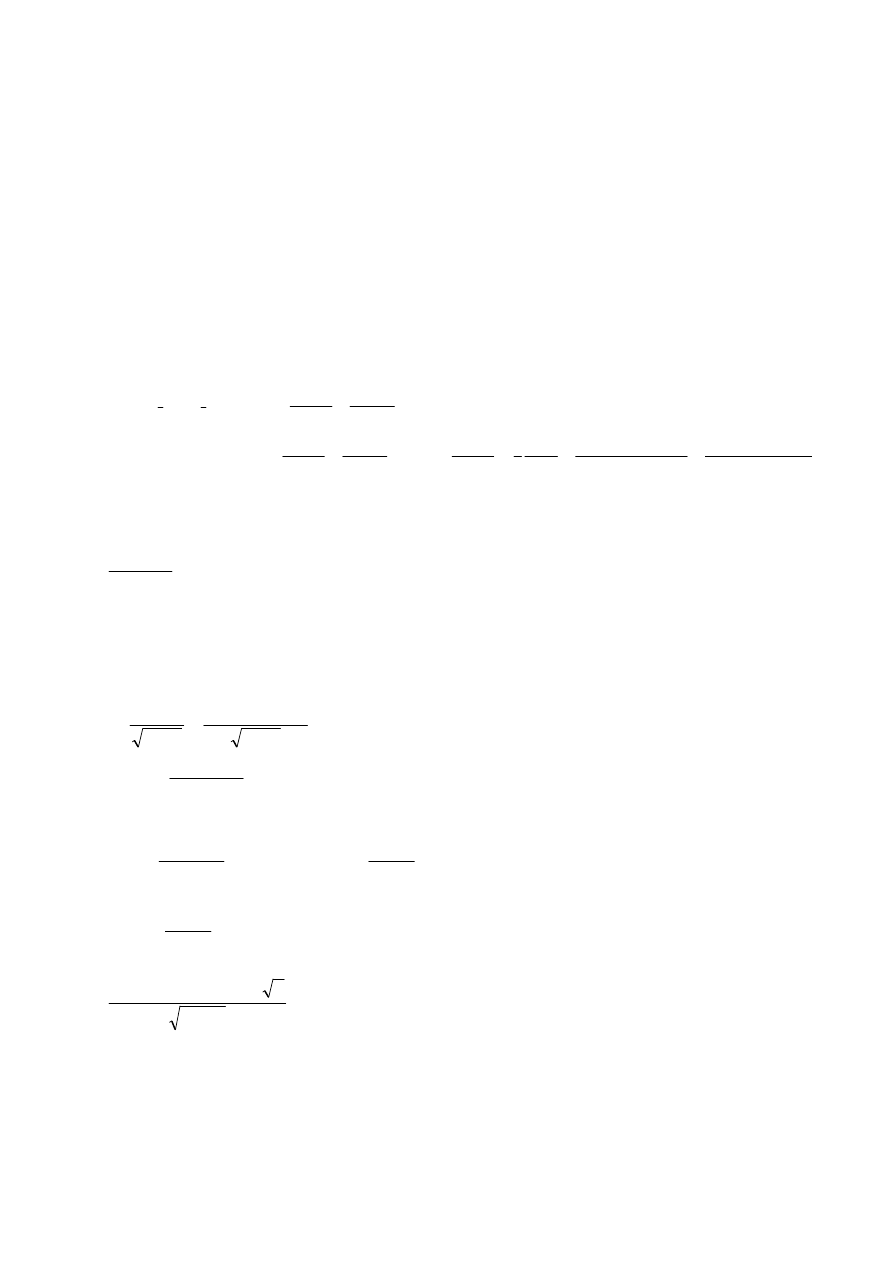
Egzamin dla Aktuariuszy z 9 października 2006 r.
Matematyka Finansowa
Zadanie 1
+
+
+
+
+
⋅
+
+
+
+
=
+
+
+
+
+
⋅
+
+
+
+
=
...
)
2
1
(
)
2
2
1
(
)
2
1
(
...
)
1
1
(
)
1
2
1
(
)
1
1
(
8
2
4
2
4
3
2
2
1
8
1
4
4
3
2
1
2
1
v
A
v
A
v
v
v
v
v
R
A
v
A
v
v
v
v
v
R
A
A
4
4
4
4
4
4
3
4
4
4
4
4
4
2
1
4
4
4
4
4
4
3
4
4
4
4
4
4
2
1
[
]
...)
1
(
8
4
1
+
+
+
=
−
v
v
A
v
R
k
k
k
k
v
k
i
v
v
i
v
k
v
k
va
a
A
k
3
4
4
3
3
4
1
+
−
+
−
=
+
⋅
+
=
∑
∑
∞
=
−
=
−
−
+
−
−
−
+
−
=
−
+
−
+
−
=
=
1
2
4
3
2
4
4
4
3
4
4
1
3440
)
1
)(
1
(
)
1
)(
1
(
)
(
1
1
1
1
1
1
k
k
k
v
v
v
v
v
i
v
v
v
i
v
k
v
k
i
v
v
i
v
v
R
ODP
Zadanie 2
n
1000000
- tyle w i-tą firmę
i
X - zysk z i-tej firmy
∑
=
=
n
i
i
X
Y
1
99
,
0
var
1500000
var
99
,
0
)
1500000
(
≥
−
≥
−
≥
≥
Y
EY
Y
EY
Y
P
Y
P
(
)
5
5
6
,
0
1
0
6
,
0
32000000
−
=
=
=
=
i
i
X
P
n
X
P
2
13
2
34
,
7
var
2488320
n
X
EX
n
EX
i
i
i
≈
→
=
EY=2488320
n
Y
13
34
,
7
var
=
Z tego wynika:
(
)
406
326
,
2
34
,
7
2488320
1500000
13
≥
→
−
≤
−
n
n
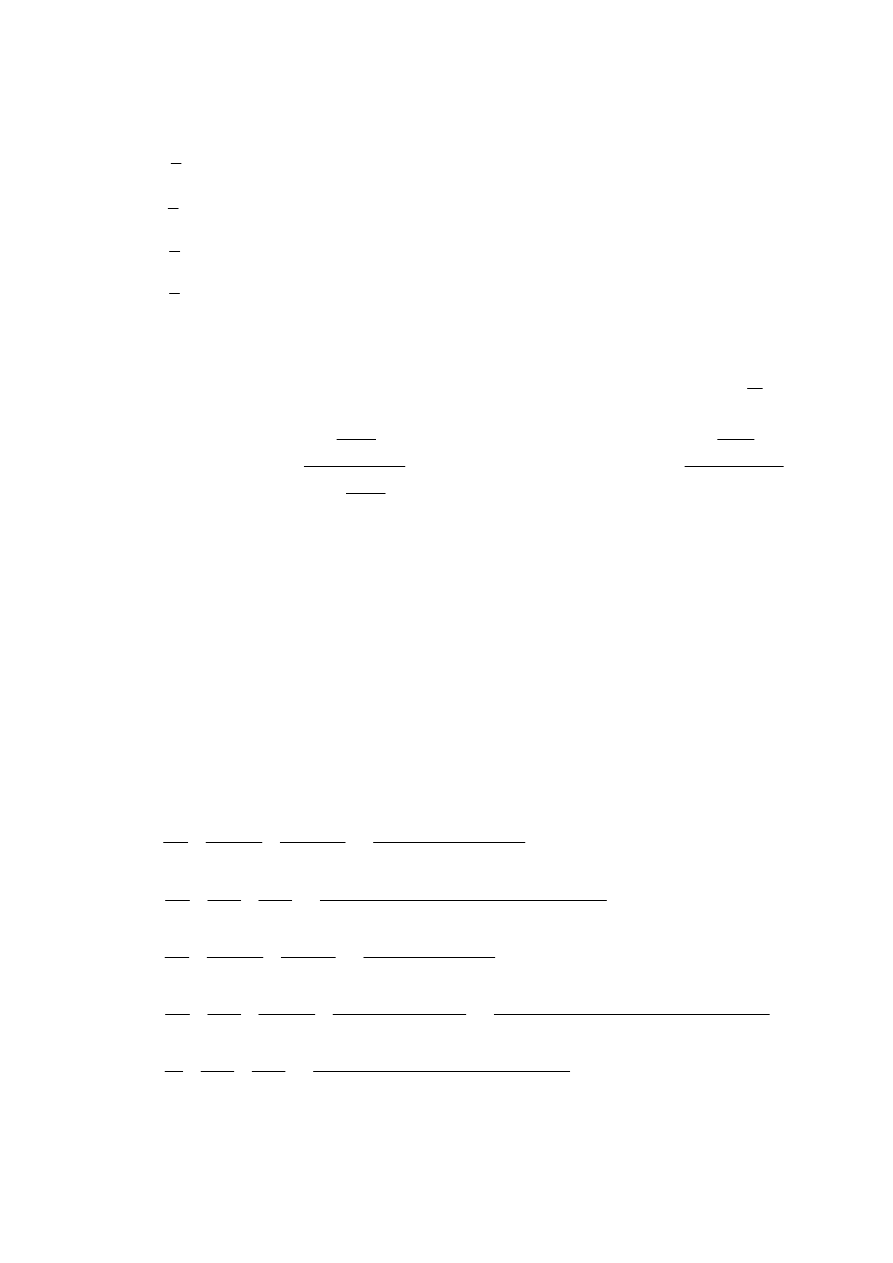
Zadanie 3
1
04
,
1
1
03
,
1
1
06
,
1
1
03
,
1
12
1
3
12
1
2
12
1
1
12
1
−
=
−
=
−
=
−
=
i
i
i
i
p
pensji
czesc
-
)
1
(
2000
479
480
X
i
WYN
p
+
=
3
;
240
479
2
479
239
2
241
240
2
240
240
2
1
239
240
2
239
1
240
2
240
1
)
1
(
2000
6
,
0
)]
1
(
)
1
(
...
)
1
(
)
1
(
)
1
(
)
1
(
)
1
)(
1
(
)
1
(
...
)
1
(
)
1
)(
1
(
)
1
(
)
1
[(
2000
i
p
p
p
p
p
p
a
i
i
i
i
i
i
i
i
i
i
i
i
i
i
i
X
+
⋅
=
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
3
240
3
479
40
1
240
1
240
2
240
1
1
1
1
)
1
(
1200
240
03
,
1
2000
1
1
1
1
1
1
)
1
(
)
1
(
2000
i
i
i
X
i
i
i
i
i
i
X
p
p
p
+
−
+
=
⋅
+
+
+
−
+
+
−
+
+
Z tego x=17,6%
Zadanie 4
=
wpp
0
placimy
gdy
1
72
x
wplywu
dodatniego
do
dojscia
bienstwem
prawdopodo
z
P
jeszcze
to
1
x
np
dodatkowo
II
wariancie
jak w
tu tak
1
,
1
wariant x
III
1
oba
lub
odwrotnie
lub
0
,
1
0
,
1
wariant x
1
1
,
0
x
wariant
72
45
60
54
72
45
60
54
45
60
−
=
→
=
=
=
=
→
=
=
=
→
=
=
x
x
x
x
II
x
tu
x
I
=
→
−
=
+
⋅
+
+
=
→
⋅
⋅
−
+
⋅
−
=
+
+
+
=
→
⋅
⋅
−
=
⋅
+
⋅
+
+
P
P
P
P
P
P
3
2
3
2
2
3
2
3
3
2
2
2
3
2
3
2
2
1
,
1
4
,
0
6
,
0
)
50
8
,
64
(
1
,
1
4
,
0
6
,
0
1
,
1
6
,
0
4
,
0
1
,
1
6
,
0
1
.
3
55
,
3
1
,
1
4
,
0
6
,
0
)
50
8
,
64
(
6
,
0
)
50
4
,
86
(
1
,
1
6
,
0
1
,
1
6
,
0
1
,
1
6
,
0
1
.
2
95
,
0
1
,
1
4
,
0
6
,
0
)
50
8
,
64
(
1
,
1
4
,
0
6
,
0
1
,
1
6
,
0
4
,
0
1
,
1
4
,
0
1
.
1
max
76
,
3
1
,
1
2
4
,
0
6
,
0
)
50
8
,
64
(
6
,
0
)
50
4
,
86
(
1
,
1
)
2
4
,
0
6
,
0
6
,
0
(
1
,
1
6
,
0
4
,
0
1
,
1
6
,
0
1
,
1
6
,
0
1
.
4
3
2
3
3
2
3
2
2
2
=
→
⋅
−
+
−
=
⋅
+
+
⋅
+
+
+
P
P
15
76
,
3
4
:
03
,
3
1
,
1
4
,
0
6
,
0
)
50
8
,
64
(
6
,
0
)
50
4
,
86
(
1
,
1
6
,
0
1
,
1
6
,
0
1
,
1
1
1
.
5
3
2
3
3
2
2
2
≈
⋅
=
→
−
+
−
=
+
+
+
ODP
P
P
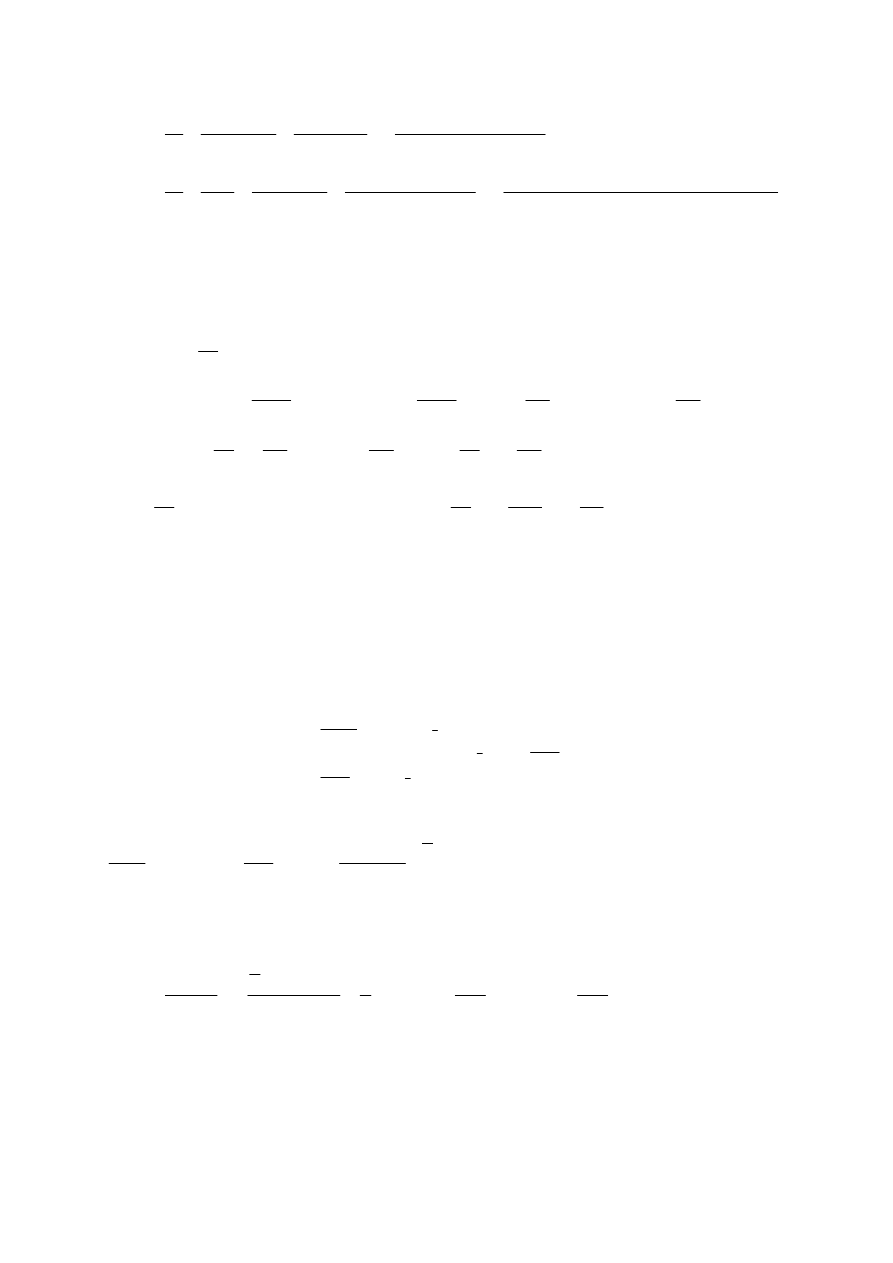
(
)
46
,
3
1
,
1
3
4
,
0
6
,
0
)
50
8
,
64
(
6
,
0
)
50
4
,
86
(
1
,
1
6
,
0
2
4
,
0
6
,
0
1
,
1
6
,
0
4
,
0
2
1
,
1
6
,
0
1
,
1
1
1
.
7
269
,
1
1
,
1
2
4
,
0
6
,
0
)
50
8
,
64
(
1
,
1
4
,
0
6
,
0
2
1
,
1
6
,
0
4
,
0
2
1
,
1
1
1
.
6
3
2
3
3
2
2
2
2
2
3
2
3
2
2
=
→
⋅
−
+
−
=
+
⋅
+
⋅
⋅
+
+
+
=
→
⋅
−
=
⋅
+
⋅
⋅
+
+
P
P
P
P
Zadanie 5
)
90
;
30
(
~ J
X
1
50
4
,
0
)
0
;
55
max(
5
6
,
0
50
4
,
0
)
0
;
55
max(
5
6
,
0
)
1
(
:
2
1
50
:
1
−
+
−
=
→
+
−
=
+
−
=
X
X
i
X
K
X
K
i
K
PORT
X
i
PORT
105
,
0
1
50
4
,
0
60
1
1
50
4
,
0
)
55
(
5
6
,
0
60
1
:
2
90
55
55
30
=
−
+
−
+
−
=
∫
∫
X
X
X
Ei
PORT
(
)
≈
+
−
+
+
−
=
∫
∫
90
55
2
2
2
55
30
2
2
1
50
8
,
0
50
4
,
0
60
1
012544
,
0
2544
,
1
36
,
31
60
1
x
x
x
x
Ei
Stąd
661908
,
0
)
var(
≈
i
12
,
0
)
1
(
var
=
PORT
i
5
,
5
≈
ODP
Zadanie 6
)
1
(
)
(
1
20
+
−
−
=
k
v
P
k
OD
P
a
a
P
a
v
P
v
P
v
P
k
k
k
k
400
6
6
400
6
1600
)
1
(
400
)
1
(
1600
6
6
6
14
20
15
1
20
6
1
1
20
−
=
→
−
=
−
=
→
−
=
−
=
∑
∑
=
+
−
=
+
−
i wstawiamy do pierwszego
1
200
3
800
3
)
400
6
(
6
1600
14
1
14
−
−
−
=
→
−
−
=
−
P
P
i
P
v
P
Zadanie 7
∫
∫
∫
+
+
+
=
+
+
+
=
+
−
+
=
+
=
t
t
t
t
t
t
t
t
t
1
1
)
1
ln(
1
1
)
1
ln(
2
1
)
1
(
1
)
2
2
(
2
1
)
1
(
2
2
2
δ

t
B
B
t
t
B
t
t
B
t
t
t
B
t
t
B
ds
s
s
B
e
t
t
B
ds
s
t
s
t
B
s
t
t
t
B
t
t
t
t
t
t
t
s
t
t
s
t
+
=
′
→
+
−
+
=
+
+
+
+
+
+
−
+
+
′
→
+
−
+
+
=
+
+
→
+
−
+
+
+
+
+
+
−
+
=
∫
∫
−
1
1
1
1
exp
)
1
(
1
2
exp
)
1
(
1
1
exp
1
1
1
1
exp
1
1
exp
)
1
(
1
1
exp
)
1
(
1
1
exp
)
1
(
1
1
exp
1
1
exp
1
1
)
1
(
1
1
exp
)
1
(
3
2
0
3
1
0
2
C
t
B
t
)
1
(
+
=
B(0)=1
Stąd
C=1 i B(t)=1+t dlatego B(2)=3
Zadanie 8
Stopa dyskontowa oznacza, że dyskonto "z góry" tzn. pierwsza płatność dyskontowana stopa
dla k=0 itd.
∑
∏
∑
∏
∞
=
−
=
∞
=
−
=
+
−
+
=
+
−
+
=
0
1
0
1
1
0
1
1
1
1
1
1
k
k
j
k
k
j
j
j
i
k
k
j
j
i
k
k
ODP
(
)
−
−
=
−
−
−
−
=
=
−
+
−
−
=
−
+
+
=
−
+
=
+
−
∏
∏
∏
−
=
−
=
−
=
k
i
i
k
i
i
k
k
i
i
i
j
k
i
k
j
i
j
j
i
k
k
k
k
k
j
k
k
j
k
j
1
1
)
1
(
1
1
)
1
(
)
1
(
1
1
1
)
1
(
1
1
!
)
1
(
!
)
1
(
1
1
1
1
0
1
0
1
0
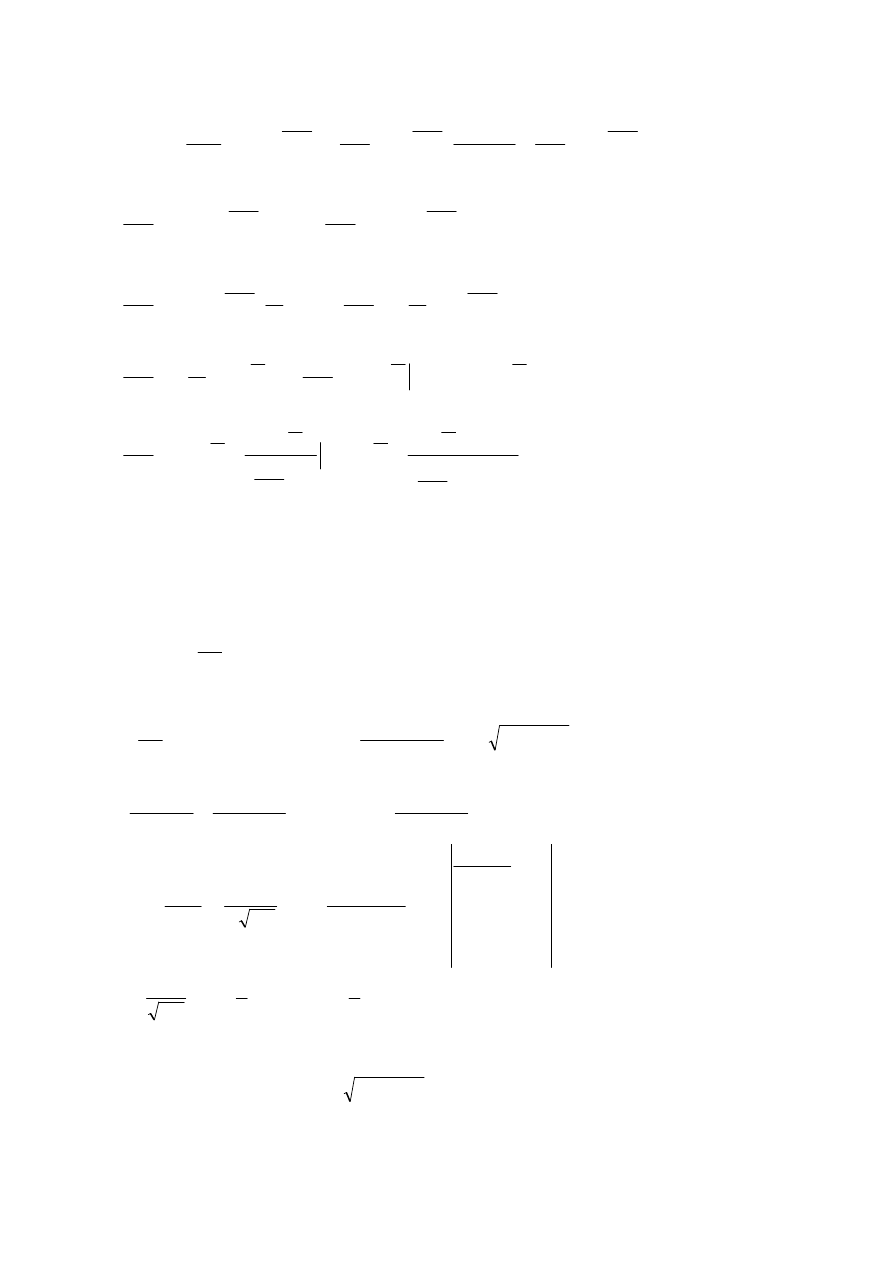
( )
5
,
12
1
1
1
1
1
1
1
1
)
1
(
)
1
(
1
1
)
1
(
)
1
(
1
1
)
1
(
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
)
1
(
1
1
1
1
1
1
)
1
(
1
1
1
1
1
1
1
0
1
1
1
1
1
1
0
1
0
1
1
1
0
1
1
1
1
1
0
1
0
0
0
1
0
1
0
0
1
0
0
0
1
0
1
0
=
−
+
−
−
−
=
+
−
+
−
−
−
=
=
+
−
+
−
=
+
−
=
=
−
−
=
−
−
=
=
−
−
=
−
−
=
=
−
−
=
+
−
−
−
=
−
−
+
=
+
−
−
−
+
−
−
−
−
−
−
−
−
−
−
∞
=
∞
=
−
−
∞
=
−
∞
=
∞
=
∞
=
−
+
∞
=
∫
∫
∫
∫
∑
∑
∫
∫
∑
∑
∑
∑
∫
∑
i
i
i
i
i
t
i
i
i
dt
t
t
t
i
dt
t
dt
d
t
i
dt
t
k
i
dt
d
t
i
dt
t
dt
d
k
i
t
i
dt
kt
k
i
t
i
dt
t
k
i
k
i
dt
t
k
i
k
i
k
i
k
i
k
i
k
i
i
k
k
ODP
i
i
i
i
i
i
i
i
i
i
i
i
i
k
k
k
k
i
i
k
k
k
k
k
k
i
k
k
k
k
Zadanie 9
(
)( )
)
1
ln(
2
)
1
ln(
1
0
2
1
2
exp
1
)
;
(
~
ln
)
(
2
2
2
2
2
2
2
2
2
2
+
=
+
−
=
→
−
=
→
=
+
−
=
+
=
Ν
=
=
≤
+
a
a
e
a
e
e
a
X
Y
p
x
x
P
p
σ
µ
σ
µ
σ
µ
σ
µ
σ
σ
µ
σ
σ
µ
σ
µ
σ
µ
−
=
→
=
−
≤
−
p
p
p
X
N
p
X
X
P
ln
ln
ln
∫
∫
∞
=
∞
+
+
=
+
+
−
−
Π
=
=
=
=
=
−
=
−
−
Π
−
=
p
p
N
x
t
t
t
dt
e
dx
e
x
t
x
dx
x
p
ODP
0
2
bo
)
2
(
2
1
exp
)
(
2
1
exp
2
1
ln
2
)
(ln
exp
2
1
1
1
2
1
2
2
2
2
µ
σ
µ
σ
σ
σ
σ
µ
σ
µ
σ
µ
σ
µ
σ
4
4
4
3
4
4
4
2
1
i dalej
;1)
N(
~
Y
gdzie
)
(
σ
p
N
Y
P
>
=
(
)
)
1
ln(
1
)
(
2
+
−
−
=
−
>
−
a
N
N
Y
P
p
p
φ
σ
σ
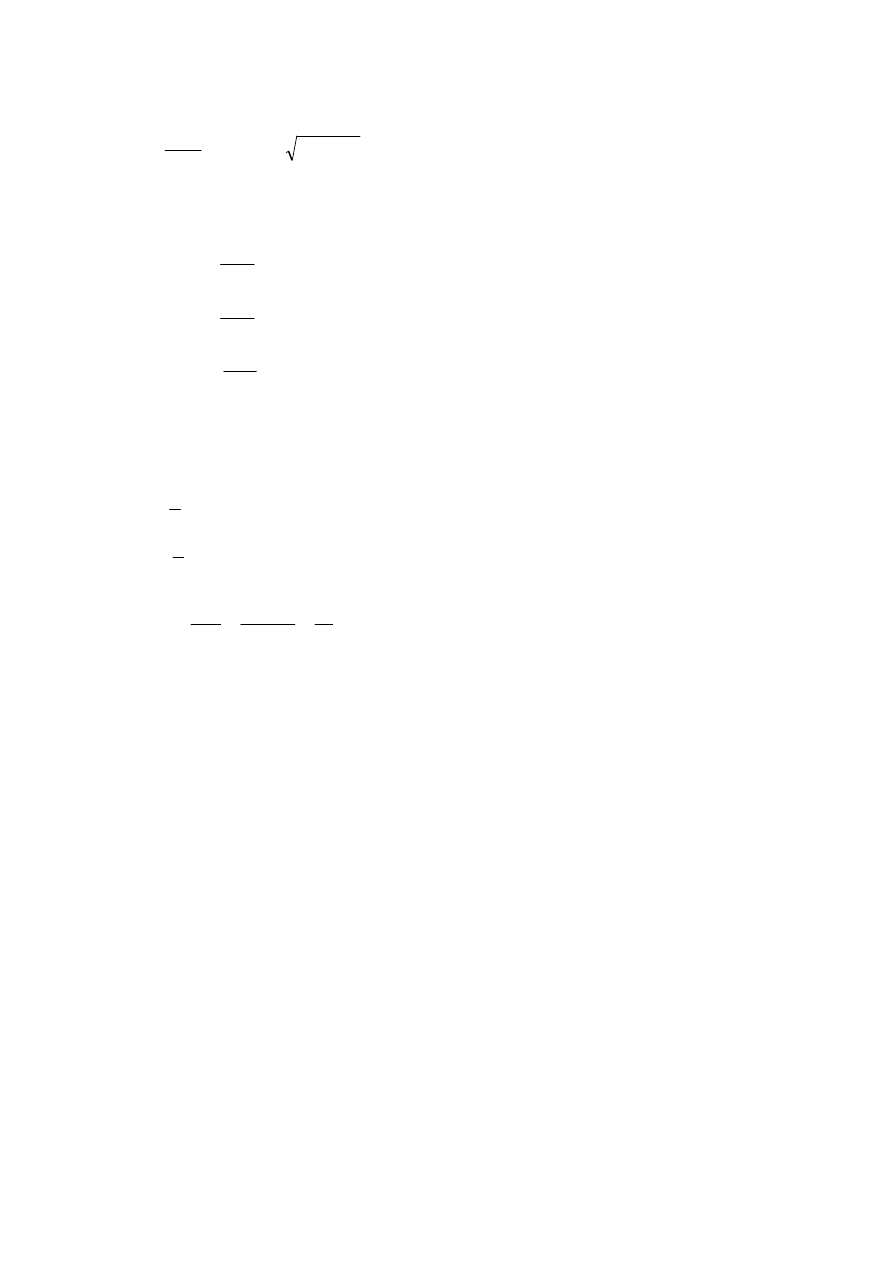
(
)
(
)
2
1
ln(
1
1
1
a
N
p
ODP
p
+
−
−
−
=
φ
Zadanie 10
+
=
+
=
+
=
∫
∫
∫
4
2
2
1
4
1
3
1
exp
)
4
,
2
(
2
1
exp
)
2
,
1
(
2
1
exp
)
4
,
1
(
dt
t
a
dt
t
a
dt
t
a
Z tego wynika:
5
7
)
4
,
2
(
3
4
)
2
,
1
(
2
)
4
,
1
(
=
=
=
a
a
a
15
2
15
28
30
5
3
7
4
2
=
−
=
⋅
⋅
−
=
ODP
Wyszukiwarka
Podobne podstrony:
1 2006.10.09 matematyka finansowa
Egzamin 2006.10.09, rozwiazania zadań aktuarialnych matematyka finansowa
2004 10 11 matematyka finansowaid 25165
1 2009 10 05 matematyka finansowaid 8924
2002 10 12 matematyka finansowaid 21647
2007.10.08 matematyka finansowa
2006.03.20 matematyka finansowa
2006.10.09 prawdopodobie stwo i statystyka
2008.10.06 matematyka finansowa
2000.12.09 matematyka finansowa
2006 06 05 matematyka finansowaid 25460
1 2009.10.05 matematyka finansowa
2004.10.11 matematyka finansowa
2010.10.04 matematyka finansowa
2003 10 11 matematyka finansowaid 21704
mat fiz 2006 10 09 id 282354 Nieznany
2010 10 04 matematyka finansowaid 27009
2007 10 08 matematyka finansowaid 25658
więcej podobnych podstron