Egzamin dla Aktuariuszy z 4 października 2010 r.
Matematyka Finansowa
Zadanie 1
CENA – początkowa koszyka
9
,
112
114
35
,
0
95
2
,
0
120
45
,
0
=
⋅
+
⋅
+
⋅
=
CENA
OD – odchylenie koszyka a wiemy, że
(
)
=
+
+
=
3
2
1
2
35
,
0
2
,
0
45
,
0
var
S
S
S
OD
(
)
( )
( )
+
⋅
⋅
⋅
⋅
⋅
+
+
+
=
2
1
2
1
3
2
2
2
1
2
,
2
,
0
45
,
0
2
var
35
,
0
var
2
,
0
var
45
,
0
S
OD
S
OD
S
S
corr
S
S
S
(
)
( )
( )
(
)
( )
( )
=
⋅
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
⋅
+
3
2
3
2
3
1
3
1
,
35
,
0
2
,
0
2
,
35
,
0
45
,
0
2
S
OD
S
OD
S
S
corr
S
OD
S
OD
S
S
corr
+
⋅
⋅
⋅
+
⋅
⋅
⋅
+
+
+
⋅
=
085
,
0
07
,
0
5
,
0
315
,
0
05
,
0
07
,
0
25
,
0
18
,
0
085
,
0
35
,
0
05
,
0
2
,
0
07
,
0
45
,
0
2
2
2
2
2
2
%
6751
,
5
...
085
,
0
05
,
0
25
,
0
14
,
0
≈
→
≈
⋅
⋅
⋅
+
OD
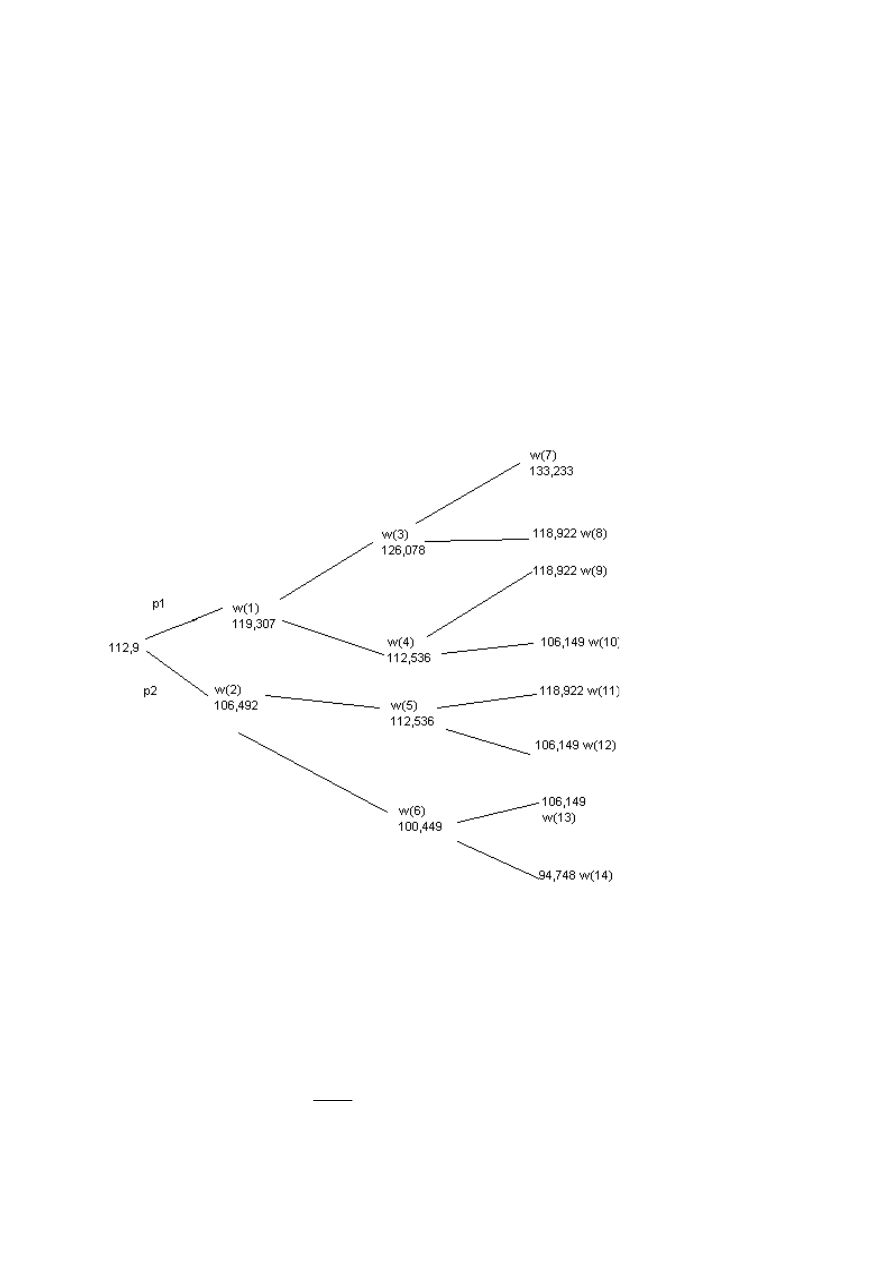
c(i) – wartość opcji w węźle i
zaczynamy od prawej strony
0
)
14
(
)
13
(
)
12
(
)
10
(
)
11
(
)
9
(
022
,
6
9
,
112
922
,
118
)
8
(
333
,
20
9
,
112
233
,
133
)
7
(
=
=
=
=
=
=
≈
−
≈
≈
−
≈
c
c
c
c
c
c
c
c
(
)
+
−
=
2
)
8
(
1
)
7
(
055
,
1
1
;
9
,
112
078
,
126
max
)
3
(
p
c
p
c
c
1
)
11
(
055
,
1
1
)
5
(
1
)
9
(
055
,
1
1
)
4
(
p
c
c
p
c
c
⋅
⋅
=
⋅
⋅
=
(
)
+
−
=
=
055
,
1
1
2
)
4
(
1
)
3
(
;
9
,
112
307
,
119
max
)
1
(
0
)
6
(
p
c
p
c
c
c
055
,
1
1
1
)
5
(
)
2
(
⋅
⋅
=
p
c
c
[
]
055
,
1
1
2
)
2
(
1
)
1
(
p
c
p
c
ODP
+
=
Z braku arbitrażu:
76
,
16
1
1
2
,
gdzie
2
1
055
,
1
1
055
,
1
2
)
1
(
1
)
1
(
≈
→
−
=
=
+
−
=
→
=
−
+
+
ODP
p
p
OD
i
i
i
p
p
i
p
i
Zadanie 2
( )
( )
( )
0
0
0
,
,
,
t
r
V
t
r
V
t
r
f
L
A
−
=
Muszą być spełnione warunki:
(
)
(
)
0
,
.
2
0
,
.
1
0
0
0
0
=
=
t
r
dr
df
t
r
f
( )
r
r
r
r
t
r
V
L
10
5
0
)
1
(
1
1000
)
1
(
1
1000
,
−
−
+
−
+
+
−
=
(
)
78
,
11123
,
0
0
≈
t
r
V
L
[
]
[
]
11
2
6
2
)
1
(
10
...
)
1
(
1000
)
1
(
5
...
)
1
(
1000
−
−
−
−
+
−
−
+
−
+
+
−
−
+
−
=
r
r
r
r
dr
dV
L
(
)
67
,
40602
,
10
1
5
1
1000
0
0
11
10
6
5
−
≈
→
−
−
+
−
−
−
=
t
r
dr
dV
i
v
i
v
i
v
i
v
v
L
( )
(
)
2
1
)
1
(
1
,
2
1
0
t
t
A
r
X
r
X
t
r
V
−
−
+
+
+
=
( )
1
2
2
1
1
1
0
2
1
)
1
(
)
1
(
,
−
−
−
−
+
−
+
−
=
t
t
A
r
X
t
r
X
t
t
r
dr
dV
Sprawdzamy:
(
)
0
0
, t
r
V
A
A,b,c i e daje około 11124 OK
d) odpada bo około 11 870
sprawdzamy:
(
)
0
0
, t
r
dr
dV
A
a)
około -73200
b)
około – 43 446
c)
około -67159
e)
około – 68461
Z tego wynika Odpowiedź b)
Zadanie 3
04
,
0
1
04
,
1
gdzie
1000
05
,
0
1000
04
,
1
)
1000
(
53
,
915
20
20
20
20
20
20
−
=
−
⋅
+
+
⋅
−
=
=
s
Rs
s
K
B
12
,
92
8
7
=
−
B
B
czyli
8
8
8
7
7
7
1000
05
,
0
1000
04
,
1
)
1000
(
1000
05
,
0
1000
04
,
1
)
1000
(
Rs
s
K
Rs
s
K
+
⋅
−
−
⋅
−
−
−
⋅
+
+
⋅
−
Wszystkie symbole
n
s są przy stopie 0,04
(
)
⋅
+
⋅
−
−
−
=
−
+
+
⋅
−
=
7
7
8
7
20
20
20
04
,
1
04
,
1
50
04
,
1
04
,
1
)
1000
(
12
,
92
50
1000
04
,
1
)
1000
(
53
,
915
R
K
Rs
s
K
Z I równania:
20
20
20
04
,
1
50
47
,
84
1000
s
Rs
K
−
+
−
=
−
i wstawiamy do równania II
(
)
7
7
7
8
20
20
20
04
,
1
04
,
1
50
04
,
1
04
,
1
04
,
1
50
47
,
84
12
,
92
⋅
+
⋅
−
−
+
−
=
R
s
Rs
(
)
(
)
7
8
20
20
7
7
7
8
20
20
04
,
1
04
,
1
04
,
1
04
,
1
04
,
1
50
04
,
1
04
,
1
04
,
1
50
47
,
84
12
,
92
−
−
⋅
+
−
+
−
=
s
s
R
067
,
0
i
zamy
wylic
1000
04
,
1
50
47
,
84
20
20
20
≈
+
−
+
−
=
K
R
s
Rs
K
Zadanie 4
+
+
+
+
+
+
+
+
+
+
=
2
2
2
2
2
2
05
,
1
1
)
1
(
1
07
,
1
1
05
,
1
1
)
1
(
1
07
,
1
1
05
,
1
1
1
1
07
,
1
1
05
,
1
1
1
1
07
,
1
1
1
1
07
,
1
1
07
,
1
1
38
,
200
1000
x
x
x
x
x
+
+
+
+
+
+
=
05
,
1
1
1
1
07
,
1
1
1
05
,
1
1
1
1
07
,
1
1
1
1
07
,
1
1
07
,
1
1
38
,
200
1000
x
x
x
OZN: 1+x=t
[
][
]
2
2
2
05
,
1
07
,
1
1
05
,
1
07
,
1
1
05
,
1
05
,
1
38
,
200
1000
t
t
t
+
⋅
+
+
=
(
)(
)
1
05
,
1
07
,
1
05
,
2
05
,
1
38
,
200
05
,
1
07
,
1
1000
2
2
2
+
⋅
+
=
⋅
t
t
t
(
)
(
)
0
05
,
2
38
,
200
05
,
1
07
,
1
05
,
2
38
,
200
05
,
1
38
,
200
07
,
1
05
,
1
38
,
200
05
,
1
07
,
1
1000
2
2
2
2
=
⋅
−
⋅
⋅
⋅
+
⋅
−
⋅
−
⋅
t
t
a
b
t
2
87
,
1461
∆
+
−
=
≈
∆
bo drugi pierwiastek ujemny
%
4
04
,
1
≈
→
≈
ODP
t
Zadanie 5
P(k) – płatność na koniec roku k
∑
=
+
=
+
+
⋅
+
+
⋅
=
+
⋅
+
+
⋅
=
+
⋅
=
k
i
i
i
k
P
P
P
1
)
1
(
....
)
1
2
(
2
)
1
1
(
1
)
(
......
)
1
2
(
2
)
1
1
(
1
)
2
(
)
1
1
(
1
)
1
(
M
L
ODP
=
∑
∑ ∑
∞
=
∞
=
=
+
=
=
1
1
1
)
1
(
)
(
i
i
i
i
j
i
v
j
j
i
v
i
iP
L
∑
∑ ∑
∞
=
∞
=
=
+
=
=
1
1
1
)
1
(
)
(
i
i
i
j
i
i
j
j
v
v
i
P
M
∑
∑
∑
=
=
=
=
+
+
+
+
=
+
+
+
+
=
+
=
+
i
j
i
j
i
j
i
i
i
i
i
i
i
i
i
i
j
j
j
j
1
1
1
2
6
)
1
(
3
)
1
2
)(
1
(
2
)
1
(
6
)
1
2
)(
1
(
)
1
(
3
)
2
)(
1
(
6
)
4
2
)(
1
(
+
+
=
+
+
=
i
i
i
i
i
i
(
)
(
)
∑
∑
∞
=
∞
=
+
+
+
+
−
=
+
+
=
+
+
=
1
1
3
2
5
2
3
4
2
11
11
1
)
1
(
3
1
2
3
3
1
3
)
2
)(
1
(
i
i
i
i
v
v
v
v
v
v
i
i
i
v
i
i
i
L
(
)
)}
1
(
)
1
(
2
4
1
)
1
(
3
{
3
1
3
2
4
v
v
v
v
v
v
v
+
−
+
+
+
−
+
(
)
(
)
∑
∑
∞
=
∞
=
−
+
+
−
+
+
+
−
=
+
+
=
+
+
=
1
1
2
3
2
4
2
3
)
1
(
2
)
1
(
)
1
(
3
4
1
)
1
(
3
1
2
3
3
1
3
)
2
)(
1
(
i
i
i
i
v
v
v
v
v
v
v
v
v
v
i
i
i
i
i
i
v
M
41
79860
3274260
=
=
=
M
L
ODP
Zadanie 6
Z parytetu: C-P+dK=S
4
,
7
35
71
,
0
40
05
,
0
≈
−
+
=
−
+
=
→
−
e
dK
P
S
ODP
Zadanie 7
Moim zdaniem (E) ale coś ze znakami jest nie tak; porównując współczynniki przy K
wychodzi (E)
R – wielkość pierwszej raty
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=
9
5
2
5
5
5
,
6
5
,
6
5
5
,
2
5
,
1
)
1
(
1
1
,
1
...
)
1
(
2
1
,
1
1
1
1
,
1
)
1
(
1
)
1
(
1
,
1
...
)
1
(
1
,
1
)
1
(
j
R
j
R
j
R
i
i
R
i
R
i
R
K
−
+
⋅
+
+
+
−
+
−
+
=
j
v
a
a
R
i
i
i
i
R
K
j
j
j
9
;
9
;
9
5
5
,
6
6
5
,
1
9
1
,
1
)
1
(
1
1
1
,
1
1
1
1
,
1
1
)
1
(
1
&
&
5
,
6
10
:
9
;
9
5
5
,
6
6
6
5
,
6
)
1
(
1
1
9
1
,
1
)
1
(
1
1
,
0
1
,
1
)
1
(
)
1
(
1
i
j
j
v
a
a
i
R
i
i
i
R
K
j
j
j
+
+
−
+
+
+
−
−
+
+
=
(
)
5
,
6
10
;
9
;
9
5
6
6
5
,
6
)
1
(
1
9
1
,
1
1
,
0
1
,
1
)
1
(
)
1
(
1
i
j
j
v
a
a
i
i
i
R
K
j
j
j
+
+
−
+
+
−
−
+
+
=
(
)
10
;
9
;
9
5
6
6
5
,
6
9
)
1
(
1
,
1
1
,
0
1
,
1
)
1
(
)
1
(
j
j
j
v
a
j
a
i
i
Rj
i
j
K
−
+
+
+
−
−
+
=
+
⋅
(
)
(
)
=
−
+
−
−
+
+
−
−
−
−
−
+
=
+
−
−
+
−
+
−
+
=
9
5
6
6
9
9
8
5
,
6
;
9
5
6
6
10
;
9
5
,
6
1
1
,
1
1
,
0
1
,
1
)
1
(
10
...
1
)
1
(
1
,
1
1
,
0
1
,
1
)
1
(
9
)
1
(
)
1
(
j
j
j
j
j
j
j
j
v
i
i
j
v
v
v
v
i
Kj
a
i
i
j
v
a
j
i
Kj
R
(
)
=
−
+
−
+
−
+
+
−
−
+
+
=
9
5
6
6
6
6
;
9
9
5
,
6
1
1
,
1
)
1
,
0
(
)
1
(
1
,
1
)
1
(
)
1
(
1
10
)
1
(
j
j
j
v
i
i
i
i
j
a
v
i
Kj
( )
(
)
9
5
6
6
;
9
9
5
,
6
1
1
,
1
1
,
0
1
,
1
1
)
1
(
1
10
)
1
(
j
i
j
j
v
i
v
i
j
a
v
i
Kj
−
+
−
−
+
−
−
+
+
=
Zadanie 8
a-ilość obligacji P(0,1)
b-ilość obligacji P(0,2)
c-ilość obligacji P(0,3)
d-ilość obligacji P(0,4)
a,b,c,d-całkowite, mogą być ujemne
a)
0,9a+0,81b+0,729c+0,6561d=0 bo wydajemy 0
Ż
eby nie było arbitrażu to w każdym wariancie zarobimy 0 tzn:
=
+
+
+
=
+
+
+
=
+
+
+
0
89
,
0
92
,
0
93
,
0
0
82
,
0
85
,
0
9
,
0
0
67
,
0
88
,
0
d
c
b
a
d
c
b
a
xd
c
b
a
a)mnożymy przez
0
729
,
0
81
,
0
9
,
0
)
9
10
=
+
+
+
→
d
c
b
a
b
b)uwzględniamy rozpisując układ równań:
→
=
+
+
−
=
=
−
−
+
→
=
+
+
=
+
=
−
+
−
−
*)
*
(*
0
16,1d
11c
3b
(**)
1
,
9
4
(*)
0
)
729
,
0
(
100
14
2
0
161
,
0
11
,
0
03
,
0
0
091
,
0
04
,
0
0
)
729
,
0
(
14
,
0
02
,
0
d
c
x
d
c
b
d
c
b
d
c
d
x
c
b
729
,
0
100
14
2
+
+
=
→
d
c
b
x
Z (**)
d
d
c
275
,
2
4
1
,
9
−
=
−
=
i wstawiamy do (***)
47
,
0
729
,
0
275
,
2
14
,
0
975
,
2
02
,
0
975
,
2
0
1
,
16
11
275
,
2
3
=
+
⋅
−
⋅
=
→
=
→
=
+
⋅
−
x
d
b
d
d
b
Zadanie 9
(
)
3
)
3
,
0
(
1
1
1000
)
0
(
r
P
+
⋅
=
(
)
+
=
2
)
2
,
1
(
1
1
1000
)
1
(
r
E
P
(
)
+
=
)
1
,
2
(
1
1
1000
)
2
(
r
E
P
889
04
,
1
1
1000
)
0
(
3
=
=
P
+
=
2
)
04
,
1
(
1
1000
)
1
(
x
E
P
+
=
)
04
,
1
(
1
1000
)
2
(
x
E
P
∫
∫
∫
−
−
−
=
=
=
+
=
+
=
+
=
+
=
+
04
,
0
04
,
0
08
,
1
1
2
2
2
04
,
0
04
,
0
08
,
1
1
1
5
,
12
1
5
,
12
04
,
1
)
04
,
1
(
1
08
,
0
1
)
04
,
1
(
1
08
,
1
ln
5
,
12
)
04
,
1
(
1
08
,
0
1
04
,
1
1
dt
t
t
x
dx
x
X
E
dx
x
X
E
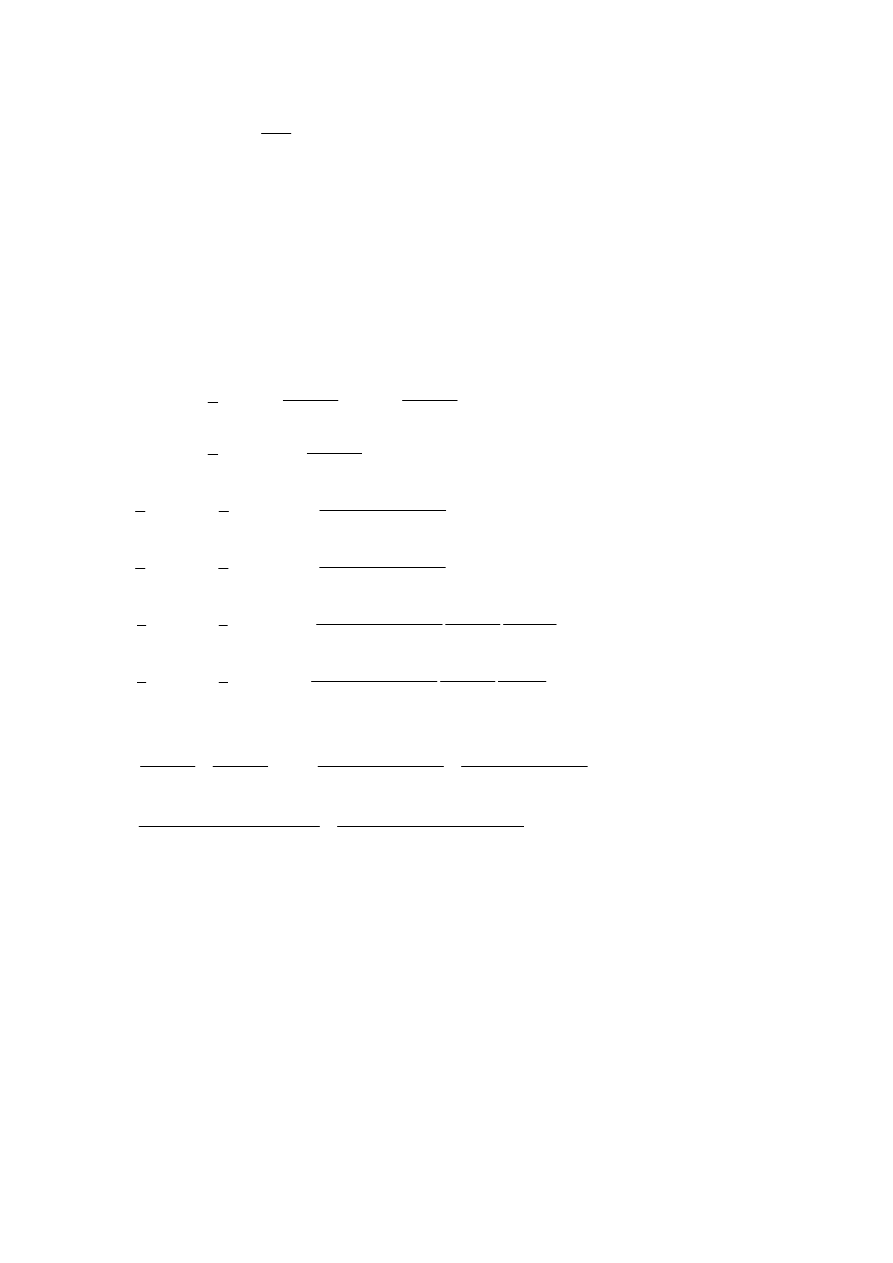
93
,
925
08
,
1
1
1
5
,
12
1000
)
1
(
=
−
⋅
=
P
01
,
962
08
,
1
ln
5
,
12
1000
)
2
(
=
⋅
=
P
Zadanie 10
1
A
- pierwotna rata osoby A
2
A
- rata osoby A po pierwszej zmianie
3
A - rata osoby A po drugiej zmianie
i
B - analogiczne oznaczenie dla osoby B
40
07
,
0
1
40
07
,
0
1
07
,
0
;
40
1
1
21000
07
,
0
1
300000
v
A
v
A
a
A
−
=
→
−
=
=
40
08
,
0
1
08
,
0
;
40
1
1
24000
300000
v
B
a
B
−
=
→
=
(
)
(
)(
)
40
07
,
0
25
08
,
0
25
07
,
0
2
08
,
0
;
25
2
07
,
0
;
25
1
1
1
1
24000
v
v
v
A
a
A
a
A
−
−
−
=
→
=
(
)
(
)(
)
25
09
,
0
40
08
,
0
25
08
,
0
2
09
,
0
;
25
2
08
,
0
;
25
1
1
1
1
27000
v
v
v
B
a
B
a
B
−
−
−
=
→
=
(
)
(
)(
)
10
11
,
0
10
08
,
0
40
07
,
0
25
08
,
0
25
07
,
0
3
11
,
0
;
10
3
08
,
0
;
10
2
1
11
,
0
08
,
0
1
1
1
1
24000
v
v
v
v
v
A
a
A
a
A
−
−
−
−
−
=
→
=
(
)
(
)(
)
10
1
,
0
10
09
,
0
25
09
,
0
40
08
,
0
25
08
,
0
3
1
,
0
;
10
3
09
,
0
;
10
2
1
1
,
0
09
,
0
1
1
1
1
27000
v
v
v
v
v
B
a
B
a
B
−
−
−
−
−
=
→
=
(
)
(
) (
)
=
−
+
−
+
−
=
3
3
2
2
1
1
5
15
5
A
B
A
B
A
B
ODP
(
)
(
)(
)
(
)
(
)(
)
+
−
−
−
−
−
−
−
+
−
−
−
=
40
07
,
0
25
08
,
0
25
07
,
25
09
,
0
40
08
,
0
25
08
,
0
40
07
,
0
40
08
,
0
1
1
1
24000
1
1
1
27000
15
1
21000
1
24000
5
v
v
v
v
v
v
v
v
(
)(
)
(
)(
)(
)
(
)(
)
(
)(
)(
)
57000
1
1
1
1
1
33000
1
1
1
1
1
30000
5
10
11
,
0
40
07
,
0
25
08
,
0
10
08
,
0
25
07
,
0
10
1
,
0
25
09
,
0
40
08
,
0
10
09
,
0
25
08
,
0
≈
−
−
−
−
−
−
−
−
−
−
−
+
v
v
v
v
v
v
v
v
v
v