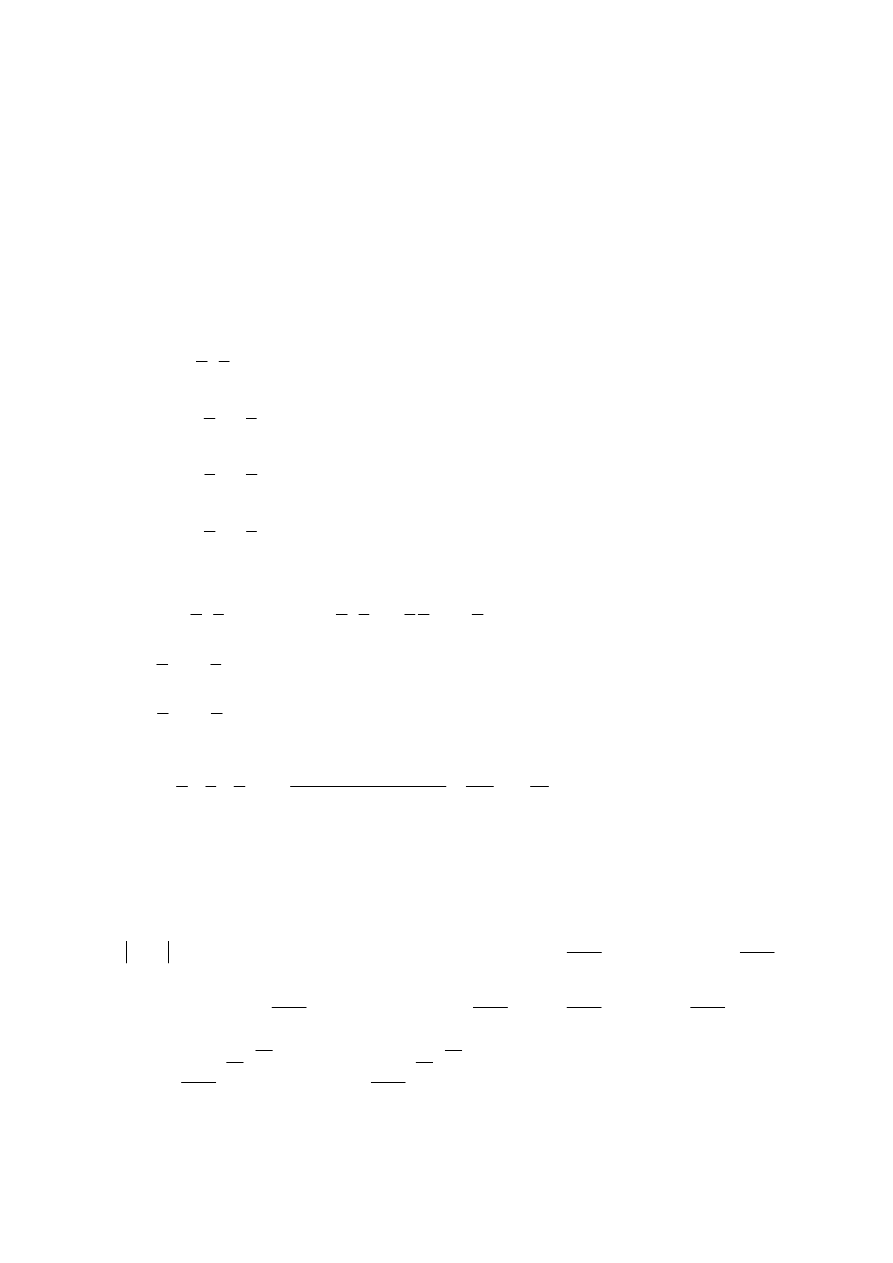
Egzamin dla Aktuariuszy z 20 czerwca 2011 r.
Prawdopodobieństwo i Statystyka
Zadanie 1
X – ilość powtórzeń
i
Y - czas oczekiwania na i-tą cyfrę
5
4
3
2
1
Y
Y
Y
Y
X
+
+
+
+
=
Rozkład
i
Y jest geometryczny:
(
)
(
)
(
)
(
)
5
1
5
4
5
2
5
3
5
3
5
2
,....
2
,
1
5
1
5
4
1
5
1
4
1
3
1
2
−
−
−
−
=
=
=
=
=
=
=
=
=
k
k
k
k
k
Y
P
k
Y
P
k
Y
P
k
k
Y
P
5
4
3
2
1
EY
EY
EY
EY
EX
+
+
+
+
=
∑
∑
∞
=
∞
=
−
=
+
=
+
=
=
1
0
1
2
4
5
1
4
5
5
1
5
1
5
4
)
1
(
5
1
5
4
k
l
l
k
l
k
EY
5
1
4
2
5
1
2
3
3
5
1
3
2
5
4
3
=
+
=
=
+
=
=
+
=
EY
EY
EY
12
5
11
12
137
12
60
30
20
15
12
5
2
5
3
5
4
5
1
=
=
+
+
+
+
=
+
+
+
+
=
EX
Zadanie 2
)
1
,
0
(
J
X
i
≅
(
)
(
)
(
)
(
)
(
)
n
i
n
n
n
t
t
X
P
t
X
X
P
t
X
X
P
)
1
(
1
1
,...,
min
1
,...
min
1
1
−
−
=
>
−
=
>
−
=
<
(
)
(
)
(
)
(
)
=
+
−
<
∨
+
+
>
=
−
<
∨
+
>
=
>
−
1
1
,...
min
1
1
,...,
min
1
1
1
1
1
n
X
X
n
X
X
P
T
T
P
T
P
n
n
n
n
n
ε
ε
ε
ε
ε
(
)
(
)
n
n
n
n
n
n
n
X
X
P
n
X
X
P
+
−
−
−
+
+
+
−
=
+
−
<
+
+
+
>
=
1
1
1
1
1
1
1
1
1
,...
min
1
1
,...,
min
1
1
ε
ε
ε
ε
=
+
−
−
−
+
+
+
−
⋅
+
−
−
+
⋅
+
+
+
+
∞
→
n
n
n
n
n
n
n
n
n
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
lim
ε
ε
ε
ε
ε
ε
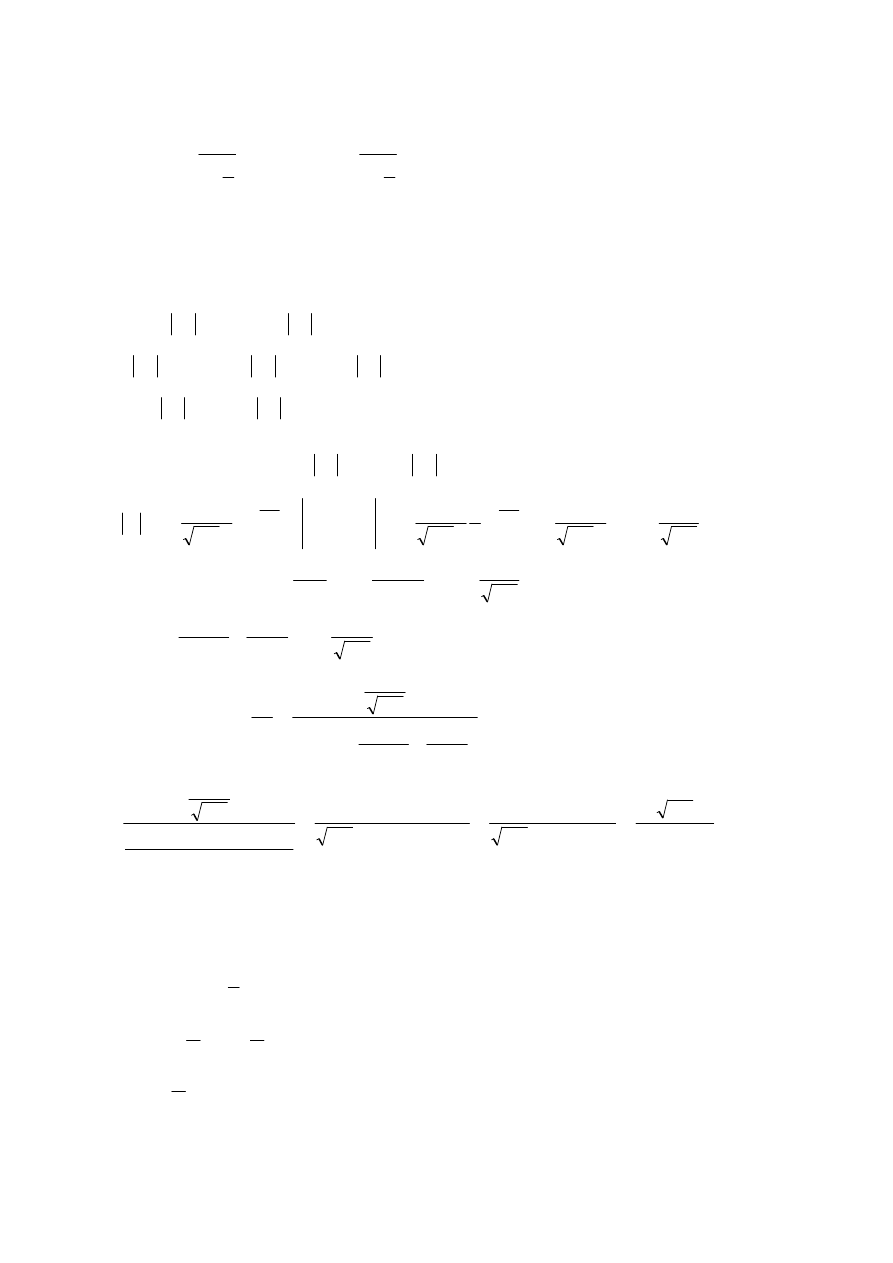
1
1
1
1
1
1
lim
exp
1
1
1
1
lim
exp
−
−
−
∞
→
∞
→
+
−
=
+
−
−
−
+
+
+
−
=
ε
ε
ε
ε
e
e
n
n
n
n
Zadanie 3
( )
( ) ( )
( ) ( ) ( )
θ
θ
θ
θ
θ
θ
θ
−
=
+
=
−
ˆ
ˆ
,
ˆ
ˆ
ˆ
2
2
2
E
b
b
D
E
∑
∑
=
=
=
n
i
i
n
i
i
X
c
X
c
1
2
1
var
var
i
i
i
i
X
E
X
E
EX
X
2
2
2
2
var
−
=
−
=
σ
∑
∑
=
=
=
n
i
i
n
i
i
X
E
c
X
c
E
1
1
(
)
(
)
∑
∑
=
=
−
+
−
=
−
n
i
n
i
i
i
c
X
E
c
X
E
c
E
1
2
1
2
2
2
2
ˆ
σ
σ
σ
σ
Π
=
Π
=
Π
=
=
=
=
Π
=
∫
∫
∞
−
∞
−
2
2
2
2
1
2
1
2
1
2
2
2
1
2
2
0
2
2
0
2
2
2
2
σ
σ
σ
σ
σ
σ
σ
dt
e
dt
xdx
t
x
xe
X
E
t
x
(
)
=
+
Π
−
Π
+
Π
−
=
−
2
2
2
2
2
2
2
2
2
2
2
2
4
2
4
ˆ
σ
σ
σ
σ
σ
σ
σ
σ
cn
n
c
n
n
c
E
c
min
2
4
2
2
2
2
2
2
2
2
2
→
+
Π
−
Π
−
Π
+
=
σ
σ
σ
σ
σ
c
n
c
n
n
n
Minimum dla
=
Π
−
Π
+
Π
=
−
=
n
n
n
n
a
b
c
2
2
2
2
2
2
2
2
2
4
2
σ
σ
σ
σ
(
)
(
)
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
−
+
Π
Π
=
−
+
Π
Π
Π
=
−
+
Π
Π
Π
=
Π
−
+
Π
Π
=
n
n
n
n
n
n
n
n
n
σ
σ
σ
σ
σ
σ
Zadanie 4
x
i
e
X
−
≅
≅
4
1
;
2
.dwum
uj
N
+
=
2
1
2
var
m
p
q
m
p
q
r
S
N
1
m
p
q
r
ES
N
=
)
(
1
IX
E
m
=

(
)
2
2
2
X
I
E
m
=
2
1
1
2
1
)
(
)
(
1
=
⋅
=
=
X
E
I
E
m
(
)
( )
1
1
1
2
1
2
2
2
2
2
=
+
=
=
EX
EI
X
I
E
18
13
3
2
12
13
4
1
3
1
1
3
2
5
,
0
75
,
0
25
,
0
1
75
,
0
25
,
0
2
var
2
=
=
+
=
⋅
+
⋅
=
N
S
3
1
2
1
3
1
2
5
,
0
75
,
0
25
,
0
2
=
⋅
⋅
=
⋅
⋅
=
N
ES
2
13
18
9
13
3
18
13
=
⋅
=
⋅
=
ODP
Zadanie 5
)
4
,
5
(
)
4
,
2
(
)
4
,
3
(
Γ
≅
+
Γ
≅
Γ
≅
Y
X
Y
X
(
)
M
L
s
f
dxdy
ye
e
x
y
x
s
Y
X
Y
X
E
Y
X
y
x
=
⋅
−
=
=
+
−
+
∆
−
−
∫
)
(
16
32
)
(
4
4
2
∈
−
=
−
−
=
→
=
+
>
>
=
∆
)
;
0
(
2
0
0
s
x
s
x
y
x
x
s
y
s
y
x
y
x
∫
=
−
⋅
⋅
−
=
−
−
−
s
x
s
x
dx
e
x
s
e
x
s
x
L
0
)
(
4
4
2
)
(
16
32
)
2
(
(
)
∫
=
−
−
=
+
−
−
=
−
−
s
s
s
s
x
s
x
sx
e
dx
sx
s
x
xs
x
e
0
0
3
2
5
4
4
2
2
2
4
3
5
2
4
3
512
2
2
512
5
4
5
4
5
5
5
4
60
512
60
20
24
45
512
3
5
2
4
3
512
s
e
s
e
s
s
s
e
s
s
s
−
−
−
=
−
−
=
−
−
=
s
Y
X
e
s
s
f
4
4
5
)
5
(
4
)
(
−
+
Γ
=
s
s
s
e
s
s
e
ODP
s
s
5
1
120
24
4
24
60
512
)
5
(
4
60
512
5
4
4
5
5
4
=
=
⋅
=
Γ
=
−
−
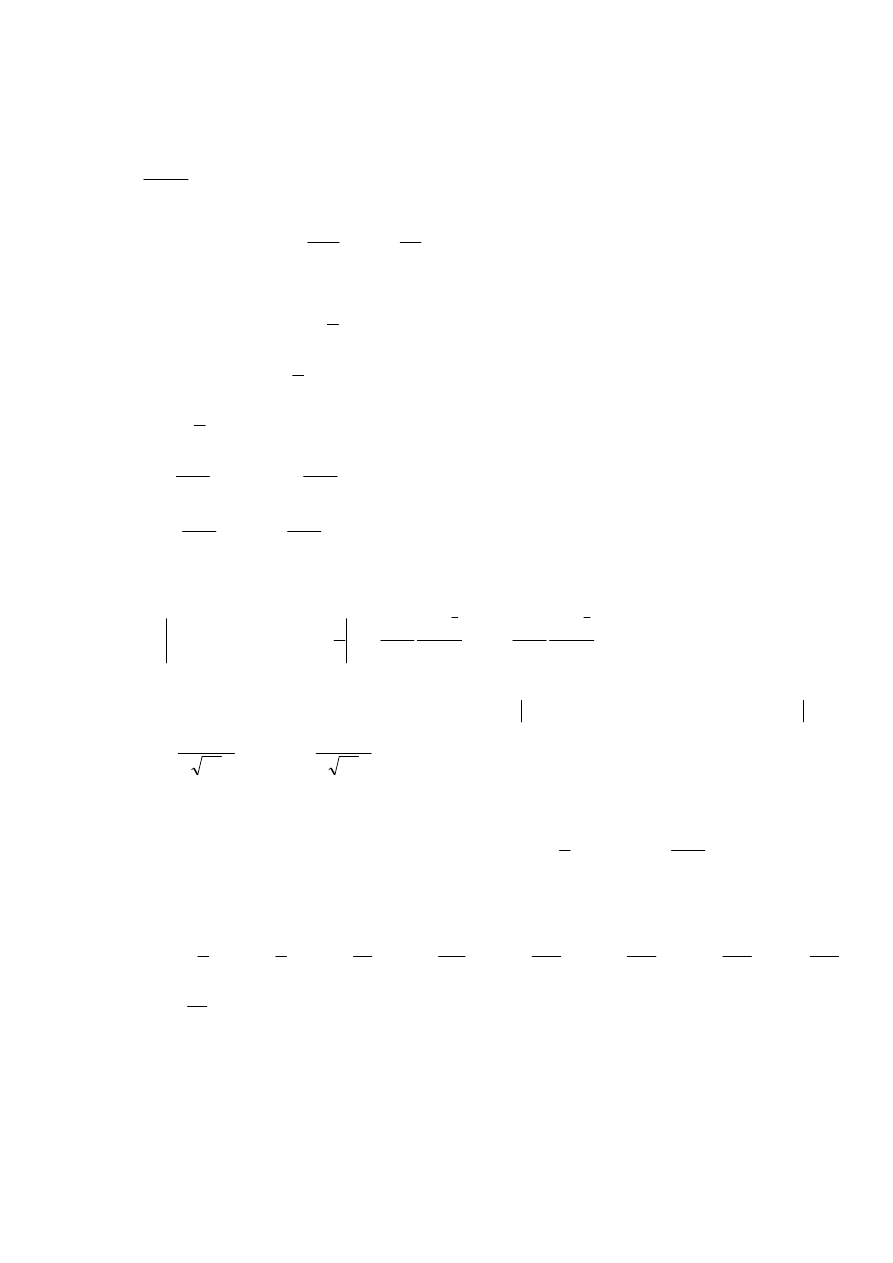
Zadanie 6
(
)
P
t
x
P
t
x
P
t
x
P
i
i
H
i
H
i
H
=
+
>
=
>
=
>
∑
∏
∏
=
8
1
2
8
2
8
2
ln
2
ln
8
ln
2
2
0
0
0
(
)
(
)
∫
≅
−
=
−
=
=
<
=
<
−
+
t
t
e
t
e
t
i
i
wykl
e
x
dx
x
e
x
P
t
x
P
1
1
1
)
(
1
1
ln
θ
θ
θ
θ
θ
)
;
8
(
ln
θ
Γ
≅
→
∑
i
x
α
=
+
>
=
∑
t
x
P
P
K
i
H
ln
2
1
2
ln
4
ln
:
0
+
<
∑
t
x
P
i
H
ln
2
1
2
ln
4
ln
:
1
β
t
w
ln
2
1
2
ln
4
+
=
∫
∫
∞
−
−
→
Γ
+
Γ
=
w
w
x
x
dx
e
x
dx
e
x
w
f
0
2
7
8
4
7
8
)
8
(
2
)
8
(
4
)
(
szukamy minimum po w
2
ln
4
0
)
8
(
2
)
8
(
4
)
(
2
7
8
4
7
8
=
→
=
Γ
+
Γ
−
=
′
−
−
w
e
w
e
w
w
f
w
w
)
2
ln
4
(
f
ODP
=
∫
∫
∞
−
−
Γ
+
Γ
=
=
=
w
w
x
x
dx
e
x
dx
e
x
t
x
w
f
8
4
0
8
2
7
8
2
7
2
)
8
(
1
2
)
8
(
1
2
iach
podstawien
po
)
(
i to są całki po
gęstościach z rozkładu
)
16
(
2
χ
(
)
=
=
>
+
<
=
<
<
−
=
normalnym
rozkladem
emy
aproksymuj
)
8
(
)
4
(
8
4
1
)
(
w
X
P
w
X
P
w
X
w
P
w
f
=
−
+
−
=
>
+
−
<
≈
−
>
+
−
<
=
36214
,
0
5
,
0
30785
,
0
5
,
0
)
09
,
1
(
)
87
,
0
(
32
16
8
32
16
4
N
P
N
P
w
N
P
w
N
P
=0,33001 czyli najbliżej odpowiedź B
Ewentualnie po podstawieniu przy f(w) w pierwszej całce
∫
−
Γ
−
=
=
w
w
x
dx
e
x
w
f
t
x
2
2
7
8
)
8
(
2
1
)
(
2
I obliczamy całkę:
∫
−
x
e
x
2
7
Po żmudnych rachunkach:
∫
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
=
x
x
x
x
x
x
x
x
x
e
xe
e
x
e
x
e
x
e
x
e
x
e
x
e
x
2
2
2
2
2
3
2
4
2
5
2
6
2
7
2
7
32
630
16
630
16
630
8
210
8
105
4
21
4
7
2
1
gdzie
A
ODP
,
!
7
2
1
8
⋅
−
=
2
16
1
8
2
2
a
a
A
−
−
−
=
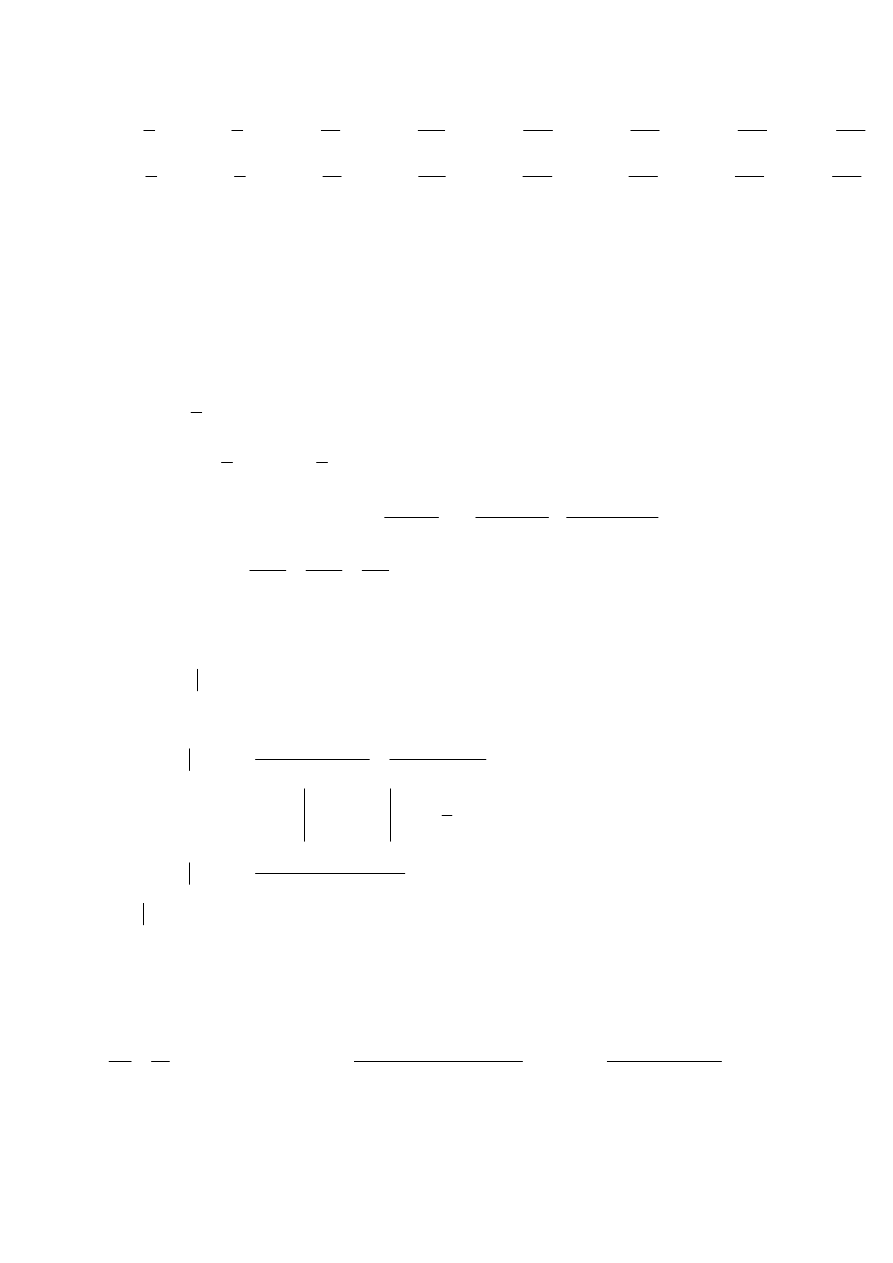
(
)
32
630
)
2
ln
4
(
16
630
)
2
ln
4
(
16
630
)
2
ln
4
(
8
210
)
2
ln
4
(
8
105
)
2
ln
4
(
4
21
)
2
ln
4
(
4
7
2
ln
4
2
1
2
3
4
5
6
7
1
+
+
+
+
+
+
+
=
a
32
630
)
2
ln
8
(
16
630
)
2
ln
8
(
16
630
)
2
ln
8
(
8
210
)
2
ln
8
(
8
105
)
2
ln
8
(
4
21
)
2
ln
8
(
4
7
)
2
ln
8
(
2
1
2
3
4
5
6
7
2
+
+
+
+
+
+
+
=
a
3336
,
0
=
→
ODP
Zadanie 7
(
)
)
,
,
(
)
,
,
(
:
:
p
n
l
Q
p
n
k
Q
X
z
X
P
n
l
p
n
k
−
=
≤
≤
∑
=
−
−
=
n
k
i
i
n
i
p
p
i
n
p
n
k
Q
)
1
(
)
,
,
(
U nas:
10
,
7
,
3
,
2
1
=
=
=
=
n
l
k
p
∑
∑
=
=
=
−
=
−
=
10
3
10
7
10
10
5
,
0
10
5
,
0
10
2
1
,
10
,
7
2
1
,
10
,
3
i
i
i
i
Q
Q
ODP
=
⋅
⋅
⋅
⋅
+
⋅
⋅
⋅
⋅
+
⋅
⋅
=
+
+
+
=
10
10
5
,
0
120
10
9
8
7
6
24
10
9
8
7
2
6
10
9
8
5
,
0
6
10
5
10
4
10
3
10
(
)
128
99
1024
792
1024
1
252
420
120
=
=
+
+
=
Zadanie 8
(
)
∏
=
>
=
10
1
1
i
i
i
x
y
f
L
(
)
)
1
(
3
)
1
(
)
1
1
(
1
1
1
1
2
3
>
=
>
+
<
<
=
>
<
−
∫
+
−
X
P
dx
e
x
X
P
t
X
P
X
t
X
P
t
x
θ
θ
[
]
3
3
3
3
3
1
3
3
3
)
(
2
3
2
t
t
w
t
w
t
x
e
e
dw
e
dw
dx
x
w
x
dx
e
x
t
X
P
θ
θ
θ
θ
θ
θ
−
∞
−
∞
−
∞
−
=
−
=
=
=
=
=
=
>
∫
∫
(
)
(
)
θ
θ
θ
θ
θ
+
+
−
−
−
+
−
−
=
−
−
−
=
>
<
−
3
3
)
1
(
)
1
(
1
1
1
1
1
t
t
e
e
e
e
X
t
X
P
(
)
3
3
)
1
(
2
2
)
1
(
)
1
(
3
)
1
(
3
1
+
−
+
−
+
=
+
⋅
=
>
t
t
i
i
e
e
t
t
e
e
x
y
f
θ
θ
θ
θ
θ
θ
( )
(
)
(
)
∏
=
+
−
∑
+
=
10
1
1
2
10
3
1
3
i
y
i
i
e
y
e
L
θ
θ
θ
( )
(
)
(
)
∑
∑
=
=
+
−
+
+
=
10
1
3
10
1
1
1
ln
2
3
ln
10
ln
i
i
i
i
y
y
e
L
θ
θ
θ
(
)
(
)
(
)
10
1
10
ˆ
0
1
10
10
0
1
10
10
10
1
3
3
10
1
3
−
+
=
→
=
+
−
+
→
=
+
−
+
=
∂
∂
∑
∑
∑
=
=
i
i
i
i
i
y
y
y
θ
θ
θ
θ
θ
θ
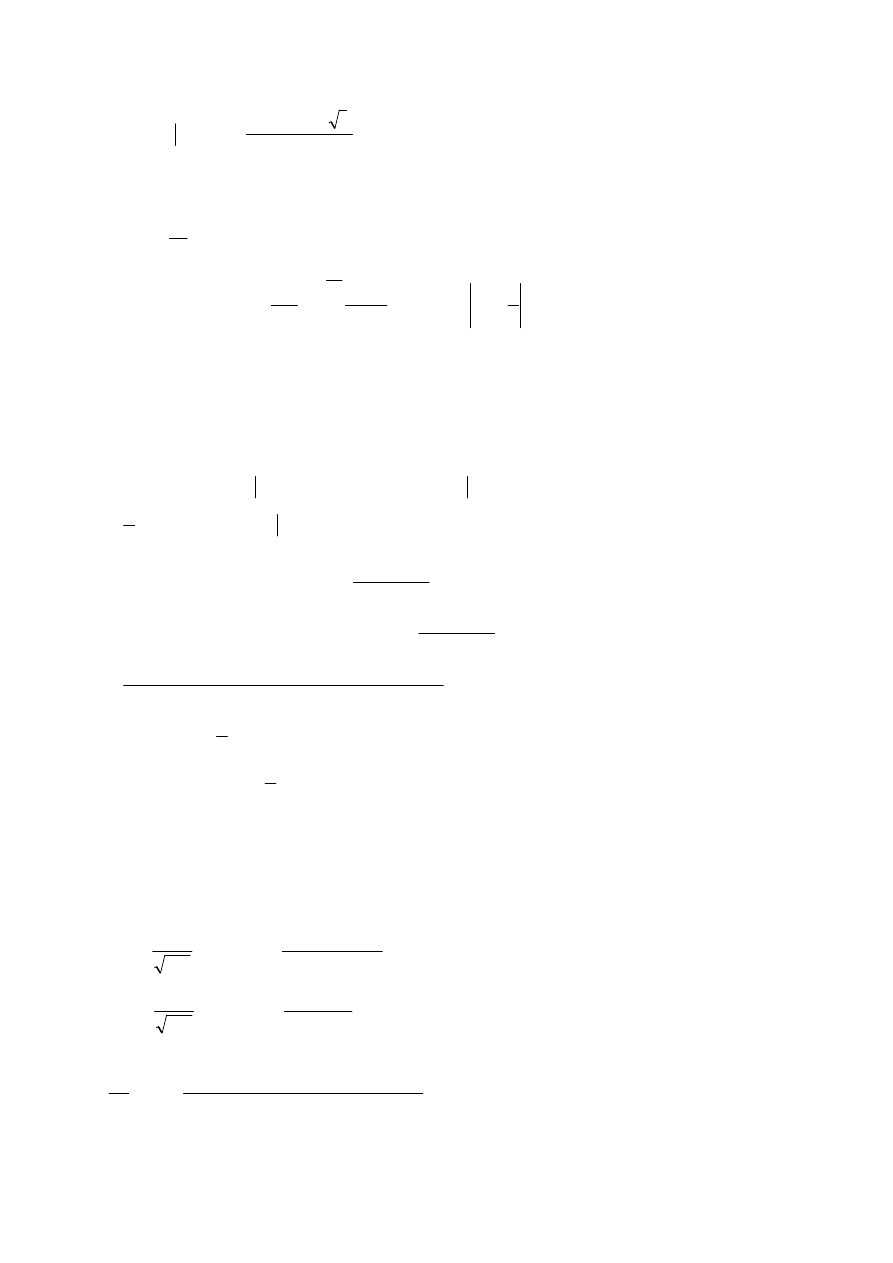
(
)
(
)
(
)
)
1
;
(
1
1
1
)
1
(
3
3
θ
θ
wykl
e
X
P
t
X
P
t
X
t
X
P
t
i
i
i
i
→
−
=
>
<
<
=
>
<
−
−
przesunięty wykładniczy
(
)
∑
∑
=
=
Γ
≅
−
→
Γ
≅
→
10
1
10
1
3
3
)
;
10
(
10
y
przesuniet
10
;
;
10
i
i
i
i
X
X
θ
θ
)
;
10
(
,
95
,
0
10
θ
θ
Γ
≅
=
<
X
gdzie
X
c
P
(
)
∫
∫
→
=
=
=
=
Γ
=
<
=
<
−
c
c
x
t
x
dx
e
x
c
X
P
c
X
P
20
0
2
10
0
9
10
95
,
0
)
20
(
2
)
10
(
10
10
χ
θ
θ
θ
θ
θ
θ
57
,
1
41
,
31
20
≈
→
=
→
c
c
Zadanie 9
(
)
1
3
0
=
≤
Y
P
(
)
(
)
(
)
(
)
(
)
=
<
<
≤
+
=
=
≤
=
≤
≥
4
4
3
4
4
3
3
2
n
n
n
n
n
n
n
X
P
X
Y
P
X
P
X
Y
P
Y
P
n
dla
(
)
(
)
4
4
4
4
4
3
4
4
4
4
4
2
1
A
n
n
n
X
X
Y
P
4
3
,
min
4
3
1
<
≤
=
−
(
)
(
) (
)
=
<
⋅
<
≤
=
−
4
1
4
,
3
,
min
1
n
n
n
n
X
P
X
X
Y
P
A
(
) (
)
[
]
(
)
=
<
≤
>
+
<
≤
=
−
−
4
1
3
,
3
4
,
3
1
1
n
n
n
n
n
X
P
X
Y
P
X
Y
P
(
) (
) (
) (
)
(
)
(
)
(
)
(
)
1
3
1
3
4
3
3
4
3
1
1
1
1
=
≤
−
+
≤
=
<
≤
>
+
<
≤
=
−
−
−
−
n
n
n
n
n
n
n
Y
P
Y
P
X
P
X
P
Y
P
X
P
Y
P
(
)
4
3
3
=
≤
→
n
Y
P
ciąg stały
Czyli
(
)
4
3
3
lim
=
≤
∞
→
n
n
Y
P
Zadanie 10
Przy
( )
1
;
:
0
i
i
x
N
Y
H
≅
Przy
(
)
1
;
1
2
:
1
−
≅
i
i
x
N
Y
H
(
)
+
−
−
Π
=
∑
=
n
i
i
i
n
x
Y
f
1
2
1
2
1
2
exp
2
1
(
)
−
−
Π
=
∑
=
n
i
i
i
n
x
Y
f
1
2
0
2
exp
2
1
(
)
(
)
−
+
+
−
−
=
∑
∑
=
=
2
1
2
exp
1
2
1
2
0
1
n
i
i
i
n
i
i
i
x
Y
x
Y
f
f
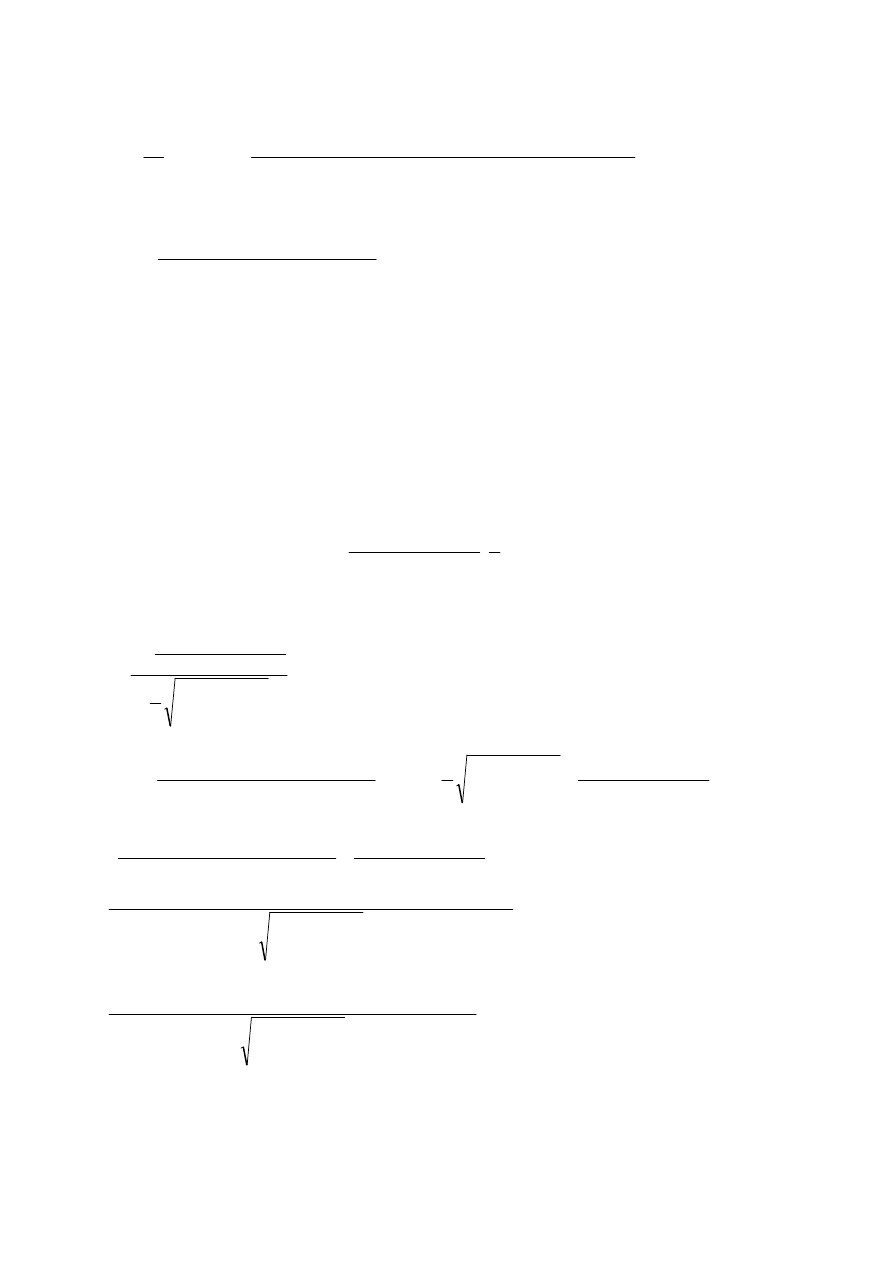
(
)
=
>
−
+
−
−
+
−
+
−
=
>
∑
=
t
x
Y
x
Y
x
Y
x
Y
x
Y
P
t
f
f
P
n
i
i
i
i
i
i
i
i
i
i
i
H
H
2
1
4
2
4
4
2
1
2
2
2
2
0
1
0
0
(
)
05
,
0
2
4
1
2
3
2
1
2
0
=
>
+
−
−
−
=
∑
=
t
x
Y
x
Y
x
P
Z
n
i
i
i
i
i
i
H
4
4
4
4
4
3
4
4
4
4
4
2
1
Przy
:
0
H
∑
∑
=
=
−
−
=
n
i
i
n
i
i
x
n
x
EZ
1
2
1
2
(
)
∑
=
−
=
n
i
i
x
Z
1
2
2
2
var
Szukamy t:
(
)
(
)
−
−
−
≅
=
>
∑
∑
∑
=
=
=
n
i
i
n
i
i
n
i
i
H
x
x
n
x
N
W
gdzie
t
W
P
1
2
1
2
1
2
2
4
1
;
2
2
,
05
,
0
0
(
)
645
,
1
2
2
2
1
2
2
1
2
1
2
1
=
−
−
−
−
→
∑
∑
∑
=
=
=
n
i
i
n
i
i
n
i
i
x
x
n
x
t
(
)
(
)
2
2
2
2
2
1
645
,
1
2
4
1
2
3
2
:
1
2
1
1
2
1
2
∑
∑
∑
∑
=
=
=
=
−
−
+
−
⋅
>
+
−
−
−
n
i
i
n
i
i
n
i
i
n
i
i
i
i
i
i
x
n
x
x
x
Y
x
Y
x
ODP
(
)
(
)
645
,
1
2
2
2
2
2
2
4
1
2
3
2
1
2
1
2
1
1
2
>
−
⋅
−
−
−
+
−
−
−
∑
∑
∑
∑
=
=
=
=
n
i
i
n
i
i
n
i
i
n
i
i
i
i
i
i
x
x
n
x
x
Y
x
Y
x
(
)
645
,
1
2
2
2
4
2
2
2
1
2
1
1
1
1
2
1
>
−
+
−
+
−
−
−
∑
∑
∑
∑
∑
∑
=
=
=
=
=
=
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
i
x
n
x
x
n
Y
x
Y
x

(
)
645
,
1
2
2
2
2
2
2
1
2
1
1
1
2
1
>
−
+
−
−
∑
∑
∑
∑
∑
=
=
=
=
=
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
i
x
x
Y
x
Y
x
(
)(
)
(
)
645
,
1
1
1
1
2
1
>
−
−
−
∑
∑
=
=
n
i
i
n
i
i
i
i
x
x
x
Y
Wyszukiwarka
Podobne podstrony:
2011.06.20 prawdopodobie stwo i statystyka
2002 06 15 prawdopodobie stwo i statystykaid 21643
2011 04 04 prawdopodobie stwo i statystykaid 27339
2008.06.02 prawdopodobie stwo i statystyka
1997.06.21 prawdopodobie stwo i statystyka
2008 06 02 prawdopodobie stwo i statystykaid 26454
1999.06.19 prawdopodobie stwo i statystyka
2001.06.02 prawdopodobie stwo i statystyka
2001 06 02 prawdopodobie stwo i statystykaid 21607
2006 06 05 prawdopodobie stwo i statystykaid 25461
2002.06.15 prawdopodobie stwo i statystyka
2004.06.07 prawdopodobie stwo i statystyka
2006.03.20 prawdopodobie stwo i statystyka
1999 06 19 prawdopodobie stwo i statystykaid 18597
2006 03 20 prawdopodobie stwo i statystykaid 25453
2006.06.05 prawdopodobie stwo i statystyka
2011.04.04 prawdopodobie stwo i statystyka
2000 06 17 prawdopodobie stwo i statystykaid 21573
więcej podobnych podstron