Program ekonomii matematycznej

Studia SSL

1. Modele matematyczne w ekonomii

2. Podstawowe zależności funkcyjne w wyborze konsumenta

3. Decyzje przedsiębiorstwa

4. Teoria gier

5. Teoria ryzyka

Podręczniki:

1. A. Blajer-Gołębiewska, L. Czerwonka, E. Pankau, M. Zielenkiewicz, Ekonomia matematyczna w zadaniach, Wyd. Uniw. Gdańskiego, Gdańsk 2006

2. A. C. Chiang: Podstawy ekonomii matematycznej, PWE, Warszawa 1994

3. A. C. Chiang: Elementy dynamicznej optymalizacji, Warszawa 2002

4. T. Kamińska: Przydatność modeli matematycznych w ekonomii, [w:] Wybrane problemy współczesnej gospodarki rynkowej, Studia i materiały MBA UG nr 2/2003

5. W. Łyszkiewicz: Industrial organization. Organizacja rynku i konkurencja, Warszawa 2000

6. E. Panek: Ekonomia matematyczna, AE w Poznaniu, Poznań 2000

7. D. Witkowska, Podstawy ekonometrii i teorii prognozowania, Oficyna Ekonomiczna, Kraków 2005

MODELE MATEMATYCZNE W EKONOMII

Ekonomia matematyczna to zastosowanie matematyki do rozumowania ekonomicznego opartego na dedukcji, czyli wyciąganiu wniosków na podstawie przesłanek (odrzuca się indukcję, ponieważ pomija się empiryczne badanie rzeczywistości i uogólnienie faktów płynących z jej obserwacji).

Zalety podejścia matematycznego:

1. stosowany język jest zwięzły i precyzyjny,

2. można korzystać z bogactwa twierdzeń matematycznych,

3. ponieważ niezbędnym warunkiem stosowania twierdzeń matematycznych jest formułowanie wszystkich przyjętych założeń w sposób jawny („jeśli ................, to ...........”), to jest to zabezpieczenie przed nieporozumieniami i błędami, jakie mogłyby powstać przy przyjęciu pewnych milczących założeń,

4. pozwala na badanie ogólnego przypadku n-wymiarowego.

Formułowanie modeli

Model ekonomiczny to celowo uproszczony schemat analityczny rzeczywistości gospodarczej. Jako struktura teoretyczna może być zbiorem założeń, definicji i zależności przyczynowo-skutkowych.

Jeśli oparty jest na modelu matematycznym (ekonometrycznym), to jest układem zależności opisujących jego strukturę.

Zależności te (równania, nierówności, relacje) wyrażają pewne związki między zmiennymi i nadają w ten sposób matematyczną postać przyjętym założeniom ekonomicznym.

Składniki modelu matematycznego

Do opisu rzeczywistości gospodarczej za pomocą matematycznego sposobu formułowania zależności między kategoriami ekonomicznymi niezbędne są:

• zmienne objaśniane i objaśniające (endogeniczne i egzogeniczne), tj. wielkości, które mogą przyjmować różne wartości (praca, zysk, przychód, koszt, dochód narodowy, konsumpcja, inwestycje, eksport, import).

W modelach zawierających jedno równanie zmienna objaśniana jest opisywana (objaśniana) danym równaniem. W modelach wielorównaniowych odpowiednikiem zmiennych objaśnianych są zmienne endogeniczne, ponieważ są generowane od wewnątrz, tj. wartości określa się na podstawie skonstruowanego modelu ekonomicznego, innymi słowy oblicza się wartości rozwiązań dla pewnego zbioru zmiennych.

Zmienne objaśniające to zmienne, które opisują (objaśniają) kształtowanie się zmiennej objaśnianej. W modelach wielorównaniowych odpowiednikiem zmiennych objaśniających są zmienne egzogeniczne, gdyż są wprowadzone do modelu z zewnątrz (ich wartości są dane i ustalone). Wśród nich rozróżnia się zmienne ściśle egzogeniczne, zwane zmiennymi autonomicznymi i zmienne sterujące. Kryterium rozróżnienia opiera się na zależności od woli użytkownika modelu i jego wpływu na ustalanie poziomu zmiennych. Zmienne autonomiczne są niezależne, gdyż użytkownik nie jest w stanie oddziaływać na ich wielkość (np. kursy walut); zmienne sterujące mogą być pod wpływem decyzji użytkownika modelu (np. stawki opodatkowania podatkiem dochodowym).

Ta sama kategoria ekonomiczna np. podaż pieniądza w jednym modelu może mieć charakter zmiennej endogenicznej, np. wyznaczenie poziomu kreacji pieniądza przez bank, w innym - egzogenicznej, np. w wyznaczeniu równowagi na rynku pieniężnym.

• stałe - to wielkości, które nie zmieniają się w przyjętych warunkach, np. skłonność do oszczędzania s w modelu równowagi ogólnej. Gdy występuje łącznie z inną zmienną, to jest współczynnikiem (liczba lub symbol), np. 5Q przy obliczeniu kosztów całkowitych produkcji TC oznacza, że koszty zmienne, z każdą następną jednostką, rosną o 5 jp.

• parametry są rodzajem zmiennej egzogenicznej, tj. ustaloną wielkością stałą, wprowadzoną do modelu pod postacią symbolu, np. α w modelu Cobba - Douglasa, informująca o wpływie zmian zatrudnienia na zmianę wielkości produkcji firmy (produktu krajowego). Parametry mają reprezentować pewną stałą o wyższym poziomie ogólności, która może przyjmować dowolną wartość. Chociaż można im przypisywać różne wartości, to w modelu pełnią funkcję stałej, ponieważ jest ona dana. Stąd w literaturze przedmiotu bywa określana mianem stałej parametrycznej.

Etapy konstrukcji modelu

1. Określenie zmiennych objaśnianych i objaśniających (endogenicznych i egzogenicznych) (np. Y, K, L) oraz parametrów (np. skłonność do oszczędzania s, relacja kapitał/produkcja v), które chce się włączyć do modelu. W relacji do zmiennych parametry są stałe, ale w badaniach porównawczych można obserwować zmiany wyniku, gdy zmienia się jakiś parametr.

2. Sformułowanie warunków, jakie zakłada się jako niezbędne do działania modelu. Występują one w formie:

• definicji lub tożsamości, określających związki zachodzące z definicji, np. przychody ze sprzedaży TR są sumą iloczynów ceny p_i i ilości sprzedaży poszczególnych rodzajów produktów x_i TR=Σx_ip_i lub inwestycje równe oszczędnościom ex post I≡A z definicji obliczania dochodu narodowego.

• zależności funkcjonalnych, czyli zależności przyjętych ex ante w modelu, np. wielkość produkcji zależy od nakładów pracy i kapitału q_x=f(L,K).

• założeń odnośnie do równowagi lub nierównowagi w działaniu modelu, które można dla wygody podzielić na warunki strumieni i warunki zasobów. Np. w kategoriach okresowych można przyjąć w modelu taki warunek strumienia, który wyraża jednookresowe opóźnienie w dostosowaniu się produkcji rynkowej do zgłaszanego zapotrzebowania na dobro x: Q_xt=Q_d(t-1).

Warunek zasobu wyraża założenie o wykorzystaniu zasobu kapitału K w czasie t przy poziomie pełnych mocy wytwórczych (wynikających z relacji poziomu produkcji do wielkości kapitału, tj. Y_t/K_t = 1/v, a więc produkt krajowy Y_t odpowiadający pełnym mocom jest dany jako równanie: K_t=vY_t.

3. Sprowadzenie warunków modelu do jednego równania względem jednej ze zmiennych wybranej z punktu widzenia wygody działania (jeśli warunków tyle, ile zmiennych).

Z powyższego wynika występowanie trzech typów równań w zastosowaniach ekonomicznych:

1. definicyjne - ustanawia tożsamość dwu wyrażeń, które mają dokładnie taki sam sens; używa się znaku identyczności lub równości, czyli: obliczając PKB metodą wydatków przyjmuje się, że poziom produktu krajowego brutto Y w gospodarce otwartej kształtują wydatki gospodarstw domowych C, przedsiębiorstw I, rządu G i salda obrotów handlowych z zagranicą (E_x - I_m), tj. Y≡C+I+G+(E_x - I_m);

2. behawioralne, określa sposób, w jaki zachowuje się zmienna w reakcji na przyrosty innych zmiennych, np. produkt krańcowy znajduje się pod wpływem zmian produktu całkowitego w zależności od zmian zatrudnienia o jednostkę, tj.
   ;

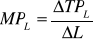
3. warunki równowagi, tylko wtedy, gdy model dotyczy pojęcia równowagi; warunek równowagi jest równaniem opisującym niezbędne warunki osiągnięcia równowagi, np. w równowadze rynkowej Q_d=Q_s lub przedsiębiorstwa maksymalizującego zysk MC=MR.

Rozwiązanie modelu polega na:

1. znalezieniu wartości liczbowej odpowiadającej poziomowi statycznemu,

2. utrzymaniu stopy wzrostu lub ścieżki czasowej,

3. znalezieniu pozostałych zmiennych na podstawie warunków modelu.

Przykładowy model - równowaga konsumenta

Algebraiczne rozwiązanie punktu optymalnego wyboru dotyczy maksymalizacji użyteczności konsumenta przy ograniczonym dochodzie.

Jeśli:

• funkcja użyteczności jest ciągła i różniczkowalna i przyjmuje postać U(X,Y)

• analiza ograniczona jest do dwóch dóbr

• ograniczenie budżetowe ma formułę P_XX + P_YY = I,

to możliwa jest każda struktura konsumpcji, która spełnia nierówność

I ≥ P_XX + P_YY,

a wybrana przez konsumenta wiązka dóbr ma dobrze zdefiniowane ilościowe interpretacje.

Różniczka całkowita pozwala obliczyć takie kombinacje X i Y, dla których poziom użyteczności jest stały
.

, po przekształceniu
.

Lewa strona równania wskazuje na MRS krzywej obojętności, a prawa na jej nachylenie równe relacji użyteczności krańcowych

Y Równowaga konsumenta

B

Y_E E

U₄

A U₃

U₂

U₁ I I₁

X_E X

Problem, przed którym stoi konsument to

przy warunku I ≥ P_XX + P_YY

Jeśli konsument znajduje się na linii ograniczenia budżetowego, to

I - P_XX - P_YY = 0,

a rozwiązanie problemu można uzyskać za pomocą funkcji Lagrange'a.

Istota metody mnożnika Lagrange'a polega na sprowadzeniu znalezienia ekstremum warunkowego do postaci, w której można zastosować warunek pierwszego rzędu typowy dla poszukiwania ekstremum bezwarunkowego.

V (X,Y,λ) = U(X,Y) + λ(I - P_XX - P_YY)

gdzie: λ - mnożnik Lagrange'a (tyle mnożników, ile warunków ograniczających).

Warunkami koniecznymi, aby zaistniał punkt optymalny, są pierwsze pochodne funkcji V względem wszystkich zmiennych, które muszą być równe zeru:

,

,

.

Przekształcone dwa pierwsze warunki pozwalają obliczyć użyteczności krańcowe konsumpcji X i Y, tj.

oraz
,

po podzieleniu otrzymuje się punkt równowagi konsumenta:

,

gdzie: lewa strona równania to nachylenie krzywej obojętności, czyli MRS, a prawa to nachylenie linii budżetowej.

Mnożnik Lagrange'a λ i jego interpretacja ekonomiczna

oraz
,

wówczas

,

.

λ pokazuje zmianę użyteczności spowodowaną zmianą wydatków odpowiednio na dobro X lub Y.

λ mierzy więc użyteczność krańcową dochodu pieniężnego.

Jego zniknięcie z formuły punktu równowagi konsumenta świadczy o tym, że wielkość użyteczności krańcowej nie ma wpływu na optymalne rozwiązanie problemu. Jeśli wartość użyteczności nie ma żadnego wpływu na wynik równowagi, to wystarczająca jest użyteczność porządkowa (ordynalna), nie kardynalna.

PODSUMOWANIE

Dotychczas posługiwano się w ekonomii głównie metodą geometryczną. Algebra pozwala na:

1. lepszą ekonomiczną interpretację otrzymanych rezultatów,

2. zastosowanie użytecznej metody sprawdzania poprawności rozwiązań geometrycznych,

3. rozszerzenie zasięgu analizy do n dóbr, gdzie n jest skończoną liczbą dodatnią.

Por. Z. Czerwiński, W. Gedymin, R. Kiedrowski, E. Panek, Makroekonomiczny średniookresowy model gospodarki Polski, KEMPO 1994, s. 5.

Zob. A.C. Chiang, Podstawy ekonomii matematycznej, PWN, Warszawa 1994, s. 20.

makroekonomia

mikroekonomia

matematyka

Ekonometria

statystyka

Ekonomia matematyczna

Prognozowanie i symulacje

Ocena projektów

inwestycyjnych

OBSERWACJA

Zmiana definicji i/lub hipotez

Pojęcia, definicje, klasyfikacja

Uogólnienia informacji, czyli hipotezy (INDUKCJA)

Wyprowadzenie wniosków (DEDUKCJA)

Usunięcie błędu logicznego

Test empiryczny - konfrontacja z rzeczywistością

(KRYTYKA NAUKOWA)

Test logiczny poprawności wnioskowania

(KRYTYKA NAUKOWA)

Falsyfikacja

Brak falsyfikacji

Niespójność logiczna

Poprawność logiczna

Odrzucenie teorii i zastąpienie jej teorią konkurencyjną

Przejściowa wartość teorii

TEORIA

---