TREŚCI ZADAŃ WRAZ Z ROZWIĄZANIAMI

ZAD. 1

Dla poniższych modeli rynku wyznacz ceny i wielkości w punkcie równowagi rynkowej. Wykonaj ilustrację graficzną dla każdego modelu.

a) Qd = 100 - 3P Qs = 15 +2P

b) Qd = 40 - 8P Qs = -8 +3P

c) Qd - 20 + 4P = 0 Qs + 5 - 2P = 0

ROZWIĄZANIE:

a)

Qd = 100 - 3P

Qs = 15 +2P

W celu wyznaczenia punktu równowagi rynkowej rozwiązujemy układ równań złożony z funkcji popytu i podaży:

Qd = 100 - 3P

Qs = 15 +2P

Układ ten rozwiązujemy eliminując równania i zmienne przez podstawienie.

Pamiętając o warunku równowagi przyjmujemy, że Qe = Qs = Qd i podstawiamy pierwsze równanie do drugiego. Otrzymujemy w ten sposób jedno równanie z jedną zmienną:

100 - 3P = 15 + 2P

Z tego równania wyznaczamy cenę równowagi rynkowej:

100 - 15 = 3P + 2P

85 = 5P

P = 85/5

P = 17

Zatem cena równowagi rynkowej Pe wynosi 17

Aby obliczyć wartość równowagi Qe = Qs = Qd, podstawiamy wyznaczoną cenę równowagi rynkowej do równania popytu (można podstawić do równani podaży):

Qe = Qd = 100 - 3 x 17 = 100 - 51 = 49

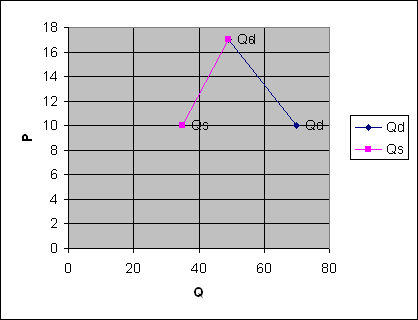
W ten sposób wyznaczona została wartość równowagi rynkowej Qe = Qs = Qd = 49 oraz cena równowagi rynkowej Pe = 17

Ilustracja graficzna z pliku Excel.

	Qd=100-3P	Qs=15+2P
	DANE
	Qd	P	Qs	P
	49	17	49	17
	70	10	35	10

b)

Qd = 40 - 8P

Qs = -8 +3P

W celu wyznaczenia punktu równowagi rynkowej rozwiązujemy układ równań złożony z funkcji popytu i podaży:

Qd = 40 - 8P

Qs = -8 +3P

Układ ten rozwiązujemy eliminując równania i zmienne przez podstawienie.

Pamiętając o warunku równowagi przyjmujemy, że Qe = Qs = Qd i podstawiamy pierwsze równanie do drugiego. Otrzymujemy w ten sposób jedno równanie z jedną zmienną:

40 - 8P = -8 +3P

Z tego równania wyznaczamy cenę równowagi rynkowej:

40 + 8 = 8P + 3P

48 = 11P

P = 48/11

P = 4,36

Zatem cena równowagi rynkowej Pe wynosi 4,36

Aby obliczyć wartość równowagi Qe = Qs = Qd, podstawiamy wyznaczoną cenę równowagi rynkowej do równania popytu (można podstawić do równani podaży):

Qe = Qd = 40 - 8 x 4,36 = 40 - 34,88 = 5,12

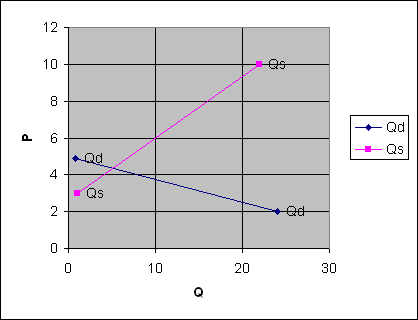
W ten sposób wyznaczona została wartość równowagi rynkowej Qe = Qs = Qd = 5,12 oraz cena równowagi rynkowej Pe = 4,36

Ilustracja graficzna z pliku Excel.

	Qd=40-8P	Qs=-8+3P
	DANE
	Qd	P	Qs	P
	24	2	1	3
	0,8	4,9	22	10

c)

Qd + 5 + 7P = 0

Qs + 11 + 4P = 0

Dokonujemy przekształceń obu równań w celu uzyskania klasycznej formy liniowej

(y= ax + b)

Zatem:

Qd - 20 + 4P = 0

Qs + 5 - 2P = 0

Qd = -4P + 20

Qs = 2P - 5

W celu wyznaczenia punktu równowagi rynkowej rozwiązujemy układ równań złożony z funkcji popytu i podaży:

Qd = -4P + 20

Qs = 2P - 5

Układ ten rozwiązujemy eliminując równania i zmienne przez podstawienie.

Pamiętając o warunku równowagi przyjmujemy, że Qe = Qs = Qd i podstawiamy pierwsze równanie do drugiego. Otrzymujemy w ten sposób jedno równanie z jedną zmienną:

-4P + 20 = 2P - 5

Z tego równania wyznaczamy cenę równowagi rynkowej:

20 + 5 = 4P + 2P

25 = 6P

P = 25/6

P = 4,16

Zatem cena równowagi rynkowej Pe wynosi 4,16

Aby obliczyć wartość równowagi Qe = Qs = Qd, podstawiamy wyznaczoną cenę równowagi rynkowej do równania popytu (można podstawić do równani podaży):

Qe = Qd = -4 x 4,16 + 20 = -16,64 + 20 = 3,36

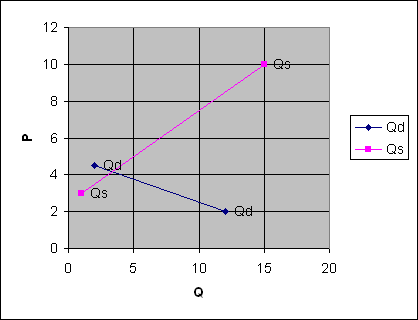
W ten sposób wyznaczona została wartość równowagi rynkowej Qe = Qs = Qd = 3,36 oraz cena równowagi rynkowej Pe = 4,16

Ilustracja graficzna z pliku Excel.

	Qd=-4P+20	Qs=2P-5
	DANE
	Qd	P	Qs	P
	12	2	1	3
	2	4,5	15	10

ZAD. 2

Dla podanych poniżej funkcji popytu, ceny równowagi i wielkości podaży w punkcie równowagi, wyznacz nadwyżkę konsumenta.

p = 250 - 0,2 q² + 0,1q

Q₀ = 10

P₀ = 200

Aby wyznaczyć nadwyżki konsumenta musimy podstawić do wzoru funkcję popytu i punkt i punkt równowagi:

CS = ¹⁰₀∫ (250 - 0,2 q² + 0,1 q - 200)dq

Rozwiązujemy całkę oznaczoną:

CS = ¹⁰₀∫ (250 - 0,2 q² + 0,1 q - 200)dq

CS = ¹⁰₀∫ (50- 0,2 q² + 0,1 q)dq

CS = (50q - 0,2 q³ / 2+ 0,1 q² / 1)¹⁰₀

CS = (50q - 0,1 q³ + 0,1 q² )¹⁰₀

Po podstawieniu za q wartości 10 i 0 otrzymamy:

CS = (50 x 10 - 0,1 x 10³ + 0,1 x 10²) - (50 x 0 - 0,1 x 0³ + 0,1 x 0) = (500 - 100 + 10) - (0) = = 410

Całkowita korzyść finansowa jaką osiągną konsumenci, którzy byliby skłonni zakupić dane dobro po cenie wyższej niż cena równowagi rynkowej P₀ = 200 wyniesie 410.

ZAD. 3

Mając daną funkcję popytu Q_d=100 - 2P - 2P², wyznacz funkcję elastyczności cenowej popytu. Oblicz punktowy współczynnik elastyczności cenowej popytu dla poziomów ceny:

P₁ = 2 i P₂ = 4. Zinterpretuj otrzymane wskaźniki elastyczności.

ROZWIĄZANIE:

E_PD = [ (100 - 2P - 2P²)^` x P ] / 100 - 2P - 2P² = [ (-2 - 4P) x P ] / 100 - 2P - 2P² =

= (-2P - 4P²) / 100 - 2P - 2P²

Elastyczność punktowa dla P₁ = 2:

E_P=2 = (-2 x 2 - 4 x 2²) / (100 - 2 x 2 - 2 x 2²) = (-4 - 4 x 4) / (100 - 4 - 2 x 4) =

= (-4 - 16) / (100 - 4 - 8) = - 20 / 88 = -0,227

E_P=2 = (-) 0,227 → 0 < E < 1 → popyt nieelastyczny

Elastyczność punktowa dla P₂ = 4:

E_P=4 = (-2 x 4 - 4 x 4²) / (100 - 2 x 4 - 2 x 4²) = (-8 - 4 x 16) / (100 - 8 - 2 x 16) =

= (-8 - 64) / (100 - 8 - 32) = - 72 / 60 = - 1,2

E_P=2 = (-) 1,2 → E > 1 → popyt elastyczny

---