1

Wykład 5

5.1 Przemiany gazu idealnego

5.2 Makroskopowe własności materii

5.3 Analiza procesów energetycznych w układach otwartych

5.4 Bilans energii i konwencja dotycząca znaku energii

5.5 Analiza układu otwartego – objętość kontrolna

2

5.1 Przemiany gazu idealnego

Zmiana stanu gazu idealnego może odbywać się przy
różnych warunkach narzuconych na podstawowe
parametry opisujące stan gazu. Ogólną przemianę gazu
przy zmianie przynajmniej dwóch parametrów opisuje
przemiana politropowa.

C

v

p

C

const

pv

ln

ln

ln















(5.26)

Istnieje kilka dobrze znanych przemian gazu idealnego,
tóre tutaj przytoczymy.

1. Przemiana izotermiczna, T=const,



=1.0

2. Przemiana izobaryczna, p=const,



=0

3

3. Przemiana izochoryczna v=const



=±

4. Przemiana adiabatyczna Q=0



=c

p

/c

v

5. Przemiana politropowa



dowolne

Dla gazu idealnego pV = n



T.

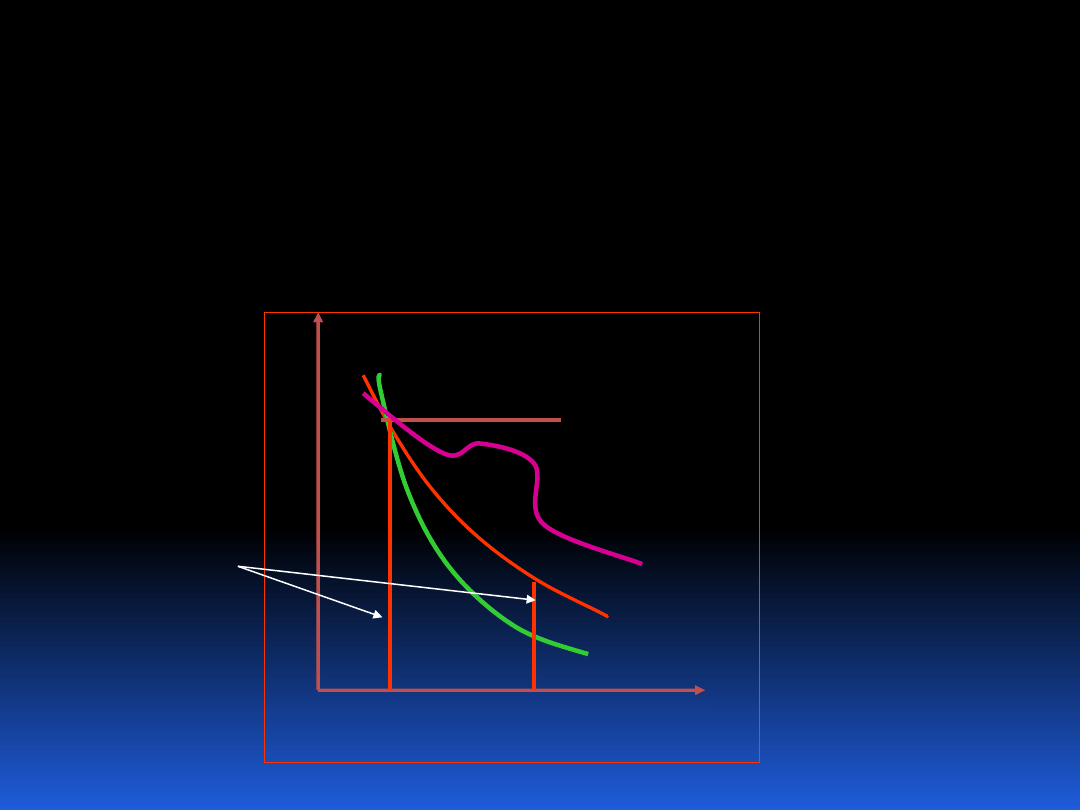
p

V

V

1

V

2

izobara

izoterma

adiabata

ogólna

izochora

4

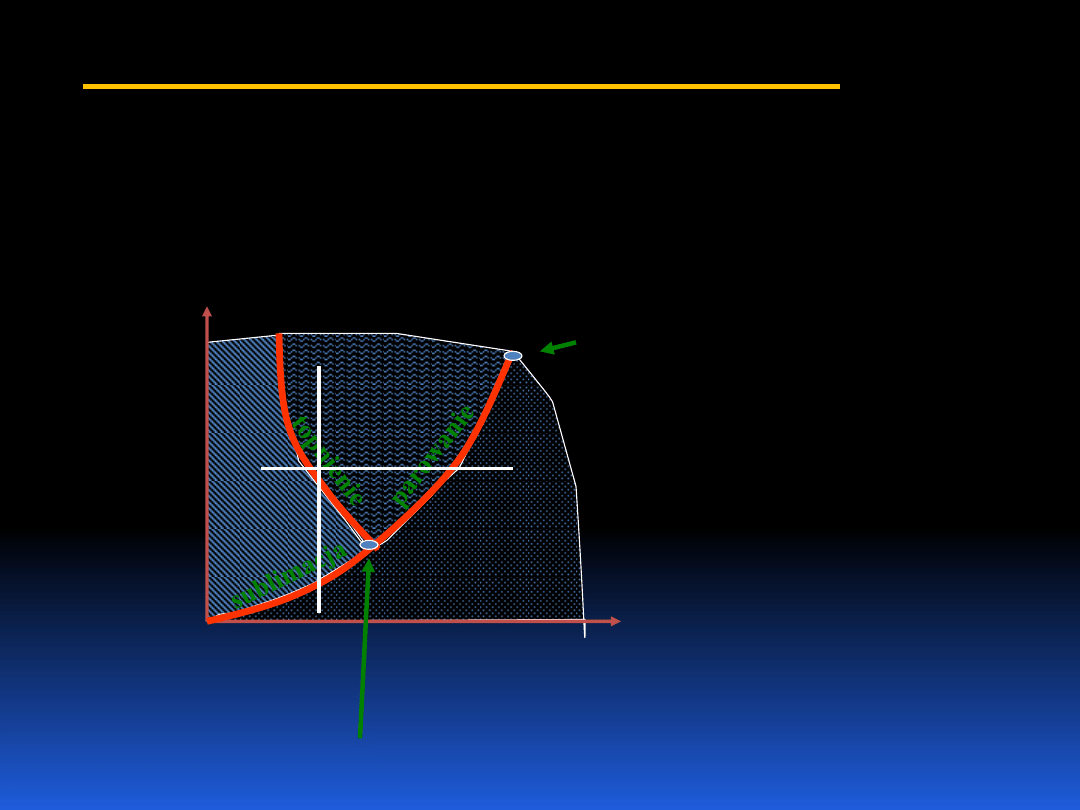
5.2 Makroskopowe własności materii

Własności materii zmieniają się, jeśli zmienimy V, p i T.
Substancje mogą istnieć w różnych fazach. Prześledźmy to
dla wody.

Linia AB pokazuje,
że woda może
równocześnie
znajdować się w
trzech fazach

T

p

Punkt potrójny

Punkt krytyczny

c. stałe

ciecz

para

gaz

A

B

5

Innymi własnościami makroskopowymi są możliwości zmiany
kształtów geometrycznych. Określają to odpowiednie
współczynniki.

Współczynnik objętościowej rozszerzalności temperaturowej
definiujemy jako:





p

T

T

p

V

V



















,

1



(5.1)

Z kolei izotermiczny współczynnik ściśliwości jest równy:





T

p

T

p

V

V





















,

1



(5.2)

6





V

T

T

V

p

p





















,

1



Warto zauważyć, że trzy wymienione współczynniki (



,



,



)

są ze sobą powiązane. Wynika to z zależności pomiędzy
pochodnymi cząstkowymi trzech zmiennych, pomiędzy
którymi istnieje zależność funkcyjna. Jeżeli zapiszemy w
oparciu o równanie stanu gazu doskonałego, że V zależy od
ciśnienia i temperatury w następujący sposób V(p,T), to
zachodzi zależność:

p

V

T

V

T

p

T

V

p





















  



























(5.3)

Można jeszcze zdefiniować współczynnik prężności



, który

ma następującą postać:

7

Mnożąc po prawej stronie równania licznik i mianownik
przez V, oraz obydwie strony równania przez p uzyskujemy
zależność:







p

1



Jeżeli znamy z pomiarów



i



, to nie musimy już mierzyć



,

tylko możemy je obliczyć z powyższego równania.

Dla gazu idealnego uzyskujemy
również:

p

T

1

1









Praca, którą należy wykonać ażeby sprężyć izotermicznie
gaz idealny wynosi;







dV

p

W

T

8

W oparciu o równanie :





2

1

2

2

2

2

1

p

p

V

dp

V

p

W

dp

V

dV

T

p

p

T

T

T

























T

p

T

p

V

V





















,

1



otrzymujemy że:

9

5.3. Analiza procesów energetycznych w
układach otwartych

4.1 Wstęp

Dotychczas omówiliśmy analityczną postać I zasady
termodynamiki, oraz podaliśmy przykłady wyliczania
termodynamicznych własności substancji.

W tym rozdziale rozszerzymy omawianie zagadnień
termodynamiki do układów, w których masa substancji może
przekraczać granice układu, czyli do układów otwartych.
Ażeby w pełni móc podać zależności opisujące procesy
zachodzące w takich układach, należy postępować według
pewnej procedury pozwalającej dokładnie scharakteryzować
układ i zachodzące procesy. Należy m.in. rozważyć
następujące problemy:

10

1. W jaki sposób jest opisany układ termodynamiczny, który mamy

analizować,

2. Jaką substancję zawiera rozważany układ i czy są znane własności

tej substancji,

3. Czy układ jest otwarty czy zamknięty,

4. W jaki sposób należy opisać zachodzący proces termodynamiczny,

5. Czy rozważany układ jest stacjonarny, czy zmienny w czasie.

Po znalezieniu odpowiedzi na te pytania, należy należy dokonać
analizy matematycznej problemu, która może przebiegać
następująco:

1. Naszkicowanie układu i określenie wlotu i wylotu masy i energii,
2. Matematyczne sformułowanie dostępnej informacji,
3. Przeprowadzenie bilansu energii,
4. Napisanie relacji opisujących proces,
5. Połączenie wszystkich informacji i otrzymanie wyniku.

Pytania:

11

5.4 Bilans energii i konwencja dotycząca
znaku energii

W rozdziale 2 omówiliśmy relacje energetyczne dotyczące
układów zamkniętych, czyli takich dla których nie zachodzi
transport masy poprzez granice układu. Przyjęliśmy
przyjmować za dodatnią energię dodaną do układu, a za
ujemną energię oddawaną przez układ, który rozważamy.

Nie możemy oczywiście zapomnieć o zasadzie zachowania
energii:

Energia, którą układ pobiera jest równa energii, którą
oddaje plus energia akumulowana w układzie.

Analiza układu opierać się będzie na relacjach poznanych
na poprzednim wykładzie.
Pamiętamy, że dla układów zamkniętych można zapisać
pierwszą zasadę termodynamiki jako:

12

dE

W

d

Q

d









(5.1)

Użyliśmy we wzorze różniczek, aby móc opisać każdy
możliwy proces.

d‘Q

d‘W

d’Q+d’W=dE

W układzie zamkniętym nie
ma przepływu masy.

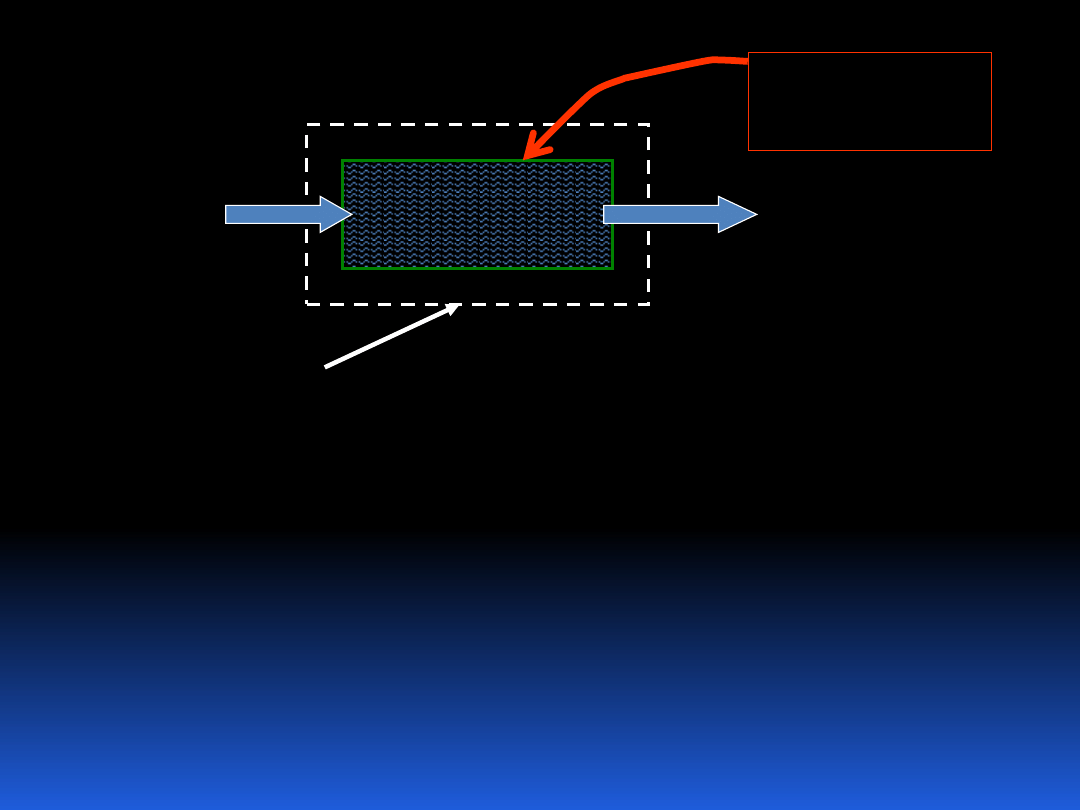
5.3 Układ otwarty

Przykładem termodynamicznego układu otwartego może
być grzejnik wody.

13

Strumień
Zimnej
wody

Ciepła
woda

Q dostarczane
ciepło

Granica
układu

Zdefiniowany układ nie bardzo zgadza się z nasza
poprzednią definicją układu termodynamicznego, jako
pewnej określonej wyodrębnionej ilości materii. Problem
ten rozwiążemy, stosując do analizy takich układów praw
dotyczących układów zamkniętych.
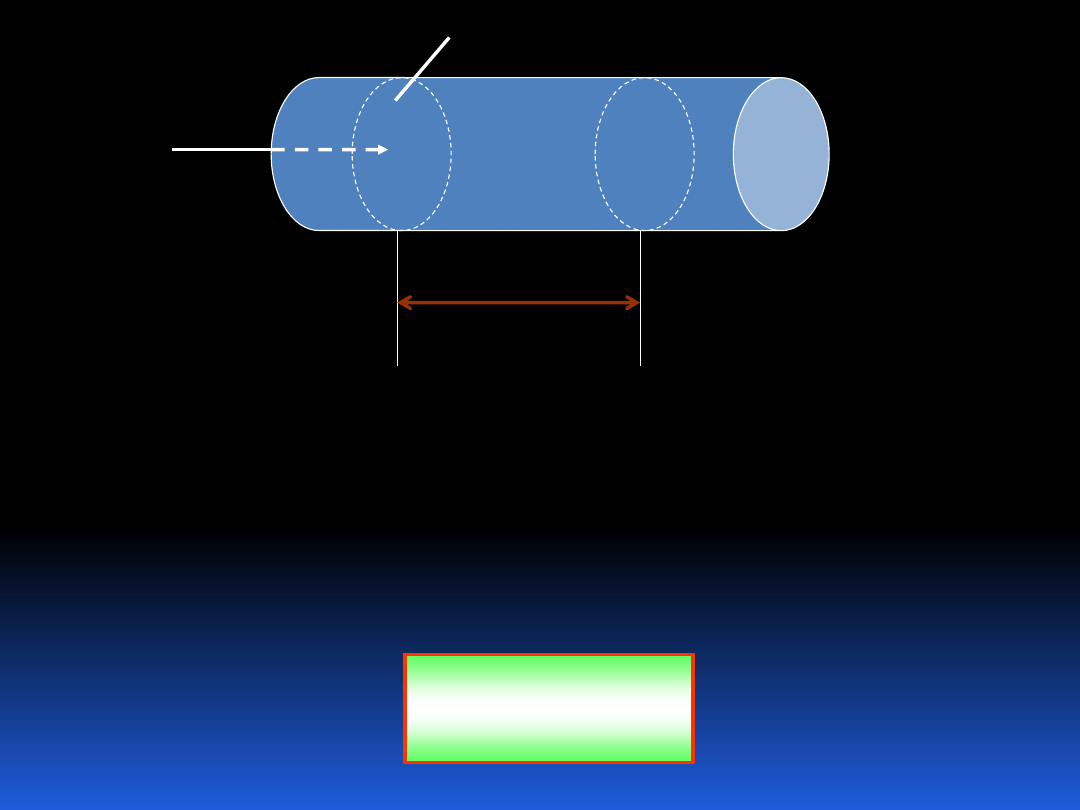
Zobaczmy w jaki sposób możemy opisać przepływ masy.
Można tego dokonać definiując jej strumień.

14

1

2

A

m





s

Jeśli przez V

=



s/dt oznaczymy średnią prędkość

przepływającej substancji, której gęstość oznaczymy przez



, wtedy strumień masy przepływającej na jednostkę czasu

przez układ wynosi:

m

AV





(5.2)

15

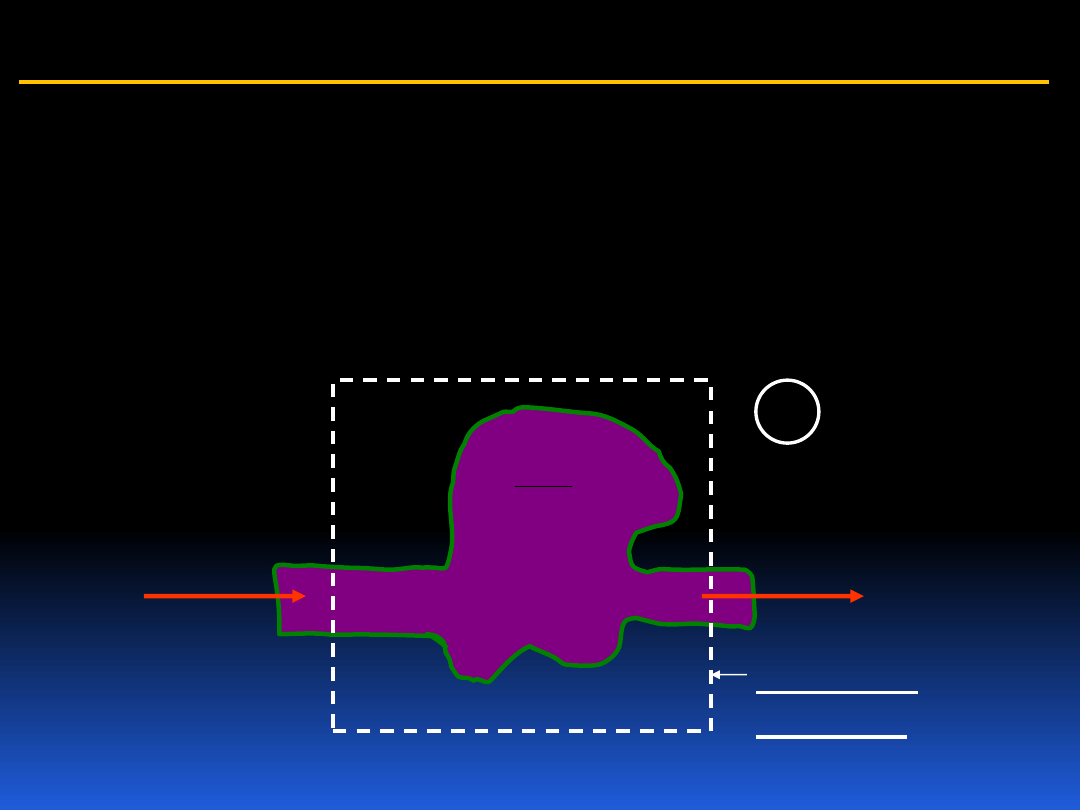
5.5 Analiza układu otwartego – objętość kontrolna

Aby móc analizować procesy termodynamiczne w układach
otwartych wprowadzamy pojęcie objętości kontrolnej. Jest
to pewna część przestrzeni, określona granicą, w której
obserwujemy przepływ masy i energii.















dt

dm



i

m



e

m



objętość

kontrolna

bilans
masy

A

16

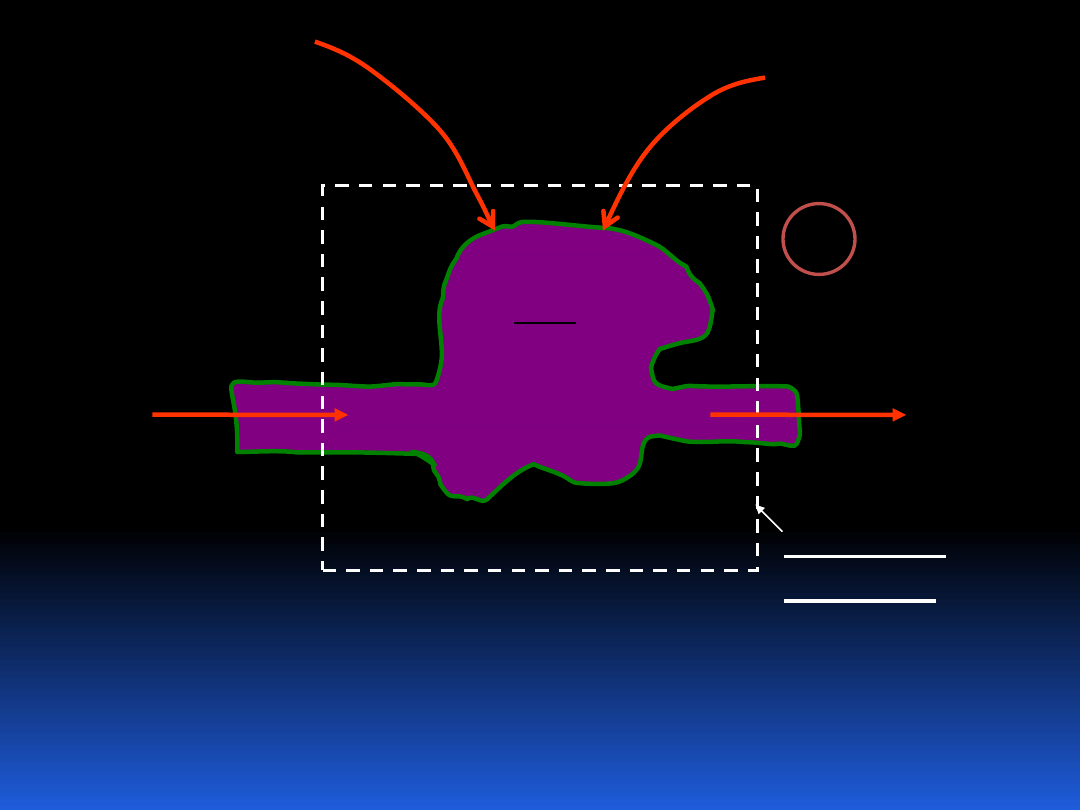
Literą e oznaczyliśmy ilość energii na jednostkę masy.















dt

dE



i

m

B



e

m



objętość

kontrolna

bilans
energii

e

i

e

e

dt

Q

d '

dt

W

d '

17

Masa wpływająca do objętości kontrolnej jest równa masie
wypływającej z niej plus wzrost masy wewnątrz objętości
kontrolnej.

e

dt

dm

i

m

m























(5.3)

Jest oczywiste, że nasz układ może mieć wiele wlotów i
wylotów. Wtedy równanie (4.3) przyjmuje postać:

























e

i

e

dt

dm

i

m

m



(5.4)

W celu analizy bilansu energii w całym obszarze kontrolnym,
rozważmy ustaloną masę, która porusza się przez objętość
kontrolną.
Odpowiada to zachowaniu się układu zamkniętego, w którym
następuje ruch masy przez objętość kontrolną.

18

Układ ten może być poddany ciśnieniu otoczenia. Może
nastąpić transfer ciepła przez granicę układu, mogą na niego
działać różne siły wykonujące pracę.
Energia wewnętrzna układy zamkniętego może zmieniać się
na wskutek ruchu z jednego miejsca do drugiego, jak również
na wskutek zmiany prędkości.

Niezależnie od obserwowanych zjawisk możemy zastosować
zasadę zachowania energii. Całkowity przepływ masy do i z
objętości kontrolnej można rozważyć jako ciąg elementów
dm, czyli małych zamkniętych układów termodynamicznych.
Możemy uważać, że strumień masy przepływający przez
układ transportuje energię wewnętrzną przez granice naszego
układu.

19

Transport energii wewnętrznej do objętości kontrolnej +
ciepło dodane do objętości kontrolnej, + praca wykonana na
wszystkich elementach w czasie ich ruchu przez układ,
są równe wzrostowi energii wewnętrznej wewnątrz objętości
kontrolnej + transport energii wewnętrznej z objętości
kontrolnej.

Analityczny zapis jest następujący:

e

dt

dE

dt

W

d

dt

Q

d

i

E

E



























'

'

(5.5)

Gdzie E

i

i E

e

oznaczają transport energii wewnętrznej na

jednostkę czasu odpowiednio na wlocie i wylocie układu.
Możemy wielkości te wyrazić następująco:

.

.

Dla takiego układu możemy sformułować zasadę zachowania
energii następująco:

20

e

e

i

i

e

m

e

e

m

i

E

E













(5.6)

Równanie (5.6) można stosować do analizy układów otwartych.
Można jednak wyrazić inaczej człon odpowiadający pracy.
Aby masa przepływała przez układ potrzebna jest siła. Siła ta jest
dana przez ciśnienie w układzie.
Element masy o objętości A ·



s ażeby być przetransportowany

do lub z objętości kontrolnej musi być poddany działaniu siły p·A
na drodze



s , przy czym niezależnie od wielkości masy



s=V/A.

Praca potrzebna na przepchanie masy do lub z objętości
kontrolnej jest równa:

V

p

A

V

A

p

s

F

ds

F

W























(5.7)

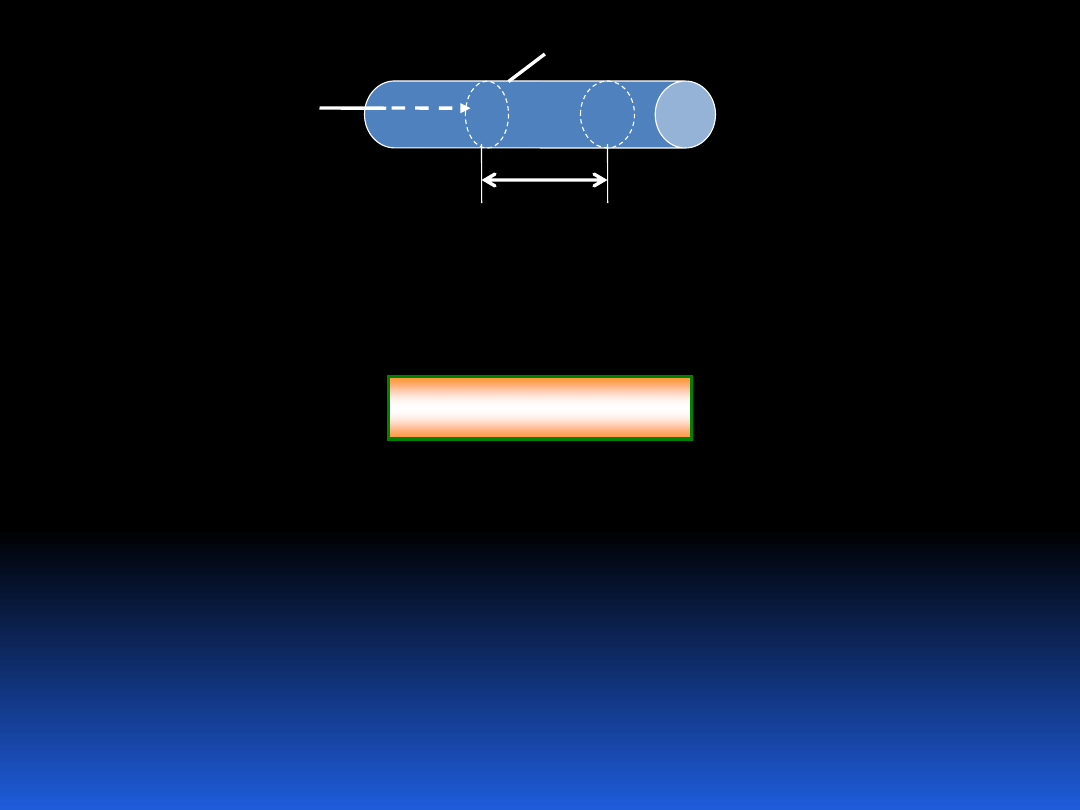
21

1

2

m





s

A

Wypadkowa praca wykonana na układzie przy przesunięciu
masy z punktu 1 do punktu 2 wynosi

2

2

1

1

V

p

V

p

W

wyp





p

1

V

1

jest pracą wykonaną na objętości przy wprowadzaniu

jej w objętość kontrolną, a p

2

V

2

odpowiednio przy

wyprowadzaniu jej z objętości kontrolnej. Różnica jest równa
wypadkowej pracy dodanej.

pV jest pracą strumienia substancji i należy tą wielkość
rozpatrywać oddzielnie od pracy wprowadzonej z zewnątrz.

22

Równanie energetyczne przyjmie więc postać:

)

(

'

'

)

(

e

e

e

e

zew

i

i

i

i

v

p

e

m

dt

dE

dt

W

d

dt

Q

d

v

p

e

m































(5.8)

Przypominam, że v

i,e

oznaczają objętość jednostki masy. W

zew

jest

pracą dostarczoną objętości kontrolnej przez siły zewnętrzne.

Równanie (5.8) przedstawia ogólny bilans energii dla układu
otwartego.

W przypadku, kiedy rozważany układ otwarty zachowuje się
jak stan stacjonarny, tzn. że nie ma w objętości kontrolnej
zmiany w czasie, czyli

0

0

dE

dm

i

dt

dt

































23

Wtedy m

i

= m

e

i równanie (5.8) przechodzi w:





)

(

)

(

'

'

i

i

i

e

e

e

zew

v

p

e

v

p

e

m

dt

W

d

dt

Q

d













(5.9)

Ażeby móc ostatecznie sformułować bilans energii dla układu
otwartego, przypomnijmy sobie od jakich wielkości zależy
energia wewnętrzna r.(3.13), (E=U+E

k

+E

p

+E

chem

+ .....) oraz

definicję entalpii r.(3.18) (h=u+pv).

Entalpia jest własnością układu, gdyż zależy tylko od wielkości
stanowiących własność układu. Ma ona fizyczne znaczenie w
zastosowaniu do układu otwartego, które nie jest już ważne
dla układu zamkniętego. A to dlatego, że iloczyn pv w układzie
zamkniętym nie stanowi pracy strumienia substancji.

.

.

24

Wprowadzając do bilansu energii (r.(5.8)) entalpię i
zakładając, że układ otwarty może mieć więcej wlotów i
wylotów, możemy zasadę zachowania zapisać następująco:

...)

(

'

'

...)

(









































e

e

i

i

chem

k

e

e

e

zew

chem

k

i

i

i

E

E

h

m

dt

dE

dt

W

d

dt

Q

d

E

E

h

m



(5.10)

Równanie to jest dość skomplikowane, ale w rozważaniach
praktycznych okazuje się, że można go jeszcze uprościć. Np.
dla gazu idealnego, czy układu woda-para wodna można
zaniedbać energię chemiczną.

25

1000J/kg = 1/2v

2

v=44.7 m/s.

Jest to prędkość znacznie większa niż w większości
rozważanych przypadków (nie biorąc oczywiście pod
uwagę turbiny gazowej, czy silnika odrzutowego) takich
jak strumień wody czy powietrza, pary w rurociągu, czy
freonu w chłodnicy.

Prędkości są zwykle tak małe, że można zaniedbać energię
kinetyczną w porównaniu z entalpią czy energią
wewnętrzną.

Oceńmy rolę energii kinetycznej.
Policzmy jaka prędkość jest potrzebna aby uzyskać
energię kinetyczną 1kJ/1kg.