1

Wykład 8

8.1 Cykle termodynamiczne maszyn cieplnych

8.2 Nierówność Clausiusa

8.3 Makroskopowa definicja entropii oraz zasada wzrostu
entropii

8.4 Entropia dla czystej substancji

8.6 Cykl Carnota

8.5 Entropia dla gazu doskonałego

8.7 Energia dostępna i niedostępna

8.8 II zasada termodynamiki dla układu otwartego

8.9 Mikroskopowa interpretacja entropii

2

8.1.1 Temperatura termodynamiczna

8.1 Cykle termodynamiczne maszyn cieplnych

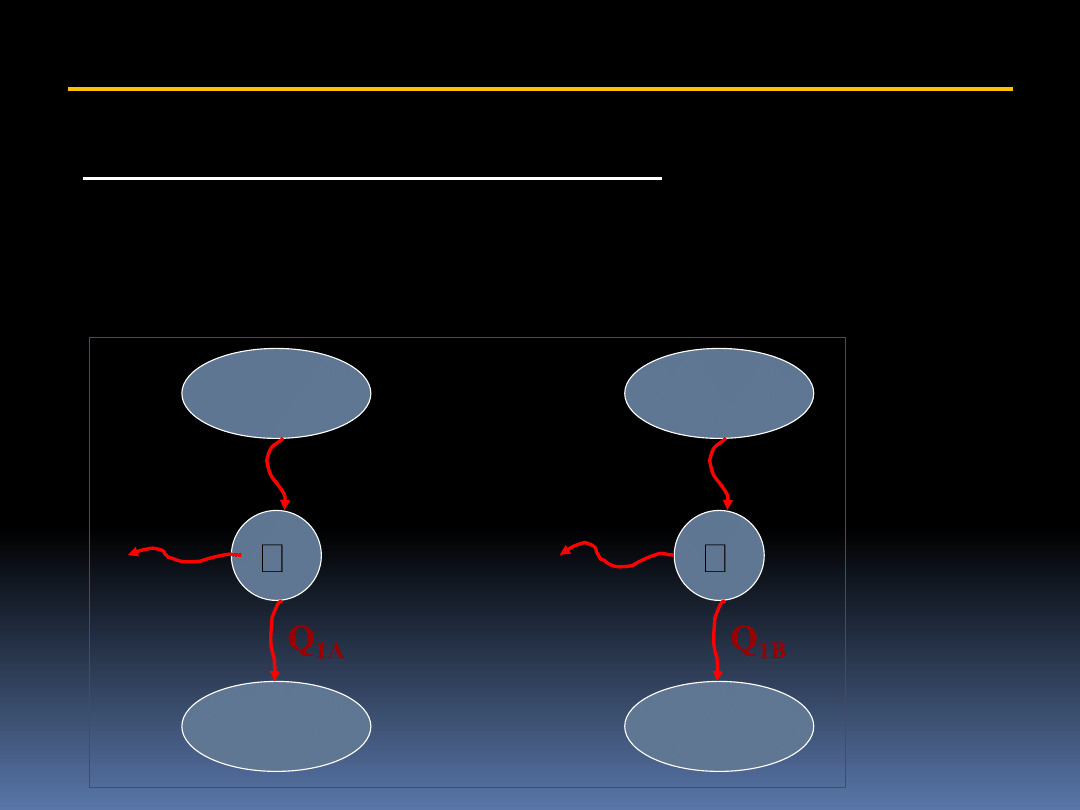
Załóżmy, że mamy do dyspozycji dwie dwie odwracalne
maszyny cieplne pracujące cyklicznie:

T

2

T

1

Q

2A

T

2

T

1

Q

2B

W

A

W

B





3



t

= =

energia użyteczna

energia włożona

uzyskana praca

zużyte ciepło

W rozważanym przypadku będzie to:

2

Q

W

t





Cykle A i B mogą być skonstruowane różnie. Załóżmy, że
wydajność cyklu A jest większa od wydajności cyklu B, oraz
że
Q

2A

= Q

2B

Wtedy W

A

> W

B

i Q

1A

< Q

1B.

Ponieważ obydwie maszyny są odwracalne, maszynę B
można odwrócić i połączyć z maszyną A. Uzyskujemy wtedy
sytuację jaka jest przedstawiona na następnym rysunku.

Wydajność cieplna



t

cyklicznej maszyny cieplnej jest

zdefiniowana następująco:

4

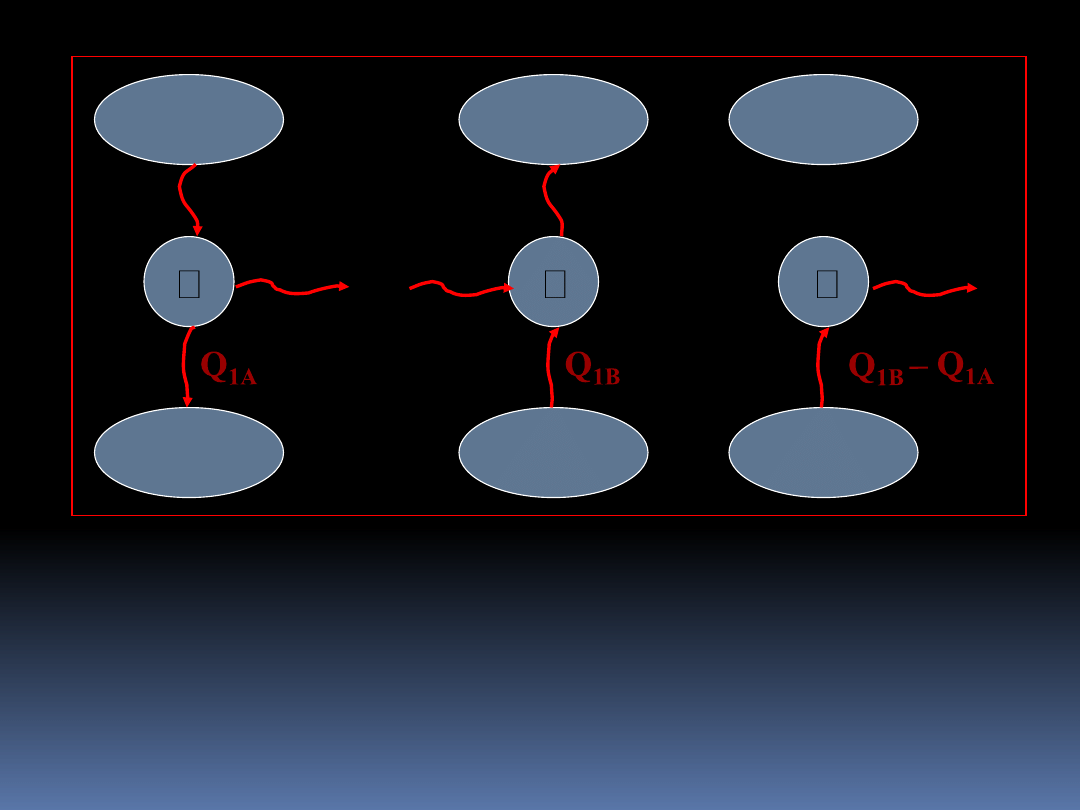
Widzimy, że otrzymalibyśmy cykl, w którym
W

A

- W

B

= Q

1B

– Q

1A

, jednak narusza sformułowanie

Kelvina-Plancka II zasady termodynamiki . Czyli założenie,
że



A

>



B

było niesłuszne.

T

2

T

1

Q

2A

W

A

W

B

T

2

T

1

Q

2B

+

W

A

- W

B

T

2

T

1

=







5

Można więc stwierdzić, że: „wszystkie odwracalne maszyny
cieplne pracujące pomiędzy tymi samymi temperaturami,
mają tą samą wydajność”.

2

1

2

1

2

2

1

Q

Q

Q

Q

Q

Q

W

t













Możemy również wyciągnąć wniosek, że Q

1

/Q

2

jest funkcją tych

temperatur. Mielibyśmy więc zależność:

)

,

(

2

1

2

1

T

T

f

Q

Q



Można pokazać, że,

)

(

)

(

2

1

2

1

T

F

T

F

Q

Q



Gdzie F jest pewną nową funkcją.

6

Zależność ta

może być spełniona przez wiele funkcji F.

Kelvin zaproponował, aby przyjąć najprostszą postać tej
funkcji, czyli

2

1

2

1

T

T

Q

Q



i równocześnie uznać to równanie za definicję bezwzględnej
temperatury termodynamicznej.

Wydajność odwracalnej maszyny cieplnej pracującej
pomiędzy dwoma zbiornikami ciepła o temperaturach T

N

–

niższej i T

W

– wyższej, jest dana przez wyrażenie;

W

N

t

T

T





1



7

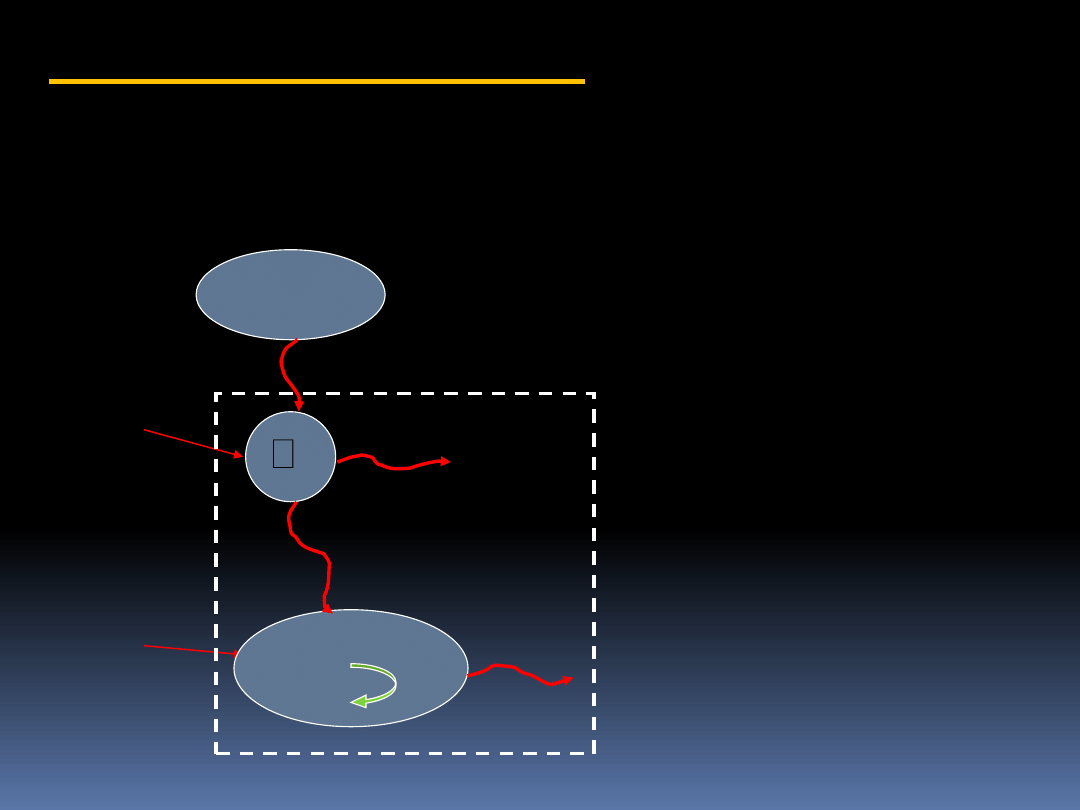
8.2 Nierówność Clausiusa

Rozważmy urządzenie, które obiera

ilość ciepła d’Q

Z

ze zbiornika o stałej

temperaturze T

Z

i transportuje to

ciepło do dwracalnej maszyny Z
produkującej pracę w ilości d’W

Z

.

Ciepło odrzucone przez
maszynę Z zasila cykliczną
maszynę

C produkującą

pracę w ilości d’W

C

.

Rozważając obydwie
maszyny jako jeden
system, całkowita praca
wykonana jest równa:

d’W =d’W

Z

+ d’W

C

Maszyna
cykliczna

Maszyna
odwracalna

T

Z

d’Q

Z

d’W

Z

d’Q

Z

d’W

C

C

T



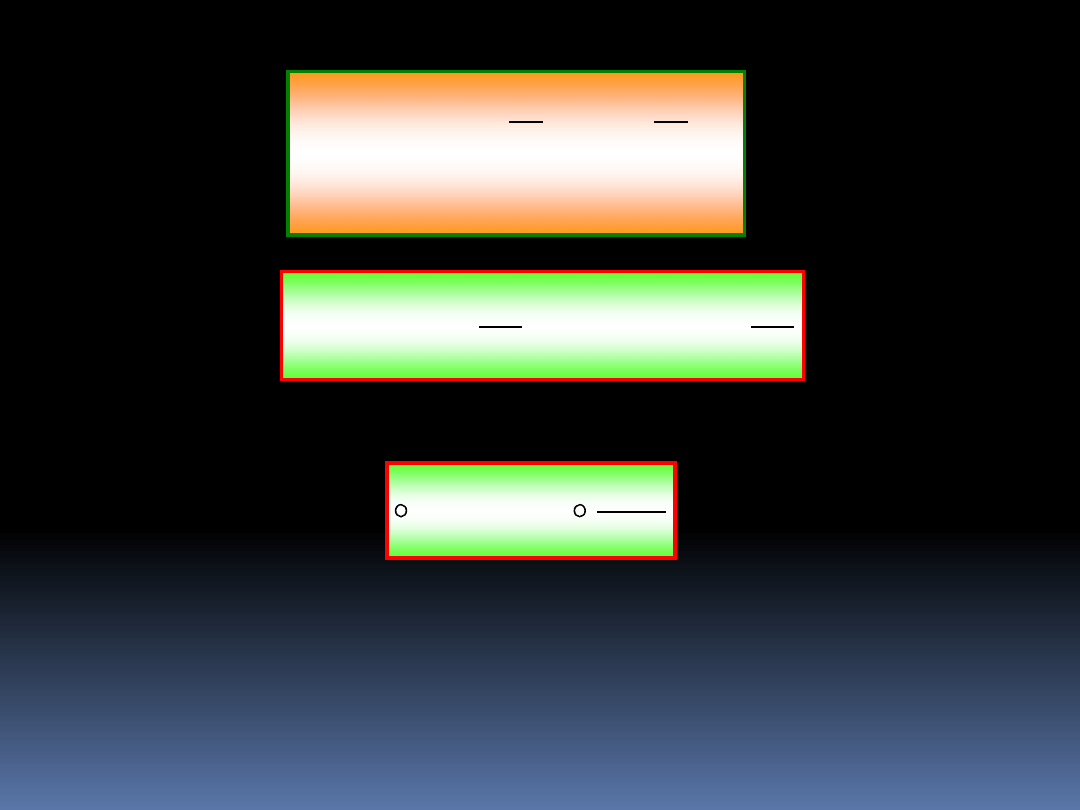
8

Q

d

W

d

T

T

Q

d

T

T

Q

d

W

d

C

Z

Z

Z

Z

'

'

)

1

(

'

)

1

(

'

'











czyli

T

T

Q

d

T

T

Q

d

W

d

Z

Z

'

)

1

1

(

'

'









Równanie to dla pełnego cyklu przyjmuje postać







T

Q

d

T

W

d

Z

'

'

Urządzenie pokazane na rysunku nie może wykonać pracy,
gdyż proces jest sprzeczny ze sformułowaniem Kelvina -
Plancka II zasady termodynamiki.
Urządzenie to może pracować tylko z cyklicznym wkładem
pracy i cyklicznym przekazywaniem ciepła do zbiornika.

W oparciu o wydajność odwracalnego silnika Z, możemy
napisać:

9

Matematycznie oznacza to





0

'W

d

gdzie d’W jest wynikową pracą. Można również
napisać, że

0

'





T

Q

d

Ta ostatnia nierówność jest nazywana nierównością
Clausiusa.

Do tej pory nie braliśmy pod uwagę faktu, że silnik C może
być odwracalny. Załóżmy, że tak jest, oraz, że





0

'W

d

10





0

'W

d

Jest to niemożliwe, gdyż stworzylibyśmy perpetuum mobile
II rodzaju. Wynika stąd, że dla procesów odwracalnych w
równaniu musi obowiązywać równość, czyli

0

)

'

(





odwr

T

Q

d

8.3 Makroskopowa definicja entropii oraz
zasada wzrostu entropii

Wyrażenie pod całką musi być różniczką zupełną
pewnej funkcji stanu. Możemy więc napisać

odwr

T

Q

d

dS

)

'

(



Jeżeli C jest silnikiem odwracalnym, to otrzymujemy,

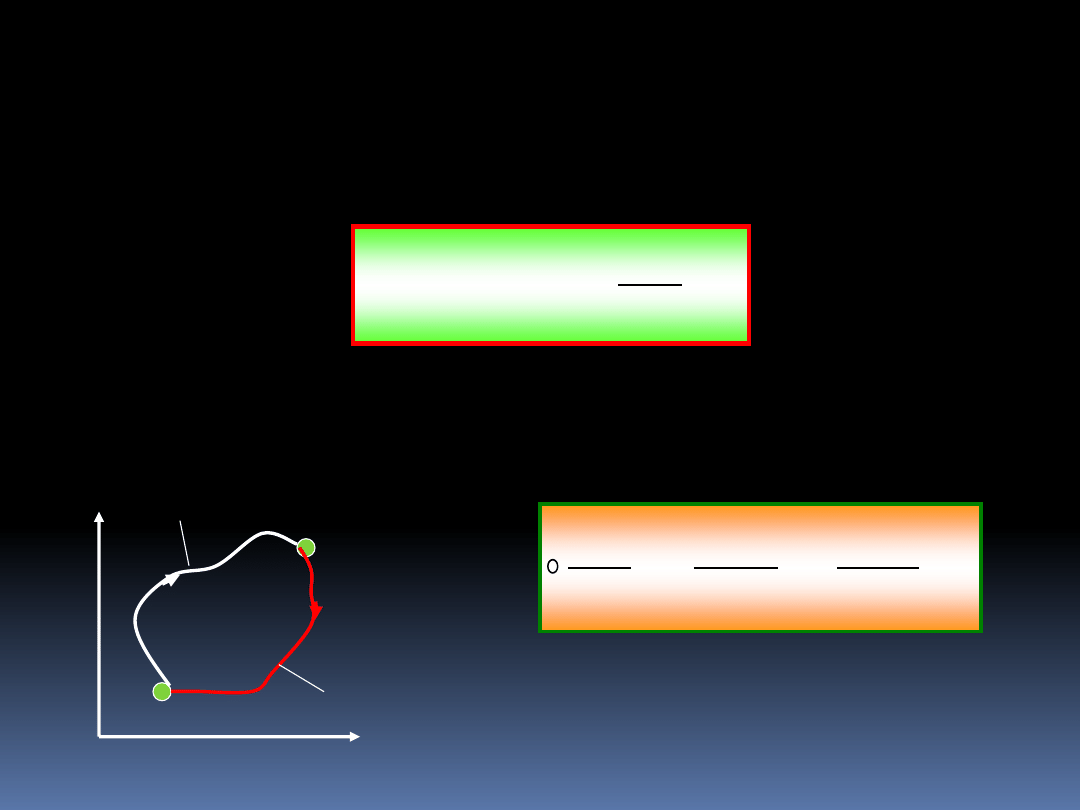
11

Funkcję S w ostatnim równaniu nazywamy entropią.
Równanie to przedstawia makroskopową definicję entropii.
Entropia jest zdefiniowana tylko dla procesów
odwracalnych, a zmianę wartości entropii można policzyć z
zależności;

odwr

T

Q

d

S

S

S

)

'

(

2

1

1

2











Rozważmy dwa dowolne punkty stanu naszego układu.

Proces
Nieodwracalny

1

2

Proces
Odwracalny

Cykl=N+O

Zgodnie z równaniem

0

'

'

'

1

2

2

1













T

Q

d

T

Q

d

T

Q

d

O

N

Użyliśmy znaku nierówności,
gdyż cały cykl jest
nieodwracalny.

12

Wiedząc, że

2

1

2

1

'

S

S

T

Q

d

O







Możemy poprzednie równanie napisać jako;















2

1

1

2

2

1

2

1

'

lub

0

'

T

Q

d

S

S

S

S

T

Q

d

N

N

W ogólnym przypadku możemy
napisać;







2

1

1

2

'

T

Q

d

S

S

Znak nierówności jest ważny dla procesów nieodwracalnych, a
znak równości dla odwracalnych

13

Dla procesu adiabatycznego d’Q = 0, czyli S

2

– S

1

 0. Jeżeli

będzie to proces adiabatyczny odwracalny, zmiana entropii
będzie równa zero. Proces ten nazywamy procesem
izentropowym.

Można powiedzieć, że żaden proces rzeczywisty nie jest
odwracalny. Gdy proces jest nieodwracalny i adiabatyczny,
entropia musi wzrastać.
Dla układu izolowanego,

0



izol

S



W oparciu o równanie

możemy znaleźć, że dla
odwracalnego procesu
izotermicznego

S

T

Q

izoterm

odwr







W układzie współrzędnych T i S możemy przedstawić
adiabatyczny proces odwracalny i nieodwracalny.

odwr

T

Q

d

dS

)

'

(



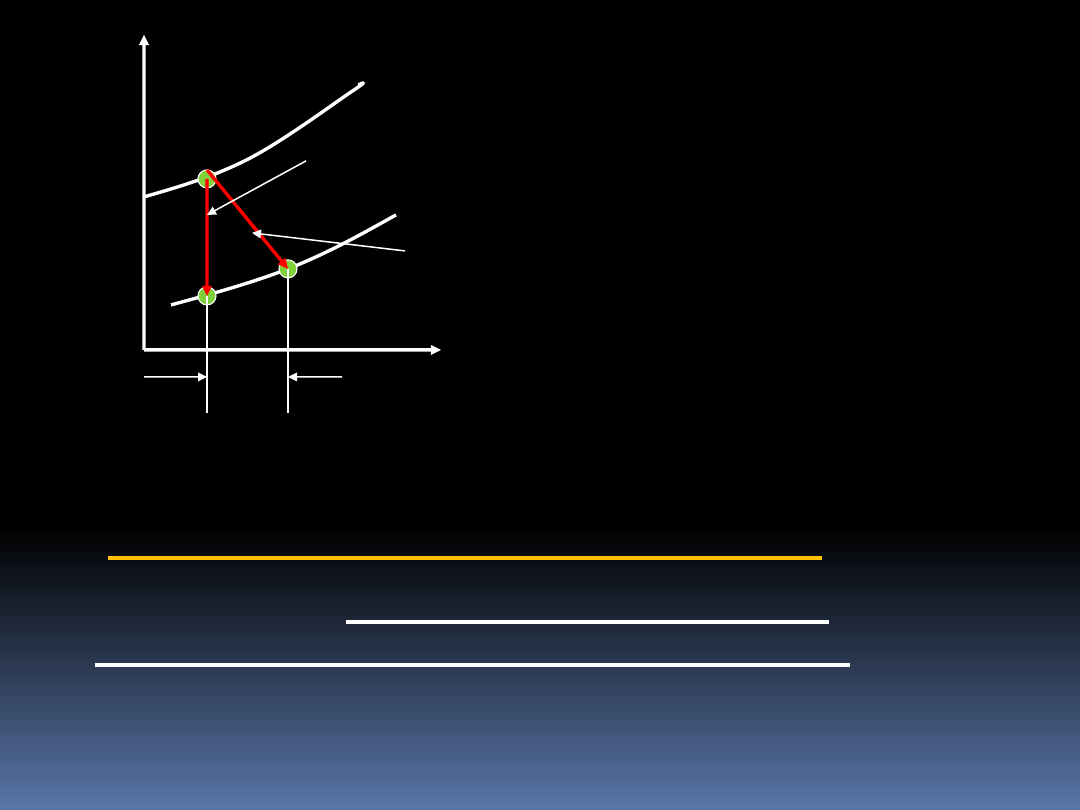
14

Pr. nieodwr.
adiab.

1

2

2’

T

S

Pr. odwracalny
adiab.



S

nieodwr.-

adiab.

Im większy jest wzrost entropii,
tym bardziej proces jest
nieodwracalny. Powodem
mniejszej lub większej
nieodwracalności procesów są
wszelkiego rodzaju tarcia, tak
samo jak mieszanie warzechą w
zupie.

8.4 Entropia dla czystej substancji

Pokazaliśmy, że entropia jest własnością układu
termodynamicznego i to własnością ekstensywną. Jest
taką samą własnością jak energia całkowita, wewnętrzna
i entalpia. Można ją liczyć z entropii właściwej.

15

s

m

S



Dla czystych substancji entropia może być stablicowana tak
jak entalpia, objętość właściwa, czy inna własność
termodynamiczna. Podaje się dwojakiego rodzaju wykresy,
zależność temperatury od entropii, czy zależność entalpii od
entropii. Ta ostatnia zależność nazywa się wykresem
Moliera.

8.5 Entropia dla gazu doskonałego

Opierając się na już wyprowadzonych zależnościach,

dT

c

dh

dT

c

du

p

V





Oraz faktu, że dla procesu odwracalnego d’Q=Tds i
przyjmując, że gaz idealny jest cieczą ściśliwą możemy
napisać:

16

ds

T

dv

p

du

Q

d







'

czyli

dv

T

p

T

du

ds





Korzystając z równania gazu doskonałego, mamy

v

R

T

p



czyli

v

dv

R

T

dT

c

ds

V





Dla c

V

= const otrzymujemy na zmianę entropii pomiędzy

dwoma stanami gazu idealnego wyrażenie

1

2

1

2

1

2

ln

ln

v

v

R

T

T

c

s

s

V







17

Równanie to można również napisać inaczej w oparciu o
zależności

p

dp

R

T

dT

c

ds

Tds

vdp

dh

Q

d

p











'

jako

2

1

2

1

1

2

ln

ln

p

p

R

T

T

c

s

s

p







W powyzszych rownaniach zmiana entropii jest liczona
między dwoma stanami układu termodynamicznego (p

1

,v

1

,T

1

)

i (p

2

,v

2

,T

2

). Ponieważ entropia jest funkcja stanu, jej zmiana

nie powinna zależeć od procesu.

18

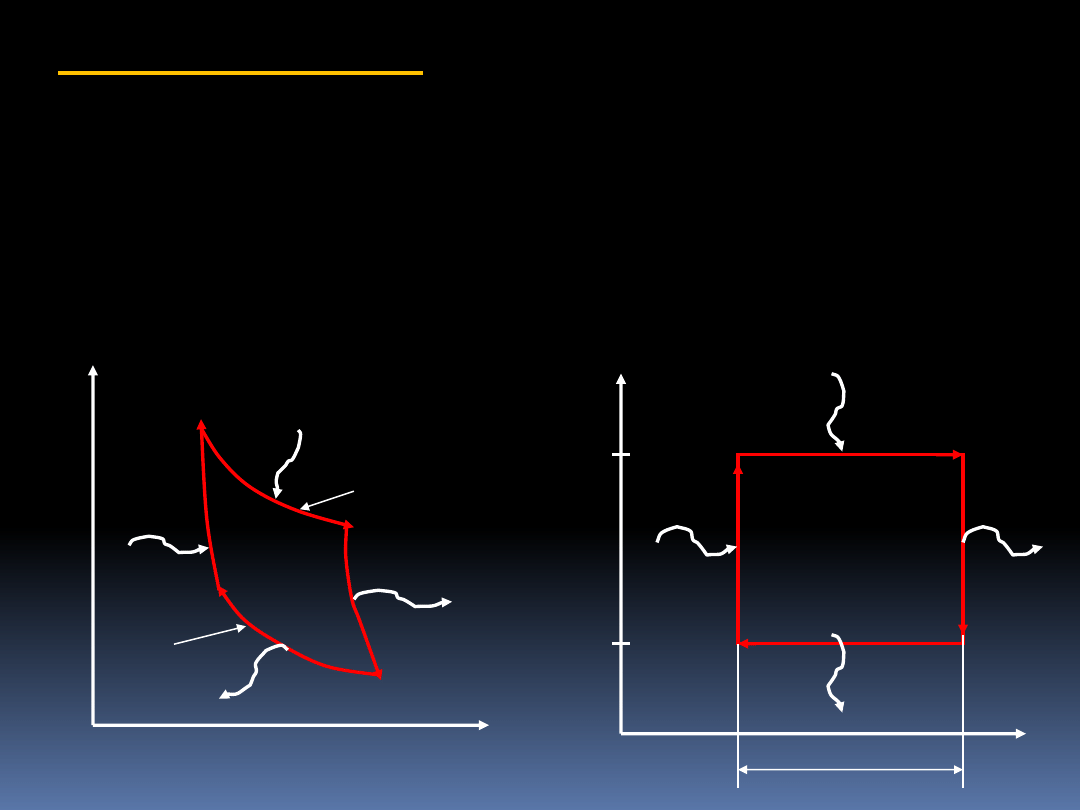
8.6 Cykl Carnota

Stwierdziliśmy do tej pory, że wydajności wszystkich cyklów
odwracalnych pracujących pomiędzy tymi samymi
temperaturami są takie same i dane odpowiednim rownaniem

.

Przykładem takiego cyklu jest cykl Carnota.

p

V

W

W

Q

W

Q

N

T

W

=const

T

N

=const

D

A

B

C

T

S

T

W

T

N

Q

W

Q

N

W

W



S

19

1. Odwracalna przemiana izotermiczna z pobraniem

ciepła

2. Odwracalna przemiana adiabatyczna z pracą

wykonana przez układ

3. Odwracalna przemiana izotermiczna z oddaniem

ciepła

4. Odwracalna przemiana adiabatyczna z praca

wykonana na układzie

W oparciu o diagram T-S znajdujemy,

S

T

Q

S

T

Q

N

N

W

W









Praca uzyskana jest równa:

S

T

T

Q

Q

W

N

W

N

W

netto



)

(









Na diagramie T-S praca wykonana jest równa powierzchni
prostokąta.

20

Zgodnie z definicją wydajności maszyny cieplnej,
otrzymujemy na wydajność cyklu Carnota wartość

W

N

W

N

W

W

netto

t

T

T

S

T

S

T

T

Q

W















1

)

(



Możemy podać ogólne stwierdzenie, że dla każdego cyklu
Odwracalnego wypadkowa praca jest równa powierzchni
zakreślonej na diagramie T-S.

8.7 Energia dostępna i niedostępna

Otrzymaliśmy wyrażenie na wydajność cyklicznej maszyny
cieplnej operującej w oparciu o dwa zbiorniki ciepła o
różnych temperaturach. Wydajność ta zależy od najniższej
dostępnej temperatury T

0

, która normalnie jest średnią

temperaturą atmosferyczną.

21

Praca jaką możemy uzyskać pobierając ciepło d’Q ze
zbiornika o temperaturze T jest równa:

Q

d

T

T

W

d

'

)

1

(

'

0





Energią dostępną dla danego ukłądu nazywamy część ciepła
dodaną do układu, która może zostać zamieniona w pracę
przez szereg odwracalnych maszyn pracujących pomiędzy
temperaturą układu a T

0

.

Q

d

T

T

W

'

)

1

(

0

max







Energia niedostępna jest równa różnicy pomiędzy
całkowitym ciepłem dodanym a uzyskaną pracą. Dla
przejścia ze stanu 1 do 2 zakładając, że ciepło jest oddane w
procesie odwracalnej maszyny, zachodzi;

22

)

(

'

)

1

(

1

2

0

max

2

1

0

2

1

0

max

S

S

T

Q

W

dS

T

Q

Q

d

T

T

W

odwr



















Praca niedostępna wynosi więc:

)

(

1

2

0

S

S

T

W

nied





8.8 II zasada termodynamiki dla układu
otwartego

Omawialiśmy I zasadę termodynamiki dla układów otwartych,
oraz poznaliśmy metody obliczania bilansów energii i ciepła.
Zajmijmy się analizą układu otwartego zawartego w pewnej
objętości kontrolnej z punktu widzenia II zasady
termodynamiki.

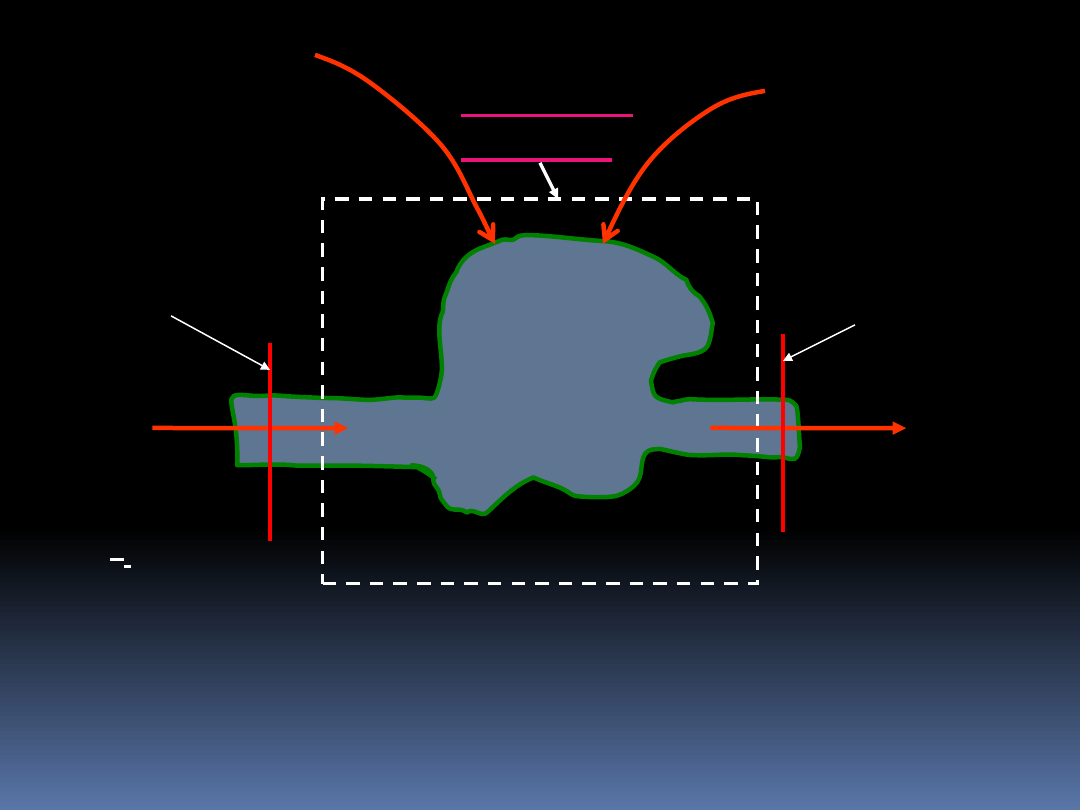
23



Objętość

kontrolna

e

i

e

e

dt

Q

d '

dt

W

d

zewn

'

m

i

h

i

s

i

m

e

h

e

s

e

wlot-input

wylot-exit

Ponieważ entropia jest funkcją stanu może być
transportowana tak jak entalpia czy energia wewnętrzna.
Ciepło i praca są dodawane do granicy objętości kontrolnej.

24

Entropia może wnikać do objętości kontrolnej przez transport
masy lub ciepła. Entropia wpływająca z transferem ciepła może
przenikać do objętości kontrolnej w różnych miejscach o różnej
temperaturze i możemy ją zapisać jako:

dt

Q

d

T

dt

dS

i

pow

i

'

1





T

i

odpowiada temperaturze powierzchni dla ciepła Q

i

.

Równocześnie wzrost entropii może następować na wskutek
pewnych procesów nieodwracalnych. Może istnieć wiele
strumieni wpływających i wypływających do objętości
kontrolnej. Dla krótkiego przedziału czasu produkcja
entropii będzie wynosiła;













































dt

dS

dt

Q

d

T

s

m

s

m

dt

dS

i

pow

i

i

in

i

e

out

e

wytw

'

1

25

Zgodnie z II zasadą termodynamiki

0















wytw

dt

dS

Pamiętamy że znak = odnosi się dla procesów odwracalnych, a
znak > dla procesów nieodwracalnych.
Dla stałego strumienia masy i stacjonarnego stanu naszego
układu zachodzi , wtedy





















e

i

m

m

dt

dS

oraz

0



dt

Q

d

T

s

m

s

m

i

i

in

i

e

out

e

'

1

















Dla procesu adiabatycznego i stałego strumienia masy

i

e

s

s



26

8.9 Mikroskopowa interpretacja entropii

Przy rozważaniu zjawisk mikroskopowych stwierdziliśmy, że
istnieje charakterystyczna funkcja stanu, która zachowuje się tak
jak makroskopowa entropia.

Stwierdziliśmy też, że w izolowanym układzie cząstki dążą do
rozkładu najbardziej prawdopodobnego, spośród wszystkich
możliwych stanów energetycznych. Pokazaliśmy również, że
odstępstwa parametrów cząstek od tych dla stanu najbardziej
prawdopodobnego są mało prawdopodobne. Jest to równoważne
stwierdzeniu, że entropia układu izolowanego dąży do swojej
maksymalnej wartości i jest wysoce mało prawdopodobne, by
zmniejszyła swą wartość, osiągnąwszy ją.

Mikroskopowa definicja entropii zawiera więc tą samą informację
co równanie -



S

izol

≥ 0, z wyjątkiem tego, że zasada wzrostu

entropii staje sie zachowaniem najbardziej prawdopodobnym.
Innym nastepstwem tego jest fakt, ze II zasada termodynamiki
staje sie stwierdzeniem tego co najbardziej prawodopodobne.