1

2. PRAKTYCZA REALIZACJA PRZEMIAY ADIABATYCZEJ

2.1 Wprowadzenie

Przemiana jest adiabatyczna, jeśli dla każdych dwóch stanów l, 2 leżących na tej prze-

mianie Q

1-2

= 0. Z tej definicji wynika, że aby zrealizować wyżej wymieniony proces, np.

ekspansję gazu w cylindrze z ruchomym tłokiem, to cylinder i tłok muszą być wykonane

z materiału będącego doskonałym izolatorem cieplnym.

Analogicznie, jeśli opróżnia się zbiornik napełniony wcześniej gazem (powietrzem)

przez otwarcie zaworu, to aby stan gazu w zbiorniku zmieniał się według adiabaty, ściany

zbiornika muszą być idealnie izolowane termicznie. Ponieważ nie ma doskonałej izolacji,

więc w praktyce możemy co najwyżej zrealizować adiabatę w przybliżeniu. Miarą tego przy-

bliżenia jest wskaźnik:

1

2

2

1

U

U

Q

Y

z

−

=

−

(1)

gdzie:

Q

z

l-2

- całkowita ilość ciepła (dodatnia lub ujemna) dostarczona do gazu w czasie ∆τ,

U

2

– U

1

 - całkowita zmiana energii wewnętrznej gazu przy przejściu od stanu 1 do stanu 2.

Jeśli Y = O, to oznacza, że zrealizowano adiabatę. W przeciwnym wypadku

w zależności od konkretnej wartości tego wskaźnika można mówić o adiabacie zrealizowanej

z dokładnością wynikającą z wartości Y.

Dla konkretnego procesu oszacowanie stopnia przybliżenia adiabaty wymaga więc

pomiaru wielkości występujących we wzorze (l). Nie jest to zadanie łatwe.

Problem w sposób istotny upraszcza się, jeśli należy zrealizować adiabatę dla gazu

spełniającego równanie Clapeyrona oraz warunek c

v

= const.

Wtedy bowiem adiabata jest politropą tzn. jej równanie w układzie współrzędnych

(p - υ) ma postać:

p υ

k

= idem

(2)

Wykładnik “k” (wykładnik adiabaty) jest związany z wielkościami c

v

i c

p

równaniem:

k = c

p

/ c

v

(3)

W układzie logarytmicznym równanie to przekształca się w prostą.

2.2 Cel doświadczenia

Celem doświadczenia jest:

• sprawdzić, czy adiabata gazu doskonałego jest politropą,
• sprawdzić, że dekompresja zbiornika ze sprężonym powietrzem jest procesem

(w przybliżeniu) adiabatycznym,

• oszacować dokładność realizacji adiabaty.

2

2.3 Opis doświadczenia.

1. Zbiorniki A i B o stałej objętości V należy napełnić powietrzem aż do uzyskania

nadciśnień odpowiednio ∆p

A1i

oraz

∆p

B1i

(np. wskazanych w arkuszu pomiarowym) w celu

uzyskania relacji:

p

A1i

> p

B1i

≥ p

o

(4)

gdzie p

o

– ciśnienie otoczenia,

p

A1i

= p

o

+ ∆p

A1i

oraz p

B1i

= p

o

+ ∆p

B1i

.

Temperatura gazu w zbiornikach ma być, po zakończeniu pompowania (należy pompować

powoli, a po napompowaniu odczekać aż ciśnienie w zbiorniku się ustabilizuje), równa

temperaturze otoczenia t

o

tzn.:

t

A1i

= t

B1i

= t

o

(5)

2. Należy na okres (około) 1 sekundy otworzyć zawór łączący zbiorniki A i B. Następuje

szybki przepływ powietrza, który kończy się gdy wyrównają się ciśnienia tzn.:

p

A2i

= p

B2i

= p

mi

> p

o

(6)

Temperatury osiągają wtedy wartości:

t

A2i

< t

o

, t

B2i

> t

o

(7)

7

3

Uwaga:

Ciśnienia p

m

nie mierzy się

ponieważ dla gazu doskonałego może być obliczone z wzoru:

2

1

1

B

A

m

p

p

p

+

=

Wyprowadzenie wzoru:
W przedziale czasu od otwarcia zaworu do jego zamknięcia nie jest wykonywana praca
zewnętrzna, a dopływy ciepła są znikome z powodu dużej szybkości procesu. Dlatego
można przyjąć że całkowita energia wewnętrzna układu nie zmienia się (w fazie
wyrównywania temperatur już tak nie jest ! )
Dla gazu doskonałego energia wewnętrzna dana jest wzorem:

0

1

U

k

pV

U

+

−

=

Wobec tego warunek stałości energii dla układu wyraża równanie:

1

1

1

1

2

2

1

1

−

+

−

=

−

+

−

k

V

p

k

V

p

k

V

p

k

V

p

B

A

B

A

Podstawiając p

A2

= p

B2

= p

m

otrzymuje się szukany wzór.

3. Po zamknięciu zaworu i należy odczekać aż temperatura powietrza w zbiornikach

ponownie osiągnie wartość

t

A3i

= t

B3i

= t

o

(8)

Wówczas można odczytać ciśnienia ∆p

A3i

i wyliczyć wartość p

A3i

:

p

A3i

> p

B3i

> p

o

(9)

Opisane wyżej czynności należy powtórzyć dla kilku różnych ciśnień p

Bi

i tej samej wartości

początkowej ciśnienia p

Ai

.

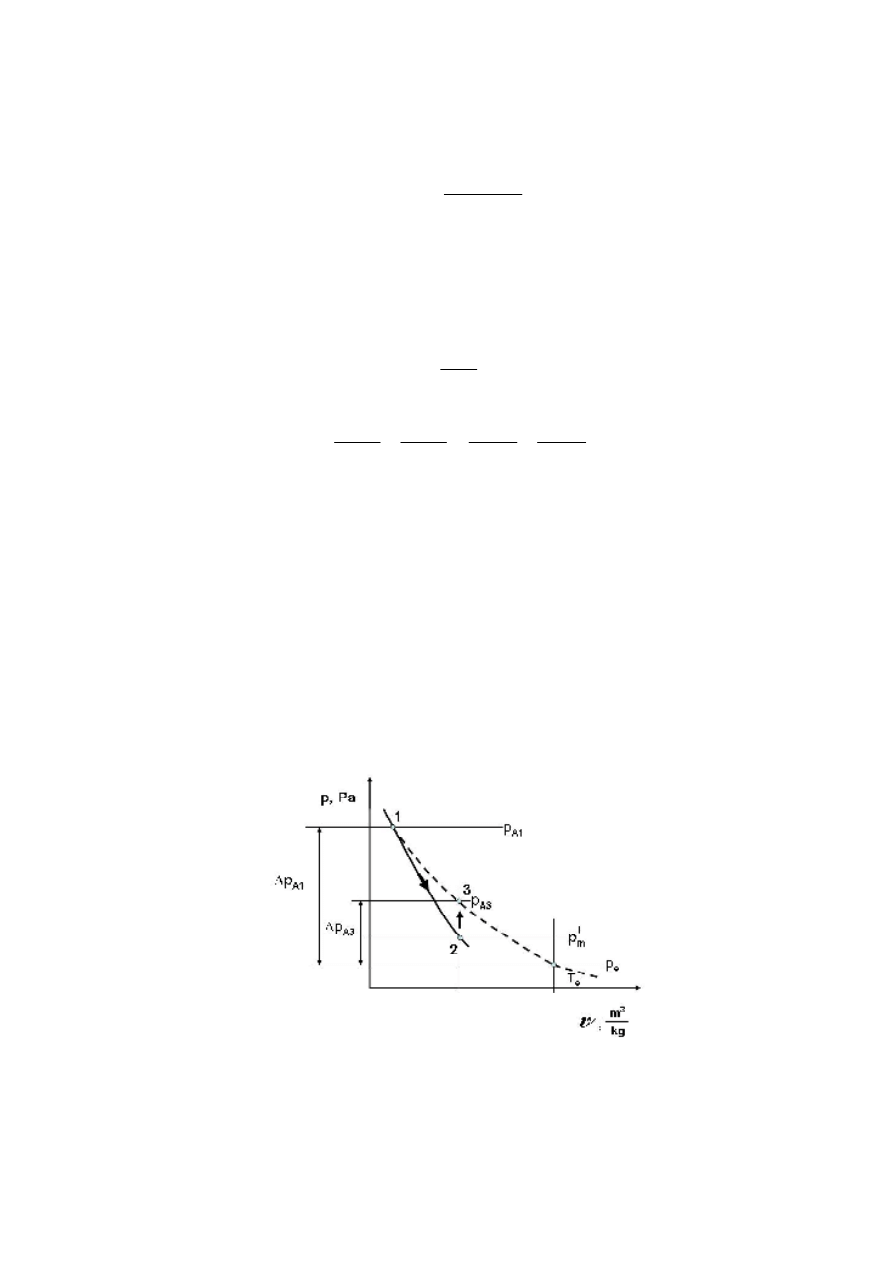
Rys. 2 Tak wygląda proces dekompresji w zbiorniku A przedstawiony w układzie (p - υ)

Obowiązują następujące zależności:

T

2

< T

o

mi

i

A

p

p

=

2

(i = 1, 2, ....,5)

T

3

= T

o

m

i

A

p

p

〉

3

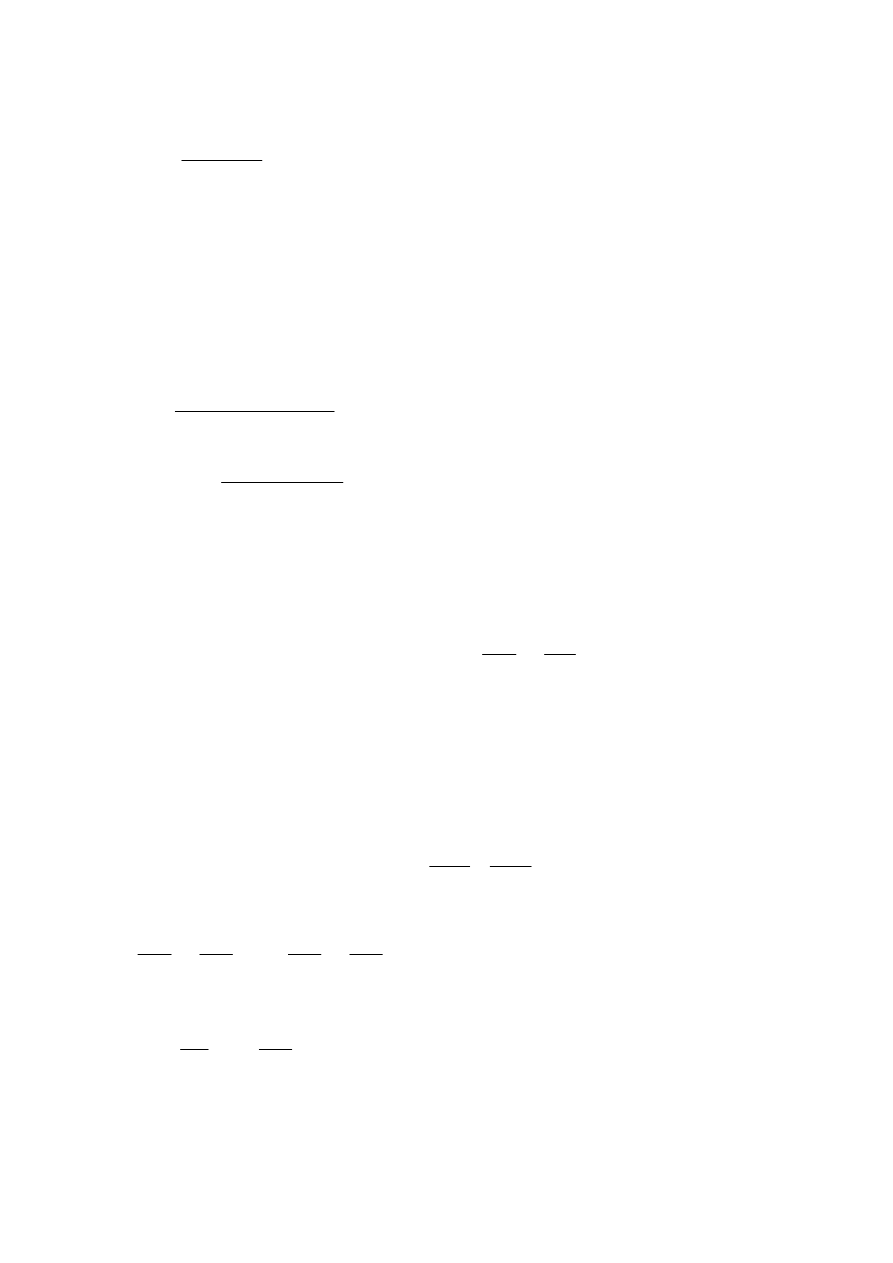
4

0

0

0

RT

p

=

υ

(R = 0,287 kJ/kg K)

2

1

1

i

B

i

A

mi

p

p

p

+

=

p

A1i

= p

o

+ (

∆

p )

A1i

i

B

i

B

p

p

p

1

0

1

)

(∆

+

=

1

1

)

(

)

(

A

i

A

p

p

∆

=

∆

- stałe np. 800 mm H

2

0 ( to jest ważne aby być stale na tej samej

politropie).

i

B

p

1

)

(∆

- 0, 150, 300, 450, 600, mm H

2

0

2

)

(

)

(

1

1

i

B

o

A

o

mi

p

p

p

p

p

∆

+

+

∆

+

=

lub

2

)

(

)

(

1

1

i

B

A

o

mi

p

p

p

p

∆

+

∆

+

=

i

A

o

i

A

p

p

p

3

3

)

(∆

+

=

Stany gazu „1”, „2” leżą na politropie, wobec tego spełniają równanie p υ

w

= idem:

mi

w

i

A

i

A

w

A

A

p

p

p

=

=

2

2

1

1

υ

υ

υ

w

stąd:

w

A

i

A

i

A

A

p

p













=

1

2

2

1

υ

υ

Stany gazów „1” i „3” leżą na izotermie T = T

o

wobec tego spełniają równanie:

=

1

1

A

A

p

υ

i

A

i

A

p

3

3

υ

Ponieważ

i

A

i

A

2

3

υ

υ

=

to

=

1

1

A

A

p

υ

i

A

i

A

p

2

3

υ

i

i

A

p

A

p

A

i

A

3

1

1

2

=

υ

υ

i ostatecznie:

w

i

A

A

i

A

A

p

p

p

p













=

3

1

2

1

lub

w

i

A

A

i

A

A

p

p

p

p













=

3

1

3

1

Logarytmując otrzymuje się:

i

A

A

mi

A

p

p

w

p

p

3

1

1

ln

ln

=

co można zapisać w postaci:

i

i

w

ξ

η

=

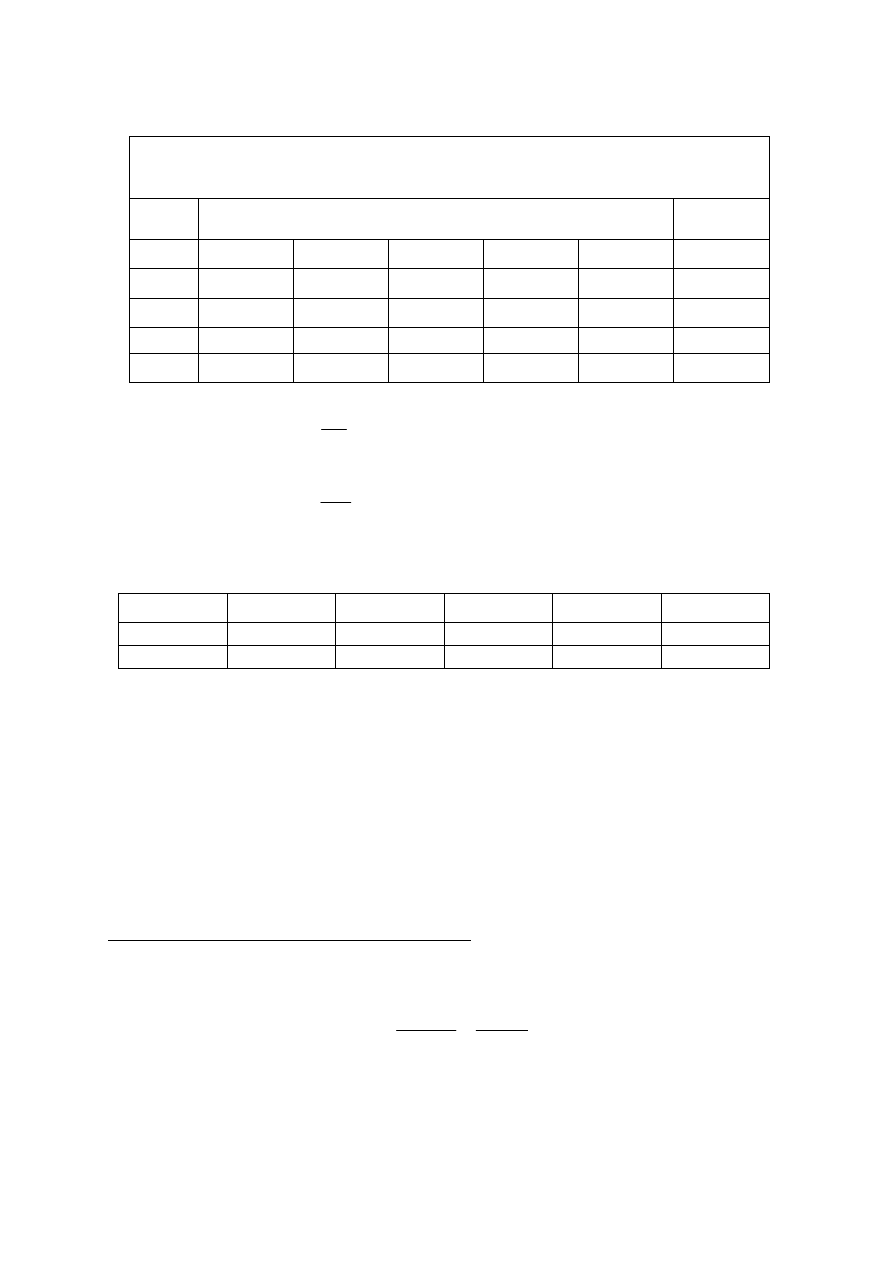
5

2.4 Opracowanie wyników.

1. Wyniki pomiarów umieścić w tabeli

Tabela wyników pomiarów

1

)

(

A

p

∆

800 mm H

2

0

ustalić

i

B

p

1

)

(∆

0

150

300

450

600

ustalić

i

A

p

3

)

(∆

mierzyć

mi

p

wyliczyć

1

A

p

wyliczyć

i

A

p

3

wyliczyć

2. Obliczyć :

mi

A

i

P

P

1

ln

=

η

i

i

A

A

i

P

P

3

1

ln

=

ξ

3. Obliczone wartości

ηηηη

i

i

ξξξξ

i

wstawić do tabeli

i

B

p

1

)

(∆

0

150

300

450

600

η

i

ξ

i

i przedstawić na wykresie

ηηηη

= f(

ξξξξ

).

4. Wyznaczyć tzw. linię trendu w postaci

ξ

η

w

=

+ u (wielomianu pierwszego stopnia).

5. Wyznaczyć postać analityczną linii trendu (równanie) oraz współczynnik determinacji

R

2

.

Tak wyznaczona wartość „w” jest przybliżeniem wykładnika „k” adiabaty gazu
doskonałego.

6. Wyznaczyć wskaźnik dokładności oszacowania Y oraz błąd względny pomiaru b

(wyznaczonej wartości w w stosunku do oczekiwanej wartości k).

Oszacowanie dokładności odwzorowania adiabaty

We wstępie podano że można dokładność tego oszacowania określić wskaźnikiem:

1

2

2

1

1

2

2

1

u

u

q

U

U

Q

Y

z

z

−

=

−

=

−

−

Ponieważ w ≠ k i w = idem ( bo zrealizowana przemiana jest politropą ), to ciepło tej

przemiany

Q

w1-2

= m c

w

(T

2

– T

1

)

oraz

6

1

−

−

=

w

R

c

c

w

σ

Ponieważ U

2

– U

1

= m c

v

(T

2

– T

1

)

Podstawiając w/w zależności do „Y” otrzymuje się:

1

−

−

=

w

k

w

Y

Dla powietrza k = 1,4

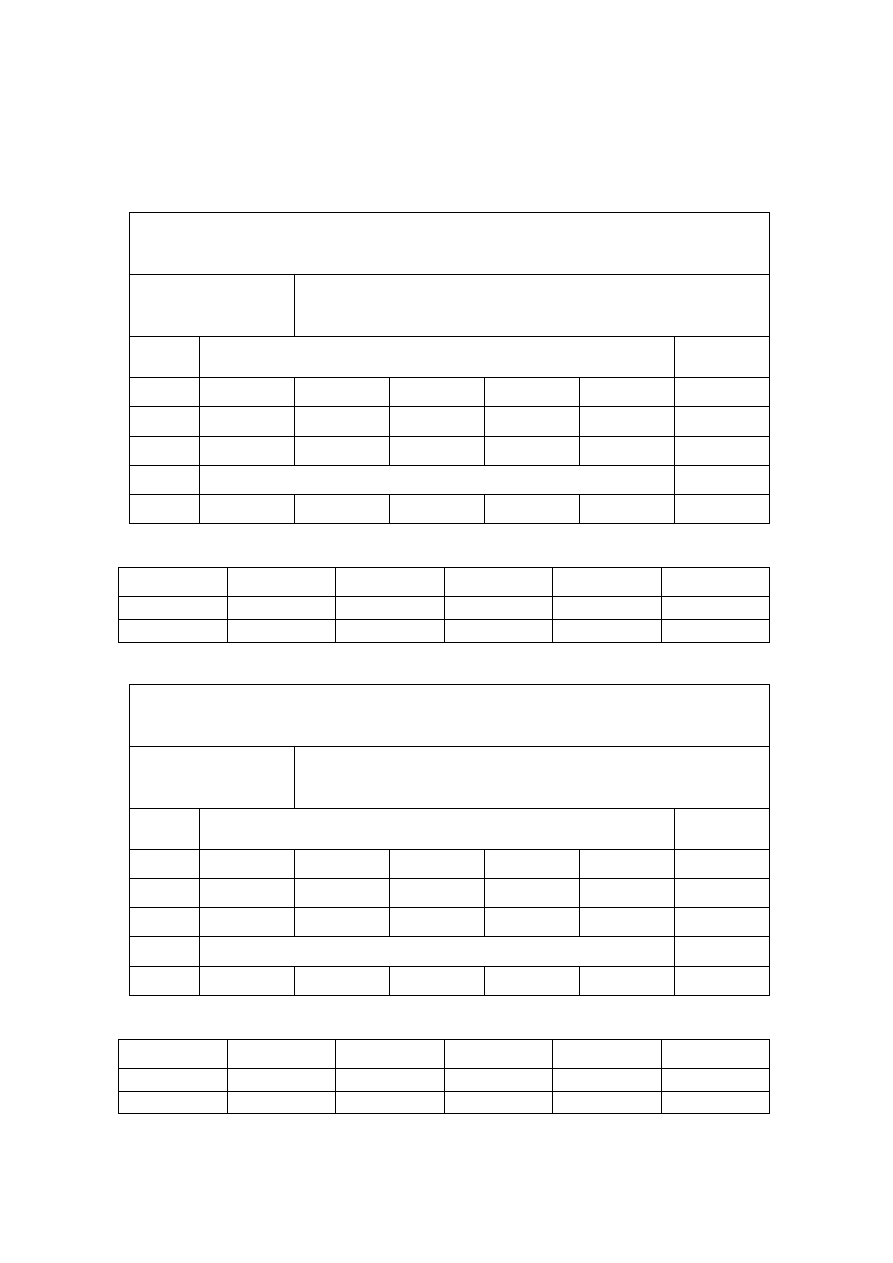
Wyznaczenie błędu względnego pomiaru:

,%

100

k

k

w

b

−

=

7

wzór tabel

Ćw. 2 Praktyczna realizacja przemiany adiabatycznej

data: ................................. godz.: ....................................

Układ pomiarowy 1:

Tabela wyników pomiarów

p

o

, hPa/p

o

, mm H

2

O

/

1

)

(

A

p

∆

800 mm H

2

0

ustalić

i

B

p

1

)

(∆

0

150

300

450

600

ustalić

i

A

p

3

)

(∆

mierzyć

mi

p

wyliczyć

1

A

p

wyliczyć

i

A

p

3

wyliczyć

Dane do wykresu - obliczone wartości η

i

i ξ

i

:

i

B

p

1

)

(∆

0

150

300

450

600

η

i

ξ

i

Układ pomiarowy 2:

Tabela wyników pomiarów

p

o

, hPa/p

o

, mm H

2

O

/

1

)

(

A

p

∆

800 mm H

2

0

ustalić

i

B

p

1

)

(∆

0

150

300

450

600

ustalić

i

A

p

3

)

(∆

mierzyć

mi

p

wyliczyć

1

A

p

wyliczyć

i

A

p

3

wyliczyć

Dane do wykresu - obliczone wartości η

i

i ξ

i

:

i

B

p

1

)

(∆

0

150

300

450

600

η

i

ξ

i