c

c

2009-05-04

@

c

! "

# $c %"

&' & ()"

& ) ) *"+,

- )*".++/

01*,2"+/

% ) 3

01*3+++3

014

c

A certain something associated with a certain system always increases.

We have two classical problems;

1.

m ½ewtons laws are always reversible

2.

m Volume is preserved in phase space

@

confusion up to ~1980s or so;boltzman started but «.

The key is the idea of chaos

It is not that complete time reverse cannot occur ± it is that it is unlikely to go to a certain state.
A sudden reverse of entropy (molecules going from disorder to order) is not impossible, just
unlikely.

(note susskind uses ³lump´ ± better ³volume in phase space´
uses probability distribution to indicate the system is inside a lump
P=0, outside of lump (volume in phase space)
P=constant inside

The Probability distribution has entropy associated with it.entropy is log(number of states in the
system)

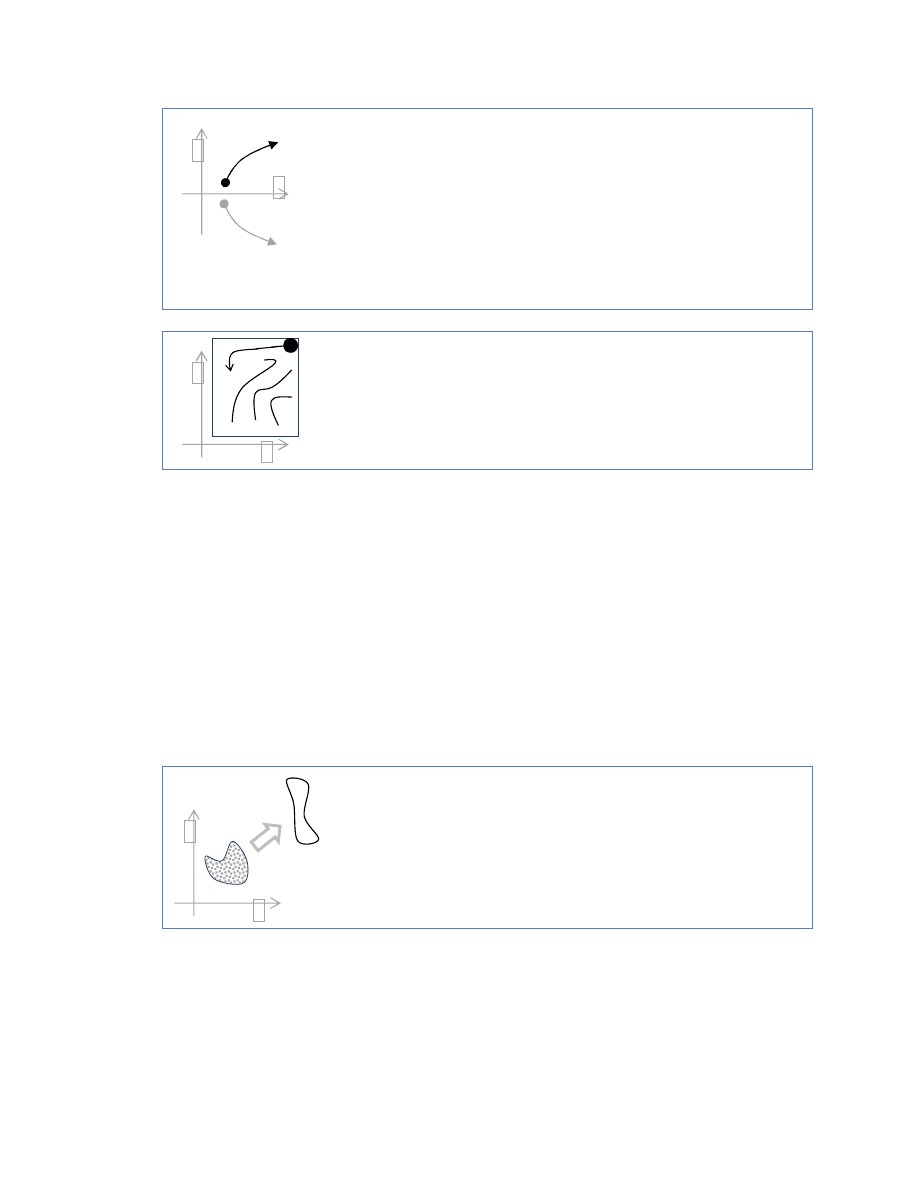
How systems evolve in phase space


phase space (x,p) (position,momentum) - phase space is multi-
dimensional ± but can only be shown as 2-D; p,x

points start within a certain volume (middle),
evolve (change shape) over time ± always equal volume

x

p

phase space (x,p) (position,momentum)

example of molecules dispersing from a point (upper rh
corner)
if we could get into that system, and reverse trajectory of
every molecule, then everything would go back to the corner

x

p

phase space (x,p) (position,momentum)

a point in phase space. starts at a point, moves to another point
cannot just ³reverse´ trajectory ± you have to also reverse velocity

assume a second trajectory (bottom) which is just the mirror image
of the (top) trajectory
other than the velocity being reversed ± newtons laws are
completely reversible

x

p

in classical (infinite) systems, counting number of states not possible,
---- divide states into cells
thenentropy is proportional to the log(volume in phase space)

But volume is preserved ± this is inconsistent with entropy increasing, how we know systems
behave
so what is the meaning of entropy, or 2

nd

law

@

Billiard Ball Analogy
Take a pool table (3-cushion billiards, no pockets); ideal conditions: perfectly reflecting, no
friction, etc.

Initially all at rest, when cue ball struck (system starts in motion) then if we know the motions
with precisely we can reverse. However if there was a small deviation initially, then the
deviations build up exponentially.

systems where this does not occur (simple systems only ???)
one ball on a square, ideal table; or, better, a ball moving back-forth on a line
---- nothing to increment exponentially ± system is stable
---- (my note: sort of like ground state in QM)

@ c !@ "

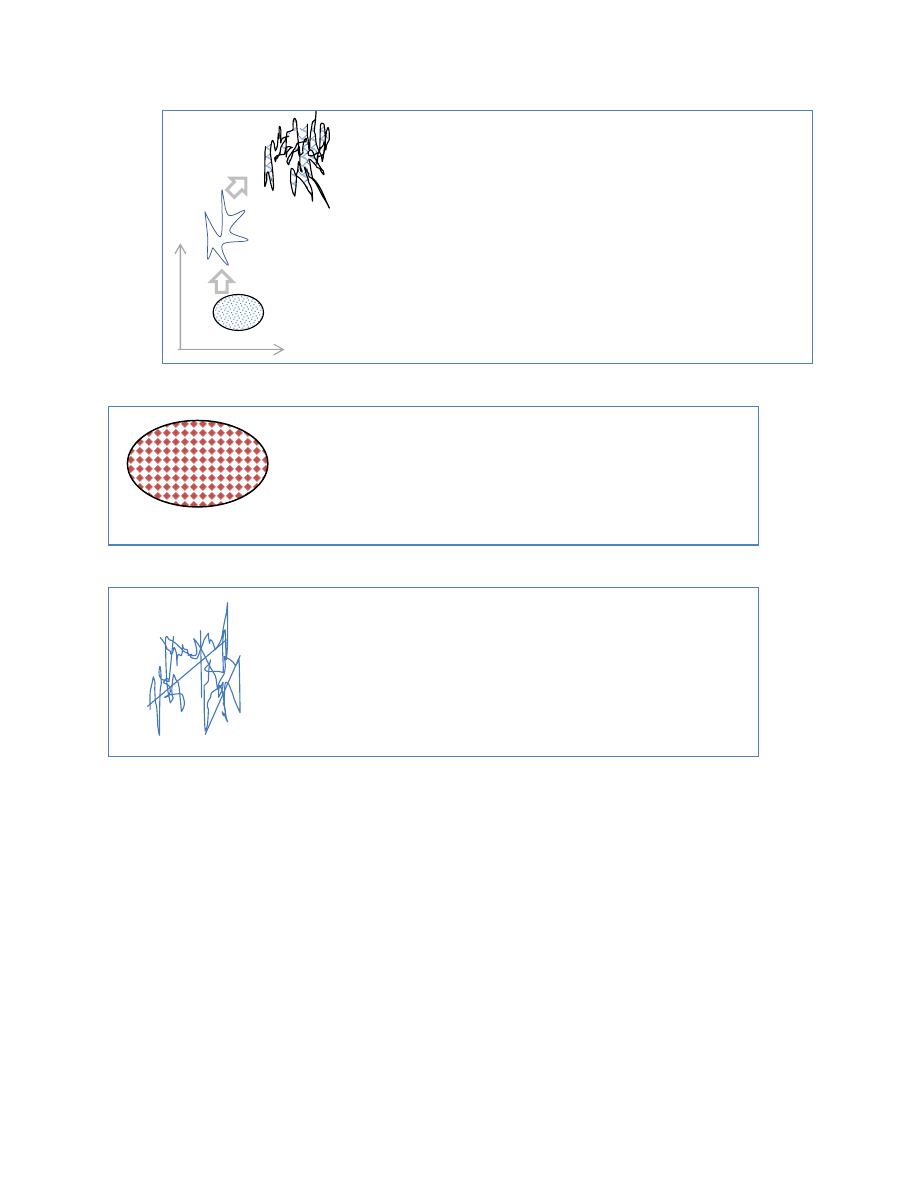
two systems, initially close together in phase space, will start exponentially deviating.
6.1

two systems, apart initially, grow apart exponentially in time

(ǻ depends, is defined by, the system, where you are in phase space, etc)
the exponent is called ±, related to degrees of
freedom (dimensionality), a measure of the chaos in phase space ± degree of instability.

R

#@ R$%

(covered in classical mechanics, lecture 7, coarse graining)

R

% @ % &'(

Fine grained entropy is the exact logarithm of the volume of the phase space keeping track of the
fine grain structure of phase space.
The fine grained entropyphase space volume never increases, frozen by Louiville¶s theorem.

The logarithm of the Coarse grained entropy volume increases. It is the Coarse grained logarithm
that defines entropy in thermodynamics.

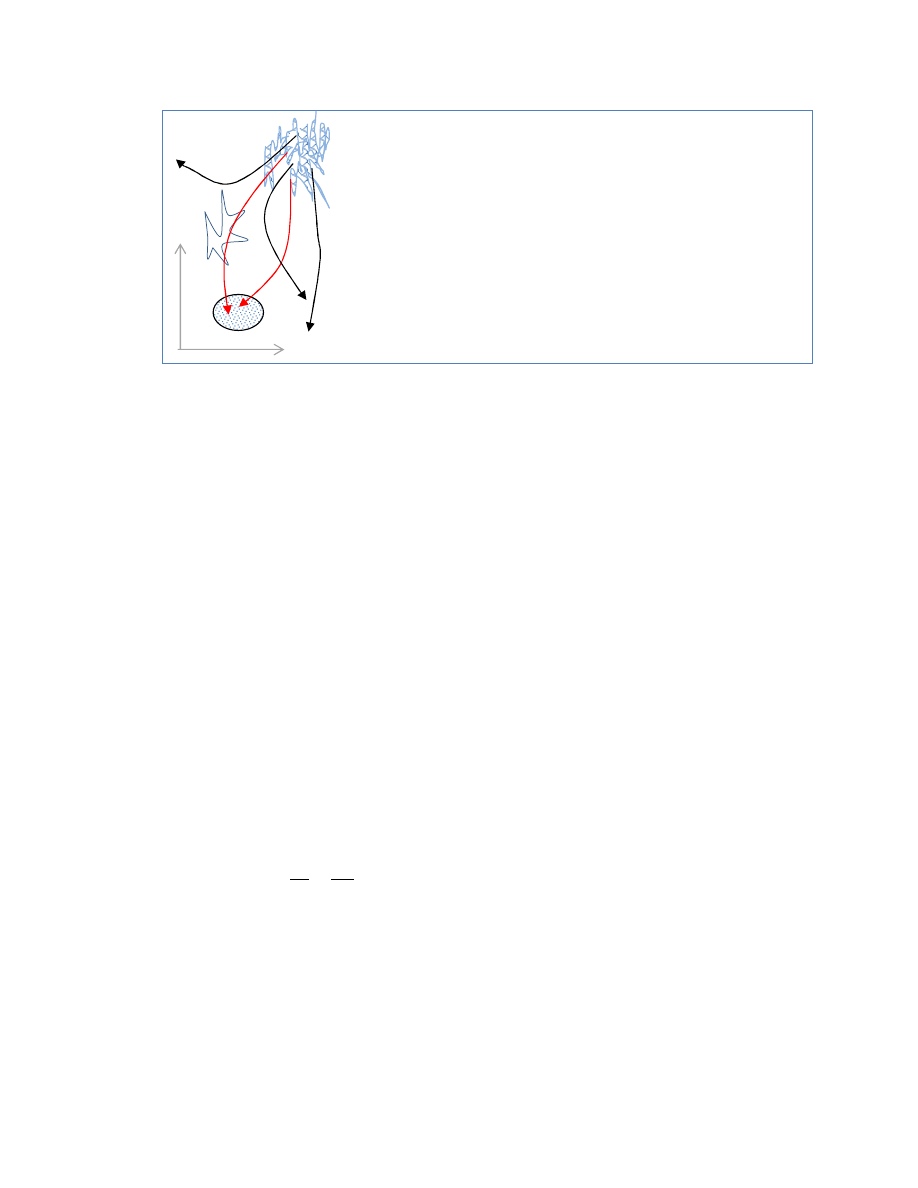
Coarse Graining

coarse graining ³blobs´ too big to distinguish branches in the
fractal. now as you coarse-grain the ™ of the coarse grain
particles exceed to original volume. have to distinguish
between fine grained entropy and corase grain entropy

Coarse Graining

start with a small ³cells´ which represents our ability to
represent it, track, measure, etc. that cover initial area
almost equal to initial volume (some overlap on edges) ± but
insignificant

As a system evolves in time the trajectories within that
volume of space become fractalized, that is, the paths branch
to finer paths.

While the exact volume mat be constant our ability to
distinguish points in phase space is limited ± especially the
ability to track an exponentially increasing number of points
and paths.

x

p

@ )%&'*((

The system evolves on

) )5

6 ' ))

% *,/++

% )

am

) 78

am

8 ) '
)$

am

)) 8*

l9:; )

% )

am

) 8

am

+ &,-'(

let us suppose that the internal motion of a molecule is described by a harmonic oscillator (not
the overall motion)

6.2

ƒ ƒ ƒ

start with classical to determine energy

where:

1

st

term is KE

2

nd

term is PE

k is spring constant

x is a coordinate which describes the oscillation.
(x is not position of center of mass of the molecule)

Running the system backwards

if we start tracing back from the fine structures of fractal
volume.
A coarse grained blob exactly on a filament will exactly
trace back. Just slightly off the filament the traceback will
diverge to some wildly different place.

If you could reverse every particle exactly ± they would all
return to the corner. The slightest deviation will fluctuate
wildly,, expanding into an even larger fractal area.

x

p

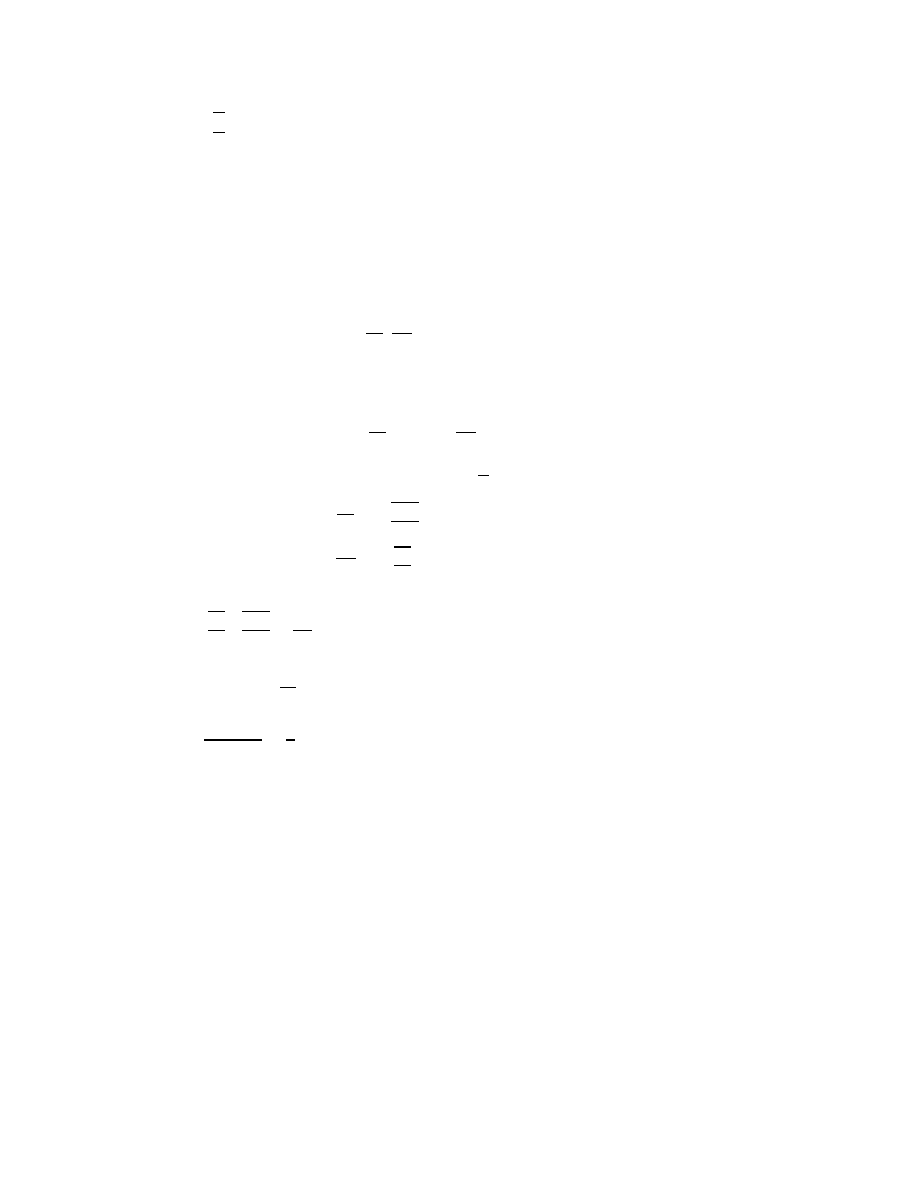
6.3

Å

frequency is k/m (2

nd

derivative

Each molecule has a different oscillation frequency. The oscillation frequency also depends on
the temperature. When k,Ȧ becomes very large, corresponds to a very low temperature, it
becomes very difficult to excite any motion and the molecule becomes a point particle.

@! %

calculate Boltzman, Heimholtz free energy. Start by determining the partition function:

6.4

!

partition function, energy from (6.2)

This integral was solved in previous lessons (Lecture 4, Gauss Integral)

(x,p) are independent, integral can be split in two

6.4a

!

substitute in Gauss Integral (

)

6.4b

6.4c

6.5

!

substituting Ȧ from (6.3)

6.6

!

(-log Z needed in equations)

6.7

ƒ

average energy is 1/ȕ which is temperature

Classical derivation has a problem. The energy does not depend on the frequency (spring
constant). So when the molecule is at very low temperatures (k,Ȧ very large) we expect the
molecule to behave, at the limit, like a point particle (zero internal vibrational energy).

But regardless of how stiff the molecule, how close it approoaches a point particle, the molecule
has vibrational energy.

+ &.(((

6.8

ƒ

lÅ

energy levels are discrete

6.9

!

!

l

partition function is now a sum

expand RHS - equals sum of a power series of a constant

l

"

l

#

l

#

l

$

"

"

l%

32

!

lÅ

) 9

) )

6.10

! #

"

l

6.11

ƒ

#

"

l%

l

l%

#

"

l%

6.12

ƒ

l

l%

to simplify, multiply by

l

@ @ +

High temperature, small ȕ
At the limit we expect classical physics. The vibrational energy is so large the individual
quantum increments do not matter.

l

" lÅ $

expand exponential in denominator of (6.12)

6.13

ƒ

l

l%

l

l

high temperatures , behaves classically

Low temperatures, ȕ is very large

6.14

ƒ

l

l%

the (- 1) in the denominator of (6.12) can be ignored

energy becomes exponentially small.


The cross-over point: at high temperatures energy is linear in T. at low temperatures energy
becomes exponentially small. The cross-over occurs when the molecular internal frequency

Å " or Å

This occurs when the oscillations become high enough to allow the system to have one quantum
of energy. below that, the molecule is frozen