N 1000



i

0 N





t 0.01



fo

20



czas

i

i t







2 



fo





1 0.001



x

i

sin  czas

i



1









dx

i

 cos  czas

i



1











ddx

i



2



sin  czas

i



1











1

0.5

0

0.5

1

200

100

0

100

200

dx

x

S2v t

( )

interp wsv2 wt



wv



t



(

)



wsv2 cspline wt wv



(

)



S1v t

( )

interp wsv1 wt



wv



t



(

)



wsv1 pspline wt wv



(

)



Sv t

( )

interp wsv wt



wv



t



(

)



wsv

lspline wt wv



(

)



czas

N

czas

0



10



wv

i

dx

i



wt

i

czas

i

czas

0





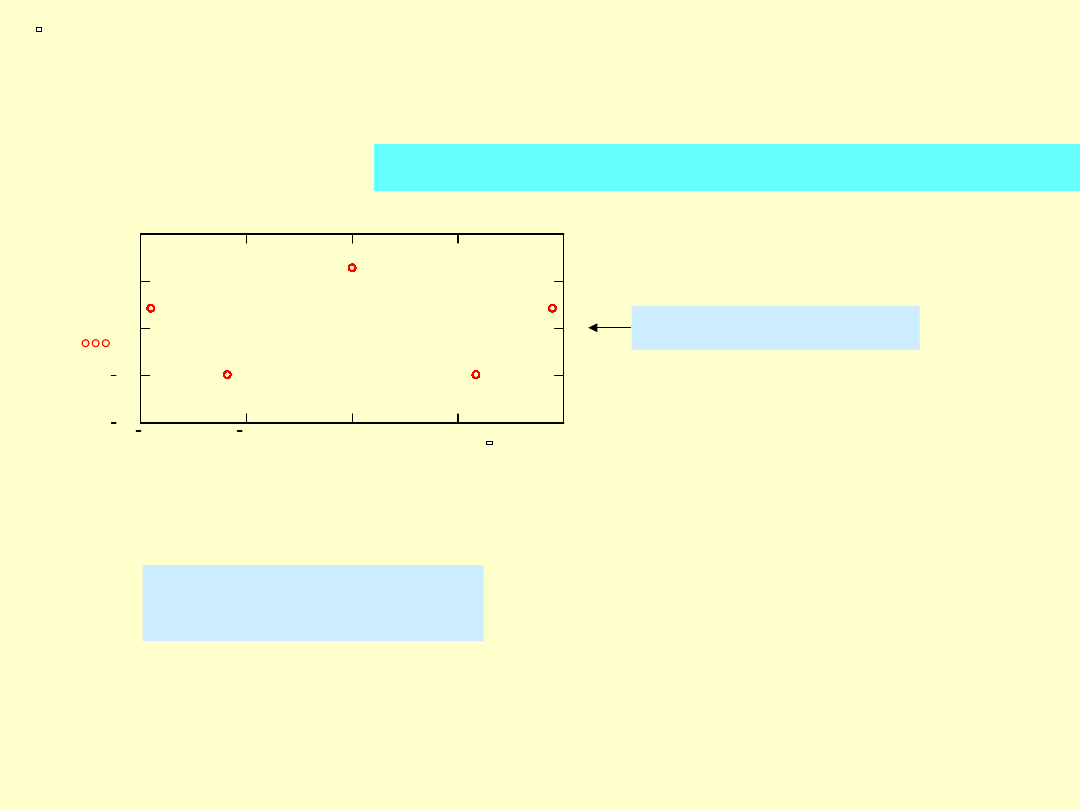
interpolacja prędkości (zamiana postaci zapisu z dyskretnej na ciągłą)

S2x t

( )

interp wsx2 wt



wx



t



(

)



wsx2 cspline wt wx



(

)



S1x t

( )

interp wsx1 wt



wx



t



(

)



wsx1 pspline wt wx



(

)



Sx t

( )

interp wsx wt



wx



t



(

)



wsx lspline wt wx



(

)



czas

N

czas

0



10



wx

i

x

i



wt

i

czas

i

czas

0





interpolacja przemieszczeń (zamiana postaci zapisu z dyskretnej na ciągłą)

Przykład numeryczny na generowanych danych

płaszczyzna fazowa

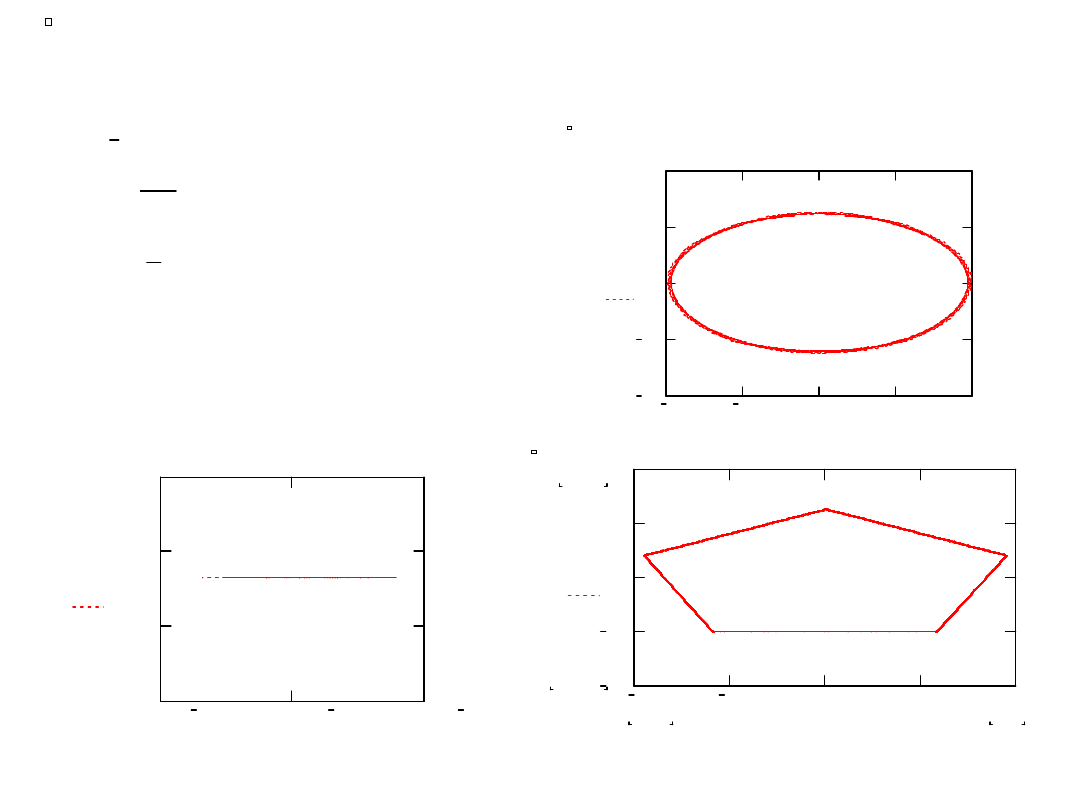
Interpolacja za pomocą
funkcji sklejanych

9.9999983310

4

9.999998332510

4

9.99999833510

4

125.5

125.6

125.7

dxr

xr

N1 200



N1 last xr

( )



dxr

n

dx

k n



(

)



dxr

jg

dx

N



dxr

0

dx

0



x

10

10 10

4







xr

1

10 10

4







xr

n

x

k n



(

)



xr

jg

x

N



xr

0

x

0



n

1 jg 1







j

0 jg





jg 200



jg

floor

N

k











k 5



krotność podziału zbioru danych

k floor

1

f t













[s] okres drgań własnych

To

1
f



[Hz] częstotliwość drgań własnych

f

18.6



[s] próbkowanie

t 0.01



t

0 t



czas

N

czas

0







t czas

2

czas

1





t1 0 To



czas

N

czas

0











1

0.5

0

0.5

1

200

100

0

100

200

Sv t1

( )

Sx t1

( )

1

0.5

0

0.5

1

200

100

0

100

200

125.664

101.738



dx

0.951

0.951



x

1

0

1

200

100

0

100

200

S2v t1

( )

S2x t1

( )

9.9999983310

4

9.999998332510

4

9.99999833510

4

125.5

125.56

125.62

125.68

125.74

125.8

dxr

xr

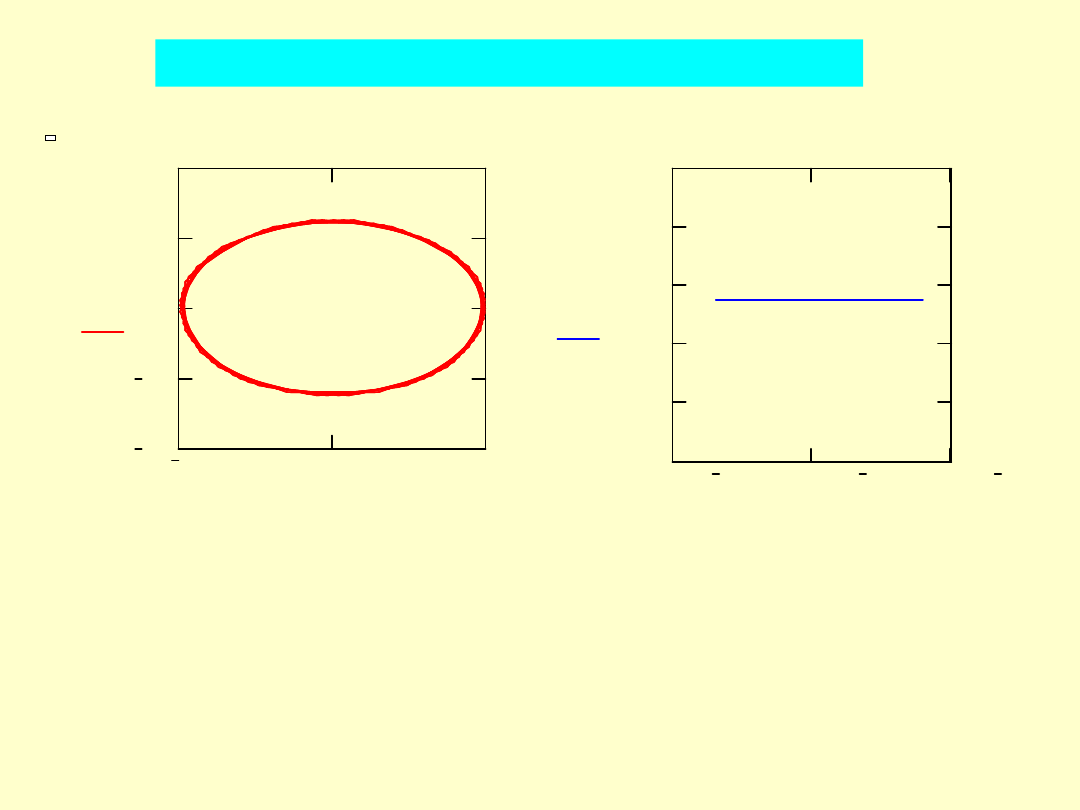
Przekrój Poincare przy
i ciagłej zmiennej t
oraz interpolowanych
splajnami wielkości v, x

To 0.054



[s]

Przybliżony przekrój Poincare
wybrano punkty z pomiarów
dyskretnych odległe o k - kroków
czyli rozłożone w czasie co Tk [s]

Tk k t





Tk 0.05



[s]

Porównanie “jakości” przekrojów Poincarego