Chaos deterministyczny

Marek Domański

Materiały pomocnicze do wykładu

Teoria Systemów

Politechnika Poznańska

© Marek Domański

Materiały są przeznaczone wyłącznie do użytku podczas zajęć

z przedmiotu Teoria Systemów prowadzonych przez

prof. Marka Domańskiego na studiach

na kierunku Elektronika i Telekomunikacja.

Uwaga:

Niektóre ilustracje pochodzą z podręczników zalecanych jako pomocnicze do przedmiotu.

Kopiowanie, rozpowszechnianie i używanie w innych celach jest

stanowczo zabronione.

W szczególności, nieuprawnione rozpowszechnianie

drogą elektroniczną np. w Internecie jest nielegalne

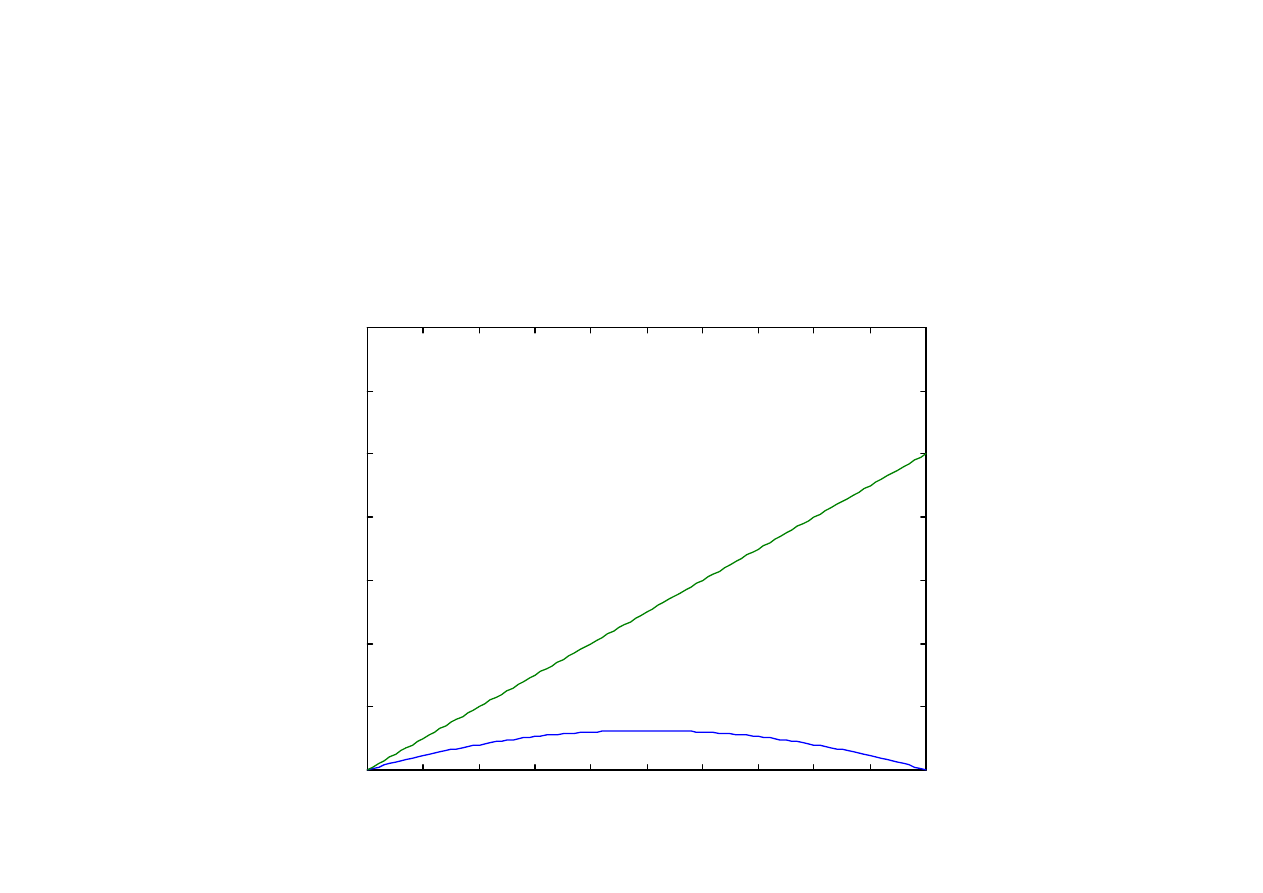
Odwzorowanie logistyczne

x(n+1) = r·x(n)[1 – x(n)]

Przypadek 0 < r < 1

Wykres odwzorowania dla r = 0,5

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.2

0.4

0.6

0.8

1

1.2

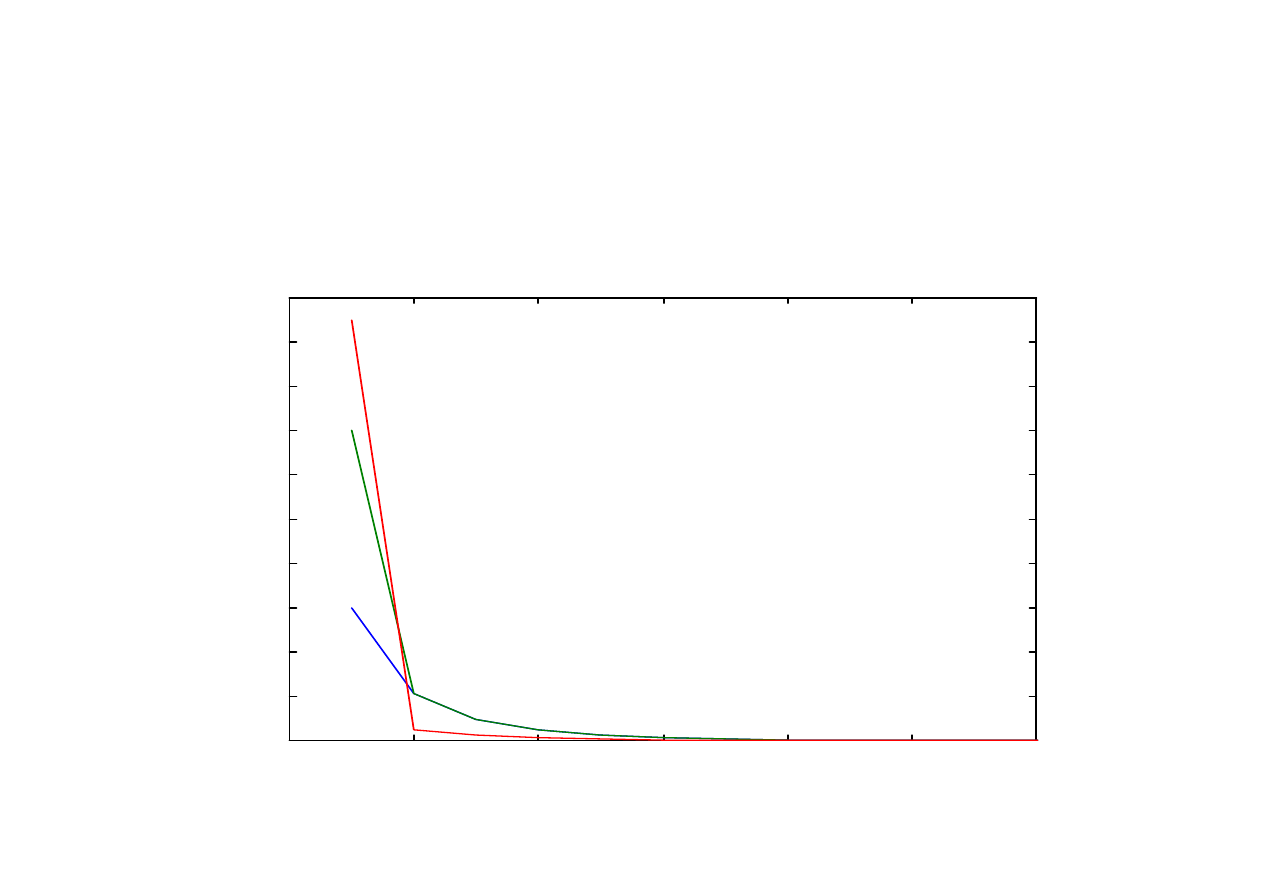
Wartości zmiennej stanu

dla warunków początkowych

x(1) = 0,300, x(1) = 0,700, x(1) = 0,950

Parametr r = 0,5

0

2

4

6

8

1 0

1 2

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

0 . 9

1

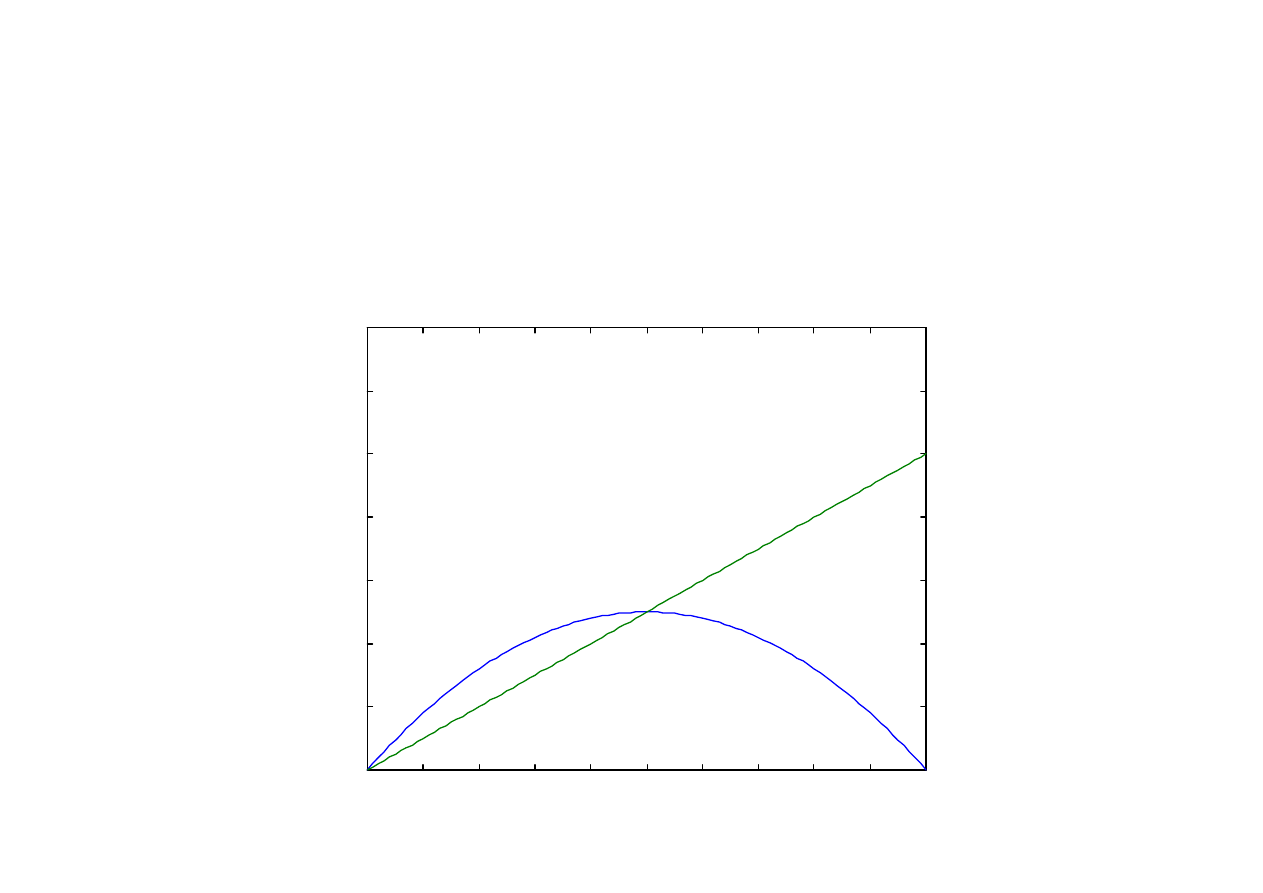
Odwzorowanie logistyczne

x(n+1) = x(n)[1 – x(n)]

Przypadek 1< r < 3

Wykres odwzorowania dla r = 2,0

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.2

0.4

0.6

0.8

1

1.2

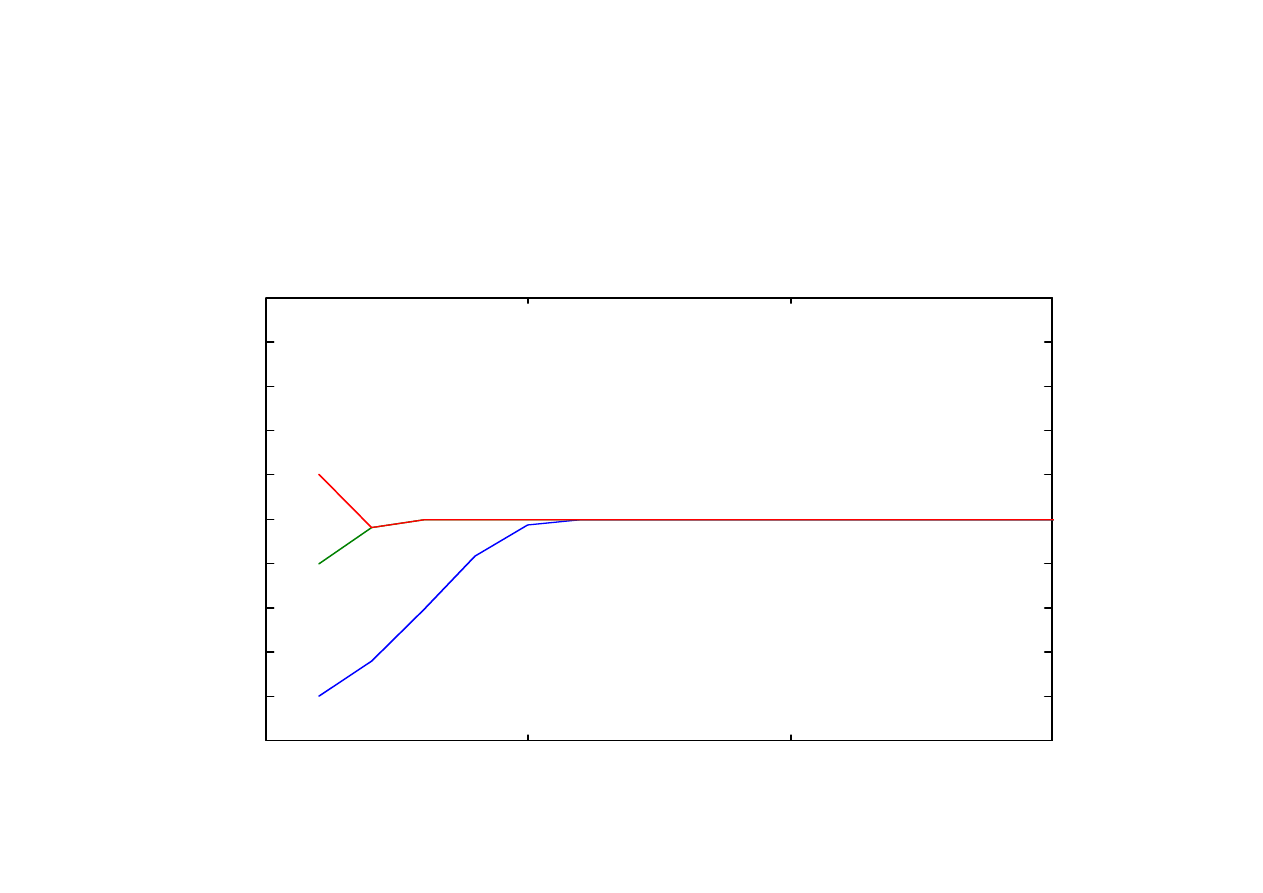
Wartości zmiennej stanu

dla warunków początkowych

x(1) = 0,1; x(1) = 0,4; x(1) = 0,6

Parametr r = 0,5

0

5

1 0

1 5

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

0 . 9

1

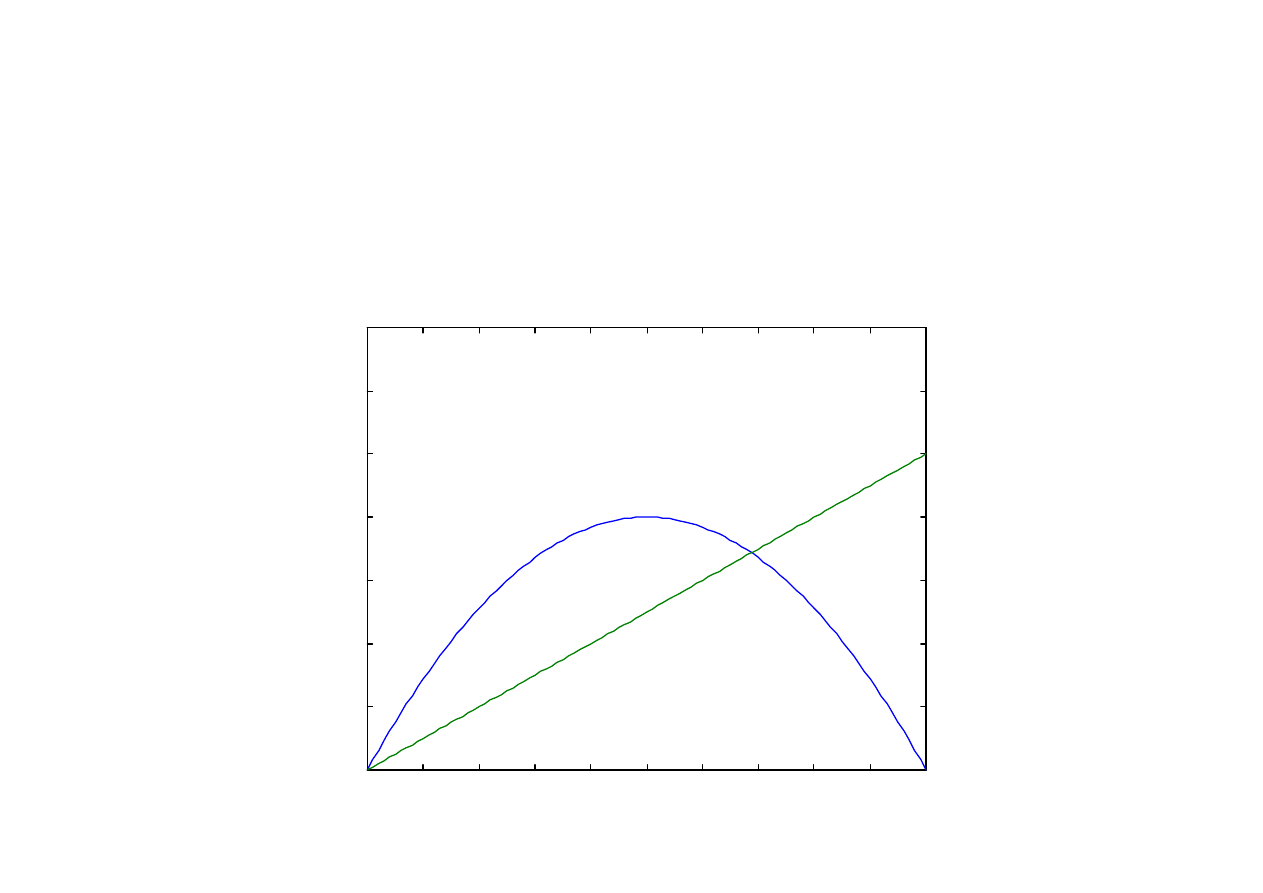
Odwzorowanie logistyczne

x(n+1) = r·x(n)[1 – x(n)]

Przypadek r > 3

Wykres odwzorowania dla r = 3,2

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.2

0.4

0.6

0.8

1

1.2

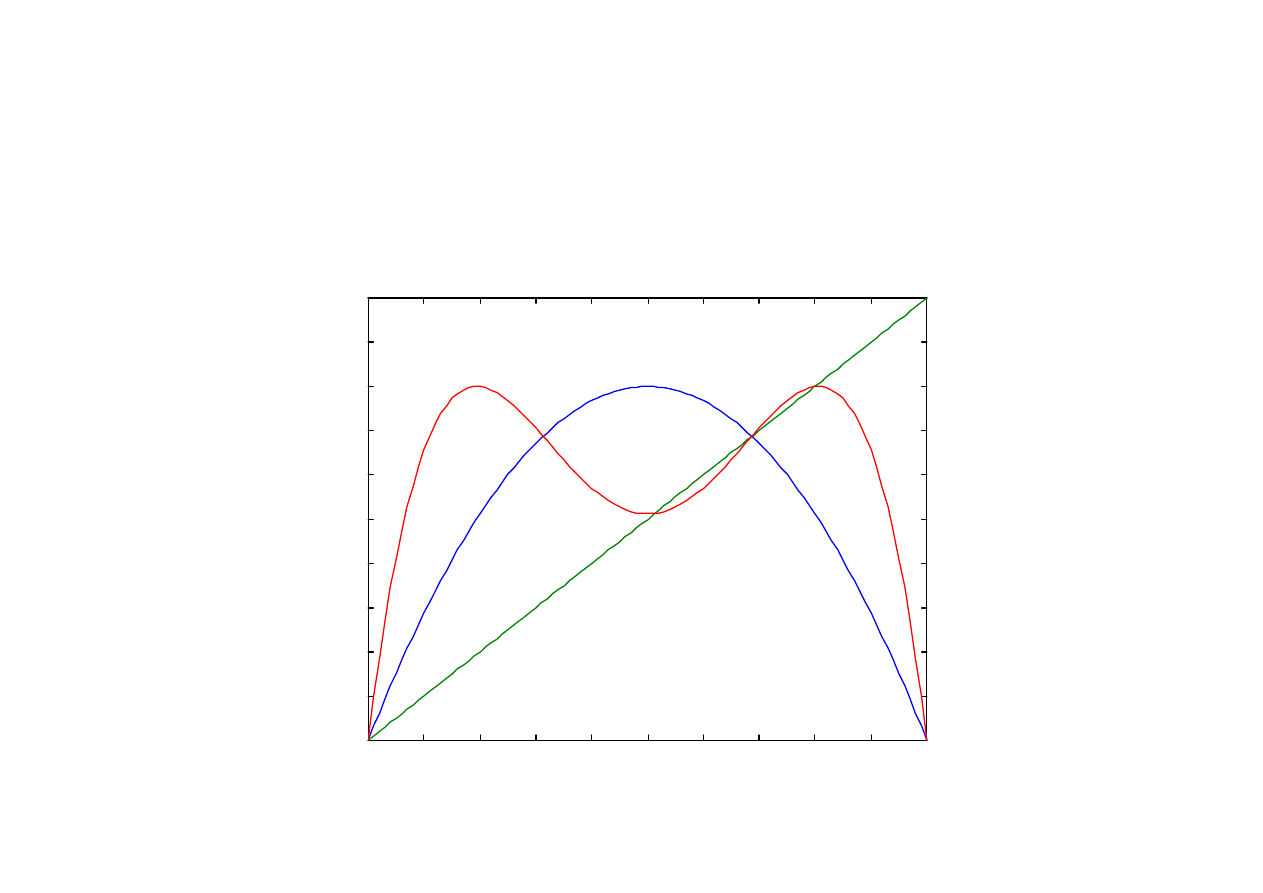
Odwzorowanie F

2

dla odwzorowania logistycznego

x(n+1) = F[x(n)] dla r = 3,2

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

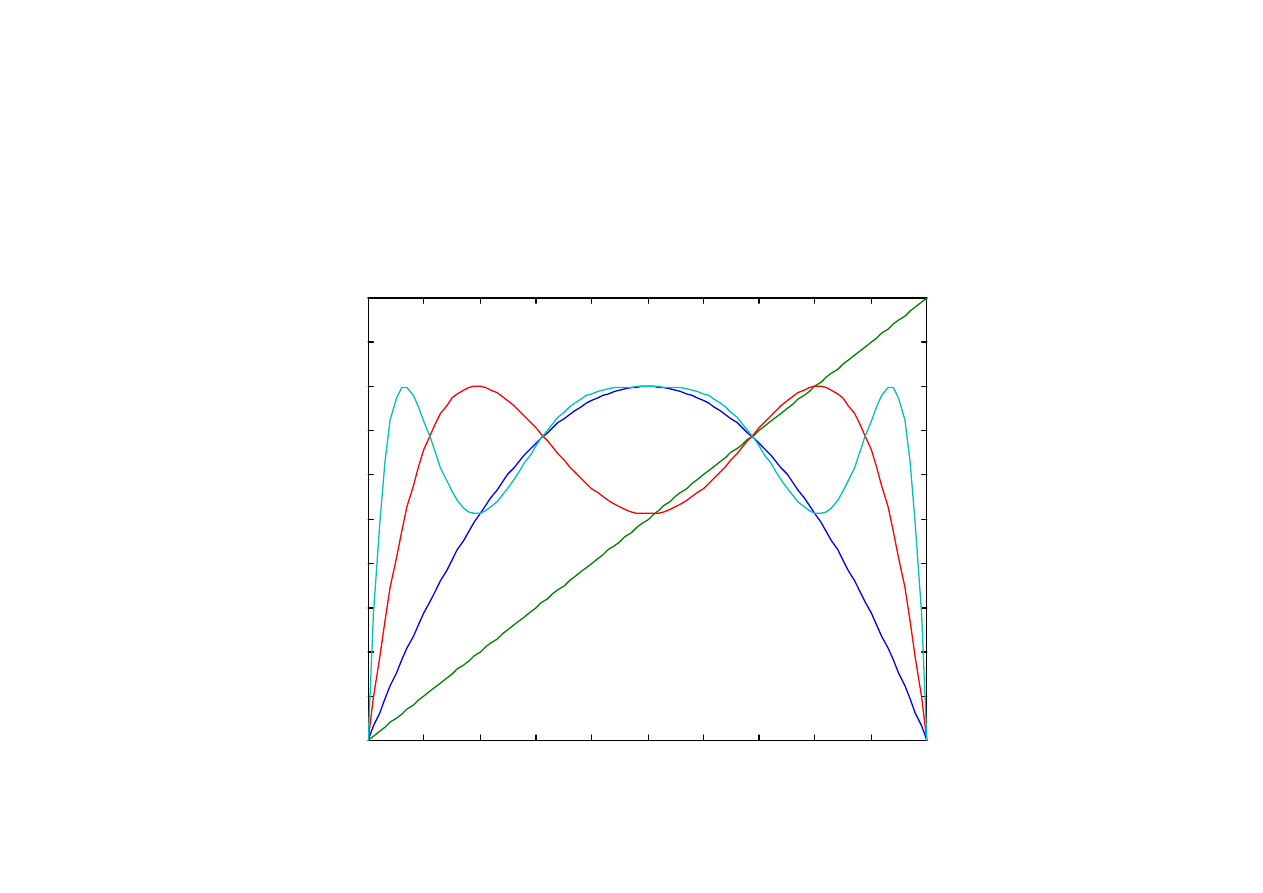
Odwzorowanie F

4

dla odwzorowania logistycznego

x(n+1) = F[x(n)] dla r = 3,2

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

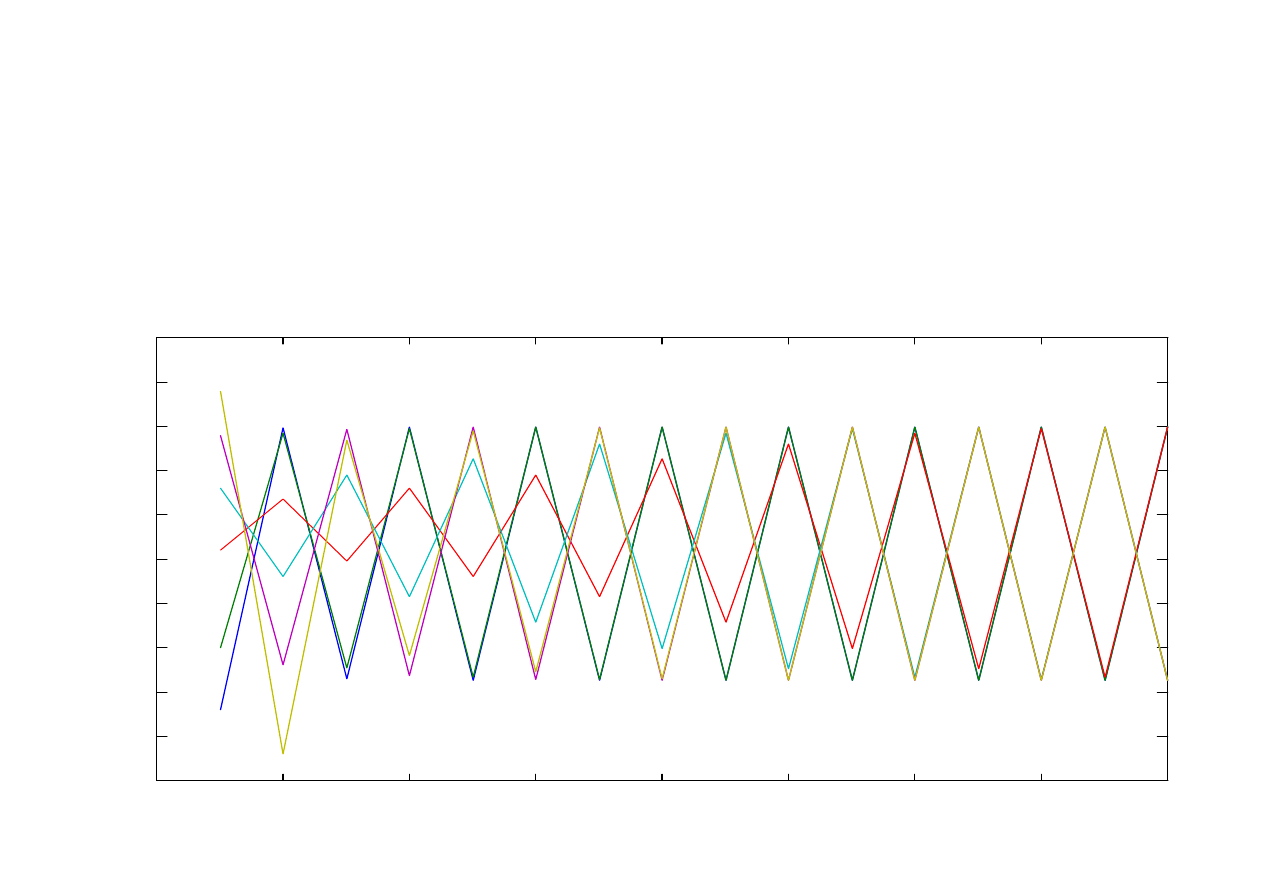
Zmienna stanu jako funkcja czasu

dla warunków początkowych

x(1) = 0,48; x(1) = 0,55; x(1) = 0,66 ;

x(1) = 0,73 ; x(1) = 0,79 ; x(1) = 0,84

Parametr r = 3,2

0

2

4

6

8

1 0

1 2

1 4

1 6

0 . 4

0 . 4 5

0 . 5

0 . 5 5

0 . 6

0 . 6 5

0 . 7

0 . 7 5

0 . 8

0 . 8 5

0 . 9

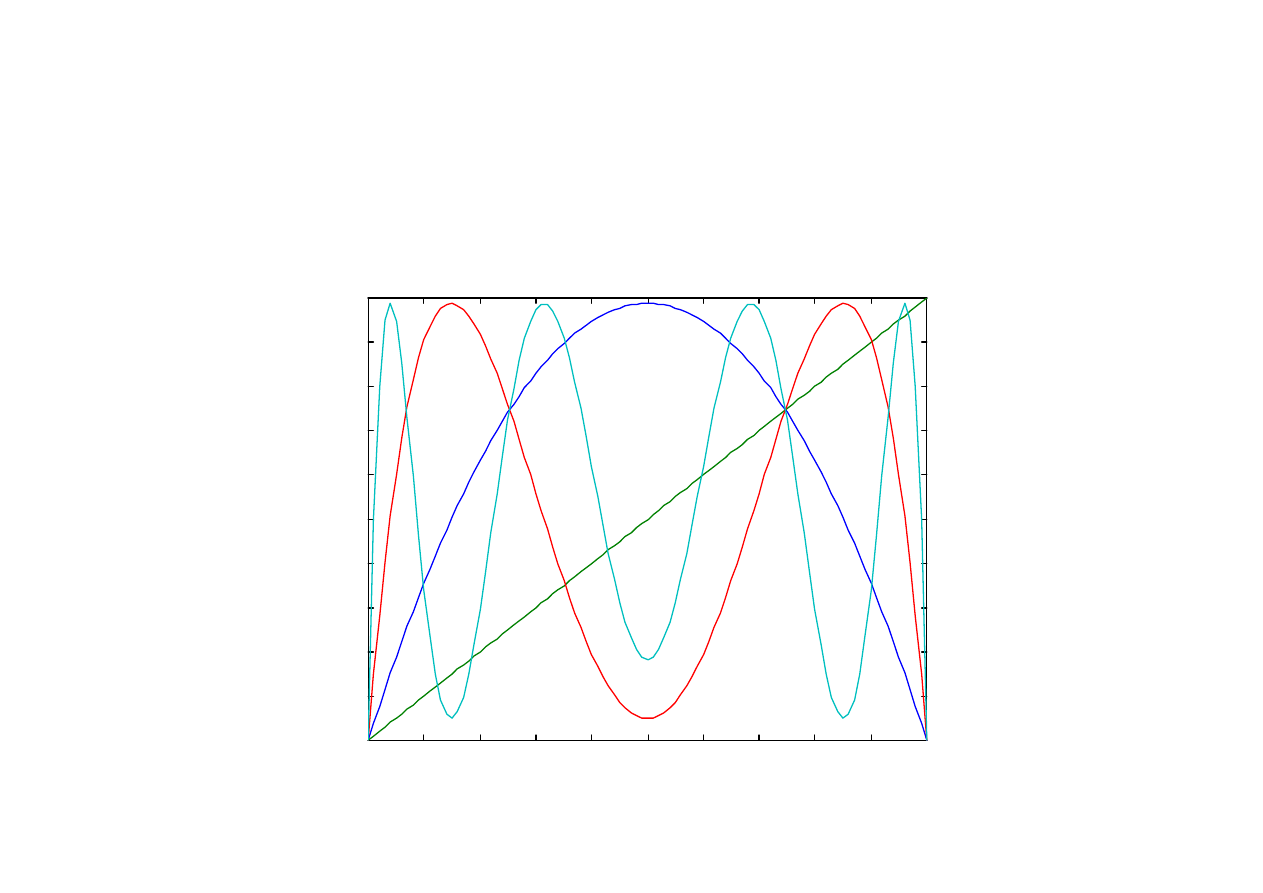
Odwzorowanie F

4

dla odwzorowania logistycznego

x(n+1) = F[x(n)] dla r = 3,95

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

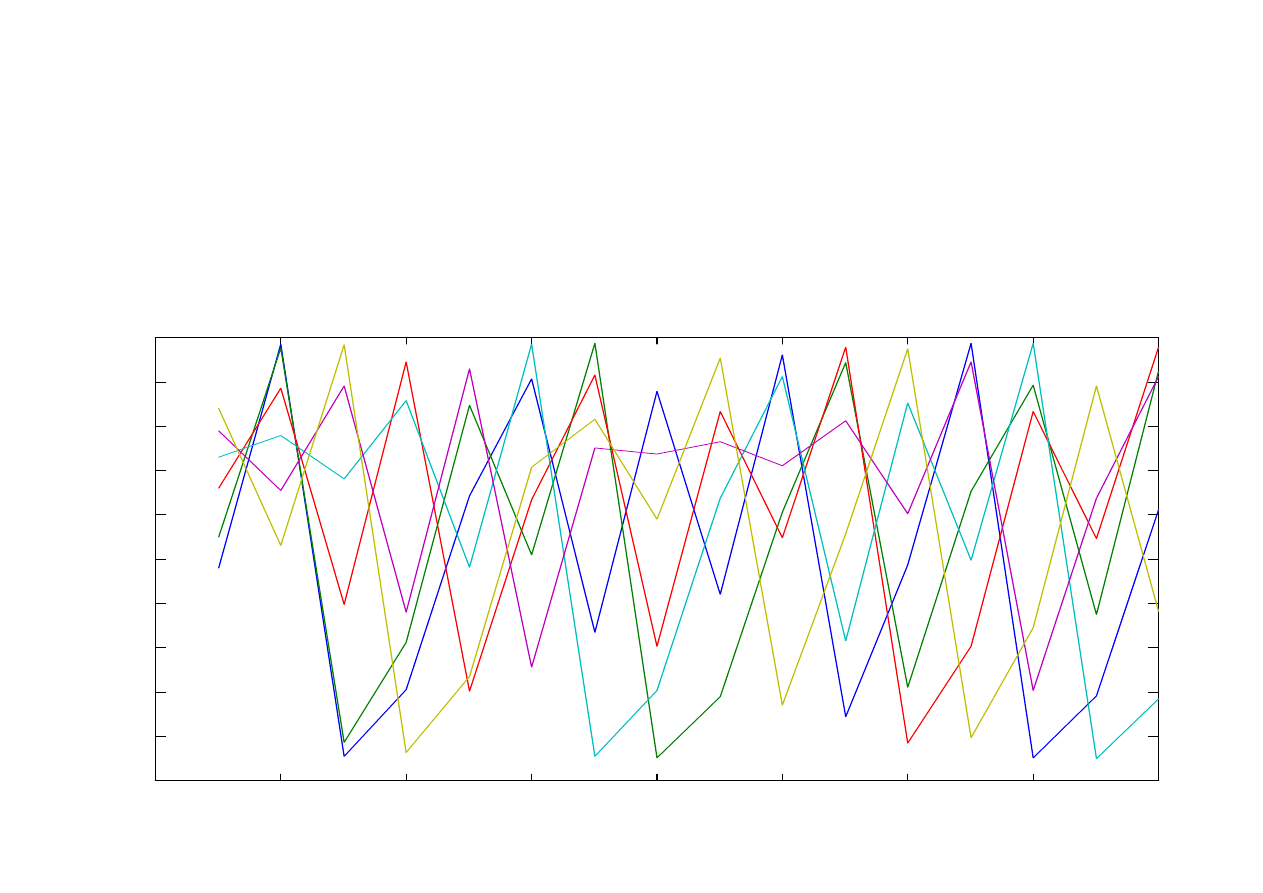
Zmienna stanu jako funkcja czasu

dla warunków początkowych

x(1) = 0,48; x(1) = 0,55; x(1) = 0,66 ;

x(1) = 0,73 ; x(1) = 0,79 ; x(1) = 0,84

Parametr r = 3,95

0

2

4

6

8

1 0

1 2

1 4

1 6

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

0 . 9

1

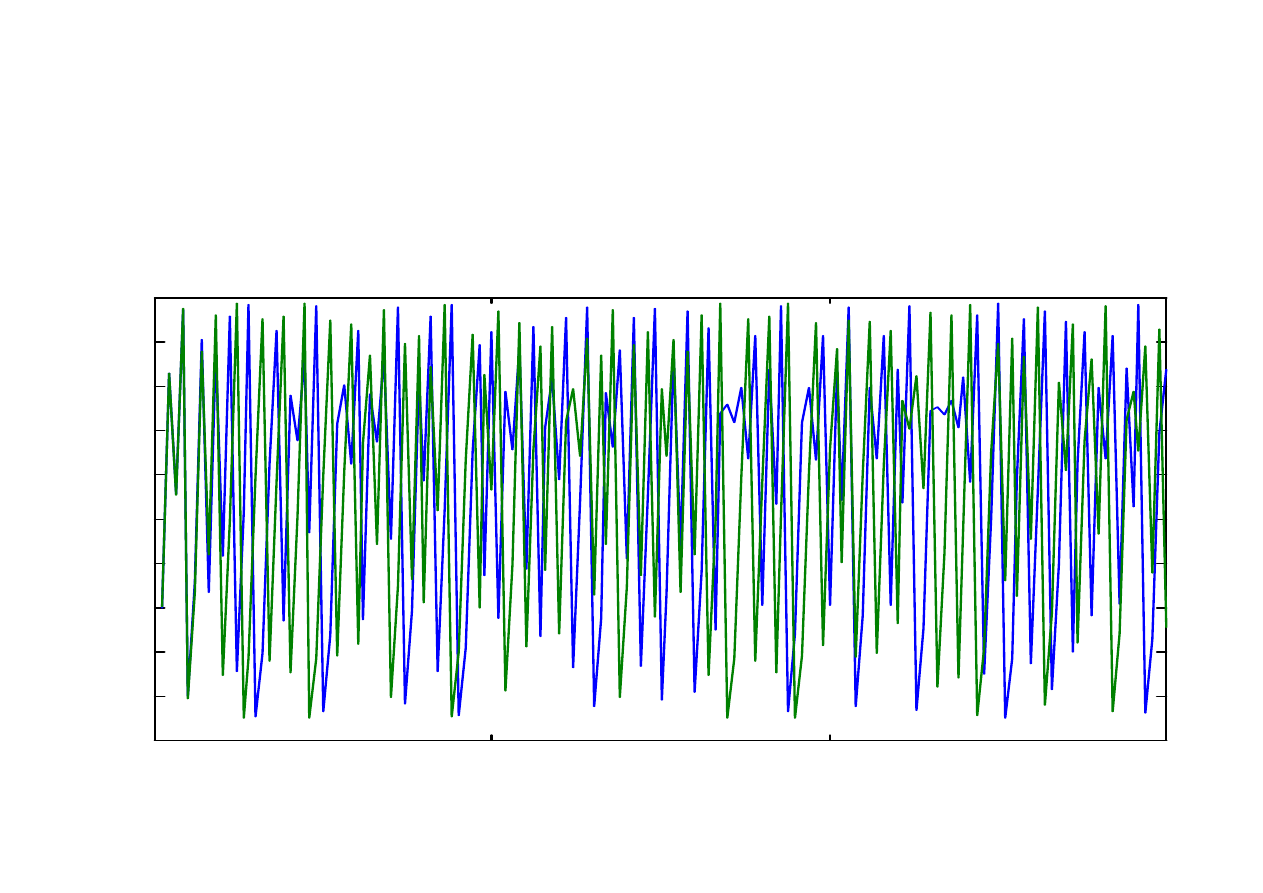
Drgania generowane dla warunków początkowych

x(1) = 0,300 (niebieska linia)

oraz x(1) = 0,301 (zielona linia)

Parametr r = 3,95

0

5 0

1 0 0

1 5 0

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

0 . 9

1

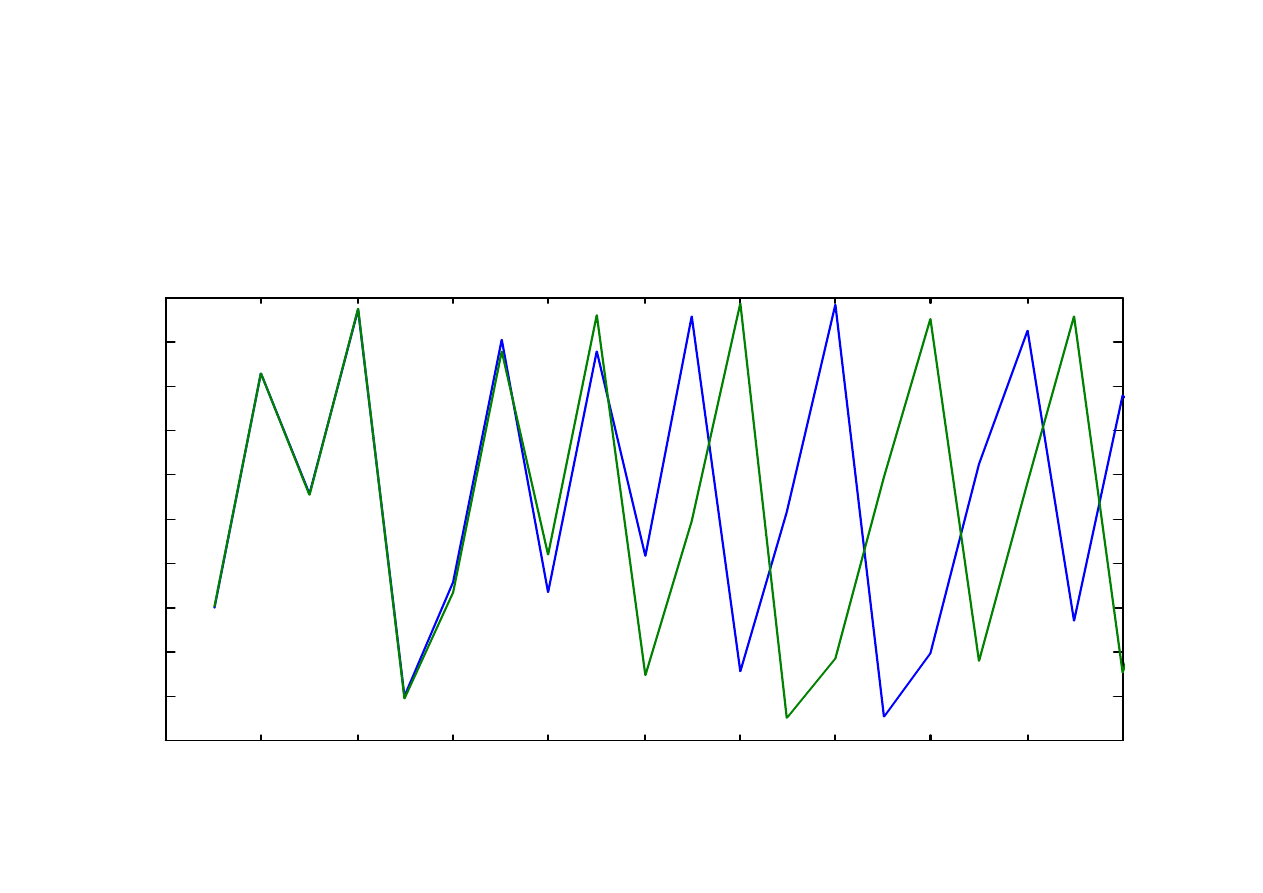
Drgania generowane dla warunków początkowych

x(1) = 0,300 (niebieska linia)

oraz x(1) = 0,301 (zielona linia);

Parametr r = 3,95; Przedział czasu <1,20>

0

2

4

6

8

1 0

1 2

1 4

1 6

1 8

2 0

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

0 . 9

1

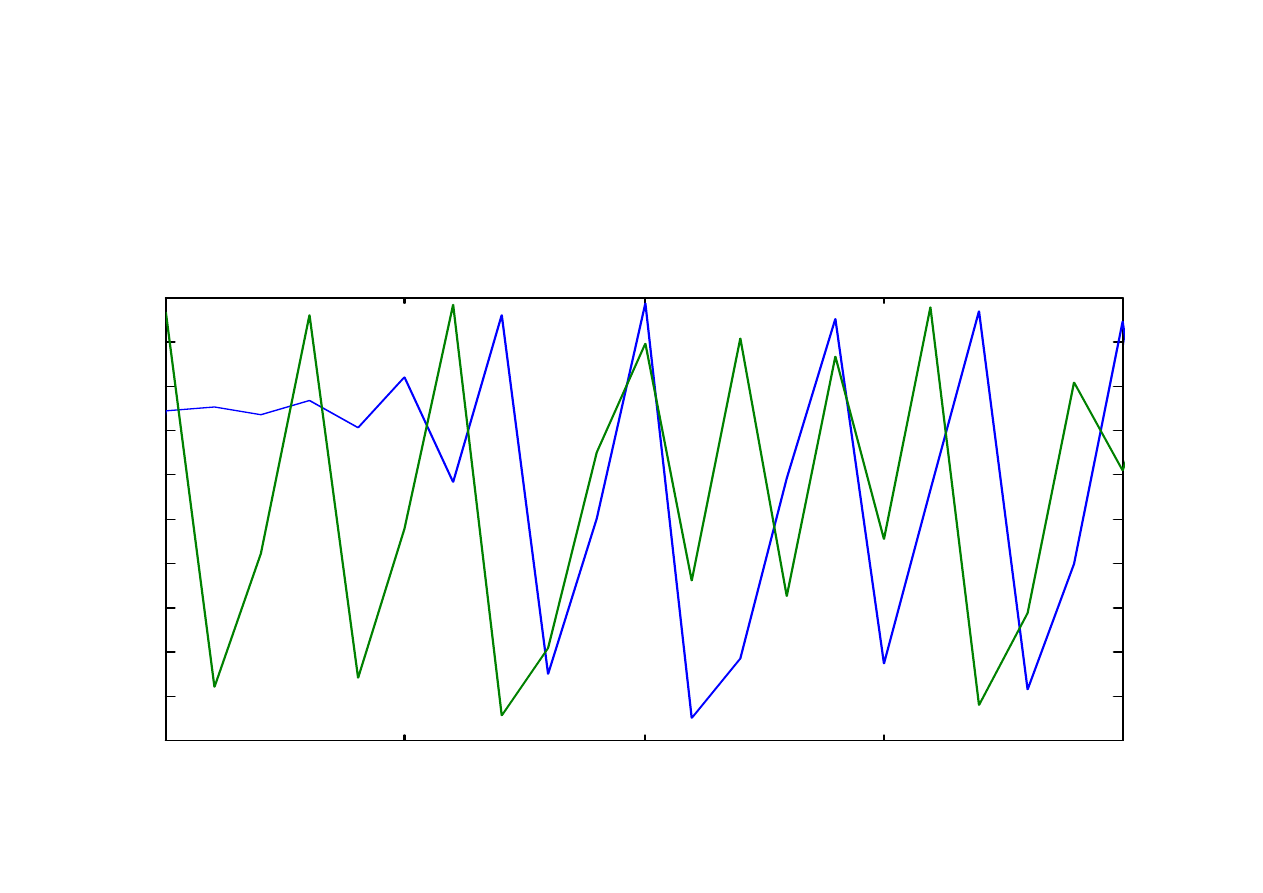
Drgania generowane dla warunków początkowych

x(1) = 0,300 (niebieska linia)

oraz x(1) = 0,301 (zielona linia);

Parametr r = 3,95; Przedział czasu <115,135>

1 1 5

1 2 0

1 25

1 30

1 3 5

0

0 .1

0 .2

0 .3

0 .4

0 .5

0 .6

0 .7

0 .8

0 .9

1

1 1 5

1 2 0

1 2 5

1 3 0

1 3 5

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

0 . 9

1

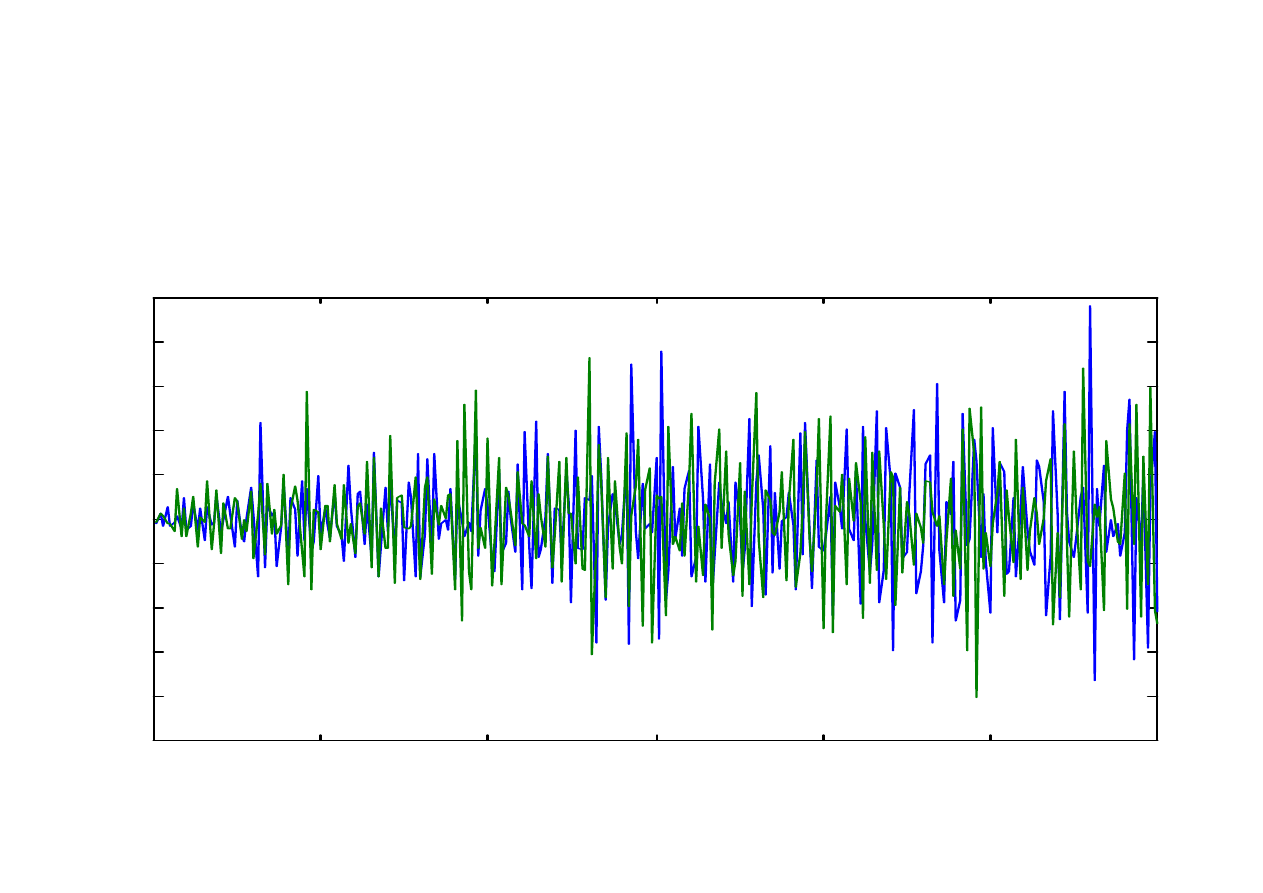
Autokowariancja drgań generowanych dla

warunków początkowych x(1) = 0,300 (niebieska

linia) oraz dla x(1)=0,301 (zielona linia);

Parametr r = 3,95

0

5 0

1 0 0

1 5 0

2 0 0

2 5 0

3 0 0

- 5

- 4

- 3

- 2

- 1

0

1

2

3

4

5

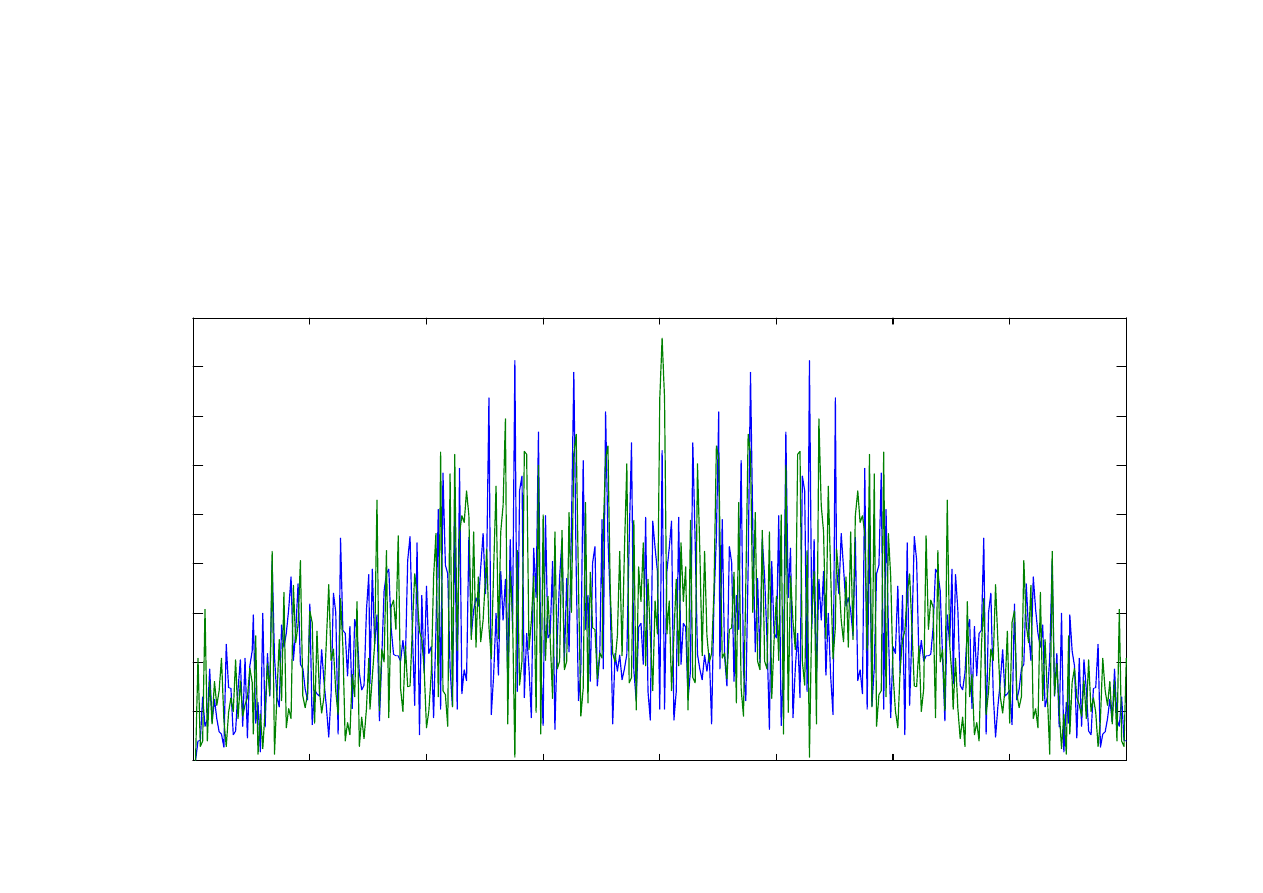
Widmo (DFT) drgań generowanych dla warunków

początkowych x(1) = 0,300 (niebieska linia) oraz dla

x(1)=0,301 (zielona linia); Parametr r = 3,95

Widmo wyznaczono dla sygnałów bez składowej stałej.

0

5 0

1 0 0

1 5 0

2 0 0

2 5 0

3 0 0

3 5 0

4 0 0

0

2

4

6

8

1 0

1 2

1 4

1 6

1 8

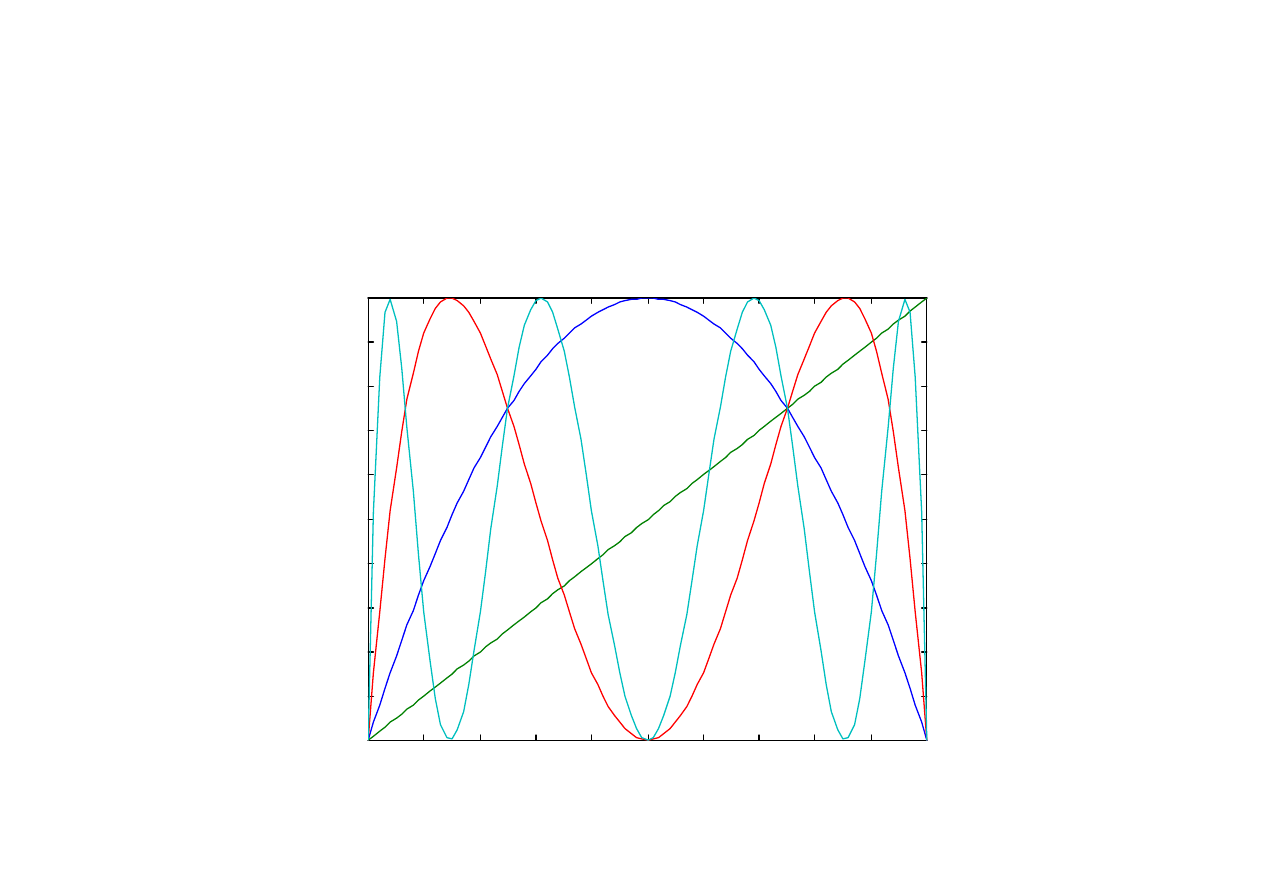
Odwzorowanie F

4

dla odwzorowania logistycznego

x(n+1) = F[x(n)] dla r = 4,00

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

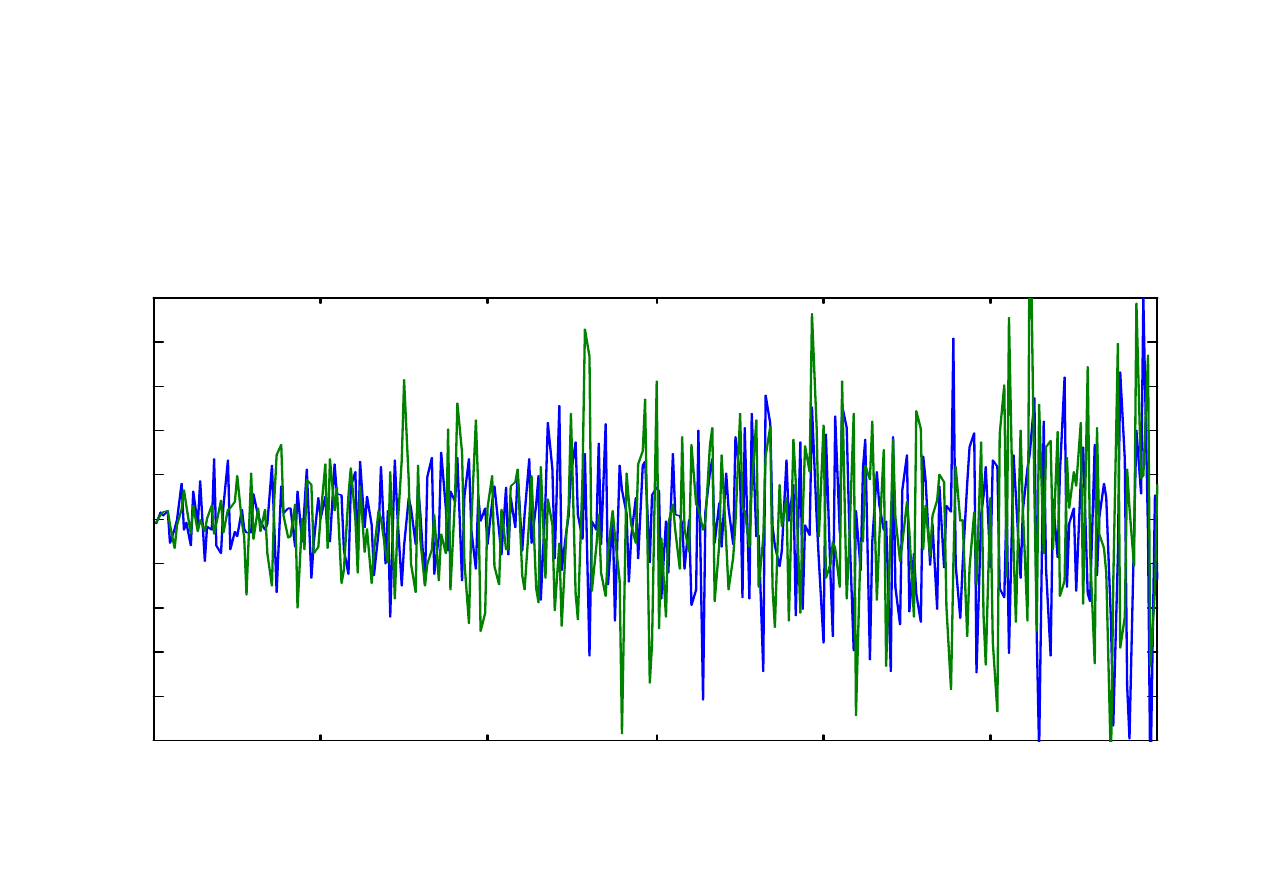
Autokowariancja drgań generowanych dla

warunków początkowych x(1) = 0,300 (niebieska

linia) oraz dla x(1)=0,301 (zielona linia);

Parametr r = 4,00

0

5 0

1 0 0

1 5 0

2 0 0

2 5 0

3 0 0

- 5

- 4

- 3

- 2

- 1

0

1

2

3

4

5