Lecture

5

THE RANK

DETERMINANTS AND THE INVERSE MATRIX

1. THE RANK OF A MATRIX

Definition

The leading coefficient of a row in a matrix is the first nonzero
entry in that row. So, for example,

The numbers 1, 2, 4 are the leading coefficints.

Definition
A matrix is in row echelon form if is satisfies the following

requirements:

1. All nonzero rows are above any rows of all zeroes.

2. The leading coefficient of a row is always to the right of the

leading coefficient of the row above it.

3. All entries below a leading coefficient, if any, are zeroes.

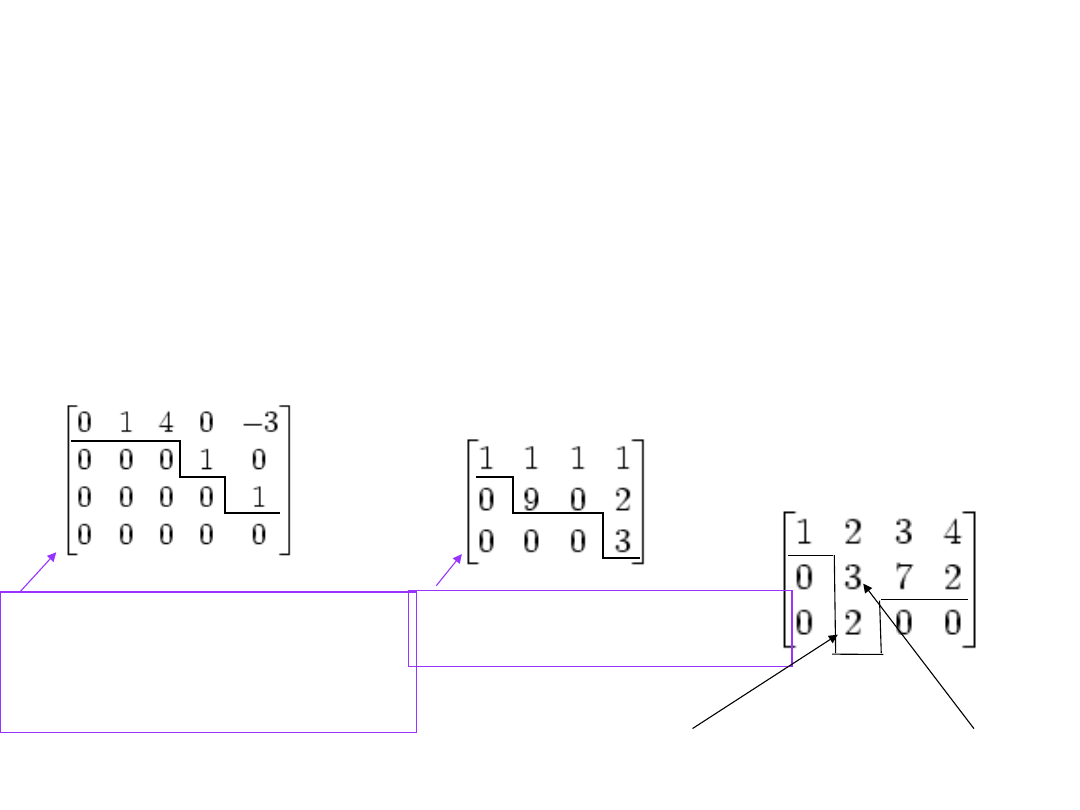
This matrix is in row echelon
form.
It has three leading
elements

As is this one. It also has
three leading elemnts

However, this matrix is not in row echelon form,
as it has nonzero entries below the leading
coefficient of the second row.

Typical structure in row echelon form

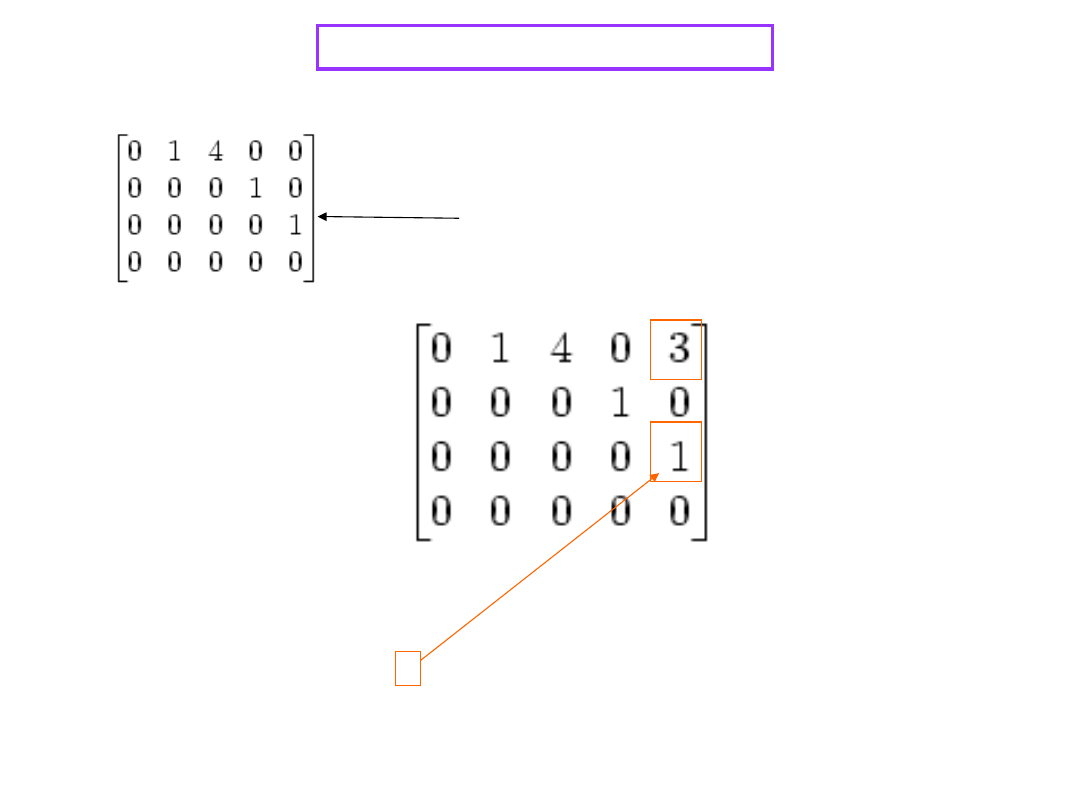
This matrix is in reduced row echelon form:
It has three leading elements

However, the obove matrix is not in reduced row
echelon form, as the 1 in the third row is not
the only nonzero entry in its column:

REDUCED ROW ECHELON FORM

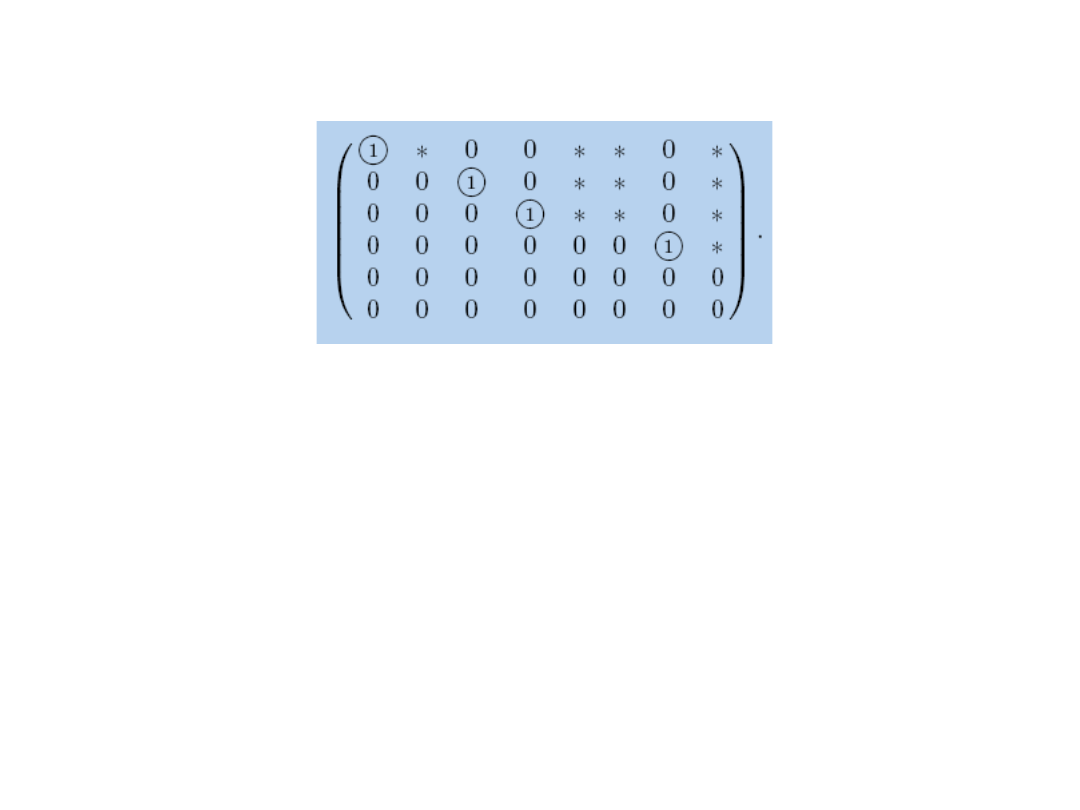
Typical structure in reduced row echelon form

A matrix is in reduced row echelon form (also known as row

canonical form) if it satisfies the following requirements:

1. All nonzero rows are above any rows of all zeroes.
2. The leading coefficient of a row is always to the right of the leading

coefficient of the row above it.

3. All entries below a leading coefficient, if any, are zeroes.
4. All leading coefficients are 1.
5. All leading coefficients are the only nonzero entries in a given column

(equivalently: all leading coefficients have zeros both above and
below them).

Every matrix can be transformed by elementary row operations into
an infinite number of echelon forms (they can all be multiples of each
other).
However, all matrices and their row echelon forms correspond to exactly
one matrix in
reduced row echelon form.

The

first three requirements

above are precisely those that determine a

matrix in row echelon form

RANK OF A MATRIX

Suppose that A

m x n

is reduced by row operations to an echelon form E.

The rank of A is defined to be the number;

rank(A) = number of leading elements
= number of nonzero rows in E
= number of basic columns in A.

Definition
The basic columns of A are defined to be those columns in A that contain
the positions of the leading elements.,

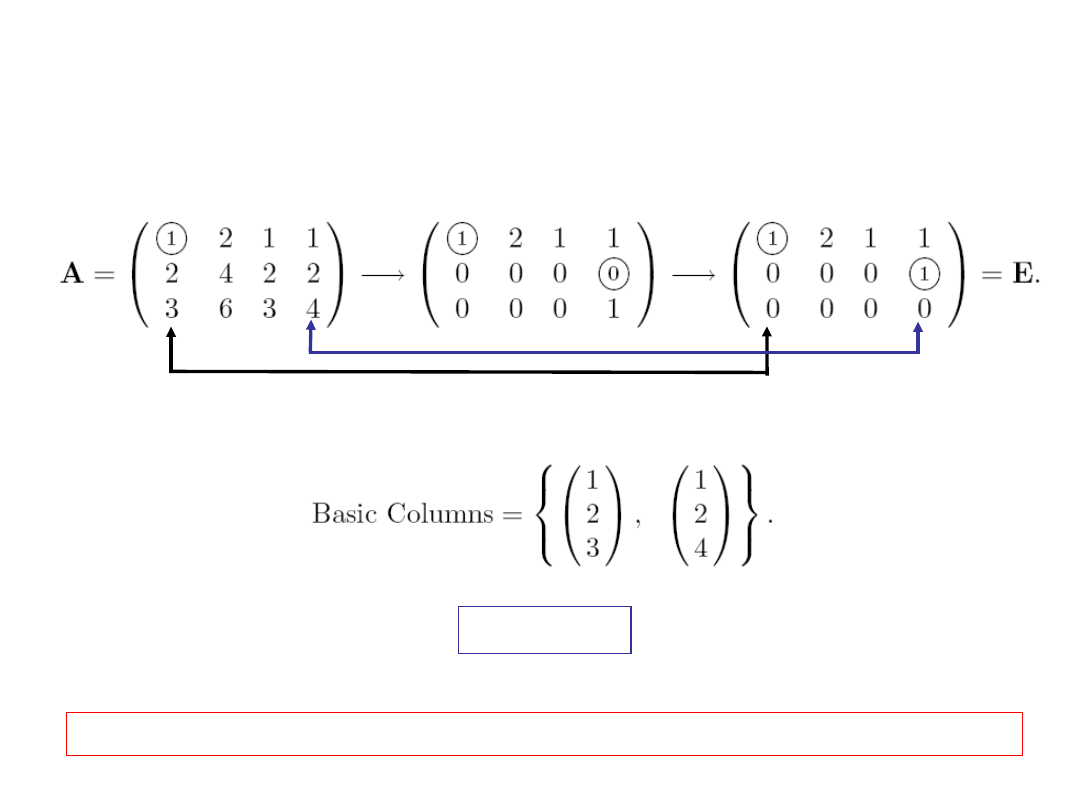
Example

We reduce the marix to row echelon form:

There are two leading lements, so rank(A) = 2, and

Note that the basic columns are extarcted from A not from E.

rank A =2

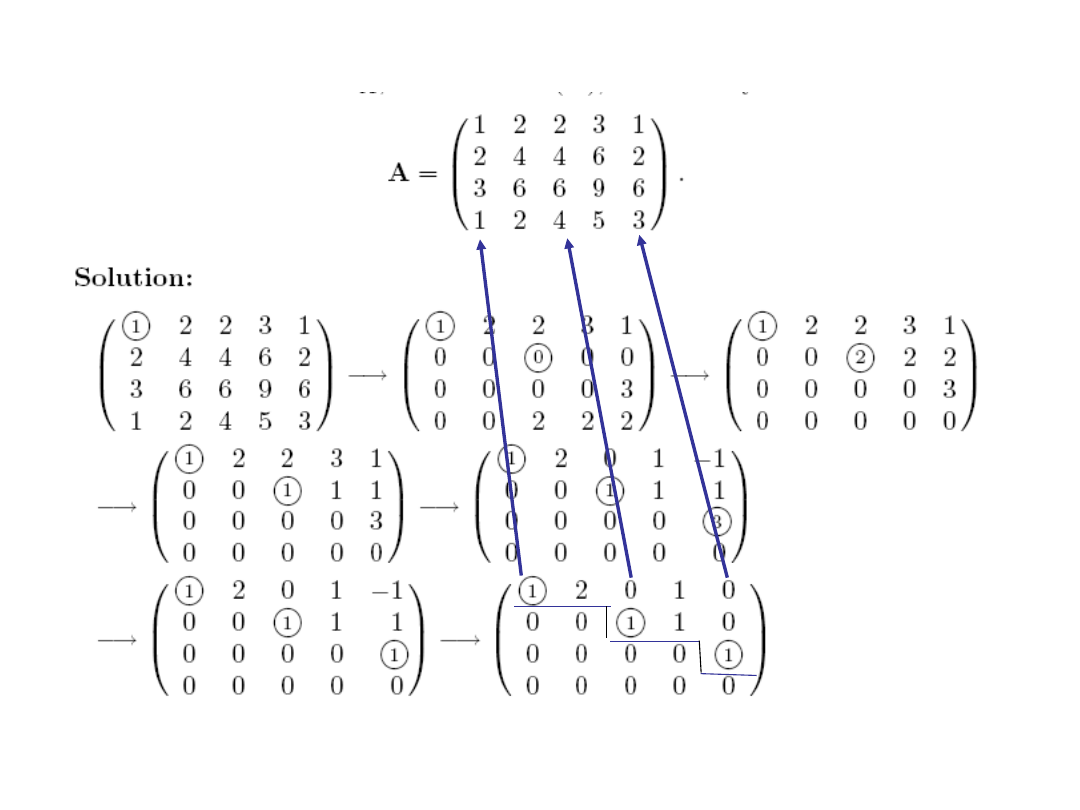
Find the rank and the basic columns of

The rank(A)=3, the basic columns are (1,2,3,1)

T

, (2,4,6,4)

T

, (1,2,6,3)

T

.

.

Example

DETERMINANT

THE ORIGIN OF THE DETERMINANT















B

dy

cx

A

by

ax



















d

/

B

dy

cx

c

/

A

by

ax

1

2

R

R

aB

ady

acx

cA

bcy

acx

































cA

aB

y

)

bc

ad

(

cA

bcy

acx

























bc

ad

cA

aB

y

bc

ad

Bb

Ad

x

DETERMINANT

Definition
The determinant of a 2 by 2 matrix

A

is equal to

bc

ad

d

c

b

a

Det

A

Det



















Notation

Det A, det A,

d

c

b

a

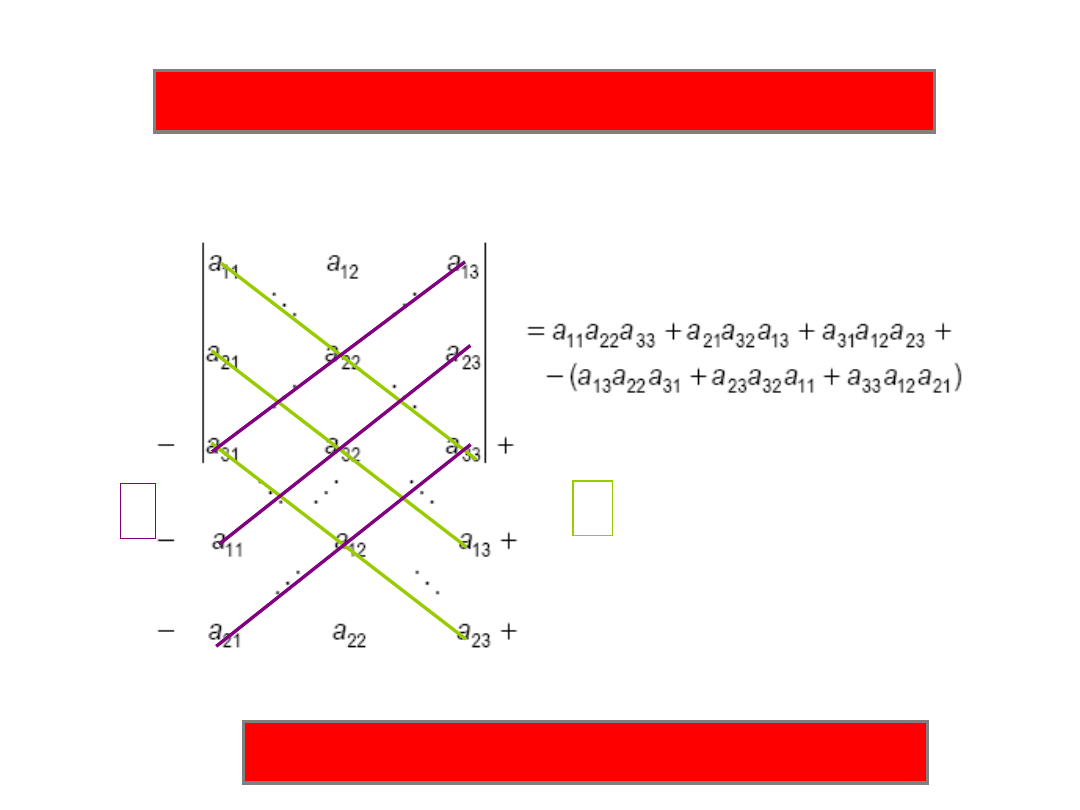
The Sarrus Method for 33 matrices

+

-

it works ONLY for 33 matrices

DEFINITION OF DETERMINANT - expansion along the first row















































1

1

1

1

1

1

1

1

1

2

21

21

1

1

1

12

11

n

n

n

n

n

n

nn

n

n

n

n

a

a

a

a

a

a

a

a

a

a

a

a

a

,

,

,

,

,

,

















A =













































1

1

1

1

1

1

1

1

2

21

21

1

1

1

12

11

n

n

n

n

nn

n

n

n

n

a

a

a

a

a

a

a

a

a

a

a

a

,

,

,

,

,











• 

We cross out the first row and the i-th column. In

this way we obtain a matrix n by n and name it

A

1,i

1.

2.

3.

Type I Elementary Row Operation

The determinant of a matrix in which every element of a row (column) is zero
is also zero.

The determinant of a matrix with two identical rows (columns) is zero

Some properties of determinants

The determinant of a square matrix is equal to the determinant of its transpose

Det A = Det A

T

Property 2.

4.

5
.

The determinant of a matrix in which one of the rows (columns) is a
linear combinationof the others is equal to zero.

The determinant of a matrix which has the elements of one row (column)
equal to the sum of two determinants is equal to the sum of two determinants
of matrices with the elemnets of appropriate rows replaced by the components
of the sum.

Type III Elementary Row Operation

OTHER METHODS OF CALCULATING THE DETERMINANT

1. We can reduce the matrix using type III Elementary Row Operations,
and then calculate the determinant.

2. We can expand the determinant along another row or column.

To explain the second method we need more definitions...

Some definitions

Definition
A kk minor determinant of A is the determinant of a k  k square submatrix of A





































1

2

3

3

9

5

1

3

4

4

0

2

7

2

3

1

e.g. a minor of A is

20

21

1

1

3

7

1





















det

Definition
A submatrix of A is formed by removing whole columns or rows from
the original matrix.



























1

2

0

2

5

4

3

2

1

A

The cofactor :

1

1

0

3

1

1

2

2

22

























det

)

(

D

Especially important are the (n - 1) × (n - 1) minors of an n × n

square

matrix

- these are often denoted M

ij

, and are derived by removing the i-

th row and the j-th column.

Definition
The cofactor

D

ij

of A is defined as

(−1)

i + j

times the minor

M

ij

of

A

.

D

ij

= (−1)

i + j

M

ij

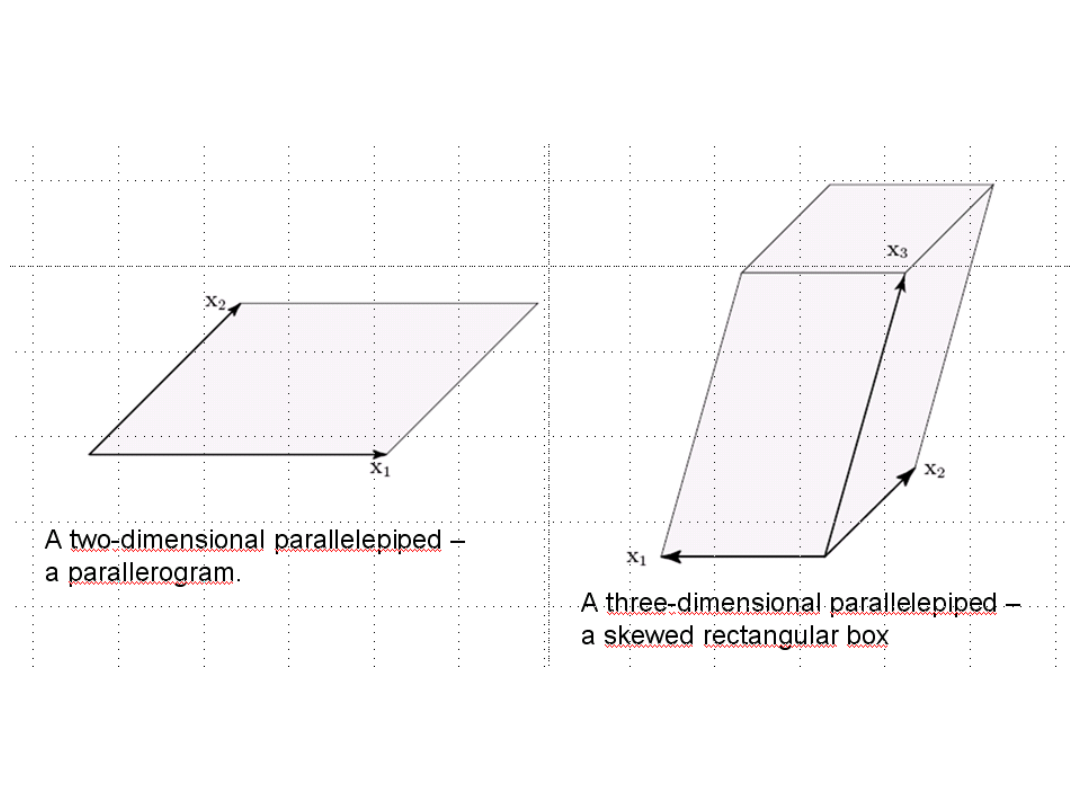
GEOMETRICAL INTERPRETATION

Example
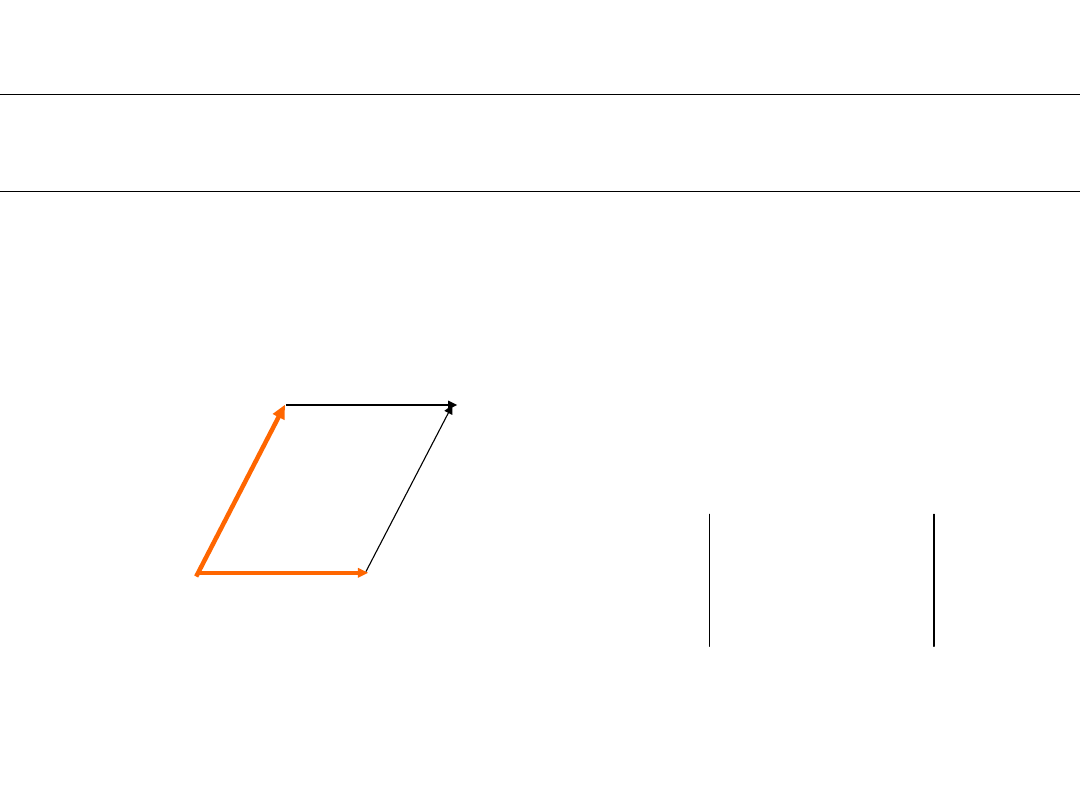
The area (2-dim volume) of a parallelogram described by vectors [2,0]
and [1,2] is

4

2

0

1

2















 det

AREA

Vector [2,0]

vector[1,2]

The volume V of a parallelepiped generated by the columns of a matrix A is
V= [det (A A

T

)]

1/2

.

In particular, if A is square, then V = | det A | .

THEOREM (ON THE DETERMINANT OF A PRODUCT OF TWO MATRICES).

Let A and B be square matrices of the same order, then:

det ( A B) = det A  det B.

THE INVERSE OF A MATRIX

DEFINITION
A matrix A is called non-singular iff
Det A  0

If an inverse exists then we can 'cancel' matrix terms:

A·B = A·C

A

-1

·/

A·B = A·C

A

-1

·A ·B = A

-

1

·A·C

(A

-1

·A) ·B =(A

-1

·A)

·C
I·B = I·C
B =C

We multiply from the
R-HS

INVERSE OF MATRIX
Definition
The inverse matrix of a square matrix

A

is a matrix denoted by

A

-1

,

such that:

A

-1

 A = A  A

-1

= 1

B · A = C · A

B · A = C · A

/

·

A

-1

B · A · A

-1

= C · A · A

-1

B ·(A

-1

·A) = C ·(A

-1

·A)

B · I = C · I

B = C

Or

We multiply from the L-HS

THEOREM

1) An invertible matrix

A

( one for which an inverse matrix

exists) is nonsingular, that is

Det

A

 0.

2) The inverse matrix

A

-1

of a non-singular matrix is non-singular

(A

-1

)

-1

= A

3) The determinant of the inverse matrix

A

-1

is equal to the

reciprocal of the determinant of matrix

A

:

DetA

1

A

Det

1





Det (AB) = DetA DetB

Theorem

The inverse matrix can be found from the
formula



.

A

A

A

D

1





Definition
If you replace each element of a square matrix A with its own
cofactor and transpose the result, then you have made the adjoint
matrix (new term adjugate) of A.

 

T

ij

D

D

A 

To prove the formula

.

A

A

A

D

1





We will first prove the following cofactors property, for 3x3 matrices,
The method of the proof is universal.

Cofactors property

Theorem : When we multiply the elements of a row of a square matrix with the
corresponding cofactors of another row, then the sum of these product is 0.
Proof:

Take

Let

A, B, C, D, E, F, G, H, I

be the cofactors of

a, b, c, d, e, f, g, h, i

.

We multiply the elements of a row, say the second, with the corresponding
cofactors of another row, say the the first.
We have to prove that

dA + eB + fC = 0

.

Take now the matrix

Since the matrix has two equal rows, its determinant is

0

. So

Det(Q) = 0

.

Furthermore, the cofactors of corresponding elements of the first row of

P

and

Q

are the same. These cofactors are

A, B

and

C

.

Hence the calculation of

Det(Q)

emanating from the first row gives

dA+eB+fC

.

Since we know that

det(Q) = 0, dA+eB+fC =

0

.

Q.E.D.























i

h

g

f

e

d

c

b

a

P























i

h

g

f

e

d

f

e

d

Q

Now we shall prove the formula

for a 3 x 3 matrix,
the method of the proof for is universal.

.

P

P

P

D

1





The diagonal elements of this matrix are

Det P



































































































iI

hH

gG

iF

hE

gD

iC

hB

gA

fI

eH

dG

fF

eE

dD

Cf

eB

dA

cI

bH

aG

cF

bE

aD

cC

Bb

aA

I

F

C

H

E

B

G

D

A

i

h

g

f

e

d

c

b

a

First we calculate the product P times (adjoint P)

P P

D

=



































iI

hH

gG

0

0

0

fF

eE

dD

0

0

0

cC

Bb

aA

Because of the cofactors property,

I

P

Det

1

0

0

0

1

0

0

0

1

P

Det

P

Det

0

0

0

P

Det

0

0

0

P

Det

















































In the same way ,

P

D

P = Det P I

So

I

P

DetP

P

and

I

DetP

P

P

D

D





thu
s

P

Det

p

P

D

1





QED

Use elementary row operations on the augmented matrix [

A | I

],

as in the Gaussian Elimination Method, to reduce

A

to the unit matrix

I

, then

transform the unit matrix to

A

-1

that is

[

A | I

] is reduced to [

I | A

-1

].

Justification

1

1

A

I

A

x

I

I

x

A











Another method to find the inverse
matrix

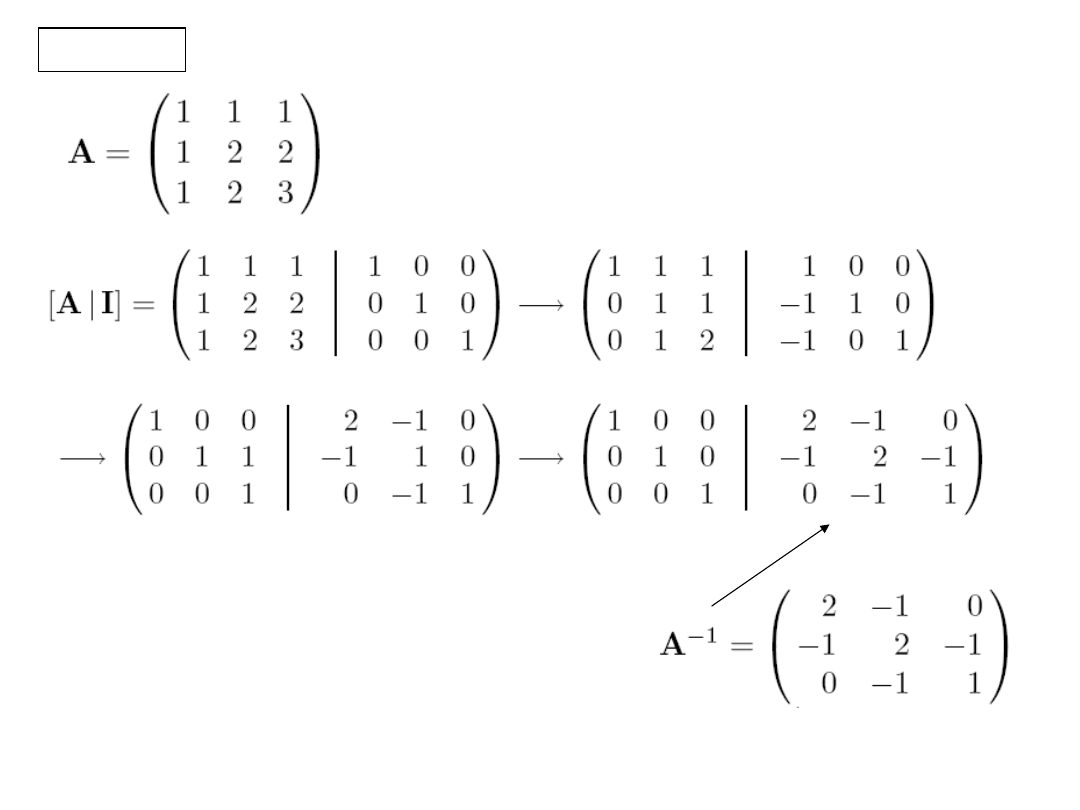
EXAMPLE

Let A and B be two nonsingular matrices then,

 

   

1

T

T

1

1

1

1

A

A

.

3

)

inversion

for

law

order

reverse

the

(

A

B

AB

.

2

r

nonsingula

also

is

AB

product

The

.

1















If

0

A

Det 

then the inverse matrix A

-1

exists.

.

A

Det

A

A

D

1



