Seminarium SEP o/Gliwice
30 marca 2010
Zastosowanie zespołów prądotwórczych do awaryjnego zasilania sieci
elektroenergetycznej nN
Ppłk w st. sp. mgr inż. Julian Wiatr
WBSPBiL Warszawa
CKSIiUE SEP
elektro.info
1. Podstawy obliczania prądów zwarciowych zwarcia
Podczas zwarć następuje przepływ prądów wielokrotnie większych od wartości
znamionowych, na które zostały dobrane przekroje przewodów i ich zabezpieczenia.
Przepływający prąd powoduje szybki wzrost temperatury przewodu, przez co stwarza
możliwość jego uszkodzenia. Wzrost temperatury przewodu stwarza również zagrożenie
pożarowe. W celu uniknięcia tych zagrożeń projektowane urządzenia oraz ich zabezpieczenie
muszą spełniać określone wymagania.
W niniejszym rozdziale zostaną pokrótce omówione zasady obliczeń prądów zwarciowych,
które stanowią ważny element przy doborze przewodów i ich zabezpieczeń.
1.1.
Obliczanie zwarć. Początkowy prąd zwarciowy
Zwarcie polega na połączeniu dwóch lub więcej punktów obwodu elektrycznego o różnych
potencjałach, w tym ziemi, przez pomijalnie małą impedancję. Zwarcie może być
przypadkowe lub celowe. Zwarcie ze względu na liczbę torów można podzielić na (rysunek
1.1.1):
- zwarcie trójfazowe i trójfazowe doziemne,
- zwarcie dwufazowe i dwufazowe doziemne,
- zwarcie jednofazowe.
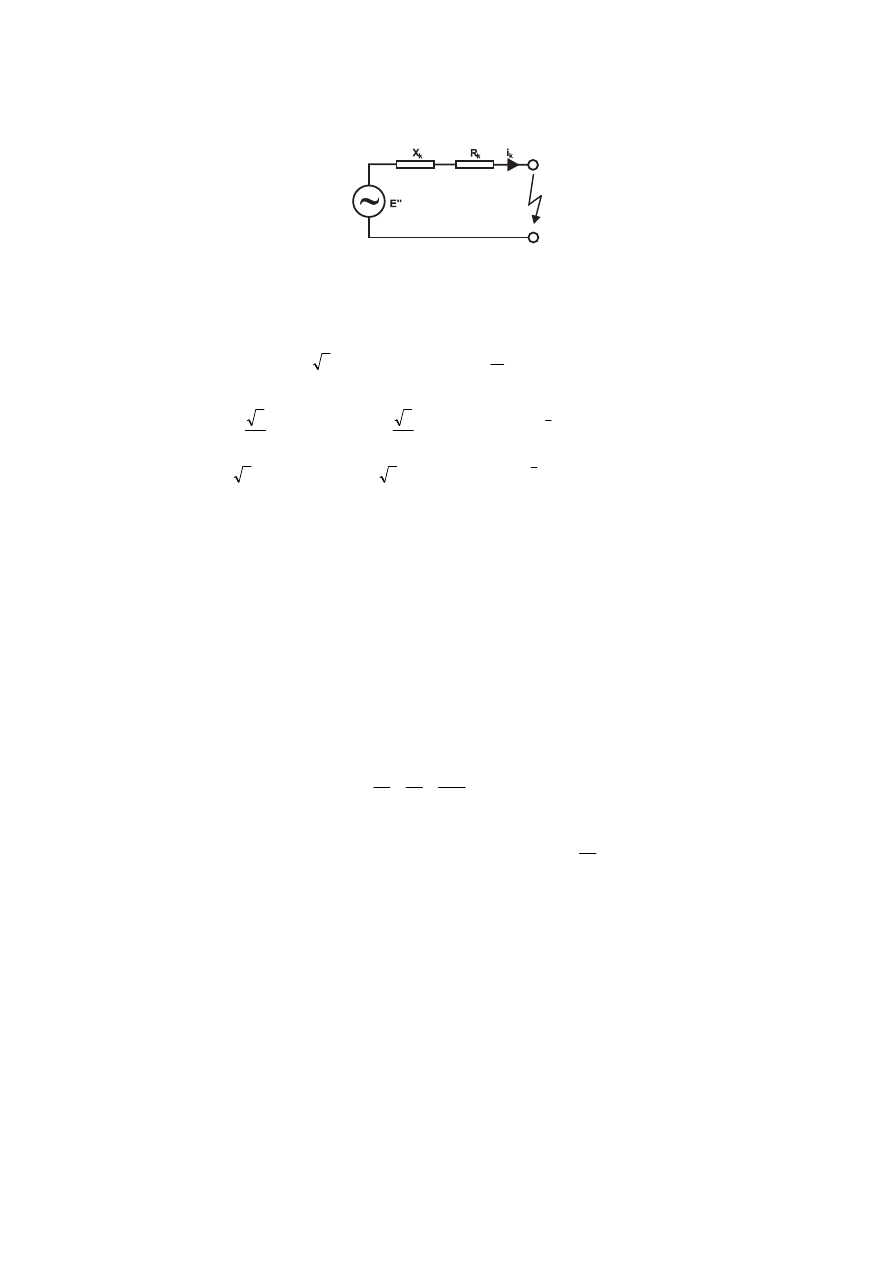
Na rysunku 1.1.1 przedstawiony został najprostszy obwód zwarciowy. Jest on
scharakteryzowany przez rezystancję R
k
oraz reaktancję X
k
, a tym samym przez impedancję
obwodu zwarciowego wyrażoną wzorem:
gdzie:
R
k
- wypadkowa rezystancja obwodu zwarciowego, w [
],
X
k
- wypadkowa reaktancja obwodu zwarciowego, w [
],
Z
k
- wypadkowa impedancja obwodu zwarciowego, w [
].
1.
Rysunek 1.1.1. Rodzaje zwarć [19]:
2
k
2
k
k
X
R
Z
(1.1.1.)
a) trójfazowe symetryczne; b) dwufazowe; c) dwufazowe doziemne; d) jednofazowe doziemne w sieci uziemionej
bezpośrednio lub przez
impedancję; e) jednofazowe doziemne w sieci z izolowanym punktem neutralnym
2.
Rysunek 1.1.2. Najprostszy obwód zwarciowy prądu przemiennego [19]
Przedstawiony na rysunku 1.1.2 obwód można opisać równaniem różniczkowym (przy
założeniu, że prąd w obwodzie tuż przed zwarciem miał pomijalną wartość w stosunku do
prądu zwarciowego, a kąt fazowy napięcia w chwili zwarcia wynosił
):
Rozwiązanie tego równania prowadzi do następującej zależności:
gdzie:
i
k
- wartości chwilowe prądu zwarciowego, w [A],
T - elektromagnetyczna stała czasowa określona wzorem 1.1.4, w [s],
i
AC
- chwilowa wartość składowej okresowej prądu zwarciowego, w [A],
i
DC
- chwilowa wartość składowej nieokresowej prądu zwarciowego, w [A],
"
k
I - początkowy prąd zwarciowy, w [A].
Prąd płynący podczas zwarcia zawiera składową nieokresową (i
DC
), która wraz z upływem
czasu zwarcia zanika oraz składową okresową (i
AC
) prądu zwarciowego.
Składowa okresowa prądu zwarcia posiada przebieg sinusoidalny, natomiast składowa
nieokresowa zanika wykładniczo wraz
z upływem czasu trwania zwarcia T
k
.
Czas zanikania składowej okresowej jest uzależniony od elektromagnetycznej stałej czasowej
T, której wartość zależy od parametrów obwodu zwarciowego i wyraża się wzorem:
gdzie:
k
- argument impedancji obwodu zwarciowego
)
R
X
tg
,
arctg
(
k
k
k
k
k
,
L
k
- indukcyjność obwodu zwarciowego, w [H],
R
k
- rezystancja obwodu zwarciowego, w [
],
X
k
- impedancja obwodu zwarciowego, w [
],
=2f - pulsacja, w [-],
f - częstotliwość, w [Hz].
Przykładowy przebieg prądu zwarciowego przedstawia rysunek 1.1.3, na którym
przedstawiono również przebieg czasowy składowej nieokresowej (i
DC
) oraz składowej
okresowej (i
AC
) prądu zwarciowego.
dt
di
*
L
*
i
*
R
)
t
sin(
*
E
*
2
(1.1.2.)
DC
AC
T
t
k
"
k
T
t
k
k
k
i
i
e
*
)
t
sin(
*
"I
*
2
)
t
sin(
*
I
*
2
e
*
)
t
sin(
*
E
*
Z
2
)
t
sin(
*
E
*
Z
2
i
(1.1.3.)
k
k
k
k
k
tg
R
X
R
L
T
(1.1.4.)
3.
Rysunek 1.1.3. Przebieg prądu zwarciowego [24]
Wartość chwilowa prądu zwarciowego zgodnie ze wzorem 1.1.3, jest sumą obydwu
składowych (okresowej i nieokresowej):
gdzie:
i
DC
– nieokresowa składowa prądu zwarciowego, w [A],
i
AC
– okresowa składowa prądu zwarciowego, w [A].
Początkowy prąd zwarciowy (
"
k
I ) można wyznaczyć z następującego wzoru:
gdzie:
"
k
I – początkowy prąd zwarciowy (wartość skuteczna składowej okresowej prądu
zwarciowego w chwili powstania
zwarcia, t = 0), w [A],
E
”
– podprzejściowa wartość siły elektromotorycznej, w [V],
Z
k
– wypadkowa impedancja obwodu zwarciowego, w [
].
Prąd ten nie jest największym prądem powstającym w miejscu zwarcia, ale stanowi podstawę
do prowadzenia dalszych obliczeń zwarciowych.
Uwaga!
Wszelkim źródłom zasilającym prąd zwarciowy (system elektroenergetyczny, lokalny
generator lub silnik) w urządzeniu o napięciu znamionowym U
n
przypisuje się jednakową
wartość siły elektromotorycznej E
"
:
gdzie:
c - współczynnik określony zgodnie z tabelą 1.1.1, w [-],
U
n
- znamionowe napięcie międzyfazowe, w [V].
Zwarcie może nastąpić w pobliżu generatora lub w głębi systemu elektroenergetycznego,
przez co rozróżniamy zwarcia:
- bliskie,
- odległe.
Przebiegi czasowe zwarcia odległego oraz zwarcia bliskiego przedstawiają rysunki 1.1.4 oraz
1.1.5:
DC
AC
k
i
i
i
(1.1.5.)
k
"
"
k
Z
E
I
(1.1.6.)
3
U
*
c
E
n
''
(1.1.7.)
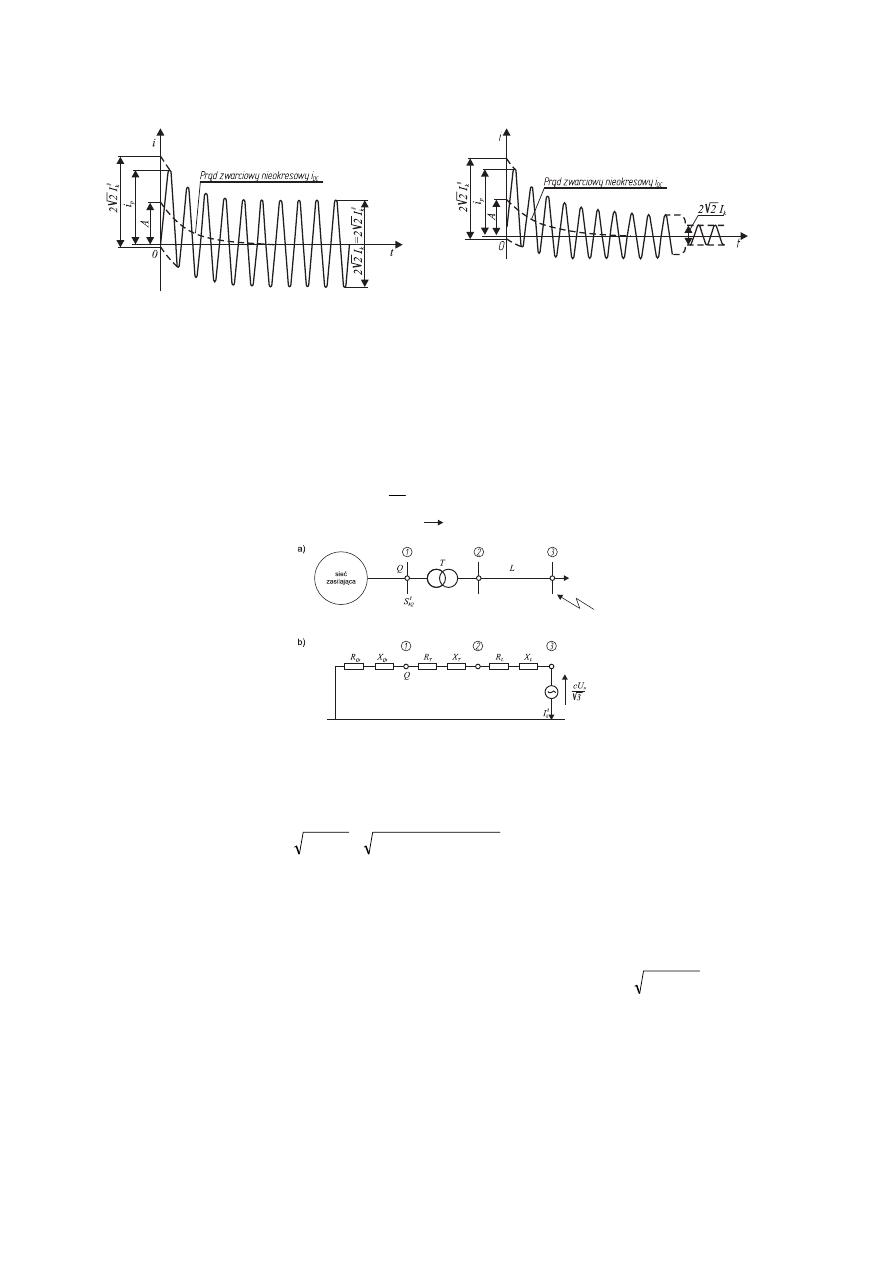
4. Rysunek 1.1.4. Przebieg prądu zwarciowego – zwarcie
odległe [4] (i
p
-prąd udarowy – patrz pkt 1.3.1)
5. Rysunek 1.1.5. Przebieg prądu zwarciowego – zwarcie
bliskie [4]
W przypadku zwarcia odległego początkowy prąd zwarciowy
"
k
I posiada przez cały czas
trwania zwarcia niezmienną wartość (rysunek 1.1.4).
Schemat obwodu zwarciowego w ogólnym przypadku dla zwarć zachodzących w systemie
elektroenergetycznym przedstawia rysunek 1.1.6.
Zwarcie odległe przy zasilaniu bezpośrednio z generatora występuje, gdy zachowany jest
stosunek:
6. Rysunek
1.1.6.
Przykładowy schemat zastępczy obwodu zwarciowego [4]:
a) schemat sieci; b) schemat zastępczy obwodu zwarciowego
Przy zwarciu w systemie elektroenergetycznym zwarcie odległe występuje, gdy spełniony jest
warunek:
gdzie:
R
L
- rezystancja linii zasilającej, w [
],
R
T
- rezystancja transformatora, w [
],
X
L
- reaktancja linii zasilającej, w [
],
X
T
- reaktancja transformatora, w [
],
Z
kQ
- zastępcza impedancja systemu elektroenergetycznego, w [
] (
2
kQ
2
kQ
kQ
X
R
Z
),
R
kQ
– zastępcza rezystancja systemu elektroenergetycznego, w [
],
X
kQ
- zastępcza reaktancja systemu elektroenergetycznego, w [
],
"
k
I - początkowy prąd zwarcia, w [A],
I
nG
- znamionowy prąd generatora, w [A].
Do celów projektowych w sieciach i instalacjach nN wystarczającym jest obliczenie prądów
zwarciowych przy zwarciach trójfazowych oraz jednofazowych. Prądy przy zwarciach
2
I
I
nG
"
k
(1.1.8.)
kQ
2
L
T
2
L
T
2
k
2
k
k
Z
2
)
X
X
(
)
R
R
(
X
R
Z
(1.1.9.)
trójfazowych stanowią podstawę doboru aparatów, kabli oraz przewodów, gdyż
charakteryzują najgorsze warunki zwarciowe dla obwodu. Zwarcia te obliczane są na
początku linii lub instalacji tak, jakby wystąpiły zaraz za zabezpieczeniem. Natomiast prądy
zwarć jednofazowych obliczane w najdalszym punkcie instalacji służą do oceny skuteczności
samoczynnego wyłączenia, powszechnie stosowanego jako środek ochrony
przeciwporażeniowej przy uszkodzeniu.
Podstawowe wzory do obliczenia początkowego prądu zwarciowego można przedstawić w
następującej postaci:
a) dla zwarć trójfazowych symetrycznych
b) dla zwarć jednofazowych
gdzie:
"
3
k
I
- prąd zwarcia trójfazowego (symetrycznego), w [A],
"
1
k
I
- prąd zwarcia jednofazowego, w [A],
U
1f
- napięcie fazowe, w [V],
U
n
- napięcie międzyfazowe, w [V],
Z
k1
- impedancja zwarciowa dla zwarć jednofazowych, w [
],
Z
k3
- impedancja pętli zwarciowej dla zwarć trójfazowych, w [
],
X
p
– reaktancja przewodu, w [
],
R
p
– rezystancja przewodu, w [
],
c
max
- współczynnik korekcyjny siły elektromotorycznej obwodu zwarciowego w zależności
od napięcia znamionowego w sieci przyjmowany z tabeli 1.1.1, w [-].
Uwaga!
Wzór 1.1.10 dotyczy obliczenia największego prądu zwarciowego w obwodach
jednofazowych. Dla celów ochrony przeciwporażeniowej oblicza się najmniejszą wartość
spodziewanego prądu zwarcia jednofazowego.
1) Tabela 1.1.1. Współczynniki korekcyjne siły elektromotorycznej zasilającej obwód zwarciowy [25]
Napięcie znamionowe
c
max
przy obliczaniu I
kmax
c
min
przy obliczaniu I
kmin
3x230/400 V
1,00
0,95
Inne wartości nN
1,05
1,00
Wysokie napięcie U > 1 kV
1,10
1,00
1.2. Parametry elementów obwodu zwarciowego
1.2.1. Parametry zwarciowe systemu elektroenergetycznego
Dla oceny parametrów zwarciowych systemu elektroenergetycznego nie jest konieczna
znajomość jego konfiguracji. Przedsiębiorstwa energetyczne dysponują wartościami mocy
zwarciowej S"
kQ
1
w charakterystycznych punktach systemu elektroenergetycznego.
1
Moc zwarciowa nie posiada sensu fizycznego, ale umożliwia obliczanie szeregu parametrów zwarciowych.
2
p
L
T
kQ
2
p
L
T
kQ
3
k
3
k
n
max
"
k
"
3
k
)
R
R
R
R
(
)
X
X
X
X
(
Z
;
Z
3
U
c
I
I
(1.1.10.)
2
p
L
T
kQ
2
p
L
T
kQ
1
k
1
k
0
max
1
k
"
)
R
R
(
2
R
R
[
)]
X
X
(
2
X
X
[
Z
;
Z
U
*
c
I
(1.1.10.)
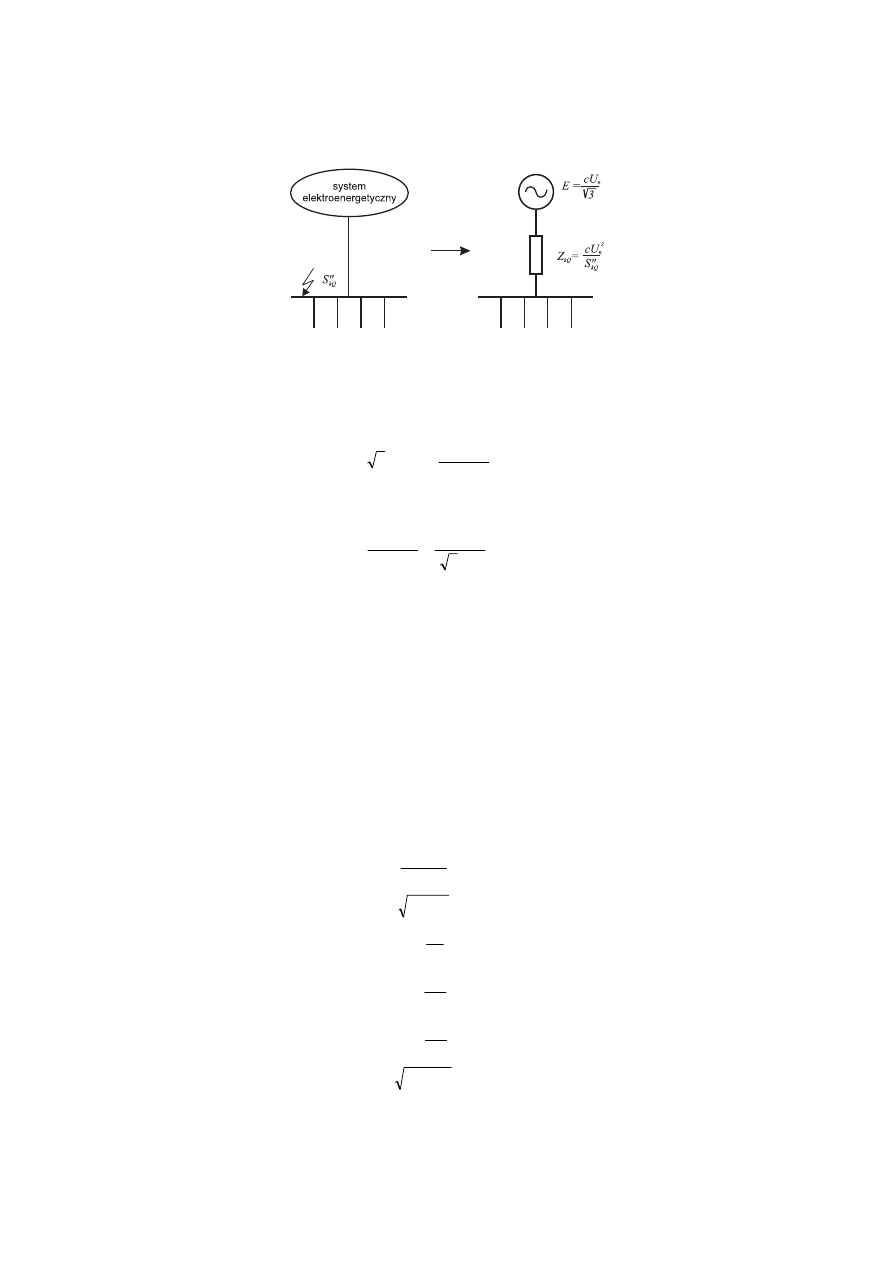
Zgodnie z takim założeniem zastępczy obwód zwarciowy możemy przedstawić tak jak na
rysunku 1.2.1.
7.
Rysunek 1.2.1. Parametry zastępcze poprzedzającego układu zasilania wyznaczone z mocy zwarciowej podanej dla określonego miejsca w
sieci [25]
Poszczególne parametry zwarciowe systemu elektroenergetycznego w charakterystycznych
jego punktach są określane przez podanie mocy zwarciowej S"
kQ
:
która stanowi podstawę do wyznaczania jego zastępczej impedancji, rezystancji oraz
reaktancji. Parametry te wyznacza się z następujących wzorów:
gdzie:
S"
kQ
- moc zwarciowa systemu elektroenergetycznego w charakterystycznym punkcie sieci
elektroenergetycznej podawana przez przedsiębiorstwo energetyczne, w [MVA],
Z
kQ
– impedancja (zastępcza) systemu elektroenergetycznego, w [
],
R
kQ
= 0,1*X
kQ
rezystancja (zastępcza) systemu elektroenergetycznego, w [
],
X
kQ
= 0,995*Z
kQ
– reaktancja (zastępcza) systemu elektroenergetycznego, w [
],
U
n
– znamionowe napięcie w miejscu zwarcia, w [V].
1.2.2. Parametry zwarciowe pozostałych elementów obwodu zwarciowego
Transformatory dwuuzwojeniowe
Impedancję zwarciową oraz pozostałe parametry składowe impedancji zwarciowej
transformatora oblicza się z poniższych zależności:
gdzie:
kQ
2
n
max
k
n
kQ
Z
U
*
c
"I
*
U
*
3
"
S
(1.2.1.)
k
n
max
kQ
2
n
max
kQ
"I
*
3
U
*
c
S
U
*
c
Z
(1.2.2.)
T
zn
_
obc
Rr
S
P
u
2
R
2
k
Xr
u
u
u
T
2
T
k
T
S
U
u
Z
T
2
T
k
T
S
U
u
X
T
2
T
R
T
S
U
u
R
2
T
2
T
T
R
X
Z
(1.2.3.)
(1.2.4.)
(1.2.5.)
(1.2.6.)
(1.2.7.)
(1.2.8.)
S
T
- moc znamionowa transformatora, w [kVA],
U
T
- napięcie znamionowe transformatora, przy którym oblicza się impedancję zwarciowe, w
[V],
u
k
- napięcie zwarciowe, w [-],
u
x
- składowa bierna napięcia zwarciowego, w [-],
P
obc_zn
- znamionowe obciążeniowe straty mocy, w [kW],
R
u
- składowa czynna napięcia zwarciowego, w [-],
X
T
- reaktancja transformatora, w [
],
R
T
- rezystancja transformatora, w [
],
Z
T
- impedancja transformatora, w [
].
Linie zasilające
W linii występują dwie składowe impedancji zwarciowej obliczane bez uwzględniania
poziomu napięcia:
- R
L
- rezystancja linii, w [
],
- X
L
- reaktancja linii, w [
].
Rezystancje linii obliczamy z poniższego wzoru:
gdzie:
- konduktywność przewodów, w [m/(mm
2
)],
L - długość przewodu, w [m],
S - przekrój przewodu, w [mm
2
].
Reaktancję linii obliczamy następująco:
a) linie kablowe
U < 1 kV: X = 0,08*L [
/km]
U > 1 kV: X = 0,1*L [
/km]
b) linia napowietrzna
U < 1 kV: X = 0,30*L [
/km]
U > 1 kV: X = 0,40*L [
/km]
Zespoły prądotwórcze
Zespół prądotwórczy - w przeciwieństwie do systemu elektroenergetycznego - stanowi źródło
„miękkie", ponieważ jego impedancja ulega zmianie wraz z upływem czasu trwania zwarcia,
co powoduje odmienność warunków zwarciowych w stosunku do sieci elektroenergetycznej,
która stanowi źródło „sztywne" (impedancja źródła zasilania nie ulega zmianie wraz z
upływem czasu zwarcia). Przed przystąpieniem do wyjaśnienia kolejności obliczeń, która nie
różni się od obliczania zwarć zasilanych przez źródło „sztywne", zostaną wyjaśnione zjawiska
zachodzące podczas zwarcia w generatorze synchronicznym. Rozpatrzone zostanie zwarcie
trójfazowe generatora: wewnątrz statora z trzema uzwojeniami fazowymi (a, b, c) wiruje z
prędkością o rotor mający uzwojenia wzbudzenia i klatki tłumiące w obu osiach d i q
(rysunek 1.2.2).
Rysunek 1.2.2 przedstawia schematyczny przekrój przez maszynę synchroniczną:
F - symbol uzwojenia wzbudzenia;
D - symbol klatki tłumiącej, a
1
, a
2
b
1
, b
2
, c
1
, c
2
- początki i końce uzwojeń poszczególnych
faz A, B, C;
a, b, c - osie uzwojeń poszczególnych faz;
d – podłużna oś wirnika;
q – poprzeczna oś wirnika;
S
L
R
L
(1.2.9.)
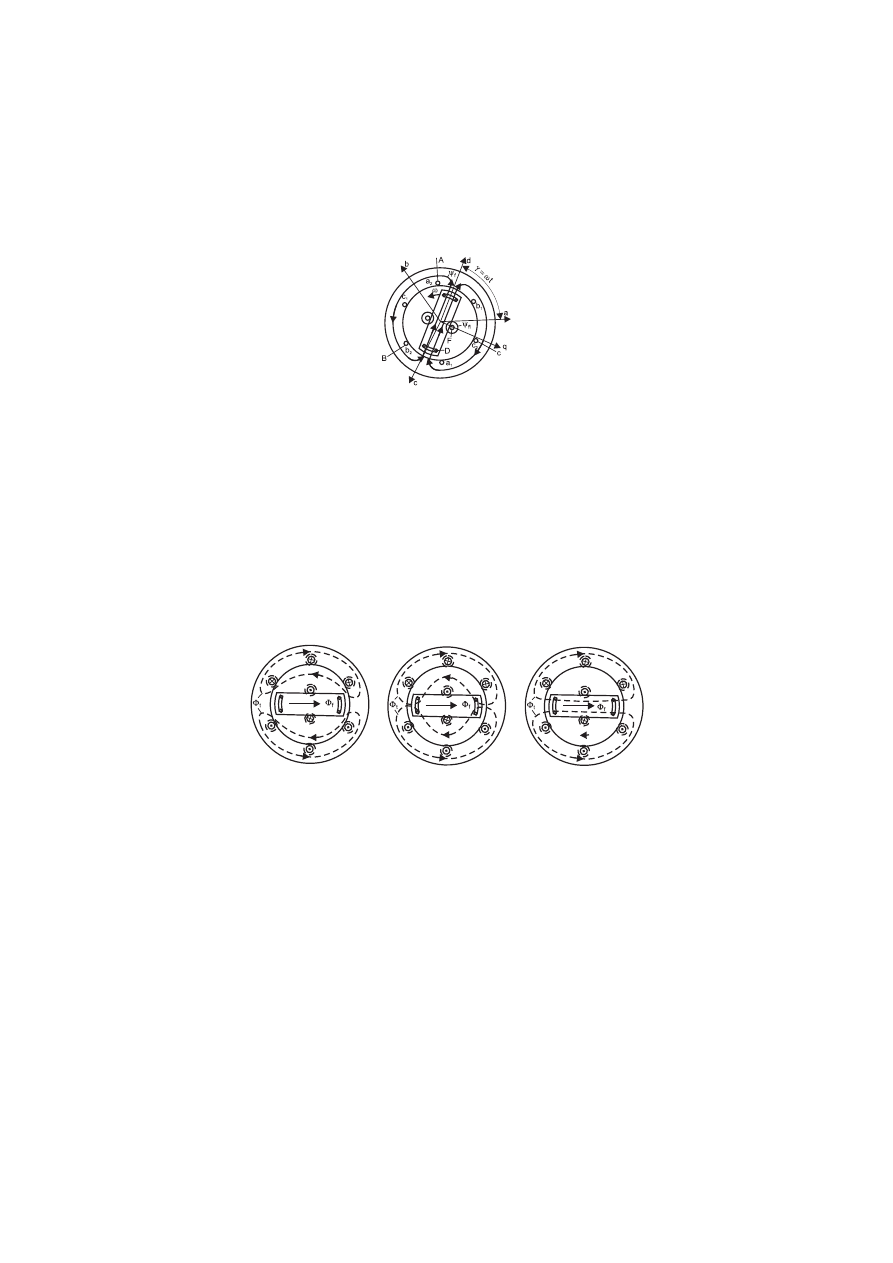
f
- strumień wzbudzenia;
fl
- strumień rozproszenia uzwojenia wzbudzenia;
= * t - kąt położenia osi d wirnika względem osi uzwojenia fazy A. Mierzony od osi fazy
A kąt osi wzdłużnej d wirnika wynosi
= * t. Strumień wirnika wywołuje podczas pracy ustalonej gwiazdę SEM w uzwojeniach
statora. Przed wystąpieniem zwarcia, każde z uzwojeń posiada pewną energię magnetyczną.
8. Rysunek
1.2.2.
Schematyczny przekrój przez maszynę synchroniczną [49]
Zwarcie generatora jako źródła napięcia powoduje powstanie okresowego prądu
zwarciowego. Dla zachowania ciągłości skojarzeń magnetycznych, w każdym z zamkniętych
uzwojeń wyzwalają się prądy pochodzące od energii pola magnetycznego. W uzwojeniu
wzbudzenia i w uzwojeniach tłumiących, w pierwszym momencie zwarcia powstają prądy
podtrzymujące poprzednie wartości strumienia skojarzonego z tymi uzwojeniami. W
rezultacie strumień stojana pochodzący od prądu zwarciowego w pierwszej chwili nie może
przejść przez uzwojenie wirnika. Stan maszyny synchronicznej, w którym strumień omija
wirnik, nazywa się stanem podprzejściowym. Przebieg zmiany drogi strumienia przedstawia
rysunek 1.2.3.
9.
Rysunek 1.2.3. Przebieg wypychanego poza wirnik strumienia stojana:
a) stan podprzejściowy; b) stan przejściowy; c) stan ustalony [23]
Rezystancja uzwojeń wirnika powoduje, że powstałe w nich prądy zanikają wskutek zamiany
energii magnetycznej uzwojenia na ciepło. Rezystancja uzwojeń tłumiących jest duża i prąd
bardzo szybko zanika. Dlatego też w krótkim czasie po wystąpieniu zwarcia, strumień stojana
pochodzący od prądu zwarciowego może wejść w część wirnika. Stan generatora, w którym
strumień stojana jest jeszcze wypychany poza uzwojenia wzbudzenia, nazywa się stanem
przejściowym. Zanikanie prądu w uzwojeniu wzbudzenia jest dość powolne (małe
rezystancje). Prąd zanika jednak po pewnym czasie i strumień stojana może bez przeszkód
przejść przez cały wirnik. Stan ten nazywa się stanem ustalonym zwarcia. Reaktancja
uzwojenia zależy od drogi strumienia tego uzwojenia, a ten z kolei przechodzi przez drogę o
zmieniającej się oporności magnetycznej i dlatego można powiedzieć, że reaktancja
generatora zmienia się w czasie trwania zwarcia. W pierwszej chwili zwarcia (stan
podprzejściowy) strumień omija cały wirnik, przechodząc przez długą szczelinę. Reaktancja
odpowiadająca tej sytuacji jest mała, nazywana podprzejściową i oznaczana
"
d
X . W stanie
przejściowym strumień częściowo przechodzi przez wirnik i reaktancja odpowiadająca tej
sytuacji nosi nazwę przejściowej, wyraża ją symbol
'
d
X . W stanie ustalonym zwarcia
występuje reaktancja synchroniczna i jest oznaczana X
d
. Dla przykładu (wartości te podawane
są w katalogach producentów generatorów):
"
d
X
= 10%
'
d
X
= 36%
d
X
= (200-300)%
w stosunku do impedancji generatora, którą należy określić następującym wzorem:
gdzie:
Z
kG
- impedancja znamionowa generatora, w [
],
U
nG
- napięcie znamionowe generatora, w [kV],
S
nG
- moc znamionowa generatora, w [MVA],
X
nG
– reaktancja znamionowa generatora, w [
].
Uwaga!
Wartości reaktancji zwarciowych podawane w katalogach producentów. Dla generatorów nN
do praktycznych obliczeń przyjmowane są wartości reaktancji podłużnej X
D
. Reaktancja
poprzeczna X
q
może zostać pominięta. Obliczenia wykonywane bez jej udziału obarczone są
niewielkim błędem mieszczącym się w dopuszczalnych granicach.
Przy zwarciu zasilanym z sieci elektroenergetycznej, mamy do czynienia ze zwarciem o
zmieniającej się reaktancji. W rezultacie zmian reaktancji generatora, zmianie musi ulegać
amplituda składowej okresowej prądu zwarciowego.
W przebiegu czasowym zwarcia można wyróżnić trzy składowe odpowiadające
poszczególnym stanom. Pierwsza część składowej okresowej zanika ze stałą czasową T’
d
zanikania prądu w uzwojeniu tłumiącym. Część druga zanika ze stałą czasową T’'
d
. Część
trzecia odpowiada reaktancji synchronicznej i jest stała. Przebieg prądu zwarciowego w stanie
jałowym generatora przedstawia rysunek 1.2.4.
10. Rysunek 1.2.4. Przebieg prądów z uwzględnieniem stałych czasowych [49]
a) składowa okresowa prądu fazy A; b) składowa nieokresowa prądu zwarciowego; c) wypadkowy prąd fazy A;
d) prąd w uzwojeniu wzbudzenia; e) prąd w klatce tłumiącej
nG
kG
nG
2
nG
kG
X
X
S
U
Z
(1.2.10.)
Przedstawione rozważania dotyczą generatora w stanie jałowym, co jest wystarczające dla
zrozumienia zachodzących w nim zjawisk podczas zwarcia. W stanie obciążonym przebiegi
czasowe posiadają podobny kształt, lecz różne wartości sił elektromotorycznych,
występujących na jego zaciskach powodują, że poszczególne części składowe prądu
zwarciowego mogą się różnić od przebiegów stanu ustalonego. Na przebieg prądu
zwarciowego ma również duży wpływ sposób regulacji napięcia i niesymetria magnetyczna
wirnika. Wpływ regulacji napięcia na prądy zwarciowe zależy od rodzaju wzbudzenia i
parametrów regulatora wzbudzenia. Niesymetria magnetyczna wirnika jest powodem tego, że
reaktancja podprzejściowa przyjmuje wartości pośrednie między X
d
i X
q
, przy czym zmiany
wokół wartości średniej zachodzą z podwójną częstotliwością, co powoduje, że w prądzie
zwarcia pojawia się składowa z podwójną częstotliwością. Obliczenie początkowego prądu
zwarciowego
"
kG
I
na zaciskach generatora wykonuje się przy wykorzystaniu następujących
wzorów:
gdzie:
E” – siła elektromotoryczna podprzejściowa, w [kV],
"
d
x
– względna reaktancja podprzejściowa, w [-],
"
d
X
- reaktancja podprzejściowa generatora, w [
]
nG
3
nG
"
d
"
d
S
U
x
X
,
R
G
– rezystancja generatora, w [Ω ] (dla generatorów o napięciu U
n
< 1 kV przyjmuje się R
kG
= 0,03•X
kG
(X
kG
według wzoru 1.2.10),
I
nG
– prąd znamionowy generatora [kA],
nG
nG
nG
U
3
S
I
,
sinφ
nG
– obliczany na podstawie współczynnika mocy znamionowej generatora cosφ
nG
, w [-],
K
G
– współczynnik korekcyjny impedancji generatora, w [-],
U
n
– napięcie w miejscu zwarcia, w [V],
U
rG
– napięcie na zaciskach generatora, w [V].
Konieczność wprowadzenia współczynnika korekcyjnego impedancji generatora (K
G
) wynika
z normatywnej konieczności stosowania jednakowej wartości siły elektromotorycznej
każdego źródła prądu zwarciowego, która różni się od siły elektromotorycznej
podprzejściowej generatora. Na rysunku 1.2.5 został przedstawiony uproszczony wykres
wektorowy maszyny synchronicznej, wyjaśniający konieczność wprowadzenia
współczynnika korekcyjnego (K
G
), którego celem jest wyeliminowanie błędu, jaki powstałby
w przypadku przyjęcia wartości znamionowej reaktancji podprzejściowej generatora.
kG
G
n
max
//
d
G
G
rG
max
kG
''
//
kG
"
Z
*
K
*
3
U
*
c
jX
R
K
3
U
c
Z
E
I
rG
//
d
max
rG
n
G
sin
x
1
c
U
U
K
2
"
d
2
G
kG
)
X
(
R
"
Z
nG
2
nG
cos
1
sin
(1.2.11.)
(1.2.12.)
(1.2.13.)
(1.2.14.)
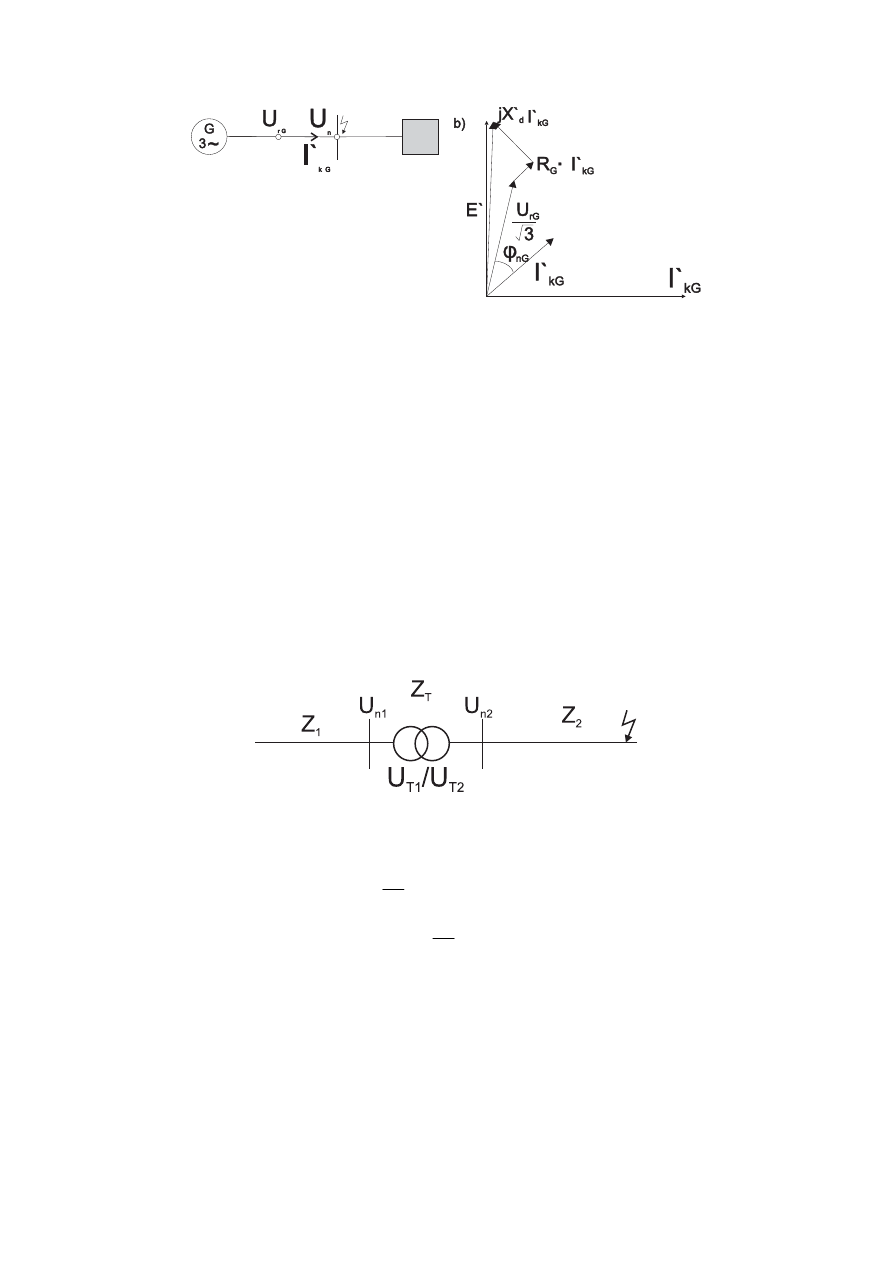
11. Rysunek 1.2.5. Korekta impedancji generatora przy zwarciu zlokalizowanym w jego pobliżu [23]:
a) lokalizacja zwarcia; b) uproszczony wykres wektorowy maszyny synchronicznej
Sprowadzanie do jednego poziomu napięcia
Wolno dodawać do siebie impedancję obwodu zwarciowego pod warunkiem, że wszystkie
zostały sprowadzone do tego samego poziomu napięcia. Podstawą przeliczania impedancji
obwodów zwarciowych i prądów na inny poziom napięcia jest przekładnia transformatorowa.
W żadnym przypadku nie wolno przyjmować za podstawę tych przeliczeń napięć
znamionowych sieci przyłączonych do górnych lub dolnych uzwojeń transformatora [25].
Uwaga!
Jest to uproszczone postępowanie, które wprowadza błąd dopuszczalny w obliczeniach
praktycznych [25]. Przy dokładnym obliczaniu impedancji obwodu zwarciowego należy
dodawać osobno rezystancję i reaktancję, a następnie obliczyć moduł impedancji.
Przeliczenie wartości impedancji wykonujemy zgodnie ze wzorami (1.2.15) i (1.2.16), które
wynikają z rysunku 1.2.6.
12. Rysunek 1.2.6. Sprowadzenie impedancji elementów obwodu Z do jednego napięcia [25] (U
T1
; U
T2
–
- napięcie znamionowe pierwotnej i wtórnej strony transformatora) [25]
2
U
/
T
2
1
T
2
T
1
k
Z
Z
U
U
Z
Z
2
T
(1.2.15.)
1.3. Obliczanie
prądów zwarciowych
1.3.1. Prąd zwarciowy udarowy
Zgodnie z tym, co zostało przedstawione na rysunkach: 1.1.3, 1.1.4 oraz 1.1.5, początkowy
prąd zwarciowy
"
k
I
nie jest największą wartością prądu zwarciowego. Stanowi on natomiast
podstawę do prowadzenia dalszych obliczeń. Z chwilą powstania zwarcia pojawia się prąd
T
T
2
k
U
/
T
S
U
u
Z
2
T
(1.2.16.)
udarowy i
p
. Wartość jego jest większa w stosunku do składowej okresowej o wartość
"
k
I
2
.
Znaczący wpływ posiada również składowa nieokresowa i
DC
, której wpływ na całkowity prąd
zwarciowy charakteryzuje się poprzez współczynnik
. Prąd ten charakteryzuje narażenia
elektrodynamiczne urządzeń zainstalowanych w obwodzie zwarciowym.
Prąd udarowy można wyrazić następującą zależnością:
gdzie:
i
p
- prąd udarowy, w [A],
- współczynnik udaru, w [-],
R
k
- rezystancja obwodu zwarciowego, w [
],
X
k
- reaktancja obwodu zwarciowego, w [
].
Współczynnik udaru
obrazuje krotność wzrostu maksymalnej amplitudy prądu
"
k
I
wynoszącej
"
k
I
*
2
spowodowaną wystąpieniem składowej nieokresowej prądu zwarciowego
i
DC
.
Jeżeli wartość stosunku
k
k
X
R
jest nieznana, w przeciętnych warunkach można przyjmować
następujące wartości współczynnika
:
- 1,8 - w urządzeniach wysokiego napięcia,
- 1,4 - w urządzeniach niskiego napięcia,
- 1,64 - dla generatora niskonapięciowego.
Jeżeli stosunek wynosi
2
,1
X
R
k
k
=>
=1, wówczas prąd udarowy
"
k
p
I
2
i
.
Uwaga!
Przy
2
,1
X
R
k
k
stała czasowa T jest tak mała, że następuje szybkie tłumienie składowej
nieokresowej. Prąd udarowy jest równy wartości szczytowej początkowego prądu
zwarciowego. W odległej instalacji odbiorczej praktycznie
= 1.
1.3.2. Prąd zwarciowy wyłączeniowy
Prąd zwarciowy wyłączeniowy jest to umowna (bieżąca) wartość skuteczna prądu
zwarciowego w chwili t
min
, kiedy otwierają się styki wyłącznika i zapala się między nimi łuk
elektryczny. Wartość prądu zwarciowego wyłączeniowego wyznaczamy w zależności od
rodzaju zwarcia:
a) dla zwarć bliskich (w pobliżu generatorów lub silników):
Uwaga!
"
k
b
I
I
- prąd wyłączeniowy symetryczny, w [A].
Współczynnik
, konieczny do wyznaczenia prądu zwarciowego wyłączeniowego
symetrycznego generatora lub silnika można odczytać z rysunku 1.3.1.
"
k
p
I
2
i
(1.3.1.)
K
K
X
R
3
e
98
,
0
02
,
1
(1.3.2.)
T
t
2
2
"
k
2
DC
2
b
basym
min
e
2
I
i
I
I
(1.3.3.)
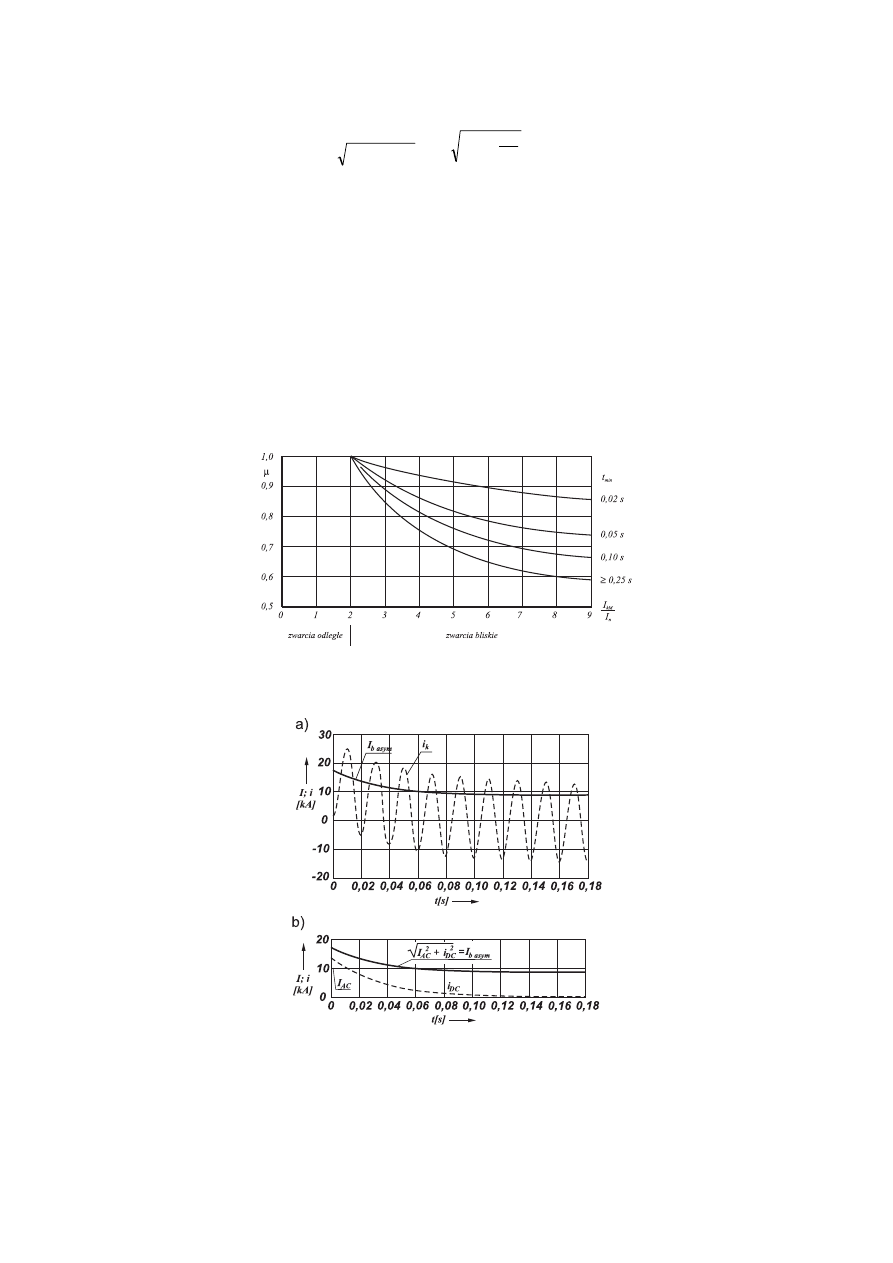
b) dla zwarć odległych:
gdzie:
T - stała czasowa obwodu zwarciowego, w [s],
t
min
-
czas własny otwierania wyłącznika stanowiącego zabezpieczenie obwodu zwarciowego,
w [ms] (czas przedłukowy dla bezpieczników topikowych), dla wyłączników na ogół nie
przekracza 20 ms.
Prąd znamionowy wyłącznika, czyli jego zdolność wyłączeniowa, powinien mieć wartość
równą lub większą od wartości I
basym.
Uwaga!
Prąd znamionowy wyłączalny wkładki bezpiecznikowej porównuje się z prądem zwarciowym
początkowym
"
k
I . Jeżeli t
min
> 1,5 T, wpływ prądu nieokresowego można pominąć i za
podstawę doboru wyłącznika przyjmować prąd wyłączeniowy symetryczny. Czyli
"
k
b
basym
I
I
I
.
13. Rysunek 1.3.1. Współczynnik
do obliczania prądu zwarciowego wyłączeniowego symetrycznego generatorów i silników (dla wartości
pośrednich t
min
należy stosować interpolację) [25]
Przykładowe przebiegi czasowe prądu wyłączeniowego przedstawia rysunek 1.3.2.
14. Rysunek
1.3.2.
Prąd wyłączeniowy w chwili t
min
otwarcia styków wyłącznika:
a) przebieg prądu zwarciowego i
K
oraz jego bieżącej wartości skutecznej; b) przebieg bieżących wartości skutecznych obu składowych I
AC
oraz i
DC
prądu zwarciowego i ich sumy geometrycznej [24]
T
t
2
"
k
2
DC
2
"
k
basym
min
e
2
1
I
)
i(
)
I(
I
(1.3.4.)
Jeżeli zwarcie jest zasilane z kilku źródeł, należy wyznaczyć poszczególne składowe prądu
zwarciowego dla każdego źródła osobno dla chwili t
min
, a następnie wyznaczyć wypadkowy
prąd zwarciowy wyłączalny niesymetryczny I
basym
korzystając z poniższego wzoru:
gdzie:
l
bi
- prąd symetryczny i-tego źródła zasilającego zwarcie, w [kA],
I
DCi
- składowa asymetryczna i-tego źródła zasilającego zwarcie, w [kA].
1.3.3. Prąd zwarciowy zastępczy cieplny
Prąd znamionowy zastępczy cieplny I
th
jest to wartość skuteczna prądu zwarciowego w czasie
trwania zwarcia T
k
. Czyli wartość średniokwadratowa prądu zwarciowego i
k
= i
AC
+ i
DC
obliczona w czasie trwania zwarcia. Na jego wartość mają wpływ zarówno składowa
okresowa i
AC
, jak i składowa nieokresowa i
DC
.
Z jego wartością porównuje się, podaną dla takiego samego czasu T
k
, obciążalność cieplną
urządzeń:
- prąd znamionowy n-sekundowy łączników, przekładników prądowych dławików
przeciwzwarciowych,
- obciążalność zwarciową cieplną szyn, kabli i przewodów instalacyjnych.
Prąd zastępczy cieplny można wyrazić zależnością:
- dla
zwarć bliskich:
gdzie:
n - współczynnik zależny od stosunku
nG
"
k
I
I
oraz czasu trwania zwarcia T
k
, odczytany z
rysunku 1.3.3b, uwzględniany tylko przy zwarciach bliskich,
m - współczynnik zależny od wartości współczynnika udaru
wyznaczony ze wzoru (1.3.7)
lub odczytany z rysunku 1.3.3a.
- dla
zwarć odległych:
2
n
1
i
DCi
2
n
1
i
bi
th
)
I
(
)
I
(
I
(1.3.5.)
m
n
I
I
"
k
th
(1.3.6.)
)
e
1
(
T
T
m
T
T
2
k
k
(1.3.7.)
m
1
I
I
"
k
th
(1.3.8.)
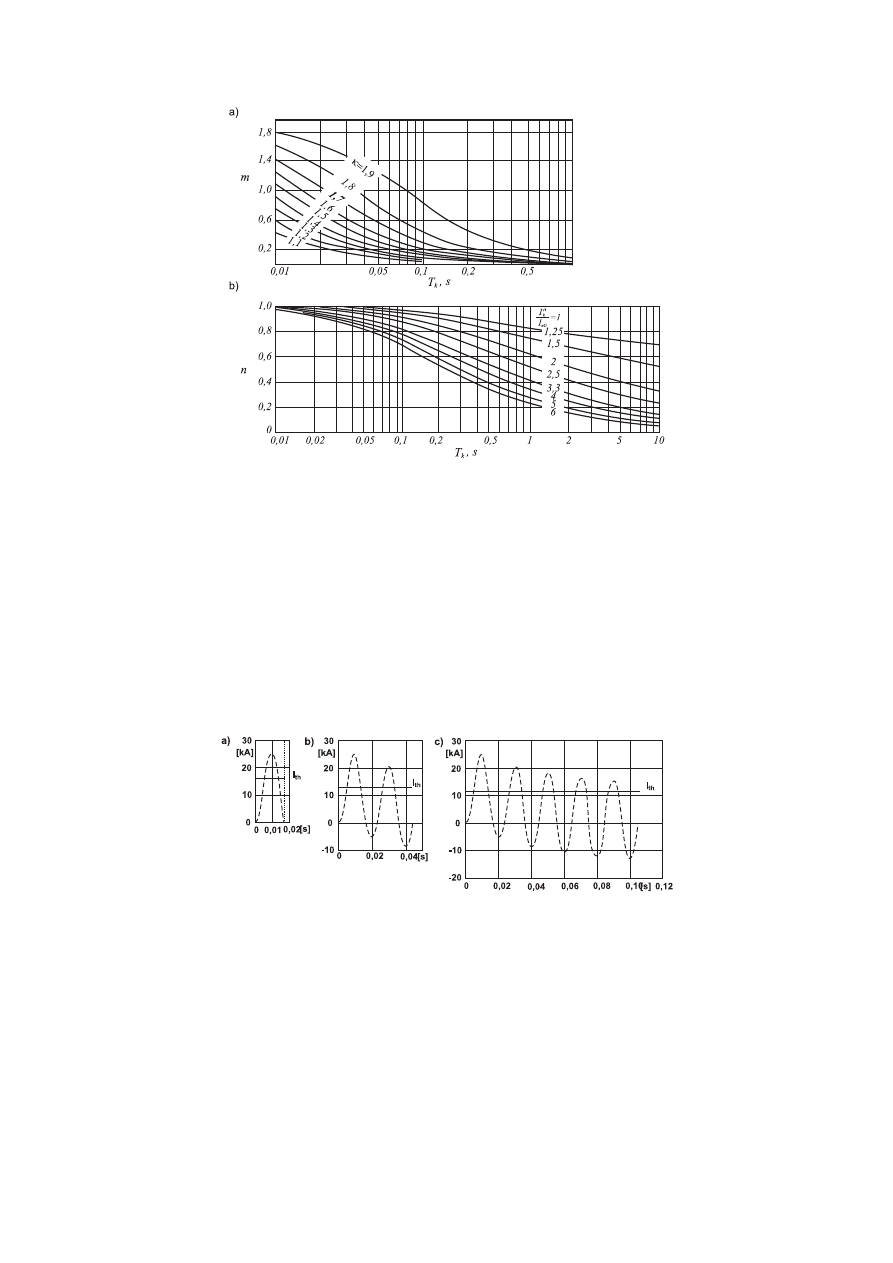
15. Rysunek
1.3.3.
Zależność współczynników m i n od czasu trwania zwarcia T
k ;
[25]:
a) współczynnik m; b) współczynnik n
Wpływ składowej nieokresowej i
DC
prądu zwarciowego na zastępczy prąd zwarciowy cieplny
I
th
wraz z upływem czasu trwania zwarcia T
k
przedstawia rysunek 1.3.4. Wraz ze wzrostem
czasu trwania zwarcia T
k
, wpływ składowej nieokresowej i
DC
na prąd zwarciowy I”
k
maleje.
W przypadku, gdy czas trwania zwarcia T
k
> 10 T można przyjmować
"
k
th
I
I
. W praktyce
inżynierskiej korzysta się z zależności I
2
th
*T
k
, zwanej dalej skutkiem cieplnym. Wartość ta
jest nazywana całką Joule'a i oznaczana w katalogach producentów aparatów elektrycznych
jako I
2
t
w
[A
2
s]. Stanowi ona wartość energii cieplnej, jaką przepuszcza do obwodu urządzenie
zabezpieczające i jaką powinny mieć wytrzymałość przewody i inne elementy urządzeń
elektrycznych.
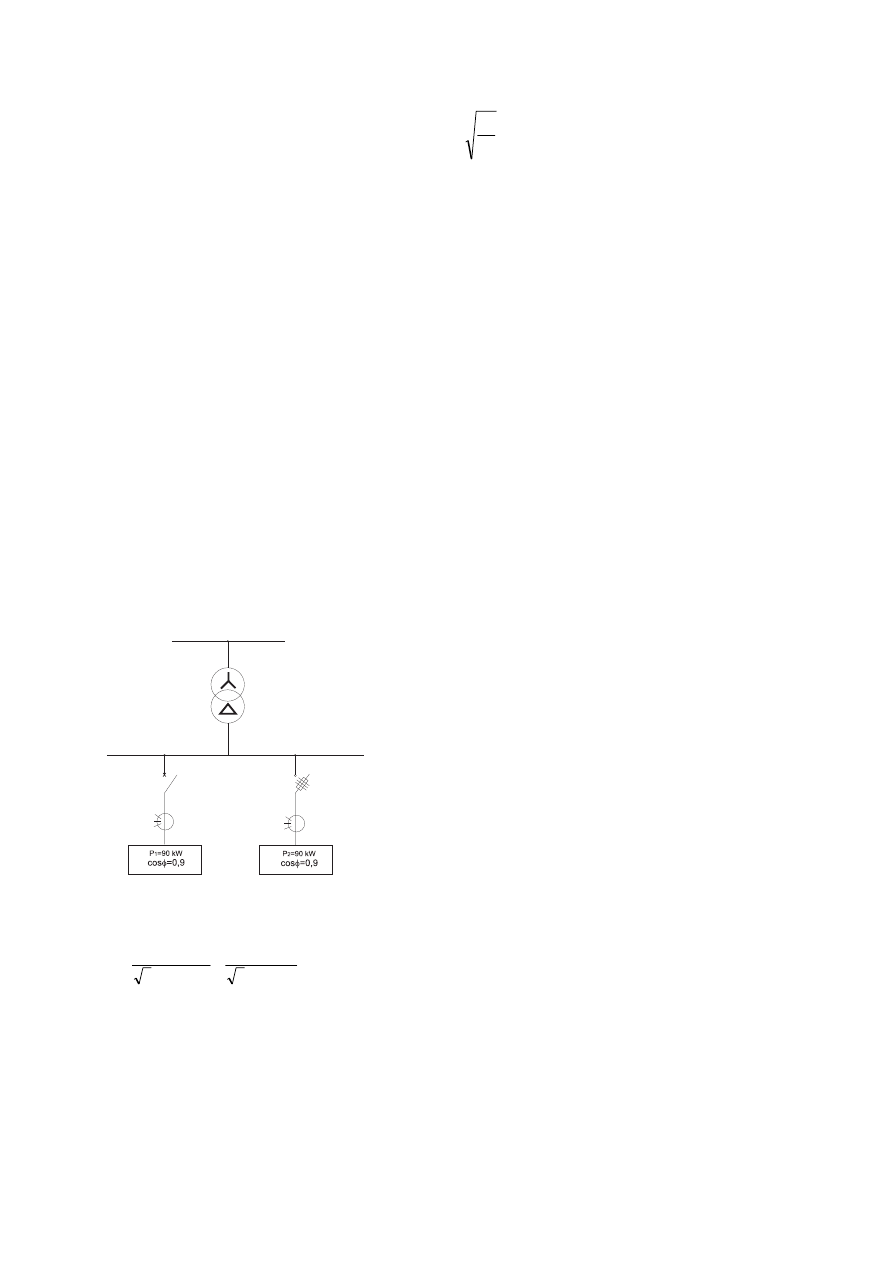
16. Rysunek
1.3.4.
Prąd zastępczy cieplny l
th
przy przebiegu prądu zwarciowego dla następujących parametrów zwarciowych
I”k=10 kA, R/X=0,076, T=42 ms,
=1,80 dla różnych wartości czasu trwania zwarcia:
a) I
th
= 16,20 kA przy T
k
= 17 ms; b) I
th
= 13,30 kA przy T
k
= 44 ms; c) I
th
= 11,80 kA przy T
k
= 105 ms
(Ith
I”
k
, przy zwiększającym się czasie trwania zwarcia T
k
) [23]
Uwaga!
Producenci urządzeń podają odporność cieplną urządzeń dla czasu T
n
= {0,05; 0,1; 0,25; 0,5;
1} s. Urządzenie elektryczne ma dostateczną obciążalność zwarciową cieplną, jeżeli
spełniony jest następujący warunek:
dla T
k
T
n
cwTn
th
I
I
(1.3.9.)
gdzie:
T
n
- czas przepływu krótkotrwałego prądu n-sekundowego wytrzymywanego przez
urządzenie, podawanego przez producenta (0,05; 0,1; 0,25; 1; 3 s),
I
cwTn
- znamionowy prąd krótkotrwały wytrzymywany w czasie T
n
podanym przez producenta
zabezpieczeń, w [A].
I
th
– prąd zwarciowy zstępczy cieplny, w [A]
Przedstawioną elementarną teorię obliczania zwarć w zastosowaniach praktycznych ilustrują
przykłady rachunkowe 1.1 -1.3.
Przykłady [195]
Przykład 1.1
Dobrać kable i ich zabezpieczenia oraz przekładniki prądowe dla dwóch przypadków:
a) zabezpieczenie wykonane jest wyłącznikiem mocy typu DPX produkcji FAEL
LEGRAND,
b) zabezpieczenie wykonane jest bezpiecznikiem topikowym zainstalowanym w
rozłączniku bezpiecznikowym.
Pozostałe dane przedstawia rysunek P.1.1.
1. Dobór zabezpieczenia oraz kabla na długotrwałą obciążalność i przeciążalność prądową:
- prąd obciążenia
17. Rysunek P.1.1. Schemat zasilania do przykładu 1.1
A
33
,
144
9
,
0
400
3
90000
cos
U
3
P
I
n
n
B
S
KQ
= 250 MVA
S
T
= 400 kVA
u
k
= 0,045
P
obczn
= 4,6 kW
= 35,7
dla T
k
>T
n
k
n
cwTn
th
T
T
I
I
(1.3.10.)
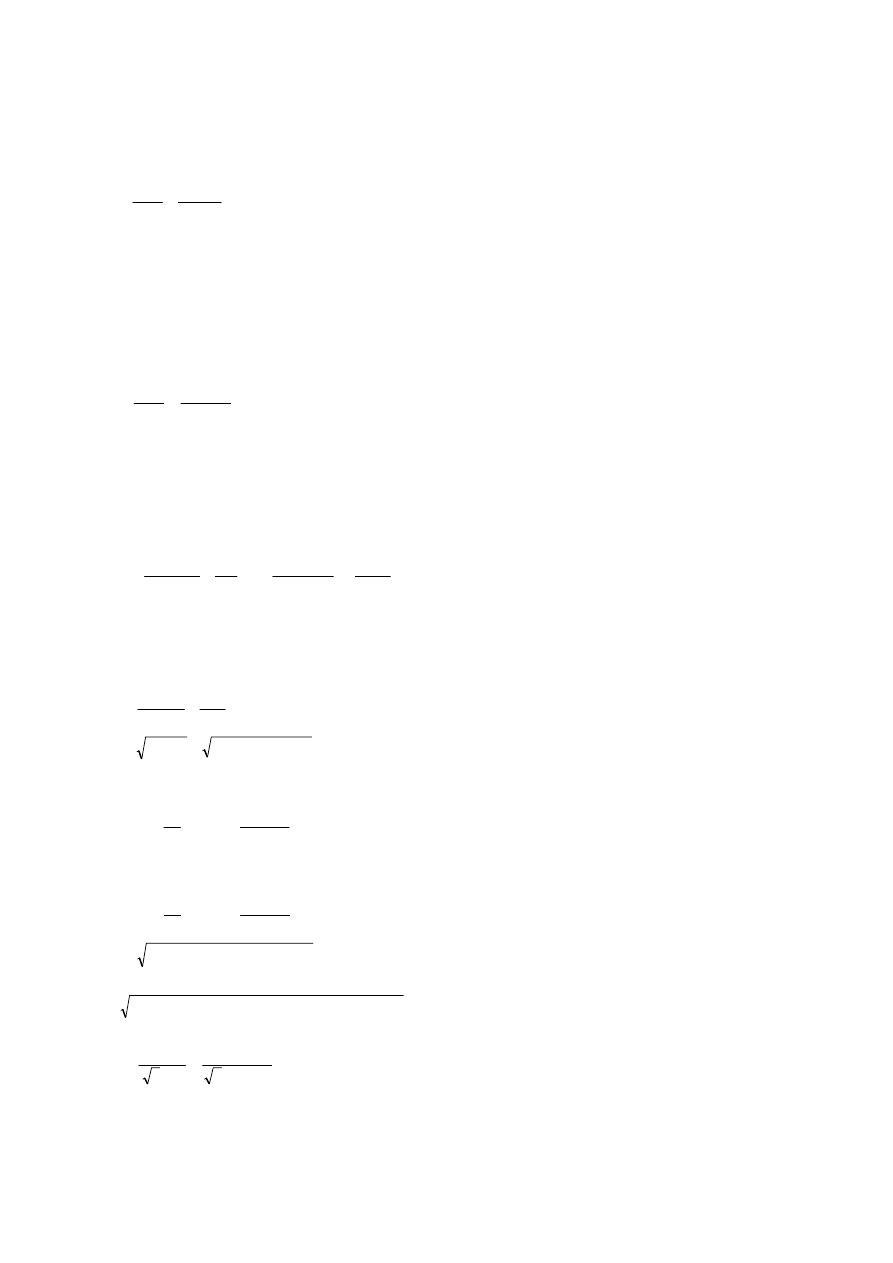
- dobór
zabezpieczeń i kabla
a. przy zabezpieczeniu bezpiecznikiem WTN00gG160
z
n
B
I
A
160
I
A
33
,
144
I
A
55
,
176
45
,
1
160
6
,1
45
,1
I
k
I
n
2
Z
Na podstawie PN-IEC 60364-5-523 [72] warunki długotrwałej obciążalności oraz
przeciążalności prądowej przy dobranym zabezpieczeniu spełni kabel YKXS 4x70, dla
którego I
dd
= 178 A > I
z
=176,55 A.
b. przy zabezpieczeniu wyłącznikiem DPX 160-160- 3P
z
n
B
I
A
160
I
A
33
,
144
I
A
160
45
,1
160
45
,1
45
,
1
I
k
I
n
2
Z
Na podstawie PN-IEC 60364-5-523 [72] warunki długotrwałej obciążalności oraz
przeciążalności prądowej przy dobranym zabezpieczeniu spełni kabel YKXS 4x70, dla
którego I
dd
= 178 A > I
z
=160 A.
- parametry obwodu zwarciowego
000776
,
0
15000
420
10
250
15000
1
,1
U
U
S
U
c
Z
2
6
2
2
1
T
2
T
kQ
1
n
2
max
kQ
000772
,
0
000776
,
0
995
,
0
Z
995
,
0
X
kQ
kQ
000077
,
0
000772
,
0
1
,
0
X
1
,
0
R
kQ
kQ
0115
,
0
400
60
,
4
S
P
u
T
zn
_
obc
R
0435
,
0
0115
,
0
0450
,
0
u
u
u
2
2
2
R
2
k
x
0050715
,
0
10
400
420
0115
,
0
S
U
u
R
3
2
T
2
T
R
kT
0191835
,
0
10
400
420
0435
,
0
S
U
u
X
3
2
T
2
T
X
kT
2
kT
kQ
2
kT
kQ
k
R
R
X
X
Z
02061
,
0
005072
,
0
000077
,
0
019184
,
0
000772
,
0
2
2
- początkowy prąd zwarcia symetrycznego
kA
2
,
11
A
25
,
11205
02061
,
0
3
400
00
,1
Z
3
U
c
I
k
n
max
''
3
k
- elektromagnetyczna
stała czasowa obwodu zwarciowego
25
,
0
cos
8757
,
3
005149
,
0
019956
,
0
R
R
X
X
R
X
tg
kT
kQ
kQ
kQ
k
k
- współczynnik udarowy oraz udarowy prąd zwarciowy
47
,1
e
98
,
0
02
,
1
019956
,
0
005149
,
0
3
kA
28
,
23
2
,
11
2
47
,
1
I
2
i
''
k
p
Uwaga!
Na podstawie charakterystyki prądowo-czasowej t = f(l
k
), przy spodziewanym początkowym
prądzie zwarciowym, czas wyłączenia wynosi odpowiednio:
a)
dla bezpiecznika WTN00gG160 - t < 0,1 s
b) dla
wyłącznika DPX 160 - 3P - T
k
= 0,2 s.
Zabezpieczenie kabla bezpiecznikiem topikowym WTN00gG160:
przy spodziewanym początkowym prądzie zwarciowym I”
k3
charakterystyki prądów
ograniczonych i
0
= f(I
K
)
odczytuje się wartość prądu ograniczonego I
o/I”k3
=9,2 kVA,
natomiast znamionowy prąd wyłączalny bezpiecznika wynosi
l
cn
= 100 kA > I’’
k3
= 11 ,2 kA.
Sprawdzenie dobranego kabla na warunek zwarciowy:
2
2
w
2
mm
70
mm
19
,
3
1
185000
135
1
1
t
I
k
1
S
Dobrany kabel spełnia zatem warunki odporności zwarciowej.
Należy również pamiętać, że rozłącznik bezpiecznikowy, w którym będą zainstalowane
bezpieczniki WTN00gG160, musi spełniać następujące wymagania:
- znamionowy prąd szczytowy i znamionowy prąd załączalny l
cm
i
p
= 23,28 kA
- prąd wytrzymywany ograniczony l
ow
I’’
k3
= 11,2 kA.
Zabezpieczenie kabla wyłącznikiem DPX 160-160-3P:
kA
2
,
11
I
kA
36
I
''
3
k
CU
kA
2
,
11
I
kA
27
I
''
3
k
CS
kA
28
,
23
i
kA
75
I
p
cm
Ponieważ T
k
= 0,2 s, T= 0,0123 s, zatem
T
10
T
26
,
16
0123
,
0
2000
,
0
T
T
k
k
Na tej podstawie należy przyjąć
''
3
k
tn
I
I
. Ponieważ
T
5
,1
T
t
k
min
, również wpływ zwarciowego
prądu nieokresowego jest pomijany.
Zatem skutek cieplny wywołany przez prąd zwarciowy należy wyrazić następująco:
s
A
25088000
2
,
0
11200
T
I
T
I
2
2
k
2
''
3
k
k
2
tn
Na tej podstawie należy obliczyć wymagany minimalny przekrój kabla:
2
2
k
2
''
3
k
k
2
th
mm
70
mm
10
,
37
1
25088000
135
1
1
T
I
k
1
1
T
I
k
1
S
Dobór przekładników:
a) przy zabezpieczeniu kabla bezpiecznikiem topikowym WTN00gG160 należy dobrać
przekładnik prądowy 150/5 A/A o następujących parametrach:
- znamionowy prąd dynamiczny I
dyn
9,2 kA (wymagane parametry zwarciowe
przekładników prądowych dobiera się do warunków zwarciowych ograniczonych przez
bezpiecznik);
- znamionowy
krótkotrwały prąd cieplny (1 -sekundowy):
A
430
1
185000
1
t
I
I
t
I
1
I
w
2
1
thT
w
2
2
1
thT
;
- znamionowy
prąd dynamiczny: I
dyn
i
0
= 9,2 kA;
b) przy zabezpieczeniu wyłącznikiem DPX 160-160-3P należy dobrać przekładnik
prądowy 150/5 A/A o następujących parametrach:
- znamionowy
krótkotrwały prąd cieplny (1-sekundowy):
A
8
,
5008
1
25088000
1
T
I
1
T
I
I
k
2
''
3
k
2
th
1
thT
- znamionowy
prąd dynamiczny I
dyn
i
p
= 23,28 kA.
Na podstawie wyznaczonych wymaganych minimalnych parametrów zwarciowych, należy
np. dobrać odpowiednie typy przekładników z katalogu producenta, w zależności od ich
przeznaczenia (układ pomiarowy lub sterowanie) - w zadaniu nie określono ich
przeznaczenia.
Przykład 1.2
Prąd znamionowy 1-sekundowy stycznika T
n
= 1s, wynosi l
thT1
= 10 kA. Sprawdzić czy może
on zostać zainstalowany w obwodach prądu przemiennego, w których występują następujące
parametry zwarciowe:
a) l
th
= 15 kA przy T
k
= 0,5 s;
b) l
th
= 10 kA przy T
k
= 0,5 s;
c) l
th
= 10 kA przy T
k
= 1,5 s;
ad. a) T
k
= 0,5 s < T
n
= 1,0 s
l
th
=15 kA > l
thT1
warunek nie jest spełniony
ad. b) T
k
= 0,5s<T
n
= 1,0 s
l
th
=10 kA = l
thT1
= 10 kA warunek jest spełniony
ad. c) T
k
= 1,5 s >T
n
= 1,0 s
kA
16
,
8
5
,1
0
,1
10
T
T
I
kA
10
I
k
n
1
thT
th
warunek nie jest spełniony
Przykład 1.3
Stacja transformatorowa 15/0,42 kV poprzez linię napowietrzną 3x230/400 V 4xAl70 o
długości L = 400 m zasila rozdzielnicę nN. Obliczyć warunki zwarciowe na szynach
rozdzielnicy nN stacji oraz na końcu linii.
Dane transformatora:
U
T1
= 15 kV; U
T2
= 420 V; ∆P
obc_zn
= 9,45 kW; u
k
= 0,06; S
T
= 630 kVA.
Napięcie zasilające transformator U
n1
= 15 kV.
Moc zwarciowa w miejscu przyłączenia zacisków górnego uzwojenia transformatora do linii
SN wynosi
MVA
250
S
"
kQ
. Schemat obwodu zwarciowego przedstawia rysunek P.1.3.
18. Rysunek P.1.3. Schemat obwodu zwarciowego do przykładu 1.3
000772
,
0
000776
,
0
995
,
0
Z
995
,
0
X
000776
,
0
15000
420
10
250
15000
10
,1
U
U
S
U
c
Z
kQ
kQ
2
6
2
2
1
T
2
T
"
kQ
2
1
n
max
kQ
0042
,
0
10
630
420
015
,
0
S
U
u
R
01176
,
0
10
630
420
042
,
0
S
U
u
X
042
,
0
015
,
0
045
,
0
u
u
u
015
,
0
630
45
,
9
S
P
u
0000774
,
0
000772
,
0
1
,
0
X
1
,
0
R
3
2
T
2
T
R
kT
3
2
T
2
T
X
kT
2
2
2
R
2
k
x
T
zn
_
obc
R
kQ
kQ
Parametry zwarciowe linii napowietrznej:
12
,
0
4
,
0
30
,
0
L
*
X
X
163
,
0
70
35
400
S
*
L
R
'
L
L
A) Zwarcie na szynach stacji:
kA
70
,
33
66
,
33
5
,
17
2
36
,1
I
2
i
36
,1
e
98
,
0
02
,
1
e
98
,
0
02
,1
kA
5
,
17
A
17442
01324
,
0
3
400
00
,1
Z
3
U
c
I
01324
,
0
01253
,
0
00428
,
0
X
R
Z
01253
,
0
01176
,
0
000772
,
0
X
X
X
00428
,
0
0042
,
0
000077
,
0
R
R
R
''
k
p
001253
,
0
00428
,
0
3
X
R
3
k
n
max
''
k
2
2
2
k
2
k
k
kT
kQ
k
kT
kQ
k
k
k
Zwarcie należy uznać za odległe, ponieważ:
001552
,
0
Z
2
01249
,
0
01176
,
0
0042
,
0
X
R
Z
kQ
2
2
2
kT
2
kT
kT
B) Zostanie obliczony prąd wyłączeniowy i zastępczy cieplny prąd dla czasów T
k
= 20
ms oraz T
k
= 100 ms, przy zwarciu na szynach nN stacji:
a) dla T
k
= 20 ms = 0,02 s
46
,
0
e
1
20
3
,
9
e
1
T
T
m
kA
14
,
21
46
,
0
1
5
,
17
m
1
I
I
kA
73
,
17
87
,
2
50
,
17
i
I
I
ms
3
,
9
s
0093
,
0
314
93
,
2
50
2
00428
,
0
01253
,
0
R
X
tg
T
kA
87
,
2
e
5
,
17
2
e
I
2
i
30
,
9
20
2
T
T
2
k
''
k
th
2
2
2
DC
2
''
k
basym
k
k
k
0093
,
0
02
,
0
T
T
''
k
DC
k
k
b) dla T
k
=100ms
''
k
b
basym
0093
,
0
100
,
0
T
T
''
k
DC
I
I
I
kA
0
e
5
,
17
2
e
I
2
i
k
Czego można było się spodziewać, gdyż T
k
=0,1s>1,5T
093
,
0
e
1
100
3
,
9
e
1
T
T
m
kA
30
,
18
093
,
0
1
5
,
17
m
1
I
I
30
,
9
100
2
T
T
2
k
''
k
th
k
czego można było się spodziewać, gdyż T
k
=0,1s>10 T ≈ 10·0,0093 = 0,093s
C) Prądy zwarciowe na końcu linii, stanowiące podstawę doboru obciążalności
zwarciowej urządzeń nN tam dołączonych:
- prąd zwarcia symetrycznego
s
0027
,
0
314
16728
,
0
13948
,
0
R
X
tg
T
13948
,
0
1200
,
0
01176
,
0
000772
,
0
Q
Q
Q
Q
16728
,
0
1630
,
0
00420
,
0
000077
,
0
R
R
R
R
k
k
k
L
T
kQ
k
L
T
kQ
k
- początkowy prąd zwarciowy
kA
062
,1
A
58
,
1061
16728
,
0
13948
,
0
3
400
00
,1
Z
3
U
c
I
2
2
k
n
max
''
k
- prąd udarowy
kA
58
,1
062
,1
2
05
,
1
I
2
i
05
,
1
e
98
,
0
02
,
1
e
98
,
0
02
,1
''
k
p
13948
,
0
016728
3
X
R
3
k
k
D) Prąd wyłączeniowy oraz zwarciowy zastępczy prąd cieplny dla czasu T
k
=20 ms oraz
T
k
=100 ms:
a) T
k
=20 ms
T
5
,1
T
gdyż
,
kA
062
,1
I
I
I
kA
00091
,
0
e
062
,1
2
e
I
2
i
k
''
k
b
basym
7
,
2
20
T
T
3
''
k
DC
k
135
,
0
e
1
20
7
,
2
e
1
T
T
m
kA
13
,1
135
,
0
1
062
,1
m
1
I
I
7
,
2
20
2
T
T
2
k
''
k
th
k
b) T
k
=100ms
027
,
0
e
1
100
7
,
2
e
1
T
T
m
I
kA
076
,1
027
,
0
1
062
,1
m
1
I
I
kA
0
,
0
e
062
,
1
2
e
I
2
i
7
,
2
100
2
T
T
2
k
''
k
''
k
th
7
,
2
100
T
T
''
k
DC
k
k
wynika to ze spełnienia upraszczającego warunku I
th
=
"
k
I gdyż, T
k
> 10T.
Udział silników w prądzie zwarciowym
Początkowy prąd zwarciowy silnika
"
kM
I
(grupy silników) jest w przybliżeniu równy jego
prądowi rozruchowemu I
r
(sumie prądów rozruchowych
n
1
i
ri
I
) przy rozruchu bezpośrednim.
Jeżeli wartość tego prądu przekracza 5% (wartość powszechnie akceptowalna [25]) wartości
prądu zwarciowego obliczonego dla konkretnego obwodu zwarciowego, w sąsiedztwie
którego jest zainstalowany silnik lub grupa silników, należy uwzględnić udział silników jako
dodatkowego źródła zasilającego zwarcie.
Silnik elektryczny, w pobliżu którego występuje zwarcie, przestaje być zasilany energią
elektryczną z sieci. Kosztem zgromadzonej energii kinetycznej oraz magnetycznej przechodzi
z pracy silnikowej do pracy generatorowej, co symbolicznie zostało przedstawione na
rysunku 1.4.1. Silnik w takim przypadku przez krótki czas, trwający kilka okresów, zasila
zwarcie prądem równym w przybliżeniu jego prądowi rozruchowemu, jaki występuje przy
rozruchu bezpośrednim.
19. Rysunek 1.4.1. Silnik jako dodatkowe źródło zasilające zwarcie [195]
W układach napędowych prądu przemiennego powszechnie stosowane są silniki indukcyjne,
a w niektórych przypadkach silniki synchroniczne. Silnik synchroniczny w czasie wybiegu
zachowuje się jak generator i powinien być tak traktowany w obliczeniach zwarciowych.
Natomiast silnik indukcyjny, który nie posiada stałego wzbudzenia, zasila zwarcie przez 2-5
okresów. Na skutek silnego tłumienia składowa okresowa zanika do zera. Impedancja silnika
synchronicznego wyraża się wzorem 1.4.1:
gdzie:
Z
M
- impedancja silnika, w [
],
n
r
r
I
I
k
- współczynnik rozruchu, w [-],
cos
U
3
P
I
n
n
n
- prąd znamionowy, w [A],
I
r
-
prąd rozruchowy silnika, w [A],
P
n
- moc czynna znamionowa silnika, w [W],
U
n
-
napięcie znamionowe silnika, w [V],
S
n
- moc pozorna silnika, w [VA],
-
sprawność silnika, w [-],
cos
- współczynnik mocy, w [-].
Prąd zwarciowy początkowy przy zwarciu trójfazowym na zaciskach silnika oblicza się ze
wzoru:
Jeżeli pomiędzy silnikiem o impedancji zwarciowej Z
M
a miejscem zwarcia występuje
znaczna impedancja linii i/lub transformatora, to prąd początkowy należy zmniejszyć do
wartości [25]:
gdzie:
L
T
M
M
zm
Z
Z
Z
Z
k
- współczynnik zmniejszający, w [-] [24],
Z
M
– impedancja silnika, w [Ω],
Z
T
– impedancja transformatora, w [Ω],
Z
L
– impedancja linii, w [Ω].
W celu wyznaczenia prądu udarowego silnika zasilającego zwarcie, wprowadza się umowny
współczynnik
3
,1
M
, co powoduje, że wzór na prąd udarowy silnika przyjmuje postać:
Podobnie jak przy prądzie początkowym zwarcia, gdy pomiędzy miejscem zwarcia występuje
znaczna impedancja linii i/lub transformatora prąd udarowy ulega zredukowaniu:
n
r
2
n
n
2
n
r
M
P
k
cos
U
S
U
k
1
Z
(1.4.1.)
M
n
max
"
kM
Z
*
3
U
*
c
I
(1.4.2.)
zm
"
kM
km
"
k
I
)
I(
(1.4.3.)
"
kM
"
kM
M
pM
I
84
,1
I
2
i
(1.4.4.)
zm
pM
'
pM
k
i
i
(1.4.5.)
Udział silnika w prądzie zwarciowym niesymetrycznym uwzględnia się obliczając składową
i
AC
oraz składową nieokresową i
DC
:
gdzie:
I
basym
– prąd zwarciowy wyłączeniowy niesymetryczny, w [A],
"
kMi
bi
I
*
I
- prąd wyłączeniowy pochodzący z i-tego źródła, w tym z i-tego silnika, w [A],
T
t
"
kMi
DCi
min
e
*
I
*
2
i
- prąd nieokresowy zwarcia pochodzący z i-tego źródła, w tym z i-tego
silnika, w [A],
- współczynnik ustalony na podstawie rysunku 1.3.1,
t
min
- czas własny otwierania wyłącznika (zapłonu łuku w bezpieczniku topikowym).
Prąd wyłączeniowy symetryczny silnika indukcyjnego wynosi:
gdzie:
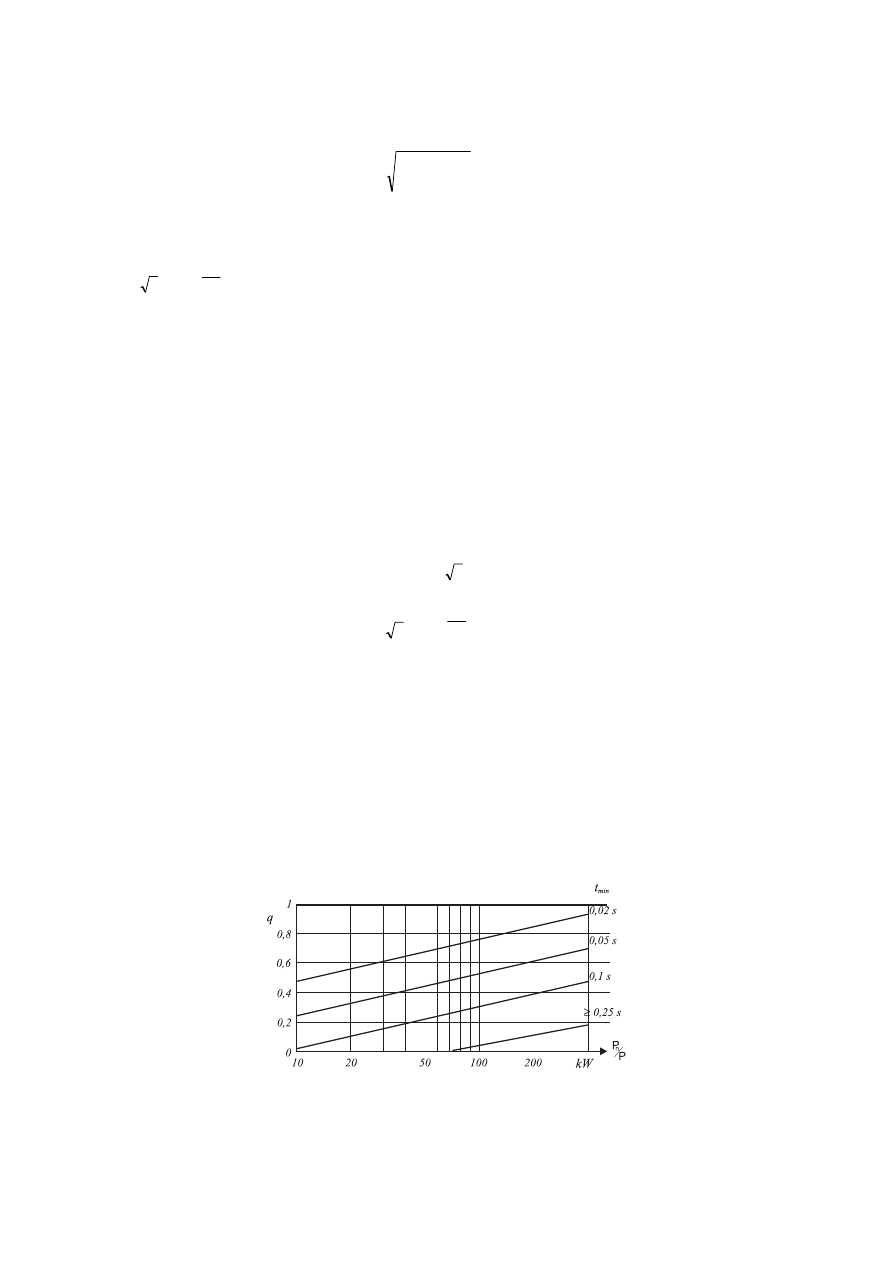
q - współczynnik zależny od mocy silnika przypadający na parę biegunów (
p
/
P
n
) odczytany z
rysunku 1.4.2 (jest to współczynnik uwzględniający dodatkowy czynnik tłumiący składową
nieokresową wynikający z fizyki działania silnika w stanie wybiegu).
W czasie zwarcia na zaciskach silnika składowa nieokresowa prądu zwarciowego ma w
chwili początkowej wartość nie większą jak
"
kM
I
2
, a w chwili t
min
przy zanikaniu ze stałą
czasową posiada wartość nie większą niż:
Zależność stałej czasowej T
DC
zanikania składowej nieokresowej (i
DC
) przy zwarciu na
zaciskach silnika indukcyjnego, w zależności od mocy silnika indukcyjnego przypadającej na
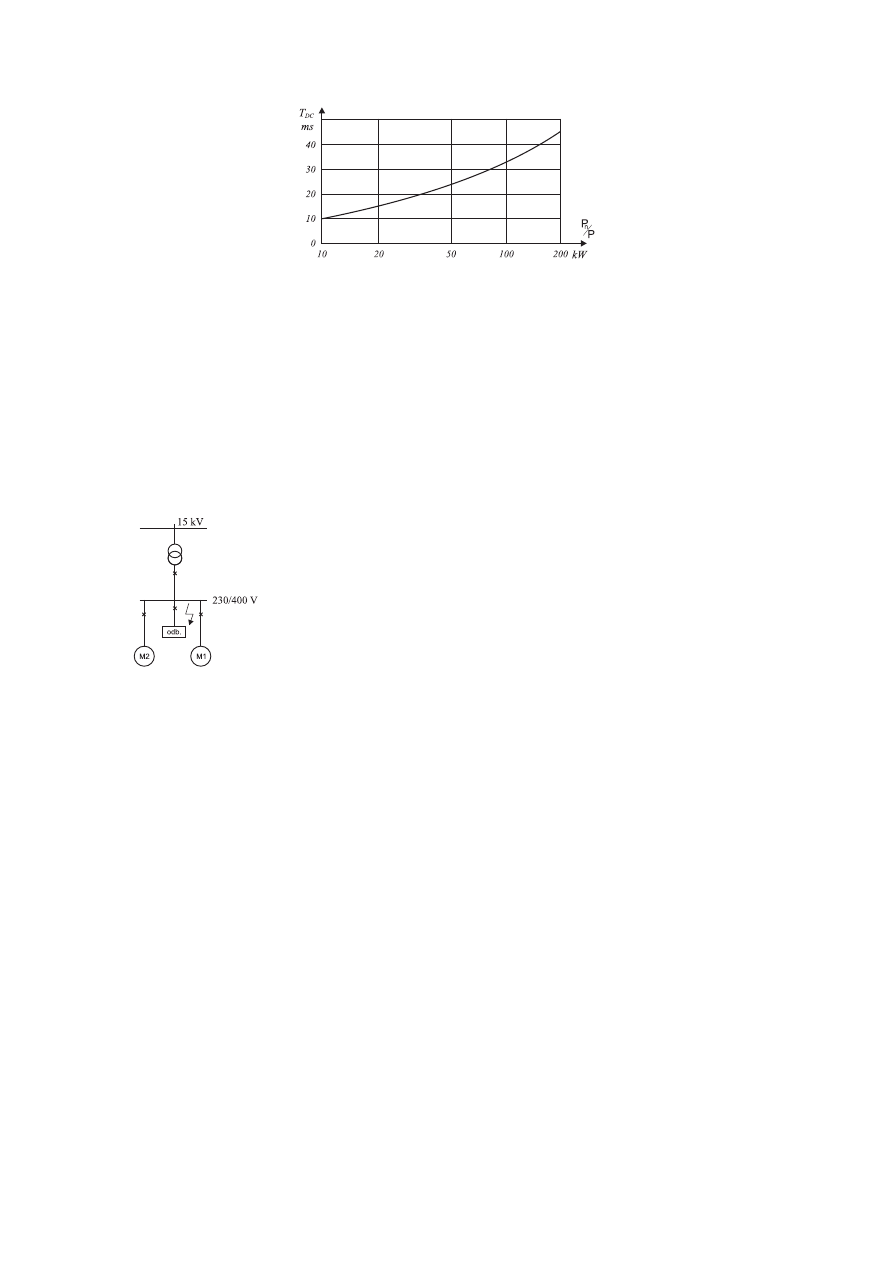
parę biegunów, przedstawia rysunek 1.4.3.
Całkowity prąd zwarciowy jest algebraiczną sumą prądów:
Podobnie prąd udarowy:
20. Rysunek
1.4.2.
Współczynnik q obrazujący znikanie prądu zwarciowego okresowego silnika indukcyjnego, z powodu znikania prądu wirnika
w zależności od mocy silnika przypadającej na parę biegunów (dla wartości pośrednich t
min
należy stosować interpolację) [25] (p- para
biegunów)
n
1
i
DCi
n
1
i
bi
basym
I
I
I
(1.4.6.)
"
kM
bM
I
*
*
q
I
(1.4.7.)
DC
min
T
t
"
kMi
DCM
e
*
I
*
2
i
(1.4.8.)
"
kM
"
kQ
"
kc
I
I
I
(1.4.9.)
pM
pQ
p
i
i
i
(1.4.10.)
21.
Rysunek 1.4.3. Przebieg zależności
p
/
P
f
T
n
DC
[25] (p- liczba par biegunów)
Przedstawione rozumowanie zostanie zilustrowane przykładem rachunkowym:
Przykład 1.4
Obliczyć początkowy prąd zwarcia trójfazowego
"
3
k
I dla obwodu przedstawionego na rysunku
P 1.4 oraz prąd udarowy dla dwóch przypadków:
a) silniki M1 i M2 – odłączone,
b) silniki M1 i M2 – załączone.
22. Rysunek P.1.4. Schemat jednokreskowy obwodu zwarciowego do przykładu 1.4
Dane SEE:
MVA
250
S
"
kQ
Dane transformatora Tr
SN/nN:
15/0,42 kV,
S
T
=250 kVA,
u
k
= 0,045,
∆P
obc_zn
=4,5 kW,
U
T1
=15kV; U
T2
=0,42kV
Dane silników:
P
M1
=P
M2
=30kW,
6
k
9
,
0
9
,
0
cos
r
gdzie:
U
T1
- napięcie znamionowe strony pierwotnej transformatora, w [kV],
U
T2
- napięcie znamionowe strony wtórnej transformatora, w [kV],
S
T
- moc pozorna znamionowa transformatora, w [kVA],
P
M
- moc czynna znamionowa silnika, w [kW],
- sprawność silnika, w [-],
cos
- współczynnik mocy silnika, w [-],
u
k
- napięcie zwarcia transformatora w jednostkach względnych, w [-],
k
r
- krotność prądu rozruchu silnika, w [-],
∆P
obc_zn
- znamionowa moc czynna strat transformatora, w [kW].
a) silniki odłączone
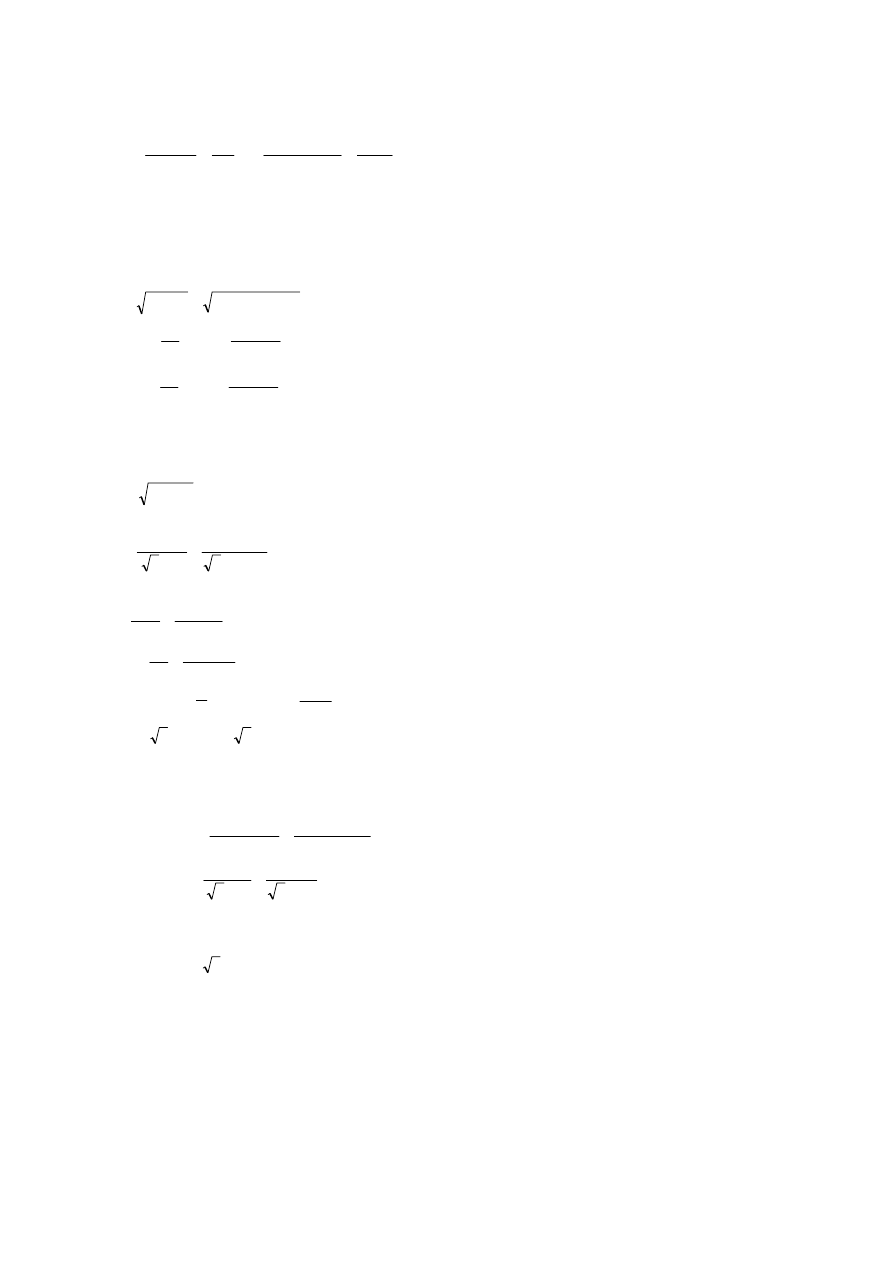
- parametry zwarciowe systemu elektroenergetycznego
0000772
,
0
000772
,
0
1
,
0
X
1
,
0
R
000772
,
0
000776
,
0
995
,
0
Z
995
,
0
X
000776
,
0
15000
420
10
250
15000
10
,1
U
U
S
U
c
Z
kQ
kQ
kQ
kQ
2
6
2
2
2
T
1
T
''
kQ
2
1
n
max
KQ
- parametry obwodu zwarciowego
0289
,
0
10
250
420
041
,
0
S
U
u
X
0127
,
0
10
250
420
018
,
0
S
U
u
R
041
,
0
018
,
0
045
,
0
u
u
u
3
2
T
2
T
x
T
3
2
T
2
T
R
T
2
2
2
R
2
k
x
0323
,
0
X
R
Z
012777
,
0
0127
,
0
0000077
,
0
R
R
R
029672
,
0
0289
,
0
000772
,
0
X
X
X
2
k
2
k
k
T
kQ
k
T
kQ
k
kA
05
,
13
15
,
7
2
29
,1
I
2
i
29
,1
e
98
,
0
02
,1
98
,
0
02
,1
32
,
2
012777
,
0
029672
,
0
R
X
tg
ms
4
,
7
50
2
32
,
2
tg
T
395
,
0
cos
kA
15
,
7
0323
,
0
3
400
0
,1
Z
3
U
c
I
''
3
k
p
029672
,
0
01277
,
0
3
X
R
k
k
k
k
k
k
n
max
''
3
k
k
k
b) silniki załączone
A
320
72
,
0
3
400
1
Z
3
U
c
I
I
I
72
,
0
30000
6
9
,
0
9
,
0
400
P
k
cos
U
Z
Z
Z
M
n
max
''
2
kM
''
1
kM
''
kM
2
n
r
2
n
2
M
1
M
M
kA
23
,
14
59
,
0
2
05
,
13
i
2
i
i
kA
59
,
0
32
,
0
84
,1
I
2
i
i
kA
79
,
7
32
,
0
32
,
0
15
,
7
I
I
I
I
pM
pQ
pc
''
kM
M
2
pM
1
pM
''
2
kM
''
1
kM
''
kQ
''
kc
Przedstawiony przykład wyjaśnia, jak dużym prądem podczas wybiegu silniki indukcyjne
zasilają zwarcie. Prąd pochodzący od dwóch silników stanowi 9% prądu zwarciowego
płynącego ze źródła podstawowego. Zatem zgodnie z wcześniejszymi wyjaśnieniami, gdy
prąd zwarciowy pochodzący od silników przekracza 5% wartości prądu
"
kQ
I
obliczonego bez
ich udziału, powinien on zostać uwzględniony w wyznaczeniu całkowitego prądu
początkowego zwarcia oraz prądu udarowego. Nieuwzględnienie tych prądów może
skutkować złym doborem aparatów elektrycznych wchodzących w skład zasilanego obwodu.
Może to spowodować wzrost zagrożenia pożarowego. Wskutek uszkodzenia aparatów
zabezpieczających prądy zwarciowe nie ulegną przerwaniu, co może doprowadzić do
szybkiego wzrostu temperatury izolacji, nie wykluczając w konsekwencji zapłonu.
W celu umożliwienia szybkiej oceny konieczności uwzględniania udziału silników w prądzie
zwarciowym można skorzystać ze wzoru:
gdzie:
ri
I
– prąd rozruchowy i-tego silnika w grupie, w [A],
''
kQ
I
- początkowy prąd zwarcia zasilanego przez źródło podstawowe (system
elektroenergetyczny lub generatora), [A].
Uwaga!
Wartości prądów
ri
I
oraz
''
kQ
I
mogą być wyrażane w [kA].
Jeżeli spełniona jest nierówność (1.4.11) należy uwzględnić udział silników w prądzie
zwarciowym. Autorom znane są skutki nie uwzględnienia przez projektantów udziału
silników w prądzie zwarciowym. W jednym przypadku prądy, dopływające do miejsca
zwarcia z silników zainstalowanych na hali produkcyjnej, spowodowały tak duży wzrost
prądu zwarciowego, że rozdzielnica uległa całkowitemu zniszczeniu.
"
kQ
n
1
i
ri
I
05
,
0
I
(1.4.11.)