Z. Kąkol-Notatki do Wykładu z Fizyki

23-1

Wykład 23

23. Indukcja elektromagnetyczna, energia pola magnetycznego

23.1 Indukcyjność

23.1.1 Transformator

Gdy dwie cewki są nawinięte na tym samym rdzeniu (często jedna na drugiej) to prąd
zmienny w jednej wywołuje SEM indukcji w drugiej.
N

1

- liczba zwojów w cewce pierwotnej, N

2

- liczba zwojów w cewce wtórnej

t

N

U

B

d

d

2

2

φ

−

=

oraz

t

N

U

B

d

d

1

1

φ

−

=

Stosunek napięć

1

2

1

2

N

N

U

U

=

(23.1)

Widać, że regulując ilość zwojów w cewkach możemy zamieniać małe napięcia na duże
i odwrotnie.

Przykład 1

Obliczmy straty mocy w linii przesyłowej o oporze 10

Ω

przesyłanej z generatora

10 MW gdy napięcie wynosi 1.5·10

4

oraz 10

5

V.

P = IU
P

strat

= I

2

R = (P/U)

2

R

P

strat1

= 4.4 MW (44%)

P

strat2

= 0.1 MW (1%)

23.1.2 Indukcyjność własna

Gdy natężenie prądu przepływającego przez cewkę zmienia się to zmienia się też

strumień przez każdy zwój tej cewki więc zgodnie z prawem indukcji Faradaya induku-
je się SEM. Tę siłę elektromotoryczną nazywamy

siłą elektromotoryczną samoindukcji

.

t

N

d

d

φ

ε

−

=

(23.2)

Wielkość N

φ jest całkowitym strumieniem zawartym w obwodzie i nosi nazwę strumie-

nia skojarzonego. Strumień skojarzony jest proporcjonalny do prądu płynącego przez
cewkę.

N

φ = LI

(23.3)

Z. Kąkol-Notatki do Wykładu z Fizyki

23-2

Stała proporcjonalności

L = N

φ/I

(23.4)

nazywana jest

indukcyjnością.

Zróżniczkowanie(po czasie) równania (23.3) daje

t

I

L

t

N

d

d

d

d

=

φ

Stąd

t

I

L

d

d

−

=

ε

(23.5)

Jednostką L jest henr. 1 H = 1 Vs/A
Jako przykład obliczmy indukcyjność cewki o długości l

0

i N zwojach.

Strumień przez każdy zwój wynosi

φ = BS

gdzie B dla cewki wynosi

B =

µ

0

nI =

µ

0

I(N/l

0

)

Zatem

I

l

NS

0

0

µ

φ

=

Indukcyjność L otrzymujemy mnożąc strumień przez N/I

0

2

0

l

S

N

L

µ

=

(23.6)

Zauważmy, że L zależy tylko od geometrii.

23.1.3 Indukcja wzajemna

Omawiając transformator pokazywaliśmy, że dwie cewki mogą oddziaływać na sie-

bie. Prąd zmienny w jednej wywoływał SEM w drugiej. Tym razem strumień przecho-
dzący przez cewkę 2 jest proporcjonalny do prądu płynącego przez cewkę 1.

N

2

φ

21

= M

21

I

1

Stałą proporcjonalności M

21

nazywamy

indukcją wzajemną.

Różniczkując to równanie otrzymujemy

t

I

M

t

N

d

d

d

d

1

21

21

2

=

φ

Stąd

t

I

M

d

d

1

21

2

−

=

ε

Z. Kąkol-Notatki do Wykładu z Fizyki

23-3

Jeżeli zmieniamy prąd I

2

to analogicznie

t

I

M

d

d

2

12

1

−

=

ε

Można pokazać (ale w skomplikowany sposób), że

M

12

= M

21

= M

Podobnie jak L tak samo M zależy tylko od

geometrii układu

.

23.2 Obwody RC i RL, stałe czasowe

Zaczniemy teraz zajmować się prądami zmieniającymi się w czasie.

23.2.1 Obwód RC

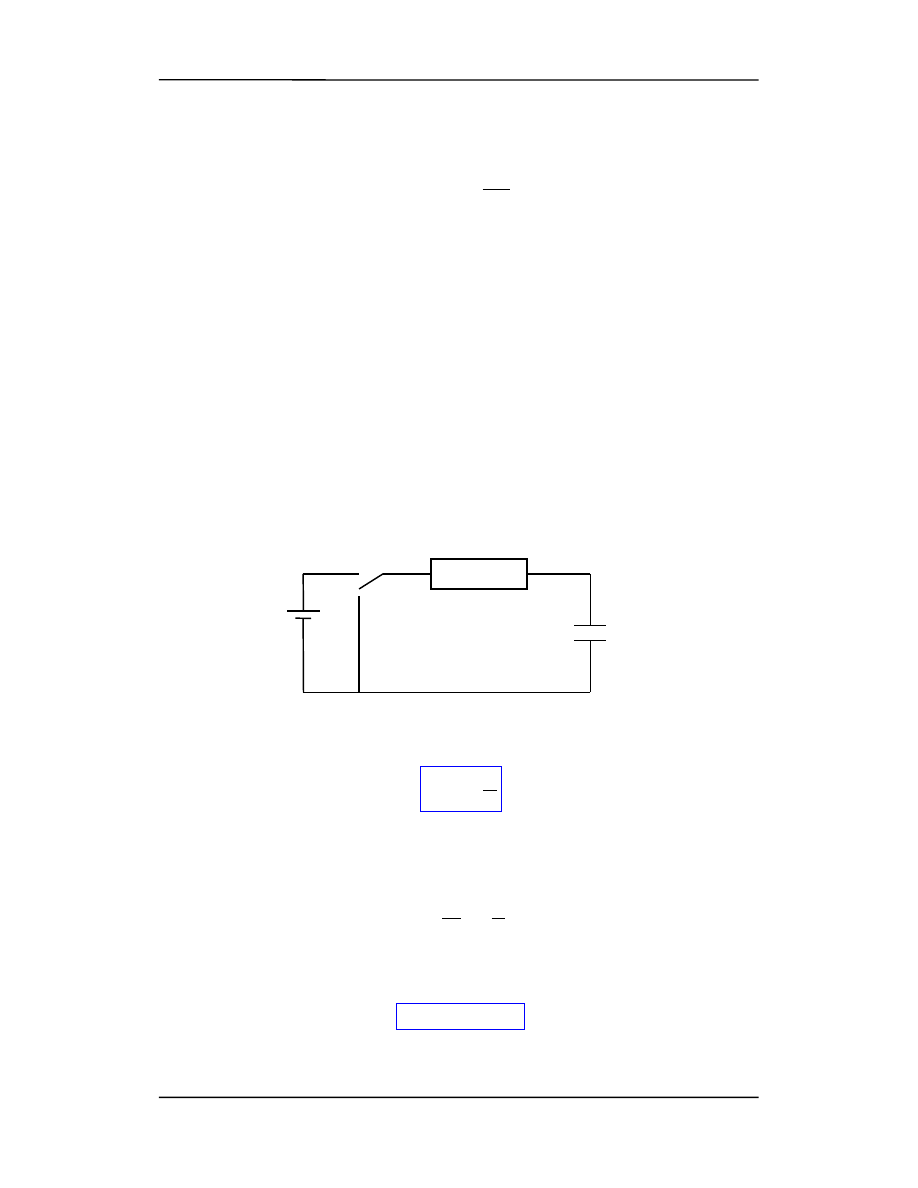
Rozpatrzmy jaki prąd popłynie w obwodzie po zamknięciu wyłącznika do pozy-

cji (a).

Korzystamy z prawa Kirchoffa.

C

q

IR

+

=

ε

(23.7)

W równaniu tym są dwie niewiadome I oraz q. Ale możemy skorzystać ze związku
I = dq/dt. Otrzymujemy równanie różniczkowe

C

q

R

t

q

+

=

d

d

ε

Szukamy rozwiązania q(t). Ma ono postać

)

1

(

/ RC

t

e

C

q

−

−

=

ε

(23.8)

Możemy sprawdzić czy funkcja ta jest rozwiązaniem równania różniczkowego poprzez
jej podstawienie.

ε

R

C

a

b

Z. Kąkol-Notatki do Wykładu z Fizyki

23-4

Prąd obliczamy różniczkując dq/dt

RC

t

e

R

t

q

I

/

d

d

−

=

=

ε

Rysunki przedstawiają zależność q(t) oraz I(t).
Jeżeli teraz przełączymy wyłącznik do pozycji (b) to będziemy rozładowywać konden-
sator. Teraz w obwodzie nie ma

ε i prawo Kirchoffa przyjmuje postać

0

=

+

C

q

IR

czyli

0

d

d

=

+

C

q

t

q

R

Rozwiązanie ma postać

RC

t

e

q

q

/

0

−

=

(23.9)

gdzie q

0

jest ładunkiem początkowym na kondensatorze.

Natężenie prądu przy rozładowaniu wynosi

RC

t

e

RC

q

t

q

I

/

0

d

d

−

−

=

=

W równaniach opisujących ładowanie i rozładowanie kondensatora wielkość RC ma
wymiar czasu i jest nazywana

stałą czasową

obwodu. Opisuje ona fakt, że ładunek na

kondensatorze nie osiąga od razu wartości końcowej lecz zbliża się do niej wykładni-
czo. Podobnie przy rozładowaniu.

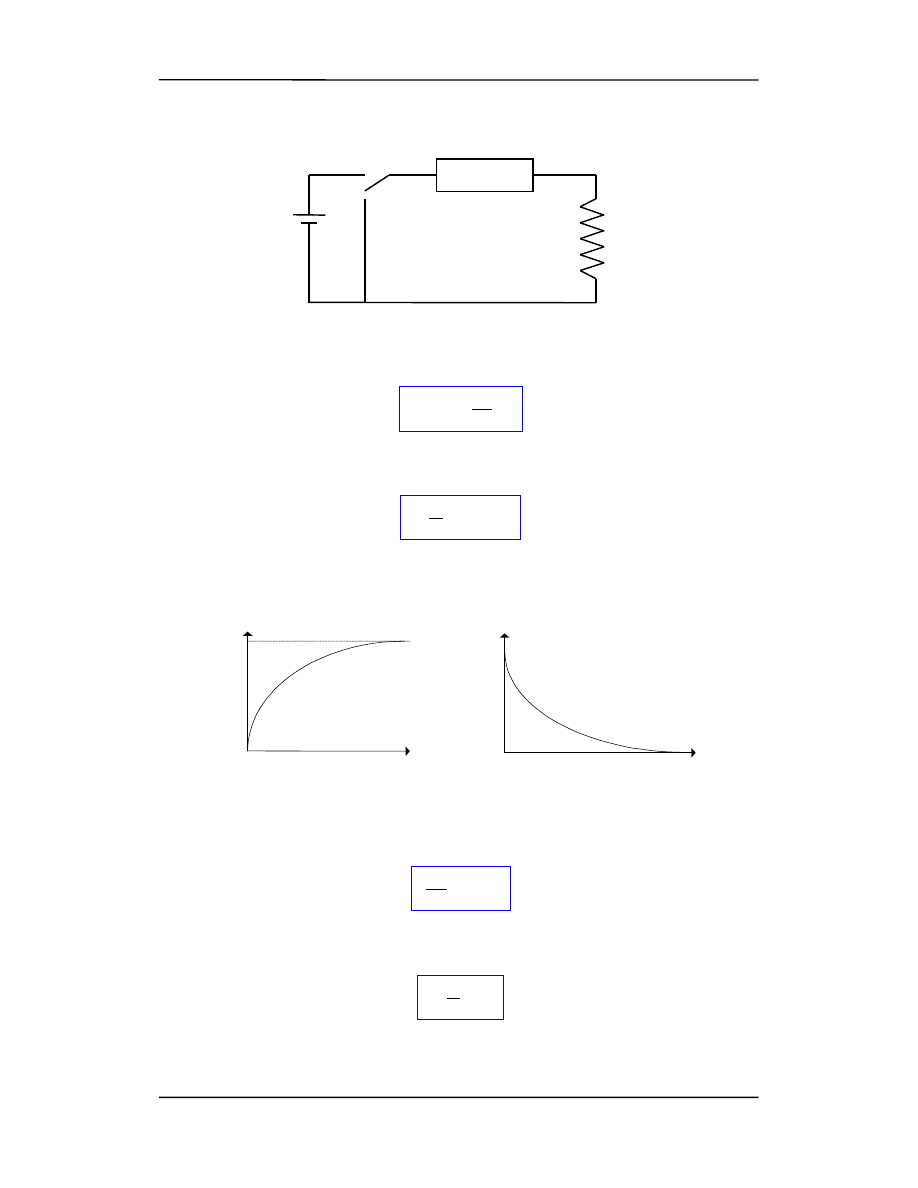
23.2.2 Obwód RL

Analogicznie opóźnienie w narastaniu i zanikaniu prądu pojawia się w obwodzie RL

przy włączaniu lub wyłączaniu źródła SEM.
Gdyby nie było cewki prąd osiągnąłby natychmiast wartość

ε/R. Dzięki cewce w obwo-

dzie pojawia się dodatkowo SEM samoindukcji

ε

L

, która zgodnie z regułą Lenza prze-

ciwdziała wzrostowi prądu (po włączeniu) co oznacza, że jej zwrot jest przeciwny do

ε.

q

t

C

ε

I

ε

/R

t

Z. Kąkol-Notatki do Wykładu z Fizyki

23-5

Z prawa Kirchoffa otrzymujemy

0

d

d

=

−

−

t

I

L

IR

ε

(23.10)

Poszukujemy rozwiązania tego równania różniczkowego w postaci I(t).
Ma ono postać

)

1

(

/ L

Rt

e

R

I

−

−

=

ε

(23.11)

Sprawdzamy poprzez podstawienie do równania. Napięcie na oporniku i cewce pokaza-
ne jest na rysunkach poniżej.

Narastanie prądu w obwodzie jest opisane stałą czasową

τ

L

= L/R.

Jeżeli przełącznik ustawimy w pozycji (b) to wyłączmy źródło SEM i otrzymamy

0

d

d

=

+

IR

t

I

L

(23.12)

z rozwiązaniem

L

Rt

e

R

I

/

−

=

ε

(23.12)

ε

R

L

a

b

V

R

t

ε

V

L

ε

t

Z. Kąkol-Notatki do Wykładu z Fizyki

23-6

23.3 Energia, a pole magnetyczne

Pozostańmy przy obwodzie RL. Z prawa Kirchoffa otrzymaliśmy

t

I

L

IR

d

d

+

=

ε

Mnożąc to równanie przez I dostajemy

t

I

LI

R

I

I

d

d

2

+

=

ε

Interpretacja tego równania z punktu widzenia pracy i energii jest następująca:

•

lewa strona równania przedstawia szybkość (moc =

εI tj εdq/dt) z jaką źródło prze-

kazuje do obwodu energię

εq.

•

pierwszy wyraz po prawej stronie to szybkość (moc) wydzielania ciepła na oporze R.

•

drugi wyraz po prawej stronie to szybkość z jaką energia gromadzi się w polu ma-
gnetycznym.

To ostatnie możemy zapisać jako

t

I

LI

t

W

B

d

d

d

d

=

czyli

I

LI

dW

B

d

=

Po scałkowaniu otrzymujemy

2

2

1

d

d

LI

I

LI

W

W

B

B

=

=

=

∫

∫

(23.13)

Równanie określa

całkowitą energię magnetyczną

zawartą w cewce o indukcyjności L

przez, którą płynie prąd I.
Porównajmy to z energią naładowanego kondensatora

C

q

W

C

2

2

1

=

(23.14)

23.4 Gęstość energii a pole magnetyczne

Rozpatrzmy solenoid o długości l i powierzchni przekroju S czyli o objętości lS.
Tak więc gęstość energii

lS

W

w

B

B

=

Ponieważ

Z. Kąkol-Notatki do Wykładu z Fizyki

23-7

2

2

1

LI

W

B

=

więc

lS

LI

w

B

2

2

1

=

Przypomnijmy, że

l

S

N

L

2

0

µ

=

oraz

l

N

I

In

B

0

0

µ

µ

=

=

co w połączeniu daje wyrażenie

0

2

2

1

µ

B

w

B

=

(23.15)

opisujące

gęstość energii

zawartej w każdym punkcie przestrzeni w której jest indukcja

magnetyczna B.

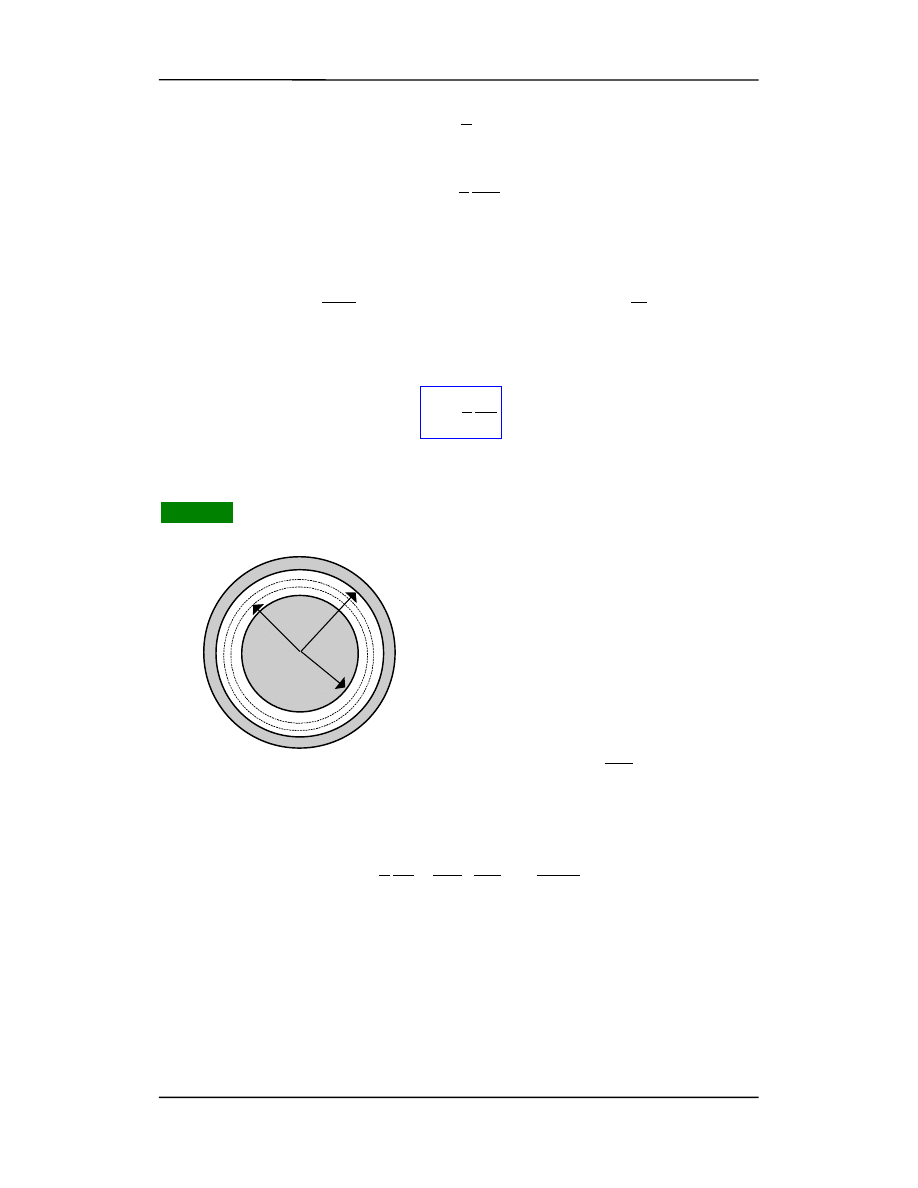
Przykład 2

Długi koncentryczny kabel składa się z cylin-
drycznych przewodników o promieniach
a i b. Obliczmy energię zawartą w polu ma-
gnetycznym kabla na odcinku o długości l

0

oraz jego indukcyjność.
Stosując prawo Ampera dla przestrzeni po-
między cylindrami otrzymamy

I

rB

0

2

µ

π

=

czyli

r

I

B

π

µ
2

0

=

Gęstość energii w punktach pomiędzy przewodami

2

2

2

0

2

0

0

0

2

8

2

2

1

2

1

r

I

r

I

B

w

B

π

µ

π

µ

µ

µ

=













=

=

Rozpatrzmy teraz cienką (dr) warstewkę pomiędzy cylindrami. Objętość tej warstewki
wynosi:

dV = 2

πrdrl

0

dla odcinka kabla o długości l

0

.

Energia w tej objętości wynosi więc

-

+

a

b

r

dr

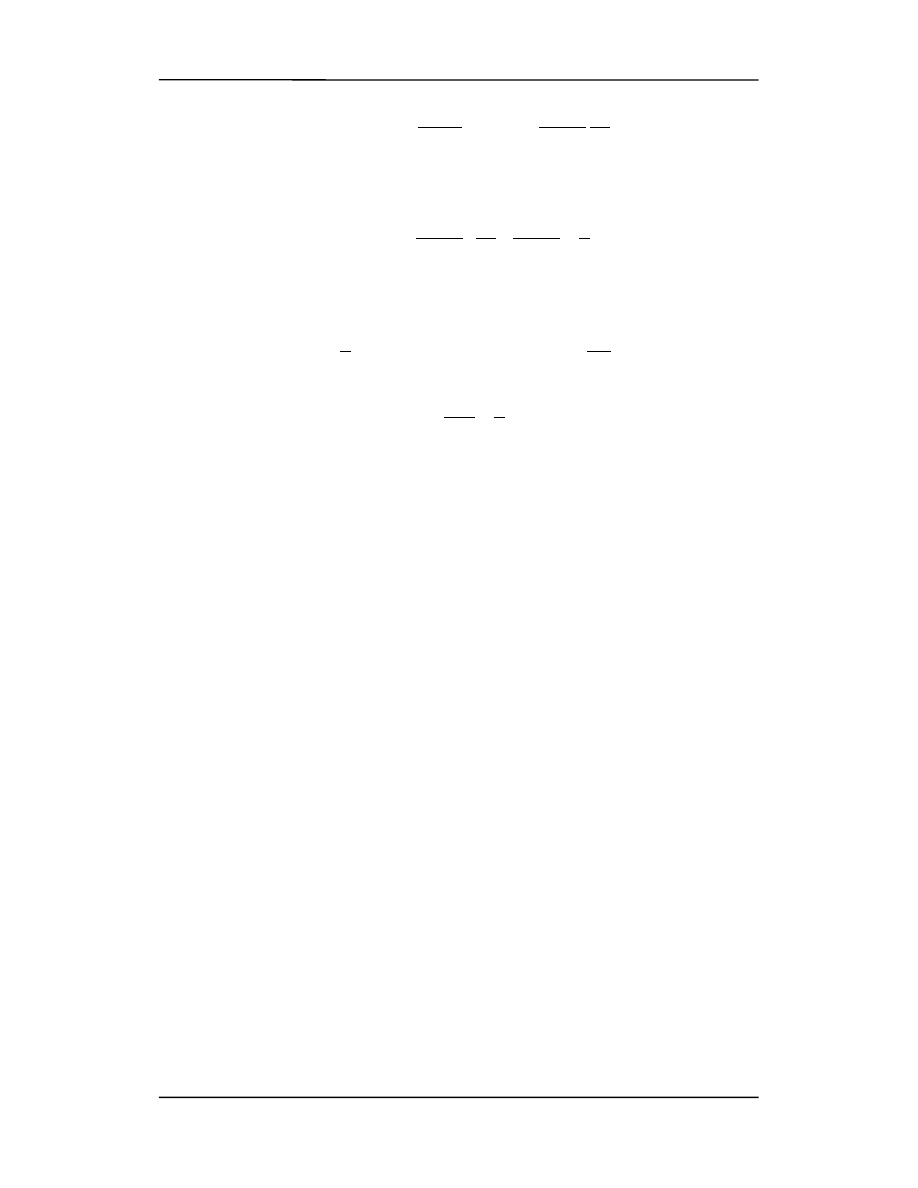
Z. Kąkol-Notatki do Wykładu z Fizyki

23-8

r

r

l

I

rl

r

r

I

V

w

W

B

d

4

d

2

8

d

d

0

2

0

0

2

2

2

0

π

µ

π

π

µ

=

=

=

Sumując (całkując) po całej objętości obliczamy całkowitą energię W

a

b

l

I

r

r

l

I

W

W

b

a

ln

4

d

4

d

0

2

0

0

2

0

π

µ

π

µ

∫

∫

=

=

=

Indukcyjność znajdziemy z zależności

2

2

1

LI

U

=

czyli

2

2

I

U

L

=

a

b

l

L

ln

2

0

0

π

µ

=

L zależy tylko od czynników geometrycznych.