Ć w i c z e n i e 43

BADANIE TRANSFORMACJI ENERGII MECHANICZNEJ

W KRĄŻKU MAXWELLA

43.1 Opis teoretyczny

Krążek Maxwella jest to masywne ciało (w naszym przypadku jest to koło zamachowe) zawieszone
na cienkim pręcie (osi obrotu), który przechodzi przez środek masy ciała. Do każdej części pręta
(po obu stronach krążka) są umocowane cienkie linki. Całość jest zawieszona na statywie tak, że
pręt zachowuje pozycję poziomą (rys. 43.1). Po nawinięciu linek na oś krążek unosi się do góry. Po
swobodnym puszczeniu krążka z górnego położenia, linki zaczynają się odwijać z pręta, a całość
opadać ku dołowi coraz szybciej ruchem jednostajnie przyśpieszonym.
Jednostajnie przyśpieszonemu ruchowi postępowemu ku dołowi towarzyszy jednostajnie przyśpie-
szony ruch obrotowy krążka. Przyśpieszenie kątowe ruchu obrotowego (ε) związane jest z przyśpie-
szeniem liniowym ruchu postępowego (a) zależnością:

R

a

ε

=

(43.1)

gdzie R – promień ośki na której nawinięte są linki.
Zastosujmy zasadę zachowania energii mechanicznej dla krążka Maxwella spadającego z wysoko-
ści h. Jego początkowa energia potencjalna E

p

po spadku z wysokości h zostaje całkowicie zamie-

niona na energię kinetyczną ruchu postępowego E

kp

oraz na energię kinetyczną ruchu obrotowego

E

ko

:

2

J

2

mV

mgh

2

0

2

ω

+

=

(43.2)

gdzie: m – masa krążka razem z ośką, J

0

– moment bezwładności krążka z ośką względem osi ob-

rotu, V – prędkość liniowa ruchu postępowego, ω – prędkość kątowa ruchu obrotowego.
Całkowita energia początkowa układu (mającej postać energii potencjalnej w jednorodnym polu
grawitacyjnym Ziemi) dzieli się na dwie postacie energii kinetycznej. W ćwiczeniu wyznaczamy
wartości obu energii kinetycznych, ich wzajemny stosunek oraz określamy, w jaki sposób zmieniają
się one w czasie. W tym celu musimy najpierw wyznaczyć moment bezwładności krążka J

0

wzglę-

dem centralnej osi obrotu. Wielkość fizyczna, jaką jest moment bezwładności została szczegółowo
przedstawiona w ćwiczeniu nr 36 przy opisie działania maszyny Atwooda.

Stosując zależność

R

V

=

ω

do zasady zachowania energii (43.2) mamy:











 +

=

2

0

2

mR

J

1

V

2gh

(43.3).

Rys. 43.1. Krążek Maxwella. Fotografia stanowiska laboratoryjnego.

i stąd po przekształceniach możemy obliczyć moment bezwładności J

0

:













−

=

1

V

2gh

mR

J

2

2

0

(43.4)

Moment bezwładności krążka Maxwella można określić też na innej drodze, rozpatrując jego
chwilowy ruch obrotowy względem osi przebiegającej przez punkt styczności nici z prętem (rys.
43.2)

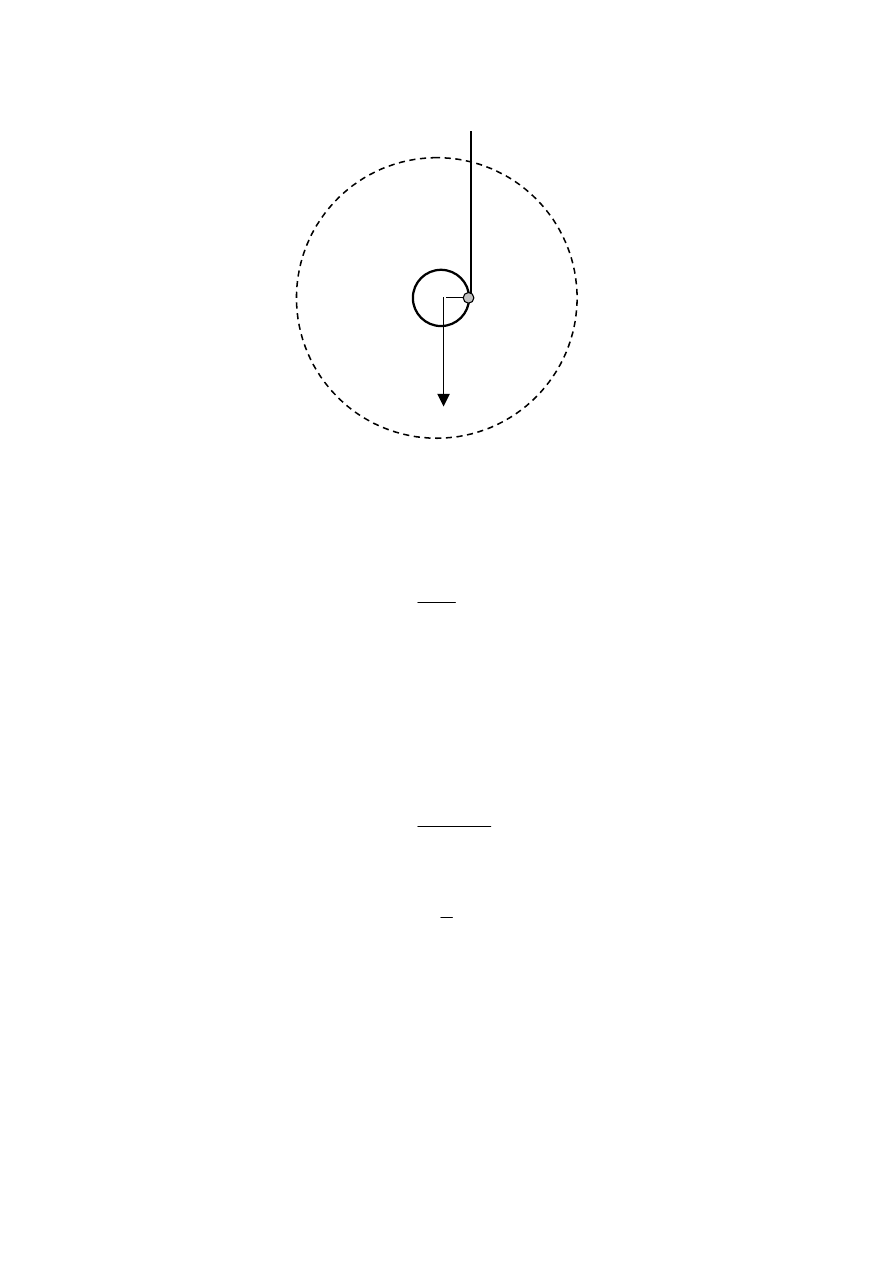
R

mg

Rys. 43.2. Chwilowy ruch obrotowy krążka względem osi przebiegającej przez punkt stycz-

ności z nicią zaznaczony literą A

.

Stosując drugą zasadę dynamiki dla ruchu obrotowego otrzymujemy:

J

mgR

ε

=

(43.5).

gdzie: mgR – moment siły obracający ciało względem osi A, J – moment bezwładności krążka
względem osi A,
Na mocy twierdzenia Steinera (o osiach równoległych - patrz ćw. nr 4) momenty bezwładności J i
J

0

są związane ze sobą zależnością:

2

0

mR

J

J

+

=

(43.6).

w efekcie:

2

0

mR

J

mgR

ε

+

=

(43.6).

i stąd:











 −

=

R

ε

g

mR

J

0

(43.7).

Wyznaczając ε można znaleźć J

0

– moment bezwładności ciała (tu krążka z prętem) względem osi

przechodzącej przez jego środek masy. Zaprezentowana metoda dobrze nadaje się do eksperymen-
talnego wyznaczania momentów bezwładności względem takich osi. Ważne jest to, że nie jest wy-
magana kołowa symetria badanego ciała. Oś obrotu musi przechodzić tylko przez środek jego masy
(rys. 43.3).

A

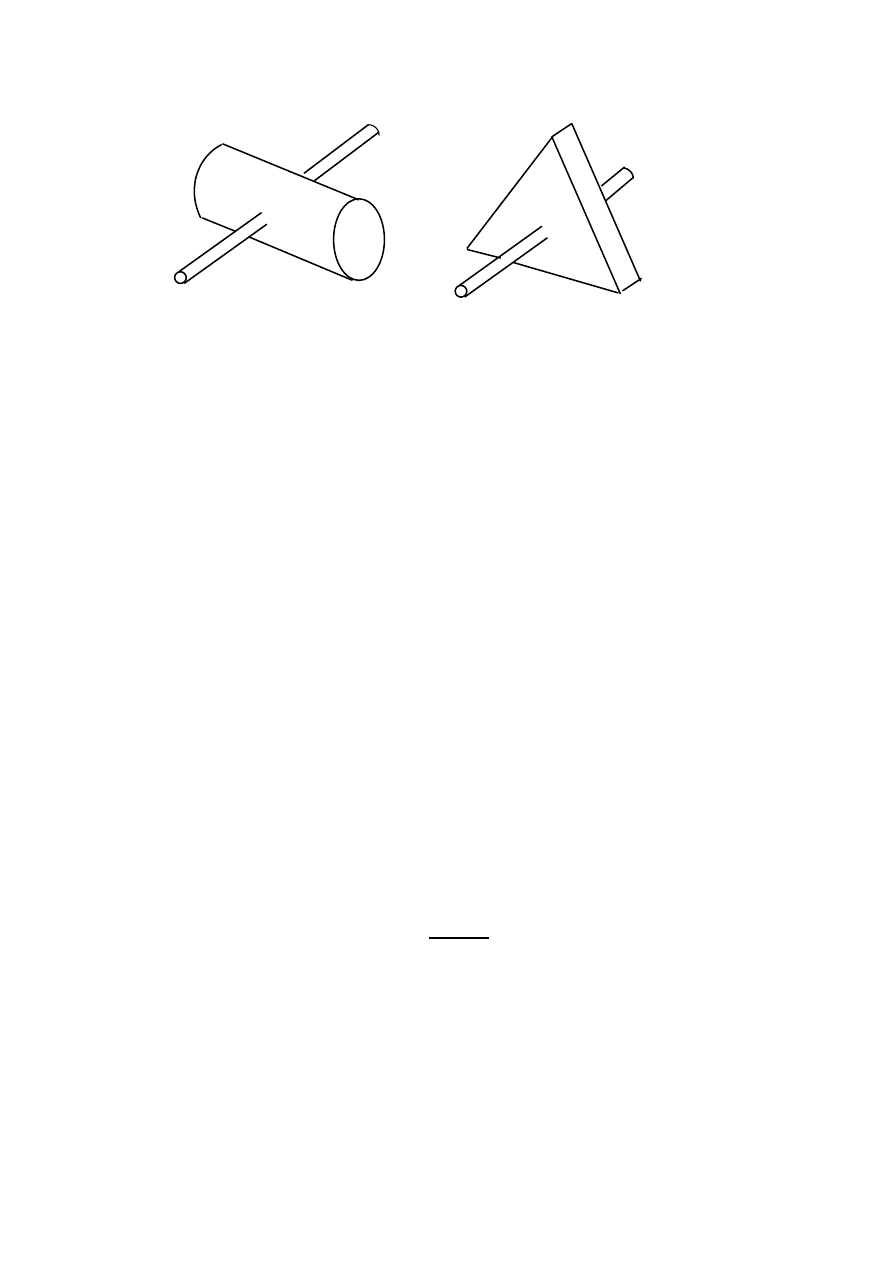
a

b

Rys. 43.3. Przykładowe kształty ciał, których momenty bezwładności można wyznaczyć

stosowaną w ćwiczeniu metodą: a) oś obrotu przebija prostopadle walec w środ-
ku masy, b) oś obrotu przebija prostopadle trójkątną płytę w środku masy.

43.2 Opis układu pomiarowego

Zastosowany w ćwiczeniu krążek Maxwella ma kształt koła zamachowego umocowanego na ośce o
promieniu

mm

0,1

2,5

r

±

=

. Masa koła z ośką 0,001

0,436

m

±

=

kg. Możliwy do zrealizowania

maksymalny spadek ciała wynosi około 65 cm. Całość jest umocowana na specjalnym wypozio-
mowanym statywie. Po nawinięciu linek na ośkę, krążek blokuje się w górnym położeniu za pomo-
cą specjalnego mechanicznego wyzwalacza. Krążek posiada umieszczone na obwodzie otwory
umożliwiające tę blokadę. Wyzwalacz jest sprzęgnięty elektronicznie z fotobramką. Całość umoż-
liwia pomiar czasu spadku krążka Maxwella z dokładnością do 0,001s. W fotobramce zastosowano
fotokomórkę reagującą na wąską wiązkę światła z zakresu podczerwieni. Wysokość położenia foto-
bramki można zmieniać przesuwając ją wzdłuż statywu.

Całość zaopatrzona jest w pionowo ustawiony liniał. Znaczniki umieszczone na liniale

umożliwiają wyznaczenie położeń ośki krążka oraz fotokomórki w fotobramce z dokładnością do
1 mm.

43.3 Przebieg pomiarów

1. Zablokować wężyk wyzwalacza w pozycji „wciśnięty”.
2. Ostrożnie nawinąć linki, na których jest zawieszony krążek na jego ośki i zablokować go w
górnym położeniu.
3. Ustawić fotobramkę na żądanej wysokości. Uważać aby oś krążka Maxwella przy spadku prze-
cinała światło fotokomórki ( wiązka światła jest niewidoczna, gdyż fotokomórka działa na pod-
czerwień) i nie uderzała w samą bramkę.
4. Za pomocą znaczników liniału ustalić górne położenie krążka Maxwella oraz fotokomórki.
Różnica odczytanych wartości równa jest wysokości (h) spadku krążka Maxwella.
5. Wcisnąć przycisk „Set” na bramce. W polu wyświetlania bramki powinny zapalić się trzy krop-
ki.
6. Zwolnić blokadę wężyka wyzwalacza i gdy koło rozwijając się z nici zacznie opadać, ponow-
nie nacisnąć wężyk i trzymać go w pozycji wciśniętej , aż do momentu gdy oś krążka Maxwella
przetnie strumień światła wiązki fotokomórki a na wyświetlaczu ukaże się wynik pomiaru czasu
spadku krążka.

7. Czynności 1-6 powtórzyć przynajmniej pięciokrotnie.
8. Czynności 1-7 powtórzyć dla pięciu wysokości (h) spadku różniących się o ~ 10cm.
9. Wyniki zebrać w poniższej tabeli.

Lp.

h

1

h

2

h

t

1

t

2

t

3

t

4

t

5

t

śr

1
2
3
4
5

43.4 Opracowanie wyników pomiarów.

Dla każdej serii pomiarowej (punkty 1-7 poprzedniego rozdziału) wykonać następujące ob-

liczenia:

1. Obliczyć wysokość spadku h i oszacować maksymalny błąd jej wyznaczenia

∆h.

2. Obliczyć średni czas spadku

śr

t

i jego średni błąd kwadratowy

t

σ

.

3. Obliczyć przyśpieszenie liniowe spadku krążka ze wzoru

2
śr

t

h

2

a

=

i średni błąd kwadratowy jego

wyznaczenia.

4. Obliczyć końcową prędkość ruchu postępowego:

śr

K

t

a

V

=

i

K

V

σ

5. Obliczyć końcową energię kinetyczną ruchu postępowego:

2

2

K

K

V

m

E

P

=

;

(

)

2

2

2

2

K

P

K

V

K

K

E

V

m

m

V

σ

σ

+













∆

=

6. Obliczyć moment bezwładności krążka J

0

ze wzoru (44.4) oraz jego średni błąd kwadratowy:

2

3

2

2

2

2

2

2

2

2

J

V

4gh

mR

V

2g

mR

1

V

2gh

2mR

1

V

2gh

mR

0













+













∆

+













∆













−













−

=

V

h

R

σ

σ

7. Obliczyć przyśpieszenie kątowe spadku krążka ze wzoru (44.1) oraz błąd

2

2

2

1













∆

+













=

R

R

a

R

a

σ

σ

ε

8. Obliczyć moment bezwładności krążka J

0

ze wzoru (44.7) i porównać otrzymany wynik z wyni-

kiem otrzymanym w punkcie 6. Wyciągnąć odpowiedni wniosek.

9. Obliczyć końcową prędkość kątową krążka:

śr

K

t

ε

ω =

;

(

) (

)

2

2

ε

ω

σ

σ

ε

σ

śr

t

t

+

=

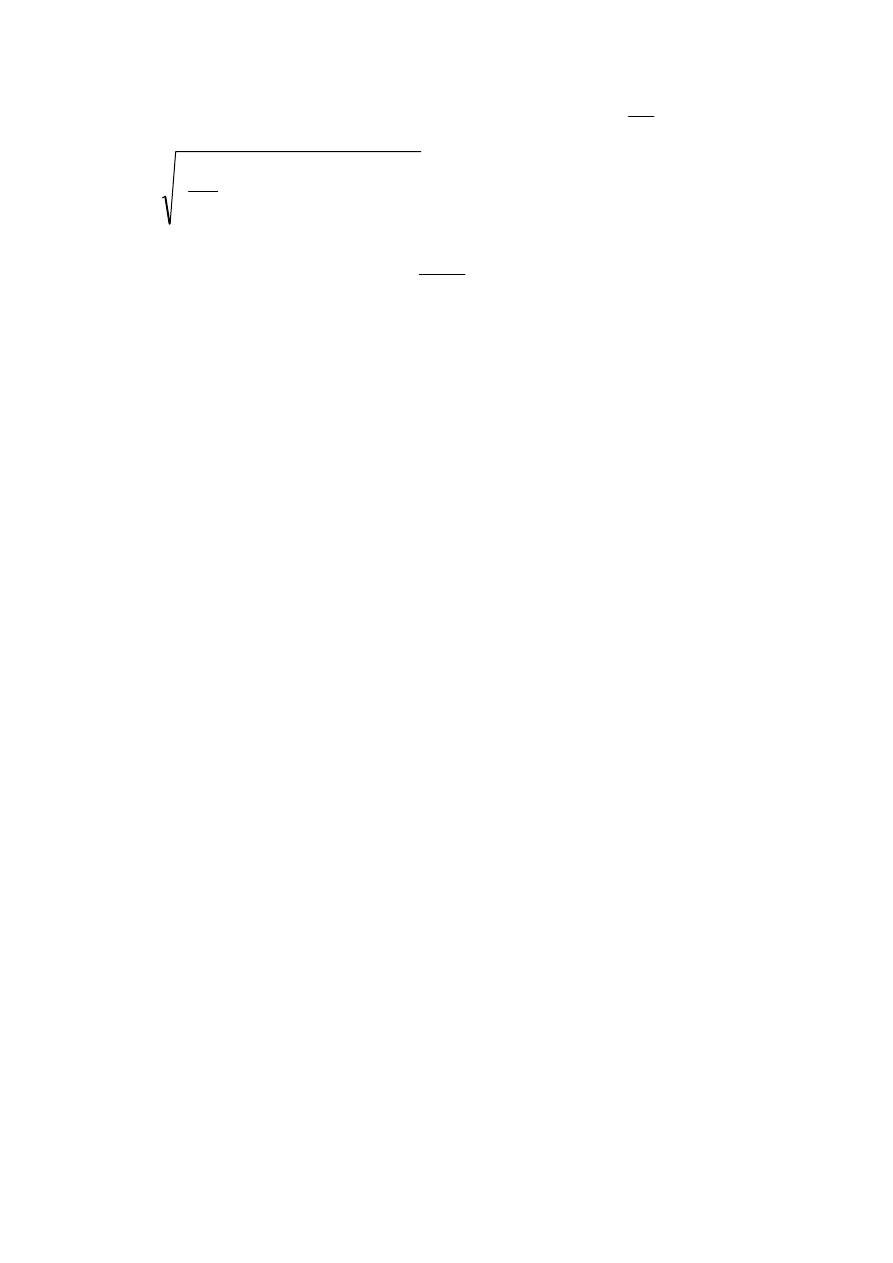
10.

Obliczyć końcową energię kinetyczną ruchu obrotowego:

2

0

2

K

K

J

E

obr

ω

=

;

(

)

2

0

2

2

2

ω

σ

ω

σ

ω

σ

K

J

E

J

obr

K

+













=

.

11. Obliczyć stosunek energii kinetycznych

P

obr

K

K

E

E

.

12. Obliczyć początkową energię potencjalną krążka

h

g

m

E

P

=

i błąd jej wyznaczenia

h

g

m

P

E

∆

=

σ

.

Zestawić w tabeli wyniki otrzymane ze wszystkich serii pomiarowych. Wykonać wykresy energii

obr

P

K

P

K

E

E

E

,

,

od kwadratu czasu (t

2

). Po naniesieniu punktów pomiarowych aproksymować je

prostymi. (Teoretycznie powinny to być proste. Dlaczego?). Sprawdzić czy eksperyment potwier-
dza teorię. Wyciągnąć ogólne wnioski z całego przebiegu doświadczenia, szczególnie odnośnie
sprawdzania się zasady zachowania energii.

43.5. Pytania kontrolne

1. Wyprowadzić wzór na chwilową wartość przyspieszenia podczas ruchu w dół krążka Maxwella.

2. Sformułować drugą zasadę dynamiki dla ruchu postępowego i obrotowego.
3. Zdefiniować moment bezwładności bryły. Od czego on zależy?.
4. Sformułować zasadę zachowania energii mechanicznej.

L i t e r a t u r a

[1] Piekara A. Mechanika ogólna,. PWN, Warszawa 1970.
[2] Leyko J. Mechanika ogólna, PWN, Warszawa 2002.