Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

1

Analiza współzależności zmiennych mierzalnych

Korelacja i regresja

Część II

W I części analizy współzależności zajmowaliśmy się badaniem siły i kierunku
związków między zmiennymi.

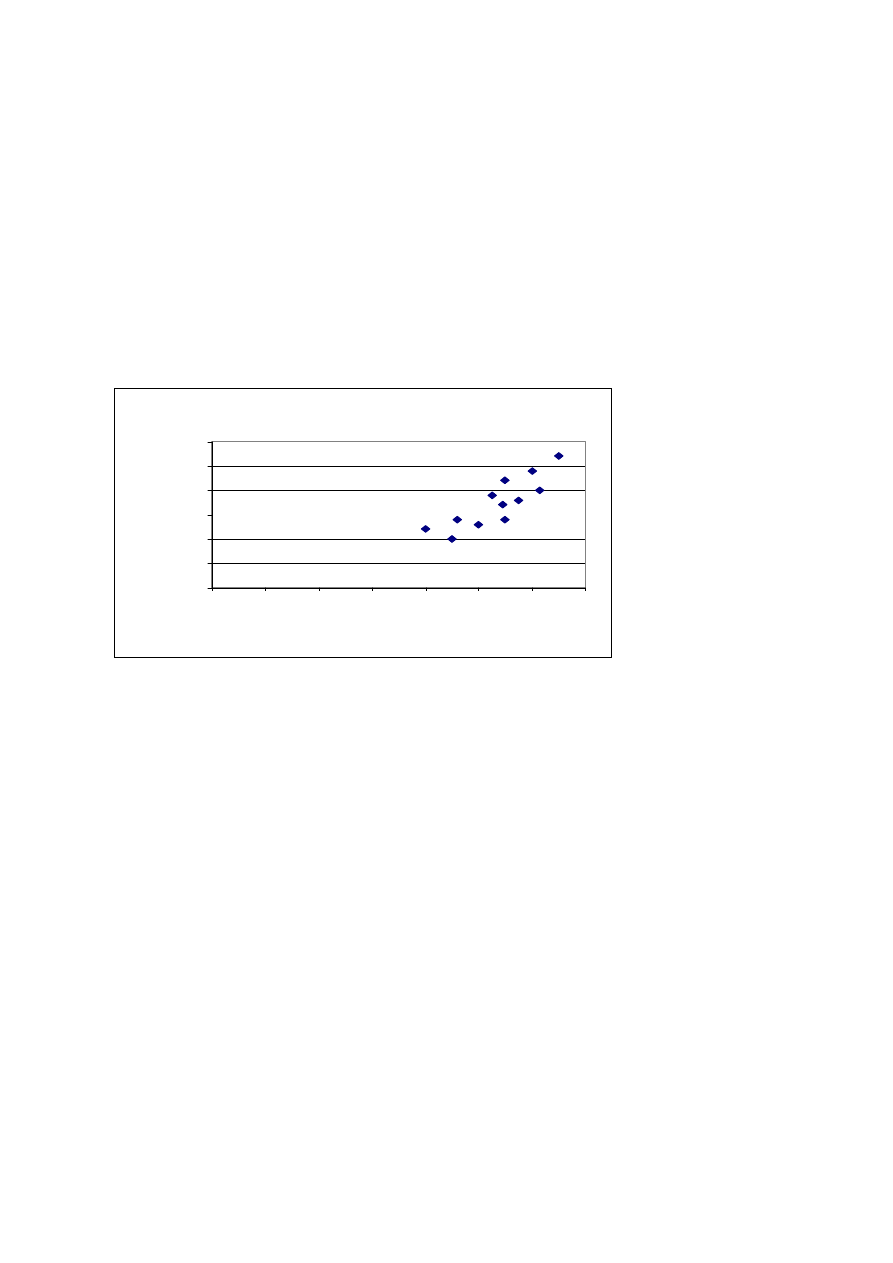
Podstawą szacunkowej oceny stopnia i kierunku zależności jest diagram korelacyjny.
Na podstawie przykładowego diagramu korelacyjnego: (Y– szybkość czytania, X– IQ)
możemy ocenić, że związek między Y i X jest dodatni i stosunkowo silny.

Diagram korelacyjny

(Y - szybkość czytania; X - IQ)

0

50

100

150

200

250

300

0

20

40

60

80

100

120

140

Dalsza część analizy zależy właśnie od tego czy związek między Y i X jest słaby czy
silny.

• Jeżeli związek jest słaby, kończymy analizę współzależności badanych

zmiennych Y i X. Formułujemy stosowny wniosek i rozpoczynamy
poszukiwanie relacji między Y i inną zmienną

• Jeżeli związek jest silny przystępujemy do dalszego etapu analizy, czyli

szacowania linii regresji

W jakim celu szacujemy linię regresji i w jaki sposób to robimy?
Przy silnym związku między zmiennymi łatwo sobie wyobrazić, że między punktami
przebiega pewna funkcja np. liniowa, która z pewną dokładnością może służyć do
opisu prawidłowości jaka ma miejsce między Y i X i następnie do prognozy Y na
podstawie wartości X.
Opisanie układu punktów nie jest łatwe i nie jest jednoznaczne. Można spróbować
opisać diagram powyższy diagram korelacyjny. Prawdopodobnie wersji byłoby tyle,
ile autorów. Odbiór też byłby różny.
Ale gdybyśmy założyli, że udałoby się do tych punktów empirycznych dopasować
linię, wówczas podając równanie tej linii można opisać relację między Y i X w sposób
jednoznaczny.

Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

2

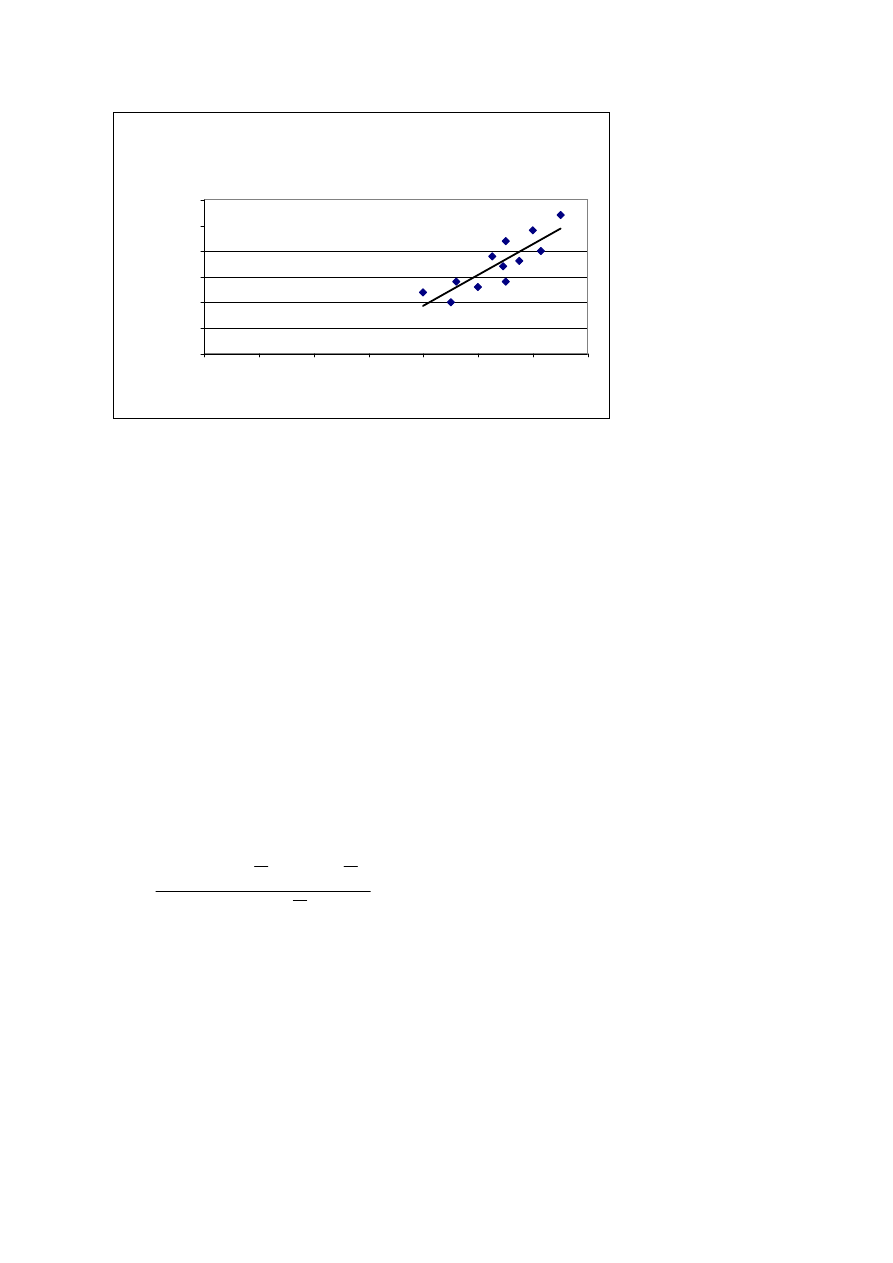
Diagram korelacyjny

(Y - szybkość czytania; X - IQ)

Oszacowana linia regresji:

Y^ = 3,02X - 148,48

0

50

100

150

200

250

300

0

20

40

60

80

100

120

140

Podsumowując ten fragment: będziemy dążyć do jednoznacznego opisu relacji między
Y i X przy pomocy równania odpowiedniej funkcji.
Najczęściej, wstępnie zakładamy, że związek YX jest liniowy i szacujemy parametry
równania.
Zakładamy, że relacja między Y i X jest liniowa, czyli :

Y = aX + b + e

lub inne oznaczenia

Y = a

1

X + a

0

+ e

gdzie:

a i b parametry równania, w tym:

a – współczynnik kątowy (parametr przy zmiennej X),

b – wyraz wolny
e –składnik losowy
Parametry równania a i b są nieznane i możemy jedynie oszacować ich wartość na
podstawie zebranych danych empirycznych, czyli znaleźć przybliżone wartości,
odpowiednio: a^ i b^ .
Wzory na oszacowanie parametrów a i b metodą najmniejszych kwadratów (MNK):

∑

∑

−

−

−

=

2

)

(

)

)(

(

ˆ

x

x

y

y

x

x

a

i

i

i

x

a

y

b

v

w ˆ

ˆ

−

=

Po oszacowaniu parametrów a i b oszacowaną linię regresji zapiszemy jako:

b

X

a

Y

ˆ

ˆ

ˆ

+

=

lub inne oznaczenia

0

1

ˆ

ˆ

ˆ

a

X

a

Y

+

=

(S

aˆ

) (S

bˆ

) standardowe błędy oszacowania parametrów

(W

aˆ

%) (W

bˆ

%) względne błędy oszacowania parametrów

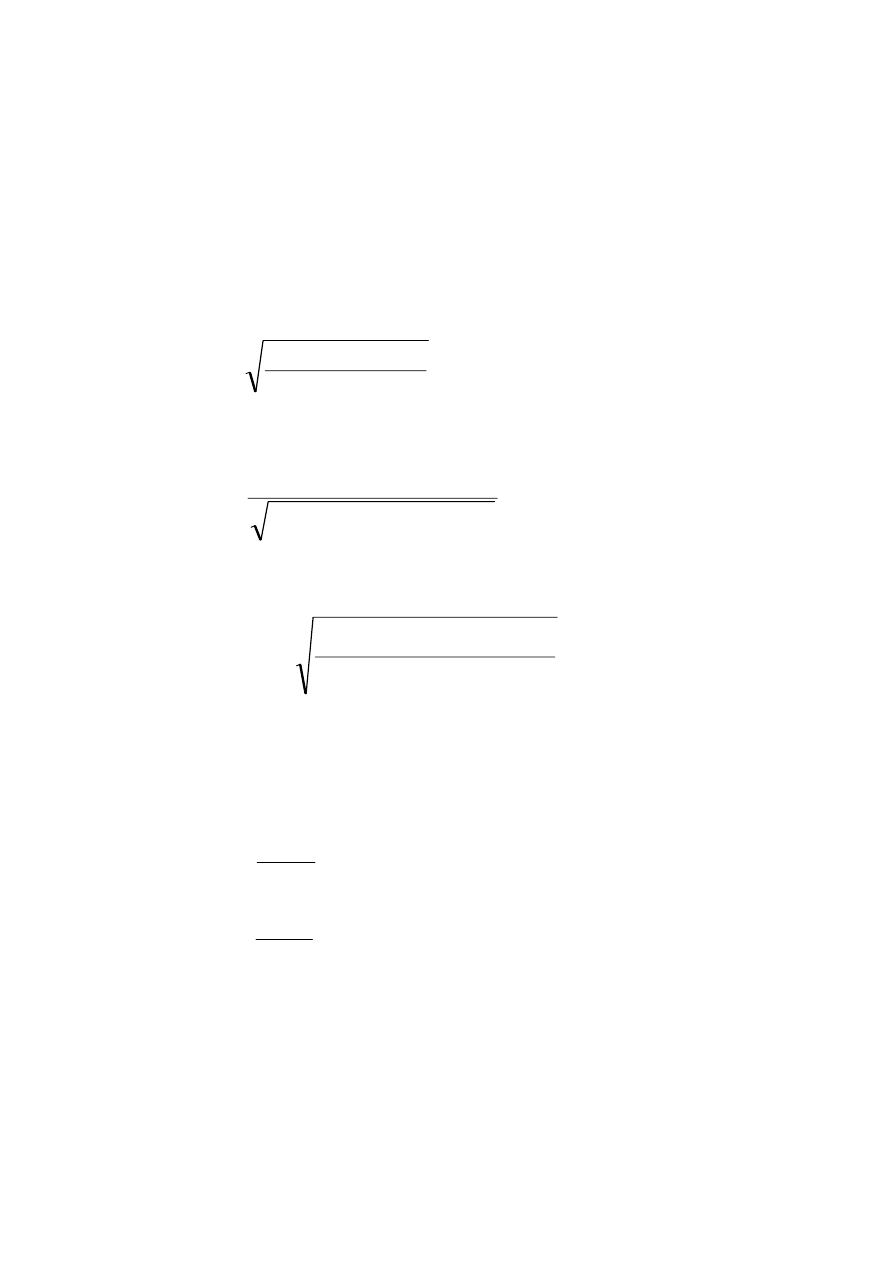
Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

3

Ocena oszacowania funkcji regresji

1) r

2

(kwadrat r) – współczynnik determinacji; przyjmuje wartości od 0 do 1

i oznacza % zmienności Y wyjaśniony zmiennością X.

Np.

r

2

=0,67 oznacza, że zróżnicowanie Y można w 67% wyjaśnić

zróżnicowaniem X.

2)

S(e)

– Standardowy błąd oszacowania funkcji regresji (modelu)

k

n

y

y

e

S

i

i

−

−

=

∑

2

)

ˆ

(

)

(

Gdzie k – liczba szacowanych parametrów (dla funkcji liniowej k=2)

3)

)

ˆ

(a

S

-

Standardowy błąd oszacowania współczynnika kątowego,

(

)

n

x

x

e

S

a

S

i

i

/

)

(

)

ˆ

(

2

2

∑

∑

−

=

4)

)

ˆ

(b

S

-

Standardowy błąd oszacowania wyrazu wolnego

(

)

[

]

n

x

x

n

x

e

S

b

S

i

i

i

/

)

(

)

ˆ

(

2

2

2

∑

∑

∑

−

=

5) względne błędy oszacowania (w %)

W(

aˆ

), W(

bˆ

) – względne błędy oszacowania

aˆ

,

bˆ

w %

%

100

ˆ

)

ˆ

(

)

ˆ

(

a

a

S

a

W

=

%

100

ˆ

)

ˆ

(

)

ˆ

(

b

b

S

b

W

=

Interpretacja

Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

4

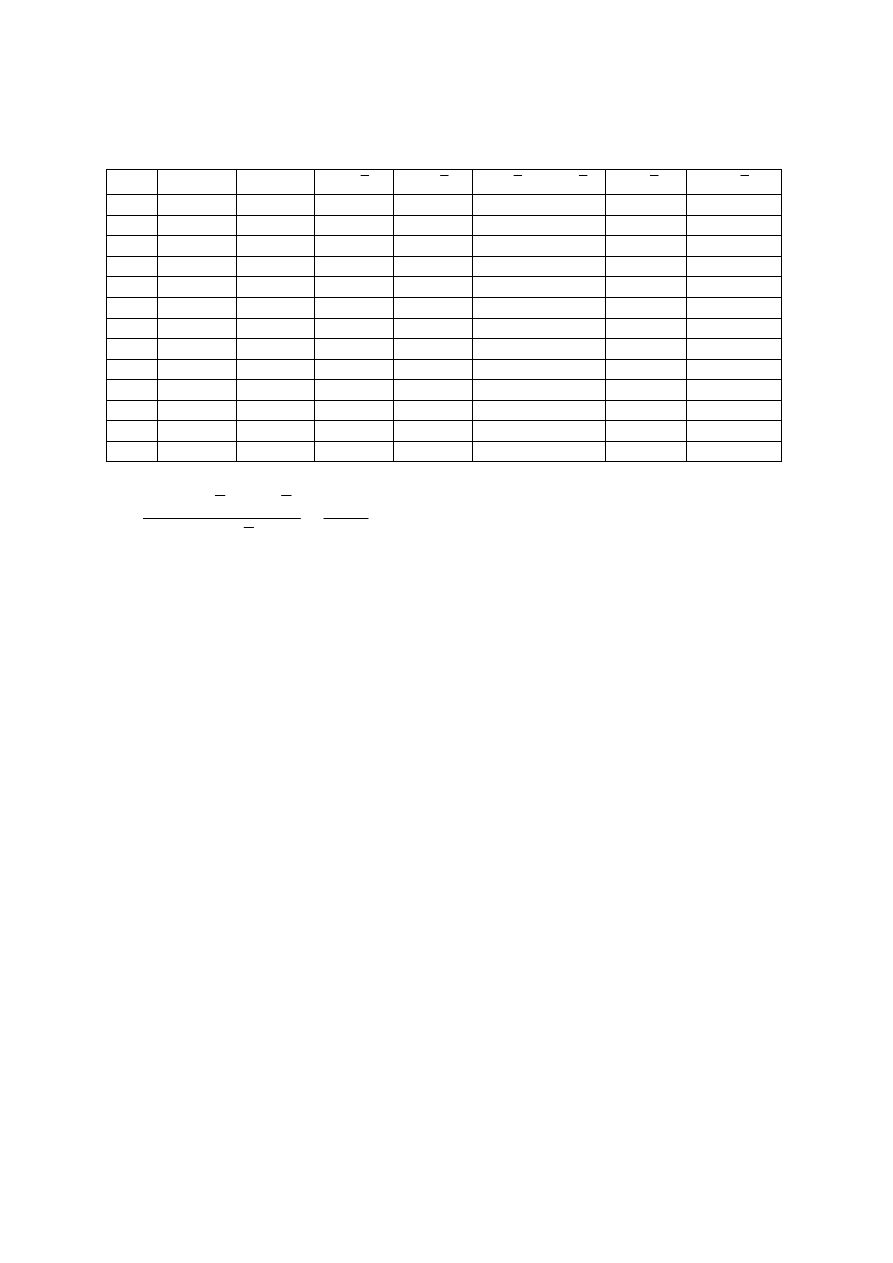
Przykład 1. Oszacować regresję Y względem X (Y – szybkość czytania i X – iloraz
inteligencji (IQ).

lp

x

i

y

i

x

i

- x

y

i

- y (x

i

- x )*( y

i

- y )

(x

i

- x )

2

( y

i

- y )

2

1 80

120

-27

-55

1485

729

3025

2 92

140

-15

-35

525

225

1225

3 90

100

-17

-75

1275

289

5625

4 109

170 2

-5

-10

4 25

5 100

130 -7

-45

315

49

2025

6 105

190 -2

15

-30

4 225

7 110

220 3

45

135

9

2025

8 110

140 3

-35

-105

9

1225

9 115

180 8

5

40

64 25

10 120

240 13

65

845

169 4225

11 123

200 16

25

400

256 625

12 130

270 23

95

2185

529 9025

Suma 1284 2100 X

X

7060

2336 29300

Średnia X= 107 Średnia Y= 175

02

,

3

2336

7060

)

(

)

)(

(

ˆ

2

=

=

−

−

−

=

∑

∑

x

x

y

y

x

x

a

i

i

i

x

a

y

b

v

w ˆ

ˆ

−

=

= 175 – 3,02 x 107 = - 148,14

Oszacowane równanie:

^
Y = 3,02X – 148,14 (np. x=115 y=203

Błędy oszacowania
S(

aˆ

)=0,58 S(

bˆ

)=63,0

W(

aˆ

)=0,58/3,02*100%= 19,2%

W(

bˆ

)=63/148,14*100%=42,5%

Współczynnik determinacji
r

2

= 0,73

aˆ

- oznacza tempo wzrostu/spadku funkcji, czyli odpowiada na pytanie o ile

wzrośnie (zmniejszy się Y) jeśli X wzrośnie o 1.

Interpretacja:
Związek między Y i X jest silny i dodatni, co oznacza, że osoby o wyższym IQ
szybciej czytają. Współczynnik determinacji 0,73 oznacza, że zróżnicowanie
szybkości czytania można w 73% wyjaśnić zróżnicowaniem IQ.

aˆ

= 3,02 oznacza, że zwiększenie IQ o 1 (większy IQ o 1) powoduje zwiększenie

szybkości czytania o 3.

Wykres oszacowanej funkcji:
wyznaczamy 2 punkty, x1= … i y1= … oraz x2=… i y2= … (patrz diagram korelat.)

Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

5

Szacowanie funkcji regresji (parametrów funkcji regresji) w arkuszu Excel.

1. wprowadzamy dane w kolumny X Y
2. w zakładce Narzędzia

>Analiza danych, a następnie >Regresja

>Zaznaczenie zakresu Y, X oraz miejsca na wynik (opcje wyjścia)

Otrzymujemy wynik:

PODSUMOWANIE - WYJŚCIE

Statystyki regresji

Wielokrotność R

0,853364

R kwadrat

0,728231

Dopasowany R
kwadrat

0,701054

Błąd standardowy

28,21851

Obserwacje

12

ANALIZA WARIANCJI

df

SS

MS

F

Istotność F

Regresja

1 21337,16

21337,16 26,79591 0,000415191

Resztkowy

10 7962,842

796,2842

Razem

11

29300

Współczynniki

Błąd

standardowy

Obliczenia własne

Względne błędy

oszacowania

Przecięcie -148,382

63,00029

42,45822

X 3,02226

0,583845

19,31816

-

Przecięcie

oznacza wyraz wolny w równaniu regresji

-

X

oznacza współczynnik kątowy

Czyli oszacowana wartość wyrazu wolnego wynosi – 148,4,
a oszacowana wartość współczynnika kątowego wynosi +3,02.

A zatem oszacowane równanie regresji:

b

X

a

Y

ˆ

ˆ

ˆ

+

=

to:

Yˆ

= 3,02 X – 148,4

błędy standardowe

(0,58) (63,0)

błędy względne

[29,3%] [42,4%]

Interpretacja:

aˆ

= 3,02 oznacza, że jeśli X (czyli iloraz IQ) zwiększy się o 1, to Y (szybkość czytania)

zwiększy się o 3,02.

bˆ

= -148,4 nie ma tu rozsądnej interpretacji, gdyż dosłownie oznacza wartość Y, gdy X = 0.

A trudno mówić o realnej sytuacji gdy iloraz IQ jest równy 0. W takim przypadku nie
interpretujemy

bˆ

.

Materiały dydaktyczne dla studentów IPSiR UW © Beata Gruszczyńska

6

Wykres oszacowanej linii regresji

Wykorzystujemy diagram korelacyjny i na nim wykreślamy oszacowaną linię regresji.
Do wykreślenia linii wystarczą dwa punkty.

Te dwa punkty uzyskujemy przyjmując dwie dowolne wartości X i obliczając z równania
odpowiadają im dwie wartości Y.

np.

X

1

= 100, wtedy

Yˆ

1

= 3,02 x 100 – 148,4 = 153,6,

X

2

= 120, wtedy

Yˆ

2

= 3,02 x 120 – 148,4 = 214,

czyli
pierwszy punkt ma współrzędne (100; 153,6),
drugi punkt ma współrzędne ( 120; 214),
a linia regresji (odcinek linii) znajduje się na wykresie.

Diagram korelacyjny

(Y - szybkość czytania; X - IQ)

0

50

100

150

200

250

300

0

20

40

60

80

100

120

140