Analiza regresji

Regresja - metoda badania wpływu zmiennych uznanych za niezależne (objaśniające) na zmienną uznaną za zależną (objaśnianą). Narzędziem badania mechanizmu powiązań między zmiennymi jest funkcja regresji. W przypadku liniowej zależności pomiędzy dwiema zmiennymi funkcja regresji liniowej przyjmuje postać:

gdzie

y - zmienna zależna (objaśniana)

x - zmienna niezależna (objaśniająca)

i
- parametry strukturalne modelu

- składnik losowy

Parametry strukturalne funkcji regresji nie są znane i należy je oszacować na podstawie próby losowej.

gdzie
- składniki losowe (resztowe)

Parametr a nazywamy współczynnikiem kierunkowym regresji i obliczamy na podstawie jednego ze wzorów:

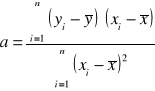
lub
,

gdzie r - współczynnik korelacji liniowej Pearsona, S(x), S(y) - odchylenia standardowe

Parametr a pokazuje o ile zmieni się y (zmienna zależna), jeśli x (zmienna niezależna) wzrośnie o 1.

Parametr b nazywamy wyrazem wolnym, pokazuje miejsce przecięcia się prostej regresji z osią OY. Obliczamy według wzoru:

Po oszacowaniu otrzymujemy następujące równanie regresji:
,

- wartości teoretyczne.

Przykład 1: Tabela podaje dane dotyczące zużycia pewnego surowca X (w kg) wykorzystywanego do produkcji wyrobu Y (w t). Oszacować równanie regresji oraz zinterpretować otrzymane wyniki. Narysować prostą regresji na wykresie. Jaka będzie spodziewana produkcja wyrobu, jeśli zostanie zużyte 180 kg surowca?

1	90	40	-15	-60	900	3600	37,42	2,58	6,67
2	85	35	-20	-65	1300	4225	35,95	-0,95	0,91
3	110	50	-5	-40	200	1600	43,28	6,72	45,19
4	125	45	-10	-25	250	625	47,67	-2,67	7,15
5	120	40	-15	-30	450	900	46,21	-6,21	38,54
6	150	63	8	0	0	0	55,00	8,00	64,00
7	140	45	-10	-10	100	100	52,07	-7,07	49,98
8	160	61	6	10	60	100	57,93	3,07	9,42
9	200	70	15	50	750	2500	69,65	0,35	0,12
10	190	61	6	40	240	1600	66,72	-5,72	32,74
11	220	86	31	70	2170	4900	75,51	10,49	109,96
12	210	64	9	60	540	3600	72,58	-8,58	73,67
Suma	1800	660	0	0	6960	23750	533,04	0	438,35
	150	55

Na ile dobra jest regresja?

Wariancja i odchylenie standardowe składnika resztowego - miary rozproszenia punktów empirycznych wokół prostej regresji. Są to miary nienormowane (przyjmują dowolne dodatnie wartości i nie mogą służyć do porównania).

Składnik resztowy:

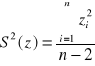
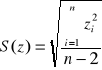
Współczynnik determinacji
jest miarą unormowaną,

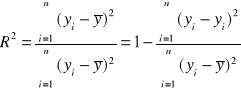
Związek między współczynnikiem determinacji
a współczynnikiem korelacji liniowej Pearsona r:
lub

Zadanie 1. Ocenić na ile dobra jest regresja z przykładu 1.

Zadanie 2. Badając zależność między ilością osób w rodzinie a ilością osób pracujących zawodowo uzyskano następujące wyniki:

- wariancja ilości osób pracujących zawodowo wynosi 1,44;

- współczynnik regresji w równaniu
wynosi 0,6;

- średnia ilość osób w rodzinie wynosi 3,42;

- współczynnik zmienności dla ilości osób w rodzinie wynosi 0,3.

Na podstawie tych informacji należy ustalić siłę związku korelacyjnego między ilością osób w rodzinie a ilością pracujących zawodowo.

Zadanie 3. Badając współzależność między wielkością produkcji a kosztami jednostkowymi uzyskano następujące równanie regresji:

, .
Czy takie wyniki są możliwe? Odpowiedź uzasadnić.

1

---