ANALIZA DYNAMIKI ZJAWISK

(badanie szeregu czasowego)

Podstawową formą prezentacji danych w analizie dynamiki jest szereg czasowy.

I. Szereg czasowy - ciąg wartości badanego zjawiska obserwowanego w kolejnych jednostkach czasu. Szereg czasowy składa się z dwóch kolumn (wierszy) - w pierwszej są jednostki czasu t, a w drugiej jest poziom badanego zjawiska y_t.

t	1	2	…	n
yt	y1	y2		yn

II. MIARY DYNAMIKI ZJAWISKA - o podstawie stałej lub ruchomej

MIARY	jednopodstawowe - za podstawę przyjęto poziom zjawiska w okresie t=1	łańcuchowe
Przyrosty absolutne
Przyrosty względne
Indeksy (indywidualne)

Przyrost względny
= procentowy przyrost względny (w %)

Indeks
= indeks w %

Uwaga! i = 1 + d oraz d = i - 1

Interpretacja indeksów:

jeśli 0 < i < 1 spadek zjawiska; jeśli i > 1 wzrost zjawiska

Przykład:

Analiza dynamiki średniej temperatury w Warszawie w dn. 1-10 lipca 2003 r.

data	Temperatura ( ْC )	Przyrosty absolutne ( ْC)		Przyrosty względne		Indeksy
				jednopodst.	łańcuchowe	jednopodst.	łańcuchowe	jednopodst.	łańcuchowe
t	yt	Δt/1	Δt/t-1	dt/1	dt/t-1	it/1	it/t-1
1	27	0	-	0	-	1	-
2	29	2	2	0,0741	0,0741	1,0741	1,0741
3	23	-4	-6	-0,1481	-0,2069	0,8519	0,7931
4	31	4	8	0,1481	0,3478	1,1481	1,3478
5	37	10	6	0,3704	0,1935	1,3704	1,1935
6	34	7	-3	0,2593	-0,0811	1,2593	0,9189
7	28	1	-6	0,0370	-0,1765	1,0370	0,8235
8	25	-2	-3	-0,0741	-0,1071	0,9259	0,8929
9	27	0	2	0,0000	0,0800	1,0000	1,0800
10	30	3	3	0,1111	0,1111	1,1111	1,1111

III. ŚREDNIE TEMPO ZMIAN ZJAWISKA W CZASIE

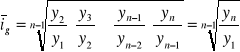
lub

Dla przykładu: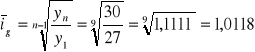

IV. PRZEKSZTAŁCENIE INDEKSÓW

*łańcuchowych w jednopodstawowe *jednopodstawowych w łańcuchowe

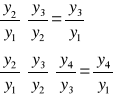
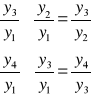
czyli
czyli

---