8.à$'<=)$=2:37/635=)(1,$
=:5271(*2

:352:$'=(1,(

8NáDG\ ] ID]RZ SWO VSU]*HQLD ]ZURWQHJR F]VWR QD]\ZDQH

SWODPL ID]RZ\PL 3// DQJ SKDVH ORFNHG ORRS ]QDMGXM EDUG]R

V]HURNLH ]DVWRVRZDQLH ZH ZVSyáF]HVQHM HOHNWURQLFH GR V\QFKURQL]DFML

SRG]LDáXSRZLHODQLD

F]VWRWOLZRFL

SRUHGQLHM

GHPRGXODFML

F]VWRWOLZRFL SU]HPLDQ\ F]VWRWOLZRFL LWS &LJOH URVQF\ REV]DU

OLF]Q\FK L Uy*QRURGQ\FK ]DVWRVRZD SWOL ID]RZHM Z XNáDGDFK

SU]HWZDU]DQLDV\JQDáyZDQDORJRZ\FKLF\IURZ\FKZL*HVL]W\P*H

SDUDPHWU\XNáDGyZ]SWO3//VQDRJyáNRU]\VWQLHMV]HQL*SDUDPHWU\

XNáDGyZNRQZHQFMRQDOQ\FK

8NáDG\ ] SWO 3// Z\WZDU]DQH V Z SRVWDFL RGG]LHOQ\FK

PRQROLW\F]Q\FKXNáDGyZ VFDORQ\FK OXE Z\NRU]\VW\ZDQH V MDNR EORNL

IXQNFMRQDOQH EDUG]LHM ]áR*RQ\FK XNáDGyZ VFDORQ\FK : ]DOH*QRFL RG

URG]DMXLWHFKQLNLSU]HWZDU]DQLDV\JQDáyZUR]Uy*QLDP\SWOHDQDORJRZH

$3// DQJ DQDORJXH SKDVH ORFNHG ORRS L F\IURZH '3// DQJ

GLJLWDOSKDVHORFNHGORRS

3WOD ID]RZD MHVW XNáDGHP VLOQLH QLHOLQLRZ\P VWG MHM DQDOL]D

SR]ZDODQDMF]FLHMQDX]\VNDQLHMHG\QLHZ\QLNyZSU]\EOL*RQ\FKOXEZ

SRVWDFLQXPHU\F]QHM

: ZLNV]RFL SUDNW\F]Q\FK ]DVWRVRZD LQWHUHVXMH QDV SUDFD Z

W]ZVWDQLHV\QFKURQL]DFMLNLHG\WRSU]\VSHáQLHQLXSHZQ\FKZDUXQNyZ

MHM G]LDáDQLH PR*QD RSLVDü PRGHOHP OLQLRZ\P ]QDF]QLH SURVWV]\P GR

DQDOL]\

: QLQLHMV]\P UR]G]LDOH QDV]H UR]ZD*DQLD RJUDQLF]\P\ GR

RPyZLHQLD SRGVWDZRZ\FK ZáDFLZRFL L Z\EUDQ\FK ]DVWRVRZD

DQDORJRZ\FKSWOLID]RZ\FK

=$6$'$'=,$à$1,$02'(/37/,)$=2:(-

3RGVWDZRZ\ VFKHPDW EORNRZ\ SWOL ID]RZHM SU]HGVWDZLRQR QD

U\V

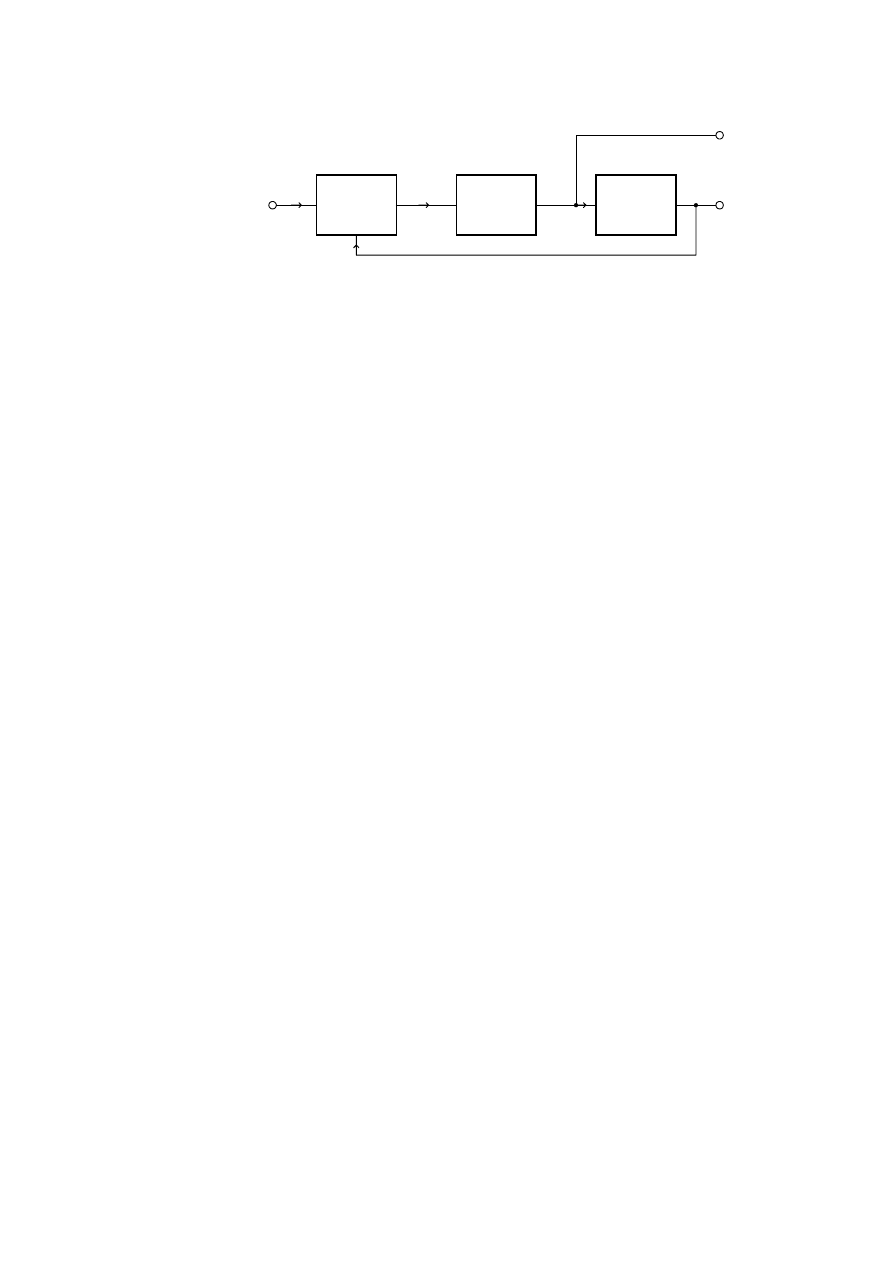
)'3

'HWHNWRU

ID]\

9&2

( )

X W

L

( )

ϕ

L

W

( )

X W

'

( )

X W

2

( )

X W

J

( )

X W

2

( )

ϕ

J

W

[ ]

UDG

[

]

9 UDG

[ ]

9

[ ]

9 9

[ ]

9

[

]

UDG 9

[ ]

UDG

5\V6FKHPDWEORNRZ\XNáDGX]ID]RZSWOVSU]*HQLD]ZURWQHJR

3WOD ID]RZD VNáDGD VL ]DVDGQLF]R ] WU]HFK SRGVWDZRZ\FK

EORNyZ GHWHNWRUD ID]\ ILOWUX GROQRSU]HSXVWRZHJR )'3 L JHQHUDWRUD

SU]HVWUDMDQHJRQDSLFLHP9&2DQJYROWDJHFRQWUROOHGRVFLOODWRU-HVW

WR XNáDG DXWRPDW\F]QHM UHJXODFML NWyUHJR ]DGDQLHP MHVW OHG]HQLH

FKZLORZHM ID]\ V\JQDáX ZHMFLRZHJR

( )

( )

ϕ

ϕ

i

g

t

t

−

SU]H] V\JQDá

( )

u t

g

Z\WZDU]DQ\ZORNDOQ\PJHQHUDWRU]H9&2

9&2 MHVW JHQHUDWRUHP NWyUHJR F]VWRWOLZRü GUJD MHVW

SURSRUFMRQDOQDGRQDSLFLDVWHUXMFHJR

( )

u t

O

'HWHNWRUID]\SRUyZQXMH

ID]\ V\JQDáyZ

( )

u t

i

L

( )

u t

g

D Z Z\QLNX WHJR SRUyZQDQLD Z\WZDU]D

V\JQDáEáGX

( )

u t

D

,

]DOH*Q\RGUy*QLF\ID]3RRGILOWURZDQLX]V\JQDáX

( )

u t

D

QLHSR*GDQ\FK VNáDGRZ\FK SU]H] ILOWU GROQRSU]HSXVWRZ\ L

HZHQWXDOQ\P Z]PRFQLHQLX RWU]\PXMH VL V\JQDá

( )

u t

O

NWyU\ VWHUXMH

9&2 Z WDNL VSRVyE DE\ Uy*QLFD ID] XOHJáD ]PQLHMV]HQLX : ODG ]D

OHG]HQLHP FKZLORZHM ID]\ V\JQDáX ZHMFLRZHJR X]\VNXMH VL WDN*H

OHG]HQLH FKZLORZHM F]VWRWOLZRFL WHJR V\JQDáX SU]H] V\JQDá

( )

u t

g

8NáDG Z\ND]XMH ZáDFLZRFL V\QFKURQL]DFML REX V\JQDáyZ D V\JQDá

ZHMFLRZ\

( )

u t

i

QRVL QD]Z V\JQDáX RGQLHVLHQLD OXE V\JQDáX

V\QFKURQL]XMFHJR 1D U\V ]D]QDF]RQR UyZQLH* MHGQRVWNL

Z\PLDURZH Z NWyU\FK Z\UD*DQH V FKDUDNWHU\VW\NL SU]HMFLRZH

SRV]F]HJyOQ\FKEORNyZRUD]V\JQDá\QDZHMFLXLZ\MFLXW\FKEORNyZ

=Dáy*P\ *H V\JQDá ZHMFLRZ\

( )

u t

i

L V\JQDá Z\WZDU]DQ\ Z

JHQHUDWRU]H9&2VRNUHORQH]DOH*QRFLDPL

( )

( )

[

]

( )

( )

[

]

u t

U

t

t

u t

U

t

t

i

i

i

g

g

g

=

+

=

+








sin

cos

ω

ϕ

ω

ϕ

0

0

JG]LH

( )

( )

ϕ

ϕ

i

g

t

t

L

VID]DPLFKZLORZ\PLND*GHJR]V\JQDáyZ

3XOVDFMHFKZLORZHV\JQDáyZRNUHODM]DOH*QRFL

( )

( )

[ ]

( )

( )

[ ]

ω

ω

ϕ

ω

ω

ϕ

i

i

g

g

t

d

dt

t

t

d

dt

t

=

+

=

+













0

0

-DNRGHWHNWRUID]\]DVWRVXMHP\XNáDGPQR*F\RSLVDQ\ZUR]G]

*G\QDMHJRZHMFLDSRGDP\V\JQDá\RSRVWDFLWRQDMHJRZHMFLX

RWU]\PDP\V\JQDá

( )

u t

D

RSLVDQ\]DOH*QRFL

( )

( ) ( )

( )

( )

[

]

u t

k u t u t

k U U

t

t

D

m

i

g

m

i

g

i

g

=

=

−

+

1

2

sin

ϕ

ϕ

( )

( )

[

]

+

+

+

1

2

2

0

k U U

t

t

m

i

g

i

g

sin

ω

ϕ

ϕ

JG]LH

k

m

MHVWVWDáXNáDGXPQR*FHJR

3LHUZV]\VNáDGQLNZ\UD*HQLDMHVWV\JQDáHPZROQR]PLHQQ\P

QDWRPLDVW GUXJL VNáDGQLN PD ZLGPR VNXSLRQH ZRNyá SXOVDFML

2

0

ω

-H*HOL URO GHWHNWRUD ID]\ SHáQL XNáDG PQR*F\ WR ] V\JQDáX

( )

u t

D

QDOH*\XVXQüQLHSR*GDQ\VNáDGQLNZLHONLHMF]VWRWOLZRFL]DSRPRF

ILOWUXGROQRSU]HSXVWRZHJRRWU]\PXMF

( )

( )

( )

[

]

( )

[

]

( )

X W

N 8 8

W

W

N

W

8

'

P

L

J

L

J

'

E

E

'

E

=

−

=

=















VLQ

VLQ

VLQ

PD[

ϕ

ϕ

ϕ

ϕ

ϕ

OXE

X

'

SU]\F]\P

( )

( )

( )

ϕ

ϕ

ϕ

b

i

g

t

t

t

=

−

MHVWEáGHPID]\

D

N

N 8 8

'

P

L

J

=

VWDQRZLZ]PRFQLHQLHGHWHNWRUDID]\ E

U

D max

PDNV\PDOQDZDUWRüQDSLFLDGHWHNWRUDID]\

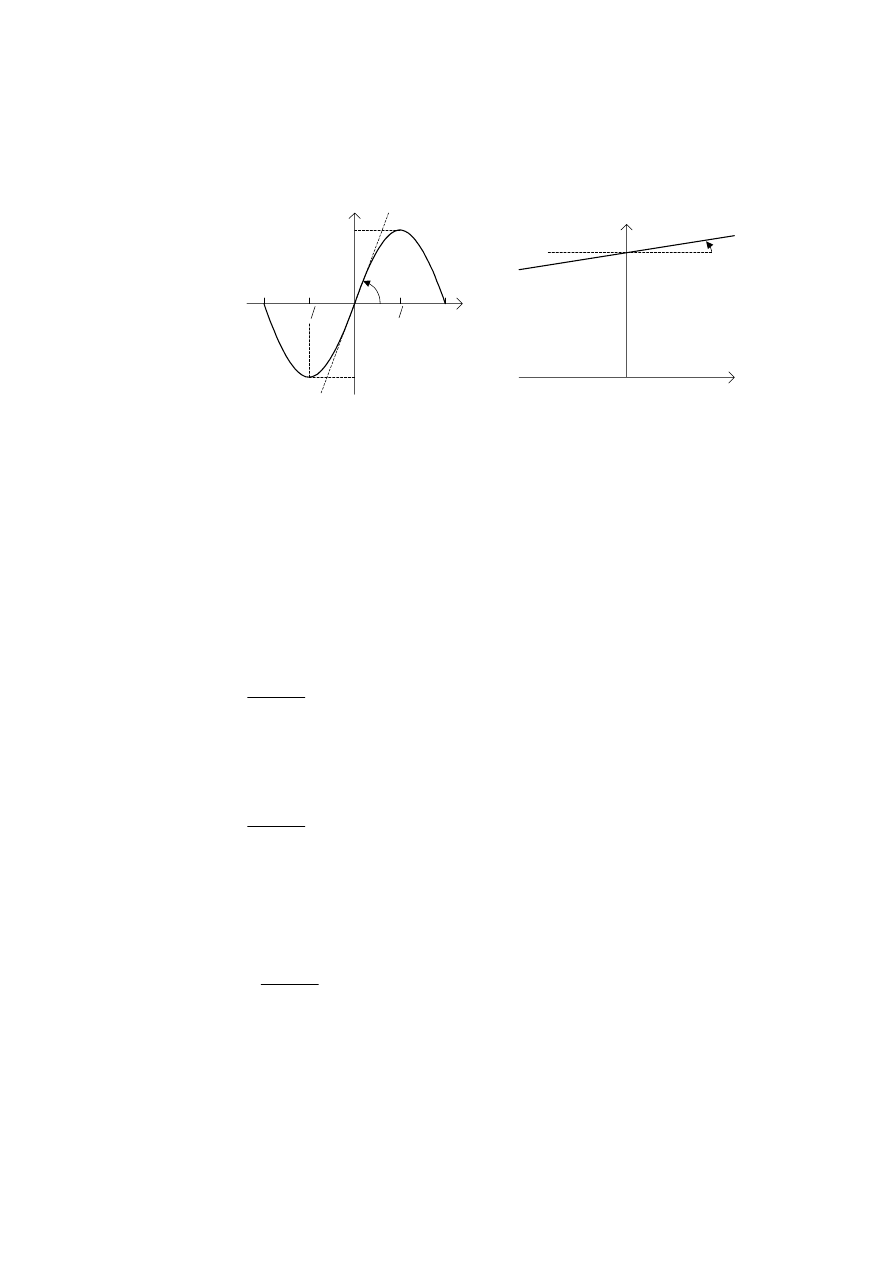
5yZQDQLHRSLVXMHFKDUDNWHU\VW\NGHWHNWRUDID]\NWyUDMHVW

IXQNFMVLQXVRLGDOQRRNUHVLH 2

π

DMHMQDFK\OHQLHZSXQNFLH

ϕ

b

=

0

RNUHODZVSyáF]\QQLN

k

D

U\VD

3U]\ ]DáR*HQLX *H ILOWU GROQRSU]HSXVWRZ\ )'3 XVXQLH

QLHSR*GDQHVNáDGRZH]V\JQDáXZ\MFLRZHJRGHWHNWRUDID]\

( )

u t

D

LQLH

EG]LHP\LFKUR]SDWU\ZDüZGDOV]\FKUR]ZD*DQLDFKWRQDSLFLHQDMHJR

Z\MFLXRNUHORQHMHVWVSORWHPIXQNFML

( )

( ) ( )

( )

[

]

( )

( ) (

)

X W

X W K W

N

W K W

N

W K W GW

2

'

'

E

'

W

E

=

∗

=

∗

=

−

∫

VLQ

VLQ

ϕ

ϕ

τ

JG]LH

( )

h t

MHVW RGSRZLHG]L LPSXOVRZ

( )

( )

[ ]

h t

H s

=

−

L

1

ILOWUX

RSLVDQHJRWUDQVPLWDQFM

( )

H s

8

' PD[

X

'

−

8

' PD[

DUFWJ N

'

−

π

ϕ

E

−

π

2

π

π

2

ω

J

ω

0

DUFWJ N

*

X

*

b)

a)

5\V D &KDUDNWHU\VW\ND SU]HMFLRZD GHWHNWRUD ID]\ E FKDUDNWHU\VW\ND

SU]HVWUDMDQLDJHQHUDWRUD9&2

-DNSRND]DQRQDU\VESXOVDFMDJHQHUDWRUD9&2SRZLQQDE\ü

OLQLRZ IXQNFM QDSLFLD VWHUXMFHJR

( )

u t

O

Z FDá\P ]DNUHVLH

F]VWRWOLZRFLSUDF\

=DWHP

( )

( )

ω

ω

g

G

O

t

k u t

=

+

0

=SRUyZQDQLD]DOH*QRFLLRWU]\PXMHP\

( )

( )

d

t

dt

k u t

g

G

O

ϕ

=

6\JQDá

( )

u t

O

PRGXOXMHF]VWRWOLZRüGUJDJHQHUDWRUD9&2SU]\

F]\PQDSRGVWDZLHUyZQDDRWU]\PXMHP\

( )

( )

( )

[

]

( )

{

}

d

t

dt

k k

t

t

h t

g

G

D

i

g

ϕ

ϕ

ϕ

=

−

∗

sin

3RGVWDZLDMF

K

k k

G

D

=

SU]\ F]\P

K

MHVW Z]PRFQLHQLHP SWOL

[

]

VHF RWU]\PXMHP\RVWDWHF]QHUyZQDQLHRSLVXMFH]ZL]HNSRPLG]\

ID]V\JQDáXZHMFLRZHJRLID]JHQHUDWRUD9&2

( )

( )

( )

[

]

( )

{

}

d

t

dt

K

t

t

h t

g

i

g

ϕ

ϕ

ϕ

=

−

∗

=

sin

( )

( )

(

)

=

−

−

∫

K

t

t h t

d

t

i

g

sin [

]

0

ϕ

ϕ

τ τ

,QQ SRVWDü WHJR UyZQDQLD PR*HP\ RWU]\PDü QD SRGVWDZLH ]DOH*QRFL

DL

( )

( )

{

}

d

t

dt

d

t

dt

K

t

h t

b

i

b

ϕ

ϕ

ϕ

=

−

∗

=

( )

sin

( )

( )

(

)

=

−

−

∫

d

t

dt

K

t h t

d

i

t

b

ϕ

ϕ

τ τ

( )

sin

0

3WOD 3// RSLVDQD UyZQDQLDPL MHVW XNáDGHP VLOQLH

QLHOLQLRZ\P ] SRZRGX QLHOLQLRZRFL FKDUDNWHU\VW\NL SU]HMFLRZHM

GHWHNWRUD ID]\ 1DFK\OHQLH FKDUDNWHU\VW\NL SU]HM FLRZHM

( )

u

D

b

ϕ

GHWHNWRUDID]\ZSU]\SDGNX]DVWRVRZDQLDXNáDGXPQR *FHJRXOHJDQLH

W\ONR ]QDF]Q\P ]PLDQRP FR GR ZDUWRFL OHF] UyZQLH* ]PLHQLD VZyM

]QDNSU]\]PLDQLHEáGXID]\RG

ϕ

ϕ

b

b

= − ∞

= + ∞

GR

U\VD3U]\

]PLDQDFK EáGX ID]\ Z SU]HG]LDáDFK

ϕ

π

π

π

E

Q

= −

+









±

GR

GODQ

=

QDFK\OHQLH FKDUDNWHU\VW\NL MHVW GRGDWQLH L Z W\P

SU]\SDGNX Z SWOL Z\VWSXMH ID]RZH XMHPQH VSU]*HQLH ]ZURWQH 'OD

SR]RVWDá\FK

ϕ

b

QDFK\OHQLH FKDUDNWHU\VW\NL SU]HMFLRZHM GHWHNWRUD MHVW

XMHPQHLZSWOLZ\VWSXMHID]RZHGRGDWQLHVSU]*HQLH]ZURWQH

37/$:67$1,(6<1&+521,=$&-,

/LQLRZ\PRGHOSWOLID]RZHM

3WOD]QDMGXMHVLZVWDQLHV\QFKURQL]DFMLJG\

( )

( )

ω

ω

i

g

t

t

=

1DSRGVWDZLH]DOH*QRFLLPR*HP\VWZLHUG]Lü *HZVWDQLH

V\QFKURQL]DFML

( )

( )

ϕ

ϕ

ϕ

i

g

t

t

const

−

=

E

:VWDQLHV\QFKURQL]DFML

ϕ

π

b0

2

≤

FRR]QDF]D*HSXQNWSUDF\GHWHNWRUD

ID]\ OH*\ Z SRGVWDZRZ\P SU]HG]LDOH MHJR FKDUDNWHU\VW\NL Z NWyU\P

MHVWRQDPRQRWRQLF]QDàDWZRPR*HP\Z\]QDF]\ü]DNUHVSU]HVWUDMDQLD

ORNDOQHJRJHQHUDWRUDSWOLZRNyáVZHMSXOVDFMLVSRF]\QNRZHM

ω

0

SU]H]

V\JQDá

( )

u t

O

'ODKDUPRQLF]QHJRV\JQDáXZHMFLRZHJR

( )

u t

i

RVWDáHMSXOVDFML

( )

u t

const

i

i

=

=

ω

QD Z\MFLX GHWHNWRUD ID]\ UyZQ RWU]\PXMHP\ VNáDGRZ VWDá

QDSLFLD

( )

U

u t

k U U

k

D

D

m

s

g

b

D

b

0

0

0

1

2

=

=

=

sin

sin

ϕ

ϕ

3U]\

− ≤

≤

π ϕ π

2

2

0

b

QDSLFLHWR]DZLHUDVLZJUDQLFDFK

−

≤

≤

k

U

k

D

D

D

0

6NáDGRZDVWDáD

U

D0

SRSU]HQLHVLHQLXSU]H]ILOWUSU]\MPXMHZDUWRü

( )

H

U

D

0

0

L SR HZHQWXDOQ\P Z]PRFQLHQLX

( )

(

)

H 0

1

>

VWHUXMH

JHQHUDWRUHP 9&2 1DMF]FLHM Z]PRFQLHQLH QLH MHVW SRWU]HEQH WM

( )

H 0

1

=

=JRGQLH]]DOH*QRFLSXOVDFMDJHQHUDWRUD9&2PR*HSU]\MPRZDü

ZDUWRFL]SU]HG]LDáX

( )

( )

ω

ω

ω

0

0

0

0

−

≤

≤

+

k k H

k k H

G

D

g

G

D

-H*HOL]DNUHV]PLDQSXOVDFMLV\JQDáXZHMFLRZHJR

( )

u t

i

EG]LHVL

XWU]\P\ZDü Z SU]HG]LDOH RNUHORQ\P Z\UD*HQLHP WR ZyZF]DV

SWODID]RZDSR]RVWDMHZVWDQLHV\QFKURQL]DFML

7HQZáDQLHSU]HG]LDáSXOVDFMLV\JQDáXZHMFLRZHJRGODNWyU\FK

SWOD ID]RZD SR]RVWDMH Z VWDQLH V\QFKURQL]DFML QRVL QD]Z ]DNUHVX

WU]\PDQLD DQJ KROG LQ UDQJH OXE ]DNUHVX OHG]HQLD DQJ WUDFNLQJ

UDQJHWHMSWOL

: UR]ZD*DQ\P SU]\SDGNX ]DNUHV WU]\PDQLD MHVW V\PHWU\F]Q\

Z]JOGHPSXOVDFML

ω

0

LZ\QRVL

( )

∆

ω

T

G

D

k k H

K

=

=

0

SU]\F]\PQDMF]FLHM

( )

H 0

1

=

: VWDQLH V\QFKURQL]DFML EáG ID]\

ϕ

b0

MHVW PDá\ L PR*HP\

]DáR*\ü *H

E

ϕ

π

3U]\ W\P ]DáR*HQLX FKDUDNWHU\VW\ND

GHWHNWRUDID]\PR*HE\üDSURNV\PRZDQD]DOH*QRFLOLQLRZ

(

) (

)

U

k

k

k

D

D

i

g

D

i

g

D

b

0

0

=

−

≈

−

=

sin

ϕ ϕ

ϕ

ϕ

ϕ

3RGVWDZLDMF]DOH*QRüGRUyZQDLRWU]\PXMHP\

( )

( )

( )

[

]

( )

( )

( )

( )

[

]

( )

G

W

GW

.

W

W K W

G

W

GW

G W

GW

.

W K W

J

L

J

E

L

E

ϕ

ϕ

ϕ

ϕ

ϕ

ϕ

=

−

∗

=

−

∗













5yZQDQLD V OLQLRZH ]DWHP VWRVXMF SU]HNV]WDáFHQLH /DSODFH¶D

RWU]\PXMHP\UyZQDQLDDOJHEUDLF]QHZSRVWDFL

( )

( )

( )

[

]

( )

( )

( )

( ) ( )

V

V

.

V

V + V

V

V

V V

.

V + V

J

L

J

E

L

E

φ

φ

φ

φ

φ

φ

=

−

=

−








JG]LH

( ) ( ) ( ) ( )

φ

φ

φ

g

i

b

s

s

s

H s

,

,

,

V WUDQVIRUPDWDPL /DSODFH¶D Z\UD*H

( ) ( ) ( )

( )

( )

ϕ

ϕ

ϕ

J

L

E

W

W

W

K W

+ V

RUD]

D

MHVWWUDQVPLWDQFMILOWUX)'3

1D SRGVWDZLH UyZQD PR*HP\ Z\]QDF]\ü WUDQVPLWDQFM

]DPNQLWHMSWOLID]RZHM

( )

( )

( )

( )

( )

G s

s

s

K H s

s

K H s

g

i

=

=

+

φ

φ

ZNWyUHM

( )

φ

i

s

MHVWZ\PXV]HQLHP]D

( )

φ

g

s

RGSRZLHG]LXNáDGX

3RGREQLHPR*HP\Z\]QDF]\üWUDQVPLWDQFMRGQLHVLRQGREáGX

ID]\

( )

φ

b

s

( )

( )

( )

( )

( )

G s

s

s

G s

s

s

K H s

b

b

i

=

= −

=

+

φ

φ

1

1D SRGVWDZLH UyZQDQLD PR*HP\ Z\]QDF]\ü WUDQVPLWDQFM

VDPHJRJHQHUDWRUD9&2

( )

( )

φ

g

O

G

s

U

s

k

s

=

F]\OLJHQHUDWRU9&2]DFKRZXMHVLMDNXNáDGFDáNXMF\

= SU]HSURZDG]RQHM DQDOL]\ Z\QLND *H Z VWDQLH V\QFKURQL]DFML

SU]\

_ _

E

ϕ

π

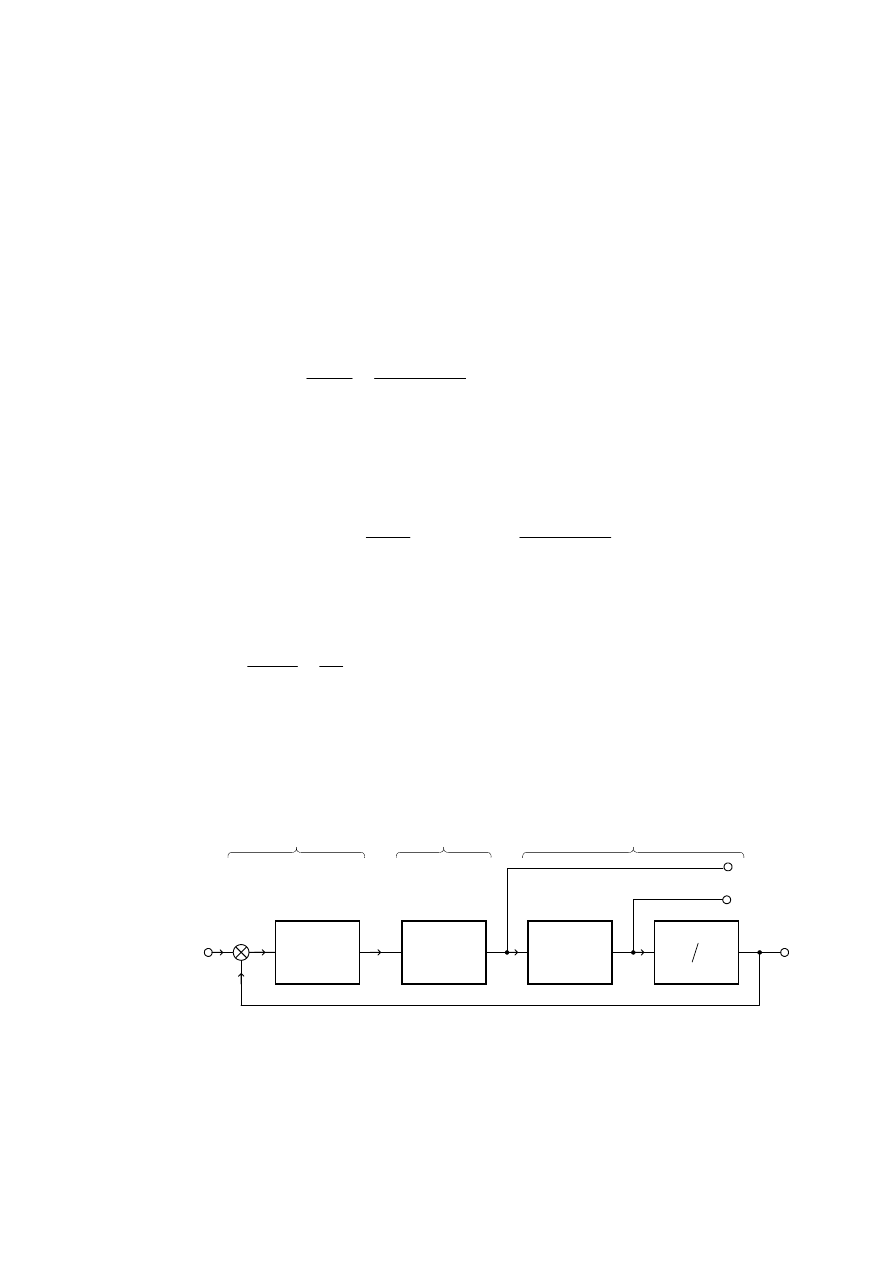
VFKHPDW EORNRZ\ SWOL PR*H E\ü ]DVWSLRQ\

PRGHOHPOLQLRZ\PSU]HGVWDZLRQ\PQDU\V

( )

+ V

N

'

N

*

( )

φ

L

V

( )

8 V

'

( )

8 V

2

( )

φ

J

V

( )

8 V

2

[

]

9 UDG

[ ]

9 9

[

]

UDG 9V

( )

φ

E

V

)D]D

1

V

3XOVDFMD

( )

Ω

J

V

( )

Ω

J

V

+

−

( )

φ

J

V

9&2

)LOWU

'HWHNWRU ID]\

5\V/LQLRZ\PRGHOSWOLID]RZHMZVWDQLHV\QFKURQL]DFML

1DSRGVWDZLHVFKHPDWXEORNRZHJR] U\VPR*HP\Z\]QDF]\ü

WUDQVPLWDQFMSWOLRWZDUWHM

( )

( )

( )

( )

( )

G s

s

s

k k

H s

s

K

H s

s

O

g

i

O

D

G

=









 =

=

φ

φ

JG]LH.MDNR]QDF]RQRZF]HQLHMMHVWZ]PRFQLHQLHPSWOL

= ]DOH*QRFL L PR*QD ]DXZD*\ü *H

k

G

Z\UD*D VL Z

UDG

9 VHF











N

'

Z 9

UDG







VWGZ]PRFQLHQLHSWOLPDZ\PLDU

1

sec







:áDFLZRFLSWOLZLVWRWQ\VSRVyE]DOH*RGWUDQVPLWDQFML

( )

H s

ILOWUX GODWHJR QL*HM UR]SDWU]\P\ NLOND SU]\NáDGyZ NWyUH PDM

QDMZLNV]H]QDF]HQLHSUDNW\F]QH

:Sá\ZWUDQVPLWDQFMLILOWUXQDZáDFLZRFLOHG]FHSWOL

:áDFLZRFLOHG]FHSWOLID]RZHMZTXDVLOLQLRZ\P]DNUHVLHMHM

SUDF\ Z LVWRWQ\ VSRVyE ]DOH* RG WUDQVPLWDQFML ]DVWRVRZDQHJR ILOWUX

GROQRSU]HSXVWRZHJR:\Uy*QLDVLSU]\W\PNLONDQDMEDUG]LHMW\SRZ\FK

XNáDGyZ ILOWUyZ GROQRSU]HSXVWRZ\FK SLHUZV]HJR U] GX NWyUH V

QDMF]FLHMVWRVRZDQHZSWODFKID]RZ\FK3//-DNZ\QLND]]DOH*QRFL

]DVWRVRZDQLHILOWUXJRU]GXSRZRGXMH*HWUDQVPLWDQFMDSWOLZ

]DNUHVLH TXDVLOLQLRZ\P MHVW JR U]GX : OLWHUDWXU]H SWOH ID]RZH

NODV\ILNXMH VL MDN XNáDG\ DXWRPDW\F]QHM UHJXODFML Z RSDUFLX R

WUDQVPLWDQFMH SWOL RWZDUWHM UyZQ SU]\ F]\P OLF]ED ELHJXQyZ

( )

G s

O

RNUHODU]GSWOLQDWRPLDVWOLF]EDELHJXQyZZSRF]WNXXNáDGX

ZVSyáU]GQ\FKRNUHODW\SSWOL

1DMF]FLHMUR]ZD*DVLSWOHID]RZHJRU]GXEH]ILOWUXRUD]

SWOH JR U]GX ] W\SRZ\PL SDV\ZQ\PL OXE DNW\ZQ\PL ILOWUDPL JR

U]GX 'RNRQXMF WHM NODV\ILNDFML SRGREQLH MDN Z >@ QL*HM

SU]HGVWDZLRQR QDMEDUG]LHM W\SRZH WUDQVPLWDQFMH VWRVRZDQ\FK ILOWUyZ

( )

H s

L ZL*FH VL ] QLPL ]JRGQLH ] UyZQ WUDQVPLWDQFMH SWOL

( )

G s

3WODSLHUZV]HJRU]GXW\SXSLHUZV]HJR

( )

H s

0

1

=

D

( )

G s

K

s

K

=

+

E

3WOD GUXJLHJR U]GX W\SX SLHUZV]HJR ] SDV\ZQ\P ILOWUHP

FDáNXMF\PRVWUXNWXU]H

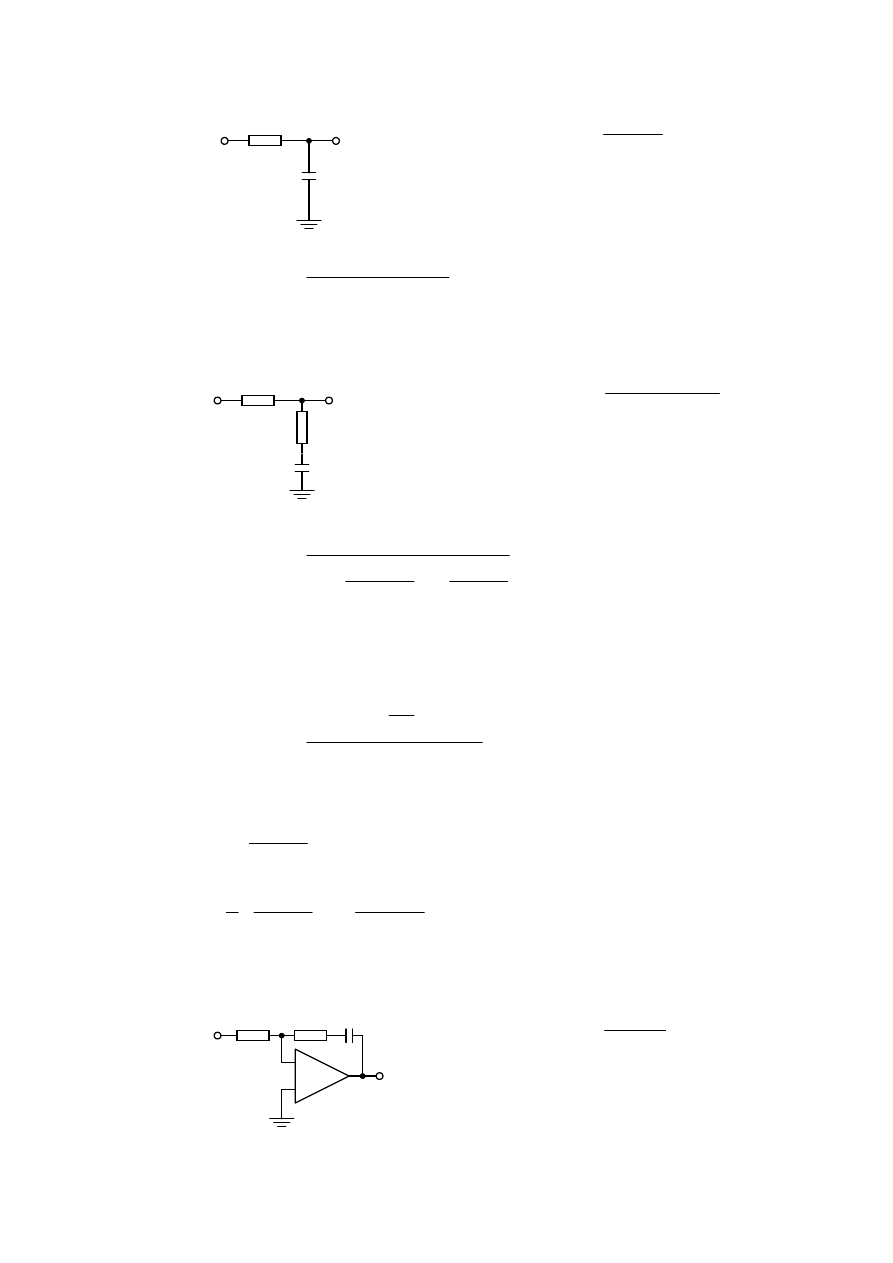
5

1

&

( )

( )

H s

H s

s

=

=

+

1

1

1

1

τ

JG]LH

τ

1

1

=

R C

( )

G s

K

s

s

K

=

+

+

−

−

−

τ

τ

τ

1

1

2

1

1

1

1

3WOD GUXJLHJR U]GX W\SX SLHUZV]HJR ] SDV\ZQ\P ILOWUHP

SURSRUFMRQDOQRFDáNXMF\PRVWUXNWXU]H

5

1

5

2

&

( )

( )

H s

H s

s

s

=

=

+

+

+

2

2

1

2

1

1

τ

τ

τ

(

)

JG]LH

τ
τ

1

1

2

2

=

=

R C

R C

( )

G s

K

s

s

K

s

K

=

+

+

+ +

+

+

+

−

(

) (

)

1

1

2

1

2

1

2

2

1

2

1

2

τ

τ τ

τ

τ

τ

τ

τ

7UDQVPLWDQFMD

( )

G s

RNUHORQD ]DOH*QRFL PR*H E\ü

Z\UD*RQDZGRJRGQLHMV]HMXQRUPRZDQHMSRVWDFL

( )

G s

K

s

s

s

n

n

n

n

n

=

−







 +

+

+

ω

ξ ω

ω

ξ ω

ω

2

2

2

2

2

D

JG]LH

ω

τ

τ

n

K

=

+











1

2

1 2

/

MHVWSXOVDFMGUJDVZRERGQ\FKSWOL E

ξ

τ τ

τ

=

+











+









1

2

1

1

2

1 2

2

K

K

K

/

MHVWZVSyáF]\QQLNLHPWáXPLHQLD F

3WOD GUXJLHJR U]GX W\SX GUXJLHJR ] DNW\ZQ\P ILOWUHP

SURSRUFMRQDOQRFDáNXMF\PRVWUXNWXU]H

5

1

5

2

&

−
+

( )

( )

H s

H s

s

s

=

= +

3

2

1

1

τ

τ

JG]LH

τ
τ

1

1

2

2

=

=

R C

R C

( )

(

)

G s

K

s

s

K

s

K

=

+

+









 +

−

1

2

1

1

2

2

1

1

τ

τ

τ

τ

τ

OXEZSRVWDFLXQRUPRZDQHM

( )

G s

s

s

s

n

n

n

n

=

+

+

+

2

2

2

2

2

ξ ω

ω

ξ ω

ω

D

JG]LH

ω

τ

n

K

=











1

1 2

/

E

ξ τ

τ

=











2

1

1 2

2

K

/

F

: ]DVDG]LH Z\VWDUF]\ UR]ZD*Dü WUDQVPLWDQFMH ILOWUyZ R SRVWDFL

( )

H s

2

UyZQ OXE

( )

H s

3

UyZQ ERZLHP SU]\ LFK SRPRF\ PR*QD

RSLVDü WUDQVNRQGXNWDQFMH GRZROQHJR ILOWUX JR U]GX 3U]\NáDGRZR

ILOWURWUDQVPLWDQFML

( )

H s

1

UyZQ MHVW V]F]HJyOQ\P SU]\SDGNLHP

ILOWUXRWUDQVPLWDQFML

( )

H s

2

UyZQGOD

τ

2

0

=

.

3RGREQLHDNW\ZQ\ILOWUFDáNXMF\]UHDOL]RZDQ\QDZ]PDFQLDF]X

RSHUDF\MQ\PLSRVLDGDMF\WUDQVPLWDQFM

( )

H s

s

4

1

1

=

τ

MHVWV]F]HJyOQ\PSU]\SDGNLHPILOWUXRWUDQVPLWDQFML

( )

H s

3

UyZQ

GOD

τ

2

0

=

%DGDMF UR]NáDG ]HU L ELHJXQyZ WUDQVPLWDQFML SWOL

( )

G s

GOD

Uy*Q\FK ILOWUyZ PR*HP\ RNUHOLü FKDUDNWHU RGSRZLHG]L XNáDGX SU]\

VNRNRZ\FK ]PLDQDFK ID]\ V\JQDáX ZHMFLRZHJR 2GSRZLHG( WD Z

LVWRWQ\ VSRVyE ]DOH*\ RG ZVSyáF]\QQLND WáXPLHQLD

ξ

RUD] RG SXOVDFML

GUJD VZRERGQ\FK

ω

n

L PR*H E\ü RVF\ODF\MQD DSHULRG\F]QR

NU\W\F]QDOXEDSHULRG\F]QD

&KDUDNWHU\VW\ND DPSOLWXGRZR F]VWRWOLZRFLRZD SWOL ID]RZHM

JR U]GX MHVW WDND MDN GROQRSU]HSXVWRZHM WUDQVPLWDQFML

MHGQRELHJXQRZHM SU]\ F]\P Z]PRFQLHQLH S WOL

.

MHVW ]DUD]HP

V]HURNRFL SDVPD SWOL 3RQLHZD* Z]PRFQLHQLH SWOL EH]SRUHGQLR

ZSá\ZD QD ]DNUHV WU]\PDQLD

(

)

∆

ω

T

SWOL GODWHJR WD ZVSyá]DOH*QRü

V]HURNRFLSDVPDSWOLL]DNUHVXWU]\PDQLDSRZRGXMH*HSWODID]RZD

JRU]GXMHVWEDUG]RU]DGNRVWRVRZDQDZSUDNW\FH

'OD ZV]\VWNLFK UR]ZD*DQ\FK WUDQVPLWDQFML ILOWUyZ WM

( )

( )

H s

H s

0

4

−

SWOD MHVW VWDELOQD >@ FKRFLD* Z SUDNW\FH PR*H VL

]GDU]\ü*HQLHXZ]JOGQLRQHZWUDQVPLWDQFMLSWOLELHJXQ\SDVR*\WQLF]H

RGVXQLWH RG ELHJXQyZ GRPLQXMF\FK Z NLHUXQNX ZLHONLFK

F]VWRWOLZRFL ZQRV] GRGDWNRZH SU]HVXQLFLD ID]\ SURZDG]FH GR

QLHVWDELOQRFL XNáDGX 0DUJLQHV\ VWDELOQRFL SWOL Z TXDVLOLQLRZ\P

]DNUHVLH SUDF\ GOD Uy*Q\FK WUDQVPLWDQFML ILOWUyZ PRJ E\ü áDWZR

Z\]QDF]RQHZRSDUFLXRWUDQVPLWDQFMHSWOLRWZDUW\FKUyZQ

1D U\V SU]HGVWDZLRQR FKDUDNWHU\VW\NL F]VWRWOLZRFLRZH

DPSOLWXGRZH L ID]RZH SWOL RWZDUW\FK GOD WU]HFK WUDQVPLWDQFML ILOWUyZ

( )

H s

0

( )

H s

1

( )

H s

2

3XOVDFMD

ω

C

SU]\NWyUHMPRGXáWUDQVPLWDQFMLSWOLRWZDUWHMRVLJD

ZDUWRü UyZQ

(

)

(

)

G

j

O

C

ω

=

1

QD]\ZD VL SXOVDFM RGFLFLD DQJ

FURVVRYHUIUHTXHQF\

7UDQVPLWDQFMD

( )

G j

0

ω

SWOL GUXJLHJR U]GX W\SX SLHUZV]HJR ]

SDV\ZQ\P ILOWUHP FDáNXMF\P NWyUHJR SXOVDFMD

ω

1

MHVW ]QDF]QLH

PQLHMV]DRG

.

DE\RVLJQüZVNLHSDVPRSRZRGXMH*HSU]HVXQLFLH

ID]\ SWOL MHVW EOLVNLH

−

π

SU]\ SXOVDFML RGFLFLD

ω

c

U\VE

:\QLNLHPWHJRPR*HE\üQLHVWDELOQRüSWOL]DPNQLWHM

=DVWRVRZDQLHILOWUXRWUDQVPLWDQFMLMHGQRELHJXQRZHM]]HUHPXPR *OLZLD

]ZLNV]HQLHPDUJLQHVXID]\MDNSRND]XMHU\VF=DXZD *P\*HGOD

WHJR SU]\SDGNX V]HURNRü SDVPD SWOL NWyUD MHVW UyZQD SXOVDFML

RGFLFLD PR*H E\ü ]QDF]QLH PQLHMV]D RG

.

0R*OLZRü QLH]DOH*QHM

UHJXODFML V]HURNRFL SDVPD SWOL RUD] Z]PRFQLHQLD SWOL

.

MHVW ]DOHW

VWRVRZDQLDWHJRW\SXILOWUyZ

: VWDQLH V\QFKURQL]DFML SWOD OHG]L ]PLDQ\ F]VWRWOLZRFL

V\JQDáX ZHMFLRZHJR 3U]\NáDGRZR MH*HOL V\JQDáHP W\P MHVW V\JQDá

]PRGXORZDQ\ F]VWRWOLZRFLRZR )0 WR QDSLFLH

( )

u t

O

NWyUH MHVW

QDSLFLHP ZHMFLRZ\P JHQHUDWRUD 9&2 MHVW SU]HELHJLHP

RGZ]RURZXMF\P ]PLDQ\ F]VWRWOLZRFL V\JQDáX ZHMFLRZHJR F]\OL

Z\VWSXMHSURFHVGHPRGXODFML)0

=Dáy*P\*HZVWDQLHSRF]WNRZ\PJG\SWOD3//MHVWZVWDQLH

V\QFKURQL]DFML QDVWSXMH ]DEXU]HQLH Z V\JQDOH ZHMFLRZ\P NWyUH

Z\ZRáXMHSURFHVSU]HMFLRZ\=DEXU]HQLHWRMHVWQDW\OHPDáH *HQDGDO

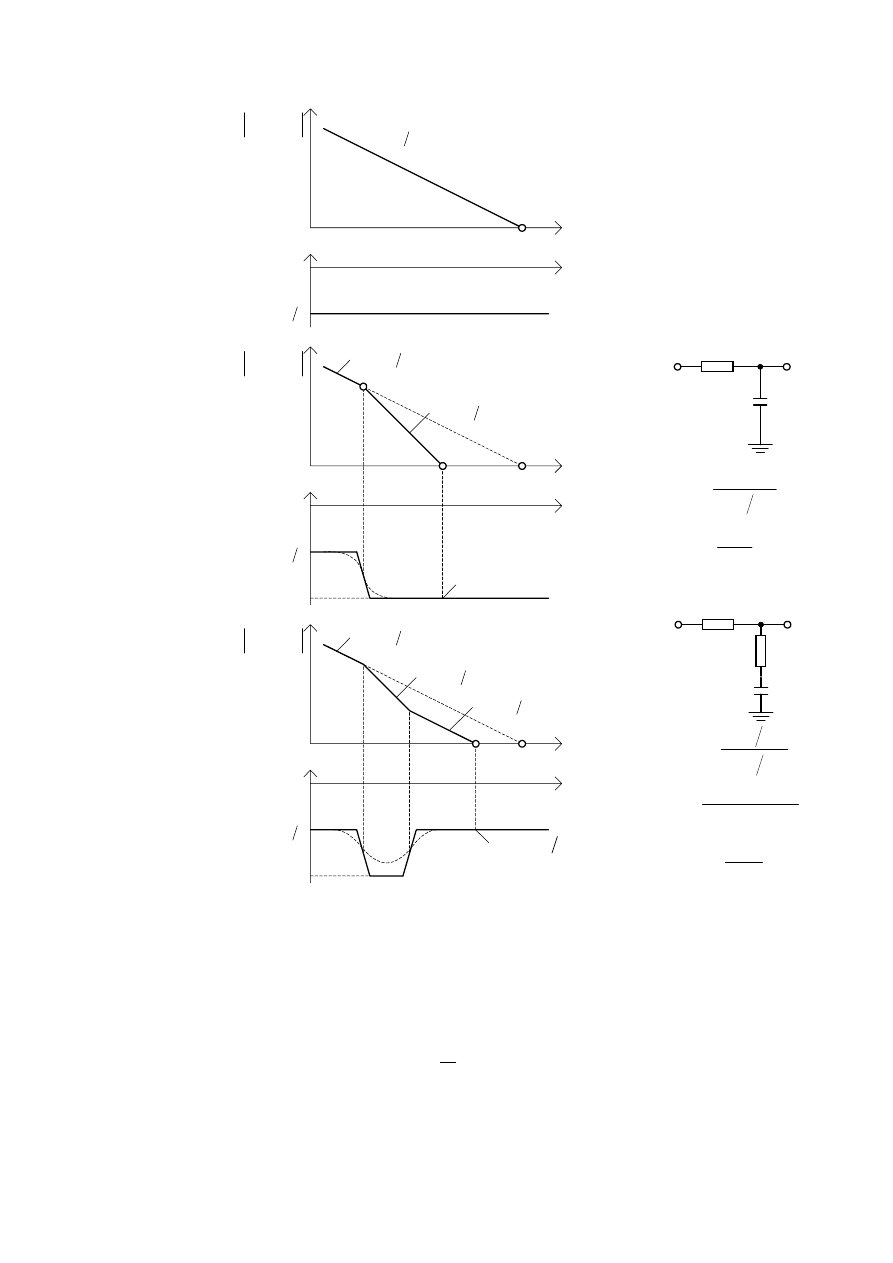
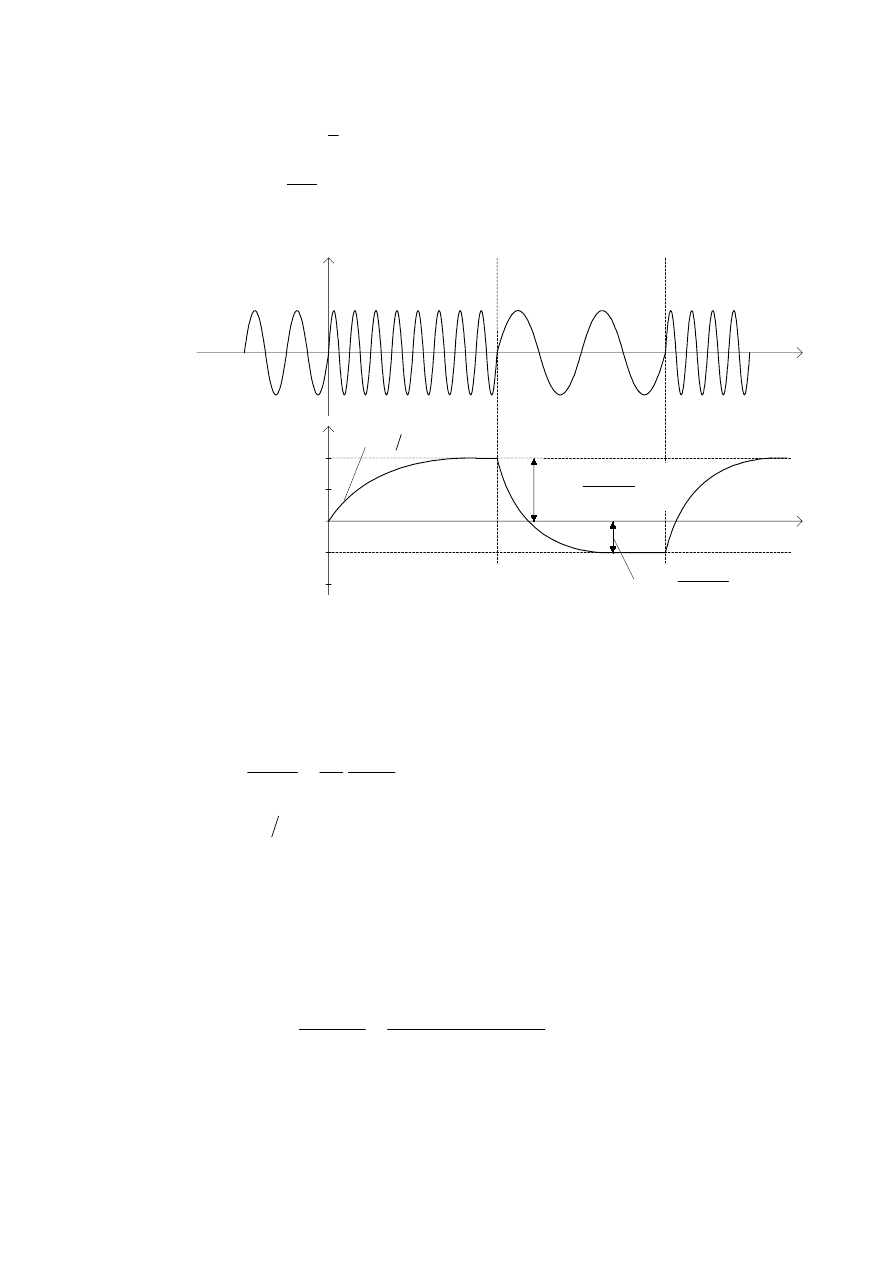
RERZL]XMHPRGHOOLQLRZ\SWOL1DU\VSU]HGVWDZLRQRSU]\NáDGRZR

SU]HELHJL F]DVRZH QDSLFLD QD ZHMFLX JHQHUDWRUD 9&2

( )

u t

O

SWOL

ID]RZHM SLHUZV]HJR U]GX

( )

(

)

H s

0

1

=

QD VLQXVRLGDOQ\ V\JQDá

ZHMFLRZ\ZNWyU\PQDVWSLáR]DEXU]HQLHZSRVWDFLVNRNRZHM]PLDQ\

F]VWRWOLZRFL

ω

F

.

=

( )

* M

2

ω

−

π

−

π

2

a)

( )

DUJ * M

2

ω

1

0

ω

F

( )

* M

2

ω

−

π

2

b)

( )

DUJ * M

2

ω

1

0

ω

1

.

−

20

G% GHN

−

20

G% GHN

−

40

G% GHN

ω

1

<<

.

∆

ϕ ≈

0

( )

+ V

0

1

=

ω

1

1

1

=

5 &

ω

F

0

ω

1

.

−

20

G% GHN

−

40

G% GHN

∆

ϕ

π

≈ −

2

−

20

G% GHN

−

π

2

−

π

1

( )

* M

2

ω

( )

DUJ * M

2

ω

ω

2

( )

+ V

V

V

2

2

1

1

1

= +

+

ω

ω

(

)

ω

1

1

2

1

=

+

5 5 &

( )

+ V

V

1

1

1

1

=

+

ω

ω

2

2

1

=

5 &

c)

5

1

5

2

&

5

1

&

ZSá\Z F]áRQX

FDáNXMFHJR 9&2

ω
ω

ω

ω

ω
ω

5\V &KDUDNWHU\VW\NL F]VWRWOLZRFLRZH DPSOLWXGRZH L ID]RZH RWZDUW\FK SWOL

ID]RZ\FKGODUy*Q\FKWUDQVPLWDQFMLILOWUXD

( )

+ V

E

( )

+ V

F

( )

+ V

3U]HELHJ QDSLFLD

( )

u t

O

QD U\V ]RVWDá Z\]QDF]RQ\ GOD SWOL

SLHUZV]HJRU]GXRSDUDPHWUDFK

[ ] [ ]

N

UDG

N+]

9

*

=







π

[ ]

.

V

I

=







=

=

ω

π

+]

(

)

ω

π

L

+]

=

2

250

(

)

ω

π

L

N+]

=

2

1

(

)

ω

π

L

N+]

=

2

1

(

)

ω

π

L

+]

=

2

500

X W

L

X W

2

0 5

−

0 5

−

0 25

0 25

0

W

W

τ

=

=

1

2

N

PV

8

N

9

2

L

*

1

0

0 5

=

−

=

ω ω

8

N

9

2

L

*

2

0

0 25

=

−

= −

ω ω

5\V 2GSRZLHG( SWOL ID]RZHM SLHUZV]HJR U]GX QD VLQXVRLGDOQ\ V\JQDá

ZHMFLRZ\]HVNRNRZ]PLDQF]VWRWOLZRFL

6WDá F]DVRZ ]PLDQ QDSLFLD QD ZHMFLX JHQHUDWRUD 9&2

PR*HP\Z\]QDF]\üQDSRGVWDZLHWUDQVPLWDQFML

( )

( )

U

s

s

k

K

s

K

O

i

G

Ω

=

+

1

VWG

τ

=

=

.

PVHF

=PLDQ\SXOVDFMLJHQHUDWRUD9&2RSLVXMH]DOH*QRü

ω

ω

g

G

O

k u

=

+

0

=DWHP SU]\ VNRNRZHM ]PLDQLH F]VWRWOLZRFL V\JQDáX ZHMFLRZHJR ]

+] GR N+] QDSLFLH QD ZHMFLX JHQHUDWRUD 9&2 ]PLHQLD VL

Z\NáDGQLF]R]HVWDáF]DVRZ

τ

RGZDUWRFLGR

U

O1

8

N

2

L

*

=

−

=

−

≈

ω ω

π

π

π

9

3U]\VNRNRZHM]PLDQLHF]VWRWOLZRFL

f

i

RGZDUWRFLN+]GRZDUWRFL

+] QDSLFLH VWHUXMFH JHQHUDWRUHP 9&2 Z\NáDGQLF]R ]PLHQLD VL

GRZDUWRFL

U

O2

8

N

2

L

*

=

−

=

−

= −

ω ω

π

π

π

9

=GROQRüOHG]HQLDSU]H]SWO]PLDQID]\V\JQDáX ZHMFLRZHJR

RNUHODVL]Z\NOHGODVWDQGDUGRZ\FK]DEXU]HWHJRV\JQDáXRSRVWDFL

VNRNRZHM]PLDQ\ID]\

VNRNRZHM]PLDQ\F]VWRWOLZRFL

OLQLRZHM]PLDQ\F]VWRWOLZRFL

3U]\MPXMF *H ]DEXU]HQLH V\JQDáX ZHMFLRZHJR QDVWSLáR Z FKZLOL

t

=

0

Z\PLHQLRQH WU]\ V\JQDá\ VWDQGDUGRZH L LFK WUDQVIRUPDW\

/DSODFH¶DSU]HGVWDZLRQRZWDEHOL

=GROQRüOHG]HQLDSU]H]SWO]PLDQID]\V\JQDáX ZHMFLRZHJR

Z\]QDF]\P\ Z RSDUFLX R UyZQDQLH RNUHODMFH WUDQVPLWDQFM

SWOLRGQLHVLRQGREáGXID]\

( )

( ) ( )

φ

φ

b

i

s

s

s

K H s

s

=

+

:\NRU]\VWXMFUyZQDQLHPR*HP\Z\]QDF]\ü

( )

φ

b

s

DW\P

VDP\P

( )

ϕ

b

t

GOD Z\EUDQHM WUDQVPLWDQFML ILOWUX ]DVWRVRZDQHJR Z S WOL

RUD]GODND*GHJR]SRGDQ\FKZWDEHOLSREXG]H

5R]ZL]DQLH UyZQDQLD PR*QD GRNRQDü GREU]H ]QDQ\PL

PHWRGDPL : QDV]\FK UR]ZD*DQLDFK RJUDQLF]\P\ VL MHG\QLH GR

Z\]QDF]HQLD ZDUWRFL DV\PSWRW\F]Q\FK UR]ZL]D V]F]HJyáRZ\FK GOD

t

→ ∞

7$%(/$

:G]LHG]LQLHF]DVX /WUDQVIRUPDWD

6NRNRZD]PLDQDID]\

( )

( )

ϕ

ϕ

i

t

t

= ∆

1

( )

φ

ϕ

i

s

s

=

∆

6NRNRZD]PLDQDSXOVDFML

( )

( )

ϕ

ω

i

t

t

t

= ∆

1

( )

φ

ω

i

s

s

= ∆

2

/LQLRZD]PLDQDSXOVDFML

( )

( )

ϕ

υ

ω

i

t

t

t

=

1

2

1

2

( )

φ

υ

ω

i

s

s

=

3

:\NRU]\VWXMF WZLHUG]HQLH R ZDUWRFL JUDQLF]QHM Z RGQLHVLHQLX

GRUyZQDQLDRWU]\PXMHP\

( )

( )

( ) ( )

lim

lim

lim

t

b

b

s

b

s

i

t

s

s

s

s

K H s

s

→∞

→

→

=

=

=

+

ϕ

ϕ

φ

φ

0

0

0

2

D6NRNRZD]PLDQDID]\

( )

( )

lim

lim

t

b

b

s

t

s

s

K H s

→∞

→

=

=

+

=

ϕ

ϕ

ϕ

0

0

0

∆

=UyZQDQLDZ\QLND *HSWODMHVWZVWDQLH OHG]LüND*G]PLDQ

ID]\

∆

ϕ

PXVLE\üPDáHDE\PR*QDVWRVRZDüPRGHOOLQLRZ\SWOLMHOL

W\ONR

( )

H 0

0

≠

.

:W\PSU]\SDGNXEáGID]\ZVWDQLHXVWDORQ\PRVLJD

ZDUWRü]HURZ
E6NRNRZD]PLDQDSXOVDFML

( )

( )

( )

lim

lim

t

b

b

s

t

s

K H s

K H

→∞

→

=

=

+

=

ϕ

ϕ

ω

ω

0

0

0

∆

∆

$V\PSWRW\F]QDZDUWRüEáGXID]\]DOH*\RGURG]DMX]DVWRVRZDQHJRZ

SWOLILOWUX'ODILOWUyZRWUDQVPLWDQFMDFK

( )

H s

0

L

( )

H s

1

PDP\

( )

H 0

1

=

]DWHP

( )

lim

t

b

b

t

K

→∞

=

=

ϕ

ϕ

ω

0

∆

: W\P SU]\SDGNX ZDUWRü EáGX ID]\ Z VWDQLH XVWDORQ\P ]DOH*\ RG

Z]PRFQLHQLD SWOL RUD] RG SRF]WNRZHM Uy*QLF\ SXOVDFML V\JQDáyZ

( )

( )

u t

u t

i

g

L

'ODILOWUXRWUDQVPLWDQFML

( )

H s

3

DV\PSWRW\F]QDZDUWRüEáGX

ϕ

b0

0

=

SRQLHZD*

( )

H s

3

= ∞

SU]\ s

→

0

F/LQLRZD]PLDQDSXOVDFML

'ODILOWUyZRWUDQVPLWDQFMDFK

( )

( )

( )

H s

H s

H s

0

1

2

,

,

WMWDNLFKGOD

NWyU\FK

( )

K H 0

PDZDUWRüVNRF]RQ

( )

( )

lim

lim

t

b

s

t

s s

K H s

→∞

→

=

+

= ∞

ϕ

υ

ω

0

1

%áGID]\QDUDVWDQLHRJUDQLF]HQLH]V]\ENRFL

( )

( )

[

]

( )

lim

lim

lim

t

b

s

b

s

d

t

dt

s s

s

s

s

s

K H s

s

K

→∞

→

→

=

=

+

=

ϕ

υ

υ

ω

ω

0

0

2

3

Φ

%áG ID]\ QDUDVWD Z PLDU XSá\ZX F]DVX SRZRGXMF Z\MFLH

GHWHNWRUDID]\]OLQLRZHJRREV]DUXSUDF\D *SU]\SHZQHMZDUWRFLEáGX

ID]\QDVWSXMHXWUDWDV\QFKURQL]DFML

'ODSWOL]ILOWUHPRWUDQVPLWDQFML

( )

H s

3

( )

( )

( )

lim

lim

t

b

b

s

t

t

s

s

s

K H s

s

→∞

→

=

=

+

ϕ

ϕ

υ

ω

0

0

3

3

3RGVWDZLDMFLEGRRWU]\PXMHP\

ϕ

υ

ξ ω

ω

υ
ω

ω

ω

b

s

n

n

n

s

s

0

0

2

2

2

2

2

=

+

+

=

→

lim

'OD Z\VWDUF]DMFR GX*HJR ZVSyáF]\QQLND WáXPLHQLD

ξ

SU]HELHJ

( )

ϕ

b

t

RVLJD ZDUWRü DV\PSWRW\F]Q Z VSRVyE DSHULRG\F]Q\ WM EH]

RVF\ODFML R GX*\FK DPSOLWXGDFK L SU]\ GRVWDWHF]QLH PDá\P VWRVXQNX

υ ω

ω

/

n

2

SWODSR]RVWDMHZVWDQLHV\QFKURQL]DFML

-H*HOL ]DVWRVXMHP\ ILOWU R WUDQVPLWDQFML

( )

( ) ( )

H s

H s H s

5

3

4

=

UyZQZyZF]DVRWU]\PXMHP\SWOID]RZJRU]GXW\SX

WU]HFLHJR NWyUHM EáG ID]\ SU]\ OLQLRZHM ]PLDQLH SXOVDFML V\JQDáX

ZHMFLRZHJRZTXDVLOLQLRZ\P]DNUHVLHSUDF\Z\QRVL]HUR

0LQLPDOL]DFMDEáGXOHG]HQLDID]\ZVWDQLHV\QFKURQL]DFMLSU]\

]PLDQDFK F]VWRWOLZRFL ZHMFLRZHM QLH VWDQRZL MHG\QHJR NU\WHULXP

GRERUX Z]PRFQLHQLD SWOL L WUDQVPLWDQFML ILOWUX GROQRSU]HSXVWRZHJR

=DUyZQRZ]PRFQLHQLHSWOLMDNLWUDQVPLWDQFMDILOWUXZLVWRWQ\VSRVyE

ZSá\ZDM UyZQLH* QD ZáDFLZRFL V]XPRZH SWOL FKDUDNWHU\]RZDQH

W]ZSDVPHPV]XPRZ\P

B

n

>@

( )

( )

B

j

j

df

n

g

i

=

∞

∫

ϕ

ϕ

Ω

Ω

2

0

1DOH*\ SU]\ W\P SRGNUHOLü *H XNáDG\ ] SWODPL ID]RZ\PL

Z\ND]XM EDUG]R NRU]\VWQH ZáDFLZRFL ]PQLHMV]DQLD VWRVXQNX

V\JQDáV]XPQDZ\MFLXXNáDGXZSRUyZQDQLXGRZHMFLD'ODSWOL3//
JRRUD]JRU]GX]ILOWUHPFDáNXMF\P

( )

(

)

H s

1

SDVPRV]XPRZH

B

n

]DOH*\ W\ONR RG Z]PRFQLHQLD SWOL L Z\QRVL

B

K

n

=

/ 4

:]URVW

Z]PRFQLHQLD ] MHGQHM VWURQ\ ]PQLHMV]D EáG OHG]HQLD ID]\ OHF]

]DUD]HP SRZLNV]D SDVPR V]XPRZH

B

n

ZVNXWHN F]HJR SWOD MHVW

EDUG]LHM SRGDWQD QD V]XP\ L SRJDUV]D VL VWRVXQHN V\JQDáV]XP QD

Z\MFLX XNáDGX =QDF]QLH NRU]\VWQLHMV]H ZáDFLZRFL V]XPRZH

Z\ND]XM SWOH 3// ] ILOWUHP SURSRUFMRQDOQR FDáNXMF\P

( ) ( )

(

)

H s H s

2

3

,

NWyUH SRQDGWR ]DOH*QLH RG URG]DMX Z\PXV]HQLD

FKDUDNWHU\]XMVLWDNLPLVDP\PLOXEPQLHMV]\PLVWDW\F]Q\PLEáGDPL

ID]\=WHJRSRZRGXVQDMF]FLHMVWRVRZDQHZSUDNW\FH

352&(6<6<1&+521,=$&-,37/,3//

'RFKRG]HQLHGRVWDQXV\QFKURQL]DFML]DNUHVFKZ\WDQLD

0RGHO OLQLRZ\ SWOL QLH PR*H E\ü Z\NRU]\VWDQ\ GR RNUHOHQLD

VWDQXSU]HMFLRZHJRZSWOL3URFHVWHQRUD]RNUHOHQLHZDUXQNyZSU]\

NWyU\FK SWOD PR*H GRMü GR VWDQX V\QFKURQL]DFML PR*HP\ ]QDOH(ü

Z\áF]QLHZGURG]HUR]ZL]DQLDQLHOLQLRZHJRUyZQDQLDUy*QLF]NRZHJR

RSLVXMFHJR W SWO =Dáy*P\ *H Z FKZLOL W SWOD VSU]*HQLD

]ZURWQHJR MHVW UR]ZDUWD Z PLHMVFX SRáF]HQLD GHWHNWRUD ID]\ L ILOWUX

GROQRSU]HSXVWRZHJRDGRZHMFLDMHVWSU]\áR*RQ\V\JQDá

( )

( )

[

]

u t

U

t

i

i

i

i

=

+

sin

ω

ϕ

0

0

QDWRPLDVWSU]HELHJZ\WZDU]DQ\SU]H]JHQHUDWRU9&2PDSRVWDü

( )

( )

[

]

( )

[

]

u t

U

t

t

U

t

g

g

g

t

g

g

=

+

=

+

=

cos

cos

ω

ϕ

ω

ϕ

0

0

0

0

3XOVDFMHREXV\JQDáyZUy*QLVLRGVLHELHR

∆

ω

W]Q

ω

ω

ω

i 0

0

−

= ∆

6\JQDá

( )

u t

i

PR*HP\]DWHP]DSLVDüZSRVWDFL

( )

( )

[

]

X

L

t

U

t

t

i

i

=

+

sin

ω

ϕ

0

JG]LH

( )

( )

ϕ

ω

ϕ

i

i

t

t

=

+

∆

0

D

6NáDGRZDZROQR]PLHQQDQDSLFLDQDZ\MFLXGHWHNWRUDID]\RSLVDQDMHVW

ZWHG\]DOH*QRFL

( )

( )

[

]

( )

( )

( )

u

t

k

t

D

D

b

b

i

g

1

0

0

0

0

=

+

=

−








sin

∆

ω

ϕ

ϕ

ϕ

ϕ

JG]LH

MHVWSRF]WNRZ\PEáGHPID]\

:F]DVLH

t

≥

0

QDVWSXMH ]DPNQLFLH SWOL VSU]*HQLD ]ZURWQHJR

LUR]SRF]\QD VL SURFHV SU]HMFLRZ\ GRFKRG]HQLD GR VWDQX

V\QFKURQL]DFML

'OD

t

≥

0

RJyOQH UyZQDQLH SWOL SU]\ Z\NRU]\VWDQLX

]DOH*QRFLSU]\MPXMHSRVWDü

( )

( ) ( )

d

t

dt

K

t

h t

b

b

ϕ

ω

ϕ

=

−

∗

∆

sin

3R ]DPNQLFLX SWOL VSU]*HQLD ]ZURWQHJR VNáDGRZD

ZROQR]PLHQQD QD Z\MFLX GHWHNWRUD QLH MHVW MX* SU]HELHJLHP

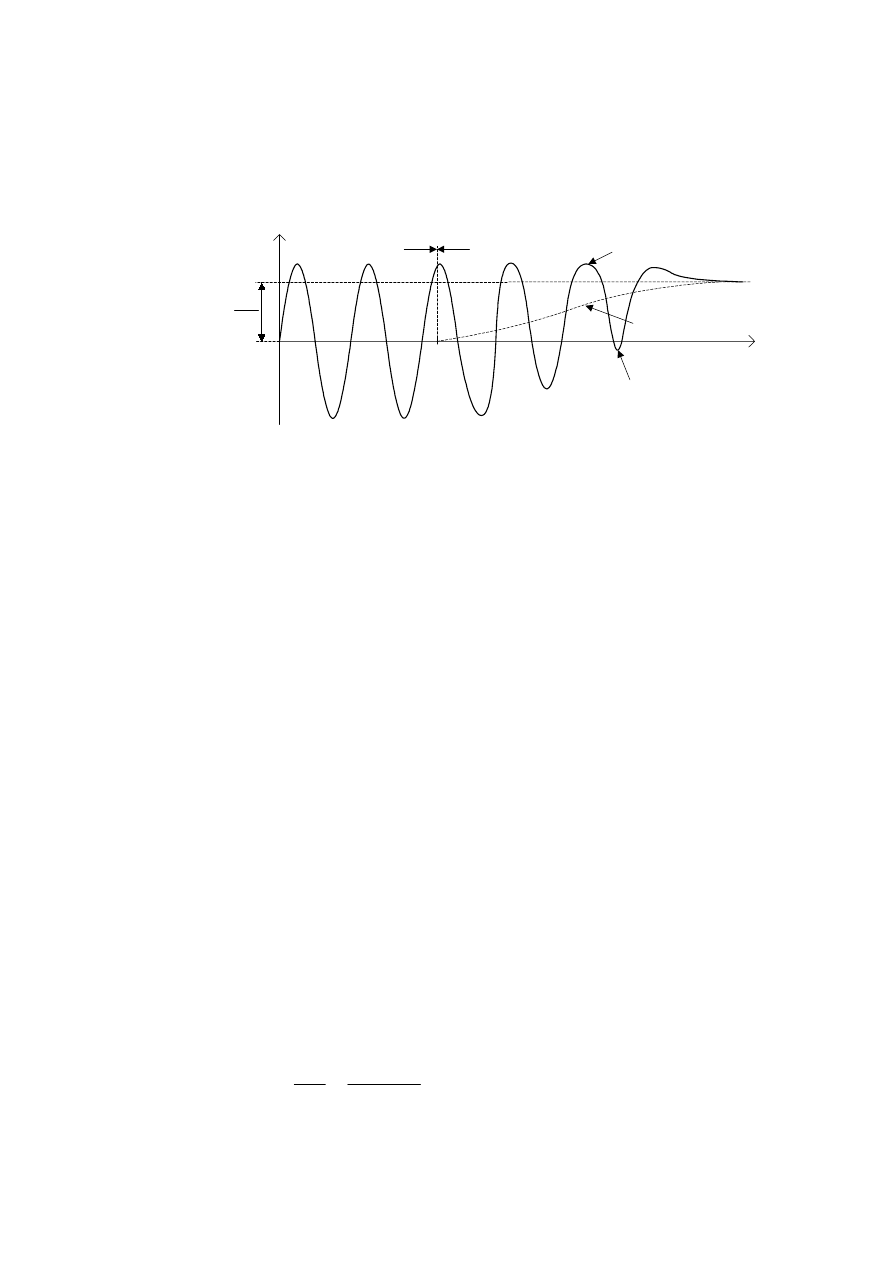
VLQXVRLGDOQ\PRSLVDQ\PUyZQDQLHP

&KDUDNWHU\VW\F]Q\SU]HELHJQDSLFLD

( )

u t

O

QDZHMFLXJHQHUDWRUD

9&2ZSWOL RVLJDMFHM VWDQ V\QFKURQL]DFML SU]\ ]DáR*HQLX

ω

ω

i 0

0

>

SU]HGVWDZLRQRQDU\V

X

2

W

8

N

2

*

= ∆

ω

0

0

SWOD RWZDUWD

SURFHV FKZ\WDQLD

F]VWRWOLZRFL ]EOL*RQH

F]VWRWOLZRFL RGGDORQH

VNáDGRZD ZROQR]PLHQQD

5\V 1DSLFLH

( )

u t

O

QD ZHMFLX JHQHUDWRUD 9&2 SWOL RVLJDMFHM VWDQ

V\QFKURQL]DFML

1DSLFLH

( )

u t

O

NWyUH RWU]\PXMHP\ Z Z\QLNX SU]HMFLD QDSLFLD

( )

u

t

D1

SU]H] ILOWU GROQRSU]HSXVWRZ\ L HZHQWXDOQLH Z]PDFQLDF]

PRGXOXMH Z F]VWRWOLZRFL JHQHUDWRU 9&2 3U]\ ]DPNQLWHM SWOL

QDSLFLH

( )

u

t

D1

QD Z\MFLX GHWHNWRUD MHVW Z\QLNLHP PQR*HQLD

ZHMFLRZHJR SU]HELHJX VLQXVRLGDOQHJR

( )

u t

i

L ]PRGXORZDQHJR Z

F]VWRWOLZRFLSU]HELHJX

( )

u t

g

6]\ENRü ]PLDQ QDSLFLD QD Z\MFLX JHQHUDWRUD 9&2

( )

du t

dt

O

/

ZVND]XMH UyZQRF]HQLH QD Z]DMHPQ UHODFM SRPLG]\ SXOVDFMDPL

( )

ω

J

W

L

( )

ω

L

W *G\]PLDQ\QDSLFLD

( )

u t

O

]DFKRG] ZROQR WR

R]QDF]D*HSXOVDFMD

( )

ω

g

t

JHQHUDWRUD 9&2]EOL*DVLGRZDUWRFL

ω

i 0

:]URVWEH]Z]JOGQHMZDUWRFL

( )

du t

dt

O

/

R]QDF]D*HSXOVDFMD

( )

ω

g

t

RGGDOD VL RG ZDUWRFL

ω

i 0

U\V -DN ZLGDü QD U\V SU]HELHJ

( )

u t

O

Z VWDQLH QLHXVWDORQ\P MHVW QLHV\PHWU\F]Q\ Z]JO GHP RVL F]DVX

=DZLHUDRQVNáDGRZZROQR]PLHQQOLQLDSU]HU\ZDQDQDU\VNWyUD

Z\PXV]D]EOL*HQLHZDUWRFLUHGQLHMSXOVDFML

( )

ω

g

t

GR

ω

i 0

: VWDQLH XVWDORQ\P QDSLFLH

( )

u t

O

RVLJD ZDUWRü Z\QLNDMF ]

FKDUDNWHU\VW\NL SU]HVWUDMDQLD JHQHUDWRUD UyZQ L RNUH ORQH MHVW

]DOH*QRFL

U

k

k

O

G

i

G

=

=

−

∆

ω ω

ω

0

0

=JRGQLH ] ZF]HQLHMV]\PL UR]ZD*DQLDPL UyZ GRSXV]F]DOQD

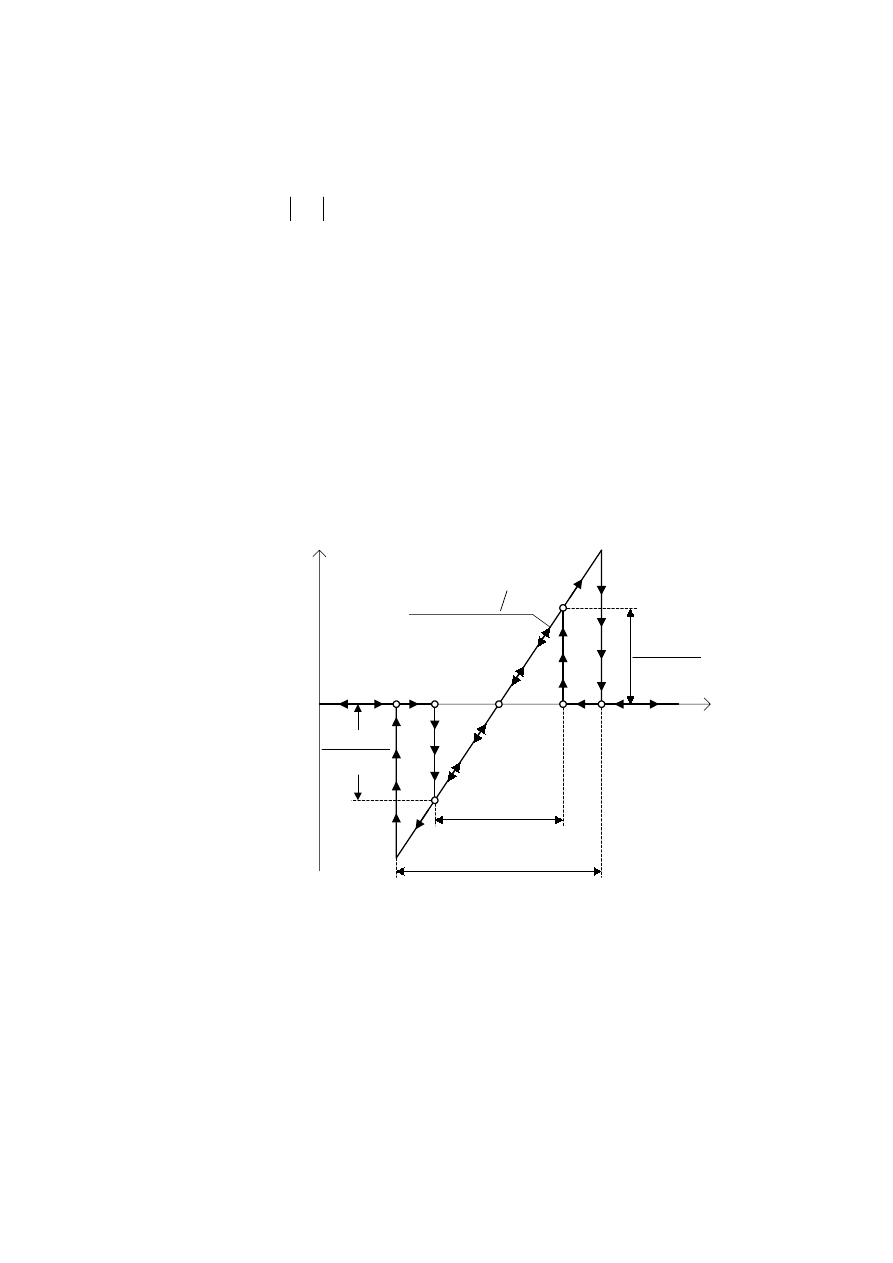
SRF]WNRZD Uy*QLFD SXOVDFML

∆

ω

QLH PR*H SU]HNURF]\ü ]DNUHVX

WU]\PDQLD SWOL

∆

ω

T

ERZLHP Z SU]HFLZQ\P Z\SDGNX QLHPR*OLZH

E\áRE\ZHMFLHZVWDQV\QFKURQL]DFML=DWHP

PD[

∆

∆

ω

ω

≤

T

=XZDJLQDNRQLHF]QRüHOLPLQDFMLV]XPyZZHMFLRZ\FKZSWOL

ID]RZHMVWRVXMHVLILOWU\RSDPLHSU]HQRV]HQLD]QDF]QLHPQLHMV]\PRG

∆

ω

T

: W\P SU]\SDGNX RPyZLRQ\ Z\*HM HIHNW SU]HFLJDQLD

F]VWRWOLZRFL JHQHUDWRUD 9&2 Z SURFHVLH SU]HMFLRZ\P EG]LH ]E\W

VáDE\DE\GRSURZDG]LüGR]UyZQDQLDF]VWRWOLZRFL

ω

iO

L

( )

ω

g

t

0DNV\PDOQUy*QLFSXOVDFMLV\JQDáyZ

( )

( )

ω

ω

g

i

t

t

L

SU]\VNRNRZ\P

RGVWURMHQLX RG SXOVDFML URGNRZHM

ω

0

SU]\ NWyUHM SWOD RVLJD VWDQ

V\QFKURQL]DFMLQD]\ZDP\ ]DNUHVHPFKZ\WDQLDDQJFDSWXUHUDQJHOXE

]DNUHVHP ZFLJDQLD DQJ SXOO LQ UDQJH L R]QDF]DP\ SU]H]

∆

ω

C

:]DMHPQH XV\WXRZDQLH ]DNUHVyZ FKZ\WDQLD L WU]\PDQLD LOXVWUXMH

U\V

X

2

ω

L

N

*

∆

ω

&

∆

ω

7

ω

ω

0

− ∆

F

*

N

3

4

3

1

3

0

3

3

3

2

ω

0

ω

ω

0

+ ∆

F

*

N

QDFK\OHQLH

]DNUHV FKZ\WDQLD

]DNUHV WU]\PDQLD

5\V=DNUHV\FKZ\WDQLDLWU]\PDQLDSWOLID]RZHM

&KDUDNWHU\VW\NL QD U\V SU]HGVWDZLDM ]DOH*QRü QDSLFLD

u

O

QD ZHMFLX JHQHUDWRUD 9&2 RG SXOVDFML V\JQDáX ZHMFLRZHJR

( )

ω

i

t

Z\]QDF]RQSU]\EDUG]RZROQ\FK]PLDQDFKF]VWRWOLZRFLV\JQDáX

-H*HOL SRF]WNRZD SXOVDFMD V\JQDáX ZHMFLRZHJR MHVW EDUG]R

PDáDWR

u

O

DJHQHUDWRU9&2Z\WZDU]DQDSLFLHRF]VWRWOLZRFL

VSRF]\QNRZHM

ω

0

3U]\ Z]URFLH SXOVDFML V\JQDáX QDSLFLH

u

O

MHVW

UyZQH ]HUX QLHFR Uy*QH RG ]HUD ZVNXWHN RPDZLDQHM MX* QLHV\PHWULL

SU]HELHJX QD Z\MFLX GHWHNWRUD ID]\ D* GR NUDFD ]DNUHVX FKZ\WDQLD

SXQNW 3

QD U\V NLHG\ WR VNRNRZR RVLJD ZDUWRü Z\QLNDMF ]

FKDUDNWHU\VW\NLSU]HVWUDMDQLDJHQHUDWRUD9&2

(

)

U

k

O

G

g

=

−

−

1

0

ω

ω

3U]\GDOV]\PZ]URFLHSXOVDFMLV\JQDáXZHMFLRZHJRQDSLFLH

u

O

MHVW OLQLRZ IXQNFM

ω

i

R QDFK\OHQLX k

G

−

1

D* GR JyUQHJR NUDFD

]DNUHVX WU]\PDQLD SXQNW 3

QD U\V NLHG\ WR QDVWSXMH SRZUyW

QDSLFLD

u

O

GRZDUWRFL]HURZHMDSXOVDFMDJHQHUDWRUD9&2SRZUDFDGR

ZDUWRFL

ω

0

=PQLHMV]DMF ] NROHL SXOVDFM V\JQDáX RVLJQLHP\

V\QFKURQL]DFM JHQHUDWRUD SR ]EOL*HQLX VL GR JyUQHJR NUDFD ]DNUHVX

FKZ\WDQLD SXQNW 3

QD U\V :WHG\ QDSLFLH

u

O

RVLJD VNRNRZR

ZDUWRü

(

)

ω

ω

0

+ ∆

C

G

k

/

D SXOVDFMD JHQHUDWRUD 9&2 Z\QRVL

(

)

ω

ω

0

+ ∆

C

=HUZDQLH V\QFKURQL]DFML QDVWSL SU]\ SXOVDFML V\JQDáX

UyZQHM

ω

ω

0

− ∆

T

NLHG\WR]RVWDQLHRVLJQLW\GROQ\NUDQLHF]DNUHVX

WU]\PDQLDSXQNW3

QDU\V

3URFHVV\QFKURQL]DFMLSWOLSLHUZV]HJRU]GX

3WOD SLHUZV]HJR U]GX QLH ]DZLHUD ILOWUX SUDNW\F]QLH

]DVWRVRZDQ\ ILOWU GROQRSU]HSXVWRZ\ PD SDVPR V]HUV]H RG ]DNUHVX

WU]\PDQLD7UDQVPLWDQFML

( )

H s

=

1

RGSRZLDGD

( ) ( )

h t

t

=

δ

ZREHFF]HJR

Z\UD*HQLHSU]\MPXMHSRVWDü

( )

( )

[

]

d

t

dt

K

t

b

b

ϕ

ω

ϕ

=

−

∆

sin

,VWRWQH LQIRUPDFMH R ]DFKRZDQLX XNáDGX PR*HP\ RWU]\PDü QD

SRGVWDZLH RGZ]RURZDQLD UyZQDQLD QD SáDV]F]\(QLH R

ZVSyáU]GQ\FK

( )

( )

d

t

dt

t

b

b

ϕ

ϕ

/

L

]ZDQHMSáDV]F]\]QID]RZ

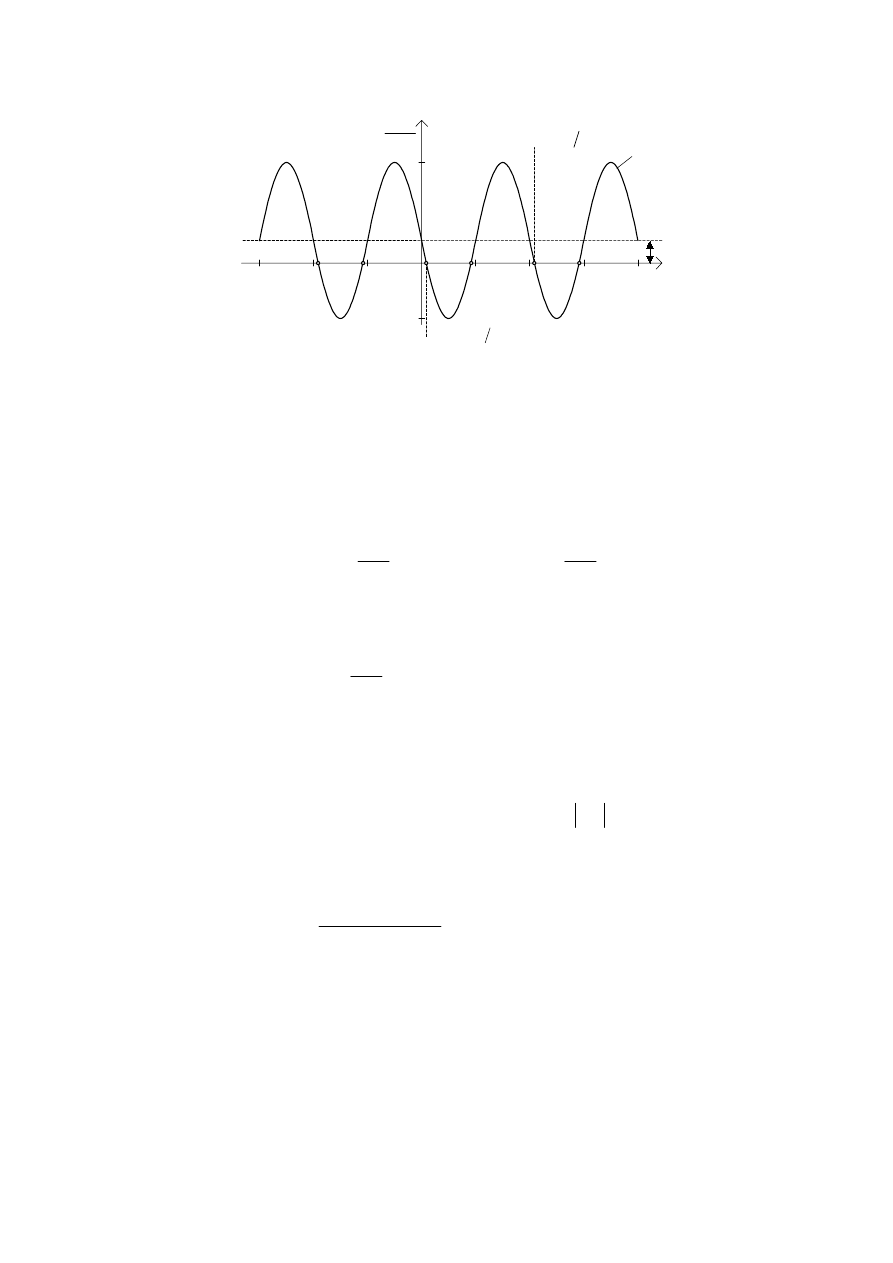
*UDILF]QH UR]ZL]DQLH UyZQDQLD QD SáDV]F]\(QLH ID]RZHM

RWU]\PXMHP\ZSRVWDFLWUDMHNWRULLID]RZHMJG]LHND *G\SXQNWWUDMHNWRULL

REUD]XMHVWDQXNáDGXZFKZLOL WF]DVWMHVWSDUDPHWUHP-DNSRND]DQR

QD U\V RWU]\PDQD WUDMHNWRULD MHVW VLQXVRLG SU]HVXQLW QD RVL

U]GQ\FKR

∆

ω

3XQNW\ Z NWyU\FK WUDMHNWRULD SU]HFLQD R RGFLW\FK V SXQNWDPL

RGZ]RURZXMF\PL VWDQ UyZQRZDJL XNáDGX

(

)

d

dt

b

ϕ

/

.

=

0

6SRUyG

SXQNWyZ ZLGRF]Q\FK QD U\V SXQNW\ 3

3

3

V SXQNWDPL

UyZQRZDJLWUZDáHMQDWRPLDVWZSXQNWDFK3

3

3

XNáDGMHVWZVWDQLH

UyZQRZDJL QLHWUZDáHM :\QLND WR VWG *H MHOL

d

dt

b

ϕ

/

>

0

WR

( )

ϕ

b

t

PXVLZ]UDVWDüMHOLQDWRPLDVW

( )

d

dt

t

b

b

ϕ

ϕ

/

,

<

0

WR

PXVLPDOHü

3

2

−

3

π

∆

ω ω

ω

=

−

L0

0

−

2

π

−

π

0

3

1

π

2

π

3

π

4

π

3

3

3

4

2

π

ω

+

DUFVLQ

∆

.

∆

ω

+

.

∆

ω

ϕ

+

.

E

VLQ

∆

ω

−

.

DUFVLQ

∆

ω

.

ϕ

E

G

GW

E

ϕ

3

5

3

6

5\V2GZ]RURZDQLHUyZQDQLDQDSáDV]F]\(QLHID]RZHM

3R ]V\QFKURQL]RZDQLX SWOD ID]RZD ]DZV]H ]QDMGXMH VL Z

MHGQ\P]HVWDQyZUyZQRZDJLWUZDáHM-DNZ\QLND]U\VZDUXQNLHP

Z\VWSLHQLDSXQNWyZUyZQRZDJLWUZDáHMMHVWDE\ZVWSQHUR]VWURMHQLH

∆

ω

E\áRFRQDMZ\*HMUyZQHZ]PRFQLHQLXSWOL

.

-H*HOLSRF]WNRZ\EáGID]\

( )

ϕ

b

0

]DZDUW\MHVWZSU]HG]LDOH

( )

− −

<

< −

π

ω ϕ

π

ω

K

K

b

arcsin

arcsin

∆

∆

0

WR QDMEOL*V]\P SXQNWHP UyZQRZDJL WUZDáHM MHVW SXQNW 3

NWyUHJR

ZVSyáU]GQDQDRVL

ϕ

b

Z\QRVL

ϕ

ω

b

K

0

=

arcsin

∆

3U]HELHJ EáGX ID]\

( )

ϕ

b

t

RG ZDUWRFL SRF]WNRZHM

( )

ϕ

b

0

RNUHORQHM ]DOH*QRFL GR ZDUWRFL XVWDORQHM

ϕ

b0

RNUHORQHM

]DOH*QRFLMHVWDSHULRG\F]QIXQNFMF]DVX&]DV

T

ε

SRXSá\ZLH

NWyUHJR EáG ID]\ ]EOL*\ VL QD RGOHJáRü

ε

GR ZDUWRFL XVWDORQHM

(

)

ϕ

ϕ

b

b

t

= ∞ =

0

PR*HP\Z\]QDF]\ü]HZ]RUXNWyU\RWU]\PXMHP\SU]H]

RGSRZLHGQLHVFDáNRZDQLHUyZQDQLD

( )

T

K

d

b

b

b

b

ε

ϕ

ϕ

ε

ω

ϕ

ϕ

=

−

+

∫

1

0

0

∆

sin

SU]\F]\P

( )

( )

ε

ϕ

ϕ

ε

ϕ

ϕ

<

<

>

>

0

0

0

0

0

0

GOD
GOD

b

b

b

b

:LHONRü

T

ε

QD]\ZDP\ F]DVHP RVLJDQLD V\QFKURQL]DFML OXE

F]DVHPFKZ\WDQLDDQJDFTXLVLWLRQWLPH&]DV

T

ε

SU]\XVWDORQ\P

ε

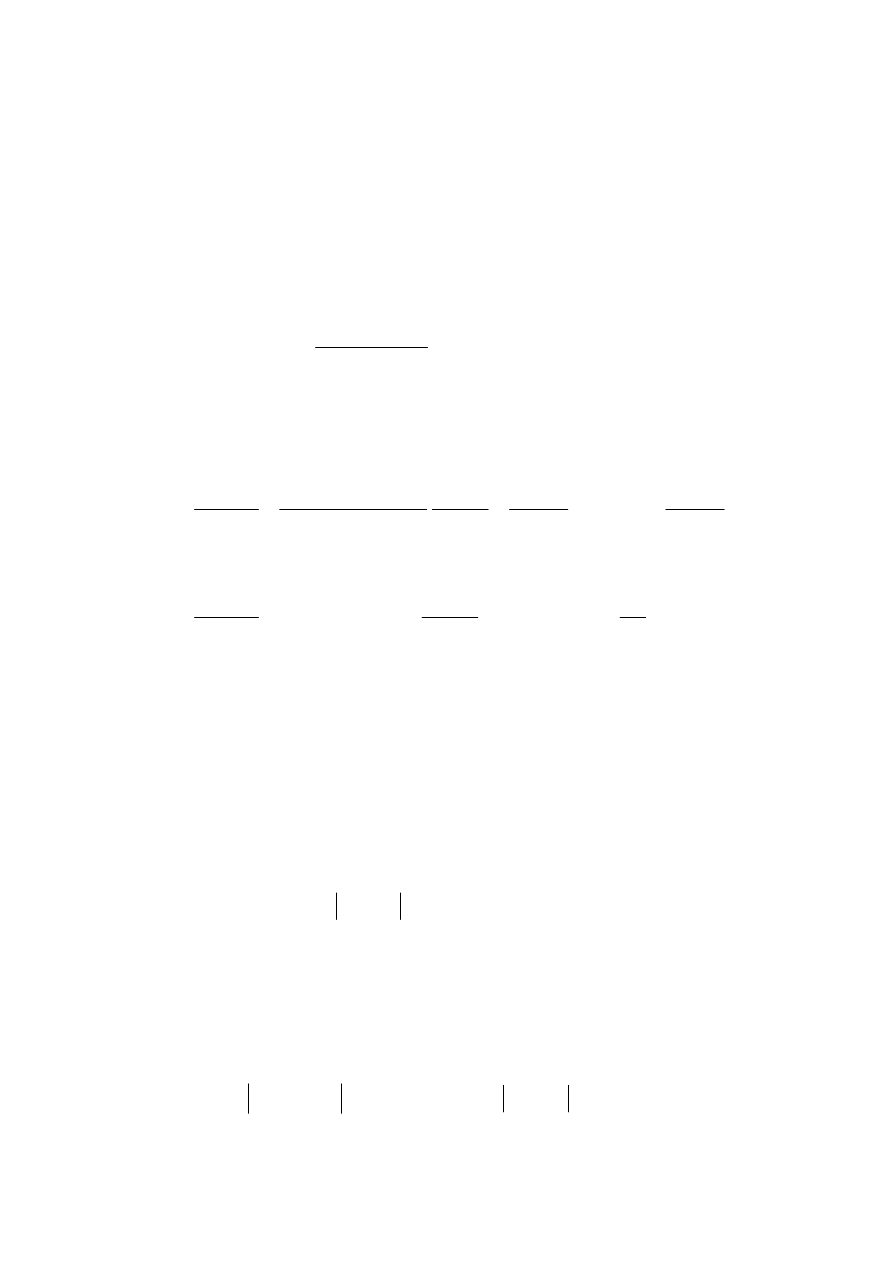
MHVWV]F]HJyOQLHGáXJLJG\

( )

ϕ

b

0

PDZDUWRü]EOL*RQGRZVSyáU]GQHM

VWDQXUyZQRZDJLQLHVWDELOQHM

3URFHVV\QFKURQL]DFMLSWOLGUXJLHJRU]GX

%DUG]R F]VWR Z SWOL ID]RZHM GUXJLHJR U]GX VWRVRZDQ\ MHVW

GROQRSU]HSXVWRZ\ILOWUSURSRUFMRQDOQRFDáNXMF\RWUDQVPLWDQFML

( )

(

)

H s

s

s

2

2

1

2

1

1

=

+

+

+

τ

τ

τ

5yZQDQLH Uy*QLF]NRZH RSLVXMFH SWO ID]RZ SREXG]RQ

VNRNLHPF]VWRWOLZRFL

∆

ω

WDNVDPRMDNZSWOLSLHUZV]HJRU]GXL

]DZLHUDMFHMILOWURWUDQVPLWDQFML

( )

H s

2

PDSRVWDü

( )

( )

( )

( )

d

t

dt

K

t d

t

dt

K

t

b

b

b

b

2

2

2

1

2

1

2

1

2

1

ϕ

τ

ϕ

τ

τ

ϕ

τ

τ

ϕ

ω

τ τ

+

+

+

+

+

=

+

cos

sin

∆

-H*HOL

1

2

/

,

τ

<<

K

WRUyZQDQLHXSUDV]F]DVLGRSRVWDFL

( )

( )

( )

( )

d

t

dt

t

d

t

dt

t

K

b

n

b

b

n

b

n

2

2

2

2

2

ϕ

ξ ω

ϕ

ϕ

ω

ϕ

ω

ω

+

+

=

cos

sin

∆

%DGDQLHSURFHVXV\QFKURQL]DFMLSWOLGUXJLHJRU]GX]HZ]JOGX

QD QLHOLQLRZRü UyZQDQLD Uy*QLF]NRZHJR QDMOHSLHM MHVW

SURZDG]LüPHWRGDPLQXPHU\F]Q\PL1L*HMSURFHVWHQ]RVWDQLHRSLVDQ\

UDF]HMSRJOGRZRRUD]]RVWDQSU]\WRF]RQHQLHNWyUHZ\QLNLNRFRZHQD

SRGVWDZLHOLWHUDWXU\>@

3U]\W\FKVDP\FK]DáR*HQLDFKMDNLHSRF]\QLRQRSU]\DQDOL]LHSWOL

SLHUZV]HJR U]GX QDSLFLH

( )

u t

O

QD ZHMFLX JHQHUDWRUD 9&2 Z

PRPHQFLH UR]SRF]FLD SURFHVX V\QFKURQL]DFML RNUHORQH MHVW

]DOH*QRFL

( )

( )

(

)

u t

k

H

t

O

D

≈

∆

∆

ω

ω

sin

5yZQDQLH RWU]\PDQR QD SRGVWDZLH ]DOH*QRFL SU]\

SRPLQLFLXSRF]WNRZ\FKID]V\JQDáyZ

6\JQDá

( )

u t

O

PRGXOXMH JHQHUDWRU 9&2 SU]\ F]\P PDNV\PDOQD

RGFK\áNDSXOVDFML

( )

ω

ω

g

t

RG

0

]JRGQLH]]DOH*QRFLDPLL

Z\QRVL

( )

( )

ω

ω

ω

g

G

O

t

k U

K H

−

=

≈

0 max

max

∆

JG]LH

K

k k

D

G

=

MHVWZ]PRFQLHQLHPSWOL

-H*HOLPDNV\PDOQDRGFK\áND

( )

ω

g

t

EG]LHUyZQDOXEZLNV]DRG

∆

ω

W]QJG\VSHáQLRQD]RVWDQLHQLHUyZQRü

( )

K H

∆

∆

ω

ω

≥

WRZyZF]DVMDN]D]QDF]RQRQDU\VZFLJX MHGQHJR RNUHVX

( )

u t

O

Z\VWSLPRPHQW]UyZQDQLDVLSXOVDFML

( )

ω

g

t

]SXOVDFM

ω

i 0

LZFKZLOL

WHMQDVWSLV\QFKURQL]DFMDSU]HELHJyZ

( )

( )

u t

u t

i

g

L

.

ω

L0

ω

0

0

W

( )

. +

∆

∆

ω

ω

=

( )

ω

J

W

( )

ω

J

W

5\V2VLJDQLHVWDQXV\QFKURQL]DFMLZFLJXMHGQHJRRNUHVX

( )

u t

O

=DNUHVSXOVDFML

∆

ω

L

VSHáQLDMF\ZDUXQHN

(

)

K H

L

L

∆

∆

ω

ω

=

QD]\ZDP\ ]DNUHVHP FKZ\WDQLD Z NWyU\P QDVWSXMH V\QFKURQL]DFMD Z

FLJXMHGQHJRRNUHVX

( )

u t

O

DQJORFNLQUDQJH

0R*QD Z\ND]Dü *H SU]\ ]DVWRVRZDQLX ILOWUX R WUDQVPLWDQFML

( )

H s

1

UyZQVáXV]QDMHVW]DOH*QRü

∆

ω

ω

L

n

≈

1DWRPLDVW Z SU]\SDGNX ILOWUX R WUDQVPLWDQFML

( )

H s

2

UyZQ

RWU]\PXMHVL

∆

ω

ξ ω

L

n

≈

2

:REXSU]\SDGNDFKVWDQV\QFKURQL]DFMLRVLJDVLSRF]DVLH

t

L

n

≈

1 /

ω

: SU]\SDGNX JG\ PDNV\PDOQD RGFK\áND

( )

ω

ω

g

t

RG

0

Z\UD*HQLH MHVW PQLHMV]D RG SRF]WNRZHM Uy*QLF\ SXOVDFML
V\JQDáyZ

( )

( )

u t

u t

i

g

L

R]QDF]RQHM SU]H]

∆

ω

WR SRF]WNRZR QLH

Z\VWSL Z *DGQ\P PRPHQFLH ]UyZQDQLH VL SXOVDFML

( )

ω

g

t

RUD]

ω

i 0

W\FKV\JQDáyZ3URFHVSU]HFLJDQLDSXOVDFMLJHQHUDWRUD9&2GRSXOVDFML

V\JQDáXZHMFLRZHJR

ω

i 0

]RVWDáRSLVDQ\SRJOGRZRZUR]G]

6NáDGRZDZROQR]PLHQQD

( )

u

t

D1

QDZ\MFLXGHWHNWRUDID]\PDSRVWDü

( )

( )

[

]

X W

N

W W

'

'

U

=

VLQ

∆

ω

JG]LH

( )

( )

∆

ω

ω

ω

r

i

g

t

t

=

−

0

D

MHVWFKZLORZUy*QLFSXOVDFMLV\JQDáXZHMFLRZHJRLJHQHUDWRUD9&2

:LHONRüWD]PLHQLDVLZF]DVLHLW\ONRZPRPHQFLH

t

=

0

PDZDUWRü

( )

∆

∆

ω

ω ω

ω

r

i

0

0

0

=

=

−

1DSLFLHSU]HVWUDMDMFHJHQHUDWRU9&2PDWHUD]SRVWDü

( )

( )

[

]

( )

[

]

X W

N +

W

W W

2

'

U

U

=

∆

∆

ω

ω

VLQ

SU]\F]\PSXOVDFMD

( )

ω

g

t

QLH]PLHQLDVLVLQXVRLGDOQLH

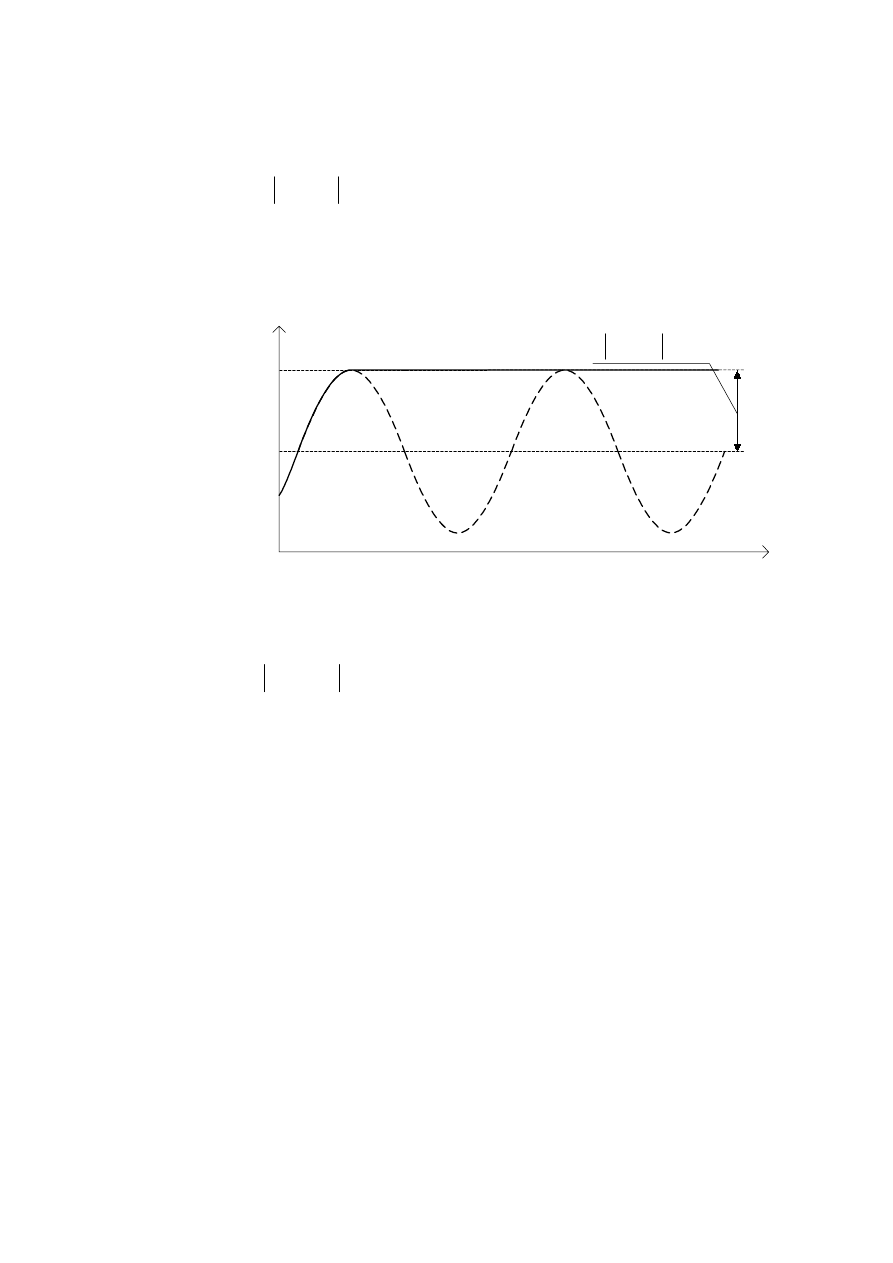
.V]WDáW SU]HELHJX QDSLFLD

( )

u t

O

RUD] ZLHONRFL

( )

∆

ω

r

t

Z

SURFHVLHV\QFKURQL]DFMLSU]HGVWDZLRQRSRJOGRZRQDU\V

X

2

W

W

∆

ω

U

∆

ω

U

a)

b)

ω

ω

L0

0

−

( )

( )

∆

ω

ω

ω

U

L

J

W

W

=

−

PDáH F] ]EOL*RQH ILOWU QLH WáXPL

GX*H

F] RGGDORQH ILOWU WáXPL

5\V3URFHVV\QFKURQL]DFMLSWOLID]RZHMDSU]HELHJQDSLFLD

( )

u t

O

ESU]HELHJ

Uy*QLF\SXOVDFML

( )

( )

∆

ω

ω

ω

U

L

J

W

W

=

−

&]ü RNUHVX SU]HELHJX

( )

u t

O

NLHG\

( )

∆

ω

r

t

MHVW PDáH MHVW

GáX*V]D QL* F]ü RNUHVX WHJR SU]HELHJX JG\

( )

∆

ω

r

t

MHVW GX*H

:\QLNLHP WHM DV\PHWULL MHVW SRMDZLHQLH VL VNáDGRZHM ZROQR]PLHQQHM

SU]HELHJX

( )

u t

O

L GRSURZDG]HQLH Z RNUHORQ\FK ZDUXQNDFK GR VWDQX

V\QFKURQL]DFMLSWOL3RF]WNRZDUy*QLFDSXOVDFML

∆

∆

ω

ω

=

C

V\JQDáyZ

( )

( )

u t

u t

i

g

L

,

SU]\ NWyUHM Z\VWSL MHV]F]H Z XNáDG]LH V\QFKURQL]DFMD

MHVW ]DNUHVHP FKZ\WDQLD : M]\NX DQJLHOVNLP GOD RGUy*QLHQLD RG

SU]\SDGNXRPyZLRQHJRSRSU]HGQLRVWRVXMHVLQD]ZSXOOLQUDQJH

3RPLG]\ZLHONRFLDPL

∆

∆

∆

ω

ω

ω

L

C

T

,

L

]DFKRG]UHODFMH

∆

∆

∆

ω

ω

ω

L

C

T

<

'ODSWOLGUXJLHJRU]GX]DNUHVFKZ\WDQLDZ\QRVL>@

∆

ω

π

ξ ω ω

C

n

n

K

≈

−

8

2

&]DVWUZDQLDSURFHVXV\QFKURQL]DFMLRNUHORQ\MHVW]DOH*QRFL

( )

t

C

n

≈

∆

ω

ξ ω

2

2

2

&]DVV\QFKURQL]DFML

t

C

PR*HE\üGáXJLJG\

∆

ω

MHVW]EOL*RQHGR

∆

ω

C

6&$/21(37/()$=2:(

:V]\VWNLHEORNLIXQNFMRQDOQHWZRU]FHSWOID]RZVáDWZHGR

Z\WZDU]DQLD Z WHFKQRORJLL PRQROLW\F]QHM VWG WH* REHFQLH SURGXNXMH

VL ZLHOH VFDORQ\FK SWOL ID]RZ\FK SUDFXMF\FK Z V]HURNLP SDPLH

F]VWRWOLZRFL L Z\PDJDMF\FK PLQLPDOQHM OLF]E\ HOHPHQWyZ

GRáF]DQ\FK]]HZQWU]

*áyZQ\PL HOHPHQWDPL SWOL ID]RZHM V JHQHUDWRU SU]HVWUDMDQ\

QDSLFLHPOXESUGHPGHWHNWRUID]\RUD]ILOWUGROQRSU]HSXVWRZ\

'HWHNWRUID]\

: VFDORQ\FK XNáDGDFK 3// MDNR GHWHNWRU\ ID]\ SRZV]HFKQLH

VWRVXMH VL PRGXODWRU\ ]UyZQRZD*RQH QDMSURVWV]H XSURV]F]RQH

F]WHURüZLDUWNRZHXNáDG\PQR*FHRSLVDQHZUR]G]

:SURZDG]DMFQRZHR]QDF]HQLD]PLHQQ\FKZUR]G]PRGXODWRU

]UyZQRZD*RQ\UR]ZD*DQRMDNRXNáDGPQR*F\

( )

( )

( )

( )

u

t

u t

u t

u t

X

i

Y

g

=

=

,

SU]HDQDOL]XMHP\ WU]\ PR*OLZH SU]\SDGNL SRG NWHP Z\NRU]\VWDQLD

PRGXODWRUDMDNRGHWHNWRUDID]\

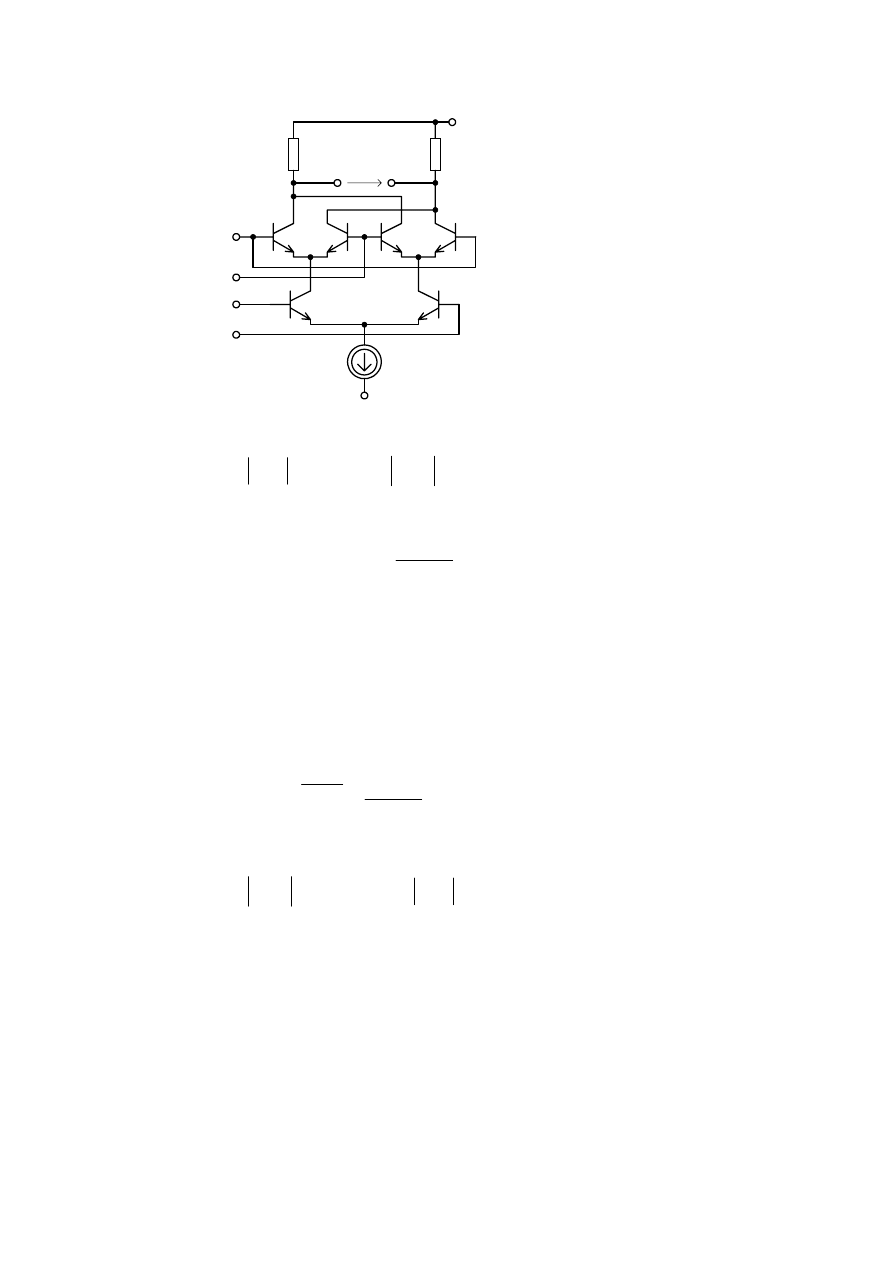
8SURV]F]RQ\ VFKHPDW LGHRZ\ PRGXODWRUD ]UyZQRZD *RQHJR

SU]HGVWDZLRQRQDU\V

−

8

((

T

4

T

3

T

5

T

6

T

2

T

1

( )

X W

L

( )

X W

J

,

((

+

8

&&

5

&

5

&

( )

X W

G

5\V

6FKHPDW

LGHRZ\

PRGXODWRUD]UyZQRZD*RQHJR

3U]\SDGHN

( )

( )

u t

u t

i

T

g

T

<<

<<

ϕ

ϕ

;

'ODXNáDGX]U\V]DOH*QRüSU]HNV]WDáFDVLGRSRVWDFL

( )

( )

( ) ( )

u t

i t R

I

R

u t u t

D

R

C

EE

C

T

i

g

=

=

4

2

ϕ

'ODGZyFKSU]HELHJyZSU]HVXQLW\FKZID]LH

( )

(

)

( )

u t

U

t

u t

U

t

i

i

g

g

=

+

=








cos

cos

ω

ϕ

ω

0

0

QD SRGVWDZLH ]DOH*QRFL RWU]\PXMHP\ FKDUDNWHU\VW\N

XNáDGXMDNRGHWHNWRUDID]\

( )

U

u t

I

R

U U

D

D

EE

C

T

g

i

0

2

8

=

=

ϕ

ϕ

cos

3U]\SDGHN

( )

( )

u t

u t

g

T

i

T

>>

<<

2

2

ϕ

ϕ

;

7UDQ]\VWRU\7

7

U\VVWHURZDQHV\JQDáHP

( )

u t

g

RGX*HM

DPSOLWXG]LH ]DFKRZXM VL Z SU]\EOL*HQLX MDN VWHURZDQH NOXF]H -HOL

V\JQDá

( )

u t

g

PDZDUWRüGRGDWQLWRZWHG\WUDQ]\VWRU\7

L7

PR*QD

WUDNWRZDüMDNRNOXF]H]ZDUWHDWUDQ]\VWRU\7

L7

MDNRNOXF]HUR]ZDUWH

'OD XMHPQHM ZDUWRFL V\JQDáX

( )

u t

g

WUDQ]\VWRU\ SU]\MPXM VWDQ\

SU]HFLZQH:W\PSU]\SDGNXQDSLFLHZ\MFLRZHX]DOH*QLRQHMHVWW\ONR

RG SR]LRPX QDSLFLD

( )

u t

i

3U]HELHJ QDSLFLD Z\MFLRZHJR MHVW

Z\QLNLHP PQR*HQLD V\JQDáX

( )

u t

i

R PDáHM DPSOLWXG]LH ]

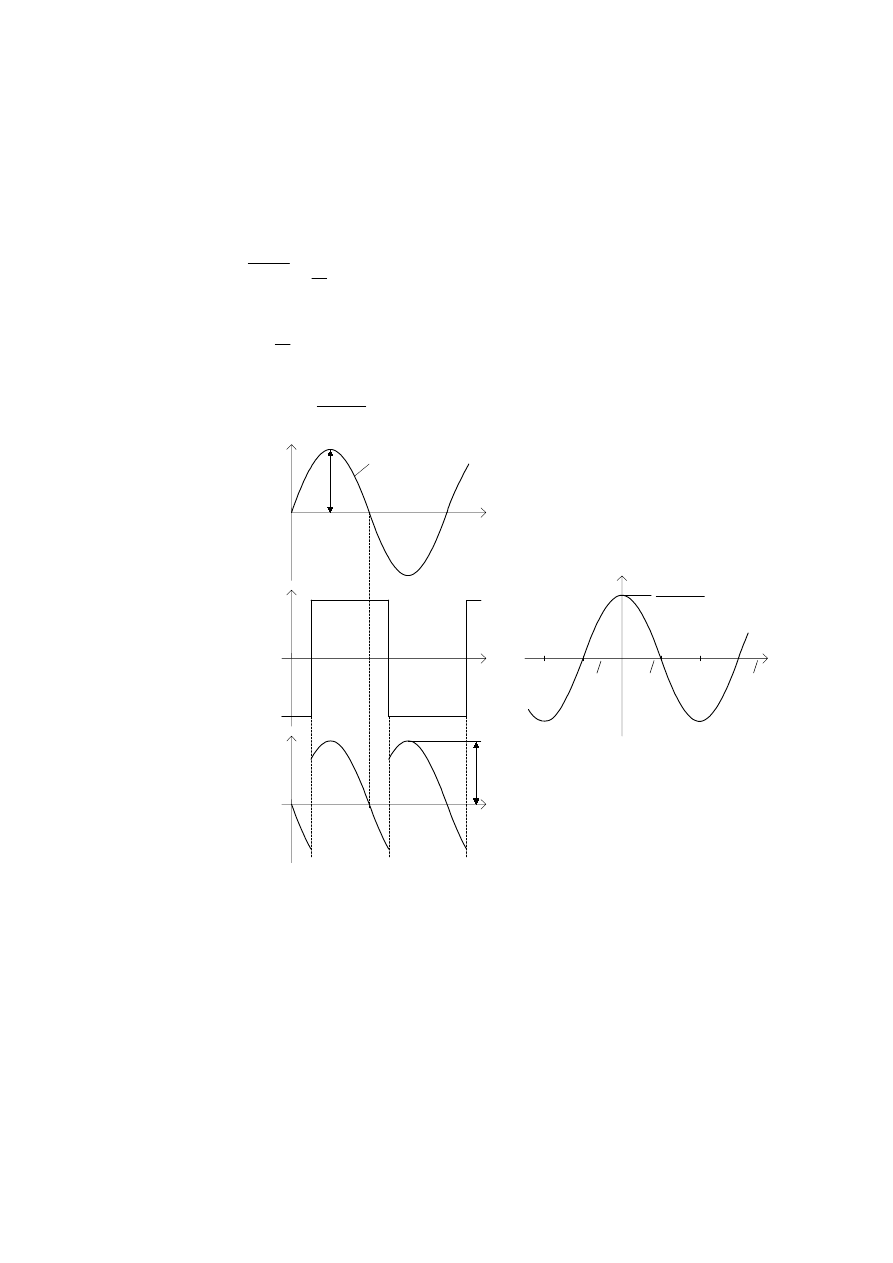
V\QFKURQL]RZDQ\P SU]HELHJLHP SURVWRNWQ\P NWyUHJR DPSOLWXGD MHVW

GX*D L QLH PD ZSá\ZX QD Z\QLN PQR*HQLD 2GSRZLHGQLH SU]HELHJL

F]DVRZH SU]\ VLQXVRLGDOQ\P SU]HELHJX

( )

u t

i

SU]HGVWDZLRQR QD

U\VD

UHGQLDZDUWRüQDSLFLDZ\MFLRZHJR

U

D0

GHWHNWRUDZ\QRVL

( )

( ) ( )

( )

( )

U

u t

u t d

t

U

t d

t

U

t d

t

D

D

D

Dm

Dm

0

0

0

1

1

=

=

=

=

−

+









 =

∫

∫

∫

π

ω

π

ω

ω

ω

ω

π

ϕ

ϕ

π

sin

sin

=

2U

Dm

π

ϕ

cos

8

'0

−

π

ϕ

−

π

2

b)

( )

X W

L

ω

W

a)

( )

X W

J

ω

W

( )

X W

'

ω

W

π

2

π

ϕ

8

'P

2

π

π

ϕ

8

L

8

W

L

L

VLQ

ω

0

π

2

π

3

2

π

2

J 5 8

P &

L

π

0

0

0

5\V 0RGXODWRU ]UyZQRZD*RQ\ VWHURZDQ\ V\JQDáHP VLQXVRLGDOQ\P

L V\QFKURQL]RZDQ\ SU]HELHJLHP SURVWRNWQ\P D SU]HELHJL F]DVRZH

EFKDUDNWHU\VW\NLGHWHNWRUD

$PSOLWXG

U

Dm

QDSLFLD Z\MFLRZHJR

( )

u t

D

PR*QD X]DOH*QLü RG

DPSOLWXG\

U

i

QDSLFLDZHMFLRZHJR

( )

u t

i

U

g R U

Dm

m

C

i

=

JG]LH

g

m

MHVWWUDQVNRQGXNWDQFMWUDQ]\VWRUyZ7

L7

= UyZQD RWU]\PXMHP\ FKDUDNWHU\VW\N GHWHNWRUD

U\VE

U

g R U

D

m

C

i

0

2

=

π

ϕ

cos

0DNV\PDOQHQDFK\OHQLHFKDUDNWHU\VW\NLGHWHNWRUDID]\Z\QRVL

k

dU

d

U

g R

D

D

i

m

C

=

= −

0

2

ϕ

π

max

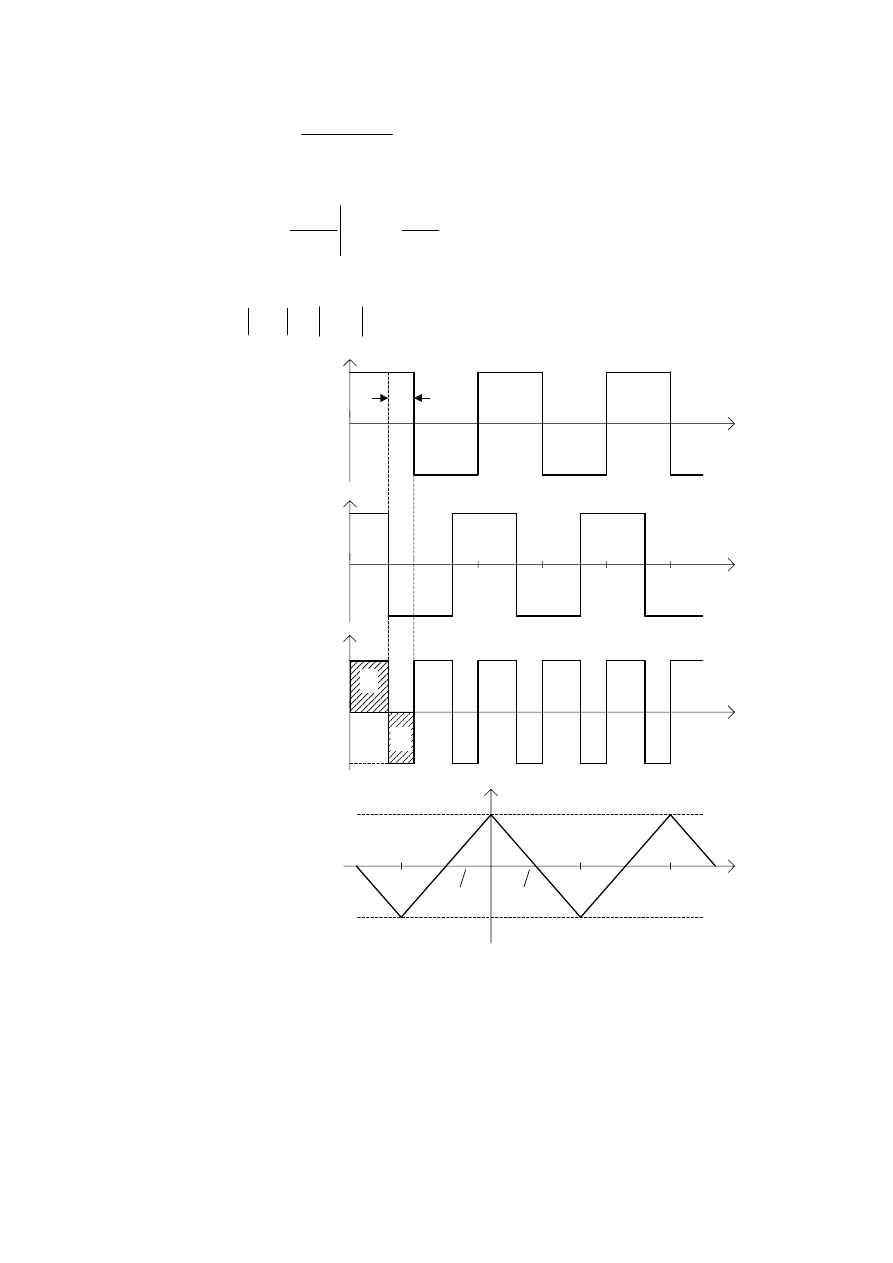
3U]\SDGHN

( )

( )

u t

u t

i

g

T

,

>>

2

ϕ

a)

( )

X W

J

ω

W

2

π

π

0

3

π

4

π

5

π

( )

X W

L

ω

W

2

π

π

0

3

π

4

π

5

π

( )

X W

'

ω

W

2

π

π

0

3

π

4

π

5

π

6

1

6

2

, 5

(( &

−

, 5

(( &

ϕ

−

, 5

(( &

, 5

(( &

8

'0

ϕ

2

π

π

π

2

−

π

2

−

π

b)

5\V 0RGXODWRU ]UyZQRZD*RQ\ GOD GX*\FK DPSOLWXG V\JQDáyZ ZHMFLRZ\FK

DSURVWRNWQHV\JQDá\VWHUXMFHEFKDUDNWHU\VW\NDGHWHNWRUD

-H*HOL RE\GZD XNáDG\ ZHMFLRZH PDM RGSRZLHGQLR GX*H

DPSOLWXG\WRZV]\VWNLHWUDQ]\VWRU\SUDFXMMDNRGZXVWDQRZHNOXF]H

3R Z\PQR*HQLX RGSRZLHGQLFK SURVWRNWQ\FK SU]HELHJyZ

NOXF]XMF\FKSU]HáF]DMF\FKSUG

I

EE

LSRVFDáNRZDQLXRWU]\PXMHP\

FKDUDNWHU\VW\N

GHWHNWRUD

2GSRZLHGQLH

SU]HELHJL

F]DVRZH

SU]HGVWDZLRQRQDU\VD

UHGQLDZDUWRü

U

D0

QDSLFLDZ\MFLRZHJRGHWHNWRUDZ\QRVL

( ) ( )

U

u t d

t

I

R

I

R

I

R

D

D

EE

C

EE

C

EE

C

0

0

1

1

2

=

=

− −

=

=

−









∫

π

ω

π ϕ

π

ϕ

π

ϕ

π

π

3U]HELHJ FKDUDNWHU\VW\NL

( )

U

f

D0

=

ϕ

GHWHNWRUD ID]\ SU]HGVWDZLRQR QD

U\VE 1DFK\OHQLH FKDUDNWHU\VW\NL GHWHNWRUD ID]\ Z SU]HG]LDOH

0

≤ ≤

ϕ π

Z\QRVL

k

dU

d

I

R

D

D

EE

C

=

= −

0

2

ϕ

π

*HQHUDWRU\SU]HVWUDMDQHQDSLFLHP9&2

3WOD ID]RZD G]LDáD SRSUDZQLH ]DUyZQR JG\ ]RVWDQLH Z QLHM

]DVWRVRZDQ\ JHQHUDWRU 9&2 GUJD VLQXVRLGDOQ\FK MDN UyZQLH* GUJD

SURVWRNWQ\FK -HVW WR NRQVHNZHQFM G]LDáDQLD GHWHNWRUD ID]\ NWyU\

SRUyZQXMH ID]\ SU]HELHJyZ ZHMFLRZ\FK D QLH LFK NV]WDáW\ :

VFDORQ\FK SWODFK 3// VWRVXMH VL JHQHUDWRU\ 9&2 Z SRVWDFL

PXOWLZLEUDWRUyZ Z\WZDU]DMF\FK SU]HELHJL SURVWRNWQH 6SHáQLDM RQH

Z ]DGRZDODMF\ VSRVyE Z\PDJDQLD VWDZLDQH JHQHUDWRURP 9&2 WDNLH

MDN

OLQRZD]DOH*QRüF]VWRWOLZRFLRGQDSLFLD

GREUDVWDELOQRüF]VWRWOLZRFL

áDWZRüJHQHURZDQLDZF]

GX*DVSUDZQRüHQHUJHW\F]QD

V]HURNL]DNUHVOHG]HQLD

áDWZRüSU]HVWUDMDQLD

:UyGPXOWLZLEUDWRUyZVWRVXMHVLQDMF]FLHMGZDXNáDG\9&2W\SX

LQWHJUDWRUSU]HU]XWQLN L 9&2 W\SX PXOWLZLEUDWRU ] SRMHPQR FLRZ\P

VSU]*HQLHPHPLWHURZ\P

D9&2W\SXLQWHJUDWRUSU]HU]XWQLN

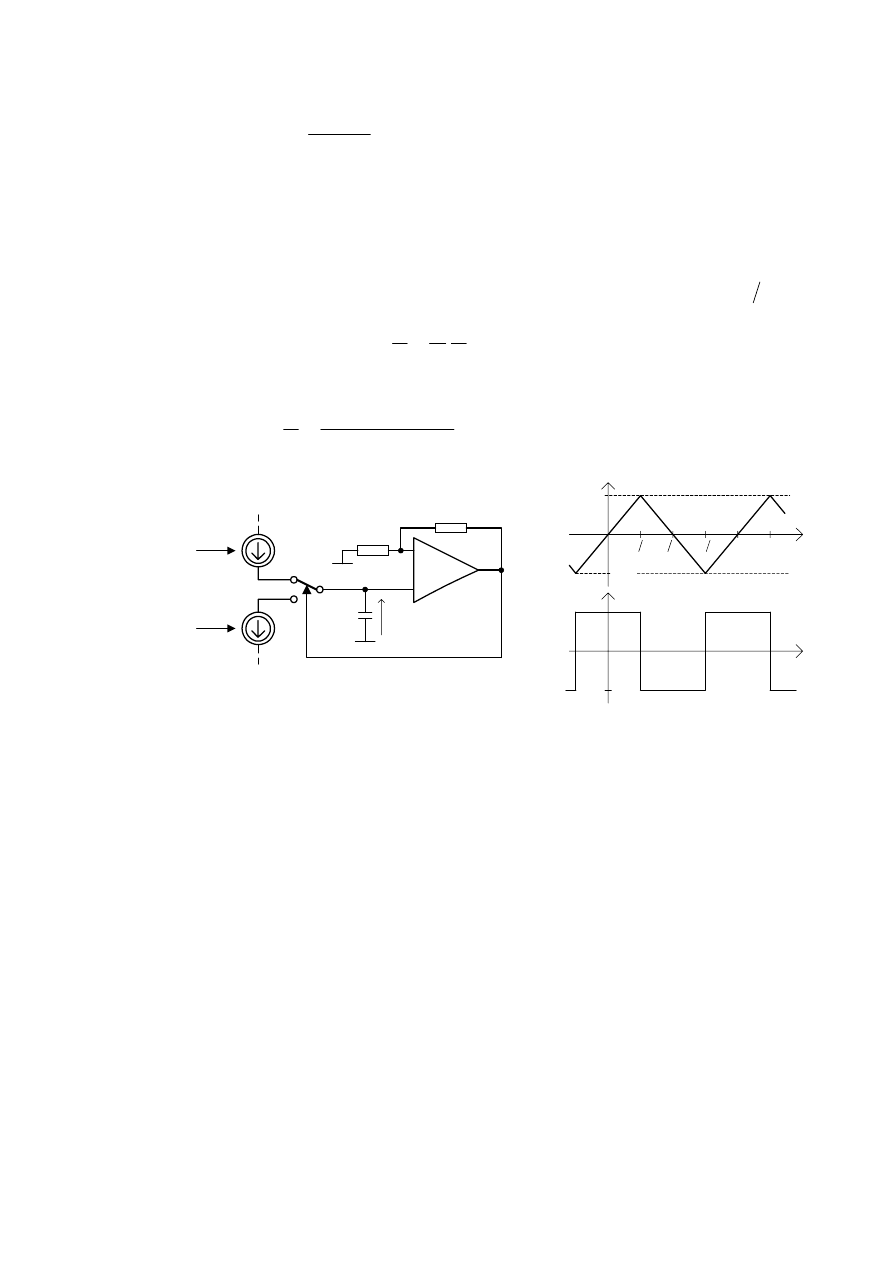
6FKHPDW LGHRZ\ XNáDGX ZUD] ] LGHDOL]RZDQ\PL SU]HELHJDPL

F]DVRZ\PL QDSLü Z XNáDG]LH SU]HGVWDZLRQR QD U\VXQNX

0LG]\V]F]\WRZHZDUWRFLQDSLFLDQD NRQGHQVDWRU]H NWyU\ RNUHVRZR

MHVWáDGRZDQ\LUR]áDGRZ\ZDQ\]UHJXORZDQ\FK (UyGHáVWDáRSUGRZ\FK

RNUHORQHVSURJRZ\PLQDSLFLDPLNRPSDUDWRUD]KLVWHUH]

U

R

R

R

U

p

k

1 2

1

1

2

1 2

,

,

=

+

JG]LH U

k 1 2

,

RGSRZLHGQLR PDNV\PDOQH L PLQLPDOQH QDSL FLH QD

Z\MFLXNRPSDUDWRUD

&]VWRWOLZRü JHQHURZDQHJR SU]HELHJX PR*HP\ Z\]QDF]\ü ]

ZDUXQNX *H NRQGHQVDWRU & SU]HáDGRZ\ZDQ\ MHVW VWDá\P SU GHP , RG

SURJRZHMZDUWRFLQDSLFLD

U

P1

GR

U

P 2

ZFLJXSRáRZ\RNUHVX

T 2

U

U

tg

T

I

C

T

P

P

1

2

2

2

−

=

=

α

6NG

(

)

f

T

I

C U

U

P

P

= =

−

1

2

1

2

&

5

1

5

2

+

−

NRPS

X

1

2

X

5(*

X

5(*

X

&

8

32

8

31

X

&

8

.1

8

.2

X

7 4 7 2

3

4

7

7

W

W

5\V9&2W\SXLQWHJUDWRUSU]HU]XWQLN

-DN ZLGDü F]VWRWOLZRü GUJD MHVW OLQLRZ IXQNFM SUGX ,

=DSHZQLDMFOLQLRZHX]DOH*QLHQLHSUGX,RGQDSLFLDVWHUXMFHJR

u

REG

RWU]\PXMHP\OLQLRZFKDUDNWHU\VW\NSU]HVWUDMDQLDJHQHUDWRUD

E 9&2 W\SX PXOWLZLEUDWRU ] SRMHPQRFLRZ\P VSU]*HQLHP

HPLWHURZ\PXNáDG%RZHVD*UHEHQH¶D

0XOWLZLEUDWRU\ ] SRMHPQRFLRZ\P VSU]*HQLHP HPLWHURZ\P

ZUD]]LFKOLF]Q\PLPRG\ILNDFMDPLXNáDGRZ\PLSR]ZDODMQDJHQHUDFM

SU]HELHJyZ Z V]HURNLP ]DNUHVLH F]VWRWOLZRFL GR NLONXVHW 0+] D

QDZHWGR*+]8NáDG\WHVQDMEDUG]LHMSRSXODUQ\PLUR]ZL]DQLDPL

JHQHUDWRUyZ9&2ZVFDORQ\FKSWODFKID]RZ\FK

1D U\VD SU]HGVWDZLRQR VFKHPDW LGHRZ\ PXOWLZLEUDWRUD ]

SRMHPQRFLRZ\P VSU]*HQLHP HPLWHURZ\P Z NWyU\P ]DVWRVRZDQR

GRGDWNRZHVSU]*HQLHNU]\*RZHNROHNWRUyZLED]WUDQ]\VWRUyZZFHOX

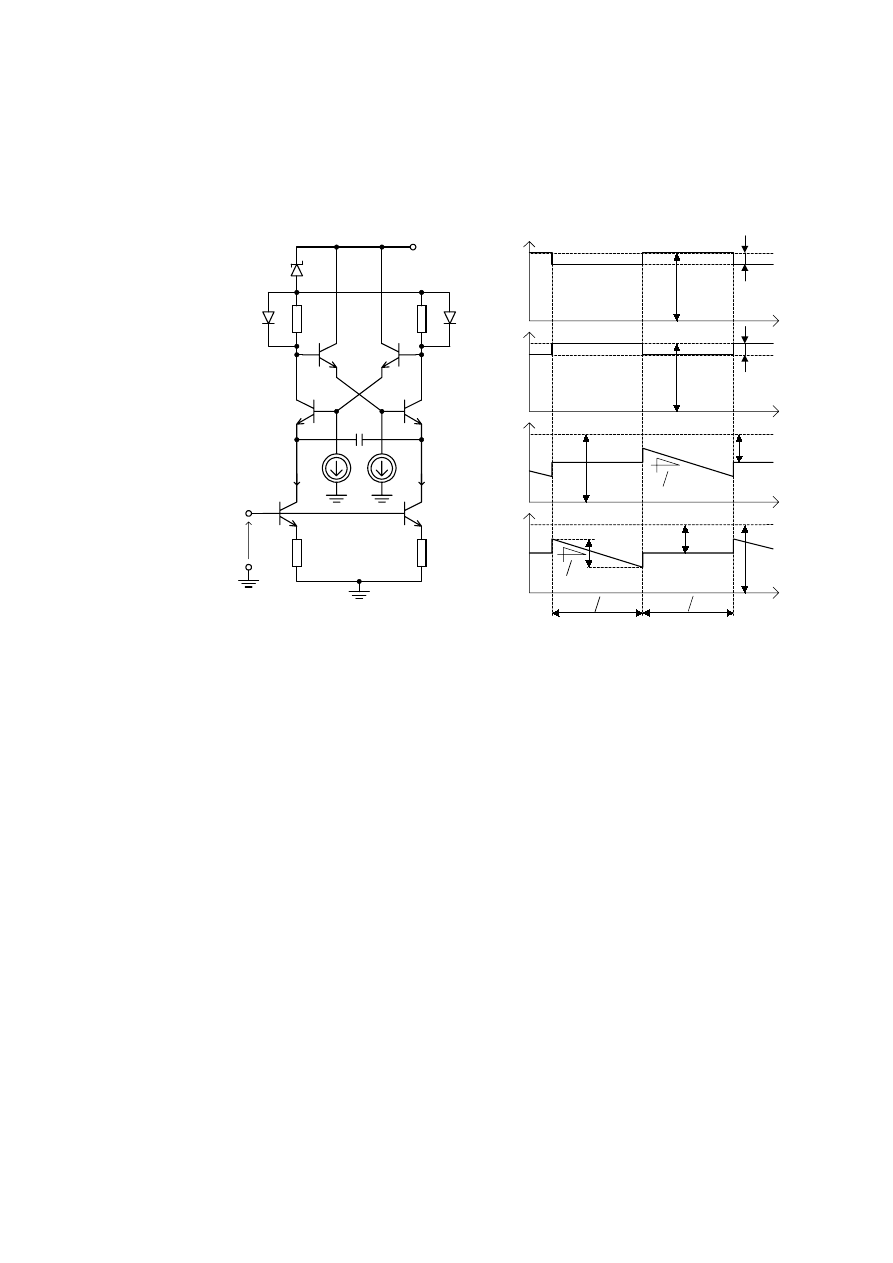
SU]\VSLHV]HQLDSURFHVXSU]HU]XWXZXNáDG]LH

6SU]*HQLH NU]\*RZH UHDOL]RZDQH MHVW ]D SRUHGQLFWZHP

ZWyUQLNyZ ] WUDQ]\VWRUDPL 7

7

]DVLODQ\FK ] RGG]LHOQ\FK (UyGHá

SUGRZ\FK

I

E

X

&1

5

(

X

5(*

T

6

T

5

5

(

,

(

,

(

T

1

T

3

T

4

T

2

&

5

&

'

2

'

1

5

&

'=

8

&&

8

&&1

X

&2

X

( 2

X

(1

,

,

X

&2

X

( 2

X

(1

X

&1

7 2

7 2

2

8

%(3

2

8

%(3

a

, &

, &

2

8

%(3

8

&&1

8

&&1

W

W

W

W

8

&&1

8

&&1

8

)

8

)

a)

b)

5\V*HQHUDWRU9&2Z]PRG\ILNRZDQ\PXNáDG]LH%RZHVDDVFKHPDWLGHRZ\

ELGHDOL]RZDQHSU]HELHJLF]DVRZHQDSLüZXNáDG]LH

7UDQ]\VWRU\ 7

7

]QDMGXM VL QD SU]HPLDQ Z VWDQLH RGFLFLD OXE

SU]HZRG]HQLD ZREHF F]HJR SUG , MHGQHJR ]H (UyGHá SUGRZ\FK Z

REZRGDFKHPLWHUyZW\FKWUDQ]\VWRUyZSU]HSá\ZDSU]H]NRQGHQVDWRU&

UD] Z MHGQ\P UD] Z GUXJLP NLHUXQNX Z\ZRáXMF QD QLP SU]HELHJ

QDSLFLDRNV]WDáFLHWUyMNWQ\P7UDQ]\VWRU\7

7

RQDSLFLX

u

REG

QD

ED]DFK SHáQL URO (UyGHá SUGRZ\FK Z REZRGDFK HPLWHUyZ 7

7

R

ZDUWRFLDFK SUGX , OLQLRZR X]DOH*QLRQ\FK RG QDSLFLD VWHUXMFHJR

u

REG

'LRG\ '

'

WUDQ]\VWRU\ Z SRáF]HQLX GLRGRZ\P RJUDQLF]DM

QLHSR*GDQH]PLDQ\DPSOLWXG\QDSLüQDNROHNWRUDFKWUDQ]\VWRUyZ7

7

RUD]XVWDODMSR]LRP\QDSLüSU]\NWyU\FKQDVWSXMH]DáF]HQLHW\FK

WUDQ]\VWRUyZ1DU\VESU]HGVWDZLRQRSU]HELHJLF]DVRZHQDSLüZ

XNáDG]LH

$QDOL] SUDF\ XNáDGX UR]SRF]QLHP\ RG PRPHQWX Z NWyU\P 7

MHVW ]DWNDQ\ D 7

SU]HZRG]L VXP SUGyZ

2I

:WHG\ QDSLFLH QD

NROHNWRU]H 7

MHVW PQLHMV]H RG QDSLFLD ]DVLODMFHJR

U

CC1

R QDSLFLH

GLRG\ SU]HZRG]FHM

U

F

QDWRPLDVW QDSLFLH QD MHJR HPLWHU]H MHVW

PQLHMV]H RG

U

CC1

R

2

2

U

U

BEP

F

≈

SU]\ SRPLQLFLX EDUG]R PDáHJR

VSDGNXQDSLFLDQDUH]\VWDQFML

5

&

RGSUGXED]\

I

B 4

WUDQ]\VWRUD7

:VNXWHNSU]HáDGRZ\ZDQLDNRQGHQVDWRUD&SRWHQFMDáHPLWHUDWUDQ]\VWRUD

7

REQL*DVL]SUGNRFL

I C

ZVNXWHNF]HJRQDVWSXMHMHJRRGHWNDQLH

Z FKZLOL RVLJQLFLD SR]LRPX

u

U

U

U

C

BEP

CC

BEP

1

1

2

3

−

≈

−

2GHWNDQLH

WUDQ]\VWRUD 7

Z\ZRáXMH UHJHQHUDF\MQ\ SU]HU]XW Z F]DVLH NWyUHJR

WUDQ]\VWRU 7

XOHJD ]DWNDQLX D VXP SUGyZ

2I

SU]HZRG]L WUDQ]\VWRU

7

6NRNRZ\ ]DQLN SUGX NROHNWRUD 7

Z\ZRáXMH GRGDWQL VNRN

QDSLFLDRZDUWRü

U

U

F

BEP

≈

QDNROHNWRU]HNWyU\SU]HQRVLVLSU]H]

ZWyUQLN 7

L SRZRGXMH VNRNRZ\ SU]\URVW QDSLFLD HPLWHUD WUDQ]\VWRUD

7

D SU]H] NRQGHQVDWRU & UyZQLH* HPLWHUD WUDQ]\VWRUD 7

6NRNRZD

]PLDQD SRWHQFMDáX HPLWHUD 7

GR ZDUWRFL

U

U

CC

BEP

1

2

−

MHVW

XWU]\P\ZDQDDZVNXWHNSU]HáDGRZ\ZDQLDNRQGHQVDWRUD&]DF]\QDVL

REQL*DüSRWHQFMDáHPLWHUDWUDQ]\VWRUD7

0LG]\V]F]\WRZDZDUWRüQDSLFLDWUyMNWQHJRQDNRQGHQVDWRU]H

Z\QRVL

2 U

BEP

: FLJX SRáRZ\ RNUHVX GUJD PXOWLZLEUDWRUD

NRQGHQVDWRUáDGXMHVL]SUGNRFL

I C

DQDSLFLHQDQLP]PLHQLDVL

R ZDUWRü PLG]\V]F]\WRZ

2 U

BEP

6WG F]VWRWOLZRü L RNUHV GUJD

Z\QRV]

f

T

I

U

C

BEP

= =

1

4

2SLVDQ\ XNáDG XPR*OLZLD JHQHUDFM SU]HELHJX SURVWRNWQHJR R

F]VWRWOLZRFL GR 0+] G]LNL SUDF\ WUDQ]\VWRUyZ Z REV]DU]H

DNW\ZQ\PEH]ZFKRG]HQLDZVWDQQDV\FHQLD1DSLFLHZ\MFLRZHMHVW

SU]HELHJLHP SURVWRNWQ\P R DPSOLWXG]LH

U

BE

SU]\OHJDMF\P GR

QDSLFLD

U

CC1

.

&]VWRWOLZRü GUJD JHQHUDWRUD MHVW ]DOH*QD RG WHPSHUDWXU\

SRSU]H]WHUPLF]Q]DOH*QRüQDSLFLD

(

)

8

G8

G7

%(

%(

α

≈ −

P9 &

R

1DSRGVWDZLH]DOH*QRFLRWU]\PXMHP\

ω

ω

α

α

G

G7

8

G8

G7

%(3

%(3

= −

=

=

=

=

P9 &

P9

&

SSP &

R

R

R

:XNáDG]LHPR*QDX]\VNDüFDáNRZLWNRPSHQVDFMWHUPLF]Q\FK]PLDQ

SXOVDFML URGNRZHM SRSU]H] X]DOH*QLHQLH SUGX (UyGHá 7

7

RG

WHPSHUDWXU\&KDUDNWHU\VW\NDSU]HVWUDMDQLDPR*HE\üOLQLRZDZ]DNUHVLH

GHNDG

1D LGHQW\F]QHM ]DVDG]LH V EXGRZDQH XNáDG\ 9&2 ] WUDQ]\VWRUDPL

026]NDQDáHPZ]ERJDFDQ\P

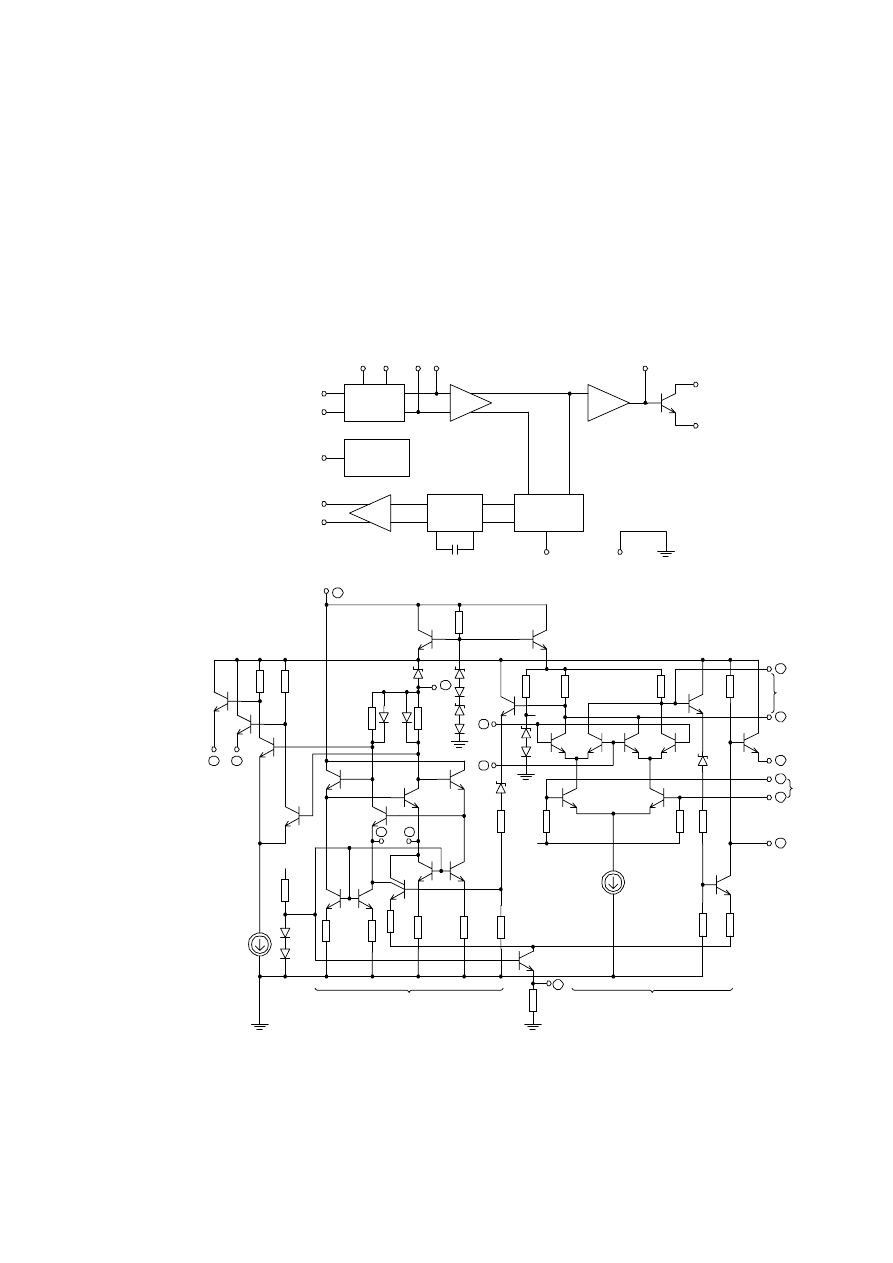
3U]\NáDGUHDOL]DFMLXNáDGXVFDORQHJR3//

1D U\V SU]HGVWDZLRQR VFKHPDW EORNRZ\ L VFKHPDW LGHRZ\

XNáDGX3//W\SX1(ILUP\6LJQHWLFVZ\NRQDQHJRZPRQROLW\F]QHM

WHFKQRORJLL ELSRODUQHM >@ 6FKHPDW EORNRZ\ SU]HGVWDZLRQ\ QD

U\VD Uy*QL VL RG UR]ZD*DQHJR ZF]HQLHM QD U\V W\P *H SWOD

]DZLHUD GRGDWNRZ\ Z]PDFQLDF] R Z]PRFQLHQLX $ G]LNL F]HPX

FDáNRZLWHZ]PRFQLHQLHSWOLZ\QRVL

K

k k A

D

G

=

.

T

1

T

2

T

3

:\MFLH

9&2

4

3

T

4

T

11

T

14

T

13

T

24

T

23

T

12

3RMHPQRü

JHQ 9&2

5

6

&

0

T

20

T

21

T

2 2 B

T

2 2 A

T

29

%LDV

5()

1

1

N

1

N

16

8

&&

7

9

2 5

N

N

N

7

9

8

N

8

N

T

26

T

27

T

5

D

8

D

9

D

10

D

11

D

3

D

2

D

1

D

4

D

12

D

13

D

6

D

7

7 4

N

T

6

T

9

T

8

T

7

2

N

2

N

4

9

5 3

N

14

9

14

9

:H

HNW

ID]\

GHW

2

15

1

N

500

Ω

8 2

N

8 2

N

T

1 0

T

19

T

25

T

17

T

18

D

5

14

13

9

12

11

10

'HHPID]D

)LOWU

9&2

'HWHNWRU ID]\

7

=DNUHV

W M L

12

N

0 75

P$

2 0

P$

:\

:HMFLH

HNWRUD

ID]\

GHW

9&2

2JUDQLF]QLN

$

'HWHNWRU

ID]\

8NáDG\

SRODU\]DFML

:]PDFQLDF]

)LOWU

)'3

( )

:HMFLH

V\JQDáX X W

L

:HMFLH

9&2

:\MFLH

9&2

'HHPID]D

:\MFLH

9

+

&

0

6

5

4

3

1

2

15

11

12 13

14

10

16

9

8

7

=DNUHV

SU]HVWUDMDQLD

a)

b)

N

5\V3WODID]RZDW\SX1(ILUP\6LJQHWLFVDVFKHPDWEORNRZ\

EVFKHPDWLGHRZ\

8NáDG VFDORQ\ VNáDGD VL ] GHWHNWRUD ID]\ Z SRVWDFL PRGXODWRUD

]UyZQRZD*RQHJR VNRPSHQVRZDQHJR WHUPLF]QLH JHQHUDWRUD 9&2 W\SX

PXOWLZLEUDWRU ] SRMHPQRFLRZ\P VSU]*HQLHP HPLWHURZ\P XNáDG

%RZHVD*UHEHQH¶DZ]PDFQLDF]DLGRáF]RQHJR]HZQWU]QLHILOWUX

8NáDG ]DVLODQ\ MHVW SRMHG\QF]\P QDSLFLHP

U

CC

SU]\ F]\P

RGG]LHOQH QL*V]H QDSLFLD ]DVLODMFH JHQHUDWRU 9&2 L GHWHNWRU ID]\

Z\WZDU]DQH V ZHZQWU]QLH SU]\ SRPRF\ WUDQ]\VWRUyZ 7

7

L

WHUPLF]QLH VNRPSHQVRZDQ\FK QDSLü RGQLHVLHQLD ]UHDOL]RZDQ\FK QD

GLRGDFK=HQHUDLWUDQ]\VWRUDFKZSRáF]HQLXGLRGRZ\P

%D]\ WUDQ]\VWRUyZ 7

7

GHWHNWRUD ID]\ V VSRODU\]RZDQH

ZHZQWU]QLH QDSLFLHP VWDá\P 9 GODWHJR V\JQDá ZHMFLRZ\

( )

u t

i

QDOH*\ GRáF]\ü SRSU]H] ]HZQWU]QH NRQGHQVDWRU\ VSU]JDMFH :

XNáDG]LHQLHPDVWDáHJRSRáF]HQLDJHQHUDWRUD9&2]GHWHNWRUHPID]\

3RáF]HQLH WR PR*H E\ü ]UHDOL]RZDQH ]HZQWU]QLH DOER SRSU]H]

EH]SRUHGQLHSRáF]HQLHZ\MüZWyUQLNRZ\FKJHQHUDWRUD9&2Z\MFLD

]ZHMFLDPLGHWHNWRUDID]\ZHMFLHDOER]DSRUHGQLFWZHP

GRGDWNRZHJR]HZQWU]QHJRG]LHOQLNDF]VWRWOLZRFLZFHOXSRV]HU]HQLD

]DNUHVX F]VWRWOLZRFLRZHJR JHQHUDWRUD 9&2 7UDQ]\VWRU\ 7

7

]DSHZQLDM QLVNRLPSHGDQF\MQH Z\MFLH Uy*QLFRZH JHQHUDWRUD 9&2

*HQHUDWRU9&2]UHDOL]RZDQ\QDWUDQ]\VWRUDFK7

7

VWHURZDQ\MHVW

] Z\MFLD Uy*QLFRZHJR GHWHNWRUD ID]\ SRSU]H] ZWyUQLNL HPLWHURZH ]

WUDQ]\VWRUDPL7

7

LZ]PDFQLDF]Uy*QLFRZ\]WUDQ]\VWRUDPL7

7

:]PDFQLDF]Uy*QLFRZ\7

7

SHáQLUROSU]HWZRUQLNDQDSLFLHSUG

ERZLHP SRáRZD SUGX Z\MFLRZHJR WUDQ]\VWRUD 7

R SRGZyMQ\P

NROHNWRU]HMHVW]DZV]HF]FLSUGXáDGRZDQLDSRMHPQRFLHPLWHURZHM

C

0

JHQHUDWRUD 9&2 : F]DVLH JG\ SU]HZRG]L WUDQ]\VWRU 7

NRQGHQVDWRU

C

0

MHVW áDGRZDQ\ SUGHP (UyGáD VWDáRSUGRZHJR ]

WUDQ]\VWRUHP7

LSUGHPNROHNWRUDWUDQ]\VWRUD7

%

QDWRPLDVWZF]DVLH

SU]HZRG]HQLD WUDQ]\VWRUD 7

SUG áDGRZDQLD MHVW VXP SUGX (UyGáD

VWDáRSUGRZHJR ] WUDQ]\VWRUHP 7

L SUGX Z\MFLRZHJR WUDQ]\VWRUD

7

$

&]VWRWOLZRüZáDVQDJHQHUDWRUD9&2MHVW]PLHQLDQD]DSRPRF

SRMHPQRFL

C

0

ZJUDQLFDFKRGNLONX+]GR0+]:FHOXSRND]DQLD

SRáF]H DSOLNDF\MQ\FK QD U\V SU]HGVWDZLRQR VFKHPDW

GHPRGXODWRUD)0]XNáDGHP1(

1DZ\MFLXGHPRGXODWRUD]DVWRVRZDQRUyZQLH*ILOWUGHHPID]\

&

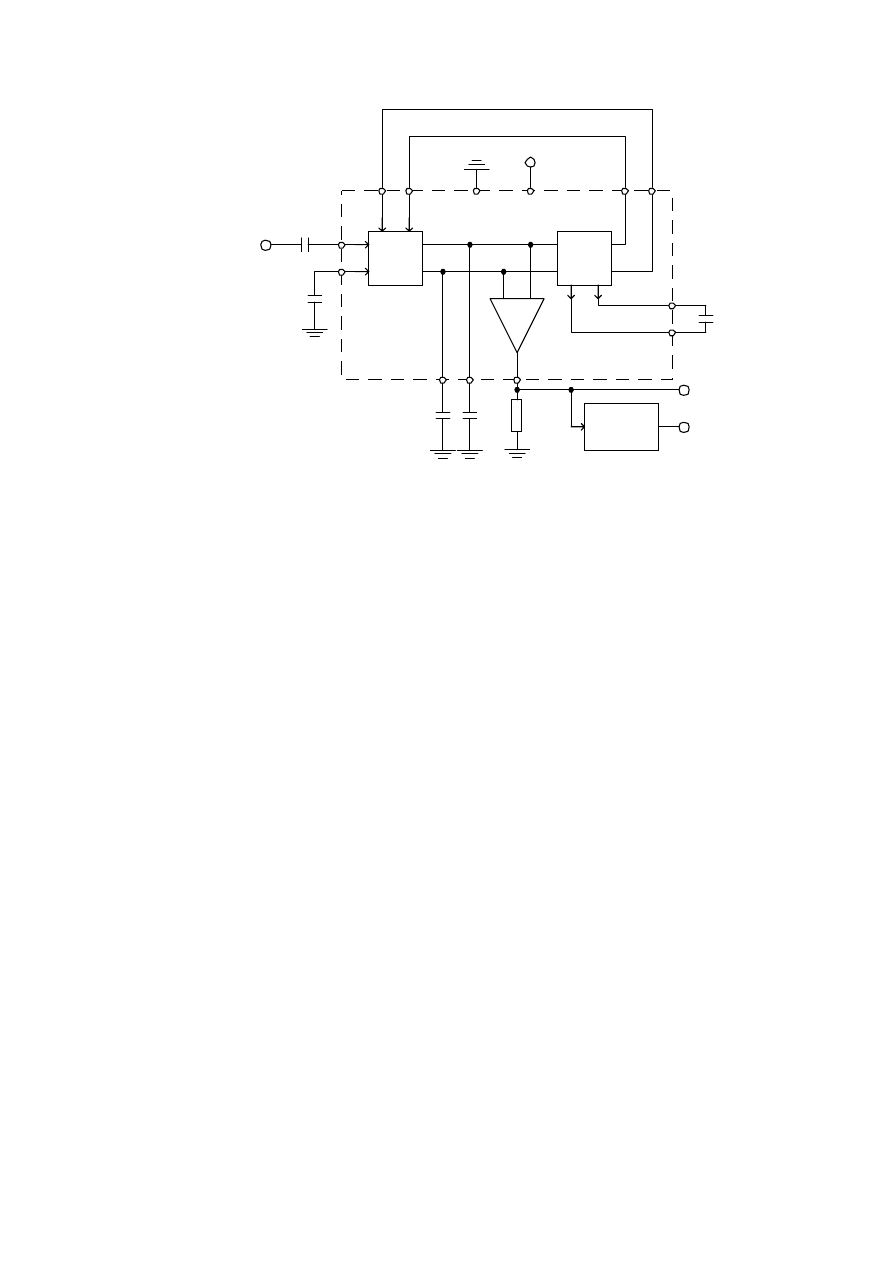
0

1 2

9&2

')

+

−

1 3

1 5

1 6

8

2

4

3

+

8

9

&&

25

S)

1

Q)

1

Q)

15

N

Ω

)LOWU

GHHPID]\

:<2

:<1

5

6

9

1 5

1 4

10

Q)

S)

N E 5 6 2

I

L

5\V6FKHPDWGHPRGXODWRUD)0]XNáDGHP1(ILUP\6LJQHWLFV