
Akademia Górniczo-Hutnicza im. Stanisława Staszica
w Krakowie
Wydział Inżynierii Mechanicznej i Robotyki
Podstawy Konstrukcji Maszyn 2
Projekt nr 3 – Sprzęgło
Wykonał:
Tomasz Siudak
Grupa 5
1

Temat:
Skonstruować wielopłytkowe sprzęgło cierne dla następujących danych:
2
W
Moc przenoszona
, obroty
25
N
k
=
300
min
obr
n
=
, współczynnik przeciążenia
1,3
k
=

Dane Obliczenia Wynik
1. Obliczenia wstępne
1.1 Prędkość kątowa:
2
300
31,42
60
30
30
n
n
π
π
π
ω
⋅
=
=
=
=
1
s
−
1.2 Moment nominalny
[ ]
9550
N
N
N
M
Nm
n
=
[ ]
25
9550
300
N
M
Nm
=
795,83
N
M
Nm
=
1.3 Moment obliczeniowy
W ogólnym przypadku moment obliczeniowy dla sprzęgieł ciernych
wyznaczamy z zależności:
O
N
M
K M
= ⋅
gdzie:
K - współczynnik przeciążeniowy, i dla sprzęgieł ciernych jest on
równy:
m
v
K
k
k
β
=
⋅
β
- współczynnik zależny od rodzaju maszyny
m
k - współczynnik zależny od liczby włączeń sprzęgła
(
)
1 0,002
1
m
g
k
m m
= −
−
<
r
m
- liczba włączeń sprzęgła na godzinę
gr
m - graniczna liczba włączeń sprzęgła na godzinę (
50 100
÷
)
v
k - współczynnik zależny od prędkości poślizgu
Ponieważ z tematu zadania mamy już dany współczynnik
przeciążeniowy , zatem można od razu policzyć moment
obliczeniowy:
K
1,3 795,83
o
M
Nm
=
⋅
1034,58
o
M
Nm
=
2. Dobór materiału
Dobieram materiał na wał z zależności na dopuszczalne naprężenia
skręcające. Wstępnie dobieram materiał na wał – stal konstrukcyjną
podwyższonej jakości: C60 (60) – ulepszaną cieplnie.
3. Obliczenia wytrzymałościowe
3.1 Naprężenia dopuszczalne:
Wał będzie obustronnie skręcany, zatem dla w/w materiału
wytrzymałość zmęczeniowa na obustronnie zmienne obciążenie
skręcające wynosi:
215
so
Z
MPa
=
(wg badań). Ponieważ nie znam
przebiegu obciążenia oraz dokładnego ukształtowania wału przyjmuje
stosunkowo wysoki współczynnik bezpieczeństwa: 3,5
z
x
=
Zatem dopuszczalne naprężenia przy skręcaniu obustronnie zmiennym
wynoszą:
215
61,43
3,5
so
so
so
z
Z
k
k
x
=
⇒
=
=
3
MPa
3.2 Obliczanie średnicy wału:
Naprężenia skręcające:

s
s
so
s
M
k
W
τ
=
≤
gdzie:
s
M - moment skręcający, w tym przypadku
s
o
M
M
=
s
W - wskaźnik wytrzymałościowy przekroju na skręcanie
Dla przekroju kołowego:
3
16
s
d
W
π
⋅
=
Zatem:
3
3
16
16
s
s
so
so
M
M
k
d
d
k
π
π
⋅
⋅
≤
⇒ ≥
⋅
⋅
3
6
1034,58
16
0,044
61,43 10
Nm
d
d
Pa
π
⋅
≥
⇒ ≥
⋅
⋅
m
m
m
44,1
d
m
≥
Przyjmuje średnice wału
ze względu na osłabienie przekroju
ze względu na występowanie wielowypustów, oraz wytrzymałość
zmęczeniową.
50
d
m
=
4. Dobór materiału na płytki cierne
Płytki cierne zrobione będą z żeliwa. Zakładam również, że będą
pracować na sucho. Dla pary ciernej żeliwo – stal, bez smarowania
orientacyjne wartości parametrów pracy są następujące:
Współczynnik tarcia:
0,15 0,2
μ
=
÷
- przyjmuje
0,18
μ
=
Dopuszczalna (krótkotrwała) temperatura pracy:
300
dop
t
C
=
D
Dopuszczalna (długotrwała) temperatura pracy:
200
dop
t
C
=
D
Naciski dopuszczalne:
0,8 1,4
dop
p
MPa
=
÷
- przyjmuje
1,1
dop
p
MPa
=
( )
2 4
dop
MN
pv
m s
= ÷
⋅
5. Obliczanie podstawowych wymiarów sprzęgła
4.1 Średnia średnica tarcia
Wymiary tarcz często są ustalane w zależności od wymagań
konstrukcyjnych (np. od wymiarów gabarytowych maszyn).
Orientacyjne wartości
sr
D można przyjmować w zależności od średnicy
wału, dla sprzęgieł wielopłytkowych:
(
)
2 4
sr
D
=
÷ d
. Zakładam, że
średnia średnica tarcia będzie trzy razy większa od przyjętej średnicy
wału, zatem:
3
sr
D
d
= ⋅
3 50
sr
D
mm
= ⋅
150
sr
D
mm
=
4.2 Szerokość czynna płytek
W celu równomiernego rozkładu nacisków na powierzchniach ciernych
konstrukcja sprzęgła powinna być sztywna, zaleca się, zatem dla
sprzęgieł, wielopłytkowych, aby
(
)
0,1 0,25
sr
b
D
≈
÷
Przyjmuje 0,18
sr
b
D
=
zatem:
0,18 150
b
mm
=
⋅
27
b
mm
=
4.2 Średnica zewnętrzna i wewnętrzna
Średnica zewnętrzna wynosi:
4

5
m
150 27
z
sr
z
D
D
b
D
=
+ ⇒
=
+
177
z
D
m
=
Średnica wewnętrzna wynosi:
150 27
w
sr
w
D
D
b
D
=
− ⇒
=
−
123
w
D
mm
=
6. Obliczenia powierzchni ciernych
6.1 Obliczanie liczby powierzchni ciernych
Liczbę powierzchni ciernych oblicza się z zależności:
2
2
o
dop
sr
z
M
z
p
b D
k
π μ
=
⋅ ⋅
⋅ ⋅
⋅
, gdzie:
z
k - współczynnik zmniejszenia nacisku w wyniku tarcia płytek w
rowkach wpustowych – zależny od liczby płytek w sprzęgle.
Dla sprzęgieł suchych
1
z
k
=
(
)
2
6
3
3
2 1034,58
0,18 1,1 10
27 10
150 10
1
Nm
z
Pa
m
m
π
−
−
⋅
=
⋅
⋅ ⋅
⋅
⋅
⋅
⋅
⋅
2069,16
377,89
z
=
5,48
z
=
, przyjmuję
6
z
=
6.2 Liczba tarcz ciernych w członie czynnym
1
1
6
1,5
4
4
z
z
z
= ⇒ = =
, czyli:
1
2
z
=
6.3 Liczba tarcz ciernych w członie biernym
2
2
6
1
1
4
4
z
z
z
= + ⇒
= + = 2,5 , czyli:
2
3
z
=
Uwaga powyższe obliczenia liczby tarcz ciernych były przeprowadzone
przy założeniu, że uwzględniamy obydwie powierzchnie cierne dwóch
skrajnych płytek. Przy założeniu że w/w powierzchnie nie biorą udziału
w przenoszeniu momentu obrotowego, wówczas liczba tarcz ciernych w
członie czynnym i członie biernym należy wyliczyć odpowiednio z
zależności:
1
2
z
z
= ,
2
1
2
z
z
= +
6.4 Całkowita liczba tarcz ciernych
Ponieważ moment tarcia w sprzęgle nie jest proporcjonalny do liczby
tarcz, lecz zależy również od tarcia na wypustach tarcz, całkowita liczba
tarcz ciernych w sprzęgle, wielotarczowym nie powinna przekraczać
(
)
25 30
÷
, warunek ten jest spełniony, gdyż:
1
2
5
z
z
+
=
7. Maksymalna siła docisku tarcz
Maksymalną siła docisku tarcz z warunku na dopuszczalne naciski
powierzchniowe (maksymalna siła osiowa włączania sprzęgła) wynosi:
w
dop
P
p
b D
sr
π
≤
⋅ ⋅ ⋅
6
1,1 10
0,027
0,150
w
P
Pa
m
π
≤ ⋅ ⋅
⋅
⋅
m
13,995,8
w
P
N
≤
14
w
P
kN
≤
8. Maksymalny moment tarcia
6
z
Maksymalny moment tarcia przenoszony przez sprzęgło jest równy:
0,5
T
w
sr
M
P
D
z k
μ
=
⋅ ⋅
⋅
⋅ ⋅
3
14 10
0,18 0,5 0,15
6 1
T
M
N
m
= ⋅
⋅
⋅
⋅
⋅ ⋅
1134
T
M
Nm
=
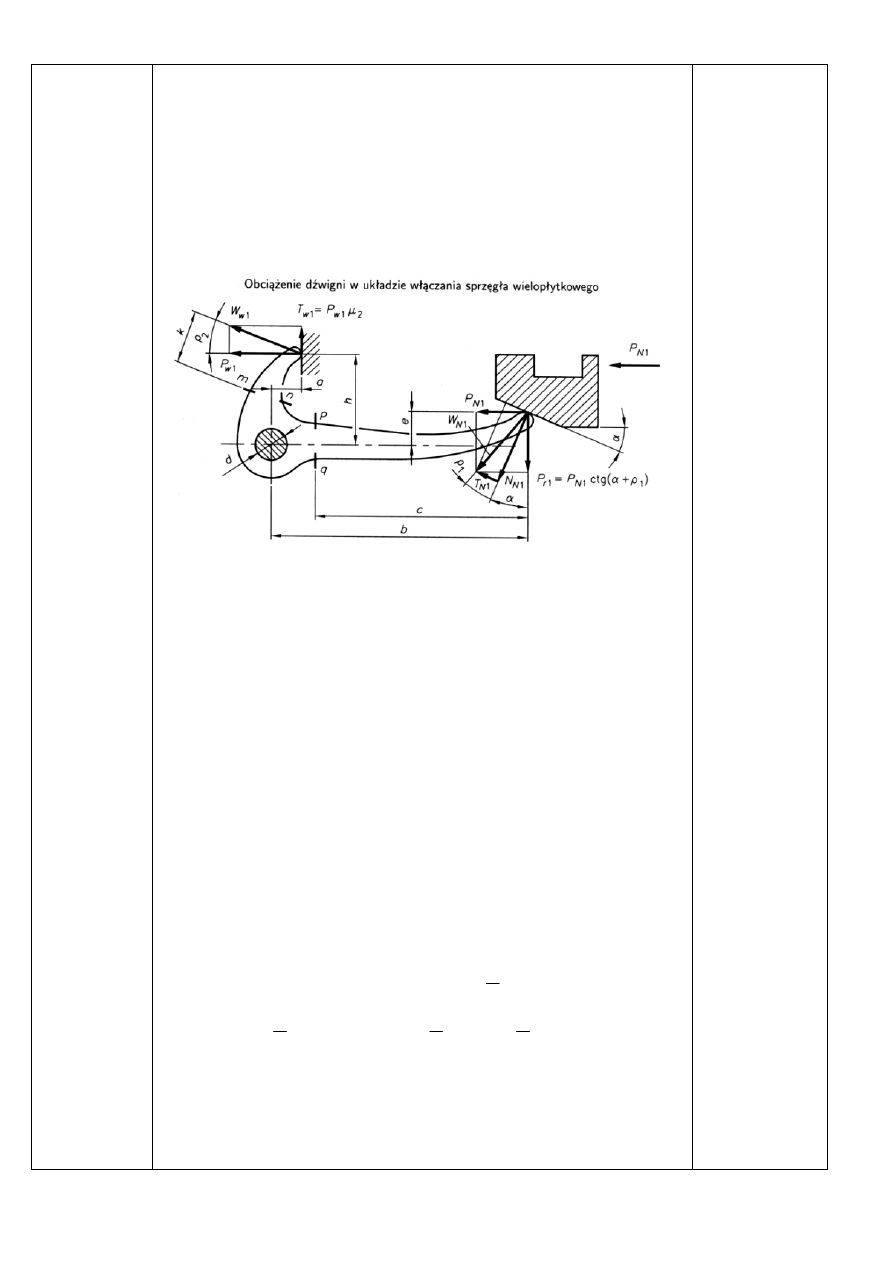
9. Obliczenia układu włączania sprzęgieł wielopłytkowych.
9.1 Założenia konstrukcyjne.
Sprzęgło będzie włączane za pośrednictwem powszechnie znanego
mechanizmu:
Na powierzchniach kontaktu dźwigni z innymi elementami występują
następujące współczynniki tarcia:
- między dźwignią i nasuwą -
1
1
tg
μ
ρ
=
- między dźwignią i płytką dociskającą przenoszącą siłę
-
1
w
P
2
2
tg
μ
ρ
=
- między dźwignią i sworzniem -
3
μ
Zakładam, że wszystkie współczynniki tarcia mają taką samą wartość:
1
2
3
0,08
μ
μ
μ
=
=
=
, oraz kąt
25
α
=
D
- liczba dźwigni – 4
Przyjmuje następujące wymiary dźwigni:
30
a
mm
=
420
b
mm
=
380
c
mm
=
30
d
mm
=
30
e
mm
=
80
h
mm
=
9.2 Obliczenia wymaganej siły włączania dźwigni
Równanie sumy momentów względem osi sworznia dźwigni w chwili
wywierania maksymalnego nacisku (wg rysunku) ma postać:
(
)
(
)
1
1
1
1 3
1
1 2
1 3
1
1
3
1 2 3
2
0
2
2
2
N
N
N
w
w
w
N
w
d
M
P e
P bctg
P
P h
P
a
d
d
d
P
P ctg
P
α ρ
μ
μ
μ
α ρ μ
μ μ
Σ
=
−
+
+
+
+
+
+
−
+
+
=
gdzie:
1
N
P - siła wywierana przez obsługę, przypadająca na jedną dźwignię.
1
w
P - siła docisku płytek wywierana przez pojedynczą dźwignię.
Stąd największa wartość siły, jakiej należy użyć do nasunięcia nasuwy
(siłą wymagana od obsługi do włączenia dźwigni), występuje w chwili,

gdy dźwignie chowają się pod nasuwę, i wynosi:
(
)
(
)
2
3
2
1
1
1
3
1
2
2
2
N
w
d
h
a
P
P
d
d
ctg
b
e
μ
μ
μ
3
α ρ
μ
+
+
+
=
⎛
⎞
+
+
− −
⎜
⎟
⎝
⎠
μ
, gdzie:
1
1
arctg
ρ
μ
=
,
2
arctg
2
ρ
μ
=
zatem ostatecznie:
(
)
(
)
2
3
2
1
1
1
3
1
2
2
2
N
w
d
h
a
P
P
d
d
ctg
arctg
b
e
μ
μ
μ
3
α
μ
μ
+
+
+
=
⎛
⎞
+
+
− −
⎜
⎟
⎝
⎠
μ
Siła włączania wszystkich dźwigni obliczamy ze wzoru:
(
)
(
)
2
3
2
1
3
1
2
2
2
N
w
d
h
a
P
P
d
d
ctg
arctg
b
e
μ
μ
μ
3
α
μ
μ
+
+
+
=
⎛
⎞
+
+
− −
⎜
⎟
⎝
⎠
μ
(
)
(
)
3
80 0,08 30 15 0,08 1 0,08
14 10
(25
4 34'26'') 420 15 0,08
30 15 0,08
N
P
N
ctg
+
⋅
+ ⋅
⋅ +
=
⋅
⋅
+
+ ⋅
−
−
D
D
⋅
3
14 10 (80 2, 4 1, 296)
1,76 421, 2 30 1, 2
N
P
N
⋅
⋅
+
+
=
⋅
−
−
3
14 10 83,696
1171744
741,312 31, 2
710,112
N
P
N
⋅
⋅
=
⇒
−
N
N
1,65
N
P
k
=
Składowe siły przypadającej na jedną dźwignię wynoszą:
1
1,65
4
N
N
P
k
P
n
=
=
N
1
412,5
N
P
N
=
(
)
(
)
1
1
1
412,5
25
0,08
r
N
r
P
P ctg
arctg
P
ctg
arctg
α
μ
=
+
⇒
=
⋅
+
D
1
726,9
r
P
N
=
9.3 Obliczenia wytrzymałościowe
Aby zapewnić wymaganą siłę docisku płytek w czasie pracy sprzęgła,
dźwignia powinna doznać odkształceń sprężystych. Zaleca się, by
ugięcie końca dźwigni było rzędu 5 mm. Przy założeniu takiej
zmienności przekroju dźwigni na jej długości, by miała stałą
wytrzymałość, wzór na ugięcie jej końca ma postać:
3
1
max
3
4
r
d
d
P b
f
Eb h
=
, gdzie:
,
d
d
b h - szerokość i wysokość przekroju dźwigni w punkcie podparcia (w
przekroju p-q według rysunku)
E – moduł sprężystości podłużnej
Przyjmuje, że
2
d
d
b
h
= oraz
max
5
f
mm
=
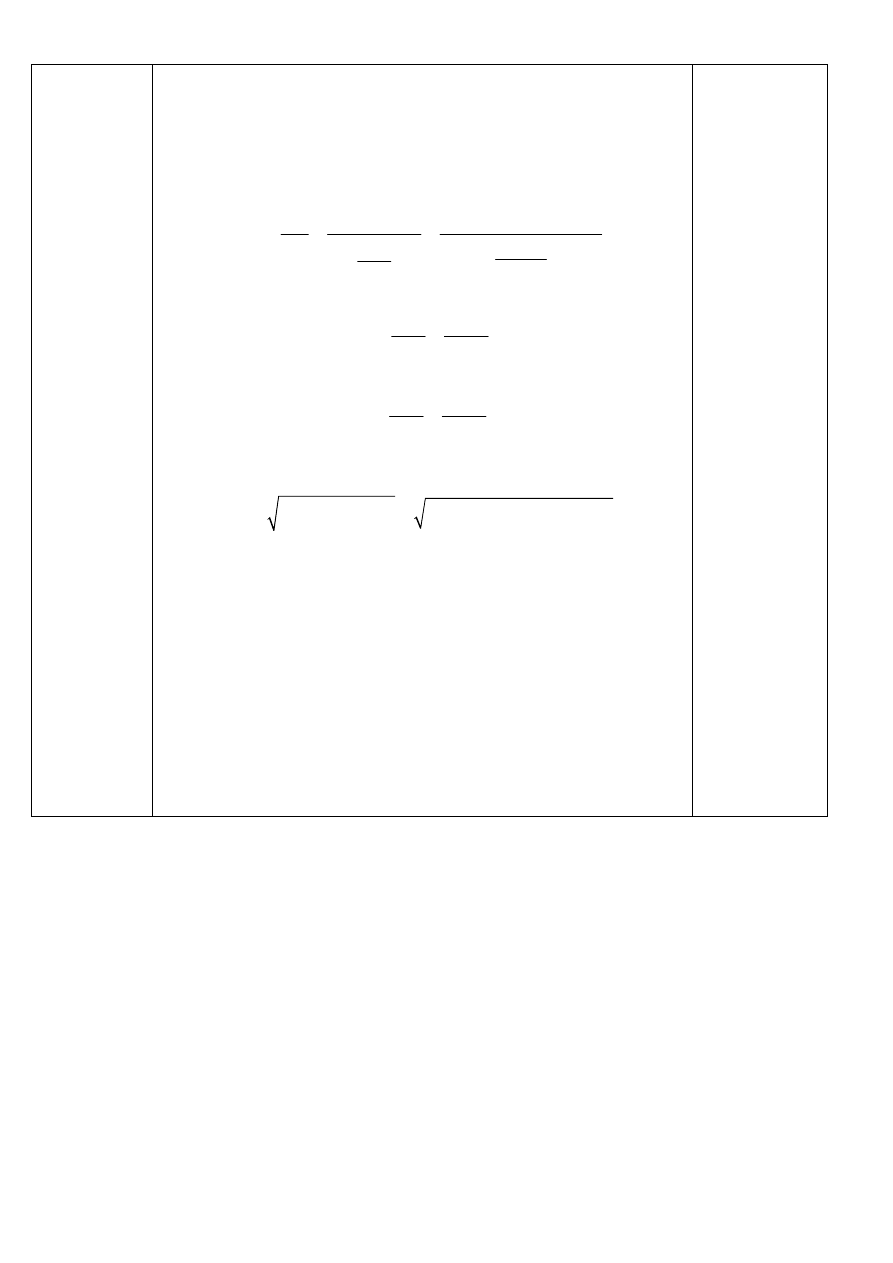
Zatem po przekształceniu w/w wzoru wysokość przekroju dźwigni
wyniesie:
3
3
1
4
4
5
max
4
4 726,9 420
2
2 2,06 10 5
r
d
P b
h
Ef
⋅
⋅
=
=
⋅
⋅
⋅
7
8
m
18
d
h
m
=
Szerokość przekroju wynosi, więc:
2
2 18
d
d
b
h
mm
=
= ⋅
36
d
b
mm
=
Przekrój p-q dźwigni jest zginany, ściskany oraz ścinany. Wartości
poszczególnych naprężeń wynoszą
1
1
2
2
726,9 380 412,5 30
36 18
6
6
g
r
N
g
p
p
x
M
P c
P
e
b h
W
σ
⋅ −
⋅
⋅
−
⋅
=
=
=
⋅
135,72
g
MPa
σ
=
1
412,5
36 18
N
c
p
p
P
b h
σ
=
=
⋅
0,64
c
MPa
σ
=
1
726,9
36 18
r
t
p
p
P
b h
τ
=
=
⋅
1,12
t
MPa
τ
=
Naprężenia zastępcze w przekroju p-q wynoszą:
(
)
(
)
2
2
2
2
3
135,72 0,64
3 1,12
z
g
c
t
σ
σ
σ
τ
=
+
+
=
+
+ ⋅
136,37
z
MPa
σ
=
Na dźwignie będzie zastosowana stal stopowa konstrukcyjna ulepszana
cieplnie: 30G2, dla której granica plastyczności wynosi
540
e
R
MPa
=
Document Outline
Wyszukiwarka
Podobne podstrony:
projekt Sprzeglo Oceloot id 397906
projekt Sprzeglo ver2 Oceloot id 397907
projekt - Sprzęgło ver2 - Oceloot, PKM projekty, PROJEKTY - Oceloot, Projekt VII - Sprzęgło, Projekt
projekt Sprzęgło ver2 Oceloot
PROJEKT sprzęgła
Projekt2-Sprzeglo, sprz-niedzwiecki, Algorytm przeprowadzenia eksperymentu.
sprzeglo, PROJEKT SPRZEGĹA SAMONASTAWNEGO ok, PROJEKT SPRZEGŁA SAMONASTAWNEGO
sprzeglo, PROJEKT SPRZEGĹA SAMONASTAWNEGO ok, PROJEKT SPRZEGŁA SAMONASTAWNEGO
Projekt2 Sprzeglo Sprzeglo id 8 Nieznany
Zakresy-projektów, Semestr V PK, Semestr Zimowy V (2013-2014), Podstawy konstrukcji maszyn, Przykład
Projekt2 Sprzeglo Sprzeglo
Projekt sprzęgła
Projekt sprzegła ciernego3, Sprzegla
SprzegloW972003, PWr, PKM, PKM, Projekt2-Sprzeglo
projekt Sprzęgło kołnierzowe
wymiary-normalne, Semestr V PK, Semestr Zimowy V (2013-2014), Podstawy konstrukcji maszyn, Przykłado
więcej podobnych podstron