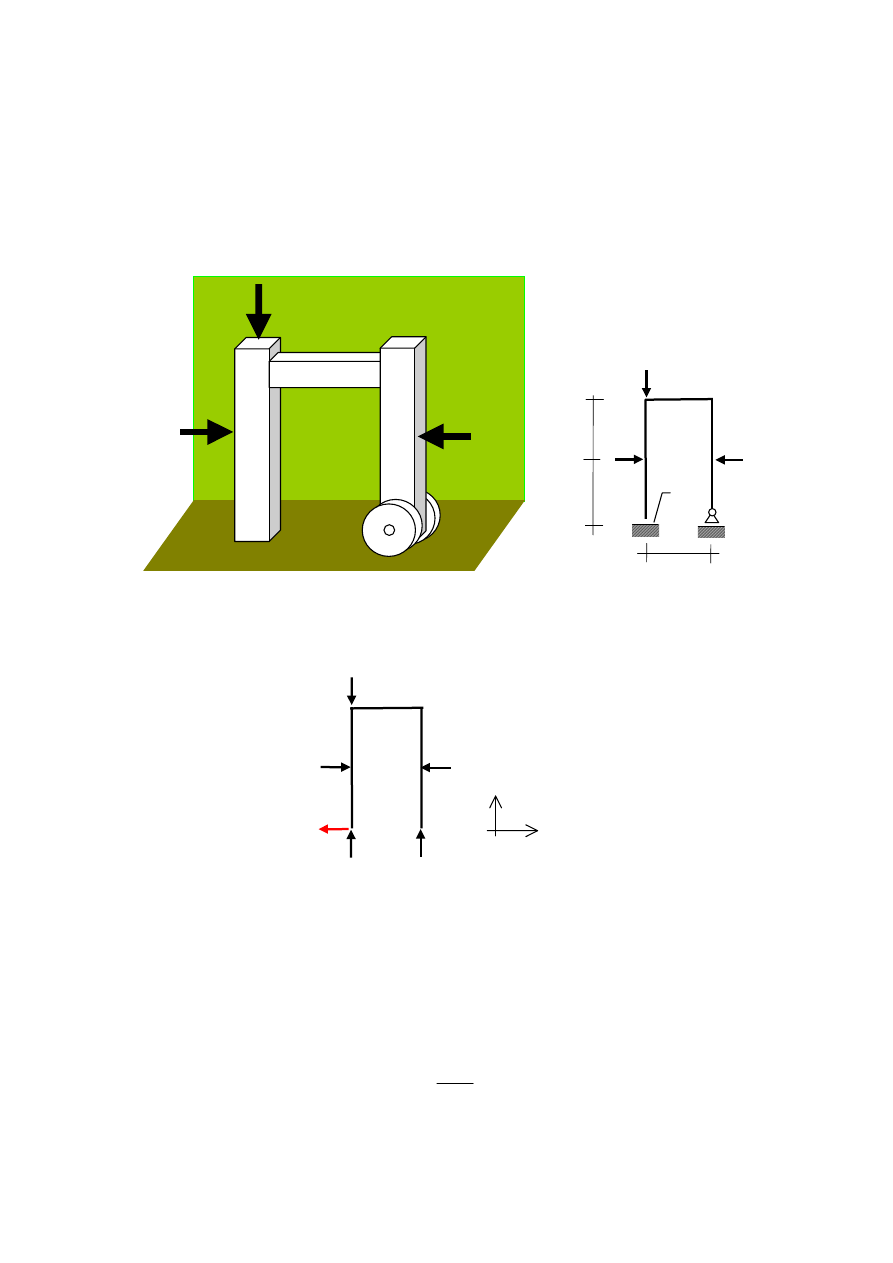
3U]\NáDG5DPDREFL*RQDVLáR

zmiennej

ZDUWRFL

: OHZHM SRGSRU]H SU]HGVWDZLRQHM UDP\ PR*H Z\VWSRZDü WDUFLH :VSyáF]\QQLN WDUFLD

wynosi

µ

5DPDMHVWQLHZD*ND2EFL*HQLHUDP\VWDQRZLSLRQRZDVLáD

P

VWDáDSR]LRPDVLáD

P i zmienna X

:\]QDF]\üZMDNLFKJUDQLFDFKPR*H]PLHQLDü VL ZDUWRü VLá\

X

DE\ XNáDG

SR]RVWDZDáZUyZQRZDG]H

3RQL*HMSU]HGVWDZLRQRU\VXQHNUDP\LMHMVFKHPDWVWDW\F]Q\QDNWyU\PRNUHORQRZ\PLDU\

X

l

l

l

2P

µ

P

A

B

x

2P

P

5R]ZL]DQLH

8NáDGVLáSRXZROQLHQLXRGZL]yZSU]HGVWDZLRQRQDU\VXQNXSRQL*HM

X

T

A

N

A

V

B

2P

P

y

x

6NáDGRZD SR]LRPD UHDNFML Z SRGSRU]H $ MHG\QD UHDNFMD SR]LRPD PXVL UyZQRZD*\ü

REFL*HQLH SR]LRPH -HM ]ZURW EG]LH ]DWHP ]DOH*Hü RG ZDUWRFL VLá\ ; 3RQLHZD* VNáDGRZD

SR]LRPD Z SXQNFLH $ MHVW VLá WDUFLD PXVL VSHáQLDü QLHUyZQRü



T

A

≤

µ

N

A

. Obliczmy z

UyZQDUyZQRZDJLVNáDGRZHUHDNFML7

A

i N

A

:\VWDUF]\]DWHPZ\NRU]\VWDüUyZQDQLD

0

M

i

iB

=

∑

⇒

-N

A

l – P l + 2P l + Xl = 0 i

0

P

i

ix

=

∑

⇒

-T

A

+ P– X

DE\RWU]\PDü

N

A

= P + X, T

A

3;=Dáy*P\*H;

≤

3DZLF7

A

3;MHVWZLHONRFLGRGDWQL

:DUXQHNWDUFLDSU]\MPXMHSRVWDü3;

≤

µ

(P + X), a to prowadzi do warunku:

P

X









+

−

≥

µ

µ

1

1

.

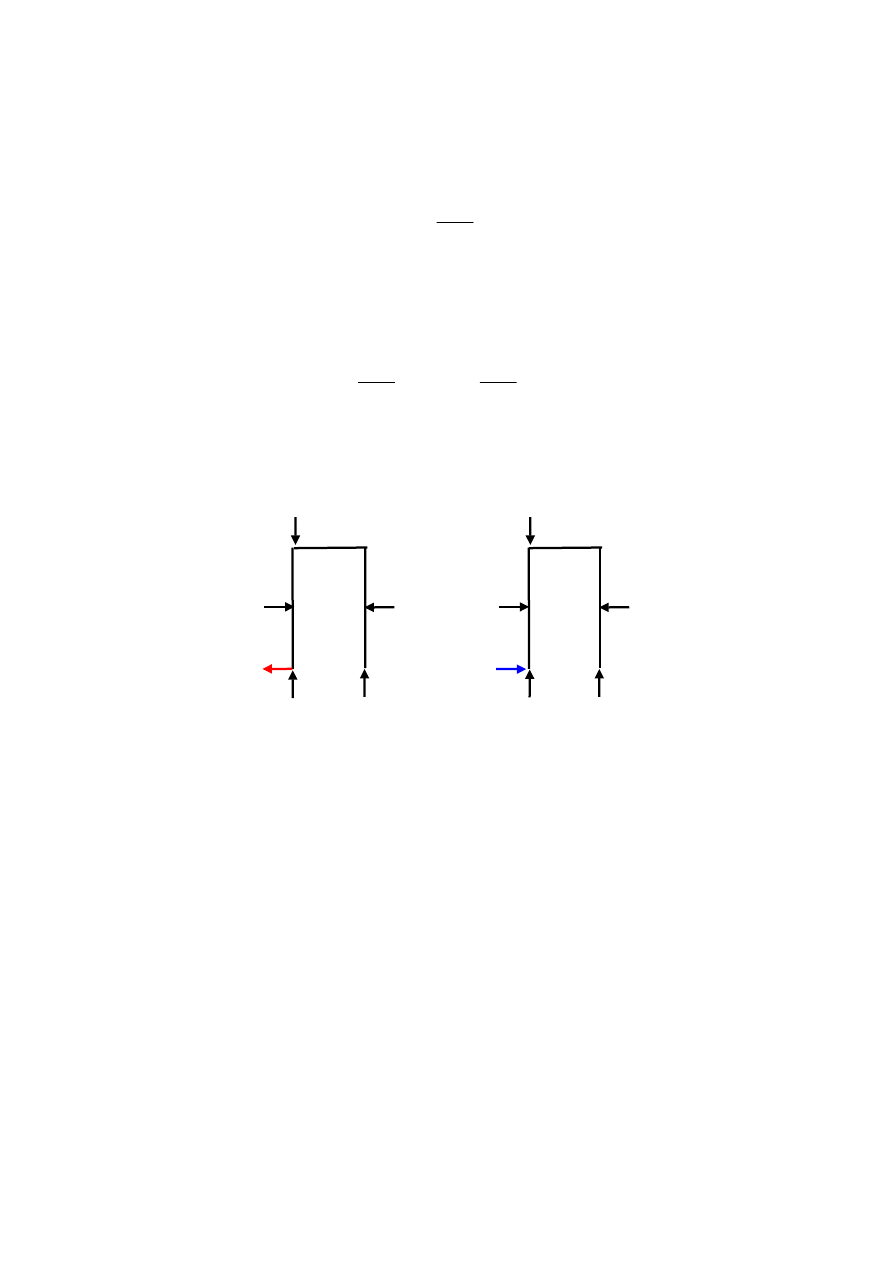
2

5R]ZD*P\ WHUD] SU]\SDGHN RGZURWQ\ JG\ 3

≤

; 3U]\ WDNLP ]DáR*HQLX 7

A

= P- X jest

ZLHONRFL XMHPQ :DUXQHN WDUFLD SU]\MPXMH SRVWDü 7

A

≤

µ

N

A

, a to prowadzi do

warunku: -(P-X)

≤

µ

3; 3RGVWDZLDMF RWU]\PDQH ] ZDUXQNyZ UyZQRZDJL ZLHONRFL

X]\VNXMHP\GUXJLHRJUDQLF]HQLDQDZLHONRü;

P

X









−

+

≤

µ

µ

1

1

.

2VWDWHF]QLH PR*HP\ VWZLHUG]Lü *H XNáDG SR]RVWDQLH Z UyZQRZDG]H JG\ ZDUWRü VLá\

F]\QQHM;]QDMGRZDüVLEG]LHZSU]HG]LDOH

P

X

P









−

+

≤

≤









+

−

µ

µ

µ

µ

1

1

1

1

.

:\NRU]\VWXMF GR REOLF]H SUDZR &RXORPED Z NWyU\P Z\VWSXMH PRGXá VLáD WDUFLD

UR]ZD*\OLP\RE\GZDSU]\SDGNL]ZURWXVLá\WDUFLD]DOH*QHRGVWRVXQNXVLá\;GRVLá\3

5]HF]\ZLVWH]ZURW\VLá\WDUFLDSU]HGVWDZLRQRSRQL*HMQDU\VXQNX

3U]HDQDOL]XMP\ RWU]\PDQH UR]ZL]DQLH GOD NRQNUHWQHM ZDUWRFL ZVSyáF]\QQLND WDUFLD QS

µ

=1/5. Wtedy 2/3P

≤

X

≤

3 :DUWR ]DXZD*\ü *H JUDQLF]Q\P ZDUWRFLRP REFL*HQLD

; 3L; 3RGSRZLDGDMUy*QHZDUWRFLSR]LRPHMUHDNFMLRGSRZLHGQLR3L3

X

T

A

N

A

V

B

2P

P

X

T

A

N

A

V

B

2P

P

Dla przypadku,
gdy

X<P

Dla przypadku,
gdy

X>P