Politechnika Rzeszowska

Rok akademicki 2012/2013

Wydział Budownictwa i Inżynierii Środowiska
Katedra Mechaniki Konstrukcji

METODY OBLICZENIOWE

Projekt nr 1

METODA RÓŻNIC SKOŃCZONYCH

Konsultował:

Wykonał:

mgr inż. Dominika Ziaja

Arkadiusz Dubiel

III BZ, LP-1

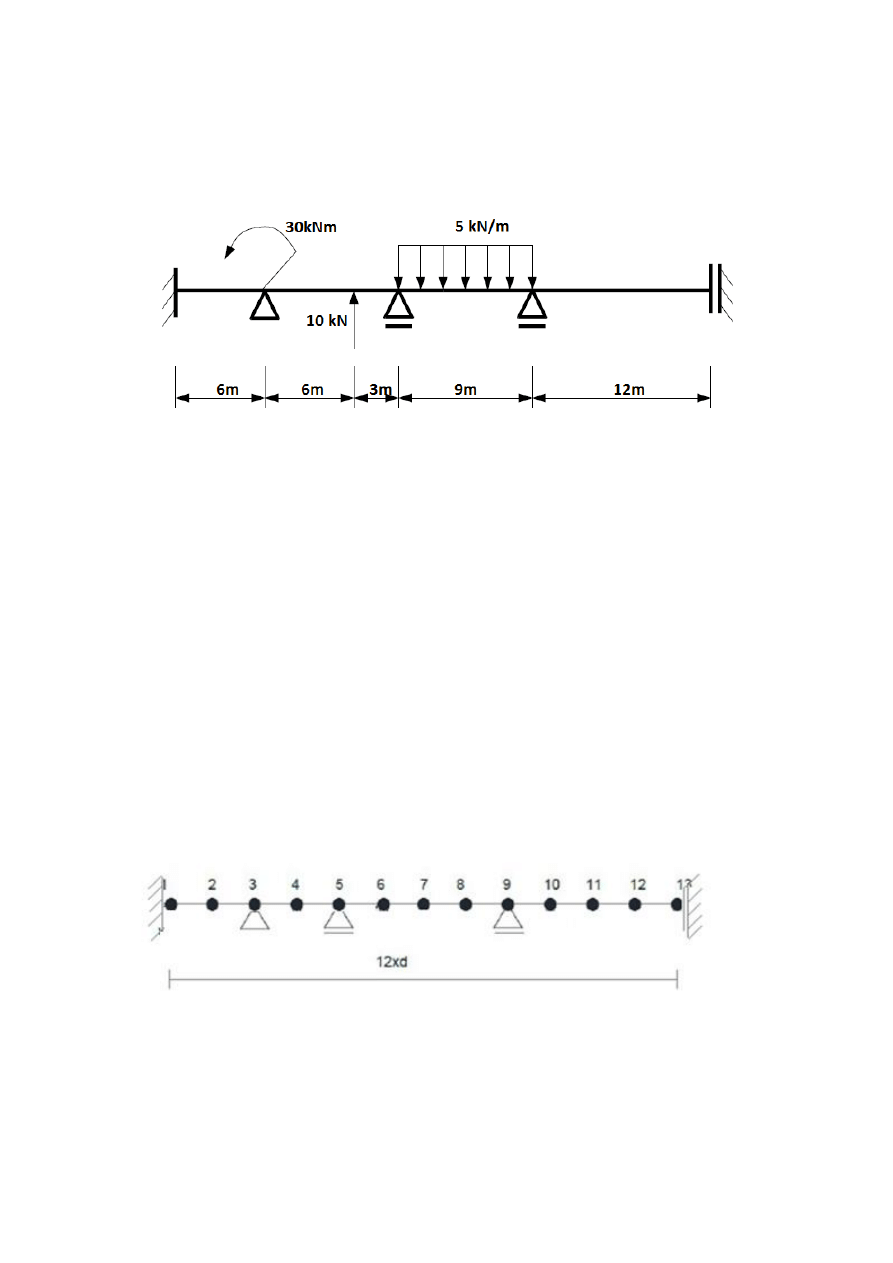
1. Schemat statyczny:

Dane:
q =5/m
P=10kN
M=30kNm
E=30*10^9N/m^2

2. Dyskretyzacja układu:

q=[0; -15000; 0; 15000;10000; -5000; -5000; -5000; -5000; 0;0;0;0;];

d = 3 m

3. Warunki brzegowe:

Dla utwiedzenia z lewej strony

Dla dwóch ostatnich równań:

wiersz 1 0;-4;0
wiersz 2 0;1;0

w

2

= 0,

w

5

= 0,

w

9

= 0,

Dla utwierdzenia przesuwnego z prawej strony:

Dla dwóch ostatnich równań:

wiersz 1 0;1;0
wiersz 2 1;-4;0

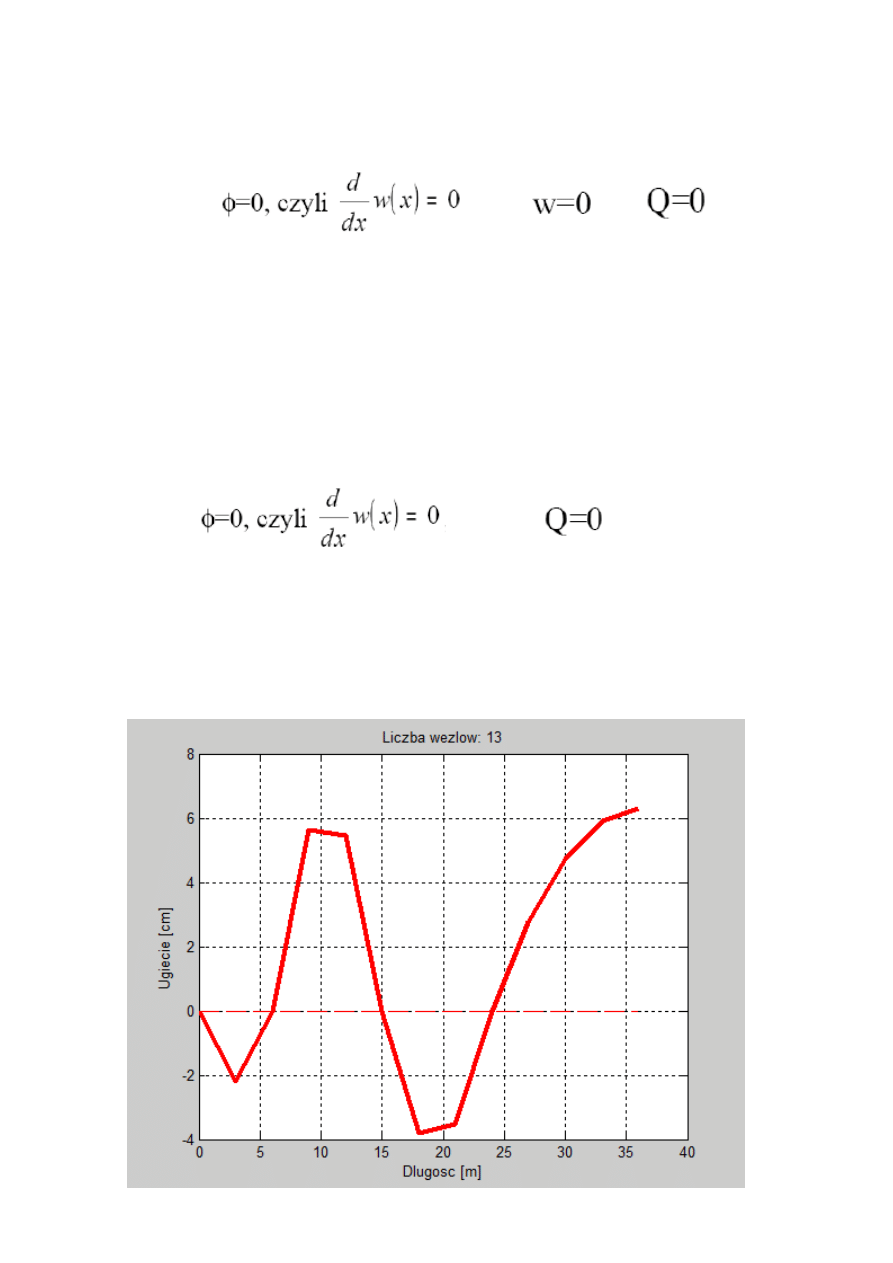
4. Wykres

ugięcia belki:

% Metoda Różnic Skończonych

% Wyznaczanie ugięcia belki

clear

all

close

all

% liczba węzłow wynosi 13 (od 0 do 12)

% lewy koniec - utwierdzenie

% prawy koniec utwierdzenie przesówne

l = 36;

% długość całej belki [m]

E = 30e9;

% moduł Younga [N/m^2]

liczba_wezlow = 13;

zerowe_ugiecie = [1 3 6 9];

niezerowe_ugiecie=1:liczba_wezlow;

% konstruowanie początkowej macierzy współczynników:

L = eye(liczba_wezlow)*6;

L(2:end,1:end-1) = L(2:end,1:end-1) - 4*eye(liczba_wezlow-1);

L(1:end-1,2:end) = L(1:end-1,2:end) - 4*eye(liczba_wezlow-1);

L(3:end,1:end-2) = L(3:end,1:end-2) + 1*eye(liczba_wezlow-2);

L(1:end-2,3:end) = L(1:end-2,3:end) + 1*eye(liczba_wezlow-2);

% a) utwierdzenie z lewej strony

L(1:2,1:3) = L(1:2,1:3) + [0 -4 0; 0 1 0];

% b) utwierzdenie przesuwne z prawej strony

L(end-1:end,end-2:end) = L(end-1:end,end-2:end) + [0 1 0; 1 -4 0];

% wektor prawych stron: h^4*q/EI

q=[0; -15000; 0; 15000; 10000; -5000; -5000; -5000; -5000; 0; 0; 0;
0;];

I= (6667e-8)*ones(13,1);

P=(l/6)^4 * (q ./ (E*I));

%% uwzglednienie zerowych ugiec

L(zerowe_ugiecie,:)=[];

L(:,zerowe_ugiecie)=[];

P(zerowe_ugiecie)=[];

niezerowe_ugiecie(zerowe_ugiecie)=[];

% L*W=P co odpowiada równaniu linii ugięcia belki: d2/dx2(EI
d2w/dx2) = q

W = inv(L)*P;

Ugiecia=zeros(liczba_wezlow,1);

Ugiecia(niezerowe_ugiecie) = W;

%% Rysunek

figure(1)

plot([0 l],[0 0],

'--r'

);

% os poczatkowa

hold

on

;

plot(0:l/12:l,Ugiecia,

'-r'

,

'linewidth'

,3);

% os odksztalcona

grid

on

title([

'Liczba wezlow: '

,num2str(liczba_wezlow)])

xlabel(

'Dlugosc [m]'

)

ylabel(

'Ugiecie [cm]'

)