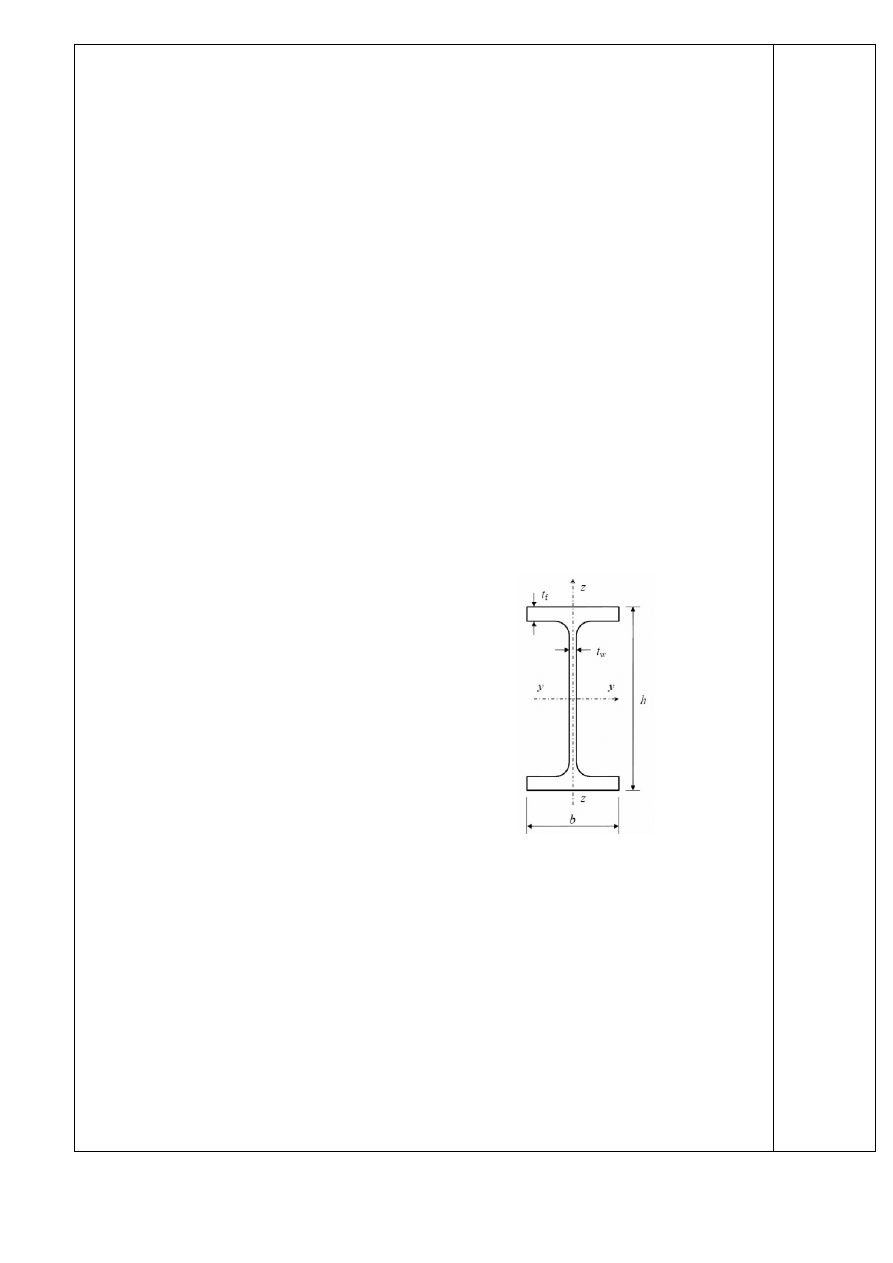
Przykład: Belka stropowa wieloprzęsłowa

1. Dane podstawowe

Częściowe współczynniki bezpieczeństwa

 



G

= 1,35 (oddziaływania stałe)

 



Q

= 1,50 (oddziaływania zmienne)

 



M0

= 1,0 (współczynnik częściowy dla nośności przekroju)

 



M1

= 1,0 (współczynnik częściowy dla nośności elementów)

Założenia projektowe

 Ilość przęseł: 4
 Rozpiętość przęsła: 6,00 m
 Rozstaw belek: 2,50 m
 Obciążenia stałe: płyta żelbetowa gr. 12cm, styropian gr. 5cm, posadzka betonowa gr.

6cm, wykładzina PCW

 Obciążenie użytkowe: 2,50 kN/m

2

 Gatunek stali: S235

Charakterystyka przekroju

Dobrano przekrój belki IPE330

 Szerokość półki

bf=160mm

 Grubość półki

tf=11,5mm

 Grubość środnika

tw=7,5mm

 Wysokość przekroju

h=330mm

 Promień wyokrąglenia

r=18mm

 Masa jednostkowa

49,1 kg/m

 Moment bezwładności względem osi y

J

y

=11770cm

4

 Moment bezwładności względem osi z

J

z

=788cm

4

 Wskaźnik wytrzymałości względem osi y W

y

=713cm

3

 Wskaźnik wytrzymałości względem osi z W

z

=98,5cm

3

 Wskaźnik oporu plastycznego

W

y,pl

=804cm

3

 Pole przekroju poprzecznego

A=62,6cm

2

 Moment bezwładności przy skręcaniu

J

T

=28,8cm

4

 Wycinkowy moment bezwładności

J

w

=199100cm

6

PN-EN
1990
PN-EN
1993-1-1
§ 6.1

,

= 100

,

= 91,0

2. Zebranie obciążeń

L.p.

Rodzaj obciążenia

Obciążenie

charakterystyczne

[kN/m]

Obciążenia stałe G

1

Wykładzina PCW

0,07 *2,50

0,18

2

Posadzka betonowa

21*0,06*2,50

3,15

3

Styropian

0,45*0,05*2,50

0,06

4

Płyta żelbetowa

25*0,12*2,50

7,5

5

Ciężar własny belki IPE330

0,48

0,48

11,37

Obciążenia zmienne Q

6

Obciążenie użytkowe

2,50*2,50

6,25

Dla obliczeń SGN: (nośność na zginanie, zwichrzenie, ścinanie)
γ

G

*G + γ

Q

*Q = 1,35*11,37+1,5*6,25=24,7kN/m

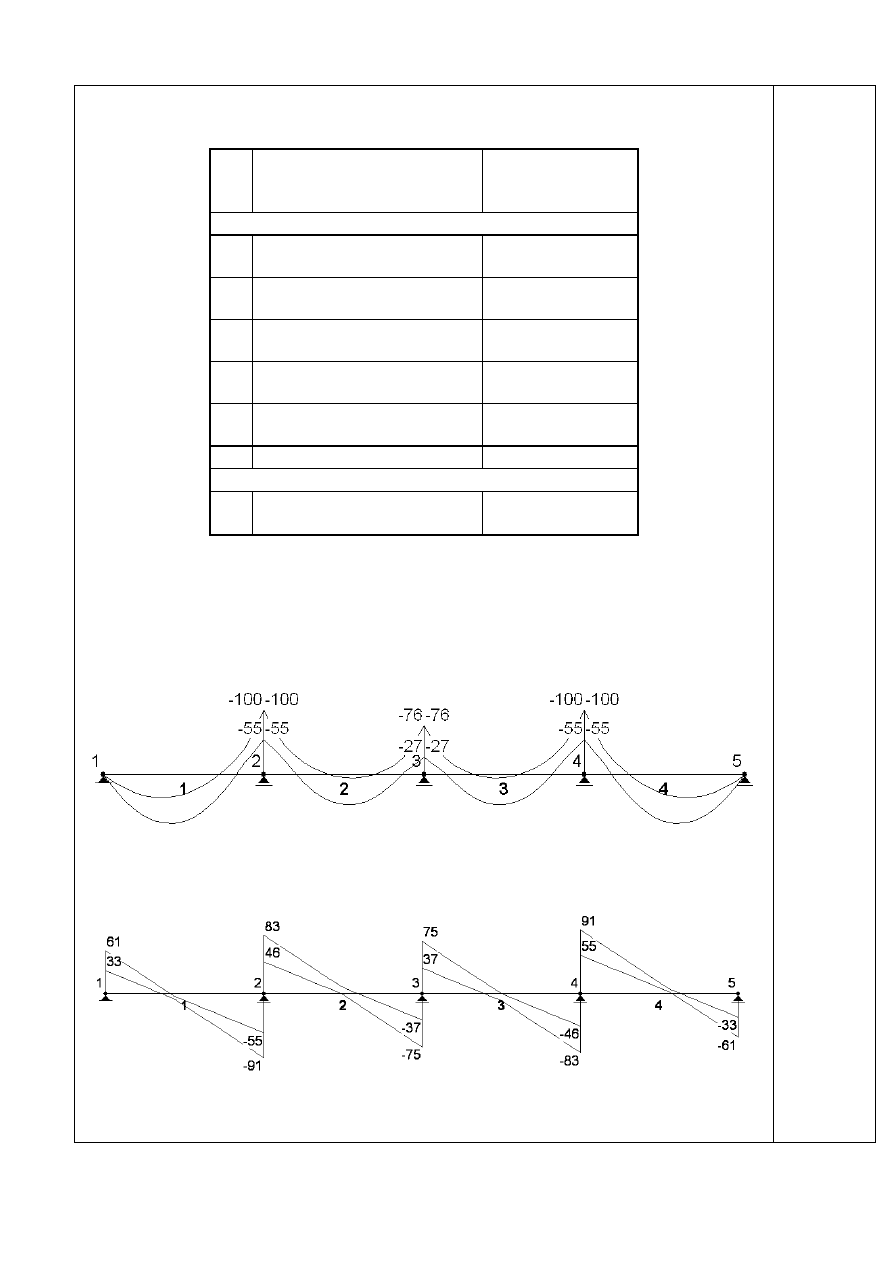
3. Ustalenie sił wewnętrznych – na podstawie programu RM-Win

Największy obliczeniowy moment zginający w środku przęsła:

Największa obliczeniowa siła ścinająca na podporze:

PN-EN
1990
§ 6.4.3.2
§ 6.5.3
Tabl.
A1.2(B)

=

235/

= 1

=

,

≤

,

,

4. Ustalenie klasy przekroju

Gatunek stali S235
Największa grubość ścianki wynosi 11,5 mm < 40 mm, więc:
f

y

= 235 MPa

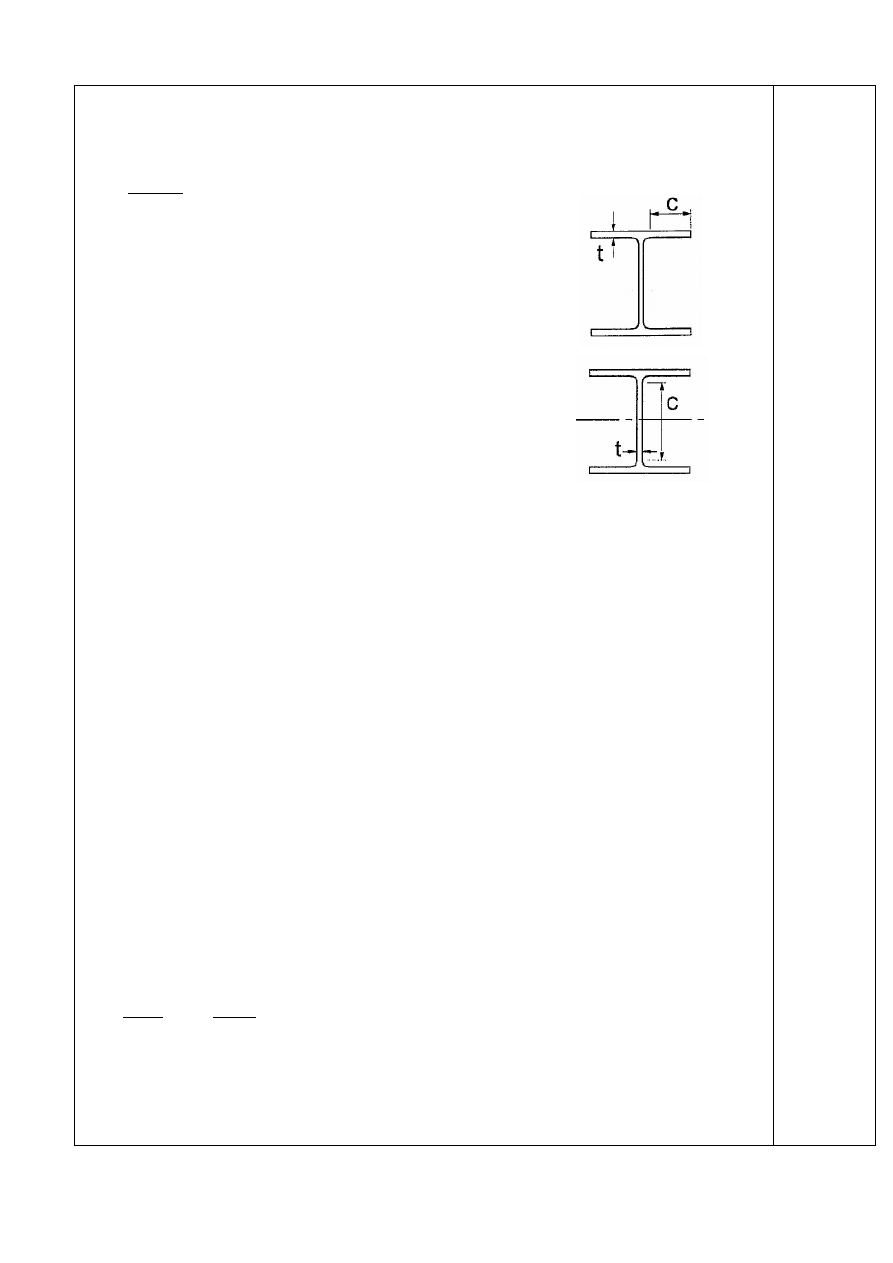
Półka - ściskanie
c = (b – t

w

– 2 r) / 2 = (160 – 7,5 – 2 × 18)/2 = 58,25 mm

c/t

f

= 58,25 / 11,5 = 5,07 ≤ 9

= 9 Klasa 1

Środnik - zginanie
c = h – 2 t

f

– 2 r = 330 – 2 × 11,5 – 2 × 18 = 271 mm

c / t

w

= 271 / 7,5 = 36,1 < 72

= 72 Klasa 1

Wniosek: Przekrój jest klasy 1

5. Nośność przekroju przy zginaniu (SGN)

Obliczeniowa nośność przekroju przy zginaniu dla klas 1 i 2
M

c,Rd

= M

pl,Rd

= W

pl,y

f

y

/



M0

= (804 × 23,5 / 1,0) = 18864kNcm=189kNm

M

y,Ed

/ M

c,Rd

= 100 / 189 = 0,529≤1 Nośność na zginanie jest wystarczająca

6. Nośność elementu na zwichrzenie (SGN)

a.) Belka zabezpieczona przed zwichrzeniem w strefie przęsłowej

W strefie przęsłowej:
Przyjęto, że ściskany pas górny belki został zatopiony w płycie żelbetowej – belka
zabezpieczona przed zwichrzeniem na całej długości -



LT,mod

= 1,0

W strefie przypodporowej:
Dla najbardziej niekorzystnego przypadku obciążenia gdy M

y,Ed

=99,9 kNm długość belki

niezabezpieczonej przed zwichrzeniem (odcinek przypodporowy obciążony momentem
ujemnym) wynosi L

c

=1,57m (wg RM-Win)

Elementy, w których pas ściskany jest stężony punktowo w kierunku
bocznym, nie są narażone na zwichrzenie, jeśli rozstaw pomiędzy
stężeniami bocznymi L

c

i wynikająca z niego smukłość zastępczego pasa ściskanego

spełnia warunek:

k

c

- współczynnik poprawkowy uwzględniający rozkład momentu zginającego pomiędzy

stężeniami;

Rozkład momentu zginającego pomiędzy stężeniami w przypodporowej części belki, założono

PN-EN
1993-1-1
Tablica 3.1




PN-EN
1993-1-1
Tablica 5.2








PN-EN
1993-1-1
§ 6.2.5



















PN-EN
1993-1-1
6.3.2.4

(1)B



PN-EN

=

=

0,6 + 0,4 = 0,775

,

=

393,6/23,62 = 4,08

=

0,775 ∗ 157

4,08 ∗ 93,9

= 0,317 < 0,4 ∗

189

100,0

= 0,757

=

,

≤

,

,

jako liniowy ψ= 0

i

f

,

z

- promień bezwładności przekroju pasa zastępczego, składającego się z pasa ściskanego i

1/3 ściskanej części środnika, względem osi z-z przekroju;

I

f,z

= [788 - (2/3 × (33-2*1,15) ) × 0,75

3

/ 12] / 2 = 393,6 cm

4

A

f,z

= [62,6 - (2/3 × (33-2*1,15)) × 0,75] / 2 = 23,62 cm

2

= 93,9 = 93,9




c0

- smukłość graniczna pasa,



c0

= 0,40

Belka jest zabezpieczona przed zwichrzeniem

b.) Belka niezabezpieczona przed zwichrzeniem

Obliczenie wpływu zwichrzenia na podstawie uproszczonej oceny zwichrzenia belek w
budynkach

Elementy, w których pas ściskany jest stężony punktowo w kierunku
bocznym, nie są narażone na zwichrzenie, jeśli rozstaw pomiędzy
stężeniami bocznymi L

c

i wynikająca z niego smukłość zastępczego pasa ściskanego

spełnia warunek:

L

c

= 600cm – przyjęto stężenia na podporach w rozstawie co 600cm

k

c

- współczynnik poprawkowy uwzględniający rozkład momentu zginającego pomiędzy

stężeniami, PN-EN 1993-1-1 Tablica 6.6;
Rozkład momentu zginającego pomiędzy podporami wg Tablicy B.3

Przęsło 12 (45):
M

2

= –100,0kNm

M

1

= 0

ψ=0

α

s

= M

12

/ M

2

= 72,6/(–100,0)= –0,727

C

mLT

= 0,1–0,8*α

s

= 0,1+0,8*0,727=0,68

Przęsło 23 (34):
M

2

= –100,0kNm

M

3

= –51,5kNm

M

23

= 4,70kNm

ψ=51,5*100,0=0,515

α

s

= M

23

/ M

2

= 4,70/(–100,0)= –0,047

C

mLT

= 0,1–0,8*α

s

= 0,1+0,8*0,047=0,138

1993-1-1
NA.17
Tablica B.3










PN-EN
1993-1-1
NA.18














PN-EN
1993-1-1
6.3.2.4

(1)B




PN-EN
1993-1-1
NA.17
Tablica B.3


Siły wew-
nętrzne wg
Rm-Win

=

=

0,68 = 0,825

,

=

393,6/23,62 = 4,08

=

0,825 ∗ 600

4,08 ∗ 93,9

= 1,29 > 0,4 ∗

189

100,0

= 0,757

,

=

,

,

≤

,

= 0,5 1 +

−

,

+

= 0,5[1 + 0,49(1,29 − 0,4) + 0,75 ∗ 1,29 ] = 1,34

=

1

+

−

=

1

1,34 + 1,34 − 0,75 ∗ 1, 29

= 0,481

,

= 1,1 ∗ 0,481 ∗ 189 = 100

=

(

)

+

+

(

)

+

.

−

Decyduje większa wartość C

mLT

= 0,68

i

f

,

z

- promień bezwładności przekroju pasa zastępczego, składającego się z pasa ściskanego i

1/3 ściskanej części środnika, względem osi z-z przekroju;

I

f,z

= [788 - (2/3 × (33-2*1,15) ) × 0,75

3

/ 12] / 2 = 393,6 cm

4

A

f,z

= [62,6 - (2/3 × (33-2*1,15)) × 0,75] / 2 = 23,62 cm

2

= 93,9 = 93,9




c0

- smukłość graniczna pasa,



c0

= 0,40

Belka nie jest zabezpieczona przed zwichrzeniem, nośność na zwichrzenie przybiera postać:

h/b=330/160=2,06>2 – krzywa c (α

LT

=0.49)

k

fl

= 1,1

M

y,Ed

/ M

b,Rd

= 100 / 100 = 1,0≤1

Nośność na zwichrzenie jest spełniona

Obliczenie wpływu zwichrzenia na podstawie obliczeń momentu krytycznego

Sprężysty moment krytyczny przy zwichrzeniu belki o stałym przekroju bisymetrycznym:

Współczynnik k odnosi się do obrotu końca elementu w planie. Jest on analogiczny do
współczynnika długości wyboczeniowej w stosunku do długości elementu ściskanego.
Współczynnik k powinien być brany jako nie mniejszy niż 1,0 chyba że wartości mniejsze od
1,0 mogą być uzasadnione

Przyjęto k=1,0

Współczynnik k

w

odnosi się do spaczenia końca elementu. W przypadku braku specjalnych

usztywnień przeciwdziałających spaczeniu, k

w

powinien być przyjmowany jako 1,0.

Przyjęto k

w

=1,0

PN-EN
1993-1-1
NA.18






PN-EN
1993-1-1
6.3.2.4
(2)B

PN-EN
1993-1-1
6.3.2.3. (1)
NA. 19









SN003a

=–

8

=–

24,7 ∗ 6,00

8 ∗ 100,0

=– 1,11

=

,

∗

/

=

804 ∗ 23.5/14504 = 1,14

= 0,5 1 +

−

,

+

= 0,5[1 + 0,49(1,14 − 0,4) + 0,75 ∗ 1,14 ]

= 1,17

=

1

+

−

=

1

1,11 + 1,11 − 0,75 ∗ 1,14

= 0,556

,

=

( /√3)

=

3080(235/√3)

1,0

= 418

,

=

91,0

418

= 0,217 < 1

ψ=0

C

1

=1,85

C

2

=0,82

z

g

=16,5cm

= 1,85

.

∗

( , ∗

)

+

+

( , ∗

)

∗

,

.

∗

+ (0,82 ∗ 16,5)

.

− 0,82 ∗

16,5 = 838,4 ∗ 17,3 = 14504

Smukłość względna dla zwichrzenia

h/b=330/160=2,06>2 – krzywa c (α

LT

=0.49)

Nośność na zwichrzenie przyjmuje postać:

M

b,Rd

=



LT,

W

pl,y

f

y

/



M1

M

b,Rd

= 0,556 × 804 × 23,5 / 1,0

= 105 kNm

M

y,Ed

/ M

b,Rd

= 100,0 / 105 = 0,951 ≤1 Nośność na zwichrzenie jest spełniona

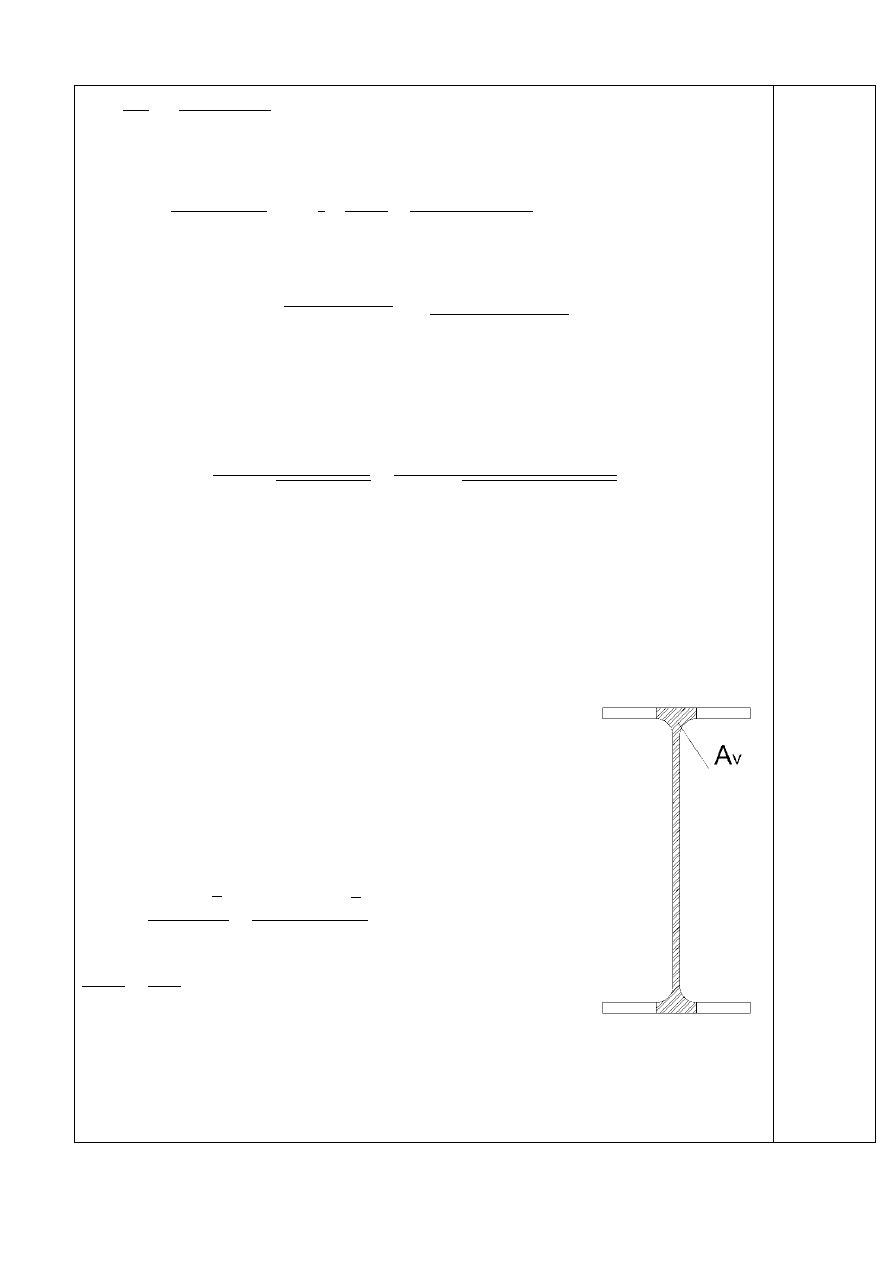
7. Nośność przekroju na ścinanie (SGN)

Pole przekroju czynnego przy ścinaniu

A

v

= A – 2 b t

f

+ (t

w

+ 2 r) t

f

A

v

= 6260 – 2 × 160 × 11,5 + (7,5 + 2 × 18) × 11,5 = 3080 mm

2

Obliczeniowa nośność plastyczna przy ścinaniu (przy braku
skręcania)

Sprawdzenie warunku stateczności środnika przy działaniu siły poprzecznej
nie jest wymagane, gdy:
h

w

/ t

w

≤ 72 / 

Można w przybliżeniu przyjmować

 =1.0

SN003a




PN-EN
1993-1-1
6.3.2.2 (1)
6.3.2.3 (1)









PN-EN
1993-1-1
6.3.2.1. (3)






PN-EN
1993-1-1
§ 6.2.6 (3)
a)



PN-EN
1993-1-1
§ 6.2.6 (2)

PN-EN
1993-1-1
§ 6.2.6 (1)

PN-EN
1993-1-1
§ 6.2.6

(6)

ℎ

=

330 − 2 ∗ 11,5

7,5

= 40,9 < 72 ∗

1
1

= 72

Nośność przekroju nie ulega redukcji wskutek wyboczenia czy ścinaniu.
Siła poprzeczna nie przekracza 50% nośności plastycznej przekroju przy ścinaniu.

Wniosek: Można pominąć wpływ siły poprzecznej na nośność przekroju przy zginaniu.

8. Ugięcie (SGU)

Ugięcie maksymalne odczytane z programu RM-Win dla kombinacji obciążeń stałych

i zmiennych w przęsłach 1 i 3:

f=0,71cm

Ugięcie dopuszczalne f

dop

= L/250=600/250=2,40cm

f=0,71cm < f

dop

= 2,40cm

PN-EN
1990
§ 6.5.3

PN-EN
1993-1-1
NA.22