1

Wprowadzenie do klasycznej teorii pola

##########################################################################################
Autor : R. Waligóra ;
data powstania dokumentu : 2008-11-10 ; ostatnie poprawki z dnia: 2012-04-01
##########################################################################################

WPROWADZENIE

Tekst ten wprowadza ogólne pojęcia stosowane w klasycznej teorii pola. Dla jego zrozumienia konieczna jest
znajomość mechaniki analitycznej (aparatu kanonicznego), podstaw STW oraz podstaw rachunku wariacyjnego.
W klasycznej teoria pola stosujemy metody klasycznej tj. nie uwzględniającej przejścia kwantowego.
Czytelnikowi przed zapoznaniem się z tekstem , powinny być znane takie pojęcia jak : współrzędne uogólnione,
prędkości i pędy uogólnione, lagranżjan i hamiltonian - układu mechanicznego, reprezentacja grupy Lorentza
( Poincarego ). Należy również mieć na uwadze, że nie wyczerpuje on tematu i jest tekstem jedynie poglądowym
i może on stanowić pewien wstęp do poruszanych zagadnień.
W pierwszej kolejności wprowadzę wspomniane wyżej wielkości dla przypadku nierelatywistycznego, następnie
pojęcia te zostaną rozszerzone na układy o nieskończonej ( w granicy ) liczbie stopni swobody tj. ośrodki ciągłe.
Dla układów takich współrzędne uogólnione zostają zastąpione (ciągłymi) funkcjami pola, lagranżjan i
hamiltonian zastępujemy odpowiednio gęstością lagranżjanu i gęstością hamiltonianu, przejście to właściwie już
uwzględnia polowy charakter zmiennych działania. Na końcu formalizmowi temu nadam relatywistyczną
niezmienniczość wprowadzając tym samym pojecie „pola relatywistycznie niezmienniczego”.
W tekście podkreślono kluczową dla teorii pola (zarówno klasycznego jak i kwantowego ) rolę zasad
zachowania wynikających z istnienia odpowiednich grup symetrii równań wariacyjnych.
( twierdzenie E. Noether ). Pojęcie pola i cząstek (cząstki) odpowiadających temu polu jest we współczesnej
fizyce podstawą zrozumienia zasad funkcjonowania wszechświata – zarówno w skali makro jak i mikro (tego w
szczególności).
Warto również wspomnieć , że obecnie bardzo duży nacisk kładzie się na pola obdarzone szczególnym rodzajem
symetrii - chodzi o symetrie cechowania, jak również pola, dla których pojecie symetrii (związanej z pewną
niezmienniczością ) zostało rozszerzone, mówię tutaj o tzw. supersymetrii.

Przyjęty schemat postępowania będzie następujący :
Wychodzimy od mechaniki analitycznej i związanego z nią aparatu kanonicznego ( formalizm Lagrange’a i
Hamiltona, przekształcenia kanoniczne , nawiasy Poissona , twierdzenie Noether , współrzędne cykliczne )
Następnie przechodzimy do rozpatrzenia formalizmu kanonicznego dla ośrodków ciągłych wprowadzając
pojęcie pola jako zmiennej funkcjonału działania. W wyniku tego przejścia otrzymujemy charakterystyczną
zamianę wielkości dynamicznych na odpowiadające im gęstości. Rozpatrując niezmienniczość równań
polowych ze względu na grupę ich symetrii ( twierdzenie Noether dla teorii pola ) otrzymujemy nowe wielkości
zachowane tj. zachowane prądy i ładunki Noether. Ostatnie uogólnienie polega na takim sformułowaniu równań
pola aby stały się niezmiennicze względem pewnej reprezentacji grupy Lorentza. Otrzymujemy w ten sposób
relatywistyczna teorię pola (klasycznego ).
Zobacz również teks pt. „Szkic o fizyce i jej historii, matematyce i filozofii”

Teoria pola (teorie pola ) – szczególnie pola skwantowanego, jak wspomniałem jest podstawą na której opiera
się cała fizyka teoretyczna. W jej metodach , a zwłaszcza używanych narzędziach matematycznych odbite jest
całe bogactwo i różnorodność fizyki. Należy od razu powiedzieć , że jest to jednak okupione wieloma
trudnościami zarówno natury fizycznej jak i matematycznej. Teoria pola ukazuje w pełni swoje możliwości
kiedy zastosujemy odpowiedni formalizm matematyczny , do arsenału którego nalezą m.in. takie pojęcia jak :
tensor, forma różniczkowa , pochodna kowariantna , pochodna Liego, rozmaitość Riemannowska.
Aby zorientować się nieco w takim wyłożeniu polecam przejrzeć książkę :
W. Thirring „Fizyka matematyczna” tom 2 – klasyczna teoria pola. ; PWN 1985
Początkującym, jednak w pierwszej kolejności proponuje zapoznać się z artykułem pt. :
„Teoria pola” M. Kupczyńskiego napisanym dla „Encyklopedii fizyki współczesnej” PWN 1984
W celu dalszego pogłębiania naszkicowanego materiału polecam odwołać się do przytoczonej na końcu
literatury.

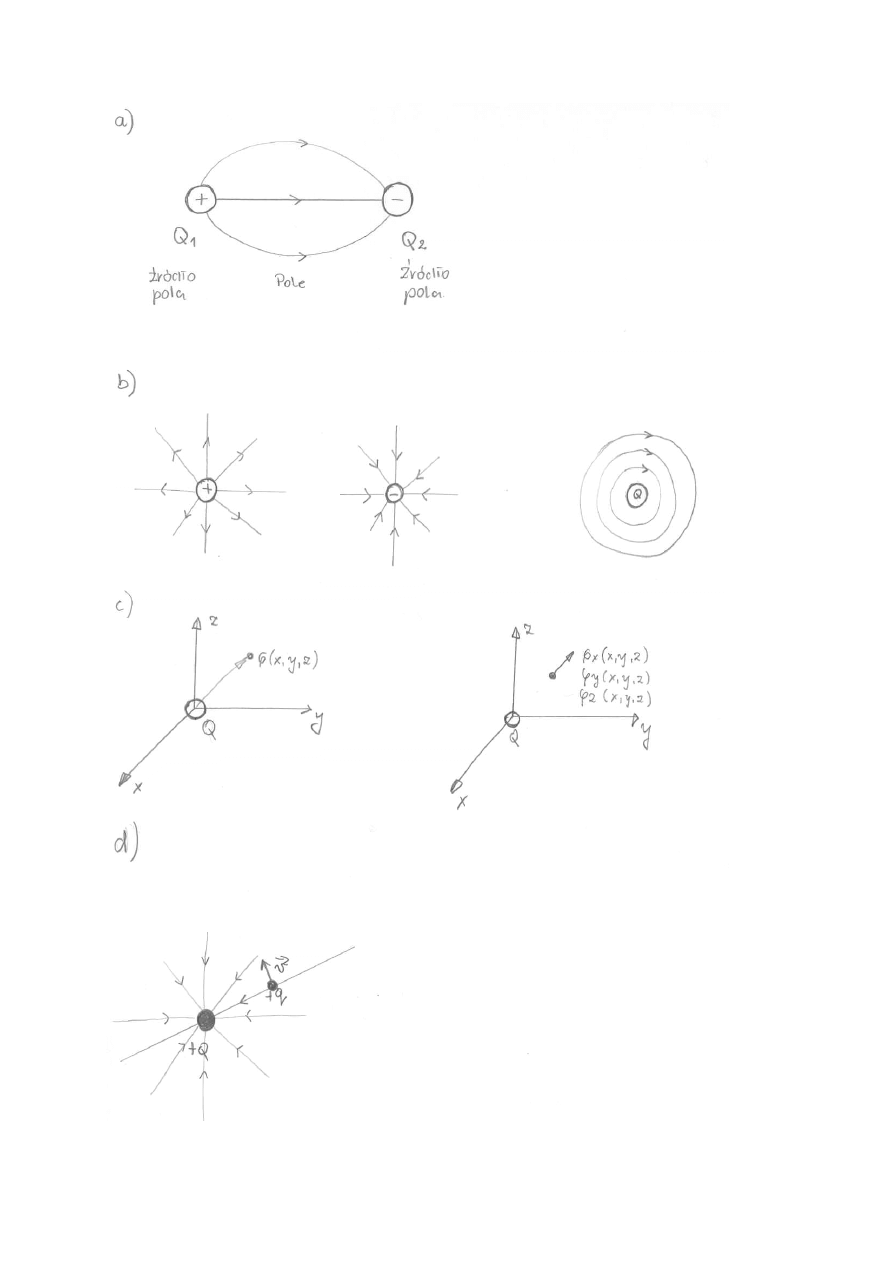
2

Rys. 1.1 a) Podstawowa koncepcja pojęcia pola – dwa ładunki (źródła pola ) oraz pole jako „ośrodek” za
pomocą którego realizuje się oddziaływanie między dwoma ładunkami ( tutaj ładunki mają przeciwne znaki )

3

Mamy zatem następujący model

cząstka A

⇐

pole fizyczne ⇒ cząstka B

b) Przykłady linii sił pola – dla ładunków o przeciwnych znakach pola wektorowe o zerowej rotacji, dla ładunku
Q pole o niezerowej rotacji. c) Przykłady dwóch podstawowych rodzaii pól – skalarnego i wektorowego
d) Podstawowa koncepcja dynamiki ładunku próbnego q ( o niezerowym wektorze prędkości początkowej v ) w
polu ładunku Q ( pole skalarne o zerowej rotacji ).

I. PODSTAWOWE POJ

ĘCIA

Przypomnijmy pewne standardowe oznaczenia stosowane w mechanice analitycznej :
qi(t) - współrzędne uogólnione punktu materialnego lub układu mechanicznego składającego się z wielu
punktów materialnych . i = 1 ... N ; N – liczba stopni swobody układu mechanicznego.
Gdy na układ składający się z n – punktów materialnych , nałożono m – więzów, to : N = 3n - m

dqi(t)/dt

≡

q

.

i(t) – prędkości uogólnione.

Przestrzeń konfiguracyjna układu mechanicznego wyznaczona jest przez współrzędne uogólnione tego układu.
Każdy układ mechaniczny może być scharakteryzowany poprzez pewną funkcję współrzędnych uogólnionych ,
prędkości uogólnionych i czasu.

L = L(qi(t) , q

.

i(t) , t )

Funkcje tą nazywamy „lagranżjanem” ( w niektórych publikacjach spotyka się pisownie „lagrangian” ) układu
mechanicznego (ogólnie układu fizycznego). Wielkość :

∂

L/

∂

q

.

i = pi(t) - nazywamy pędem uogólnionym.

Rozpatrzmy funkcjonał postaci :
t1
S [

γ

] =

∫

L dt (1.1)

t0
S [

γ

] – oznacza zależność funkcjonalną S od

γ

;

γ

- jest pewną krzywą w przestrzeni konfiguracyjnej.

Funkcjonał o takiej postaci nazywamy „działaniem”.

Do podstawowych zasad mechaniki należy zasada stacjonarnego działania, zwana niesłusznie z matematycznego
punktu widzenia zasadą najmniejszego działania. Głosi ona iż :
Rzeczywisty ruch układu mechanicznego w przestrzeni konfiguracyjnej opisywany jest przez taką krzywą

γ

, dla

której działanie (1.1) osiąga ekstremum (w szczególności może to być minimum ).

Zgodnie z podstawowym twierdzeniem rachunku wariacyjnego możemy powiedzieć :
warunkiem koniecznym aby działanie S osiągało ekstremum jest spełnienie równania Eulera-Lagrange’a :

d/dt (

∂

L/

∂

q

.

i )

−

∂

L/qi = 0 lub p

.

−

fi = 0 lub p

.

= fi (1.2)

gdzie : fi =

∂

L/qi – jest siłą uogólnioną.

Równanie to wynika z równania wariacyjnego o postaci :

δ

S = 0 (1.3)

Rozwiązania równania : p

.

= fi – nazywamy „ekstremalnymi” funkcjonału S.

Wprowadzając pojęcie pochodnej wariacyjnej (pochodnej Hamiltona ) :

hL / hqi = d/dt (

∂

L/

∂

q

.

i ) – (

∂

L/qi ) (1.4)

( literka h symbolizuje różniczkowanie w sensie Hamiltona ) otrzymamy warunek :
hL / hqi = 0
Należy zauważyć, że lagranżjan jest określony niejednoznacznie. Wynika to z tego, że lagranżjan postaci :
L’ = L + d/dt f (qi , t )
również spełnia równania (1.4).
W ogólności będziemy mieli następującą niejednoznaczność :
₤

→

₤’ = ₤ +

∂µ

F

µ

która nie będzie naruszała działania tj. S = S’ ( zatem i odpowiednich równań ruchu )
Własność ta jest słuszna dla określonych zależności topologicznych.

4

Asymptotyczna addytywność lagranżjanu.
Jeżeli będziemy rozpatrywali dwa układy mechaniczne znajdujące się w znacznej odległości jeden od drugiego
to jest oczywiste , że procesy zachodzące w jednym układzie nie powinny wpływać na procesy zachodzące w
drugim układzie. Z drugiej strony jednak, nie można zabronić aby rozpatrywać te dwa układy jako jeden układ
złożony z dwóch odległych przestrzennie części I i II.
Jeżeli pewien układ ( I + II ) rozdzielimy na dwa pod układy I i II w taki sposób , że minimalna odległość

między punktami materialnymi układu I i II rI II

→

∝

, to funkcje Lagrange’a układu I + II możemy rozłożyć na

dwie (osobne ) funkcje Lagrange’a :
LI + II

→

LI

+ L

II

r I II

→

∞

Jest to warunek asymptotycznej addytywności funkcji Lagrange’a.

Przykład 1.
Rozważmy układ zachowawczy fizyczny (mechaniczny) składający się z jednego punktu materialnego o jednym
stopniu swobody. Dla takiego układu jak wiadomo lagranżjan ma postać :
L = T – U ; gdzie : T – to energia kinetyczna , U – to energia potencjalna.
I odpowiednio, dla energii tych mamy zależności postaci :

T = ½ mv2 ; U = U(x)
Równanie Eulera–Lagrange’a przyjmuje postać :

p

.

= fi (jest to uogólniona II zasada dynamiki Newtona )

Dla naszego przypadku mamy jednak :
p =

∂

L/

∂

v = mv ; f =

∂

L/

∂

x =

∂

U/

∂

x

zatem :
dp/dt = f ⇒ ma = F ⇒ ma =

−

∂

U/

∂

x

Co oczywiście pokrywa się z „klasycznie” rozumianym II prawem Newtona.

Równania Hamiltona
Jak wiadomo równania mechaniki możemy zapisać ( w formie równoważnej ) w formaliźmie Hamiltona.
Funkcje Hamiltona związana jest z funkcją Lagrange’a następująco :

H (qi(t) , pi(t) , t ) =

Σ

pj q

.

j (p , q , t) – L ( q , q

.

(p , q , t) , t ) (1.5)

Funkcjonał działania (1.1) możemy zapisać również wykorzystując funkcje Hamiltona :
t1 t1

S [

γ

] =

∫

L dt =

∫

[

Σ

pj q

.

j (p, q, t ) – L ( q , q

.

(p, q, t ) , t ) ] (1.6)

t0 t0
Wariacja takiego funkcjonału prowadzi do równań kanonicznych Hamiltona postaci :

q

.

j =

∂

H/

∂

pj ; p

.

j =

−

∂

H/

∂

qj ; j = 1 … n - liczba stopni swobody układu. (1.7)

Równania (1.7) są równoważne równaniom (1.2).
Dla formalizmu Lagrange’a mamy n – równań różniczkowych drugiego rzędu, dla formalizmu Hamiltona mamy
2n – równań różniczkowych pierwszego rzędu.

II. PRAWA ZACHOWANIA W KLASYCZNEJ TEORII POLA

Jak wspomniano podstawową rolę w teorii pola odgrywa twierdzenie Emmi (ang. Emmy ) Noether.
Dla układu równań różniczkowych , które mogą być otrzymane z zasady wariacyjnej Eulera-Lagrange’a,
każdemu jednoparametrycznemu przekształceniu ciągłemu pozostawiającemu funkcjonał wariacyjny
inwariantnym odpowiada jedno różniczkowe prawo zachowania. Jeżeli ciągła grupa przekształceń (grupa Liego)
zawiera m parametrów , to z inwariantności tego funkcjonału względem tej grupy wynika m- różniczkowych
praw zachowania.
Zatem , jeżeli funkcjonał postaci (1.1) jest niezmienniczy względem ciągłej m-parametrycznej grupy
przekształceń to równaniom (1.2) odpowiada m – różniczkowych praw zachowania
Przypominam , że różniczkowym prawem zachowania (w ogólności ) nazywamy wielkość :

∇µ

T

µν

= 0 ; gdzie :

∇µ

- jest pochodną kowariantną ; T

µν

- pewnym tensorem.

Dla naszych celów wystarczy jednak szczególny przypadek tego prawa , mianowicie :

d/dt [ f ( (qi(t) , q

.

i(t) ) ] = 0 (2.1)

Z różniczkowego prawa zachowania wynika, że pewna wielkość jest zachowana w czasie tj. :

5

f ( (qi(t) , q

.

i(t) ) = const.

Można pokazać , że różniczkowe prawo zachowania dla przypadku funkcjonału postaci (1.1) ma postać :

d/dt { [ L

−

Σ

(

∂

L/

∂

q

.

i )q

.

i ]

Λ

+

Σ

(

∂

L/

∂

q

.

i )

Λ

i } (2.2)

Transformacje współrzędnych mają postać :
t ⇒ t’ = t +

Λ

(q, t )

ε

; qi (t) ⇒ q’i (t’) = qi (t) +

Λ

i (q, t)

ε

;

ε

- pewien parametr ciągły

Zgodnie z tym :

Q = [ L

−

Σ

(

∂

L/

∂

q

.

i )q

.

i ]

Λ

+

Σ

(

∂

L/

∂

q

.

i )

Λ

i = const. (2.3)

Zatem wielkość : Q = Q ((qi(t) , q

.

i(t) ) = const.

Zasada zachowania energii.
Aby otrzymać zasadę zachowania całkowitej energii układu mechanicznego zachowawczego przyjmijmy ,
transformacje dla których :

Λ

(q, t ) = 1 ,

Λ

i (q, t) = 0

Mamy zatem :
t ⇒ t’ = t +

ε

; qi (t) ⇒ q’i (t’) = qi (t)

Jest to jak widać transformacja polegająca jedynie na przesunięciu (translacji) czasu.
Mamy dalej :

d/dt [ L

−

Σ

(

∂

L/

∂

q

.

i )q

.

i ] = 0

czyli :

[ L

−

Σ

(

∂

L/

∂

q

.

i )q

.

i ] = const. =

−

E ; E – energia całkowita układu zachowawczego

Jak wiemy wielkość :

L

−

Σ

(

∂

L/

∂

q

.

i )q

.

i = H ; gdzie : H – jest funkcją Hamiltona.

Zatem : dH /dt = 0 => H = const.
Dla układu zachowawczego mamy :
L = T

−

U

−

E = T – U

−

Σ

(

∂

T/

∂

q

.

i )q

.

i

W układzie kartezjańskim mamy q

.

i = vi , T = ½ mv

2 ,

∂

T/

∂

q

.

=

∂

T/

∂

v = mv ; U = U(x, y, z)

- E = T

−

U

−

2T =

−

( U + T ) => E = T + U

Zatem dla układu zachowawczego z jednorodności czasu wynika zasada zachowania energii całkowitej układu.

Zasada zachowania pędu.
Aby otrzymać zasadę zachowania pędu przyjmijmy :

Λ

(q, t ) = 0 ,

Λ

i (q, t) = 1

Mamy odpowiednio wielkość zachowaną postaci :

d/dt [

Σ

(

∂

L/

∂

q

.

i ) ] = 0

Σ

(

∂

L/

∂

q

.

i ) = const.

Przyjmijmy L = T

−

U

Σ

(

∂

L/

∂

q

.

i ) =

Σ

∂

T/

∂

q

.

i = const. ⇒ p =

∂

T/

∂

v = mv = const.

Zatem dla układu zachowawczego z przesunięcia w przestrzeni (jednorodności przestrzeni) wynika prawo
zachowania pędu.
Można pokazać ponadto , że z obrotu w przestrzeni ( izotropowość przestrzeni) wynika prawo zachowania
momentu pędu.

III. UKŁADY CI

ĄGŁE – OŚRODKI CIĄGŁE.

Do tej pory rozpatrywaliśmy układy mechaniczne składające się z dyskretnie rozłożonych punktów
materialnych. Takich punktów mogło być kilka lub w skrajnych przypadkach nieskończenie wiele. Jednak
zawsze zakładaliśmy, że jest ich przeliczalna ilość. Rozszerzając formalizm kanoniczny możemy rozpatrywać po
pierwsze układy złożone z pewnych podukładów które to mogą znowu składać się z pewnych układów. Funkcja
Lagrange’a całego układu będzie oczywiście w myśl zasady addytywności lagranżjanu , sumą wszystkich
składowych (naturalnie, jeśli odległości między poszczególnymi podukładami będą dostatecznie małe )
k

6

Lcałkowity. =

Σ

Li ; k = liczba pod układów.

i = k
Po drugie, formalizm możemy uogólniać rozpatrując układ składający się z nieprzeliczalnej liczby punktów tj.
możemy rozpatrywać ruch mechaniczny pewnego ośrodka ciągłego.
Rolę współrzędnych uogólnionych dla tego przypadku odgrywają już nie poszczególne współrzędne , ale
funkcje ciągłe współrzędnych przestrzennych ( uogólnionych w „klasycznym” rozumieniu ) i czasu :

η

=

η

( qi , t ) lub dla współrzędnych kartezjańskich

η

=

η

( x, y ,z , t )

Klasycznym przykładem wprowadzenia takiego formalizmu jest układ liniowy oscylatorów harmonicznych –
przy przejściu granicznym układ ten modeluje ruch drgający struny.
Funkcja Lagrange’a dla ośrodka ciągłego przyjmuje postać :

L =

∫ ∫ ∫

₤ dV (3.1)

V
Wielkość : ₤ - nazywamy „gęstością funkcji Lagrange’a”
dV = dxdydz - dla przypadku trój wymiarowej przestrzeni Euklidesa.
Dla ogólnego przypadku mamy :

₤ = ₤ (

η

,

η

.

,

∂η

/

∂

qi ) ;

η

.

= d

η

/ dt (3.2)

W szczególnym przypadku ;

∂η

/

∂

qi ⇒

∂η

/

∂

x ,

∂η

/

∂

y ,

∂η

/

∂

z

Równania ruchu ośrodka ciągłego możemy otrzymać podobnie jak dla układów dyskretnych wariując pewne
działanie :
t1
S =

∫ ∫ ∫ ∫

₤ dVdt (3.3)

t0 V
Warunek stacjonarnego działania przyjmuje postać :

δ

S = 0

prowadzi on do równań analogicznych (1.2), dla układu dyskretnego :

d/dt (

∂

L/

∂η

.

) -

∂

L/

∂η

= 0

W przypadku jeszcze ogólniejszym lagranżjan może zależeć nie od jednej funkcji ciągłej

η

, a od

s – funkcji

η

s =

η

s (qi , t ) , a wtedy :

₤ = ₤ (

η

(qi , t ) ,

∂η

s /

∂

t ,

∂η

s /

∂

qi ,qi , t )

Dla tego przypadku równania Eulera- Lagrange’a przyjmują postać :

d/dt (

∂

L/

∂η

.

s ) +

Σ

d/dqi [

∂

L/

∂

(

∂η

s /

∂

qi )]

−

∂

L/

∂η

s = 0

Jak łatwo można się domyśleć, również metoda Hamiltona może być rozszerzona na ośrodki ciągłe.
Na początku jednak musimy zamienić pęd (uogólniony) na odpowiadającą mu gęstość pędu:
(należy zauważyć że przejście : pewna wielkość

→

gęstość tej wielkości , jest charakterystyczne dla metod teorii

pola )

π =

∂

L/

∂η

.

Dla przypadku

η

s =

η

s ( qi , t ) mamy :

πs =

∂

L/

∂η

.

s .

Wielkość tak określona w teorii pola nazywamy „pędem sprzężonym z polem”

Gęstość funkcji Hamiltona określona jest następująco :

Ħ =

Σ

πs

η

.

s

−

₤ (3.4)

s
Funkcja Hamiltona będzie miała postać :
H =

∫ ∫ ∫

Ħ dV (3.5)

V
Z wariacji funkcjonału
t1
S =

∫ ∫ ∫

∫

Ħ dVdt (3.6)

t0 V
otrzymujemy równania kanoniczne dla ośrodków ciągłych postaci :

7

η

.

s =

∂

H /

∂

πs ; π

.

s =

−

{ (

∂

H /

∂η

s )

−

Σ

d/dqi [

∂

H/

∂

(

∂η

s /

∂

qi )] } (3.7)

Wprowadzając uogólnienie pochodnej wariacyjnej o postaci :

δ

H/

δη

s = (

∂

H /

∂η

s )

−

Σ

d/dqi [

∂

H/

∂

(

∂η

s /

∂

qi )]

otrzymamy :

η

.

s =

δ

H /

δ

πs ; π

.

s =

−δ

H/

δη

s (3.8)

Równania te przypominają zapis (1.7).

Funkcje

η

s =

η

s ( qi , t ) ( w szczególnym przypadku :

η

s =

η

s ( t, x, y, z ) ) pod względem matematycznym są

funkcjami określającymi pewne pole (pola ). Mogą to być pola : wektorowe, skalarne, tensorowe lub spinorowe.

Mamy zatem następującą odpowiedniość :
Mechanika punktu materialnego lub ich układu pole

x

µ

i , i = 1, 2, ... , N

ϕ

(x

µ

)

N

L(t) =

ΣΣΣΣ

₤( xi ) L(t) =

∫

d3x ₤(x )

i=1 przestrzeń
t2
S =

∫

₤(t ) dt S =

∫

₤(t )dt =

∫

d4x ₤(x )

t1 czas czaso-przestrzeń

IV POLA W PRZESTRZENI MINKOWSKIEGO.

Rozpatrzmy układ pól zadanych w przestrzeni Minkowskiego :

ϕ

a =

ϕ

a (x

µ

) ;

µ

= 0,1,2,3 ; a = 1 ... n

x0 = t ; r = r (x1 , x2 , x3 )
Lagranżjan ma postać :

L =

∫ ∫ ∫

₤(

ϕ

a (x

µ

),

∂µϕ

a (x

µ

) ) dV ; dV = d3x (4.1)

gdzie :

∂µ

= (

∂

/

∂

t ,

∂

/

∂

xi ) ; i = 1,2,3

Postać gęstości lagranżjanu ₤(

ϕ

a (x

µ

),

∂µϕ

a (x

µ

) ) wybrana jest nie przypadkowo, nakładamy bowiem na

niego pewne warunki wynikające z danych doświadczalnych jak i wynikłych po uwzględnieniu samozgodności
teorii fizycznych.

Zakładamy po pierwsze ,że nie zależy ona jawnie od x

µ

- co zapewnia niezmienniczość translacyjną, po drugie

nie zależy ona od pochodnych wyższych niż pierwsza – w przeciwnym razie prowadziłaby do równań pola
niezgodnych z doświadczeniem. Po trzecie musi być funkcją lokalną ( pochodne pól brane są w jednym i tym
samym punkcie ) i rzeczywistą.
Wszystkie fundamentalne teorie pola ( teoria oddziaływań elektrosłabych, silnych i grawitacji ) są zbudowane w
oparciu o tak przyjmowaną gęstość lagranżjanu.
Działanie określamy następująco :
t1
S =

∫ ∫ ∫ ∫

₤ dVdt (4.2)

t0 V
Równania wariacyjne otrzymujemy oczywiście wariujac działanie (4.2) :

δ

S = 0

Z czego otrzymujemy ( równanie Eulera – Lagrange’a ) równania pola :

∂

L/

∂ϕ

a

−

∂µ

[

∂

L /

∂

(

∂µϕ

a ) ] = 0 (4.3)

Najprostszym przypadkiem pola jest pole skalarne , dla którego :

ϕ

=

ϕ

(x

µ

)

V. TWIERDZENIE NOETHER W TEORII POLA.

Rozpatrzmy przekształcenia postaci :

x

µ

→

x’

µ

= x

µ

+

Λµ

A (x)

ε

A. (5.1)

ϕ

a (x)

→

ϕ

’a (x) =

ϕ

a (x) +

Λ

ab

A

ϕ

b (x)

ε

A. (5.1)

gdzie :

ε

A – jest pewnym parametrem ciągłym.

8

Można pokazać , że z niezmienniczości równań pola (4.3) względem przekształceń (5.1) wynika różniczkowe
prawo zachowania :

∂

J

µ

a /

∂

x

µ

= 0 ( lub

∂µ

J

µ

a = 0 ) (5.2)

Wielkość :

J

µ

a = T

µν

Λν

A + [

∂

L/

∂

(

∂µϕ

a )]

ϕ

b

Λ

ab

A (5.3)

nazywamy „prądem Noether“.
Równanie (5.2) stwierdza zatem, że prąd Noether jest zachowany.
Wielkość

T

µν

=

δµν

L

−

[

∂

L /

∂

(

∂µϕ

a )]

ϕ

a

ν

(5.4)

δµν

- delta Kroneckera

nazywamy „kanonicznym tensorem energii-pędu”. W przypadku kiedy lagranżjan nie zależy jawnie od x

µ

,

zachowanym prądem jest kanoniczny tensor energii-pędu.

∂µ

T

µν

= 0 (5.5)

Uwaga. Równość (5.5) jest w istocie stwierdza ,że 4-dywergencja tensora energii-pędu jest równa zeru. W
ogólności tensor ten nie musi być symetryczny, jednak w wielu teoriach pola np. w teorii grawitacji żądamy aby
był on symetryczny. Oczywiście, równość (5.5) jest szczególnym przypadkiem równości (5.2) - zatem
kanoniczny tensor energii-pędu jest szczególną postacią prądu Noether.
Całkując (5.2) względem dowolnej 4-objętości ( pamiętajmy , że rozważamy pole w przestrzeni Minkowskiego )

oraz stosując twierdzenie Gaussa otrzymujemy, że 4-strumień wektora J

µ

a przez ograniczającą tą 4-objetość

hiperpowierzchnię jest równy zeru. W szczególności dochodzimy do równania :

Qa (t) =

∫

J0a (x) dx

3 = 0 (5.6)

t=const.
Wielkość : Qa – nazywamy „ładunkami Noether“. Równanie (5.6) stwierdza zatem , że ładunek Noether jest
stały w czasie. (są one całkami ruchu w teorii pola ).
Jest to również tzw. całkowe wyrażenie twierdzenia Noether.
(całkowe prawo zachowania ). Można pokazać , że w szczególności, ładunki zachowane są to składowe 4-pędu :

P

µ

=

∫

T0

µ

dx3 = 0 (5.7)

VI. KLASYCZNE POLA SWOBODNE.

Poprzez pole swobodne rozumiemy pole które nie oddziałuje z innymi polami. Przykładem takiego pola jest pole
elektromagnetyczne w próżni.
Opis każdego pola rozpoczynamy od zapostulowania gęstości funkcji Lagrange’a. Kształt tej funkcji (jej
matematyczna postać ) wybierana jest zgodnie z pewnymi „przepisami”. Do najważniejszych z nich należą :
a) Relatywistyczna niezmienniczość. Działanie powinno być inwariantem grupy Poincarego.
b) Lokalność. Funkcje pola od których zależy jest funkcjonał działania , powinny zależeć od jednego i tego

samego punktu x ( w przestrzeni Minkowskiego zatem x

≡

x

µ

,

µ

= 0, 1, 2, 3 ).

c) Rzeczywistość. W działanie powinny wchodzić tylko rzeczywiste kombinacje funkcji pola i ich pochodne.
d). Do lagranżjanu powinny wchodzić pochodne funkcji pola nie wyższe niż pierwsze.

Pola skalarne.

Jak już wspominałem najprostszym polem jest pole skalarne (rzeczywiste). Pole skalarne

ϕ

(x) lub

ϕ

=

ϕ

( x0, x1, x2, x3 ) transformuje się przy przekształceniach Lorentza jak skalar lub pseudoskalar tj.

ϕ

(x) =

ϕ

(x’). Pole to odpowiada cząstkom neutralnym o spinie 0.

Gęstość funkcji Lagrange’a dla takiego pola jest następująca :
₤ = ½ { [

∂ϕ

(x)/

∂

x

µ

]2

−

m2

ϕ

2(x) } (6.1)

lub
₤ =

∂µϕ

(x)

∂µϕ

(x) – ½m2

ϕ

2(x) (6.1a)

m – jest pewną stałą. ( możemy ją związać z masą kwantów pola )
Równanie pola skalarnego to równanie Kleina-Gordona , postaci (przyjmujemy układ jednostek w którym c=1 ):

( + m2 )

ϕ

(x) = 0 (6.2)

gdzie :

≡

∂µ

∂µ

= c-2

∂

t

2

−

∇

2 – jest operatorem d’Alamberta

Równanie Kleina –Gordona uzyskujemy z równań wariacyjnych postaci :

9

∂

L/

∂ϕ

−

∂µ

[

∂

L /

∂

(

∂µ

ϕ

)] = 0

Równanie (6.2) jest dobrze znane z relatywistycznej mechaniki kwantowej. Było ono pierwszym
relatywistycznym równaniem falowym, uzyskanym w mechanice kwantowej i zostało ono otrzymane w wyniku
relatywistycznego uogólnienia równania Schrödingera.
Tensor gęstości energii-pędu dla pola skalarnego ma postać :

T

µν

= (

∂ϕ

/

∂

x

µ

)(

∂ϕ

/

∂

x

ν

)

−

g

µν

L (6.3)

Gdzie : g

µν

- jest tensorem metrycznym w przestrzeni Minkowskiego.

Z równania tego otrzymujemy, że gęstość energii pola skalarnego jest równa :

T00 = ½ [ (

∂ϕ

/

∂

t )2 + (

∇ϕ

)2 + m2

ϕ

2 ] (6.4)

Rozwiązaniem szczególnym równania (6.2) jest fala płaska :

ϕ

(x) = A e -ipx (6.5)

gdzie : p2

≡

(p0 )2 – p2 = m2 .

Oprócz pól skalarnych w dalszej kolejności rozważać możemy pola wektorowe, pola z ładunkiem, pola ze
spinem ( pola spinorowe, bispinorowe ). Za każdym razem przyjmując odpowiednią postać lagranżajnu
(kierując się raczej metodą heurystyczną , nie ma bowiem jednej i ustalonej metody budowy funkcji Lagrange’a)
a następnie wyznaczając ( o ile jest to możliwe ) rozwiązanie równań pola.

Pola wektorowe.

a) masywne pole wektorowe (pole wektorowe z masą ).
Pole wektorowe Aµ składa się z czterech składowych transformujących się przy przekształceniu Lorentza jak
wektor :

A’µ(x) =

Λ

µ

ν

Aν (x) ,

Λ

µ

ν

- macierz Lorentza.

Lagranżjan pola wektorowego możemy zadać jako sumę czterech lagranżjanów swobodnych pól skalarnych A0
, A1, A2 , A3 , po jego wariowaniu dostaniemy cztery niezależne równania Kleina-Gordona, przypadek ten nie
wnosi niczego interesującego z fizycznego punktu widzenia. Pole o nowych własnościach otrzymamy nakładając
na pole Aµ dodatkowy warunek, zmniejszający liczbę niezależnych składowych ( do trzech ) :

∂

µ Aµ = 0

Te trzy niezależne składowe będą odpowiadać trzem wewnętrznym stopniom swobody cząstki o spinie równym
1 i masie różnej od zera. ( pole skalarne reprezentuje cząstkę o spinie zero, pole wektorowe reprezentuje cząstkę
o spinie jeden )
Lagranżjan dla pola wektorowego możemy wybrać np. w postaci :

£ = - ¼ F

µν Fµν + ½ m2 Aµ Aµ

gdzie : Fµν =

∂

µA

ν -

∂

ν A

µ

Równanie pola wynikające z tego lagranżjanu ma postać :

Aµ

−

∂

µ (

∂

ν A

µ ) + m2 Aµ = 0

Zespolone pole skalarne.

Zespolone pole skalarne posiada dwie niezależne składowe : φ(x) oraz sprzężoną do niej składową φ*(x). Może
być ono jednak rozpatrywane jako pole o dwóch niezależnych składowych rzeczywistych φ1(x), φ2(x)
związanych z polem zespolonym następująco :
φ(x) = φ1(x) + iφ2(x) lub φ(x) = (1/

√

2) ( φ1(x) + iφ2(x) )

φ*(x) = φ1(x) - iφ2(x) φ*(x) = (1/

√

2) ( φ1(x) - iφ2(x) )

Lagranżjan takiego pola ma postać :

£ =

∂

µ

φ*

∂

µφ – m

2φ*φ

Obie składowe pola spełniają równanie Kleina-Gordona :

( + m2 ) φ(x) = 0 ( + m2 ) φ*(x) = 0
Tensor energii-pędu pola zespolonego jest dany następująco :

Tµν =[ (

∂

φ*/

∂

xµ ) (

∂

φ/

∂

xν ) + (

∂

φ*/

∂

xν ) (

∂

φ/

∂

xµ ) ] - g

µν £

Ze wzoru tego otrzymujemy następującą zależność na gęstość energii zespolonego pola skalarnego :

T00 =

ΣΣΣΣ

[ (

∂

φ*/

∂

xk ) (

∂

φ/

∂

xk ) ] + m2 φ*φ

oraz dla gęstości pędu :

T0i = - [ (

∂

φ*/

∂

x0 ) (

∂

φ/

∂

xi ) - (

∂

φ*/

∂

xi ) (

∂

φ/

∂

x0 ) ]

10

Wprowadzony lagranżjan posiada bardzo ważną symetrie, związaną z globalną transformacją cechowania – jest
on mianowicie niezmienniczy względem następującego przekształcenia składowych pola :
φ’(x) = e+iα φ(x)
φ*’(x) = e-iα φ(x)
gdzie : α – stała (rzeczywista), niezależna od współrzędnych czasoprzestrzennych.
Dla małych α możemy zapisać infinitezymalne przekształcenia cechowania :
δφ = iαφ
δφ* = -iαφ
Ponieważ α nie zależy od współrzędnych czasoprzestrzennych infinitezymalne przekształcenia pochodnych pola
maja następującą postać :
δ(

∂

µφ ) = iα

∂

µφ

δ (

∂

µφ* ) = -iα

∂

µφ*

Rozpatrując dwa równoważne podejście, z zastosowaniem dwóch pól rzeczywistych transformację tą możemy
zapisać następująco ( zapis macierzowy ) :
( φ1’ ) = ( cosα -sinα ) ( φ1 )
( φ2’ ) = ( sinα cosα ) ( φ2 )
( jest to oczywiście transformacja polegająca na obrocie o kąt α )
Jest to przekształcenie zadawane przez elementy grupy Liego, konkretnie grupy U(1)

Wprowadzony lagranżjan charakteryzuje się również prądem zachowanym o postaci :
jµ = - i (φ*

∂

µφ - φ

∂

µ φ* ) ;

∂

µjµ

≡

(

∂

j0/

∂

t ) + div j = 0

Obecność takiego prądu zgodnie z twierdzeniem Noether związane jest z wskazaną globalną transformacją
cechowania.
Równanie

∂

µjµ = 0 pociąga za sobą istnienie ładunku zachowanego :

Q =

∫

j0 d

4x

Rozważmy teraz lokalne przekształcenie cechowania
φ’(x)

→

e-iα(x) φ(x)

Zauważmy dalej, że

∂

µφ pod działaniem globalnego przekształcenia cechowania przekształca się jak samo pole

tj. φ(x)
Jednak pod działaniem lokalnego przekształcenia cechowania pojawia się dodatkowy człon

∂

µφ’(x)

→

e-iα(x)

∂

µφ(x) + φ(x)

∂

µe

-iα(x)

Widać więc, że gęstość £ ( φ,

∂

µφ ) nie jest inwariantna względem lokalnych przekształceń cechowania. Aby

uczynić ją inwariantną należy zamienić

∂

µφ(x) na wyrażenie przekształcające się jak samo pole tj. φ(x). W tym

celu wprowadzimy pole wektorowe Aµ(x) ( pole cechowania ), które przekształca się pod działaniem lokalnego
przekształcenia cechowania w następujący sposób :
Aµ(x)

→

Aµ(x) + (1/e)

∂

µα(x) ; e – pewna stała rzeczywista ( skalująca )

Wtedy „pochodna kowariantna” :
Dµφ(x)

≡

[

∂

µ + ieAµ(x) ] φ(x)

Będzie przekształcała się już jak samo pole tj. :

Dµφ(x)

→

e-iα(x) Dµφ(x)

Gęstość £ ( φ, Dµφ ) będzie zatem inwariantna względem lokalnego przekształcenia cechowania, zawiera on
jednak pole wektorowe Aµ(x ) jako pole zewnętrzne, nie wynikające z teorii. Aby sprawić aby teoria była pełna
należy dodać do lagranżjanu człon kwadratowy względem

∂

µAµ(x) :

£ = - ¼ F

µν Fµν + £0( φ, Dµφ ) gdzie : Fµν =

∂

µA

ν

−

∂

ν A

µ – jest to tensor pola EM

Sytuacja jest zatem następująca : wprowadzony lagranżjan £ =

∂

µ

φ*

∂

µφ – m

2φ*φ posiada globalną symetrię

cechowania U(1) ( odpowiadającą pewnemu przesunięciu fazy ). Ponieważ z fizycznego punktu widzenia
bardziej interesuje nas lokalna symetria cechowania ( co wynika m.in. z wymogu relatywistycznej postaci teorii
fizycznych, który globalna symetria cechowania łamie ) chcielibyśmy aby lagranżjan ten był niezmienniczy
względem właśnie takiej symetrii. Ponieważ występują dodatkowe człony ( nie inwariantne względem lokalnej
symetrii cechowania ) musimy zamienić zwykłą pochodną na pochodną innego typu – pochodną kowariantną.
Poprzez tą modyfikacje wprowadzamy jednak dodatkowe pole wektorowe – pole cechowania Aµ

,o

własnościach transformacyjnych :

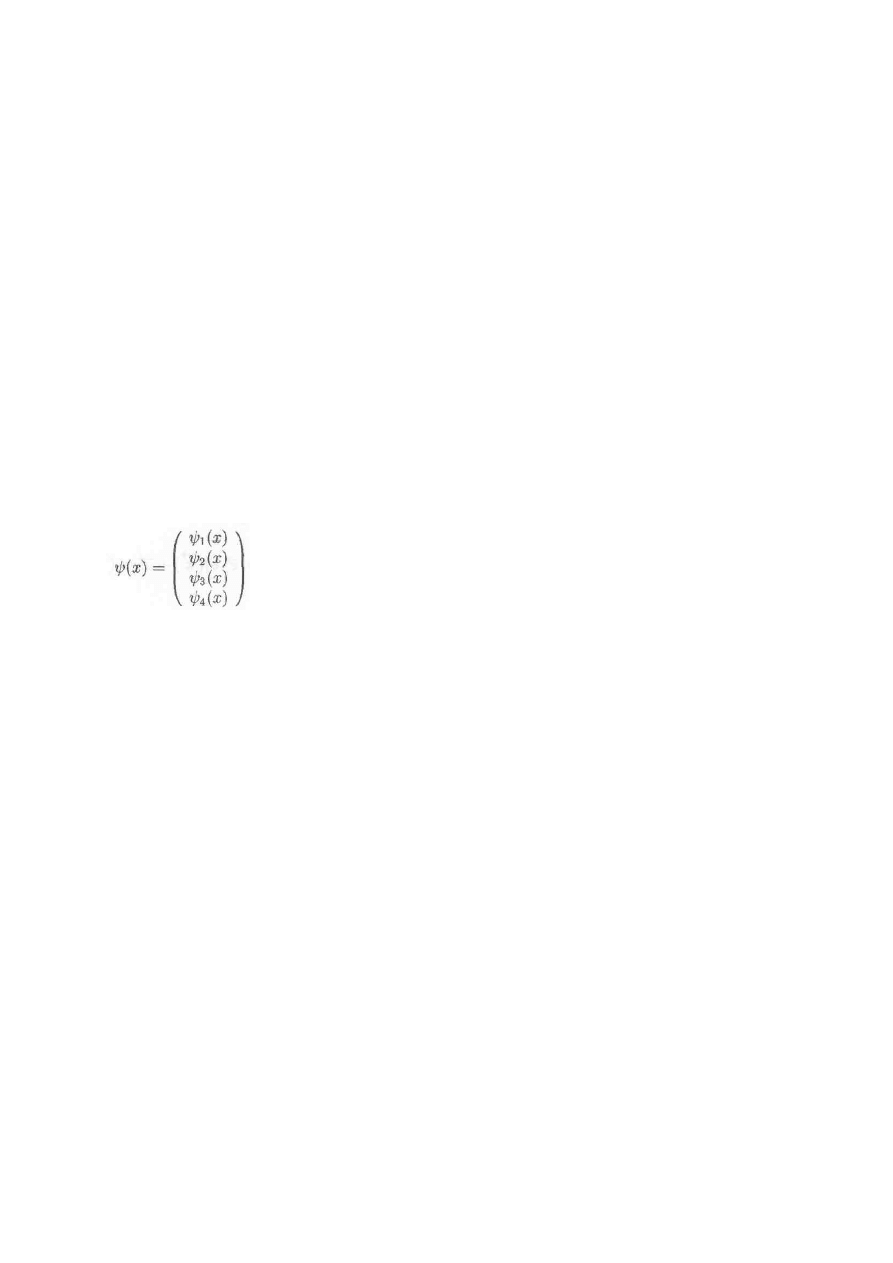
11

Aµ

(x)

→

A’µ

= Aµ (x) + q

∂

µα (x) ; q- pewna stała

Pole cechowania należy teraz wpasować do wejściowego lagranżjanu tak aby stało się ono pewną immanentną

składową naszej teorii – musimy dodać do lagranżjanu człon z jego pochodnymi członem takim jest człon β Fµν
Fµν , β –stała
Zatem nasz całkowity lagranżjan ma teraz postać :

£ = (

∂

µφ + ieAµφ ) (

∂

µ

φ*

−

ieAµφ* ) – m

2φ*φ – ¼ Fµν Fµν ; e - ma oczywiście sens ładunku elektrycznego

Widać więc, że pole EM pojawia się naturalnie w naszym lagranżjanie ( teorii zespolonego pola skalarnego )
jako wymóg inwariantności działania względem lokalnego przekształcenia cechowania. Pole EM jest zatem
polem cechowania, które należy wprowadzić aby zagwarantować inwariantność działania względem lokalnych
U(1)-przekształceń cechowania. Warto zauważyć, że równania Maxwella wynikają z wariowania powyższego
lagranżjanu ( wariując względem potencjałów Aµ

).

Mamy również nową interpretacje bezmasowości pola EM – pole EM jest polem bezmasowym ponieważ
wymaga tego inwariantność względem U(1)-cechowania.
Widać więc, że elektrodynamika jest teorią z U(1)-cechowaniem.

Pola spinorowe.

Dla pól spinorowych lagranżjan ma postać :

£ =

ψ

-(x) i

γµ

∂

µ

ψ

(x) – m

ψ

-(x )

ψ

(x)

wariowanie tego lagranżjanu prowadzi do równania ruchu nazywanego równaniem Diraca :
( i

∂

^ – m )

ψ

(x) = 0

∂

^

≡

γµ∂µ

,

γµ

- macierz Diraca ( zobacz tekst pt. Wprowadzenie do mechaniki kwantowej” )

Pole spinorowe

ψ

a(x ) ma postać kolumny ( spinor Diraca ) :

LITERATURA.

1) „Droga do rzeczywistości” - R. Penrose. Prószyński i S-ka 2004
2) „Klasyczna teoria pola” - K. Meissner. WN-PWN 2002
3) „Teoria pola” - L. D. Landau, E. M. Lifszyc PWN 1977
4) „Elementy klasycznej i kwantowej teorii pola” - J. Karaśkiwewicz. UMCS Lublin 2003
5) „Wprowadzenie w teorię pól klasycznych” - A.A. Bogusz, L. G. Moroz
Mińsk 1968 (język rosyjski)
6) „Podstawy fizyki teoretycznej” - B. W. Medwedew.
Moskwa Nauka 1977 (język rosyjski)
7) „Podstawowe zasady mechaniki klasycznej i - E. Schmutzer
klasycznej teorii pola” Moskwa Mir 1976 (język rosyjski)
8) „Teoria pola - część I” - J. Rzewuski. PWN 1964
(język angielski)
9) „Współczesna geometria – - B.A. Dubrownin, S. P. Nowikow
metody i zastosowania” A. T. Fomenko
Moskwa Nauka 1986 (język rosyjski )
10) „Mechanika klasyczna” - J. Leech
Moskwa 1961 (język rosyjski )
11) „Elektrodynamika i klasyczna teoria pola - A. O. Barut
oraz cząstek” New York 1980 (język angielski )
12) „Encyklopedia fizyki matematycznej” - red. L. D. Faddeew.
( hasło : „Twierdzenie Noether” ) Moskwa 1988 (język rosyjski)
13) „Rachunek wariacyjny” - I. M. Gelfand, S. W. Fomin PWN 1972
14) „Pola klasyczne” - D. W. Galcow, Ju. W. Grac , W, C. Żukowskij
( przekład własny )
15) „Wprowadzenie do symetrii i supersymetrii -- Jan Łopuszański
w kwantowej teorii pola” World Scientific
(język angielski)
16) „Wstęp do teorii pól kwantowych” -- Iwo Białynicki-Birula
PWN 1971

12

17) „Kwantowa teoria pola” -- Lewis H. Ryder ( przekład własny )

18) „Teoria pola. Współczesne wprowadzenie” -- Pierre Ramond ( przekład własny )