
1
###########################################################################
Podstawowe zasady mechaniki klasycznej i klasycznej teorii pola
(aparat kanoniczny )
E. Schmutzer
VEB Deutscher Verlag der Wissenschaften Berlin 1973
**************************************************************************
Tłumaczenie rosyjskie : G. M. Iłiczewoj, pod redakcją : S. P. Allilujewa
Moskwa „Mir” 1976
***************************************************************************
tłumaczenie z rosyjskiego : R. Waligóra
Ostatnia modyfikacja : 2008-12-29
Tłumaczenie całości książki.
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
Wprowadzenie do tłumaczenia
Prezentowane tłumaczenie książki znanego fizyka teoretyka Ernesta Schmutzera przedstawia w
„skondensowanej” formie podstawy mechaniki analitycznej wraz z najbardziej reprezentatywnymi przykładami
jej zastosowania. Jest to wykład bardzo klarowny i konsekwentnie trzymający się wybranego kierunku tj. mający
głównie za zadanie wprowadzenie do klasycznej teorii pola. Przed lekturą dobrze było by „odświeżyć”
wiadomości związane z tematem sięgając np. po książki :
1). W. Rubinowicz , W. Królikowski – „Mechanika teoretyczna” . WN-PWN 1988
2). R. Gutowski – „Mechanika analityczna”. PWN 1971
3). Gantmacher – „Wykłady z mechaniki analitycznej” PWN 1972
Słowo wstępne tłumacza i redaktora
Istotą prezentowanej książki jest wskazanie tego gdzie „kończy się” mechanika teoretyczna i „zaczyna się „
fizyka teoretyczna. Postawienie linii podziału między tymi dyscyplinami jest w znacznym stopniu sprawą
umowną , przykładowo autor tej monografii uważa, że w zasadzie jest możliwe rozszerzenie pojęć mechaniki, w
taki sposób aby miały one sens również w teorii pola. Obecnie mechanika klasyczna i teoria pola są wykładane
oddzielnie i są przedstawiane w różnych książkach. Właśnie dlatego interesującym jest próba jednolitego
wyłożenia tych zagadnień z ogólnego punktu widzenia, dokonana w przedstawionej czytelnikowi książce.
Podstawą dla wykładu jest formalizm Lagrange’a – Hamiltona oraz związane z tym formalizmem koncepcje –
tzn. wszystko to, co w skrócie nazywamy „aparatem kanonicznym” lub „formalizmem kanonicznym”, - mając to
za podstawę, autor daje jednolity wykład mechaniki i teorii pola. Przy każdej sposobności pokazuje on
możliwości „wyjścia” z mechaniki w obszar teorii pola oraz demonstruje organiczny związek tych dwóch gałęzi
fizyki (przykładowo – autor, w nie standardowy sposób formułuje ogólne twierdzenia Noether, stosując je
najpierw w teorii pola a dopiero potem w mechanice )
Wszystko to sprawia , że książka powinna być interesująca dla szerokiego kręgu odbiorców, chociaż nie
zdecydowalibyśmy się rekomendować jej dla początkującego w temacie czytelnika.
Profesor Uniwersytetu w Jenie -Ernest Schmutzer specjalizuje się w teorii grawitacji , przewodniczy grupie
naukowej zajmującej się aktualnymi problemami relatywistycznej teorii pola. Jest m.in. autorem monumentalnej
monografii pt. „Relativistische phisik” (fizyka relatywistyczna – przypis własny) (zobacz spis literatury).
Radzieckiemu (obecnie, oczywiście Rosyjskiemu – przypis własny ) czytelnikowi znany jest przekład jego
przeglądowej pracy dotyczącej własności symetrii w mechanice klasycznej (włączając w to relatywistyczną ) i
kwantowej. ( E. Schmutzer – „Symetrie i prawa zachowania w fizyce” Mir Moskwa 1974 )
Książkę obecnie prezentowaną można traktować jako, pewnego rodzaju wprowadzenie do książki wyżej
wymienionej - napisane już po jej wydaniu .
Prezentowany w przedstawionej monografii materiał, jest w znacznej mierze odbiciem punktu widzenia autora
na przedmiot , stanowiąc jednocześnie wyraz kręgu jego zainteresowań.
W części A - książki przy wykładzie mechaniki dostrzec można wpływ koncepcji Hertza , dosyć powiedzieć ,że
siły nie potencjalne traktowane są równorzędnie z siłami reakcji więzów nieholonomicznych (rozdział 5.1 i 5.2 –

2
jak wiadomo Hertz w swojej mechanice usunął pojęcie siły rozumianej w takiej postaci w jakiej było ono
przedstawione w mechanice Newtona a rozpatrywał siły jako efekty obecności ukrytych lub jawnych więzów)
W części B , poświęconej klasycznej teorii pola , wybór konkretnych pól którymi ilustrowana jest ogólna teoria,
w pełni podyktowany jest gustem autora. W praktyce są to te same pola, jakie występują w jego pracy „Symetrie
i prawa zachowania w fizyce”, przykładów związanych z ruchem środowiska ciągłego autor nie stosuje.
Zarówno ze względu na dobór materiału jak i na sposób jego wyłożenia należy podkreślić dwie okoliczności.
Po pierwsze - w części A, książka daleka jest od tradycjonalnego wykładu materiału mechaniki analitycznej ;
poruszane są jedynie te rozdziały, które mogą stanowić pomost między mechaniką i teorią pola.
Po drugie - książka jest opracowanym zapisem wykładów co często znajduje swoje charakterystyczne odbicie w
prezentowanym tekście. W jednych rozdziałach autor w sposób pełny prowadzi swoje wykłady (niekiedy dosyć
uciążliwe), w innych szkicuje tylko zarys problemu. Niejednokrotnie wprowadza nie wykorzystywane dalej
pojęcia (pochodna Liego, tensor momentu obrotu w teorii pola i inne) – robi to chyba po to aby „wzbogacić”
ogólną wiedzę słuchacza. Miejscami - przyjęte założenia nie są omawiane w sposób dokładny (znane uściślenia
dodane są w dopiskach redaktora przekładu i tłumacza, jednak tylko tam gdzie mogłyby wyniknąć
nieporozumienia o zasadniczym charakterze ). Niekiedy autor dokładnie omawia pojęcia wyjściowe oraz
dokładnie rozpisuje sformułowane zależności , a niekiedy traktuje je w sposób ogólny. W takich przypadkach
czytelnik może sięgnąć do materiałów źródłowych, których spis dany jest w bibliografii.
Przy przekładzie poprawiono szereg błędów drukarskich , oraz dokonano kilku poprawek zgodnych z sugestiami
autora - za co jesteśmy mu wdzięczni.
W ogólności książka ta stanowi cenny wkład do obszernej literatury dotyczącej mechaniki analitycznej i teorii
pola. Może być ona wykorzystana zarówno jako podręcznik dla studentów uniwersytetów i szkół
pedagogicznych jak i studentów politechnik. Oprócz tego może ona służyć jako pomoc dla pracowników
naukowych oraz dla wszystkich zainteresowanych fizyką teoretyczną.
S. Allilujew
G. Iłiczjewa
Słowo wstępne autora
Stały postęp nauki w sposób naturalny prowadzi do koncentracji materiału wykładanego przy nauczaniu fizyki w
szkołach wyższych. W szczególności , okazuje się koniecznym - od samego początku wykładać fizykę
eksperymentalną i teoretyczną w ścisłym powiązaniu jedna z drugą. Mając na uwadze jedności teorii i praktyki
takie wyłożenie posiada wiele zalet, związanych z tym, że wyniki teoretyczne cały czas muszą mieć oparcie w
faktach eksperymentalnych. Jednak rzeczywista realizacja takiego programu nieubłaganie prowadzi do obniżenia
roli logiczno-dedukcyjnej w budowie fizyki teoretycznej, a jak wiadomo rola taka jest konieczna w tym , aby
student mógł zorientować się w ogólnej koncepcji fizyki teoretycznej, a przez to orientować się w fizyce jako
nauce. Dlatego na naszym uniwersytecie został wprowadzony cykl wykładów „Podstawowe zasady mechaniki
klasycznej i klasycznej teorii pola” na którym przedstawiana jest kwintesencja klasycznych rozdziałów fizyki
teoretycznej (z wyłączeniem termodynamiki i fizyki statystycznej), w szczególności nacisk położono na aparat
kanoniczny. Przygotowałem taki wykład i dwa razy go wygłosiłem. Ważność tego materiału dla podstaw fizyki i
brak jednego i spójnego jego wyłożenia w podręcznikach pobudził mnie do redakcji i udostępnienia tego
wykładu w formie prezentowanej książki.
Przy przygotowaniu niniejszej publikacji wykorzystałem notatki prowadzone przez studentów , za co chciałbym
im podziękować.
E. Schmutzer Jena czerwiec 1973

3
CZ
ĘŚĆ A
MECHANIKA KLASYCZNA
1. RÓWNANIA LAGRANGE’A PIERWSZEGO RODZAJU
Będziemy rozpatrywali układ N punktów materialnych , przyjmując następujące oznaczenia:
m
Ω
- masa Ω-go punktu materialnego
x
Ω
, y
Ω
, z
Ω
- współrzędne ortogonalne kartezjańskie, Ω-go punktu materialnego, położenie którego określone
jest wektorem wodzącym : r
Ω
(„tłusta” czcionka oznacza – wektor , przypis własny)
K
Ω
x , K
Ω
y , K
Ω
z – rzuty na osie ortogonalnego kartezjańskiego układu współrzędnych siły aktywnej : K
Ω
-
działającej na Ω-ty punkt materialny.
Z
Ω
x , Z
Ω
y , Z
Ω
z – rzuty na osie ortogonalnego kartezjańskiego układu współrzędnych siły reakcji : Z
Ω
,
działającej na Ω-ty punkt materialny.
Duże greckie litery (Ω, Γ itd.) w indeksach oznaczają numery punktów materialnych.
Jak wiadomo, równanie Newtona (drugie prawo Newtona; Lex secunda, 1687 rok) dotyczące ruchu Ω -go
punktu materialnego , na który działa tylko siła aktywna (siła pasywna to siła reakcji więzów – przypis własny),
w inercjalnym układzie odniesienia (IUO – przypis własny ) zapisywane jest w następujący sposób :
m
Ω
r..
Ω
= K
Ω
(gdzie r..
Ω
- oznacza drugą pochodną po czasie wektora r
- przypis własny) (1.1)
W całej książce będziemy wykorzystywali tylko IUO i dlatego nie będziemy uwzględniać tak zwanych sił
inercji. (tj. sił pozornych – przypis własny)
W charakterze przykładu sił aktywnych można wskazać siły elektromagnetyczne , siły jądrowe , siły
grawitacyjne (siły ciążenia - w ramach teorii Newtonowskiej ) i inne tego typu.
Jeśli na rozpatrywany punkt materialny działa oprócz siły aktywnej , siła reakcji - będąca wynikiem pewnych
ograniczeń nałożonych na poruszający się punkt (przykładowo przez warunek mówiący, że punkt materialny
może się poruszać tylko po pewnej powierzchni), to siła ta wchodzi do równania (1.1) jako dodatkowy składnik :
m
Ω
r..
Ω
= K
Ω
+ Z
Ω
(1.2a)
lub , przedstawiając je jako rzuty (równanie (1.2a) jest równaniem wektorowym w trójwymiarowej przestrzeni
Euklidesa możemy rozpisać go składowe zgodne z osiami wprowadzonego kartezjańskiego układu
współrzędnych – przypis własny) na osie układu :
m
Ω
x..
Ω
= K
Ω
x + Z
Ω
x (1.2a)
m
Ω
y..
Ω
= K
Ω
y + Z
Ω
y (1.2a)
m
Ω
z..
Ω
= K
Ω
z + Z
Ω
z (1.2a)
To rozszerzenie (uwzględniające siły reakcji) równań będziemy nazywali „równaniami Lagrange’a pierwszego
rodzaju” (1788 rok) (równaniami Lagrange’a pierwszego rodzaju zwykle nazywa się równania (3.4) – przypis
tłumacza )
2. WI
ĘZY
2.1 RÓWNANIA WIĘZÓW
W tym rozdziale wyprowadzimy zależności między równaniami więzów a siłami reakcji będącymi wynikiem
obecności tych więzów (reakcjami więzów). Naśladując podejście G. Hertza zapiszemy dla m-tego
więzu nałożonego na układ N punktów materialnych , równania w postaci różniczkowej :
N
duµ ≡ cµ dt + ∑ aµΩ dxΩ + bµΩ dyΩ + cµΩ dzΩ = 0 ; µ = 1,2,3, ..., m (2.1)
Ω =1
(małe greckie litery przy indeksach oznaczają numery równań więzów)
Współczynniki formy różniczkowej (2.1) są funkcjami współrzędnych cząstki (pojęcie „cząstka” i „punkt
materialny” wykorzystywane są jako synonimy) i czasu.
Wprowadzając następujące wektory :
aµΩ = i aµΩ + j bµΩ + k cµΩ (2.2)
równania (2.1) można zapisać w następującej postaci :

4
N
duµ ≡ cµ dt + ∑ aµΩ drΩ = 0 (2.3)
Ω =1
Ponieważ każdy punkt materialny posiada trzy stopnie swobody , liczba stopni swobody dla układu jako całości
(na mocy obecności m równań więzów) jest dana równaniem :
f = 3N – m (2.4)
Jeśli nie rozpatrywać przypadku równowagi , to należy przyjąć, że spełniona jest nierówność : m < 3N
2.2 KLASYFIKACJA WIĘZÓW
Więzy klasyfikujemy według ich dwóch różnych własności (* Zwykle więzy klasyfikujemy również według
innych własności. Dzielą się one na : utrzymujące i nie utrzymujące (przedstawiane są one za pomocą
odpowiednio równości i nierówności ). Oprócz tego możemy wyróżnić klasę więzów idealnych , mających tą
własność , że suma prac elementarnych sił reakcji tych więzów, na dowolnym wirtualnym przesunięciu (zobacz
rozdział 3.1) jest równa zeru. Autor nie wprowadza tych pojęć , ponieważ ogranicza się on w swoich
rozważaniach do więzów utrzymujących , idealnych – przypis tłumacza *)
(W literaturze polskiej więzy utrzymujące nazywane są dwustronnymi a nie utrzymujące jednostronnymi –
przypis własny)
a) Zależność (lub nie zależność) odpowiadającej im formy różniczkowej od czasu. Jeśli cµ = 0 i
∂
aµΩ /
∂
t = 0 to więzy nazywamy „skleronomicznymi”. Jeśli współczynniki nie spełniają tych
warunków , to forma różniczkowa zależna jest od czasu i więzy nazywamy „reonomicznymi”
b) Całkowalności (lub niecałkowalności) odpowiadającej im formy różniczkowej. Jeśli forma różniczkowa
(2.1) jest różniczka zupełną , to więzy nazywamy „holonomicznymi”. Ma to miejsce w przypadku ,
kiedy:
∂
aµΩ /
∂
xΓ =
∂
aµΓ /
∂
xΩ ;
∂
cµ /
∂
xΩ =
∂
aµΩ /
∂
t ; itd. (2.5)
W tym przypadku istnieją funkcje : Fµ (xΩ ,t ) , takie ,że duµ = dFµ = 0 i dlatego równanie więzów
holonomicznych można zapisać w następującej postaci :
Fµ (rΩ ,t ) – const. = 0 (2.6)
Wtedy :
cµ =
∂
Fµ/
∂
t i aµΩ =
∂
Fµ/
∂
rΩ = grad rΩ Fµ (2.7)
Jeśli forma (2.1) nie jest różniczką zupełną , jednak istnieje dla niej pewien mnożnik całkujący , to takie więzy,
również nazywamy holonomicznymi.
Jeśli forma (2.1) nie jest różniczką zupełną i nie może być w nią przekształcona za pomocą jakiegokolwiek
mnożnika całkującego , to więzy nazywamy „nieholonomicznymi”. Więzy takie przed Hertzem rozpatrywał
A. Foss (1884 r. )
3. ZASADY RÓ
śNICZKOWE
3.1 ZASADA D’ALEMBERTA
Zasada D’Alemberta jest najbardziej znaną ze wszystkich zasad różniczkowych. Aby ją sformułować ,
konieczne jest wprowadzenie pojęcia „przemieszczenia (przesunięcia) wirtualnego”.
Wirtualne przesunięcie – jest to dopuszczalne przez więzy, nieskończenie małe przemieszczenie punktu w
pewnej ustalonej i stałej chwili czasu. Przesunięcie wirtualne Ω-tego punktu materialnego oznaczamy przez :
δrΩ (w odróżnieniu od rzeczywistego nieskończenie małego przesunięcia drΩ ,zachodzącego w ciągu pewnej
chwili czasu ).
Zasadę D’Alemberta (równanie (3.1) nazywamy również ogólnym równaniem dynamiki – przypis tłumacza)
Zapisujemy w następujący sposób :
N
Σ (mΩ – r..ΩKΩ ) δrΩ = 0 (3.1)
Ω =1
Na mocy faktu , że przesunięcie wirtualne δrΩ nie jest niezależnym , z równania tego nie wynika równanie
ruchu (1.1). Dlatego wynika pytanie - jakie równanie ruchu jest równoważne równości (3.1) ?
Dla wirtualnych przesunięć δrΩ równanie więzów (2.3) przyjmuje postać :
N
Σ aµΩ δrΩ = 0 (3.2)
Ω =1

5
Zgodnie z metodą mnożników Lagrange’a , pomnożymy każde z tych równań przez odpowiadający mu mnożnik
λµ , a następnie z sumujemy wyniki względem wszystkich m więzów i odejmiemy otrzymaną sumę od równości
(3.1). To daje nam :
N m
Σ (mΩ r..Ω - KΩ - Σ λµaµΩ ) δrΩ = 0 (3.3)
Ω =1 µ =1
Stąd możemy otrzymać równanie ruchu w następującej formie :
m
mΩ r
..
Ω = KΩ + Σ λµaµΩ (3.4)
µ =1
Wybierzmy m mnożników λµ , w taki sposób, że dla m składowych wchodzących do równania (3.3) wielkości
stojące w nawiasie staną się równe zeru. Po tej operacji pozostanie suma zawierająca f =3N-m składowych.
Ponieważ rozpatrywany układ ma f stopni swobody , f z przemieszczeń - δxΩ , δyΩ , δzΩ można wybrać
dowolnie , w szczególności można wszystkie , oprócz jednego wybrać równe zeru. Wtedy współczynnik przy
tym niezerowym przemieszczeniu (wielkość stojąca w odpowiednim nawiasie) powinien być równy zeru. Zatem
,wszystkie wielkości stojące w nawiasach powinny być równe zeru.
3N równań (3.4) i m równań (2.1) razem przedstawiają układ 3N + m równań określających 3N współrzędnych
xΩ , yΩ , zΩ i m nieokreślonych mnożników Lagrange’a - λµ .
Porównując równanie (3.4) i (1.2a) , znajdujemy następujące wyrażenie dla sumarycznej siły reakcji więzów ,
działającej na Ω-ty punkt materialny :
m
ZΩ = Σ λµaµΩ (3.5)
µ =1
Zatem, przedstawiliśmy siły reakcji przez współczynniki wchodzące do równania więzów. Na mocy równości
(3.2) z równości (3.5) wynika ,że:
N
Σ ZΩ δrΩ = 0 (3.6)
Ω =1
Będziemy interpretować iloczyn skalarny ZΩ δrΩ , jako pracę wirtualną , wykonywaną przez siłę reakcji
ZΩ działającą na Ω-ty punkt materialny , wtedy równanie (3.6) stanie się równoważne następującemu
stwierdzeniu :
„sumaryczna praca wirtualna wszystkich sił reakcji działających na układ mechaniczny jest równa zeru”.
W szczególnym przypadku równowagi ( r..Ω= 0 ) zasada D’Alemberta nazywa się „zasadą wirtualnych
przesunięć”. Zasada ta wykorzystywana jest w celu wyprowadzenia równań równowagi.
Aby wyjaśnić powyższe ogólne teoretyczne wywody , wyobraźmy sobie układ składający się z dwóch punktów
materialnych o równej masie , na które działa tylko siła ciążenia. Punkty te połączone są między sobą za pomocą
nie rozciągliwej nici przerzuconej przez bloczek. Ruch tych punktów nie jest ruchem swobodnym : równania
więzów otrzymujemy z warunku połączenia punktów nicią o stałej długości , dlatego
wirtualne przesunięcie jednego z punktów pociąga za sobą wirtualne przesunięcie drugiego z punktów.
Przy tym sumaryczna praca wirtualna będzie równa zeru. W przypadku punktu izolowanego , na ruch którego
nałożono jeden holonomiczny więz, wyrażenie (3.5) na reakcje tego więzu przyjmuje postać :
Z = λa = λ(
∂
F/
∂
r) = λ grad F (3.7)
(zobacz równość (2.7)). Odpowiednio, siła reakcji danego więzu jest prostopadła do powierzchni F= const.
np. do powierzchni stołu. Zatem wyjaśniliśmy ,że przy wirtualnym przemieszczeniu punktu po tej powierzchni
praca sił reakcji jest równa zeru.
Dla oznaczenia wirtualnego przesunięcia wykorzystaliśmy symbol wariacji δ. Ponieważ czas jest stały
(i ustalony) w rzeczywistości chodzi o nieskończenie małą zmianę (wariację) współrzędnych. Dlatego
odpowiadające matematyczne rachunki wykonywane są tak samo jak w rachunku wariacyjnym, w szczególności
obliczenie wariacji funkcji prowadzi się analogicznie jak obliczenie różniczki zupełnej.
3.2 RÓWNANIE ZACHOWANIA ENERGII DLA UKŁADU Z WIĘZAMI
Zbadamy zmianę energii układu mechanicznego z nałożonymi więzami , przy jego ruchu rzeczywistym.
Mnożąc równanie Lagrange’a pierwszego rodzaju (3.4) przez drΩ i rozpatrując prace elementarną ,
wykonywaną przez działającą na Ω-ty punkt materialny siłę aktywną :
dAΩ = KΩdrΩ

6
oraz energię kinetyczną Ω-tego punktu materialnego :
TΩ = ½ mΩ r
..2
Ω (3.8)
Otrzymamy równanie zachowania energii dla tego układu :
m
dTΩ = dAΩ + Σ λµaµΩdrΩ (3.9)
µ =1
W przypadku więzów holonomicznych możemy podstawić do tego równania wyrażenie (2.7) dla aµΩ a
następnie przepiszemy go następująco :
m
dTΩ = dAΩ + Σ λµ(
∂
Fµ /
∂
rΩ) drΩ (3.10)
µ =1
Z zależności (2.6) mamy :
m
dFµ = (
∂
Fµ /
∂
t) dt +
Σ (
∂
Fµ /
∂
rΩ) drΩ (3.11)
µ =1
Sumując równania (3.10) po wszystkich punktach materialnych i przyjmując do wiadomości równości (3.11)
oraz zakładając :
N N
dT =
Σ TΩ ; dA = Σ dAΩ (3.12)
Ω =1 Ω =1
Otrzymamy równanie zachowania dla różniczki sumarycznej energii kinetycznej T i sumarycznej pracy
elementarnej A :
m
dT = dA -
Σ λµ(
∂
Fµ /
∂
t )dt (3.13)
µ =1
Druga składowa w prawej części tego równania przedstawia pracę elementarną , wykonywaną przez siły reakcji
więzów reonomicznych (przykładowo – zmiana energii kinetycznej piłeczki tenisowej przy przesunięciu rakiety
, płaszczyznę której przedstawia równanie (2.6), a która obrazuje więzy holonomiczno- reonomiczne ).
Jeśli siły aktywne , działające na układ są siłami potencjalnymi to ma miejsce równość :
dA = -dU (3.14)
gdzie : U – jest energią potencjalną. Zakładając :
dE = dT + dU (3.15)
gdzie : E- jest energią całkowitą układu , z równania (3.13) otrzymamy równanie zachowania energii w postaci :
m
dE = -
Σ λµ(
∂
Fµ /
∂
t )dt (3.16)
µ =1
Dla układu z więzami holonomiczno-skleronomicznymi, z zależności tej bezpośrednio wynika prawo
zachowania energii :
dE = 0 lub E = const. (3.17)
3.3 PRZYKŁAD WIEZÓW HOLONOMICZNYCH
(RÓWNOWAGA WAHADŁA SFERYCZNEGO)
Wykorzystując zasadę wirtualnych przesunięć , znajdziemy położenie równowagi punktu materialnego ,
znajdującego się w jednorodnym polu grawitacyjnym (polu ciążenia) i poruszającego się po sferze.
(wahadło sferyczne). Jeśli promień sfery jest równy R (rysunek nr 1) to równanie więzu holonomiczno-
skleronomicznego przyjmuje postać :
F - const = x2 + y2 + z2 - R2 = 0 (3.18)
Energia potencjalna dana jest wyrażeniem :
U = U0 + mgz (3.19)
gdzie g – jest przyspieszeniem grawitacyjnym,
oraz :
K = - grad U = -mg k
(3.20)
Obecność więzów ogranicza ruch rozpatrywanego punktu i wyklucza jeden z trzech stopni swobody, zatem
dysponujemy dwoma niezależnymi współrzędnymi. Położenia równowagi będziemy poszukiwać w następujący
sposób : znajdziemy ekstremum energii potencjalnej U(z) uwzględniając ,to że współrzędna z jest wybrana nie w

7
sposób dowolny ,ale spełnia równanie (3.18). W analizie matematycznej wykorzystuje się dwie metody
znajdowania ekstremum funkcji : metoda rugowania i metoda mnożników Lagrange’a.
Rys. 1
Posługując się metodą rugowania , podstawimy do wyrażenia (3.19) wartość z otrzymaną z równania (3.18) , co
daje nam :
U = U0 + mg sqrt( R
2 - x2 - y2 )
(3.21)
Gdzie x , y – są współrzędnymi niezależnymi. Warunki konieczne na ekstremum są następujące :
∂
U/
∂
x = - mgx / sqrt( R2 - x2 - y2 ) = 0 ;
∂
U/
∂
y = - mgy / sqrt( R2 - x2 - y2 ) = 0
(3.22)
z czego wynika, że :
x = 0 ; y = 0
(3.23)
oraz na mocy (3.18) : z =
±
R
(3.24)
( plus odpowiada położeniu równowagi nietrwałej a minus – położeniu równowagi trwałej )
Wykorzystując metodę mnożników Lagrange’a , poszukujemy ekstremum funkcji :
U’ = U0 + mgz – λ (x
2 + y2 + z2 - R2 )
(3.25)
Mamy tutaj nową zmienną - mnożnik λ, i dlatego wszystkie współrzędne x, y, z można uważać za niezależne.
Wtedy konieczne warunki na ekstremum zapisujemy w postaci :
∂
U’/
∂
x = -2λx = 0 ;
∂
U’/
∂
y = -2λy = 0 ;
∂
U’/
∂
z = mg-2λz = 0 ;
(3.26)
skąd wynika ,że : x = 0 ; y = 0 ; λ = mg / 2z
(3.27)
Na mocy (3.18) mamy : z =
±
R
(3.28)
I dlatego : λ =
±
mg / 2R
(3.29)
Wykorzystanie przedstawionej powyżej metody mnożników Lagrange’a jest równoważne wykorzystaniu
metody przesunięć możliwych. Istotnie - w przypadku równowagi równanie wektorowe (3.4) sprowadza się do
równości :
Kx + λ(
∂
F/
∂
x) = 0; Ky + λ(
∂
F/
∂
y) = 0; Kz + λ(
∂
F/
∂
z) = 0;
(3.30)
Które można przepisać w postaci :
∂
U/
∂
x = λ(
∂
F/
∂
x);
∂
U/
∂
y = λ(
∂
F/
∂
y);
∂
U/
∂
z = λ(
∂
F/
∂
z);
(3.31)
lub w postaci :
∂
U’/
∂
x = 0 ;
∂
U’/
∂
y = 0 ;
∂
U’/
∂
z = 0 ;
(3.32)
tj. w postaci równości (3.26). Siła reakcji określona jest zgodnie z zależnością (3.7) i ma postać :
Z = λ grad F = 2λ(ix + jy + kz)
(3.33)
W położeniu równowagi siła ta przyjmuje wartość :
Z = kmg
(3.34)
3.4 PRZYKŁAD WIĘZU NIEHOLONOMICZNEGO ( TOCZĄCY SIĘ DYSK )
W charakterze przykładu ruchu układu o więzach nieholonomicznych G. Hamel badał toczący się dysk po
powierzchni szorstkiej. Podkreślmy , że teraz rozpatrujemy ruch ciała sztywnego , a nie punktu materialnego.
Wybierzmy układ współrzędnych kartezjańskich w taki sposób aby płaszczyzna x, y pokrywała się z
płaszczyzną nieruchomą (rys. 2 )
wtedy współrzędne x, y będą określały położenie punktu P styku dysku ( o promieniu r ) z tą płaszczyzną.
Oznaczmy przez:
ζ
- kąt między osią obrotu a osią z, przez
ψ
- kąt między styczną do toru w punkcie styczności
a osią x ,
ϕ
- kąt między promieniem przechodzącym przez punkt styczności i pewnym ustalonym promieniem r
, toczącego się okręgu , kąt ten odczytujemy w kierunku obrotu dysku.

8
Rys. 2
Zatem – położenie dysku określone jest pięcioma współrzędnymi : x, y,
ψ
,
ζ
,
ϕ
. jednak , ponieważ obrotowi
odbywającego się bez poślizgu, konieczne towarzyszy przemieszczenie , powinien być spełniony warunek :
ds. = a d
ϕ
Rzutując ten warunek na oś współrzędnych , otrzymujemy dwa równania więzów :
dx = a d
ϕ
cos (
ψ
) , dy = a d
ϕ
sin (
ψ
) (3.35)
lub :
dF1 = dx - a d
ϕ
cos (
ψ
) = 0 ; dF2 = dy - a d
ϕ
sin(
ψ
) = 0 (3.36)
Ponieważ warunki całkowalności nie są tutaj spełnione mamy dwa równania więzów nieholonomicznych , zatem
dysk infinitezymalnie ma tylko trzy stopnie swobody. Tą ilość stopni swobody należy odróżniać od liczby
współrzędnych niezależnych , które mogą być zadane w charakterze wartości początkowych przy ruchu dysku
( liczby stopni swobody w ogólności) *) Liczbę stopni swobody układu o więzach nieholonomicznych zwykle
określa się jako liczbę niezależnych różniczek ( „liczbę infinitezymalnych stopni swobody” – zgodnie z
terminologią autora ), przy tym pojęcia „liczba stopni swobody w ogólności” zazwyczaj się nie wykorzystuje –
przypis tłumacza *)
3.5 ZASADA GAUSSA (ZASADA NAJMNIEJSZEGO PRZYMUSU )
(zobacz [2] str. 107, literatury podanej we wprowadzeniu – przypis własny )
W związku ze swoją metoda najmniejszych kwadratów Gauss ( 1829 rok ) sformułował zasadę najmniejszego
przymusu. Według Gaussa miarą przymusu jest wielkość :
N N
Z =
Σ m
Ω
[ r
..
Ω – (KΩ/m
Ω
)]
2 = Σ m
Ω
[ x
..
Ω – (KΩx/m
Ω
)]
2 + [ y..Ω – (KΩy/m
Ω
)]
2 +
Ω
=1
Ω
=1
+ [ z..Ω – (KΩz/m
Ω
)]
2 (3.37)
Ponieważ ruch układu mechanicznego przy zdjęciu nałożonych na niego więzów, opisywany byłby przez prawo
Newtona (1.1) przymus w istocie przedstawia sobą miarę odchylenia układu od ruchu swobodnego. Składowe
kwadratowe odpowiadają kwadratom błędu w teorii błędów ,a masy – wagą.
Zgodnie z Gaussem , ruch rzeczywisty na który nałożono więzy zachodzi tak aby zdefiniowany powyżej
przymus, osiągał minimum, tj. :
δ
Z = 0 (3.38)
Przy tym wariacja
δ
Z brana jest przy ustalonych wartościach współrzędnych i prędkości wszystkich punktów :
δ
rΩ = 0 ,
δ
r.Ω = 0 (3.39)
Ze wzoru (3.37) wynika , że :
N
δ
Z = 2
Σ ( m
Ω
r
..
Ω – KΩ )
δ
r..Ω (3.40)
Ω
=1
Zgodnie z równaniami więzów (2.3) :
N
du
µ
/dt = c
µ
+ 2
Σ a
µΩ
r.Ω = 0 (3.41)
Ω
=1

9
skąd różniczkując w sposób zupełny po czasie znajdujemy :
N N N N
d2u
µ
/dt2 =
Σ (
∂
c
µ
/
∂
rΩ )r
.
Ω + Σ a
µΩ
r.Ω + Σ [ ( r
.
Ω
∇Γ
) a
µΩ
] r.Ω + (
∂
c
µ
/
∂
t) +
Σ (
∂
a
µΩ
/
∂
t)r.Ω = 0
Ω
=1
Ω
=1
Ω
=1
Ω
=1
(3.42)
Po uwzględnienieniu równości (3.39) otrzymamy :
N
Σ a
µΩ
δ
r..Ω = 0 (3.43)
Ω
=1
Pomnożymy to równanie przez mnożnik Lagrange’a
λµ
i zsumujemy względem wszystkich więzów :
m N
Σ Σ
λµ
a
µΩ
δ
r..Ω = 0 (3.44)
µ
=1
Ω
1
Równość tą pomnożymy przez dwa i człon po członie odejmiemy od zależności (3.40). Po tej operacji warunek
(3.38) możemy zapisać w następującej postaci :
N m
δ
Z = 2
Σ (m
Ω
r..Ω - K
Ω
-
Σ
λµ
a
µΩ
)
δ
r..Ω = 0 (3.45)
Ω
=1
µ
=1
Stąd można wyprowadzić równania Lagrange’a pierwszego rodzaju (3.4) , w sposób podobny jak w rozdziale
poświęconym zasadzie d’Alemberta.
Zasada najprostszej trajektorii Hertza (zobacz [2] str.116 literatury podanej we wprowadzeniu – przypis własny )
jest szczególnym przypadkiem zasady Gaussa i wydawać się by mogło, że nie zasługuje na osobne omówienie.
Jednak kryją się w niej głębokie fizyczne idee, pozostające aktualnymi i w chwili obecnej. H. Hertz dążył do
wykluczenia sił ze swojej teorii i rozpatrywał układy na które nie działają siły aktywne. Przy tym wychodził z
pojęcia elementu drogi ds. , toru układu w wielowymiarowej przestrzeni :
(ds.)2 =
Σ (dkk )2 (3.46)
k
oraz pojęcia krzywizny sqrt(K), tego toru :
K =
Σ (d2xk /ds2 )2 (3.47)
k
W celu rozwinięcia swojej teorii Hertz przyjmował masy wszystkich punktów jako wielokrotności pewnej masy
jednostkowej. Jego zasada najprostszej trajektorii polega na minimalizacji krzywizny :
δ
K = 0 (3.48)
Od razu widać , że idea ta jest bardzo bliska Einsteinowskiej idei teorii grawitacji , w której jak wiadomo , siła
ciążenia pojawia się jako wynik zakrzywienia czterowymiarowej czasoprzestrzeni , co powoduje , że ruch
cząstki odbywa się po geodezyjnej (po najprostszej linii w sensie geometrii Riemanna ).
4. ZASADY CAŁKOWE
4.1 ZASADA HAMILTONA
4.1.1 PODSTAWOWE ZADANIE RACHUNKU WARIACYJNEGO
Podczas gdy w zwykłej teorii poszukiwania maksimum i minimum chodzi o określenie wartości ekstremalnej
pewnej funkcji , podstawą rachunku wariacyjnego jest pytanie o osiąganie wartości ekstremalnej całki :
t1
I =
∫
F(Q, dQ/dt , t ) dt (4.1)
t0
W całce tej funkcja F(Q, dQ/dt , t ) jest zadana ale na rozpatrywanym odcinku „dopuszczamy do
współzawodnictwa” dowolnych krzywych Q(t) o ustalonych punktach początkowych i końcowych. Na
zmienność tych krzywych nałożono warunki :
Q( t0) = const. ; Q( t1) = const. (4.2)
Na rysunku 3 pokazano krzywe q = q(t) – tak zwane ekstremalne, które spełniają wymagana własność
ekstremalności całki (4.1).

10
Odpowiadające szukanej funkcji q(t) , funkcje Q(t) nazywamy funkcjami porównawczymi i zakładamy dla nich :
Q(t) = q(t) +
ε
ζ
(t) (4.3)
zakładając , że
ε
- jest nieskończenie małym parametrem. Na mocy warunków (4.2) dowolna funkcja
ζ
(t)
powinna spełniać równości :
ζ
(t0) =
ζ
(t1) = 0 (4.4)
Wielkość :
δ
q(t) =
ε
ζ
(t) (4.5)
nazywamy „wariacją funkcji q(t).Podstawiając wyrażenie (4.3) do wzoru (4.1), otrzymamy całkę zależną od
parametru
ε
:
t1
I(
ε
) =
∫
F(q +
ε
ζ
, q. +
ε
ζ
. , t ) dt (4.6)
t0
Zgodnie z definicją całka ta przyjmuje wartość ekstremalną przy
ε
=0, zatem rozpatrywane zagadnienie
wariacyjne sprowadza się do zadania znalezienia zwykłego ekstremum. Teraz bowiem warunek konieczny na to
aby I(
ε
) osiągało ekstremum możemy zapisać następująco :
[
∂
I(
ε
) /
∂ε
]
ε
=0 = 0 (4.7)
Różniczkując I względem
ε
, otrzymujemy :
t1 t1 t1
[
∂
I(
ε
) /
∂ε
] =
∫
[ (
∂
F/
∂
q)
ζ
+ (
∂
F/
∂
q. )
ζ
. ] dt =
∫
[ (
∂
F/
∂
q) – d/dt (
∂
F/
∂
q. ) ]
ζ
dt + (
∂
F/
∂
q. )
ζ
|
(4.8)
t0 t0 t0
Na mocy warunku (4.4) ostatnia składowa staje się zerem. Ponieważ funkcja
ζ
(t) może być wybrana w sposób
dowolny , wyrażenie w nawiasie kwadratowym powinno tożsamościowo być równe zeru , dochodzimy tym
sposobem do „wariacyjnego równania różniczkowego Eulera-Lagrange’a” :
(
∂
F/
∂
q) – d/dt (
∂
F/
∂
q. ) = 0 (4.9)
Równanie to jest równaniem różniczkowym zwyczajnym drugiego rzędu dla funkcji q(t). Wielkość :
δ
I = [
∂
I(
ε
) /
∂ε
]
ε
=0
ε
(4.10)
nazywamy „wariacją” całki I(
ε
). Reprezentuje ona liniowy człon rozkładu całki I(
ε
) w szereg Taylora. Aby
określić charakter ekstremum (minimum lub maksimum) konieczne jest obliczenie wariacji wyższego rzędu.
Z definicji wariacji (4.5) wynika , że :
d(
δ
q) =
ε
d
ζ
(4.11)
Na mocy równości (4.3) otrzymujemy :
dQ = dq +
ε
d
ζ
(4.12)
I dlatego , zgodnie z definicją wariacji :
δ
(dq) = dQ – dq =
ε
d
ζ
(4.13)
Stąd otrzymujemy równanie :
d(
δ
q) =
δ
(dq) (4.14)
oznaczające , że operacja obliczenia wariacji i różniczkowania są przemienne.
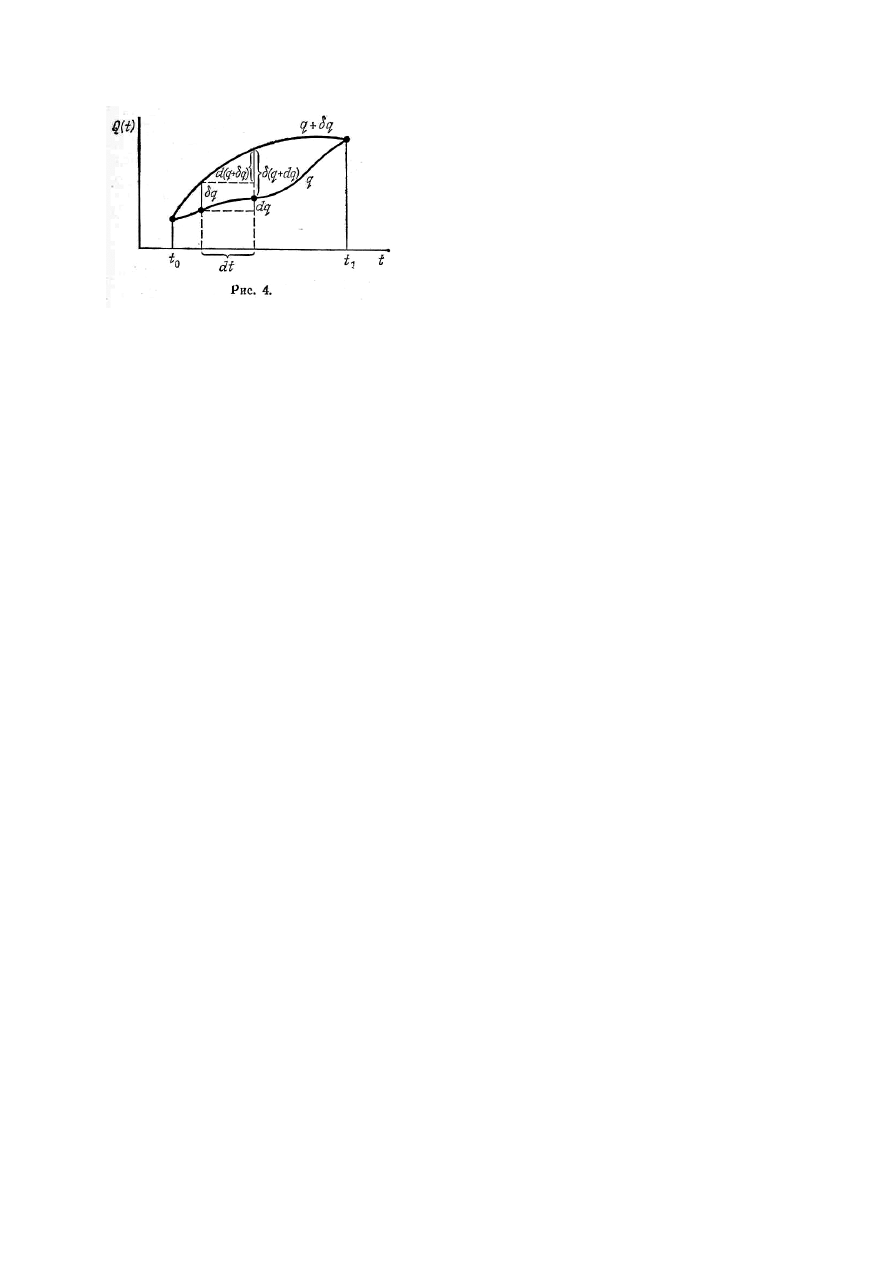
11
RYS 4
Ponieważ czas przy wariowaniu nie zmienia się , z ostatniego równania wynika zależność :
d/dt (
δ
q) =
δ
( dq/dt) (4.15)
tj. przemienność wariowania i różniczkowania po czasie.
Zależność (4.14) poglądowo przedstawiono na rysunku 4. Zgodnie z nim :
δ
q + d(q +
δ
q) = dq +
δ
(q + dq) (4.16)
Ponieważ operator wariowania jest liniowy , ma miejsce równość :
δ
( q1+ q2 ) =
δ
q1 +
δ
q2 (4.17)
Stosując tą równość dochodzimy do równania (4.14) postaci :
δ
q + dq + d(
δ
q) = dq +
δ
q +
δ
(dq)
Powyższe wywody łatwo jest uogólnić na przypadek kilku funkcji qK ( K = 1... p ).
Teraz wyprowadzimy wzór Eulera-Lagrange’a w inny sposób , bez wykorzystywania parametru
ε
.
Na miejsce całki (4.1) rozpatrzymy całkę :
t1
I =
∫
F(qK , q
.
K , t ) dt (4.18)
t0
Koniecznym warunkiem osiągania ekstremum tej całki jest teraz równość zeru wariacji tej całki. Na końcach
granicy całkowania powinny być spełnione warunki :
δ
qK( t0) =
δ
qK( t1) = 0 (4.19)
Zmieniając kolejność operacji wariowania i całkowania, otrzymujemy :
t1 p
δ
I =
∫
Σ [ (
∂
F/
∂
qK )
δ
qK + (
∂
F/
∂
q.K )
δ
q.K ] dt = 0
t0 K=1
Wykorzystując zależności :
δ
q.K = d/dt (
δ
qK )
a następnie całkując przez części , dochodzimy do równania :
t1 p t1 p
δ
I =
∫
Σ [ (
∂
F/
∂
qK )
δ
qK + (
∂
F/
∂
q.K ) d/dt (
δ
qK )] dt =
∫
Σ [ (
∂
F/
∂
qK ) - d/dt(
∂
F/
∂
q.K ) ]
δ
qK dt +
t0 K=1 t0 K=1
p t1
+
Σ [(
∂
F/
∂
q.K)
δ
qK ]
|
= 0
K=1 t0
Całkowane człony stają się równe zeru na mocy warunków (4.19). Wyrażenia w nawiasach okrągłych pod
znakiem całki również się zerują , co wynika z dowolności w wyborze wariacji
δ
qK. W rezultacie otrzymujemy
układ p – równań różniczkowych drugiego rzędu Eulera –Lagrange’a :
(
∂
F/
∂
qK ) – d/dt (
∂
F/
∂
q. K ) = 0 ; K = 1 ... p (4.20)
( Przedstawione wyniki są klasycznymi wynikami rachunku wariacyjnego , zainteresowanego czytelnika
odsyłam do książki pt. : „Rachunek wariacyjny” – I. M. Gelfand, S. W. Fomin. PWN 1972 – przypis własny )
4.1.2 ZASADA HAMILTONA.

12
Obecny rozdział poświęcimy całkowej zasadzie , ustanowionej przez R. Hamiltona w 1894 roku, oraz
równoważnym jej równaniom ruchu układu mechanicznego. W zasadzie tej kryje się głęboki sens. Jej znaczenie
stanie się w pełni jasne przy uogólnieniu jej sformułowania w teorii pola.
W charakterze punktu wyjściowego weźmiemy równanie (3.3) i scałkujemy go po czasie w granicach od t0 do t1
N t1 m
Σ
∫
[ m
Ω
r
..
Ω
δ
rΩ – ( KΩ + Σ
λµ
a
µ
Ω )
δ
rΩ ] dt = 0
Ω
=1 t0
µ
=1
Dokonamy następnie przekształcenia :
r..Ω
δ
rΩ = d/dt ( r
.
Ω
δ
rΩ ) – ½
δ
( r2. Ω ) (4.21)
oraz wykorzystamy wyrażenie (3.12) dla energii kinetycznej całego układu. To pozwala otrzymać :
t1 N m N t1
∫
[
δ
T +
Σ ( KΩ + Σ
λµ
a
µ
Ω )
δ
rΩ ] dt – Σ ( r
.
Ω
δ
rΩ ) | = 0
t0
Ω
=1
µ
=1
Ω
=1 t0
Zakładając, jak zwykle w rachunku wariacyjnym :
δ
rΩ (t0) =
δ
rΩ (t1) = 0 (4.22)
otrzymujemy :
t1 N m
∫
[
δ
T +
Σ ( KΩ + Σ
λµ
a
µ
Ω )
δ
rΩ ]dt = 0 (4.23)
t0
Ω
=1
µ
=1
Wprowadźmy funkcje :
L = L( rΩ , r
.
Ω , t ) = T – U( rΩ , r
.
Ω , t ) (4.24)
Funkcja ta ma wymiar energii , nazwiemy ją „funkcją Lagrange’a” lub lagranżjanem. Jeżeli funkcja U zależy od
prędkości , to będziemy ją nazywali „potencjałem uogólnionym”. Jeżeli nie zależy od prędkości , to U jest równe
tożsamościowo energii potencjalnej układu ( uwaga. należy rozróżniać pojęcia uogólnionego potencjału i energii
potencjalnej. ). Równanie (4.23) przyjmuje teraz postać :
t1 N m
∫
[
δ
L +
δ
U +
Σ ( KΩ + Σ
λµ
a
µ
Ω )
δ
rΩ ]dt = 0
t0
Ω
=1
µ
=1
Wprowadzając pojecie „pochodnej wariacyjnej”, zdefiniowanej dla funkcji f( rΩ , r
.
Ω , t ) następująco :
δ
f/
δ
rΩ = (
∂
f/
∂
rΩ ) – d/dt (
∂
f/
∂
r.Ω ) (4.25)
oraz przyjmując warunki (4.22), ostatnie równanie możemy zapisać w postaci :
t1 N m
∫
{
δ
L +
Σ [ (
δ
U/
δ
rΩ ) + KΩ + Σ
λµ
a
µ
Ω ]
δ
rΩ } dt = 0 (4.26)
t0
Ω
=1
µ
=1
Założymy teraz , że siły aktywne KΩ oraz potencjał uogólniony U, związane są zależnościami :
KΩ = -
δ
U/
δ
rΩ = - [ (
∂
U/
∂
rΩ ) - d/dt (
∂
U/
∂
r.Ω )] (4.27)
( w szczególnym przypadku , kiedy funkcja U nie zależy od prędkości są to znane wzory wiążące siły i energię
potencjalną ) ( tj. F = - grad U – przypis własny )
Po takim założeniu równanie (4.26) przyjmuje postać :
t1 N m
∫
(
δ
L +
Σ Σ
λµ
a
µ
Ω
δ
rΩ ) dt = 0 (4.28)
t0
Ω
=1
µ
=1
Jest to zapis zasady Hamiltona dla układu o dowolnych więzach.
Dla układu o więzach holonomicznych na mocy zależności (2.7) mamy :
t1 N m
∫
[
δ
L +
Σ Σ
λµ
(
∂
F
µ
/
∂
rΩ )
δ
rΩ ] dt = 0
t0
Ω
=1
µ
=1
lub

13
t1 N m
δ
∫
(
δ
L +
Σ Σ
λµ
F
µ
) dt = 0 (4.29)
t0
Ω
=1
µ
=1
Przy braku więzów zasadę Hamiltona zapisujemy jeszcze prościej :
t1 t1
δ
∫
δ
L dt =
δ
∫
( T – L) dt = 0 (4.30)
t0 t0
Stosując wzory (4.20) rachunku wariacyjnego do zasady Hamiltona w postaci (4.28) otrzymujemy równania
Lagrange’a dla układu o dowolnych więzach :
m
d/dt (
∂
L/
∂
r.Ω ) - (
∂
L /
∂
rΩ) = Σ
λµ
a
µ
Ω = ZΩ (4.31)
µ
=1
które dla układu o więzach holonomicznych przyjmują postać :
m
d/dt (
∂
L/
∂
r.Ω ) - (
∂
L /
∂
rΩ) = Σ
λµ
(
∂
F
µ
/
∂
rΩ ) = ZΩ (4.32)
µ
=1
Przy braku więzów równania Lagrange’a upraszczają się do postaci :
δ
L/
δ
rΩ = (
∂
L/
∂
rΩ ) - d/dt (
∂
L/
∂
r.Ω ) = 0 (4.33)
Równania Lagrange’a (4.31) reprezentują oczywiście równania Lagrange’a pierwszego rodzaju (1.2a) lub (3.4)
zapisane przez funkcje Lagrange’a L.
Definiując działanie (w sensie Hamiltona ) jako :
t1
S =
∫
L( rΩ , r
.
Ω , t )dt + S0 (4.34)
t0
przy braku więzów dochodzimy do następującego sformułowania zasady Hamiltona : ruch układu
mechanicznego w zadanym przedziale czasowym < t0 t1> odbywa się tak aby działanie (4.34) osiągało
wartość ekstremalną (nie koniecznie minimalną ). Zasada Hamiltona jako zasada całkowa , pozwala głębiej niż
sformułowanie Newtonowskie dynamiki, przeniknąć w istotę procesu ruchu.
Zapis praw przyrody w postaci równań różniczkowych stanowi bezpośrednio naszą wizję przyczynowości co
podkreśla się jeszcze tym faktem , że dany proces rozwija się od pewnego stanu początkowego. W
przeciwieństwie do tego zapisu różniczkowego , w zasadzie Hamiltona mamy pewien skończony odcinek czasu ,
w którym w jednakowy sposób potraktowano zarówno przeszłość jak i przyszłość. Dlatego też w literaturze
spotykamy się z opiniami – w stylu autora wspomnianej zasady – podobnymi do takiej : „aby osiągnąć swój cel
przyroda ze wszystkich możliwych (wymyślonych) ruchów wybiera takie w które odpowiadają działaniu
ekstremalnemu”.
4.2 INNE ZASADY CAŁKOWE.
Zasadę Hamiltona poprzedzała zasada Maupertiusa ( 1747 rok ) o priorytet sformułowania której spierał się
Leibnitz. Jednak tylko Euler i Lagrange rozpatrując układ zachowawczy posiadający energię E, zamienili
nadzwyczaj bałamutne , pierwotne sformułowanie tej zasady na ścisłe matematyczne twierdzenia.
Mimo tego ,że w zasadzie Maupertiusa działanie określone jest jako całka po czasie od energii kinetycznej T –
układu (* dokładniej od podwojonej energii kinetycznej układu – przypis tłumacza. *) , dopuszcza się w niej
jedynie wariacje względem czasu (
δ
t
≠
0) pozostawiając ustaloną energię całkowitą (
δ
E = 0). Zatem
porównuje się tylko drogi na których energia całkowita jest taka sama.
Ponieważ przy braku sił , działanie w zasadzie Maupertiusa , z dokładnością do stałego czynnika przechodzi w
całkę po czasie , widać oczywisty związek tej zasady z zasadą Fermata najkrótszej drogi optycznej. Oczywiście
w przypadku rozprzestrzeniania się światła chodzi o ruch czoła fali, która nie podlega zasadom mechaniki.
5. RÓWNANIA LAGRANGE’A
5.1 RÓWNANIA LAGRANGE’A WE WSPÓŁRZĘDNYCH UOGÓLNIONYCH
Przy rozwiązywaniu konkretnych zadań zwykle nie wykorzystujemy współrzędnych kartezjańskich , a
wybieramy współrzędne stosowne dla rozwiązywanego zagadnienia , przykładowo - zadanie które posiada
symetrię sferyczną rozwiązujemy we współrzędnych sferycznych itp.

14
Takie indywidualne podejście do budowy równań Lagrange’a stosuje się z powodzeniem w wielu przypadkach.
Przy tym współrzędne nie koniecznie maja wymiar długości (kąt , przykładowo jest wielkością bezwymiarową )
Dlatego też mówimy o „współrzędnych uogólnionych”, współrzędne takie oznaczamy przez : qk .
Rozpatrzmy układ składający się z N punktów materialnych , mających zatem 3N stopni swobody. Jeżeli na ten
układ nałożymy tylko więzy holonomiczne, to można wykorzystać równania więzów w celu wykluczenia tylu
współrzędnych ile nałożono więzów. Wtedy uwzględniając więzy zasadę Hamiltona (4.30) możemy zapisać w
postaci ;
t1
δ
∫
L( qk , q
.
k , t )dt = 0 ; k = 1 ... p (5.1)
t0
Odpowiednie równania Lagrange’a drugiego rodzaju we współrzędnych uogólnionych mają postać :
δ
L/
∂
qk =
∂
L/
∂
qk – d/dt (
∂
L/
∂
q.k ) = 0 (5.2)
Jeżeli teraz oprócz więzów holonomicznych nałożymy na układ jeszcze więzy nieholonomiczne, to otrzymamy
zapis zasady Hamiltona w postaci (4.28), przy czym równania więzów nieholonomicznych powinny być
przedstawione we współrzędnych uogólnionych.
(* Autor postępuje tutaj dosyć nietypowo. Na początku uwzględnia tylko więzy holonomiczne i wyprowadza p
niezależnych współrzędnych uogólnionych qk . To pozwala mu zapisać zależności (5.4) i (5.5) które nie były by
spełnione przy uwzględnieniu więzów nieholonomicznych . Po czym uwzględnia i więzy nieholonomiczne
( wzór (5.7) ) nie mówiąc przy tym ,że z p wariacji
δ
qk , niezależnymi pozostają tylko p – n, gdzie n – jest liczbą
więzów nieholonomicznych , i że z p równań (5.10) - n spełnionych jest poprzez odpowiedni wybór n
mnożników
λµ
. Zauważmy oprócz tego , że , zależność (5.4) ma miejsce tylko dla więzów skleronomicznych ,
w przypadku więzów reonomicznych należy ją zmienić zależnością rΩ = rΩ (qΩ , t ) – przypis tłumacza. *)
Ponieważ liczba p niezależnych współrzędnych uogólnionych spełnia nierówność :
p
≤
3N (5.3)
ma miejsce zależność :
rΩ = rΩ (qk ) (5.4)
tak , że współrzędne qk grają teraz rolę parametrów
Z równości (5.4) znajdujemy :
p
δ
rΩ = Σ (
∂
rΩ /
∂
qk )
δ
qk (5.5)
k=1
Jeżeli teraz wprowadzimy dla uproszczenia zapisu wielkość :
p
e
µ
k = Σ (
∂
rΩ /
∂
qk ) a
µΩ
(5.6)
Ω
=1
to w miejsce (4.28) otrzymamy :
t1 p m
∫
(
δ
L +
Σ Σ
λµ
e
µ
k
δ
qk ) dt = 0 (5.7)
t0 k=1
µ
=1
lub
p t1 m
Σ
∫
[ (
δ
L/
∂
qk ) + Σ
λµ
e
µ
k ]
δ
qk dt = 0 (5.8)
k=1 t0
µ
=1
Wielkości :
m
Qk = Σ
λµ
e
µ
k (5.9)
µ
=1
wiążące się z reakcjami więzów nieholonomicznych , nazywamy „siłami uogólnionymi”. Zatem z zależności
(5.8) otrzymujemy uogólnione równania Lagrange’a:
d/dt (
∂
L/
∂
q.k ) - (
∂
L/
∂
qk ) = Qk (5.10)

15
5.2 RÓWNANIA LAGRANGE’A DLA UKŁADÓW DYSYPATYWNYCH.
W tym rozdziale wyjaśnimy , czy możliwe jest opisanie ruchu układu mechanicznego , na którego punkty
działają siły oporu ośrodka , przez uogólnione równania Lagrange’a postaci (5.10) tj. przez równania :
d/dt (
∂
L/
∂
q.k ) - (
∂
L/
∂
qk ) = Rk (5.11)
gdzie : Rk – są uogólnionymi siłami oporu.
W tym celu rozpatrzymy tak zwaną „dysypatywną funkcje Rayleigha”
Φ
( r
.
Ω ), zależną jedynie od prędkości
r.Ω i z której siły oporu RΩ otrzymujemy za pomocą operatora gradientu działającego w przestrzeni prędkości :
RΩ =
∂Φ
/
∂
r
.
Ω (5.12)
Zatem uogólnione równania Lagrange’a (5.11) możemy zapisać w postaci wektorowej :
d/dt (
∂
L/
∂
r.
Ω
) -
∂
L/
∂
r
Ω
=
∂Φ
/
∂
r
.
Ω = RΩ (5.13)
Moc sił oporu (prędkość z jaką energia mechaniczna przechodzi w ciepło) jest dana :
N N N
dA(oporu) /dt =
Σ RΩ r.
Ω
=
Σ (
∂Φ
/
∂
r
.
Ω ) r
.
Ω
=
Σ [ (
∂Φ
/
∂
x
.
Ω ) x
.
Ω
+ (
∂Φ
/
∂
y
.
Ω ) y
.
Ω
+ (
∂Φ
/
∂
z.Ω )z
.
Ω
]
Ω
=1
Ω
=1
Ω
=1 (5.14)
W charakterze przykładu rozpatrzymy przypadek oporu ośrodka liniowego i anizotropowego, dla którego
funkcja Rayleigha ma postać :
N
Φ
= ½
Σ (
µ
1x
. 2
Ω
+
µ
2 y
. 2
Ω
+
µ
3 z
. 2
Ω
) (5.15)
Ω
=1
W przypadku ośrodka anizotropowego dodatnie współczynniki
µ
1,
µ
2,
µ
3 będą różne tj. wielkość siły oporu
zależna będzie od kierunku. Zgodnie z równaniem (5.12) przez różniczkowanie znajdujemy siłę oporu :
RΩ = i
µ
1x
.
Ω
+ j
µ
2 y
.
Ω
+ k
µ
3 z
.
Ω
(5.16)
wynika z niej jasno , że opór jest liniowy i anizotropowy. Podstawiając to wyrażenie do wzoru (5.14) ,
otrzymujmy :
N
dA(oporu) /dt =
Σ (
µ
1x
. 2
Ω
+
µ
2 y
. 2
Ω
+
µ
3 z
. 2
Ω
) = 2
Φ
≥
0 (5.17)
Ω
=1
Zatem, funkcja dysypatywna Rayleigha
Φ
jest miarą prędkości z jaką energia mechaniczna przechodzi w ciepło.
W przypadku oporu ośrodka liniowego i izotropowego wszystkie trzy współczynniki
µ
i są sobie równe :
µ
1 =
µ
2 =
µ
3 =
µ
(5.18)
Aby ustanowić związek między dwoma postaciami uogólnionych równań Lagrange’a (5.11) i (5.13),
wykorzystamy na początku zależność :
p
r
.
Ω= Σ ( rΩ /
∂
qk ) q
.
k (5.19)
k=1
wynikającą z równości (5.4). Ponieważ w formaliźmie Lagrange’a współrzędne uogólnione qk i prędkości
uogólnione q.k są zmiennymi niezależnymi , różniczkowanie ostatniej zależności daje nam :
∂
r.
Ω
/
∂
q.k =
∂
r
Ω
/
∂
qk (5.20)
Zauważmy ,że w rozpatrywanym przypadku liczba współrzędnych kartezjańskich x
Ω
, y
Ω
, z
Ω
, jest równa
liczbie współrzędnych uogólnionych qk. Przejścia od równań (5.11) do równań (5.13) dokonujemy w
następujący sposób : na początku zgodnie z zasadami różniczkowania funkcji złożonych znajdujemy :
N N
∂
L/
∂
qk = Σ (
∂
L/
∂
rΩ ) (
∂
rΩ /
∂
qk ) + Σ (
∂
L/
∂
r
.
Ω ) (
∂
r
.
Ω/
∂
qk ) (5.21)
Ω
=1
Ω
=1
N
∂
L/
∂
q.k = Σ (
∂
L/
∂
r
.
Ω ) (
∂
r
.
Ω/
∂
q.k ) (5.22)
Ω
=1
Podstawiając te wyrażenia do równań (5.11) i uwzględniając równość (5.20) , otrzymujemy :

16
N N
Σ [ d/dt (
∂
L/
∂
r
.
Ω ) - (
∂
L/
∂
rΩ ) ] (
∂
rΩ /
∂
qk ) + Σ (
∂
L/
∂
r
.
Ω )[d/dt (
∂
rΩ /
∂
qk ) - (
∂
r
.
Ω/
∂
qk ) ] = Rk (5.23)
Ω
=1
Ω
=1
I dalej zgodnie z zasadą różniczkowania funkcji złożonej i na mocy zależności (5.19) mamy :
p p
d/dt (
∂
rΩ /
∂
qk ) - (
∂
r
.
Ω/
∂
qk ) = Σ (
∂
2rΩ /
∂
qL
∂
qk )q
.
L - Σ (
∂
2rΩ /
∂
qk
∂
qL )q
.
L = 0
L=1 L=1
zatem :
N
Σ [ d/dt (
∂
L/
∂
r
.
Ω ) - (
∂
L/
∂
rΩ ) ] (
∂
rΩ /
∂
qk ) = Rk (5.24)
Ω
=1
Skąd znajdujemy :
N
Rk =Σ RΩ (
∂
rΩ /
∂
qk ) (5.25)
Ω
=1
6. RÓWNANIA HAMILTONA
6.1 WYPROWADZENIE RÓWNAŃ HAMILTONA PRZY POMOCY PRZEKSZTAŁCENIA LEGENDRE’A
W formaliźmie Legendre’a w charakterze podstawowej funkcji wykorzystujemy funkcje Lagrange’a L, a w
charakterze zmiennych niezależnych – współrzędne uogólnione qk i prędkości uogólnione q
.
k . Czas t ,odgrywa
rolę parametru.
W formaliźmie Hamiltona funkcją podstawową jest funkcja Hamiltona (hamiltonian) H, a zmiennymi
niezależnymi są -współrzędne uogólnione qk i nie omówione do tej pory ,pędy uogólnione pk. Czas t ,podobnie
jak wczesniej odgrywa rolę parametru.
Przejście od formalizmu Lagrange’a , w którym uwzględniono już obecność nałożonych na układ więzów
(liczba stopni swobody jest równa f ), do formalizmu Hamiltona :
qk , q
.
k , L(qk , q
.
k , t)
→
qk , pk , H(qk , pk , t) (6.1)
dokonywane jest za pomocą „przekształcenia Legendre’a“ , o postaci :
f
H(qk , pk , t) = Σ pk q
.
k - L(qk , q
.
k , t) (6.2)
k=1
Przekształcenia Legendre’a przy których razem ze zmiennymi niezależnymi przekształcają się również zmienne
zależne należą do ogólnej klasy tak zwanych przekształceń stycznościowych (kontaktowych). Wychodzą one
poza ramy zwykłych przekształceń punktowych (przykładowo przekształceń typu przejście od współrzędnych
kartezjańskich do współrzędnych biegunowych ). Zależność (6.2) jest równaniem definicyjnym omawianego
przekształcenia Legendre’a . Na mocy (6.2) mamy :
f
dH =
Σ [ pk dq.k + q.k pk – (
∂
L/
∂
dqk )dqk – (
∂
L/
∂
q.k )dq
.
k ] – (
∂
L/
∂
t) dt (6.3)
k=1
Zgodnie z definicją funkcja Hamiltona H nie powinna zależeć od q.k. Osiągniemy ten cel , określając pędy
uogólnione w następujący sposób :
pk = (
∂
L/q.k ) (6.4)
Zatem otrzymujemy :
f
dH =
Σ [ q.k dpk – (
∂
L/
∂
dqk )dqk ] – (
∂
L/
∂
t) dt (6.5)
k=1
Podstawienie wielkości (6.4) do równania (5.2) daje :
p.k =
∂
L/
∂
qk (6.6)
Zatem (6.5) możemy zapisać następująco :
f
dH =
Σ (q.k dpk – p.kdqk ) – (
∂
L/
∂
t) dt (6.7)
k=1

17
A następnie przedstawmy różniczkę zupełną funkcji H = H( qk , pk , t) :
f
dH =
Σ [ (
∂
H/
∂
qk )dqk + (
∂
H/
∂
pk) dpk ] + (
∂
H/
∂
t) dt (6.8)
k=1
Przyrównując współczynniki przy różniczkach zmiennych niezależnych w wyrażeniach (6.7) i (6.8) ,
dochodzimy do „kanonicznych równań różniczkowych Hamiltona” :
q.k =
∂
H/
∂
pk ; p
.
k = -
∂
H/
∂
qk (6.9)
Równania (6.9) to układ 2f równań różniczkowych zwyczajnych pierwszego rzędu , opisują one ruch danego
układu mechanicznego. Z matematycznego punktu widzenia jest on ekwiwalentny układowi równań Lagrange’a
, które to – jak wiadomo – są równaniami różniczkowymi zwyczajnymi drugiego rzędu.
Współrzędne uogólnione i pędy uogólnione figurujące w równaniach kanonicznych Hamiltona nazywane są
„zmiennymi kanonicznie sprzężonymi”. Z równości (6.7) wynika jeszcze jedna , ważna zależność, a mianowicie
∂
H/
∂
t = -
∂
L/
∂
t (6.10)
Przy pomocy równania Hamiltona otrzymujemy z (6.8) równość :
f
dH/dt =
Σ [ (
∂
H/
∂
qk ) dq
.
k + (
∂
H/
∂
pk) dp
.
k ] + (
∂
H/
∂
t) =
∂
H/
∂
t (6.11)
k=1
Układ mechaniczny będziemy nazywali „układem mechanicznym zachowawczym“ jeżeli dla niego funkcja
Lagrange’a nie zależy w sposób jawny od czasu tj. :
∂
L/
∂
t = 0 (6.12)
wtedy na mocy (6.10) otrzymamy również :
∂
H/
∂
t = 0 (6.13)
zatem , zgodnie z (6.11) :
dH/dt = 0 lub H = E = const. (6.14)
Stałą wielkość E będziemy nazywać energią układu zachowawczego.
Wprowadzone w ten sposób pojęcie energii pokrywa się z powszechnie rozumianym pojęciem energii
zachowawczego układu mechanicznego. Dla takiego układu potencjał U nie zależy od prędkości (i przedstawia
sobą energię potencjalną ). Wtedy w miejsce równości (4.24) mamy równość :
L = T – U(rΩ ) (6.15)
zatem w miejsce (6.4) możemy podstawić :
pk =
∂
T/
∂
q. k (6.16)
Na mocy tych zależności wyrażenie (6.2) przyjmuje postać :
f
H =
Σ [ (
∂
T/
∂
dq.k ) q
.
k - T + U (6.17)
k =1
Energia kinetyczna T przedstawia sobą formę kwadratową prędkości :
*) We wzorze (6.18) druga równość spełniona jest tylko dla układu konserwatywnego , przy czym
współczynniki akL są funkcjami współrzędnych uogólnionych. – przypis tłumacza )
N f
T = ½
Σ mΩ r.Ω2 = Σ akL q.k q.L (6.18)
Ω
=1 k,L=1
(współczynniki akL są dla nas nie istotne ). Ponieważ T – jest jednorodną funkcją drugiego rzędu , zgodnie z
twierdzeniem Eulera dotyczącym funkcji jednorodnych ma miejsce równość :
f
Σ (
∂
T/
∂
dq.k ) q
.
k = 2T (6.19)
k =1
na mocy której z (6.17) wynika :
H = T + U = E (6.20)
Co dowodzi naszego stwierdzenia.
Może się okazać , że do liczby argumentów funkcji Hamiltona nie wchodzi pewna współrzędna uogólniona qk .
Taka współrzędną nazywamy „zmienną cykliczną” (pochodzenie tej nazwy związane jest badaniem ruchu
obrotowego ). Ważność takiej współrzędnej spowodowana jest tym ,że na mocy równań Hamiltona (6.9) pęd
uogólniony odpowiadający zmiennej cyklicznej jest stałą ruchu :
p. = -
∂
H/
∂
q =
∂
L/
∂
q = 0 tj. p = const.
18
6.2 PRZYKŁAD FORMALIZMU LAGRANGE’A –HAMILTONA (WAHADŁO MATEMATYCZNE )
Na prostym przykładzie pokaże zasadnicze kroki rozwiązywania zadań mechanicznych w ramach formalizmu
Lagrange’a- Hamiltona.
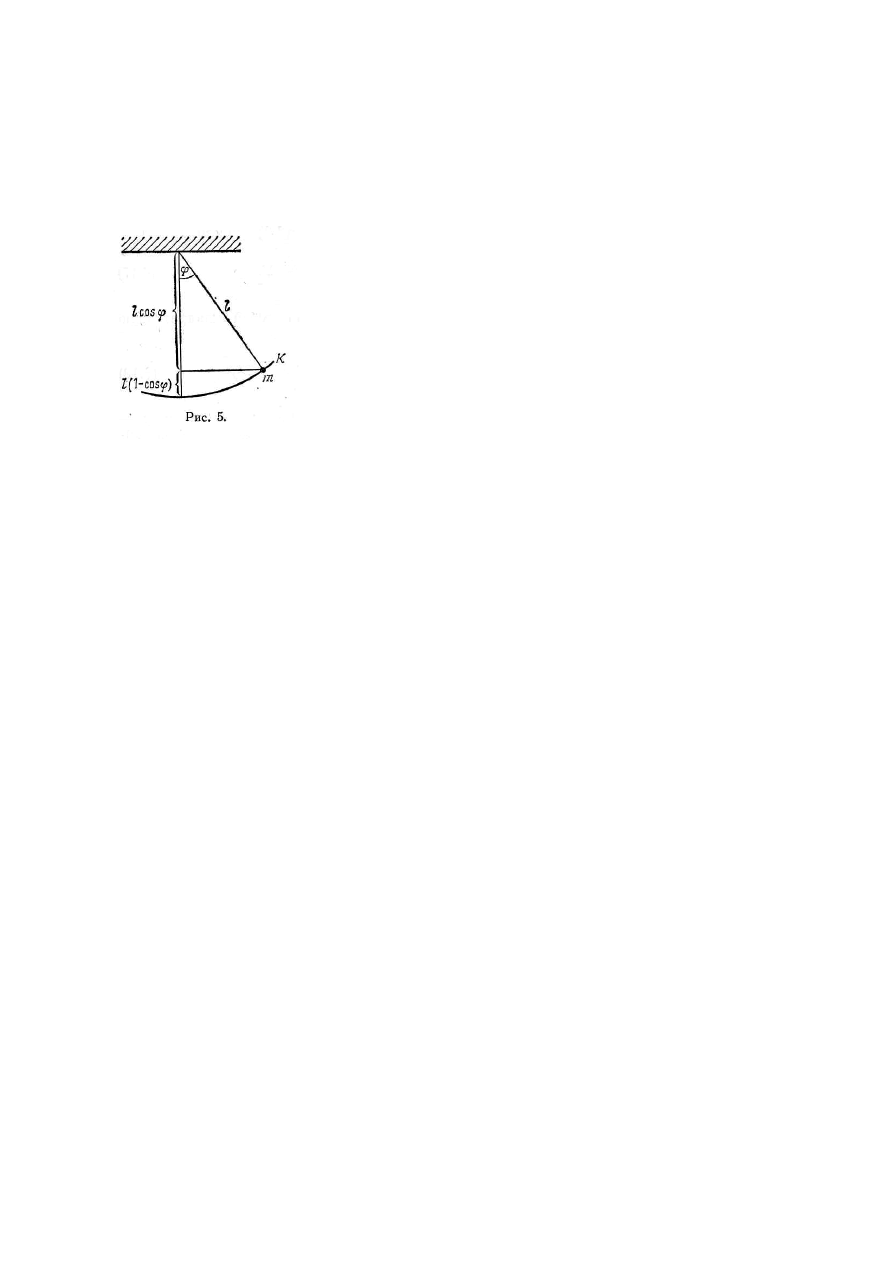
Rozpatrzmy ruch płaski punktu materialnego m , w jednorodnym polu ciążenia (rysunek 5 )
RYS 5
Ponieważ ruch jest ruchem płaskim – załóżmy, że zachodzi on na płaszczyźnie x, z – położenie punktu m
będziemy określać za pomocą współrzędnych x, y. Równanie więzów otrzymujemy z warunku , że ruch punktu
zachodzi po okręgu K. Dlatego z dwóch stopni swobody ruchu płaskiego zostaje tylko jedna.
Oczywiści taki tok rozumowania nie jest w każdej sytuacji oczywistym. W naszym zadaniu jest jasne , że za
współrzędną uogólnioną najlepiej przyjąć kąt odchylenia
ϕ
, wahadła od pionu.
Ponieważ mówimy o układzie zachowawczym w którym potencjał nie zależy od prędkości, zgodnie z (4.24)
mamy :
L = T – U = ½ mL2
ϕ
. 2 – mgL [ 1 – cos (
ϕ
) ] (6.21)
gdzie L – jest długością wahadła , g- przyspieszeniem wywołanym przez siłę ciążenia.
Dokładne rozwiązanie tego zadania prowadzi do całki eliptycznej. Ponieważ interesuje nas jedynie zasada
rozwiązywania podobnych zadań , ograniczymy się do przypadku małych katów odchylenia |
ϕ
| << 1 i dlatego
zadowolimy się przybliżeniem :
cos(
ϕ
) = 1 – ½
ϕ
2 (6.22)
Przy takim warunku wyrażenie (6.21) przyjmuje postać :
L = ½ mL2
ϕ
. 2 – ½ mg L
ϕ
2 ( 6.23)
skąd otrzymujemy :
∂
L/
∂ϕ
= - mgL
ϕ
;
∂
L/
∂ϕ
. = mL2
ϕ
. (6.24)
Równanie Lagrange’a (5.2) w naszym przypadku możemy zapisać następująco :
d/dt (
∂
L/
∂ϕ
. ) - (
∂
L/
∂ϕ
) = 0
Podstawiając do niego wyrażenia (6.24) otrzymujemy równanie różniczkowe zwyczajne drugiego rzędu :
ϕ
. . + (g/L)
ϕ
= 0 (6.25)
ogólnym rozwiązaniem tego równania jest funkcja :
ϕ
=
ϕ
0 cos [ sqrt(g/L) +
λ
0 ) (6.26)
gdzie :
ϕ
0 i
λ
0 – są stałymi całkowania.
Stąd znajdujemy częstotliwość wychylenia wahadła :
ω = sqrt (g/L) (6.27)
Pokaże teraz , jak rozwiązuje się to zadanie w formaliźmie Hamiltona. W tym celu wprowadzimy zgodnie z
(6.4) pęd uogólniony p, wykorzystując drugą równość (6.24) :
p =
∂
L/
∂ϕ
. = mL2
ϕ
. (6.28)
skąd :
ϕ
. = p/ mL2 (6.29)
Zatem stosownie do naszego zadania funkcja Hamiltona (6.2) ma postać :
H = p
ϕ
. – L (6.30)
Podstawiając do niej wyrażenie (6.23) dla L i wyrażenie (6.29) dla
ϕ
. otrzymujemy funkcje Hamiltona ,
zapisaną w jej zmiennych istotnych :

19
H = T + U = p2 / 2mL2 + ½ mgL
ϕ
2 (6.31)
Różniczkując ją znajdujemy :
∂
H/
∂ϕ
= mgL
ϕ
,
∂
H/
∂
p = p/ mL2 (6.32)
A równania Hamiltona (6.9) przyjmują postać :
ϕ
. =
∂
H/
∂
p ; p. = -
∂
H/
∂ϕ
(6.33)
Podstawiając wyrażenia (6.32) otrzymamy układ składający się z dwóch równań różniczkowych zwyczajnych
pierwszego rzędu :
ϕ
. = p/ mL2 ; p. = - mgL
ϕ
(6.34)
Teraz musimy rozwiązać ten układ równań. Możemy w tym celu wykorzystać metodę wykluczania , i
wykluczyć zmienną p, prowadzi to do równania różniczkowemu drugiego rzędu (6.25).
Ponieważ mamy do czynienia z układem zachowawczym tj. :
∂
L/
∂
t = 0 (6.35)
to ,zgodnie z (6.20) spełnione jest prawo zachowania energii :
E = ½ p / mL2 + ½ mgL
ϕ
2 = const. (6.36)
7. ZAPIS FORMALIZMU HAMILTONA PRZEZ NAWIASY POISSONA
7.1 DEFINICJA NAWIASÓW POISSONA
Przestrzeń współrzędnych uogólnionych qk nazywamy „przestrzenią konfiguracyjną”, przestrzeń pędów
uogólnionych pk nazywamy „przestrzenią pędów”. Wymiar każdej z tych przestrzeni jest równy f, iloczyn tych
dwóch przestrzeni nazywamy „przestrzenią fazową” (dokładniejszą klasyfikacje przestrzeni wprowadza się w
mechanice statystycznej ) – przestrzeń fazowa ma wymiar 2f. Przestrzeń ta można powiedzieć , jest areną
formalizmu Hamiltona. Taki formalizm możemy przenieść również na semiklasyczną mechanikę kwantową.
W ściślejszym sformułowaniu mechaniki kwantowej oraz w kwantowej teorii pola szeroko wykorzystywane jest
pojecie „komutatora”. Klasycznym obrazem takich komutatorów są – nawiasy Poissona, które odgrywają istotną
rolę przy przejściu od mechaniki klasycznej do mechaniki kwantowej. Z tego względu chciałbym dokładnie
omówić te nawiasy.
Dla dwóch dowolnych funkcji : u (qk , pk , t ) i v (qk , pk , t ) zadanych w przestrzeni fazowej nawias(nawiasy)
Poissona określone są następująco :
f
[ u, v ] =
Σ { (
∂
u/
∂
qk)(
∂
v/
∂
pk) – (
∂
v/
∂
qk) (
∂
u/
∂
pk) } (7.1)
k=1
Dla nawiasów Poissona spełnione są następujące zależności :
1. [ u, v ] = - [v, u ] (antysymetria ) (7.2)
2. [ u, c ] = 0 jeżeli c = const (7.2)
3. a) [u1+ u2, v ] = [u1, v ] + [u2, v ] (7.2)
3. b) [u1, v1+ v2 ] = [u, v1] + [u, v2 ] (7.2)
4. a) [u1u2, v ] = u1[u2, v ] + [u21, v ] u2 (7.2)
4. b) [u1, v1v2 ] = v1[u, v2] + [u, v1] v2 (7.2)
5. [ u, [v, w ] ] + [ v, [w, u] ] + [ w, [ u, v ] ] = 0 (tożsamość Jakobiego ) (7.2)
Słuszność tych zależności wynika z samej definicji (7.1). Zależność 1. możemy wywieść w oczywisty sposób z
zależność (7.1). Zależność (7.2) jest również jasna - ponieważ pochodna od stałej jest równa zeru. Zależność 3a.
wynika z tego ,że pochodna od sumy jest równa sumie pochodnych. Zależność 3b. można otrzymać z zależności
3a. na mocy zależności 1. Zależność 4a. jest następstwem zasady Leibniza dla różniczki iloczynu , zależność 4b.
otrzymujemy z 4a. na mocy 1. Zależności 5. (tożsamość Jakobiego ) można dowieść przez bezpośredni
rachunek.
Interesujące jest to ,że dla „komutatora” dwóch operatorów kwantowych
ℑ
,
ℜ
- zdefiniowanym równością :
[
ℑ
,
ℜ
] =
ℑℜ
-
ℜℑ
(7.3)
spełnione są takie same formalne zależności postaci (7.2). Dlatego wynikła nadzieja ( która się spełniła ) na
otrzymanie równań kwantowych odzwierciedlających zjawiska badane w fizyce kwantowej , poprzez formalną
zmianę nawiasów Poissona na komutator :
[ u , v ]
→
(1/i ħ )[
ℑ
,
ℜ
] (7.4)
do którego wchodzi odpowiedni czynnik wymiarowy.
( i – jest jednostką urojoną ; ħ = h /2
π
- zmodyfikowana stała Plancka ).

20
7.2 RÓWNANIA RUCHU I KLASYCZNE ANALOGI KOMUTACYJNYCH ZALEZNOŚCI HEISENBERGA
Na mocy równań Hamiltona dla dowolnej funkcji A(qk , pk , t ) spełniona jest zależność :
f f
dA/dt =
∂
A/
∂
t +
Σ [(
∂
A/
∂
qk ) q
.
k + (
∂
A/
∂
pk) p
.
k ] =
∂
A/
∂
t +
Σ [(
∂
A/
∂
qk ) (
∂
H/
∂
pk) - (
∂
A/
∂
pk ) (
∂
H/
∂
qk)]
k=1 k=1
lub stosując nawiasy Poissona :
dA/dt =
∂
A/
∂
t + [ A, H ] (7.5)
Równanie to można rozpatrywać jako ogólne prawo ruchu (zmiany w czasie ) wielkości A.
Jeżeli przyjąć w szczególności A = qk i A = pk, to otrzymamy równania Hamiltona w zupełnie symetrycznej
postaci :
q.k = [qk , H ] ; p
.
k = [ pk , H ] (7.6)
Poniżej obliczymy pewne nawiasy Poissona , które odgrywają ważną rolę przy przejściu do mechaniki
kwantowej. Ponieważ w formaliźmie Hamiltona qk , pk są zmiennymi niezależnymi , słuszne są zależności :
∂
qL /
∂
qk =
δ
Lk ;
∂
pL /
∂
pk =
δ
Lk ;
∂
pL /
∂
qk = 0 ;
∂
qL /
∂
pk = 0 (7.7)
gdzie :
δ
Lk - jest symbolem Kroneckera;
Podstawiając te wyrażenia do równości :
f
[ A, pL ] = Σ {(
∂
A/
∂
qk ) (
∂
pL/
∂
pk ) - (
∂
A/
∂
pk)(
∂
pL/
∂
qk)}
k=1
Otrzymujemy :
[ A, pL ] =
∂
A/
∂
qL (7.8)
Pochodną po pL można zapisać w sposób analogiczny :
[ A, qL ] = -
∂
A/
∂
pL (7.9)
Zastosowanie tych wzorów do przypadków szczególnych daje :
zgodnie z (7.8) dla A = qk :
[ qk , pL ] =
δ
kL (7.10)
zgodnie z (7.8) dla A = pk :
[ pk , pL ] = 0 (7.11)
zgodnie z (7.9) dla A = qk :
[ qk , qL ] = 0 (7.12)
Analogi tych trzech ważnych zależności występują w mechanice kwantowej , gdzie służą jako podstawa dla
ustanowienia zależności nieoznaczoności Heisenberga.
7.3 PRZYKŁAD (LINIOWY OSCYLATOR HARMONICZNY )
Liniowy oscylator harmoniczny jest układem zachowawczym o jednym stopniu swobody. Przy wyborze – w
charakterze współrzędnej uogólnionej zmiennej x , funkcja Lagrange’a może być zapisana w postaci :
L = T – U = ½ mx.2 – ½ kx2 (7.13)
( k- stała sprężystości sprężyny ). Pęd uogólniony możemy zatem zapisać w postaci :
p =
∂
L/
∂
x. = m x. (7.14)
co pokrywa się w tym przypadku ze zwykłym pędem znanym z mechaniki. Funkcja Hamiltona jest równa :
H = px. – L = p2/2m + ½ kx2 (7.15)
Podstawmy tę funkcję do równania Hamiltona (7.6) I wykorzystajmy własności nawiasów Poissona , daje to
nam :
x. = [ x, H ] =
∂
H/
∂
p = p/m (7.16)
p. = [ p, H ] = -
∂
H/
∂
p = -kx (7.17)
Teraz należy rozwiązać ten układ równań różniczkowych. Różniczkujemy pierwsze równanie względem t i
podstawiamy obliczoną zależność na p. ,z drugiego równania :
x.. + (k/m)x = 0 (7.18)
Równanie różniczkowe drugiego rzędu (7.18) ma ogólne rozwiązanie postaci :
x = C sin[ ω ( t – t0 ) +
λ
] = C sin ( ωt +
λ
0 ) (7.19)
( C i
λ
0 =
λ
- ωt0 - są stałymi całkowania ). Stąd otrzymujemy częstotliwość :

21
ω = sqrt ( k/m ) (7.20)
8. TEORIA HAMILTONA-JAKOBIEGO
8.1 RÓWNANIE HAMILTONA -JAKOBIEGO.
Do tej pory spotykaliśmy się z prawami ruchu mechaniki klasycznej , przedstawianymi w postaci równań
różniczkowych zwyczajnych , jak również zasad całkowych i różniczkowych. W tym rozdziale wprowadzimy
zapis tych praw mechaniki klasycznej w postaci nieliniowego równania różniczkowego pierwszego rzędu o
pochodnych cząstkowych , jest to równanie Hamiltona – Jakobiego. Pierwszy wprowadził to równanie Hamilton
(w 1827 roku a w latach 1830 i 1832 uzupełnił je ) podstawą dla ich wyprowadzenia stały się badania nad drogą
promienia światła w instrumentach optycznych. Prace Jakobiego związane są z przekształceniami kanonicznymi
oraz z dalszym rozwojem formalizmu kanonicznego.
Teoria Hamiltona – Jakobiego ma duże znaczenie dla rozumienia drogi rozwoju fizyki a ściśle przejścia od
mechaniki klasycznej do kwantowej. Przejście to we współczesnym rozumieniu miało swój analog w rozwoju
elektromagnetycznej teorii światła.
Jak wiadomo , koniec sporu miedzy korpuskularną teorią Newtona a falową Huyghensa wiąże się ze
współczesną elektrodynamiką kwantową i koncepcją dualizmu korpuskularno-falowego. W mechanice
korpuskularna teoria cząstek (punktów materialnych ) nie budziła wątpliwości aż do końca XIX wieku, kiedy to
zaczęły się badania zjawisk zachodzących w atomach. W 1924 roku L. de Broglie wysunął idee przypisaniu
cząstce klasycznej własności falowych ,wprowadzając dualizm korpuskularno-falowy cząstek.
E. Schrodinger rozwinął tą koncepcje wprowadzając w 1926 roku mechanikę falową , która okazała się
równoważna mechanice macierzowej – początki której wiążą się z pracami W. Heisenberga ( 1925 ).
Mechanika falowa i mechanika macierzowa są pod względem matematycznym równoważnymi sposobami
sformułowania mechaniki kwantowej.
W jakim stopniu w teorii Hamiltona-Jakobiego jest już obecna mechanika kwantowa ?
Na to pytanie odpowiemy w miarę jak będziemy omawiać tą teorie.
W pierwszym kroku wyjdziemy od definicji (4.34) S , przy czym funkcje Lagrange’a zapiszemy we
współrzędnych uogólnionych :
t1
S =
∫
L(qk , q
.
k , t ) dt + S0 (8.1)
t0
Przy tym stała całkowania S0 wybieramy w ten sposób aby : S(t0 ) = S0.
Jak wiadomo , zadanie polega na tym aby scałkować równania ruchu Newtona określając z nich współrzędne w
następujący sposób :
qk = qk ( t, t0 , q
0
L , q
.0
L ) ; k , L = 1 ..... f (8.2)
Jest to parametryczne przedstawienie toru cząstek. Wchodzące w niego stałe całkowania q0L i q
.0
k ( L = 1... f)
mają sens wartości początkowych odpowiednio współrzędnych i prędkości cząstek.
Chwila początkowa t0 - jest parametrem nie istotnym z fizycznego punktu widzenia. Ponieważ w mechanice
newtonowskiej nie wyróżniamy żadnej chwili czasu , problem jest jedynie w ustaleniu punktu początkowego
odczytu czasu. Różniczkowanie wyrażeń (8.2) pozwala w sposób parametryczny przedstawić prędkości :
q.k = q
.
k ( t, t0 , q
0
L , q
.0
L ) (8.3)
Przypuśćmy teraz , że rozwiązaliśmy w ten sposób przedstawione zadanie i znaleźliśmy funkcje (8.2) i (8.3).
A następnie podstawiliśmy te wyrażenia do funkcji Lagrange’a (8.1) i wykonaliśmy całkowanie po czasie. To
daje nam następującą strukturę funkcji działania :
S = ż(t, t0 , q
0
L , q
.0
L ) + S0 ; ż(t, t0 , q
0
L , q
. 0
) = 0 (8.4)
Następny krok będzie polegał na tym aby rozwiązać układ równań (8.2) względem prędkości początkowych.
Przy tym dochodzimy do układu :
q.0k = q
. 0
k ( t, t0 , qL , q
0
L ) (8.5)
Teraz podstawmy te wyrażenia do funkcji ż, co daje :
S = S(qk ,t , q
0
k , t0 , S0 ) = ż( qk , t , q
0
k , t0 ) + S0 (8.6)
gdzie
ż(q0k , t0 , q
0
k , t0 ) = 0
Przeprowadzone wyżej wywody pozwalają na sformułowanie pewnych ważnych wniosków.
Pochodna zupełna po czasie całki (8.1) równa jest :

22
dS./dt = L (8.7)
Podstawmy do funkcji podcałkowej (8.1) wyrażenie na funkcje Lagrange’a zapisane za pomocą funkcji
Hamiltona, otrzymane z zależności (6.2) :
t1 f
S =
∫
(
Σ pk q.k – H ) dt + S0 (8.8)
t0 k=1
Znak sumy można wyprowadzić poza znak całki . Oprócz tego podstawmy : q.kdt = dqk i odpowiednio do tego
zmieńmy granice całkowania :
f qk t
S =
Σ
∫
pk dqk –
∫
H dt + S0 (8.9)
k=1 q0k t0
Ponieważ : p0k = p
0(t
0 ) , wynika stąd równość :
f f
dS. =
Σ pk dqk – Σ p0k dq0k – H dt + H0 dt0 + dS0 (8.10)
k=1 k=1
która to ponownie potwierdza strukturę (8.6) działania. Z równości (8.10) wynika ,że :
pk =
∂
S/
∂
qk (8.11)
p0k = -
∂
S/
∂
q0k (8.12)
jak również :
H = -
∂
S/
∂
t (8.13)
Przepiszmy jeszcze raz ostatnią równość zapisując argumenty funkcji H ( za wyjątkiem stałych całkowania ) i
przyjmując do wiadomości zależność (8.11) :
∂
S/
∂
t = H( qk ,
∂
S/
∂
qk , t ) = 0 (8.14)
Otrzymane w ten sposób równanie jest szukanym równaniem Hamiltona –Jakobiego o pochodnych cząstkowych
dla działania S. Ponieważ funkcja Hamiltona jest funkcja kwadratową względem pędów , jest to równanie
nieliniowe pierwszego rzędu o pochodnych cząstkowych. Z fizycznego punktu widzenia równanie to jest
równoważne prawu ruchu Newtona.
Na początku tego rozdziału wspominałem , że teoria Hamiltona-Jakobiego w istocie związana jest z mechanika
falową. Dlatego też teraz , na zakończenie warto zauważyć , że równanie Hamiltona –Jakobiego (8.14)
otrzymujemy z równania falowego Schrodingera :
H ( qk , ( h/i )
∂
/
∂
qk , t )
Ψ
= iħ
∂Ψ
/
∂
t (8.15)
będącym równaniem liniowym, drugiego rzędu o pochodnych cząstkowych względem funkcji
Ψ
, w/w równanie
otrzymamy w granicy ħ
→
0. Przy tym funkcje
Ψ
, przyjmujące wartości zespolone , funkcja działania S –
przyjmująca wartości rzeczywiste i funkcja Z - przyjmująca również wartości rzeczywiste ( funkcja amplitudy )
,związane są zależnością :
Ψ
= Zei S/h (8.15)
Niniejszy rozdział zakończymy ponownym rozpatrzeniem zależności (8.12). Jest to układ f równań wiążących
wielkości : qk , q
0
k , p
0
k , t . Jeżeli rozwiążemy go względem współrzędnych qk , otrzymamy nowy układ
równań :
qk = fk ( t, t0 , q
0
L , p
0
L ) (8.16)
który odróżnia się od układu (8.2) tym, że w miejsce prędkości początkowych q. 0L wchodzą do niego pędy
początkowe p0L. Dlatego można twierdzić , że równania (8.12) odtwarzają tor.
Możemy zatem, znaleźć tor przez obliczenie działania, które otrzymujemy w wyniku rozwiązania równania
Hamiltona – Jakobiego (8.14). Oczywiście to rozwiązanie S nie jest otrzymywane w sposób automatyczny o
zadanej strukturze (8.6), a bez założenia takiej struktury nie można otrzymać zależności (8.12). W dalszej części
będziemy dokładnie zajmowali się tymi zagadnieniami.
8.2 CAŁKA ZUPEŁNA.
Na początku rozpatrzymy dowolne równanie pierwszego rzędu o pochodnych cząstkowych o n zmiennych yi :
F ( yi ,
σ
,
∂σ
/
∂
yi ) = 0 ; i = 1 ... n (8.17)

23
Całką zupełną tego równania , nazywamy funkcję
σ
- spełniającą to równanie , zależną oprócz n – zmiennych yi,
od n- zmiennych parametrów
α
i :
σ
=
σ
( yi ,
α
i ) (8.18)
Dla równania Hamiltona- Jakobiego , w szczególności mamy :
yi = (q1 , … ,qf , t ) ; n = f + 1 (8.19)
σ
= S (8.20)
F = H( qk ,
∂
S/
∂
qk , t ) +
∂
S/
∂
t (8.21)
Ponieważ funkcja S wchodzi do równania Hamiltona – Jakobiego tylko poprzez swoje pochodne , jest ona
określona tylko z dokładnością do stałej addytywnej, którą wcześniej oznaczyliśmy przez S0 , zakładając przy
tym , że : S0 (t0 ) = S0 . Teraz również będziemy trzymali się tego założenia, wtedy do funkcji S wejdzie nie
istotny parametr t0. Wielkość S0 można określić poprzez jedną ze stałych całkowania :
α
n =
α
f+1 + S0 (8.22)
wtedy zależność (8.18) przyjmie następującą postać :
S =
σ
( qk , t ,
α
k , t0 , S0 ) = ż(qk , t ,
α
k , t0 ) + S0 (8.23)
gdzie :
ż( q0k , t0 ,
α
k , t0 ) = 0
Porównując ta funkcję – znalezioną z równania Hamiltona – Jakobiego – z funkcją (8.6) – otrzymaną
bezpośrednio z definicji działania S , otrzymujemy :
ż(qk , t , q0k , t0 ) = ż(qk , t ,
α
k , t0 ) (8.24)
8.3 „SKRÓCONE“ RÓWNANIE HAMILTONA- JAKOBIEGO.
Jeżeli mamy do czynienia z układem mechanicznym zachowawczym, to funkcja Hamiltona nie zależy jawnie od
czasu , zatem równanie Hamiltona – Jakobiego (8.14) przechodzi w równanie :
∂
S/
∂
t + H (qk ,
∂
S/
∂
qk ) = 0 (8.25)
Zależność od czasu można przedstawić przez oddzielne składowe :
S = -E( t – t0 ) + W( qk , q
0
k ) (8.26)
gdzie : W(q0k , q
0
k ) = S0 ; E= const.
zatem z równania (8.25) otrzymujemy „skrócone” równanie Hamiltona – Jakobiego :
H(qk ,
∂
W/
∂
qk ) = E (8.27)
Własność taka, że t oraz t0 wchodzą do wyrażenia (8.26) w postaci różnicy , wynika z niezależności H od czasu
i wypływającej z tego inwariantności równania różniczkowego względem przesunięcia w czasie.
Z równania (8.27) od razu widać fizyczny sens stałej całkowania E – jest ona energią układu.
Teraz można przepisać zależność (8.11) następująco :
pk =
∂
W/
∂
qk (8.28)
Dane wzory otrzymujemy z (8.11) zakładając , że E przy różniczkowaniu pozostaje stałe. O tym należy pamiętać
dlatego , że E nie wchodzi w liczbę stałych od których jest zależna funkcja (8.6).
Znajdując całkę zupełną równania (8.27) dochodzimy do następującej struktury skróconego działania W :
W = Ŵ( qk ,
α
k ) (8.29)
Przy podstawieniu tego wyrażenia do równania (8.27) otrzymamy energię E jako funkcję parametrów
α
k :
E = E(
α
k ) (8.30)
Dla prostych fizycznych zadań niekiedy udaje się , częściowo lub nawet całkowicie rozdzielić zmienne
(współrzędne) wchodzące do równań Hamiltona – Jakobiego (8.27). W przypadku , kiedy zmienne można
całkowicie rozdzielić , funkcja W przyjmuje postać :
W = W1(q1) + W2(q2) + ... + Wf(qf) (8.31)
8.4 POGLĄDOWE GEOMETRYCZNE PRZEDSTAWIENIE DZIAŁANIA.
Z zależności działania S od współrzędnych i czasu wynika , że działanie można rozpatrywać jako pewne pole.
Odpowiadające mu przedstawienie geometryczne okazuje się być bardzo poglądowym w przypadku układu
zachowawczego , dlatego je przedstawię.
24
Ograniczymy się do ruchu jednej cząstki tak wiec zamiast funkcji polowej w f-wymiarowej przestrzeni
konfiguracyjnej będziemy mieli sumę funkcji polowych w trójwymiarowej przestrzeni konfiguracyjnej i liniową
funkcje czasu :
S = -E( t – t0 ) + W( r , r0 ) (8.32)
Powierzchnia S =const. , zbudowana dla pewnej ustalonej chwili czasu , przedstawia powierzchnię stałego
działania w tej trójwymiarowej przestrzeni. Przy zmianie czasu powierzchnia ta przemieszcza się zgodnie ze
wzorem (8.32). Na rysunku 6 pokazano położenia tej powierzchni w różnych chwilach czasu ( t1, t2 , ... )
dla dwuwymiarowego przypadku.
Rys. 6
Ten sam zbiór powierzchni można było by otrzymać inaczej , a mianowicie ustalić pewną stałą chwilę czasu i
rozpatrywać jako parametr samo działanie ( S1, S2 , ... ).
Chociaż równanie Hamiltona – Jakobiego nie jest równaniem falowym w jego zapisie zwykłej postaci , widać
pewne cechy typowe dla rozprzestrzeniania się fal , dlatego też można mówić o rozprzestrzenianiu się
(propagacji) tzw. „fal działania”.
Zgodnie z przedstawioną ogólna teorią otrzymujemy dla pędu ( pęd uogólniony może być zgodny ze zwykłym
pędem mechanicznym )następujące wyrażenie :
p = grad S (8.38)
Ponieważ pędy są prostopadłe do powierzchni stałego działania , tory ruchu są również prostopadłe do tych
powierzchni. Zadany stan początkowy określa tor dalszego ruchu cząstki.
Zbieżność takiego stanu rzeczy z optyka , badanie której wpłynęło na prace Hamiltona jest jak widać bardzo
widoczna.
9. PRZEKSZTAŁCENIA KANONICZNE
9.1 INWARIANTNOŚĆ RÓWNAŃ RUCHU PRZY PRZEKSZTAŁCENIACH KANONICZNYCH.
Przekształcenia kanoniczne odgrywają podstawową rolę w mechanice klasycznej. Przy nich przekształcają się
zarówno zmienne niezależne qk, i pk , jak również zmienna zależna H (a w wyniku czego również q
.
i L ) :
qk , q
.
k , pk , H, L - > q^k , q^
.
k , p^k , H
^
, L
^
.
( daszek nad literą oznacza wynik przekształcenia kanonicznego ). Przekształcenia kanoniczne - są to
przekształcenia postaci :
q^k = q^k ( qL , pL , t ) ; p^k = p^k ( qL , pL , t ) (9.1)
pozostawiają one inwariantnym cały aparat kanoniczny , przy czym funkcja Hamiltona i funkcja Lagrange’a
zmieniają się w określony sposób. Przekształcenia kanoniczne należą do klasy „przekształceń stycznościowych”.
Aby otrzymać przekształcenia kanoniczne wyjdziemy od pojęcia „funkcji prowadzącej” (generatora) :
F = F (qk , q^k , t ) (9.2)
na która nakładamy następujący warunek :
*) Należy mieć na uwadze , że teraz jak i dalej autor rozpatruje tylko szczególną klasę przekształceń
kanonicznych – przypis tłumacza *)
powinna ona być zależna tylko od starych współrzędnych qk , nowych współrzędnych q^k oraz od czasu t .
Funkcję tą wprowadzamy poprzez równanie :
f f
H^ (q^k , p^k , t ) - H (qk , pk , t ) = Σ p^k q^
.
k – Σ pk q
.
k – d/dt F (qk , q^k , t ) (9.3)
k=1 k=1

25
Mnożąc tą równość przez dt i rozwiązując wynik ze względu na dF , otrzymujemy wyrażenie na różniczkę
zupełną :
f f
dF = ( H – H^ )dt +
Σ p^k dq^k – Σ pk dqk (9.4)
k=1 k=1
Równanie to pokazuje , że funkcja F w istocie zależy jedynie od qk , q^k oraz t. Ponieważ zgodnie z definicją
przekształcenia kanonicznego zmienne z daszkiem , również powinny spełniać formalizm Hamiltona –
Lagrange’a , razem z zależnością :
f
L (qk , q
.
k , t ) = Σ pk q
.
k – H (qk , pk , t ) (9.5)
k=1
wynikającą z definicji (6.2), powinna być spełniona również zależność :
f
L^ (q^k , q^
.
k , t ) = Σ p^k q^
.
k – H^ (q^k , p^k , t ) (9.6)
k=1
Stąd wynika , że :
dF = ( L^ - L ) dt (9.7)
lub , że :
L^ (q^k , q^
.
k , t ) – L (qk , q
.
k , t ) = d/dt F (qk , q^
.
k , t ) (9.8)
Całkując to równanie w przedziale miedzy dwoma ustalonymi chwilami t0 i t1 otrzymujemy :
t1 t1
∫
L^ dt -
∫
L dt = F( t1 ) - F( t0 ) (9.9)
t0 t0
a następnie wariując tą zależność, dostajemy :
t1 t1
δ
∫
L^ dt -
δ
∫
L dt =
δ
F( t1 ) -
δ
F( t0 ) (9.10)
t0 t0
Zgodnie z założeniem dla zmiennych wejściowych słuszna jest zasada Hamiltona :
t1
δ
∫
L dt = 0
t0
Wymagamy , aby w nowym układzie, tak jak i w starym wariacja współrzędnych w punktach końcowym i
początkowym była równa zeru :
δ
q^k ( t0 ) =
δ
q^k ( t1 ) = 0
Ponieważ F jest funkcją tylko q^k , qk i t , to w punktach początkowym i końcowym zeruje się również wariacja
F. Stąd zgodnie z równością (9.9) wynika słuszność zasady Hamiltona w nowych zmiennych :
t1
δ
∫
L^ dt = 0 (9.11)
t0
a z tego bezpośrednio wynika równanie Lagrange’a :
δ
L^ /
δ
q^k =
∂
L^ /
∂
q^k - d/dt (
∂
L^ /q. ^k ) = 0 (9.12)
Przeprowadzając podobne rachunki i założenia co powyżej dla nowych zmiennych , w szczególności otrzymamy
p^k =
∂
L^ /q. ^k (9.13)
z czego od razu widać , że dla nowego układu w istocie spełnione są równania Hamiltona :
q. ^k =
∂
H^ /
∂
p^k , p
. ^
k = -
∂
H^ /
∂
q^k ,
∂
H^ /
∂
t = d H^ /dt (9.14)
9.2 BUDOWA FUNKCJI PROWADZĄCEJ ( TWORZĄCEJ ).
Aby powyższe rachunki były słuszne funkcja prowadząca F powinna mieć strukturę postaci (9.2). W dalszej
kolejności będziemy budować funkcję F wychodząc od czterech funkcji postaci :
R1(qk , q^k , t ) ; R2(pk , q^k , t ) ; R3(qk , p^k , t ) ;R4(pk , p^k , t ) (9.15)

26
które obrazują wszystkie cztery możliwe kombinacje zmiennych. Przy tym we wszystkie funkcje Ri powinna
wchodzić równa ilość starych i nowych zmiennych. Każdą funkcję Ri uzupełnimy pewnym dodatkowym
członem , który zapewni wymaganą strukturę funkcji F.
Rozpatrzmy kolejno :
Przypadek A :
F = R1(qk , q^k , t ) (9.16)
Zbudujemy różniczkę zupełną funkcji F i porównamy ją z otrzymanym wcześniej wyrażeniem (9.4), w wyniku
czego otrzymujemy :
p^k =
∂
R1/
∂
q^k , pk =
∂
R1/
∂
qk , H – H^ =
∂
R1/
∂
t (9.17)
Jest to układ równań z którego znając postać funkcji R1 możemy znaleźć qk , pk , H i tym samym rozwiązać
postawione zadanie.
Przypadek B :
f
F = R2(pk , q^k , t ) - Σ qk pk (9.18)
k=1
Aby udowodnić , że takie podejście prowadzi do celu obliczmy różniczkę zupełną :
f f f f
dF =
Σ (
∂
R2/
∂
pk ) dpk + Σ (
∂
R2/
∂
q^k ) dq^k + (
∂
R2/
∂
t)dt -
Σ pk dqk - Σ qk dpk (9.19)
k=1 k=1 k=1 k=1
Porównując ten wynik z wyrażeniem (9.4) , otrzymamy :
qk =
∂
R2/
∂
pk ; p^k =
∂
R2/
∂
q^k ; H – H^ =
∂
R2/
∂
t (9.20)
Są to wzory przekształceń dla przypadku B.
Przypadek C :
f
F = R3(qk , p^k , t ) + Σ q^k p^k (9.21)
k=1
Dla tego przypadku mamy taką sama kolejność obliczeń jak w przypadku B. Obliczając różniczkę zupełną :
f f f f
dF =
Σ (
∂
R3/
∂
qk ) dqk + Σ (
∂
R3/
∂
p^k ) dp^k + (
∂
R3/
∂
t)dt +
Σ q^k dp^k + Σ p^k dq^k (9.22)
k=1 k=1 k=1 k=1
i porównując go z wyrażeniem (9.4) dochodzimy do wzorów przekształceń postaci :
q^k = -
∂
R3/
∂
p^k ; pk = -
∂
R3/
∂
qk ; H – H^ =
∂
R3/
∂
t (9.23)
Przypadek D :
f f
F = R4(pk , p^k , t ) - Σ qk pk + Σ q^k p^k (9.24)
k=1 k=1
Obliczając różniczkę zupełną , otrzymujemy :
f f f f f
dF =
Σ (
∂
R4/
∂
pk ) dpk + Σ (
∂
R4/
∂
p^k ) dp^k + (
∂
R3/
∂
t)dt -
Σ qk dpk - Σ pk dqk + Σ q^k d^pk +
k=1 k=1 k=1 k=1 k=1
f
+
Σ p^k dq^k (9.25)
k=1
Porównując ten wynik do wyrażenia (9.4) , znajdujemy wzory na przekształcenia :
qk = -
∂
R4/
∂
pk ; q^k = -
∂
R3/
∂
p^k ; H – H^ =
∂
R4/
∂
t (9.26)
Ponieważ funkcje Ri wybrane są dowolnie , zmienne q^k , p^k tracą zupełnie charakter współrzędnych i pędów.
Aby to wyjaśnić , wybierzemy, przykładowo :
f
F = R1 = Σ qk q^k (9.27)
k=1
co odpowiada przypadkowi A. Z zależności (9.17) wynikają wzory przekształceń postaci :

27
p^k = qk ; q^k = - pk ; H^ = H (9.28)
Zatem w tym przypadku współrzędne uogólnione i pędy po prostu zamieniają się rolami ( z dokładnością do
znaku ) :
f
R3 = - Σ
λ
L ( qM, t ) p^L (9.29)
L=1
gdzie, jeśli
λ
L – są dowolnymi funkcjami to mamy przypadek C. Przy tym z zależności (9.23) wynikają wzory
przekształceń postaci :
f
q^k =
λ
k ( qM, t ) ; pk = Σ [
∂λ
L( qM, t ) /
∂
qk ] p^L (9.30)
L=1
f
H^ = H +
Σ [
∂λ
L( qM, t ) /
∂
t ] p^L (9.30)
L=1
Pierwsza z tych równości pokazuje ,że mamy do czynienia z ogólnym przekształceniem punktowym.
Odpowiednio zatem wszystkie przekształcenia punktowe są kanoniczne.
Przedstawione powyżej wyniki opierają się na tym, że zmienne qk , pk , q^k , p^k rozpatrywaliśmy jako
zmienne niezależne. Jeśli przyjmować, że między nimi zachodzą pewne związki to przebieg przedstawionego
toku rozumowania powinien ulec zmianie i tak przykładowo jeżeli : q^k
≡
qk to w przypadku A , z równości
(9.4) wynikać będą zależności :
p^k = pk +
∂
F/
∂
qk ; H – H^ =
∂
F/
∂
t .
9.3 INWARIANTNOŚĆ ZALEśNOŚCI KOMUTACYJNYCH PRZY PRZEKSZTAŁCENIACH
KANONICZNYCH
Wcześniej ( zobacz wzory (7.10) – ( 7.12) ) spotkaliśmy się z interesującą zależnością - wiążącą zmienne
kanoniczne przypominającą zależności komutacyjne Heisenberga występujące w mechanice kwantowej.
Te trzy równości w ramach mechaniki klasycznej dla uproszczenia będziemy nazywali zależnościami
komutacyjnymi. Dalej pokażę , że przy przekształceniach kanonicznych zależności te zachowują swoją postać .
Jednak na początku wprowadzimy cztery pomocnicze wzory.
Na mocy twierdzenia Schwartza o równości pochodnych mieszanych , z (9.17) , (9.23) i (9.26) wynikają
następujące zależności :
∂
p^k / q^L = -
∂
pL / q^k ;
∂
qk / q^L =
∂
pL / pk (9.31)
∂
q^k / qL =
∂
pL / p^k ;
∂
qk / p^L = -
∂
q^L / pk (9.31)
Podstawiając te ważne zależności do równości określonych przez nawiasy Poissona, otrzymamy :
f
[ q^k , q^L ] = - Σ { (
∂
q^k /
∂
qM ) (
∂
qM /
∂
p^L ) + (
∂
q^k /
∂
pM ) (
∂
pM /
∂
p^L ) } = - (
∂
q^k /
∂
p^L ) = 0 (9.32)
M=1
f
[ p^k , p^L ] = - Σ { (
∂
p^k /
∂
qM ) (
∂
qM /
∂
q^L ) + (
∂
p^k /
∂
pM ) (
∂
pM /
∂
q^L ) } = (
∂
p^k /
∂
q^L ) = 0 (9.33)
M=1
f
[ q^k , p^L ] = - Σ { (
∂
q^k /
∂
qM ) (
∂
qM /
∂
q^L ) + (
∂
q^k /
∂
pM ) (
∂
pM /
∂
q^L ) } = (
∂
p^k /
∂
q^L ) =
δ
qkL (9.34)
M=1
Pochodne cząstkowe w pierwszych dwóch równościach zerują się , ponieważ jedna ze zmiennych niezależnych
jest różniczkowana względem drugiej zmiennej niezależnej. Zatem dowiedliśmy naszego twierdzenia. Jest to
jeszcze jedna fundamentalna własność przekształceń kanonicznych.
9.4 JAKOBIAN PRZEKSZTAŁCENIA KANONICZNEGO.
Jakobian wchodzący w przekształcenie kanoniczne ma postać :
|
∂
q1 /
∂
q^1 , … ,
∂
q1 /
∂
q^f ,
∂
q1 /
∂
p^1 , ... ,
∂
q1 /
∂
p^f |
|....................................................................................... |
∆
= |
∂
qf /
∂
q^1 , … ,
∂
qf /
∂
q^f ,
∂
qf /
∂
p^1 , ... ,
∂
qf /
∂
p^f |
|
∂
p1 /
∂
q^1 , … ,
∂
p1 /
∂
q^f ,
∂
qf /
∂
p^1 , ... ,
∂
qf /
∂
p^f | (9.35)
|....................................................................................... |
|
∂
pf /
∂
q^1 , … ,
∂
pf /
∂
q^f ,
∂
pf /
∂
p^1 , ... ,
∂
pf /
∂
p^f |

28
∆
=
∂
( q1 , … , qf , p1 , … , pf ) /
∂
( q^1 , … , q^f , p^1 , … , p^f )
Rozpatrzmy ( f + 1)-wiersz. Wykorzystując wzory na przekształcenie (9.23) dla przypadku C, można zapisać
elementy tego wiersza tak :
∂
p1/
∂
q^M = - Σ (
∂
2R
3 /
∂
qM
∂
q1 )
∂
qL /
∂
q^M (9.36)
L
∂
p1/
∂
p^M = - Σ (
∂
2R
3 /
∂
qM
∂
q1 )
∂
qL /
∂
p^M = - Σ (
∂
2R
3 /
∂
qM
∂
q1 ) (
∂
qL /
∂
p^M ) + (
∂
q^M /
∂
q1 ) (9.36)
L
Podstawiając te wyrażenia do (f + 1) –wiersza i dodając je do poprzednich f-wierszy pomnożonych przez :
(
∂
2R
3 /
∂
q1
∂
q1 ) ….. (
∂
2R
3 /
∂
qf
∂
q1 )
sprowadzimy jakobian do następującej postaci :
|
∂
q1 /
∂
q^1 , … ,
∂
q1 /
∂
q^f ,
∂
q1 /
∂
p^1 , ... ,
∂
q1 /
∂
p^f |
|....................................................................................... |
∆
= |
∂
qf /
∂
q^1 , … ,
∂
qf /
∂
q^f ,
∂
qf /
∂
p^1 , ... ,
∂
qf /
∂
p^f |
| 0 , … , 0 ,
∂
qf /
∂
p^1 , ... ,
∂
qf /
∂
p^f |
|....................................................................................... |
|
∂
pf /
∂
q^1 , … ,
∂
pf /
∂
q^f ,
∂
pf /
∂
p^1 , ... ,
∂
pf /
∂
p^f |
Wykonując analogiczną operacje dla wszystkich pozostałych wierszy od (f+2) –go do 2f-go , otrzymamy :
|
∂
q1 /
∂
q^1 , … ,
∂
q1 /
∂
q^f ,
∂
q1 /
∂
p^1 , ... ,
∂
q1 /
∂
p^f |
|....................................................................................... |
∆
= |
∂
qf /
∂
q^1 , … ,
∂
qf /
∂
q^f ,
∂
qf /
∂
p^1 , ... ,
∂
qf /
∂
p^f |
| 0 , … , 0 ,
∂
qf /
∂
p^1 , ... ,
∂
qf /
∂
p^f |
|....................................................................................... |
| 0 , … , 0 ,
∂
pf /
∂
p^1 , ... ,
∂
pf /
∂
p^f |
Zgodnie z zasadami obliczenia wyznaczników , wyrażenie to możemy zapisać jako iloczyn :
|
∂
q1 /
∂
q^1 , … ,
∂
q1 /
∂
q^f | |
∂
q1 /
∂
p^1 , ... ,
∂
q1 /
∂
p^f |
|.......................................... | | ........................................... | =
∆
= |
∂
qf /
∂
q^1 , … ,
∂
qf /
∂
q^f | |
∂
qf /
∂
p^1 , ... ,
∂
qf /
∂
p^f |
= [
∂
(q1 , … , qf ) /
∂
( q^1 , … , q^f )] [
∂
(q^1 , … , q^f ) /
∂
(q1 , … , qf ) ] (9.38)
Pierwszy czynnik jest jakobianem przekształcenia qk
→
q^k przy ustalonej wartości p^k , drugi - jakobianem
przekształcenia odwrotnego. Z tego wynika , że :
∆
= 1 (9.39)
Zatem , pokazałem ,że przekształcenie kanoniczne prowadzi do zachowania objętości przestrzeni fazowej , jak
bowiem wiadomo jakobian określa zależność między objętościami przy odwzorowaniach. Bezpośrednim
następstwem takiego faktu jest to , że całka :
I =
∫
....
∫
dq1… dqf dp1 … pf (9.40)
brana względem pewnego obszaru przestrzeni fazowej , jest inwariantem , co wynika z tego ,że funkcja pod
całkowa przedstawia inwariant. Związek między tym rezultatem a twierdzeniem Liouville’a jest oczywisty.
9.5 TWIERDZENIE JAKOBIEGO O OKREŚLONOŚCI TORU.
W rozdziale 8.1 byłem zmuszony pozostawić pytanie o to jak praktycznie wykorzystać układ równań (8.12) w
celu określenia toru, działanie bowiem jak wiadomo w tym równaniu zadaje się nie zakładając jakiś konkretnych
zmiennych. Teraz mogę odpowiedzieć na to pytanie przy pomocy przekształcenia kanonicznego . Pokaże w jaki
sposób w postawionym celu można zastosować działanie w postaci całki zupełnej (8.23) ( Jakobi 1834 rok ).
Powróćmy do przypadku C. Zależności (9.23) pokazują , że funkcja R3 związana jest z działaniem S w
następujący sposób :
R3 = - S (9.41)
Zakładając , że S ma postać (8.23) , na mocy warunku swobody wyboru nowych zmiennych kanonicznych
założymy :
p^k =
α
k (9.42)
Wtedy równania (9.23) zapiszemy następująco :

29
q^k =
∂
S/
∂α
k ; pk =
∂
S /
∂
qk ; H^ = H +
∂
S/
∂
t (9.43)
Druga z tych równości jest zgodna z równaniem (8.11) – to właśnie przywiodło nas do równości (9.41).
Porównując trzecie równanie z równaniem Hamiltona – Jakobiego (8.25) otrzymujemy :
H^ = 0 (9.44)
Zatem , nowa funkcja Hamiltona jest tożsamościowo równa zeru. Wypiszemy teraz równania Hamiltona w
nowych zmiennych :
q^ .k =
∂
H^ /
∂
p^k ; p^
.
k = -
∂
H^ /
∂
q^ .k (9.45)
Z tego na mocy (9.44) , wynika , że :
q^ k = const. p^ k = const. (9.46)
Druga z tych równości w istocie jest zgodna z równością (9.42). Podstawiając dla wygody q^k =
β
k ,
sprowadzamy pierwsze równanie (9.43) do postaci :
∂
S /
∂α
k =
β
k (9.47)
Jak widać przeprowadzone przekształcenie kanoniczne prowadzi do tego ,że nowe współrzędne i pędy okazały
się wielkościami stałymi.
Istota twierdzenia Jakobiego wynika z równań (9.47) które są analogiczne do równań ( 8.12) i które są układem
równań określających tor. Praktycznie oznacza to ,że aby otrzymać układ równań opisujących tor , należy
znaleźć całkę zupełną S równania Hamiltona – Jakobiego – następnie ją zróżniczkować względem stałych
niezależnych
α
k i porównać pochodne cząstkowe do nowych stałych
β
k .
10. PRZYKŁADY ZWI
ĄZANE Z TEORIĄ HAMILTONA – JAKOBIEGO.
10.1 LINIOWY OSCYLATOR HARMONICZNY.
W rozdziale 7.3 badaliśmy oscylator harmoniczny jako przykład teorii Hamiltona. Teraz rozpatrzymy ten sam
charakterystyczny przykład w celu poglądowego przedstawienia teorii Hamiltona – Jakobiego , można bowiem
na tym przykładzie zademonstrować pewne charakterystyczne cechy tej teorii.
Funkcja Hamiltona zadana jest wzorem (7.15) :
H = p2 / 2m + ½ k x2 (10.1)
Ponieważ mamy do czynienia z układem zachowawczym , można wykorzystać równanie Hamiltona – Jakobiego
w postaci ( 8.27) :
½ (1/m) ( dW/ dx )2 + ½ k x2 = E (10.2)
Można było tutaj zamienić pochodną cząstkową W na pochodną zupełną , ponieważ x jest jedyną współrzędną
zalezną. Z równania (10.2) wynika ,że :
dW/ dx =
±
sqrt ( 2mE – m k x2 ) (10.3)
Całkując to równanie , znajdujemy W i zgodnie z wzorem (8.26) otrzymujemy :
S = - Et
±
sqrt ( 2mE )
∫
sqrt [ 1- ( kx2 /2E ) ] dx + const. (10.4)
Zatem całka zupełna została znaleziona. Jedynym istotnym parametrem ( oprócz stałej addytywnej całkowania
która jednak nie odgrywa żadnej roli ) jest energia E. W zagadnieniu tym występuje tylko jedna współrzędna x,
dlatego można podstawić E =
α
.
Ponieważ w wielu przypadkach z fizycznego punktu widzenia interesuje nas jedynie tor ruchu , można nie
obliczać całki.
Znajdziemy pochodną cząstkową od S po E :
∂
S/
∂
E = - t
±
sqrt ( m /2E)
∫
sqrt [ 1- (x2k /2E) ] dx
±
[ k sqrt ( 2mE)/4E2 ]
∫
{x2dx /sqrt [ 1- (k x2/2E) ] }dx
= - t
±
sqrt ( m /2E)
∫
dx / sqrt [ 1- ( x2k /2E ) ]
Dokonując całkowania , co na tym etapie jest konieczne, wygodnie jest podstawić :
ξ
= sqrt ( k/2E ) x (10.5)
oraz przyjmując :
ω = sqrt ( k/m) ( zobacz równość (7.2) ).
Otrzymujmy :
∂
S/
∂
E = - t
±
( 1/ω)
∫
d
ξ
/ sqrt ( 1-
ξ
2 ) = - t
±
( 1/ω) arcsin [ sqrt ( k/ 2E ) x ] (10.6)
Teraz wykorzystamy wzór (9.47) tj. podstawimy :
∂
S /
∂
E =
β
(10.7)
co prowadzi do równania :
x =
±
sqrt ( 2E / k ) sin [ ω ( t +
β
)] (10.8)

30
Wynik ten jest zgodny ze wzorem (7.19) – odróżnia się od niego jedynie wyborem stałej całkowania.
Porównanie tych dwóch wyników - w szczególności - prowadzi do zależności :
C =
±
sqrt ( 2E / k ) (10.9)
Wykorzystaliśmy ten poglądowy przykład aby na konkrecie pokazać zastosowanie wprowadzonej wcześniej
teorii , warto podkreślić jeszcze kilka interesujących w nim faktów.
Po pierwsze można zdefiniować stałą addytywną całkowania w wyrażeniu (10.4) w ten sposób aby sprowadzić
funkcję S do postaci (8.26) . Co daje nam :
x
S = - E ( t – t0 )
±
sqrt ( 2mE )
∫
sqrt [ 1 - ( kx2 /2E)] dx + S0 (10.10)
x0
gdzie : x0 = x (t0 ) – odpowiada początkowemu położeniu punktu materialnego. Dokonując całkowania ,
znajdujemy :
S = - E ( t – t0 )
±
(E/ω){ arcsin [x sqrt ( k/2E)] – arcsin [ x0 sqrt (k/2E)] + x sqrt (k/2E) sqrt ( 1 – (kx
2 /2E)) –
- x0 sqrt ( k/2E) sqrt ( 1 – (kx0
2 /2E)) + S
0 (10.11)
Porównajmy ten wynik z wyrażeniem dla działania otrzymanym przez bezpośrednie całkowanie. W tym celu
zróżniczkujmy funkcje (7.19) względem czasu :
dx/dt = C ω cos [ ω( t – t0 ) +
λ
] (10.12)
podstawmy to wyrażenie razem z wyrażeniem (7.19) do wyrażenia (7.13) co prowadzi do następującej funkcji
Lagrange’a :
L = (k/2)C2 { cos2 [ ω ( t – t0 ) +
λ
] - sin2 [ ω ( t – t0 ) +
λ
] }= (k/2)C2 cos2 [ 2ω ( t – t0 ) + 2
λ
] (10.13)
Skąd przez całkowanie , zgodnie z (8.1) , znajdujemy działanie :
S = (kC2/2) { sin [ 2ω ( t – t0 ) + 2
λ
] - sin (2
λ
) } + S0 (10.14)
Wartość początkowa współrzędnej x , na mocy (7.19) jest równa :
x0 = C sin (
λ
) (10.15)
a prędkość początkowa na mocy (10.12) jest równa :
v0 = Cω cos (
λ
) (10.16)
Wykorzystując te równania , można wyrazić stałe całkowania C i
λ
przez x0 i v0 :
C =
±
(v0 /ω) sqrt [ 1 + (x
2
0 / v
2
0 ) ] ;
λ
= arctg (x0ω / v0 ) (10.17)
Podstawiając te wartości do wyrażeń (7.19) , (10.12) i (10.14) dochodzimy do wprowadzonych wcześniej
wyrażeń postaci odpowiednio : (8.2) , (8.3) i (8.4). Rozwiązując otrzymaną z (7.19) równość względem v0 ,
znajdujemy :
v0 = [ ω / sin(ω ( t – t0 )] { x - x0 cos [ω ( t – t0 )] } (10.18)
co jest wynikiem analogicznym do (8.5). Podstawienie tego wyrażenia do (10.17) daje :
C2 ={ x2 + x20 – 2xx0 cos[ ω ( t – t0 ) ]} / sin
2 [ ω ( t – t
0 ) +
λ
] (10.19)
λ
= arctg {x0 sin[ ω ( t – t0 )] } / [ x - x0 cos [ ω ( t – t0 ) ] (10.19)
zatem wyrażenie (10.14) przyjmuje postać :
S = (k/2ω)C2 cos[ ω ( t – t0 ) + 2
λ
] + S0 .
lub – z uwzględnieniem równości :
cos[ ω ( t – t0 ) + 2
λ
] = {(x2 + x20 ) cos[ ω ( t – t0 ) ] – 2xx0}/ {x
2 + x2
0 – 2xx0 cos[ ω ( t – t0 ) ]} (10.20)
postać :
S = {(k/2ω)(x2 + x20 ) cos[ ω ( t – t0 ) ] – 2xx0}/ sin[ ω ( t – t0 )] (10.21)
- która odpowiada strukturze funkcji (8.6).
Podkreślam jeszcze raz następujący fakt : wyrażenie dla działania (10.11) przedstawia sobą całkę zupełną
równania Hamiltona- Jakobiego , podczas gdy zależność (10.21) podaje działanie, opisujące faktyczny proces
ruchu i dlatego też proces ten ma odzwierciedlenie w tej zależności poprzez wzory (7.19) i (10.12). Dlatego ,
wykorzystując równania (7.19) można sprowadzić wyrażenie (10.11) do postaci (10.21). Co zapisałem poniżej.
uwzględniając równość :
arcsin ( A) – arcsin(B) = arcsin [ A – sqrt(1 - B2 ) – B sqrt ( 1- A2 ) ] (10.22)
wyrażenie (10.11) można przepisać następująco :
S = - E ( t – t0 )
±
(E/ω) arcsin [x sqrt ( k/2E) sqrt ( 1 – (kx2 /2E) - x0 sqrt (k/2E)sqrt ( 1 – (kx
2 /2E)] +
+ x sqrt (k/2E) sqrt ( 1 – (kx2 /2E) ) – x0 sqrt (k/2E)sqrt ( 1 – (kx0
2 /2E) + S
0 . (10.23)

31
Na mocy (10.9) wynika z tego , że :
S = - E ( t – t0 ) + (E/ω) arcsin {(x/C)sqrt [ 1 – (x0
2/C2 ) ] – (x
0 / C) sqrt [ 1 – (x
2/C2 )] } +
+ (x / C) sqrt [ 1 – (x2/C2 )] – (x0 / C) sqrt [ 1 – (x0
2/C2 )] + S
0 . (10.24)
Podstawiając wyrażenie (7.19) otrzymujemy :
S = - E ( t – t0 ) + (E/ω) { arcsin [sin [ ω ( t – t0 ) +
λ
] cos (
λ
) – sin(
λ
)cos [ ω ( t – t0 ) +
λ
] ] +
+ sin[ ω ( t – t0 ) +
λ
] cos[ ω ( t – t0 ) +
λ
] – sin(
λ
) cos(
λ
) } + S0 . (10.25)
lub :
S =( E/2ω) { sin[ 2ω ( t – t0 ) + 2
λ
] – sin (2
λ
)} + S0 . (10.25)
Wynik ten jest zgodny z wyrażeniem (10.14), co dowodzi naszego stwierdzenia.
Rozbudujmy dalej nasz przykład. Różniczkowanie funkcji (10.21) daje :
∂
S/
∂
x = {k [x cos[ ω ( t – t0 ) ] - x0 }/ ω sin[ ω ( t – t0 )] (10.26)
∂
S/
∂
x0 = {k [x0 cos[ ω ( t – t0 ) ] - x }/ ω sin[ ω ( t – t0 )] (10.26)
A następnie wykorzystując (10.19), wyrażenie (10.12) można sprowadzić do następującej postaci :
dx/dt = { ω/sin[ ω ( t – t0 )] } { x cos[ ω ( t – t0 )] – x0 } (10.27)
Przy pomocy tego wzoru i wzoru (10.18) ze wzoru (10.26) otrzymamy równości :
∂
S/
∂
x = m (dx/dt) ;
∂
S/
∂
x0 = - mv0 (10.28)
bezpośrednio odpowiadającą zależnościom (8.11) i (8.12) w teorii ogólnej.
Różniczkując oprócz tego funkcję (10.21) względem czasu otrzymujemy :
∂
S/
∂
t =- (k/2) [ x2 + x0
2 – 2x
0 x cos [ ω ( t – t0 )] ] / sin
2[ ω ( t – t
0 )] (10.29)
Z drugiej strony , zgodnie z (10.1) mamy :
H = E = (k/2)[ x2 + x0
2 – 2x
0 x cos [ ω ( t – t0 )] ] / sin
2[ ω ( t – t
0 )] (10.30)
Co jeszcze raz potwierdza , że działanie S, spełnia równanie Hamiltona – Jakobiego.
10.2 ZAGADNIENIE KEPLERA.
Zastosowanie teorii Hamiltona – Jakobiego do zagadnienia Keplera nie tylko pozwala rozwiązać samo to
zagadnienie ale posiada również duże znaczenie dla przybliżenia półklasycznego teorii kwantowej. Na początku
będziemy rozpatrywali ruch płaski i zapiszemy funkcję Lagrange’a we współrzędnych biegunowych :
L = ½ m ( r. 2 + r2
ϕ
. 2 ) + K/r (10.31)
gdzie : K =
γ
N Mm (dla pola grawitacyjnego)
K = - eQ (dla pola Coulombowskiego)
γ
N – stała grawitacyjna, m – (odpowiednio e ) – masa (ładunek ) poruszającej się cząstki
M – ( Q ) – masa ( ładunek ) ciała centralnego .
W tym zagadnieniu punkt posiada dwa stopnie swobody , czego odzwierciedleniem są dwie współrzędne
biegunowe r ,
ϕ
. Znajdziemy pędy uogólnione :
pr =
∂
L/
∂
r. = mr. ; p
ϕ
=
∂
L/
∂
ϕ
. = mr2
ϕ
. (10.32)
Wtedy funkcja Hamiltona przyjmuje postać :
H = prr
. + p
ϕϕ
. - L = ½ m ( r. 2 + r2
ϕ
. 2 ) – (K/r ) = (1/2m) [ p
r
2 + (1/r2 ) p
ϕ
2 ] – (K/r ) (10.33)
Ponieważ chodzi o zagadnienie stacjonarne , można wyjść bezpośrednio z równania Hamiltona – Jakobiego w
postaci (8.27) :
(1/2m) [ (
∂
W/
∂
r)2 + (1/r2 )(
∂
W/
∂ϕ
)2 ] – (K/r) = E (10.34)
przy czym :
pr
=
∂
W/
∂
r ; p
ϕ
=
∂
W/
∂ϕ
(10.35)
Zgodnie z zależnością (8.31) zakładamy , że :
W = R(r) +
Φ
(
ϕ
) (10.36)
podstawiając to wyrażenie do równania (10.34), otrzymujemy :
R’2 + (1/r2 )
Φ
2 – (2mK/r) = 2mE
lub :
r2 R’2 – 2mKr – 2mEr2 =
Φ
’2
Ponieważ wielkości stojące po różnych stronach tego równania zależne są od różnych zmiennych niezależnych ,
każda strona równania powinna równać się stałej. Odpowiednio ,zatem udało się rozdzielić zmienne i otrzymać
dwa równania różniczkowe zwyczajne :
p
ϕ
=
Φ
’ =
α
(10.37)

32
pr
= R’ =
±
sqrt [ 2m ( E + (k/r) ) – (
α
2 / r2 ) ] (10.38)
Pierwsza z tych równości wyraża prawo zachowania momentu pędu. Na mocy wzoru (8.26) otrzymujemy
działanie :
S = - Et
±
∫
sqrt {2m [ E + (K/r) – (
α
2 / r2 )} dr +
αϕ
+ const. (10.39)
Jest to całka zupełna równania Hamiltona – Jakobiego. Odpowiednimi parametrami niezależnymi są E i
α
.
Zgodnie z twierdzeniem Jakobiego , aby znaleźć równanie ruchu , należy zróżniczkować całkę zupełną
względem tych parametrów. Na początku zróżniczkujemy względem
α
:
β
=
∂
S/
∂α
=
±
α
∫
{2m [ E + (K/r) – (
α
2 / r2 )}-1/2 dr/r2 +
ϕ
Przejście do nowej zmiennej całkowania s = 1/r daje :
β
-
ϕ
=
±
α
∫
[ 2m (E + Ks) –
α
2 s2 ]-1/2 ds =
±
∫
ds / sqrt [ ( s – s1) ( s2 – s ) ] (10.40)
Wykorzystaliśmy tutaj pierwiastki trójmianu s1 i s2 , dla których zachodzi równość :
s1 s2 = -2mE/
α
2 , s
1 + s2 = 2mK/
α
2 (10.41)
Fizyczny sens tych pierwiastków jest następujący :
s1 - jest wielkością odwrotną do odległości peryhelium.
s2 – jest wielkością odwrotną do odległości w aphelium.
Dalej, należy dokonać podstawienia :
s = ½ (s1 + s2 ) + ½ (s2 – s1 ) u (10.42)
które sprowadza równanie (10.40) do postaci :
β
-
ϕ
=
±
∫
du / sqrt ( 1 – u2 ) =
±
arcsin (u ) =
±
arcsin { [ 2 / ( s2 – s1 )] [ (1/r) – ½ (s2 + s1 )} (10.43)
Stąd otrzymujemy :
1/r = ½ (s2 + s1)
±
½ ( s2 – s1 )] sin (
β
-
ϕ
) (10.44)
Przywołując zależności wiążące wielkości s1 i s2 z półosią wielką a i mimośrodem
ε
tj. zależności :
s1 = 1 / a(1 +
ε
) ; s2 = 1/ a( 1-
ε
) (10.45)
równanie (10.44) można zapisać w postaci :
1/r = [ 1
±
ε
sin (
ϕ
-
β
) ] / a ( 1 -
ε
2 ) (10.46)
Jest to równanie wiążące r oraz
ϕ
, określa ono postać geometryczną toru , który jest przecięciem stożka.
Drugie równanie opisujące prawo ruchu w czasie – otrzymujemy przez zróżniczkowanie funkcji (10.39)
względem E. Zgodnie z twierdzeniem Jakobiego mamy :
γ
=
∂
S/
∂
E = - t
±
m
∫
{ 2m [E + (K/r)] – (
α
2 / r2 )}-1/2 dr
Dokonując zamiany zmiennych całkowania i wykorzystując wyżej wprowadzone oznaczenia , znajdujemy :
t +
γ
=
±
(m/
α
)
∫
ds / s2 sqrt [ ( s – s1) ( s2 – s )] (10.47)
tj. ustanawiamy zależność między t i r. Całki tej jednak nie będziemy obliczać.
Jak widać z wyrażenia (10.31) w tym przykładzie kąt
ϕ
przedstawia współrzędną cykliczną.
11. RUCH PERIODYCZNY I WARUKOWO-PERIODYCZNY (quasiokresowy)
11 UKŁAD PERIODYCZNY Z JEDNYM STOPNIEM SWOBODY.
Libracja. W tym przypadku współrzędna i pęd są periodycznymi funkcjami czasu o jednakowym okresie
τ
:
q( t +
τ
) = q(t) ; p( t +
τ
) = p(t) (11.1)
Jako przykład libracji może służyć ruch liniowego oscylatora harmonicznego oraz wahadła matematycznego w
przypadku braku tarcia.
Na skutek periodyczności q i p ruch w dwuwymiarowej przestrzeni fazowej (na płaszczyźnie fazowej ) odbywa
się po pewnej krzywej zamkniętej. Taka krzywą nazywaną „trajektorią fazową” przedstawiono na rysunku 7.
Rozłożenie w szereg Fouriera daje :
∝
q =
Σ q0L exp [ 2
π
i L (
ν
t +
γ
) ] (11.2)
L = -
∝
33
Rys. 7
∝
p =
Σ p0L exp [ 2
π
i L (
ν
t +
γ
) ] (11.2)
L = -
∝
gdzie :
ν
= 1/
τ
- jest częstotliwością drgań,
γ
- to stała fazowa. Wykorzystując zmienną :
ω =
ν
t +
γ
(11.3)
zmieniającą się o jeden przez okres, można odzwierciedlić okresowość współrzędnej q poprzez następujący
zapis :
q(w + 1) = q(w) (11.4)
Wtedy rozkład w szereg Fouriera dla tej współrzędnej przyjmie postać :
∝
q =
Σ q0L exp ( 2
π
i L w ) ] (11.5)
L = -
∝
Obrót.
Wybierając przy ruchu szczególną postać współrzędnej , którą oznaczymy przez w, i którą możemy
rozpatrywać jako kąt w procesie ruchu ( będzie ona wzrastała z czasem).
Chociaż periodyczność „w” , w czasie nie jest zakładana , w czasie
τ
układ powraca do swojego punktu
początkowego. W czasie
τ
współrzędna w zmienia się o jednostkę :
w = (1/
τ
) ( t – t0) + w0 =
ν
t +
γ
(11.6)
W przeciwieństwie do niej pęd J przedstawia periodyczną funkcję współrzędnej w :
J( w + 1) = J(w)
(11.7)lub na mocy równości (11.6) – periodyczną funkcję czasu :
J ( t +
τ
) = J(t) (11.8)
Ten przypadek przedstawiono na rysunku 8.
Rys. 8
Przykładami takiego rodzaju ruchu są różne przypadki obrotu wokół stałej osi. Aby znormalizować okres tak
jak to było zrobione powyżej między współrzędną w i kątem obrotu
ϕ
wokół osi należy ustanowić następującą
zależność :
w =
ϕ
/ 2
π
(11.9)
Jeśli dla opisania ruchu wykorzystamy współrzędne ortokartezjańskie XK ( XK -oznacza współrzędne postaci :
x
Ω
, y
Ω
, z
Ω
) , to współrzędna i pęd okażą się funkcjami okresowymi czasu , zatem w tym przypadku pozostaje
w mocy równość (11.4) :
XK ( w + 1 ) = XK (w ) (11.10)

34
11.2 UKŁAD PERIODYCZNY Z WIELOMA STOPNIAMI SWOBODY.
Układem periodycznym z wieloma stopniami swobody będziemy nazywać taki układ , którego ruch opisywany
we współrzędnych ortokartezjańskich możemy – uogólniając zależności (11.4) lub (11.10) przedstawić za
pomocą funkcji :
XK ( w1 + 1 , w2 + 1 , ... ) = X
K ( w
1, w2 , ... ) (11.11)
Przy tym mają miejsce następujące uogólnione równości (11.3) :
w1 =
ν
1t +
γ
1 , w2 =
ν
2t +
γ
2 , ... , (11.12)
gdzie :
ν
1 = 1/
τ
1,
ν
1 = 1/
τ
1 , ... a wielkości :
τ
1,
τ
2, .. przedstawiają okresy zmienności zmiennych w1, w2, ...
Analogicznie do (11.5) można przedstawić funkcję XK jako szereg Fouriera :
∝
XK =
Σ CKL1,L2 exp [ 2
π
i (L1w1 + L2 w2 + ... ) ] (11.13)
L1L1= -
∝
Uwzględniając równości (11.12) rozkład ten można zapisać następująco :
∝
XK =
Σ DKL1,L2 exp [ 2
π
i (L1
ν
1 + L2
ν
2 + ... ) ] (11.14)
L1L1= -
∝
( gdzie wszystkie stałe fazowe są odpowiednio uwzględniane poprzez współczynniki DKL1,L2 ).
W ogólnym przypadku szereg Fouriera (11.14) nie przedstawia okresowej w czasie t, funkcji - chociaż każda
oddzielnie wzięta eksponenta może być okresowa. Periodyczność będzie miała miejsce tylko wtedy , kiedy
częstotliwości
ν
1,
ν
2 ... będą się miały do siebie jak liczby całkowite. Dlatego układy z wieloma stopniami
swobody nazywane są „układami warunkowo periodycznymi”.
Ilość częstotliwości których stosunek wyrażony być może liczbą całkowitą określa tzw. „stopień
zdegenerowania” układu. Jeżeli nie ma takich częstotliwości układ jest niezdegenerowany. Jeżeli wszystkie
częstotliwości związane są przez zależności całkowite , to układ nazywamy „zupełnie zdegenerowanym” – w
tym przypadku mamy do czynienia z okresową funkcją czasu.
Omówiony wcześniej przykład zagadnienia Keplera , jest przykładem układu zdegenerowanego o dwóch
stopniach swobody ( niezależne współrzędne r ,
ϕ
) , w którym istnieje tylko jedna częstotliwość . Poprzez
nałożenie pewnego zaburzenia (perturbacji) możemy pozbyć się degeneracji , jednak wtedy ruch odbywać się
będzie po rozecie.
W charakterze przykładu układu warunkowo periodycznego , można przywołać oscylator anizotropowy tj. punkt
materialny , dla którego stałe sprężystości są różne w różnych kierunkach . Tor takiego punktu przedstawia
pewną figurę Lissajous – jest to krzywa nie zamknięta w sposób gęsty pokrywająca pewien obszar. Ruch jest
periodyczny tylko w przypadku zdegenerowanym.
Układ mechaniczny może poruszać się ruchem periodycznym tylko w przypadku konserwatywności – wynika to
z warunków energetycznych. Dlatego w dalszej części przyjmiemy , że :
H = H(qK , pK ) (11.15)
Przy badaniu ruchu periodycznego wygodnie jest wykorzystywać przekształcenia kanoniczne.
11.3 ZMIENNE KĄT-DZIAŁANIE.
Rozpatrzmy przypadek C , przekształcenia kanonicznego , tj. zastosujmy wzory przekształcenia (9.23) :
q^k = -
∂
R3(qk ,p^k , t) /
∂
p^k ; pk = -
∂
R3(qk ,p^k , t)/
∂
qk ;
H – H^ =
∂
R3(qk ,p^k , t)/
∂
t (11.16)
Przy pomocy takiego przekształcenia równania Hamiltona w nowych zmiennych kanonicznych przyjmą postać
q. ^k = -
∂
H^ /
∂
p^k ; p
. ^
k = -
∂
H^ /
∂
q^k (11.17)
Funkcje R3 , względem której wcześniej nie zakładaliśmy żadnych dodatkowych warunków , teraz wybieramy
tak aby nowa funkcja Hamiltona zależała tylko od nowych pędów :
H^ = H^ (p. ^k ) (11.18)
W tym przypadku z drugiego równania Hamiltona wynika , że :
p^k = const. (11.19)
I dlatego z pierwszego całkowania otrzymujemy równości :
q^k =
ν
^k t +
γ
^k (11.20)

35
gdzie :
ν
^k ,
γ
^k - są stałymi. Wtedy :
ν
^k =
∂
H^ ( p^k ) /
∂
p^k (11.21)
Wcześniej, współrzędne które nie wchodziły do funkcji Hamiltona nazwaliśmy „zmiennymi cyklicznymi”.
Zatem, jak widać zmienna cykliczna rośnie liniowo w czasie. Jeśli zmienna cykliczna posiada w szczególności ,
własność , taką że w okresie rośnie do jedności , to nazywamy ją „zmienną kątową”. Dlatego zgodnie z już
wykorzystywanymi we wzorach (11.3) i (11.6) oznaczeniami przyjmiemy dla niej symbol w. Mnożąc równość
(11.20) przez pewną stałą
λ
, możemy przejść od współrzędne q^k do odpowiadającej jej zmiennej wk :
wk =
ν
^k t +
γ
^k (11.22)
gdzie :
wk =
λ
q^k ,
ν
k =
λν
^k ,
γ
k =
λϕ
^k (11.23)
Pęd – sprzężony kanonicznie ze zmienną wk nazywamy „zmienną działania” i oznaczamy ją przez Jk , zatem
zależności (11.21) możemy przepisać do postaci :
ν
k =
∂
H^ /
∂
Jk (11.24)
gdzie :
Jk =
∂
p^k /
λ
(11.25)
Ponieważ , na mocy warunków (11.15) i (11.18) lewa strona trzeciego ze wzorów (11.16) nie zależny w sposób
jawny od czasu , funkcja R3 może być liniową funkcją czasu. Bez ograniczenia ogólności możemy założyć :
∂
R3 /
∂
t = 0 (11.26)
Zatem , z (11.16) wynikają wzory przekształcenia :
wk = -
∂
R3 /
∂
Jk ; pk = -
∂
R3 /
∂
qk ; H = H^ = E (11.27)
Ostatni z nich przedstawia skrócone równanie Hamiltona – Jakobiego a drugi ustanawia tożsamość :
R3 = - W (11.28)
( W – jest skróconym działaniem ). Dlatego wzory (11.27) można zapisać następująco :
wk =
ν
k t +
γ
k =
∂
W /
∂
Jk , pk =
∂
W/
∂
qk , H( qk ,
∂
W/
∂
qk ) =E (11.29)
11.4 UKŁADY O ZMIENNYCH ROZDZIELONYCH.
Aby mieć możliwość rozwinięcia dalej teorii w żądanym kierunku , musimy ograniczyć się do układów o
zmiennych rozdzielonych. Nasze dalsze kroki będą polegały na tym co następuje.
Będziemy poszukiwali całki zupełnej skróconego równania Hamiltona – Jakobiego w postaci sumy :
W =
Σ WL (qL ,
α
M ) = W1 (q1 ,
α
M ) + W2 (q2 ,
α
M ) + ... (11.30)
L
Przy tym otrzymamy :
E = E (
α
M ) (11.31)
Wtedy pierwsze i drugie równanie (11.29) wyglądać następująco :
wk =
ν
k t +
γ
k = Σ (
∂
WL /
∂
JK ) , pk =
∂
Wk /
∂
qk (11.32)
Ustalmy następnie wartość wszystkich współrzędnych , oprócz qk , i dla ruchu wzdłuż odpowiadającej linii
współrzędnościowej ( zakładając Jk = const. ) znajdujemy :
dM wk = (
∂
2W
M /
∂
qM
∂
JK ) dqM (11.33)
Całkując w okresie , znajdujemy przyrost :
∆
M wk =
∂
/
∂
JK
∫
(
∂
WM /
∂
qM) dqM =
∂
/
∂
JK
∫
pM dqM (11.34)
τ
τ
(symbol
∫
- oznacza , że całkowania dokonujemy w ciągu pełnego okresu ). Przy M = K otrzymujemy
τ
∆
M wk = 1, skąd wynika , że :
JK =
∫
pK dqK (11.35)
τ
zakładając stałe całkowania równe zeru. Przy M
≠
K otrzymamy :
∆
M wk = 0, chociaż wartość wk zmienia się
podczas ruchu.
Całkę po prawej stronie równości (11.35) nazywamy „całką fazową” jest ona identyczna z odpowiadającą jej
zmienną działania. Dlatego zmienna działania równa jest powierzchni obszaru zakreskowanego na rysunkach
7 i 8 .

36
Ponieważ w całce , wchodzącej do równania (11.35) całkowanie prowadzimy względem współrzędnej wchodzi
do niej jeszcze również parametr
α
M , możemy zatem zapisać :
JK = JK (
α
M ) (11.36)
Rozwiązując ten układ względem
α
M :
α
M =
α
M ( JK ) (11.37)
a następnie podstawiając wynik do wzoru (11.31) , otrzymamy :
E = E (
α
M ( JK ) ) (11.38)
Obliczając pochodną cząstkową od tej wielkości względem JK i uwzględniając równości (11.27) i (11.24)
znajdujemy wartości częstotliwości :
ν
K =
∂
E(
α
M ( JK )) /
∂
JK (11.39)
Podsumowując najistotniejsze z otrzymanych rezultatów możemy powiedzieć :
1. Rozwiązując równanie Hamiltona – Jakobiego , otrzymujmy funkcję tworzącą przekształcenia kanonicznego.
2. Obliczając całki fazowe (11.35) , znajdujemy zmienne działania , kanonicznie sprzężone do zmiennych
kątowych (11.22). Tym samym rozpatrywane zagadnienie dynamiczne okazuje się rozwiązywalna w nowych
zmiennych. Przekształcenie odwrotne do zmiennych pierwotnych można wykonać przy pomocy wspomnianej
powyżej funkcji tworzącej.
3. Zgodnie z równościami (11.39) , różniczkowanie energii względem zmiennych działania daje wartości
częstotliwości.
11.5 ZASADA KWANTOWANIA BOHRA – SOMMERFELDA.
Przejście do pół klasycznej mechaniki kwantowej dokonywane jest z zastosowaniem do całki fazowej zasady
kwantowania Bohra – Sommerfelda :
JK =
∫
pK dqK = nK h (11.40)
τ
( h - jest stałą Plancka ). Przy tym liczba kwantowa nK może przyjmować wartości ze zbioru liczb całkowitych.
Pochodna cząstkowa (11.39) przechodzi w zależność różnicową , co związane jest z tym ,że na mocy warunku :
∆
JK = h (11.41)
zmiana zmiennej działania mniejsza niż h jest niemożliwa. Stąd otrzymujemy następująca zależność :
ν
=
∆
E / h lub
∆
E =
ν
h (11.42)
w której rozpoznajemy wzory Plancka.
Stosując zasadę Bohra – Sommerfelda (11.40) do rozpatrywanego w rozdziale 10.2 zagadnienia Keplera ,
otrzymamy zgodnie z równaniem (10.37) :
J
ϕ
=
∫
p
ϕ
d
ϕ
= 2
πα
= n
ϕ
h lub
α
= (h /2
π
) n
ϕ
= ħ n
ϕ
(11.43)
τ
( wielkość n
ϕ
nazywamy „azymutalną liczbą kwantową” )
i zgodnie z równaniem (10.38) :
rmax
Jr =
∫
pr dr =
±
∫
sqrt [ 2m ( E + (k/r) ) – [ ( ħ n
ϕ
)2 / r2 ] ] dr = ħ nr (11.44)
τ
rmin
( wielkość nr nazywamy „radialna liczbą kwantową” ; ħ = h /2
π
)
Wybieramy zazwyczaj znak plus aby nr , mogło przyjmować tylko dodatnie wartości. Wielkości :
rmin = 1/ s2 , rmax = 1/ s1 reprezentują minimalną I maksymalną wartość kąta biegunowego.
Obliczenie całki ( przykładowo na płaszczyźnie zespolonej ) daje :
Jr = - n
ϕ
h - 2
π
i [ mK/ sqrt (2mE) ] = h nr
skąd otrzymujemy dyskretne poziomy energii :
En = - ( mK
2/ 2ħ2r2 ) (11.45)
do którego wchodzi „główna liczba kwantowa“ :
n = nr + n
ϕ
(11.46)
Energia jest ujemna dlatego , że mamy stany związane. Odpowiednio z wprowadzonymi powyżej oznaczeniami
dla atomów stosujemy K = - eQ. Wzór (11.45) jest słuszny dla atomu wodoru , jak również dla układów
wodoropodobnych.

37
12. TOR JAKO CHARAKTERYSTYKI RÓWNANIA HAMILTONA – JAKOBIEGO.
W tym rozdziale dokładnie zaznajomimy się z matematycznymi aspektami teorii Hamiltona – Jakobiego. Przy
tym będziemy opierali się dokładnie na opracowaniu teorii równań o pochodnych cząstkowych drugiego rzędu.
Jak wiadomo charakterystykami takiego równania różniczkowego są specjalnie wydzielone krzywe osobliwe. W
dalszej części pokaże , że charakterystyki równania Hamiltona – Jakobiego odpowiadają torom punktu
materialnego.
Powróćmy do rozdziału 8.2 , w którym podana była definicja całki zupełnej , równania o pochodnych
cząstkowych pierwszego rzędu o n zmiennych niezależnych – przyjęto dla tej całki następujące oznaczenie :
σ = σ ( yi ,
α
i ) (12.1)
Całka ogólną równania o pochodnych cząstkowych pierwszego rzędu o n zmiennych niezależnych nazywamy
rozwiązanie tego równania , zawierające pewną dowolną funkcję n-1 zmiennych . Całkę ogólna można znaleźć z
całki zupełnej w następujący sposób.
Załóżmy , że :
α
n = f (
α
i , … ,
α
n-1 ) (12.2)
gdzie f – jest dowolna funkcją n-1 zmiennych , wtedy całka zupełna (12.1) przechodzi w funkcję :
σ = σ ( yi ,
α
i , … ,
α
n-1, f(
α
i , … ,
α
n-1)) =
τ
( yi ,
α
i , … ,
α
n-1) (12.3)
Funkcja
τ
, oczywiście , jest również rozwiązaniem naszego równania różniczkowego
Funkcje (12.1) obrazują n-parametryczny zbiór rozwiązań. Przy podstawieniu (12.2) otrzymujemy (n-1) –
parametryczny zbiór rozwiązań (12.3). Różniczkując (12.3) względem parametrów
α
i , … ,
α
n-1, otrzymujemy
układ (przypomina to budowę krzywej rozwijającej ) :
∂
σ/
∂α
i + (
∂
σ
∂
f)(
∂
f/
∂α
1) = 0 , … ,
∂
σ/
∂α
n-1 + (
∂
σ
∂
f)(
∂
f/
∂α
n-1) = 0 (12.4)
składający się z n-1 równań. Rozwiązując ten układ względem
α
i , … ,
α
n-1 , znajdujemy :
α
i =
α
1(yi ) , … ,
α
n-1 =
α
n-1(yi ) (12.5)
Do zależności tych wchodzi dowolna funkcja f. Wynikiem podstawienia wyrażeń (12.5) do wzorów (12.3)
będzie całka ogólna :
σ =
τ
( yi ,
α
1(yi ) , … ,
α
n-1(yi ) ) (12.6)
Całkę osobliwą równania o pochodnych cząstkowych pierwszego rzędu , otrzymujemy w analogiczny sposób.
Z (12.1) można wyprowadzić układ :
∂
σ( yi ,
α
i )/
∂
α
1 = 0 , … ,
∂
σ( yi ,
α
i )/
∂
α
n = 0 (12.7)
Składający się z n równań. Rozwiązując ten układ względem zmiennych
α
i , dochodzimy do n zależności
postaci :
α
1 = h1(yi ) , … ,
α
n hn (yi ) (12.8)
Podstawiając te wyrażenia do (12.1) otrzymamy funkcję :
σ = σ( yi , hi (yi )) (12.9)
Jeśli funkcja ta spełnia równanie różniczkowe , to nazywamy ją całką osobliwą. Opisuje ona ogólną rozwijającą
wszystkich powierzchni całkowych , wchodzących do całki zupełnej.
Rozpatrzmy teraz (n+1) – wymiarową przestrzeń zmiennych (yi , σ ), w której rozwiązanie równania
różniczkowego zapisane będzie w postaci nie jawnej :
G(yi , σ ) = 0 (12.10)
przedstawiającej pewną hiperpowierzchnię. Przy tym (n+1)-wymiar odpowiada zmiennej zależnej σ.
Niech w tej przestrzeni w sposób parametryczny będzie zadana pewna krzywa :
yi = yi (
λ
) , σ = σ (
λ
) (12.11)
(
λ
- jest parametrem krzywej). Ponieważ gradient
∂
G/
∂
yi , określa kierunek normalnej do tej hiperpowierzchni ,
każdemu ustalonemu punktowi krzywej (12.11) można przyporządkować poprzez określenie kierunków
normalnych na tej krzywej, stożek normalnych ( stożek normalny) , jest to możliwe na mocy zależności :
∂
σ/
∂
yi = - (
∂
G/
∂
yi ) / (
∂
G/
∂
σ) (12.12)
wynikających z równania różniczkowego (12.10). Przy tym w szczególnym przypadku n = 2 , mamy
dwuwymiarową powierzchnię stożkową.
W tym ustalonym punkcie krzywej, elementy powierzchni całkowych , prostopadłe do kierunków normalnych
również tworzą stożek – nazywany stożkiem Moongea.

38
Przy przesunięciu wzdłuż zadanej krzywej elementy powierzchni całkowej przedstawiają półoś - przedłużając tą
półoś w kierunku normalnym można zbudować powierzchnię całkową. Dokonać tego można przez rozłożenie w
szereg potęgowy funkcji σ( yi ). W celu zbudowania tej półosi wykorzystamy zależność :
n
(
∂
G/
∂
σ) (
∂
σ/
∂λ
) +
Σ (
∂
G/
∂
yi ) (
∂
yi /
∂λ
) = 0 (12.13)
i=1
spełnioną wzdłuż krzywej (12.11) i otrzymanej przez różniczkowanie równań (12.10).
Charakterystykami równania różniczkowego pierwszego rzędu są takie krzywe , dla których jednoznaczne
przedłużenie tj. jednoznaczne zbudowanie hiperpowierzchni całkowej jest nie możliwe. Zatem, charakterystyki
reprezentują sobą krzywe osobliwe , którym odpowiada nieprzeliczalny zbiór powierzchni całkowych.
Charakterystyki równania o pochodnych cząstkowych (8.17) można opisać następującym układem równań :
n
dσ/d
λ
=
Σ [
∂
F/
∂
(
∂
σ/
∂
yi )] (
∂
σ/
∂
yi ) (12.14)
i=1
dyi /
∂λ
= (
∂
F/
∂
(
∂
σ/
∂
yi )) (12.15)
d(
∂
σ/
∂
yi)/d
λ
= - (
∂
F/
∂
yi ) – (
∂
F/
∂
σ) (
∂
σ/
∂
yi ) (12.16)
Równania te zastosujemy do równania Hamiltona – Jakobiego, dla którego funkcja F określona jest wzorem
(8.21) i spełnia zależności (8.19) i (8.20). Wypisze jeszcze raz te wyniki :
F = H( qk , (
∂
S/
∂
qk ), t ) +
∂
S/
∂
t (12.17)
yi = (qk , t ) ; σ = S (12.18)
Z tego , że F nie zależy jawnie od S wynika równość :
∂
F/
∂
S = 0 (12.19)
Zatem , z układu równań (12.14) – (12.16) po uwzględnieniu równości :
∂
S/
∂
qk = pk , otrzymujemy następujące
zależności ( n = f + 1 ) :
f
dS/d
λ
=
Σ (
∂
H/
∂
pk ) pk +
∂
S/
∂
t (12.20)
k=1
dqk /d
λ
=
∂
H/
∂
pk , dt/d
λ
= 1 (12.21)
dpk /d
λ
= -
∂
H/qpk , d(
∂
S/
∂
t)/ d
λ
= -
∂
H /
∂
t (12.22)
Z drugiego równania (12.21) można bez ograniczenia ogólności założyć , że :
λ
= t (12.23)
tj. wybrać w charakterze parametru krzywej czas t. Przy tym równania (12.20) – (12.22) możemy zapisać
następująco :
f f
dS/dt = (
∂
S/
∂
t ) +
Σ (
∂
H/
∂
pk ) pk = (
∂
S/
∂
t) +
Σ (
∂
S/
∂
qk ) (dqk/dt) (12.24)
k=1 k=1
(dqk/dt) =
∂
H/
∂
pk , (dpk/dt) = -
∂
H/
∂
qk , dH/dt =
∂
H/
∂
t (12.25)
Możemy od razu rozpoznać w powyższym układ równań zapisany w formaliźmie Hamiltona , opisujący
trajektorię punktu materialnego. Tym samym twierdzenie , że tor jest charakterystyką równania Hamiltona –
Jakobiego jest dowiedzione.
Zaprezentowane poniżej wywody prowadzą do geometrycznej interpretacji twierdzenia Jakobiego o
znajdywaniu trajektorii z całki zupełnej równania Hamiltona – Jakobiego .
Wyjdziemy z zależności (8.23) , którą zapiszemy teraz następująco :
T = S – S^( qk ,t ,
α
k , t0 ) – S0 = 0 (12.26)
Zgodnie z tym co powiedziano wcześniej , równanie to przedstawia hiperpowierzchnię w (f + 2)-wymiarowej
przestrzeni zmiennych qk , t , S (jak pokazałem wcześniej t0 – jest parametrem nie istotnym). Wobec istnienia
f +1 niezależnych parametrów
α
k , S0 , hiperpowierzchnia ta jest (f + 1)-parametrycznym zbiorem
hiperpowierzchni , przy czym addytywnie wchodzący do równania (12.26) parametr powoduje jedynie
przesunięcie wzdłuż osi S. Budowa krzywych rozwijających rodziny (12.26) prowadzi do równań :
∂
T/
∂α
k = -
∂
S^/
∂α
k = 0 ;
∂
T/
∂
Sk = - 1 = 0 (12.27)
tj. jak widać do sprzeczności w drugim z równań. Zatem, względem parametru S0 ( na skutek powodowanego
przez niego przesunięcia ) rozwijające nie istnieją. Z twierdzenia Jakobiego (9.47), które można zapisać na mocy
zależności (8.23) następująco :

39
∂
S^ /
∂α
k =
β
k (12.28)
wynika, że określone przez równania (12,27) krzywe osobliwe w ogólnym przypadku nie są charakterystykami.
Jeśli , jednak, zmniejszyć liczbę parametrów o jeden i wziąć ich nie f + 1, a f – przyjmując przykładowo :
α
k =
α
k (
γ
1 , ... ,
γ
f ) =
α
k = (
γ
L ) (12.29)
S0 = S0 (
γ
1 , ... ,
γ
f ) = S0 = (
γ
L ) (12.30)
to równość (12.26) możemy zapisać w postaci :
T = S – S^( qk ,t ,
α
k (
γ
L ), t0 ) - S0 (
γ
L ) = 0 (12.31)
Budując teraz rozwinięte, względem parametrów
γ
L , tj. zakładając :
f
∂
T/
∂γ
L = Σ (
∂
S^/
∂α
k )(
∂α
k /
∂γ
k ) – (
∂
S0 /
∂γ
L ) = 0 (12.32)
k=1
otrzymujemy niejednorodny układ równań :
f
Σ (
∂
S^/
∂α
k )(
∂α
k /
∂γ
k ) = (
∂
S0 /
∂γ
L ) (12.33)
k=1
dla wielkości
∂
S^/
∂α
k . Poprzez odpowiedni wybór funkcji
α
k (
γ
L ) można osiągnąć to ,że wyznacznik złożony
ze współczynników przy tych wielkościach będzie różny od zera :
|
α
k /
γ
L |
≠
0 (12.34)
i wtedy istnieje rozwiązanie :
∂
S^/
∂α
k = Bk (12.35)
Utożsamiając wielkości Bk z dowolnie wybieranymi wielkościami
β
k , dochodzimy do stwierdzenia (12.28)
twierdzenia Jakobiego i tym samym pokazaliśmy, że trajektorię ( odpowiednio charakterystyki ) są rozwiniętymi
f-parametrycznego zbioru powierzchni (12.31).
13. NIESKOŃCZENIE MAŁE PRZEKSZTAŁCENIA KANONICZNE.
W tym rozdziale pokaże jeszcze jedną ważną możliwość zastosowania przekształceń kanonicznych. Przy tym
będę rozpatrywał nieskończenie mała zmianę zmiennych , które podlegają przekształceniu kanonicznemu.
Jak to zwykle robi się w rachunku różniczkowym, będziemy odrzucać małe drugiego rzędu w porównaniu z
małymi pierwszego rzędu.
Wyjdziemy od funkcji tworzącej postaci :
f
F = I -
Σ pk (
∂
I /
∂
pk ) (13.1)
k=1
przy czym :
I = I( qk , pk , t ) (13.2)
jest wielkością nieskończenie małą – nazwiemy ją „nieskończenie mała funkcją tworzącą”. Zatem , funkcja F
jest również nieskończenie mała. *) Właśnie z powodu małości funkcji I i F w odróżnieniu od zrobionych
wcześniej założeń ( zobacz rozdział 9) autor w tej chwili zakłada , że funkcje te zależne są tylko od starych
zmiennych – przypis redaktora. *)
Ze wzoru (13.1) otrzymujemy :
f f
dF = (
∂
I/
∂
t) dt +
Σ (
∂
I/
∂
qk ) dqk - Σ pk d (
∂
I /
∂
pk ) (13.3)
k=1 k=1
Z dokładnością do małych pierwszego rzędu wynik ten można przepisać do następującej postaci :
f f
dF = (
∂
I/
∂
t) dt +
Σ [ pk + (
∂
I/
∂
qk )] + d [ qk – (
∂
I/
∂
pk 0 ] - Σ pk dqk (13.4)
k=1 k=1
Porównując go do zależności dla przypadku ogólnego (9.4) , znajdujemy szukane wzory przekształcenia :
q^k = qk – (
∂
I/
∂
pk ) , p^k = pk – (
∂
I/
∂
qk ) , H^ = H – (
∂
I/
∂
t) (13.5)
Nieskończenie małe zmiany zmiennych w odróżnieniu od ich wirtualnych przyrostów, będziemy oznaczali
symbolem
δ
^ :
q^k = qk +
δ
^qk , p^k = pk +
δ
^pk , H^ = H +
δ
^H (13.6)
Wtedy wzory (13.5) przyjmują postać :
δ
^qk = -
∂
I/
∂
pk ,
δ
^pk = -
∂
I/
∂
qk ,
δ
^H = -
∂
I/
∂
t (13.7)

40
Poniżej pokaże , że proces ruchu układu mechanicznego w czasie można interpretować jako następstwo
nieskończenie małych przekształceń kanonicznych ( zmianie zmiennych w interwale między dwoma chwilami
czasu odpowiada zmiana tych zmiennych na skutek nieskończenie małego przekształcenia kanonicznego ).
W związku z tym zapiszemy równania Hamiltona w następujący sposób :
dqk = (
∂
H/
∂
pk ) dt ; dpk = (
∂
H/
∂
qk ) dt (13.8)
W związku z dowodzonym twierdzeniem utożsamimy różniczki w równaniach (13.8) z nieskończenie małymi
zmianami (13.7) :
dqk =
δ
^qk ; dpk =
δ
^pk (13.9)
Przy tym z równań (13.7) I (13.8) wynika , że :
(
∂
H/
∂
pk) dt = - (
∂
I/
∂
pk ) ; (
∂
H/
∂
qk) dt = - (
∂
I/
∂
qk ) (13.10)
ponieważ czas nie wpływa w żaden sposób na różniczkowanie względem współrzędnych , otrzymujemy stąd , że
nieskończenie mała funkcja tworząca ma następującą postać :
I = - H dt (13.11)
Zależność (13.11) pokazuje , że w czasie ruchu funkcja Hamiltona w określony sposób wchodzi w nieskończenie
małą funkcję tworzącą.
Na mocy ogólnego wzoru (7.5) dla nieskończenie małej funkcji tworzącej spełniona jest równość :
dI/dt =
∂
I/
∂
t + [ I , H ] (13.12)
W szczególnym przypadku , kiedy I przyjmuje postać wyrażenia (13.11), otrzymujemy :
dI/dt =
∂
I/
∂
t (13.13)
zatem , dla tego przypadku ostatnia z równości (13.6) może być zapisana następująco :
H^ = H + (
∂
H/
∂
t) dt (13.14)
14. PRZEKSZTAŁCENIA SYMETRII.
Zdefiniujmy wielkość
∆
^H równością :
∆
^H = H( q^k , p^k , t ) – H( qk , pk , t ) (14.1)
Zauważmy , że w ogólnym przypadku :
H( q^k , p^k , t )
≠
H^( q^k , p^k , t ) (14.2)
Rozkładając prawą stronę równania (14.1) w szereg Taylora względem qk i pk otrzymamy :
f f
∆
^H =
Σ (
∂
H/
∂
qk )
δ
^qk + Σ (
∂
H/
∂
qk )
δ
^pk (14.3)
k=1 k=1
Po uwzględnieniu zależności (13.7) otrzymamy :
f
∆
^H =
Σ [ - (
∂
H/
∂
qk )(
∂
I/
∂
pk ) + (
∂
H/
∂
pk )(
∂
I/
∂
qk )] = [ I, H ] (14.4)
k=1
Zgodnie z (13.12) dla pochodnej zupełnej względem czasu mamy :
dI/dt =
∂
I/
∂
t + [ I , H ] (14.5)
Skąd otrzymujemy , że :
dI/dt =
∂
I/
∂
t +
∆
^H (14.6)
Jest to nasza podstawowa zależność.
Przekształcenie symetrii zdefiniowane jest warunkiem :
∂
I/
∂
t +
∆
^H = 0 (14.7)
Zatem , chodzi o nieskończenie małe przekształcenie kanoniczne posiadające taką własność , że podstawienie
przekształconych zmiennych do funkcji Hamiltona , zgodnie z równaniem (14.1) prowadzi do takiej wielkości
∆
^H , która związana jest z pochodną cząstkową względem czasu nieskończenie małej funkcji tworzącej
zależnością (14.7). Dlatego dla przekształceń symetrii , zgodnie z (14.6) , mamy :
dI/dt = 0 lub I = const. (14.8)
Zatem , nieskończenie mała funkcja tworząca poddana przekształceniu symetrii jest stałą ruchu. Ponieważ
parametry wchodzą do takiej funkcji tworzącej w sposób liniowy , otrzymujemy stąd tyle niezależnych stałych
ruchu ile mamy niezależnych parametrów. Dalej zademonstruje konkretny sposób działania takiej metody.
Na mocy (13.7) i (14.7) dla przekształcenia symetrii :
∆
^H =
δ
^H lub H^ = H( q^k , p^k , t ) (14.9)

41
15. PRAWA ZACHOWANIA MECHANIKI NEWTONOWSKIEJ.
Zastosujmy teraz rozwinięty powyżej formalizm do układu zamkniętego, składającego się z N punktów
materialnych , poddanych działaniu tylko sił wewnętrznych. Wyjdziemy z nieskończenie małej funkcji tworzącej
, zawierającej wszystkie znane symetrię mechaniki newtonowskiej, odzwierciedlające ważne fizyczne rezultaty
będące owocem wielu lat jej rozwoju. Funkcja o której mowa wygląda następująco :
N N N N
I = - a
Σ p
Ω
+
ξ
H - d
Σ (r
Ω
×
p
Ω
) – v [ t
Σ r
Ω
-
Σ m
Ω
r
Ω
] (15.1)
Ω
=1
Ω
=1
Ω
=1
Ω
=1
Gdzie : a ,
ξ
, d , v – są nieskończenie małymi parametrami (
ξ
- jest parametrem skalarnym , reszta to parametry
wektorowe ).
Zgodnie z ogólną teorią , potrzebne nam będą pochodne cząstkowe od I względem różnych zmiennych , dlatego
znajdujemy :
∂
I/
∂
r
Ω
=
ξ
(
∂
H/
∂
r
Ω
) + ( d
×
p
Ω
) – v m
Ω
(15.2)
∂
I/
∂
p
Ω
= -a +
ξ
(
∂
H/
∂
p
Ω
) - ( d
×
r
Ω
) – v t (15.3)
N
∂
I/
∂
t =
ξ
(
∂
H/
∂
t) + v
Σ p
Ω
(15.4)
Ω
=1
Stąd , zgodnie ze wzorami (13.5) , teorii ogólnej, obliczamy przekształcone zmienne i przekształcone funkcje
Hamiltona :
r^
Ω
= r
Ω
-
∂
I/
∂
p
Ω
= r
Ω
+ a + ( d
×
r
Ω
) - v t -
ξ
(dr
Ω
/dt ) (15.5)
p^
Ω
= p
Ω
-
∂
I/
∂
r
Ω
= p
Ω
+ ( d
×
p
Ω
) - v m
Ω
-
ξ
(dp
Ω
/dt ) (15.6)
N
H^ = H -
∂
I/
∂
t = H - v
Σ p
Ω
-
ξ
(
∂
H/
∂
t ) (15.7)
Ω
=1
Równości te przedstawiają wzory na przekształcenia odpowiednich wielkości , otrzymane przy pomocy
nieskończenie małej funkcji tworzącej.
Teraz wyjaśnię sens nieskończenie małych parametrów i rozpatrzę wzór dotyczący przekształcenia zmiennej
r^
Ω
. Widać , że :
a – określa przesunięcie przestrzenne
d – określa obrót przestrzenny.
v – określa ruch jednostajny.
ξ
- określa przesunięcie czasu.
Przy przekształceniach Lorentza czterowymiarowej przestrzeni , a i
ξ
opisują przesunięcie czasoprzestrzenne , a
d i v – obrót czasoprzestrzenny.
Mając do dyspozycji te wyniki zbadamy funkcje Hamiltona dla zamkniętego układu mechanicznego ,
składającego się z N punktów materialnych . Miedzy tymi punktami mogą działać siły potencjalne , które
zależne są tylko od wartości różnicy wektorów wodzących punktów materialnych. A tego, na mocy
zachowawczości układu wynika , że :
N
H = T + U =
Σ ½ m
Ω
(dr
Ω
/dt )2 + U (r
ΩΓ
) (15.8)
Ω
=1
lub :
N
H = ½
Σ ( p2
Ω
/m
Ω
) + U (r
ΩΓ
) ( r
ΩΓ
= | r
Ω
- r
Γ
| ) (15.9)
Ω
=1
Teraz nasze zadanie polega na tym aby znaleźć symetrię w tej funkcji Hamiltona, ponieważ zgodnie z ogólną
teorią , każda symetria daje pewne prawo zachowania ( całkę pierwszą ).
Jak już wspomniałem , wprowadzona powyżej nieskończenie mała funkcja tworząca I wyczerpuje wszystkie
symetrię funkcji Hamiltona. Należy również pokazać , że spełniona jest równość :
(
∂
I/
∂
t ) +
∆
^H = 0 (15.10)
Zgodnie ze wzorem (14.1) obliczmy wielkość :
N N
∆
^H = ½
Σ ( p^2
Ω
/m
Ω
) + U (r^
ΩΓ
) – ½
Σ ( p2
Ω
/m
Ω
) + U (r
ΩΓ
)
Ω
=1
Ω
=1

42
W to wyrażenie należy podstawić wartości czterech zmiennych p
Ω
, p^
Ω
, r^
Ω
, r
Ω
. Przy zmiennych
podniesionych do kwadratu ,należy mieć na uwadze , że małe drugiego rzędu odrzucamy :
Obliczmy :
r^
ΩΓ
= | r
Ω
- r
Γ
| :
r^
ΩΓ
= sqrt ( r^
Ω
- r^
Γ
) = sqrt { [ r
Ω
- r
Γ
+ d
×
( r
Ω
- r
Γ
) -
ξ
( r.
Ω
- r.
Γ
)]2 } =
= [ ( r
Ω
- r
Γ
)2 + 2 ( r
Ω
- r
Γ
) [d
×
( r
Ω
- r
Γ
)] - 2
ξ
( r
Ω
- r
Γ
) ( r.
Ω
- r.
Γ
)]1/2 (15.11)
Dalej mamy :
N
∆
^H = ½
Σ (1/m
Ω
)[ p^2
Ω
+ 2 p
Ω
(d
×
p
Ω
) - 2m
Ω
p
Ω
v - 2
ξ
p.
Ω
p
Ω
- p2
Ω
] +
Ω
=1
U {[ ( r
Ω
- r
Γ
)2 + 2 ( r
Ω
- r
Γ
) [d
×
( r
Ω
- r
Γ
)] - 2 ( r
Ω
- r
Γ
) ( r.
Ω
- r.
Γ
)
ξ
]1/2 } – U (r
ΩΓ
) (15.12)
Uproszczając ( uwzględniając m.in. to ,że iloczyn mieszany wektorów do którego wchodzą równe czynniki jest
równy zeru ) otrzymamy :
N N
∆
^H = - v
Σ p
Ω
- ½
ξ
d/dt
Σ (p^2
Ω
/ m
Ω
) + U ( r
ΩΓ
sqrt [1- 2
ξ
d/dt ( ln (r
ΩΓ
)] ) – U(r
ΩΓ
) }
Ω
=1
Ω
=1
( o słuszności wyrażenia stojącego pod pierwiastkiem można się przekonać różniczkując je ).
Teraz możemy rozłożyć pierwiastek , wchodzący jako argument funkcji U, w szereg Taylora :
sqrt [1- 2
ξ
d/dt ( ln (r
ΩΓ
) ]
≈
1 -
ξ
d/dt [ ln (r
ΩΓ
) ] (15.13)
Zatem , rozkładając w szereg Taylora samą funkcję U otrzymamy :
N
U = U ( r
ΩΓ
-
ξ
r
ΩΓ
d/dt [ ln (r
ΩΓ
) ] = U(r
ΩΓ
) - ½
ξ
Σ (
∂
U/
∂
r
ΩΓ
) (dr
ΩΓ
/dt) (15.14)
Ω
,
Γ
=1
Ponieważ do sumy po prawej stronie , każda ze składowych wchodzi dwukrotnie postawiliśmy przed znakiem
sumy czynnik ½ . W wyniku tego wyrażenie
∆
^H przyjmuje postać :
N N N
∆
^H = - v
Σ p
Ω
- ½
ξ
d/dt
Σ (p^2
Ω
/ m
Ω
) - ½
ξ
Σ (
∂
U/
∂
r
ΩΓ
) (dr
ΩΓ
/dt) (15.15)
Ω
=1
Ω
=1
Ω
,
Γ
=1
Ponieważ :
N N
dH/dt =1/2 d/dt
Σ (p^2
Ω
/ m
Ω
) + ½
Σ (
∂
U/
∂
r
ΩΓ
) (dr
ΩΓ
/dt) (15.16)
Ω
=1
Ω
,
Γ
=1
ostatecznie otrzymujemy :
N
∆
^H = - v
Σ p
Ω
-
ξ
dH/dt (15.17)
Ω
=1
Teraz obliczmy pochodną zupełną względem czasu wielkości I :
N N
dI/dt =
∂
I/
∂
t +
∆
^H = v
Σ p
Ω
+
ξ
dH/dt - v
Σ p
Ω
-
ξ
dH/dt (15.18)
Ω
=1
Ω
=1
Z tego , na mocy równości (6.11) wynika warunek postaci :
dI/dt = 0 lub I = const. (15.19)
Zatem nasza nieskończenie mała funkcja tworząca jest stałą ruchu , rozpatrywanego układu mechanicznego.
Wyjaśnię teraz co oznacza taki wynik.
Ponieważ parametry wybrane zostały dowolnie , można ustalić wartość jednego z nich , a pozostałe przyjąć
równe zeru. Wykonując kolejno tą procedurę do każdego z parametrów, znajdujemy dla każdego z nich stałą
wielkość , będącą mnożnikiem przy danym parametrze w wyrażeniu (15.1). Rozpatrzmy otrzymywane w taki
sposób wyrażenia :
1). a
≠
0 , d = 0 , v = 0 ,
ξ
= 0
Z (15.1) wynika równość :
N
a
Σ p
Ω
= const.
Ω
=1

43
Zatem :
N
Σ p
Ω
= const. ( zachowanie pędu ) (15.20)
Ω
=1
Zatem ,jak widać , prawo zachowania pędu otrzymaliśmy z symetrii funkcji Hamiltona , względem przesunięcia
przestrzennego. Dlatego w przestrzeni konfiguracyjnej wszystkie punkty są „równouprawnione” żadnego z
punktów nie można uprzywilejować. Własność ta nazywamy „jednorodnością przestrzeni”.
2).
ξ
≠
0 , d = 0 , v = 0 , a = 0
W tym przypadku z (15.1) wynika równość :
ξ
H = const.
i dlatego :
H = E = const. ( zachowanie energii ) (15.21)
Prawo zachowania energii jest wynikiem symetrii funkcji Hamiltona względem przesunięcia czasowego.
Dlatego żadna chwila czasu nie jest uprzywilejowana , stwierdzenie to nazywamy „jednorodnością czasu”.
3). d
≠
0 , a = 0 , v = 0 ,
ξ
= 0
Przy tych warunkach ze wzoru (15.1) otrzymujemy :
N
d
Σ ( r
Ω
×
p
Ω
) = const.
Ω
=1
Odpowiednio zatem :
N
Σ ( r
Ω
×
p
Ω
) = const. ( zachowanie momentu pędu ) (15.22)
Ω
=1
Jak widzimy prawo zachowania momentu pędu wynika z symetrii funkcji Hamiltona względem obrotu
przestrzennego. Własność ta nazywa się „izotropowością” przestrzeni.
4). v
≠
0 , a = 0 , d = 0 ,
ξ
= 0
Zgodnie ze wzorem (15.1) mamy :
N N
v [ t
Σ r
Ω
-
Σ m
Ω
r
Ω
] = const.
Ω
=1
Ω
=1
skąd otrzymujemy :
N N
Σ m
Ω
r
Ω
- t
Σ p
Ω
= const. (prawo zachowania prędkości środka masy ) (15.23)
Ω
=1
Ω
=1
Zatem , jednostajny i prostoliniowy ruch środka masy wynika z odpowiedniej symetrii funkcji Hamiltona. W
podejściu czterowymiarowym fakt ten dotyczy obrotu czasoprzestrzennego ( obrót lorentzowski ), któremu
odpowiada „izotropowość continuum czasoprzestrzennego )
Prawa zachowania pędu, momentu pędu i prędkości środka masy wyrażone są równaniami wektorowymi , każde
takie równanie równoważne jest trzem równaniom skalarnym, zatem te trzy prawa łącznie dają dziewięć stałych
ruchu. Przy spełnieniu wszystkich wskazanych powyżej symetrii w mechanice istnieje dziesięć stałych ruchu
( włączając stałą energii )
16.MECHANIKA RELATYWISTYCZNA PUNKTU MATERIALNEGO W TRÓJWYMIAROWYM
FORMALIŹMIE.
Przy dużych prędkościach ruchu mechanika Newtonowska nie jest już słuszna i należy stosować wzory
szczególnej teorii względności stworzonej przez A. Einsteina w 1905 roku. Mechanika relatywistyczna układu
punktów materialnych nie istnieje , ponieważ wysokoenergetyczne cząstki oddziałują wzajemnie w wyniku
czego występują zjawiska których wyjaśnienie wymaga wyjścia poza ramy mechaniki ( przykładowo : anihilacja
par cząstek i promieniowanie fal elektromagnetycznych ).
W relatywistycznym sformułowaniu równanie ruchu punktu zapisujemy następująco :
d/dt { m0 r
. / sqrt [ 1 – (
r
. 2 / c2 )] } = K (16.1)
Równanie to przedstawia uogólnienie równania ruchu Newtona.
W mechanice relatywistycznej masa nie jest stała ale jest zmienną dynamiczną, zależną od prędkości :

44
m = m0 / sqrt ( 1 – ( r
. 2 / c2 ) ) ( masa relatywistyczna ) (16.2)
Pokaże teraz , że można przenieść do mechaniki relatywistycznej teorię Lagrange’a – Jakobiego w
trójwymiarowym sformułowaniu.
Zdefiniujmy działanie w sposób analogiczny jak wcześniej ( zobacz wyrażenie ( 8.1 ) ) :
t1
S =
∫
L(r , r
.
, t ) dt + S0 (16.3)
t0
Ponieważ nie nakładamy na funkcję Lagrange’a żadnych ograniczeń , zasadę Hamiltona otrzymamy również w
znanej postaci :
t1
δ
∫
L(r , r. , t ) dt = 0 , przyczym :
δ
r ( t1) =
δ
r (t0 ) = 0 (16.4)
t0
Odpowiednio zatem równanie Lagrange’a wygląda następująco :
δ
L/
δ
r =
∂
L/
∂
r – d/dt (
∂
L/
∂
r. ) = 0 (16.5)
Równanie ruchu (16.1) możemy otrzymać przy pomocy relatywistycznej funkcji Lagrange’a :
L = m0 c
2 [ 1 – (
r
. 2 / c2 ) ]1/2 - U(r , r. , t ) (16.6)
Rozłożenie wyrażenia pod pierwiastkiem w szereg Taylora daje :
[ 1 – ( r
. 2 / c2 ) ]1/2
≈
1 – ½ (r. 2 / c2 ) (16.7)
Jeżeli rozpatrujemy małe prędkości w porównaniu z prędkością światła ( r
. 2 << c2 ) , to człony wyższych
rzędów można odrzucić. Wtedy z dokładnością do stałej addytywnej , która jak wiadomo nie figuruje w
równaniach ruchu , otrzymujemy już znaną postać funkcji Lagrange’a mechaniki newtonowskiej (4.24):
L
≈
- m0 c
2 + ½ m r. 2 – U (16.8)
Pokaże teraz ,że ta relatywistyczna funkcja Lagrange’a prowadzi do prawidłowych równań ruchu. Różniczkując
ją znajdujemy :
∂
L/
∂
r = -
∂
U/
∂
r (16.9)
p =
∂
L/
∂
r. = { m0 r
. / sqrt [ 1 – (
r
. 2 / c2 ) ] } -
∂
U/
∂
r. (16.10)
Wprowadzając masę relatywistyczną (16.2) otrzymujemy :
p = mr. -
∂
U/
∂
r. (16.11)
Podstawmy to wyrażenie do równania Lagrange’a :
d/dt ( mr. ) = -
∂
U/
∂
r +d/dt (
∂
U/
∂
r. ) (16.12)
Porównując go z równaniem ruchu otrzymamy wyrażenie dla siły :
K = -
∂
U/
∂
r +d/dt (
∂
U/
∂
r. ) (16.13)
identyczne z wyrażeniem (4.27).
Zastosujmy powyższe wzory do opisu ruchu cząstki naładowanej poruszającej się w dowolnym polu
elektromagnetycznym ( efekty kwantowo-mechaniczne pomijamy ) i sprawdźmy czy otrzymamy znany wzór :
K = eE + (e/c) v
×
B (16.14)
gdzie : E – jest natężeniem pola elektrycznego, B – jest natężeniem pola magnetycznego.
W danym przypadku potencjał uogólniony wygląda następująco :
U = e
ϕ
- (e/c) Ar. (16.15)
Podstawiając ten potencjał do wzoru (16.13) otrzymamy :
K = e(
∂ϕ
/
∂
r) + (e/c)
∂
/
∂
r < A ,r. > - (e/c) dA/dt (16.16)
Aby dojść do ogólnego wyrażenia na siłę należy przekształcić ten wynik. W tym celu przejdziemy od zapisu
wektorowego do zapisu we współrzędnych. ( Indeksy górne greckie przybierają wartości od 1 do 3 .
Zgodnie z umową sumacyjną stosujemy również sumowanie względem powtarzających się indeksów )
Mamy zatem :
K
µ
= - e (
∂ϕ
/
∂
x
µ
) + (e/c) (
∂
A
ν
/
∂
x
µ
)x.
ν
- (e/c) (
∂
A
µ
/dt ) (16.17)
Przy tym uwzględniliśmy , że w formaliźmie Lagrange’a współrzędne i prędkości rozpatruje się jako zmienne
niezależne. Dalsze przekształcenia pokazują , że :
K
µ
= - e (
∂ϕ
/
∂
x
µ
) + (e/c) [ (
∂
A
ν
/
∂
x
µ
) – (
∂
A
µ
/
∂
x
ν
)x.
ν
- (
∂
A
µ
/dt ) ] (16.18)
Przyjmując zależność między natężeniami pól i potencjałem skalarnym
ϕ
oraz wektorowym A, postaci :
E = - grad
ϕ
- (1/c)
∂
A/
∂
t) , B = rot A (16.19)
lub w zapisie we współrzędnych :

45
E
µ
= - (
∂ϕ
/
∂
x
µ
) - (1/c) (
∂
A
µ
/
∂
t ) ; B1 = (
∂
A3/
∂
x2 ) – (
∂
A2/
∂
x3 ) itd (16.20)
wzory (16.18) dla
µ
= 1 można przedstawić w następującej postaci :
K1 = eE1 + (e/c) { [(
∂
A2/
∂
x1 ) – (
∂
A1/
∂
x2 )] x.2 – [(
∂
A1/
∂
x3 ) – (
∂
A3/
∂
x1 )] x.3 } =
= eE1 + (e/c)( B3x
.2 – B
2x
.3 ) = eE
1 + (e/c)( v
×
B)1
Dla pozostałych składowych można przeprowadzić analogiczne rachunki, otrzymując zapis we współrzędnych
wzoru (16.14) . Zatem pokazaliśmy , że (16.15) przedstawia prawidłowe wyrażenie dla potencjału uogólnionego.
Następnym etapem będzie obliczenie funkcji Hamiltona z funkcji Lagrange’a – w tym celu wykorzystamy wzór
(6.2) :
H( r ,p , t ) = r. p – L( r, r. , t ) (16.21)
W naszym przypadku spełnione są również równania kanoniczne (6.9) – (6.11) których zapis wektorowy ma
postać :
r. =
∂
H/
∂
p ; p. = -
∂
H/
∂
r ; dH/dt =
∂
H/
∂
t = -
∂
L/
∂
t (16.22)
Podstawiając wyrażenia (16.6) do wzoru (16.21) otrzymamy :
H = r. p + m0 c
2 sqrt [ 1 – (
r
. 2 / c2 ) ] + U (16.23)
Ponieważ H jest funkcją współrzędnych i pędu r. należy wyrazić przez p. Jednak celowe wydaje się
przeprowadzić to następująco : na początku wyrazić p przez r. a potem przejść od r. do p .
Zgodnie z definicją pędu kanonicznego (6.4) :
p =
∂
L/
∂
r. = { r. m0 / sqrt [ 1 – ( r
. 2 / c2 ) ] } -
∂
U/
∂
r. (16.24)
Podstawiając to wyrażenie do wzoru (16.23) , otrzymamy :
H = { r. m0 / sqrt [ 1 – ( r
. 2 / c2 ) ] } + m
0 c
2 sqrt [ 1 – (
r
. 2 / c2 ) ] + U – (
∂
U/
∂
r. ) r. =
= m0 c
2 + U - (
∂
U/
∂
r. ) r. (16.25)
Zatem , dochodzimy do interesującego wyniku. W mechanice relatywistycznej energii kinetycznej odpowiada
wielkość m0 c
2. Jednak do funkcji Lagrange’a wyrażenie to nie wchodzi tj. w mechanice relatywistycznej już
nie zachodzi zależność postaci ;
L = T – U
Teraz zapiszemy w funkcji Hamiltona r. przez p dla przypadku ruchu cząstki naładowanej w polu
elektromagnetycznym. W tym celu podstawimy do wyrażenia (16.25) potencjał uogólniony (16.15) , co pozwoli
otrzymać :
H = m c2 + e
ϕ
= { m0 c
2 / sqrt [ 1 – (
r
. 2 / c2 ) ] } + e
ϕ
(16.26)
Stąd wynika , że :
( H - e
ϕ
)2 = m0
2 c2 / [ 1 – (
r
. 2 / c2 ) ] (16.27)
I dalej , zgodnie ze wzorem (16.24) *) Zauważmy ,że tutaj nie spełniona jest równość p = mr. , chociaż
wykorzystujemy współrzędne kartezjańskie. *) :
p = { r. m0 / sqrt [ 1 – ( r
. 2 / c2 ) ] } + (e/c) A = mr. + (e/c) A (16.28)
skąd :
[ p – (e/c) A ]2 = m0
2
r
. 2 / [ 1 – (
r
. 2 / c2 ) ] (16.29)
Rozwiązując to równanie względem r
. 2 / c2 , otrzymamy :
r. 2 / c2 = ( 1/c2 )[ p – (e/c) A ]2 / [ m0
2 + ( 1/c2 )[ p – (e/c) A ]2 (16.30)
I dalej :
1 - ( r
. 2 / c2 ) = { 1 + (1/m
0
2 c2 ) [ p – (e/c) A ]2 }-1 (16.31)
I ostatecznie (16.27) możemy zapisać w następujący sposób :
( H - e
ϕ
)2 = m0
2 c4 + c2 [ p – (e/c) A ]2 (16.32)
Przy podstawieniu do tego równania następujących zależności :
p =
∂
S/
∂
r ; H = -
∂
S/
∂
t (16.33)
(jak to było robione przy wyprowadzaniu równania Hamiltona – Jakobiego ) , otrzymujemy równanie Hamiltona
- Jakobiego dla cząstki relatywistycznej poruszającej się w polu elektromagnetycznym :
[ (
∂
S/
∂
r) – (e/c) A ]2 – (1/c2 ) [ (
∂
S/
∂
t) + e
ϕ
]2 + m0
2 c2 = 0 (16.34)
W dalszej kolejności będziemy przyjmowali , że indeksy łacińskie przyjmują wartości od 1 do 4 , zgodnie z
liczbą wymiarów czasoprzestrzeni. Umowa sumacyjna pozostaje w mocy.
W zapisie czterowymiarowym równanie (16.34) znacznie się upraszcza. Wektor wodzący ma cztery składowe :

46
xi = ( x, y, z , ct ) (16.35)
a czteropotencjał ma postać :
Ai = ( A, -
ϕ
) = ( A1, A2 , A3 , -
ϕ
) (16.36)
W STW tensor metryczny ma postać :
gij = g
ij = ( 1 0 0 0 ) (16.37)
( 0 1 0 0 )
( 0 0 0 1 )
( 0 0 0 –1 )
Po uwzględnieniu tych zależności równanie (16.34) przyjmuje postać :
gij [ (
∂
S/
∂
xi ) – (e/c) Ai ] [ (
∂
S/
∂
xi ) – (e/c) Aj ] + m0
2 c2 = 0 (16.38)
Jest to relatywistyczne równanie Hamiltona –Jakobiego . Poprzez niego ustanawia się związek z równaniem
Kleina-Gordona mechaniki kwantowej , opisującym ruch relatywistyczny cząstki przy braku spinu.
CZ
ĘŚĆ B
KLASYCZNA TEORIA POLA
17. WPROWADZENIE W TEORIE POLA.
Ta część książki poświęconą jest klasycznej teorii pola. Na pierwszy plan wysuniemy formalizm kanoniczny,
mając wzgląd na prostotę i objętość książki , nie będę jednak poruszał zagadnień metodologicznych związanych
z poruszanym tematem. Podstawowa ideą wykładu klasycznej teorii pola będzie polegała na wyjaśnieniu do
jakiego stopnia można wykorzystać w klasycznej teorii pola, pojęcia mechaniki klasycznej i odpowiadający jej
formalizm. Jak pokażę – na klasyczna teorie pola ,można przenieść całe rozdziały formalizmu Hamiltona –
Lagrange’a ; dlatego zasada Hamiltona , równania Lagrange’a i równania Hamiltona związane są ze sobą w taki
sam sposób jak w mechanice kanonicznej. Oczywiście pojęcia mechaniczne należy rozszerzyć w taki sposób aby
miały one sens w teorii pola.
Podczas gdy w mechanice centralne miejsce zajmuje układ składający się z N-punktów materialnych , przy
czym proces ruchu opisujemy za pomocą wektorów wodzących lub współrzędnych uogólnionych :
rΩ = rΩ ( t ) lub qk = qk(t) (17.1)
w klasycznej teorii pola mamy do czynienia z układem pól klasycznych , który w ogólnym przypadku składa się
z pól różnych rodzajów ( postaci ). Układ ten można opisać za pośrednictwem N funkcji polowych ( funkcji pól )
UΩ = UΩ (x
i ) = UΩ (r , t ) (17.2)
Indeksy :
Ω
,
Γ
itd. w tej części książki przybierają wartości od 1 do N , jednak w obecnym przypadku N posiada
inny sens fizyczny.
Porównując równania (17.1) i (17.2) możemy ustanowić pewną analogię :
rΩ ( lub qk )
→
UΩ ; t
→
xi (17.3)
Zatem – uogólnionym współrzędnym mechaniki odpowiadają funkcje polowe , a mechanicznemu parametrowi
czasu - cztery czasoprzestrzenne współrzędne galileuszowe (xi ) = ( x
µ
, ct). W teorii względności
współrzędne przestrzenne x
µ
i współrzędna czasowa t , są nierozłącznie związane , wiąże się to z tym ,że tylko
przy takim związku jest słuszna STW , zgodnie z ta teorią prawa przyrody zapisane we współrzędnych
Galileusza , zachowują swoja formę przy przejściu od jednego IUO do drugiego IUO tj. przy przekształceniach
Lorentza
( mówimy wtedy o inwariantności lub kowariantności praw przyrody ) ( inwariantność i kowariantność to dwa
różne ( ogólnie ) pojęcia - przypis własny )
Z drugiej strony , również w teorii pola przy opisie procesu ruchu czas odgrywa odmienną role niż współrzędne
przestrzenne - ruch w ogólności odbywa się bowiem w czasie.
Jednak zgodnie z wyrażeniem (17.2) do funkcji pola razem z czasem wchodzi wektor wodzący w postaci trzech
parametrów zmieniających się w sposób ciągły. Dlatego w odróżnieniu od mechaniki w której mieliśmy
skończoną liczbę stopni swobody, w teorii pola mówimy o układach z nieskończoną ( nieprzeliczalną ) liczbą
stopni swobody.

47
18. ZASADA HAMILTONA.
W teorii pola funkcja Lagrange’a L przedstawia sobą całkę względem ustalonego obszaru w trójwymiarowej
przestrzeni współrzędnych , funkcje podcałkową nazywamy „gęstością lagranżjanu” ₤ :
L =
∫
₤ ( UΩ ,
∂
UΩ/
∂
r ,
∂
UΩ/
∂
t , r , t ) d3x (18.1)
V3
Gęstość lagranżjanu zależy od funkcji pola i ich pochodnych , jak również może zależeć w sposób jawny od
współrzędnych przestrzennych i czasu. Analogia z funkcją Lagrange’a (4.24) jest oczywista. W zapisie
relatywistycznym gęstość lagranżajnu ma postać :
₤ = ₤ ( UΩ , UΩ | i , xi ) (18.2)
przy czym kreska pionowa w indeksie oznacza pochodną cząstkową :
UΩ | i =
∂
UΩ/
∂
xi (18.3)
Wprowadzona w taki sposób gęstość lagranżjanu nazywa się „gęstością lagranżjanu pierwszego rzędu”,
ponieważ wchodzą do niej tylko pochodne pierwszego stopnia.
Gęstość lagranżjanu odgrywa w teorii pola tak ważną rolę jak funkcja Lagrange’a w mechanice. Aby oparta na
tych podstawach teoria była zgodna z STW , gęstość lagranżjanu powinna być relatywistycznym inwariantem.
Związane z postawionym tematem problemy będziemy dokładnie rozpatrywać w dalszym ciągu pracy.
Całkując równość (18.1) względem czasu od t0 do t oraz uwzględniając , że czterowymiarowy element objętości
d4x = d3x dx4 = c d3x dt (18.4)
jest również relatywistycznym inwariantem, otrzymujemy ( analogicznie do (8.1) ) następujące relatywistyczne
wyrażenie dla działania S :
t
S =
∫
∫
₤ d3x dt = (1/c)
∫
₤d4x (18.5)
t0 V3 V3
Przy tym czterowymiarowa objętość , względem której całkujemy , określona jest odpowiednim zapisem
trójwymiarowym. Dlatego dla ustalonego czterowymiarowej objętości czasoprzestrzennej działanie również jest
inwariantem. Dla uproszczenia wywodów będziemy , gdzie tylko to będzie możliwe posługiwali się
czterowymiarową forma zapisu. Oprócz tego , przypomnimy przyjęte wcześniej zasady :
1). litery greckie w indeksach przybierają wartości od 1 do 3
2). litery łacińskie w indeksach przybierają wartości od 1 do 4
3). duże litery greckie
Ω
,
Γ
,
Λ
itd. w indeksach przybierają wartości od 1 do N ( N – liczba funkcji polowych )
Dla wszystkich postaci indeksów stosujemy Einsteinowska umowę o sumowaniu , przy czym sumowanie
prowadzimy względem wszystkich zmiennych odpowiadającym wymiarom danej przestrzeni. Wprowadzimy
zapis w taki sposób aby z dwóch jednakowych indeksów , względem których prowadzimy sumowanie , jeden
był kowariantny (dolny ) drugi kontrawariantny (górny ). Przy tym operator różniczkowy
∂
i =
∂
/
∂
xi uważamy za
wielkość kowariantną , a operator różniczkowy :
∂
i =
∂
/
∂
xi = g
ij
∂
j – za wielkość kontrawariantną.
Tak jak i wcześniej będziemy wykorzystywali rzeczywiste współrzędne Galileusza xi. W porównaniu ze
współrzędnymi Minkowskiego ( x
µ
, i ct ) posiadają one ta własność , że nie wnoszą warunkowej ( sztucznej )
zespoloności, zatem ciało liczb zespolonych pojawia się tylko w związku teorią kwantową. I w tym przypadku
należy ściśle przestrzegać rozróżnienia między indeksami ko- i kontrawariantnymi.
Teraz , po takim przygotowaniu możemy uogólnić równość (4.30) – formułując zasadę Hamiltona jako zasadę
kowariantną relatywistycznie. Zapiszemy ją następująco :
δ
∫
₤ ( UΩ , UΩ | i , x
i ) d4x = 0 (18.6)
V4
Wariację funkcji polowych bierzemy w standardowy sposób stosowany w rachunku wariacyjnym. Analogicznie
do warunku (4.22) funkcje polowe powinny być stałe na granicy całkowania obszaru V4 :
δ
UΩ | V4 = 0 (18.7)
19. RÓWNANIA LAGRANGE’A
W tym rozdziale wyprowadzimy dla teorii pola analog równań mechanicznych Lagrange’a. Jak wiadomo w
mechanice równania te przedstawiają sobą równania ruchu układu mechanicznego. W teorii pola równania
Lagrange’a również należy rozpatrywać jako równania ruchu układu. Teraz jednak nazywają się one
„równaniami pola”.

48
Obliczmy wariację działania w zasadzie Hamiltona :
δ
∫
₤ ( UΩ , UΩ | i , x
i ) d4x =
∫
[ (
∂
₤/
∂
UΩ )
δ
UΩ + (
∂
₤/
∂
UΩ | i )
δ
UΩ | i ] d
4x = 0 (19.1)
V4 V4
zmieńmy porządek operacji wariowania i różniczkowania, wtedy otrzymamy :
∫
[ (
∂
₤/
∂
UΩ )
δ
UΩ + (
∂
₤/
∂
UΩ | i ) (
δ
UΩ ) | i ] d
4x = 0
V4
lub :
∫
{ (
∂
₤/
∂
UΩ )
δ
UΩ + [ (
∂
₤/
∂
UΩ | i )
δ
UΩ ] | i – [ (
∂
₤/
∂
UΩ | i ) | i
δ
UΩ ] } d
4x = 0 (19.2)
V4
W dalszych przekształceniach wykorzystamy twierdzenie Gaussa – Ostrogradskiego dla czterowymiarowej
przestrzeni. Przypomnijmy wektorowy zapis tego twierdzenia dla przypadku trójwymiarowego :
∫
div a d3x =
∫
a d
σ
V3 V3
Ponieważ zapis wektorowy jest charakterystyczny dla przestrzeni trójwymiarowej ale nie wygodny dla
przypadku czterowymiarowego , przepisze to twierdzenie do zapisu indeksowego :
∫
a
µ
|
µ
d
3x =
∫
a
µ
dσ
µ
(19.3)
V3 V3
Przy tym tensorowy element powierzchni dσ
µ
określony jest w następujący sposób :
dσ
µ
= ½
εµαβ
dV
αβ
(19.4)
gdzie :
εµαβ
- jest trójwymiarowym tensorem Levi-Civity, charakteryzującym się własnością absolutnej
antysymetrii , zatem :
ε
123 = 1 (19.5)
dV
αβ
- jest trójwymiarowym tensorowym elementem o określonej ( wewnętrznie ) orientacji , przy pewnym
specjalnym wyborze współrzędnych ma on postać :
( dV
αβ
) = ( 0 dx
1
dx
2
-dx
1
dx
3 ) (19.6)
( -dx1 dx
2
0 dx
2
dx
3 )
( dx1 dx
3
-dx
2
dx
3 0 )
W szczególności , wynika z tego , że :
dσ1 = dx
2
dx
3
; dσ2 = dx
3
dx
1
; dσ3 = dx
1
dx
2
(19.7)
W przestrzeni trójwymiarowej twierdzenia Gaussa- Ostrogradskiego dowodzimy tak samo jak w przestrzeni
trójwymiarowej , co prowadzi to do następującej, analogicznej do (19.3) postaci :
∫
am | m d
4x = i
∫
am dfm (19.8)
V4 V4
Trójwymiarowy element tensorowy hiperpowierzchni w czterowymiarowej przestrzeni zdefiniowany jest
następująco :
dfm = (1/6i )
ε
mijk dV
ijk
(19.9)
ε
mijk – jest czterowymiarowym tensorem Levi-Civity , również absolutnie antysymetrycznym , zatem o
własności :
ε
1234 = 1 (19.10)
dVijk - jest absolutnie antysymetrycznym czterowymiarowym elementem tensorowym o określonej orientacji.
Do wzoru (19.8) celowo wprowadzono mnożnik i , ponieważ będzie on miał związek z liczbą wymiarów
przestrzennych.
Wykorzystamy twierdzenie Gaussa – Ostrogradskiego w celu przekształcenia drugiej składowej równości (19.2)
w całkę po hiperpowierzchni :
∫
[ (
∂
₤/
∂
UΩ | i ) | i
δ
UΩ ] d
4x = i
∫
[ (
∂
₤/
∂
UΩ | i )
δ
UΩ ]
df
i
V4
∂
V4
(poprzez
∂
V4 oznaczam brzeg hiperpowierzchni V4- przypis własny )

49
Ponieważ zgodnie z założeniem (18.7) funkcje polowe są ustalone i stałe na brzegu czterowymiarowej
powierzchni całkowania , funkcja podcałkowa na brzegu hiperpowierzchni V4 staje się równa zeru , zatem cała
całka jest równa zeru. Dlatego w miejsce wzoru (19.2) mamy :
∫
[ (
∂
₤/
∂
UΩ ) - (
∂
₤/
∂
UΩ | i ) ]
δ
UΩ d
4x = 0 (19.11)
V4
Na mocy dowolności wyboru wielkości
δ
UΩ , z równości zeru całki wynika równość zeru funkcji podcałkowej.
Tym samym otrzymujemy równania Lagrange’a teorii pola :
(
δ
₤/
δ
UΩ ) = (
∂
₤/
∂
UΩ ) – (
∂
₤/
∂
UΩ | i ) | i = 0 (19.12)
równania te wyrażają ten fakt , że „pochodna wariacyjna” gęstości lagranżjanu jest równa zeru. Struktura tych
równań odpowiada strukturze równań mechaniki Lagrange’a.
Ponieważ wyszliśmy od inwariantnego działania a następnie prowadziliśmy rachunki w sposób kowariantny ,
równania Lagrange’a są kowariantne. Odpowiednio zatem , spełniają one warunki STW i dlatego zapisane być
mogą w jednakowy sposób w dowolnym IUO.
20. RÓWNANIA HAMILTONA.
W teorii pola można wprowadzić równania przedstawiające sobą analog równań mechaniki Hamiltona. W tym
celu wprowadzimy – analogicznie do pojęcia pędu kanonicznego (6.4) wielkości :
ΠΩ
i =
∂
₤ /
∂
UΩ | i (20.1)
Podczas gdy w mechanice mają miejsce zależności :
qk
→
pk =
∂
L/
∂
p.k
w teorii pola istnieje zależność relatywistyczna :
UΩ
→
ΠΩ
i =
∂
₤ /
∂
UΩ | i (20.2)
W mechanice - jednej uogólnionej współrzędnej qk w miarę sposobności odpowiada jeden pęd uogólniony pk .
Jeśli jednak w teorii pola ściśle trzymać się zasad formalnych, to jednej funkcji pola UΩ należało by
przyporządkować cztery wielkości postaci :
ΠΩ
i .
Wymaganie zgodności z ideami mechaniki zmusza nas jednak do odejścia od tej „dyrektywy” i wprowadzenia
pojęcia pędu stowarzyszonego z polem :
ΠΩ
i = (1/c)
ΠΩ
4 = (1/c)
∂
₤ /
∂
UΩ | 4 =
∂
₤ /
∂
(
∂
UΩ | t ) (20.3)
Zatem otrzymujemy następujące przyporządkowanie :
UΩ
→
ΠΩ
(20.4)
jednak jest ono okupione tym ,że wydzielamy czwartą składową (czas) i tym samym wychodzimy poza ramy
ścisłego czterowymiarowego formalizmu.
Analogicznie do funkcji Hamiltona (6.2) wprowadzamy w teorii pola „gęstość hamiltonianu” :
Ħ =
ΠΩ
(
∂
UΩ/
∂
t) - ₤ =
ΠΩ
4 UΩ | 4 - ₤ (20.5)
Tutaj jednak również odchodzimy od kowariantności , ponieważ przy określaniu w/w wielkości wydzielamy
czas. Odpowiednio zatem otrzymywane z tego równania Hamiltona nie powinny pojawiać się w
czterowymiarowym formaliźmie. Osiągamy tutaj pewną granicę ,do której można jeszcze stosować idee
mechaniki.
Zbudujmy różniczkę zupełną wielkości Ħ :
dĦ = (
∂
UΩ/
∂
t) d
ΠΩ
+
ΠΩ
d (
∂
UΩ/
∂
t) – (
∂
₤ /
∂
UΩ ) - (
∂
₤ /
∂
UΩ | i ) dUΩ | i - (
∂
₤ /
∂
xi )jaw dx
i (20.6)
Zapis (
∂
₤ /
∂
xi )jaw – oznacza pochodną względem współrzędnej x
i wchodzącej w sposób jawny do funkcji ₤ ,
w charakterze zmiennej niezależnej. Wielkości (
∂
₤ /
∂
xi ) i (
∂
₤ /
∂
xi )jaw – związane są następującymi
zależnościami :
(
∂
₤ /
∂
xi ) = (
∂
₤ /
∂
UΩ )UΩ | i + (
∂
₤ /
∂
UΩ | i ) UΩ | j | i + (
∂
₤ /
∂
xi )jaw (20.7)
Z zależności :
ΠΩ
(
∂
UΩ/
∂
t) - (
∂
₤ /
∂
UΩ | i ) UΩ | i = - (
∂
₤ /
∂
UΩ |
µ
) UΩ |
µ
(20.8)
Wynika , że :
dĦ = (
∂
UΩ/
∂
t) d
ΠΩ
- (
∂
₤ /
∂
UΩ ) dUΩ - (
∂
₤ /
∂
UΩ |
µ
) UΩ |
µ
- (
∂
₤ /
∂
xi )jaw dx
i (20.9)
Stąd widać , że Ħ ma postać :

50
Ħ = Ħ ( UΩ , UΩ |
µ
,
ΠΩ
, xi ) (20.10)
jeśli UΩ i
ΠΩ
są niezależne. Będziemy rozwijać teorię właśnie dla takiego przypadku.
Możemy teraz zapisać następujące równania :
∂
UΩ/
∂
t =
∂
Ħ/
∂ΠΩ
;
∂
Ħ/
∂
UΩ = -
∂
₤ /
∂
UΩ (20.11)
∂
Ħ/
∂
UΩ |
µ
=
∂
₤ /
∂
UΩ |
µ
; (
∂
Ħ/
∂
xi )jaw = - (
∂
₤ /
∂
xi )jaw (20.12)
I dalej – dokonamy pewnego przekształcenia równania Lagrange’a :
∂
₤ /
∂
UΩ = (
∂
₤ /
∂
UΩ | i ) | i = (
∂
₤ /
∂
UΩ |
µ
) |
µ
+
∂
/
∂
t [ (
∂
₤ /
∂
(
∂
UΩ /
∂
t ) ] =
= (
∂
₤ /
∂
UΩ |
µ
) |
µ
+
∂ΠΩ
/
∂
t (20.13)
Stąd wynika , że :
∂ΠΩ
/
∂
t = (
∂
₤ /
∂
UΩ ) - (
∂
₤ /
∂
UΩ |
µ
) |
µ
(20.14)
Podstawiając te wyrażenia do układu (20.11) daje równania Hamiltona teorii pola :
∂
UΩ /
∂
t =
∂
Ħ/
∂ΠΩ
;
∂ΠΩ
/
∂
t = - [ (
∂
Ħ/
∂ΠΩ
) - (
∂
₤ /
∂
UΩ |
µ
) |
µ
] (20.15)
Równania te można przybliżyć do postaci podobnej do równań mechaniki Hamiltonowskiej , jeśli wprowadzić
pojęcie – „pochodnej funkcjonalnej”. Pochodne funkcjonalne od pewnego wyrażenia całkowego :
F =
∫
f( UΩ , UΩ |
µ
,
ΠΩ
, xi ) d3x (20.16)
V3
definiujemy w następujący sposób :
*) Należy zauważyć , że autor rozróżnia pochodną wariacyjną i funkcjonalną – przypis redaktora *)
∂Φ
F/
∂Φ
UΩ =
∂
f/
∂
UΩ – (
∂
f/
∂
UΩ |
µ
) |
µ
;
∂Φ
F/
∂ΦΠΩ
=
∂
f/
∂ΠΩ
(20.17)
Przedstawimy funkcję Hamiltona jako całkę gęstości hamiltonianu względem przestrzennej objętości :
H =
∫
Ħ ( UΩ , UΩ |
µ
,
ΠΩ
, xi ) d3x (20.18)
V3
Biorąc pochodne funkcjonalne od H i podstawiając je do powyższego równania Hamiltona , otrzymamy :
∂
UΩ /
∂
t =
∂Φ
H/
∂ΦΠΩ
;
∂ΠΩ
/
∂
t = -
∂Φ
H/
∂Φ
UΩ (20.19)
tj. ustanowiliśmy daleko idącą formalną odpowiedniość z równaniami mechaniki Hamiltona (6.9).
*) Zauważmy , że równania Lagrange’a teorii pola (19.12) zapisane przez pochodne funkcjonalne funkcji
Lagrange’a L (18.1) mają postać :
∂Φ
L/
∂Φ
UΩ = -
∂
/
∂
t [
∂Φ
L/
∂Φ
(
∂
UΩ/
∂
t) ] = 0
i formalnie odpowiadają mechanicznym równaniom Lagrange’a (5.2) – przypis redaktora *)
21. ZAPIS FORMALIZMU HAMILTONA PRZY POMOCY NAWIASÓW POISSONA.
Na początku wyjdziemy od tych samych idei od jakich wyszliśmy definiując nawiasy Poissona w mechanice, w
tym celu rozpatrzymy dwie funkcje f , g , o następującej postaci :
f = f ( UΩ , UΩ |
µ
,
ΠΩ
, xi ) ; g = g( UΩ , UΩ |
µ
,
ΠΩ
, xi ) (21.1)
Dalej wprowadzimy wielkości F ,G jako całki względem przestrzennej objętości , funkcji f i g :
F =
∫
f d3x ; g =
∫
g d3x ; (21.2)
V3 V3
Nawiasy Poissona od F i G definiujemy przez pochodne funkcjonalne (20.17) w następujący sposób :
[ F, G ] =
∫
{ (
∂Φ
F/
∂Φ
UΩ ) (
∂Φ
G/
∂ΦΠΩ
) – (
∂Φ
G/
∂Φ
UΩ )(
∂Φ
F/
∂ΦΠΩ
) } d3x (21.3)
V3
Wykorzystując tą definicję , obliczymy nawiasy Poissona dla pewnych funkcji F , G szczególnej postaci.
Otrzymane wyniki odgrywają ważną rolę przy formalnym przejściu do kwantowej teorii pola. Przy wyborze
jednej z tych funkcji – funkcji Hamiltona H otrzymamy :
[ F, H ] =
∫
{ (
∂Φ
F/
∂Φ
UΩ ) (
∂Φ
H/
∂ΦΠΩ
) – (
∂Φ
H/
∂Φ
UΩ )(
∂Φ
F/
∂ΦΠΩ
) } d3x (21.4)
V3
Zamieniając pochodne funkcjonalne od H równymi im na mocy równań Hamiltona wyrażeniami (20.19) i
zapisując pochodne funkcjonalne od F w postaci (20.17) dochodzimy do następującego wyniku :

51
[ F , H ] =
∫
{ (
∂
f/
∂
UΩ – (
∂
f/
∂
UΩ |
µ
) |
µ
)(
∂
UΩ /
∂
t) + (
∂
F/
∂ΠΩ
)(
∂ΠΩ
/
∂
t) }d3x (21.5)
V3
Pozbywając się nawiasów w wyrażeniu pod całkowym oraz wykorzystując wzory dla pochodnej iloczynu ,
otrzymujemy :
[ F , H ] =
∫
{ (
∂
f/
∂
UΩ )(
∂
UΩ/
∂
t ) - (
∂
f/
∂
UΩ |
µ
)(
∂
UΩ /
∂
t) + (
∂
f/
∂
UΩ |
µ
)(
∂
UΩ |
µ
/
∂
t) +
V3
+ (
∂
f/
∂ΠΩ
)(
∂ΠΩ
/
∂
t) }d3x (21.6)
Zastosujmy do drugiej składowej po prawej stronie tego równania twierdzenie Gaussa- Ostrogradskiego :
∫
(
∂
f/
∂
UΩ |
µ
) (
∂
UΩ /
∂
t) d3x =
∫
(
∂
f/
∂
UΩ |
µ
) (
∂
UΩ /
∂
t)dσ
µ
(21.7)
V3
∂
V3
Jeśli przyjmiemy ,że przy przejściu granicznym do całki po nieskończonej objętości , funkcja całkowa w całce
po powierzchni dąży do zera szybciej niż pole obszaru tej powierzchni dąży do nieskończoności , to całka ta
dążyć będzie do zera.
Ponieważ :
∂
f/
∂
t = (
∂
f/
∂
UΩ )(
∂
UΩ /
∂
t) + (
∂
f/
∂
UΩ |
µ
)(
∂
UΩ |
µ
/
∂
t) + (
∂
f/
∂
UΩ )(
∂ΠΩ
/
∂
t) + (
∂
f/
∂
t )jaw (21.8)
to mamy :
[ F , H ] =
∫
[ (
∂
f/
∂
t) - (
∂
f/
∂
t )jaw ] d
3x (21.9)
V3
Teraz można dokonać całkowania , ponieważ operacje – całkowania względem czasu i całkowania względem
objętości przestrzennej są zamienne, w wyniku tego otrzymujemy :
dF/dt =
∂
F/
∂
t + [ F , H ] (21.10)
Jest to „równanie ruchu“ dla wielkości F w teorii pola. Podstawiając , w szczególności F = H , otrzymamy :
dH/dt =
∂
H/
∂
t (21.11)
Jeśli funkcja Hamiltona nie zależy w sposób jawny od czasu to H jest stałą ruchu i można utożsamić powyższą
zależność z prawem zachowania energii.
dH/dt = 0 (21.12)
lub
H = const. (21.13)
W teorii pola nie przypadkowo wybraliśmy dla funkcji Lagrange’a L, funkcji Hamiltona H i działania S te same
symbole co i w mechanice. Nie bacząc na rozszerzenie fizycznych aspektów , mamy do czynienia z tą samą
fizyczna treścią - odpowiada to ciągłości procesu rozwoju fizyki.
Zastosujemy teraz ogólne równania ruchu (21.10) do przypadków : F = UΩ i F =
ΠΩ
. Zgodnie z zależnościami
(21.2) wykorzystamy przy tym wyrażenia całkowe dla wielkości UΩ i
ΠΩ
, wyrażonych przy pomocy funkcji
delta Diraca :
UΩ (x
µ
, t ) =
∫
UΩ (
ξµ
, t )
δ
(x
µ
-
ξµ
)d3
ξ
(21.14)
V3
ΠΩ
(x
µ
, t ) =
∫
ΠΩ
(
ξµ
, t )
δ
(x
µ
-
ξµ
)d3
ξ
(21.15)
V3
Ponieważ nie występuje tutaj jawna zależność od czasu , z równania (21.10) otrzymujemy następujące
„równanie ruchu” dla funkcji polowych i pędów sprzężonych :
∂
UΩ /
∂
t = [ UΩ , H ] ;
∂ΠΩ
/
∂
t = [
ΠΩ
, H ] (21.16)
Równania te są „równaniami polowymi Hamiltona“ zapisanymi przez nawiasy Poissona.
Poniżej obliczymy nawiasy Poissona dwóch funkcji polowych od dwóch funkcji pędów stowarzyszonych. Mając
na uwadze zastosowania kwantowomechaniczne , będziemy również mówić o zależnościach komutacyjnych.
Przy obliczeniach będziemy wykorzystywali reprezentacje całkowe (21.14) i (21.15). Zgodnie z ogólną teorią
zakładamy :
F = UΩ (x
µ
, t ) i f = UΩ (
ξµ
, t )
δ
(x
µ
-
ξµ
) (21.17)
jak również :
G =
ΠΩ
(x
µ
, t ) i g =
ΠΩ
(
ξµ
, t )
δ
(x
µ
-
ξµ
) (21.18)
Nawiasy Poissona od dwóch funkcji polowych zapisujemy następująco :

52
[ UΩ(x
µ
, t ) ,U
Γ
(x^
µ
, t )] =
∫
{(
∂Φ
UΩ /
∂Φ
U
Λ
)(
∂Φ
U
Γ
/
∂ΦΠΛ
) – (
∂Φ
U
Γ
/
∂Φ
U
Λ
)(
∂Φ
UΩ /
∂ΦΠΛ
) }d3
ξ
(21.19)
V3
należy przy tym, wnikliwie śledzić względem jakiego argumentu bierzemy pochodne.
Zgodnie z definicją pochodnej funkcjonalnej (20.17) , otrzymujemy :
(
∂Φ
U
Γ
/
∂ΦΠΛ
) =
∂
/
∂Π
{U
Γ
δ
(x
µ
-
ξµ
) } = 0 (21.20)
co jest konsekwencją m.in. tego , że funkcje polowe U
Γ
i funkcje pędu
ΠΛ
zakładamy jako niezależne jedna od
drugiej. Zatem z równości (21.19) wynika zależność komutacyjna :
[ UΩ (x
µ
, t ) , U
Γ
(x^
µ
, t )] = 0 (21.21)
Obliczymy teraz nawiasy Poissona od dwóch funkcji pędów
ΠΩ
i
ΠΓ
:
[
ΠΩ
(x
µ
, t ),
ΠΓ
(x^
µ
, t ) ] =
∫
{(
∂ΦΠΩ
/
∂Φ
U
Λ
)(
∂ΦΠΓ
/
∂ΦΠΛ
) – (
∂ΦΠΓ
/
∂Φ
U
Λ
)(
∂ΦΠΩ
/
∂ΦΠΛ
) }d3
ξ
(21.22)
V3
Następnie ponownie wykorzystamy definicję pochodnej funkcjonalnej (20.17) i znajdziemy :
(
∂ΦΠΩ
/
∂Φ
U
Λ
) =
∂
/
∂
U
Λ
{
ΠΩ
δ
(x
µ
-
ξµ
) } – {
∂
/
∂
U
Λ
|
µ
(
ΠΩ
δ
(x
µ
-
ξµ
) ) }|
µ
= 0 (21.33)
co wynika z tego , że wielkości
ΠΩ
i U
Λ
|
µ
również rozpatrujemy jako niezależne. Dlatego też z równości
(21.22) wynika zależność komutacyjna :
[
ΠΩ
(x
µ
, t ),
ΠΓ
(x^
µ
, t ) ] = 0 (21.24)
Na zakończenie wprowadzimy zależności komutacyjne zawierające funkcje polową UΩ i funkcje pędu
ΠΓ
:
[UΩ (x
µ
, t ),
ΠΓ
(x^
µ
, t ) ] =
∫
{
∂
/
∂
U
Λ
[ UΩ
δ
(x
µ
-
ξµ
)]
∂
/
∂ΠΛ
[ (
ΠΓδ
(x^
µ
-
ξµ
)] -
∂
/
∂
U
Λ
[
ΠΓδ
(x^
µ
-
ξµ
)]
V3
∂
/
∂ΠΛ
[ UΩ
δ
(x
µ
-
ξµ
)] }d3
ξ
(21.25)
Ostatnia składowa zeruje się na mocy niezależności U
Λ
i
ΠΓ
. Uwzględniając wyniki różniczkowania :
∂
/
∂
U
Λ
[ UΩ
δ
(x
µ
-
ξµ
)] =
δ
Ω
Λ
δ
Ω
δ
(x
µ
-
ξµ
) (21.26)
∂
/
∂ΠΛ
[ (
ΠΓδ
(x^
µ
-
ξµ
)] =
δΛΓ
δ
Ω
δ
(x^
µ
-
ξµ
) (21.27)
dochodzimy do równości :
UΩ (x
µ
, t ),
ΠΓ
(x^
µ
, t ) ] =
∫
{
δ
Ω
Λ
δ
Ω
δ
(x
µ
-
ξµ
)
δΛΓ
δ
Ω
δ
(x^
µ
-
ξµ
) }d3
ξ
(21.28)
V3
Stąd poprzez całkowanie otrzymujemy zależność komutacyjną :
[UΩ (x
µ
, t ),
ΠΓ
(x^
µ
, t ) ] =
δ
Ω
Γ
δ
(x
µ
- x^
µ
) (21.29)
W odróżnieniu od poprzednich wyników teraz nawiasy Poissona są różne od zera, jeśli zawierają one funkcje
polową i odpowiadającą jej funkcję pędu, przy czym wartości obu tych wielkości brane są w jednej i tej samej
chwili czasu i w jednym i tym samym punkcie przestrzeni.
Na zakończenie tego rozdziału obliczymy jeszcze nawiasy Poissona od dowolnej wielkości F i funkcji polowej
UΩ , oraz od dowolnej wielkości F i funkcji pędu
ΠΩ
. Mamy zatem :
[ F, UΩ (x
µ
, t ) ] =
∫
{(
∂Φ
F/
∂Φ
U
Λ
)(
∂Φ
UΩ /
∂ΦΠΛ
) – (
∂Φ
UΩ /
∂Φ
U
Λ
)(
∂Φ
F/
∂ΦΠΛ
) }d3
ξ
(21.30)
V3
W wyrażeniu podcałkowym pierwsza składowa zeruje się na mocy niezależności UΩ i
ΠΛ
, zatem pozostaje :
[ F, UΩ (x
µ
, t ) ] =
∫
{
δ
Ω
Λ
(
∂
f /
∂ΠΛ
)
δ
(x
µ
-
ξµ
) }d3
ξ
(21.31)
V3
Po całkowaniu otrzymujemy :
[ F , UΩ ] = - (
∂Φ
F/
∂ΦΠΩ
) (21.32)
Analogicznie prowadzimy obliczenia dla :
[ F ,
ΠΩ
(x
µ
, t ) ] =
∫
{(
∂Φ
F/
∂Φ
U
Λ
)(
∂Φ
ΠΩ
/
∂ΦΠΛ
) – (
∂Φ
ΠΩ
/
∂Φ
U
Λ
)(
∂Φ
F/
∂ΦΠΛ
) }d3
ξ
(21.33)
V3
Teraz zeruje się druga składowa w wyrażeniu podcałkowym , zatem pozostaje :

53
[ F ,
ΠΩ
(x
µ
, t ) ] =
∫
{ [ (
∂
f/
∂
U
Λ
) - (
∂
f/
∂
U
Λ
|
µ
) |
µ
]
δΛΩ
δ
(x
µ
-
ξµ
) }d3
ξ
(21.34)
V3
Zatem poprzez całkowanie otrzymujemy :
[ F ,
ΠΩ
(x
µ
, t ) ] =
δΛΩ
[ (
∂
f/
∂
U
Λ
) - (
∂
f/
∂
U
Λ
|
µ
) |
µ
] = (
∂
f/
∂
U
Ω
) - (
∂
f/
∂
U
Ω
|
µ
) |
µ
(21.35)
lub – przy wykorzystaniu pochodnej funkcjonalnej :
[ F ,
ΠΩ
] = (
∂Φ
F/
∂Φ
U
Ω
) (21.36)
Dla równań (21.32) i (21.36) istnieją mechaniczne analogi – równania (7.8) i (7.9).
Wprowadzone w tym rozdziale zależności , w których figurują nawiasy Poissona , mają zasadnicze znaczenie
przy formalnym przejściu do kwantowej teorii pola, jest tak ponieważ w kwantowej teorii pola nawiasy Poissona
są komutatorami od odpowiadających im polowych operatorów, podobnie jak to było dla zależności
mechanicznych (7.4).
22. TEORIA NOETHER
22.1 PODSTAWOWE IDEE
W rozdziałach 13 – 15 rozpatrywaliśmy w ramach mechaniki newtonowskiej na początku nieskończenie małe
przekształcenia kanoniczne w ich ogólnej postaci , m.in. ich szczególny przypadek - przekształcenia symetrii, na
końcu badaliśmy ich zastosowanie do układu N punktów materialnych.
Kwintesencją wszystkich prowadzonych tam rozważań był wniosek , że każda symetria funkcji Hamiltona
prowadzi do „istnienia” pewnego zachowania , odpowiadającego tej symetrii.
Te pryncypialne dla rozwoju fizyki wnioski ( idee ) zostały sformułowane przez Emmę Noethet ( 1918 ), z
wykorzystaniem metody teorii grup w teorii pola o symetriach ciągłych . Prace Noether poprzedzały pisma
Poincarego dotyczące mechaniki. Przy tym nie rozpatrywano symetrii dyskretnych występujących w mechanice
kwantowej , co tłumaczy się faktem ,że mechanika kwantowa ukształtowała się później.
W 1921 roku Bessel-Hagen zastosował teorię Noether w swym autorskim , abstrakcyjnym sformułowaniu do
konkretnych pól fizycznych i tym samym udostępnił ją fizykom. Przez dziesięciolecia teoria Noether
pozostawała w cieniu aż w połowie XX wieku w związku z różnymi aktualnymi problemami fizyki , w
szczególności dotyczącymi fizyki cząstek elementarnych i ich symetriami , doceniono jej ważność do tego
stopnia ,że w tej chwili trudno się bez niej obejść. Proces prawidłowej oceny i ważności symetrii w fizyce został
przyspieszony kiedy okazało się , że łamane jest prawo „zachowania parzystości” , które to zawdzięczamy Lee i
Yangowi ( 1956 ).
22.2 PRZEKSZTAŁCENIA WŁAŚCIWE ( CIĄGŁE ) LORENTZA.
W teorii Noether podstawowa rolę odgrywają przekształcenia dwóch różnych postaci.
Po pierwsze – „przekształcenia współrzędnych” – pociągające za sobą przekształcenia funkcji polowych UΩ -
które są obiektami geometrycznymi ( np. tensorami ,spinorami, bispinorami ) o ściśle określonych prawach
transformacyjnych.
Po drugie - istnieją przekształcenia , które przy ustalonych współrzędnych zmieniają postać zależności
funkcjonalnych – co będziemy nazywać „przekształceniami funkcjonalnymi” , do takich przekształceń należą
przekształcenia cechowania , fazowe itp.
W teorii Noether , w których mowa o symetriach ciągłych ( w odróżnieniu od wspomnianych symetriach
dyskretnych ), przekształcenia obu rodzajów ograniczone są szczególnym przypadkiem nieskończenie małych
przekształceń , co sprawia, że upraszczają się one pod względem matematycznym.
Jak to było do tej pory będziemy oznaczali przekształcenia współrzędnych apostrofem przy indeksie , a
przekształcenia funkcjonalne - daszkiem nad odpowiednią literą.
W poprzednich rozdziałach wykorzystywaliśmy w charakterze współrzędnych czasoprzestrzennych współrzędne
Galileusza. Tym samym kładliśmy nacisk na wykorzystanie IUO , w których powinny być opisane zjawiska
fizyczne. Jak wiadomo, przy wykorzystaniu takich współrzędnych, przejście od jednego IUO do drugiego IUO
dokonuje się za pomocą przekształcenia Lorentza, związanych oczywiście z szczególną zasadą względności.
Ponieważ einsteinowska teoria grawitacji ( 1915 ) w zasadzie wykorzystuje zakrzywioną czasoprzestrzeń, w
której nie można już stosować współrzędnych Galileusza , zjawiska grawitacyjne pozostawiamy poza ramami
naszego wykładu. Aby je uwzględnić musielibyśmy zastosować aparat matematyczny OTW , który oparty jest
na ogólnej zasadzie względności i która to wprowadza opis zjawisk fizycznych we współrzędnych
krzywoliniowych.
W STW podstawowym przekształceniem współrzędnych są jednorodne i niejednorodne przekształcenia
Lorentza. Połączenie tych dwóch grup przekształceń nazywa się „grupą Poincarego”.

54
( W literaturze polskiej przyjęto niekiedy, nazywać grupą Poincarego niejednorodne przekształcenia Lorentza –
przypis własny )
W ogólnym przypadku jednorodne i niejednorodne przekształcenia Lorentza ( oba są to przekształcenia
liniowe) mogą być zapisane łącznie w następujący sposób :
xi’ = Ai’j x
j +
α
i’ (22.1)
Stałe mnożniki :
Ai’j =
∂
xi’ /
∂
xj (22.2)
nazywamy “współczynnikami Lorentza”. Określają one jednorodne przekształcenia Lorentza ( obroty
lorentzowskie). Stałe
α
i’ charakteryzują niejednorodne przekształcenia Lorentza , opisują one przesunięcia
czasoprzestrzenne.
Ponieważ przekształcenia Lorentza pozostawiają metrykę niezmienioną , spełniają one na mocy prawa
transformacji tensora metrycznego (16.37) :
gi’k’ = (
∂
xi’/
∂
xm ) (
∂
xk’/
∂
xn ) gmn (22.3)
równania różniczkowe postaci :
(
∂
xi’/
∂
xm ) (
∂
xk’/
∂
xn ) = gik (22.4)
Zależności te prowadzą do następujących związków :
| Ai’m |
2 = 1 lub | Ai’
m | =
±
1 (22.5)
Właściwe (ciągłe ) przekształcenia Lorentza określone są warunkiem :
| Ai’m | = 1 przy A
4
4 > 0 (warunek ortochroniczności) (22.6)
Rozpatrzmy te przekształcenia dokładniej.
Pierwszy z warunków (22.6) jest warunkiem bardziej matematycznym ( nie koniecznie fizycznym ) – jest to
warunek dla przekształcenia ciągłego., drugi gwarantuje zachowanie wejściowej orientacji czasu.
( zachowanie wybranego kierunku upływu czasu – przypis własny )
Fakt ,że tensor metryczny jest inwariantny względem przesunięć czasoprzestrzennych
α
i’ , oznacza
„jednorodność czasoprzestrzeni”, a fakt , że jest on inwariantny względem obrotów czasoprzestrzennych Ai’j
jest wynikiem „izotropowości czasoprzestrzeni”.
W przypadku nieskończenie małych przekształceń Lorentza otrzymujemy :
Ai’j = g
i
j +
α
i
j i A
k
j’ = g
k
j +
α
k
j (22.7)
α
k
j – są wielkościami nieskończenie małymi.
Wzory te można sprawdzić podstawiając je do zależności (22.4) :
Ai’j A
k
i’ = g
k
j (22.8)
Podstawienie wyrażeń (22.7) do równania (22.4) prowadzi do warunku antysymetryczności :
α
i
j = -
α
j
i (22.9)
przy tym wykorzystaliśmy prawa podnoszenia i opuszczania indeksów , przykładowo :
t… i… = g
ik t…
k .. lub t
…
k ... = gkm t
…m
... (22.10)
Zatem właściwe przekształcenia Lorentza (22.1) możemy zapisać w następującej postaci :
xi’ = xi +
ξ
i = xi +
α
i
j +
α
i tj.
ξ
i =
α
i
j x
i +
α
i (22.11)
α
i - to wielkości nieskończenie małe, w określony sposób związane z wielkościami
α
i’ .
Szesnaście współczynników Lorentza Ai’j związanych jest dziesięcioma warunkami (22.4), tak , że pozostaje
tylko sześć współczynników niezależnych. Tymi niezależnymi współczynnikami są :
α
1
2 ,
α
1
3 ,
α
1
4 ,
α
2
3 ,
α
2
4 ,
α
3
4 ,
nazywamy je “nieskończenie małymi parametrami obrotów lorentzowskich”. Opisują one :
trzy wielkości - obroty przestrzenne (tylko przestrzenne )
trzy wielkości - obroty czasoprzestrzenne ( w tym ruch jednostajny )
Do nich możemy jeszcze dołączyć cztery niezależne wielkości opisujące translacje czasoprzestrzenne tj. :
trzy wielkości – translacje przestrzenne.
jedna wielkość – przesunięcie czasu.
Teraz powiem kilka słów o tensorach i ich własnościach.
Tensor t ij ..
km .. przedstawia pewien obiekt geometryczny , który przy przekształceniu współrzędnych
charakteryzuje się ściśle określonymi prawami transformacyjnymi , przykładowo przy przekształceniu Lorntza

55
( tj, przejściu od jednego IUO do drugiego IUO ) Ilość indeksów nazywamy rzędem tensora. Indeksy dolne ,
nazywamy kowariantnymi, górne - kontrawariantnymi. Jeśli działanie dodawania ma być kowariantne , to
dodawać możemy tylko tensory o jednakowym „rozkładzie” indeksów.
Indeksy kowariantne przekształcają się według prawa :
t ..i’ .. ( x
k’ ) = Aj
i’ t .. j .. (x
k ) (22.12)
a kontrawariantne :
t ..i’ .. ( xk’ ) = Ai’j t
.. j .. (xk ) (22.13)
W powyższym zapisie pokazano argumenty odnoszące się do odpowiedniego układu współrzędnych. Często
argumenty te jako domyślne będziemy opuszczali. Jeżeli jednak na ich miejsce należało by wpisać inne
argumenty to aby uniknąć nieporozumień należy je wypisać w jawnej postaci.
Dla nieskończenie małych przekształceń Lorentza wskazane wyżej zasady na mocy zależności (22.7) przyjmują
postać :
t ..i’ .. ( x
k’ ) = t
.. i .. (x
k ) -
α
j
i t .. j .. (x
k ) (22.14)
t ..i’ .. ( xk’ ) = t .. i .. (xk ) +
α
i
j t
.. j .. (xk ) (22.15)
Wzory przekształceń spinorów lub bispinorów przy skończonych przekształceniach Lorentza są bardziej
złożone. Przy nieskończenie małych przekształceniach Lorentza dla bispinorów
Ψ
^ otrzymujemy wzory
przekształcenia postaci :
Ψ
’( xk’ ) =
Ψ
( xk ) + ¼ i
α
ij
ϑ
ij
Ψ
( xk ) (22.16)
Ψ
^’ ( xk’ ) =
Ψ
^( xk ) + ¼ i
α
ij
Ψ
^( xk )
ϑ
ij (22.17)
Przy tym macierz
ϑ
ij zbudowana jest z wykorzystaniem macierzy Diraca
γ
i w sposób następujący :
ϑ
ij = (1/2i) (
γ
i
γ
j -
γ
j
γ
i ) (22.18)
Uogólniając zależności (22.14) – (22.17) na dowolne funkcje polowe U
Ω
, możemy zapisać :
U
Ω
’ ( x
k’ ) = U
Ω
( x
k ) + S
ΓΩ
ij
α
ij U
Γ
( x
k ) (22.19)
Zatem człon dopełniający związany z nieskończenie małym przekształceniem jest , jak widać proporcjonalny do
nieskończenie małych współczynników Lorentza. Stała S
ΓΩ
ij zależna jest od charakteru rozpatrywanego
obiektu geometrycznego. Na mocy warunku antysymetrii (22.9) można bez utraty ogólności zapisać :
S
ΓΩ
ij = - S
ΓΩ
ji (22.20)
Porównanie (22.19) z (22.14) pozwala otrzymać zależność dla tensorów :
S
ΓΩ
ij
→
Skmij = ½ ( gim g
k
j - g
k
i gjm ) (22.21)
a z (22.16) – dla bispinorów :
S
ΓΩ
ij
→
Sij = ¼ i
ϑ
ij (22.22)
22.3 WARIACJA MATERIAŁOWA I WARIACJA LOKALNA.
Po pewnych przygotowaniach prowadzonych powyżej , jesteśmy gotowi do wprowadzenia definicji „wariacji
materiałowej” funkcji polowej. Pod tym pojęciem rozumiemy następująca wielkość :
∆
S U
Ω
= U
Ω
’ ( x
i’ ) - U
Ω
( x
i ) (22.23)
∆
S U
Ω
’ | k = U
Ω
’ | k’ ( x
i’ ) - U
Ω
| k ( x
i ) itd. (22.24)
Różniczkując wyrażenie (22.23) względem xi , stwierdzamy , że operacja wariacji materiałowej jest nie
zamienna z różniczkowaniem cząstkowym. Zgodnie z zasadą różniczkowania funkcji złożonej mamy :
U
Ω
’ | k’ = U
Ω
| i A
i
k’ + (
∆
S U
Ω
) | k’ (22.25)
Ponieważ
∆
S U
Ω
jest wielkością nieskończenie małą , można podstawić :
(
∆
S U
Ω
) | k’
→
(
∆
S U
Ω
) | k (22.26)
Podstawiając dla współczynników Aik’ wartości (22.7) , otrzymamy :
U
Ω
’ | k’ = U
Ω
| k - U
Ω
| i
α
i
k + (
∆
S U
Ω
) | k’ (22.27)
Porównanie tego wyniku z definicją (22.24) prowadzi do zależności :
(
∆
S U
Ω
) | k =
∆
S U
Ω
| k + U
Ω
| i
α
i
k (22.28)
która dowodzi naszego twierdzenia. ( o nie przemienności wariacji materiałowej z różniczkowaniem
cząstkowym – przypis własny )

56
Teraz zdefiniujemy drugi typ wariacji , a mianowicie „wariacje lokalną”, charakteryzującą się własnością
przemienności z różniczkowaniem cząstkowym . Aby to osiągnąć dodamy do wyrażenia na wariacje
materiałową nieskończenie mały człon poprawkowy :
∆
L U
Ω
=
∆
SU
Ω
- U
Ω
| i
ξ
i
(22.29)
∆
L U
Ω
| k =
∆
SU
Ω
| k - U
Ω
| k | i
ξ
i
(22.30)
Różniczkując wyrażenie (22.29) , znajdujemy :
(
∆
L U
Ω
)| k = (
∆
S U
Ω
)| k - U
Ω
| i | k
ξ
i
- U
Ω
| i
ξ
i
| k
Na mocy (22.11) możemy przepisać ten wynik w następującej postaci :
(
∆
L U
Ω
)| k = (
∆
S U
Ω
)| k - U
Ω
| i | k
ξ
i
- U
Ω
| i
α
i
k =
∆
S U
Ω
| k - U
Ω
| i | k
ξ
i
(22.31)
Na mocy równości pochodnych mieszanych U
Ω
| i | k = U
Ω
| k | i mamy :
(
∆
S U
Ω
)| k = (
∆
L U
Ω
)| k (22.32)
co tym samym dowodzi przemienności operacji lokalnego wariowania i różniczkowania cząstkowego.
W teorii pola ważną role odgrywa jeszcze jedno pojęcie , jest to „pochodna Liego” :
∆
£ U
Ω
= -
∆
L U
Ω
(22.33)
Aby lepiej wyjaśnić pojęcie wariacji lokalnej, przekształcimy troszkę jej wyrażenie. Z definicji (22.29) wynika
następująca zależność :
∆
L U
Ω
= U
Ω
’ ( x
j’ ) - U
Ω
( x
j ) - U
Ω
| j
ξ
j
(22.34)
Rozłożenie jej w szereg Taylora pozwala otrzymać :
U
Ω
’ ( x
j’ ) - U
Ω
’ ( x
j ) + U
Ω
’ | j
ξ
j
lub – w przybliżeniu :
U
Ω
’ ( x
j’ ) - U
Ω
’ ( x
j ) + U
Ω
| j
ξ
j
(22.35)
Zatem otrzymujemy :
∆
L U
Ω
= U
Ω
’ ( x
j ) - U
Ω
( x
j )
(22.36)
Jak zatem widać lokalną wariację można interpretować jako zmianę funkcji polowej przy przekształceniu
współrzędnych , przy czym do funkcji podstawiane są „stare” ( nie przekształcone) argumenty. W odróżnieniu
od tego wariacja materiałowa reprezentuje sobą zmianę funkcji polowej w której, jak pokazują indeksy,
uwzględniane są również zmiany argumentów przy przejściu do nowego układu odniesienia.
Wykorzystując definicje wariacji materiałowej i lokalnej , łatwo pokazać , że dla obu z nich słuszna jest
następująca zasada pochodnej iloczynu :
∆
S (U
Ω
V
Γ
) = (
∆
S U
Ω
) V
Γ
+ U
Ω
(
∆
SV
Γ
) (22.37)
∆
L (U
Ω
V
Γ
) = (
∆
L U
Ω
) V
Γ
+ U
Ω
(
∆
LV
Γ
) (22.38)
Przytoczę schemat dowodu powyższych równości dla wariacji materiałowej :
∆
S (U
Ω
V
Γ
) = U
Ω
’ V
Γ
’ + U
Ω
V
Γ
= ( U
Ω
+
∆
S U
Ω
) ( V
Γ
+
∆
SV
Γ
) = (
∆
S U
Ω
) V
Γ
+ U
Ω
(
∆
SV
Γ
) +
+ (
∆
S U
Ω
) + (
∆
SV
Γ
)
Ponieważ ostatnia składowa po prawej stronie jest małą drugiego rzędu , możemy ją odrzucić – co kończy
dowód.
Zgodnie z definicją (22.29) wariacja lokalna różni się od materiałowej tylko o pewien człon dodatkowy
zawierający pochodną cząstkową. Zatem , na mocy faktu , że zasada różniczkowania iloczynu jest słuszna dla
różniczkowania cząstkowego , jest ona również słuszna dla wariacji lokalnej.
22.4 WARIACJA FUNKCJONALNA I WARIACJA ZUPEŁNA.
Wariacje które rozpatrywaliśmy do tej pory otrzymywane były w wyniku zmiany układu współrzędnych. Dla
wariacji funkcjonalnej , jak wspominałem wcześniej, zmieniamy nie układ współrzędnych , a strukturę funkcji
polowej. Zmieniona funkcję będziemy oznaczali tyldą. Zatem „wariacja funkcjonalna”
δ
U
Ω
zdefiniowana jest
następująco :
δ
U
Ω
= U
~
Ω
- U
Ω
(22.39)
Ponieważ obliczenie wariacji funkcjonalnej i przekształcenie współrzędnych są operacjami niezależnymi można
zmieniać ich porządek :
( U~
Ω
)’ = ( U
Ω
’ )
~
= U
~
Ω
’ (22.40)
Wariacja zupełna , którą oznaczymy przez
∆
U
Ω
, zgodnie z definicją reprezentuje sobą zmianę funkcji polowej
przy jednoczesnym przekształceniu funkcjonalnym i przekształceniu współrzędnych , mamy zatem :

57
∆
U
Ω
= U
~
Ω
’ - U
Ω
(22.41)
Wariacja zupełna jest sumą wariacji materiałowej i funkcjonalnej, dowodzimy tego przez następujące obliczenia
, w których małe drugiego rzędu odrzucamy :
∆
U
Ω
= U
~
Ω
’ - U
~
Ω
+ U~
Ω
- U
Ω
=
∆
S U
~
Ω
+
δ
U
Ω
=
∆
S U
Ω
+
δ
U
Ω
(22.42)
Ponieważ wariowanie funkcjonalne nie wpływa na współrzędne , oczywista jest jego przemienność z
różniczkowaniem cząstkowym :
(
δ
U
Ω
)| k =
δ
U
Ω
| k (22.43)
Ta zależność przypomina analogiczną zależność (4.15) z mechaniki. Dlatego też nie przypadkowo
wykorzystaliśmy również tutaj ten sam symbol dla wariacji ( zauważmy ,że ten sam symbol zastosowaliśmy
również przy wyprowadzeniu równań Lagrange’a z zasady Hamiltona w teorii pola ).
Z definicji (22.39) wariacji funkcjonalnej oraz z przeprowadzonych wyliczeń, wynika , że dla wariacji tej
słuszna jest zasada różniczkowania iloczynu :
δ
(U
Ω
V
Γ
) = (
δ
U
Ω
)V
Γ
+ U
Ω
δ
V
Γ
(22.44)
Zatem na mocy równości (22.42) i (22.37) zasada różniczkowania iloczynu jest spełniona również dla wariacji
zupełnej :
∆
(U
Ω
V
Γ
) = (
∆
U
Ω
)V
Γ
+ U
Ω
∆
V
Γ
(22.45)
22.5 WARIACJA ZUPEŁNA GĘSTOŚCI LAGRANśJANU.
W tym rozdziale rozwiniemy wprowadzony wcześniej formalizm, wprowadzając go dla gęstości lagranżjanu.
Ograniczymy się do gęstości lagranżjanu pierwszego rzędu :
£ = £( U
Ω
, U
Ω
| i , x
i
) (22.46)
Wariację zupełną tej gęstości definiujemy następująco :
∆
£( U~
Ω
’ , U
~
Ω
’ | i’ , x
i’
) - £( U
Ω
, U
Ω
| i , x
i
) (22.47)
W związku z definicją (22.41) wynika z tego :
∆
£( U
Ω
+
∆
U
Ω
, U
Ω
| i , +
∆
U
Ω
| i , x
i’
+
ξ
i
) – £( U
Ω
, U
Ω
| i , x
i
) (22.48)
Rozłożenie tej równości w szereg Taylora pozwala otrzymać :
∆
£ = (
∂
£ /
∂
U
Ω
)
∆
U
Ω
+ (
∂
£ /
∂
U
Ω
| j )
∆
U
Ω
| j + (
∂
£ /
∂
xi )jaw
ξ
i
(22.49)
Na mocy równości (22.42) i (22.29) wielkość
∆
U
Ω
możemy wyrazić w następujący sposób :
∆
U
Ω
=
∆
LU
Ω
+ U
Ω
| i
ξ
i
+
δ
U
Ω
(22.50)
Dla U
Ω
| j otrzymujemy analogiczne wyrażenie :
U
Ω
| j =
∆
L U
Ω
| j + U
Ω
| j | i
ξ
i
+
δ
U
Ω
| j (22.51)
Zatem , wyrażenie (22.49) dla
∆
£ przyjmuje postać :
∆
£ = (
∂
£ /
∂
U
Ω
) (
∆
LU
Ω
- U
Ω
| i
ξ
i
+
δ
U
Ω
) + (
∂
£ /
∂
U
Ω
| j ) (
∆
LU
Ω
| j + U
Ω
| j | i
ξ
i
+
δ
U
Ω
| j ) +
+ (
∂
£ /
∂
xi)jaw
ξ
i
(22.52)
Na tym etapie wyrazimy pewne pochodne cząstkowe przez pochodną wariacyjną , która , zgodnie z równaniem
(19.12) , określimy następująco :
δ
£/
δ
U
Ω
=
∂
£ /
∂
U
Ω
- (
∂
£/
∂
U
Ω
| i ) | i (22.53)
Dodamy do tego wyrażenia dwa dodatkowe człony , a potem odejmiemy je i miarę możliwości zamienimy dwa
wyrażenia w jednej pochodnej wariacyjnej. Wyglądać to będzie następująco :
∆
£ = (
∂
£ /
∂
U
Ω
)
δ
U
Ω
- (
∂
£ /
∂
U
Ω
| j ) | j
δ
U
Ω
+ (
∂
£ /
∂
U
Ω
| j )U
Ω
| j + (
∂
£/
∂
U
Ω
| j ) | j
δ
U
Ω
+ (
∂
£ /
∂
U
Ω
)
∆
LU
Ω
+ (
∂
£ /
∂
U
Ω
| j )
∆
LU
Ω
| j + (
∂
£ /
∂
U
Ω
| j ) | j
∆
LU
Ω
+ [ (
∂
£ /
∂
xi)jaw + (
∂
£ /
∂
U
Ω
)U
Ω
| i + (
∂
£ /
∂
U
Ω
| j )
U
Ω
| j | i ]
ξ
i
.
Skąd otrzymujemy :
∆
£ = (
∂
£ /
∂
U
Ω
)
δ
U
Ω
+ [ (
∂
£ /
∂
U
Ω
| j )] | j + (
∂
£ /
∂
U
Ω
)
∆
LU
Ω
+ [(
∂
£/
∂
U
Ω
| j )
∆
LU
Ω
] | j +
+ [ (
∂
£ /
∂
xi)jaw + (
∂
£ /
∂
U
Ω
)U
Ω
| i + (
∂
£ /
∂
U
Ω
| j )U
Ω
| j | i ]
ξ
i
. (22.54)
W dalszym ciągu wykorzystamy oznaczenia (20.1) i wyrugujemy pochodne (
∂
£ /
∂
xi )jaw przy pomocy
zależności :
(£ g ji ) | j = £ | i = (
∂
£/
∂
U
Ω
)U
Ω
| i + (
∂
£ /
∂
U
Ω
| j )U
Ω
| j | i + (
∂
£ /
∂
xi)jaw (22.55)
Przy tym wielkość
∆
£ zapisujemy w postaci :

58
∆
£ = (
∂
£ /
∂
U
Ω
)
δ
U
Ω
+ (
ΠΩ
j
δ
U
Ω
)| j + (
δ
£ /
δ
U
Ω
| j)
∆
LU
Ω
+ (
ΠΩ
j
∆
LU
Ω
)| j + (£ g
j
i ) | j
ξ
i
(22.56)
Wyrażając zgodnie ze wzorem (22.29) wariacje lokalną przez materiałową , otrzymujemy :
∆
£ = (
∂
£ /
∂
U
Ω
)
δ
U
Ω
+ (
ΠΩ
j
δ
U
Ω
)| j + (
δ
£ /
δ
U
Ω
) (
∆
SU
Ω
+ U
Ω
| i
ξ
i
) + [
ΠΩ
j (
∆
LU
Ω
- U
Ω
| i
ξ
i
)] | j +
+ (£ gji ) | j
ξ
i
(22.57)
Przekształcimy ostatni składnik zgodnie z zasadą różniczkowania iloczynu oraz uwzględniając warunek
α
j
i =
ξ
i
| i = 0 :
(£ gji ) | j
ξ
i
= (£ g
j
i
ξ
i
) | j - £ g
j
i
ξ
i
| j = (£ g
j
i
ξ
i
) | j - £
ξ
i
| i = (£ g
j
i
ξ
i
) | j
Zatem , dla
∆
£ ostatecznie otrzymujemy następujące wyrażenie :
∆
£ = (
∂
£ /
∂
U
Ω
) (
δ
U
Ω
+
∆
SU
Ω
- U
Ω
| i
ξ
i
) + (
ΠΩ
j
δ
U
Ω
) | j + [
ΠΩ
j
∆
SU
Ω
- (
ΠΩ
j
∆
SU
Ω
| i - £ g
j
i )
ξ
i
] | j
(22.58)
W przypadku szczególnym – wariacji czysto funkcjonalnej , z powyższego wynika , że :
δ
£ = (
∂
£ /
∂
U
Ω
)
δ
U
Ω
+ (
ΠΩ
j
δ
U
Ω
) | j (22.59)
Całkowanie tego wyrażenia względem ustalonej czterowymiarowej objętości V4 pozwala otrzymać :
δ
∫
£ d4x =
∫
[(
∂
£ /
∂
U
Ω
)
δ
U
Ω
+ (
ΠΩ
j
δ
U
Ω
) | j ] d
4x (22.60)
V4 V4
Wynik ten jest zgodny z równaniem (19.2) , które zgodnie z tym, wchodzi do formalizmu Noether jako jego
szczególny przypadek. Odpowiednio zatem , symbol wariacji w zapisie zasady Hamiltona jest identyczny z
symbolem wykorzystanym dla wariacji funkcjonalnej.
22.6 PRZEKSZTAŁCENIA SYMETRII.
W mechanice pod przekształceniem symetrii rozumiemy przekształcenie określone przez nieskończenie małą
funkcją tworzącą , nie zależne od czasu na mocy definicji (14.7) i gwarantujące inwariantność formy funkcji
Hamiltona. W teorii pola na pierwszy plan w miejsce formalizmu Hamiltona wprowadza się, jako wiodący
formalizm Lagrange’a , związane jest to z tym ,że zapewnia on relatywistyczną inwariantność. Dlatego przy
definiowaniu przekształcenia symetrii wyjdziemy z gęstości lagranżjanu i wymaganej inwariantnej formy
gęstości ( względem wariacji funkcjonalnej i wariacji współrzędnych ) lagranżjanu określonej z dokładnością do
pewnej dywergentnej składowej. Odpowiednio zatem, przekształcenie symetrii określimy przez równanie :
∆
£ = - Ŋ~j | j (22.61)
tj. przez równość :
£ ( U~
Ω
’ , U
~
Ω
’ | i’ , x
i’ ) = £ ( U
Ω
, U
Ω
| i , x
i ) - Ŋ~j
| j (22.62)
gdzie : Ŋ~j = Ŋ
ξ
j +
δ
Ŋj – jest tensorem pierwszego rzędu, charakteryzującym się następującą strukturą
funkcjonalną : Ŋ~j = Ŋ~j ( U
Ω
, U
~
Ω
, x
i )
Całkując (22.62) względem czterowymiarowej objętości i stosując czterowymiarowy analog twierdzenia
Gaussa-Ostrogradskiego , otrzymujemy :
∫
£ ( U~
Ω
’ , U
~
Ω
’ | i’ , x
i’ ) d4x =
∫
£ ( U
Ω
, U
Ω
| i , x
i ) d4x -
∫
Ŋ~j dfi (22.63)
V4 V4
∂
V4
Ponieważ czterowymiarowy element objętości jest inwariantem , po lewej stronie d4x można zamienić na d4x’.
Weźmy teraz wariacje funkcjonalną od tego równania i zażądajmy aby dla układu wejściowego ( układu nie
primowanego ) słuszna była zasada Hamiltona. Wtedy będzie ona również słuszna dla układu otrzymanego w
wyniku przekształcenia symetrii ( układu primowanego ) , wynika to z tego ,że wariacja całki względem
hiperpowierzchni jest zerem. Zatem otrzymujemy :
∫
£ ( U~
Ω
’ , U
~
Ω
’ | i’ , x
i’ ) d4x’ =
δ
∫
£ ( U
Ω
, U
Ω
| i , x
i ) d4x = 0 (22.64)
V4 V4
Stąd wynika ,że również dla układu primowanego spełnione są równania Lagrange’a :
δ
£ /
δ
U~
Ω
’ =
∂
£ /
∂
U~
Ω
’ – [
∂
£ /
∂
U~
Ω
’ | i’ ] | i’ = 0 (22.65)
Wprowadzimy teraz jedno ważne pojęcie - kanonicznego tensora energii-pędu Ŧij :
Ŧij =
ΠΩ
i U
Ω
| j - £ g
i
j (22.66)
Jest on zbudowany podobnie jak w mechanice funkcja Hamiltona :

59
f
H =
Σ pk qk – L
k=1
stąd bierze się określenie “kanoniczny”.
Dla przekształcenia symetrii z równości (22.58) wynika zalezność :
δ
£ /
δ
U
Ω
= (
δ
U
Ω
+
∆
SU
Ω
- U
Ω
| i
ξ
i
) + (
ΠΩ
j
δ
U
Ω
+
δ
Ŋj ) | j + [
ΠΩ
j
∆
SU
Ω
- Ŧ
i
j
ξ
i
+ Ŋ
ξ
i
) | j = 0 (22.67)
którą należy rozpatrywać jako „matematyczne sformułowanie twierdzenia Noether” dla gęstości lagranżjanu
pierwszego rzędu. Strukturę tego równania rozpatrzymy dalej.
Twierdzenie Noether w tej formie jest tak zwanym „słabym prawem zachowania”. Tylko przy wypełnieniu
równań pola otrzymujemy prawo zachowania w postaci czterowymiarowego równania ciągłości.
W odróżnieniu od słabego prawa zachowania „silne prawo zachowania” reprezentuje spełnioną tożsamościowo
równość, słuszną nie zależnie od tego czy spełnione są równania pola. (* zatem silne zasady zachowania
odzwierciedlają tylko formalne własności lagranżjanu. W odróżnieniu od nich , słabe prawa zachowania
spełnione są tylko przy uwzględnieniu równań pola, mających fizyczną interpretacje – przypis tłumacza. *)
22.7 RÓśNICZKOWE PRAWA ZACHOWANIA.
Przy założeniu , że równania pola są spełnione, tj. że pochodne wariacyjne gęstości lagranżjanu są równe zeru,
zależność (22.67) przyjmuje postać :
(
ΠΩ
j
δ
U
Ω
+
δ
Ŋj ) | j + [
ΠΩ
j
∆
SU
Ω
- Ŧ
i
j
ξ
i
+ Ŋ
ξ
i
) | j = 0 (22.68)
Ponieważ przekształcenia współrzędnych i przekształcenia funkcjonalne przedstawiają sobą wzajemnie
niezależne operacje , równość ta rozpada się na dwa różniczkowe prawa zachowania :
(
ΠΩ
j
δ
U
Ω
+
δ
Ŋj ) | j = 0 (22.69)
[
ΠΩ
j
∆
SU
Ω
- Ŧ
i
j
ξ
i
+ Ŋ
ξ
i
) | j = 0 (22.70)
mają one strukturę równań ciągłości tj. stwierdzają one równość zeru czterowymiarowej dywergencji.
Jak wiadomo „równanie ciągłości” w trójwymiarowym sformułowaniu tj. o postaci :
div j +
∂ρ
/
∂
t = 0 (22.71)
można , zakładając j4 = c
ρ
, zdefiniować w postaci czterowymiarowej :
jm| m = j
µ
|
µ
+ j4| 4 = div j +
∂ρ
/
∂
t = 0 (22.72)
Jak widać równanie to ma taka strukturę jak (22.69) i (22.70).
Zakładając , że wariacje funkcjonalną można zapisać w postaci :
δ
U
Ω
= i a e
ΓΩ
U
Γ
(22.73)
w której : a- jest nieskończenie małym parametrem , e
ΓΩ
- są pewnymi współczynnikami, oraz wprowadzając
4-wektor gęstości prądu :
jm =
ΠΩ
m e
ΓΩ
U
Γ
(22.74)
z (22.69) otrzymamy ( zakładając
δ
Ŋj = 0 ) różniczkowe prawo zachowania :
jm| m = 0 (22.75)
Teraz pozostaje nam dać fizyczną interpretację równości (22.70). Podstawiając do tego równania , wyrażenia
otrzymane ze wzoru (22.19) dla wariacji materiałowej :
∆
SU
Ω
= S
ΓΩ
mn
α
mn U
Γ
(22.76)
na mocy (22.11) otrzymamy ( przy założeniu Ŋ = 0 ) :
U
Γ
( S
ΓΩ
m
n
ΠΩ
jU
Γ
- Ŧm
j xn
) | j -
α
m Ŧ
m
j
| j = 0 (22.77)
Na mocy niezależności translacji i obrotu , wynika z tego „różniczkowe prawo zachowania energii-pędu” :
Ŧmj | j = 0 (22.78)
Wprowadzając oznaczenie :
ℵ
j
m
n
= S
ΓΩ
m
n
ΠΩ
jU
Γ
= -
ℵ
jn
m (22.79)
zapiszemy pozostałą część równania (22.77) następująco :
α
m
n (
ℵ
j
m
n
- Ŧm
j xn
) | j = 0 (22.80)

60
Ponieważ wielkości
α
m
n są antysymetryczne nie można od razu zakładać ,że współczynniki przy tych
wielkościach są zerami, na początku należy wydzielić w tych współczynnikach część symetryczną i
antysymetryczną. Ponieważ człony odpowiadające symetrycznej części są tożsamościowo równe zeru , pozostaje
α
mn [
ℵ
jmn – ½ ( Ŧmjxn
- Ŧ
njxm
) ] | j = 0
z czego wynika , że :
( Ŧnjxm - Ŧ
mjxn
+ 2
ℵ
jmn )
| j = 0 (22.81)
Jeśli wprowadzimy „tensor momentu pędu” :
Dmnj = (1/c) ( Ŧmjxn - Ŧ
njxm
+ 2
ℵ
jmn )
(22.82)
to równanie (22.81) przyjmie postać różniczkowego prawa zachowania momentu pędu i prędkości środka mas :
Dmnj | j = 0 (22.83)
Niekiedy może być pomocne rozłożenie tensora momentu pędu na składową orbitalną :
(orbit) Dmni = (1/c) ( Ŧmixn
- Ŧ
nixm
) (22.84)
oraz składową spinową, nie zależną od współrzędnych :
(spin) Dmni = (2/c)
ℵ
inm (22.85)
Zatem :
Dmni = (orbit) Dmni + (spin) Dmni (22.86)
Na końcu pokaże , że prawo zachowania energii-pędu (22.78) zawiera cztery równania , a prawo zachowania
momentu pędu i prędkości środka mas (22.83) – sześć równań.
Fizyczny sens tych zależności będzie wyjaśniony mając na uwadze ich związek z odpowiadającymi im
całkowymi prawami zachowania. Jednak, śledząc przytoczony tok rozumowania , już teraz można ustanowić
związek symetrii i odpowiadających jej praw zachowania, zupełnie analogicznie jak to zrobiliśmy w mechanice.
Związki te są następujące :
translacja przestrzenna
→
zachowanie pędu } jednorodność czasoprzestrzeni.
translacja czasowa
→
zachowanie energii }
obrót przestrzenny
→
zachowanie momentu pędu } izotropowość czasoprzestrzeni.
ruch jednostajny
→
zachowanie prędkości środka mas }
22.8 SYMETRYCZNY TENSOR ENERGII-PĘDU.
Chociaż kanoniczny tensor energii-pędu (22.66) Ŧs
i
odgrywa istotną rolę w aparacie kanonicznym , nie spełnia
on pewnych istotnych z punktu widzenia fizyki wymagań , przykładowo nie jest inwariantny ze względu na
przekształcenie cechowania dla przypadku pola maxwellowskiego.
Oprócz tego tensora istnieje „symetryczny tensor energii-pędu” :
Ts
i = Ti
s (22.87)
który wykorzystywany jest w einsteinowskich równaniach pola grawitacyjnego i definiowany jest w ramach
OTW. Belinfante i inni podjęli próbę wprowadzenia takiego tensora ad hoc , i otrzymali :
Ts
i = Ŧ
s
i + (
ℵ
s
im
+
ℵ
i
s
m
+
ℵ
mi
s )| m (22.88)
Różniczkując to wyrażenie względem xi i przyjmując do wiadomości równanie (22.78) oraz warunek
antysymetrii (22.79) otrzymamy :
Ts
i
| i =
ℵ
s
im
| m | i +
ℵ
i
s
m
| m | i +
ℵ
mi
s | i | m
Pierwsza składowa po prawej stronie jest tożsamościowo równa zeru ( zawężenie wyrażeń antysymetrycznego i
symetrycznego ), druga i trzecia wzajemnie się znoszą przy zmianie indeksów m
↔
i , po których sumujemy.
Zatem , również dla symetrycznego tensora energii-pędu mają miejsce różniczkowe prawa zachowania :
Ts
i
| i = 0 (22.89)
W związku z tym , niektórzy autorzy , nie stosując formalizmu Noether , definiują tensor momentu pędu przez
symetryczny tensor energii-pędu , podstawiając :
D^mni = (1/c) ( Tmixn - T
nixm
) = - D^
nmi
(22.90)
Różniczkując to wyrażenie oraz uwzględniając równość (22.89) jak również warunek symetrii (22.87),
dochodzimy do wniosku ,że słuszne jest, podobnie jak (22.83) , różniczkowe prawo zachowania :
D^mni | i = 0 (22.91)

61
Tensor który otrzymamy działając na tensor momentu pędu Dimj operatorem dywergencji a następnie mnożąc
wynik przez c :
Lik = c Dikj | j (22.92)
nazywamy „tensorem momentu obrotowego” – uogólnia on odpowiadające mu pojęcie tensora momentu
bezwładności w mechanice.
22.9 CAŁKOWE PRAWA ZACHOWANIA.
Przy wyprowadzaniu całkowych praw zachowania wyjdziemy od otrzymanych w rozdziale 22.7 różniczkowych
praw zachowania (22.75) , (22.78) i (22.83), formalnie odpowiadającym z równaniem ciągłości.
Przy tym operatorem dywergencji będziemy działali :
- w prawie (22.75) na tensor pierwszego rzędu jk .
- w prawie (22.78) na tensor drugiego rzędu Ŧm
j
.
- w prawie (22.83) na tensor trzeciego rzędu Dnmj.
Ponieważ współczynniki przekształcenia Lorentza są stałe, można je wprowadzić pod znak pochodnej , tak ,że
wyprowadzenie całkowych praw zachowania dla tensorów o wspomnianym typie nie jest związane z jakimiś
szczególnymi problemami – nie dotyczy to OTW w której występuje problem z istnieniem prawa zachowania
energii-pędu.
Możemy zatem wyprowadzić całkowe prawo zachowania odpowiadające równaniu (22.75), a następnie
zmieniając indeksy swobodne w wyrażeniu różniczkowym , przenieść otrzymane wyniki na pozostałe przypadki.
W sformułowaniu trójwymiarowym wyprowadzenie tego całkowego prawa zachowania będzie przebiegać
następująco :
Równanie ciągłości (22.71) całkujemy względem trójwymiarowej objętości V3 a następnie stosujemy do
uzyskanego wyniku twierdzenie Gaussa-Ostrogradskiego :
dQ/dt = -
∫
div j d3x = -
∫
div j d
σ (22.93)
V3
∂
V3
gdzie :
Q =
∫
ρ
d3x (22.94)
V3
Jeśli całka po powierzchni zeruje się ( przykładowo jeśli prąd wewnątrz skończonego obszaru jest równy
prądowi na zewnątrz lub jeśli przy granicy obszaru dążącej do nieskończoności gęstość prądu ubywa szybciej
niż rośnie pole ograniczone tym obszarem ) to otrzymamy całkowe prawo zachowania
dQ/dt = 0 lub Q = const. (22.95)
Wyprowadzenie tego wzoru może być również dokonane w formaliźmie czterowymiarowym. Równanie
ciągłości (22.75) całkujemy po czterowymiarowym obszarze a następnie stosujemy twierdzenie Gaussa-
Ostrogradskiego :
∫
jm | m d
4x = i
∫
jm dfm = 0 (22.96)
V4
∂
V4
Wyobraźmy sobie czterowymiarowy obszar całkowania w postaci cylindra, który ograniczony jest „od góry” i
od „dołu” trójwymiarowymi przestrzennopodobnymi obszarami V3 i V^3 , a po „boku” czasoprzestrzenną
hiperpowierzchnią M, wtedy równość (22.96) można zapisać następująco :
∫
jm dfm -
∫
jm dfm +
∫
jm dfm = 0 (22.97)
V^3 V3 M
Ostatnią składową po lewej stronie można przyjąć równą zeru, podobnie jak w trójwymiarowym formaliźmie.
Z tego otrzymujemy prawo zachowania postaci :
∫
jm dfm = -
∫
jm dfm (22.98)
V^3 V3 M
Możemy przekonać się o równoważności tego wyniku i równości (22.95) przyjmując równość :
Q = (1/ic)
∫
jm dfm (22.99)
V3
Wynika ona z tego ,że jeśli w charakterze tójwymiarowego obszaru wybierzemy hiperpowierzchnię
przestrzennopodobną t = const. , to elementy tensorowe hiperpowierzchni (19.9) przyjmą postać :

62
df
µ
= 0 ; df4 = i d
3x (22.100)
zatem z (22.99) i (22.94) wynika równość :
Q = (1/c)
∫
j4 d3x =
∫
ρ
d3x (22.101)
t = const. t = const.
Tym kończymy omówienie prawa (22.75). Należy jedynie podkreślić , że pytanie o fizyczny sens wielkości Q do
tej pory pozostaje otwarte. Dalej pokaże jedynie ,że w przypadku pola maxwellowskiego: jm – reprezentuje
4-wektor gęstości prądu elektrycznego , a Q – ładunek elektryczny.
Aby omówić prawo (22.78) wprowadzę , analogicznie do wielkości (22.99) 4-pęd jako całkę :
Pm = (i/c)
∫
Ŧm
j df
j (22.102)
V3
Wybierając również dla tego przypadku obszar V3 w postaci hiperpowierzchni t = const, otrzymamy :
Pm = - (1/c)
∫
Ŧm
4 d3x (22.103)
t =const.
Prowadząc, podobne jak wcześniej rachunki dochodzimy do całkowego prawa zachowania energii-pędu :
d Pm / dt = 0 lub Pm = const. (22.104)
Trójwymiarowy pęd możemy przedstawić za pomocą trzech wielkości składowych przestrzennopodobnych
(22.103) , tj. :
P
µ
= - (1/c)
∫
Ŧ
µ
4 d3x (22.105)
t = const.
Całkowe prawo zachowania trójwymiarowego pędu wyrażamy równościami postaci :
d P
µ
/ dt = 0 lub P
µ
= const. (22.106)
Energia układu związana jest z czwartą składową 4-pędu następująco :
ℜ
= - cP4 =
∫
Ŧ4
4 d3x (22.107)
t = const.
Całkowe prawo zachowania energii ma postać :
d
ℜ
/ dt =0 lub
ℜ
= const. (22.108)
Jeżeli przy dowodzie zachowania energii-pędu wyjdziemy od symetrycznego tensora energii-pędu tj. z
różniczkowego prawa zachowania (22.89) to otrzymamy te same wyniki , związane jest to z tym ,że
dywergentny człon w wyrażeniu (22.88) przy całkowaniu względem przestrzeni można wyzerować.
Zajmiemy się teraz prawem (22.83) i zdefiniujemy całkowy tensor momentu pędu :
Dnm = (1/ i)
∫
Dnmj dfj (22.109)
V3
Wybierając obszar całkowania w taki sam sposób jak wcześniej , otrzymujemy :
Dnm =
∫
Dmn4 d3x (22.110)
t = const.
Wprowadzając pojęcia „całkowego tensora orbitalnego momentu pędu” :
(orbit) Dnm =
∫
(orbit)Dnm4 d3x (22.111)
t = const.
oraz „całkowego tensora spinowego momentu pędu” :
(spin) Dnm =
∫
(spin)Dnm4 d3x (22.112)
t = const.
możemy zapisać równość :
Dnm = (orbit) Dnm + (spin) Dnm (22.113)
Postępując tak jak wcześniej , otrzymamy całkowe prawo zachowania momentu pędu i prędkości środka mas :
dDnm /dt = 0 lub Dnm = const. (22.114)
Zbadam teraz przestrzenną część D
µν
powyższego tensora i pokaże , że ta stała ruchu odpowiada pojęciu
zwykłego momentu pędu. Ona również składa się z części orbitalnej i spinowej :
D
µν
= (orbit) D
µν
+ (spin) D
µν
(22.115)

63
Zgodnie z definicją (22.84) , mamy :
(orbit) D
µν
=
∫
(orbit)D
µν
4 d3x =
∫
( x
µ
(kan)
πν
- x
ν
(kan)
πµ
) d3x (22.116)
t = const. t = const.
w równaniu tym wprowadziliśmy „kanoniczną gęstość pędu” :
(kan)
πµ
= - (1/c) Ŧ
µ
4 (22.117)
To wszystko , oczywiście jest zgodne z mechaniczną definicją orbitalnego momentu pędu :
D = r
×
p lub D1 = D
23 = x2p
3 – x
3p
2 (22.118)
Dla całkowego tensora momentu pędu spinowego ze wzoru (22.85) otrzymujemy :
(spin) D
µν
=
∫
(spin)D
µν
4 d3x = (2/c)
∫
ℵ
4
νµ
d
3x (22.119)
t = const. t = const.
Całkowe prawo zachowania momentu pędu zapisujemy następująco :
dD
µν
/dt = 0 lub D
µν
= const. (22.120)
Ponieważ tensor D
µν
jest tensorem antysymetrycznym , równanie to jest równoważne trzem równaniom we
współrzędnych.
Rozpatrzymy teraz , pozostałą część równania (22.114), a dokładnie równanie :
dD
µ
4 /dt = 0 lub D
µ
4 = const. (22.121)
które jest również równoważne trzem równaniom zapisanym we współrzędnych. Wprowadzając kanoniczny
tensor gęstości energii postaci :
(kan) w = Ŧ
4
4 (22.122)
oraz uwzględniając wzór (22.82), równaniu (22.122) można nadać postać :
d/dt
∫
[ ( (kan)w /c2 ) x
µ
-
πµ
t +2 c2
ℵ
44
µ
] d
3x = 0 (22.123)
t = const.
Definiując centrum mas równaniem :
x^
µ
=
∫
( (kan)w /c2 ) x
µ
d
3x / ( (kan)w /c2 ) d3x (22.124)
otrzymamy :
x^
µ
= [ t
∫
( (kan)
πµ
d3x - 2 c2
∫
ℵ
44
µ
d3x + const. ] /
∫
(kan)w /c2 d
3x (22.125)
Równość tą możemy interpretować jako prawo zachowania prędkości środka mas.
Do takich samych wyników doszlibyśmy jeśli wyszlibyśmy od różniczkowego prawa zachowania (22.91),
opartego na symetrycznym tensorze energii-pędu , wynika to z tego, że dodatkowy człon przy całkowaniu
względem przestrzeni można wyzerować.
23. ZASTOSOWANIE TEORII DO MECHANIKI NEWTONOWSKIEJ.
Chociaż prawa zachowania w mechanice newtonowskiej , już omówiliśmy stosując formalizm Hamiltona ,
pouczające będzie pokazanie, w jaki sposób prawa te można włączyć do teorii Noether , opartej na formaliźmie
Lagrange’a.
Teoria Noether w poprzednich rozdziałach była rozwinięta w teorii pola. Pokaże jednak , że teorię tą możemy
stosować również do mechaniki newtonowskiej, w której funkcję Lagrange’a zadaje wzór (4.24) :
L = L( rΩ , r
.
Ω , t ) (23.1)
Zanim ustalimy konkretny związek z teorią Noether, rozszerzymy na formalizm Lagrange’a teorię nieskończenie
małych przekształceń kanonicznych , którą wyłożyłem w rozdziałach 13 i 14.
Przy tym , tak jak i wcześniej, wyjdziemy z nieskończenie małego przekształcenia kanonicznego , opisywanego
wzorami (13.6) , które to w zapisie wektorowym mają postać :
r^Ω = rΩ +
δ
^ rΩ ; p^Ω = pΩ +
δ
^ pΩ ; H^ = H +
δ
^H (23.2)
Ponieważ w formaliźmie Lagrange’a wykorzystujemy zmienne rΩ , r
.
Ω oraz L , sensownie jest podstawić :
r^Ω = rΩ +
δ
^ rΩ ; r^
.
Ω= r
.
Ω +
δ
^ r.Ω ; L^ = L +
δ
^L (23.3)
Ten formalny zapis będzie uzasadniony tylko przy dokładnym wyjaśnieniu sensu wielkości r^.Ω. Powróćmy
teraz do układu punktów materialnych , rozpatrzonym w rozdziale 15, i zauważmy , że różniczkując wyrażenie
(15.5) względem czasu a następnie porównując wynik z wyrażeniem (15.6) , dochodzimy do równości :
r^. Ω = r
. ^Ω (23.4)
z której wynika równość :

64
d (
δ
^ rΩ ) / dt =
δ
^ r.Ω (23.5)
Przy przekształceniu kanonicznym wymagane jest aby związki :
N N
H =
Σ pΩ r.Ω – L oraz H^ = Σ p^Ω r. ^Ω – L^ (23.6)
Ω
=1
Ω
=1
były zachowane , a z tego wynika :
N
δ
^L =
Σ (r.Ω
δ
^ pΩ + pΩ
δ
^ r.Ω ) -
δ
^H (23.7)
Ω
=1
Zależności (13.7) można również przedstawić w formie wektorowej :
δ
^ rΩ = -
∂
I/
∂
pΩ ;
δ
^ pΩ = -
∂
I/
∂
rΩ ;
δ
^H = -
∂
I/
∂
t (23.8)
Podstawiając te wyrażenia do (23.7) , otrzymamy :
N N
δ
^L =
∂
I/
∂
t +
Σ [ (
∂
I/
∂
rΩ )r
.
Ω - pΩ d/dt (
∂
I/
∂
pΩ )] = d/dt [ I – Σ (
∂
I/
∂
pΩ ) pΩ] (23.9)
Ω
=1
Ω
=1
Zgodnie z ostatnim z równań (23.3) możemy zatem znaleźć L^.
Analogicznie do wielkości (14.1) zdefiniujemy wielkość :
∆
^L = L( r^Ω , r^
.
Ω , t ) – L( rΩ , r
.
Ω , t ) = L( rΩ +
δ
^rΩ , r
.
Ω +
δ
^r. Ω , t ) – L ( rΩ , r
.
Ω , t ) (23.10)
Rozłożenie w szereg Taylora daje :
N N N
∆
^L =
Σ [ (
∂
L/
∂
rΩ )
δ
^rΩ + (
∂
L/
∂
r.Ω )
δ
^r. Ω ] = Σ (
∂
L/
∂
rΩ )
δ
^rΩ + d/dt Σ pΩ
δ
^rΩ (23.11)
Ω
=1
Ω
=1
Ω
=1
Uwzględniając zależność (23.6) , wyrażenie (23.10) można sprowadzić do postaci :
N N
∆
^L =
Σ ( p^Ω r^. Ω - pΩ r. Ω ) -
∆
^H = d/dt [ I -
Σ (
∂
I/
∂
pΩ ) pΩ ] -
∂
I/
∂
t -
∆
^H (23.12)
Ω
=1
Ω
=1
Z porównania tego wyniku z wyrażeniem (23.9) wynika równość :
δ
^L =
∆
^L +
∂
I/
∂
t +
∆
^H (23.13)
Przy pomocy zależności (14.6) spełnionej przy dowolnych warunkach , wielkość (23.12) można ostatecznie
zapisać w postaci :
N
∆
^L = - d/dt
Σ (
∂
I/
∂
pΩ ) pΩ (23.14)
Ω
=1
identycznej z (23.11) na mocy równań ruchu.
Przyjmując do wiadomości również zależność (13.1), która wiąże funkcje tworzącą F i nieskończenie małą
funkcje tworzącą I , a która w postaci wektorowej przedstawia się następująco :
N
F = I -
Σ (
∂
I/
∂
pΩ ) pΩ (23.15)
Ω
=1
Wzory (23.9) i (23.14) można zapisać następująco :
δ
^L = dF /dt (23.16)
∆
^L = (dF/dt) – dI/dt (23.17)
Jak pokazałem wcześniej , nasze wywody oparte są na nieskończenie małych przekształceniach kanonicznych .
Ograniczając jeszcze bardziej wykorzystywane przekształcenia , tj. zakładając że są to przekształcenia symetrii ,
określone zależnością (14.7) – podstawiając do wzoru (23.17) wynik (14.8) dochodzimy do równania :
(dF/dt ) -
∆
^L = 0 (23.18)
Jest to definicja przekształcenia symetrii w formaliźmie Lagrange’a , które należy rozpatrywać jako analog
definicji (14.7).
I dalej, z równości (23.13) otrzymujemy analog zależności (14.9) tj. :
∆
^L =
δ
^L lub L^ = L( r^Ω , r
. ^Ω , t ) (23.19)
Łącząc teraz otrzymane powyżej wyniki z wynikami uzyskanymi w teorii pola dochodzimy do następujących
odpowiedniości :
UΩ
→
rΩ , x
i
→
t , ₤
→
L (23.20)
W teorii pola wprowadziliśmy przekształcenie współrzędnych i przekształcenie funkcjonalne :

65
xi’ = xi +
ξ
i , U~Ω’ (xi ) = UΩ(xi ) +
∆
LUΩ +
δ
UΩ (23.21)
Jak pokazuje powyższy przykład , analogiczne zależności , postaci :
t’ = t +
ξ
, r^Ω (t) = rΩ (t) +
∆
LrΩ +
δ
rΩ (23.22)
kryją się za badanymi wcześniej przekształceniami kanonicznymi , zachodzi zatem odpowiedniość :
U~Ω’ (x
i )
→
r^Ω (t) (23.23)
przy czym :
∆
LrΩ = r
.
Ω
ξ
(23.24)
Na mocy równości (22.29) wynika z tego ,że
∆
SrΩ = 0.
W dalszej kolejności będziemy zakładali , że rozpatrywane przekształcenia są przekształceniami symetrii.
Przepisując zależność (22.61) teorii pola do odpowiadającej mechanice postaci , otrzymujemy (Ŋ^j
→
Ŋ^ ) :
∆
L + dŊ^ /dt = 0 (23.25)
gdzie :
Ŋ^ =
δ
Ŋ + Ŋ
ξ
przy czym różniczkowe prawa zachowania (22.69) i (22.70) przechodzą w prawa :
N
d/dt [
Σ pΩ
δ
r Ω +
δ
Ŋ ] = 0 (23.26)
Ω
=1
oraz
d/dt [ ( H - Ŋ )
ξ
] = 0 (23.27)
Teraz musimy znaleźć związek między
∆
L i
∆
^L. Ponieważ w definicji
∆
^L wszędzie figuruje jeden i ten sam
argument t, podczas gdy w definicji
∆
L do jednego członu wchodzi argument t’ , a do drugiego argument t , ten
związek jest następujący :
∆
L =
∆
^L + (dL/dt)
ξ
(23.28)
Podstawiając tutaj wartości
∆
L i
∆
^L , otrzymanych ze wzorów (23.18) i (23.25) odpowiednio otrzymamy :
dŊ^ /dt = - dF/dt – (dL/dt)
ξ
= d(
δ
Ŋ/dt) + (dŊ /dt )
ξ
(23.29)
Dla poglądowego wyjaśnienia tej ogólnej teorii zastosujemy przedstawiony powyżej formalizm do naszego
przypadku układu punktów materialnych. W tym celu koniecznie musimy znaleźć wielkości
δ
Ŋ i Ŋ , wchodzące
do praw zachowania (23.26) i (23.27).
Zgodnie z równaniem (15.5) , mamy :
δ
r Ω = a + d
×
r Ω - v
t (23.30)
Wyrażenie to podstawimy do prawa (23.26). Z równania (15.8) otrzymujemy odpowiadającą naszemu
przypadkowi funkcję Lagrange’a :
N
L = T – U =
Σ ( mΩ / 2) r. Ω2 – U( r Ω
Γ
) (23.31)
Ω
=1
Skąd po uwzględnieniu równości (15.5) mamy :
N N N N
∆
^L = - v
Σ mΩ r. Ω – ½
ξ
[ d/dt
Σ mΩ r. Ω2 – Σ (
∂
U/
∂
r Ω
Γ
)(d r
Ω
Γ
/dt)] = - v Σ mΩ r
.
Ω–
ξ
(dL/dt) (23.32)
Ω
=1
Ω
=1
Ω
=1
Ω
=1
Na mocy zależności (23.28) porównanie tego wyniku ze wzorem (23.25) daje :
N
dŊ^ /dt = v
Σ mΩ r. Ω (23.33)
Ω
=1
Zatem , zgodnie z równaniem (23.29) :
N
d(
δ
Ŋ/dt) = v d/dt
Σ mΩ r. Ω ; dŊ/dt = 0 (23.34)
Ω
=1
Podstawienie tych zależności do wyrażenia (23.30) dla
δ
rΩ do równania (23.26) i (23.27) prowadzi do znanych
praw zachowania :
N N N N
d/dt [ a
Σ pΩ + d Σ r Ω
×
p Ω – v ( Σ pΩ - Σ mΩ rΩ ) ] = 0 (23.35)
Ω
=1
Ω
=1
Ω
=1
Ω
=1
d/dt (
ξ
H) = 0 (23.36)

66
które dokładnie zostały omówione w rozdziale 15.
Podstawiając wyrażenie (15.1) dla nieskończenie małej funkcji tworzącej I do wzoru (23.15) , dla funkcji
tworzącej F, otrzymujemy :
N
F = - v
Σ mΩ rΩ -
ξ
L (23.37)
Ω
=1
co w pełni zgadza się z zależnościami (23.29) i (23.33).
24. ZASTOSOWANIE TEORII DO POLA SCHRÖDINGEROWSKIEGO.
W niniejszym rozdziale będziemy rozpatrywali pole schrödingerowskie ( pole typu Schrödingera ) Ψ,
oddziałujące wzajemnie z zewnętrznym polem elektromagnetycznym A,
ϕ
. Jeżeli wyjdziemy od gęstości
lagranżjanu , symetrycznej względem funkcji polowej Ψ i sprzężonej do niej w sposób zespolony ( hermitowsko
sprzężonej – przypis własny ) funkcji polowej Ψ*, postaci :
₤ = ½ ħ2/m0 { (grad Ψ*+ i
α
A Ψ* )(grad Ψ + i
α
A Ψ ) + (im0 /ħ ) [ (
∂
Ψ*/
∂
t) Ψ - Ψ*(
∂
Ψ*/
∂
t) ] +
+ (2m0V/ħ
2 ) Ψ* Ψ } (24.1)
gdzie :
α
= e/ ħc , V = e
ϕ
- jest energią potencjalną .
to gęstość taka będzie wielkością rzeczywistą :
₤ = ₤* (24.2)
a to znacznie uprości nam obliczenia.
Różniczkując wyrażenie (24.1) i wykorzystując oznaczenia wprowadzone w rozdziale 20, otrzymamy wzory :
∂
₤/
∂
Ψ = - (½ ħ2/m0) [ -i
α
A (grad Ψ*+ i
α
A Ψ* ) + (im0 /ħ) (
∂
Ψ*/
∂
t)+ (2m0V/ħ
2 ) VΨ* ] (24.3)
Π
µ
=
∂
₤/
∂
Ψ|
µ
= - ½ ħ
2/m
0 ( Ψ
*|
µ
+ i
α
A
µ
Ψ* ) (24.4)
Π =
∂
₤/
∂
(
∂
Ψ/
∂
t) = - ½ ħ
2/m
0 ( - im0Ψ
*/ ħ ) (24.5)
Warunek rzeczywistości gęstości lagranżjanu (24.2) daje nam tą dogodność , że odpowiednie wzory odnoszące
się do Ψ*, otrzymujemy poprzez prostą zamianę wszystkich wielkości - wielkościami zespolenie sprzężonymi.
Równanie Lagrange’a (19.12) rozpada się w tym przypadku na dwa równania :
δ
₤/
δ
Ψ =
∂
₤/
∂
Ψ – (
∂
₤/
∂
Ψ|
µ
) |
µ
-
∂
/
∂
t [
∂
₤/
∂
(
∂
Ψ/
∂
t) ] = 0 (24.6)
δ
₤/
δ
Ψ* =
∂
₤/
∂
Ψ* – (
∂
₤/
∂
Ψ*|
µ
) |
µ
-
∂
/
∂
t [
∂
₤/
∂
(
∂
Ψ*/
∂
t) ] = 0 (24.7)
Podstawiając do ostatniego równania otrzymane wcześniej wyrażenia dla pochodnych cząstkowych , prowadzi
do znanego ( z mechaniki kwantowej ) równania Schrödingera :
∆Ψ – 2i
α
Agrad Ψ - i
α
divA Ψ -
α
2A2 Ψ - (2m
0V/ħ
2 )Ψ = (2m
0/ iħ
) (
∂
Ψ /
∂
t) (24.8)
Równanie (24.6) przy tym przekształca się do równania Schrödingera dla funkcji hermitowsko sprzężonej.
Zgodnie z równaniem (20.5) , znajdujemy gęstość hamiltonianu :
Ħ = Π (
∂
Ψ/
∂
t) + Π* (
∂
Ψ*/
∂
t) - ₤ = (½ ħ2/m0) [ (grad Ψ
*+ i
α
A Ψ* )(grad Ψ + i
α
A Ψ ) +
+ (2m0V/ħ
2 ) Ψ* Ψ ] (24.9)
która również jest rzeczywista :
Ħ = Ħ* (24.10)
Na mocy równości (24.5) wyrażenie (24.9) można zapisać w następującej postaci :
Ħ = - (iħ/m0) [ (grad Π+ i
α
AΠ ) (grad Ψ + i
α
A Ψ ) + (2m0V/ħ
2 ) Π Ψ ] (24.11)
W tym przykładzie mamy do czynienia z pewnym osobnym przypadkiem , wynikającym z tego ,że na mocy
równości (24.5) funkcja pędu Π , z dokładnością do pewnego stałego czynnika jest zgodna z funkcją pola Ψ*;
analogiczna zależność istnieje również między Π*i Ψ. Na tą okoliczność należy zwrócić dokładniejszą uwagę ,
dlatego, że teraz nie jest już spełniony warunek niezależności wielkości UΩ i Π
Ω , wprowadzony w rozdziale 20
i odpowiednio zatem wprowadzone w tym rozdziale wzory nie są stosowalne bezpośrednio. W związku z tymi
związkami w wyrażeniach dotyczących gęstości hamiltonianu pojawiają się człony grad Π i grad Π* , , należy
zatem uogólnić równania Hamiltona (20.19) w następujący sposób :
∂
Ψ/
∂
t =
∂
ΦH/
∂
ΦΠ = (
∂
Ħ/
∂
Π) – (
∂
Ħ/
∂
Π|
µ
) |
µ
(24.12)
∂
Π/
∂
t = -
∂
ΦH/
∂
ΦΨ = - [ (
∂
Ħ/
∂
Π) – (
∂
Ħ/
∂
Ψ|
µ
) ] (24.13)
Zgodnie z tym powinniśmy wybrać odpowiednie wyrażenie dla gęstości Hamiltona. Uwzględniając zależność :
Π Ψ = Π* Ψ* (24.14)

67
wyrażenie (24.11) można zapisać w następującej ,symetrycznej postaci :
Ħ = - (iħ/2m0) [ (grad Π+ i
α
AΠ ) (grad Ψ + i
α
AΨ ) - (grad Π*+ i
α
AΠ* )(grad Ψ* + i
α
AΨ* ) +
+ (2m0V/ħ
2 ) ( Π Ψ - Π* Ψ* ) ] (24.15)
Skąd znajdujemy :
∂
Ħ/
∂
Ψ = - (iħ/2m0) [ -i
α
A(grad Π + i
α
AΠ ) + (2m0V/ħ
2 )Π ] (24.16)
∂
Ħ/
∂
grad Ψ = - (iħ/2m0) ( grad Π + i
α
AΠ ) (24.17)
∂
Ħ/
∂
Π = - (iħ/2m0) [ i
α
A(grad Ψ + i
α
AΨ ) + (2m0V/ħ
2 )Ψ ] (24.18)
∂
Ħ/
∂
grad Π = - (iħ/2m0) ( grad Ψ + i
α
AΨ ) (24.19)
Podstawiając te wyrażenia do równania Hamiltona (24.12) i (24.13) , otrzymamy :
∂
Ψ/
∂
t = (iħ/2m0) [ ∆Ψ – i
α
divAΨ - 2 i
α
grad Ψ -
α
2A2 Ψ - (2m
0V/ħ
2 )Ψ ) (24.20)
∂
Π/
∂
t = - (iħ/2m0) [ ∆Π – i
α
divAΠ - 2 i
α
grad Π -
α
2A2 Π - (2m
0V/ħ
2 )Π ) (24.21)
W tych dwóch równaniach Hamiltona bez trudu rozpoznajemy równania Schrödingera dla funkcji Ψ i Ψ* .
Teraz przejdę , konkretnie do zastosowania teorii Noether. Ponieważ teoria Schrödingera nie jest
relatywistycznie inwariantna nie będziemy zajmować się symetriami związanymi z przekształceniem
współrzędnych , zbadamy tylko „symetrię fazową”.
Przez bezpośrednie podstawienie można przekonać się , że gęstość lagranżjanu (24.1) jest inwariantna względem
„przekształcenia fazowego” :
Ψ~ = Ψei
η
; Ψ~* = Ψ*e-i
η
(24.22)
gdzie :
η
- jest pewną stałą rzeczywistą.
Dla nieskończenie małego przekształcenia ( z nieskończenie małą wartością
η
) mamy :
Ψ~ = Ψ + i
η
Ψ ; Ψ~* = Ψ* - i
η
Ψ* (24.23)
lub
δ
Ψ = i
η
Ψ ;
δ
Ψ* = - i
η
Ψ* (24.24)
Przy zastosowaniu ogólnej teorii wyjdziemy od różniczkowego prawa zachowania (22.69). Na mocy
inwariantności gęstości lagranżjanu mamy ;
δ
Ŋj = 0 , zatem :
(Πj
δ
Ψ + Π*j
δ
Ψ* ) | j = (Π
µ
δ
Ψ + Π*
µ
δ
Ψ* ) |
µ
+
∂
/
∂
t (Π
δ
Ψ + Π*
δ
Ψ* ) = 0 (24.25)
Podstawiając do tego równania wyrażenia (24.4) , (24.5) i (24.24) dochodzimy do równania ciągłości :
∂
/
∂
t ( Ψ Ψ* ) + (iħ/2m0) ( Ψ
* |
µ
Ψ - Ψ |
µ
Ψ* + 2 i
α
A
µ
Ψ* Ψ ) |
µ
= 0 (24.26)
W równaniu tym występuje „gęstość prawdopodobieństwa” :
w = Ψ Ψ* (24.27)
oraz „gęstość prądu prawdopodobieństwa” :
J = (ħ/2im0) ( Ψ
* grad Ψ - Ψ grad Ψ* - 2 i
α
A Ψ* Ψ ) (24.28)
Zatem , z symetrii fazowej wynika prawo zachowania prawdopodobieństwa. W teorii jednocząsteczkowej prawo
to można utożsamić z prawem zachowania ładunku elektrycznego.
25. ZASTOSOWANIE TEORII DO UKŁADU POLA MAXWELOWSKIEGO I KLEIN-
GORDONOWSKIEGO.
Oznaczmy zespoloną funkcję falową pola Kleina-Gordona , przez
Φ
, a 4-potencjał pola Maxwella przez Ai
( tak jak w rozdziale 16 ) następnie zauważmy ,że tensor pola elektromagnetycznego Bmn związany jest z 4-
potencjałem w następujący sposób :
Bmn = An | m – Am | n (25.1)
Gęstość lagranżjanu dla naszego układu dwóch pól będzie maiła postać :
₤ = - (ħ2/ 2m0 ) [ (
Φ
* | m + i
α
Am
Φ
* )(
Φ
| m + i
α
Am
Φ
) + (m0
2c2/ħ2)
Φ
*
Φ
] – ¼ BmnB
mn (25.2)
gdzie :
α
= e/ħc , m0 – jest masą spoczynkową.
Przy tym 4-potencjał zgodnie z równaniem (16.36) , zbudowany jest z potencjału wektorowego A i potencjału
skalarnego
ϕ
:
Ai = ( A , -
ϕ
)
a tensor pola elektromagnetycznego wyrażony jest przez składowe E
µ
i B
µ
- natężenia pól , odpowiednio
elektrycznego i magnetycznego :

68
[ 0 B3 -B2 | E1 ]
Bmn = [ -B
3 0 B1 | E
2 ] (25.3)
-----------------------
[ -E1 -E2 -E3 | 0 ]
Układy równań Maxwella przy cyklicznym przestawieniu indeksów :
Bmn | k = Bmn | k + Bkm | n + Bnk | m = 0 (25.4)
w trójwymiarowym zapisie mające postać :
rot E = - (1/c)
∂
B/
∂
t ; div B = 0 (25.5)
są tożsamościami na mocy (25.1)
Trójwymiarowy zapis zależności (25.1) wygląda następująco :
E = - grad
ϕ
- (1/c) (
∂
A/
∂
t ) ; B = rot A (25.6)
Gęstość lagranżjanu (25.2) jest wielkością rzeczywistą :
₤ = ₤* (25.7)
Dla dalszych obliczeń korzystnie będzie jeśli zapiszemy wyrażenie (25.2) w trójwymiarowej postaci , zakładając
V = e
ϕ
:
₤ = - (ħ2/ 2m0 ) { (grad
Φ
* + i
α
A
Φ
* )(grad
Φ
+ i
α
A
Φ
) – (1/c2) [ (
∂Φ
*/
∂
t) – (iV/ħ)
Φ
* )]
[(
∂Φ
/
∂
t) – (iV/ħ)
Φ
)] + (m0
2c2/ħ2)
Φ
*
Φ
} + ½ ( E2 – B2 ) (25.8)
Różniczkując to wyrażenie , otrzymujemy następujące zależności :
(
∂
₤ /
∂Φ
) = - (ħ2/ 2m0
) [ -i
α
Am (
Φ
* | m + i
α
Am
Φ
* ) + (m0
2c2/ħ2)
Φ
* ] (25.9)
Πm = (
∂
₤ /
∂Φ
| m ) = - (ħ
2/ 2m
0
) (
Φ
* | m + i
α
Am
Φ
* ) (25.10)
Π
µ
= (
∂
₤ /
∂Φ
|
µ
) = - (ħ
2/ 2m
0
) (
Φ
* |
µ
+ i
α
A
µ
Φ
* ) (25.11)
Π =
∂
₤ /
∂
(
∂Φ
/
∂
t) = - (ħ
2/ 2m
0
) { - (1/c2) [(
∂Φ
*/
∂
t) – (iV/ħ)
Φ
* ] (25.12)
(
∂
₤ /
∂
Ai
) = (eħ /2m
0ci) (
Φ
*
Φ
| i -
Φ
* | i
Φ
- 2i
α
Φ
*
Φ
Ai ) (25.13)
π
ij =
∂
₤ /
∂
A i | j = B
ij (25.14)
π
i = (1/c)
π
i4 =
∂
₤ /
∂
(
∂
Ai
/
∂
t) = (1/c)Bi4 (25.15)
πµ
= (1/c)
πµ
4 =
∂
₤ /
∂
(
∂
A
µ
/
∂
t) = - (1/c)Ei (25.16)
π
=
π
4 = (1/c)
π
44 = 0 (25.17)
Aby nie utracić ogólnej perspektywy , jeszcze raz oddzielnie wypiszemy kanonicznie sprzężone zmienne :
Φ
↔
Π
;
Φ
*
↔
Π
* ; A
µ
↔
- (1/c)E
µ
;
ϕ
↔
0 (25.18)
Zatem , dla potencjału skalarnego nie istnieje kanonicznie sprzężona funkcja pędu. Z danego wyniku wypływają
daleko idące wnioski dotyczące elektrodynamiki kwantowej , nie mam jednak możliwości zająć się tym
problemem dokładniej.
Równanie Lagrange’a (19.12) rozbijemy na trzy równania :
(
δ
₤ /
δΦ
) = (
∂
₤ /
∂Φ
) – (
∂
₤ /
∂Φ
| m )| m
= 0 (25.19)
(
δ
₤ /
δΦ
*) = (
∂
₤ /
∂Φ
*) – (
∂
₤ /
∂Φ
*| m )| m
= 0 (25.20)
(
δ
₤ /
δ
Ai ) = (
∂
₤ /
∂
Ai ) – (
∂
₤ /
∂
Ai | j )| j
= 0 (25.21)
Podstawienie do równania (25.20) wyrażeń hermitowsko sprzężonych do wyrażeń (25.9) i (25.10) pozwala
otrzymać równanie Kleina-Gordona :
Φ
| j
| j - 2i
α
Aj
Φ
| j
-
α
2 A
j A
j
Φ
- i
α
A| j | j
Φ
- (m
0
2c2/ħ2)
Φ
= 0 (25.22)
Równanie (25.19) przy tym przechodzi w równanie Kleina –Gordona dla funkcji hermitowsko sprzężonej.
Wprowadzimy skrócone oznaczenia :
j i = (eħ/2m0i) (
Φ
*
Φ
| i -
Φ
*| i
Φ
- 2 i
α
Φ
*
Φ
Ai ) (25.23)
dla 4-wektora gęstości prądu elektrycznego , odpowiadającemu polu Kleina –Gordona , wtedy z równania
(25.21) otrzymamy układ niejednorodnych równań Maxwella :
Bij | j = j
i
/ c (25.24)
Przechodząc do trójwymiarowego zapisu i zakładając :
ji = ( j , c
ρ
) (25.25)
otrzymamy znane równania Maxwella :
*) Równania (25.26) różnią się od bardziej rozpowszechnionej formy zapisu brakiem mnożnika 4
π
przy j oraz
ρ
.
Czynnik ten otrzymamy automatycznie jeżeli w wyrażeniu (25.2) dla gęstości lagranżjanu zmienimy

69
współczynnik – ¼ , w ostatniej składowej na – 1/16
π
i odpowiednio we wzorze (25.8) zamienimy ½ na 1/8
π
-
przypis redaktora *)
rot B = (1/c) [ (
∂
E/
∂
t) + j ) , div E =
ρ
(25.26)
Teraz ze wzoru (20.5) obliczymy gęstość hamiltonianu :
Ħ =
Π
(
∂Φ
/
∂
t) +
Π
* (
∂Φ
*/
∂
t) +
πµ
(
∂
A
µ
/
∂
t) - ₤ = (ħ2/2m0)[ (grad
Φ
* + i
α
A
Φ
* )(grad
Φ
+ i
α
A
Φ
) +
+ (1/c2)(
∂Φ
*/
∂
t)(
∂Φ
/
∂
t) – (V2/c2ħ2)
ΦΦ
* + (m0
2c2/ħ2)
ΦΦ
* ] + ½ ( E2 – B2 ) + E grad
ϕ
(25.27)
Przy pomocy zależności (25.12) i (25.16) można nadać temu wyrażeniu elegancką formę
Ħ = (2m0c2/ħ2) [
Π
*
Π
+ ( iVħ/2m0c
2) (
Π
*
Φ
* -
ΠΦ
)] + ½ c2
πµ
πµ
- c
πµ
ϕ
|
µ
+ (25.28)
+ ( ħ2/2m0) [ (grad
Φ
* + i
α
A
Φ
* )(grad
Φ
+ i
α
A
Φ
) + (m0
2c2/ħ2)
ΦΦ
* ] + ½ ( A
τ
|
χ
- A
χ
|
τ
) A
τ
|
χ
.
Przy tym zapisie wykorzystaliśmy tożsamość :
( rot A )2 = ( A
τ
|
χ
- A
χ
|
τ
) A
τ
|
χ
(25.29)
Różniczkując , otrzymujemy wzory postaci :
∂
Ħ/
∂Φ
= ( ħ2/2m0) [ - i
α
A (grad
Φ
* + i
α
A
Φ
* ) + (m0
2c2/ħ2)
Φ
* ] – (iV/ħ)
Π
(25.30)
∂
Ħ/
∂
grad
Φ
= ( ħ2/2m0) (grad
Φ
* + i
α
A
Φ
* ) (25.31)
∂
Ħ/
∂Π
= (2m0c
2/ħ2) [
Π
* - ( iVħ/2m0c
2)
Φ
) (25.32)
∂
Ħ/
∂
A = ( ieħ2/2m0c) (
Φ
* grad
Φ
-
Φ
grad
Φ
* - 2 i
α
A
Φ
*
Φ
) = - (1/c) j (25.33)
∂
Ħ/
∂
A
µ
|
ν
= B
νµ
(25.34)
∂
Ħ/
∂πµ
= c2
πµ
- c
ϕ
|
µ
(25.35)
∂
Ħ/
∂ϕ
= (ie/ħ ) (
Π
*
Φ
* -
ΠΦ
) (25.36)
∂
Ħ/
∂ϕ
|
µ
= -c
πµ
(25.37)
Równania Hamiltona (20.19) przyjmują następującą postać :
∂Φ
/
∂
t =
∂Φ
Ħ/
∂ΦΠ
=
∂
Ħ/
∂Π
(25.38)
∂Π
/
∂
t = -
∂Φ
Ħ/
∂ΦΠ
= - [ (
∂
Ħ/
∂Π
) – (
∂
Ħ/
∂Φ
|
µ
) |
µ
] (25.39)
∂
A
µ
/
∂
t =
∂Φ
Ħ/
∂Φπµ
=
∂
Ħ/
∂πµ
(25.40)
∂ϕ
/
∂
t =
∂Φ
Ħ/
∂Φπ
=
∂
Ħ/
∂π
(25.41)
∂πν
/
∂
t = -
∂Φ
Ħ/
∂Φ
A
ν
= - [ (
∂
Ħ/
∂
A
ν
) - (
∂
Ħ/
∂
A
ν
|
µ
) |
µ
] (25.42)
∂π
/
∂
t = -
∂Φ
Ħ/
∂Φϕ
= - [ (
∂
Ħ/
∂ϕ
) - (
∂
Ħ/
∂ϕ
|
µ
) |
µ
] (25.43)
Jeśli do równania (25.38) podstawimy wyrażenie (25.32) i wykorzystamy wzór (25.12) , to otrzymamy
tożsamość.
Podstawienie (25.30) i (25.31) do (25.39) daje :
∂Π
/
∂
t = (iV/ħ )
Π
+ ( ħ2/2m0) [
∆Φ
* + i
α
div A
Φ
* + 2i
α
A grad
Φ
* -
α
2A2
Φ
* - (m0
2c2/ħ2)
Φ
* ] (25.44)
Przy pomocy wzoru (25.12) równanie to możemy zapisać jako równanie Kleina-Gordona dla funkcji
hermitowsko sprzężonej :
Φ
* | m |m + i
α
Am |m
Φ
* + 2i
α
Am
Φ
* |m -
α
2Am A
m
Φ
* - (m0
2c2/ħ2)
Φ
* = 0 (25.45)
Równanie (25.40) po uwzględnieniu równości (25.35) prowadzi do znanego już nam równania :
E = - grad
ϕ
- (1/c) (
∂
A/
∂
t) (25.46)
równania (25.41) dalej już nie będziemy wykorzystywać.
Równanie (25.42) przy podstawieniu do niego wyrażeń (25.33) i (25.34) przekształca się w równanie Maxwella :
B
νµ
|
µ
= (1/c) [ (
∂
E
ν
/
∂
t) + j
ν
] lub rot B = (1/c) [ (
∂
E/
∂
t) + j ] (25.47)
a z równania (25.43) i wzoru (25.12) wynika , że :
πµ
µ
= -i
α
(
Π
*
Φ
* -
ΠΦ
) = (eħ/2m0c
3i ) [
Φ
* (
∂Φ
/
∂
t) -
Φ
(
∂Φ
*/
∂
t) + (2iV/ħ)
Φ
*
Φ
] (25.48)
Odpowiednio do zależności (25.25) gęstość ładunku dla pola Kleina –Gordona definiowana jest zgodnie ze
wzorem :
ρ
= (ieħ/2m0c
2 ) [
Φ
* (
∂Φ
/
∂
t) -
Φ
(
∂Φ
*/
∂
t) + (2iV/ħ)
Φ
*
Φ
] (25.49)
i dlatego na mocy równania (25.16) równanie (25.48) zapisujemy następująco :
div E =
ρ
(25.50)
Ponieważ dla pola maxwellowskiego w charakterze wyjściowych funkcji polowych bierzemy A i
ϕ
, a B
definiujemy równością : B = rot A , skąd wynika , że :

70
div B = 0 (25.51)
a ponieważ zastosowanie operatora rot, do równania (25.46) prowadzi do równania :
rot E = - (1/c)
∂
B/
∂
t (25.52)
możemy dojść do stwierdzenia , że równania Hamiltona odpowiadają równaniom kombinowanego pola
Maxwella-Kleina-Gordona.
Zbadajmy teraz symetrię tego pola. Na mocy inwariantności gęstości lagranżjanu (25.2) przy przekształceniach
jednorodnych Lorentza wynikają z tego prawa zachowania energii-pędu (22.78) ( odpowiednio również (22.89) )
, prawa zachowania momentu pędu oraz prawo zachowania prędkości środka mas (22.83 ) ( odpowiednio
również (22.91). Ogólne zależności teoretyczne przedstawiliśmy powyżej , dalej zatem możemy nimi się nie
zajmować. W tej chwili znajdziemy tylko tensory – energii-pędu (22.66) i (22.88) otrzymując tym samym
najistotniejsze informacje.
Kanoniczny tensor energii-pędu (22.66) ma teraz postać :
Ŧji =
Π
i
Φ
| j +
Π
*i
Φ
* | j +
π
ki A
k | j - ₤g
i
j (25.53)
Podstawmy do tego wzoru wyrażenia (25.10) I (25.14) , co pozwoli otrzymać :
Ŧji = (ħ2/2m0) [
Φ
*| i
Φ
| j +
Φ
*| j
Φ
| i + i
α
Ai (
Φ
*
Φ
| j -
Φ
Φ
*| j ) ] + B
k
i Ak | j - ₤gji (25.54)
Aby otrzymać symetryczny tensor energii-pędu (22.88) należy przede wszystkim obliczyć wielkość (22.79).
Ponieważ pole Kleina-Gordona jest polem skalarnym , odpowiednie współczynniki S
ΓΩ
m
n
zerują się , co
powoduj e, że do sumy (22.79) wejdzie tylko 4-potencjał :
Ħjmn = Sikmn
π
kj
Ai (25.55)
Dla tensorów spełniona jest zależność (22.21), dlatego :
Ħjmn = ½ ( gmk gin - gim g nk )
π
kj
Ai = ½ ( Bm
j An
- B
nj
Am ) (25.56)
Podstawimy teraz ten rezultat do wzoru (22.88) I zgodnie z (25.24) otrzymamy :
Tji = Ŧji + ( B
im
Aj )| m = Ŧji + (1/c) ji Aj + Bi
k
Aj | k (25.57)
Zmiana ji na wyrażenie (25.23) prowadzi do ostatecznego wyrażenia dla symetrycznego tensora energii-pędu :
Tji = - (ħ
2/2m
0){ [ (
Φ
*| i + j
α
Aj
Φ
*) (
Φ
| i - i
α
Ai
Φ
) + (
Φ
*| i + i
α
Ai
Φ
*) (
Φ
| j - i
α
Aj
Φ
) ] –
- gmk [ (
Φ
*| m + i
α
Am
Φ
*) (
Φ
| m k - i
α
Am
Φ
) + (m0
2c2/ħ2)
Φ
*
Φ
] } + Eji (25.58)
Elektromagnetyczna część tego tensora :
Eji = Bj
k B
ki + ¼ gji BmnB
mn
(25.59)
nazywa się „tensorem Minkowskiego“.
Podstawową rolę odgrywa gęstość energii :
T4
4 = (ħ/2m
0) [(grad
Φ
* + i
α
A
Φ
* )(grad
Φ
+ i
α
A
Φ
) + (1/c2)(
∂Φ
*/
∂
t) (
∂Φ
/
∂
t) + (V2/c2/ħ2)
Φ
*
Φ
+
+ (m0
2c2/ħ2)
ΦΦ
* + (iV/c2ħ)[ (
∂Φ
*/
∂
t)
Φ
- (
∂Φ
/
∂
t)
Φ
* ] + ½ ( E2 – B2 ) (25.60)
Odejumując to wyrażenie od wyrażenia (25.27) oraz wykorzystując wzór (25.49), otrzymujemy :
Ħ -T44 = E grad
ϕ
- ( ieħ/2m0c
2)
ϕ
[ (
∂Φ
*/
∂
t) (
∂Φ
/
∂
t) + (V2/c2/ħ2)
Φ
*
Φ
] = E grad
ϕ
+
ρϕ
= div (
ϕ
E ) (25.61)
Zatem gęstość energii różni się od gęstości hamiltonianu o człon dywergentny. Kiedy ten człon staje się równy
zeru podczas całkowania względem przestrzeni funkcja Hamiltona zrównuje się z energia układu pól.
Na zakończenie rozpatrzymy „symetrię cechowania” – jedyną postać symetrii , która pozostała nam do zbadania.
Gęstość lagranżjanu w oczywisty sposób jest inwariantna względem „przekształcenia cechowania” :
A~i = Ai +
χ
| i ;
Φ
~ =
Φ
ei
αχ
;
Φ
~* =
Φ
*e-i
αχ
(25.62)
gdzie :
χ
- funkcja rzeczywista cechowania.
Dla nieskończenie małej funkcji
χ
, mamy :
A~i = Ai +
χ
| i ;
Φ
~ =
Φ
~ i
αχΦ
~ ;
Φ
~* =
Φ
* - i
αχΦ
* (25.63)
lub
δ
Ai =
χ
| i ;
δΦ
= i
αχΦ
;
δΦ
* = - i
αχΦ
* (25.64)
Stosując do tego przypadku różniczkowe prawo zachowania (22.69) na mocy równości :
δ
Ŋj = 0 przyjmuje ono
następującą postać :
(
Π
i
δΦ
+
Π
*i
δΦ
* +
π
ki
δ
Ak ) | i = 0 (25.65)
Podstawiając do tego równania wartości :
Π
i ,
π
ki ,
δ
A,
δΦ
,
δΦ
* , odpowiadające odpowiednio wzorom (25.10)
, (25.14) i (25.64) oraz wprowadzając wielkość ji zgodnie ze wzorem (25.23) , otrzymujemy :
[ Bki | i - (1/c) j
k ]
χ
| k - (1/c) j
i
| i
χ
= 0 tj . ji | i = 0 (25.66)

71
Zatem , z warunku symetrii cechowania wynika prawo zachowania ładunku.
26. ZASTOSOWANIE TEORII DO UKŁADU PÓL MAXWELLOWSKIEGO I DIRAKOWSKIEGO.
Oznaczmy przez
Ψ
bispinor Diraca , opisujący pole Diraca , przez
Ψ
+ - bispinor hermitowsko sprzężony.
, a przez :
Ψ
^ =
Ψ
+
β
(26.1)
bispinor sprzężony. Wykorzystując „macierze Diraca”
γ
k spełniające zależność :
γ
k
γ
m +
γ
m
γ
k = 2gkm (26.2)
gęstość lagranżjanu można zapisać w następującej postaci :
₤ = - ½ ħc [
Ψ
^
γ
k (
Ψ
| k - i
α
Ak
Ψ
) – (
Ψ
^
| k
+ i
α
Ak
Ψ
^ )
γ
k
Ψ
+ (2m0c/ħ)
ΨΨ
^ ] – ¼ B
mnB
mn
(26.3)
Uwzględniając zależności komutacyjne :
βγ
k +
γ
k
+
β
= 0 (26.4)
wiążące
β
= i
γ
4 i
γ
k , możemy pokazać , że gęstość lagranżjanu jest rzeczywista :
₤ = ₤* (26.5)
Różniczkując otrzymamy następujące zależności :
∂
₤/
∂Ψ
= - ½ ħc [ -
Ψ
^
| k
γ
k - 2i
α
Ak
Ψ
γ
k + (2m
0c/ħ)
Ψ
^ ] (26.6)
∂
₤/
∂Ψ
+ = - ½ iħc
γ
4 [
γ
4
Ψ
| k - 2i
α
Ak
Ψ
γ
k + (2m
0c/ħ)
Ψ
] (26.7)
Π
i =
∂
₤/
∂Ψ
| i = - ½ ħc
Ψ
^
γ
i (26.8)
Π
i+ =
∂
₤/
∂Ψ
+
| i = ½ ħc
γ
4
γ
i
Ψ
(26.9)
Πµ
=
∂
₤/
∂Ψ
|
µ
= - ½ ħc
Ψ
^
γµ
(26.10)
Πµ
+ =
∂
₤/
∂Ψ
+
|
µ
= ½ ħc
γ
4
γµ
Ψ
(26.11)
Π
=
∂
₤/
∂
(
∂Ψ
/
∂
t ) = ½ ħc
Ψ
+
(26.12)
Π
+ =
∂
₤/
∂
(
∂Ψ
+
/
∂
t) = ½ ħc
Ψ
(26.13)
Wprowadzając , dla uproszczenia zapisu, „dirakowski 4-wektor gęstości prądu” :
jk = iec
Ψ
^
γ
k
Ψ
(26.14)
otrzymamy :
∂
₤/
∂
Ai = (1/c) j
i (26.15)
Oprócz tego . mają miejsce podobne wzory jaki wprowadziliśmy w poprzednim rozdziale :
π
ij =
∂
₤/
∂
Ai | j = B
ij (26.16)
π
i = (1/c)
π
i4 =
∂
₤/
∂
(
∂
Ai /
∂
t) = (1/c) Bi4 (26.17)
πµ
= (1/c)
πµ
4 =
∂
₤/
∂
(
∂
A
µ
/
∂
t) = (1/c) Bi
µ
(26.18)
π
=
π
44 /c = 0 (26.19)
Między kanonicznie sprzężonymi zmiennymi dirakowskiego pola mają miejsce następujące odpowiedniości :
Ψ
↔
Π
= ½ ħc
Ψ
+
;
Ψ
+
↔
Π
+
= - ½ ħc
Ψ
(26.20)
Zatem , funkcje polowe i funkcje pędów nie są wielkościami wzajemnie niezależnymi – jest to sytuacja taka jak
dla pola schrödingerowskiego. Równanie Lagrange’a (19.12) zawiera obecnie trzy równania postaci :
δ
₤/
δΨ
=
∂
₤/
∂Ψ
- (
∂
₤/
∂Ψ
| m ) | m = 0 (26.21)
δ
₤/
δΨ
+ =
∂
₤/
∂Ψ
+ - (
∂
₤/
∂Ψ
+
| m ) | m = 0 (26.22)
δ
₤/
δ
Ai =
∂
₤/
∂
Ai – (
∂
₤/
∂
Ai | j ) | j = 0 (26.23)
Na mocy zależności (26.15) od razu staje się jasne , że ostatnie równanie odtwarza układ niejednorodnych
równań Maxwella.
Podstawiając wyrażenia (26.9) do równania (26.22) otrzymujemy znane równanie Diraca :
γ
k (
Ψ
| k - i
α
Ak
Ψ
) + (m0c/ħ)
Ψ
= 0 (26.24)
i przy tym równanie (26.21) przechodzi w równanie Diraca dla funkcji sprzężonej :
(
Ψ
^ | k - i
α
Ak
Ψ
^ )
γ
k - (m
0c/ħ)
Ψ
^ = 0 (26.25)
Przy podstawieniu tych równań pola do gęstości lagranżjanu składowe, związane z polem dirackowskim
tożsamościowo równają się zeru , zatem z wyrażenia (26.3) otrzymamy :

72
₤ = ¼ BmnBmn (26.26)
Obliczymy teraz gęstość hamiltonianu zgodnie ze wzorem (20.5) :
Ħ =
Π
(
∂Ψ
/
∂
t) + (
∂Ψ
+/
∂
t)
Π
+ +
πµ
(
∂
A
µ
/
∂
t) - ₤ = ½ iħ [
Ψ
+ (
∂Ψ
/
∂
t) - (
∂Ψ
+/
∂
t)
Ψ
] + ½ ( E2 – B2 ) +
+ E grad
ϕ
(26.27)
Aby nadać temu wyrażeniu wymaganą strukturę , wykluczymy pochodne cząstkowe względem czasu przy
pomocy równań Diraca , co pozwala otrzymać w pierwszej kolejności :
Ħ = ½ iħc [
Ψ
+
γ
4
γµ
(
Ψ
|
µ
- i
α
A
µΨ
) - (
Ψ
+
|
µ
+ i
α
A
µΨ
+ )
γ
4
γµ
Ψ
- (2iV/ħc)
ΨΨ
+ + (2m
0c/ħ)
Ψ
+
γ
4
Ψ
] +
+ ½ ( E2 – B2 ) + E grad
ϕ
= ½ iħc [
Ψ
+
γ
4
γµ
Ψ
|
µ
-
Ψ
+
|
µ
γ
4
γµ
Ψ
+ (2m0c/ħ)
Ψ
+
γ
4
Ψ
] – (1/c) jm Am +
+ ½ ( E2 – B2 ) + E grad
ϕ
(26.28)
a następnie , przyjmując do wiadomości zależności (26.12) i (26.13) otrzymujemy :
Ħ = c [
Π
γ
4
γµ
Ψ
|
µ
-
Π
|
µ
γ
4
γµ
Ψ
+ (2m0c/ħ)
Π
γ
4
Ψ
] - (1/c) jm A
m + ½ ( E
2 – B2 ) + E grad
ϕ
(26.29)
Równanie to jest analogiczne do równania (24.11) w teorii Schrödingera. Uwagi przedstawione w związku z
równaniem (24.11) pozostają w mocy również obecnie.
W związku z zależnością miedzy funkcjami polowymi a funkcjami pędów równania Hamiltona dla pola Diraca
powinny mieć następującą postać :
∂Ψ
/
∂
t =
∂Φ
Ħ/
∂ΦΠ
=
∂
Ħ/
∂Π
- (
∂
Ħ/
∂Π
|
µ
) |
µ
(26.30)
∂Π
/
∂
t =
∂Φ
Ħ/
∂ΦΨ
= - [ (
∂
Ħ/
∂Ψ
) - (
∂
Ħ/
∂Ψ
|
µ
) |
µ
(26.31)
Przy tym gęstość hamiltonianu należy przedstawić w postaci symetrycznej :
Ħ = ½ c [
Π
γ
4
γµ
Ψ
|
µ
-
Ψ
+
|
µ
γ
4
γµ
Π
+
|
µ
+
Ψ
+
|
µ
γ
4
γµ
Π
+ -
Π
|
µ
γ
4
γµ
Ψ
+
+ 2i
α
A
µ
(
Ψ
+
|
µ
γ
4
γµ
Π
+ -
Π
γ
4
γµ
Ψ
) – (2iV/ħc) (
ΠΨ
-
Ψ
+
Π
+ ) + (2m
0c/ħ) (
Πγ
4
Ψ
-
Ψ
+
γ
4
Π
+ ) ] +
+ ½ ( E2 – B2 ) + E grad
ϕ
(26.32)
o symetryczności takiego zapisu możemy od razu przekonać się z zależności postaci :
Π
....
Ψ
= -
Ψ
+ ....
Π
+ (26.33)
Różniczkując znajdujemy :
∂
Ħ/
∂Ψ
= ½ c [ -
Πµ
γ
4
γµ
- 2i
α
A
µ
Π
γ
4
γµ
– (2iV/ħc)
Π
+ (2m0c/ħ)
Πγ
4 ] (26.34)
∂
Ħ/
∂Ψ
|
µ
= ½ c
Πµ
γ
4
γµ
(26.35)
∂
Ħ/
∂Π
= ½ c [
γ
4
γµ
Ψ
+
|
µ
- 2i
α
A
µγ
4
γµ
Ψ
– (2iV/ħc)
Ψ
+ (2m0c/ħ)
γ
4
Ψ
] (26.36)
∂
Ħ/
∂Π
|
µ
= ½ c
γ
4
γµ
Ψ
(26.37)
∂
Ħ/
∂
A
µ
= i
α
c (
Ψ
+
γ
4
γµ
Π
+ -
Π
γ
4
γµ
Ψ
) = - (1/c) j
µ
(26.38)
∂
Ħ/
∂
A
µ
|
ν
= B
νµ
(26.39)
∂
Ħ/
∂πµ
= c2
πµ
- c
ϕ
|
µ
(26.40)
∂
Ħ/
∂ϕ
= - (ie/ħ) (
ΠΨ
-
Ψ
+
Π
+ ) (26.41)
∂
Ħ/
∂ϕ
|
µ
= - c
πµ
(26.42)
Podstawmy teraz te wyrażenia do równania Hamiltona (26.30) I (26.31). Przy tym pierwsze z nich zapiszemy
następująco :
∂Ψ
/
∂
t = c [
γ
4
γµ
Ψ
|
µ
- 2i
α
A
µ
γ
4
γµ
Ψ
– (iV/ħc)
Ψ
+ (m0c/ħ)
γ
4
Ψ
] (26.43)
a drugie :
∂Π
/
∂
t = c [
Π
|
µ
γ
4
γµ
- 2i
α
A
µ
Πγ
4
γµ
– (iV/ħc)
Π
+ (m0c/ħ)
Π
γ
4 ] (26.44)
Prostymi rachunkami możemy udowodnić , że te równania Hamiltona są identyczne jak równania Diraca (26.24)
i (26.25).
Dla wielkości elektromagnetycznych można otrzymać równania Hamiltona w postaci równań (25.40) – (25.43).
Przy tym niczego nowego nie otrzymujemy - należy jedynie uwzględnić to ,że dla 4-wektor gęstości prądu ma
teraz składowe :
j
µ
= iec
Ψ
^
γ
4
Ψ
,
ρ
= e
Ψ
+
Ψ
(26.45)
Teraz , podobnie jak w poprzednim rozdziale , zbadamy symetrię pola.
Na mocy inwariantności gęstości lagranżjanu (26.3) przy niejednorodnych przekształceniach Lorentza znów
spełnione jest prawo zachowania energii-pędu (22.78) ( odpowiednio (22.89) ) oraz prawo zachowania momentu
pędu i prędkości środka mas (22.83). (odpowiednio (22.91) ). Obliczmy tensor energii-pędu , który jest dla nas
wielkością kluczową.

73
Dla kanonicznego tensora energii-pędu (22.66) mamy :
Ŧij =
Π
i
Φ
| j +
Ψ
+
| j
Π
i+ +
π
ki A
k | j + ¼ g
i
j Bmn B
mn
(25.46)
Podstawiając do tego wyrażenia wartości (26.8) I (26.9) dla
Π
i i
Π
i+ , otrzymamy :
Ŧij = - ½ ħc [
Ψ
^
γ
i
Ψ
| j -
Ψ
^ | j
γ
i
Ψ
] + Bk i Ak | j + ¼ g
i
j Bmn B
mn
(25.47)
Dla pól spinorowych znalezienie symetrycznego tensora energii-pędu , otrzymywanego z einsteinowskich
równań pola , związane jest z dosyć skomplikowanymi obliczeniami. ( zobacz Schmutzer [1] )
Dlatego wprowadzę tylko ostateczny wynik takich obliczeń tego symetrycznego tensora :
Ŧji = - ¼ ħc {
Ψ
^ [
γ
i (
Ψ
| i - i
α
Ai
Ψ
) +
γ
i (
Ψ
| j - i
α
Aj
Ψ
)] – [ (
Ψ
^| j - i
α
Aj
Ψ
^ )
γ
i + (
Ψ
^| i - i
α
Ai
Ψ
^ )
γ
j ]
Ψ
} + Eji (25.48)
Przy tym część elektromagnetyczna tensora, określona jest wzorem (25.59).
Stąd dla gęstości energii otrzymujemy następujące wyrażenie :
Ŧ44 = ½ ħc [
Ψ
+ (
∂Ψ
/
∂
t) – (
Ψ
+/
∂
t)
Ψ
+(2iV/ħ)
Ψ
+
Ψ
] + ½ ( E2 – B2 ) (25.49)
Odejmując to wyrażenie od wyrażenia (26.27) dla gęstości hamiltonianu , dochodzimy do następującego wyniku
Ħ - Ŧ44 = E grad
ϕ
+
ϕρ
= div (E
ϕ
) (26.50)
tj. do takiego samego wyniku co dla pola Maxwella-Kleina-Gordona. Odpowiednio zatem , również dla pola
Maxwella-Diraka funkcja Hamiltona i energia układu są , jak być powinno ,równe.
Pole Maxwella-Diraka charakteryzuje się również symetrią cechowania tj. gęstość lagranżjanu jest inwariantna
względem przekształceń cechowania :
A~i = Ai +
χ
| i ;
Ψ
~ =
Ψ
ei
αχ
;
Ψ
^~ =
Ψ
^ e-i
αχ
(26.51)
(
χ
- rzeczywista funkcja cechowania ). Dla nieskończenie małej funkcji
χ
, otrzymujemy :
A~i = Ai +
χ
| i ;
Ψ
~ =
Ψ
+ i
αχΨ
;
Ψ
^~ =
Ψ
^ - i
αχΨ
(26.52)
lub :
δ
Ai =
χ
| i ;
δΨ
= i
αχΨ
;
δΨ
^~ = - i
αχΨ
(26.53)
Stosując do tego przypadku różniczkowe prawo zachowania (22.69) na mocy równości :
δ
Ŋj = 0 przyjmuje ono
następującą postać :
(
Π
i
δΨ
+
δΨ
+
Π
I+ +
π
ki
δ
Ak ) | i = 0 (26.54)
Podstawiając tutaj wyrażenia (26.8) , (26.9) , (26.16) I (26.53) z uwzględnieniem równości (26.14) otrzymujemy
[ Bki| i – (1/c)j
k )
χ
| k - (1/c) j
i
| i
χ
= 0 ; tj. ji | i = 0 (26.55)
Zatem również w tym przypadku prawo zachowania ładunku jest następstwem inwariantności ze względu na
cechowanie.

74
Wyszukiwarka
Podobne podstrony:
Wprowadzenie do klasycznej teorii pola
Zasady dzienne PKM, IŚ Tokarzewski 27.06.2016, V semestr COWiG, PKM (Podstawy konstrukcji mechaniczn
podstawy zarządzania, Szkoła klasyczna
mechanika klasyczna, Studia
Podstawowe projekcje w radiografii klasycznej
Masaż (zasady masażu klasycznego), Masaże, Masaż
Podstawowe projekcje w radiografii klasycznej, Fizjoterapia, Anatomia
Urbański P Geometryczne podstawy teorii pola
C5 (X7) B3DG010WP0 2 05 08 2013 Demontaż Montaż Wahacz wzdłużny tylnego zawieszenia (Z zawiesz
Dynamika punktu materialnego w mechanice klasycznej
podstawy zarzadzania wyklad3 klasyczne techniki zarzadzania
Niektore implikacje Klasycznej Teorii Testow
rzepka, podstawy teorii pola elektromagnetycznego,test
Mickiewiczowska Oda do m odoÂci wobec klasycystycznej teorii gatunku
Zasady warunkowania klasycznego, artykuł I Pawłow
mechanika klasyczna kolokwium
więcej podobnych podstron