Politechnika Śląska

Gliwice, 2006/2007

Wydział: Automatyki, Elektroniki i Informatyki

Semestr: 6 (letni)

Kierunek: Automatyka i robotyka

Podstawy Automatyki

– laboratorium

Ćw 8. Regulacja dyskretna w czasie.

Data ćwiczeń laboratoryjnych:

18.04.2007

Grupa: 1
Sekcja: 3

Skład osobowy sekcji:
Zięba Andrzej
Bojko Marcin
Pawliczek Krystian

1. Cel ćwiczenia:

Celem ćwiczenia było przeanalizowanie działania dyskretnego układu regulacji.

Należało na podstawie odpowiednich charakterystyk jak też odpowiedzi skokowych układu
dokonać porównania układu ciągłego z dyskretnym w zależności od zadanych okresów
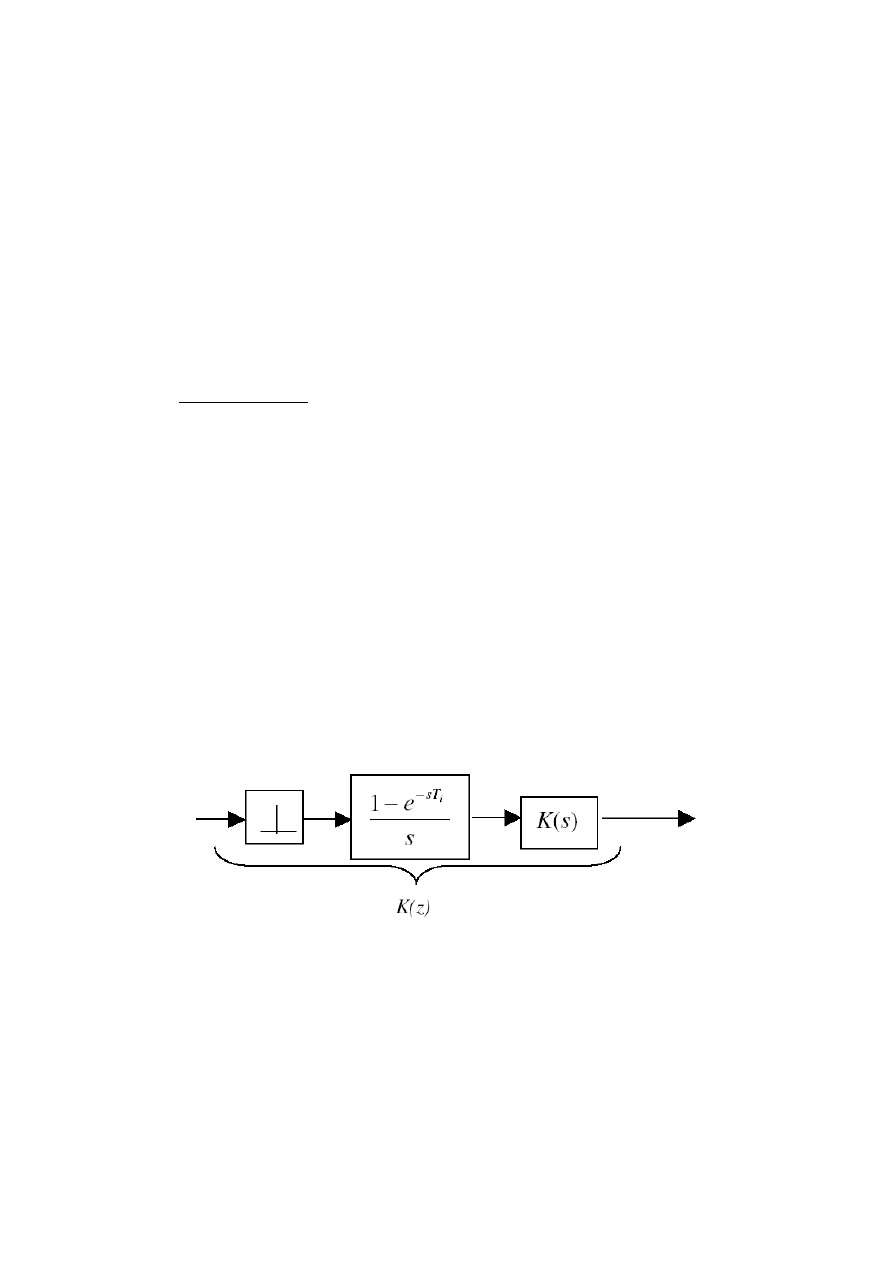
próbkowania. Badania należało przeprowadzić dla zadanego układu ciągłego (transmitancja zadana
przez prowadzącego) z wykorzystaniem impulsatora idealnego i ekstrapolatora zerowego rzędu.

2. Program ćwiczenia:

I. ANALIZA UKŁADU OTWARTEGO:
1. Wykreślić odpowiedź skokową i charakterystyki częstotliwościowe: amplitudowo-fazową,

modułu i fazy dla obiektu o zadanej przez prowadzącego transmitancji:

K  s=

1



1sT

1



1sT

2



; T

1

=

3 s ; T

2

=

4,5 s .

2. Dla zadanego czasu próbkowania T

i

= T

1

wyznaczyć analitycznie transmitancję dyskretną K(z)

obiektu pokazanego na rysunku 1, obliczyć jej wzmocnienie, zera i bieguny.

3. Dla czasów próbkowania T

i

= 0,1 T

1

; 0,2 T

1

; 0,5 T

1

; 1,0 T

1

; 3,0 T

1

:

a)

Odczytać transmitancje dyskretną, wzmocnienie, zera, bieguny ze środowiska Matlab.

b)

Zaznaczyć położenia zer i biegunów na płaszczyźnie z.

c)

Narysować odpowiedź skokową obiektu.

d)

Wykreślić charakterystykę amplitudowo-fazową do pulsacji Nyquista ω

i

= π/T

i

,

odczytać wartość modułu transmitancji dla ω

i

.

e)

Wykreślić charakterystyki częstotliwościowe modułu i fazy do pulsacji będącej
wielokrotnością ω

i

(liniowa skala pulsacji), odczytać maksymalne wartości modułu i

odpowiadające im wartości pulsacji.

4. Przeanalizować wpływ okresu próbkowania na położenie zer i biegunów transmitancji

dyskretnej, postać przebiegów czasowych i charakterystyk częstotliwościowych. Porównać
otrzymane przebiegi i charakterystyki z analogicznymi wykresami uzyskanymi dla układu
ciągłego w czasie. Wybrać „optymalną” wartość czasu próbkowania.

Rysunek 1. Schemat blokowy układu otwartego.

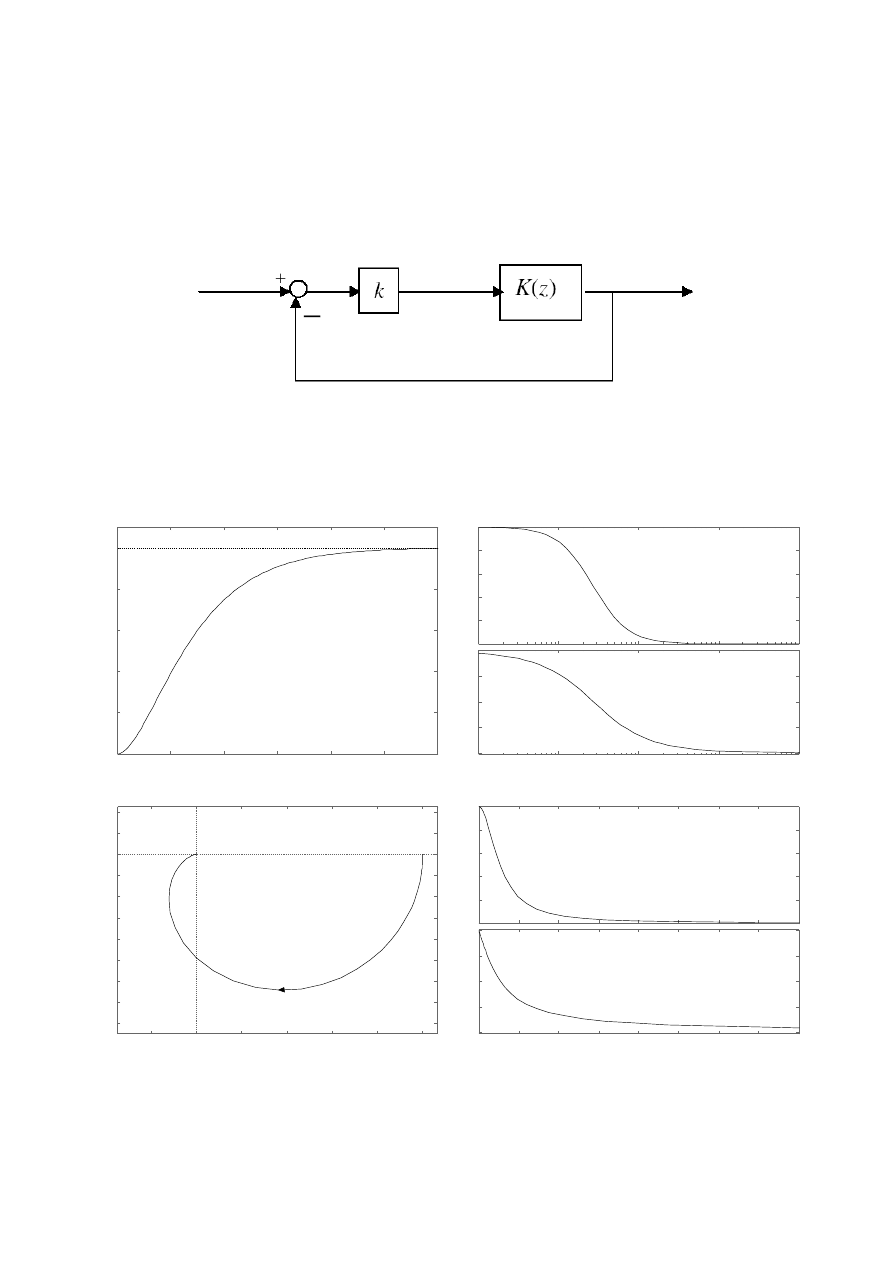
II. ANALIZA UKŁADU ZAMKNIĘTEGO:
5. Wyznaczyć analitycznie transmitancje dyskretną K(z) układu otwartego (struktura jak na

rysunku 1) dla „optymalnego” okresu próbkowania (z punktu 4), oraz wyznaczyć wzmocnienie
graniczne układu zamkniętego o strukturze jak na rysunku 2.

6. Wykreślić linie pierwiastkowe układu. Odczytać wzmocnienia, dla których równanie

charakterystyczne posiada:
a)

pierwiastki rzeczywiste: dodatnie, ujemne, różnych znaków.

b)

pierwiastki zespolone o częściach rzeczywistych: dodatnich, ujemnych, różnych
znaków.

7. Dla wzmocnień wybranych ze znalezionych powyżej zakresów wykreślić odpowiedzi skokowe

dyskretnego układu zamkniętego i porównać je.

8. Dla wzmocnień wybranych w punkcie 7 wykreślić odpowiedzi skokowe ciągłego układu

zamkniętego.

9. Dla innej niż „optymalna” wartości okresu próbkowania wyznaczyć analitycznie K(z) oraz

wzmocnienie graniczne układu zamkniętego. Dla wybranych w punkcie 7 wartości wzmocnień
sprawdzić położenie pierwiastków równania charakterystycznego i narysować odpowiedzi
skokowe.

10. Przeanalizować wpływ okresu impulsowania na działanie układu zamkniętego. Porównać z

działaniem układu ciągłego.

Rysunek 2. Schemat blokowy układu zamkniętego.

3. Analiza układu otwartego:

Ad 1. Przebiegi i charakterystyki dla obiektu ciągłego.

0

5

1 0

1 5

2 0

2 5

3 0

0

0 . 2

0 . 4

0 . 6

0 . 8

1

S t e p R e s p o n s e

T i m e ( s e c )

A

m

p

lit

u

d

e

0

0 . 2

0 . 4

0 . 6

0 . 8

1

M

a

g

n

it

u

d

e

(

a

b

s

)

1 0

- 2

1 0

- 1

1 0

0

1 0

1

1 0

2

- 1 8 0

- 1 3 5

- 9 0

- 4 5

0

P

h

a

s

e

(

d

e

g

)

B o d e D i a g r a m

F r e q u e n c y ( r a d / s e c )

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 0 . 8

- 0 . 7

- 0 . 6

- 0 . 5

- 0 . 4

- 0 . 3

- 0 . 2

- 0 . 1

0

0 . 1

0 . 2

N y q u i s t D i a g r a m

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

0

0 . 2

0 . 4

0 . 6

0 . 8

1

M

a

g

n

it

u

d

e

(

a

b

s

)

0

0 . 5

1

1 . 5

2

2 . 5

3

3 . 5

4

- 1 8 0

- 1 3 5

- 9 0

- 4 5

0

P

h

a

s

e

(

d

e

g

)

B o d e D i a g r a m

F r e q u e n c y ( r a d / s e c )

Ad 2.

●

Wyprowadzenie transmitancji zespolonej K(z) dla obiektu jak na rysunku 1, transmitancji
K(s) jak w punkcie 1 i okresie próbkowania T

i

= T

1

.

K  s=

1−e

−

sT

i

s 1sT

1



1sT

2



=

1

s 1sT

1



1sT

2



−

e

−

sT

i

s 1sT

1



1sT

2



K t=

[

1−

T

2

T

2

−

T

1

e

−

t

T

2



T

1

T

2

−

T

1

e

−

t

T

1

]

⋅

1t −

[

1−

T

2

T

2

−

T

1

e

−

t−T

i

T

2



T

1

T

2

−

T

1

e

−

t −T

i

T

1

]

⋅

1t−T

i



K t=0=0 Spełniony warunek nieantycypacji.

A

1

=

T

1

T

2

−

T

1

A

2

=

T

2

T

2

−

T

1

K nT

i

=

[

1−A

2

e

−

nT

i

T

2



A

1

e

−

nT

i

T

1

]

⋅

1 nT

i

−

[

1− A

2

e

−



n−1T

i

T

2



A

1

e

−



n−1 T

i

T

1

]

⋅

1n−1T

i



D

1

=

e

−

T

i

T

1

D

2

=

e

−

T

i

T

2

K  z =

z

z−1

−

A

2

z

z−D

2



A

1

z

z −D

1

−

1

z−1



A

2

z −D

2

−

A

1

z−D

1

K  z =

A

1



z−1

z−D

1

−

A

2



z−1

z−D

2

K  z =

A

1



z−1 z− D

2

−

A

2



z −1 z −D

1



z−D

1



z− D

2





z −D

1



z−D

2



K  z =z

2



1 A

1

−

A

2



z  A

2

−

A

1



D

1



A

2

−

1−D

2



A

1



1 D

1

D

2



A

1

D

2

−

A

2

D

1



A

1

−

A

2

=

T

1

T

2

−

T

1

−

T

2

T

2

−

T

1

=−

1

K  z =

z 1 A

1

D

1

−

A

2

D

2



D

1

D

2



A

1

D

2

−

A

2

D

1





z −D

1



z −D

2



Ogólna postać transmitancji dyskretnej K(z):

K  z =



1 A

1

D

1

−

A

2

D

2





z 

D

1

D

2



A

1

D

2

−

A

2

D

1

1 A

1

D

1

−

A

2

D

2





z −D

1



z−D

2



gdzie :

A

1

=

T

1

T

2

−

T

1

; A

2

=

T

2

T

2

−

T

1

; D

1

=

e

−

T

i

T

1

; D

2

=

e

−

T

i

T

2

Podstawiając wartości liczbowe:

T

1

=

3 ; T

2

=

4,5 ; T

i

=

3

A

1

=

2 ; A

2

=

3 ;

D

1

=

0,3679 ; D

2

=

0,5134

K  z =

0,1955 z 0,5732



z−0,3679 z −0,5134

Transmitancja została przedstawiona w takiej postaci ze względu na to, że jawnie można odczytać
wzmocnienie, bieguny i zera transmitancji.

●

Wzmocnienie: k = 0,1955

●

Zera:

z

1

= -0,5732

●

Bieguny:

b

1

= 0,3679; b

2

= 0,5134

Ad 3.

T

i

= 0,1 T

1

= 0,3 s

a)

K  z =

0.0031539 z0.946



z−0.9355 z −0.9048

b)

c)

d)

e)

ω

i

= 10,47 rad/s

M

max

= 1

M(ω

i

) = 46,2 · 10

-6

ω

1

= 0 rad/s; ω

2

= 20,9 rad/s; ω

3

= 41,9 rad/s;

T

i

= 0,2 T

1

= 0,6 s

a)

K  z =

0.011942 z0.8948



z −0.8752 z−0.8187

b)

c)

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

P o l e - Z e r o M a p

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

1 . 2

- 0 . 7

- 0 . 6

- 0 . 5

- 0 . 4

- 0 . 3

- 0 . 2

- 0 . 1

0

0 . 1

0 . 2

S y s t e m : G
R e a l : - 4 . 6 2 e - 0 0 5
I m a g : 9 . 7 e - 0 2 0
F r e q u e n c y ( r a d / s e c ) : 1 0 . 5

N y q u i s t D i a g r a m

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

0

5

1 0

1 5

2 0

2 5

3 0

3 5

4 0

- 7 2 0

- 5 4 0

- 3 6 0

- 1 8 0

0

P

h

a

s

e

(

d

e

g

)

0

0 . 2

0 . 4

0 . 6

0 . 8

1

S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 0 . 0 0 1
M a g n i t u d e ( a b s ) : 1

S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 2 0 . 9
M a g n i t u d e ( a b s ) : 1

M

a

g

n

it

u

d

e

(

a

b

s

)

B o d e D i a g r a m

F r e q u e n c y ( r a d / s e c )

0

5

1 0

1 5

2 0

2 5

3 0

0

0 . 2

0 . 4

0 . 6

0 . 8

1

T i m e ( s e c )

A

m

p

lit

u

d

e

S t e p R e s p o n s e

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

P o l e - Z e r o M a p

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

0

5

1 0

1 5

2 0

2 5

3 0

0

0 . 2

0 . 4

0 . 6

0 . 8

1

T i m e ( s e c )

A

m

p

lit

u

d

e

S t e p R e s p o n s e

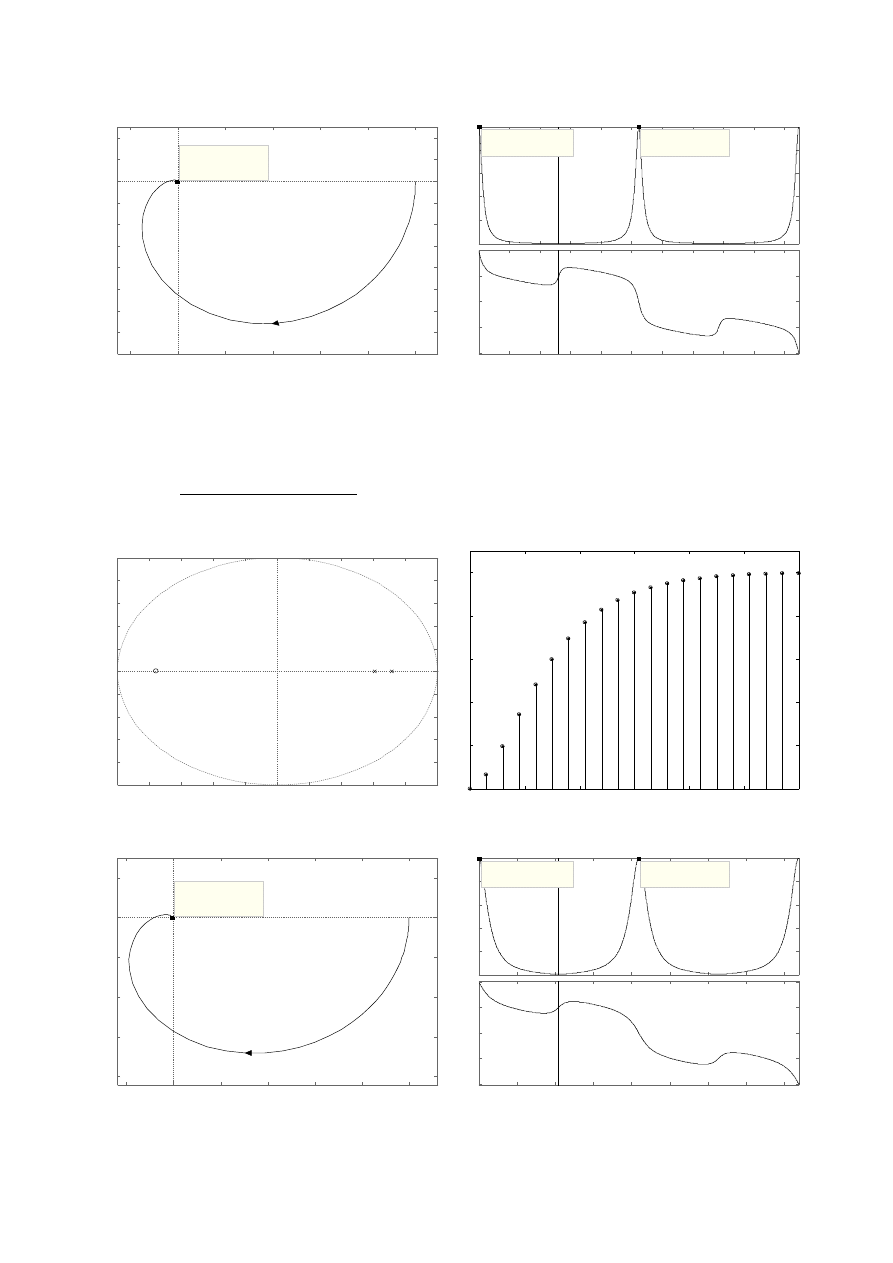
d)

e)

ω

i

= 5,24 rad/s

M

max

= 1

M(ω

i

) = 36,8 · 10

-6

ω

1

= 0 rad/s; ω

2

= 10,5 rad/s; ω

3

= 20,9 rad/s;

T

i

= 0,5 T

1

= 1,5 s

a)

K  z =

0.063467 z 0.7574



z −0.7165 z−0.6065

b)

c)

d)

e)

ω

i

= 2,09 rad/s

M

max

= 1

M(ω

i

) = 5,58 · 10

-3

ω

1

= 0 rad/s; ω

2

= 4,19 rad/s; ω

3

= 8,38 rad/s;

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 0 . 7

- 0 . 6

- 0 . 5

- 0 . 4

- 0 . 3

- 0 . 2

- 0 . 1

0

0 . 1

0 . 2

S y s t e m : G
R e a l : - 0 . 0 0 0 3 6 8
I m a g : 3 . 0 6 e - 0 1 8
F r e q u e n c y ( r a d / s e c ) : 5 . 2 4

N y q u i s t D i a g r a m

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

0

2

4

6

8

1 0

1 2

1 4

1 6

1 8

2 0

- 7 2 0

- 5 4 0

- 3 6 0

- 1 8 0

0

P

h

a

s

e

(

d

e

g

)

0

0 . 2

0 . 4

0 . 6

0 . 8

1

S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 0 . 0 0 1
M a g n i t u d e ( a b s ) : 1

S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 1 0 . 5
M a g n i t u d e ( a b s ) : 1

M

a

g

n

it

u

d

e

(

a

b

s

)

B o d e D i a g r a m

F r e q u e n c y ( r a d / s e c )

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

P o l e - Z e r o M a p

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

S y s t e m : G
R e a l : - 0 . 0 0 5 5 8
I m a g : 1 . 8 e - 0 1 8
F r e q u e n c y ( r a d / s e c ) : 2 . 0 9

N y q u i s t D i a g r a m

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

0

1

2

3

4

5

6

7

8

- 7 2 0

- 5 4 0

- 3 6 0

- 1 8 0

0

P

h

a

s

e

(

d

e

g

)

0

0 . 2

0 . 4

0 . 6

0 . 8

1

S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 0 . 0 0 1
M a g n i t u d e ( a b s ) : 1

S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 4 . 1 9
M a g n i t u d e ( a b s ) : 1

M

a

g

n

it

u

d

e

(

a

b

s

)

B o d e D i a g r a m

F r e q u e n c y ( r a d / s e c )

0

5

1 0

1 5

2 0

2 5

3 0

0

0 . 2

0 . 4

0 . 6

0 . 8

1

T i m e ( s e c )

A

m

p

lit

u

d

e

S t e p R e s p o n s e

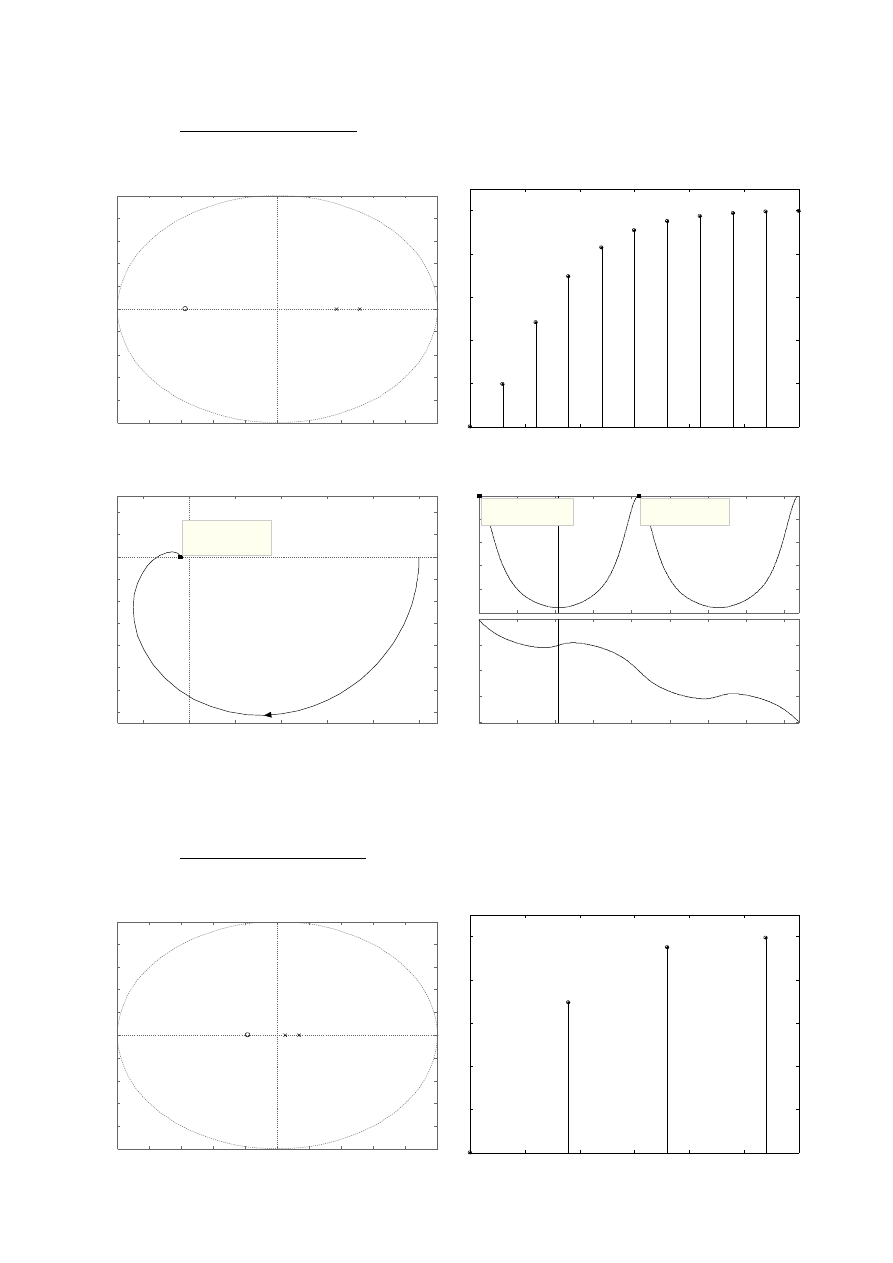
T

i

= 1,0 T

1

= 3,0 s

a)

K  z =

0.19551 z 0.5732



z −0.5134 z−0.3679

b)

c)

d)

e)

ω

i

= 1,05 rad/s

M

max

= 1

M(ω

i

) = 40,3 · 10

-3

ω

1

= 0 rad/s; ω

2

= 2,09 rad/s; ω

3

= 4,19 rad/s;

T

i

= 3,0 T

1

= 9,0 s

a)

K  z =

0.69357 z 0.1846



z −0.1353 z−0.04979

b)

c)

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

P o l e - Z e r o M a p

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 0 . 7

- 0 . 6

- 0 . 5

- 0 . 4

- 0 . 3

- 0 . 2

- 0 . 1

0

0 . 1

0 . 2

S y s t e m : G
R e a l : - 0 . 0 4 0 3
I m a g : - 4 . 9 4 e - 0 1 8
F r e q u e n c y ( r a d / s e c ) : 1 . 0 5

N y q u i s t D i a g r a m

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

0

0 . 5

1

1 . 5

2

2 . 5

3

3 . 5

4

- 7 2 0

- 5 4 0

- 3 6 0

- 1 8 0

0

P

h

a

s

e

(

d

e

g

)

0

0 . 2

0 . 4

0 . 6

0 . 8

1

S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 0 . 0 0 1
M a g n i t u d e ( a b s ) : 1

S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 2 . 0 9
M a g n i t u d e ( a b s ) : 1

M

a

g

n

it

u

d

e

(

a

b

s

)

B o d e D i a g r a m

F r e q u e n c y ( r a d / s e c )

0

5

1 0

1 5

2 0

2 5

3 0

0

0 . 2

0 . 4

0 . 6

0 . 8

1

T i m e ( s e c )

A

m

p

lit

u

d

e

S t e p R e s p o n s e

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

P o l e - Z e r o M a p

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

0

5

1 0

1 5

2 0

2 5

3 0

0

0 . 2

0 . 4

0 . 6

0 . 8

1

T i m e ( s e c )

A

m

p

lit

u

d

e

S t e p R e s p o n s e

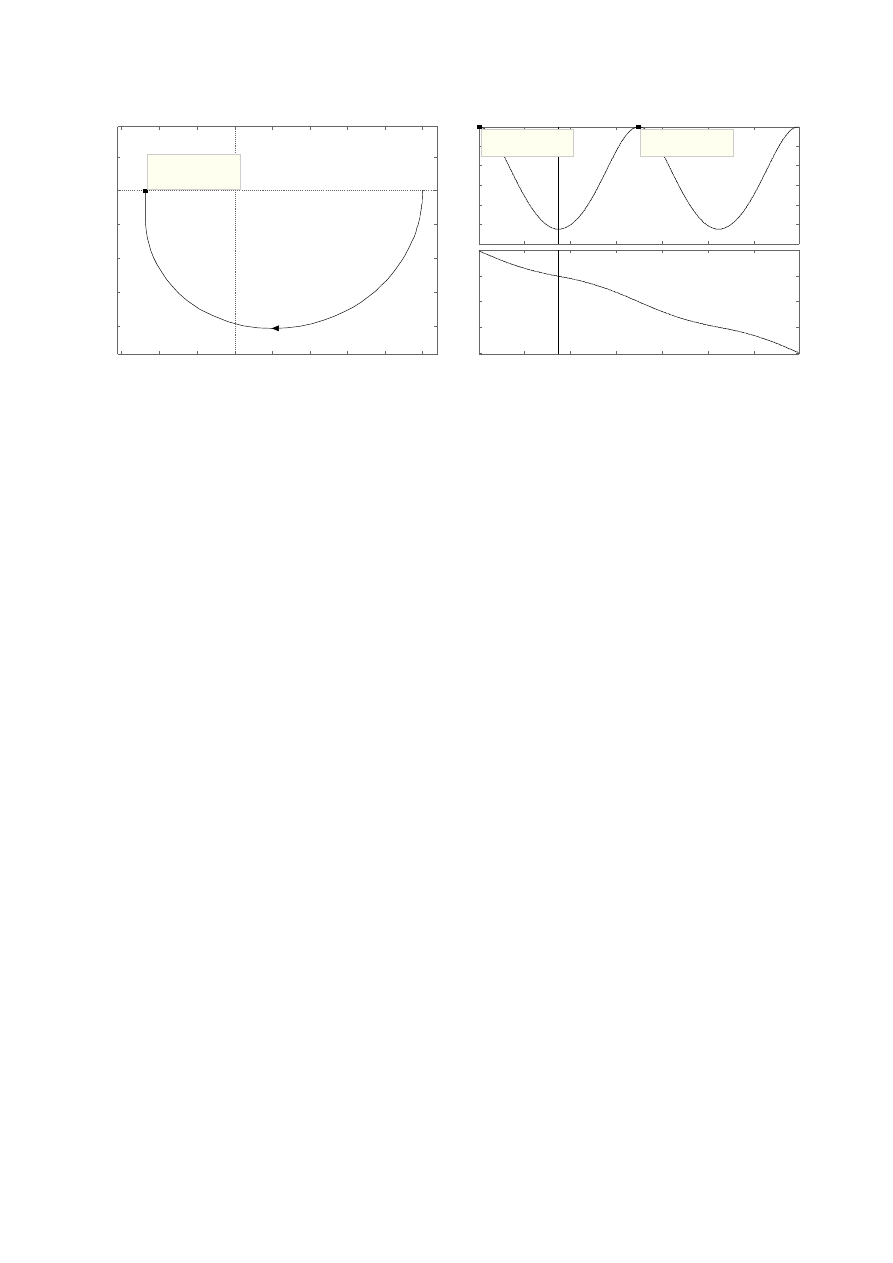
d)

e)

ω

i

= 0,35 rad/s

M

max

= 1

M(ω

i

) = 474 · 10

-3

ω

1

= 0 rad/s; ω

2

= 0,70 rad/s; ω

3

= 1,40 rad/s;

Ad 4. Wnioski:

●

Ze wzrostem okresu próbkowania zarówno bieguny jak i zera transmitancji K(z) zbliżają się
do centrum płaszczyzny z, to znaczy do punktu o współrzędnych (0,j0). Im mniejsza jest
wartość okresu próbkowania tym bliżej wrysowanego okręgu jednostkowego o środku w
punkcie o współrzędnych (0,j0) znajdują się zarówno zera jak i bieguny transmitancji K(z).
Zauważono również, że dla tak zdefiniowanej transmitancji K(z) zmienia się odległość
pomiędzy biegunami w taki sposób, że dla niskich wartości czasu próbkowania jest ona
stosunkowo mała i rośnie do pewnego momentu ze wzrostem tegoż okresu, a następnie
zaczyna maleć z dalszym wzrostem okresu próbkowania.

●

Ze wzrostem okresu próbkowania zmniejsza się gęstość izolowanych punktów odpowiedzi
skokowych. Jak widać dla bardzo małych wartości T

i

w porównaniu do najmniejszej stałej

czasowej części ciągłej układu próbkowanie jest tak gęste, że układ dyskretny zachowuje się
jak ciągły. Punkty izolowane odpowiedzi skokowych układu dyskretnego w każdym z
przypadków pokrywają się z punktami osobliwymi układu ciągłego dla tych chwil czasu w
których zachodzi próbkowanie.

●

Charakterystyka amplitudowo-fazowa dla małych wartości okresu próbkowania w stosunku
do najmniejszej stałej czasowej części ciągłej układu jest niemalże jednakowa z
charakterystyką nyquista obiektu ciągłego. Ze wzrostem okresu próbkowania maleje
pulsacja (częstotliwość) Nyquista i rośnie wartość modułu transmitancji przy tej pulsacji. W
pewnych granicach zaobserwowano że charakterystyka amplitudowo-fazowa przechodzi
przez ćwiartkę drugą płaszczyzny Nyquista. Oznacza to, że układzie dyskretnym występują
przesunięcia fazowe większe niż w układzie ciągłym. Przy dalszym wzroście powyżej
pewnej pulsacji nie obserwujemy już przejścia charakterystyki do ćwiartki drugiej. Dla
bardzo dużych wartości okresu próbkowania układ dyskretny ma zbliżoną charakterystykę
amplitudowo-fazową do przesuwnika-fazowego.

●

Na charakterystykach częstotliwościowych modułu i fazy widzimy również potwierdzenie
wniosku powyższego (fragment charakterystyk do pulsacji Nyquista oznaczonej pionową
linią). Charakterystyki te wykonano do wielokrotności pulsacji Nyquista w celu
zobrazowania błędnej interpretacji przez układ wymuszeń o wyższych częstotliwościach od
częstotliwości Nyquista. Mamy dla tych częstotliwości do czynienia ze zjawiskiem aliasingu
wynikającym z niespełnienia założenia twierdzenia Kotielnikowa-Shannona. Na tych
charakterystykach możemy doszukać się pewnych symetrii i na ich podstawie możemy
wnioskować, że aby zapewnić odpowiednie warunki pracy w układach dyskretnych
rzeczywistych powinno się do ich wejść podłączać filtry dolnoprzepustowe w celu
stłumienia wysokich harmonicznych sygnału dyskretyzowanego. Odpowiednie

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

S y s t e m : G
R e a l : - 0 . 4 7 4
I m a g : - 5 . 8 1 e - 0 1 7
F r e q u e n c y ( r a d / s e c ) : 0 . 3 4 9

N y q u i s t D i a g r a m

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

0

0 . 2

0 . 4

0 . 6

0 . 8

1

1 . 2

- 7 2 0

- 5 4 0

- 3 6 0

- 1 8 0

0

P

h

a

s

e

(

d

e

g

)

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

0 . 9

1

S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 0 . 0 0 1
M a g n i t u d e ( a b s ) : 1

S y s t e m : G
F r e q u e n c y ( r a d / s e c ) : 0 . 6 9 6
M a g n i t u d e ( a b s ) : 1

M

a

g

n

it

u

d

e

(

a

b

s

)

B o d e D i a g r a m

F r e q u e n c y ( r a d / s e c )

charakterystyki częstotliwościowe dla układu ciągłego wskazują że układ ciągły nie może
odwrócić fazy sygnału poniżej -180

o

(-180

o

dla ω → ∞) i nie nadąża za sygnałami o

wysokich częstotliwościach M(∞) = 0. Fakt występowania w układzie dyskretnym
okresowego przebiegu M(ω) sprawia, że przy niekorzystnym warunkach (np. wymuszeniu
sinusoidalnym o pulsacji nieznacznie mniejszej od pulsacji Nyquista i zakłóceniu o
wysokiej częstotliwości ω

z

spełniającej równanie ω

z

= 2 · ω

i

· k, gdzie k wysoka liczba

naturalna) układ będzie działał w sposób błędny i niepożądany. W rzeczywistych układach
kiedy chcemy uzyskać zadowalające działanie układu konieczna jest praca w układzie
zamkniętym, a w szczególnych przypadkach stosowanie filtrów stroboskopowych.

●

Ze względu na przeprowadzone symulacje i uzyskane charakterystyki dla różnych wartości
okresu próbkowania za optymalną wartość przyjęto połowę najmniejszej stałej czasowej
części ciągłej układu (T

i opt

= 1,5 s). Wybór ten został dokonany na drodze kompromisów i

wynika z następujących faktów:

○

Położenie zera i biegunów transmitancji K(z) jest stosunkowo korzystne, to znaczy nie
leżą zbyt blisko okręgu jednostkowego ani w pobliżu jego środka.

○

Punkty izolowane odpowiedzi na skok jednostkowy obiektu o transmitancji K(z) nie są
zbyt gęsto usytuowane.

○

Charakterystyka amplitudowo-fazowa obiektu dyskretnego w znacznej części jest
zbliżona do charakterystyki amplitudowo-fazowej obiektu ciągłego.

○

Niska wartość moduł transmitancji K(z) dla pulsacji Nyquista.

○

Przesunięcie fazowe w niedużym przedziale jest mniejsze od -180

o

.

○

Stosunkowo dobra charakterystyka modułu od pulsacji (w przedziale pulsacji od 0 do
pulsacji Nyquista).

4. Analiza układu zamkniętego:

Ad 5.

●

Wyprowadzenie transmitancji zespolonej K(z) dla obiektu jak na rysunku 1, transmitancji
K(s) jak w punkcie 1 i okresie próbkowania T

i

= T

i opt

= 0,5 T

1

= 1,5 s.

Wykorzystując ogólną postać transmitancji dyskretnej K(z) (patrz punkt 2) i podstawieniu
odpowiednich wartości liczbowych otrzymujemy:

T

1

=

3 ; T

2

=

4,5 ; T

i

=

1,5

A

1

=

2 ;

A

2

=

3 ;

D

1

=

0,6065 ; D

2

=

0,7165

K  z =

0,0635 z 0,7574



z −0,6065 z−0,7165

●

Wyznaczenie wzmocnienia granicznego układu:

Równanie charakterystyczne:



z−0,6065 z −0,7165k⋅0,0635 z 0,7574=0

z

2



z  k⋅0,0635−1,3230 k⋅0,04810,4346=0

Podstawiamy:

z =

w1
w−1



w1

2



w1 w−1 k⋅0,0635−1,3230w−1

2



k⋅0,04810,4346=0

w

2



k⋅0,11160,1116w1,1308−k⋅0,09621,8884−k⋅0,1116=0

Stosując kryterium Hurwitza otrzymujemy następujące warunki:

k −1
k 11,7547
k 16,9211

Na podstawie uzyskanych warunków i założeniu k>0 uzyskujemy wartość k

gr

powyżej którego

układ jest niestabilny.

k

gr



11,7547

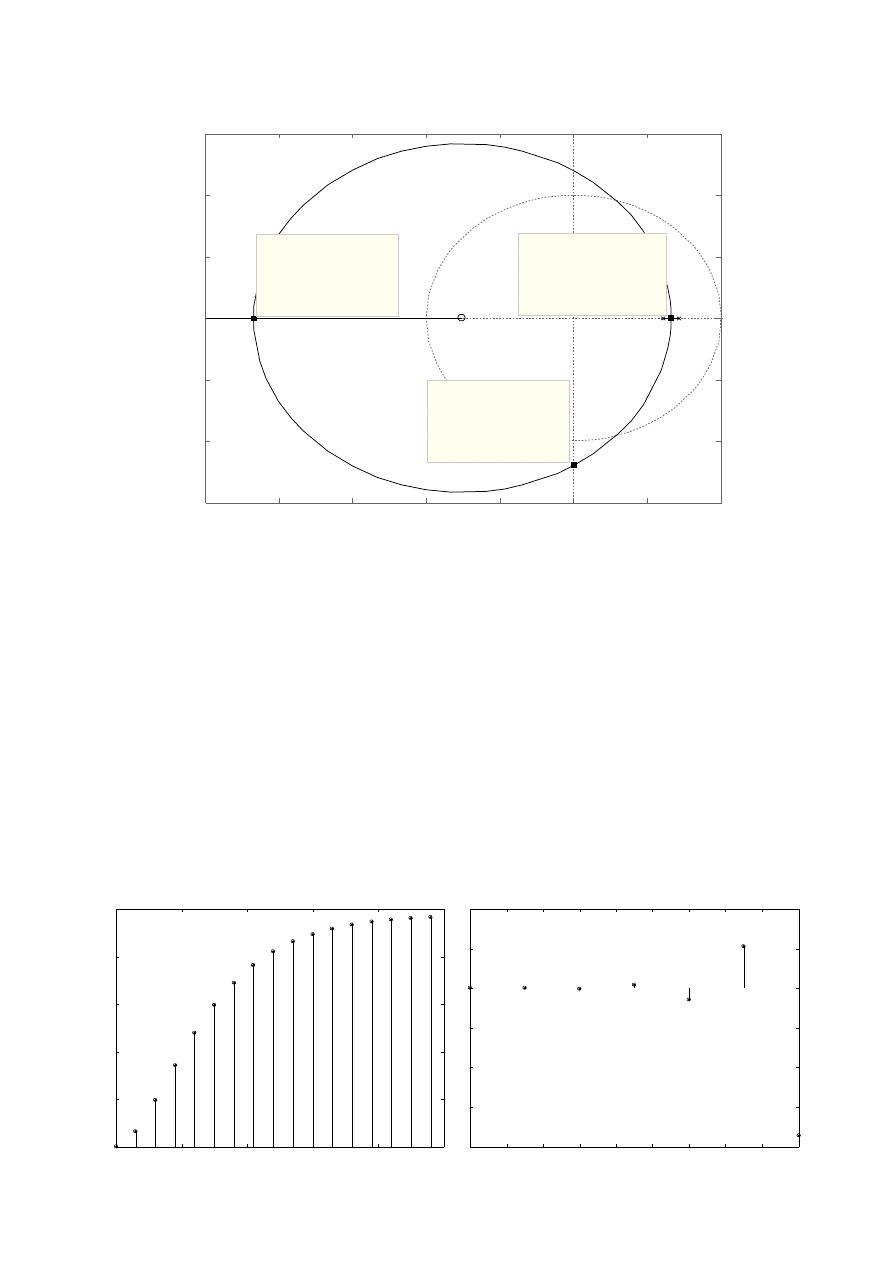
Ad 6.

Równanie charakterystyczne posiada:

a)

pierwiastki rzeczywiste dodatnie dla k 0,0336 ;
pierwiastki rzeczywiste ujemne dla

k 89,4

;

nie posiada pierwiastków rzeczywistych różnych znaków;

b)

pierwiastki zespolone o częściach rzeczywistych dodatnich dla

k 0,0336∩k 20,8

;

pierwiastki zespolone o częściach rzeczywistych ujemnych dla

k 20,8∩k 89,4

;

nie posiada pierwiastków zespolonych o częściach rzeczywistych różnych znaków.

Ad 7.

Wybrane wartości wzmocnień tak aby równanie charakterystyczne 1+K(z)=0 posiadało:
a) pierwiastki rzeczywiste dodatnie: k = 0,025;
b) pierwiastki rzeczywiste ujemne: k = 100;
c) pierwiastki zespolone o części rzeczywistej dodatniej: k = 10;
d) pierwiastki zespolone o części rzeczywistej ujemnej: k = 30.

a)

b)

- 2 . 5

- 2

- 1 . 5

- 1

- 0 . 5

0

0 . 5

1

- 1 . 5

- 1

- 0 . 5

0

0 . 5

1

1 . 5

S y s t e m : G o
G a i n : 8 9 . 4
P o l e : - 2 . 1 8
D a m p i n g : - 0 . 2 4
O v e r s h o o t ( % ) : 2 1 8
F r e q u e n c y ( r a d / s e c ) : 2 . 1 6

S y s t e m : G o

G a i n : 2 0 . 8

P o l e : 0 . 0 0 1 2 4 - 1 . 2 i

D a m p i n g : - 0 . 1 1 4

O v e r s h o o t ( % ) : 1 4 3

F r e q u e n c y ( r a d / s e c ) : 1 . 0 5

S y s t e m : G o

G a i n : 0 . 0 3 3 6

P o l e : 0 . 6 6 + 8 . 7 3 e - 0 0 9 i

D a m p i n g : 1

O v e r s h o o t ( % ) : 0

F r e q u e n c y ( r a d / s e c ) : 0 . 2 7 7

R o o t L o c u s

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

0

5

1 0

1 5

2 0

2 5

0

0 . 0 0 5

0 . 0 1

0 . 0 1 5

0 . 0 2

0 . 0 2 5

T i m e ( s e c )

A

m

p

li

tu

d

e

S t e p R e s p o n s e

0

1

2

3

4

5

6

7

8

9

- 4 0 0 0

- 3 0 0 0

- 2 0 0 0

- 1 0 0 0

0

1 0 0 0

2 0 0 0

T i m e ( s e c )

A

m

p

li

tu

d

e

S t e p R e s p o n s e

c)

d)

Wnioski:

W przypadku kiedy cały obszar takich nastaw, że równanie charakterystyczne posiada

dwa dodatnie pierwiastki rzeczywiste zawiera się w obszarze stabilnych nastaw, to dyskretny układ
zamknięty z regulatorem o tak dobranej nastawie będzie miał odpowiedź skokową aperiodyczną. W
naszym przypadku wzmocnienie regulatora jest niskie więc nawet w granicznym przypadku więc
uchyb regulacji w stanie ustalonym ma dużą wartość. Zaletą jest szybki czas regulacji.

W przypadku kiedy równanie charakterystyczne będzie posiadało pierwiastki zespolone

o części rzeczywistej dodatniej to dla naszego obiektu możemy wyróżnić dwa przypadki. Pierwszy
gdy nastawione wzmocnienie k jest mniejsze od wyznaczonego w punkcie 5 k

gr

, wówczas mamy do

czynienia z układem zamkniętym o periodycznym charakterze odpowiedzi skokowej, czas regulacji
jest dłuższy niż dla układu z równaniem charakterystycznym o dodatnich rzeczywistych
pierwiastkach, natomiast uchyb regulacji w stanie ustalonym ma stosunkowo małą wartość. W
drugim przypadku (k>k

gr

) nasz układ zamknięty jest niestabilny.

W pozostałych przypadkach (b i d) k>k

gr

czyli układ niestabilny.

Ad 8.

Dla wzmocnień jak w punkcie 7 – rozpatrujemy ciągły układ zamknięty:

a)

b)

0

2

4

6

8

1 0

1 2

- 1 0

- 8

- 6

- 4

- 2

0

2

4

6

8

1 0

T i m e ( s e c )

A

m

p

lit

u

d

e

S t e p R e s p o n s e

0

2 0

4 0

6 0

8 0

1 0 0

1 2 0

0

0 . 2

0 . 4

0 . 6

0 . 8

1

1 . 2

1 . 4

1 . 6

1 . 8

T i m e ( s e c )

A

m

p

lit

u

d

e

S t e p R e s p o n s e

0

5

1 0

1 5

2 0

2 5

0

0 . 0 0 5

0 . 0 1

0 . 0 1 5

0 . 0 2

0 . 0 2 5

S t e p R e s p o n s e

T i m e ( s e c )

A

m

p

li

tu

d

e

0

2

4

6

8

1 0

1 2

1 4

1 6

1 8

2 0

0

0 . 2

0 . 4

0 . 6

0 . 8

1

1 . 2

1 . 4

1 . 6

1 . 8

S t e p R e s p o n s e

T i m e ( s e c )

A

m

p

li

tu

d

e

c)

d)

Wnioski:

Jak zaobserwowano periodyczność pojawia się wówczas gdy wzmocnienie k

przekroczy wartość dla której rozwiązaniem równania charakterystycznego 1+K(z)=0 przestaną być
pierwiastki rzeczywiste dodatnie. Poniżej tej granicy zamknięty układ ciągły jest aperiodyczny. Ze
względu na to, że zamknięty układ ciągły jest stabilny strukturalnie wzmocnienie k możemy
dowolnie zwiększać. Ze wzrostem k dla zamkniętego układu ciągłego rośnie stopień
oscylacyjności, maleje uchyb regulacji w stanie ustalonym, czas regulacji jest w przybliżeniu stały.

Ad 9.

Dla T

i

= 9 s:

K  z =

0,6936 z 0,1846



z −0,0498 z−0,1353

k

gr



2,11

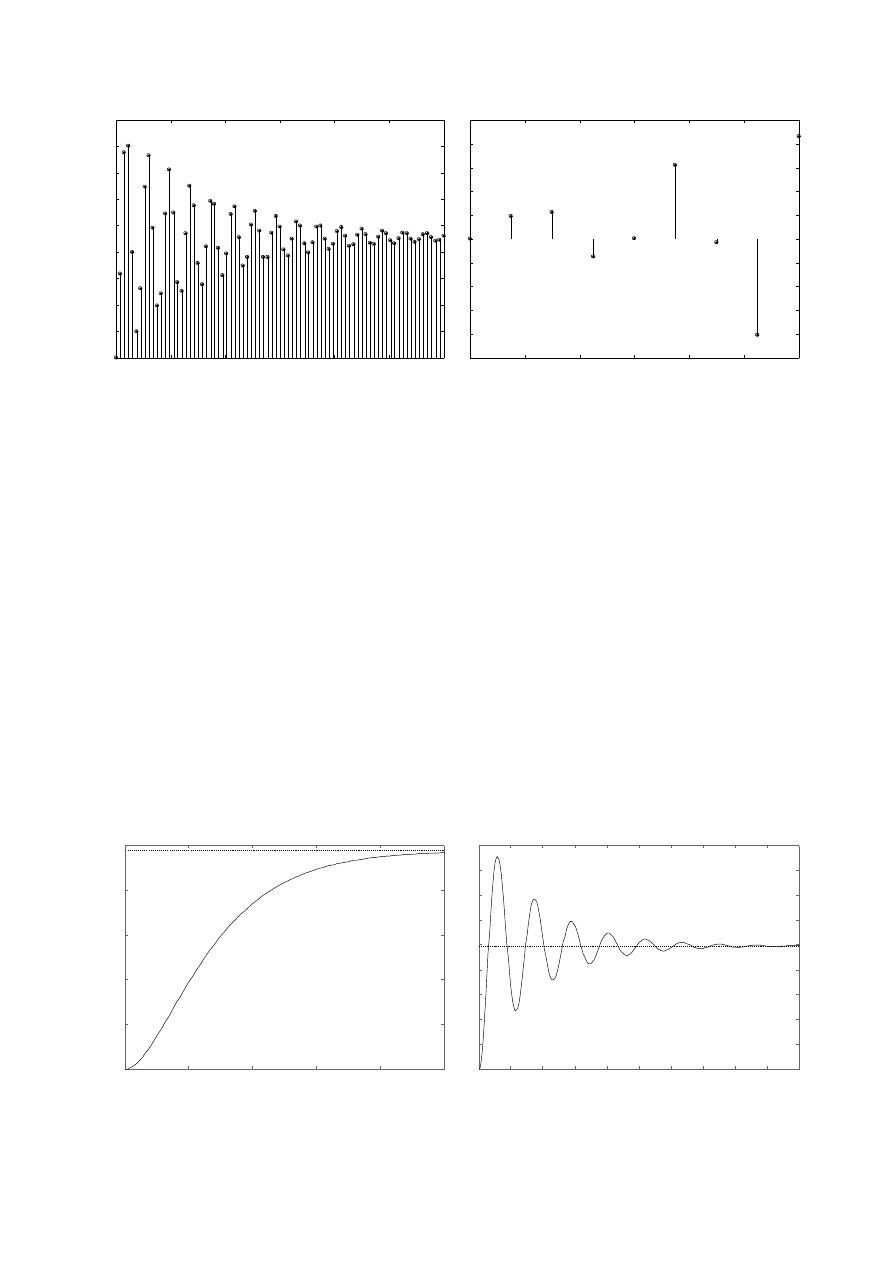
Ze względu na trudność w zobrazowaniu usytuowania pierwiastków dla tak dużego rozrzutu

wzmocnień przedstawiono tylko przypadek dla k = 0,025. Pozostałe pierwiastki odczytano z
wykresu w środowisku Matlab.

x – bieguny transmitancji K(z)
o – zero transmitancji K(z)
◊ – pierwiastki równania charakterystycznego dla danego wzmocnienia k.

0

2

4

6

8

1 0

1 2

1 4

1 6

1 8

2 0

0

0 . 2

0 . 4

0 . 6

0 . 8

1

1 . 2

1 . 4

S t e p R e s p o n s e

T i m e ( s e c )

A

m

p

lit

u

d

e

0

2

4

6

8

1 0

1 2

1 4

1 6

1 8

2 0

0

0 . 2

0 . 4

0 . 6

0 . 8

1

1 . 2

1 . 4

1 . 6

S t e p R e s p o n s e

T i m e ( s e c )

A

m

p

li

tu

d

e

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

- 1

- 0 . 8

- 0 . 6

- 0 . 4

- 0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

R o o t L o c u s

R e a l A x i s

Im

a

g

in

a

ry

A

x

is

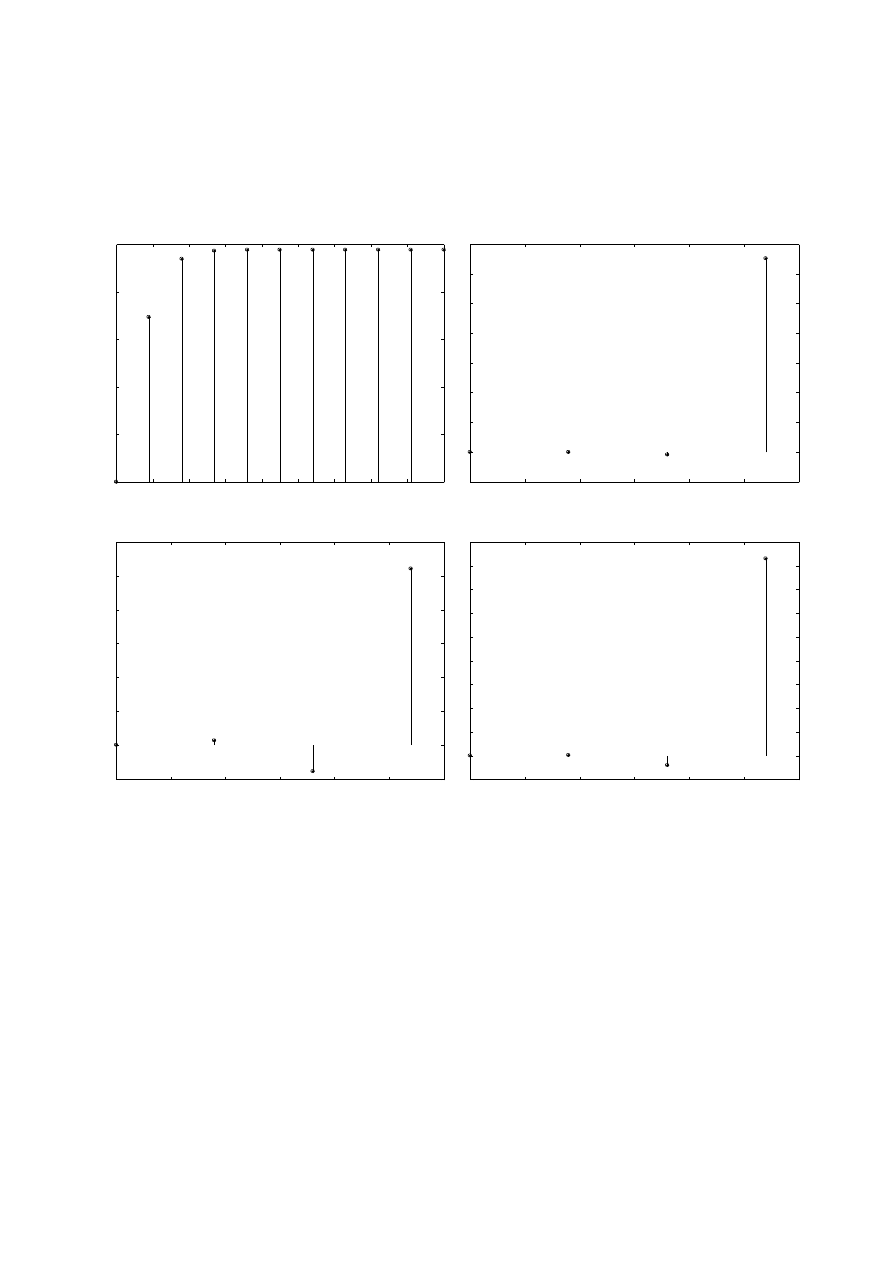
a) k = 0,025

z

1,2

= 0.0839 ± j0.0539

b) k = 100

z

1

= -69;

z

2

= -0,186

c) k = 10

z

1

= -6,55; z

2

= -0,196

d) k = 30

z

1

= -20,4; z

2

= -0,188

Odpowiedzi skokowe:
a)

b)

c)

d)

Wnioski:

Tylko w przypadku (a) k<k

gr

. Pomimo iż przebieg odpowiedzi skokowej w tym

przypadku nie wygląda na oscylacyjny to nieznaczne zwiększenie wartości wzmocnienia ujawnia
oscylacje. Teoretycznie uzyskany przebieg też powinien być oscylacyjny – być może doszło do
przekłamań numerycznych bądź błędów zaokrągleń. Wynika to z usytuowania pierwiastków a
mianowicie pierwiastki równania charakterystycznego 1+K(z)=0 są zespolone.

Ad 10.

Wnioski:

●

Dla bardzo małych okresów próbkowania transformata Z traci sens i należy w takim
wypadku potraktować, taki układ jako ciągły.

●

Dla bardzo dużych okresów próbkowania transformata Z zmierza do opóźnienia
dyskretnego.

●

Ze wzrostem T

i

maleje wzmocnienie graniczne k

gr

decydujące o stabilności układu.

●

Ze wzrostem T

i

maleje częstotliwość Nyquista.

●

Ze wzrostem T

i

maleją graniczne wartości przedziałów dla których pierwiastki są

określonego typu (rzeczywiste, zespolone i ich znaki).

●

Ze wzrostem T

i

wzrasta stopień oscylacyjności układu.

0

1 0

2 0

3 0

4 0

5 0

6 0

7 0

8 0

9 0

0

0 . 0 0 5

0 . 0 1

0 . 0 1 5

0 . 0 2

0 . 0 2 5

T i m e ( s e c )

A

m

p

li

tu

d

e

S t e p R e s p o n s e

0

5

1 0

1 5

2 0

2 5

3 0

- 0 . 5

0

0 . 5

1

1 . 5

2

2 . 5

3

3 . 5

x 1 0

5

T i m e ( s e c )

A

m

p

li

tu

d

e

S t e p R e s p o n s e

0

5

1 0

1 5

2 0

2 5

3 0

- 5 0

0

5 0

1 0 0

1 5 0

2 0 0

2 5 0

3 0 0

T i m e ( s e c )

A

m

p

lit

u

d

e

S t e p R e s p o n s e

0

5

1 0

1 5

2 0

2 5

3 0

- 1 0 0 0

0

1 0 0 0

2 0 0 0

3 0 0 0

4 0 0 0

5 0 0 0

6 0 0 0

7 0 0 0

8 0 0 0

9 0 0 0

T i m e ( s e c )

A

m

p

li

tu

d

e

S t e p R e s p o n s e