Politechnika Śląska
Gliwice, 2006/2007
Wydział: Automatyki, Elektroniki i Informatyki
Semestr: 6 (letni)
Kierunek: Automatyka i robotyka
Podstawy Automatyki
– laboratorium
Ćw 5. Regulacja PID.
Data ćwiczeń laboratoryjnych:
28.03.2007
Grupa: 1
Sekcja: 3
Skład osobowy sekcji:
Zięba Andrzej
Bojko Marcin
1. Cel ćwiczenia:
Celem ćwiczenia była analiza własności układów regulacji oraz wskazanie możliwości
poprawy jego działania poprzez dobór odpowiednich regulatorów. Badany był wpływ typu oraz
nastaw regulatora dobieranych według: kryterium M
max
, metody Zieglera-Nicholsa (Z-N), metody
QDR oraz zadanego zapasu fazy.
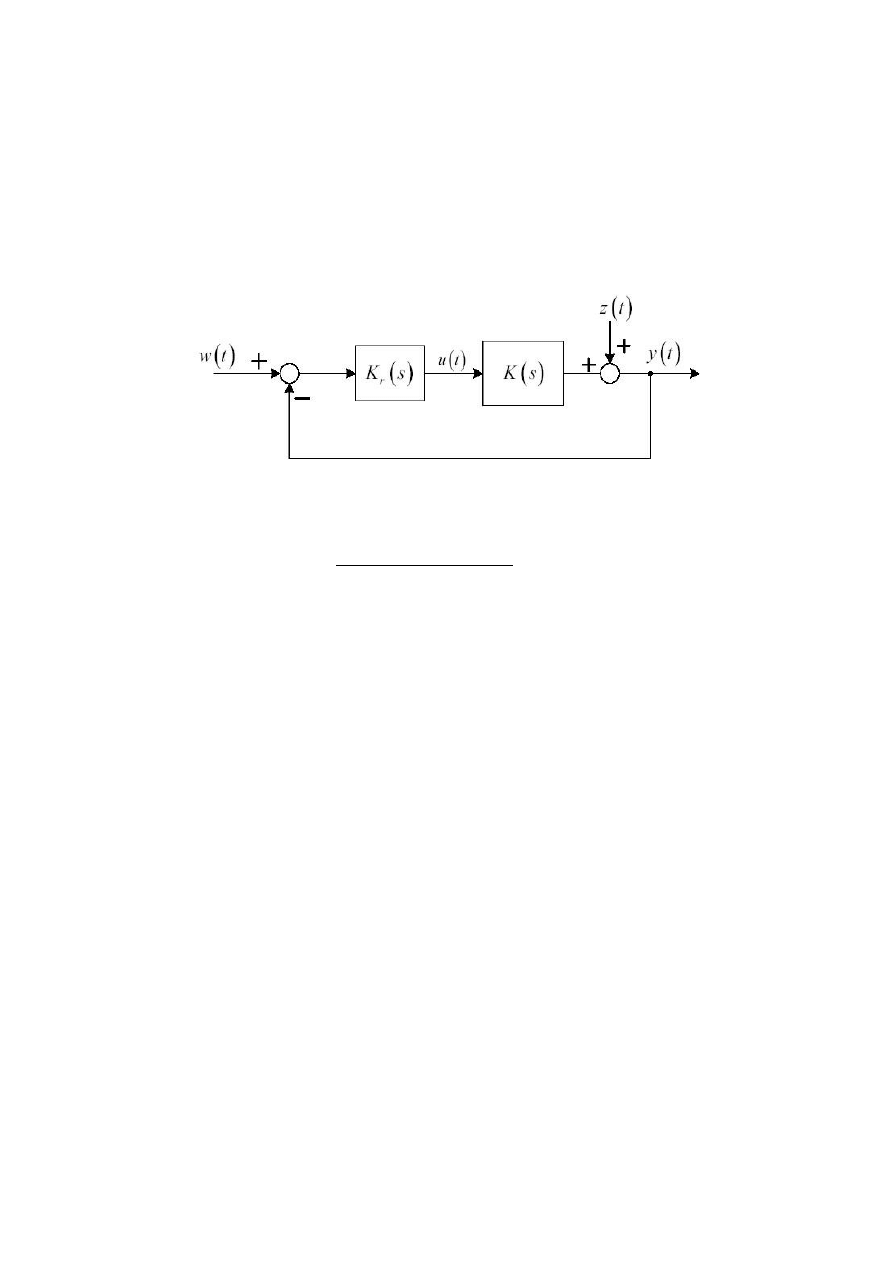
2. Program ćwiczenia:
Rysunek 1: Zamknięty układ regulacji.
A. Część pierwsza – porównanie działania układów z regulatorami dobieranymi według
różnych kryteriów.
Przeprowadź analizę zamkniętego układu regulacji przedstawionego na rysunku 1. z
obiektem o transmitancji: K s=
k
as1sT
1
1sT
2
; gdzie : k=3, T
1
=
5, T
2
=
7.6 , a=1.
1. Zakładając K
r
(s) = 1 zbadać własności obiektu regulacji K(s).
1.1.
Wykreślić charakterystykę Nyquista układu otwartego – zaznaczyć zapas amplitudy oraz
zapas fazy.
1.2.
Wykreślić odpowiedź skokową układu zamkniętego.
1.3.
Wykreślić przebieg wskaźników częstotliwościowych M(ω) i q(ω).
2. Zbadać wpływ nastaw regulatora P.
2.1.
Dobrać k
r
korzystając z:
a) kryterium M
max
;
b) zapasu fazy (przyjąć Δφ = π/6);
c) metody Zieglera-Nicholsa;
d) metody QDR.
2.2.
Dla poszczególnych układów regulacji wykreślić:
a) charakterystykę Nyquista;
b) odpowiedź skokową;
c) przebieg wskaźników częstotliwościowych.
Poszczególne charakterystyki należy przedstawić w sposób zbiorczy porównując je z
odpowiednimi charakterystykami układu bez regulatora (punkt A.1).
2.3.
Na podstawie otrzymanych wyników wskazać „optymalną” nastawę regulatora i
uzasadnić swój wybór.
3. Zbadać wpływ nastaw regulatora PI.
W tym celu należy dobrać nastawy regulatora wykorzystując poszczególne kryteria
(2.1 a,b,c,d) i wykreślić komplet charakterystyk (2.2 a,b,c). Na podstawie otrzymanych
wyników wskazać „optymalną” nastawę regulatora i uzasadnić swój wybór.
4. Zbadać wpływ nastaw regulatora PID.
W tym celu należy dobrać nastawy regulatora wykorzystując poszczególne kryteria
(2.1 a,b,c,d) i wykreślić komplet charakterystyk (2.2 a,b,c). Na podstawie otrzymanych
wyników wskazać „optymalną” nastawę regulatora i uzasadnić swój wybór.
B. Część druga – porównanie działania układów z regulatorami P, PI, PID.
Przeprowadź analizę zamkniętego układu regulacji przedstawionego na rysunku 1. z
obiektem o transmitancji: K s=
k
1sT
1
n
1sT
2
; k =3, T
2
=
7.5 , T
1
=
0.1⋅T
2
=
0.75 , n=5.
1. Zakładając K
r
(s) = 1 zbadać własności obiektu regulacji K(s).
1.1.
Wykreślić charakterystykę Nyquista układu otwartego.
1.2.
Wykreślić odpowiedź skokową układu zamkniętego.
1.3.
Wykreślić przebieg wskaźników częstotliwościowych.
2. Dobrać nastawy regulatorów P, PI, PID według metody Zieglera-Nicholsa.
2.1.
Dla poszczególnych układów regulacji wykreślić:
a) charakterystykę Nyquista;
b) przebiegi wskaźników: nadążania i regulacji.
Zbadać wpływ regulatorów P, PI, PID na zapas stabilności oraz przebiegi wskaźników
częstotliwościowych. Poszczególne charakterystyki należy przedstawić w sposób
zbiorczy porównując je z odpowiednimi charakterystykami układu bez regulatora (B.1).
2.2.
Wykreślić odpowiedzi skokowe układów z regulatorami P, PI, PID i porównać z
odpowiedzią skokową układu zamkniętego bez regulatora (B.1.2) – co daje pojawienie
się kolejnych elementów w regulatorze.
2.3.
Dla każdego typu regulatora porównać odpowiedzi skokowe układów przy nastawach
Zieglera-Nicholsa i nastawach dobranych w oparciu o inne kryterium (2.1 a,b,d) – czy
można polepszyć działanie układu odchodząc od nastaw Zieglera-Nicholsa.
3. Kod źródłowy programu:
Część A:
close all;
clear all;
clc;
% Zdefiniowanie transmitancji obiektu:
s=tf('s');
K=3/(s+1)/(5*s+1)/(7.5*s+1);
% Zdefiniowanie transmitancji regulatorow:
k_kr=5.666666; % wzmocnienie reg. P dla ktorego uklad znajdzie sie na granicy stabilnosci
T_kr=10.5; % okres wystepujacych wowczas oscylacji niegasnacych
k_p=3; % wzmocnienie procesu (uklad otwarty)
t1=14.38; % czas po ktorym odpowiedz skokowa uzyska 63,2% wartosci w stanie ustalonym
t2=7.4764; % czas po ktorym odpowiedz skokowa uzyska 28,3% wartosci w stanie ustalonym
T_p=1.5*(t1-t2); % zastepcza stala czasowa
T0_p=t1-T_p; % zastepczy czas opuznienia
% P:
Kr1=1.330;
Kr2=2.075;
Kr3=0.5*k_kr;
Kr4=T_p/k_p/T0_p;
% PI:
% Kr1=1.07*(1+1/(s*25));
% Kr2=1.12*(1+1/(s*10));
% Kr3=0.45*k_kr*(1+1/(s*0.85*T_kr));
% Kr4=(0.9*T_p/k_p/T0_p)*(1+1/(s*3.33*T0_p));
% PID:
% Kr1=3.7*(1+1/(s*10)+s*2);
% Kr2=11.5*(1+1/(s*20)+s*5);
% Kr3=0.6*k_kr*(1+1/(s*0.5*T_kr)+s*0.12*T_kr);
% Kr4=1.2*T_p/k_p/T0_p*(1+1/(s*2*T0_p)+s*0.5*T0_p);
% Wykreslenie odpowiednich charakterystyk:
figure;
hold on;
nyquist(K);
nyquist(minreal(K*Kr1));
nyquist(minreal(K*Kr2));
nyquist(minreal(K*Kr3));
nyquist(minreal(K*Kr4));
figure;
hold on;
step(minreal(K/(K+1)));
step(minreal(K*Kr1/(K*Kr1+1)));
step(minreal(K*Kr2/(K*Kr2+1)));
step(minreal(K*Kr3/(K*Kr3+1)));
step(minreal(K*Kr4/(K*Kr4+1)));
legend('Uklad bez regulatora','Kryterium M_{max}','Zapewnienie zapasu fazy 30^{o}',...
'Metoda Zieglera-Nicholsa','Metoda QDR',4);
figure;
hold on;
bodemag(minreal(K/(K+1)));
bodemag(minreal(K*Kr1/(K*Kr1+1)));
bodemag(minreal(K*Kr2/(K*Kr2+1)));
bodemag(minreal(K*Kr3/(K*Kr3+1)));
bodemag(minreal(K*Kr4/(K*Kr4+1)));
legend('Uklad bez regulatora','Kryterium M_{max}','Zapewnienie zapasu fazy 30^{o}',...
'Metoda Zieglera-Nicholsa','Metoda QDR',2);
xlim([10^(-3) 10^(2)]);
figure;
hold on;
bodemag(minreal(1/(K+1)));
bodemag(minreal(1/(K*Kr1+1)));
bodemag(minreal(1/(K*Kr2+1)));
bodemag(minreal(1/(K*Kr3+1)));
bodemag(minreal(1/(K*Kr4+1)));
legend('Uklad bez regulatora','Kryterium M_{max}','Zapewnienie zapasu fazy 30^{o}',...
'Metoda Zieglera-Nicholsa','Metoda QDR',2);
xlim([10^(-3) 10^(2)]);
Część B:
close all;
clear all;
clc;
% Zdefiniowanie transmitancji obiektu:
s=tf('s');
K=3/((0.75*s+1)^5)/(7.5*s+1);
% Zdefiniowanie transmitancji regulatorow - metoda Zieglera-Nicholsa:
k_kr=1.8538273; % wzmocnienie reg. P dla ktorego uklad znajdzie sie na granicy stabilnosci
T_kr=12.4; % okres wystepujacych wowczas oscylacji niegasnacych
Kr1=0.5*k_kr;
Kr2=0.45*k_kr*(1+1/(s*0.85*T_kr));
Kr3=0.6*k_kr*(1+1/(s*0.5*T_kr)+s*0.12*T_kr);
% Wykreslenie odpowiednich charakterystyk:
figure;
hold on;
nyquist(K);
nyquist(minreal(K*Kr1));
nyquist(minreal(K*Kr2));
nyquist(minreal(K*Kr3));
figure;
hold on;
bodemag(minreal(K/(K+1)));
bodemag(minreal(K*Kr1/(K*Kr1+1)));
bodemag(minreal(K*Kr2/(K*Kr2+1)));
bodemag(minreal(K*Kr3/(K*Kr3+1)));
legend('Uklad bez regulatora','Uklad z regulatorem P',...
'Uklad z regulatorem PI','Uklad z regulatorem PID',2);
xlim([10^(-2) 10^(2)]);
figure;
hold on;
bodemag(minreal(1/(K+1)));
bodemag(minreal(1/(K*Kr1+1)));
bodemag(minreal(1/(K*Kr2+1)));
bodemag(minreal(1/(K*Kr3+1)));
legend('Uklad bez regulatora','Uklad z regulatorem P',...
'Uklad z regulatorem PI','Uklad z regulatorem PID',2);
xlim([10^(-2) 10^(2)]);
figure;
hold on;
step(minreal(K/(K+1)));
step(minreal(K*Kr1/(K*Kr1+1)));
step(minreal(K*Kr2/(K*Kr2+1)));
step(minreal(K*Kr3/(K*Kr3+1)));
legend('Uklad bez regulatora','Uklad z regulatorem P',...
'Uklad z regulatorem PI','Uklad z regulatorem PID',4);
% Definicja nastaw regulatorow dla innych metod:
k_p=3; % wzmocnienie procesu (uklad otwarty)
t1=11.4491; % czas po ktorym odpowiedz skokowa uzyska 63,2% wartosci w stanie ustalonym
t2=6.298; % czas po ktorym odpowiedz skokowa uzyska 28,3% wartosci w stanie ustalonym
T_p=1.5*(t1-t2); % zastepcza stala czasowa
T0_p=t1-T_p; % zastepczy czas opuznienia
% P:
Kr1a=0.84;
Kr1b=1.22;
Kr1d=T_p/k_p/T0_p;
% PI:
Kr2a=0.767*(1+1/(s*25));
Kr2b=0.915*(1+1/(s*10));
Kr2d=(0.9*T_p/k_p/T0_p)*(1+1/(s*3.33*T0_p));
% PID:
Kr3a=1.125*(1+1/(s*10)+s*2);
Kr3b=0.973*(1+1/(s*20)+s*5);
Kr3d=1.2*T_p/k_p/T0_p*(1+1/(s*2*T0_p)+s*0.5*T0_p);
% Odpowiedzi skokowe:
% Regulatory P:
figure;
hold on;
step(minreal(K*Kr1/(K*Kr1+1)));
step(minreal(K*Kr1a/(K*Kr1a+1)));
step(minreal(K*Kr1b/(K*Kr1b+1)));
step(minreal(K*Kr1d/(K*Kr1d+1)));
legend('Metoda Zieglera-Nicholsa','Kryterium M_{max}',...
'Zapewnienie zapasu fazy 30^{o}','Metoda QDR',4);
% Regulatory PI:
figure;
hold on;
step(minreal(K*Kr2/(K*Kr2+1)));
step(minreal(K*Kr2a/(K*Kr2a+1)));
step(minreal(K*Kr2b/(K*Kr2b+1)));
step(minreal(K*Kr2d/(K*Kr2d+1)));
legend('Metoda Zieglera-Nicholsa','Kryterium M_{max}',...
'Zapewnienie zapasu fazy 30^{o}','Metoda QDR',4);
% Regulatory PID:
figure;
hold on;
step(minreal(K*Kr3/(K*Kr3+1)));
step(minreal(K*Kr3a/(K*Kr3a+1)));
step(minreal(K*Kr3b/(K*Kr3b+1)));
step(minreal(K*Kr3d/(K*Kr3d+1)));
legend('Metoda Zieglera-Nicholsa','Kryterium M_{max}',...
'Zapewnienie zapasu fazy 30^{o}','Metoda QDR',4);
4. Realizacja zadań części pierwszej (A):
1. Badanie własności obiektu regulacji:
Ad 1.1.
Δφ = 60
o
ΔL = 15.1
Δk = 5.69
- 2
- 1 . 5
- 1
- 0 . 5
0
0 . 5
1
1 . 5
2
2 . 5
3
- 2
- 1 . 5
- 1
- 0 . 5
0
0 . 5
S y s t e m : K
G a i n M a r g i n ( d B ) : 1 5 . 1
A t f r e q u e n c y ( r a d / s e c ) : 0 . 6
C l o s e d L o o p S t a b l e ? Y e s
S y s t e m : K
P h a s e M a r g i n ( d e g ) : 6 0
D e l a y M a r g i n ( s e c ) : 4 . 6 9
A t f r e q u e n c y ( r a d / s e c ) : 0 . 2 2 4
C l o s e d L o o p S t a b l e ? Y e s
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
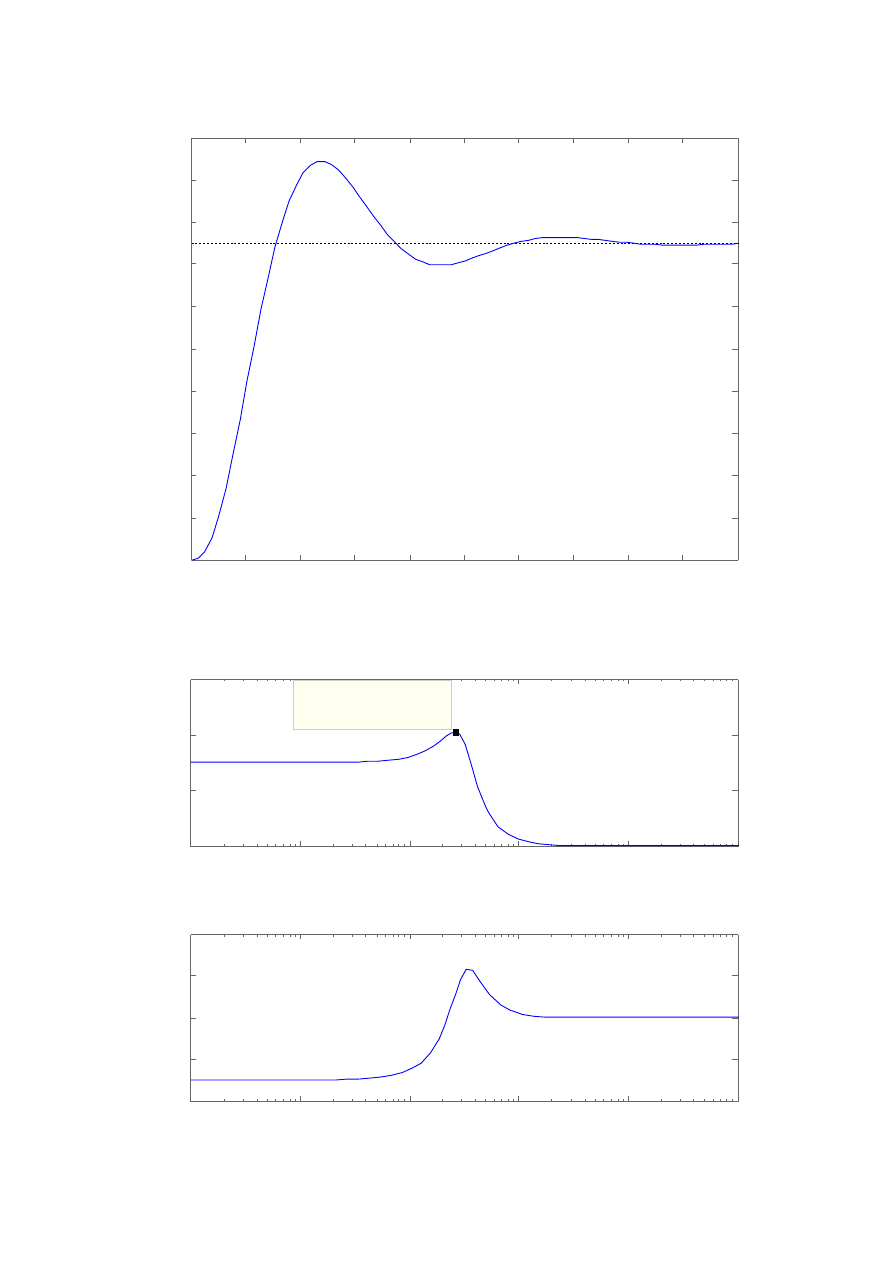
Ad 1.2.
Ad 1.3.
Kolejno: wskaźnik nadążania M(ω); wskaźnik regulacji q(ω).
0
5
1 0
1 5
2 0
2 5
3 0
3 5
4 0
4 5
5 0
0
0 . 1
0 . 2
0 . 3
0 . 4
0 . 5
0 . 6
0 . 7
0 . 8
0 . 9
1
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
2
M
a
g
n
it
u
d
e
(
a
b
s
)
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : u n t i t l e d 1
F r e q u e n c y ( r a d / s e c ) : 0 . 2 6 2
M a g n i t u d e ( a b s ) : 1 . 0 3
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
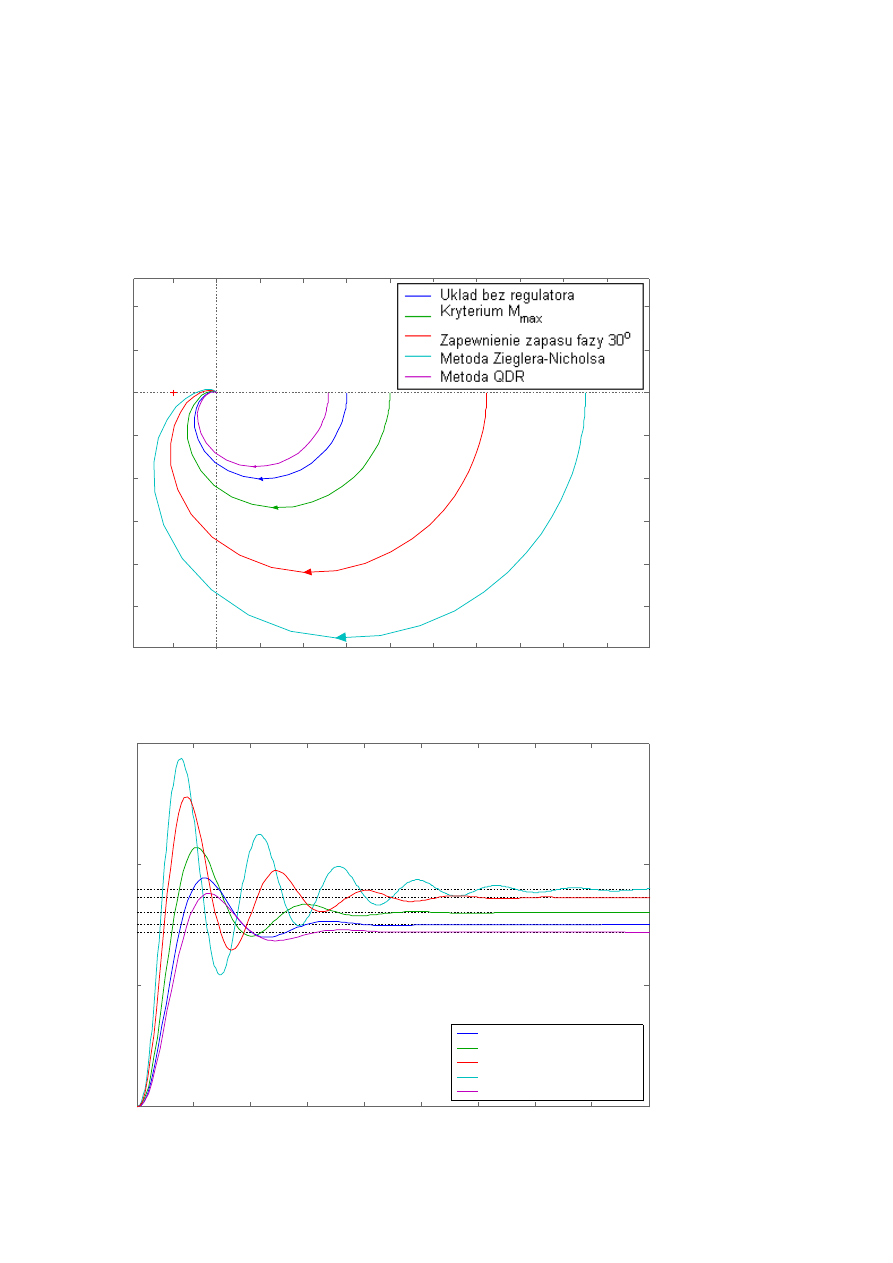
2. Wpływ nastaw regulatora P.
Ad 2.1. Nastawy regulatora:
a) Kryterium M
max
k
r
= 1.330
b) Zapewnienie zapasu fazy Δφ = π / 6
k
r
= 2.075
c) Metoda Zieglera-Nicholsa
k
r
= 2.833
d) Metoda QDR
k
r
= 0.858
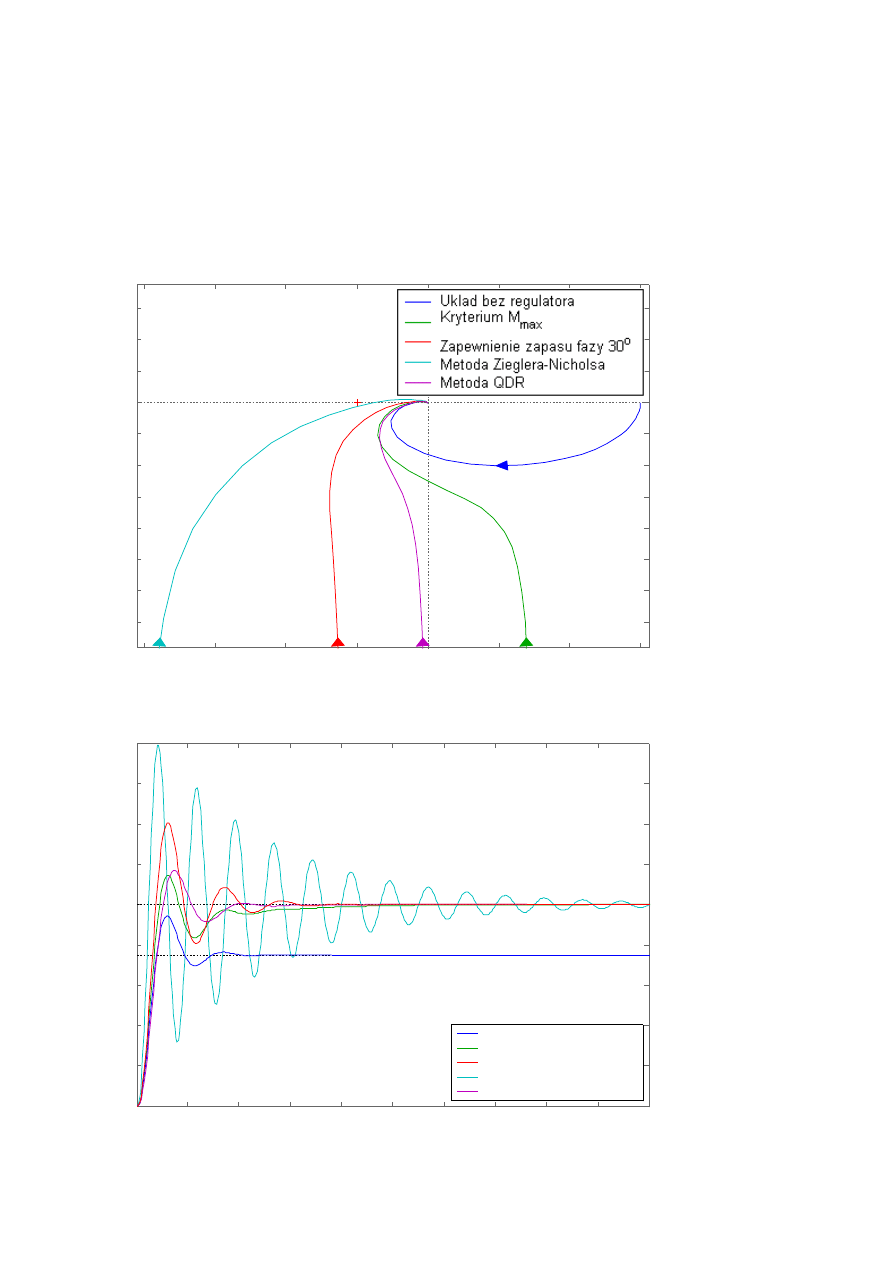
Ad 2.2.a)
Bez regulatora:
Δφ = 60
o
ΔL = 15.1
Δk = 5.69
a) Δφ = 47.1
o
ΔL = 12.6
Δk = 4.27
b) Δφ = 30.0
o
ΔL = 8.73
Δk = 2.73
c) Δφ = 19.7
o
ΔL = 6.02
Δk = 2.00
d) Δφ = 67.9
o
ΔL = 16.4
Δk = 6.61
Ad 2.2.b)
Bez regulatora:
y
ust
= 0.750
y
p
= 0.193
t
r
= 37.4 s
a) y
ust
= 0.800
y
p
= 0.270
t
r
= 42.2 s
b) y
ust
= 0.861
y
p
= 0.419
t
r
= 56.7 s
c) y
ust
= 0.894
y
p
= 0.546
t
r
= 71.6 s
d) y
ust
= 0.720
y
p
= 0.159
t
r
= 38.4 s
- 1
0
1
2
3
4
5
6
7
8
9
- 5
- 4
- 3
- 2
- 1
0
1
2
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
0
0 . 5
1
1 . 5
U k l a d b e z r e g u l a t o r a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Z i e g l e r a - N i c h o l s a
M e t o d a Q D R
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
y
ust
– wartość odpowiedzi skokowej w stanie ustalonym
y
p
– wartość przeregulowania odpowiedzi skokowej
t
r
– czas regulacji – czas po którym |y(t) - y
ust
| < y
ust
· 1%
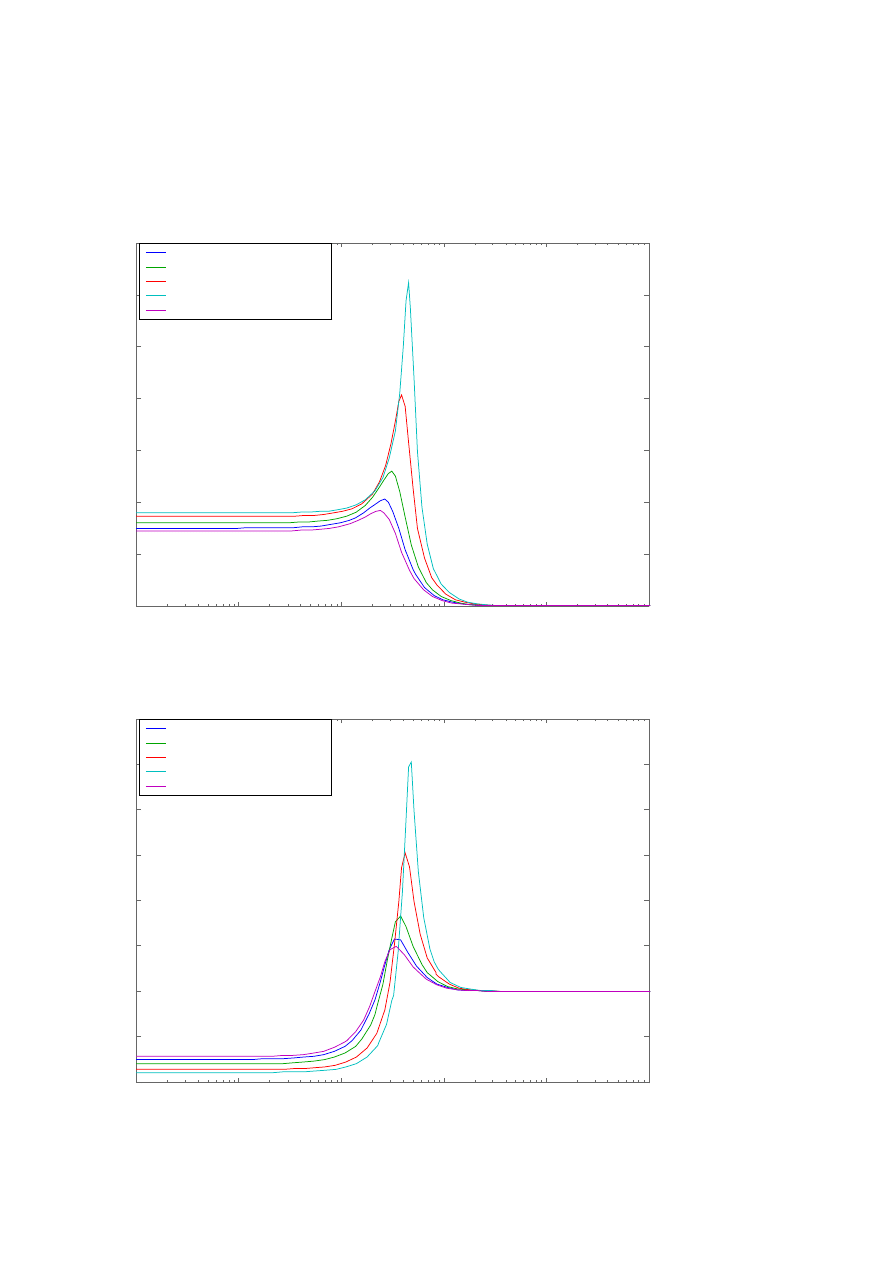
Ad 2.2.c)
Wskaźnik nadążania:
Bez regulatora:
M
max
= 1.03
ω
r
= 0.262
rad
/
s
a) M
max
= 1.30
ω
r
= 0.310
rad
/
s
b) M
max
= 2.03
ω
r
= 0.389
rad
/
s
c) M
max
= 3.11
ω
r
= 0.449
rad
/
s
d) M
max
= 0.92
ω
r
= 0.238
rad
/
s
Wskaźnik regulacji:
Bez regulatora:
q
max
= 1.58
ω
r
= 0.326
rad
/
s
a) q
max
= 1.83
ω
r
= 0.377
rad
/
s
b) q
max
= 2.52
ω
r
= 0.418
rad
/
s
c) q
max
= 3.52
ω
r
= 0.477
rad
/
s
d) q
max
= 1.49
ω
r
= 0.346
rad
/
s
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
2
2 . 5
3
3 . 5
M
a
g
n
it
u
d
e
(
a
b
s
)
U k l a d b e z r e g u l a t o r a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Z i e g l e r a - N i c h o l s a
M e t o d a Q D R
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
2
2 . 5
3
3 . 5
4
M
a
g
n
it
u
d
e
(
a
b
s
)
U k l a d b e z r e g u l a t o r a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Z i e g l e r a - N i c h o l s a
M e t o d a Q D R
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
Ad 2.3.
a) Kryterium M
max
:
●
Zapewnia spełnienie wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Uchyb regulacji stanowi 20.0% wymuszenia.
●
Przeregulowanie względne to 33,75%
●
Czas regulacji jest o 4.8 sekundy dłuższy niż w układzie bez regulatora (wynosi 42.2 s).
●
Wartość M
max
wynosi 1.3 i jest optymalna, ω
r
= 0.310
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.244
rad
/
s
.
b) Zapewnienie zapasu fazy równego 30
o
:
●
Zapewnia spełnienie wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Uchyb regulacji stanowi 13.9% wymuszenia.
●
Przeregulowanie względne to 48.66%
●
Czas regulacji jest o 19.3 sekundy dłuższy niż w układzie bez regulatora (wynosi 56.7 s).
●
Wartość M
max
wynosi 2.03 i jest zbyt duża, ω
r
= 0.389
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.285
rad
/
s
.
c) Metoda Zieglera-Nicholsa:
●
Nie zapewnia spełnienia wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Uchyb regulacji stanowi 10.6% wymuszenia.
●
Przeregulowanie względne to 61.07%
●
Czas regulacji jest o 34.2 sekundy dłuższy niż w układzie bez regulatora (wynosi 71.6 s).
●
Wartość M
max
wynosi 3.11 i jest zbyt duża, ω
r
= 0.449
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.323
rad
/
s
.
d) Metoda QDR:
●
Zapewnia spełnienie wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji – najwyższe wartości ponieważ nastawa wzmocnienia jest
najmniejsza.
●
Uchyb regulacji stanowi 28.0% wymuszenia.
●
Przeregulowanie względne to 22.08%
●
Czas regulacji jest o 1.0 sekundy dłuższy niż w układzie bez regulatora (wynosi 38.4 s).
●
Wartość M
max
wynosi 0.92 i jest zbyt mała, ω
r
= 0.238
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.214
rad
/
s
.
Wybór optymalnej nastawy:
k
r
= 1.330 (z kryterium M
max
).
Uzasadnienie:
Nastawa wynikająca z metody Zieglera-Nicholsa jest nieodpowiednia ze względu na nie
spełnienie wymagań związanych z wartościami zapasu fazy i wzmocnienia. Dodatkowo wartość
przeregulowania jest zbyt duża i mogłaby w pewnych warunkach doprowadzić do zniszczenia
obiektu. Czas regulacji jest zbyt długi (niemalże dwa razy większy niż w przypadku układu bez
regulatora).
Nastawa wynikająca z metody QDR jest nieodpowiednia ze względu na duży uchyb
regulacji w stanie ustalonym oraz najniższą wartość pulsacji dla której zakłócenia są tłumione.
Nastawa wynikająca z zapewnienia żądanego zapasu fazy została odrzucona ze względu
na zbyt wielkie przeregulowanie (prawie 50%), co jest równoważne zbyt wysokiej wartości M
max
.
Wadą nastawy wynikającej z kryterium M
max
jest stosunkowo duża wartość uchybu w
stanie ustalonym. W przypadku sterowania procesami w których dokładność musiałaby być
większa należałoby wykorzystać nastawy zapewniające ją (nastawy wynikające z zapasu fazy bądź
Zieglera-Nicholsa). Jednakże w procesach w których wymagana jest stosunkowo duża dokładność
stosuje się regulatory PI bądź PID.
3. Wpływ nastaw regulatora PI.
Ad 3.1. Nastawy regulatora:
a) Kryterium M
max
k
r
= 1.070 T
c
= 25,000
b) Zapewnienie zapasu fazy Δφ = π / 6
k
r
= 1.120 T
c
= 10,000
c) Metoda Zieglera-Nicholsa
k
r
= 2.550 T
c
= 8,925
d) Metoda QDR
k
r
= 0.772 T
c
= 13,402
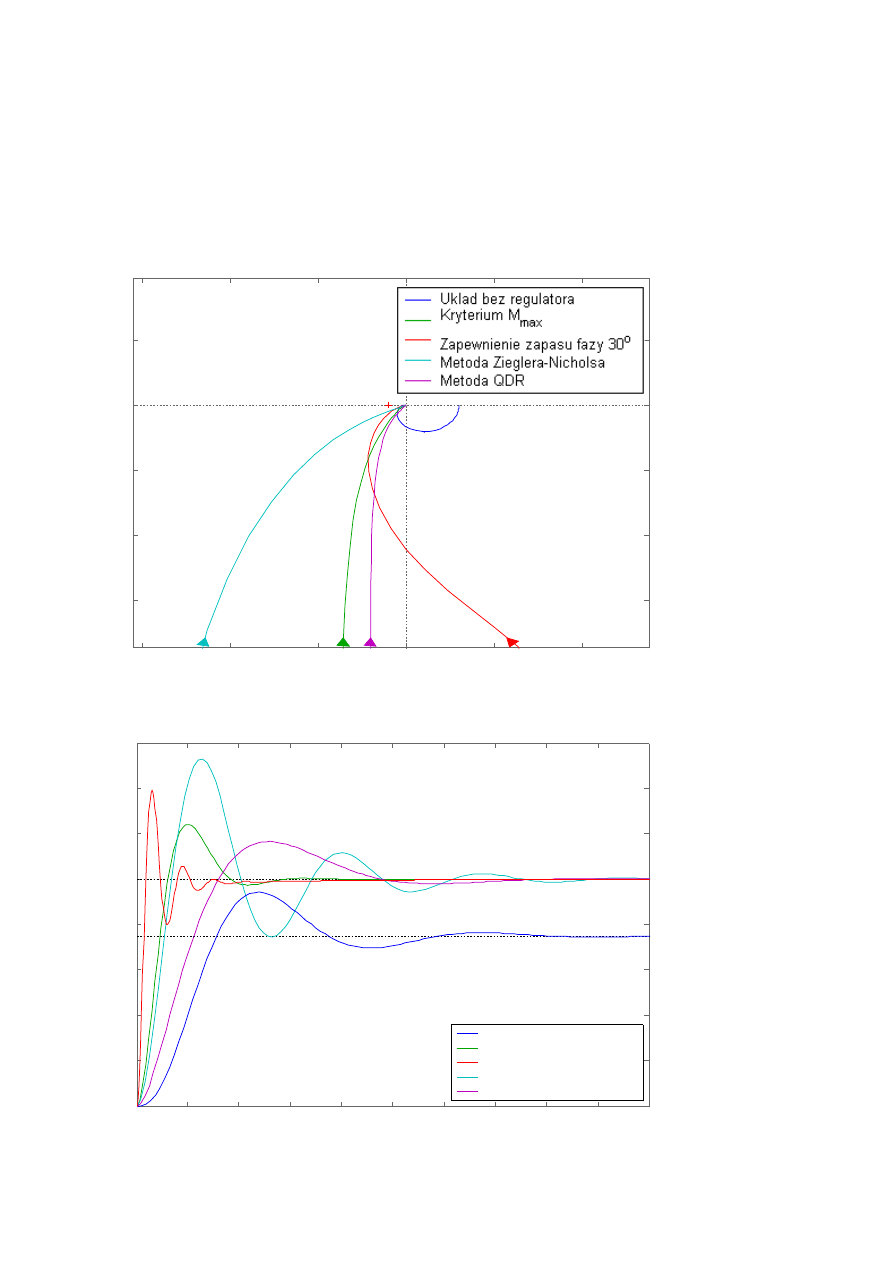
Ad 3.2.a)
Bez regulatora:
Δφ = 60
o
ΔL = 15.1
Δk = 5.69
a) Δφ = 46.5
o
ΔL = 13.1
Δk = 4.52
b) Δφ = 30.0
o
ΔL = 10.2
Δk = 3.24
c) Δφ = 6.56
o
ΔL = 2.50
Δk = 1.33
d) Δφ = 48.7
o
ΔL = 14.6
Δk = 5.37
Ad 3.2.b)
Bez regulatora:
y
ust
= 0.750
y
p
= 0.193
t
r
= 37.4 s
a) y
ust
= 1.000
y
p
= 0.150
t
r
= 84.7 s
b) y
ust
= 1.000
y
p
= 0.410
t
r
= 60.1 s
c) y
ust
= 1.000
y
p
= 0.790
t
r
= 213 s
d) y
ust
= 1.000
y
p
= 0.170
t
r
= 36.6 s
- 4
- 3
- 2
- 1
0
1
2
3
- 7
- 6
- 5
- 4
- 3
- 2
- 1
0
1
2
3
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
2 0
4 0
6 0
8 0
1 0 0
1 2 0
1 4 0
1 6 0
1 8 0
2 0 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
1 . 6
1 . 8
U k l a d b e z r e g u l a t o r a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Z i e g l e r a - N i c h o l s a
M e t o d a Q D R
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
y
ust
– wartość odpowiedzi skokowej w stanie ustalonym
y
p
– wartość przeregulowania odpowiedzi skokowej
t
r
– czas regulacji – czas po którym |y(t) - y
ust
| < y
ust
· 1%
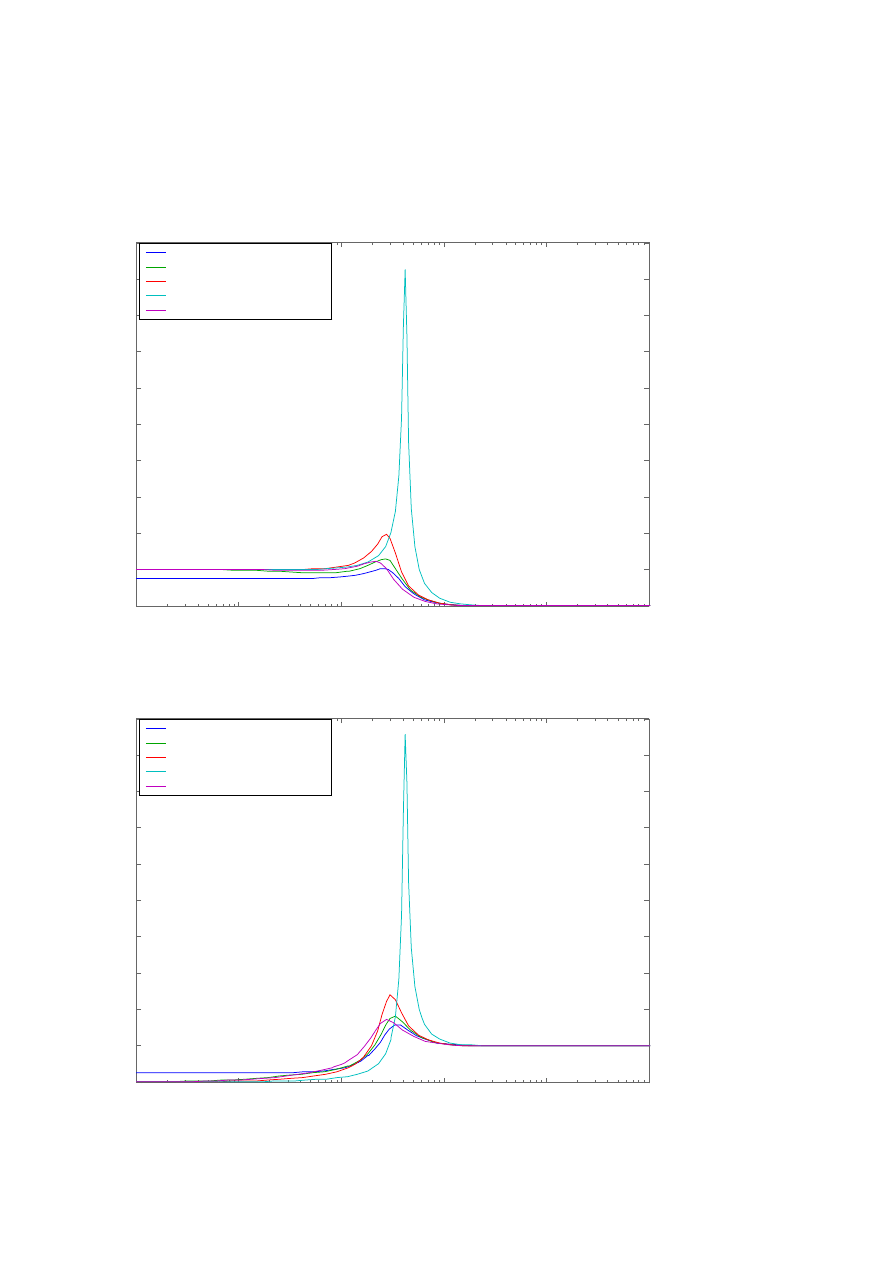
Ad 3.2.c)
Wskaźnik nadążania:
Bez regulatora:
M
max
= 1.03
ω
r
= 0.262
rad
/
s
a) M
max
= 1.30
ω
r
= 0.268
rad
/
s
b) M
max
= 1.98
ω
r
= 0.274
rad
/
s
c) M
max
= 9.26
ω
r
= 0.417
rad
/
s
d) M
max
= 1.23
ω
r
= 0.215
rad
/
s
Wskaźnik regulacji:
Bez regulatora:
q
max
= 1.58
ω
r
= 0.326
rad
/
s
a) q
max
= 1.81
ω
r
= 0.338
rad
/
s
b) q
max
= 2.41
ω
r
= 0.299
rad
/
s
c) q
max
= 9.59
ω
r
= 0.417
rad
/
s
d) q
max
= 1.72
ω
r
= 0.275
rad
/
s
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
1
2
3
4
5
6
7
8
9
1 0
M
a
g
n
it
u
d
e
(
a
b
s
)
U k l a d b e z r e g u l a t o r a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Z i e g l e r a - N i c h o l s a
M e t o d a Q D R
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
1
2
3
4
5
6
7
8
9
1 0
M
a
g
n
it
u
d
e
(
a
b
s
)
U k l a d b e z r e g u l a t o r a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Z i e g l e r a - N i c h o l s a
M e t o d a Q D R
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
Ad 3.3.
a) Kryterium M
max
:
●
Zapewnia spełnienie wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Zerowy uchyb regulacji dla wymuszenia skokowego.
●
Przeregulowanie względne to 15%
●
Czas regulacji jest o 47.3 sekundy dłuższy niż w układzie bez regulatora (wynosi 84.7 s).
●
Wartość M
max
wynosi 1.3 i jest optymalna, ω
r
= 0.268
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.209
rad
/
s
.
b) Zapewnienie zapasu fazy równego 30
o
:
●
Zapewnia spełnienie wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Zerowy uchyb regulacji dla wymuszenia skokowego.
●
Przeregulowanie względne to 41%
●
Czas regulacji jest o 22.7 sekundy dłuższy niż w układzie bez regulatora (wynosi 60.1 s).
●
Wartość M
max
wynosi 1.98 i jest zbyt duża, ω
r
= 0.274
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.196
rad
/
s
.
c) Metoda Zieglera-Nicholsa:
●
Nie zapewnia spełnienia wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Zerowy uchyb regulacji dla wymuszenia skokowego.
●
Przeregulowanie względne to 79%
●
Czas regulacji jest o 175.6 sekundy dłuższy niż w układzie bez regulatora (wynosi 213 s).
●
Wartość M
max
wynosi 9.26 i jest zbyt duża, ω
r
= 0.417
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.288
rad
/
s
.
d) Metoda QDR:
●
Zapewnia spełnienie wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Zerowy uchyb regulacji dla wymuszenia skokowego.
●
Przeregulowanie względne to 17%
●
Czas regulacji jest o 0.8 sekundy krótszy niż w układzie bez regulatora (wynosi 36.6 s).
●
Wartość M
max
wynosi 1.23 i jest bliska optymalnej, ω
r
= 0.215
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.170
rad
/
s
.
Wybór optymalnej nastawy:
k
r
= 0.772 T
c
= 13,402 (z metody QDR).
Uzasadnienie:
Nastawa wynikająca z metody Zieglera-Nicholsa jest nieodpowiednia ze względu na nie
spełnienie wymagań związanych z wartościami zapasu fazy i wzmocnienia. Dodatkowo wartość
przeregulowania jest zbyt duża i mogłaby w pewnych warunkach doprowadzić do zniszczenia
obiektu. Czas regulacji jest zbyt długi (ponad pięć razy większy niż w przypadku układu bez
regulatora).
Nastawa wynikająca z kryterium M
max
została odrzucona z powodu długiego czasu
regulacji.
Nastawa wynikająca z zapewnienia żądanego zapasu fazy została odrzucona ze względu
na zbyt wielkie przeregulowanie (ponad 40%), co jest równoważne zbyt wysokiej wartości M
max
.
Nastawa wynikająca z metody QDR jest najkorzystniejsza ze względu na czas regulacji,
niezbyt wielkie przeregulowanie, wartości M
max
oraz q
max
. Jej największą zaletą są stosunkowo duże
zapasy fazy oraz wzmocnienia. Niestety nastawa ta charakteryzuje najgorszą charakterystyką
tłumienia zakłóceń. Z tego powodu przy tak dobranej nastawie układ nie powinien być narażony na
działanie zakłóceń o dużej amplitudzie i częstotliwości. Gdy warunki wymagałyby lepszych
własności układu ze względu na tłumienie zakłóceń lepszą nastawą byłaby ta wynikająca z zapasu
fazy.
4. Wpływ nastaw regulatora PID.
Ad 4.1. Nastawy regulatora:
a) Kryterium M
max
k
r
= 3.700 T
c
= 10,000 T
d
= 2,000
b) Zapewnienie zapasu fazy Δφ = π / 6
k
r
= 11.500 T
c
= 20,000 T
d
= 5,000
c) Metoda Zieglera-Nicholsa
k
r
= 3.400 T
c
= 5,250 T
d
= 1,260
d) Metoda QDR
k
r
= 1.029 T
c
= 8,049 T
d
= 2,012
Ad 4.2.a)
Bez regulatora:
Δφ = 60
o
ΔL = 15.1
Δk = 5.69
a) Δφ = 46.7
o
ΔL = ∞
Δk = ∞
b) Δφ = 30.0
o
ΔL = ∞
Δk = ∞
c) Δφ = 24.3
o
ΔL = ∞
Δk = ∞
d) Δφ = 53.8
o
ΔL = ∞
Δk = ∞
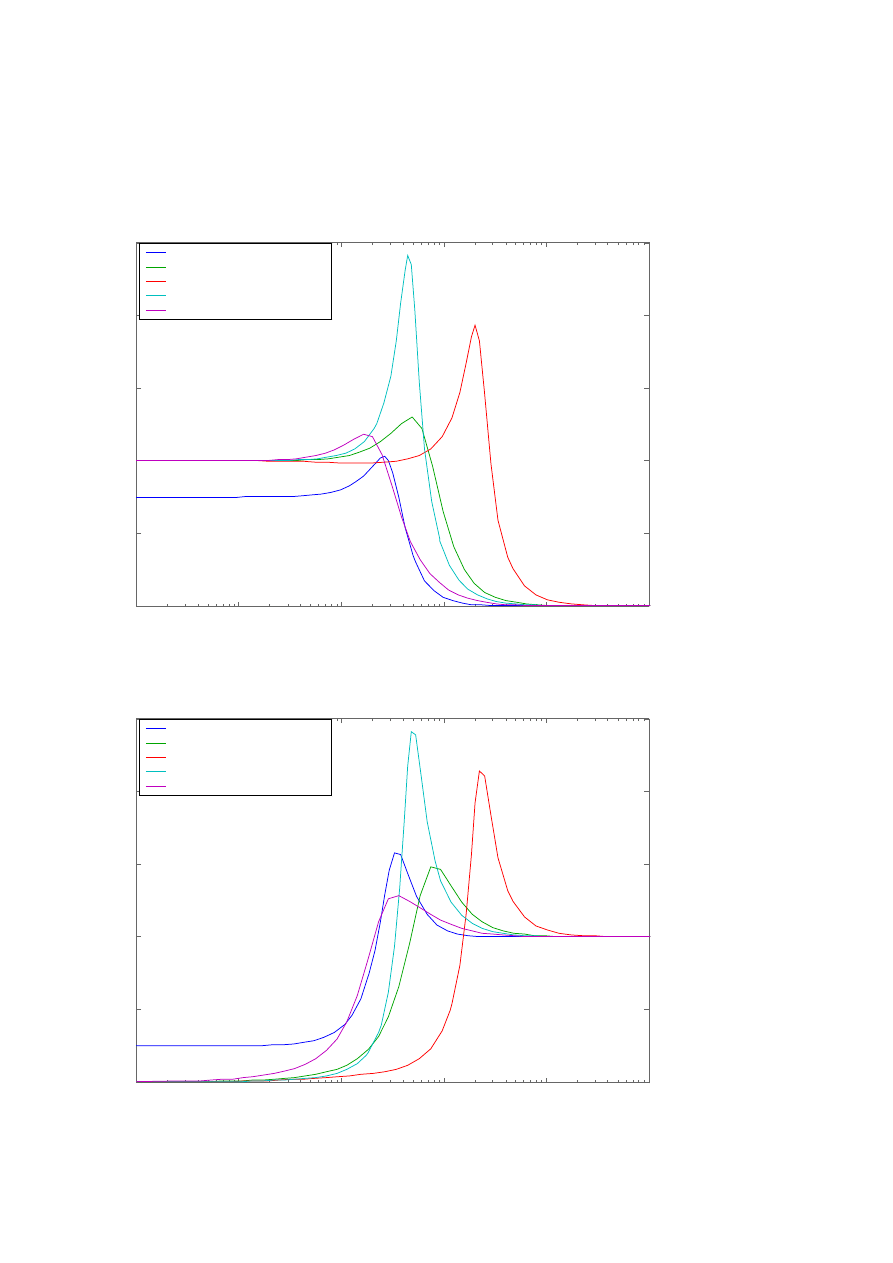
Ad 4.2.b)
Bez regulatora:
y
ust
= 0.750
y
p
= 0.193
t
r
= 37.4 s
a) y
ust
= 1.000
y
p
= 0.240
t
r
= 13.1 s
b) y
ust
= 1.000
y
p
= 0.390
t
r
= 13.0 s
c) y
ust
= 1.000
y
p
= 0.530
t
r
= 41.9 s
d) y
ust
= 1.000
y
p
= 0.170
t
r
= 34.4 s
- 1 5
- 1 0
- 5
0
5
1 0
- 1 5
- 1 0
- 5
0
5
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
5
1 0
1 5
2 0
2 5
3 0
3 5
4 0
4 5
5 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
1 . 6
U k l a d b e z r e g u l a t o r a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Z i e g l e r a - N i c h o l s a
M e t o d a Q D R
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
y
ust
– wartość odpowiedzi skokowej w stanie ustalonym
y
p
– wartość przeregulowania odpowiedzi skokowej
t
r
– czas regulacji – czas po którym |y(t) - y
ust
| < y
ust
· 1%
Ad 4.2.c)
Wskaźnik nadążania:
Bez regulatora:
M
max
= 1.03
ω
r
= 0.262
rad
/
s
a) M
max
= 1.30
ω
r
= 0.485
rad
/
s
b) M
max
= 1.93
ω
r
= 2.02
rad
/
s
c) M
max
= 2.42
ω
r
= 0.444
rad
/
s
d) M
max
= 1.18
ω
r
= 0.163
rad
/
s
Wskaźnik regulacji:
Bez regulatora:
q
max
= 1.58
ω
r
= 0.326
rad
/
s
a) q
max
= 1.48
ω
r
= 0.737
rad
/
s
b) q
max
= 2.14
ω
r
= 2.21
rad
/
s
c) q
max
= 2.41
ω
r
= 0.480
rad
/
s
d) q
max
= 1.28
ω
r
= 0.365
rad
/
s
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
2
2 . 5
M
a
g
n
it
u
d
e
(
a
b
s
)
U k l a d b e z r e g u l a t o r a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Z i e g l e r a - N i c h o l s a
M e t o d a Q D R
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
2
2 . 5
M
a
g
n
it
u
d
e
(
a
b
s
)
U k l a d b e z r e g u l a t o r a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Z i e g l e r a - N i c h o l s a
M e t o d a Q D R
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
Ad 4.3.
a) Kryterium M
max
:
●
Zapewnia spełnienie wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Zerowy uchyb regulacji dla wymuszenia skokowego.
●
Przeregulowanie względne to 24%
●
Czas regulacji jest o 24.3 sekundy krótszy niż w układzie bez regulatora (wynosi 13.1 s).
●
Wartość M
max
wynosi 1.3 i jest optymalna, ω
r
= 0.485
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.479
rad
/
s
.
b) Zapewnienie zapasu fazy równego 30
o
:
●
Zapewnia spełnienie wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Zerowy uchyb regulacji dla wymuszenia skokowego.
●
Przeregulowanie względne to 39%
●
Czas regulacji jest o 24.4 sekundy krótszy niż w układzie bez regulatora (wynosi 13.0 s).
●
Wartość M
max
wynosi 1.93 i jest zbyt duża, ω
r
= 2.02
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 1.55
rad
/
s
.
c) Metoda Zieglera-Nicholsa:
●
Nie zapewnia spełnienia wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Zerowy uchyb regulacji dla wymuszenia skokowego.
●
Przeregulowanie względne to 53%
●
Czas regulacji jest o 4.5 sekundy dłuższy niż w układzie bez regulatora (wynosi 41.9 s).
●
Wartość M
max
wynosi 2.42 i jest zbyt duża, ω
r
= 0.444
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.339
rad
/
s
.
d) Metoda QDR:
●
Zapewnia spełnienie wymagań związanych z zapasem fazy i zapasem wzmocnienia
stawianych układowi regulacji.
●
Zerowy uchyb regulacji dla wymuszenia skokowego.
●
Przeregulowanie względne to 17%
●
Czas regulacji jest o 3.0 sekundy krótszy niż w układzie bez regulatora (wynosi 34.4 s).
●
Wartość M
max
wynosi 1.18 i jest bliska optymalnej, ω
r
= 0.163
rad
/
s
.
●
Zdolność tłumienia zakłóceń o pulsacji mniejszej od 0.209
rad
/
s
.
Wybór optymalnej nastawy:
k
r
= 11.500 T
c
= 20,000 T
d
= 5,000 (z Δφ = 30
o
).
Uzasadnienie:
Nastawa wynikająca z metody Zieglera-Nicholsa jest nieodpowiednia ze względu na nie
spełnienie wymagań związanych z wartościami zapasu fazy i wzmocnienia. Dodatkowo wartość
przeregulowania jest zbyt duża i mogłaby w pewnych warunkach doprowadzić do zniszczenia
obiektu. Czas regulacji jest zbyt długi.
Nastawa wynikająca z metody QDR została odrzucona ze względu na zbyt długi czas
regulacji i najgorsze własności tłumienia zakłóceń w paśmie podrezonansowym.
Nastawa wynikająca z kryterium M
max
jest stosunkowo dobra (czas regulacji, wielość
przeregulowania) jednakże za optymalną nastawę przyjęto tą wynikającą z żądania zapasu fazy
równego 30
o
. Zdecydowało o tym wyborze szerokie pasmo tłumienia zakłóceń pomimo większego
przeregulowania na odpowiedź skokową.
5. Realizacja zadań części drugiej (B):
1. Badanie własności obiektu regulacji:
Ad 1.1.
Δφ = 44.9
o
ΔL = 5.36
Δk = 1.85
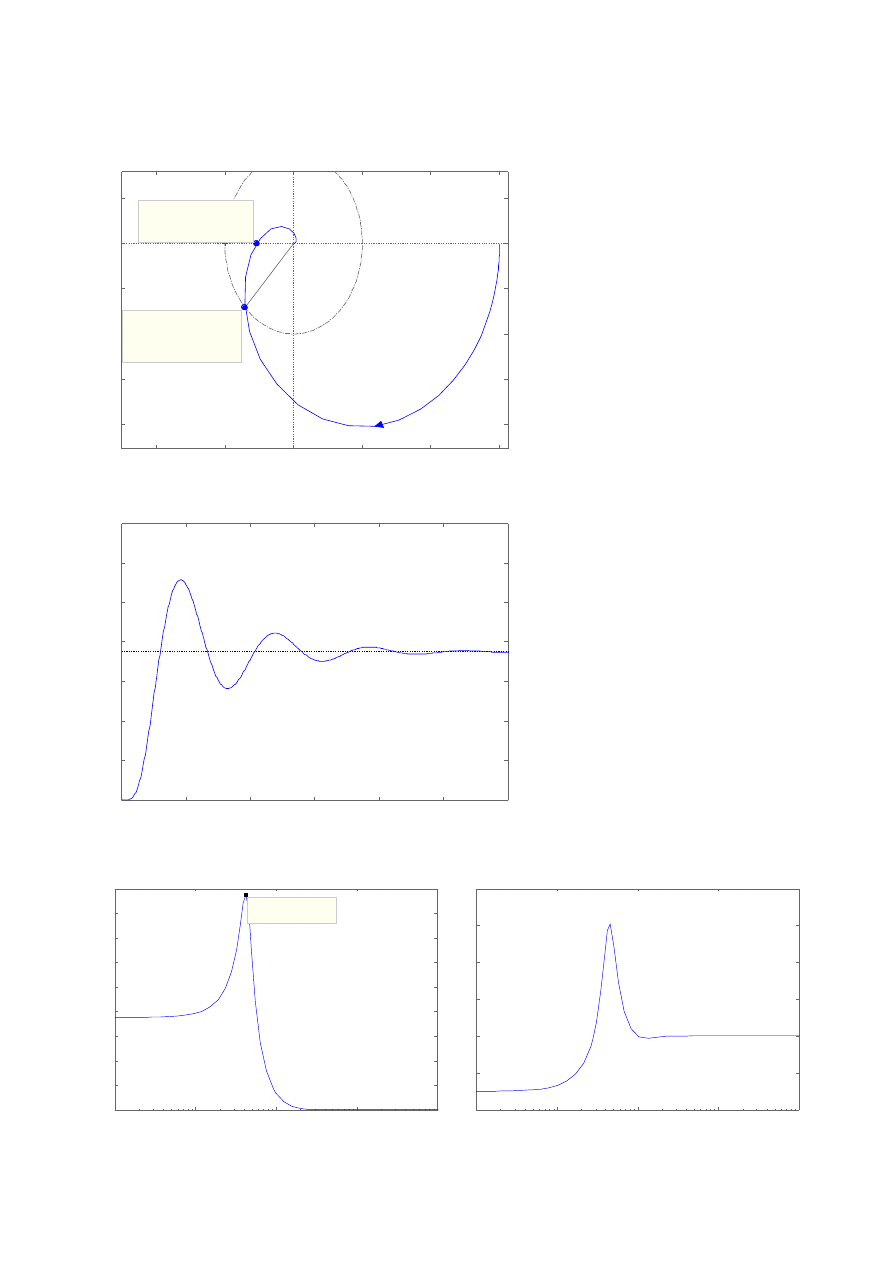
Ad 1.2.
Ad 1.3.
Wskaźnik nadążania M(ω):
Wskaźnik regulacji q(ω):
- 2
- 1
0
1
2
3
- 2
- 1 . 5
- 1
- 0 . 5
0
0 . 5
S y s t e m : K
G a i n M a r g i n ( d B ) : 5 . 3 6
A t f r e q u e n c y ( r a d / s e c ) : 0 . 5 1
C l o s e d L o o p S t a b l e ? Y e s
S y s t e m : K
P h a s e M a r g i n ( d e g ) : 4 4 . 9
D e l a y M a r g i n ( s e c ) : 2 . 4 4
A t f r e q u e n c y ( r a d / s e c ) : 0 . 3 2 1
C l o s e d L o o p S t a b l e ? Y e s
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
0
1 0
2 0
3 0
4 0
5 0
6 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
1 . 6
1 . 8
M
a
g
n
it
u
d
e
(
a
b
s
)
S y s t e m : u n t i t l e d 1
F r e q u e n c y ( r a d / s e c ) : 0 . 4 2
M a g n i t u d e ( a b s ) : 1 . 7 5
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
1 0
- 2
1 0
- 1
1 0
0
1 0
1
1 0
2
0
0 . 5
1
1 . 5
2
2 . 5
3
M
a
g
n
it
u
d
e
(
a
b
s
)
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
2. Porównanie regulatorów P, PI, PID – nastawy według metody Zieglera-Nicholsa.
a) Regulator P:
k
r
= 0.927
b) Regulator PI:
k
r
= 0.834 T
c
= 10,54
c) Regulator PID:
k
r
= 1.112 T
c
= 6,200 T
d
= 1,488
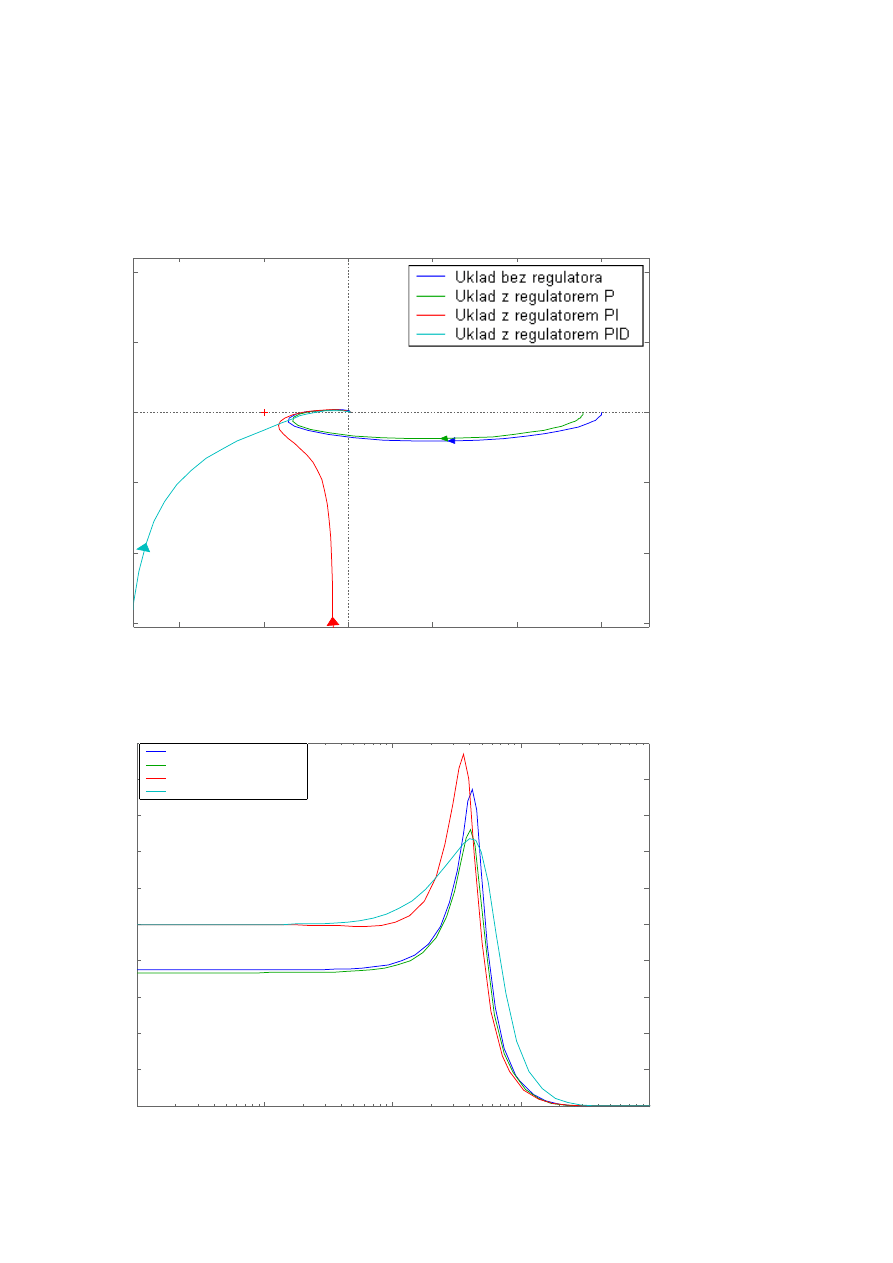
Ad 2.1.a)
Bez regulatora:
Δφ = 44.9
o
ΔL = 5.36
Δk = 1.85
Z regulatorem P:
Δφ = 50.7
o
ΔL = 6.02
Δk = 2.00
Z regulatorem PI:
Δφ = 36.4
o
ΔL = 5.31
Δk = 1.84
Z regulatorem PID:
Δφ = 40.5
o
ΔL = 7.37
Δk = 2.34
Ad 2.1.b)
Wskaźnik nadążania:
Bez regulatora:
M
max
= 1.75
ω
r
= 0.420
Z regulatorem P:
M
max
= 1.52
ω
r
= 0.407
Z regulatorem PI:
M
max
= 1.94
ω
r
= 0.357
Z regulatorem PID:
M
max
= 1.47
ω
r
= 0.402
- 2
- 1
0
1
2
3
- 1 5
- 1 0
- 5
0
5
1 0
N y q u i s t D i a g r a m
R e a l A x i s
Im
a
g
in
a
ry
A
x
is
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
1 . 6
1 . 8
2
M
a
g
n
it
u
d
e
(
a
b
s
)
U k l a d b e z r e g u l a t o r a
U k l a d z r e g u l a t o r e m P
U k l a d z r e g u l a t o r e m P I
U k l a d z r e g u l a t o r e m P I D
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
Wskaźnik regulacji:
Bez regulatora:
q
max
= 2.52
ω
r
= 0.455
Z regulatorem P:
q
max
= 2.31
ω
r
= 0.444
Z regulatorem PI:
q
max
= 2.66
ω
r
= 0.390
Z regulatorem PID:
q
max
= 2.07
ω
r
= 0.546
Jeżeli obiekt regulacji można w dostatecznym stopniu aproksymować obiektem o
transmitancji będącej iloczynem opóźnienia, wzmocnienia i inercji pierwszego rzędu (jak w
przykładzie) wówczas wpływ typu regulatora z nastawami dobranymi przy pomocy metody
Zieglera-Nicholsa jest następujący (odnośnie zapasów stabilności i wskaźników
częstotliwościowych):
●
Zapas wzmocnienia wynosi około Δk = 2 (około 6 dB) dla wszystkich typów regulatorów.
Zapas ten równy jest 2 dla regulatora typu P – wynika to bezpośrednio z zastosowanej
metody.
●
Zapas fazy jest wynikiem ustawienia danego zapasu wzmocnienia w układzie regulacji.
●
Wartość maksymalnego modułu jest najniższa dla układu z regulatorem PID z czego można
wnioskować że w układzie tym będą występować najmniejsze oscylacje i przeregulowanie.
W układzie z regulatorem PI mamy sytuację odwrotną, to znaczy największą wartość
maksymalnego modułu.
●
Częstotliwość rezonansowa charakterystyk nadążania jest najwyższa dla układu z
regulatorem PID a najniższa dla układu z regulatorem PI. Zaletom zastosowania regulatora
P jest najszersze pasmo nadążania.
●
Z przebiegów wskaźnika nadążania można wnioskować o zerowym uchybie regulacji w
stanie ustalonym dla układów z regulatorami PI i PID. Dla układu z regulatorem P uchyb ten
nie jest zerowy.
●
Wnioskiem z przebiegu wskaźników regulacji jest fakt całkowitego tłumienia stałych w
czasie zakłóceń dla układów z regulatorami PI i PID. Przy zastosowaniu regulatora
proporcjonalnego zakłócenia nie są całkowicie tłumione w całym zakresie ich
częstotliwości.
●
Najszerszym pasmem tłumienia zakłóceń charakteryzują się układy z regulatorami P i PID.
Zakres tłumienia zakłóceń układu z regulatorem PI jest nieco mniejszy.
1 0
- 3
1 0
- 2
1 0
- 1
1 0
0
1 0
1
0
0 . 5
1
1 . 5
2
2 . 5
3
M
a
g
n
it
u
d
e
(
a
b
s
)
U k l a d b e z r e g u l a t o r a
U k l a d z r e g u l a t o r e m P
U k l a d z r e g u l a t o r e m P I
U k l a d z r e g u l a t o r e m P I D
B o d e D i a g r a m
F r e q u e n c y ( r a d / s e c )
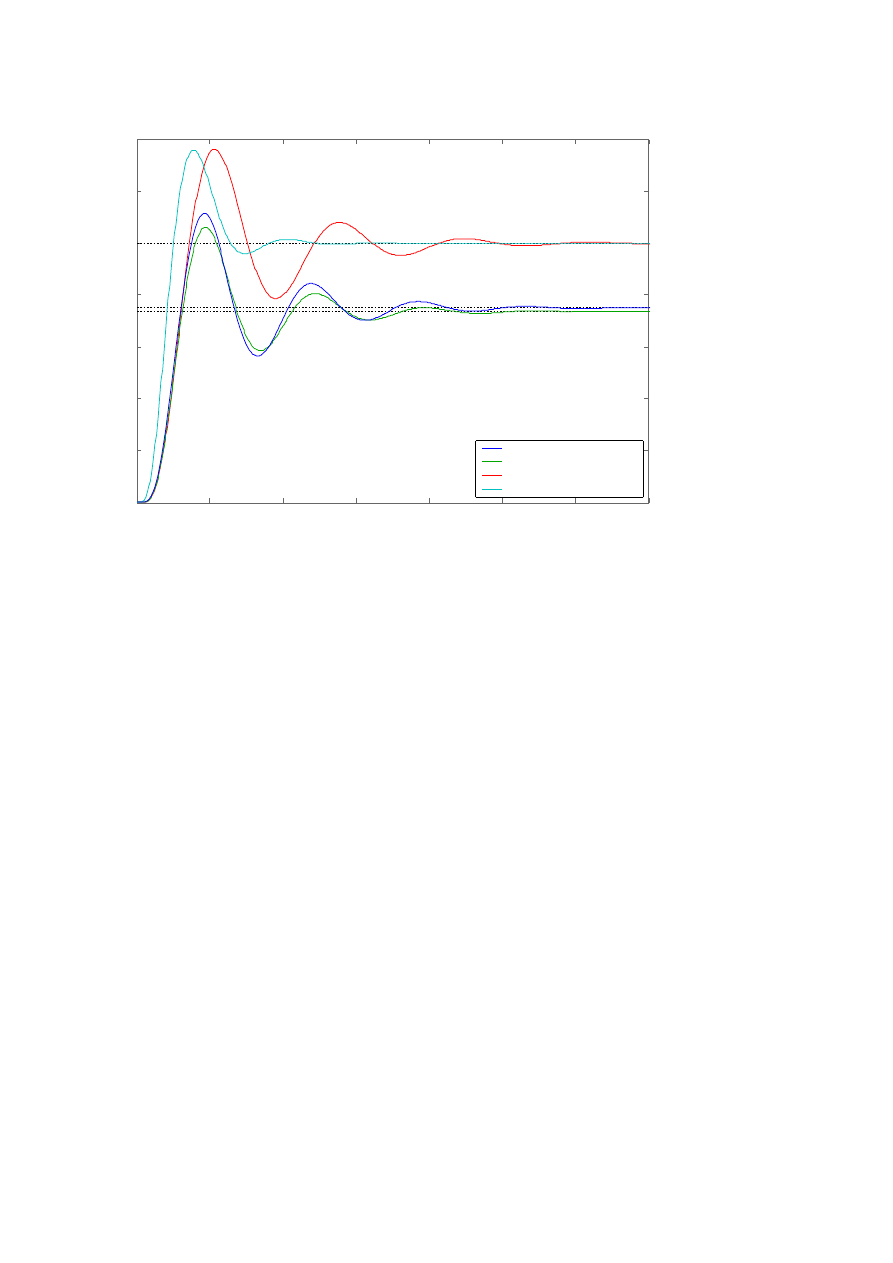
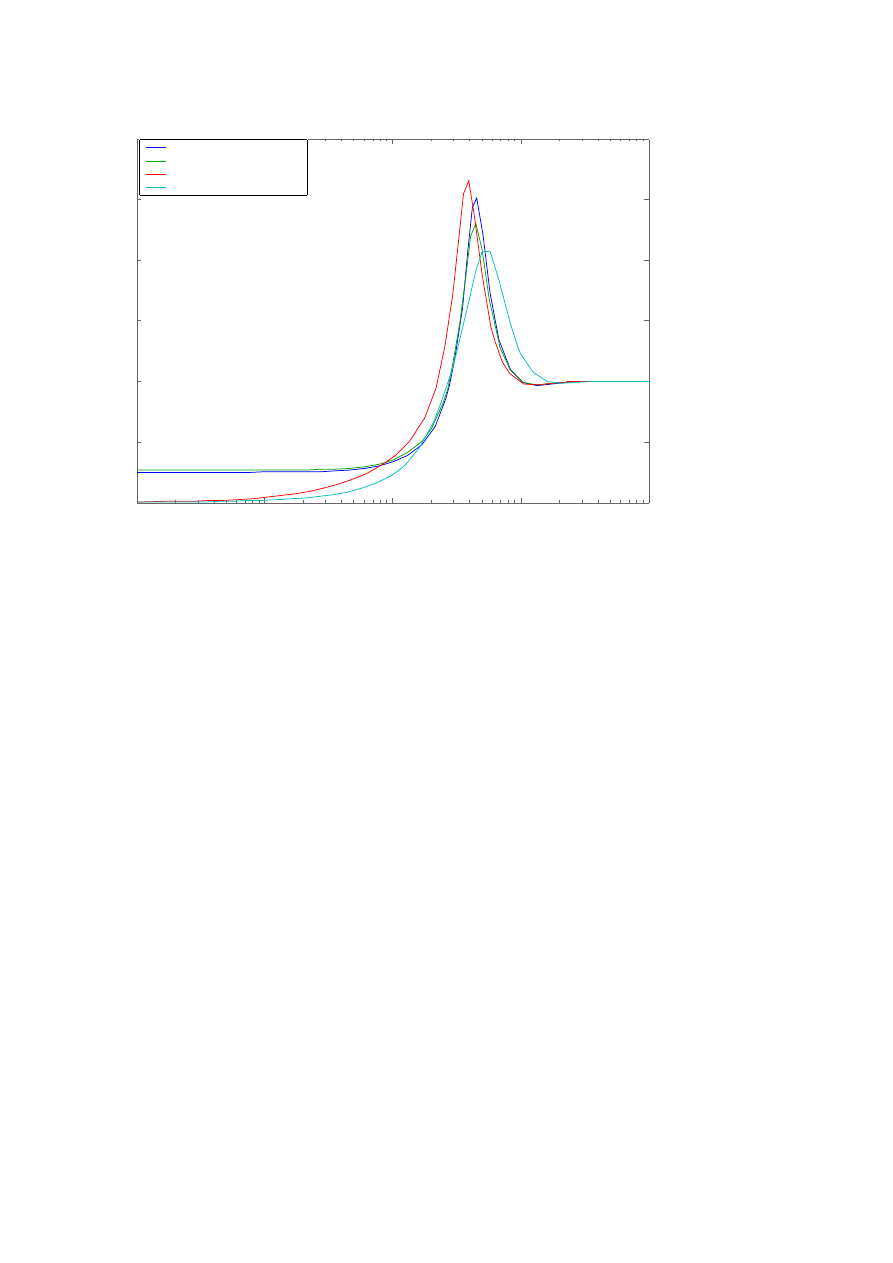
Ad 2.2.
Bez regulatora:
y
ust
= 0.751
y
p
= 0.359
t
r
= 48.4 s
Z regulatorem P:
y
ust
= 0.736
y
p
= 0.324
t
r
= 41.9 s
Z regulatorem PI:
y
ust
= 1.000
y
p
= 0.360
t
r
= 54.3 s
Z regulatorem PID:
y
ust
= 1.000
y
p
= 0.360
t
r
= 22.3 s
y
ust
– wartość odpowiedzi skokowej w stanie ustalonym
y
p
– wartość przeregulowania odpowiedzi skokowej
t
r
– czas regulacji – czas po którym |y(t) - y
ust
| < y
ust
· 1%
Część proporcjonalna (regulator P):
Wiąże się bezpośrednio z ustawieniem w układzie zapasu wzmocnienia Δk = 2.
Konsekwencje tej zmiany powodują zmianę: wartości uchybu w stanie ustalonym, wartości
przeregulowania, czasu regulacji, czasu zanikania oscylacji. W pewnym stopniu (zależnym od
dopasowania do układu inercyjnego I rzędu z opóźnieniem) przebieg regulacji jest normalizowany.
Część całkująca (regulator PI):
Całka wprowadza do układu astatyzm I rzędu (zerowy uchyb regulacji w stanie
ustalonym dla wymuszenia skokowego). Zwiększa się oscylacyjność układu i czas regulacji.
Część różniczkująca (regulator PID):
Znacząco zmniejsza czas regulacji. Zwiększa szybkość reakcji układu na wymuszenie
sterujące. Oscylacje są bardzo szybko tłumione.
Najkorzystniejsza regulacja zachodzi przy zastosowaniu regulatora PID.
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
U k l a d b e z r e g u l a t o r a
U k l a d z r e g u l a t o r e m P
U k l a d z r e g u l a t o r e m P I
U k l a d z r e g u l a t o r e m P I D
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
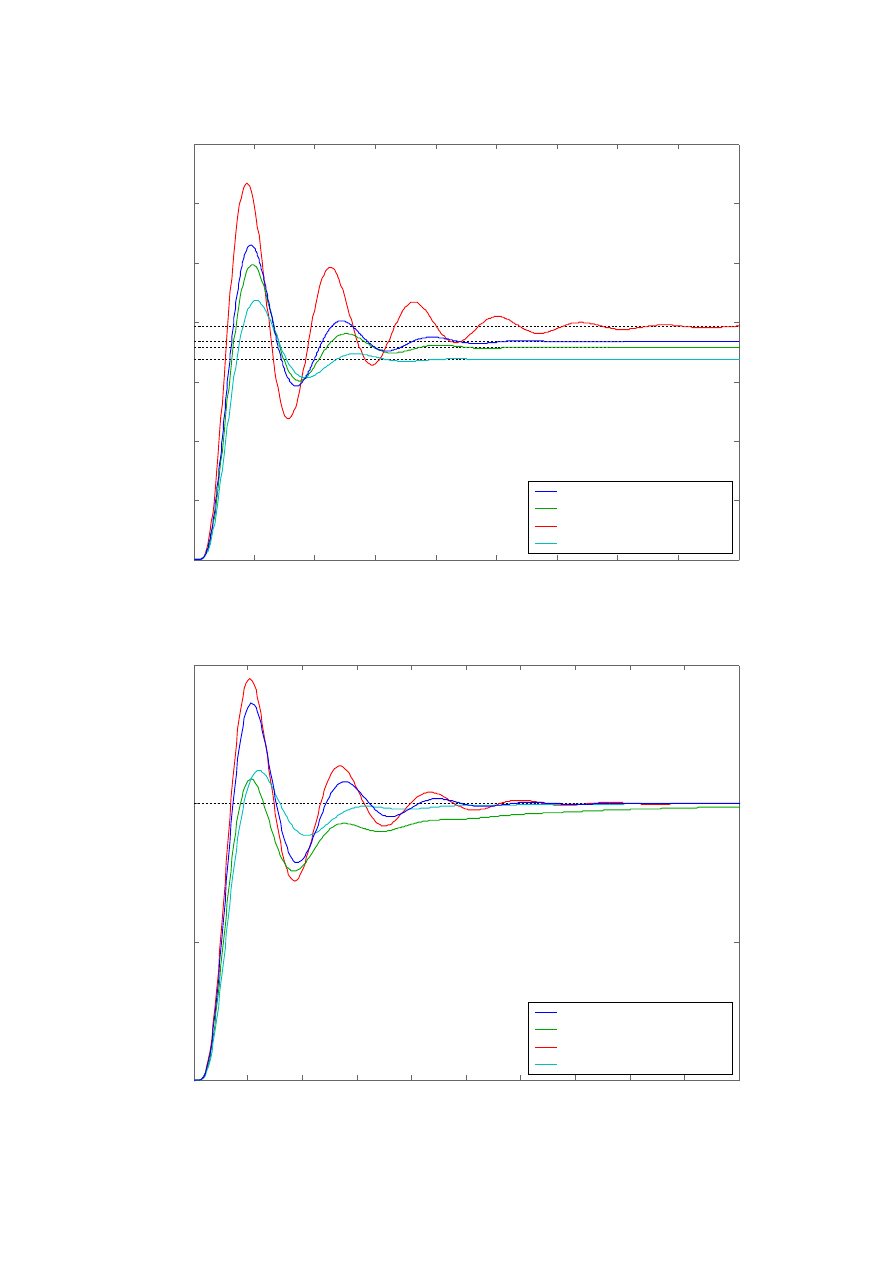
Ad 2.3.a) Regulatory P:
Ad 2.3.b) Regulatory PI:
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
M e t o d a Z i e g l e r a - N i c h o l s a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Q D R
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
9 0
1 0 0
0
0 . 5
1
1 . 5
M e t o d a Z i e g l e r a - N i c h o l s a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Q D R
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e
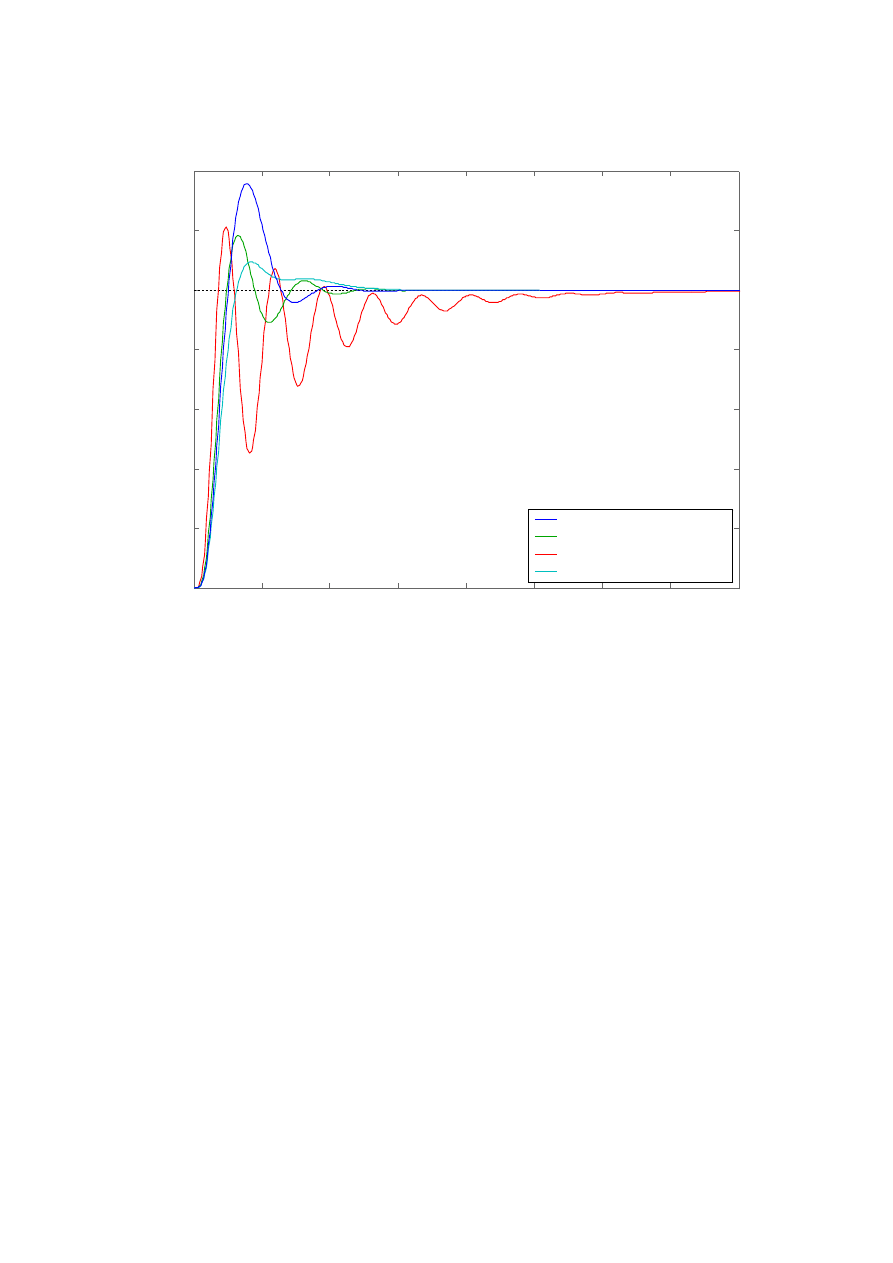
Ad 2.3.c) Regulatory PID:
Dla wszystkich przypadków regulatorów dla badanego obiektu nastawy wynikające z
metody Zieglera-Nicholsa są optymalne. Wynika to z faktu iż transmitancję obiektu regulacji
można z dużą dokładnością aproksymować iloczynem transmitancji elementu inercyjnego I rzędu i
opóźnienia. Najgorszym kryterium doboru nastaw w tym przypadku okazuje się kryterium bazujące
na zapasie fazy równym 30
o
.
6. Wnioski:
●
Dobór nastaw regulatora zależy przede wszystkim od postaci transmitancji obiektu regulacji
oraz narzuconych warunków regulacji (na przykład maksymalnego przeregulowania, które
nie uszkodzi obiektu).
●
Metodę Zieglera-Nicholsa stosujemy kiedy transmitancję obiektu regulacji można z dużą
dokładnością aproksymować iloczynem transmitancji elementu inercyjnego I rzędu i
opóźnienia.
●
Metoda QDR charakteryzuje sie czterokrotnym zmniejszeniem amplitudy kolejnych
oscylacji, .
●
Dla złożonych obiektów regulacji nie zawsze da się wyznaczyć zadowalające nastawy przy
pomocy kryteriów zobrazowanych w tym sprawozdaniu. Jednakże istnieje wiele innych
metod (np. bazujących na wskaźnikach całkowych) przy zastosowaniu których można
otrzymać lepsze nastawy.
●
Często gdy w transmitancji obiektu regulacji znajduje się czynnik całkujący, aby uzyskać
dobre parametry regulacji wystarcza regulator P bądź PD.
●
Bardzo często stosuje się aproksymacje złożonych obiektów regulacji znacznie prostrzymi
uzyskując bardzo dobre parametry regulacji.
0
1 0
2 0
3 0
4 0
5 0
6 0
7 0
8 0
0
0 . 2
0 . 4
0 . 6
0 . 8
1
1 . 2
1 . 4
M e t o d a Z i e g l e r a - N i c h o l s a
K r y t e r i u m M
m a x
Z a p e w n i e n i e z a p a s u f a z y 3 0
o
M e t o d a Q D R
S t e p R e s p o n s e
T i m e ( s e c )
A
m
p
lit
u
d
e