LABORATORIUM – AUTOMATYKA i ROBOTYKA 

Dobór optymalnych nastaw regulatora PID metodą Zieglera-Nicholsa 

 

1. 

Wstęp 

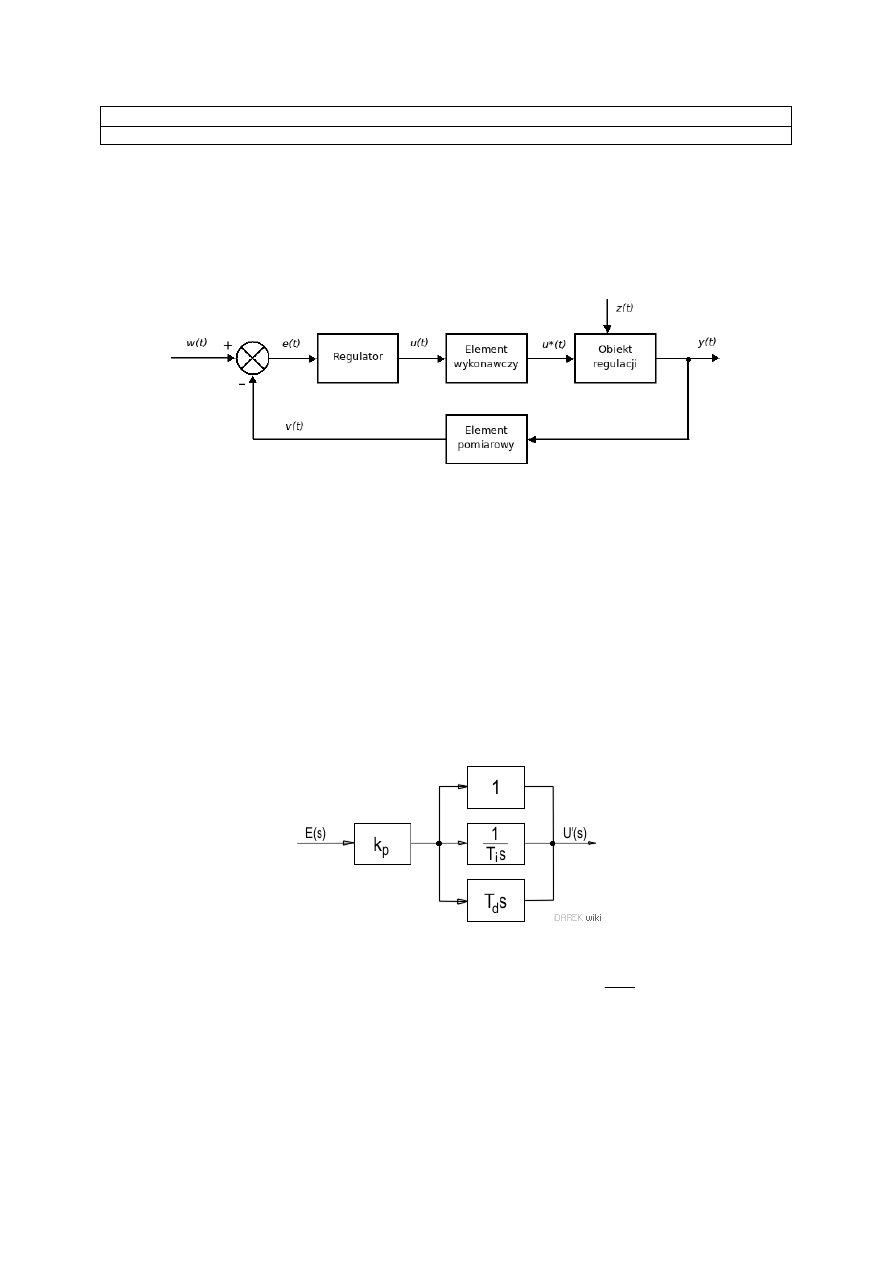
Na  Rysunku  1  pokazano  podstawową  strukturę  układu  regulacji.  Celem  regulacji  jest  uzyskanie  przez  wielkość 

regulowaną y(t) wartości zadanej w(t), co sprowadza się do sprowadzenia błędu (uchybu) regulacji do zera. Układ regulacji 

jest układem dynamicznym, tzn. osiąganie celu regulacji następuje w trakcie procesu regulacji zachodzącego w określonym 

(skończonym) czasie. 

 

Rysunek 1. Ogólny schemat układu regulacji automatycznej 

W projektowaniu układów regulacji istotne znaczenie ma dobór właściwego regulatora i jego parametrów. Dobór 

regulatora opiera się zwykle na minimalizacji pewnego wskaźnika jakości regulacji. Transmitancję regulatora wyznacza się 

na  podstawie  przyjętego  kryterium,  przy  znajomości  właściwości  dynamicznych  pozostałych  elementów  w  układzie.  W 

praktyce właściwości dynamiczne obiektu nie są zwykle znane, a ich wyznaczenie eksperymentalne jest możliwe jedynie z 

ograniczoną  dokładnością.  W  takiej  sytuacji  najczęściej  stosuje  się  regulatory  uniwersalne,  wśród  których  najszersze 

zastosowanie ma regulator PID. 

Regulator PID przetwarza sygnał wejściowy E(t) według trzech równolegle realizowanych operacji dynamicznych: 

 

wzmocnienia proporcjonalnego ze współczynnikiem k

p

, 

 

różniczkowania ze stałą czasową T

d

, 

 

całkowania ze stałą czasową T

i

. 

 

Rysunek 2. Schemat struktury regulatora PID 

Transmitancja idealnego regulatora PID ma postać: 

 

























s

T

T

s

k

s

G

i

d

p

PID

1

1

. 

Prawidłowe określenie współczynników regulatora PID (k

p

, T

d

, T

i

) wymaga znajomości (przynajmniej przybliżonej) 

właściwości  dynamicznych  toru  złożonego  z  obiektu  regulacji,  elementu  wykonawczego  i  układu  pomiarowego.  Istnieją 

również  metody  eksperymentalnego  wyznaczenia  nastaw  regulatora  PID  po  jego  zainstalowaniu  w  zamkniętym  układzie 

regulacji, bez konieczności wyznaczania parametrów obiektu. Metoda pokazana w ćwiczeniu (opracowana przez Zieglera i 

Nicholsa) prowadzi do uzyskania przebiegu aperiodycznego z przeregulowaniem 20% i minimalnym czasem regulacji. 

2. 

Przebieg ćwiczenia. 

2.1. 

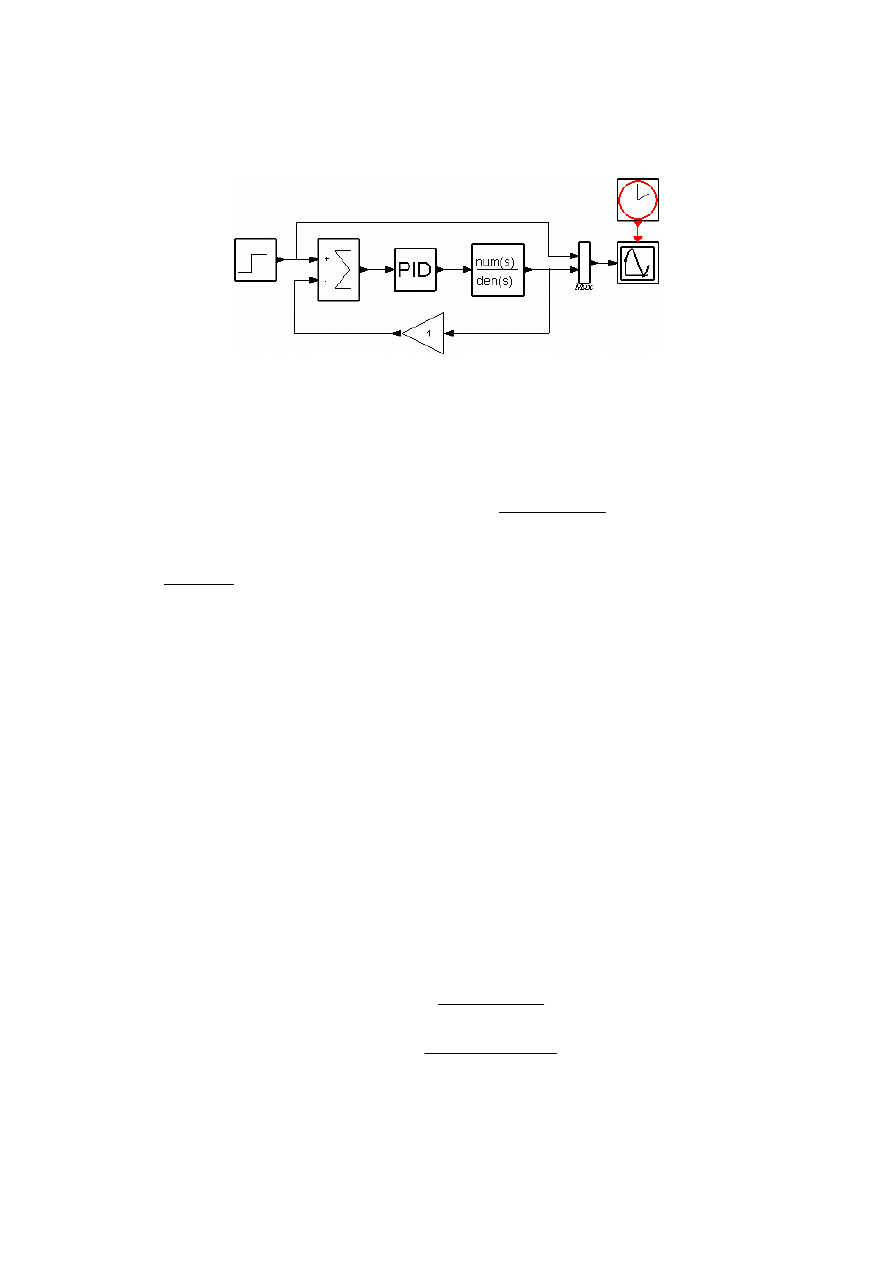
Stworzyć w module Scicos programu Scilab (Applications->Scicos) model układu regulacji z Rysunku 3. 

 

 

Rysunek 3. Model układu automatycznej regulacji z regulatorem PID 

 

2.2. 

Skonfigurować bloki modelu: 

 

Step function generator: Step time=0, Final value=1. Czyli na wejście układu podajemy skok jednostkowy. 

 

Continous transfer function - tutaj określamy własności obiektu regulacji, w postaci jego transmitancji. Pierwszym 

obiektem regulacji niech będzie obiekt o transmitancji: 

 

1

2

2

5

,

2

2

3













s

s

s

s

G

. 

 

PID regulator - tutaj określamy własności regulatora PID: Proportional=1 (wzmocnienie proporcjonalne), Integral=0 

(

odwrotność stałej czasowej członu całkującego regulatora), Derivation=0 (stała czasowa członu różniczkującego 

regulatora), 

 

Single display scope: Refresh period=50 (wzmocnienie proporcjonalne), w trakcie ćwiczenia należy odpowiednio  

modyfikować  parametry  Ymin  i  Ymax  (określające  maksimum  i  minimum  osi  y  wykresów),  tak  by  uzyskiwane 

wykresy były możliwie dokładne i czytelne. 

2.3. 

Ustawić odpowiednie parametry symulacji (Simulate->Setup): Final integration time=50, pozostałe bez zmian. 

2.4. 

Zgodnie z zasadami podanymi w punkcie 3 instrukcji wyznaczyć optymalne nastawy regulatora. Uzyskane wartości 

umieścić w protokole. 

2.5. 

Ustawić  nowe  parametry  wartości  zadanej  sygnału  (ustawiane  w bloku  Step  function  generator). Nich  przyjmuje 

ona na początku wartość 5 i po 25 sekundach zmienia się na -5. 

2.6. 

Sprawdzić i naszkicować w protokole odpowiedź układu na takie pobudzenie w czterech przypadkach: 

  układ bez regulacji (blok PID regulator: Proportional=1, Integral=0, Derivation=0, blok Gain: Gain=0), 

 

układ z regulatorami optymalnymi typu P, PI i PID (blok PID regulator: wartości obliczone w punkcie 2.4, blok Gain: 

Gain=1). 

2.7. 

W  ten  sam  sposób  dokonać  doboru  nastaw  optymalnych  regulatora  i  wypełnić  protokół  dla  obiektów  o 

transmitancjach: 

2.7.1. 

 

1

2

3

1

2

3













s

s

s

s

G

, 

2.7.2. 

 

1

2

3

5

,

0

2

3

4















s

s

s

s

s

G

. 

 

2.8. 

Mile widziane jest zamieszczenie w protokole własnych wniosków i przemyśleń. 

3. 

Metoda Zieglera-Nicholsa 

Sposób postępowania jest następujący: 

1. 

nastawić regulator na działanie czysto proporcjonalne (Integral=0, Derivation=0), 

2. 

eksperymentalnie wyznaczyć wzmocnienie krytyczne k

kr

 regulatora (Proportional) dla którego na wyjściu 

układu występują oscylacje niegasnące (o stałej amplitudzie), 

3. 

zmierzyć okres tych oscylacji T

osc

, 

4. 

znając wielkości T

osc

 i k

kr

 nastawy optymalne wg Zieglera i Nicholsa dobiera się wg Tabeli 1. 

 

Tabela 1. Optymalne nastawy regulatora PID wg metody Zieglera-Nicholsa 

Typ regulatora 

k

p 

T

i 

T

d

 

P 

0,5k

kr 

- 

- 

PI 

0,45k

kr

 

0,85T

osc 

- 

PID 

0,6k

kr

 

0,5T

osc

 

0,12T

osc

 

 
 
4. 

Literatura 

1)  Frohr  F.,  Orttenburger  F.,  „Wprowadzenie  do  elektronicznej  techniki  regulacji”,  Wydawnictwa  Naukowo-Techniczne, 

Warszawa 1977 

2)  Kiczkowiak  T.,  Ociepa  Z.,  Tarnowski  W.,  Wachowicz  E.,  Wachowicz  M.,  „Laboratorium  z  podstaw  automatyki”, 

Wydawnictwo Uczelniane Politechniki Koszalińskiej, Koszalin 1999 

3)  Pochopień B., „Automatyka przemysłowa dla elektroników”, Wydawnictwa Szkolne i Pedagogiczne , Warszawa 1976 

4)  zbiorowa pod red. Hejmo W., „Laboratorium podstaw automatyki”, Wydawnictwa Politechniki Krakowskiej, Kraków 1988 

5)  zbiorowa pod red. Zakrzewski J., „Laboratorium podstaw automatyki”, Wydawnictwo Politechniki Śląskiej, Gliwice 2001 

Opracowanie ćwiczenia: Seweryn Lipiński