AKADEMIA GÓRNICZO - HUTNICZA W KRAKOWIE			Grupa B Rafał Szemraj
EAIiE	2001/2002		Rok II Semestr IV	Elektrotechnika		Rok B Grupa 8
Temat: Regulatory PID - charakterystyki czasowe i częstotliwościowe.
Data wykonania: 2002-04-12		Data zaliczenia:			Ocena:

1. Regulatory P,PD i PI, PID a likwidacja uchybu ustalonego.

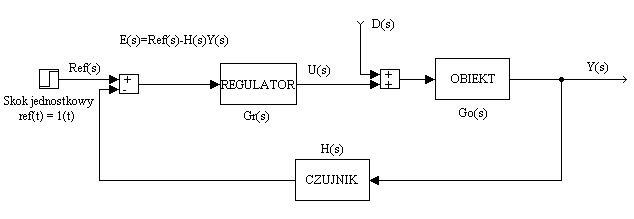
Niech Ref(s) = X(s). Zgodnie ze schematem mamy:
oraz

Zgodnie z definicją wartości końcowej:
.

Rozważmy teraz wartość uchybu e(t) w stanie ustalonym dla poszczególnych typów regulatorów.

Niech
i
i

• Regulator P (proporcjonalny):

Mamy
,
wtedy:

Widzimy, że dla regulatora proporcjonalnego w czasie ustalonym wartość uchybu jest różna od zera.

• Regulator PD (proporcjonalno - różniczkujący):

Mamy
,
wtedy:

Widzimy, że dla tego regulatora uchyb ustalony też jest różny od zera.

• Regulator PI (proporcjonalno - całkujący):

Mamy
,
wtedy:

W tym przypadku ustalona wartość uchybu wynosi zero. Spowodowało to zastosowanie członu całkującego w regulatorze.

• Regulator PID:

Mamy
,
wtedy:

Również regulator PID zawierający człon całkujący posiada zerowy uchyb ustalony.

WNIOSEK: Regulatory zawierające część całującą likwidują uchyb ustalony w przeciwieństwie do regulatorów pozbawionych tego członu.

2. Dobór parametrów regulatora PID metodą Zieglera - Nicholsa dla zadanego obiektu.

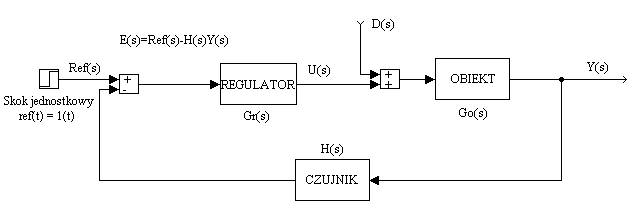
Transmitancja obiektu:

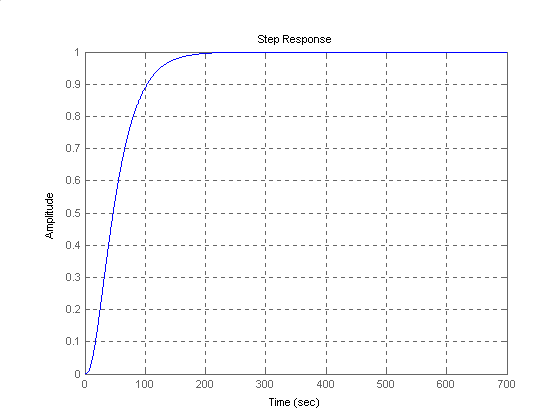
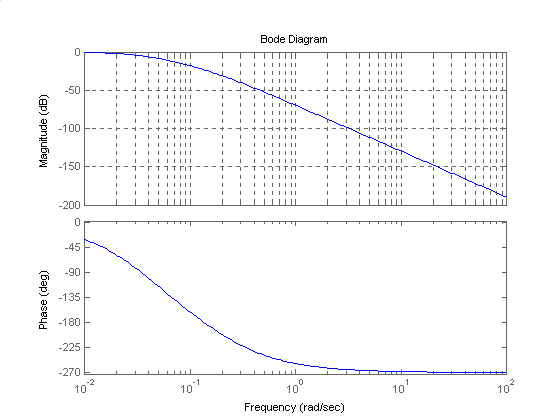
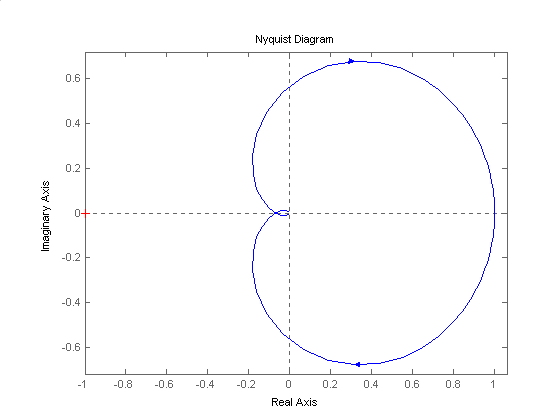
Dobierając parametry regulatora PID dla tego obiektu według metody Zieglera - Nicholsa otrzymałem następujące wyniki:

stąd mamy:

Na podstawie zależności
i
otrzymujemy ostatecznie nastawy regulatora PID:

Stąd transmitancja regulatora PID:

Zgodnie ze schematem transmitancja zastępcza układu otwartego wyniesie (w tym punkcie zakładam zerowy sygnał zakłóceń):

Jeżeli układ otwarty obejmiemy pętlą ujemnego sprzężenia zwrotnego o transmitancji H(s) = 1, to transmitancja układu zastępczego będzie wynosić:

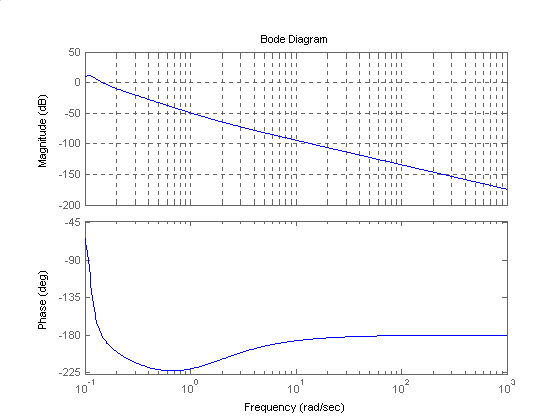
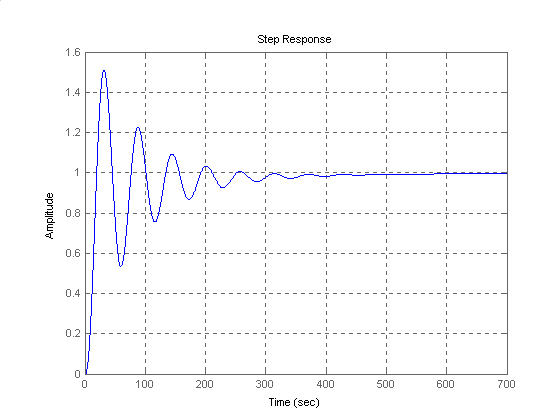
Można sprawdzić, że równanie charakterystyczne mianownika ma pierwiastki o częściach rzeczywistych w lewej półpłaszczyźnie Gauusa (układ stabilny), a w stanie ustalonym układ osiągnie amplitudę równą jedności (stosunek wyrazów wolnych licznika i mianownika).

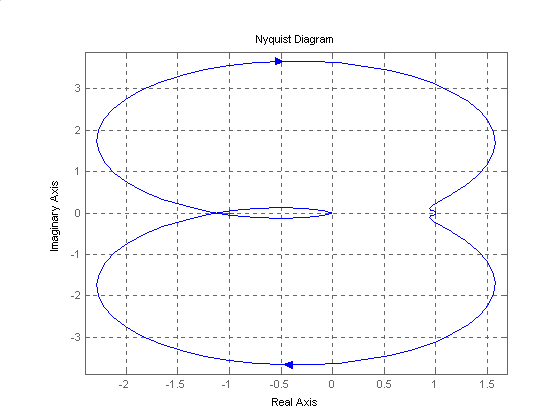
3. Wpływ zmian wartości nastawów na odpowiedź układu:

Transmitancja badanego obiektu:

Transmitancja czujnika w pętli sprzężenia zwrotnego:
.

Obliczanie nastawów regulatora dla tego obiektu z wykorzystaniem metody Zieglera- Nicholsa jest niepraktyczne, ponieważ zarówno zapas amplitudy i odpowiadająca mu częstotliwość graniczna mają nieskończone wartości. Ogólnie transmitancja regulatora ma postać:

Wtedy transmitancja zastępcza układu zamkniętego będzie miała postać:

Jak widzimy odpowiedź na wymuszenie skokowe tego układu ustali się na poziomie jedności niezależnie od wartości poszczególnych nastawów regulatora.

Zakładając następujące początkowe nastawy:

sprawdźmy jak zmienia się postać odpowiedzi układu przy zmianie jednego z nastawów (przy stałych pozostałych):

• Regulator PID - stałe nastawy K_i i K_d:

Kd = 0,2 Ki = 0,5	Czas narastania tr [s]	Przeregulowanie M.o [%]	Czas ustalenia ts [s]	Błąd w stanie ustalonym ess [%]	Szerokość pasm bw [rad/s]
Kp = 0,5	3,7164	0,4464	5,86	2,86*10^-5	0,573
Kp = 5	0,8244	2,1973	2,257	1,0499	2,8282
Kp = 10	0,4541	23,3797	0	2,0676	4,6106

Widzimy, że wzrost parametru K_p powoduje poszerzenie pasma i zmniejszenie czasu narastania. Jednak zbyt duża wartość tego parametru powoduje silne przeregulowania (powstawanie oscylacji ).

Kp = 2 Kd = 0,2	Czas narastania tr [s]	Przeregulowanie M.o [%]	Czas ustalenia ts [s]	Błąd w stanie ustalonym ess [%]	Szerokość pasm bw [rad/s]
Ki = 0,1	33,8931	0	81	1,0836	0,1447
Ki = 0,5	4,362	0	12,8	5,08*10^-3	0,9448
Ki = 1,5	1,3369	15,6108	5,2	1,56*10^-11	1,5024

Zmiany parametru K_i powodują takie same rezultaty jak zmiany współczynnika części proporcjonalnej jednak w mniejszym stopniu. Jedyna różnica - zwiększanie K_i powoduje znaczne zmniejszenie się błędu w stanie ustalonym (zaleta stosowania członu całkującego). Następuje poszerzenie pasma lecz w bardzo małym zakresie.

Kp = 2 Ki = 0,5	Czas narastania tr [s]	Przeregulowanie M.o [%]	Czas ustalenia ts [s]	Błąd w stanie ustalonym ess [%]	Szerokość pasm bw [rad/s]
Kd = 0,1	4,3054	0	12,84	0,0662	1,027
Kd = 0,5	4,6205	0	12,65	0,0552	0,7439
Kd = 1,5	5,4821	0	12,12	0,0281	0,476

Zwiększanie parametru K_d powoduje minimalne zwiększenie czasu narastania sygnału i równie małe zmniejszenie błędu ustalonego. Wadą jest zawężanie się pasma przy wzroście tego parametru.

4. Porównanie odpowiedzi różnych regulatorów na wymuszenie sygnałem referencyjnym i na wymuszenie sygnałem zakłócającym w postaci skoku jednostkowego przy zerowym sygnale referencyjnym.

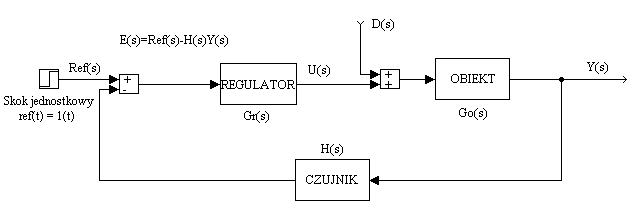
Ze schematu mamy:

oraz
. Przyjmujemy:

i

• Regulator P:

Z metody Zieglera - Nicholsa mamy następujący nastaw:

K_p = 7,29. Mamy

Dla ref(t) = 1(t) i d(t) = 0 mamy:

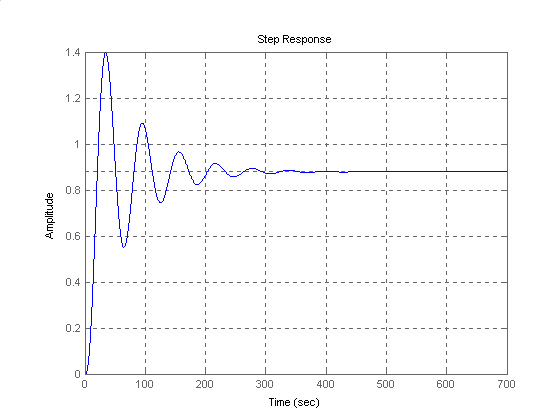
Dla ref(t) = 0 i d(t) = 1(t) mamy:

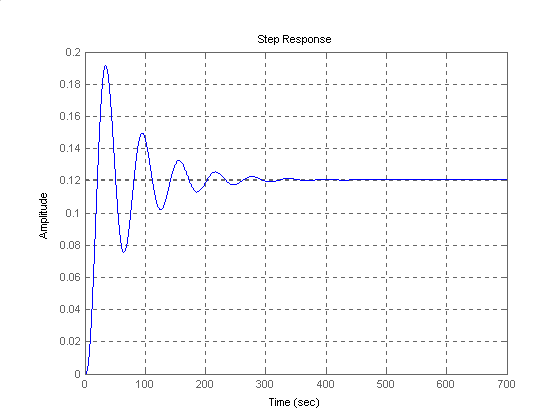
• Regulator PD:

Z metody Zieglera - Nicholsa mamy następujący nastaw:

K_p = 8,75 i K_d = 5,8. Mamy

Dla ref(t) = 1(t) i d(t) = 0 mamy:

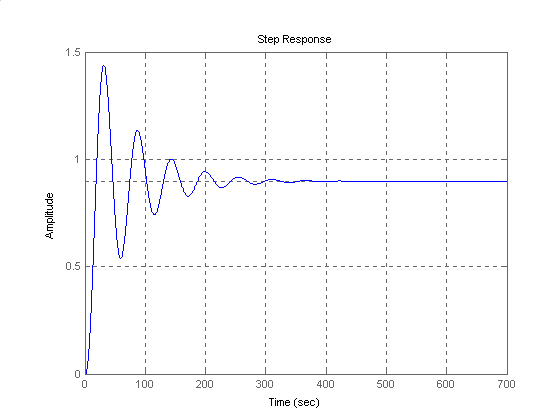
Dla ref(t) = 0 i d(t) = 1(t) mamy:

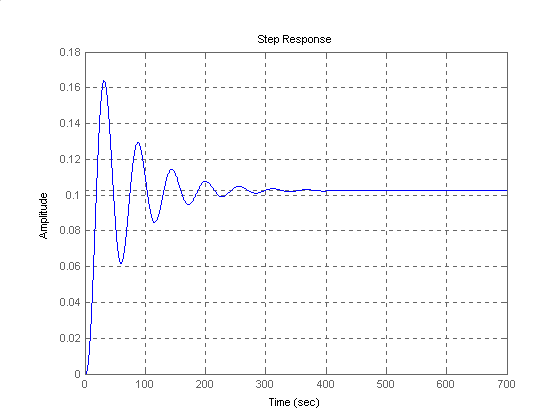
• Regulator PI:

Z metody Zieglera - Nicholsa mamy następujący nastaw:

K_p = 8,75 i K_i = 0,0431. Mamy

Dla ref(t) = 1(t) i d(t) = 0 mamy:

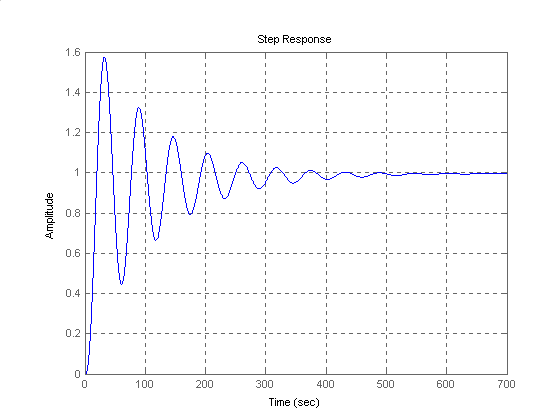
Dla ref(t) = 0 i d(t) = 1(t) mamy:

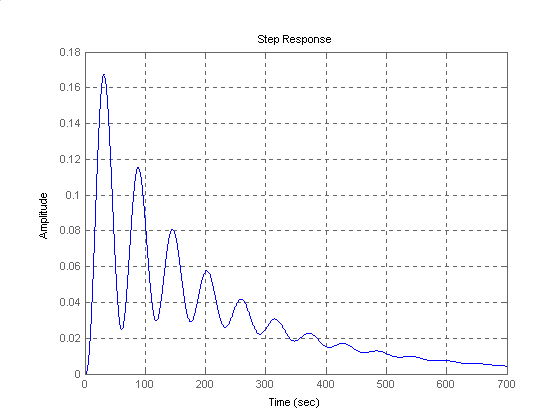
• Regulator PID:

Wyliczone nastawy regulatora PID metodą Zieglera - Nicholsa:

mamy

Dla ref(t) = 1(t) i d(t) = 0 mamy:

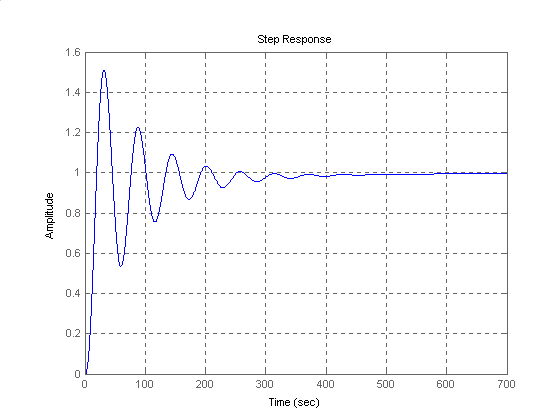
Dla ref(t) = 0 i d(t) = 1(t) mamy:

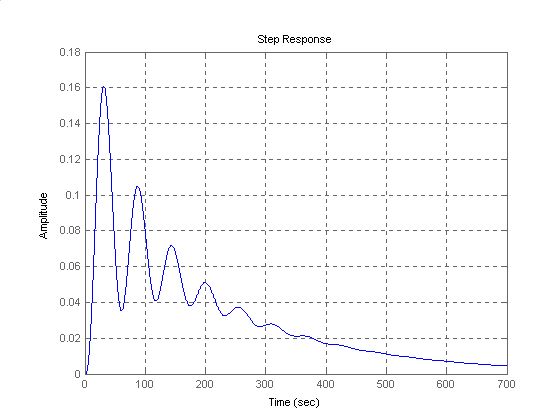
WNIOSKI:

• Obiekt regulowany regulatorem PID ma najlepsze warunki pracy - zerowy uchyb sygnału oraz silne tłumienie sygnału szumu.

• Regulator PI działa w bardzo podobny sposób jak PID ale czas ustalania się odpowiedzi jest w tym przypadku nieco dłuższy.

• Tylko regulatory z częścią całkującą gwarantują zerowy uchyb oraz tłumienie do zera sygnałów zakłucających.

2

---