POLITECHNIKA WARSZAWSKA

Wydział Samochodów i Maszyn Roboczych

Modelowanie komputerowe w praktyce

Inżynierskiej

„Symulacja drgań układu mechanicznego”

Wykonał:

Arkadiusz Kubik

Numer albumu: 257462

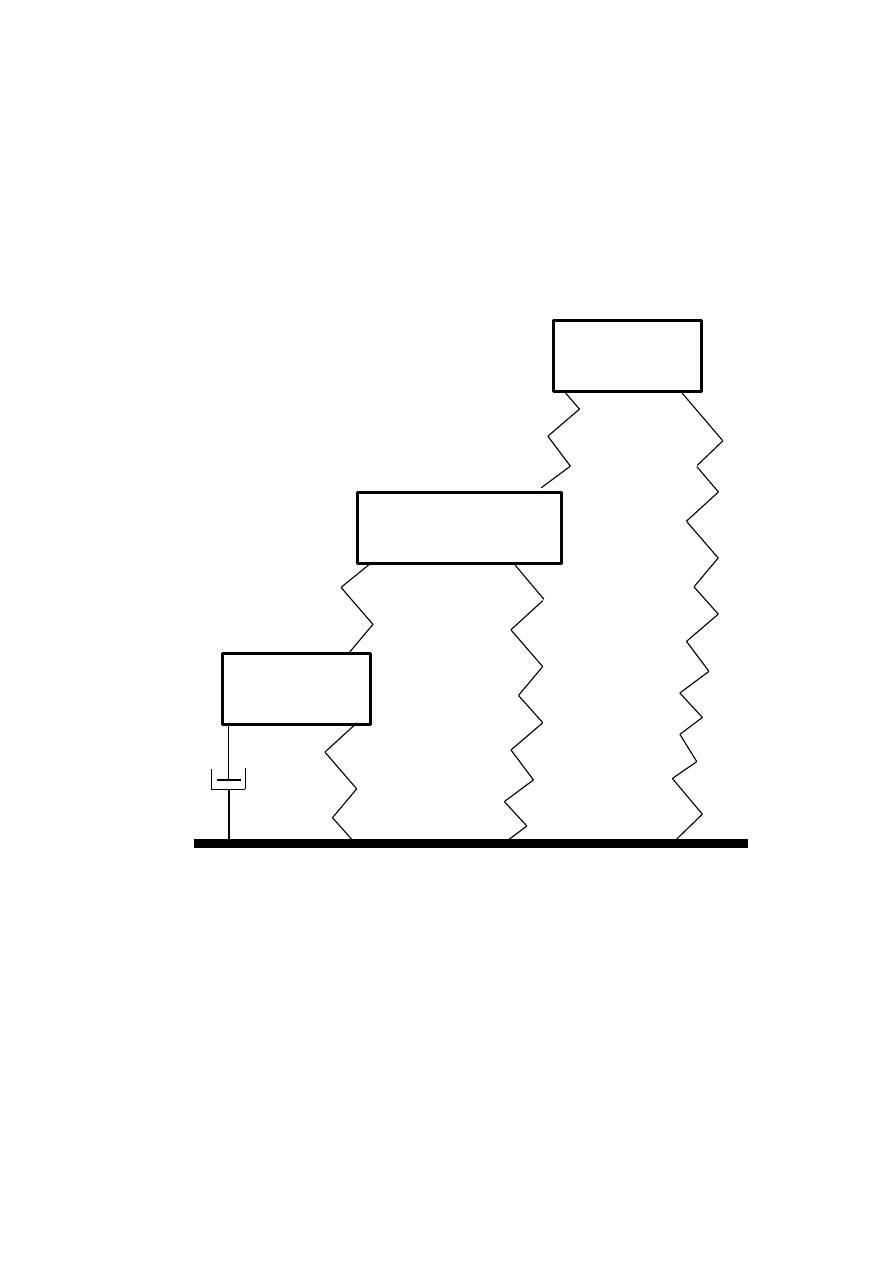
1. Schemat układu

Układ składa się z trzech mas, pięciu sprężyn oraz jednego tłumika,
rozmieszczenie elementów ilustruje poniższy rysunek:

2. Macierze sztywności, mas i tłumienia

Macierz sztywności K:

[

]

m

3

m

2

m

1

k

5

k

4

k

3

k

2

k

1

c

Ponieważ nie ma przemieszczeń podłoża, można wykreślić pierwszy
wiersz i pierwszą kolumnę. Wówczas:

[

]

Macierz tłumienia C:

[

]

Macierz mas M:

[

]

3. Dane

k

1

= 4 N/m

k

2

= 5 N/m

k

3

= 2 N/m

k

4

= 3 N/m

k

5

= 1 N/m

m

1

= 6 kg

m

2

= 13 kg

m

3

= 4 kg

Warunki początkowe:
x

1

=0 x

2

=0

x

3

=0

x

1

’=0 x

2

’=10 m/s x

3

’=0

krok dt=0,1 s

4. Rozwiązanie

Symulację przeprowadzono w programie Scilab.
Tłumienie układu otrzymamy z tłumienia Rayleigh’a:

C= α *M+β*K, gdzie α,β ϵ<0,001; 0,5>

Macierze K i M z uwzględnieniem danych wynoszą:

[

]

[

]

Rozwiązanie zadania w programie Scilab

//Obliczanie amplitud drgań układu

yy1

=

(

0

)

, yy2

=

(

0

)

, yy3

=

(

0

)

K

=

[[

9

,

-

5

,

0

]

;

[

-

5

,

10

,

-

3

]

;

[

0

,

-

3

,

4

]]

//macierz sztywności

M

=

[[

6

,

0

,

0

]

;

[

0

,

13

,

0

]

;

[

0

,

0

,

4

]]

//macierz mas

y1

=

[

0

,

0

,

0

]

'

, y2

=

[

0

,

1

,

0

]

'

h

=

0.1

, tmax

=

100

a

=

0.05

//współczynnik alfa

b

=

0.02

//współczynnik beta

F

=

0

C

=

a

*

M

+

b

*

K

// wzór Raileygh'a

t

=

h

:

h

:

tmax

for

j

=

1

:

tmax

/

h

y3

=

((

M

+

0.5

*

h

*

C

)

^-

1

)

*

(

F

*

(

h

^

2

)

+

(

2

*

M

-

K

*

(

h

^

2

))

*

y2

+

(

C

*

h

*

0.5

-

M

)

*

y1

)

y1

=

y2, y2

=

y3

yy1

(

j

)

=

y2

(

1

)

, yy2

(

j

)

=

y2

(

2

)

, yy3

(

j

)

=

y2

(

3

)

end

clf

plot2d

(

t,yy1

)

,

plot

(

t,yy2,

'b'

)

,

plot

(

t,yy3,

'g'

)

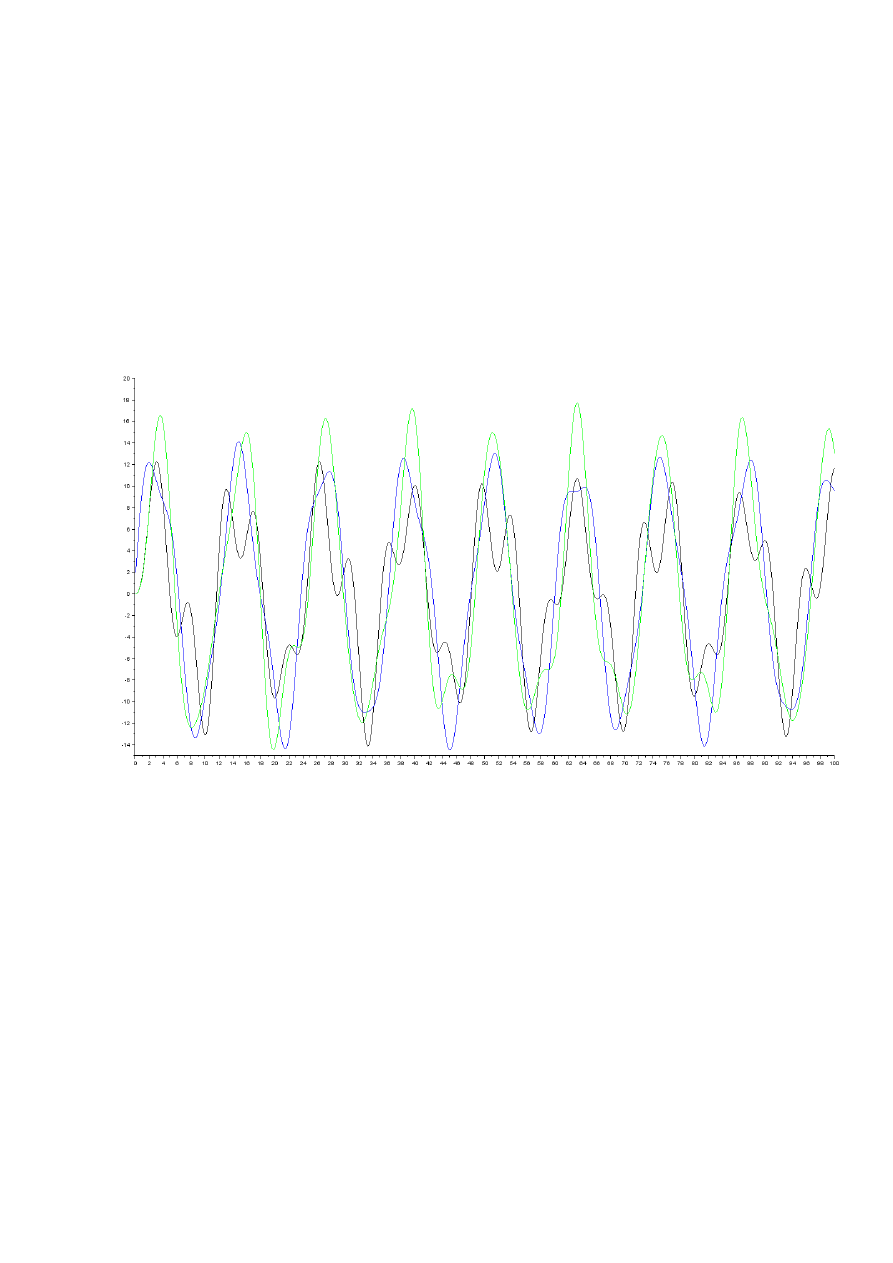
5. Wykresy

Na wykresach przedstawiono amplitudy wychyleń poszczególnych mas
układu, gdzie: kolor czarny – m

1

, zielony - m

2

, niebieski – m

3

dla α =0,001; β=0,001

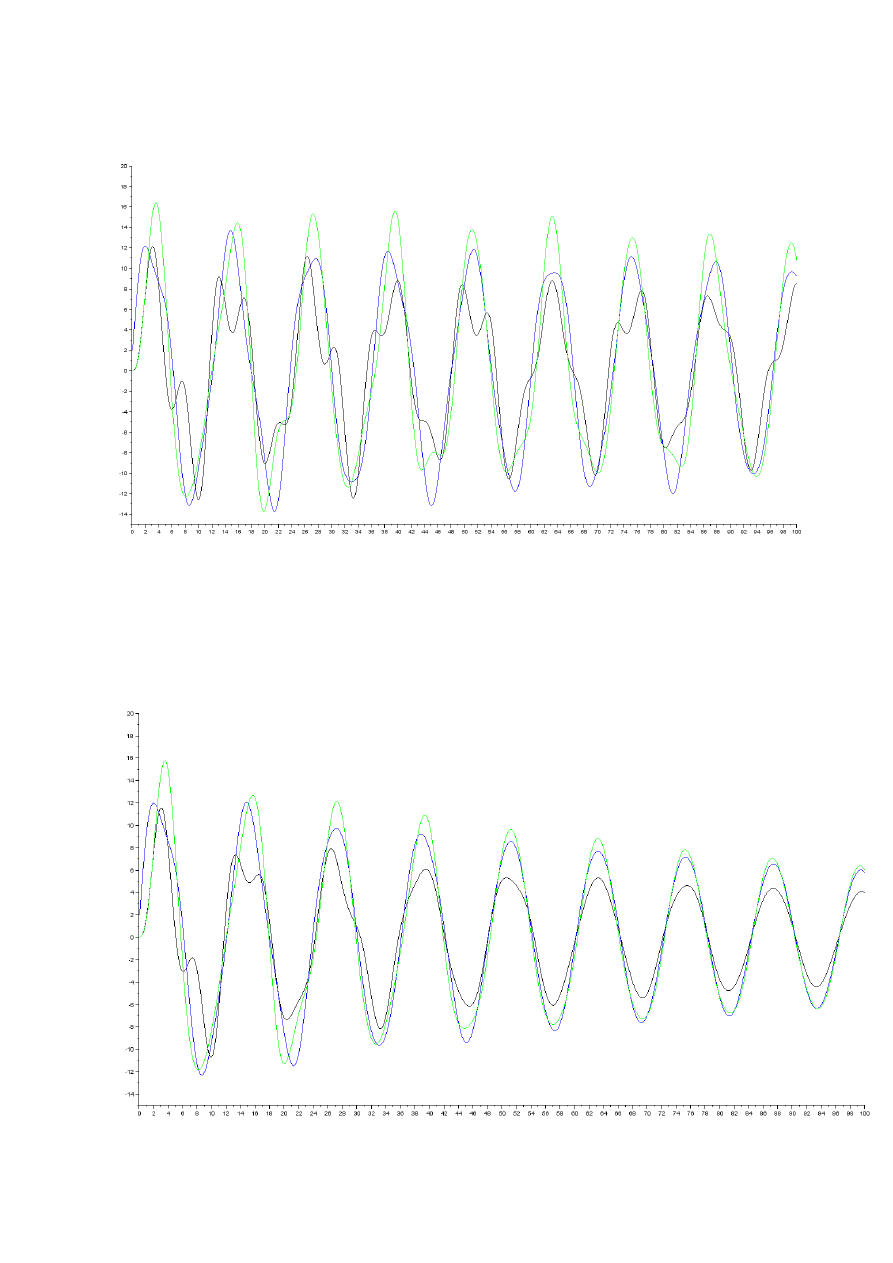
dla α =0,001; β=0,01

dla α =0,001; β=0,05

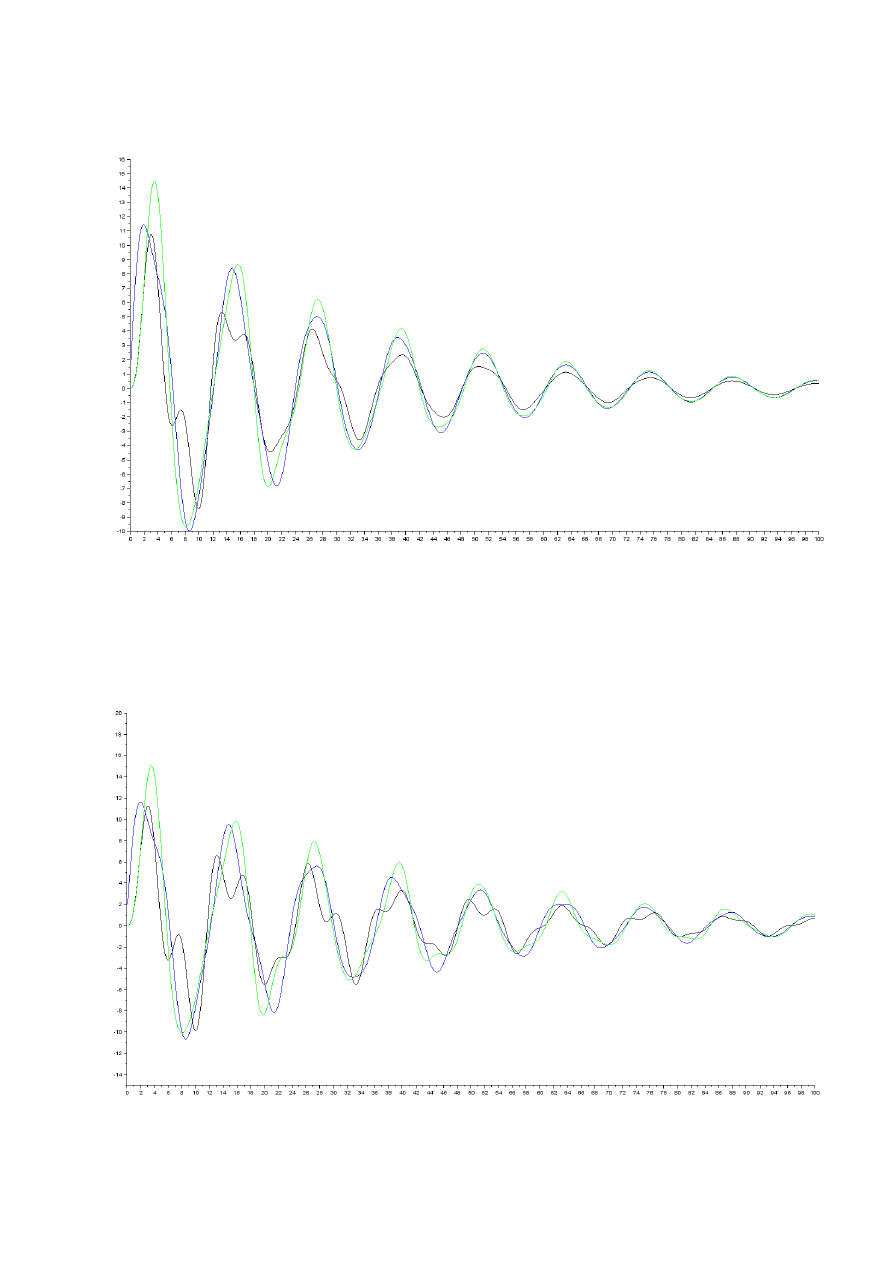
dla α =0,05; β=0,05

dla α =0,05; β=0,01

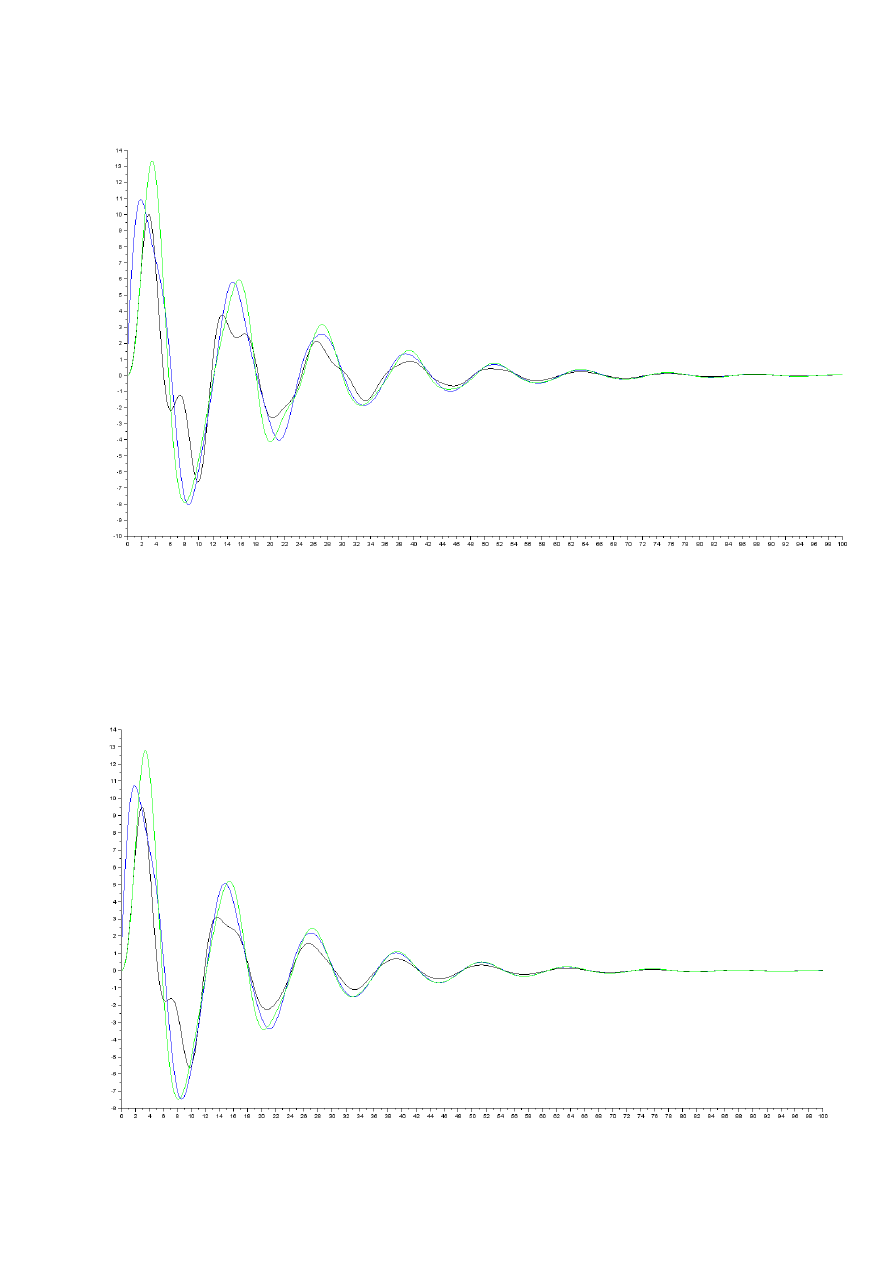
dla α =0,1; β=0,05

dla α =0,1; β=0,1

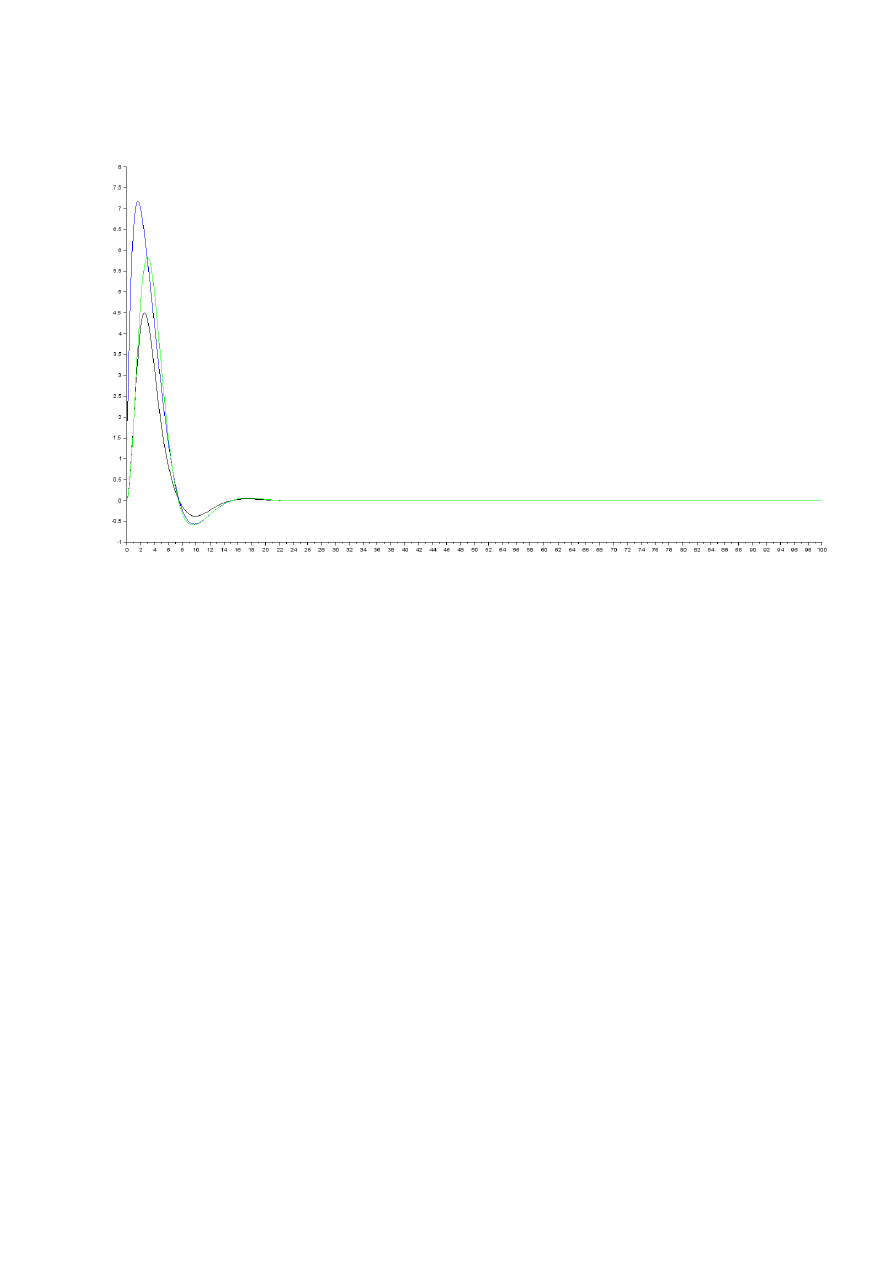
dla α =0,5; β=0,5

6. Wnioski i spostrzeżenia

Można zauważyć, że zwiększenie parametru α powoduje zwiększenie
szybkości tłumienia drgań, zaś parametr β pozwala na zmniejszenie
różnic w amplitudach drgań poszczególnych mas. Za taki stan
odpowiadają przyjęte wartości danych oraz zależność, z której została
obliczona macierz tłumienia.