RYNEK NIERUCHOMOŚCI

dr inż. Radosław Cellmer

Wykład
Modelowanie ekonometryczne cen nieruchomości

Treść wykładu:

1. Analiza regresji wielorakiej

2. Zastosowanie narzędzi obliczeniowych

3. Weryfikacja i interpretacja modelu regresji

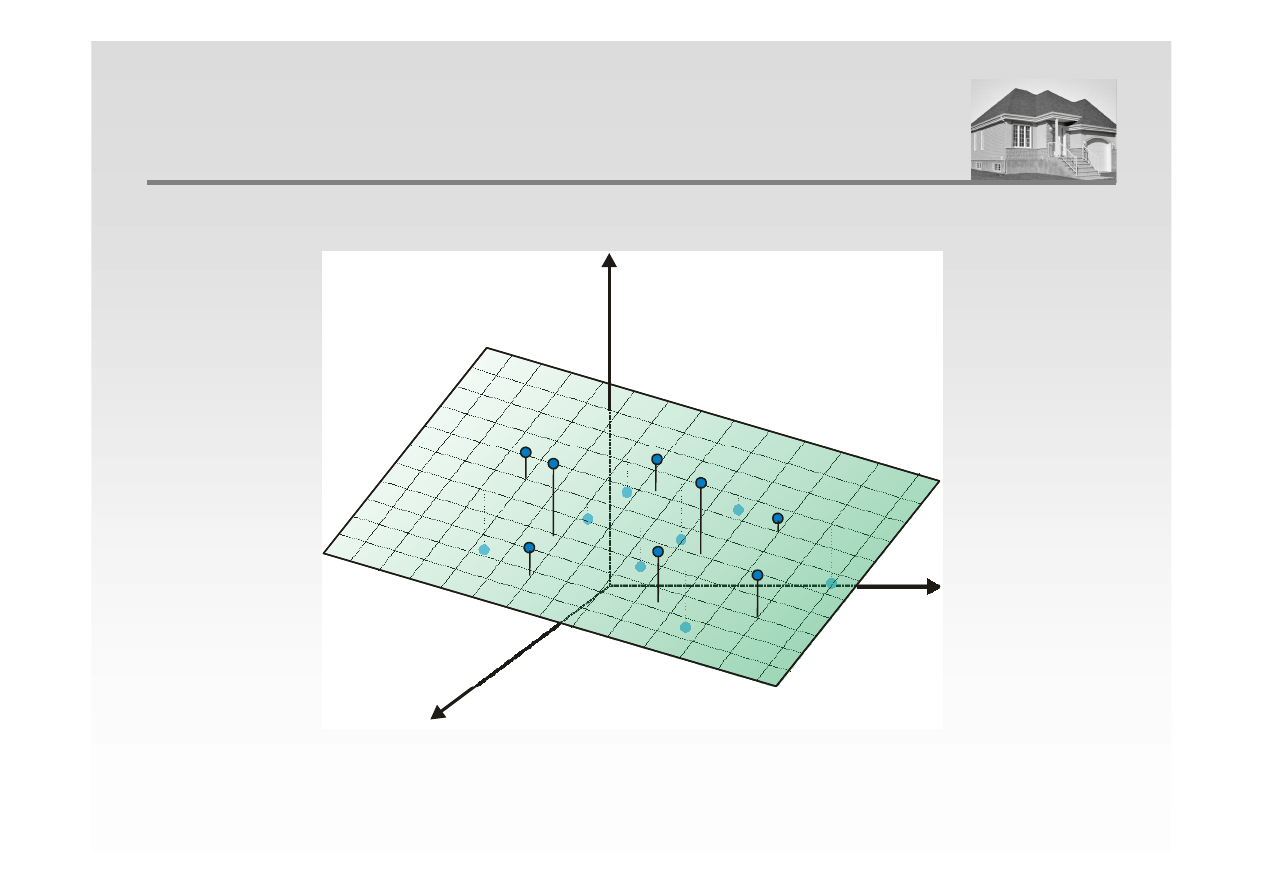
Z

PŁASZCZYZNA W PRZESTRZENI TRÓJWYMIAROWEJ

X

Y

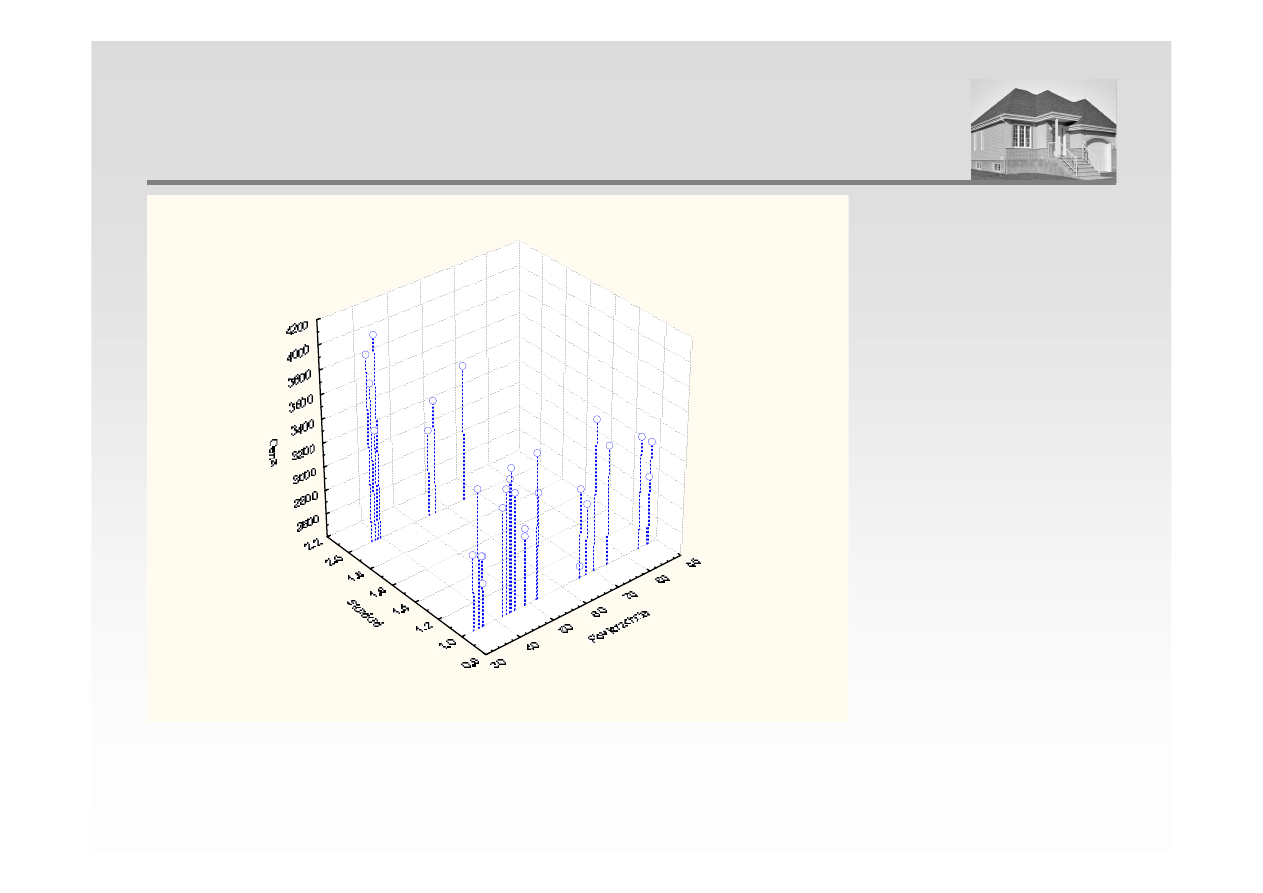
POZIOM CEN TRANSAKCYJNYCH W ZALEŻNOŚCI OD
POWIERZCHNI I STANDARDU MIESZKANIA

Rozrzutu 3W Cena wzgl

ę

dem Powierzchnia i Standard

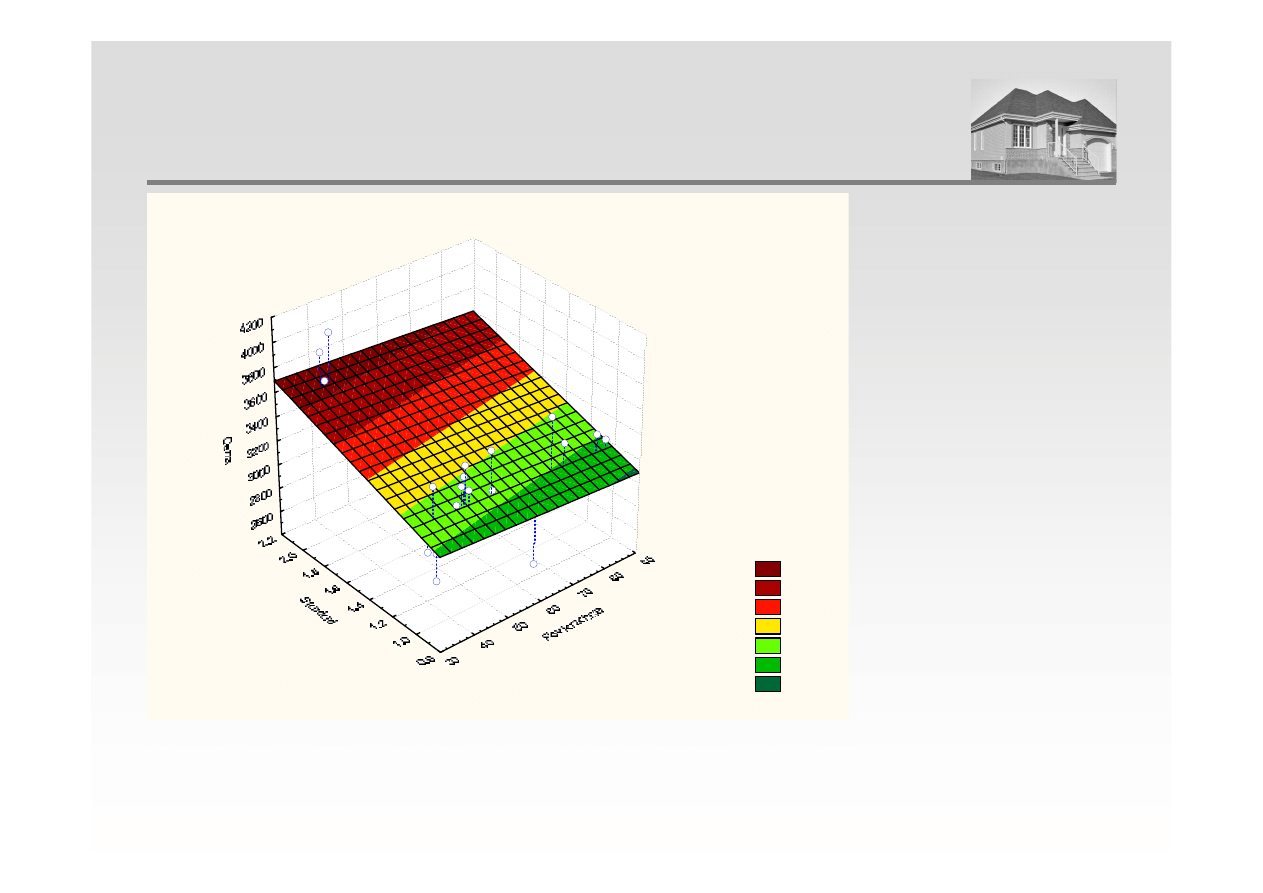
POZIOM CEN TRANSAKCYJNYCH W ZALEŻNOŚCI OD
POWIERZCHNI I STANDARDU MIESZKANIA

Cena = 2938,7641-1,6303*x+364,9833*y

> 3600
< 3600
< 3500
< 3400
< 3300
< 3200
< 3100

Ogólnym celem regresji wielokrotnej jest badanie związków pomiędzy wieloma zmiennymi
objaśniającymi (niezależnymi) a zmienną objaśnianą (zależną).

Przykładowo rzeczoznawca majątkowy określając wartość lokalu mieszkalnego zbiera dane
dotyczące podobnych lokali – powierzchnia użytkowa, liczba pomieszczeń, zużycie techniczne
itp. oraz subiektywną ocenę atrakcyjności obiektu.

Dokonując analizy regresji wielorakiej można uzyskać odpowiedź na pytanie:

REGRESJA WIELORAKA OGÓLNY CEL

Jak poszczególne wielkości wpływają na cenę lokalu?

U podstaw modelu regresji leży hipoteza o istnieniu zależności, między co najmniej dwiema
zmiennymi. Zakłada się, że wzrostowi jednej z badanych wielkości towarzyszy wzrost lub spadek
drugiej. Stąd zależność zmiennej Y od zmiennych X

1

, X

2

, ..., X

k

przedstawia się za pomocą funkcji:

Y = f(X

1

, X

2

, ..., X

k

)

1. Określenie zestawu zmiennych (cech rynkowych) i ich opis w przyjętej skali liczbowej

2. Określenie postaci analitycznej modelu

3. Estymacja parametrów modelu

4. Weryfikacja merytoryczna i statystyczna modelu

5. Zastosowanie modelu do prognozy zmiennej objaśnianej

PROCEDURA ANALIZY REGRESJI WIELORAKIEJ

5. Zastosowanie modelu do prognozy zmiennej objaśnianej

Cena = 2938,7641-1,6303*x+364,9833*y

> 3600
< 3600
< 3500
< 3400
< 3300
< 3200
< 3100

Najczęściej wykorzystywanym modelem jest model liniowy o następującej postaci:

Y =

ββββ

0

+

ββββ

1

X

1

+

ββββ

2

X

2

+ … +

ββββ

k

X

k

+

ξξξξ

gdzie:
Y

- zmienna objaśniana (zależna)

X

1

, X

2

, ..., X

k

- zmienne objaśniające (niezależne)

β

1

,

β

2

, ...,

β

k

- parametry modelu

POSTAĆ ANALITYCZNA MODELU REGRESJI WIELORAKIEJ

β

1

,

β

2

, ...,

β

k

- parametry modelu

β

0

- stała

ξ

- składnik losowy (reszta) modelu

Y

ˆ

Dane wyjściowe:

Lp.

Cena

Cena

Cena

Cena

Cecha 1

Cecha 1

Cecha 1

Cecha 1

Cecha 2

Cecha 2

Cecha 2

Cecha 2

...

Cecha k

Cecha k

Cecha k

Cecha k

1

y

1

x

11

x

12

…

x

1k

ESTYMACJA PARAMETRÓW MODELU

1

y

1

x

11

x

12

…

x

1k

2

y

2

x

21

x

22

…

x

2k

…

…

…

…

…

…

n

y

n

x

n1

x

n2

…

x

nk

Układ równań:

y

1

=

β

0

+

β

1

x

11

+

β

2

x

12

+ … +

β

k

x

1k

y

2

=

β

0

+

β

1

x

21

+

β

2

x

22

+ … +

β

k

x

2k

………………………………………
y

n

=

β

0

+

β

1

x

n1

+

β

2

x

n2

+ … +

β

k

x

nk

Układ równań w postaci macierzowej:

Y = XA

gdzie:

ESTYMACJA PARAMETRÓW MODELU

Y = XA

gdzie:

























=

n

2

1

y

...

y

y

Y

























=

nk

n2

n1

2k

22

21

1k

12

11

x

...

x

x

1

...

...

...

...

...

x

...

x

x

1

x

...

x

x

1

X

























=

k

β

β

β

...

A

1

0

Macierz parametrów modelu wyznacza się metodą najmniejszych kwadratów, wykorzystując
następujący wzór:

A = (X

T

X)

-1

X

T

Y

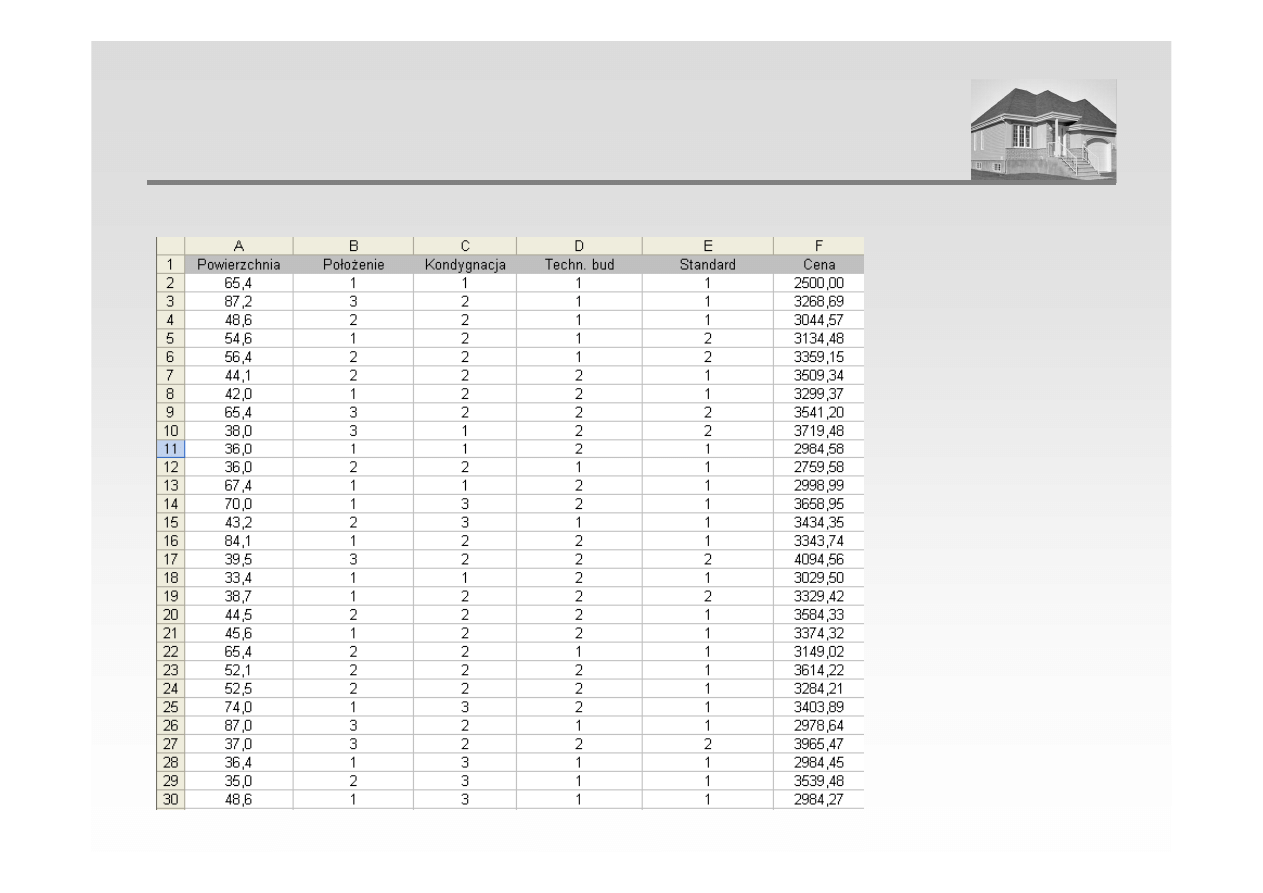
1. Określenie zestawu zmiennych (cech rynkowych) i ich opis w przyjętej skali liczbowej

ANALIZA REGRESJI WIELORAKIEJ

2. Określenie postaci analitycznej modelu

Y =

ββββ

0

+

ββββ

1

X

1

+

ββββ

2

X

2

+

ββββ

3

X

3

+

ββββ

4

X

4

+

ββββ

5

X

5

+ … +

ββββ

k

X

k

+

ξξξξ

gdzie:
Y

- zmienna objaśniana (cena transakcyjna)

X

1

- zmienna objaśniająca (powierzchnia)

X

2

- zmienna objaśniająca (położenie)

X

- zmienna objaśniająca (kondygnacja)

ANALIZA REGRESJI WIELORAKIEJ

2

X

3

- zmienna objaśniająca (kondygnacja)

X

4

- zmienna objaśniająca (technologia)

X

5

- zmienna objaśniająca (standard)

β

1

,

β

2

, ...,

β

k

- parametry modelu

β

0

- stała

ξ

- składnik losowy (reszta) modelu

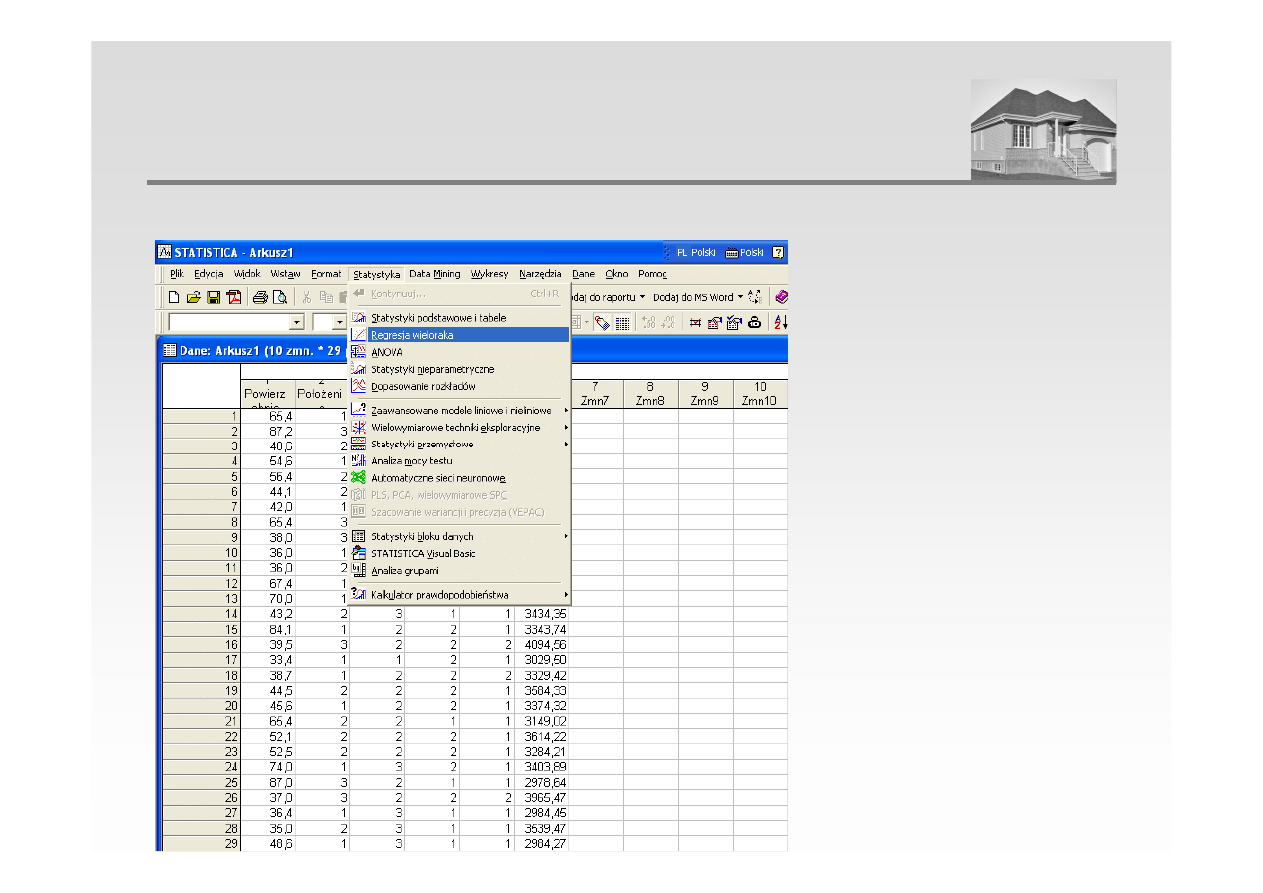
3. Estymacja parametrów modelu – przy pomocy programu STATISTICA

ANALIZA REGRESJI WIELORAKIEJ

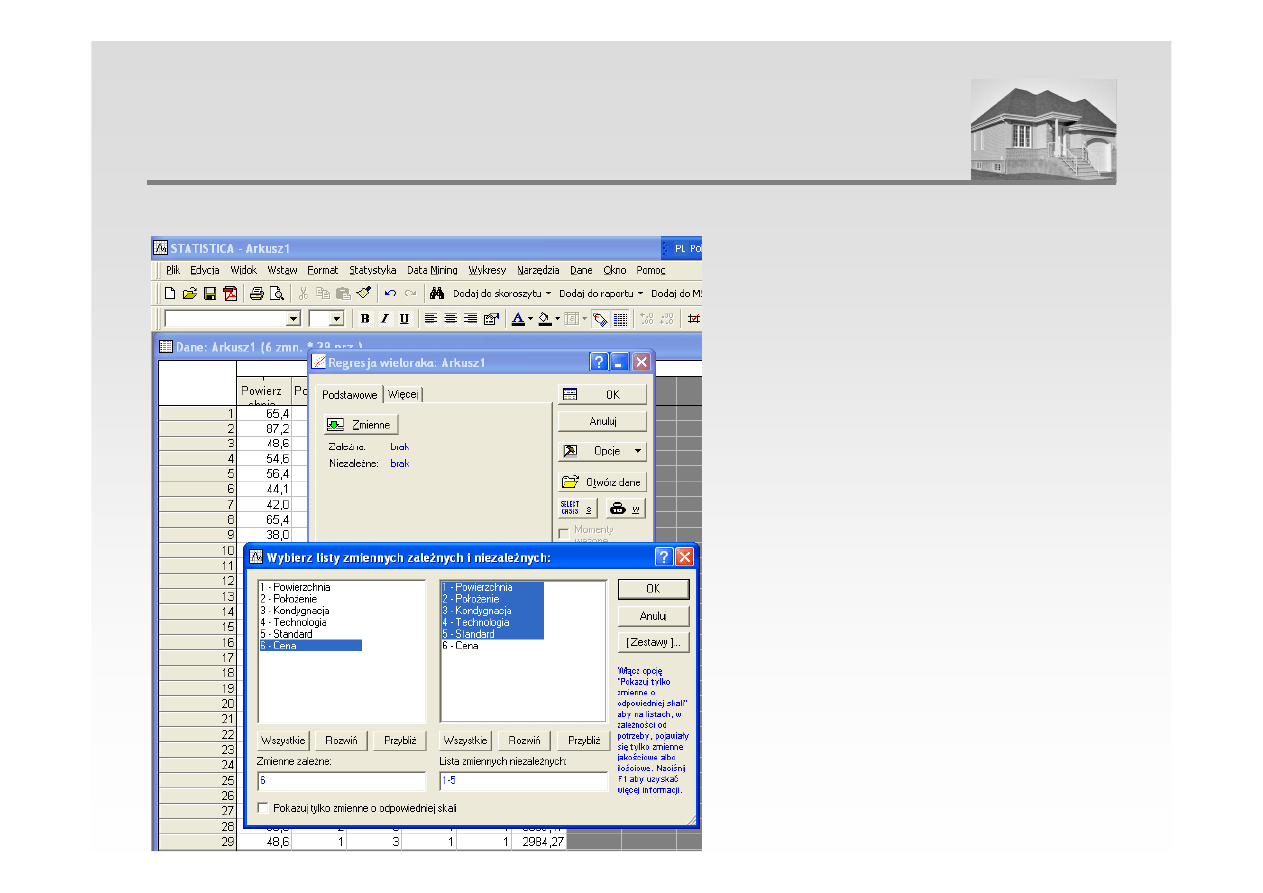
3. Estymacja parametrów modelu – przy pomocy programu STATISTICA

ANALIZA REGRESJI WIELORAKIEJ

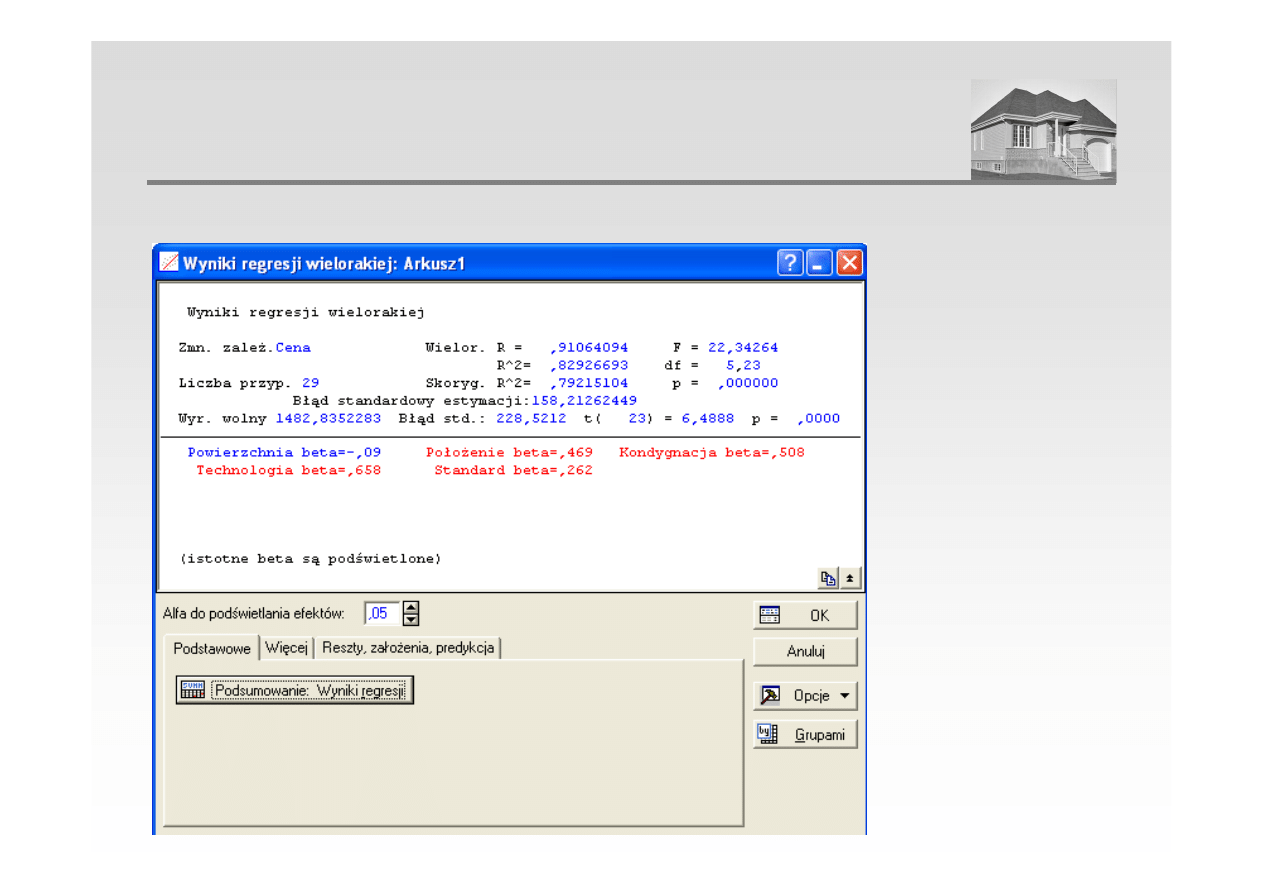
3. Estymacja parametrów modelu – przy pomocy programu STATISTICA

ANALIZA REGRESJI WIELORAKIEJ

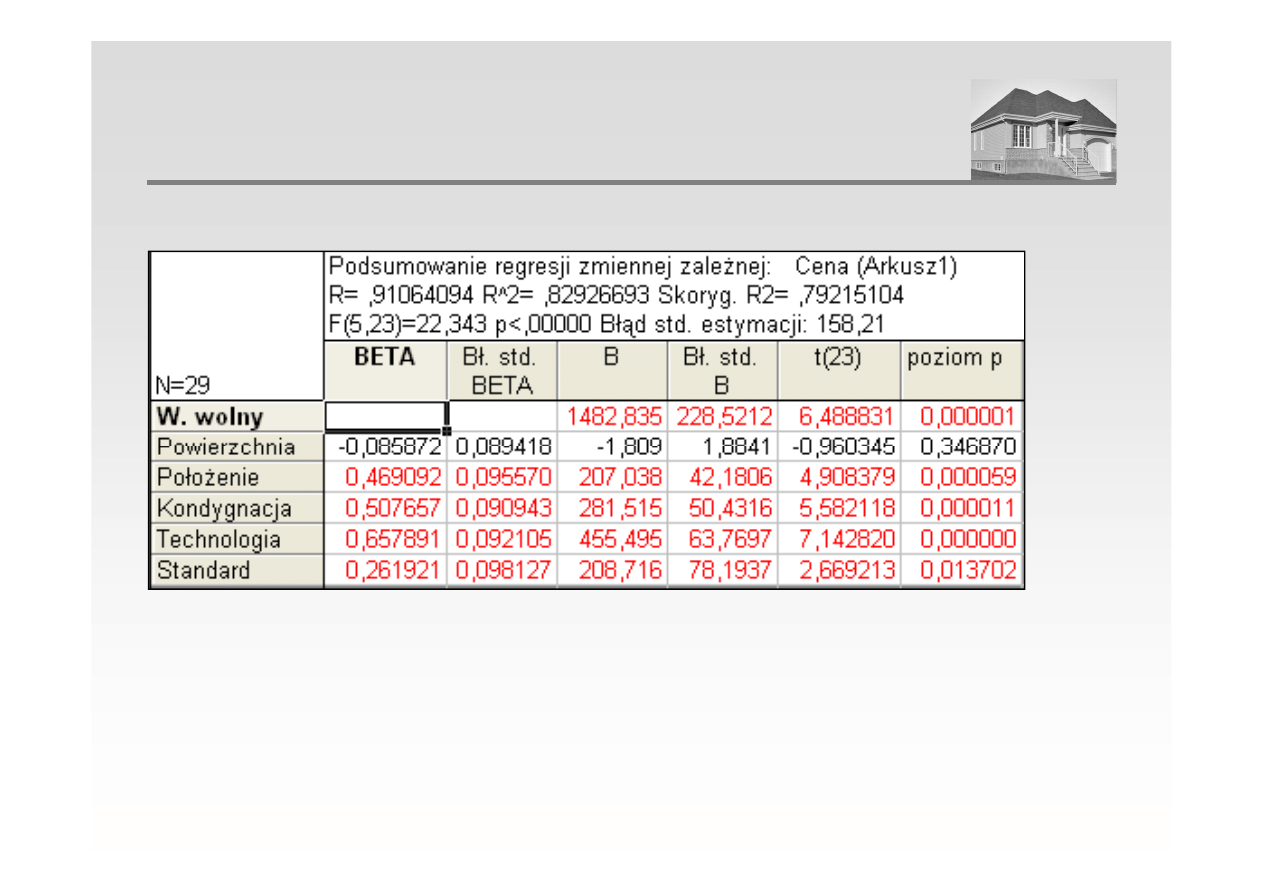
3. Estymacja parametrów modelu – przy pomocy programu STATISTICA

ANALIZA REGRESJI WIELORAKIEJ

Cena = 1482,83 – 1,81 · X

1

+ 207,04 · X

2

+ 281,51 · X

3

+ 455,49 · X

4

+ 208,72 · X

5

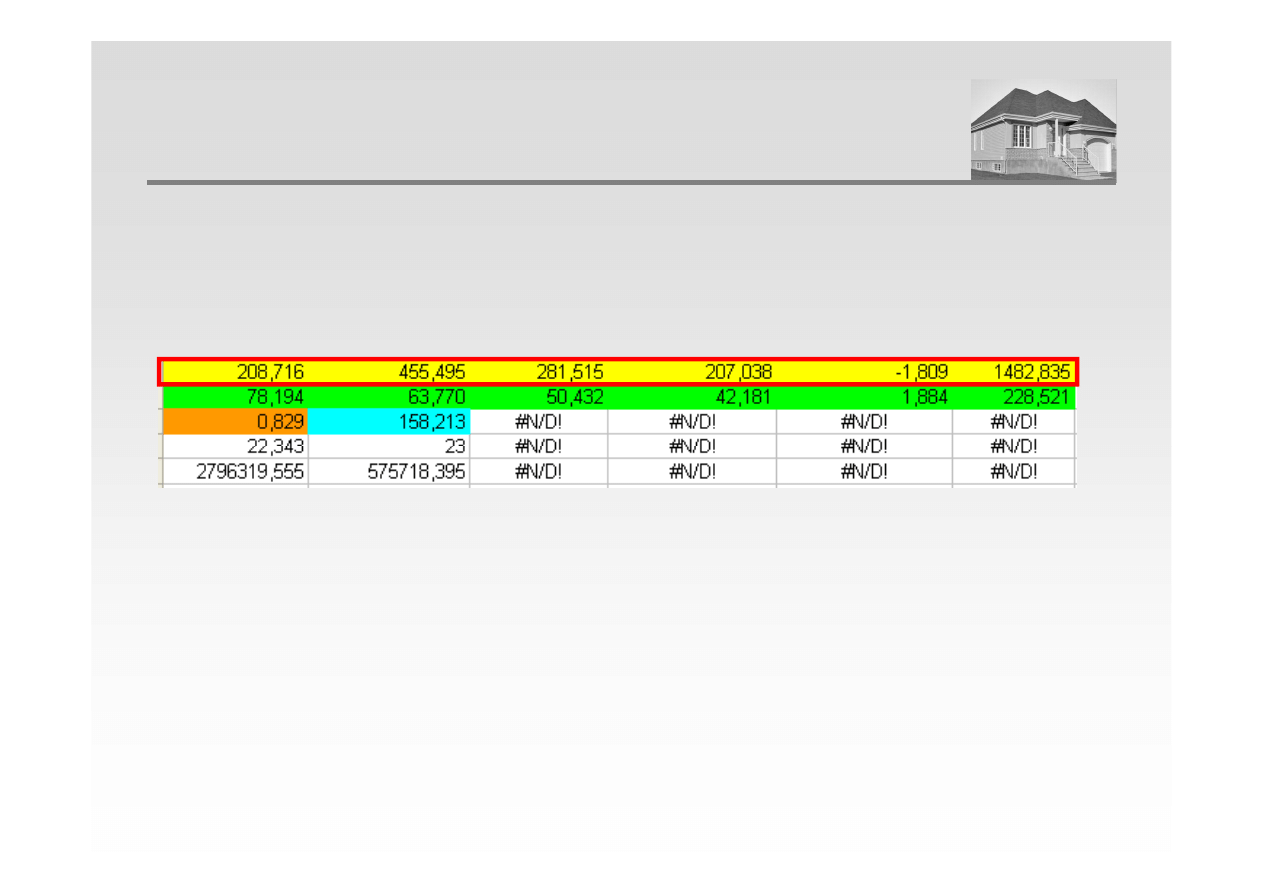
3. Estymacja parametrów modelu – przy pomocy arkusza kalkulacyjnego (polecenie REGLINP)

ANALIZA REGRESJI WIELORAKIEJ

Cena = 1482,83 – 1,81 · X

1

+ 207,04 · X

2

+ 281,51 · X

3

+ 455,49 · X

4

+ 208,72 · X

5

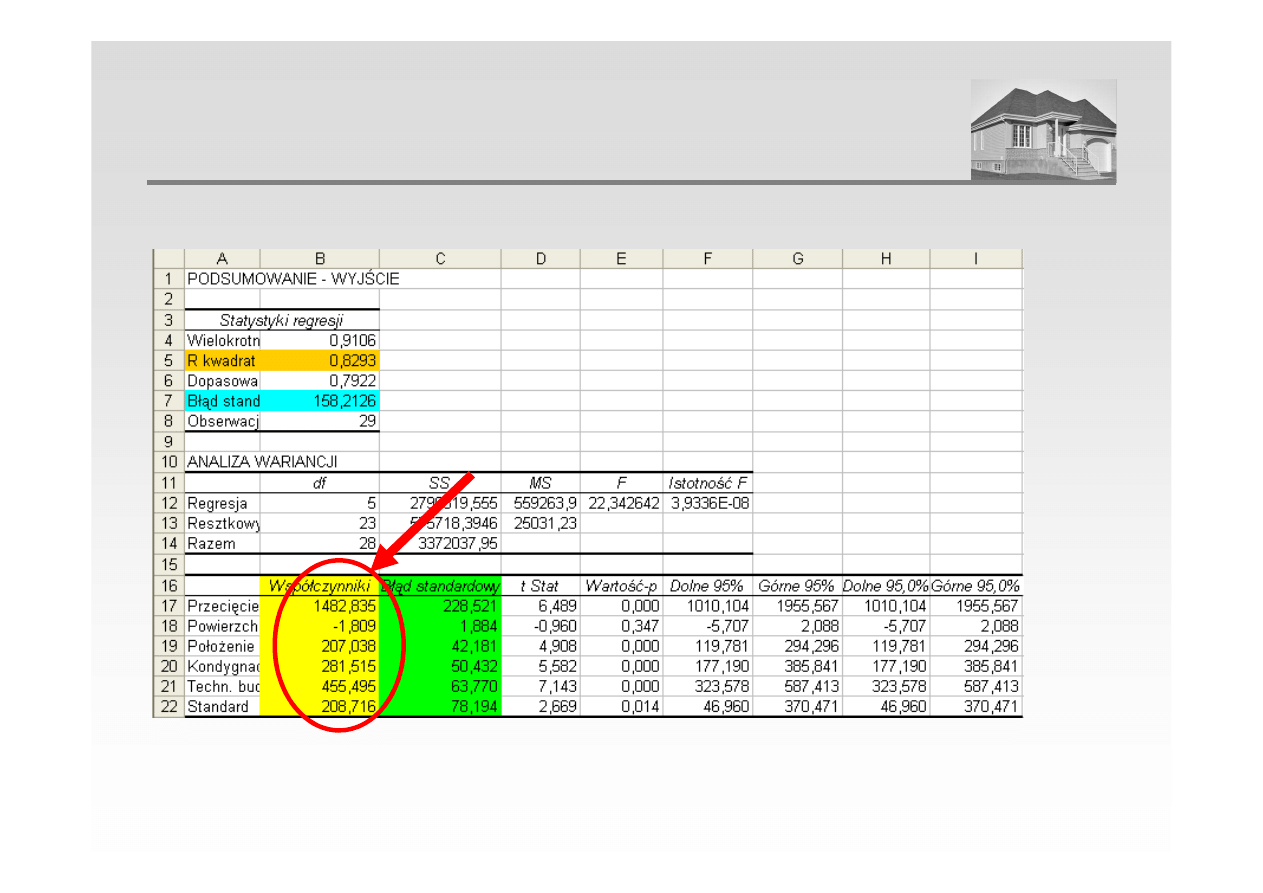
3. Estymacja parametrów modelu – przy pomocy arkusza kalkulacyjnego (narzędzie „Analiza danych”)

ANALIZA REGRESJI WIELORAKIEJ

Cena = 1482,83 – 1,81 · X

1

+ 207,04 · X

2

+ 281,51 · X

3

+ 455,49 · X

4

+ 208,72 · X

5

Przez weryfikację modelu ekonometrycznego należy rozumieć ocenę jego poprawności przy
wzięciu pod uwagę aspektów merytorycznych i statystycznych.

Weryfikacja modelu może polegać na określeniu stopnia zgodności zbudowanego modelu z
danymi empirycznymi oraz na ocenie jakości ocen parametrów strukturalnych.

Wnioskowanie z modelu jest możliwe tylko wtedy, gdy wartości miar modelu nie wskazują na
rozbieżności między modelem a rzeczywistością. Może ono polegać na interpretacji modelu

WERYFIKACJA MODELU REGRESJI WIELORAKIEJ

rozbieżności między modelem a rzeczywistością. Może ono polegać na interpretacji modelu
(diagnoza rynku), predykcji bądź symulacji.

Weryfikacja merytoryczna – to stwierdzenie zgodności modelu z wiedzą o badanych
zjawiskach i zdrowym rozsądkiem. Polega na ocenie właściwości znaków przy
obliczonych współczynnikach oraz wielkości oszacowanych współczynników.

Weryfikacja statystyczna – polega na sprawdzeniu czy model spełnia standardowe
postulaty statystyczne: istotność zmiennych objaśniających, wymagane dopasowanie
do wyników obserwacji i pożądane właściwości składnika resztowego.

WERYFIKACJA MODELU REGRESJI WIELORAKIEJ

do wyników obserwacji i pożądane właściwości składnika resztowego.

Przebieg weryfikacji statystycznej modelu

• weryfikacja hipotezy o nieistnieniu zależności pomiędzy zbiorem zmiennych

objaśniających a cenami transakcyjnymi

• ocena współczynnika determinacji

• ocena błędu standardowego estymacji

• weryfikacja hipotezy o nieistotności parametrów modelu regresji

WERYFIKACJA STATYSTYCZNA

• weryfikacja hipotezy o nieistotności parametrów modelu regresji

Hipotezę o nieistnieniu zależności pomiędzy zbiorem zmiennych objaśniających a
cenami transakcyjnymi weryfikuje się przy pomocy statystyki F Fischera-Snedecora -
stosowanej w celu zbadania czy uzyskane wyniki modelu regresji nie wystąpiły
przypadkowo.

Test F wykonuje się stawiając następujące hipotezy:
H

0

:

α

1

=

α

2

= ... =

α

k

= 0 co oznacza, że model nie przedstawia żadnej zależności

WERYFIKACJA HIPOTEZY O BRAKU ZALEŻNOŚCI OPISANEJ
PRZEZ MODEL

H

0

:

α

1

=

α

2

= ... =

α

k

= 0 co oznacza, że model nie przedstawia żadnej zależności

H

1

: co najmniej jedno

α ≠

0, co oznacza, że model przedstawia zależność statystyczną,

W celu weryfikacji hipotezy zerowej obliczoną wartość statystyki F porównujemy z
wartością krytyczną.

Wartość empiryczną statystyki F oblicza się z wzoru:

(

)

/

ˆ

1

2

















−

=

∑

=

k

y

y

F

n

i

i

WERYFIKACJA HIPOTEZY O BRAKU ZALEŻNOŚCI OPISANEJ
PRZEZ MODEL

(

)

)

1

/(

ˆ

1

2

−

−













−

=

∑

=

k

n

y

y

F

n

i

i

gdzie:

- oznacza kolejną cenę estymowaną (wartość teoretyczną - estymator ceny)
- jest to średnia arytmetyczna obliczona z cen transakcyjnych

y

i

- oznacza kolejną cenę transakcyjną

n

- jest to liczba obserwacji (liczba danych o transakcjach)

k

- oznacza liczbę zmiennych objaśniających (liczba cech przyjętych do analiz)

i

yˆ

y

Wartość krytyczną odczytuje się z tabeli wartości krytycznych rozkładu F-Snedecora dla
przyjętego poziomu istotności (równego zazwyczaj 0,01; 0,05 lub 0,10), określonej liczby
zmiennych objaśniających i stopni swobody.
Przykład:
dla liczby nieruchomości podobnych

n = 21

dla liczby zmiennych objaśniających

v

1

= 5

dla liczby stopni swobody równej n - k - 1

v

2

= 21 -5 -1 = 15

dla poziomu istotności równego

α

= 0,05

wartość krytyczna statystyki F na podstawie tabeli wartości krytycznych wynosi 2,90

WERYFIKACJA HIPOTEZY O BRAKU ZALEŻNOŚCI OPISANEJ
PRZEZ MODEL

wartość krytyczna statystyki F na podstawie tabeli wartości krytycznych wynosi 2,90

v2\v1

1

2

...

5

1

161,4

199,5

...

230,2

2

18,51

19,00

...

19,30

...

...

...

...

...

15

4,54

3,68

...

2,90

Jeżeli wartość empiryczna statystyki F jest wyższa od wartości krytycznej tzn:

F

obl

≥≥≥≥

F

kryt

to hipotezę o nieistnieniu zależności należy odrzucić (zależności opisane modelem nie wystąpiły
przypadkowo).

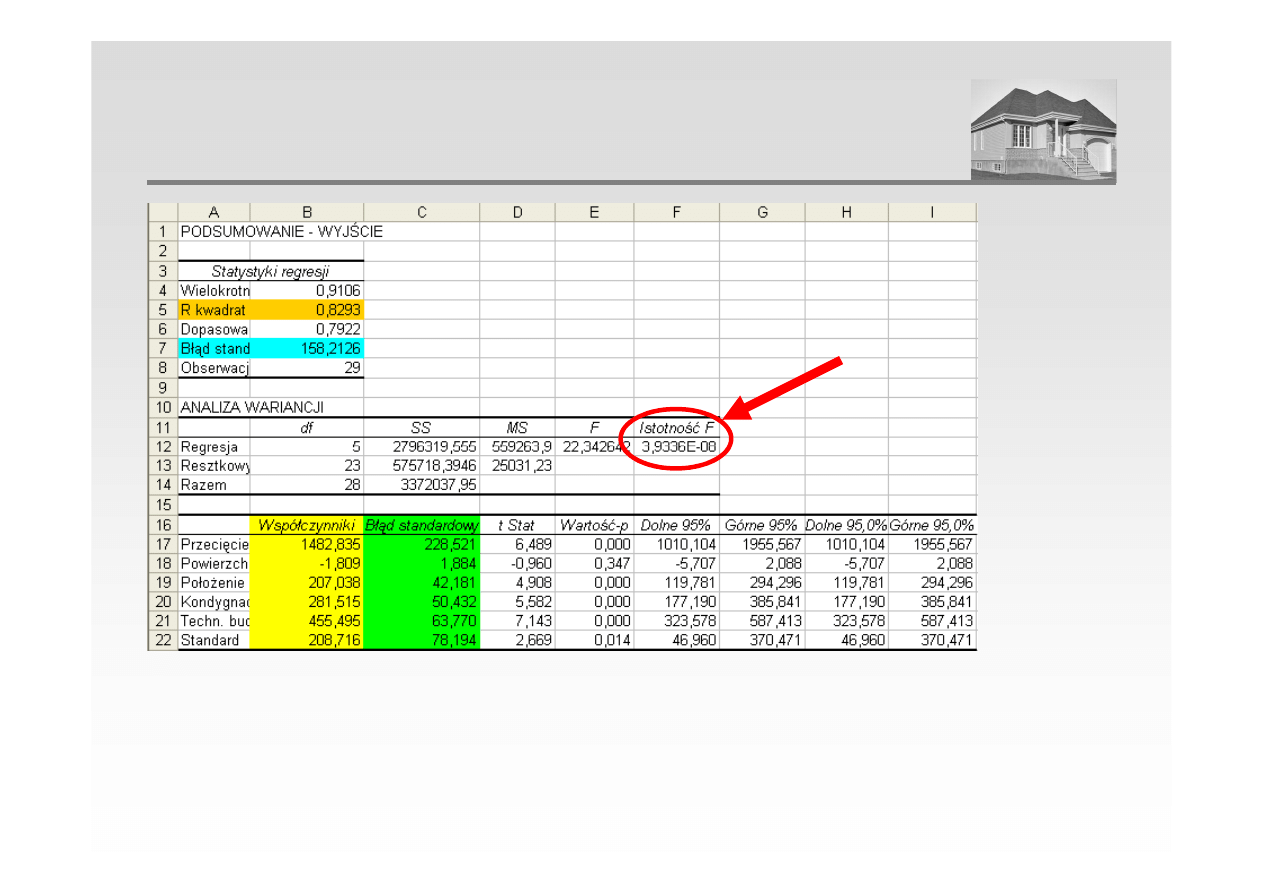
WERYFIKACJA HIPOTEZY O BRAKU ZALEŻNOŚCI OPISANEJ
PRZEZ MODEL (PRZYKŁAD)

Istotność F oznacza prawdopodobieństwo, że zależności opisane modelem wystąpiły
przypadkowo

Istotność F = 0,00000004

hipotezę o nieistnieniu zależności należy odrzucić (zależności opisane modelem nie wystąpiły
przypadkowo).

Współczynnik determinacji R

2

określa się z następującego wzoru:

(

)

(

)

(

)

(

)

∑

∑

∑

∑

=

=

=

=

−

−

−

=

−

−

=

n

i

i

n

i

i

i

n

i

i

n

i

i

y

y

y

y

y

y

y

y

R

1

2

1

2

1

2

1

2

2

ˆ

1

ˆ

WSPÓŁCZYNNIK DETERMINACJI

R

2

pomnożony przez 100% interpretuje się jako stopień wyjaśnienia całkowitej zmienności

zmiennej zależnej przez zmienność uwzględnionych w badaniu zmiennych niezależnych.
Współczynnik determinacji spełnia warunek: 0 < R

2

< 1. Im bliższy jest jedności, tym lepiej

zależność liniowa została dopasowana do danego zbioru obserwacji.

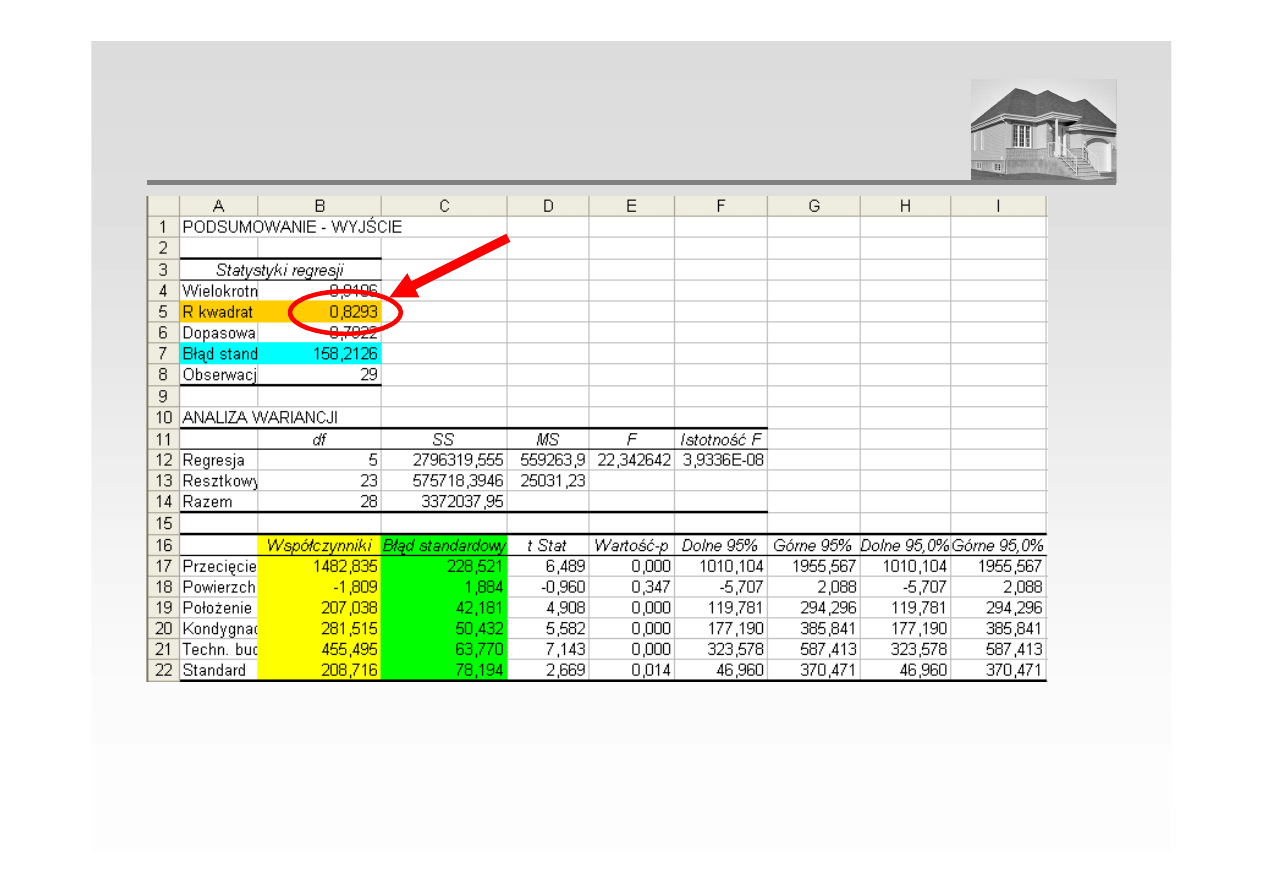
WSPÓŁCZYNNIK DETERMINACJI (PRZYKŁAD)

Współczynnik determinacji wyniósł 0,829 co oznacza, ze 83% zmienności cen zostało
wyjaśnione przez model

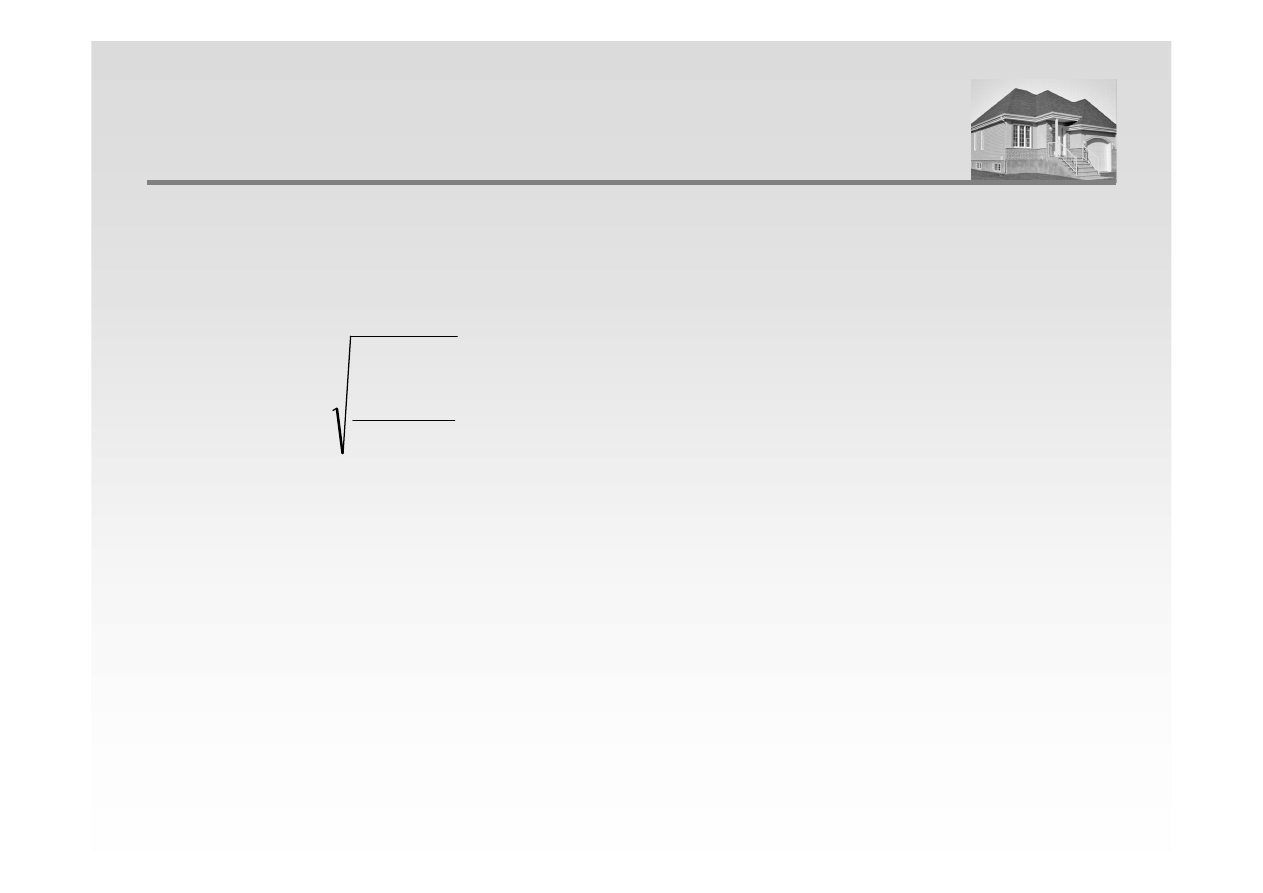
Błąd standardowy estymacji określony jest jako pierwiastek z wariancji reszt i może być
interpretowany jako błąd, który możliwy jest do popełnienia w trakcie prognozowania przy
pomocy modelu. Opisany jest następującym wzorem:

1

1

2

−

−

=

∑

=

k

n

e

S

n

i

i

e

BŁĄD STANDARDOWY ESTYMACJI
(ODCHYLENIE STANDARDOWE RESZT)

1

−

−

k

n

gdzie:
e

i

- reszta (różnica pomiędzy wartością teoretyczną i obserwowaną)

n - liczba obserwacji
k - liczba zmiennych objaśniających

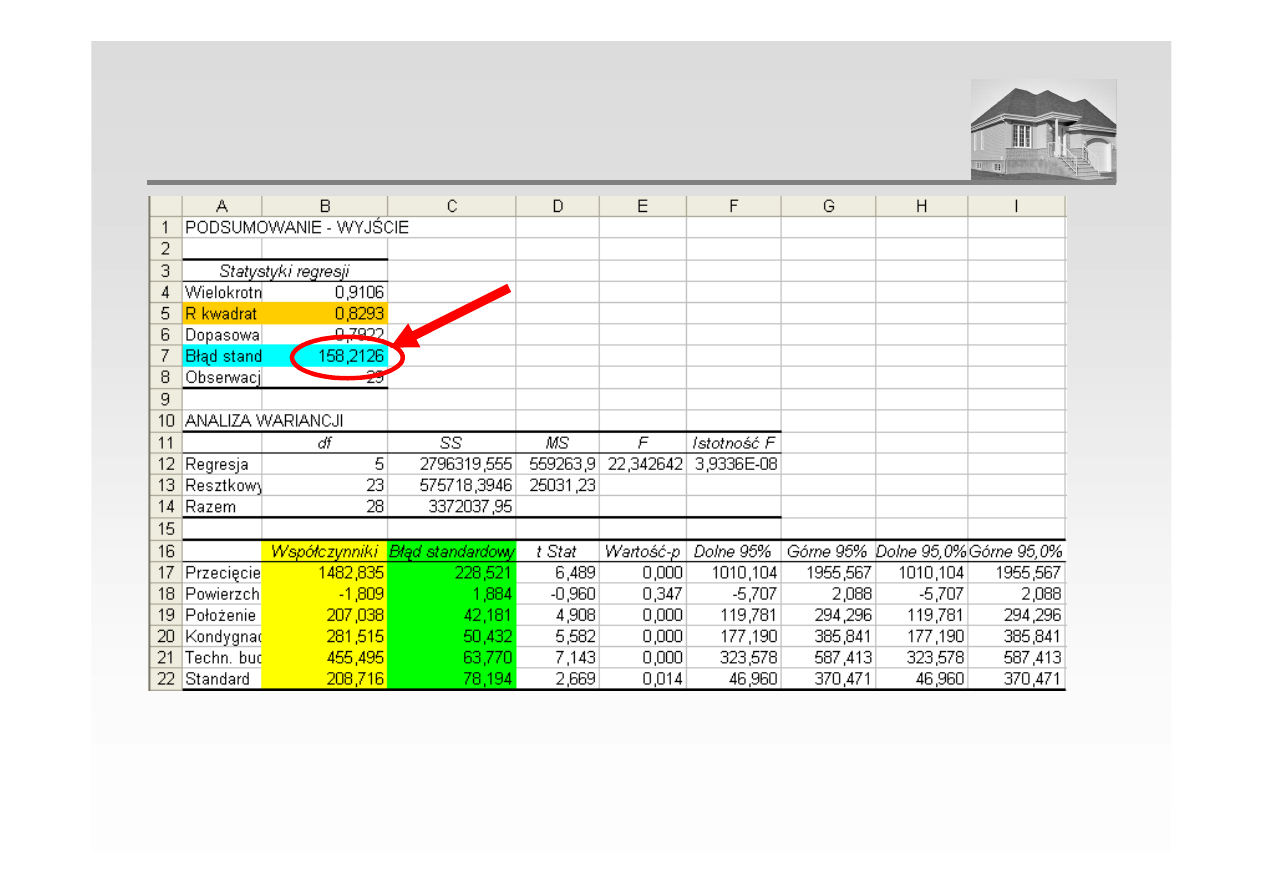
BŁĄD STANDARDOWY ESTYMACJI
(ODCHYLENIE STANDARDOWE RESZT) - PRZYKŁAD

Błąd standardowy estymacji wyniósł 158,21 zł co oznacza, że błąd prognozy będzie bliski tej
wartości

Narzędziem pozwalającym na ocenę istotności poszczególnych zmiennych niezależnych jest test t-
Studenta. Określa on, czy liniowa zależność między dwiema zmiennymi jest istotna statystycznie.
Zakłada się, że stosunek odchylenia od średniej lub innego parametru w rozkładzie statystyk z
prób do błędu standardowego tego rozkładu jest zgodny z rozkładem t.

t

i

α

=

WERYFIKACJA HIPOTEZY O NIEISTOTNOŚCI PARAMETRÓW
MODELU

i

S

t

i

α

=

gdzie:

α

i

- testowany parametr modelu regresji

S

α

i

- błąd standardowy parametru

α

i

Test t-Studenta może posłużyć do weryfikacji następującej hipotezy:
H

0

:

α

i

= 0 co oznacza, że dany parametr w stopniu nieistotnym różni się od zera (nie istnieje

zależność między daną zmienną a ceną)
H

1

:

α

i

≠

0, co oznacza, że wartość danego parametru jest statystycznie istotna

Wartość

krytyczną

rozkładu

t-Studenta

odczytuje

się

z

tablic

(lub

z

kalkulatora

prawdopodobieństwa) dla przyjętego poziomu istotności i określonej liczby stopni swobody.

WERYFIKACJA HIPOTEZY O NIEISTOTNOŚCI PARAMETRÓW
MODELU

Jeżeli wartość empiryczna statystyki t jest wyższa od wartości krytycznej tzn:

t

obl

≥≥≥≥

t

kryt

to hipotezę o nieistotności parametru należy odrzucić (parametr jest istotny statystycznie).

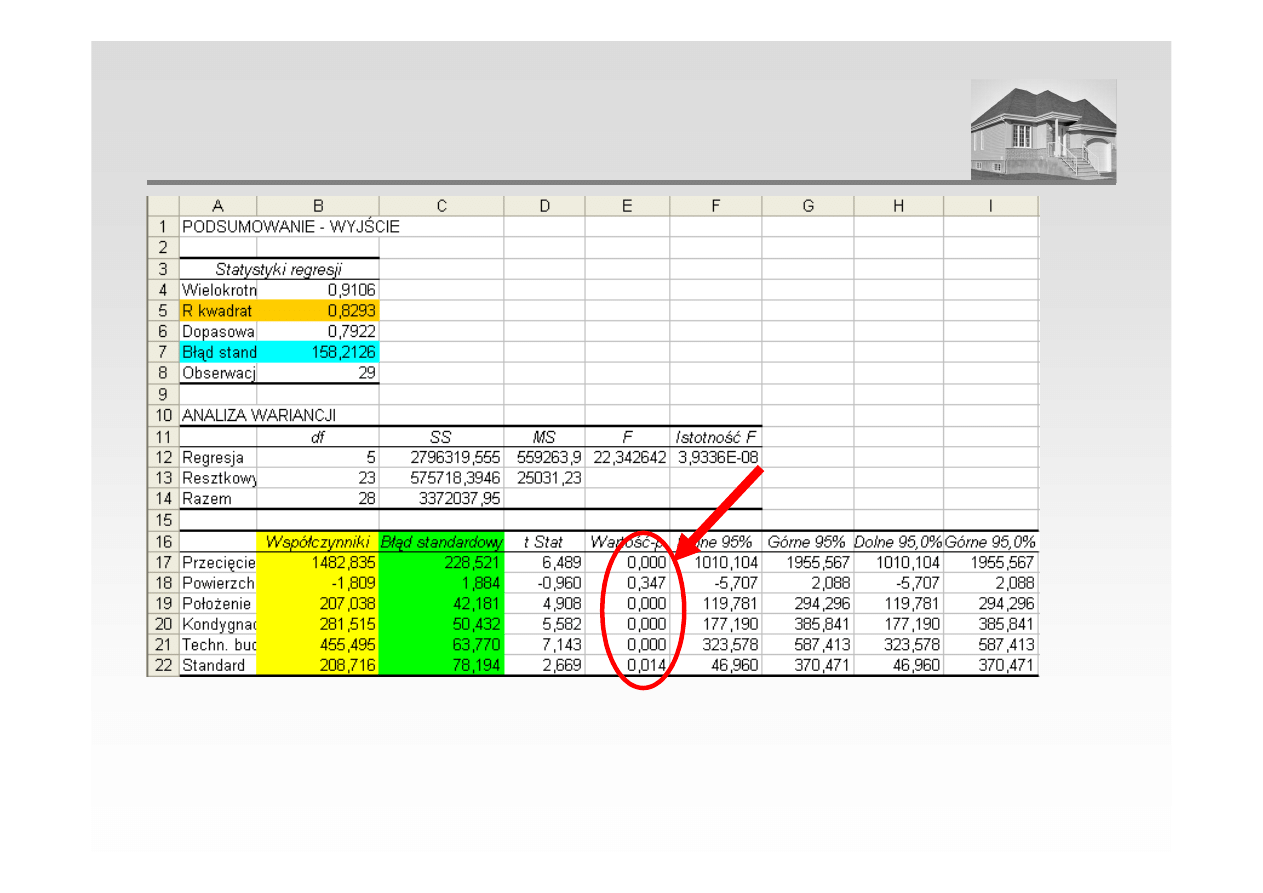
WERYFIKACJA HIPOTEZY O NIEISTOTNOŚCI PARAMETRÓW
MODELU (PRZYKŁAD)

Wartość-p oznacza prawdopodobieństwo, że dana zmienna jest statystycznie nieistotna. Za
poziom krytyczny przyjmujemy 0,05