
RYNEK NIERUCHOMOŚCI
dr inż. Radosław Cellmer

Wykład
Modelowanie ekonometryczne cen nieruchomości
Treść wykładu:
1. Analiza regresji wielorakiej
2. Zastosowanie narzędzi obliczeniowych
3. Weryfikacja i interpretacja modelu regresji
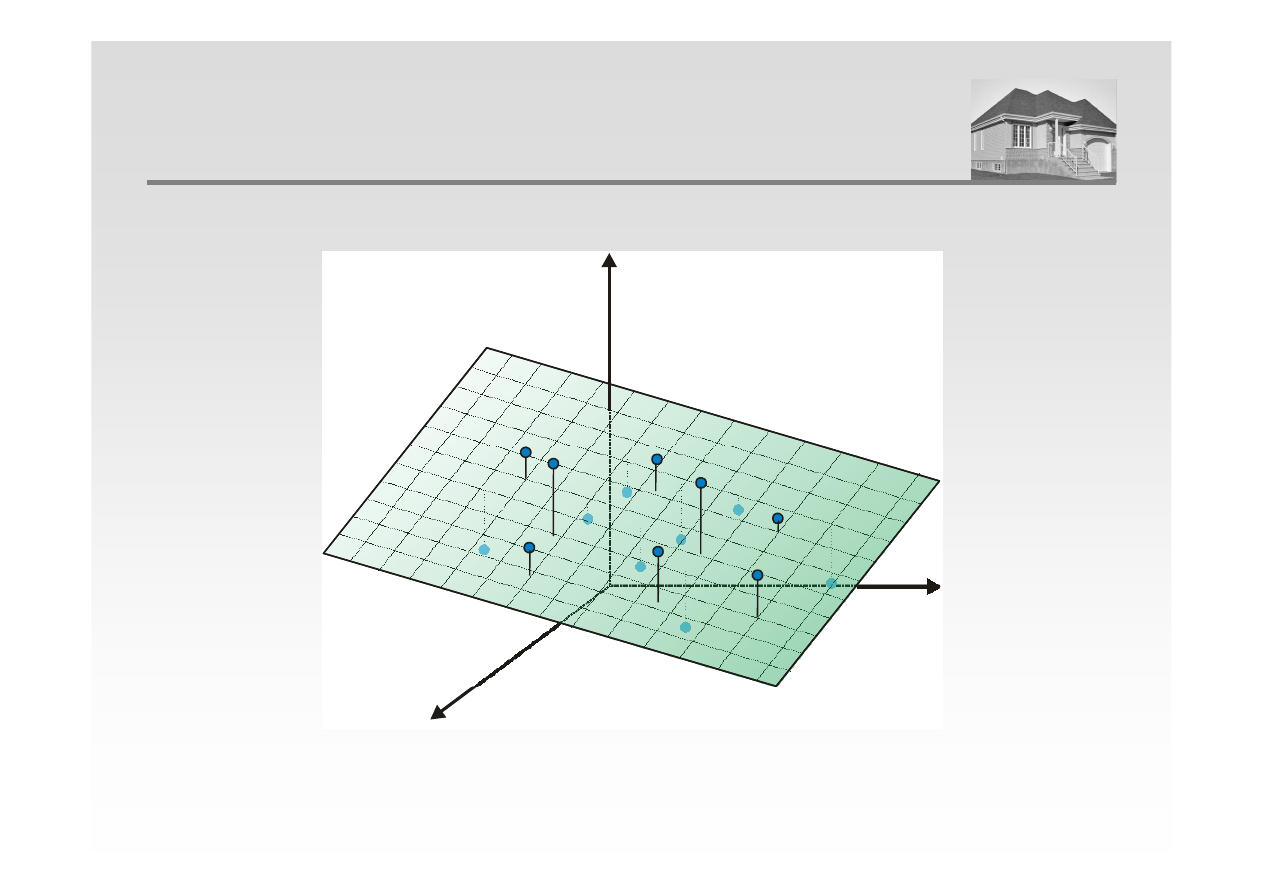
Z
PŁASZCZYZNA W PRZESTRZENI TRÓJWYMIAROWEJ
X
Y
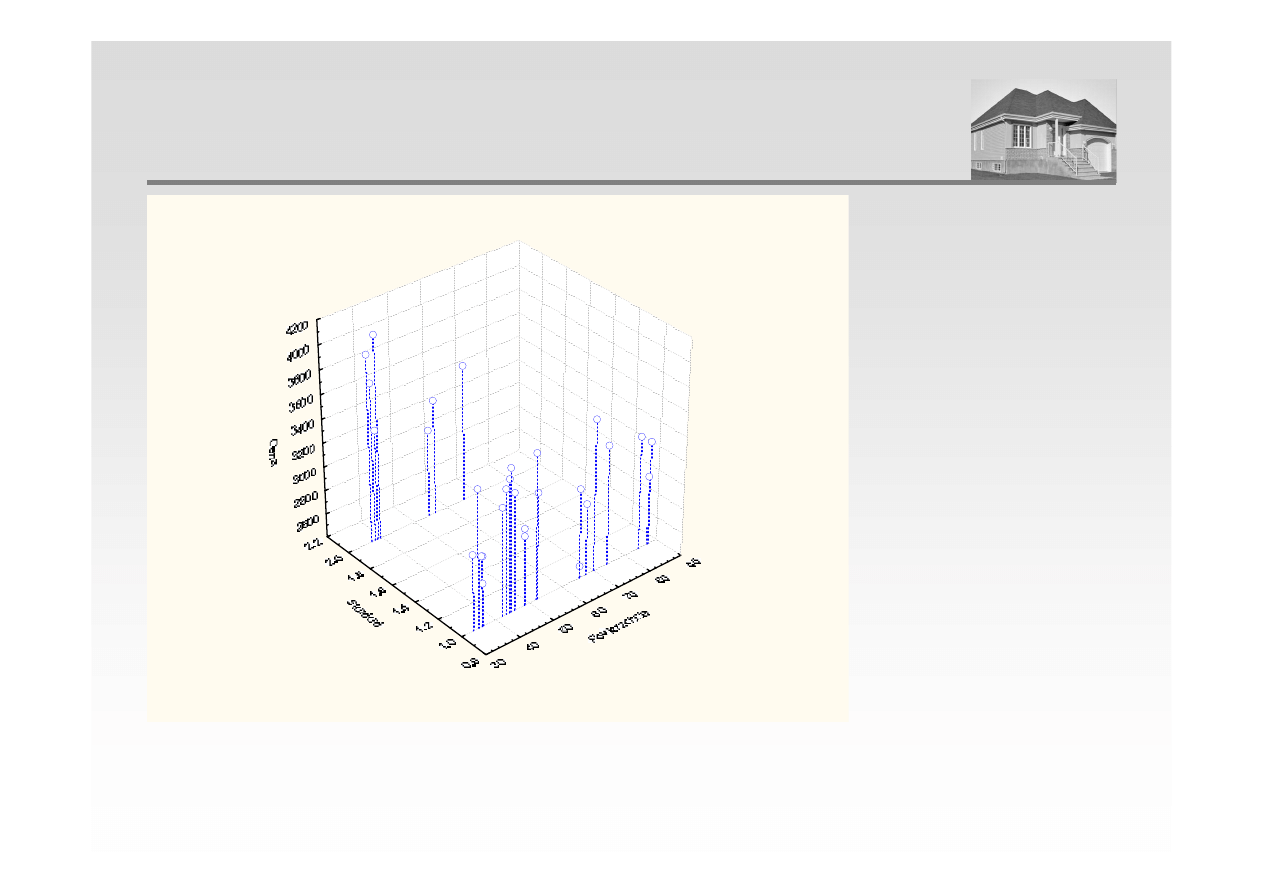
POZIOM CEN TRANSAKCYJNYCH W ZALEŻNOŚCI OD
POWIERZCHNI I STANDARDU MIESZKANIA
Rozrzutu 3W Cena wzgl
ę
dem Powierzchnia i Standard
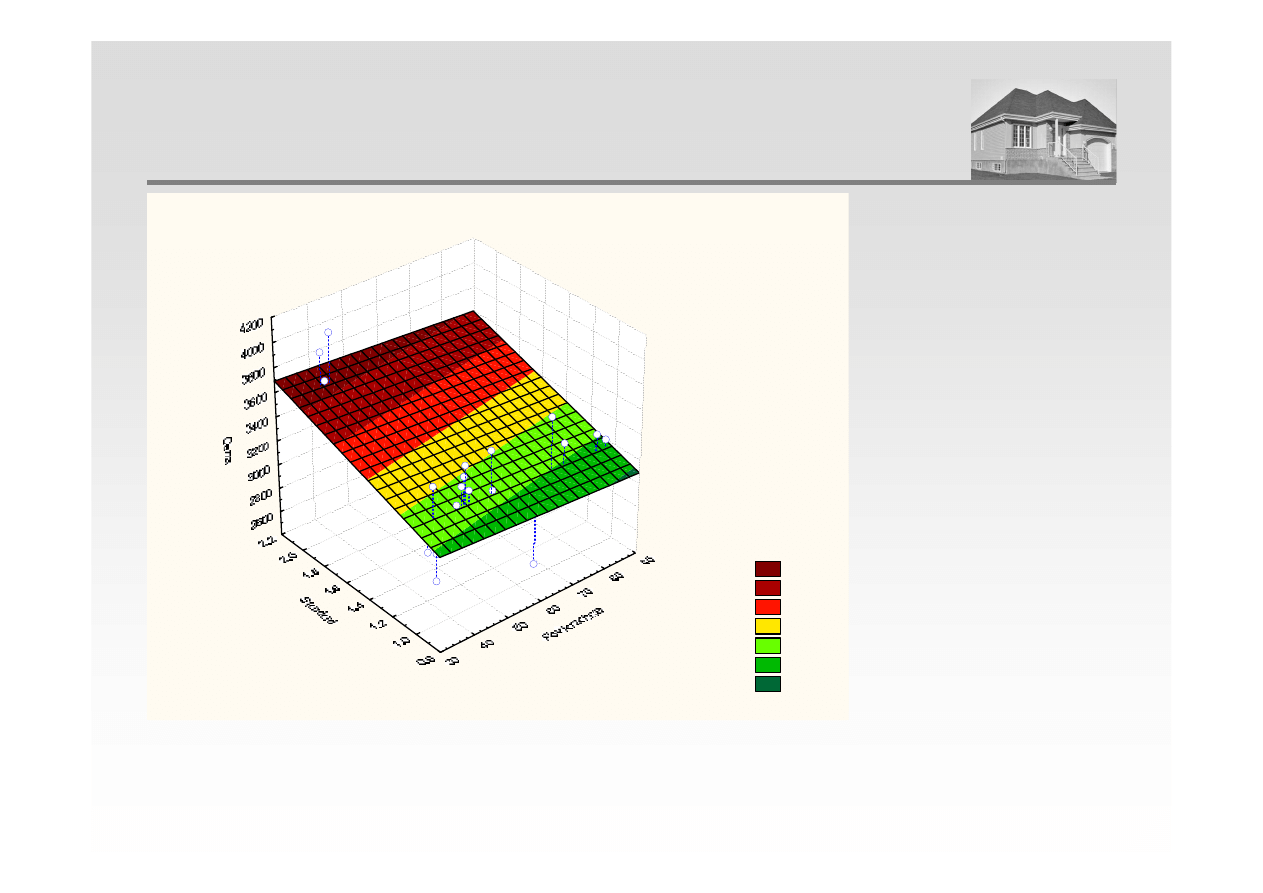
POZIOM CEN TRANSAKCYJNYCH W ZALEŻNOŚCI OD
POWIERZCHNI I STANDARDU MIESZKANIA
Cena = 2938,7641-1,6303*x+364,9833*y
> 3600
< 3600
< 3500
< 3400
< 3300
< 3200
< 3100

Ogólnym celem regresji wielokrotnej jest badanie związków pomiędzy wieloma zmiennymi
objaśniającymi (niezależnymi) a zmienną objaśnianą (zależną).
Przykładowo rzeczoznawca majątkowy określając wartość lokalu mieszkalnego zbiera dane
dotyczące podobnych lokali – powierzchnia użytkowa, liczba pomieszczeń, zużycie techniczne
itp. oraz subiektywną ocenę atrakcyjności obiektu.
Dokonując analizy regresji wielorakiej można uzyskać odpowiedź na pytanie:
REGRESJA WIELORAKA OGÓLNY CEL
Jak poszczególne wielkości wpływają na cenę lokalu?
U podstaw modelu regresji leży hipoteza o istnieniu zależności, między co najmniej dwiema
zmiennymi. Zakłada się, że wzrostowi jednej z badanych wielkości towarzyszy wzrost lub spadek
drugiej. Stąd zależność zmiennej Y od zmiennych X
1
, X
2
, ..., X
k
przedstawia się za pomocą funkcji:
Y = f(X
1
, X
2
, ..., X
k
)
1. Określenie zestawu zmiennych (cech rynkowych) i ich opis w przyjętej skali liczbowej
2. Określenie postaci analitycznej modelu
3. Estymacja parametrów modelu
4. Weryfikacja merytoryczna i statystyczna modelu
5. Zastosowanie modelu do prognozy zmiennej objaśnianej
PROCEDURA ANALIZY REGRESJI WIELORAKIEJ
5. Zastosowanie modelu do prognozy zmiennej objaśnianej
Cena = 2938,7641-1,6303*x+364,9833*y
> 3600
< 3600
< 3500
< 3400
< 3300
< 3200
< 3100

Najczęściej wykorzystywanym modelem jest model liniowy o następującej postaci:
Y =
ββββ
0
+
ββββ
1
X
1
+
ββββ
2
X
2
+ … +
ββββ
k
X
k
+
ξξξξ
gdzie:
Y
- zmienna objaśniana (zależna)
X
1
, X
2
, ..., X
k
- zmienne objaśniające (niezależne)
β
1
,
β
2
, ...,
β
k
- parametry modelu
POSTAĆ ANALITYCZNA MODELU REGRESJI WIELORAKIEJ
β
1
,
β
2
, ...,
β
k
- parametry modelu
β
0
- stała
ξ
- składnik losowy (reszta) modelu
Y
ˆ
Dane wyjściowe:
Lp.
Cena
Cena
Cena
Cena
Cecha 1
Cecha 1
Cecha 1
Cecha 1
Cecha 2
Cecha 2
Cecha 2
Cecha 2
...
Cecha k
Cecha k
Cecha k
Cecha k
1
y
1
x
11
x
12
…
x
1k
ESTYMACJA PARAMETRÓW MODELU
1
y
1
x
11
x
12
…
x
1k
2
y
2
x
21
x
22
…
x
2k
…
…
…
…
…
…
n
y
n
x
n1
x
n2
…
x
nk

Układ równań:
y
1
=
β
0
+
β
1
x
11
+
β
2
x
12
+ … +
β
k
x
1k
y
2
=
β
0
+
β
1
x
21
+
β
2
x
22
+ … +
β
k
x
2k
………………………………………
y
n
=
β
0
+
β
1
x
n1
+
β
2
x
n2
+ … +
β
k
x
nk
Układ równań w postaci macierzowej:
Y = XA
gdzie:
ESTYMACJA PARAMETRÓW MODELU
Y = XA
gdzie:
=
n
2
1
y
...
y
y
Y
=
nk
n2
n1
2k
22
21
1k
12
11
x
...
x
x
1
...
...
...
...
...
x
...
x
x
1
x
...
x
x
1
X
=
k
β
β
β
...
A
1
0
Macierz parametrów modelu wyznacza się metodą najmniejszych kwadratów, wykorzystując
następujący wzór:
A = (X
T
X)
-1
X
T
Y
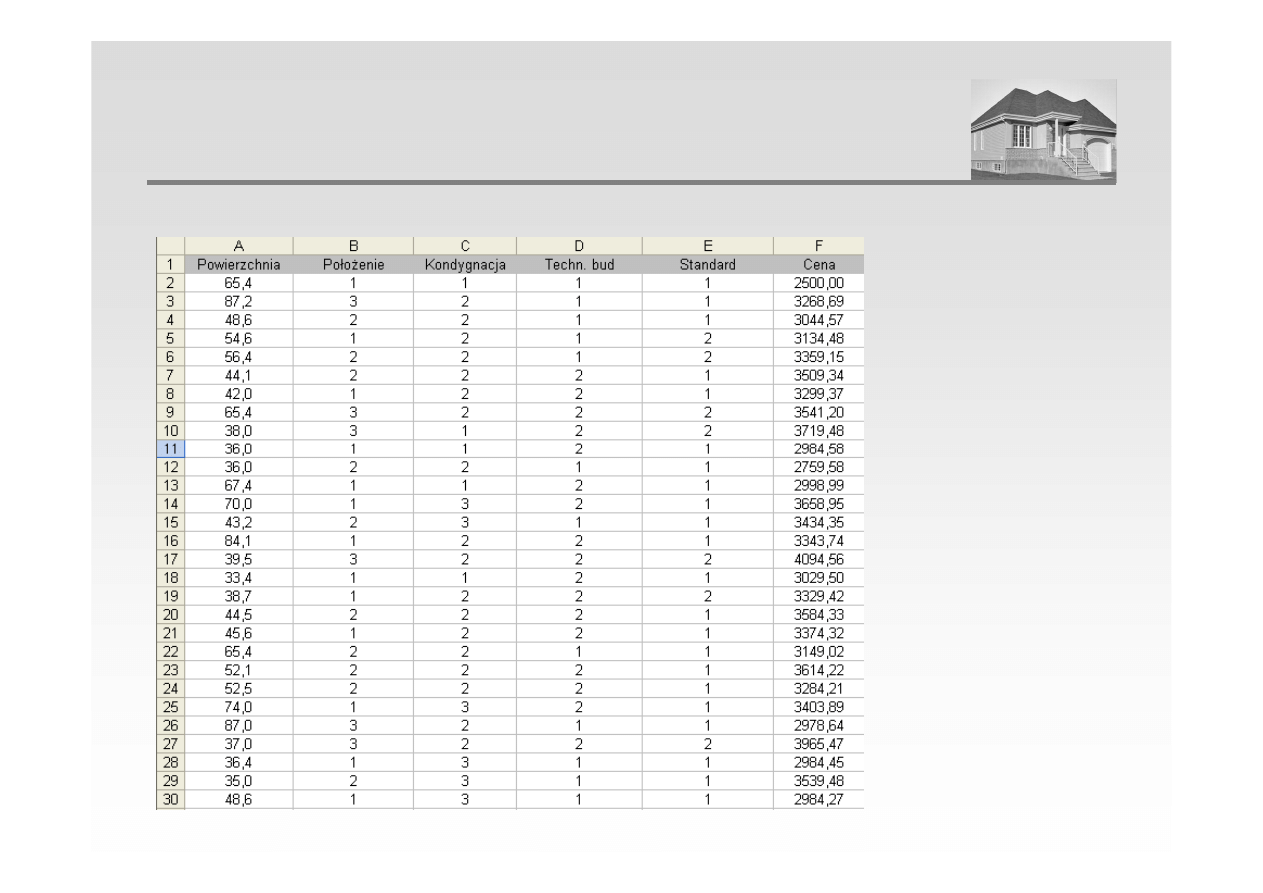
1. Określenie zestawu zmiennych (cech rynkowych) i ich opis w przyjętej skali liczbowej
ANALIZA REGRESJI WIELORAKIEJ

2. Określenie postaci analitycznej modelu
Y =
ββββ
0
+
ββββ
1
X
1
+
ββββ
2
X
2
+
ββββ
3
X
3
+
ββββ
4
X
4
+
ββββ
5
X
5
+ … +
ββββ
k
X
k
+
ξξξξ
gdzie:
Y
- zmienna objaśniana (cena transakcyjna)
X
1
- zmienna objaśniająca (powierzchnia)
X
2
- zmienna objaśniająca (położenie)
X
- zmienna objaśniająca (kondygnacja)
ANALIZA REGRESJI WIELORAKIEJ
2
X
3
- zmienna objaśniająca (kondygnacja)
X
4
- zmienna objaśniająca (technologia)
X
5
- zmienna objaśniająca (standard)
β
1
,
β
2
, ...,
β
k
- parametry modelu
β
0
- stała
ξ
- składnik losowy (reszta) modelu
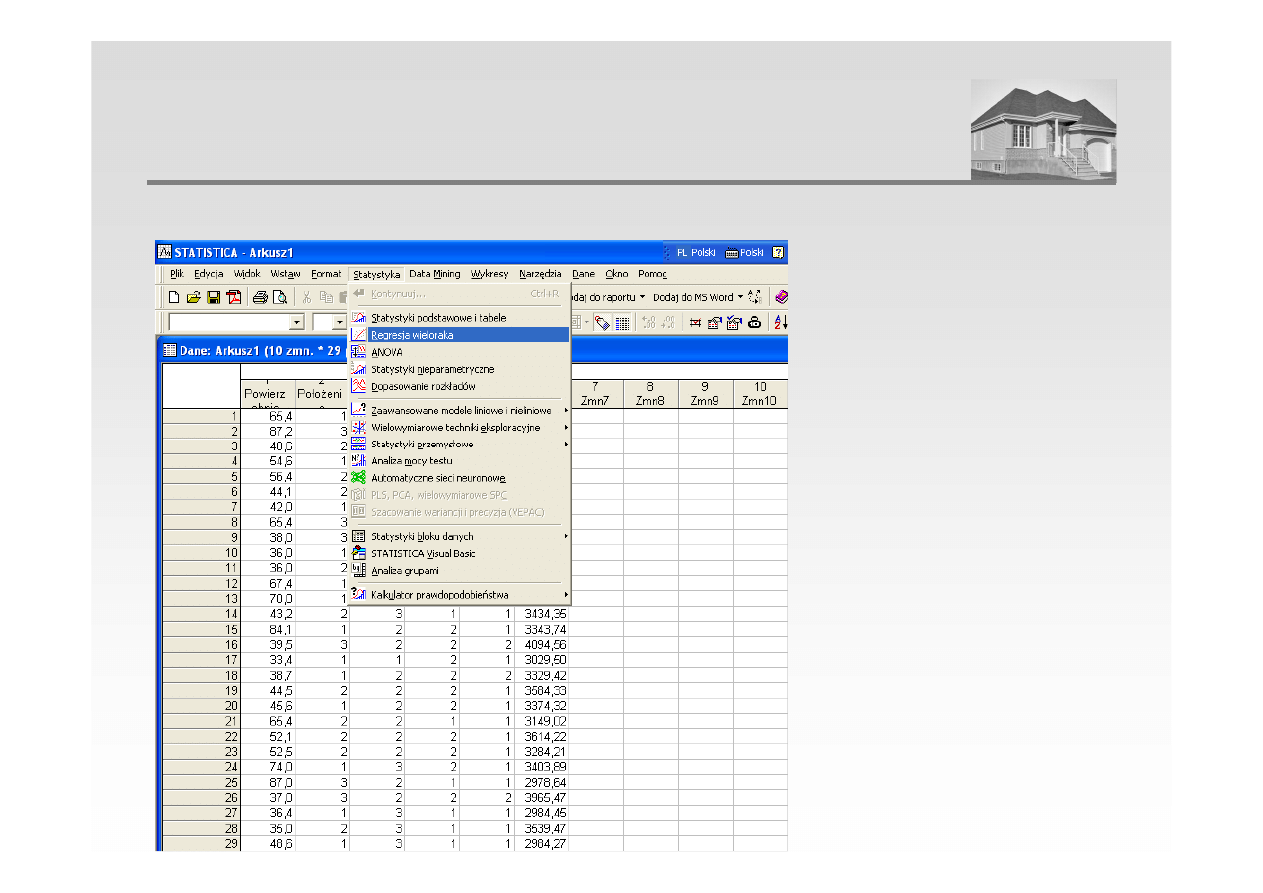
3. Estymacja parametrów modelu – przy pomocy programu STATISTICA
ANALIZA REGRESJI WIELORAKIEJ
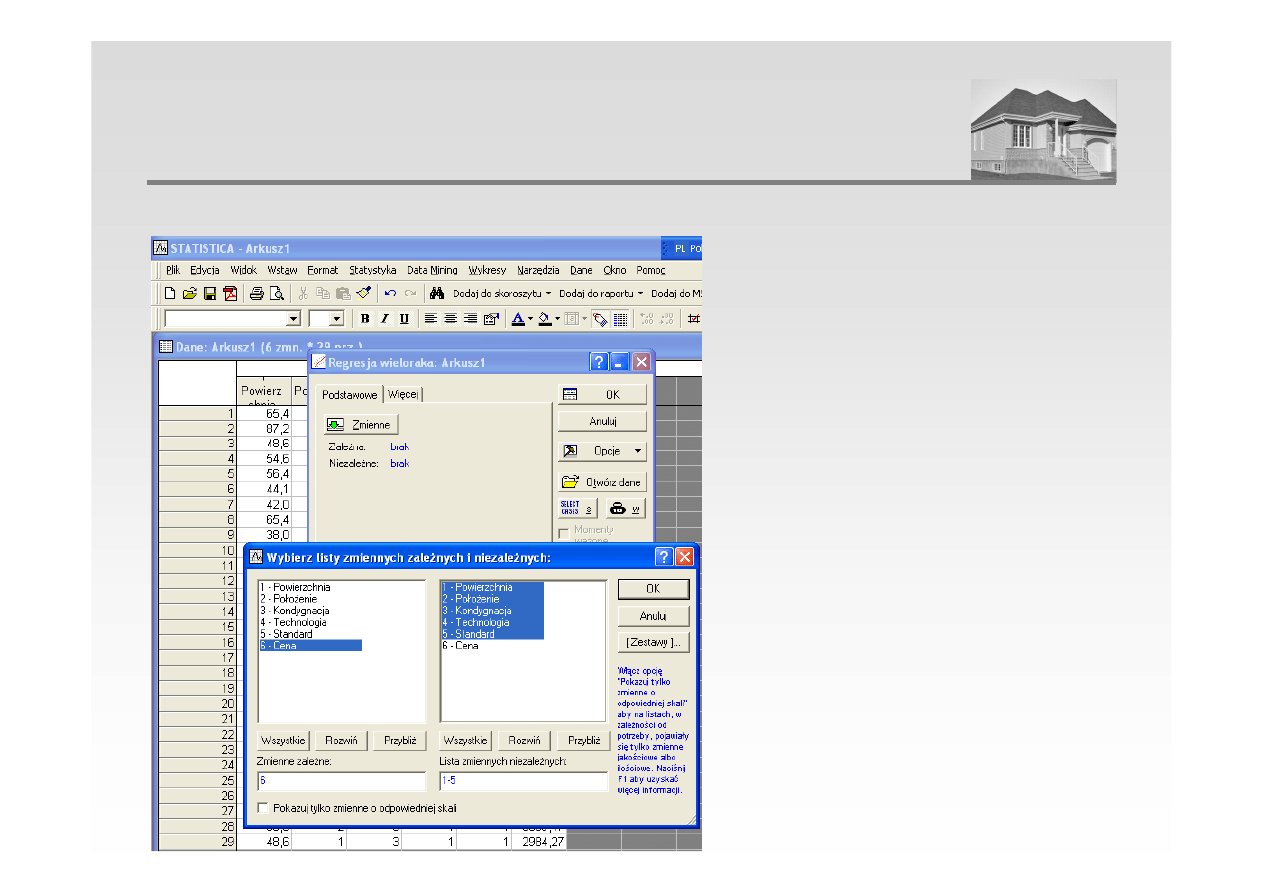
3. Estymacja parametrów modelu – przy pomocy programu STATISTICA
ANALIZA REGRESJI WIELORAKIEJ
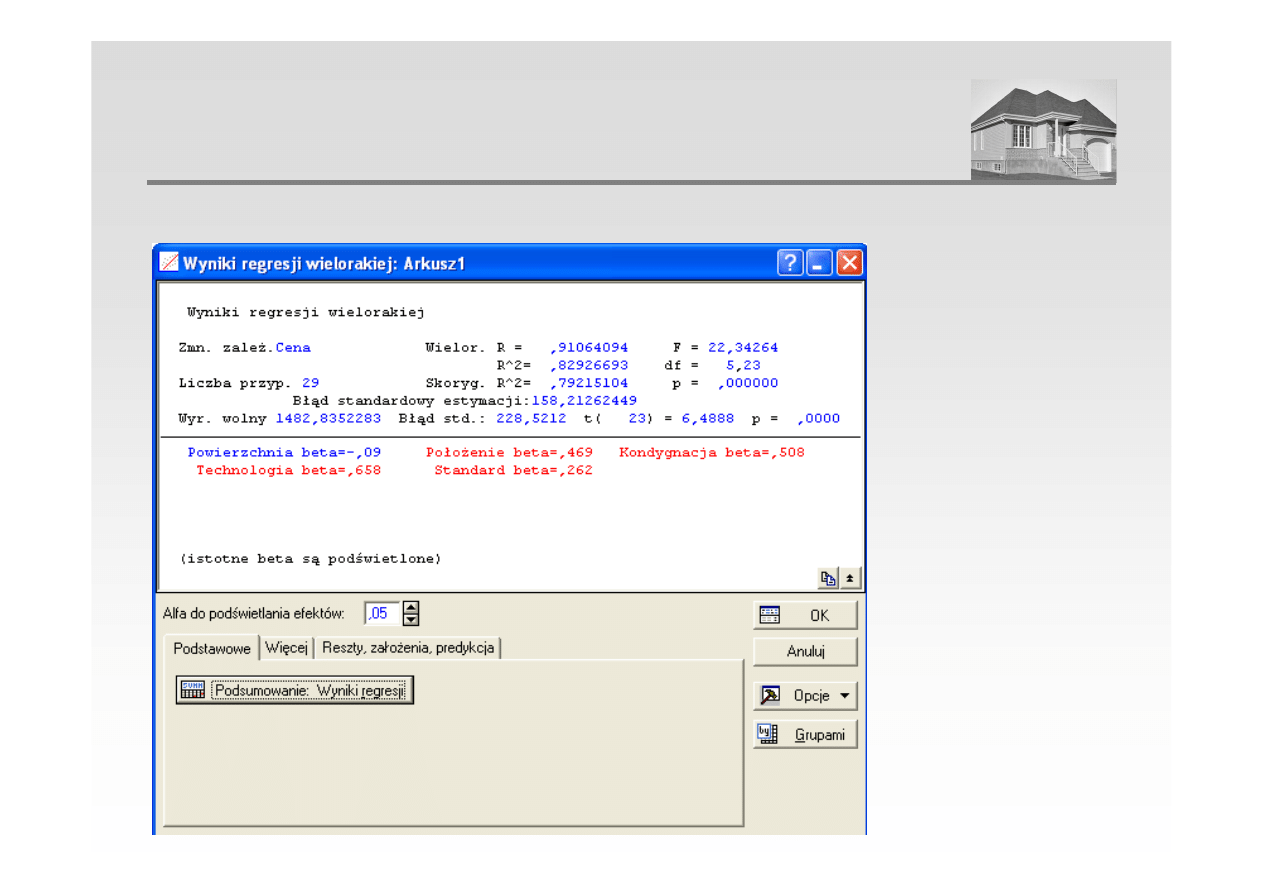
3. Estymacja parametrów modelu – przy pomocy programu STATISTICA
ANALIZA REGRESJI WIELORAKIEJ
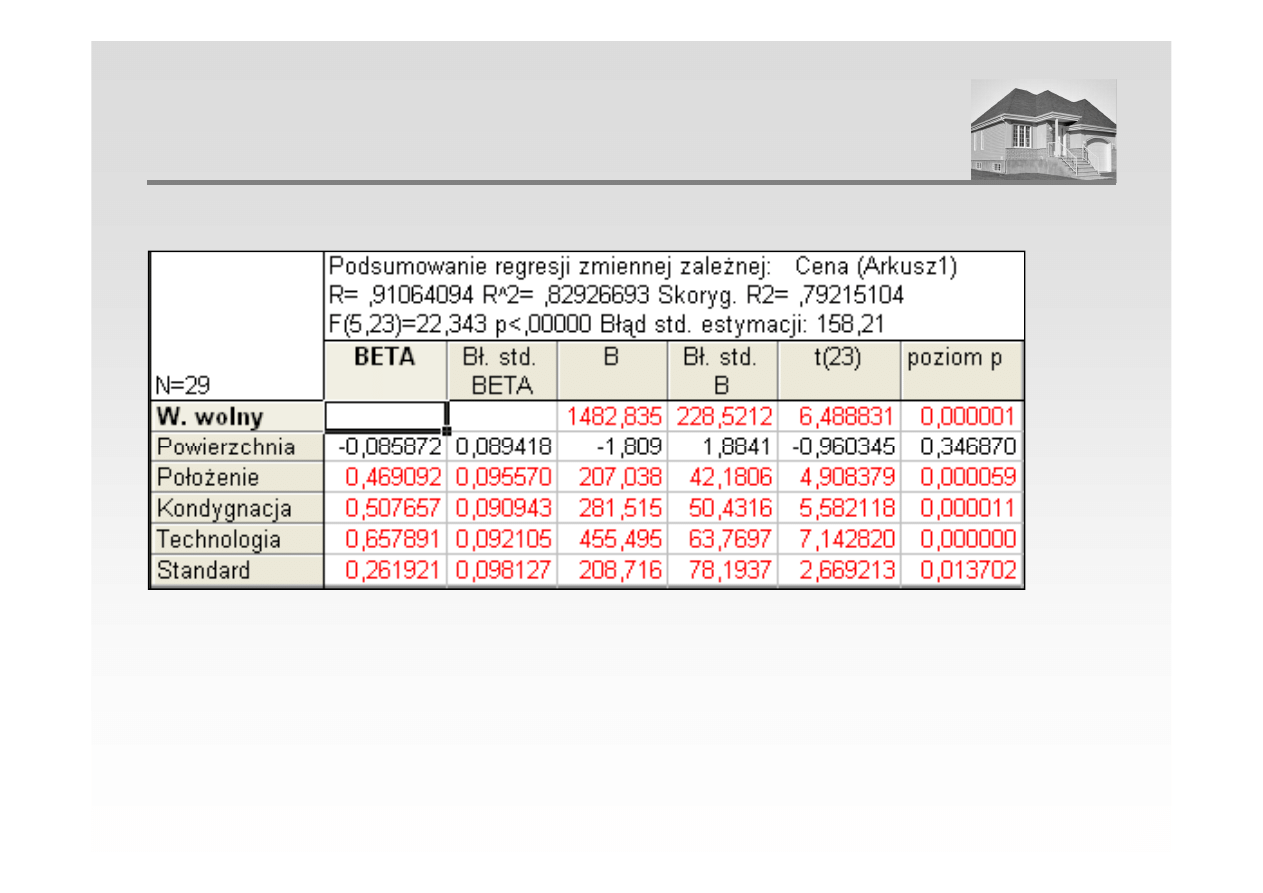
3. Estymacja parametrów modelu – przy pomocy programu STATISTICA
ANALIZA REGRESJI WIELORAKIEJ
Cena = 1482,83 – 1,81 · X
1
+ 207,04 · X
2
+ 281,51 · X
3
+ 455,49 · X
4
+ 208,72 · X
5
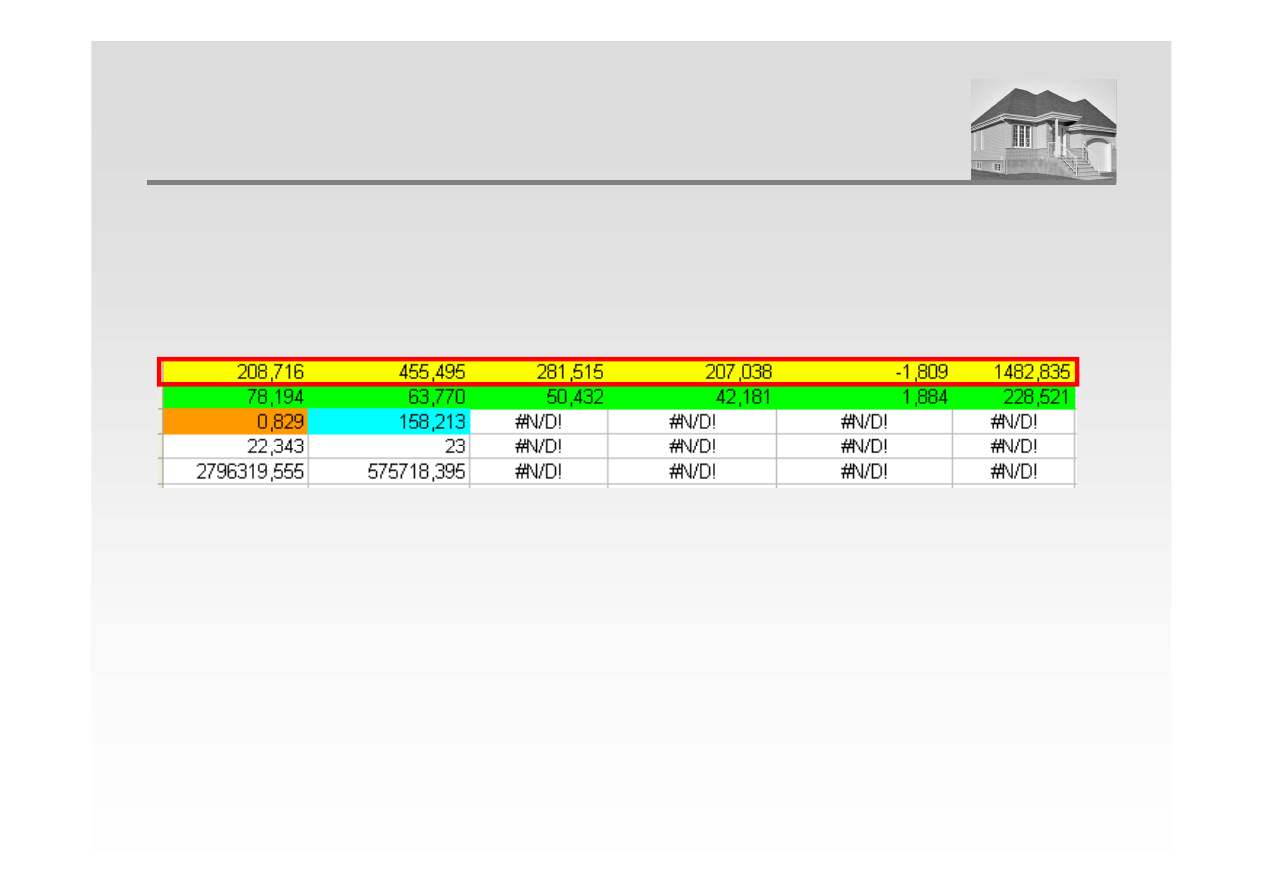
3. Estymacja parametrów modelu – przy pomocy arkusza kalkulacyjnego (polecenie REGLINP)
ANALIZA REGRESJI WIELORAKIEJ
Cena = 1482,83 – 1,81 · X
1
+ 207,04 · X
2
+ 281,51 · X
3
+ 455,49 · X
4
+ 208,72 · X
5
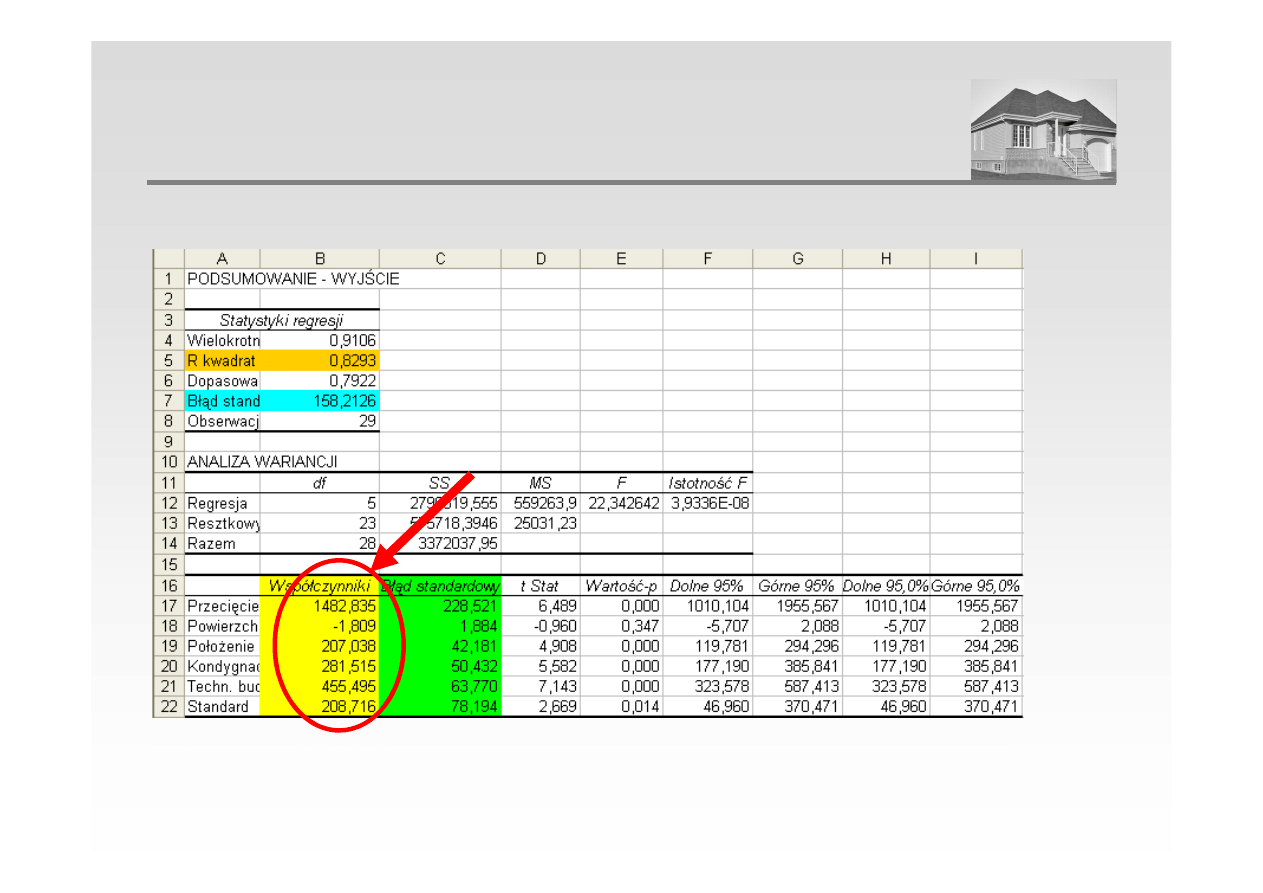
3. Estymacja parametrów modelu – przy pomocy arkusza kalkulacyjnego (narzędzie „Analiza danych”)
ANALIZA REGRESJI WIELORAKIEJ
Cena = 1482,83 – 1,81 · X
1
+ 207,04 · X
2
+ 281,51 · X
3
+ 455,49 · X
4
+ 208,72 · X
5

Przez weryfikację modelu ekonometrycznego należy rozumieć ocenę jego poprawności przy
wzięciu pod uwagę aspektów merytorycznych i statystycznych.
Weryfikacja modelu może polegać na określeniu stopnia zgodności zbudowanego modelu z
danymi empirycznymi oraz na ocenie jakości ocen parametrów strukturalnych.
Wnioskowanie z modelu jest możliwe tylko wtedy, gdy wartości miar modelu nie wskazują na
rozbieżności między modelem a rzeczywistością. Może ono polegać na interpretacji modelu
WERYFIKACJA MODELU REGRESJI WIELORAKIEJ
rozbieżności między modelem a rzeczywistością. Może ono polegać na interpretacji modelu
(diagnoza rynku), predykcji bądź symulacji.

Weryfikacja merytoryczna – to stwierdzenie zgodności modelu z wiedzą o badanych
zjawiskach i zdrowym rozsądkiem. Polega na ocenie właściwości znaków przy
obliczonych współczynnikach oraz wielkości oszacowanych współczynników.
Weryfikacja statystyczna – polega na sprawdzeniu czy model spełnia standardowe
postulaty statystyczne: istotność zmiennych objaśniających, wymagane dopasowanie
do wyników obserwacji i pożądane właściwości składnika resztowego.
WERYFIKACJA MODELU REGRESJI WIELORAKIEJ
do wyników obserwacji i pożądane właściwości składnika resztowego.

Przebieg weryfikacji statystycznej modelu
• weryfikacja hipotezy o nieistnieniu zależności pomiędzy zbiorem zmiennych
objaśniających a cenami transakcyjnymi
• ocena współczynnika determinacji
• ocena błędu standardowego estymacji
• weryfikacja hipotezy o nieistotności parametrów modelu regresji
WERYFIKACJA STATYSTYCZNA
• weryfikacja hipotezy o nieistotności parametrów modelu regresji

Hipotezę o nieistnieniu zależności pomiędzy zbiorem zmiennych objaśniających a
cenami transakcyjnymi weryfikuje się przy pomocy statystyki F Fischera-Snedecora -
stosowanej w celu zbadania czy uzyskane wyniki modelu regresji nie wystąpiły
przypadkowo.
Test F wykonuje się stawiając następujące hipotezy:
H
0
:
α
1
=
α
2
= ... =
α
k
= 0 co oznacza, że model nie przedstawia żadnej zależności
WERYFIKACJA HIPOTEZY O BRAKU ZALEŻNOŚCI OPISANEJ
PRZEZ MODEL
H
0
:
α
1
=
α
2
= ... =
α
k
= 0 co oznacza, że model nie przedstawia żadnej zależności
H
1
: co najmniej jedno
α ≠
0, co oznacza, że model przedstawia zależność statystyczną,
W celu weryfikacji hipotezy zerowej obliczoną wartość statystyki F porównujemy z
wartością krytyczną.
Wartość empiryczną statystyki F oblicza się z wzoru:
(
)
/
ˆ
1
2
−
=
∑
=
k
y
y
F
n
i
i
WERYFIKACJA HIPOTEZY O BRAKU ZALEŻNOŚCI OPISANEJ
PRZEZ MODEL
(
)
)
1
/(
ˆ
1
2
−
−
−
=
∑
=
k
n
y
y
F
n
i
i
gdzie:
- oznacza kolejną cenę estymowaną (wartość teoretyczną - estymator ceny)
- jest to średnia arytmetyczna obliczona z cen transakcyjnych
y
i
- oznacza kolejną cenę transakcyjną
n
- jest to liczba obserwacji (liczba danych o transakcjach)
k
- oznacza liczbę zmiennych objaśniających (liczba cech przyjętych do analiz)
i
yˆ
y
Wartość krytyczną odczytuje się z tabeli wartości krytycznych rozkładu F-Snedecora dla
przyjętego poziomu istotności (równego zazwyczaj 0,01; 0,05 lub 0,10), określonej liczby
zmiennych objaśniających i stopni swobody.
Przykład:
dla liczby nieruchomości podobnych
n = 21
dla liczby zmiennych objaśniających
v
1
= 5
dla liczby stopni swobody równej n - k - 1
v
2
= 21 -5 -1 = 15
dla poziomu istotności równego
α
= 0,05
wartość krytyczna statystyki F na podstawie tabeli wartości krytycznych wynosi 2,90
WERYFIKACJA HIPOTEZY O BRAKU ZALEŻNOŚCI OPISANEJ
PRZEZ MODEL
wartość krytyczna statystyki F na podstawie tabeli wartości krytycznych wynosi 2,90
v2\v1
1
2
...
5
1
161,4
199,5
...
230,2
2
18,51
19,00
...
19,30
...
...
...
...
...
15
4,54
3,68
...
2,90
Jeżeli wartość empiryczna statystyki F jest wyższa od wartości krytycznej tzn:
F
obl
≥≥≥≥
F
kryt
to hipotezę o nieistnieniu zależności należy odrzucić (zależności opisane modelem nie wystąpiły
przypadkowo).
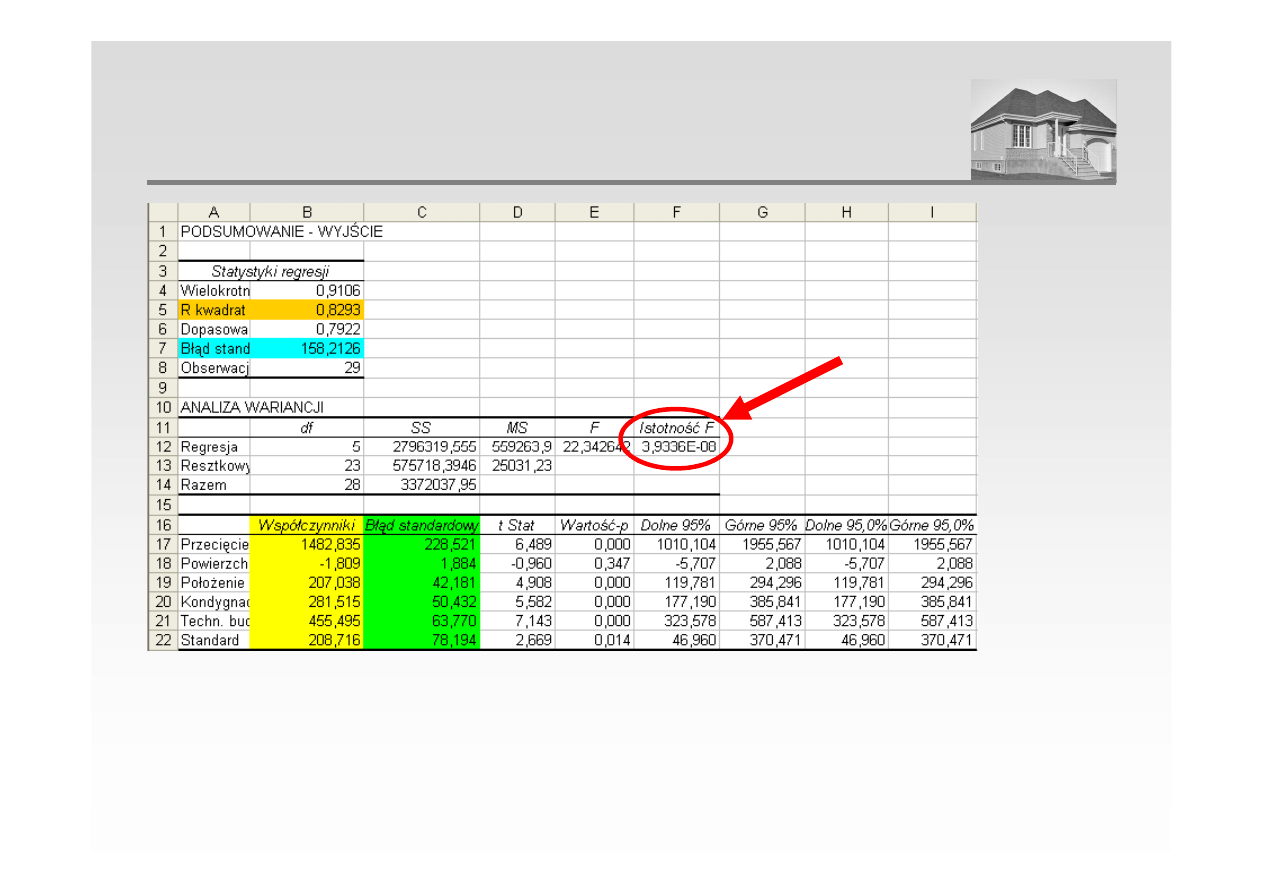
WERYFIKACJA HIPOTEZY O BRAKU ZALEŻNOŚCI OPISANEJ
PRZEZ MODEL (PRZYKŁAD)
Istotność F oznacza prawdopodobieństwo, że zależności opisane modelem wystąpiły
przypadkowo
Istotność F = 0,00000004
hipotezę o nieistnieniu zależności należy odrzucić (zależności opisane modelem nie wystąpiły
przypadkowo).
Współczynnik determinacji R
2
określa się z następującego wzoru:
(
)
(
)
(
)
(
)
∑
∑
∑
∑
=
=
=
=
−
−
−
=
−
−
=
n
i
i
n
i
i
i
n
i
i
n
i
i
y
y
y
y
y
y
y
y
R
1
2
1
2
1
2
1
2
2
ˆ
1
ˆ
WSPÓŁCZYNNIK DETERMINACJI
R
2
pomnożony przez 100% interpretuje się jako stopień wyjaśnienia całkowitej zmienności
zmiennej zależnej przez zmienność uwzględnionych w badaniu zmiennych niezależnych.
Współczynnik determinacji spełnia warunek: 0 < R
2
< 1. Im bliższy jest jedności, tym lepiej
zależność liniowa została dopasowana do danego zbioru obserwacji.
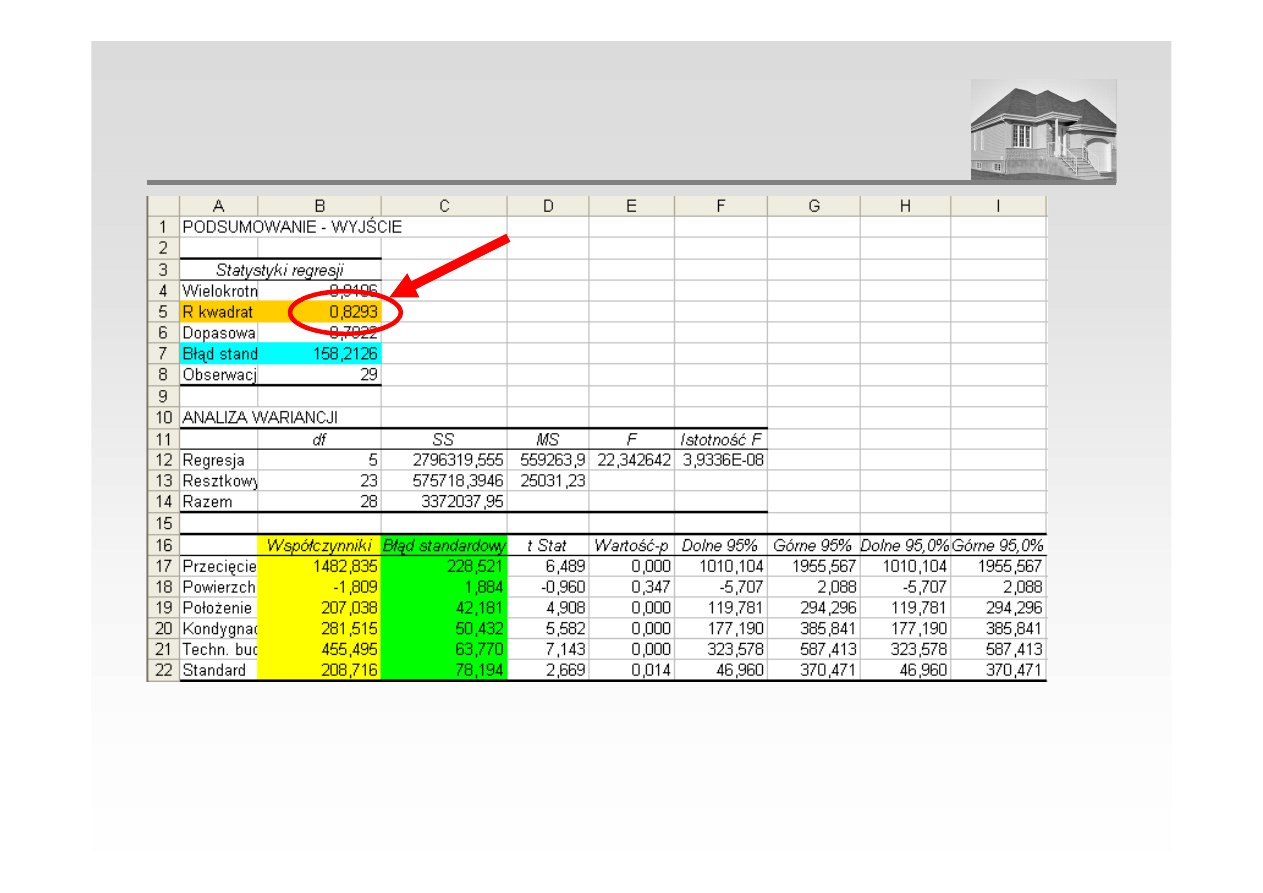
WSPÓŁCZYNNIK DETERMINACJI (PRZYKŁAD)
Współczynnik determinacji wyniósł 0,829 co oznacza, ze 83% zmienności cen zostało
wyjaśnione przez model
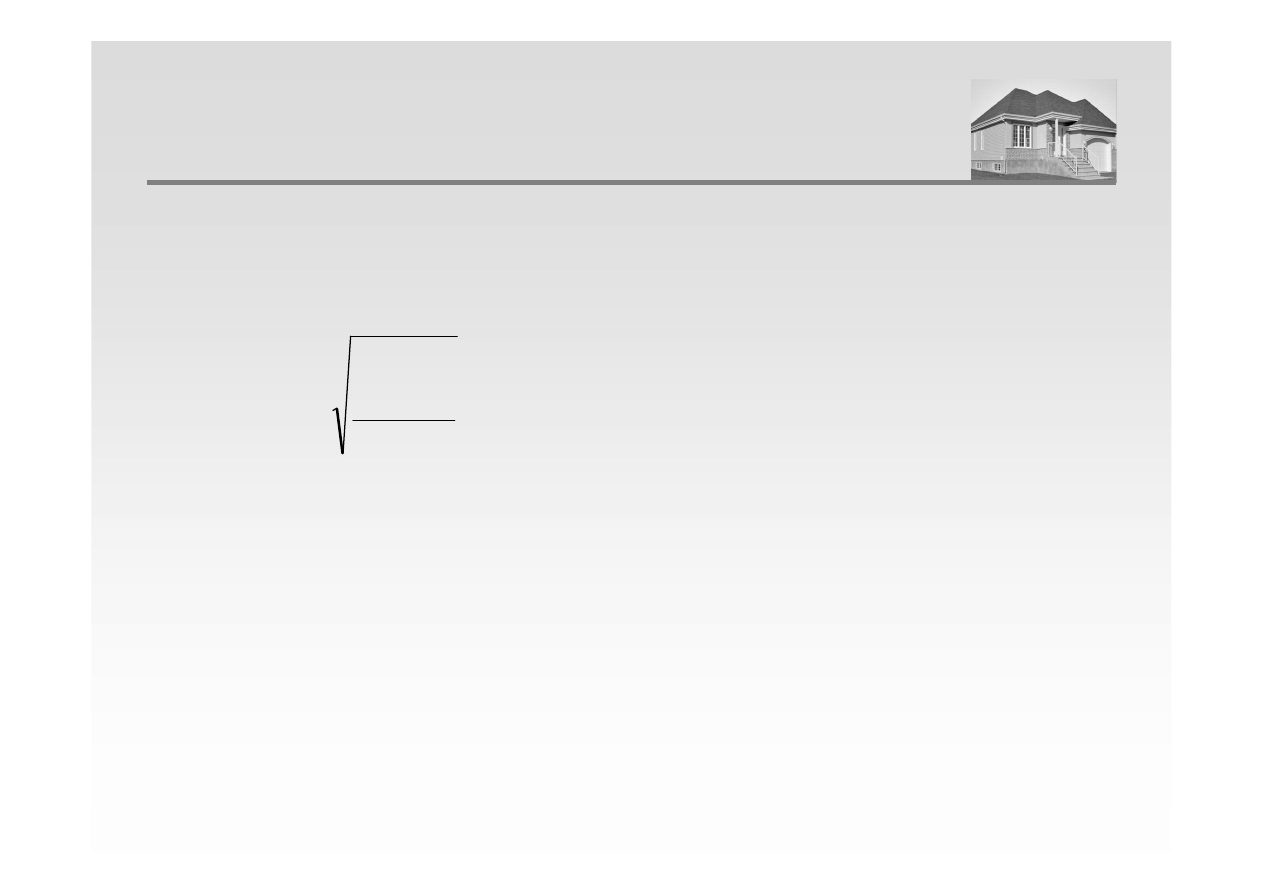
Błąd standardowy estymacji określony jest jako pierwiastek z wariancji reszt i może być
interpretowany jako błąd, który możliwy jest do popełnienia w trakcie prognozowania przy
pomocy modelu. Opisany jest następującym wzorem:
1
1
2
−
−
=
∑
=
k
n
e
S
n
i
i
e
BŁĄD STANDARDOWY ESTYMACJI
(ODCHYLENIE STANDARDOWE RESZT)
1
−
−
k
n
gdzie:
e
i
- reszta (różnica pomiędzy wartością teoretyczną i obserwowaną)
n - liczba obserwacji
k - liczba zmiennych objaśniających
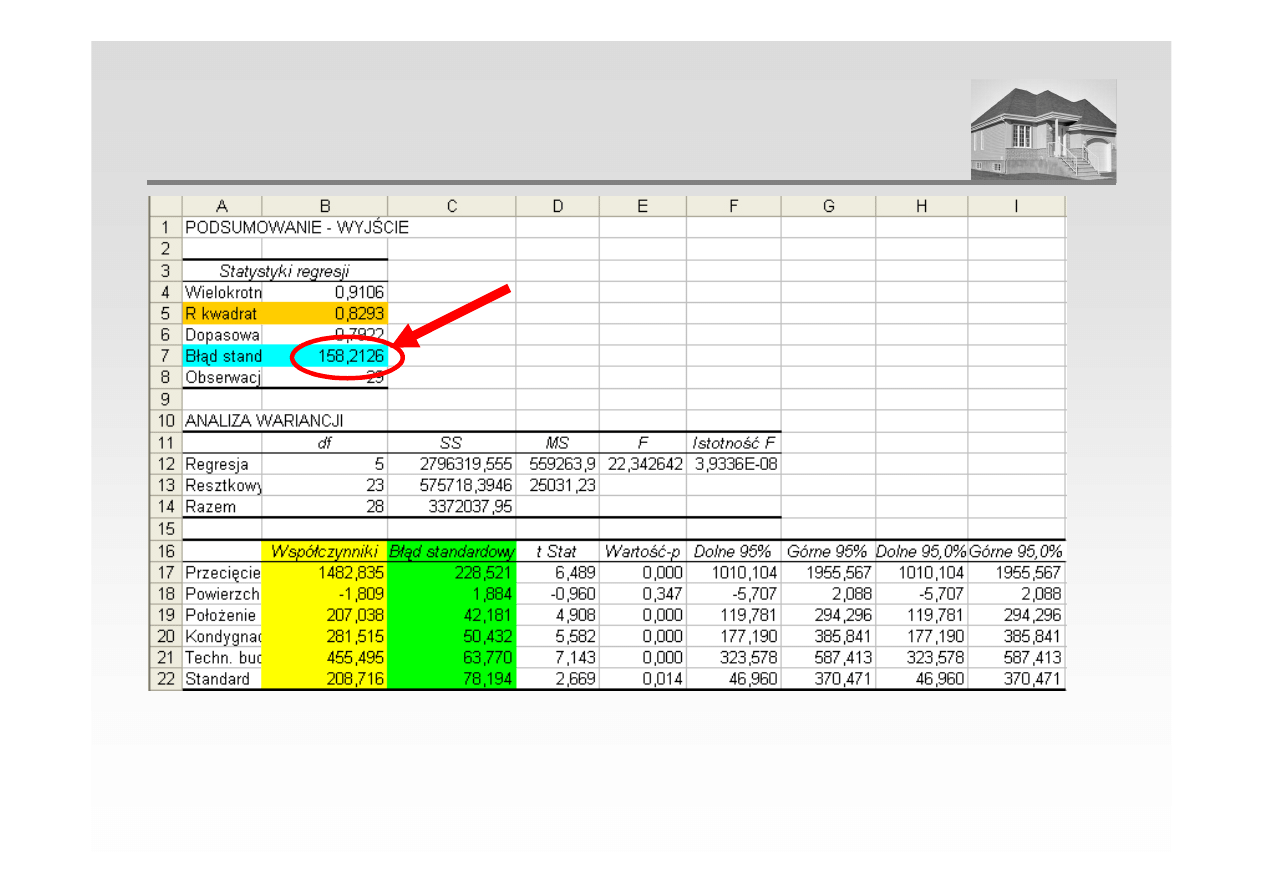
BŁĄD STANDARDOWY ESTYMACJI
(ODCHYLENIE STANDARDOWE RESZT) - PRZYKŁAD
Błąd standardowy estymacji wyniósł 158,21 zł co oznacza, że błąd prognozy będzie bliski tej
wartości

Narzędziem pozwalającym na ocenę istotności poszczególnych zmiennych niezależnych jest test t-
Studenta. Określa on, czy liniowa zależność między dwiema zmiennymi jest istotna statystycznie.
Zakłada się, że stosunek odchylenia od średniej lub innego parametru w rozkładzie statystyk z
prób do błędu standardowego tego rozkładu jest zgodny z rozkładem t.
t
i
α
=
WERYFIKACJA HIPOTEZY O NIEISTOTNOŚCI PARAMETRÓW
MODELU
i
S
t
i
α
=
gdzie:
α
i
- testowany parametr modelu regresji
S
α
i
- błąd standardowy parametru
α
i

Test t-Studenta może posłużyć do weryfikacji następującej hipotezy:
H
0
:
α
i
= 0 co oznacza, że dany parametr w stopniu nieistotnym różni się od zera (nie istnieje
zależność między daną zmienną a ceną)
H
1
:
α
i
≠
0, co oznacza, że wartość danego parametru jest statystycznie istotna
Wartość
krytyczną
rozkładu
t-Studenta
odczytuje
się
z
tablic
(lub
z
kalkulatora
prawdopodobieństwa) dla przyjętego poziomu istotności i określonej liczby stopni swobody.
WERYFIKACJA HIPOTEZY O NIEISTOTNOŚCI PARAMETRÓW
MODELU
Jeżeli wartość empiryczna statystyki t jest wyższa od wartości krytycznej tzn:
t
obl
≥≥≥≥
t
kryt
to hipotezę o nieistotności parametru należy odrzucić (parametr jest istotny statystycznie).
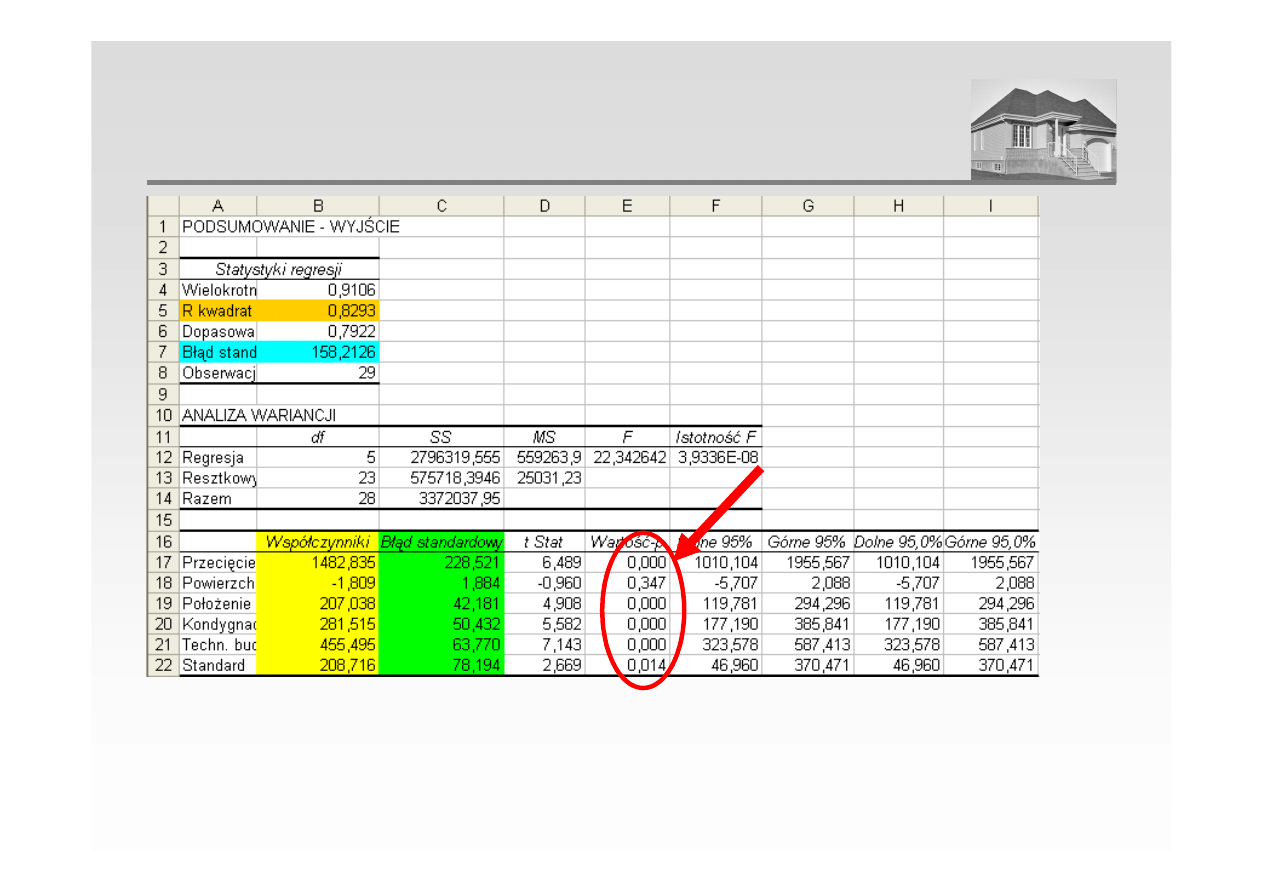
WERYFIKACJA HIPOTEZY O NIEISTOTNOŚCI PARAMETRÓW
MODELU (PRZYKŁAD)
Wartość-p oznacza prawdopodobieństwo, że dana zmienna jest statystycznie nieistotna. Za
poziom krytyczny przyjmujemy 0,05
Wyszukiwarka
Podobne podstrony:
06 regresja www przeklej pl
05 analiza stat www przeklej pl Nieznany
07 popyt podaz www przeklej pli Nieznany (2)
01 r wnanie ruchu pojazdu samochodowego www przeklej plid 2911 ppt
04 metody ilosciowe www przeklej plid 5082
wyniki cz ii ois egz norm 21 06 2011 www przeklej pl
zelbet www przeklej id 587207 Nieznany
materia y pow oki 2 www przekle Nieznany
fizyka www przeklej pl id 17708 Nieznany
phmetria www przeklej pl
06 pytanka PE opracowaneid 6379 Nieznany (2)
inventor modelowanie zespolow www przeklej pl
prob wki www.przeklej.pl, Ratownictwo Medyczne
06.regresja liniowa, STATYSTYKA
rozw j teorii literatury wyk zag do egz www przeklej pl
pytania www przeklej pl
więcej podobnych podstron