An

Extensible

SA

T-solv

er

[extended

v

ersion

1.2℄

Niklas

E

en,

Niklas

S

orensson

Chalmers

Univ

ersit

y

of

T

e

hnology

,

Sw

eden

feen,nikgs.halmers.se

Abstrat.

In

this

artile,

w

e

presen

t

a

small,

omplete,

and

eÆien

t

SA

T-solv

er

in

the

st

yle

of

onit-driv

en

learning,

as

exemplied

b

y

C

HA FF

.

W

e

aim

to

giv

e

suÆien

t

details

ab

out

implemen

tation

to

enable

the

reader

to

onstrut

his

or

her

o

wn

solv

er

in

a

v

ery

short

time.

This

will

allo

w

users

of

SA

T-solv

ers

to

mak

e

domain

sp

ei

extensions

or

adaptions

of

urren

t

state-of-the-art

SA

T-te

hniques,

to

meet

the

needs

of

a

partiular

appliation

area.

The

presen

ted

solv

er

is

designed

with

this

in

mind,

and

inludes

among

other

things

a

me

hanism

for

adding

arbitrary

b

o

olean

onstrain

ts.

It

also

supp

orts

solving

a

series

of

related

SA

T-problems

eÆien

tly

b

y

an

inremen

tal

SA

T-in

terfae.

1

In

tro

dution

The

use

of

SA

T-solv

ers

in

v

arious

appliations

is

on

the

mar

h.

As

insigh

t

on

ho

w

to

eÆien

tly

eno

de

problems

in

to

SA

T

is

inreasing,

a

gro

wing

n

um

b

er

of

prob-

lem

domains

are

suessfully

b

eing

ta

kled

b

y

SA

T-solv

ers.

This

is

partiularly

true

for

the

ele

tr

oni

design

automation

(ED

A)

industry

[BCCFZ99

,Lar92

℄.

The

suess

is

further

magnied

b

y

urren

t

state-of-the-art

solv

ers

b

eing

ex-

tended

and

adapted

to

meet

the

sp

ei

harateristis

of

these

problem

domains

[ARMS02,ES03

℄.

Ho

w

ev

er,

mo

difying

an

existing

solv

er,

ev

en

with

a

thorough

understanding

of

b

oth

the

problem

domain

and

of

mo

dern

SA

T-te

hniques,

an

b

eome

a

time

onsuming

and

b

ewildering

journey

in

to

the

m

ysterious

inner

w

orkings

of

a

ten-

thousand-line

soft

w

are

pa

k

age.

Lik

ewise,

writing

a

solv

er

from

srat

h

an

also

b

e

a

daun

ting

task,

as

there

are

n

umerous

pitfalls

hidden

in

the

in

triate

details

of

a

orret

and

eÆien

t

solv

er.

The

problem

is

that

although

the

te

hniques

used

in

a

mo

dern

SA

T-solv

er

are

w

ell

do

umen

ted,

the

details

neessary

for

an

implementation

ha

v

e

not

b

een

adequately

presen

ted

b

efore.

In

the

fall

of

2002,

the

authors

implemen

ted

the

solv

ers

S

ATZOO

and

S

AT

-

NIK

.

In

order

to

suÆien

tly

understand

the

implemen

tation

tri

ks

needed

for

a

mo

dern

SA

T-solv

er,

it

w

as

neessary

to

onsult

the

soure-o

de

of

previous

im-

plemen

tations.

1

W

e

nd

that

the

material

on

tained

therein

an

b

e

made

more

aessible,

whi

h

is

desirable

for

the

SA

T-omm

unit

y

.

Th

us,

the

prinipal

goal

of

this

artile

is

to

bridge

the

gap

b

et

w

een

existing

desriptions

of

SA

T-te

hniques

and

their

atual

implemen

tation.

W

e

will

do

this

b

y

presen

ting

the

o

de

of

a

minimal

SA

T-solv

er

M

INI

S

AT

,

based

on

the

ideas

for

onit-driv

en

ba

ktra

king

[MS96

℄,

together

with

w

at

hed

literals

and

dynami

v

ariable

ordering

[MZ01

℄.

The

original

C++

soure

o

de

1

L

IM M AT

at

http://www.inf.ethz.h/perso nal/ bier e/pro jet s/lim mat/

Z

C

HA FF

at

http://www.ee.prineton.edu/~

h aff/z haf f

(do

wnloadable

from

http://www.s.h

al

mer

s.

se/

~

e

en

)

for

M

INI

S

AT

is

under

600

lines

(not

oun

ting

ommen

ts),

and

is

the

result

of

rethinking

and

simplifying

the

designs

of

S

ATZOO

and

S

ATNIK

without

sariing

eÆieny

.

W

e

will

presen

t

all

the

relev

an

t

parts

of

the

o

de

in

a

manner

that

should

b

e

aessible

to

an

y

one

aquain

ted

with

either

C++

or

Ja

v

a.

The

presen

ted

o

de

inludes

an

inremen

tal

SA

T-in

terfae,

whi

h

allo

ws

for

a

series

of

related

problems

to

b

e

solv

ed

with

p

oten

tially

h

uge

eÆieny

gains

[ES03

℄.

W

e

also

generalize

the

expressiv

eness

of

the

SA

T-problem

form

ulation

b

y

pro

viding

a

me

hanism

for

arbitrary

onstr

aints

o

v

er

b

o

olean

v

ariables

to

b

e

dened.

P

aragraphs

disussing

implemen

tation

alternativ

es

are

mark

ed

\[Dis-

ussion℄"

and

an

b

e

skipp

ed

on

a

rst

reading.

F

rom

the

do

umen

tation

in

this

pap

er

w

e

hop

e

it

is

p

ossible

for

you

to

implemen

t

a

fresh

SA

T-solv

er

in

y

our

fa

v

orite

language,

or

to

grab

the

C++

v

ersion

of

M

INI

S

AT

from

the

net

and

start

mo

difying

it

to

inlude

new

and

in

teresting

ideas.

2

Appliation

Programming

In

terfae

W

e

start

b

y

presen

ting

M

INI

S

AT

's

external

in

terfae,

with

whi

h

a

user

appli-

ation

an

sp

eify

and

solv

e

SA

T-problems.

A

basi

kno

wledge

ab

out

SA

T

is

assumed

(see

for

instane

[MS96

℄).

The

t

yp

es

var

,

lit

,

and

V

e

for

v

ariables,

literals,

and

v

etors

resp

etiv

ely

are

explained

in

detail

in

setion

4.

lass

Solver

{

Publi

interfa

e

var

newV

ar

()

b

o

ol

addClause

(V

e

hlit

i

literals)

b

o

ol

add:

:

:

(:

:

:)

b

o

ol

simplifyDB

()

b

o

ol

solve

(V

e

hlit

i

assumptions)

V

e

hb

o

ol

i

mo

del

{

If

found,

this

ve

tor

has

the

mo

del.

The

\add

:

:

: "

metho

d

should

b

e

understo

o

d

as

a

plae-holder

for

additional

onstrain

ts

implemen

ted

in

an

extension

of

M

INI

S

AT

.

F

or

a

standard

SA

T-problem,

the

in

terfae

is

used

in

the

follo

wing

w

a

y:

V

ari-

ables

are

in

tro

dued

b

y

alling

newV

ar().

F

rom

these

v

ariables,

lauses

are

built

and

added

b

y

addClause().

T

rivial

onits,

su

h

as

t

w

o

unit

lauses

fxg

and

fxg

b

eing

added,

an

b

e

deteted

b

y

addClause(),

in

whi

h

ase

it

returns

F

alse.

F

rom

this

p

oin

t

on,

the

solv

er

state

is

undened

and

m

ust

not

b

e

used

further.

If

no

su

h

trivial

onit

is

deteted

during

the

lause

insertion

phase,

solve()

is

alled

with

an

empt

y

list

of

assumptions.

It

returns

F

alse

if

the

problem

is

unsatisable,

and

Tr

ue

if

it

is

satisable,

in

whi

h

ase

the

mo

del

an

b

e

read

from

the

publi

v

etor

\mo

del".

The

simplifyDB()

metho

d

an

b

e

used

b

efore

alling

solve()

to

simplify

the

set

of

problem

onstrain

ts

(often

alled

the

onstr

aint

datab

ase

).

In

our

imple-

men

tation,

simplifyDB()

will

rst

propagate

all

unit

information,

then

remo

v

e

all

satised

onstrain

ts.

As

for

addClause(),

the

simplier

an

sometimes

detet

a

2

onit,

in

whi

h

ase

F

alse

is

returned

and

the

solv

er

state

is,

again,

undened

and

m

ust

not

b

e

used

further.

If

the

solv

er

returns

satisable,

new

onstrain

ts

an

b

e

added

rep

eatedly

to

the

existing

database

and

solve()

run

again.

Ho

w

ev

er,

more

in

teresting

sequenes

of

SA

T-problems

an

b

e

solv

ed

b

y

the

use

of

unit

assumptions.

When

passing

a

non-empt

y

list

of

assumptions

to

solve(),

the

solv

er

temp

orarily

assumes

the

literals

to

b

e

true.

After

nding

a

mo

del

or

a

on

tradition,

these

assumptions

are

undone,

and

the

solv

er

is

returned

to

a

usable

state,

ev

en

when

solve()

return

F

alse,

whi

h

no

w

should

b

e

in

terpreted

as

unsatisable

under

assumptions.

F

or

this

to

w

ork,

alling

simplifyDB()

b

efore

solve()

is

no

longer

optional.

It

is

the

me

hanism

for

deteting

onits

indep

enden

t

of

the

assumptions

{

referred

to

as

a

top-level

onit

from

no

w

on

{

whi

h

puts

the

solv

er

in

an

undened

state.

W

e

wish

to

remark

that

the

abilit

y

to

pass

unit

assumptions

to

solve()

is

more

p

o

w

erful

than

it

migh

t

app

ear

at

rst.

F

or

an

example

of

its

use,

see

[ES03

℄.

An

alternativ

e

in

terfae

w

ould

b

e

for

solve()

to

return

one

of

three

v

alues:

[Disussion℄

satisable,

unsatisable,

or

unsatisable

under

assumptions.

This

is

indeed

a

less

error-prone

in

terfae

as

there

is

no

longer

a

pre-ondition

on

the

use

of

solve().

The

urren

t

in

terfae,

ho

w

ev

er,

represen

ts

the

smallest

mo

diation

of

a

non-

inremen

tal

SA

T-solv

er.

The

early

non-inremen

tal

v

ersion

of

S

ATZOO

w

as

made

omplian

t

to

the

ab

o

v

e

in

terfae

b

y

adding

just

5

lines

of

o

de.

3

Ov

erview

of

the

SA

T-solv

er

This

artile

will

treat

the

p

opular

st

yle

of

SA

T-solv

ers

based

on

the

DPLL

algo-

rithm

[DLL62

℄,

ba

ktra

king

b

y

onit

analysis

and

lause

reording

(also

re-

ferred

to

as

le

arning

)

[MS96

℄,

and

b

o

olean

onstrain

t

propagation

(BCP)

using

wathe

d

liter

als

[MZ01

℄.

2

W

e

will

refer

to

this

st

yle

of

solv

er

as

a

onit-driven

SA

T-solver.

The

omp

onen

ts

of

su

h

a

solv

er,

and

indeed

a

more

general

onstrain

t

solv

er,

an

b

e

oneptually

divided

in

to

three

ategories:

Represen

tation.

Someho

w

the

SA

T-instane

m

ust

b

e

represen

ted

b

y

in

ter-

nal

data

strutures,

as

m

ust

an

y

deriv

ed

information.

Inferene.

Brute

fore

sear

h

is

seldom

go

o

d

enough

on

its

o

wn.

A

solv

er

also

needs

some

me

hanism

for

omputing

and

propagating

the

diret

im-

pliations

of

the

urren

t

state

of

information.

Sear

h.

Inferene

is

almost

alw

a

ys

om

bined

with

sear

h

to

mak

e

the

solv

er

omplete.

The

sear

h

an

b

e

view

ed

as

another

w

a

y

of

deriving

information.

A

standard

onit-driv

en

SA

T-solv

er

an

represen

t

lauses

(with

t

w

o

literals

or

more)

and

assignments.

Although

the

assignmen

ts

an

b

e

view

ed

as

unit-lauses,

they

are

treated

sp

eially

in

man

y

w

a

ys,

and

are

b

est

view

ed

as

a

separate

t

yp

e

of

information.

The

only

inferene

me

hanism

used

b

y

a

standard

solv

er

is

unit

pr

op

agation.

As

so

on

as

a

lause

b

eomes

unit

under

the

urren

t

assignmen

t

(all

literals

exept

2

This

inludes

SA

T-solv

ers

su

h

as:

Z

C

HA FF

,

L

IM M AT

,

B

E RKM IN

.

3

one

are

false),

the

remaining

un

b

ound

literal

is

set

to

true,

p

ossibly

making

more

lauses

unit.

The

pro

ess

is

on

tin

ued

un

til

no

more

information

an

b

e

propagated.

The

sear

h

pro

edure

of

a

mo

dern

solv

er

is

the

most

omplex

part.

Heuris-

tially

,

v

ariables

are

pi

k

ed

and

assigned

v

alues

(assumptions

are

made),

un

til

the

propagation

detets

a

onit

(all

literals

of

a

lause

ha

v

e

b

eome

false).

A

t

that

p

oin

t,

a

so

alled

onit

lause

is

onstruted

and

added

to

the

SA

T

problem.

Assumptions

are

then

aneled

b

y

ba

ktra

king

un

til

the

onit

lause

b

eomes

unit,

from

whi

h

p

oin

t

this

unit

lause

is

propagated

and

the

sear

h

pro

ess

on

tin

ues.

M

INI

S

AT

is

extensible

with

arbitrary

b

o

olean

onstrain

ts.

This

will

aet

the

r

epr

esentation,

whi

h

m

ust

b

e

able

to

store

these

onstrain

ts;

the

infer

en

e,

whi

h

m

ust

b

e

able

to

deriv

e

unit

information

from

these

onstrain

ts;

and

the

se

ar

h,

whi

h

m

ust

b

e

able

to

analyze

and

generate

onit

lauses

from

the

onstrain

ts.

The

me

hanism

w

e

suggest

for

managing

general

onstrain

ts

is

v

ery

ligh

t

w

eigh

t,

and

b

y

making

the

dep

endenies

b

et

w

een

the

SA

T-algorithm

and

the

onstrain

ts

implemen

tation

expliit,

w

e

feel

it

rather

adds

to

the

larit

y

of

the

solv

er

than

obsures

it.

Pr

op

agation.

The

propagation

pro

edure

of

M

INI

S

AT

is

largely

inspired

b

y

that

of

C

HAFF

[MZ01

℄.

F

or

ea

h

literal,

a

list

of

onstrain

ts

is

k

ept.

These

are

the

onstrain

ts

that

may

propagate

unit

information

(v

ariable

assignmen

ts)

if

the

literal

b

eomes

Tr

ue.

F

or

lauses,

no

unit

information

an

b

e

propagated

un

til

all

literals

exept

one

ha

v

e

b

eome

F

alse.

Tw

o

un

b

ound

literals

p

and

q

of

the

lause

are

therefore

seleted,

and

referenes

to

the

lause

are

added

to

the

lists

of

p

and

q

resp

etiv

ely

.

The

literals

are

said

to

b

e

wathe

d

and

the

lists

of

onstrain

ts

are

referred

to

as

wather

lists.

As

so

on

as

a

w

at

hed

literal

b

eomes

Tr

ue,

the

onstrain

t

is

in

v

ok

ed

to

see

if

information

ma

y

b

e

propagated,

or

to

selet

new

un

b

ound

literals

to

b

e

w

at

hed.

A

feature

of

the

w

at

her

system

for

lauses

is

that

on

ba

ktra

king,

no

adjust-

men

t

to

the

w

at

her

lists

need

to

b

e

done.

Ba

ktra

king

is

therefore

v

ery

heap.

Ho

w

ev

er,

for

other

onstrain

t

t

yp

es,

this

is

not

neessarily

a

go

o

d

approa

h.

M

INI

S

AT

therefore

supp

orts

the

optional

use

of

undo

lists

for

those

onstrain

ts;

storing

what

onstrain

ts

need

to

b

e

up

dated

when

a

v

ariable

b

eomes

un

b

ound

b

y

ba

ktra

king.

L

e

arning.

The

learning

pro

edure

of

M

INI

S

AT

follo

ws

the

ideas

of

Marques-

Silv

a

and

Sak

allah

in

[MS96℄.

The

pro

ess

starts

when

a

onstrain

t

b

eomes

oniting

(imp

ossible

to

satisfy)

under

the

urren

t

assignmen

t.

The

oniting

onstrain

t

is

then

ask

ed

for

a

set

of

v

ariable

assignmen

ts

that

mak

e

it

on

tradi-

tory

.

F

or

a

lause,

this

w

ould

b

e

all

the

literals

of

the

lause

(whi

h

are

F

alse

under

a

onit).

Ea

h

of

the

v

ariable

assignmen

ts

returned

m

ust

b

e

either

an

assumption

of

the

sear

h

pro

edure,

or

the

result

of

some

pr

op

agation

of

a

on-

strain

t.

The

propagating

onstrain

ts

are

in

turn

ask

ed

for

the

set

of

v

ariable

assignmen

ts

that

fored

the

propagation

to

o

ur,

on

tin

uing

the

analysis

ba

k-

w

ards.

The

pro

edure

is

rep

eated

un

til

some

termination

ondition

is

fullled,

resulting

in

a

set

of

v

ariable

assignmen

ts

that

implies

the

onit.

A

lause

pro-

hibiting

that

partiular

assignmen

t

is

added

to

the

lause

database.

This

le

arnt

4

lause

m

ust

alw

a

ys,

b

y

onstrution,

b

e

implied

b

y

the

original

problem

on-

strain

ts.

Learn

t

lauses

serv

e

t

w

o

purp

oses:

they

driv

e

the

ba

ktra

king

(as

w

e

shall

see)

and

they

sp

eed

up

future

onits

b

y

\a

hing"

the

reason

for

the

onit.

Ea

h

lause

will

prev

en

t

only

a

onstan

t

n

um

b

er

of

inferenes,

but

as

the

reorded

lauses

start

to

build

on

ea

h

other

and

partiipate

in

the

unit

propagation,

the

aum

ulated

eet

of

learning

an

b

e

massiv

e.

Ho

w

ev

er,

as

the

set

of

learn

t

lauses

inrease,

propagation

is

slo

w

ed

do

wn.

Therefore,

the

n

um

b

er

of

learn

t

lauses

is

p

erio

dially

redued,

k

eeping

only

the

lauses

that

seem

useful

b

y

some

heuristi.

Se

ar

h.

The

sear

h

pro

edure

of

a

onit-driv

en

SA

T-solv

er

is

somewhat

im-

pliit.

Although

a

reursiv

e

denition

of

the

pro

edure

migh

t

b

e

more

elegan

t,

it

is

t

ypially

desrib

ed

(and

implemen

ted)

iterativ

ely

.

The

pro

edure

will

start

b

y

seleting

an

unassigned

v

ariable

x

(alled

the

de

ision

variable

)

and

assume

a

v

alue

for

it,

sa

y

Tr

ue.

The

onsequenes

of

x

=

Tr

ue

will

then

b

e

propa-

gated,

p

ossibly

resulting

in

more

v

ariable

assignmen

ts.

All

v

ariables

assigned

as

a

onsequene

of

x

is

said

to

b

e

from

the

same

de

ision

level,

oun

ting

from

1

for

the

rst

assumption

made

and

so

forth.

Assignmen

ts

made

b

efore

the

rst

assumption

(deision

lev

el

0)

are

alled

top-level.

All

assignmen

ts

will

b

e

stored

on

a

sta

k

in

the

order

they

w

ere

made;

from

no

w

on

referred

to

as

the

tr

ail.

The

trail

is

divided

in

to

deision

lev

els

and

is

used

to

undo

information

during

ba

ktra

king.

The

deision

phase

will

on

tin

ue

un

til

either

all

v

ariables

ha

v

e

b

een

assigned,

in

whi

h

ase

w

e

ha

v

e

a

mo

del,

or

a

onit

has

o

urred.

On

onits,

the

learning

pro

edure

will

b

e

in

v

ok

ed

and

a

onit

lause

pro

dued.

The

trail

will

b

e

used

to

undo

deisions,

one

lev

el

at

a

time,

un

til

preisely

one

of

the

literals

of

the

learn

t

lause

b

eomes

un

b

ound

(they

are

all

F

alse

at

the

p

oin

t

of

onit).

By

onstrution,

the

onit

lause

annot

go

diretly

from

oniting

to

a

lause

with

t

w

o

or

more

un

b

ound

literals.

If

the

lause

remains

unit

for

sev

eral

deision

lev

els,

it

is

adv

an

tageous

to

hose

the

lo

w

est

lev

el

(referred

to

as

b

akjumping

or

non-hr

onolo

gi

al

b

aktr

aking

[MS96

℄).

lo

op

pr

op

agate

()

{

pr

op

agate

unit

lauses

if

not

onit

then

if

all

v

ariables

assigned

then

return

Sa

tisfiable

else

de

ide

()

{

pik

a

new

variable

and

assign

it

else

analyze

()

{

analyze

onit

and

add

a

onit

lause

if

top-lev

el

onit

found

then

return

Unsa

tisfiable

else

b

aktr

ak

()

{

undo

assignments

until

onit

lause

is

unit

5

An

imp

ortan

t

part

of

the

pro

edure

is

the

heuristi

for

de

ide().

Lik

e

C

HAFF

,

M

INI

S

AT

uses

a

dynami

v

ariable

order

that

giv

es

priorit

y

to

v

ariables

in

v

olv

ed

in

reen

t

onits.

Although

this

is

a

go

o

d

default

order,

domain

sp

ei

heuristis

ha

v

e

suess-

[Disussion℄

fully

b

een

used

in

v

arious

areas

to

impro

v

e

the

p

erformane

[Stri00

℄.

V

ariable

ordering

is

a

traditional

target

for

impro

ving

SA

T-solv

ers.

A

tivity

heuristis.

One

imp

ortan

t

te

hnique

in

tro

dued

b

y

C

HAFF

[MZ01

℄

is

a

dynami

v

ariable

ordering

based

on

ativit

y

(referred

to

as

the

VSIDS

heuris-

ti).

The

original

heuristi

imp

oses

an

order

on

liter

als,

but

b

orro

wing

from

S

ATZOO

,

w

e

mak

e

no

distintion

b

et

w

een

p

and

p

in

M

INI

S

AT

.

Ea

h

v

ariable

has

an

ativity

atta

hed

to

it.

Ev

ery

time

a

v

ariable

o

urs

in

a

reorded

onit

lause,

its

ativit

y

is

inreased.

W

e

will

refer

to

this

as

bumping.

After

reording

the

onit,

the

ativit

y

of

all

the

v

ariables

in

the

system

are

m

ultiplied

b

y

a

onstan

t

less

than

1,

th

us

de

aying

the

ativit

y

of

v

ariables

o

v

er

time.

Reen

t

inremen

ts

oun

t

more

than

old.

The

urren

t

sum

determines

the

ativit

y

of

a

v

ariable.

In

M

INI

S

AT

w

e

use

a

similar

idea

for

lauses.

When

a

learn

t

lause

is

used

in

the

analysis

pro

ess

of

a

onit,

its

ativit

y

is

bump

ed.

Inativ

e

lauses

are

p

erio

dially

remo

v

ed.

Constr

aint

r

emoval.

The

onstrain

t

database

is

divided

in

to

t

w

o

parts:

the

pr

oblem

onstr

aints

and

the

le

arnt

lauses.

As

w

e

ha

v

e

noted,

the

set

of

learn

t

lauses

an

b

e

p

erio

dially

redued

to

inrease

the

p

erformane

of

propagation.

Learn

t

lauses

are

used

to

rop

future

bran

hes

in

the

sear

h

tree,

so

w

e

risk

getting

a

bigger

sear

h

spae

instead.

The

balane

b

et

w

een

the

t

w

o

fores

is

deliate,

and

there

are

SA

T-instanes

for

whi

h

a

big

learn

t

lause

set

is

ad-

v

an

tageous,

and

others

where

a

small

set

is

b

etter.

M

INI

S

AT

's

default

heuristi

starts

with

a

small

set

and

gradually

inreases

the

size.

Problem

onstrain

ts

an

also

b

e

remo

v

ed

if

they

are

satised

at

the

top-lev

el.

The

API

metho

d

simplifyDB()

is

resp

onsible

for

this.

The

pro

edure

is

par-

tiularly

imp

ortan

t

for

inremen

tal

SA

T-problems,

where

te

hniques

for

lause

remo

v

al

build

on

this

feature.

T

op-level

solver.

Although

the

pseudo-o

de

for

the

sear

h

pro

edure

presen

ted

ab

o

v

e

suÆes

for

a

simple

onit-driv

en

SA

T-solv

er,

a

solv

er

str

ate

gy

an

im-

pro

v

e

the

p

erformane.

A

t

ypial

strategy

applied

b

y

mo

dern

onit-driv

en

SA

T-solv

ers

is

the

use

of

r

estarts

to

esap

e

from

futile

parts

of

the

sear

h

tree.

In

M

INI

S

AT

w

e

also

v

ary

the

n

um

b

er

of

learn

t

lauses

k

ept

at

a

giv

en

time.

F

urthermore,

the

solve()

metho

d

of

the

API

supp

orts

inremen

tal

assumptions,

not

handled

b

y

the

ab

o

v

e

pseudo-o

de.

4

Implemen

tation

The

follo

wing

on

v

en

tions

are

used

in

the

o

de.

A

tomi

t

yp

es

start

with

a

lo

w

er-

ase

letter

and

are

passed

b

y

v

alue.

Comp

osite

t

yp

es

start

with

a

apital

letter

and

are

passed

b

y

referene.

Blo

ks

are

mark

ed

only

b

y

inden

tation

lev

el.

The

6

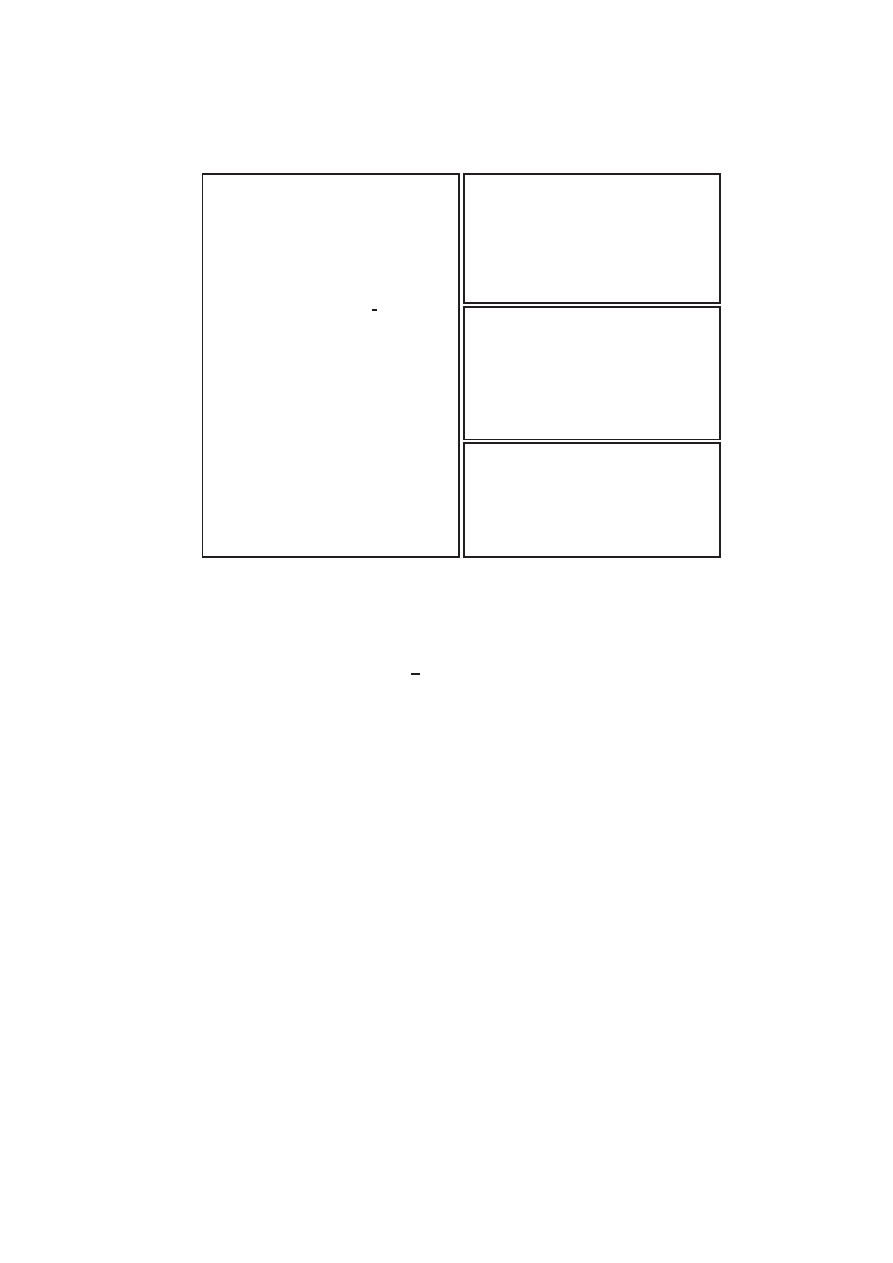
lass

V

e

hT

i

{

Publi

interfa

e

{

Construtors:

V

e

()

V

e

(int

size)

V

e

(int

size,

T

pad)

{

Size

op

er

ations:

int

size

()

void

shrink

(int

nof

elems)

void

p

op

()

void

gr

owT

o

(int

size)

void

gr

owT

o

(int

size,

T

pad)

void

le

ar

()

{

Stak

interfa

e:

void

push

()

void

push

(T

elem)

T

last

()

{

V

e

tor

interfa

e:

T

op

[

℄

(int

index)

{

Dupli

atation:

void

opyT

o

(V

e

hT

i

op

y)

void

moveT

o

(V

e

hT

i

dest)

lass

lit

{

Publi

interfa

e

lit

(var

x)

{

Glob

al

funtions:

lit

op

:

(lit

p)

b

o

ol

sign

(lit

p)

int

var

(lit

p)

int

index

(lit

p)

lass

lb

o

ol

{

Publi

interfa

e

lb

o

ol

()

lb

o

ol

(b

o

ol

x)

{

Glob

al

funtions:

lb

o

ol

op

:

(lb

o

ol

x)

{

Glob

al

onstants:

lb

o

ol

F

alse

?

,

Tr

ue

?

,

?

lass

Queue

hT

i

{

Publi

interfa

e

Queue

()

void

insert

(T

x)

T

de

queue

()

void

le

ar

()

int

size

()

Fig.

1.

Basi

abstr

at

data

typ

es

use

d

thr

oughout

the

o

de.

The

v

etor

data

t

yp

e

an

push

a

default

onstruted

elemen

t

b

y

the

push

()

metho

d

with

no

argumen

t.

The

moveT

o

()

metho

d

will

mo

v

e

the

on

ten

ts

of

a

v

etor

to

another

v

etor

in

onstan

t

time,

learing

the

soure

v

etor.

The

literal

data

t

yp

e

has

an

index

()

metho

d

whi

h

on

v

erts

the

literal

to

a

\small"

in

teger

suitable

for

arra

y

indexing.

The

var

()

metho

d

returns

the

underlying

v

ariable

of

the

literal,

and

the

sign

()

metho

d

if

the

literal

is

signed

(F

alse

for

x

and

Tr

ue

for

x

).

b

ottom

sym

b

ol

?

will

alw

a

ys

mean

undene

d

;

the

sym

b

ol

F

alse

will

b

e

used

to

denote

the

b

o

olean

false.

W

e

will

use,

but

not

sp

eify

an

implemen

tation

of,

the

follo

wing

abstrat

data

t

yp

es:

V

e

hT

i

an

extensible

v

etor

of

t

yp

e

T

;

lit

the

t

yp

e

of

literals

on

taining

a

sp

eial

literal

?

lit

;

lb

o

ol

for

the

lifted

b

o

olean

domain

on

taining

elemen

ts

Tr

ue

?

,

F

alse

?

,

and

?;

Queue

hT

i

a

queue

of

t

yp

e

T

.

W

e

also

use

var

as

a

t

yp

e

synon

ym

for

int

(for

impliit

do

umen

tation)

with

the

sp

eial

onstan

t

?

v

ar

.

The

in

terfaes

of

the

abstrat

data

t

yp

es

are

presen

ted

in

Figure

1.

4.1

The

solv

er

state

A

n

um

b

er

of

things

need

to

b

e

stored

in

the

solv

er

state.

Figure

2

sho

ws

the

omplete

set

of

mem

b

er

v

ariables

of

the

solv

er

t

yp

e

of

M

INI

S

AT

.

T

ogether

with

the

state

v

ariables

w

e

dene

some

short

help

er

metho

ds

in

Figure

3,

as

w

ell

as

the

in

terfae

of

V

arOr

der

(Figure

4),

explained

in

setion

4.6.

The

state

do

es

not

on

tain

a

b

o

olean

\onit"

to

remem

b

er

if

a

top-lev

el

[Disussion℄

onit

has

b

een

rea

hed.

Instead

w

e

imp

ose

as

an

in

v

arian

t

that

the

solv

er

m

ust

nev

er

b

e

in

a

oniting

state.

As

a

onsequene,

an

y

metho

d

that

puts

the

solv

er

7

in

a

oniting

state

m

ust

omm

uniate

this.

Using

the

solv

er

ob

jet

after

this

p

oin

t

is

illegal.

The

in

v

arian

t

mak

es

the

in

terfae

sligh

tly

more

um

b

ersome

to

use,

but

simplies

the

implemen

tation,

whi

h

is

imp

ortan

t

when

extending

and

exp

erimen

ting

with

new

te

hniques.

4.2

Constrain

ts

M

INI

S

AT

an

handle

arbitrary

onstrain

ts

o

v

er

b

o

olean

v

ariables

through

the

abstration

presen

ted

in

Figure

5.

Ea

h

onstrain

t

t

yp

e

needs

to

implemen

t

metho

ds

for

onstruting,

remo

ving,

propagating

and

alulating

reasons.

In

addition,

metho

ds

for

simplifying

the

onstrain

t

and

up

dating

the

onstrain

t

on

ba

ktra

k

an

b

e

sp

eied.

W

e

explain

the

meaning

and

resp

onsibilities

of

these

metho

ds

in

detail:

Construtor.

The

onstrutor

ma

y

only

b

e

alled

at

the

top-lev

el.

It

m

ust

reate

and

add

the

onstrain

t

to

appropriate

w

at

her

lists

after

enqueu-

ing

an

y

unit

information

deriv

able

under

the

urren

t

top-lev

el

assignmen

t.

Should

a

onit

arise,

this

m

ust

b

e

omm

uniated

to

the

aller.

Remo

v

e.

The

remo

v

e

metho

d

supplan

ts

the

destrutor

b

y

reeiving

the

solv

er

state

as

a

parameter.

It

should

disp

ose

the

onstrain

t

and

remo

v

e

it

from

the

w

at

her

lists.

Propagate.

The

propagate

metho

d

is

alled

if

the

onstrain

t

is

found

in

a

w

at

her

list

during

propagation

of

unit

information

p.

The

onstrain

t

is

remo

v

ed

from

the

list

and

is

required

to

insert

itself

in

to

a

new

or

the

same

w

at

her

list.

An

y

unit

information

deriv

able

as

a

onsequene

of

p

should

b

e

enqueued.

If

suessful,

Tr

ue

is

returned;

if

a

onit

is

deteted,

F

alse

is

returned.

The

onstrain

t

ma

y

add

itself

to

the

undo

list

of

var

(p)

if

it

needs

to

b

e

up

dated

when

p

b

eomes

un

b

ound.

Simplify

.

A

t

the

top-lev

el,

a

onstrain

t

ma

y

b

e

giv

en

the

opp

ortunit

y

to

simplify

its

represen

tation

(returns

F

alse)

or

state

that

the

onstrain

t

is

satised

under

the

urren

t

assignmen

t

and

an

b

e

remo

v

ed

(returns

Tr

ue).

A

onstrain

t

m

ust

not

b

e

simpliable

to

pro

due

unit

information

or

to

b

e

oniting;

in

that

ase

the

propagation

has

not

b

een

orretly

dened.

Undo.

During

ba

ktra

king,

this

metho

d

is

alled

if

the

onstrain

t

added

itself

to

the

undo

list

of

var

(p)

in

pr

op

agate().

The

urren

t

v

ariable

assign-

men

ts

are

guaran

teed

to

b

e

iden

tial

to

that

of

the

momen

t

b

efore

pr

op

a-

gate()

w

as

alled.

Calulate

Reason.

This

metho

d

is

giv

en

a

literal

p

and

an

empt

y

v

etor.

The

onstrain

t

is

the

r

e

ason

for

p

b

eing

true,

that

is,

during

propagation,

the

urren

t

onstrain

t

enqueued

p.

The

reeiv

ed

v

etor

is

extended

to

inlude

a

set

of

assignmen

ts

(represen

ted

as

literals)

implying

p.

The

urren

t

v

ariable

assignmen

ts

are

guaran

teed

to

b

e

iden

tial

to

that

of

the

momen

t

b

efore

the

onstrain

t

propagated

p.

The

literal

p

is

also

allo

w

ed

to

b

e

the

sp

eial

onstan

t

?

lit

in

whi

h

ase

the

reason

for

the

lause

b

eing

oniting

should

b

e

returned

through

the

v

etor.

8

lass

Solv

er

{

Constr

aint

datab

ase

V

e

hConstr

i

onstrs

{

List

of

pr

oblem

onstr

aints.

V

e

hClause

i

learn

ts

{

List

of

le

arnt

lauses.

double

la

in

{

Clause

ativity

inr

ement

{

amount

to

bump

with.

double

la

dea

y

{

De

ay

fator

for

lause

ativity.

{

V

ariable

or

der

V

e

hdouble

i

ativit

y

{

Heuristi

me

asur

ement

of

the

ativity

of

a

variable.

double

v

ar

in

{

V

ariable

ativity

inr

ement

{

amount

to

bump

with.

double

v

ar

dea

y

{

De

ay

fator

for

variable

ativity.

V

arOr

der

order

{

Ke

eps

tr

ak

of

the

dynami

variable

or

der.

{

Pr

op

agation

V

e

hV

e

hConstr

ii

{

F

or

e

ah

liter

al

'p',

a

list

of

onstr

aints

wathing

'p'.

w

at

hes

A

onstr

aint

wil

l

b

e

insp

e

te

d

when

'p'

b

e

omes

true.

V

e

hV

e

hConstr

ii

{

F

or

e

ah

variable

'x',

a

list

of

onstr

aints

that

ne

e

d

to

undos

up

date

when

'x'

b

e

omes

unb

ound

by

b

aktr

aking.

Queue

hlit

i

propQ

{

Pr

op

agation

queue.

{

Assignments

V

e

hlb

o

ol

i

assigns

{

The

urr

ent

assignments

indexe

d

on

variables.

V

e

hlit

i

trail

{

List

of

assignments

in

hr

onolo

gi

al

or

der.

V

e

hint

i

trail

lim

{

Sep

ar

ator

indi

es

for

dier

ent

de

ision

levels

in

'tr

ail'.

V

e

hConstr

i

reason

{

F

or

e

ah

variable,

the

onstr

aint

that

implie

d

its

value.

V

e

hint

i

lev

el

{

F

or

e

ah

variable,

the

de

ision

level

it

was

assigne

d.

int

ro

ot

lev

el

{

Sep

ar

ates

inr

emental

and

se

ar

h

assumptions.

Fig.

2.

In

ternal

state

of

the

solv

er.

int

Solver.nV

ars

()

return

assigns.size

()

int

Solver.nAssigns

()

return

trail.size

()

int

Solver.nConstr

aints

()

return

onstrs.size

()

int

Solver.nL

e

arnts

()

return

learn

ts.size

()

lb

o

ol

Solver.value

(var

x)

return

assigns[x℄

lb

o

ol

Solver.value

(lit

p)

return

sign

(p)

?

:assigns[var

(p)℄

:

assigns[var

(p)℄

int

Solver.de

isionL

evel

()

return

trail

lim.size()

Fig.

3.

Small

help

er

metho

ds.

F

or

instane,

nL

e

arnts()

returns

the

n

um

b

er

of

learn

t

lauses.

lass

V

arOr

der

{

Publi

interfa

e

V

arOr

der

(V

e

hlb

o

ol

i

ref

to

assigns,

V

e

hdouble

i

ref

to

ativit

y)

void

newV

ar

()

{

Cal

le

d

when

a

new

variable

is

r

e

ate

d.

void

up

date

(var

x)

{

Cal

le

d

when

variable

has

inr

e

ase

d

in

ativity.

void

up

dateA

l

l

()

{

Cal

le

d

when

al

l

variables

have

b

e

en

assigne

d

new

ativities.

void

undo

(var

x)

{

Cal

le

d

when

variable

is

unb

ound

(may

b

e

sele

te

d

again).

var

sele

t

()

{

Cal

le

d

to

sele

t

a

new,

unassigne

d

variable.

Fig.

4.

Assisting

ADT

for

the

dynami

v

ariable

ordering

of

the

solv

er.

The

onstrutor

tak

es

referenes

to

the

assignmen

t

v

etor

and

the

ativit

y

v

etor

of

the

solv

er.

The

metho

d

sele

t()

will

return

the

unassigned

v

ariable

with

the

highest

ativit

y

.

9

lass

Constr

virtual

void

r

emove

(Solver

S)

{

must

b

e

dene

d

virtual

b

o

ol

pr

op

agate

(Solver

S,

lit

p)

{

must

b

e

dene

d

virtual

b

o

ol

simplify

(Solver

S)

{

defaults

to

r

eturn

false

virtual

void

undo

(Solver

S,

lit

p)

{

defaults

to

do

nothing

virtual

void

alR

e

ason

(Solver

S,

lit

p,

V

e

hlit

i

out

reason)

{

must

b

e

dene

d

Fig.

5.

Abstrat

base

lass

for

onstrain

ts.

The

o

de

for

the

Clause

onstrain

t

is

presen

ted

in

Figure

7.

It

is

also

used

for

learn

t

lauses,

whi

h

are

unique

in

that

they

an

b

e

added

to

the

lause

database

while

the

solv

er

is

not

at

top-lev

el.

This

mak

es

the

onstrutor

o

de

a

bit

more

ompliated

than

it

w

ould

b

e

for

a

normal

onstrain

t.

Implemen

ting

the

addClause()

metho

d

of

the

var

Solver.newV

ar

()

int

index

index

=

nV

ars

()

w

at

hes

.push

()

w

at

hes

.push

()

undos

.push

()

reason

.push

(Null)

assigns

.push

(?)

lev

el

.push

(-1)

ativit

y

.push

(0)

order

.newV

ar

()

return

index

Fig.

6.

Creates

a

new

SA

T

v

ariable

in

the

solv

er.

solv

er

API

is

just

a

matter

of

alling

Clause

-

new()

and

pushing

the

new

onstrain

t

on

the

\onstrs"

v

etor,

storing

the

list

of

problem

on-

strain

ts.

F

or

ompleteness,

w

e

also

displa

y

the

o

de

for

reating

v

ariables

in

the

solv

er

(Fig-

ure

6).

There

are

a

n

um

b

er

of

tri

ks

for

smart-o

ding

[Disussion℄

that

an

b

e

used

in

a

C++

implemen

tation

of

Clause.

In

partiularly

the

\lits"

v

etor

an

b

e

implemen

ted

as

an

zero-sized

arra

y

plaed

last

in

the

lass,

and

then

extra

memory

allo

ated

for

the

lause

to

on

tain

the

data.

W

e

observ

ed

a

20%

sp

eedup

for

this

tri

k.

F

urthermore,

mem-

ory

an

b

e

sa

v

ed

b

y

not

storing

ativit

y

for

prob-

lem

lauses.

Of

the

metho

ds

dening

a

onstrain

t,

pr

op

agate()

should

b

e

the

primary

tar-

[Disussion℄

get

for

eÆien

t

implemen

tation.

The

SA

T-solv

er

sp

ends

ab

out

80%

of

the

time

propagating,

so

the

metho

d

will

b

e

alled

frequen

tly

.

In

S

ATZOO

a

p

erformane

gain

w

as

a

hiev

ed

b

y

remem

b

ering

the

p

osition

of

the

last

w

at

hed

literal

and

start

lo

oking

for

a

new

literal

to

w

at

h

from

that

p

osition.

F

urther

sp

eedups

ma

y

b

e

a

hiev

ed

b

y

sp

eializing

the

o

de

for

small

lause

sizes.

4.3

Propagation

Giv

en

the

me

hanism

for

adding

onstrain

ts,

w

e

no

w

mo

v

e

on

to

desrib

e

the

propagation

of

unit

information

on

these

onstrain

ts.

The

propagation

routine

k

eeps

a

set

of

literals

(unit

information)

that

is

to

b

e

propagated.

W

e

all

this

the

pr

op

agation

queue.

When

a

literal

is

inserted

in

to

the

queue,

the

orresp

onding

v

ariable

is

immediately

assigned.

F

or

ea

h

literal

in

the

queue,

the

w

at

her

list

of

that

literal

determines

the

onstrain

ts

that

ma

y

b

e

aeted

b

y

the

assignmen

t.

Through

the

in

terfae

desrib

ed

in

the

previous

setion,

ea

h

onstrain

t

is

ask

ed

b

y

a

all

to

its

pr

op

agate()

metho

d

if

more

unit

information

an

b

e

inferred,

whi

h

will

then

b

e

enqueued.

The

pro

ess

on

tin

ues

un

til

either

the

queue

is

empt

y

or

a

onit

is

found.

10

lass

Clause

:

publi

Constr

b

o

ol

learn

t

o

at

ativit

y

V

e

hlit

i

lits

{

Construtor

{

r

e

ates

a

new

lause

and

adds

it

to

wather

lists:

stati

b

o

ol

Clause

new

(Solver

S,

V

e

hlit

i

ps,

b

o

ol

learn

t,

Clause

out

lause)

\Implemen

tation

in

Figure

8

"

{

L

e

arnt

lauses

only:

b

o

ol

lo

ke

d

(Solver

S)

return

S.reason[var

(lits[0℄)℄

==

this

{

Constr

aint

interfa

e:

void

r

emove

(Solver

S)

remo

v

eElem(this,

S.w

at

hes[index(:lits[0℄)℄)

remo

v

eElem(this,

S.w

at

hes[index(:lits[1℄)℄)

delete

this

b

o

ol

simplify

(Solver

S)

{

only

al

le

d

at

top-level

with

empty

pr

op.

queue

int

j

=

0

for

(int

i

=

0;

i

<

lits.size

();

i++)

if

(S.value

(lits[i℄)

==

Tr

ue

?

)

return

Tr

ue

else

if

(S.value

(lits[i℄)

==

?)

lits[j++℄

=

lits[i℄

{

false

liter

als

ar

e

not

opie

d

(only

o

ur

for

i

2)

lits.shrink(lits.size

()

j)

return

F

alse

b

o

ol

pr

op

agate

(Solver

S,

lit

p)

{

Make

sur

e

the

false

liter

al

is

lits[1℄:

if

(lits[0℄

==

:p)

lits[0℄

=

lits[1℄,

lits[1℄

=

:p

{

If

0th

wath

is

true,

then

lause

is

alr

e

ady

satise

d.

if

(S.value

(lits[0℄)

==

Tr

ue

?

)

S.w

at

hes[index

(p)℄.push

(this)

{

r

e-insert

lause

into

wather

list

return

Tr

ue

{

L

o

ok

for

a

new

liter

al

to

wath:

for

(int

i

=

2;

i

<

size

();

i++)

if

(S.value

(lits[i℄)

!=

F

alse

?

)

lits[1℄

=

lits[i℄,

lits[i℄

=

:p

S.w

at

hes[index

(:lits[1℄)℄.push

(this)

{

insert

lause

into

wather

list

return

Tr

ue

{

Clause

is

unit

under

assignment:

S.w

at

hes[index

(p)℄.push

(this)

return

S.enqueue

(lits[0℄,

this)

{

enqueue

for

pr

op

agation

void

alR

e

ason

(Solver

S,

lit

p,

ve

hlit

i

out

reason)

{

invariant:

(p

==

?)

or

(p

==

lits[0℄

)

for

(int

i

=

((p

==

?)

?

0

:

1);

i

<

size

();

i++)

out

reason.push

(:lits[i℄)

{

invariant:

S.value(lits[i℄)

==

F

alse

?

if

(le

arnt

)

S.laBumpAtivit

y(this)

Fig.

7.

Implemen

tation

of

the

Clause

onstrain

t.

11

b

o

ol

Clause

new

(Solver

S,

V

e

hlit

i

ps,

b

o

ol

learn

t,

Clause

out

lause)

out

lause

=

Null

{

Normalize

lause:

if

(!learn

t)

if

("an

y

literal

in

ps

is

true")

return

Tr

ue

if

("b

oth

p

and

:p

o

urs

in

ps")

return

Tr

ue

"remo

v

e

all

false

literals

from

ps"

"remo

v

e

all

dupliates

from

ps"

if

(ps.size

()

==

0)

return

F

alse

else

if

(ps.size

()

==

1)

return

S.enqueue

(ps[0℄)

{

unit

fats

ar

e

enqueue

d

else

{

A

l

lo

ate

lause:

Clause

=

new

Clause

ps.moveT

o

(.lits)

.learn

t

=

learn

t

.ativit

y

=

0

{

only

r

elevant

for

le

arnt

lauses

if

(learn

t)

{

Pik

a

se

ond

liter

al

to

wath:

"Let

max

i

b

e

the

index

of

the

literal

with

highest

deision

lev

el"

.lits[1℄

=

ps[max

i℄,

.lits[max

i℄

=

ps[1℄

{

Bumping:

S.laBumpA

tivity

()

{

new

ly

le

arnt

lauses

should

b

e

onsider

e

d

ative

for

(int

i

=

0;

i

<

ps.size

();

i++)

S.varBumpA

tivity

(ps[i℄)

{

variables

in

onit

lauses

ar

e

bump

e

d

{

A

dd

lause

to

wather

lists:

S.w

at

hes[index

(:.lits[0℄)℄.push

()

S.w

at

hes[index

(:.lits[1℄)℄.push

()

out

lause

=

return

Tr

ue

Fig.

8.

Construtor

funtion

for

lauses.

Returns

F

alse

if

top-lev

el

onit

is

deteted.

'out

lause'

ma

y

b

e

set

to

Null

if

the

new

lause

is

already

satised

under

the

urren

t

top-lev

el

assignmen

t.

P

ost-ondition:

'ps'

is

leared.

F

or

learn

t

lauses,

all

literals

will

b

e

false

exept

`lits[0℄'

(this

b

y

design

of

the

analyze

()

metho

d).

F

or

the

propagation

to

w

ork,

the

seond

w

at

h

m

ust

b

e

put

on

the

literal

whi

h

will

rst

b

e

un

b

ound

b

y

ba

ktra

king.

(Note

that

none

of

the

learn

t-lause

sp

ei

things

needs

to

b

e

done

for

a

user

dened

onstrain

t

t

yp

e.)

12

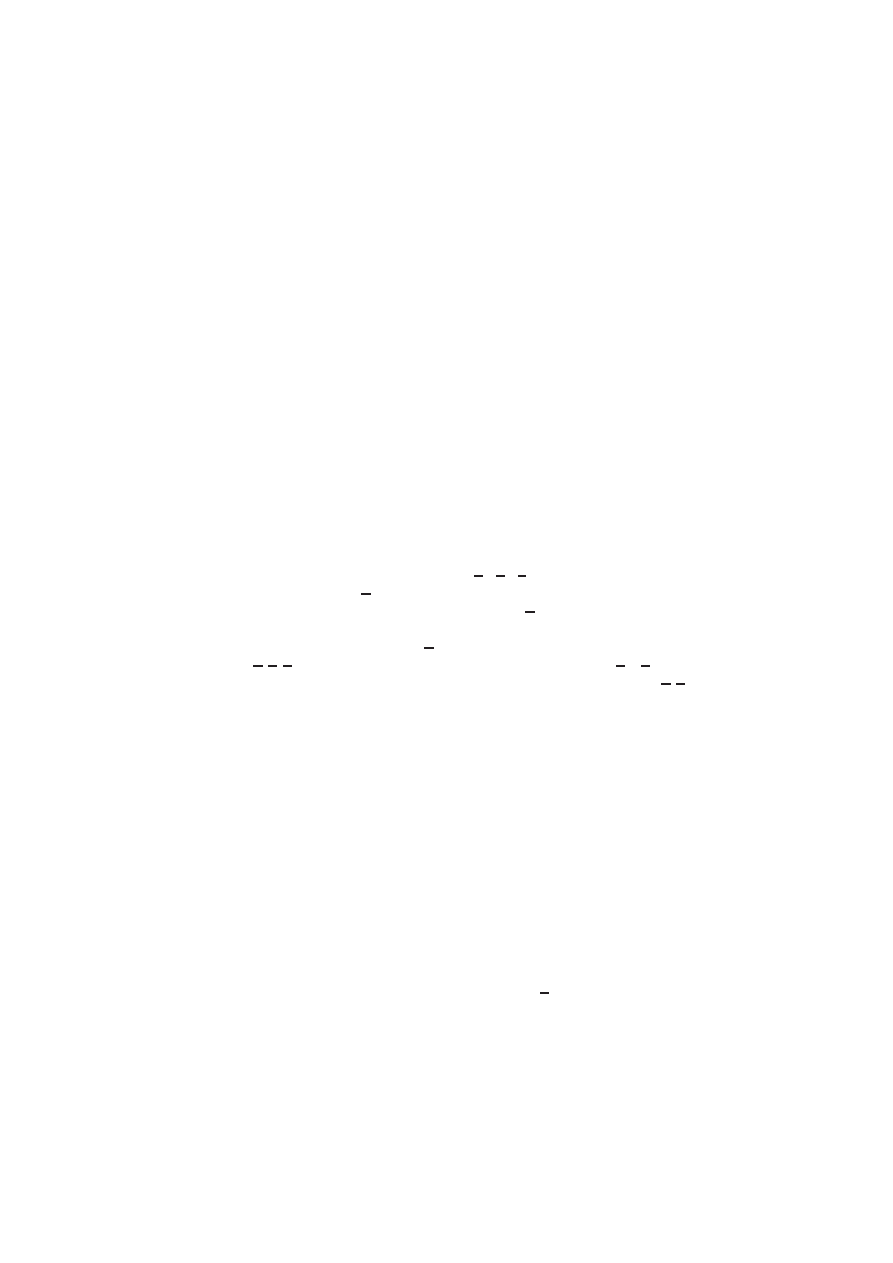
An

implemen

tation

of

this

pro

edure

is

displa

y

ed

in

Figure

9.

It

starts

b

y

dequeuing

a

literal

and

learing

the

w

at

her

list

for

that

literal

b

y

mo

ving

it

to

\tmp".

The

propagate

metho

d

is

then

alled

for

ea

h

onstrain

t

of

\tmp".

This

will

re-insert

w

at

hes

in

to

new

lists.

Should

a

onit

b

e

deteted

during

the

tra

v

ersal

of

\tmp",

the

remaining

w

at

hes

will

b

e

opied

ba

k

to

the

original

w

at

her

list,

and

the

propagation

queue

leared.

The

metho

d

for

enqueuing

unit

information

is

relativ

ely

straigh

tforw

ard.

Note

that

the

same

fat

an

b

e

enqueued

sev

eral

times,

as

it

ma

y

b

e

prop-

agated

from

dieren

t

onstrain

ts,

but

it

will

only

b

e

put

on

the

propagation

queue

one.

It

ma

y

b

e

that

later

enqueuings

ha

v

e

a

\b

etter"

reason

(determined

heuristi-

[Disussion℄

ally)

and

a

small

p

erformane

gain

w

as

a

hiev

ed

in

S

ATZOO

b

y

hanging

reason

if

the

new

reason

w

as

smaller

than

the

previously

stored.

The

hanging

aets

the

onit

lause

generation

desrib

ed

in

the

next

setion.

4.4

Learning

This

setion

desrib

es

the

onit-driv

en

lause

learning.

It

w

as

rst

desrib

ed

in

[MS96

℄

and

is

one

of

the

ma

jor

adv

anes

of

SA

T-te

hnology

in

the

last

deade.

W

e

desrib

e

the

basi

onit-analysis

algorithm

b

y

an

example.

Assume

the

database

on

tains

the

lause

fx;

y

;

z

g

whi

h

just

b

eame

unsatised

during

propagation.

This

is

our

onit.

W

e

all

x

^

y

^

z

the

reason

set

of

the

onit.

No

w

x

is

false

b

eause

x

w

as

propagated

from

some

onstrain

t.

W

e

ask

that

onstrain

t

to

giv

e

us

the

reason

for

propagating

x

(the

alR

e

ason()

metho

d).

It

will

resp

ond

with

another

onjuntion

of

literals,

sa

y

u

^

v

.

These

w

ere

the

v

ariable

assignmen

t

that

implied

x.

The

onstrain

t

ma

y

in

fat

ha

v

e

b

een

the

lause

fu

;

v

;

xg.

F

rom

this

little

analysis

w

e

kno

w

that

u

^

v

^

y

^

z

m

ust

also

lead

to

a

onit.

W

e

ma

y

prohibit

this

onit

b

y

adding

the

lause

fu

;

v

;

y

;

z

g

to

the

lause

database.

This

w

ould

b

e

an

example

of

a

le

arnt

onit

lause.

In

the

example,

w

e

pi

k

ed

only

one

literal

and

analyzed

it

one

step.

The

pro

ess

of

expanding

literals

with

their

reason

sets

an

b

e

on

tin

ued,

in

the

extreme

ase

un

til

all

the

literals

of

the

onit

set

are

deision

v

ariables

(whi

h

w

ere

not

propagated

b

y

an

y

onstrain

ts).

Dieren

t

learning

s

hemes

based

on

this

pro

ess

ha

v

e

b

een

prop

osed.

Exp

erimen

tally

the

\First

Unique

Impliation

P

oin

t"

(First

UIP)

heuristi

has

b

een

sho

wn

eetiv

e

[ZM01

℄.

W

e

will

not

giv

e

the

denition

of

UIPs

here,

but

just

state

the

algorithm:

In

a

breadth-rst

manner,

on

tin

ue

to

expand

literals

of

the

urren

t

deision

lev

el,

un

til

there

is

just

one

left.

In

the

o

de

for

analyze(),

displa

y

ed

in

Figure

10,

w

e

mak

e

use

of

the

fat

that

a

breadth-rst

tra

v

ersal

an

b

e

a

hiev

ed

b

y

insp

eting

the

trail

ba

kw

ards.

Esp

eially

,

the

v

ariables

of

the

reason

set

of

p

is

alw

a

ys

b

efore

p

in

the

trail.

F

ur-

thermore,

in

the

algorithm

w

e

initialize

p

to

?

lit

,

whi

h

will

mak

e

alR

e

ason()

return

the

reason

for

the

onit.

Assuming

x

to

b

e

the

unit

information

that

auses

the

onit,

an

alternativ

e

[Disussion℄

implemen

tation

w

ould

b

e

to

alulate

the

reason

for

x

and

just

add

x

to

that

set.

The

o

de

w

ould

b

e

sligh

tly

more

um

b

ersome

but

the

on

trat

for

alR

e

ason()

w

ould

b

e

simpler,

as

w

e

no

longer

need

the

sp

eial

ase

for

?

lit

.

13

Constr

Solver.pr

op

agate

()

while

(propQ.size

()

>

0)

lit

p

=

propQ.de

queue

()

{

'p'

is

now

the

enqueue

d

fat

to

pr

op

agate

V

e

hConstr

i

tmp

{

'tmp'

wil

l

ontain

the

wather

list

for

'p'

w

at

hes[index

(p)℄.moveT

o

(tmp)

for

(int

i

=

0;

i

<

tmp.size

();

i++)

if

(!tmp[i℄.pr

op

agate

(this,

p))

{

Constr

aint

is

oniting;

opy

r

emaining

wathes

to

'wathes[p℄'

{

and

r

eturn

onstr

aint:

for

(int

j

=

i+1;

j

<

tmp.size

();

j++)

w

at

hes[index

(p)℄.push

(tmp[j℄)

propQ.le

ar

()

return

tmp[i℄

return

Null

b

o

ol

Solver.enqueue

(lit

p,

Constr

from

=

Null)

if

(value

(p)

!=

?)

if

(value

(p)

==

F

alse

?

)

{

Coniting

enqueue

d

assignment

return

F

alse

else

{

Existing

onsistent

assignment

{

don

't

enqueue

return

Tr

ue

else

{

New

fat,

stor

e

it

assigns

[var

(p)℄

=

lb

o

ol

(!sign

(p))

lev

el

[var

(p)℄

=

de

isionL

evel

()

reason

[var

(p)℄

=

from

trail.push

(p)

propQ.insert

(p)

return

Tr

ue

Fig.

9.

pr

op

agate():

Propagates

all

enqueued

fats.

If

a

onit

arises,

the

oniting

lause

is

returned,

otherwise

Null.

enqueue():

Puts

a

new

fat

on

the

propagation

queue,

as

w

ell

as

immediately

up

dating

the

v

ariable's

v

alue

in

the

assignmen

t

v

etor.

If

a

onit

arises,

F

alse

is

returned

and

the

propagation

queue

is

leared.

The

parameter

'from'

on

tains

a

referene

to

the

onstrain

t

from

whi

h

'p'

w

as

propagated

(defaults

to

Null

if

omitted).

Finally

,

the

analysis

not

only

returns

a

onit

lause,

but

also

the

ba

k-

tra

king

lev

el.

This

is

the

lo

w

est

deision

lev

el

for

whi

h

the

onit

lause

is

unit.

It

is

adv

an

tageous

to

ba

ktra

k

as

far

as

p

ossible

[MS96

℄,

and

is

referred

to

as

b

ak-jumping

or

non-hr

onolo

gi

al

b

aktr

aking

in

the

literature.

4.5

Sear

h

The

sear

h

metho

d

in

Figure

13

w

orks

basially

as

desrib

ed

in

setion

3

but

with

the

follo

wing

additions:

Restarts.

The

rst

argumen

t

of

the

sear

h

metho

d

is

\nof

onits".

The

sear

h

for

a

mo

del

or

a

on

tradition

will

only

b

e

onduted

for

this

man

y

14

void

Solver.analyze

(Constr

on,

V

e

hlit

i

out

learn

t,

Int

out

btlev

el)

V

e

hb

o

ol

i

seen(nV

ars

(),

F

alse)

int

oun

ter

=

0

lit

p

=

?

lit

V

e

hlit

i

p

reason

out

learn

t.push

()

{

le

ave

r

o

om

for

the

asserting

liter

al

out

btlev

el

=

0

do

p

reason.le

ar

()

on.

alR

e

ason

(this,

p,

p

reason)

{

invariant

her

e:

on

!=

NULL

{

Tra

e

reason

f

or

p:

for

(int

j

=

0;

j

<

p

reason.size();

j++)

lit

q

=

p

reason[j℄

if

(!seen[var

(q)℄)

seen[var

(q)℄

=

Tr

ue

if

(lev

el[var

(q)℄

==

de

isionL

evel

())

oun

ter++

else

if

(lev

el[var

(q)℄

>

0)

{

exlude

variables

fr

om

de

ision

level

0

out

learn

t.push

(:q)

out

btlev

el

=

max

(out

btlev

el,

lev

el[var

(q)℄)

{

Selet

next

literal

to

look

a

t:

do

p

=

trail.last

()

on

=

reason[var

(p)℄

undoOne

()

while

(!seen[var

(p)℄)

oun

ter

while

(oun

ter

>

0)

out

learn

t[0℄

=

:p

Fig.

10.

Analyze

a

onit

and

pro

due

a

reason

lause.

Pre-onditions:

(1)

'out

learn

t'

is

assumed

to

b

e

leared.

(2)

Curren

t

deision

lev

el

m

ust

b

e

greater

than

ro

ot

lev

el.

P

ost-onditions:

(1)

'out

learn

t[0℄'

is

the

asserting

literal

at

lev

el

'out

btlev

el'.

Eet:

Will

undo

part

of

the

trail,

but

not

b

ey

ond

last

deision

lev

el.

void

Solver.r

e

or

d

(V

e

hlit

i

lause)

Clause

{

wil

l

b

e

set

to

r

e

ate

d

lause,

or

NULL

if

'lause[℄'

is

unit

Clause

new

(this,

lause,

Tr

ue,

)

{

annot

fail

at

this

p

oint

enqueue

(lause[0℄,

)

{

annot

fail

at

this

p

oint

if

(

!=

Null)

learn

ts.push

()

Fig.

11.

Reord

a

lause

and

driv

e

ba

ktra

king.

Pre-ondition:

'lause[0℄'

m

ust

on

tain

the

asserting

literal.

In

partiular,

'lause[℄'

m

ust

not

b

e

empt

y

.

15

onits.

If

failing

to

solv

e

the

SA

T-problem

within

the

b

ound,

all

assump-

tions

will

b

e

aneled

and

?

returned.

The

surrounding

solv

er

strategy

will

then

restart

the

sear

h,

p

ossibly

with

a

new

set

of

parameters.

Redue.

The

seond

argumen

t,

\nof

learn

ts",

sets

an

upp

er

limit

on

the

n

um

b

er

of

learn

t

lauses

that

are

k

ept.

One

this

n

um

b

er

is

rea

hed,

r

e-

du

eDB()

is

alled.

Clauses

that

are

urren

tly

the

reason

for

a

v

ariable

as-

signmen

t

are

said

to

b

e

lo

ke

d

and

annot

b

e

remo

v

ed

b

y

r

e

du

eDB().

F

or

this

reason,

the

limit

is

extended

b

y

the

n

um

b

er

of

assigned

v

ariables,

whi

h

appro

ximates

the

n

um

b

er

of

lo

k

ed

lauses.

P

arameters.

The

third

argumen

t

to

the

sear

h

metho

d

groups

some

tuning

onstan

ts.

In

the

urren

t

v

ersion

of

M

INI

S

AT

,

it

only

on

tains

the

dea

y

fators

for

v

ariables

and

lauses.

Ro

ot-lev

el.

T

o

supp

ort

inremen

tal

SA

T,

the

onept

of

a

r

o

ot-level

is

in-

tro

dued.

The

ro

ot-lev

el

ats

a

bit

as

a

new

top-lev

el.

Ab

o

v

e

the

ro

ot-lev

el

are

the

inremen

tal

assumptions

passed

to

solve()

(if

an

y).

The

sear

h

pro-

edure

is

not

allo

w

ed

to

ba

ktra

k

ab

o

v

e

the

ro

ot-lev

el,

as

this

w

ould

hange

the

inremen

tal

assumptions.

If

w

e

rea

h

a

onit

at

ro

ot-lev

el,

the

sear

h

will

return

F

alse.

A

problem

with

the

approa

h

presen

ted

here

is

onit

lauses

that

are

unit.

F

or

these,

analyze()

will

alw

a

ys

return

a

ba

ktra

k

lev

el

of

0

(top-

lev

el).

As

unit

lauses

are

treated

sp

eially

,

they

are

nev

er

added

to

the

lause

database.

Instead

they

are

enqueued

as

fats

to

b

e

propagated

(see

the

o

de

of

Clause

new()

).

There

w

ould

b

e

no

problem

if

this

w

as

done

at

top-lev

el.

Ho

w

ev

er,

the

sear

h

pro

edure

will

only

undo

un

til

ro

ot-lev

el,

whi

h

means

that

the

unit

fat

will

b

e

enqueued

there.

One

se

ar

h()

has

solv

ed

the

urren

t

SA

T-problem,

the

surrounding

solv

er

strategy

will

undo

an

y

inremen

tal

assumption

and

put

the

solv

er

ba

k

at

the

top-lev

el.

By

this

the

unit

lause

will

b

e

forgotten,

and

the

next

inremen

tal

SA

T

problem

will

ha

v

e

to

infer

it

again.

A

solution

to

this

is

to

store

the

learn

t

unit

lauses

in

a

v

etor

and

re-insert

them

at

top-lev

el

b

efore

the

next

all

to

solve().

The

reason

for

omitting

this

in

M

INI

S

AT

is

that

w

e

ha

v

e

not

seen

an

y

p

erformane

gain

b

y

this

extra

handling

in

our

appliations

[ES03

,CS03

℄.

Simpliit

y

th

us

ditates

that

w

e

lea

v

e

it

out

of

the

presen

tation.

Simplify

.

Pro

vided

the

ro

ot-lev

el

is

0

(no

assumptions

w

ere

passed

to

solve()

)

the

sear

h

will

return

to

the

top-lev

el

ev

ery

time

a

unit

lause

is

learn

t.

A

t

that

p

oin

t

it

is

legal

to

all

simplifyDB()

to

simplify

the

problem

onstrain

ts

aording

to

the

top-lev

el

assignmen

t.

If

a

stronger

simplier

than

presen

ted

here

is

implemen

ted,

a

on

tradition

ma

y

b

e

found,

in

whi

h

ase

the

sear

h

should

b

e

ab

orted.

As

our

simplier

is

not

stronger

than

normal

propaga-

tion,

it

an

nev

er

rea

h

a

on

tradition,

so

w

e

ignore

the

return

v

alue

of

simplify().

16

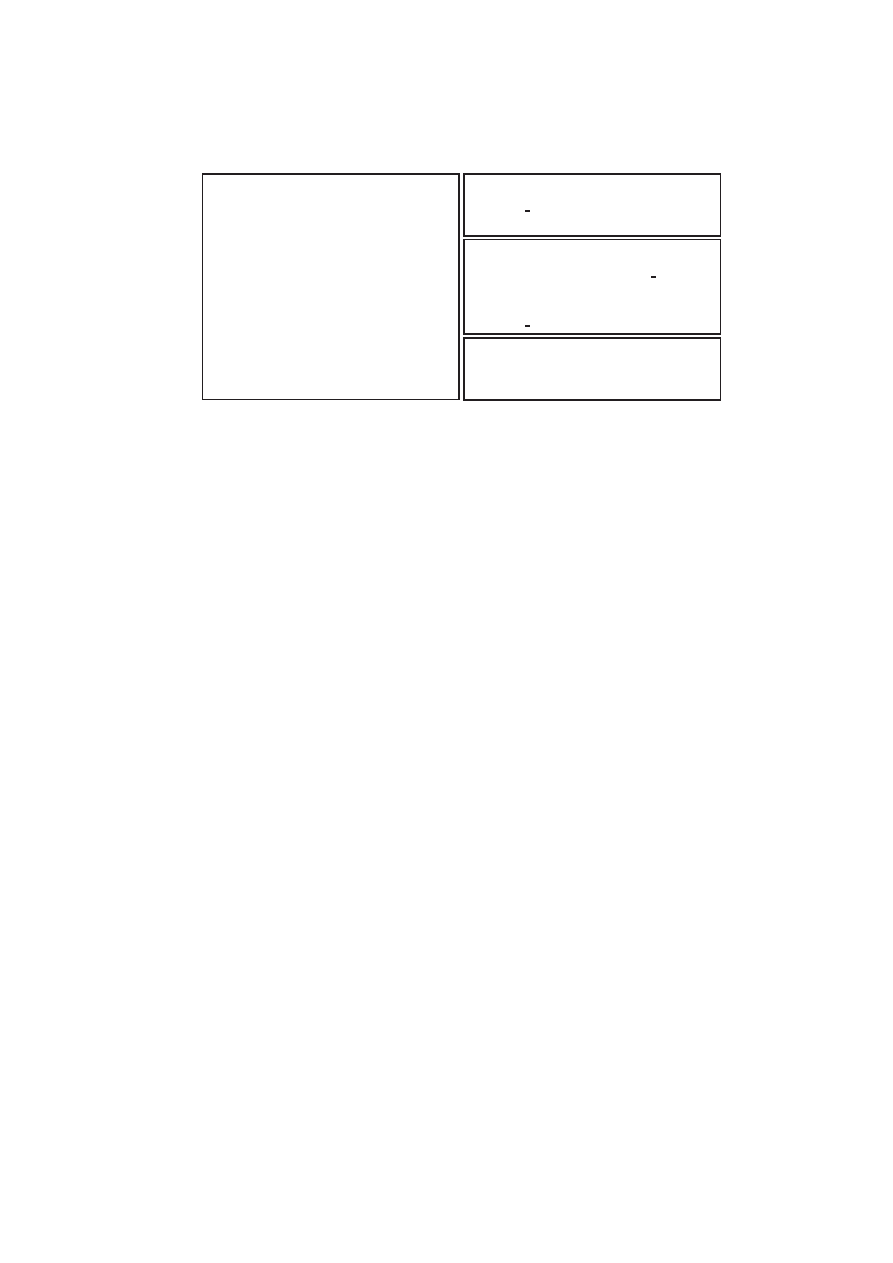
void

Solver.undoOne

()

lit

p

=

trail.last

()

var

x

=

var

(p)

assigns

[x℄

=

?

reason

[x℄

=

Null

lev

el

[x℄

=

-1

order.undo

(x)

trail.p

op

()

while

(undos[x℄.size

()

>

0)

undos[x℄.last

().undo

(this,

p)

undos[x℄.p

op

()

b

o

ol

Solver.assume

(lit

p)

trail

lim.push

(trail.size

())

return

enqueue

(p)

void

Solver.

an

el

()

int

=

trail.size

()

trail

lim.last

()

for

(;

!=

0;

)

undoOne

()

trail

lim.p

op

()

void

Solver.

an

elUntil

(int

lev

el)

while

(de

isionL

evel

()

>

lev

el)

an

el

()

Fig.

12.

assume():

returns

F

alse

if

immediate

onit.

Pre-ondition:

propaga-

tion

queue

is

empt

y

.

undoOne():

un

binds

the

last

v

ariable

on

the

trail.

an

el():

rev

erts

to

the

state

b

efore

last

push

().

Pre-ondition:

propagation

queue

is

empt

y

.

an

elUntil():

anels

sev

eral

lev

els

of

assumptions.

4.6

Ativit

y

heuristis

The

implemen

tation

of

ativit

y

is

sho

wn

in

Figure

14.

Instead

of

atually

m

ulti-

plying

all

v

ariables

b

y

a

dea

y

fator

after

ea

h

onit,

w

e

bump

v

ariables

with

larger

and

larger

n

um

b

ers.

Only

relativ

e

v

alues

matter.

Ev

en

tually

w

e

will

rea

h

the

limit

of

what

is

represen

table

b

y

a

oating

p

oin

t

n

um

b

er.

A

t

that

p

oin

t,

all

ativities

are

saled

do

wn.

In

the

V

arOr

der

data

t

yp

e

of

M

INI

S

AT

,

the

list

of

v

ariables

is

k

ept

sorted

on

ativit

y

at

all

time.

The

ba

ktra

king

will

alw

a

ys

aurately

ho

ose

the

most

ativ

e

v

ariable.

The

original

suggestion

for

the

VSIDS

dynami

v

ariable

ordering

w

as

to

sort

p

erio

dially

.

The

p

olarit

y

of

a

literal

is

ignored

in

M

INI

S

AT

.

Ho

w

ev

er,

storing

the

latest

[Disussion℄

p

olarit

y

of

a

v

ariable

migh

t

impro

v

e

the

sear

h

when

restarts

are

used,

but

it

remains

to

b

e

empirially

supp

orted.

F

urthermore,

the

in

terfae

of

V

arOr

der

an

b

e

used

for

other

v

ariable

heuristis.

In

S

ATZOO

,

an

initial

stati

v

ariable

order

omputed

from

the

lause

struture

w

as

partiularly

suessful

on

man

y

problems.

4.7

Constrain

t

remo

v

al

The

metho

ds

for

reduing

the

set

of

learn

t

lauses

as

w

ell

as

the

top-lev

el

sim-

pliation

pro

edure

an

b

e

found

in

Figure

15.

When

remo

ving

learn

t

lauses,

it

is

imp

ortan

t

not

to

remo

v

e

so

alled

lo

ke

d

lauses.

Lo

k

ed

lauses

are

those

partiipating

in

the

urren

t

ba

ktra

king

bran

h

b

y

b

eing

the

reason

(through

propagation)

for

a

v

ariable

assignmen

t.

The

redue

pro

edure

k

eeps

half

of

the

learn

t

lauses,

exept

for

those

whi

h

ha

v

e

dea

y

ed

b

elo

w

a

threshold

limit.

Su

h

lauses

an

o

ur

if

the

set

of

ativ

e

onstrain

ts

is

v

ery

small.

T

op-lev

el

simpliation

an

b

e

seen

as

a

sp

eial

ase

of

propagation.

Sine

[Disussion℄

17

lb

o

ol

Solver.se

ar

h

(int

nof

onits,

int

nof

learn

ts,

Se

ar

hPar

ams

params)

int

onitC

=

0

v

ar

dea

y

=

1

/

params.v

ar

dea

y

la

dea

y

=

1

/

params.la

dea

y

mo

del.le

ar

()

lo

op

Constr

on

=

pr

op

agate

()

if

(on

!=

Null)

{

Conflit

onitC++

V

e

hlit

i

learn

t

lause

int

ba

ktra

k

lev

el

if

(de

isionL

evel

()

==

ro

ot

lev

el)

return

F

alse

?

analyze

(on,

learn

t

lause,

ba

ktra

k

lev

el)

an

elUntil

(max

(ba

ktra

k

lev

el,

ro

ot

lev

el))

r

e

or

d

(learn

t

lause)

de

ayA

tivities

()

else

{

No

onflit

if

(de

isionL

evel

()

==

0)

{

Simplify

the

set

of

pr

oblem

lauses:

simplifyDB

()

{

our

simplier

annot

r

eturn

false

her

e

if

(learn

ts.size

()

nAssigns

()

nof

learn

ts)

{

R

e

du

e

the

set

of

le

arnt

lauses:

r

e

du

eDB

()

if

(nAssigns

()

==

nV

ars

())

{

Mo

del

found:

mo

del.gr

owT

o

(nV

ars

())

for

(int

i

=

0;

i

<

nV

ars

();

i++)

mo

del[i℄

=

(value

(i)

==

Tr

ue

?

)

an

elUntil

(ro

ot

lev

el)

return

Tr

ue

?

else

if

(onitC

nof

onits)

{

R

e

ahe

d

b

ound

on

numb

er

of

onits:

an

elUntil

(ro

ot

lev

el)

{

for

e

a

r

estart

return

?

else

{

New

variable

de

ision:

lit

p

=

lit

(order.sele

t

())

{

may

have

heuristi

for

p

olarity

her

e

assume

(p)

{

annot

r

eturn

false

Fig.

13.

Sear

h

metho

d.

Assumes

and

propagates

un

til

a

onit

is

found,

from

whi

h

a

onit

lause

is

learn

t

and

ba

ktra

king

p

erformed

un

til

sear

h

an

on

tin

ue.

Pre-

ondition:

ro

ot

lev

el

==

de

isionL

evel

().

18

void

Solver.varBumpA

tivity

(var

x)

if

((ativit

y[x℄

+=

v

ar

in)

>

1e100)

varR

es

aleA

tivity

()

order.up

date

(x)

void

Solver.varDe

ayA

tivity

()

v

ar

in

*=

v

ar

dea

y

void

Solver.varR

es

aleA

tivity

()

for

(int

i

=

0;

i

<

nV

ars

();

i++)

ativit

y[i℄

*=

1e-100

v

ar

in

*=

1e-100

void

Solver.laBumpA

tivity

(

Clause

)

void

Solver.laDe

ayA

tivity

()

void

Solver.laR

es

aleA

tivity

()

{

Similarly

implemente

d.

void

Solver.de

ayA

tivities

()

varDe

ayA

tivity

()

laDe

ayA

tivity

()

Fig.

14.

Bumping

of

v

ariable

and

lause

ativities.

it

is

p

erformed

under

no

assumption,

an

ything

learn

t

an

b

e

k

ept

forev

er.

The

freedom

of

not

ha

ving

to

store

deriv

ed

information

separately

,

with

the

abilit

y

to

undo

it

later,

mak

es

it

easier

to

implemen

t

stronger

propagation.

4.8

T

op-lev

el

solv

er

The

metho

d

implemen

ting

M

INI

S

AT

's

top-lev

el

strategy

an

b

e

found

in

Figure

16.

It

is

resp

onsible

for

making

the

inremen

tal

assumptions

and

setting

the

ro

ot

lev

el.

F

urthermore,

it

ompletes

the

simple

ba

ktra

king

sear

h

with

restarts,

whi

h

are

p

erformed

less

and

less

frequen

tly

.

After

ea

h

restart,

the

n

um

b

er

of

allo

w

ed

learn

t

lauses

is

inreased.

The

o

de

on

tains

a

n

um

b

er

of

hand-tuned

onstan

ts

that

ha

v

e

sho

wn

to

p

er-

form

reasonable

on

our

appliations

[ES03

,CS03

℄.

The

top-lev

el

strategy

,

ho

w-

ev

er,

is

a

pro

dutiv

e

target

for

impro

v

emen

ts

(p

ossibly

appliation

dep

enden

t).

In

S

ATZOO

,

the

top-lev

el

strategy

on

tains

an

initial

phase

where

a

stati

v

ari-

able

ordering

is

used.

5

Conlusions

and

Related

W

ork

By

this

pap

er,

w

e

ha

v

e

pro

vided

a

minimal

referene

implemen

tation

of

a

mo

dern

onit-driv

en

SA

T-solv

er.

Despite

the

abstration

la

y

er

for

b

o

olean

onstrain

ts,

and

the

la

k

of

more

sophistiated

heuristis,

the

p

erformane

of

M

INI

S

AT

is

omparable

to

state-of-the-art

SA

T-solv

ers.

W

e

ha

v

e

tested

M

INI

S

AT

against

Z

C

HAFF

and

B

ERKMIN

5.61

on

177

SA

T-instanes.

These

instanes

w

ere

used

to

tune

S

ATZOO

for

the

SA

T

2003

Comp

etition.

As

S

ATZOO

solv

ed

more

instanes

and

series

of

problems,

ranging

o

v

er

all

three

ategories

(industrial,

handmade,

and

r

andom

),

than

an

y

other

solv

er

in

the

omp

etition,

w

e

feel

that

this

is

a

go

o

d

test-set

for

the

o

v

erall

p

erformane.

No

extra

tuning

w

as

done

in

M

INI

S

AT

;

it

w

as

just

run

one

with

the

onstan

ts

presen

ted

in

the

o

de.

A

t

a

time-out

of

10

min

utes,

M

INI

S

AT

solv

ed

158

instanes,

while

Z

C

HAFF

solv

ed

147

instanes

and

B

ERKMIN

157

instanes.

Another

approa

h

to

inremen

tal

SA

T

and

non-lausal

onstrain

ts

w

as

pre-

sen

ted

b

y

Aloul,

Ramani,

Mark

o

v,

and

Sak

allah

in

their

w

ork

on

S

ATIRE

and

PBS

[WKS01,ARMS02

℄.

Our

implemen

tation

diers

in

that

it

has

a

simpler

19

void

Solver.r

e

du

eDB

()

int

i,

j

double

lim

=

la

in

/

learn

ts.size()

sortOnA

tivity

(learn

ts)

for

(i=j=0;

i

<

learn

ts.size

()/2;

i++)

if

(!learn

ts[i℄.lo

ke

d

(this))

learn

ts[i℄.r

emove

(this)

else

learn

ts[j++℄

=

learn

ts[i℄

for

(;

i

<

learn

ts.size

();

i++)

if

(!learn

ts[i℄.lo

ke

d

(this)

&&

learn

ts[i℄.ativity

()

<

lim)

learn

ts[i℄.r

emove

(this)

else

learn

ts[j++℄

=

learn

ts[i℄

learn

ts.shrink

(i

j)

b

o

ol

Solver.simplifyDB

()

if

(pr

op

agate

()

!=

Null)

return

F

alse

for

(int

t

yp

e

=

0;

t

yp

e

<

2;

t

yp

e++)

V

e

hConstr

i

s

=

t

yp

e

?

(V

e

hConstr

i)learn

ts

:

onstrs

int

j

=

0

for

(int

i

=

0;

i

<

s.size

();

i++)

if

(s[i℄.simplify

(this))

s[i℄.r

emove

(this)

else

s[j++℄

=

s[i℄

s.shrink

(s.size

()

j)

r

eturn

Tr

ue

Fig.

15.

r

e

du

eDB():

Remo

v

e

half

of

the

learn

t

lauses

min

us

some

lo

k

ed

lauses.

A

lo

k

ed

lause

is

a

lauses

that

is

reason

to

a

urren

t

assignmen

t.

Clauses

b

elo

w

a

ertain

lo

w

er

b

ound

ativit

y

are

also

b

e

remo

v

ed.

simplifyDB():

T

op-lev

el

simplify

of

onstrain

t

database.

Will

remo

v

e

an

y

satised

onstrain

t

and

simplify

remaining

onstrain

ts

under

urren

t

(partial)

assignmen

t.

If

a

top-lev

el

onit

is

found,

F

alse

is

returned.

Pre-ondition:

Deision

lev

el

m

ust

b

e

zero.

P

ost-ondition:

Propagation

queue

is

empt

y

.

b

o

ol

Solver.solve

(V

e

hlit

i

assumps)

Se

ar

hPar

ams

params(0.95,

0.999)

double

nof

onits

=

100

double

nof

learn

ts

=

nConstr

aints

()/3

lb

o

ol

status

=

?

{

Push

inrement

al

assumptions:

for

(int

i

=

0;

i

<

assumps.size

();

i++)

if

(!assume

(assumps[i℄)

j

j

pr

op

agate

()

!=

Null)

an

elUntil

(0)

return

F

alse

ro

ot

lev

el

=

de

isionL

evel

()

{

Sol

ve:

while

(status

==

?)

status

=

se

ar

h

((int

)nof

onits,

(int

)nof

learn

ts,

params)

nof

onits

*=

1.5

nof

learn

ts

*=

1.1

anelUn

til(0)

return

status

==

Tr

ue

?

Fig.

16.

Main

solv

e

metho

d.

Pre-ondition:

If

assumptions

are

used,

simplifyDB

()

m

ust

b

e

alled

righ

t

b

efore

using

this

metho

d.

If

not,

a

top-lev

el

onit

(resulting

in

a

non-usable

in

ternal

state)

annot

b

e

distinguished

from

a

onit

under

assumptions.

20

notion

of

inremen

talit

y

,

and

that

it

on

tains

a

w

ell

do

umen

ted

in

terfae

for

non-lausal

onstrain

ts.

Finally

,

a

set

of

referene

implemen

tations

of

mo

dern

SA

T-te

hniques

is

presen

t

in

the

O

PEN

SAT

pro

jet.

3

Ho

w

ev

er,

the

pro

jet

aim

for

ompleteness

rather

than

minimal

exp

osition,

as

w

e

ha

v

e

hosen

in

this

pap

er.

6

Exerises

1.

W

rite

the

o

de

for

an

A

tMost

onstrain

t.

The

onstrain

t

is

satised

if

at

most

n

out

of

m

sp

eied

literals

are

true.

2.

Implemen

t

a

generator

for

(generalized)

pigeon-hole

form

ulas

using

the

new

onstrain

ts.

The

generator

should

tak

e

three

argumen

ts:

n

um

b

er

of

pigeons,

n

um

b

er

of

holes,

and

hole

apait

y

.

Ea

h

pigeon

m

ust

reside

in

some

pigeon-

hole.

No

hole

ma

y

on

tain

more

pigeons

than

its

apait

y

.

3.

Mak

e

an

inremen

tal

v

ersion

that

adds

one

pigeon

to

the

problem

at

a

time

un

til

the

problem

b

eomes

unsatisable.

Referenes

[ARMS02℄

F.

Aloul,

A.

Ramani,

I.

Mark

o

v,

K.

Sak

allah.

\Generi

ILP

vs.

Sp

e-

ialized

0-1

ILP:

an

Up

date"

in

International

Confer

en

e

on

Computer

A

ide

d

Design

(ICCAD),

2002.

[BCCFZ99℄

A.

Biere,

A.

Cimatti,

E.M.

Clark

e,

M.

F

ujita,

Y.

Zh

u.

\Sym

b

oli

Mo

del

Che

king

using

SA

T

pro

edures

instead

of

BDDs"

in

Pr

o

e

e

dings

of

Design

A

utomation

Confer

en

e

(D

A

C'99),

1999.

[CS03℄

K.

Claessen,

N.

S

orensson.

\New

T

e

hniques

that

Impro

v

e

MA

CE-st

yle

Finite

Mo

del

Finding"

in

CADE-19,

Workshop

W4.

Mo

del

Computation

{

Priniples,

A

lgorithms,

Appli

ations,

2003.

[DLL62℄

M.

Da

vis,

G.

Logemann,

D.

Lo

v

eland.

\A

ma

hine

program

for

theorem

pro

ving"

in

Communi

ations

of

the

A

CM,

v

ol

5,

1962.

[ES03℄

N.

E

en,

N.

S

orensson.

\T

emp

oral

Indution

b

y

Inremen

tal

SA

T

Solv-

ing"

in

Pr

o

.

of

First

International

Workshop

on

Bounde

d

Mo

del

Che

king,

2003.

ENTCS

issue

4

v

olume

89.

[Lar92℄

T.

Larrab

ee.

\T

est

P

attern

Generation

Using

Bo

olean

Satisabilit

y"

in

IEEE

T

r

ansations

on

Computer-A

ide

d

Design,

v

ol.

11-1,

1992.

[MS96℄

J.P

.

Marques-Silv

a,

K.A.

Sak

allah.

\GRASP

{

A

New

Sear

h

Algorithm

for

Satisabilit

y"

in

ICCAD.

IEEE

Computer

So

iety

Pr

ess,

1996

[MZ01℄

M.W.

Mosk

ewiz,

C.F.

Madigan,

Y.

Zhao,

L.

Zhang,

S.

Malik.

\Cha:

Engi-

neering

an

EÆien

t

SA

T

Solv

er"

in

Pr

o

.

of

the

38

th

Design

A

utomation

Confer

en

e,

2001.

[Stri00℄

O.

Stri

hman

\T

uning

SA

T

he

k

ers

for

Bounded

Mo

del

Che

king"

in

Pr

o

.

of

12

th

Intl.

Conf.

on

Computer

A

ide

d

V

eri

ation,

LNCS:1855,

Springer-V

erlag

2000

[WKS01℄

J.

Whittemore,

J.

Kim,

K.

Sak

allah.

\SA

TIRE:

A

New

Inremen

tal

Satisabilit

y

Engine"

in

Pr

o

.

38th

Conf.

on

Design

A

utomation,

A

CM

Press

2001.

[ZM01℄

L.

Zhang,

C.F.

Madigan,

M.W.

Mosk

ewiz,

S.

Malik.

\EÆien

t

Conit

Driv

en

Learning

in

Bo

olean

Satisabilit

y

Solv

er"

in

Pr

o

.

of

the

In-

ternational

Confer

en

e

on

Computer

A

ide

d

Design

(ICCAD),

2001.

3

h

ttp://www.op

ensat.org

21

App

endix

{

What

is

missing

from

Satzo

o?

In

order

to

redue

the

size

of

M

INI

S

AT

to

a

minim

um,

all

non-essen

tial

parts

of

S

ATZOO

/

S

ATNIK

w

ere

left

out.

Sine

S

ATZOO

w

on

t

w

o

ategories

of

the

SA

T

2003

Comp

etition,

w

e

hose

to

presen

t

the

missing

parts

here

for

ompleteness.

Initial

strategies:

Burst

of

r

andom

variable

or

ders.

Before

an

ything

else,

S

ATZOO

runs

sev

eral

passes

of

ab

out

10-100

onits

ea

h

with

the

v

ariable

order

initiated

to

random.

F

or

satisable

problems,

S

ATZOO

an

sometimes

stum

ble

up

on

the

solution

b

y

this

strategy

.

F

or

hard

(t

ypially

unsatisable)

problems,

imp

or-

tan

t

lauses

an

b

e

learn

t

in

this

phase

that

is

outside

the

"lo

al

optim

um"

that

the

ativit

y

driv

en

v

ariable

heuristi

will

later

get

stu

k

in.

Stati

variable

or

dering.

The

seond

phase

of

S

ATZOO

is

to

ompute

a

stati

v

ariable

ordering

taking

in

to

aoun

t

ho

w

the

v

ariables

of

dieren

t

lauses

relates

to

ea

h

other

(see

Figure

17).

V

ariables

often

o

urring

together

in

lauses

will

b

e

put

lose

in

the

v

ariable

order.

S

ATZOO

uses

this

stati

or-

dering

for

at

least

5000

onits

and

do

es

not

stop

un

til

progress

is

halted

sev

erely

.

The

stati

ordering

often

oun

ters

the

eet

of

"sh

uing"

the

prob-

lem

(

hanging

the

order

of

lauses).

The

authors

b

eliev

e

this

phase

to

b

e

the

most

imp

ortan

t

feature

left

out

of

M

INI

S

AT

,

and

an

imp

ortan

t

part

of

the

suess

of

S

ATZOO

in

the

omp

etition.

4

Extra

v

ariable

deision

heuristis:

V

ariable

of

r

e

ent

imp

ortan

e.

Inspired

b

y

the

SA

T-solv

er

B

ERKMIN

,

o

a-

sionally

v

ariables

from

reen

t

(unsatised)

reorded

lauses

are

pi

k

ed.

R

andom.

Ab

out

1%

of

the

time,

a

random

v

ariable

is

seleted

for

bran

hing.

This

simple

strategy

seems

to

ra

k

some

extra

problems

without

inurring

an

y

substan

tial

o

v

erhead

for

other

problems.

Giv

e

it

a

try!

Other:

Equivalent

variable

substitution.

The

binary

lauses

are

he

k

ed

for

yli

impliations.

If

a

yle

is

found,

a

represen

tativ

e

is

seleted

and

all

other

v

ariables

in

the

yle

is

replaed

b

y

this

represen

tativ

e

in

the

lause

database.

This

yields

a

smaller

database

and

few

er

v

ariables.

The

simpliation

is

done

p

erio

dially

,

but

is

most

imp

ortan

t

in

the

initial

phase

(some

problems

an

b

e

v

ery

redundan

t).

Garb

age

ol

le

tion.

S

ATZOO

implemen

ts

its

o

wn

memory

managemen

t

whi

h

allo

ws

lauses

to

b

e

stored

more

ompatly

.

0-1-pr

o

gr

amming.

Pseudo-b

o

olean

onstrain

ts

are

supp

orted

b

y

S

ATZOO

.

This

an

of

ourse

easily

b

e

added

to

M

INI

S

AT

through

the

onstrain

t

in-

terfae.

4

The

pro

vided

o

de

urren

tly

has

no

further

motiv

ation

b

ey

ond

the

authors'

in

tuition.

Indeed

it

w

as

added

as

a

qui

k

ha

k

t

w

o

da

ys

b

efore

the

omp

etition.

22

void

Solver.statiV

arOr

der

()

{

Clear

a

tivity:

for

(int

i

=

0;

i

<

nV

ars

();

i++)

ativit

y[i℄

=

0

{

Do

simple

v

ariable

a

tivity

heuristi:

for

(int

i

=

0;

i

<

lauses.size

();

i++)

Clause

=

lauses[i℄

double

add

=

p

ow2

(

size

())

for

(int

j

=

0;

j

<

size

();

j++)

ativit

y[var

([j℄)℄

+=

add

{

Calula

te

the

initial

"hea

t"

of

all

la

uses:

V

e

hV

e

hint

ii

o

urs(2*nV

ars

())

{

Map

liter

al

to

list

of

lause

indi

es

V

e

hPair

hdouble

,int

ii

heat(lauses.size

())

{

Pairs

of

he

at

and

lause

index

for

(int

i

=

0;

i

<

lauses.size

();

i++)

Clause

=

lauses[i℄

double

sum

=

0

for

(int

j

=

0;

j

<

size

();

j++)

o

urs[index

([j℄)℄.push

(i)

sum

+=

ativit

y[var

([j℄)℄

heat[i℄

=

Pair

new

(sum,

i)

{

Bump

hea

t

f

or

la

uses

whose

v

ariables

our

in

other

hot

la

uses:

double

iter

size

=

0

for

(int

i

=

0;

i

<

lauses.size

();

i++)

Clause

=

lauses[i℄

for

(int

j

=

0;

j

<

size

();

j++)

iter

size

+=

o

urs[index

([j℄)℄.size

()

int

iterations

=

min

((int

)(((double

)literals

/

iter

size)

*

100),

10)

double

disapation

=

1.0

/

iterations

for

(int

=

0;

<

iterations;

++)

for

(int

i

=

0;

i

<

lauses.size

();

i++)

Clause

=

lauses[i℄

for

(int

j

=

0;

j

<

size

();

j++)

V

e

hint

i

os

=

o

urs[index

([j℄)℄

for

(int

k

=

0;

k

<

os.size

();

k++)

heat[i℄.fst

+=

heat[os[k℄℄.fst

*

disapation

{

Set

a

tivity

a

ording

to

hot

la

uses:

sort

(heat)

for

(int

i

=

0;

i

<

nV

ars

();

i++)

ativit

y[i℄

=

0

double

extra

=

1e200

for

(int

i

=

0;

i

<

heat.size

();

i++)

Clause

&

=

lauses[heat[i℄.snd℄

for

(int

j

=

0;

j

<

size

();

j++)

if

(ativit

y[var

([j℄)℄

==

0)

ativit

y[var

([j℄)℄

=

extra

extra

*=

0.995

order.up

dateA

l

l

()

v

ar

in

=

1

Fig.

17.

The

stati

v

ariable

ordering

of

S

ATZOO

.

The

o

de

is

dened

only

for

lauses,

not

for

arbitrary

onstrain

ts.

It

m

ust

b

e

adapted

b

efore

it

an

b

e

used

in

M

INI

S

AT

.

23