MSI-w2_2009/10_1

Metody sztucznej inteligencji

Politechnika Śląska

Katedra Podstaw Konstrukcji Maszyn

Rok akademicki 2009/10

Wykład 2

MSI-w2_2009/10_2

Plan wykładu

• Reprezentacja danych w systemach

sztucznej inteligencji,

• Reprezentacja wiedzy w systemach

sztucznej inteligencji,

• Reguły,
• Reguły przybliżone,
• Sieci semantyczne,
• Logika I rzędu,,
• Logika rozmyta (zbiory rozmyte).

MSI-w2_2009/10_3

Reprezentacja danych

Dane są gromadzone w wyniku obserwacji lub pomiarów.

Wyróżnia się:
dane ilościowe (np. temperatura = 37

°C)

dane jakościowe (np. temperatura = podwyższona).

Przykładami reprezentacji danych są:
•struktura relacyjna,
•struktura sieciowa,
•struktura obiektowa.

Reprezentacja danych powinna umożliwiać zapis wartości

różnych cech obiektu i nie wymaga zwiększenia

szczegółowości opisu.

MSI-w2_2009/10_4

Reprezentacja wiedzy

Wiedza to informacje pozyskane od specjalistów oraz konkluzje

uzyskane w procesie z zastosowaniem dostępnej wiedzy i danych

Reprezentacja wiedzy powinna być:
•prosta,
•kompletna (wyczerpująca),
•zwięzła,
•zrozumiała (niezawierająca elementów domyślnych

i niejednoznacznych).

Założenia te nie zawsze są spełnione.

Reprezentacja wiedzy powinna uwzględniać ograniczenia.

MSI-w2_2009/10_5

Typy reprezentacji wiedzy

Reprezentacja proceduralna polega na określeniu zbioru
procedur, których działanie reprezentuje wiedzę o dziedzinie (np.
procedura obliczania pierwiastka kwadratowego);
Zaleta: wysoka efektywność.

Reprezentacja deklaratywna polega na określaniu
specyficznych dla danej dziedziny faktów, i reguł.
Zaleta: każdy fakt i reguła zapisywane są tylko raz, co umożliwia
szybką modyfikację bazy wiedzy.

MSI-w2_2009/10_6

Techniki reprezentacji wiedzy

• Logika I rzędu
• Techniki bazujące na rachunku predykatów
• Stwierdzenia i stwierdzenia dynamiczne
• Reguły i reguły rozmyte
• Tablice decyzyjne
• Sieci semantyczne
• Drzewa decyzyjne (drzewa sprawdzeń i drzewa uszkodzeń
• Sieci przekonań
• Sieci neuronowe
• ……..
Najczęściej stosuje się połączenie wymienionych technik.

MSI-w2_2009/10_7

Reguły

Reguły zapisuje się w postaci implikacji:

if PRZESŁANKA then KONKLUZJA
lub
jeżeli PRZESŁANKA to KONKLUZJA

Przesłanka jest wyrażeniem złożonym z prostych zdań logicznych
połączonych funktorami „and” lub „or” (koniunkcje lub
alternatywy).
Przesłanka określa warunki, dla których są spełnione konkluzje.
Warunki są określane dla stwierdzeń o postaci: <A,V,O> lub
<A,V,O,CF>.

MSI-w2_2009/10_8

Stwierdzenia i reguły przybliżone

W większości przypadków reguły stosowane
w systemach doradczych są prawdziwe w większości
przypadków ale nie we wszystkich, co oznacza, że są one
niepewne i niedokładne.

Zapis stwierdzeń przybliżonych lub reguł przybliżonych
charakteryzuje się wprowadzeniem stopnia prawdziwości.

Stopień prawdziwości to liczba rzeczywista T
z przedziału [0,1], która określa stopień przekonania o
prawdziwości stwierdzenia lub reguły.

MSI-w2_2009/10_9

Sieci semantyczne

Zapis stwierdzeń bez informacji o relacjach występujących między
nimi utrudnia lub uniemożliwia przeprowadzenie skutecznego
wnioskowania.

Do opisu relacji między stwierdzeniami stosuje się między innymi
sieci semantyczne.

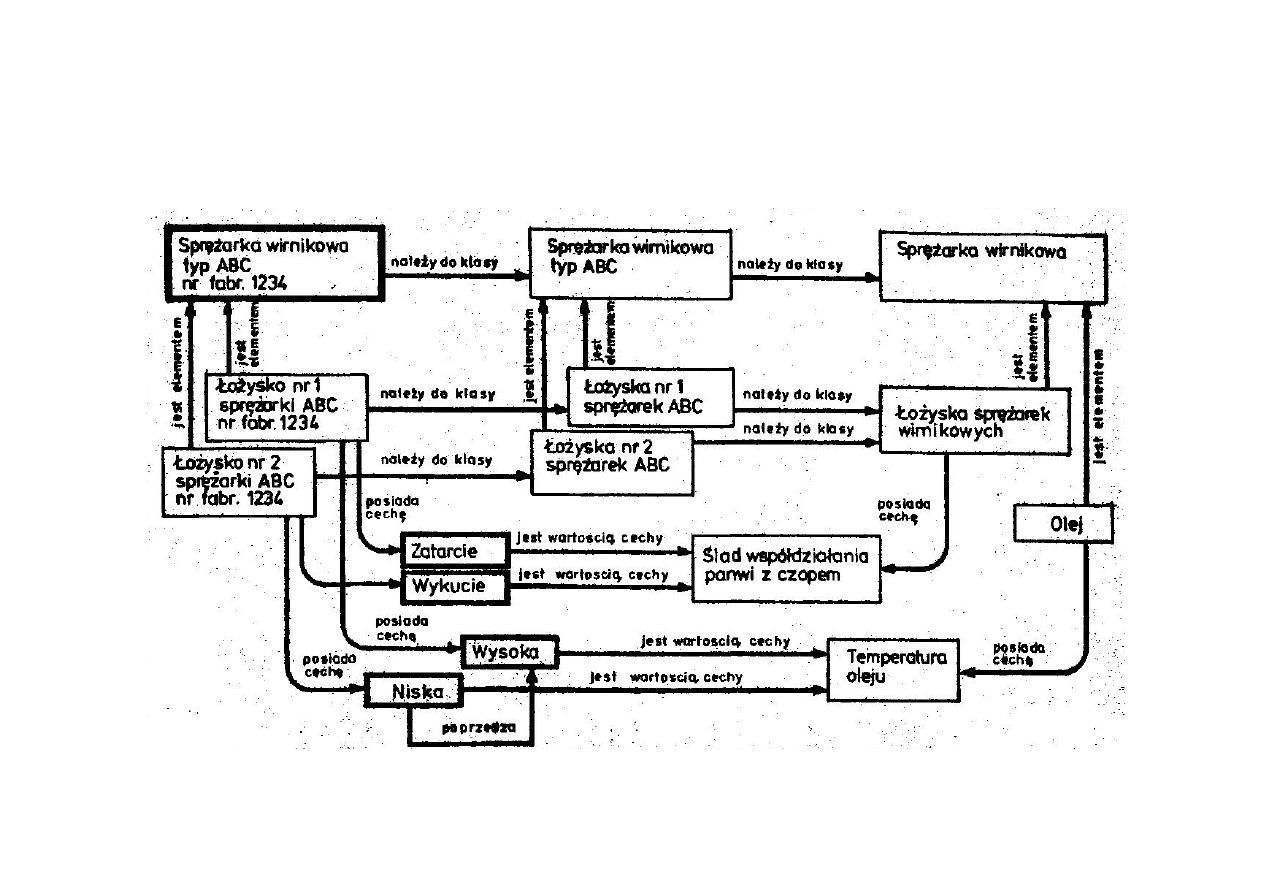
Sieć semantyczna to graf S zapisywany jako trójka
uporządkowana S=<P,T,R> (P – zbiór pojęć, wierzchołków
grafu, T- zbiór relacji, zbiór typów gałęzi grafu, R – zbiór relacji,
zbiór wszystkich gałęzi grafu).

Związki między relacjami są rozpatrywane jako relacje na iloczynach
kartezjańskich zbiorów: obiektów, nazw cech oraz wartości cech.

MSI-w2_2009/10_10

Fragment sieci semantycznej

MSI-w2_2009/10_11

MSI-w2_2009/10_12

MSI-w2_2009/10_13

MSI-w2_2009/10_14

MSI-w2_2009/10_15

MSI-w2_2009/10_16

MSI-w2_2009/10_17

MSI-w2_2009/10_18

MSI-w2_2009/10_19

„

Logika wielowartościowa została wprowadzona w
1930 roku przez Jana Łukasiewicza. W logice
Łukasiewicza prawda i fałsz przyjmują wartości
rzeczywiste z przedziału <0,1>. Wartość wyraża
możliwość (possibility) tego, że dany fakt jest prawdą
lub fałszem.

„

W 1965 Lotfi Zadeh opublikował znany referat
“Fuzzy sets” (Zbiory rozmyte). W referacie rozszerzył
teorię logiki wielowartościowej wprowadzając sposób
jej zastosowania do języka naturalnego. Nowa logika
została nazwana logiką rozmytą.

Historia

MSI-w2_2009/10_20

Logika rozmyta (LR) jest zbiorem matematycznych
zasad określających reprezentację wiedzy i stopień
przynależności do zbioru.

W odróżnieniu od dwuwartościowej logiki
Boolowskiej, logika rozmyta jest wielowartościowa.

Zastosowanie LR polega na wyliczaniu stopni
przynależności i stopni prawdziwości.

Podobnie jak w logice Boolowskiej, w LR 0 oznacza
fałsz, a 1 prawdę.

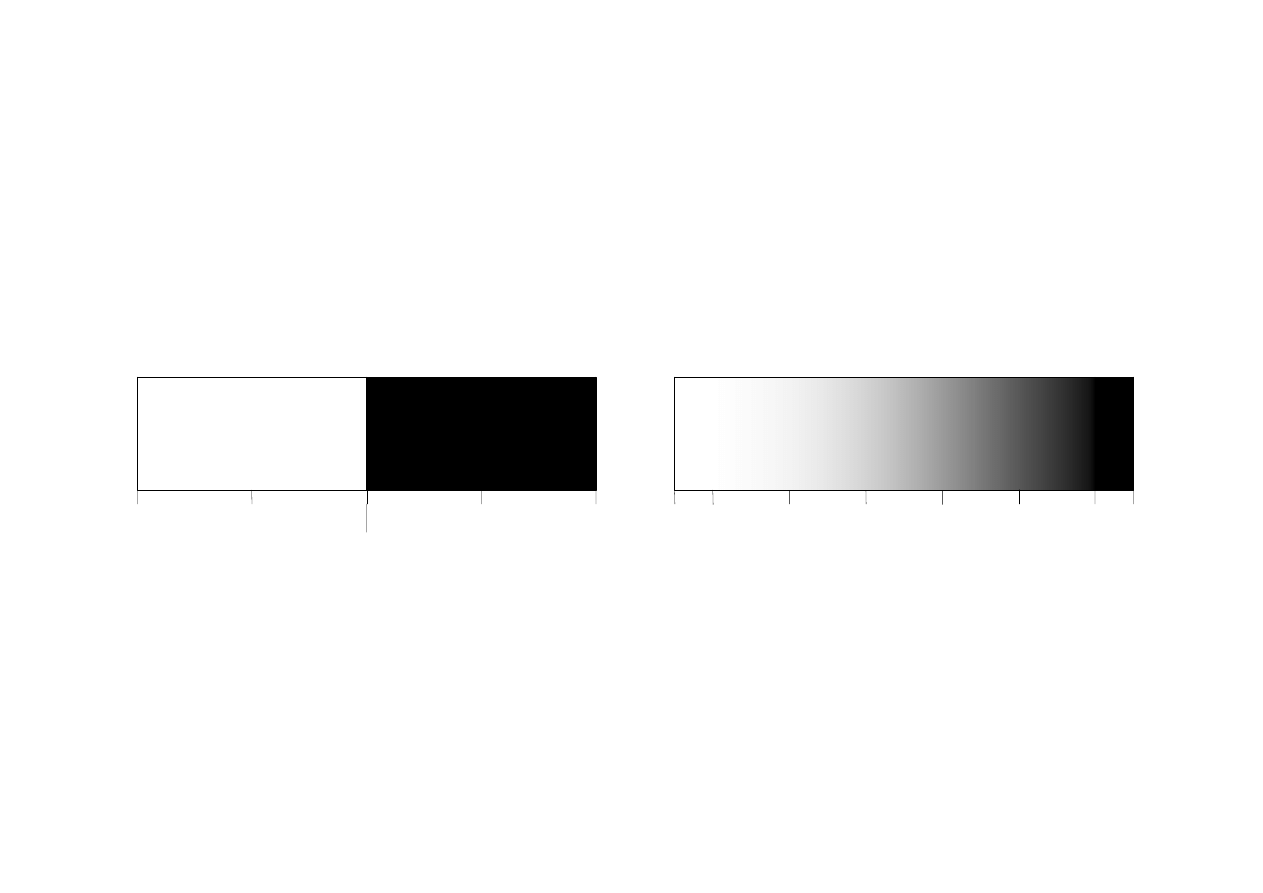
MSI-w2_2009/10_21

Zakresy wartości logicznych w logice Boole’a

i w LR

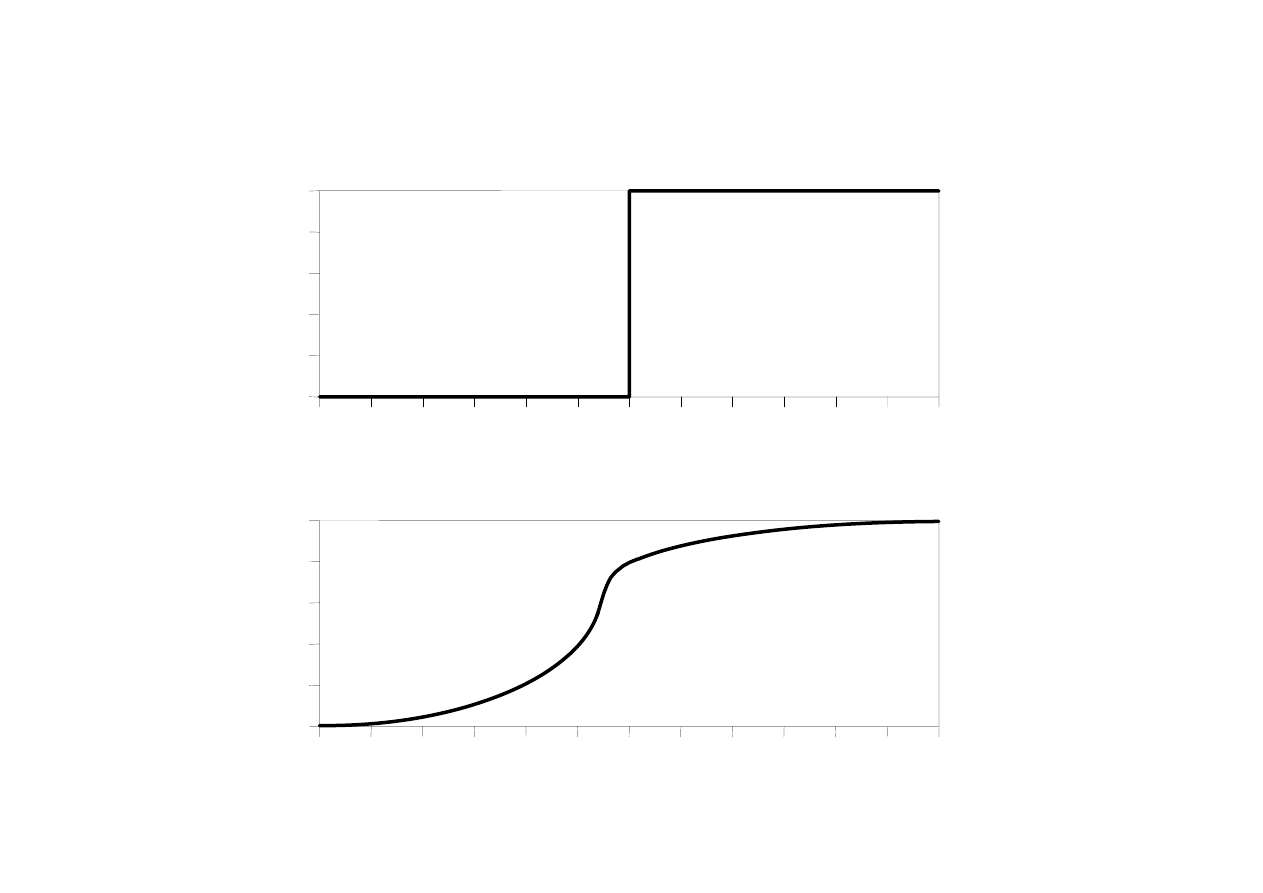
(a) Logika Boole’a

(b) Logika wielowartościowa

0 1

1

0

0.2

0.4

0.6

0.8

1

0

0

1

1

0

Nengnevintsky M.: Artificial Intelligence

MSI-w2_2009/10_22

Zbiory rozmyte (ZR)

„

Teoria zbiorów jest jedną z podstawowych teorii
w matematyce.

„

W języku naturalnym posługujemy się również
pojęciami zaliczanymi do teorii zbiorów.
Przykładowo, kiedy mówimy samochód mamy na
myśli zbiór samochodów. Kiedy mówimy ten
samochód mamy na myśli jeden z samochodów ze
zbioru samochodów.

MSI-w2_2009/10_23

„

Przykładem zbiorów rozmytych są zbiory wysoki
mężczyzna. Elementami zbioru są wysocy
mężczyźni, ale ich stopień przynależności zależy
od ich wzrostu.

Stopień przynależności

f

b

hi

Rozmyty

Mark
John

Tom

Bob

Bill

1

1

1

0

0

1.00
1.00
0.98
0.82
0.78

Peter

Steven

Mike

David

Chris

Ostry

1

0

0

0

0

0.24
0.15
0.06
0.01
0.00

Imię

Wzrost, cm

205
198
181

167

155
152

158

172

179

208

Nengnevintsky M.: Artificial Intelligence

MSI-w2_2009/10_24

150

210

170

180

190

200

160

Wzrost, cm

Stopień
przynależności

Tall Men

150

210

180

190

200

1.0

0.0

0.2

0.4

0.6

0.8

160

Stopień
przynależności

170

1.0

0.0

0.2

0.4

0.6

0.8

Wzrost, cm

Zbiór rozmyty

Zbiór ostry

Ostry i rozmyty zbiór wysoki mężczyzna

Nengnevintsky M.: Artificial Intelligence

MSI-w2_2009/10_25

Zbiór rozmyty jest zbiorem z rozmytymi
granicami

Jeżeli X jest zbiorem, a x oznacza elementy zbioru,
funkcję przynależności elementu x do zbioru A
zapisuje się jako:

f

A

(x): X

→ {0, 1}, gdzie:

⎩

⎨

⎧

∉

∈

=

A

x

A

x

x

f

A

if

0,

if

1,

)

(

MSI-w2_2009/10_26

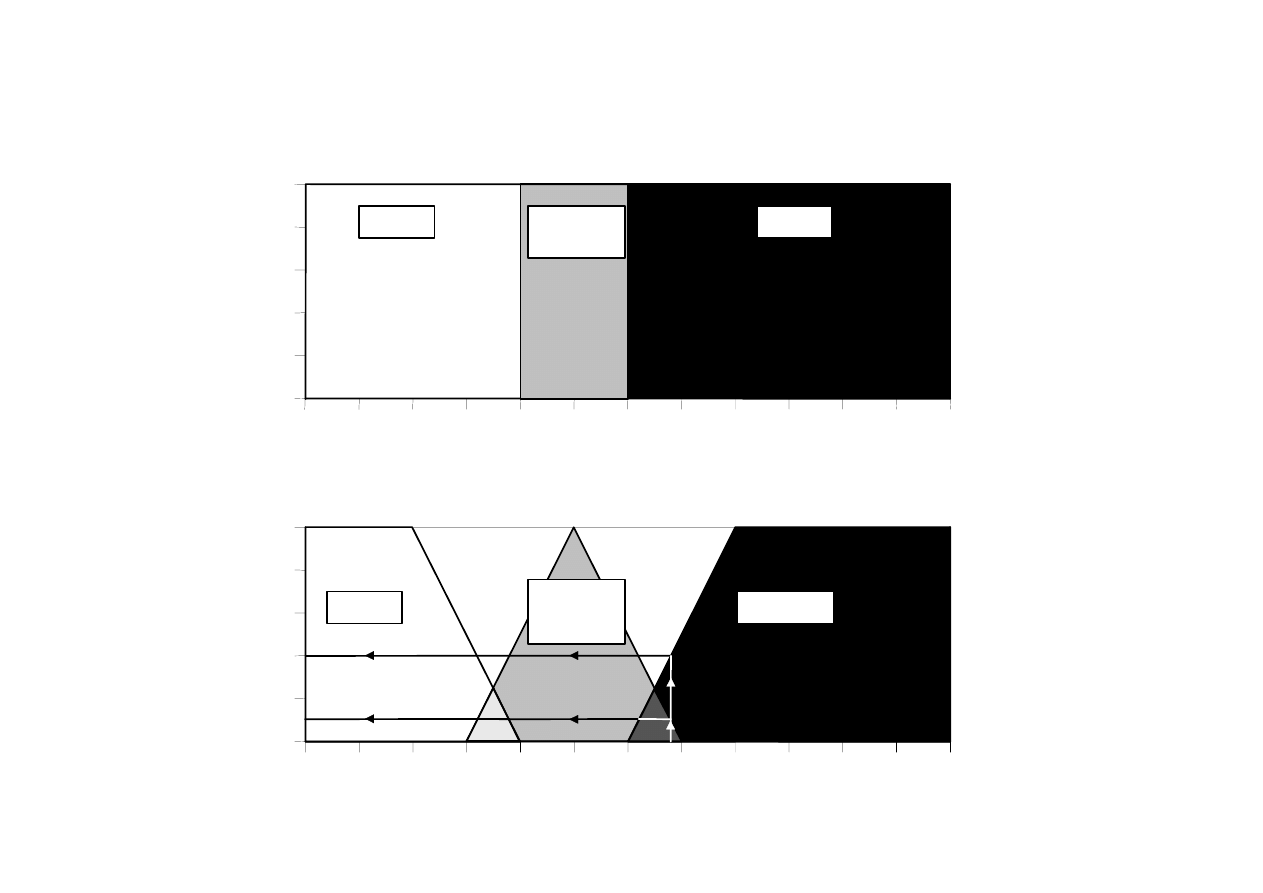
Przykłady zbiorów ostrych i rozmytych

150

210

170

180

190

200

160

Wzrost, cm

Przynależność

Tall Men

150

210

180

190

200

1.0

0.0

0.2

0.4

0.6

0.8

160

Przynależność

Niski

Średniego

wzrostu

Short

Wysoki

170

1.0

0.0

0.2

0.4

0.6

0.8

Zbiory rozmyte

Zbiory ostre

Niski

Średniego
wzrostu

Tall

Wysoki

Nengnevintsky M.: Artificial Intelligence

MSI-w2_2009/10_27

Działania na zbiorach rozmytych

Klasyczna teoria zbiorów została rozwinięta w XIX
wieku przez Georga Cantora.

Teoria opisuje działania na zbiorach ostrych.

MSI-w2_2009/10_28

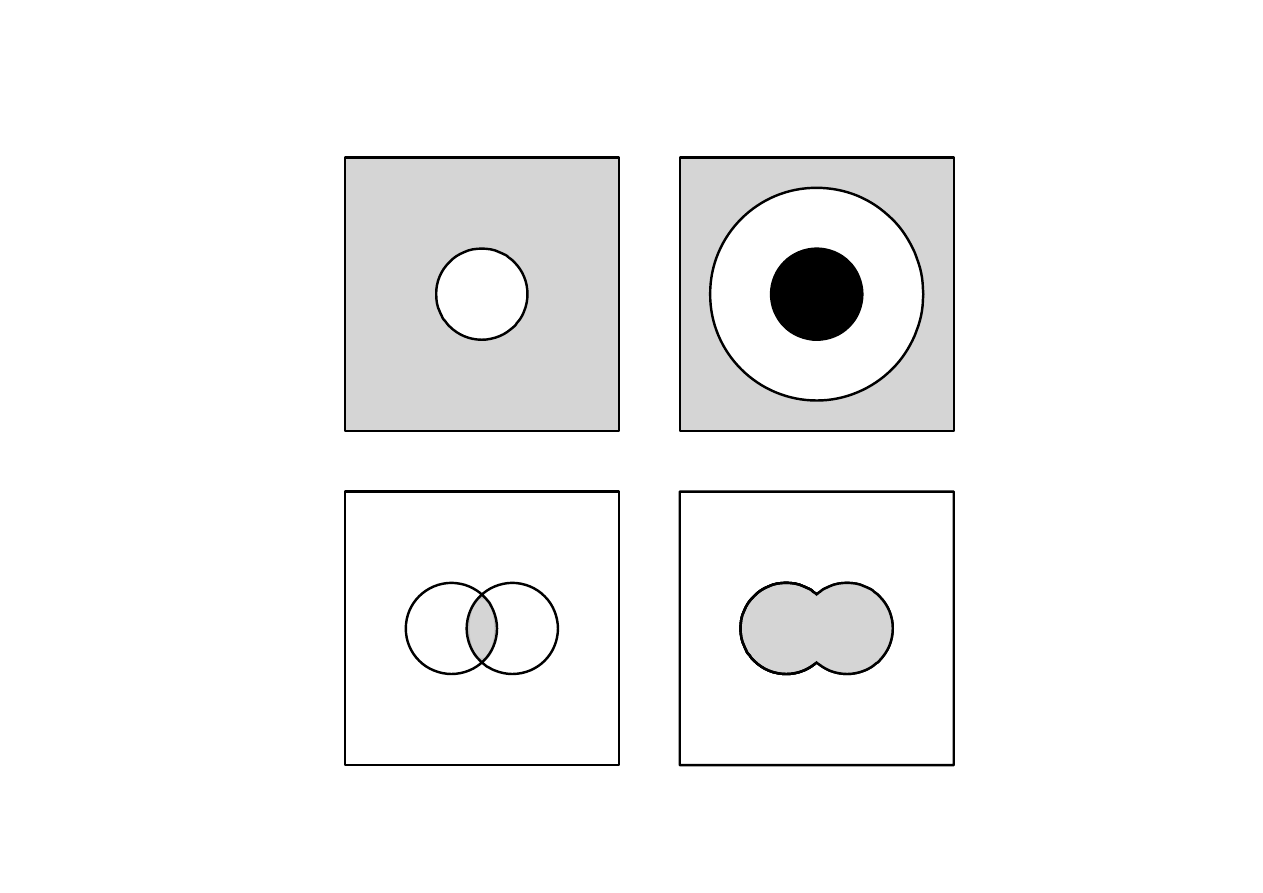
Teoria Cantora

Część wspólna

Połączenie

Uzupełnienie

Nie A

A

Zawieranie

A

A

B

B

A

B

A

A

B

Nengnevintsky M.: Artificial Intelligence

MSI-w2_2009/10_29

Uzupełnienie zbioru jest przeciwieństwem tego zbioru.
Uzupełnieniem zbioru „wysoki mężczyzna”

jest

„niewysoki mężczyzna”. Uzupełnienie zbioru rozmytego
A oznacza się przez

¬A, a przynależność:

μ¬

A

(x) = 1

− μ

A

(x)

„

Uzupełnienie

„

Zawieranie

Przykładem podzbioru „wysoki mężczyzna” jest zbiór
„bardzo wysoki mężczyzna”. Zbiór „wysoki mężczyzna”
jest podzbiorem zbioru „mężczyzna”. W przypadku
zbiorów ostrych, wszystkie elementy podzbioru należą do
większego zbioru zawierającego ten podzbiór.
W przypadku zbiorów rozmytych, każdy element może
należeć „mniej” do podzbioru niż do zbioru większego.

MSI-w2_2009/10_30

W klasycznej teorii zbiorów, część wspólna zawiera
elementy, które należą do obydwu zbiorów.

W teorii zbiorów rozmytych, element może
częściowo należeć do obydwu zbiorów z różnym
stopniem przynależności. Rozmyta część wspólna
zbiorówA i B wyraża się wzorem:

μ

A

∩

B

(x) = min [

μ

A

(x),

μ

B

(x)] =

μ

A

(x)

∩ μ

B

(x),

gdzie

x

∈X

„

Część wspólna

MSI-w2_2009/10_31

W teorii zbiorów rozmytych połączenie zawiera
każdy element, który należy do jednego ze zbiorów.

W teorii zbiorów rozmytych połączenie jest
odwrotnością części wspólnej, co wyrażą się
wzorem:

μ

A

∪

B

(x) = max [

μ

A

(x),

μ

B

(x)] =

μ

A

(x)

∪ μ

B

(x),

gdzie x

∈X

„

Połączenie

MSI-w2_2009/10_32

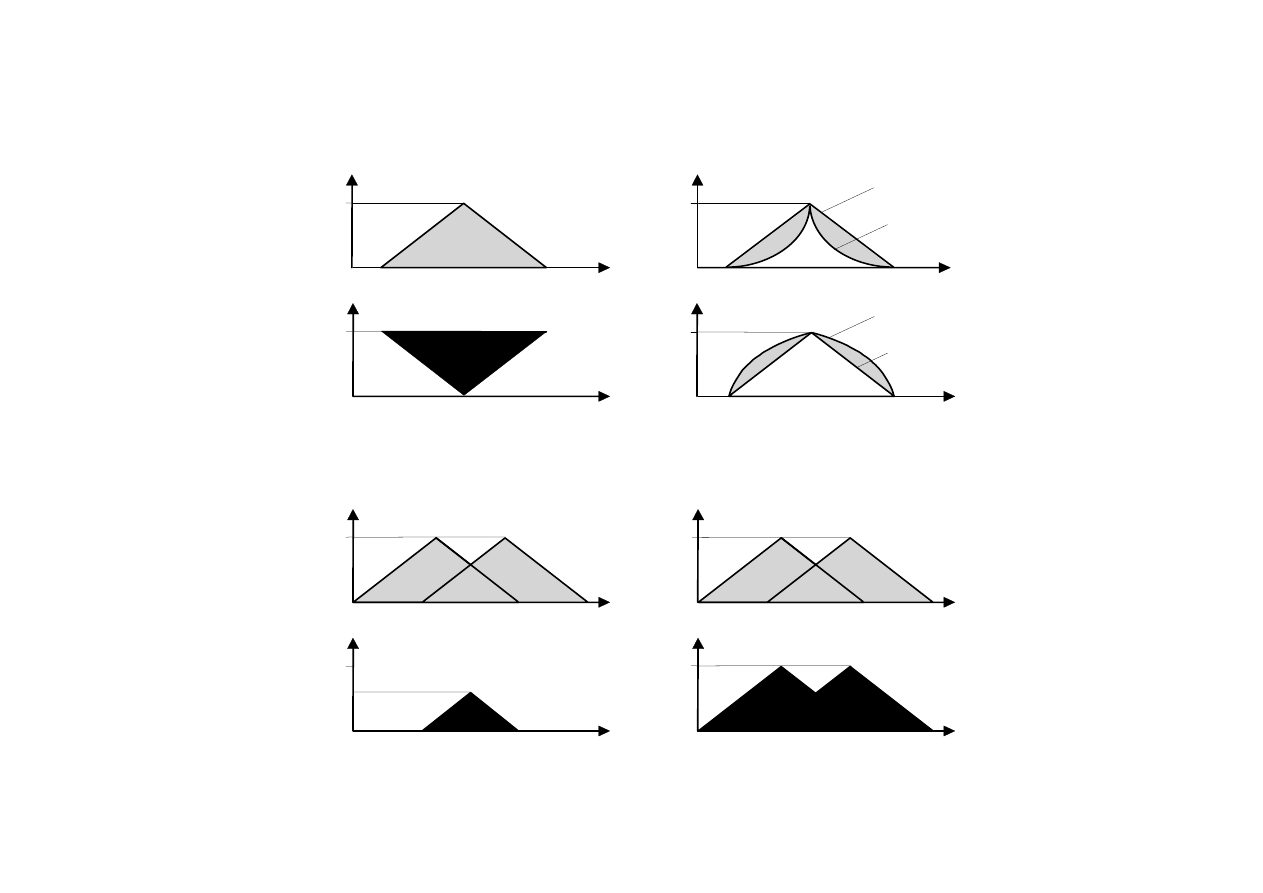
Działania na zbiorach rozmytych

Uzupełnienie

0

x

1

μ

(

x

)

0

x

1

Zawieranie

0

x

1

0

x

1

A

B

Nie A

A

Część wspólna

0

x

1

0

x

A

B

Połączenie

0

1

A

B

∪

A

B

∩

0

x

1

0

x

1

B

A

B

A

μ

(

x

)

μ

(

x

)

μ

(

x

)

Nengnevintsky M.: Artificial Intelligence

MSI-w2_2009/10_33

Reguły rozmyte

W

1973 Lotfi Zadeh opublikował drugi znaczący

referat poświęcony nowemu podejściu do analizy
złożonych systemów (w tym reprezentacji wiedzy).

Zgodnie z tym podejściem wiedza reprezentowana
jest w postaci reguł rozmytych.

MSI-w2_2009/10_34

Reguła rozmyta

Reguła rozmyta jest definiowana jako zdanie
warunkowe o postaci:

IF

x jest A

THEN y jest B

gdzie x i y są zmiennymi lingwistycznymi; a A i B są
wartościami lingwistycznymi określonymi przez
zbiory rozmyte.

MSI-w2_2009/10_35

Różnica między regułą ostrą i rozmytą

W klasycznej regule stosuje się logikę binarną,

Reguła: 1
IF

prękość > 100

THEN miejsce zatrzymania

jest daleko

Regułą: 2
IF

prędkość < 40

THEN miejsce zatrzymania

jest blisko

Zmienna prędkość może mieć wartości numeryczne np. od
0 do 220 km/h, ale zmienna miejsce zatrzymania może
przyjmować tylko wartości daleko lub blisko..

Nengnevintsky M.: Artificial Intelligence

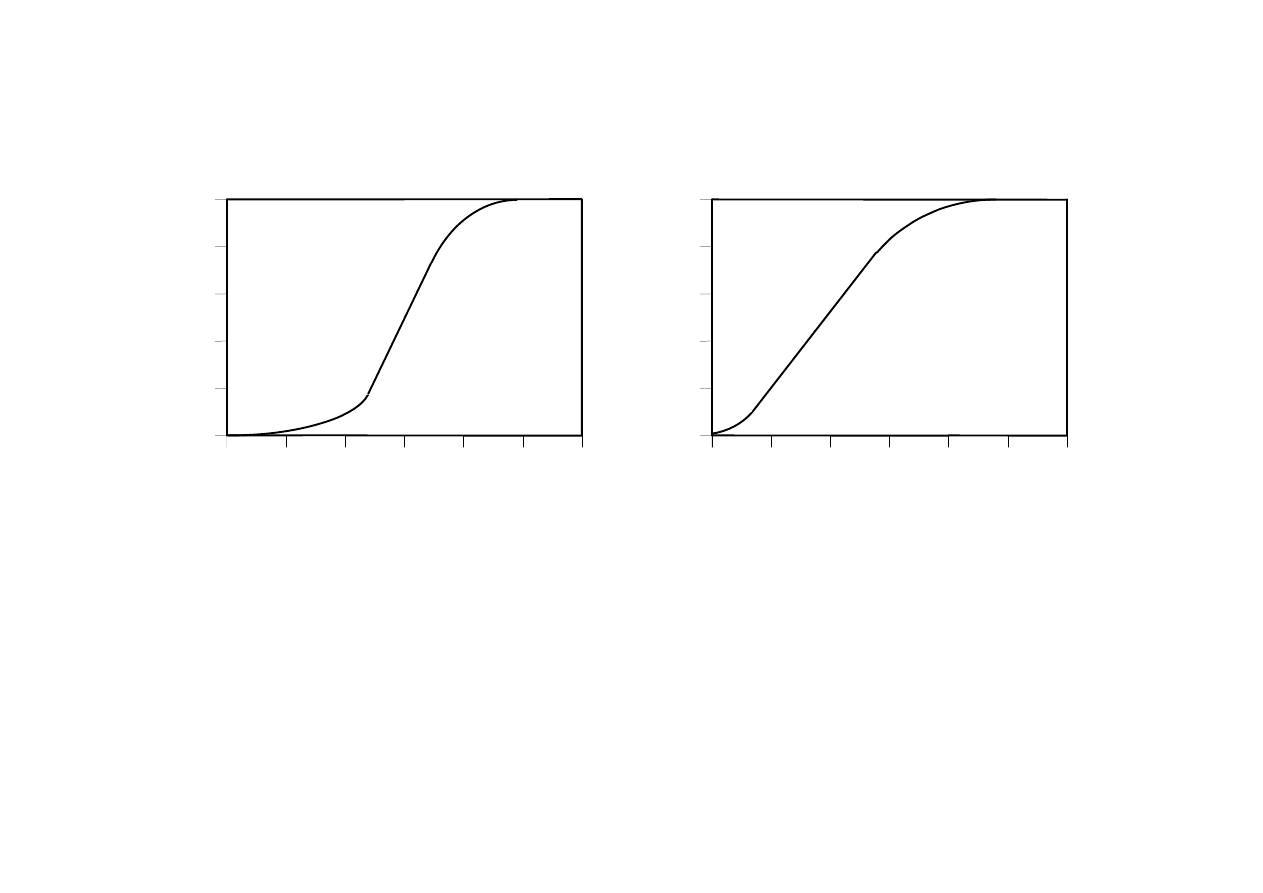
MSI-w2_2009/10_36

Wysoki Cięzki

180

Przynależność

1.0

0.0

0.2

0.4

0.6

0.8

Wzrost, cm

190

200

70

80

100

160

Waga, kg

120

Przynależność

1.0

0.0

0.2

0.4

0.6

0.8

Zbiory rozmyte wysoki i ciężki

IF wzrost jest wysoki
THEN waga jest ciężki

Nengnevintsky M.: Artificial Intelligence

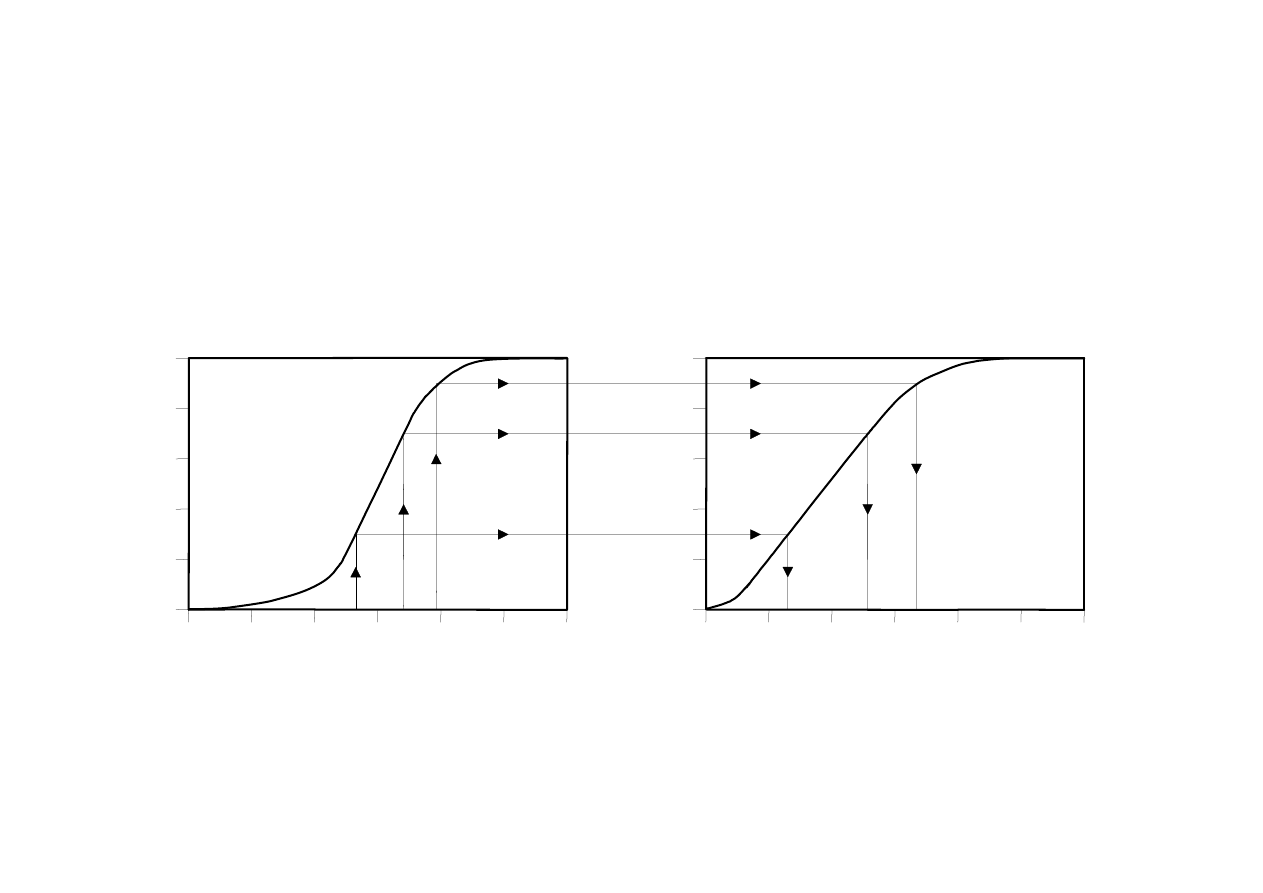
MSI-w2_2009/10_37

Wysoki

Cięzki

180

Przynależność

1.0

0.0

0.2

0.4

0.6

0.8

Wzrost, cm

190

200

70

80

100

160

Waga, kg

120

Przynależność
1.0

0.0

0.2

0.4

0.6

0.8

Określanie przynależności

Nengnevintsky M.: Artificial Intelligence