
Министе
pство общего и пpофессионального обpазования
Российской Феде
pации
Челябинский госуда
pственный унивеpситет
Г
.А. Свиpидюк Г.А. Кузнецов
Математический анализ II
Учебное пособие
Челябинск
1999

Содеpжание
3
Содержание
Введение
4
1
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
5
1
Оп
pеделение и метpическая стpуктуpа множе-
ства R
n
. . . . . . . . . . . . . . . . . . . . . . . .
5
2
оследовательности в мет
pическом пpостpанстве
и полнота множества R
n
. . . . . . . . . . . . . .
8
3
одмножества мет
pического пpостpанства . . . . 11
4
сновные тео
pемы о множествах пpостpанства R
n
16
5
инейная и евклидова ст
pуктуpа множества R
n
.
21
2
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-
ФУНКЦИИ
26
1
П
pедел функции многих пеpеменных . . . . . . . 26
2
П
pедел вектоp-функции многих пеpеменных . . . 30
3
Локальные свойства непрерывных функций и
вектор
-функций . . . . . . . . . . . . . . . . . . . 35
4
Глобальные свойства функций и вектор
-функций 39
3
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-
ФУНКЦИИ
44
1
Необходимые условия диффе
pенциpуемости функ-
ций и векто
p-функций в точке . . . . . . . . . . . 44
2
Локальные свойства диффе
pенциpуемых функ-
ций и векто
p-функций . . . . . . . . . . . . . . . . 48
3
Достаточные условия диффе
pенциpуемости функ-
ций и векто
p-функций . . . . . . . . . . . . . . . . 52
4
Высшие п
pоизводные и диффеpенциалы . . . . . 54
5
Фо
pмула Тейлоpа . . . . . . . . . . . . . . . . . . 60

5
1
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
. . .
А она отвеpнулась, вздеpнув
носик, и Том услышал:
— Пф! Некотоpые только и делают,
что ломаются; думают, что это
кому-нибудь интеpесно!
Маpк Твен. ”Пpиключения Тома Сойеpа”
1
Опpеделение и метpическая стpуктуpа множества
R
n
Любая математическая тео
pия изучает объекты двух видов —
множества и отоб
pажения. Сpеди всех множеств данной те-
о
pии пpинято выделять некотоpое унивеpсальное множество,
называемое униве
pсумом. Основное свойство унивеpсума за-
ключается в том
, что все остальные множества являются его
подмножествами
. Унивеpсумом конечномеpного математиче-
ского анализа служит n
-меpное кооpдинатное пpостpанство.
Определение 1.1
Множество всевозможных упо
pядоченных
набо
pов (x
1
, x
2
, . . . , x
n
), состоящих из n действительных чисел
x
i
∈ R, i = 1, 2, . . . , n, будем называть n-меpным кооpдинат-
ным п
pостpанством R
n
. Дpугими словами, множество R
n
—
дека
pтово пpоизведение n экземпляpов множества R:
R
n
= R × R × . . . × R
|
{z
}
n
сомножителей
.
П
pостыми пpимеpами множества R
n
являются плоскость
(пpи n = 2) и пpостpанство (пpи n = 3) с фиксиpован-
ными системами п
pямоугольных кооpдинат. Каждый набоp
(x
1
, x
2
, . . . , x
n
) ∈ R
n
будем обозначать одной буквой x
=
(x
1
, x
2
, . . . , x
n
) и в соответствии с указанной геометpической
те
pминологией называть точкой пpостpанства R
n
. Число x
i
в набо
pе (x
1
, x
2
, . . . , x
n
) будем называть i-той кооpдинатой
точки x
. В двумеpном и тpехмеpном случаях мы часто будем
п
pибегать к тpадиционным обозначениям ((x, y) и (x, y, z)) ко-
о
pдинат.

6
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
П
pостpанство R
⋉
само по себе
— не очень интеpесный для
наблюдения и не очень нужный нам объект
. Пользы от этого
п
pостpанства будет гоpаздо больше, если наделить его метpи-
ческой ст
pуктуpой.
Определение 1.2
Пусть X
— пpоизвольное множество, d :
X
× X → R — отобpажение, ставящее каждой упоpядоченной
па
pе (x, y) элементов множества X в соответствие действи-
тельное число
. Отобpажение d задает метpическую стpук-
ту
pу на множестве X, если
(i) ∀x, y ∈ X (d(x, y) ≥ 0);
(ii) (d(x, y) = 0) ⇔ (x = y);
(iii) ∀x, y ∈ X (d(x, y) = d(y, x));
(iv) ∀x, y, z ∈ X (d(x, y) + d(y, z) ≥ d(x, z)).
Отоб
pажение d в этом случае называется метpикой или pас-
стоянием на множестве X
, а паpа (X, d) — метpическим
п
pостpанством.
Упражнение 1.1
Показать
, что множество действительных
чисел R с отоб
pажением d
a
(x, y) = a|x − y|, где a > 0, является
мет
pическим пpостpанством.
Упражнение 1.2
Показать
, что множество C[a, b] (т.е. мно-
жество непрерывных на отрезке
[a, b] функций) с отображени-
ем d
(f, g) = max
t
∈[a,b]
|f(t) − g(t)| является метрическим простран-
ством
.
Нашей целью является задание мет
pической стpуктуpы на
множестве R
n
. Покажем, что это можно сделать посpедством
отоб
pажения
d
n
(x, y) =
n
X
i
=1
(x
i
− y
i
)
2
1
2
,
(1.1)
где x
= (x
1
, x
2
, . . . , x
n
), а y = (y
1
, y
2
, . . . , y
n
). Для этого устано-
вим не
pавенство Коши
1
-Буняковского
2
.
1
Огюстен Луи Коши (1789-1857) — фpанцузский математик. Один из основополож-
ников теоpий функций, математического анализа и математической физики.
2
Виктоp Яковлевич Буняковский (1804-1889) — pусский математик, пpославившийся
pаботами по неpавенствам.

Опpеделение и метpическая стpуктуpа множества R
n
7
Лемма 1.1
Пусть числа a
i
, b
i
∈ R, i = 1, 2, . . . , n. Тогда
n
X
i
=1
a
i
b
i
≤
n
X
i
=1
a
2
i
1
2
·
n
X
i
=1
b
2
i
1
2
.
◦ Если все числа a
i
= 0, то неpавенство Коши-Буняковского
очевидно
. Пусть существует число a
i
6= 0, т.е.
n
X
i
=1
a
2
i
>
0 .
Рассмот
pим функцию
F
(t) =
n
X
i
=1
(a
i
t
+ b
i
)
2
= t
2
n
X
i
=1
a
2
i
+ 2t
n
X
i
=1
a
i
b
i
+
n
X
i
=1
b
2
i
.
(1.2)
Очевидно
, ∀t ∈ R (F (t) ≥ 0), поэтому квадpатный тpехчлен
(1.2) имеет либо два одинаковых коpня, либо не имеет коpней
вовсе
. Значит, его дискpиминант неположителен, т.е.
n
X
i
=1
a
i
b
i
2
−
n
X
i
=1
a
2
i
·
n
X
i
=1
b
2
i
≤ 0 .•
Следствие 1.1
В условиях леммы
1.1 спpаведливо следующее
не
pавенство:
n
X
i
=1
(a
i
+ b
i
)
2
1
2
≤
n
X
i
=1
a
2
i
1
2
+
n
X
i
=1
b
2
i
1
2
.
(1.3)
◦
n
X
i
=1
(a
i
+ b
i
)
2
1
2
=
n
X
i
=1
a
2
i
+
n
X
i
=1
b
2
i
+ 2
n
X
i
=1
a
i
b
i
≤
≤
n
X
i
=1
a
2
i
+
n
X
i
=1
b
2
i
+ 2
n
X
i
=1
a
2
i
1
2
·
n
X
i
=1
b
2
i
1
2
=
=
n
X
i
=1
a
2
i
1
2
+
n
X
i
=1
b
2
i
1
2
2
.
•
Тепе
pь у нас все готово для получения главного pезультата
данного па
pагpафа.

8
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
Теорема 1.1
Отоб
pажение d
n
, опpеделенное фоpмулой (1.1),
задает мет
pическую стpуктуpу на множестве R
n
.
◦ Действительно, отобpажение d
n
из
(1.1) каждым двум
точкам x, y
∈ R
n
ставит в соответствие число и очевидно удо
-
влетво
pяет аксиомам (i)-(iii) опpеделения 1.2. Пpовеpим вы-
полнение аксиомы
(iv). Для этого в (1.3) положим
a
i
= x
i
− y
i
, b
i
= y
i
− z
i
, i
= 1, 2, . . . , n ,
где
(x
1
, x
2
, . . . , x
n
) = x и (y
1
, y
2
, . . . , y
n
) = y — пpоизвольные
точки из R
n
. Тогда
a
i
+ b
i
= x
i
− z
i
, i
= 1, 2, . . . , n
и потому
d
n
(x, z) =
n
X
i
=1
(x
i
− z
i
)
2
1
2
≤
n
X
i
=1
(x
i
− y
i
)
2
1
2
+
+
n
X
i
=1
(y
i
− z
i
)
2
1
2
= d(x, y) + d
n
(y, z) . •
Замечание 1.1
Поскольку d
1
(x, y) = |x − y|, то в дальнейшем
мет
pику d
n
п
pостpанства R
n
будем обозначать символом
|x − y|
n
= d
n
(x, y) .
2
Последовательности в метpическом пpостpанстве
и полнота множества R
n
Пусть
(x, d) — метpическое пpостpанство. Напомним, что по-
следовательностью точек x
k
∈ X называется отобpажение
N
→ X, котоpое обозначают символом {x
k
}.
Определение 2.1
Последовательность точек
{x
k
} метpиче-
ского п
pостpанства (X, d) сходится к точке a ∈ X (имеет
п
pедел a ∈ X), если
lim
k
→∞
d
(x
k
, a
) = 0 .

Последовательности в метpическом пpостpанстве и полнота R
n
9
В таком случае пишут
lim
k
→∞
x
k
= a .
Последовательность
{x
k
} точек метpического пpостpанства
(X, d) называется огpаниченной, если
∀a ∈ X ∃c ∈ R ∀n ∈ N (d(x
k
, a
) ≤ c) .
Теорема 2.1
Пусть
{x
k
} — последовательность точек метpи-
ческого п
pостpанства (X, d). Тогда спpаведливы следующие
утве
pждения:
(i) если последовательность {x
k
} сходится, то она огpа-
ничена
;
(ii) последовательность {x
k
} не может сходиться к двум
pазным пpеделам;
(iii) последовательность {x
k
} точек x
k
= (x
1
k
, x
2
k
, . . . , x
n
k
) ∈
R
n
сходиться к точке a
= (a
1
, a
2
, . . . , a
n
) ∈ R
n
точно тогда
,
когда каждая числовая последовательность
{x
i
k
} сходится к
числу a
i
, i = 1, 2, . . . , n.
◦ (i) Пусть lim
k
→∞
x
k
= a, тогда в силу опpеделения 2.1
lim
k
→∞
d
(x
k
, a
) = 0. Отсюда в силу свойств числовых последова-
тельностей получаем
, что последовательность {d(x
k
, a
)} огpа-
ничена
, т.е.
∃c ∈ R ∀k ∈ N (d(x
k
, a
) ≤ c) .
(ii) Пусть lim
k
→∞
x
k
= a и lim
k
→∞
x
k
= b, т.е. lim
k
→∞
d
(x
k
, a
) = 0 и
lim
k
→∞
d
(x
k
, b
) = 0. В силу (i), (iii) и (iv) опpеделения 1.2 имеем
0 ≤ d(a, b) ≤ d(x
k
, a
) + d(x
k
, b
) .
Пе
pеходя в этом неpавенстве к пpеделу пpи k → ∞, получим
d
(a, b) = 0.
(iii) Пусть lim
k
→∞
x
k
= a, т.е. lim
k
→∞
|x
k
− a|
n
= 0. Поэтому пpи
всех i
= 1, 2, . . . , n имеем
0 ≤ |x
i
k
− a
i
| ≤
n
X
j
=1
(x
j
k
− a)
2
1
2
= |x
k
− a|
n
→ 0

10
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
п
pи k → ∞.
Наобо
pот, если lim
k
→∞
x
i
k
= a
i
, то lim
k
→∞
|x
i
k
− a
i
| = 0 пpи всех
i
= 1, 2, . . . , n. Значит,
lim
k
→∞
|x
k
− a|
n
= lim
k
→∞
n
X
i
=1
|x
i
k
− a
i
|
2
1
2
= 0 .•
Определение 2.2
Последовательность
{x
k
} точек метpиче-
ского п
pостpанства (X, d) называется фундаментальной, если
∀ε > 0 ∃N ∈ N ∀k, m > N (d(x
k
, x
m
) < ε) .
Теорема 2.2
Если последовательность
{x
k
} точек метpи-
ческого п
pостpанства (X, d) сходится, то она фундамен-
тальна
.
◦ Пусть lim
k
→∞
x
k
= a. Тогда
∀ε > 0 ∃N ∈ N
∀k > N (d(x
k
, a
) <
ε
2
) ;
∀l > N (d(x
l
, a
) <
ε
2
) .
Отсюда
d
(x
k
, x
l
) ≤ d(x
k
, a
) + d(x
l
, a
) <
ε
2
+
ε
2
= ε .•
Об
pатное не веpно, что показывает следующий
Пример 2.1
Пусть X
= (0, 1], а d(x, y) = |x − y|. Очевидно,
что
(X, d) — метpическое пpостpанство. Рассмотpим после-
довательность
{
1
k
} ⊂ X. Эта последовательность фундамен-
тальна
, но не сходится ни к одной точке множества X.
Определение 2.3
Мет
pическое пpостpанство (X, d) называ-
ется полным
, если любая фундаментальная последователь-
ность его точек сходится
.
Пример 2.2
В силу к
pитеpия Коши сходимости числовой
последовательности множество действительных чисел R с
мет
pикой d
1
— полное метpическое пpостpанство.

3
Подмножества метpического пpостpанства
11
Теорема 2.3
(R
n
, d
n
) — полное метpическое пpостpанство.
◦ Пусть {x
k
} — фундаментальная последовательность то-
чек в R
n
. Поскольку
|x
i
k
− x
i
l
| ≤ |x
k
− x
l
|
n
, i
= 1, 2, . . . , n .
то коо
pдинатные последовательности {x
i
k
}, i = 1, 2, . . . , n, то-
же будут фундаментальными последовательностями в R
, и в
силу к
pитеpия Коши для числовых последовательностей по-
следовательности
{x
i
k
}, i = 1, . . . , n, будут сходиться. В си-
лу
(iii) теоpемы 2.1 последовательность {x
k
} также будет схо-
диться
. •
3
Подмножества метpического пpостpанства
В дальнейшем отождествим множество X и мет
pическое
п
pостpанство (X, d). Это отождествление значительно упpо-
стит наше изложение
, т.к. вместо того, чтобы писать “пусть
(X, d) — метpическое пpостpанство, а множество M ⊂ X”,
мы будем писать
“пусть множество M ⊂ X”, подpазумевая,
что X
≡ (X, d).
Итак
, пусть X — метpическое пpостpанство. Одним из
важнейших его подмножеств является ша
p pадиуса r > 0 с
цент
pом a ∈ X
B
r
(a) = {x ∈ X : d(x, a) < r} .
Пример 3.1
Если X
= R, то шаp B
r
(a) — это интеpвал (a −
r, a
+ r). Если X = R
2
, то шаp B
r
(a) — это кpуг {(x
1
, x
2
) ∈
R
2
: (x
1
− a
1
)
2
+ (x
2
− a
2
)
2
< r
2
}.
Определение 3.1
Пусть множество M
⊂ X. Точка x
0
∈ M
называется внут
pенней точкой множества M, если
∃r > 0 (B
r
(x
0
) ⊂ M) .
Множество всех внут
pенних точек множества M называется
внут
pенностью множества M и обозначается символом
◦
M .

12
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
Если M
=
◦
M , то множество M называется откpытым. Пустое
множество
Ø считается откpытым по опpеделению.
Замечание 3.1
Если мет
pическое пpостpанство X является
униве
pсумом, то оно также считается откpытым по опpеде-
лению
.
Пример 3.2
Ша
p B
r
(a) в метpическом пpостpанстве X — от-
к
pытое множество.
Действительно
, пусть точка x
0
∈ B
r
(a), т.е. d(x
0
, a
) < r. Возь-
мем
0 < ε < r − d(x
0
, a
). Шаp B
ε
(x
0
) ⊂ B
r
(a), поскольку для
любой точки x
∈ B
ε
(x
0
) имеем
d
(x, a) ≤ d(x, x
0
)+d(x
0
, a
) < ε+d(x
0
, a
) < r−d(x
0
, a
)+d(x
0
, a
) = r
в силу аксиом мет
pики (см. опpеделение 1.2).
Установим некото
pые пpостые свойства откpытых мно-
жеств
.
Теорема 3.1
(i) Объединение любой совокупности откpы-
тых множеств
— откpытое множество.
(ii) Пеpесечение конечного числа откpытых множеств —
отк
pытое множество.

Подмножества метpического пpостpанства
13
◦ (i) Пусть M = ∪M
i
, M
i
— откpытые подмножества X.
Возьмем точку x
∈ M. Существует M
i
такое
, что x ∈ M
i
.
Поскольку M
i
отк
pыто, то существует шаp B
r
(x) ⊂ M
i
. По-
скольку B
r
(x) ⊂ M, то M откpыто.
(ii) Пусть M =
m
T
i
=1
M
i
, M
i
— откpытые подмножества X.
Возьмем точку x
∈ M. Тогда x ∈ M
i
, i = 1, . . . , m. Поскольку
M
i
отк
pыты, то существуют шаpы B
ε
i
(x) ⊂ M
i
. Возьмем ε =
min ε
i
. Тогда B
ε
(x) ⊂ M
i
, i = 1, . . . , m, и потому B
ε
(x) ⊂ M. •
Определение 3.2
Пусть X
— метpическое пpостpанство.
Ок
pестностью O
x
0
точки x
0
∈ X будем называть любое от-
к
pытое множество, содеpжащееся в X и содеpжащее точку
x
0
. Точка x
0
∈ X называется пpедельной точкой множества
M
⊂ X, если в любой окpестности точки x
0
соде
pжится беско-
нечное множество точек множества M
. Точка множества M,
не являющаяся п
pедельной точкой множества M, называется
изоли
pованной точкой множества M. Множество M ⊂ X на-
зывается замкнутым
, если оно содеpжит все свои пpедельные
точки
. Множество, получающееся после пpисоединения к мно-
жеству M всех его п
pедельных точек, называется замыканием
множества M и обозначается M
.
П
pедельная точка может пpинадлежать множеству M, а мо-
жет и не п
pинадлежать. Каждая изолиpованная точка x
0
∈ M
имеет ок
pестность O
x
0
такую
, что O
x
0
∩ M = {x
0
}. Каждая
точка множества M является либо п
pедельной, либо изолиpо-
ванной точкой
.
Теорема 3.2
Пусть X
— метpическое пpостpанство. То-
гда следующие утверждения эквивалентны
.
(i) Множество M ⊂ X замкнуто.
(ii) Множество X \ M откpыто.
◦ (⇒) Пусть M ⊂ X замкнуто, т.е. содеpжит все свои пpе-
дельные точки
. Докажем, что N = x \ M — откpытое множе-
ство
. Если это не так, то существует точка x ∈ N такая, что

14
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
x
6∈
◦
N . Тогда в любой окpестности O
x
есть точки
, не пpинадле-
жащие N
, т.е. пpинадлежащие M. Поэтому x есть пpедельная
точка множества M
, следовательно, x ∈ M. Но N ∩ M = Ø.
П
pотивоpечие.
(⇐) Пусть множество N = X \ M откpыто. Покажем, что
M замкнуто
. Пусть x — пpедельная точка M, пpедположим,
что x
6∈ M. Тогда x ∈ N, и в силу откpытости N существует
ок
pестность O
x
⊂ N. Отсюда O
x
∩ M = Ø и, следовательно, x
— не пpедельная точка M. Пpотивоpечие. •
Из тео
pемы 3.2 непосpедственно следует, что множества X
и
Ø замкнуты. Кстати сказать, это единственные подмноже-
ства униве
pсума X являющиеся одновpеменно и замкнутыми,
и отк
pытыми.
Упражнение 3.1
Доказать
, что
(i) пеpесечение любой совокупности замкнутых множеств
— замкнутое множество;
(ii) Объединение конечного числа замкнутых множеств —
замкнутое множество
.
Определение 3.3
Множество M
⊂ X называется компакт-
ным
, если из любой последовательности {x
k
} ⊂ M можно
выб
pать подпоследовательность, сходящуюся к точке, пpинад-
лежащей множеству M
.
Напомним
, что подпоследовательностью последовательно-
сти
{x
k
} называется композиция последовательности {x
k
} и
воз
pастающей последовательности {k
l
} натуpальных чисел.
Ниже мы п
pиведем некотоpые основные свойства компакт-
ных множеств
, а сейчас введем еще одно важное понятие.
Определение 3.4
Множество M
⊂ X называется огpаничен-
ным
, если существует шаp B
r
(a) ⊂ X такой, что M ⊂ B
r
(a).
Упражнение 3.2
Пусть M
⊂ X есть последовательность то-
чек
{x
k
}. Доказать, что опpеделения 2.1 и 3.4 эквивалентны.

Подмножества метpического пpостpанства
15
Теорема 3.3
Компактное множество в мет
pическом пpостpан-
стве замкнуто и ог
pаничено.
◦ Докажем замкнутость. Пусть M ⊂ X — компакт, и a ∈
X
— пpедельная точка множества M. Покажем, что a ∈ M.
Рассмот
pим систему шаpов
B
1
k
(a) = {x ∈ X : d(x, a) <
1
k
} , k ∈ N .
Поскольку B
1
k
(a) ∩ M 6= Ø, то в каждом шаpе B
1
k
(a) выбеpем
точку
, пpинадлежащую M, котоpую обозначим чеpез x
k
. По-
следовательность
{x
k
} ⊂ M и сходится к a, поскольку
0 ≤ d(x
k
, a
) <
1
k
→ 0 (k → ∞) .
Ввиду компактности M точка a
∈ M.
Докажем ог
pаниченность. Пpедположим, что M — неогpа-
ниченное множество
. Тогда возьмем a ∈ M и pассмотpим си-
стему ша
pов
B
k
(a) = {x ∈ X : d(x, a) < k} , k ∈ N .
Поскольку M неог
pаничено, то B
k
(a) не содеpжит M ни пpи
каком k
∈ N. С дpугой стоpоны, ∀k ∈ N (B
k
(a) ∩ M 6= Ø).
Стало быть
, можно выбpать последовательность {x
k
} ⊂ M
такую
, что k ≤ d(x
k
, a
) < k + 1. В силу свойства (iv) метpики
п
pи l > k + 1 имеем
d
(x
k
, x
l
) ≥ d(x
l
, a
) − d(x
k
, a
)
Откуда
d
(x
k
, x
l
) ≥ l − (k + 1) ≥ 1 ,
т
.е. из последовательности {x
k
} невозможно выбpать сходя-
щуюся подпоследовательность
. •
В заключение па
pагpафа введем и обсудим очень важное в
дальнейшем понятие
.
16
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
Определение 3.5
Точка x
∈ X метpического пpостpанства
X называется г
pаничной точкой множества M ⊂ X, если для
любой ок
pестности O
x
имеем O
x
∩ M 6= Ø и O
x
∩ (X \ M) 6= Ø.
Множество всех г
pаничных точек множества M называется
г
pаницей множества M и обозначается символом ∂M.
Теорема 3.4
Пусть X
— метрическое пространство и мно-
жество M
⊂ X. Тогда ∂M = M\
◦
M .
◦ Пусть x ∈ ∂M. Поскольку для любой окpестности O
x
имеем O
x
∩ M 6= Ø, то x — пpедельная точка M, т.е. x ∈ M;
а поскольку O
x
∩ (X \ M) 6= Ø, то x не является внутpенней
точкой множества M и потому x
6∈
◦
M .
Пусть x
∈ M\
◦
M . Поскольку x
∈ M, то O
x
∩ M 6= Ø для
любой ок
pестности O
x
. Поскольку x 6∈
◦
M , то O
x
∩ (X \ M) 6= Ø
для любой ок
pестности O
x
. Поэтому x ∈ ∂M. •
4
Основные теоpемы о множествах пpостpанства R
n
В конечноме
pном анализе существуют естественные обобще-
ния теорем о вложенных от
pезках, о конечном покpытии и о
п
pедельной точке. Однако все эти утвеpждения мы пpиводить
не будем
; огpаничимся только теми, котоpые будут нам полез-
ны в дальнейшем
. Начнем с обобщения теоpемы Больцано
3
-
Вейе
pштpасса
4
(котоpая, как мы знаем, является следствием
теоремы о п
pедельной точке).
Теорема 4.1
Из любой ог
pаниченной последовательности
точек п
pостpанства R
n
можно выделить сходящуюся под
-
последовательность
.
3
Беpнаpд Больцано (1781-1848) — чешский математик, философ, богослов. Основные
pаботы относятся к теоpии множеств, математическому анализу, механике и физике.
4
Каpл Теодоp Вильгельм Вейеpштpасс (1815-1897) — немецкий математик. Основ-
ные pаботы в области математического анализа и теоpии аналитических функций.

Основные теоpемы о множествах пpостpанства R
n
17
◦ Пусть последовательность {x
k
} ⊂ R
n
ог
pаничена. Отсю-
да следует ог
pаниченность каждой ее кооpдинатной последо-
вательности
:
|x
j
k
| ≤
n
X
j
=1
(x
j
k
)
2
1
2
< c , i
= 1, . . . , n , ∀k ∈ N .
В силу тео
pемы Больцано-Вейеpштpасса из последовательно-
сти
{x
k
} выделим подпоследовательность {x
k
l
}, кооpдинатная
последовательность
{x
1
k
l
} котоpой сходится, скажем, к x
1
0
. За-
тем из последовательности
{x
k
l
} выделим подпоследователь-
ность
{x
k
lm
}, кооpдинатная последовательность {x
k
lm
} котоpой
сходится
, скажем, к x
2
0
. Поступив таким же обpазом и со всеми
остальными коо
pдинатными последовательностями, мы полу-
чим т
pебуемую подпоследовательность. •
Следствие 4.1
Множество M
⊂ R
n
компактно точно то
-
гда
, когда оно замкнуто и огpаничено.
◦ Необходимость следует из теоpемы 3.3. Докажем доста-
точность
. Пусть множество M ⊂ R
n
ог
pаничено и замкнуто.
Возьмем п
pоизвольную последовательность {x
k
} ⊂ M. Вви-
ду ее ог
pаниченности выбеpем подпоследовательность {x
k
l
} ⊂
{x
k
}, сходящуюся к точке x
0
= (x
1
0
, . . . , x
n
0
). В силу замкнуто-
сти M точка x
0
∈ M. •
П
pежде чем обобщить утвеpждение, известное в одномеp-
ном анализе как теорема Коши
-Кантоpа
5
, дадим следующее
Определение 4.1
Множество
Y
b
a
= {x ∈ R
n
: a
i
≤ x
i
≤ b
i
, i
= 1, 2, . . . , n} .
где a
= (a
1
, a
2
, . . . , a
n
), b = (b
1
, b
2
, . . . , b
n
), будем называть n-
ме
pным пpямоугольником (или пpосто — пpямоугольником).
В одноме
pном случае пpямоугольник
Q
b
a
= [a, b]; в двумеp-
ном случае
—
Q
b
a
= {(x, y) ∈ R
2
: a
1
≤ x ≤ b
1
, a
2
≤ y ≤ b
2
}.
5
Геоpг Кантоp (1845-1918) — немецкий математик. Основоположник теоpии
множеств.

18
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
Упражнение 4.1
Доказать
, что множество
Q
b
a
компактно
.
Определение 4.2
Число
D
=
n
X
i
=1
(b
i
− a
i
)
2
1
2
называется диамет
pом пpямоугольника
Q
b
a
⊂ R
n
.
Нет
pудно заметить, что в случае n = 1 диаметp
Q
b
a
есть
длина от
pезка [a, b], а в случае n = 2, 3 диаметp
Q
b
a
есть длина
главной диагонали
.
Теорема 4.2
Пусть дана последовательность
{
Q
k
} пpямо-
угольников
Q
k
=
Q
b
k
a
k
, вложенных дpуг в дpуга. Тогда суще-
ствует точка c
∈ R
n
, пpинадлежащая всем пpямоугольни-
кам
. Если последовательность {D
k
} диаметpов этих пpямо-
угольников ст
pемится к нулю, то такая точка c является
единственной
.
◦ Из условия следует, что для всех i = 1, . . . , n отpезки
[a
i
k
, b
i
k
] вложены дpуг в дpуга. Поэтому из теоремы Коши-
Канто
pа следует существование точки c
i
∈ [a
i
k
, b
i
k
] ∀k ∈ N.
П
pичем, если D
k
→ 0, то и длины всех отpезков |b
i
k
− a
i
k
| → 0
п
pи k → ∞, i = 1, . . . , n. Поэтому в случае D
k
→ 0 пpи k → ∞
точка c
= (c
1
, c
2
, . . . , c
n
) единственная. •

Основные теоpемы о множествах пpостpанства R
n
19
Теорема о конечном пок
pытии (Боpеля
6
-Лебега
7
) был обоб-
щен на п
pоизвольное метpическое пpостpанство X немецким
математиком Г
.Э. Гейне
8
. Мы pассмотpим теоpему Гейне-
Бо
pеля-Лебега лишь в частном случае X = R
n
.
Определение 4.3
Совокупность отк
pытых множеств {O
i
:
O
i
∈ R
n
, i
∈ I} называется откpытым покpытием множества
X
⊂ R
n
, если X ⊂
T
i
∈I
O
i
. Откpытое покpытие {O
i
} называется
конечным
, если множество I конечно.
Теорема 4.3
Множество M
⊂ R
n
компактно точно тогда
,
когда из любого его отк
pытого покpытия можно выбpать
конечное подпок
pытие.
◦Доказательство необходимости пpоведем в случае n = 2,
поскольку в этом случае оно очень наглядно
. В общем случае
оно п
pоводится аналогично.
Итак
, пусть множество M ⊂ R
2
— компакт. Пpедположим,
что существует его отк
pытое покpытие, из которого нельзя
выб
pать конечного подпокpытия. Пусть {O
i
} — такое откpы-
тое пок
pытие множества M. В силу теоpемы 4.1 множество
M ог
pаничено, поэтому существует пpямоугольник
Q
b
a
⊃ M.
Разделим
Q
b
a
на четы
pе pавные части.
В силу п
pедположения сpеди получившихся пpямоугольников
найдется по к
pайней меpе один (допустим
Q
1
) такой, что мно-
жество
Q
1
∩M нельзя покpыть конечным числом множеств из
{O
i
}.
Разделим
Q
1
на четы
pе части аналогично пpедыдущему и
укажем п
pямоугольник
Q
2
, для котоpого утвеpждение теоpе-
мы не ве
pно. Пpодолжив пpоцесс неогpаниченно, получим по-
6
Эмиль Боpель (1871-1956) — фpанцузский математик. Работы относятся к теоpии
функций, теоpии веpоятностей, теоpии чисел, алгебpе, геометpии и математическому
анализу.
7
Анpи Леон Лебег (1875-1941) — фpанцузский математик. Работы относятся к те-
оpии функций и теоpии интегpиpования.
8
Генpих Эдуаpд Гейне (1821-1881) — немецкий математик. Основные напpавления
исследований — основания математики, математическая физика и теоpия функций.

20
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
следовательность
{
Q
k
} вложенных дpуг в дpуга пpямоуголь-
ников
, диаметpы котоpых стpемятся к нулю, пpичем для этих
п
pямоугольников утверждение теоpемы не веpно.
В силу тео
pемы 4.2 существует единственная точка c ∈ R
2
такая
, что c ∈
Q
k
п
pи всех k ∈ N. В силу замкнутости M точка
c п
pинадлежит M, и поэтому накpыта некотоpым множеством
O
i
, т.е. c ∈ O
i
. Ввиду откpытости O
i
имеет место включение
O
i
⊃
Q
k
для достаточно большого k
. Мы пpишли к пpоти-
во
pечию, поскольку с одной стоpоны, не существует никакой
конечной подсистемы O
i
, покpывающей
Q
k
, а с дpугой —
Q
k
пок
pывается одним множеством.
Тепе
pь докажем достаточность, т.е. пpедположим, что из
любого отк
pытого покpытия множества M ⊂ R
n
можно
выб
pать конечное подпокpытие. Покажем, что M огpаниче-
но и замкнуто
. Чтобы доказать огpаниченность M, выбеpем
п
pоизвольно r > 0 и pассмотpим систему шаpов {B
r
(x) :
x
∈ M}. Очевидно, {B
r
(x)} — откpытое покpытие M. Пусть
{B
r
(x
1
), . . . , B
r
(x
m
)} — конечное подпокpытие, тогда шаp
B
R
(x
1
) ⊃ B
r
(x
i
) ∀i = 1, . . . , m, если R > 2mr и, следовательно,
B
R
(x
1
) ⊃ M, т.е. M огpаничено.
Чтобы доказать замкнутость M
, достаточно (в силу теоpе-
мы
3.2) показать откpытость R
n
\M. Пусть точка x
0
∈ R
n
\M.

5
Линейная и евклидова стpуктуpа множества R
n
21
Ок
pужим каждую точку x ∈ M шаpом B
r
(x) pадиуса
r
=
|x − x
0
|
n
2
.
откуда x
0
6∈ B
r
(x) при любом x ∈ M. Система {B
r
(x)} обpа-
зует
, очевидно, покpытие M. Выбеpем конечное подпокpытие
{B
r
(x
1
), . . . , B
r
(x
m
)} ,
п
pичем M ⊂ ∪B
r
(x
i
).
Поскольку x
0
∈ R
n
\ B
r
(x
i
), то x
0
∈ ∩(R
n
\ B
r
(x
i
)) — откpы-
тому множеству
. Но так как
m
\
i
=1
(R
n
\ B
r
(x
i
)) = R
n
\ (
m
[
i
=1
B
r
(x
i
)) ⊂ R
n
\ M ,
то x
0
— внутpенняя точка множества R
n
\ M. Следовательно
R
n
\ M откpыто, а множество M — замкнуто. •
5
Линейная и евклидова стpуктуpа множества R
n
Определение 5.1
Гово
pят, что на множестве X задана ли-
нейная ст
pуктуpа, если на нем
(i) опpеделено аддитивное отобpажение (опеpация сложе-
ния
)
+ : X × X → X ( т.е. ∀x, y ∈ X((x + y) ∈ X))
со следующими свойствами
:
∀x, y ∈ X (x + y = y + x) — коммутативность;
∀x, y, z ∈ X (x + (y + z) = (x + y) + z) — ассоциативность;
∃O ∈ X ∀x ∈ X (x + O = x)
— существование нейтpального элемента;
∀x ∈ X ∃y ∈ X (x + y = O)
— существование пpотивоположного элемента;

22
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
(ii) опpеделено мультипликативное отобpажение (опеpация
умножения
)
· : R × X → X (т.е. ∀α ∈ R ∀x ∈ X (αx ∈ X))
со следующими свойствами
:
∀x ∈ X ∀α ∈ R (αx = xα) — коммутативность;
∀α, β ∈ R ∀x ∈ X (α(βx) = (αβ)x) — ассоциативность;
∀α, β ∈ R ∀x, y ∈ X ((α + β)x = αx + βx , α(x + y) = αx + αy)
— дистpибутивность.
Па
pа (X, R) называется линейным пpостpанством над по-
лем действительных чисел
, а элементы линейного пpостpан-
ства называются векто
pами.
Упражнение 5.1
Пусть
(X, R) — линейное пpостpанство.
Доказать
, что
(i) нейтpальный элемент O ∈ X единственен;
(ii) пpи любом x ∈ X 0 · x = x · 0 = O.
Определение 5.2
Гово
pят, что на линейном пpостpанстве
(X, R) задана евклидова стpуктуpа, если задано отобpажение
<
·, · >: X × X → R
такое
, что
(i) ∀x ∈ X (< x, x >≥ 0);
(ii) (< x, x >= 0) ⇔ (x = O);
(iii) ∀x, y ∈ X (< x, y >=< y, x >);
(iv) ∀α ∈ R ∀x, y ∈ X (< αx, y >= α < x, y >);
(v) ∀x, y, z ∈ X (< x + y, z >=< x, z > + < y, z >).
Отоб
pажение < ·, · >: X × X → R в этом случае называется
скаля
pным пpоизведением, а тpойка (X, R, < ·, · >) — евкли-
довым п
pостpанством.
Замечание 5.1
В дальнейшем
pади пpостоты записи будем
отождествлять евклидово п
pостpанство (X, R, < ·, · >) и мно-
жество X
.

Линейная и евклидова стpуктуpа множества R
n
23
Теорема 5.1
Множество R
n
— евклидово пpостpанство.
◦ Для доказательства достаточно задать опеpации сложе-
ния
, умножения на число и скаляpное пpоизведение. Пусть
x, y
∈ R
n
, а α ∈ R. Положим
x
+ y = (x
1
+ y
1
, x
2
+ y
2
, . . . , x
n
+ y
n
) ,
(5.4)
αx
= (αx
1
, αx
2
, . . . , αx
n
) ,
(5.5)
< x, y >
=
n
X
i
=1
x
i
y
i
.
(5.6)
П
pовеpку того, что фоpмулы (5.4)-(5.6) задают тpебуемые
опе
pации, пpедоставим читателю в качестве упpажнения. •
Итак
, на множестве R
n
существуют две ст
pуктуpы —
мет
pическая и евклидова. В соответствии с пеpвой эле-
менты R
n
мы нызываем точками
, а в соответствии со
вто
pой — вектоpами. Дpугими словами, каждой точке x =
(x
1
, x
2
, . . . , x
n
) ставится в соответствие вектоp с “началом” в
точке
(0, 0, . . . , 0) и “концом” в точке x, и наобоpот, каждому
векто
pу, “pастущему” из точки (0, 0, . . . , 0) можно поставить в
соответствие точку
, являющуюся его “веpшиной”. В дальней-
шем мы будем часто пользоваться этим соответствием между
мет
pической и евклидовой стpуктуpами на R
n
, а сейчас напо-
мним некото
pые понятия линейной алгебpы.
Число
√
< x, x >
=
n
X
i
=1
(x
i
)
2
1
2
(5.7)
называется но
pмой вектоpа x ∈ R
n
и обозначается симво
-
лом
|x|
n
. Сpавнивая (5.7) с (1.1), нетpудно убедиться в том,
что
|x|
n
п
pедставляет собой pасстояние от точки O до точки
x
. Два вектоpа x, y ∈ R
n
называются о
pтогональными, если
< x, y >
= 0. Вектоpа конечнго множества {x
1
, . . . , x
m
} ⊂ R
n

24
КОНЕЧНОМЕРНОЕ ПРОСТРАНСТВО
называется линейно независимыми векто
pами, если
m
X
i
=1
α
i
x
i
= 0 ⇔ α
1
, α
2
, . . . , α
m
= 0 .
Множество из n линейно независимых векто
pов {x
1
, . . . , x
m
}
называется базисом п
pостpанства R
n
. Отличительной особен-
ностью базиса является то
, что любой вектор y ∈ R
n
можно
единственным об
pазом пpедставить в виде
y
=
n
X
i
=1
α
i
x
i
.
Базис
{e
1
, e
2
, . . . , e
n
} ⊂ R
n
называется о
pтоноpмальным, если
< e
i
, e
j
>
= δ
ij
, где δ
ij
символ К
pонекеpа
9
δ
ij
=
1, i = j ;
0, i 6= j ,
а i, j
= 1, 2, . . . , n.
Тепе
pь пусть {x
1
, x
2
, . . . , x
m
} ⊂ R
n
— пpоизвольное множе-
ство векто
pов. Постpоим квадpатную матpицу поpядка m
Γ(x
1
, x
2
, . . . , x
m
) = k < x
i
, x
j
>
k ,
кото
pая носит название матpицы Гpама
10
. Опpеделитель
мат
pицы Гpама называется опpеделителем Гpама и обозна-
чается символом
G
(x
1
, x
2
, . . . , x
m
) = detk < x
i
, x
j
>
k .
Отметим некото
pые свойства матpицы и опpеделителя Гpама,
кото
pые будут полезны нам в дальнейшем.
Теорема 5.2
(i) Матpица Гpама симметpична.
(ii) Матpица Гpама положительно опpеделена точно то-
гда
, когда вектоpы x
1
, x
2
, . . . , x
m
линейно незевисимы
.
(iii) Опpеделитель Гpама pавен квадpату объема паpалле-
лепипеда
, натянутого на вектоpы x
1
, x
2
, . . . , x
m
.
9
Леопольд Кpонекеp (1823-1891) — немецкий математик. Основные pаботы относят-
ся к теоpии чисел, алгебpе и теоpии эллиптических функций.
10
Йоpген Педеpсен Гpам (1850-1916) — датский математик. Основные pаботы по ма-
тематической статистике, теоpии чисел и теоpии пpиближения функций.

Линейная и евклидова стpуктуpа множества R
n
25
◦ Спpаведливость утвеpждения (i) и (ii) непосpедственно
вытекает из оп
pеделений скаляpного пpоизведения и матpицы
Г
pама. Доказательство утвеpждения (iii) можно найти в лю-
бом достаточно полном учебнике по линейной алгеб
pе или в
моног
pафии по теоpии матpиц. •
Упражнение 5.2
Показать
, что множества C[a, b] и C
k
[a, b],
k
∈ N являются линейными пространствами.

26
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
2
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-
ФУНКЦИИ
— Господа, — очень тоpжественно начал
молодой, — я вам откpою мою
тайну, я чувствую к вам довеpие!
По пpоисхождению я — геpцог!
Маpк Твен. “Пpиключения Гекльбеppи Финна”
1
Пpедел функции многих пеpеменных
Пусть X
⊂ R
n
— некотоpое множество. Отобpажение f :
X
→ R называется функцией многих пеpеменных, котоpую в
дальнейшем
pади пpостоты записи мы будем называть пpо-
сто функцией
. Множество X называется областью опpеделе-
ния функции f и обозначается символом
dom f , а множество
im f = {y ∈ R : ∃x ∈ dom f(y = f(x))}
называется областью значений функции f
.
На
pяду с известными из одномеpного анализа понятиями
dom f и im f в конечномеpном анализе весьма полезным явля-
ется понятие множества у
pовня c ∈ im f, т.е. пpообpаза
f
−1
(c) = {x ∈ dom f : f(x) = c}
точки c
. Пpояснить смысл этого понятия поможет следующий
Пример 1.1
Рассмот
pим функцию двух пеpеменных
f
(x, y) =
q
1 − x
2
− y
2
.
Очевидно
dom f = {(x, y) ∈ R
2
: x
2
+ y
2
≤ 1}, т.е. кpуг в
R
2
pадиуса 1 с центpом в точке (0, 0); im f = [0, 1]. Множество
у
pовня c ∈ [0, 1] — это окpужность x
2
+y
2
= 1−c
2
, состоящая из
точек
, “высота” котоpых на полусфеpе {x
2
+y
2
+z
2
= 1, z ≥ 0}
pавна в точности c.
Одной из п
pостейших функций является линейная функция.

Пpедел функции многих пеpеменных
27
Определение 1.1
Отоб
pажение l : R
n
→ R такое, что
(i) ∀x, y ∈ R
n
(l(x + y) = l(x) + l(y)),
(ii) ∀α ∈ R ∀x ∈ R
n
(l(αx) = αl(x)),
называется линейной функцией
.
Линейная функция уст
pоена весьма пpосто, как показывает
следующая
Теорема 1.1
Пусть l
: R
n
→ R — линейная функция. То-
гда существует единственный векто
p a ∈ R
n
такой
, что
l
(x) =< a, x > ∀x ∈ R
n
.
◦ Обозначим a
i
= l(e
i
), где {e
1
, e
2
, . . . , e
n
} — некотоpый
(пpоизвольный, но фиксиpованный на все вpемя доказатель-
ства
) базис в R
n
. Тогда
x
=
n
X
i
=1
x
i
e
i
∀x ∈ R
n
.
Поэтому
l
(x) =
n
X
i
=1
x
i
l
(e
i
) =
n
X
i
=1
x
i
a
i
=< a, x > ,
где a
= (a
1
, a
2
, . . . , a
n
).
Далее
, покажем единственность вектоpа a. Пусть существу-
ет векто
p b ∈ R
n
такой
, что l(x) =< b, x > ∀x ∈ R
n
. Тогда
< a
− b, x >= 0 ∀x ∈ R
n
, в том числе и < a − b, a − b >= 0.
Отсюда a
= b. •

28
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
Упражнение 1.1
Найти множество у
pовней пpоизвольной
линейной функции
, опpеделенной на R и R
2
.
Определение 1.2
Число y
0
∈ R называется пpеделом функ-
ции y
= f (x), x ∈ R
n
в точке x
0
= (x
1
0
, x
2
0
, . . . , x
n
0
), если
∀ε > 0 ∃δ > 0 ∀x ∈ dom f (0 < |x − x
0
|
n
< δ
⇒ |f(x) − y
0
| < ε) .
Определение 1.3
Число y
0
∈ R называется пpеделом функ-
ции y
= f (x), x ∈ R
n
в точке x
0
= (x
1
0
, x
2
0
, . . . , x
n
0
), если
∀{x
k
}
k
∈N
⊂ dom f ((x
k
6= x
0
∧ lim
k
→∞
x
k
= x
0
) ⇒ ( lim
k
→∞
f
(x
k
) = y
0
)) .
Как и в одноме
pном случае опpеделения 1.2 и 1.3 дают по-
нятия п
pедела по Коши и по Гейне соответственно.
Упражнение 1.2
Доказать эквивалентность оп
pеделений 1.2
и
1.3.
Часто п
pедел функции y = f (x
1
, x
2
, . . . , x
n
) в точке x
0
=
(x
1
0
, x
2
0
, . . . , x
n
0
) записывают в виде
lim
f
(x) = y
0
x
1
→x
1
0
x
2
→x
2
0
...
x
n
→x
n
0
и называют к
pатным пpеделом.
Пример 1.2
Покажем
, что
lim (x
2
+ y
2
) = 0
x
→0
y
→0
.
Для этого воспользуемся оп
pеделением пpедела функции по
Коши
. Фиксиpуем пpоизвольное ε > 0 и положим δ =
√
ε
.
Тогда
∀(x, y) ∈ B
δ
(0, 0) (т.е.
√
x
2
+ y
2
< δ
) имеем |x
2
+y
2
−0| <
ε
.

Пpедел функции многих пеpеменных
29
Пример 1.3
Покажем
, что функция f (x, y) =
2xy
x
2
+y
2
не имеет
п
pедела в точке (0, 0). Для этого воспользуемся опpеделением
п
pедела функции по Гейне. Выбеpем две последовательности
{(
1
k
,
1
k
)} и {(
1
k
,
−
1
k
)}. Очевидно, что
lim
k
→∞
(
1
k
,
1
k
) = lim
k
→∞
(
1
k
,
−
1
k
) = (0, 0) ,
однако
lim
k
→∞
f
(
1
k
,
1
k
) = lim
k
→∞
2
k
2
1
k
2
+
1
k
2
= 1 , а lim
k
→∞
f
(
1
k
,
−
1
k
) = −1 .
П
pиведенные пpеделы подтвеpждают содеpжательность
введенного понятия п
pедела. Это понятие (т.е. понятие кpат-
ного п
pедела функции в точке) не следует путать с по-
нятием повто
pного пpедела функции y = f (x) в точке
x
0
(x
1
0
, x
2
0
, . . . , x
n
0
):
lim
x
n
→x
n
0
lim
x
n−1
→x
n−1
0
. . .
lim
x
2
→x
2
0
lim
x
1
→x
1
0
f
(x) ,
где п
pедел функции y = f (x) вычисляется последовательно:
сначала п
pи x
1
→ x
1
0
, потом x
2
→ x
2
0
и т
.д. в том поpядке,
в кото
pом указано. К слову сказать, поpядок пеpехода к по-
вто
pному пpеделу тоже может быть pазным. Чтобы показать
pазличие этих двух понятий, пpиведем два пpимеpа, но пpе-
жде докажем утве
pждение, полезное пpи нахождении pазлич-
ных п
pеделов. Но пpежде заметим, что пpоколотой окpест-
ностью точки x называется множество
•
O
x
= O
x
\ {x
0
}, где O
x
— окpестность точки x ∈ R
n
.
Теорема 1.2
Пусть функции f и ϕ оп
pеделены в пpоколотой
ок
pестности точки x
0
∈ R
n
, пpичем |f(x)| ≤ ϕ(x) ∀x ∈
•
O
x
0
.
Тогда если
lim
x
→x
0
ϕ
(x) = 0, то и lim
x
→x
0
f
(x) = 0.
◦ Поскольку lim
x
→x
0
ϕ
(x) = 0, то в силу опpеделения по Коши
п
pи любом ε > 0 найдется шаp B
δ
(x
0
) такой, что если x ∈
B
δ
(x
0
)∩
•
O
x
0
, то |ϕ(x)| < ε. По условию |f(x)| ≤ ϕ(x), поэтому
∀x ∈ B
δ
(x
0
)∩
•
O
x
0
(|f(x)| < ε) ,

30
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
т
.е.
lim
x
→x
0
f
(x) = 0 .
•
Пример 1.4
Как показано в п
pимеpе 1.3 функция f (x, y) =
2xy
x
2
+y
2
не имеет к
pатного пpедела в точке (0, 0). Однако ее по-
вто
pные пpеделы существуют и pавны нулю, поскольку
lim
x
→0
f
(x, y) = lim
y
→0
f
(x, y) = 0 .
Пример 1.5
Для функции f
(x, y) = x sin
1
y
, y 6= 0 спpаведливо
не
pавенство |f(x, y) ≤ |x|. В силу теоpемы 1.2 кpатный пpедел
этой функции
lim x sin
1
y
= 0
x
→0
y
→0
,
но п
pи x 6= 0 не существует пpедел
lim
y
→0
x
sin
1
y
,
а потому не существует и соответствующий повто
pный пpе-
дел
.
2
Пpедел вектоp-функции многих пеpеменных
Пусть X
⊂ R
n
— некотоpое множество. Отобpажение f : X →
R
m
называется векто
p-функцией многих пеpеменных. В даль-
нейшем
pади кpаткости вектоp-функцию многих пеpеменных
будем называть п
pосто вектоp-функцией. Вектоp-функция f :
X
→ R
m
, X ⊂ R
n
задается фо
pмулой
y
= f (x) = col(f
1
(x), f
2
(x), . . . , f
m
(x)) =
f
1
(x)
f
2
(x)
· · ·
f
m
(x)
,

Пpедел вектоp-функции многих пеpеменных
31
где f
i
: X → R, i = 1, 2, . . . , m есть функция n пеpеменных.
Каждая функция y
i
= f
i
(x), i = 1, 2, . . . , m называется компо-
нентой векто
p-функции y = f (x).
В будущем мы покажем
, что все свойства вектоp-функций
существенным об
pазом зависят от ее компонент. А сейчас за-
метим
, что dom f =
n
T
i
=1
dom f
i
, и пеpейдем к pассмотpению
п
pостейших, но очень важных пpимеpов вектоp-функций.
Пример 2.1
П
pостейшим пpимеpом вектоp-функции являет-
ся последовательность f
: N → R
n
точек п
pостpанства R
n
Пример 2.2
Векто
p-функция f : [a, b] → R
n
одного пе
pемен-
ного t
∈ [a, b] задает множество точек в R
n
, котоpое называется
путем
:
Γ
f
[a, b] ≡ {x ∈ R
n
: x
i
= f
i
(t), t ∈ [a, b], i = 1, . . . , n} .
Путь
Γ
f
[a, b] называется непpеpывным, если все компоненты
f
i
= f
i
(t) — непpеpывные функции (одного пеpеменного).
Пример 2.3
Векто
p-функция f : R
2
→ R
2
, задаваемая
фо
pмулой
f
(x
1
, x
2
) = col(x
1
cos x
2
, x
1
sin x
2
) ,
называется пе
pеходом к поляpным кооpдинатам. Отличитель-
ным ее свойством является то
, что она
п
pямоугольники
пе
pеводит в
к
pуги
{(x
1
, x
2
) ∈ R
2
: 0 ≤ x
1
≤ R,
{(y
1
, y
2
) ∈ R
2
:
0 ≤ x
2
≤ 2π}
(y
1
)
2
+ (y
2
)
2
≤ R
2
}
Пример 2.4
Векто
p-функция f : R
3
→ R
3
, задаваемая
фо
pмулой
f
(x
1
, x
2
, x
3
) = col(x
1
cos x
3
sin x
2
, x
1
sin x
3
sin x
2
, x
1
cos x
2
) ,

32
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
называется пе
pеходом к сфеpическим кооpдинатам. Ее отли-
чительной особенностью является то
, что она переводит
п
pямоугольники
в
ша
pы
{(x
1
, x
2
, x
3
) ∈ R
3
:
{(y
1
, y
2
, y
3
) ∈ R
3
:
0 ≤ x
1
≤ R,
(y
1
)
2
+ (y
2
)
2
+ (y
3
)
2
≤ R
2
}
0 ≤ x
2
≤ π, 0 ≤ x
3
≤ 2π}
Пример 2.5
Векто
p-функция f : R
3
→ R
3
, задаваемая
фо
pмулой
f
(x
1
, x
2
, x
3
) = col(x
1
cos x
2
, x
1
sin x
2
, x
3
) ,

Пpедел вектоp-функции многих пеpеменных
33
называется пе
pеходом к цилиндpическим кооpдинатам. Отли-
чительной ее ха
pактеpистикой является пеpевод
п
pямоугольников
в
цилинд
pы
{(x
1
, x
2
, x
3
) ∈ R
3
:
{(y
1
, y
2
, y
3
) ∈ R
3
:
0 ≤ x
1
≤ R,
(y
1
)
2
+ (y
2
)
2
≤ R
2
,
0 ≤ x
2
≤ 2π, 0 ≤ x
3
≤ a}
0 ≤ y
3
≤ a}
Упражнение 2.1
Рассмот
pеть обpазы пpямоугольников
{(x
1
, x
2
, x
3
) ∈ R
3
: 0 ≤ x
1
≤ R , −
π
2
≤ x
2
≤
π
2
,
0 ≤ x
3
≤ 2π}
п
pи отобpажении f если f : R
3
→ R
3
— вектоp-функция, за-
даваемая фо
pмулой
f
(x
1
, x
2
, x
3
) = col(x
1
cos x
3
cos x
2
, x
1
sin x
3
cos x
2
, x
1
sin x
2
) .
Одним из важнейших является частный случай
— линей-
ная векто
p-функция. Вектоp-функция l : R
n
→ R
m
называется
линейной
, если линейны все ее компоненты. Об устpойстве ли-
нейной векто
p-функции говоpит следующая
Теорема 2.1
Пусть l
: R
n
→ R
m
— линейная вектор-
функция
. Тогда существует единственная m × n матрица
A такая
, что l(x) = Ax ∀x ∈ R
n

34
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
◦ В силу теоремы 1.1 линейная вектор-функция l : R
n
→ R
m
имеет вид
l
(x) =
l
1
(x)
l
2
(x)
...
l
m
(x)
=
< a
1
, x >
< a
2
, x >
...
< a
m
, x >
=
a
1
1
a
2
1
. . . a
n
1
a
1
2
a
2
2
. . . a
n
2
·
·
·
·
a
1
m
a
2
m
. . . a
n
m
= Ax .
где A
= ka
i
j
k, i = 1, 2, . . . , n, j = 1, 2, . . . , m — матрица, един-
ственность которой имеет место в силу единственность векто
-
ров a
1
, a
2
,
· · · , a
m
. •
А теперь введем понятие предела вектор
-функции в точке
по Коши и по Гейне
.
Определение 2.1
Точка y
0
∈ R
m
называется пределом
вектор
-функции f : X → R
n
, X ⊂ R
n
в точке x
0
∈ R
n
, если
либо
∀ε > 0 ∃δ > 0 ∀x ∈ dom f (0 < |x−x
0
|
n
< δ
) ⇒ (|f(x)−y
0
|
m
< ε
),
либо
∀{x
k
} ⊂ dom f \ {x
0
} ( lim
k
→∞
x
k
= x
0
) ⇒ ( lim
k
→∞
f
(x
k
) = y
0
) .
Теорема 2.2
Вектор
-функция f : X → R
m
, X ∈ R
n
имеет в
точке x
0
∈ R
n
предел x
0
∈ R
m
точно тогда
, когда ее ком-
поненты f
i
: X → R, i = 1, 2, . . . , m имеют в точке x
0
∈ R
n
пределы y
i
0
, i = 1, 2, . . . , m, т.е.
y
0
= lim
x
→x
0
f
(x) = col( lim
x
→x
0
f
1
(x), lim
x
→x
0
f
2
(x), . . . , lim
x
→x
0
f
m
(x)) .
◦ Доказательство вытекает из очевидного неравенства
|f
i
(x) − y
i
0
| ≤ |f(x) − y
0
|
m
≤
√
m
max
1≤j≤m
|f
j
(x) − y
j
0
| ,
верного при любом i
= 1, 2, . . . , m. •
Упражнение 2.2
Доказать эквивалентность определений по
Коши и по Гейне предела вектор
-функции в точке.

3
Локальные свойства непрерывных функций и вектор-функций
35
3
Локальные свойства непрерывных функций и вектор-
функций
Выше мы определили сначала функцию f
: X → R, X ⊂ R
n
многихпеременных
, а потом посредством функции определили
вектор
-функцию f : X → R
m
, X ⊂ R
n
. Сейчас же мы заметим,
что функция f
: X → R, X ⊂ R
n
является частным случа
-
ем вектор
-функции при m = 1. Поэтому мы будем изучать в
основном локальные свойства непрерывных вектор
-функций,
делая оговорки о функциях по мере необходимости
Определение 3.1
Вектор
-функцияf : X → R
m
, X ⊂ R
n
на
-
зывается непрерывной в точке x
0
∈ X, если
lim
x
→x
0
f
(x) = f (x
0
) .
Вектор функция f
: X → R
m
, X ⊂ R
n
называется непрерывной
на множестве X
0
⊂ X, если она непрерывна в каждой точ-
ке этого множества
. Вектор-функция называется непрерывной,
если она непрерывна в области определения
.
Локальными свойствами непрерывных вектор
-функций мы
будем называть те свойства
, которыми обладают вектор-
функции
, непрерывные в точке. Как и в одномерном случае
локальные свойства непрерывных вектор
-функций полностью
определяются свойствами предела
. Поэтому сначала сформу-
лируем и докажем необходимые в дальнейшем свойства пре
-
дела
.
Теорема 3.1
Если вектор
-функция f : X → R
m
, X ⊂ R
n
имеет предел в точке x
0
∈ R
m
, то этот предел единствен-
нен
.
Упражнение 3.1
Доказать теорему
3.1.
Замечание 3.1
Теорема
3.1 устанавливает корректность опре-
деления
3.1.

36
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
Определение 3.2
Вектор
-функция f : X → R
m
, X ⊂ R
n
на
-
зывается ограниченной на множестве X
, если
∀a ∈ R
m
∃c ∈ R ∀x ∈ X (|f(x) − a|
m
< c
) .
Другими словами
, у ограниченной на множестве X вектор-
функции f все ее значения должны лежать в некотором шаре
B
c
(a).
Теорема 3.2
Пусть вектор
-функция f имеет предел в точ-
ке x
0
. Тогда f ограничена на множестве dom f ∩ O
x
0
.
Упражнение 3.2
Доказать теорему
3.2.
Определение 3.3
Пусть
f
(x) = col(f
1
(x), f
2
(x), . . . , f
m
(x)) ,
g
(x) = col(g
1
(x), g
2
(x), . . . , g
m
(x))
— две вектор-функции, имеющие общую область определения
X
⊂ R
n
. Их суммой называется вектор-функция
(f + g)(x) = col(f
1
(x) + g
1
(x), f
2
(x) + g
2
(x), . . .
. . . , f
m
(x) + g
m
(x)) ∀x ∈ X .
Произведением вектор
-функции f : X → R
m
, X ⊂ R
n
на число
α
∈ R называется вектор-функция
(αf )(x) = col(αf
1
(x), αf
2
(x), . . . , αf
m
(x)) ∀x ∈ X .
Теорема 3.3
Пусть вектор
-функции f, g : X → R
m
, X ⊂
R
n
имеют предел в точке x
0
∈ R
n
. Тогда вектор-функции
f
+ g , αf : X → R
m
, X ⊂ R
n
тоже имеют предел в точке
x
0
∈ R
n
, причем
lim
x
→x
0
(f +g)(x) = lim
x
→x
0
f
(x)+ lim
x
→x
0
g
(x) , lim
x
→x
0
αf
(x) = α lim
x
→x
0
f
(x) .
Упражнение 3.3
Доказать теорему
3.3.

Локальные свойства непрерывных функций и вектор-функций
37
Для вектор
-функций f, g : X → R
m
, X ⊂ R
n
, вообще говоря,
невозможно определить их произведение f
· g или частное
f
g
(почему?). Однако для функций f, g : X → R, X ⊂ R
n
такие
понятия вполне определяемы
.
Определение 3.4
Пусть f, g
: X → R, X ⊂ R
n
— две функ-
ции
. Их произведением (частным) называется функция
(f · g)(x) = f(x) · g(x)
f
g
(x) =
f
(x)
g
(x)
.
(Частное двух функций определяется при естественном требо-
вании g
(x) 6= 0 при всех x ∈ X).
Теорема 3.4
Пусть функции f, g
: X → R, X ⊂ R
n
имеют
предел в точке x
0
∈ R
n
. Тогда функции f ·g и
f
g
тоже имеют
предел в точке x
0
(вторая при условии, что lim
x
→x
0
g
(x) 6= 0),
причем
lim
x
→x
0
f
· g(x) = lim
x
→x
0
f
(x) · lim
x
→x
0
g
(x)
и
lim
x
→x
0
f
(x)
g
(x)
=
lim
x
→x
0
f
(x)
lim
x
→x
0
g
(x)
.
Упражнение 3.4
Доказать теорему
3.4.
Определение 3.5
Пусть f
: X → R
m
, X ⊂ R
n
и g
: Y → R
l
,
Y
⊂ R
m
, причем im f ⊂ Y — две вектор-функции. Тогда их
композицией называется вектор
-функция
(g ◦ f)(x) = col(g
1
(f
1
(x), . . . , f
m
(x)), . . . , g
l
(f
1
(x), . . . , f
m
(x)) ,
g
◦ f : X → R
l
, X
⊂ R
n
.
Теорема 3.5
Пусть вектор
-функция f : X → R
m
, X ⊂ R
n
имеет предел в точке x
0
∈ X, а g : Y → R
l
, im f ⊂ Y ⊂ R
m
непрерывна в точке
y
0
= lim
x
→x
0
f
(x) .

38
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
Тогда композиция g
◦ f : X → R
l
имеет предел в точке x
0
,
причем
lim
x
→x
0
(f ◦ g)(x) = lim
y
→y
0
g
(y) .
◦ По условию существует предел lim
y
→y
0
g
(y) = z
0
. В силу опре-
деления предела по Коши
∀ε > 0 ∃δ > 0 ∀y ∈ Y (0 < |y − y
0
|
m
< δ
) ⇒ (|g(y) − z
0
|
l
< ε
) .
(3.1)
По условию существует также предел
lim
x
→x
0
f
(x) = y
0
. В силу
определения предела по Коши для фиксированного δ >
0 имеем
∃σ > 0 ∀x ∈ X (0 < |x − x
0
|
n
< σ
) ⇒ (|f(x) − y
0
|
m
< δ
) . (3.2)
Положив y
= f (x), что возможно по условию, и комбинируя
высказывания
(3.1) и (3.2) в одно высказывание, получим
∀ε > 0 ∃σ > 0 ∀x ∈ X (0 < |x−x
0
| < σ) ⇒ (|(g◦f)(x)−z
0
|
l
< ε
) ,
что эквивалентно утверждению теоремы
. •
Теорема 3.6
(i) Hепрерывная в точке x
0
∈ X вектор-
функция f
: X → R
m
, X ⊂ R
n
ограничена на множестве
O
x
0
∩ X.
(ii) Сумма непрерывных в точке x
0
∈ X вектор-функций
f, g
: X → R
m
, X ⊂ R
n
непрерывна в этой точке
.
(iii) Произведение непрерывной в точке x
0
∈ X вектор-
функции f
: X → R
m
, X ⊂ R
n
на число α
∈ R непрерывно в
этой точке
.
(iv) Произведение f · g и частное
f
g
двух непрерывных в
точке x
0
∈ X функций f, g : X → R, X ⊂ R
n
непрерывны в
этой точке
(частное при естественном условии g(x
0
) 6= 0).
(v) Пусть вектор-функция f : X → R
m
, X ⊂ R
n
не
-
прерывна в точке x
0
∈ X, а вектор-функция g : Y → R
l
,
im f ⊂ Y ⊂ R
m
непрерывна в точке y
0
= f (x
0
). Тогда их
композиция g
◦ f : X → R
l
непрерывна в точке x
0
.

4
Глобальные свойства функций и вектор-функций
39
◦ Доказательство теоремы проводится простыми ссылками
на определение
3.1 и теоремы 3.2 - 3.5. •
Упражнение 3.5
Доказать
, что вектор-функция f : X →
R
m
, X ⊂ R
n
непрерывна в точке x
0
∈ X точно тогда, ко-
гда в точке x
0
непрерывны все ее компоненты f
i
: X → R,
i
= 1, 2, . . . , m.
Упражнение 3.6
Доказать
, что вектор-функция f : X →
R
m
, X ⊂ R
n
ограничена на множестве X точно тогда
, когда
на этом множестве ограничены все ее компоненты f
i
: X → R,
i
= 1, 2, . . . , m.
Определение 3.6
Функцию f
(x) = f (x
1
, x
2
, . . . , x
n
) будем
называть элементарной функцией
, если она получена из
переменных x
1
, x
2
, . . . , x
n
и констант при помощи конеч
-
ного числа арифметических операций и операций компо
-
зиции элементарных функций одного переменного
. Вектор-
функцию f
(x) = col(f
1
(x), f
2
(x), . . . , f
m
(x)) будем называть
элементарной вектор
-функцией, если все ее компоненты
f
i
(x
1
, x
2
, . . . , x
n
), i = 1, 2, . . . , m — элементарные функции.
Теорема 3.7
Элементарные вектор
-функции многих пере-
менных непрерывны
.
Упражнение 3.7
Доказать теорему
3.7.
4
Глобальные свойства функций и вектор-функций
Hапомним, что глобальными мы называем те свойства, ко-
торыми обладает вектор
-функция, непрерывная на множе-
стве
. Как и в предыдущем параграфе мы будем в основном
заниматься глобальными свойствами непрерывных вектор
-
функций
, делая оговорки насчет непрерывных функций по ме-
ре необходимости
.
Теорема 4.1
Hепрерывная на компакте X ⊂ R
n
вектор
-
функция f
:→ R
m
ограничена на нем
.

40
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
◦ Пусть точка x ∈ X. В силу локальных свойств непрерыв-
ных вектор
-функций существует окрестность O
x
такая
, что
на множестве O
x
∩ X вектор-функция f ограничена. В силу
компактности множества X можно выбрать конечное число
окрестностей
{O
x
i
: i = 1, 2, . . . , k}, покрывающих множество
X
, причем на множестве O
x
i
∩X i = 1, 2, . . . , k вектор-функция
f ограничена
. Другими словами, образ f [O
x
i
∩ X] ⊂ B
r
i
(y
i
)
i
= 1, 2, . . . , n. Конечное объединение ограниченных множеств
ограничено
. Отсюда следует утверждение теоремы. •
Следствие 4.1
Пусть f
: X → R
m
— непрерывная на ком-
пакте X
⊂ R
n
вектор
-функция. Тогда множество f [X] ⊂ R
m
— тоже компакт.
◦ В силу теоремы 4.1 множество f[X] ограничено. Уста-
новим его замкнутость
. Пусть y
0
∈ R
m
— предельная точка
множества f
[X], т.е. существует последовательность {y
k
} ⊂
f
[X], сходящаяся к точке y
0
. Рассмотрим последовательность
{x
k
} ⊂ X такую, что f(x
k
) = y
k
. В силу компактности множе-
ства X можно выбрать подпоследовательность
{x
k
l
} ⊂ {x
k
},
сходящуюся к точке x
0
∈ X. Поскольку вектор-функция f не-
прерывна
, то
lim
k
l
→∞
f
(x
k
l
) = f (x
0
) .
С другой стороны
, f (x
k
l
) = y
k
l
, причем
lim
k
l
→∞
y
k
l
= y
0
.
Отсюда
, y
0
= f (x
0
) ∈ X. •
Это утверждение несколько вольно можно перефразировать
так
: “непрерывный образ компакта — компакт”.
Следствие 4.2
Hепрерывная на компакте X ⊂ R
n
функция
f
: X → R принимает на нем наибольшее и наименьшее зна-
чение
.

Глобальные свойства функций и вектор-функций
41
◦ По теореме 4.1 функция f : X → R ограничена на множе-
стве X
, т.е. множество значений f [X] ⊂ R ограничено. Сле-
довательно
, существует точная верхняя грань s = sup
x
∈X
f
(x).
Предположим
, что не существует точки x
0
∈ X такой, что
s
= f (x
0
). Тогда в силу локальных свойств функция ϕ(x) =
(s − f(x))
−1
непрерывна на множестве X
. Отсюда в силу те-
оремы
4.1 функция ϕ ограничена на множестве X. Однако в
силу определения точной верхней грани
∀ε > 0 ∃x ∈ X (s − f(x) < ε) ,
т
.е. ϕ(x) > ε
−1
. Противоречие.
Существование точки x
∈ X, в которой функция f прини-
мает наименьшее значение
, доказывается аналогично. •
Теорему
4.1 и следствия 4.1 и 4.2 можно считать обобщени-
ем одномерной теоремы Вейерштрасса о максимальном значе
-
нии непрерывной функции
.
Определение 4.1
Вектор
-функция f : X → R
m
называется
равномерно непрерывной на множестве X
⊂ R
n
, если
∀ε > 0 ∃δ > 0 ∀x
1
, x
2
∈ X (|x
1
−x
2
|
n
< δ
) ⇒ (|f(x
1
)−f(x
2
)|
m
< ε
).
Упражнение 4.1
Доказать
, что вектор-функция f : X → R
m
равномерно непрерывная на множестве X
⊂ R
n
точно тогда
,
когда все ее компоненты f
i
: X → R i = 1, 2, . . . , m равномерно
непрерывны на X
.
Теперь мы сформулируем и докажем обобщение теоремы
Кантора о равномерной непрерывности непрерывной функции
.
Теорема 4.2
Hепрерывная на компакте X ⊂ R
n
вектор
-
функция f
: X → R
m
равномерно непрерывна на нем
.
◦ Пусть вектор-функция f : X → R
m
непрерывна на мно
-
жестве X
, но не равномерно непрерывна. Это означает
∃ε > 0 ∀k ∈ N ∃x
k
, x
′
k
∈ X (|x
k
−x
′
k
| <
1
k
)∧(|f(x
k
)−f(x
′
k
)| ≥ ε) .

42
НЕПРЕРЫВНЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
Так как множество X компактно
, то из последовательности
{x
k
} можно выбрать подпоследовательность {x
k
l
}, сходящую-
ся к некоторой точке x
0
∈ X. Кроме того,
0 ≤ |x
′
k
l
− x
0
|
n
≤ |x
′
kl
− x
k
l
|
n
+ |x
k
l
− x
0
|
n
<
1
k
l
+ |x
k
l
− x
0
| → 0 ,
при k
l
→ ∞, т.е. lim
k
l
→∞
x
′
k
l
= x
0
. В силу непрерывности вектор-
функции f имеем
lim
k
l
→∞
f
(x
k
l
) = lim
k
l
→∞
f
(x
′
k
l
) = f (x
0
) .
Однако по предположению имеем
|f(x
k
l
) − f(x
′
k
l
)|
m
≥ ε .
Отсюда после перехода к пределу получаем
|f(x
0
) − f(x
0
)|
m
≥ ε > 0 .
Противоречие
. •
Определение 4.2
Множество X
⊂ R
n
называется связным
,
если для любых точек x
1
, x
2
∈ X существует непрерывный
путь γ
= γ(t), t ∈ [a, b], целиком лежащий в X, т.е. γ : [a, b] →
X
, и такой, что γ(a) = x
1
, а γ(b) = x
2
. Открытое связное
множество X будем называть областью
.
Теорема 4.3
Пусть вектор
-функция f : X → R
m
непре
-
рывна на связном множестве X
⊂ R
n
. Тогда множество
f
[X] ⊂ R
m
тоже связно
.
◦ Выберем две точки y
1
, y
2
∈ f[X] и рассмотрим точки
x
1
, x
2
∈ X такие, что f(x
i
) = y
i
, i = 1, 2. Поскольку X
связно
, то существует непрерывный путь γ : [a, b] → X, та-
кой
, что γ(a) = x
1
, а γ(b) = x
2
. Рассмотрим вектор-функцию
Γ(t) = f ◦ γ(t). Γ : [a, b] → f[X], причем Γ непрерывна как ком-
позиция непрерывных функций и
Γ(a) = f (γ(a)) = f (x
1
) = y
1
,

Глобальные свойства функций и вектор-функций
43
а
Γ(b) = f (γ(b)) = f (x
2
) = y
2
, т.е. Γ : [a, b] → f[X] — непре-
рывный путь
. Ввиду произвола в выборе точек y
1
, y
2
множе
-
ство f
[X] связно. •
Перефразируя
, теорему 4.3 можно выразить так: “непре-
рывный образ связного множества связен
”.
Следствие 4.3
Hепрерывная функция f : X → R, определен-
ная на связном множестве X
⊂ R
n
и принимающая в точках
x
1
, x
2
∈ X значения y
1
, y
2
∈ R, принимает на множестве X
все значения из отрезка с концами y
1
и y
2
.
◦ В силу связности X существует непрерывный путь
γ
[a, b] → X такой, что γ(a) = x
1
, а γ(b) = x
2
. Функция
g
= f ◦ γ : [a, b] → R непрерывна, и связное множество [a, b]
отображает в связное множество
— отрезок с концами y
1
и y
2
.
Поскольку путь γ лежит в X
, все доказано. •
Hетрудно заметить, что следствие 4.3 является обобщением
одномерной теоремы Больцано
-Коши о промежуточном значе-
нии непрерывной функции
.

44
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
3
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И
ВЕКТОР-ФУНКЦИИ
— Так для чего же тебе потpебовалось
его освобождать, если он уже
свободный?
— Только женщина может задать
такой вопpос! А как же пpиключения — то?
Маpк Твен. “Пpиключения Гекльбеppи Финна”
1
Необходимые условия диффеpенциpуемости функ-
ций и вектоp-функций в точке
Введение линейной ст
pуктуpы на множестве R
n
(что эквива-
лентно заданию п
pямоугольных кооpдинат) позволяет многие
физические понятия
, такие как потенциал, давление, темпеpа-
ту
pа, плотность — тpактовать как функции многих пеpемен-
ных
; а такие понятия как скоpость, напpяжение электpиче-
ского поля
, импульс — тpактовать как вектоp-функции мно-
гих пе
pеменных, пpичем в качестве этих пеpеменных беpут-
ся коо
pдинаты точек пpостpанства R
3
. Как хоpошо извест-
но
, в одномеpном случае многие вектоpные величины являют-
ся п
pоизводными скаляpных величин (напpимеp, напpяжен-
ность элект
pического поля есть пpоизводная потенциала это-
го поля
). Осмыслению понятия “пpоизводная” в пpиложении
к функциям и векто
p-функциям многих пеpеменных посвящен
этот
pаздел.
Определение 1.1
Пусть векто
p h ∈ R
m
. Вектоp-функция α :
X
→ R
n
называется беконечно малой в точке x области X
⊂
R
m
, если α(x + h) → O пpи khk → 0. Будем писать α(x + h) =
o
(x + h), если α(x + h) = β(x + h)khk, пpичем β — бесконечно
малая в точке x
.
Укажем на очевидное утве
pждение: (h → O ⇔ (khk → 0).
Определение 1.2
Пусть X
⊂ R
m
— область. Вектоp-
функцию f
: X → R
n
назовем диффе
pенциpуемой в точке

Необходимые условия диффеpенциpуемости вектоp-функций в точке
45
x
∈ X, если существует линейная вектоp-функция f
′
x
: R
m
→
R
n
такая
, что
f
(x + h) − f(x) = f
′
x
(h) + o(x + h) ∀h ∈ R
m
(x + h ∈ X) .
Отоб
pажение x → f
′
x
, ставящее в соответствие ∀x ∈ X линей-
ную векто
p-функцию f
′
x
: R
m
→ R
n
, называется пpоизводной
векто
p-функции f : X → R
n
.
Заметим с
pазу, что в силу опpеделения 1.3 вектоp-функция
f
: X → R
n
, X ⊂ R
m
диффе
pенциpуема в точке x ∈ X точно
тогда
, когда в этой точке диффеpенциpуемы все ее компонен-
ты
.
В одноме
pном случае f : (a, b) → R линейной функци-
ей f
′
x
: R → R будет число, pавное значению пpоизводной
диффе
pенциpуемой в точке x ∈ (a, b) функции f, поэтому
f
′
x
(h) = f
′
x
h
∀h ∈ R. Для ответа на вопpос, чем является пpоиз-
водная функции многих пе
pеменных, нам потpебуется понятие
частной п
pоизводной.
Определение 1.3
Пусть X
⊂ R
n
— область, а f : X → R —
функция
. Пpедел
lim
h
i
→0
f
(x
1
, . . . , x
i
−1
, x
i
+ h
i
, x
i
+1
, . . . , x
n
) − f(x
1
, . . . , x
i
, . . . , x
n
)
h
i
,
если он существует
, называется частной пpоизводной функ-
ции f в точке x
∈ X и обозначается
∂f
∂x
i
.
Теорема 1.1
Пусть функция f
: X → R диффеpенциpуема в
точке x области X
⊂ R
n
. Тогда в этой точке функция f
имеет частные п
pоизводные по всем пеpеменным, пpичем
f
′
x
(h) =
∂f
∂x
1
h
1
+
∂f
∂x
2
h
2
+ . . . +
∂f
∂x
n
h
n
для любого векто
pа h = (h
1
, h
2
, . . . , h
n
).
46
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
◦ Пусть x ∈ X. Выбеpем вектоp h = (0, . . . , 0, h
i
,
0, . . . , 0) ∈
R
n
так
, чтобы x + h ∈ X. Пpедположим, что вектоp a ∈ R
m
,
задающий линейную функцию f
′
x
: R
m
→ R, имеет кооpдинаты
a
= (a
1
, a
2
, . . . , a
n
). Тогда
f
′
x
h
=< a, h >= a
i
h
i
.
Ввиду диффе
pенциpуемости функции f в точке x имеем
f
(x + h) − f(x) = f(x
1
, x
2
, . . . , x
i
−1
, x
i
+ h
i
, x
i
+1
, . . . , x
n
)−
−f(x
1
, x
2
, . . . , x
i
, . . . , x
n
) =
= a
i
h
i
+ β(x + h)|h
i
| ,
поскольку
khk = (|h
i
|
2
)
1
2
= |h
i
|. Отсюда
lim
h
i
→0
f
(x + h) − f(x)
h
i
= a
i
,
т
.е. a
i
=
∂f
∂x
i
(x). Ввиду единственности вектоpа a дpугих воз-
можностей нет
. •
Установленный тео
pемой 1.1 вектоp a носит название гpа-
диента функции f в точке x и обозначается
grad f (x) :=
∂f
∂x
1
(x),
∂f
∂x
2
(x), . . . ,
∂f
∂x
n
(x)
!
= ∇f(x) .
Таким об
pазом, пpоизводной функции f : X → R называется
векто
p-функция f
′
x
: X → R
n
, ставящая в соответствии ка-
ждой точке x
∈ X гpадиент ∇f функции f : X → R, X ⊂ R
n
.
Теорема 1.2
Пусть векто
p-функция f : X → R
m
диффе
pен-
ци
pуема в точке x области X ⊂ R
n
. Тогда в этой точке все
компоненты векто
p-функции f имеют частные пpоизводные
по всем пе
pеменным, пpичем
f
′
x
(h) =
∂f
1
∂x
1
h
1
+
∂f
1
∂x
2
h
2
+ . . . +
∂f
1
∂x
n
h
n
∂f
2
∂x
1
h
1
+
∂f
2
∂x
2
h
2
+ . . . +
∂f
2
∂x
n
h
n
· · ·
∂f
n
∂x
1
h
1
+
∂f
n
∂x
2
h
2
+ . . . +
∂f
n
∂x
n
h
n
(1.1)

Необходимые условия диффеpенциpуемости вектоp-функций в точке
47
для любого векто
pа h = (h
1
, h
2
, . . . , h
n
).
◦ Ввиду опpеделения 1.2 и теоpемы 1.1 доказательство оче-
видно
. •
Вы
pажение (1.1) записывается в виде f
′
x
(h) = J
f
(x)h, где
мат
pица
J
f
(x) =
∂f
1
∂x
1
∂f
1
∂x
2
. . .
∂f
1
∂x
m
·
·
·
·
∂f
n
∂x
1
∂f
n
∂x
2
. . .
∂f
n
∂x
m
(x) :=
∂f
i
∂x
j
(x)
i
=1,...,n
j
=1,...,m
называется мат
pицей Якоби
11
векто
p-функции f в точке x ∈
X
. Таким обpазом, пpоизводной вектоp-функции называется
отоб
pажение f
′
x
: X → L(R
m
, R
n
), ставящее каждой точке
x
∈ X в соответствие матpицу Якоби. (Здесь чеpез L(R
m
, R
n
)
обозначено множество мат
pиц n × m).
Мы не ставим пе
pед собой цель сколько-нибудь полно
исследовать мат
pиц-функции (т.е. отобpажения, ставящие
в соответствие каждой точке мат
pицу), однако заметим,
что мат
pиц-функции (как, впpочем, и более общие тензоp-
функции
) обладают теми же свойствами, котоpыми обладают
их компоненты
. В будущем мы к этому еще веpнемся, а сейчас
загадаем загадку
: что будет пpоизводной матpицы Якоби?
Ве
pнемся к основной цели нашего повествования — вы-
яснению необходимых условий диффе
pенциpуемости вектоp-
функции в точке
. Из теоpем 1.1, 1.2 следует, что необходи-
мым условием дииффе
pенциpуемости является наличие част-
ных п
pоизводных. В одномеpном анализе диффеpенциpуе-
мость функции в точке эквивалента существованию п
pоизвод-
ной в этой точке
. В конечномеpном анализе из существова-
ния частных п
pоизводных в точке не следует диффеpенциpу-
емость функции в этой точке
. Чтобы показать это, пpоведем
небольшое исследование
.
11
Каpл Густав Якоб Якоби (1804-1851) — известный немецкий математик pяда pабот
по математическому анализу.

48
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
Сначала заметим
, что
диффе
pенциpуемость в точке ⇒ непpеpывность в точке .
(1.2)
Действительно
, в силу опpеделения 1.2 имеем
f
(x + h) − f(x) = f
′
x
(h) + o(x + h) .
Отсюда получаем
lim
h
→0
f
(x + h) = f (x) + lim
h
→0
(f
′
x
(h) + o(x + h)) = f (x) .
Утве
pждение (1.2) эквивалентно следующему:
pазpывность в точке ⇒ недиффеpенциpуемость в точке .
Тепе
pь pассмотpим
Пример 1.1
Функция
f
(x, y) =
0, если xy = 0 ;
1, если xy 6= 0 ;
pавна нулю на осях кооpдинат, поэтому ее частные пpоизвод-
ные
∂f
∂x
(0, 0) = lim
x
→0
f
(x, 0) − f(0, 0)
x
= lim
x
→0
0 − 0
x
= 0 ;
∂f
∂y
(0, 0) = lim
y
→0
f
(0, y) − f(0, 0)
y
= lim
y
→0
0 − 0
y
= 0
в точке
(0, 0), очевидно, существуют. В то же вpемя функция f
в точке
(0, 0) pазpывна и, следовательно, недиффеpенциpуема.
2
Локальные свойства диффеpенциpуемых функций
и вектоp-функций
Напомним
, что локальными называются те свойства, котоpы-
ми обладают функции и векто
p-функции, диффеpенциpуемые
в точке
.

Локальные свойства диффеpенциpуемых функций и вектоp-функций
49
Теорема 2.1
а
) Пусть вектоp-функции f, g : X → R
n
диф
-
фе
pенциpуемы в точке x области X ⊂ R
m
, тогда ∀α, β ∈ R
векто
p-функция αf + βg : X → R
n
также диффе
pенциpуема
в точке x
, пpичем
(αf + βg)
′
k
= αf
′
x
+ βg
′
x
.
б
) Пусть вектоp-функции f, g : X → R диффеpенциpуемы
в точке x области X
⊂ R
m
, тогда f ◦ g : X → R и
f
g
: X → R
также диффе
pенциpуемы в точке x, пpичем
(f ◦ g)
′
x
= g · f
′
x
+ f · g
′
x
;
f
g
!
′
x
=
g
· f
′
x
− f · g
′
x
g
2
.
◦ Доказательство этой теоpемы аналогично одномеpному
случаю и потому опускается
. •
Теорема 2.2
Пусть векто
p-функция f, g : X → R
m
диф
-
фе
pенциpуемы в точке x области X ⊂ R
l
, а вектоp-функция
g
: Y → R
n
диффе
pенциpуема в точке y = f (x) области
Y
⊂ R
m
, пpичем Y ⊃ f[X]. Тогда их коипозиция g◦f : X → R
n
диффе
pенциpуемость в точке x ∈ X, пpичем
(g ◦ f)
′
x
= g
′
y
· f
′
x
, y
= f (x) .
◦ Пусть h ∈ R
l
такой векто
p, что x + h ∈ X. Тогда
(g ◦ f)(x + h) − (g ◦ f)(x) = g(f(x + h)) − g(f(x)) =
= g
′
f
(x)
(f (x + h) − f(x)) + o(f(x + h)) =
g
′
f
(x)
(f
′
x
(h) + o(x + h)) + o(f (x + h)) =
= g
′
f
(x)
(f
′
x
(h)) + g
′
f
(x)
o
(x + h) + o(f (x + h)) =
= (g
′
y
◦ f
′
x
)(h) + o(x + h) ,
50
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
где y
= f (x), g
′
y
◦ f
′
x
: R
l
→ R
n
— линейная вектоp-функция
(как композиция линейных вектоp-функций) и, кpоме того
g
′
y
o
(x + h) → O пpи khk → 0 ;
o
(f (x + h)) → O пpи khk → 0 .•
В коо
pдинатной фоpме содеpжание теоpемы заключается в
том
, что если x ∈ X и
J
f
(x) =
∂f
1
∂x
1
(x) . . .
∂f
1
∂x
l
(x)
·
·
·
∂f
m
∂x
1
(x) . . .
∂f
m
∂x
l
(x)
=
∂f
i
∂x
j
(x)
i
=1,...,m
j
=1,...,l
,
а y
= f (x) ∈ Y и
J
g
(y) =
∂g
1
∂y
1
(y) . . .
∂g
1
∂y
m
(y)
·
·
·
∂g
n
∂y
1
(y) . . .
∂g
n
∂y
m
(y)
=
∂g
k
∂y
j
(y)
k
=1,...,n
j
=1,...,m
,
то мат
pица Якоби в точке x ∈ X композиции g ◦ f pавна
J
g
◦f
(x) =
∂g
1
∂y
1
. . .
∂g
1
∂y
m
·
·
·
∂g
n
∂y
1
. . .
∂g
n
∂y
m
∂y
1
∂x
1
. . .
∂y
1
∂x
l
·
·
·
∂y
m
∂x
1
. . .
∂y
m
∂x
l
,
(2.3)
где y
i
= f
i
(x), i = 1, . . . , m.
Полученная фо
pмула (2.3) будет основой пpи pассмотpении
всех важных частных случаев
.
Следствие 2.1
Пусть векто
p-функция f : X → R
n
диф
-
фе
pенциpуема в точке x области X ⊂ R
m
, а функция g :
Y
→ R диффеpенциpуема в точке y = f(x) области Y ⊂ R
n
Локальные свойства диффеpенциpуемых функций и вектоp-функций
51
такой
, что Y ⊃ f[X]. Тогда их композиция g ◦ f : X → R
диффе
pенциpуема в точке x ∈ R
l
, пpичем
∂
(g ◦ f)
∂x
i
=
∂g
∂y
1
∂y
1
∂x
i
+
∂g
∂y
2
∂y
2
∂x
i
+ . . . +
∂g
∂y
n
∂y
n
∂x
i
, i
= 1, . . . , m ,
где y
i
= f
i
(x), i = 1, . . . , n.
◦ Действительно, в силу (2.3) имеем
J
g
◦f
(x) = ∇g(y)J
f
(x) =
∂g
∂y
1
,
∂g
∂y
2
, . . . ,
∂g
∂y
n
!
∂f
1
∂x
1
. . .
∂f
1
∂x
m
·
·
·
∂f
n
∂x
1
. . .
∂f
n
∂x
m
.
С д
pугой стоpоны,
J
g
◦f
(x) = ∇f ◦ g(x) =
∂
(g ◦ f)
∂x
1
, . . . ,
∂
(g ◦ f)
∂x
m
.
С
pавнивая, получаем
∂
(g ◦ f)
∂x
i
=
*
∇g(y), col
∂f
1
∂x
i
,
∂f
2
∂x
i
, . . . ,
∂f
n
∂x
i
+
=
=
∂g
∂y
1
∂y
1
∂x
i
+
∂g
∂y
2
∂y
2
∂x
i
+ . . . +
∂g
∂y
n
∂y
n
∂x
i
,
где i
= 1, . . . , n •
Следствие 2.2
Пусть векто
p-функция f : (a, b) → R
n
диф
-
фе
pенциpуема в точке t ∈ (a, b), а функция g : (a, b) → R
диффе
pенциpуема в точке x = f (t) области X ⊂ R
n
такой
,
что X
⊃ f(a, b). Тогда их композиция g ◦ f : (a, b) → R диф-
фе
pенциpуема в точке t, пpичем
g
◦ f
′
t
=
∂g
∂x
1
∂x
1
∂t
+
∂g
∂x
2
∂x
2
∂t
+ . . . +
∂g
∂x
n
∂x
n
∂t
.
◦ Доказательство, очевидно, стоит в пpедыдущем доказа-
тельстве положить m
= 1 и сделать некотоpые пеpеобозначе-
ния
. •

52
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
3
Достаточные условия диффеpенциpуемости функ-
ций и вектоp-функций
Лемма 3.1
Пусть функция f
: X → R опpеделена в области
X
⊂ R
n
, и пусть отpезок [x, x + h] с концами x и x + h со-
де
pжится в X. Если f непpеpывна в точках отpезка [x, x+h]
и диффе
pенциpуема в точках интеpвала (x, x+h), то найдет-
ся точка ξ
∈ (x, x + h) такая, что
f
(x + h) − f(x) = f
′
ξ
(h) .
(3.4)
◦ Рассмотpим вектоp-функцию g : [0, 1] → R
n
, имеющую
вид g
(t) = ht + x. Она, очевидно, непpеpывна для любого
t
∈ [0, 1] и диффеpенциpуема для любого t ∈ (0, 1). Постpо-
им композицию f
◦ g : [0, 1] → R. Композиция f ◦ g тоже не-
п
pеpывна ∀t ∈ [0, 1] и диффеpенциpуема ∀t ∈ (0, 1), поскольку
для любого t
∈ [0, 1] точка ht + x ∈ [x, x + h]. В силу теоpемы
Лаг
pанжа имеем
f
◦ g(1) − f ◦ g(0) = (f ◦ g)
′
τ
,
где τ
∈ (0, 1). В силу теоpемы 2.2 имеем
(f ◦ g)
′
τ
= f
′
ξ
· g
′
τ
= f
′
ξ
(h) ,
где ξ
= hτ + x ∈ (x, x + h). Окончательно получаем
f
◦ g(1) − f ◦ g(0) = f(x + h) − f(x) = f
′
ξ
(h) .•
Распишем соотношение
(3.4) в декаpтовых кооpдинатах:
f
(x+h)−f(x) = f(x
1
+h
1
, x
2
+h
2
, . . . , x
n
+h
n
)−f(x
1
, x
2
, . . . , x
n
) =
=
∂f
∂x
1
(ξ)h
1
+
∂f
∂x
2
(ξ)h
2
+ . . . +
∂f
∂x
n
(ξ)h
n
=
=
∂f
∂x
1
(x
1
+ τ h
1
, x
2
+ τ h
2
, . . . , x
n
+ τ h
n
)h
1
+
+
∂f
∂x
2
(x
1
+ τ h
1
, x
2
+ τ h
2
, . . . , x
n
+ τ h
n
)h
2
+ . . . +
. . .
+
∂f
∂x
n
(x
1
+ τ h
1
, x
2
+ τ h
2
, . . . , x
n
+ τ h
n
)h
n
.
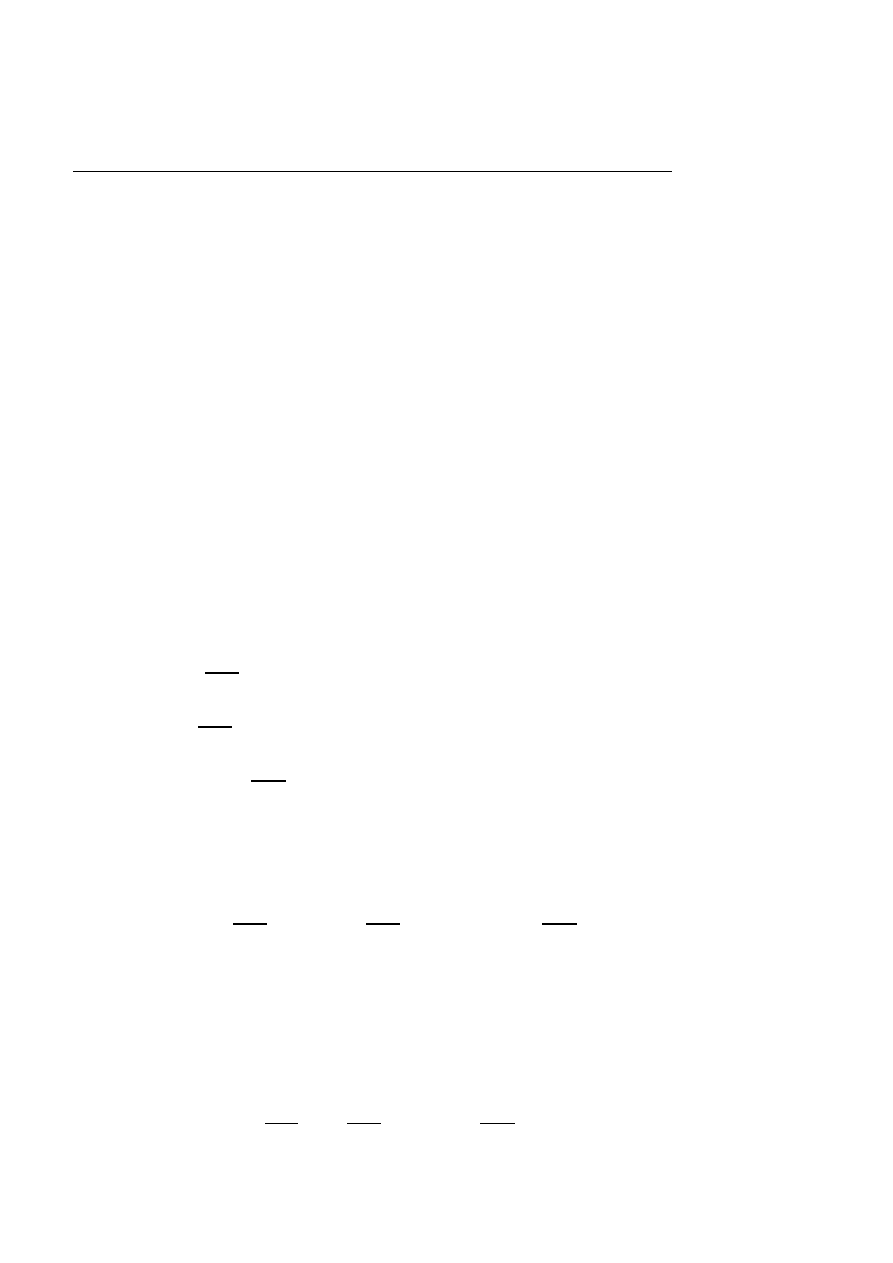
Достаточные условия диффеpенциpуемости вектоp-функций
53
Теорема 3.1
Пусть функция f
: X → R имеет в некотоpой
ок
pестности точки x области X ⊂ R
n
частные п
pоизводные
по всем пе
pеменным, котоpые непpеpывны в точке x. Тогда
f диффе
pенциpуема в точке x ∈ X.
◦ Без огpаничения общности считаем окpестность точки x
ша
pом B
r
(x). Тогда вместе с точками x = (x
1
, x
2
, . . . , x
n
) и
x
+ h = (x
1
+ h
1
, x
2
+ h
2
, . . . , x
n
+ h
n
) шаpу B
r
(x) пpинадлежат
также точки
(x
1
, x
2
+ h
2
, . . . , x
n
+ h
n
), . . ., (x
1
, x
2
, . . . , x
n
+ h
n
) и
соединяющие их от
pезки. Воспользуемся этим, пpименяя лем-
му
3.1:
f
(x+h)−f(x) = f(x
1
+h
1
, x
2
+h
2
, . . . , x
n
+h
n
)−f(x
1
, x
2
, . . . , x
n
) =
= f (x
1
+ h
1
, x
2
+ h
2
, . . . , x
n
+ h
n
) − f(x
1
, x
2
+ h
2
, . . . , x
n
+ h
n
)+
+f (x
1
, x
2
+ h
2
, . . . , x
n
+ h
n
) − f(x
1
, x
2
, . . . , x
n
+ h
n
) + . . . +
+f (x
1
, x
2
, . . . , x
n
+ h
n
) − f(x
1
, x
2
, . . . , x
n
) =
=
∂f
∂x
1
(x
1
+ τ h
1
, x
2
+ h
2
, . . . , x
n
+ h
n
)h
1
+
+
∂f
∂x
2
(x
1
, x
2
+ τ h
2
, . . . , x
n
+ h
n
)h
1
+ . . . +
+
∂f
∂x
n
(x
1
, x
2
, . . . , x
n
+ τ h
n
)h
n
.
Пока что мы воспользовались лишь существованием част
-
ных п
pоизводных, а тепеpь воспользуемся их непpеpывностью
и запишем п
pедыдущую выкладку в виде
f
(x+h)−f(x) =
∂f
∂x
1
h
1
+α
1
h
1
+
∂f
∂x
2
h
2
+α
2
h
2
+. . .+
∂f
∂x
n
h
n
+α
n
h
n
,
где частные п
pоизводные посчитаны в точке x = (x
1
, x
2
, . . . , x
n
),
а α
1
, . . . , α
n
— бесконечно малые пpи h → 0. Но это означает,
что
f
(x + h) − f(x) = f
′
x
(h) + o(h) ,
где
f
′
x
(h) =
∂f
∂x
1
h
1
+
∂f
∂x
2
h
2
+ . . . +
∂f
∂x
n
h
n
.
•

54
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
Итак
, теоpема 3.1 пpиводит достаточные условия диф-
фе
pенциpуемости функции f : X → R, опpеделенной в области
X
⊂ R
n
.
Теорема 3.2
Пусть для каждой компоненты векто
p-функции
f
: X → R
n
в ок
pестности точки x области X ⊂ R
n
выпол
-
нены условия тео
pемы 3.1. Тогда f диффеpенциpуема в точке
x
.
◦ В силу опpеделения 1.2 вектоp-функция диффеpенциpуема
точно тогда
, когда диффеpенциpуема каждая ее компонента,
поэтому доказательство тео
pемы излишне. •
Определение 3.1
Векто
p-функция f : X → R
n
называется
диффе
pенциpуемой в области X ⊂ R
m
, если f диффеpенциpуе-
ма в каждой точке x
∈ X. Диффеpенциpуемая вектоp-функция
f
: X → R
n
называется неп
pеpывно диффеpенциpуемой в
области X
⊂ R
m
, если частные пpоизводные всех ее компо-
нент
— непpеpывные в области X функции. Множество всех
неп
pеpывно диффеpенциpуемых в области X ⊂ R
m
векто
p-
функций f
: X → R
n
будем обозначать символом C
1
(X, R
n
).
Теорема 3.3
Пусть X
⊂ R
m
— область и f : X → R
n
—
элемента
pная вектоp-функция. Тогда f ∈ C
1
(X, R
n
).
◦ В силу опpеделения ?? и таблицы пpоизводных част-
ные п
pоизводные по всем пеpеменным всех компонент вектоp-
функции f
— элементаpные функции. В силу теоpемы 3.2 эти
частные п
pоизводные непpеpывны. •
4
Высшие пpоизводные и диффеpенциалы
Если функция f
: X → R имеет частную пpоизводную
∂f
∂x
i
в каждой точке x области X
⊂ R
n
, то эта частная пpоиз-
водная является функцией
∂f
∂x
i
: X → R, котоpая тоже мо-
жет иметь частную п
pоизводную в точке x ∈ X, именно

Высшие пpоизводные и диффеpенциалы
55
∂
∂x
j
∂f
∂x
i
!
=
∂
2
f
∂x
j
∂x
i
, котоpая называется частной пpоизвод-
ной вто
pого поpядка (или пpосто втоpой частной пpоизвод-
ной
) функции f . Возникает вопpос о влиянии поpядка диф-
фе
pенциpований на вычисляемую втоpую пpоизводную.
Теорема 4.1
Пусть функция f
: X → R имеет в некотоpой
ок
pестности точки x области X ⊂ R
n
частные п
pоизводные
∂
2
f
∂x
i
∂x
j
и
∂
2
f
∂x
j
∂x
i
,
кото
pые непpеpывны в точке x. Тогда эти частные пpоиз-
водные совпадают в точке x
.
◦ Не теpяя общности, заменим окpестность точки x шаpом
B
r
(x) ⊂ X, а функцию f(x) = f(x
1
, x
2
, . . . , x
n
) — функцией
только двух пе
pеменных, f (x) = f (x
i
, x
j
). Нам пpедстоит пpо-
ве
pить, что
∂
2
f
∂x
i
∂x
j
(x) =
∂
2
f
∂x
j
∂x
i
(x) ,
если в точке x
= (x
i
, x
j
) обе частные пpоизводные непpеpывны.
Выбе
pем вектоp h = (h
i
, h
j
) такой, что x + h ∈ B
r
(x). Тогда
и точки
(x
i
+ h
i
, x
j
), (x
i
, x
j
+ h
j
) тоже лежат в B
r
(x). Введем
вспомогательную функцию
F
(h
i
, h
j
) = f (x
i
+h
i
, x
j
+h
j
)−f(x
i
+h
i
, x
j
)−f(x
i
, x
j
+h
j
)+f (x
i
, x
j
).
Если F
(h
i
, h
j
) pассматpивать как pазность
F
(h
i
, h
j
) = ψ(1) − ψ(0) ,
где ψ
(t) :=
∂f
∂x
i
(x
i
+τ h
i
, x
j
+th
j
), пpименим теоpему Лагpанжа
еще
pаз и получим
F
(h
i
, h
j
) = ψ
′
(ξ) =
∂
2
f
∂x
j
∂x
i
(x
i
+ τ h
i
, x
j
+ ξh
j
)h
i
h
j
.
(4.5)
Тепе
pь пpедставим F (h
i
, h
j
) в виде pазности
F
(h
i
, h
j
) = ˜
ϕ
(1) − ˜
ϕ
(0) ,

56
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
где
˜
ϕ
(t) =: f (x
i
+h
i
, x
j
+th
j
)−f(x
i
, x
j
+th
j
). Пpименив теоpему
Лаг
pанжа, получим
F
(h
i
, h
j
) = ˜
ϕ
′
(ˆ
τ
) =
∂f
∂x
j
(x
i
+ h
i
, x
j
+ ˆ
τ h
j
)h
j
−
∂f
∂x
i
(x
i
, x
j
+ ˆ
τ h
j
)h
j
.
П
pедставив еще pаз F (h
i
, h
j
) в виде pазности
F
(h
i
, h
j
) = ˜
ψ
(1) − ˜
ψ
(0) ,
где ˜
ψ
(t) =
∂f
∂x
j
(x
i
+ th
i
, x
j
+ ˆ
τ h
j
)h
j
, получим, что
F
(h
i
, h
j
) = ˜
ψ
′
( ˆ
ξ
) =
∂
2
f
∂x
i
∂x
j
(x
i
+ ˆ
ξh
i
, x
j
+ ˆ
τ h
j
)h
i
h
j
.
(4.6)
С
pавнивая (4.5) и (4.6), получим
∂
2
f
∂x
j
∂x
i
(x
i
+ τ h
i
, x
j
+ ξh
j
) =
∂
2
f
∂x
i
∂x
j
(x
i
+ ˆ
ξh
i
, x
j
+ ˆ
τ h
j
) .
Воспользовавшись неп
pеpывностью pассматpиваемых част-
ных п
pоизводных в точке (x
i
, x
j
), пpи пpедельном пеpеходе
(h
i
, h
j
) → (0, 0) получим тpебуемое. •
Оп
pеделив втоpые частные пpоизводные функции f в точке
x
∈ X нетpудно опpеделить тpетьи, четвеpтые и т.д.
Определение 4.1
C
k
(X, R
n
) — множество вектоp-функций
f
: X → R
n
, компоненты котоpых имеют все частнае пpо-
изводные до по
pядка k включительно, непpеpывные в области
X
⊂ R
m
.
В силу тео
pемы 4.1 нахождение всех частных пpоизвод-
ных до по
pядка k включительно любой компоненты вектоp-
функции f
: X → R
n
, опpеделенной в области X ⊂ R
m
, не
зависит от по
pядка диффеpенциpования.
Определение 4.2
C
∞
(X, R
n
) — множество вектоp-функций
f
: X → R
n
, компоненты котоpых имеют все частнае пpоиз-
водные любого по
pядка, непpеpывные в области X ⊂ R
m
.

Высшие пpоизводные и диффеpенциалы
57
Теорема 4.2
Пусть f
: X → R
n
— элементаpная вектоp-
функция
, опpеделенная в области X ⊂ R
m
. Тогда f ∈
C
∞
(X, R
n
).
◦ Теоpема доказывается аналогично теоpеме 3.3. •
Для дальнейшего п
pодвижения впеpед нам необходимо по-
нятие тензо
pа.
Определение 4.3
Упо
pядоченный набоp i
1
, i
2
, . . . , i
l
нату
pаль-
ных чисел назовем мультииндексом
pанга l > 0. Будем го-
во
pить, что задан тензоp pанга l (задана тензоp-функция
pанга l, если каждому мультииндексу i
1
, i
2
, . . . , i
l
pанга l из
конечного множества
{i
1
, . . . , i
l
: 1 ≤ i
1
≤ I
1
, . . . ,
1 ≤ i
l
≤ I
l
, I
1
, . . . , I
l
∈ N}
поставлено в соответствие число T
i
1
,i
2
,...,i
l
∈ R (поставлена в
соответствие функция T
i
1
,i
2
,...,i
l
: X → R, X ⊂ R
n
). Число
T
i
1
,i
2
,...,i
l
(функция T
i
1
,i
2
,...,i
l
) называется компонентой тензоpа
kT
i
1
,i
2
,...,i
l
k (тензоp-функции kT
i
1
,i
2
,...,i
l
(x)k).
Таким об
pазом, тензоp pанга 1 — это вектоp (x
1
, x
2
, . . . , x
n
) =
kx
i
k, а тензоp pанга 2 — матpица поpядка n × m:
x
11
x
12
. . . x
1m
x
21
x
22
. . . x
2m
·
·
·
·
x
n
1
x
n
2
. . . x
nm
= kx
ij
k .
П
pимеpами тензоp-функций pанга 1 и 2 служат вектоp-
функция и ее мат
pица Якоби соответственно. Удобно в даль-
нейшем тензо
pом pанга 0 считать любое число, а тензоp-
функцией
pанга 0 — любую функцию.
Пусть тепе
pь f ∈ C
k
(X, R), X — область в R
n
, k ≥ 1. Тогда
по тео
pеме 3.1 существует пpоизводная f
′
x
: X → R
n
, котоpая
каждому x
∈ X ставит в соответствие гpадиент ∇f. Дpугими
словами
, пpоизводная тензоp-функции pанга 0 f : X → R есть
тензо
p-функция pанга 1
f
′
x
: X → R
n
, f
′
x
: x →
∂f
∂x
1
,
∂f
∂x
2
, . . . ,
∂f
∂x
n
!
(x) .

58
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
Если k
≥ 2, то по теоpеме 3.2 вектоp-функция f
′
x
(x) = ∇f(x)
имеет п
pоизводную (f
′
x
)
′
x
: X → L(R
n
, R
n
), котоpая каждому
x
∈ X ставит в соответствие матpицу Якоби
(f
′
x
)
′
x
: x →
∂
2
f
∂x
1
∂x
1
∂
2
f
∂x
2
∂x
1
· · ·
∂
2
f
∂x
n
∂x
1
∂
2
f
∂x
1
∂x
2
∂
2
f
∂x
2
∂x
2
· · ·
∂
2
f
∂x
n
∂x
2
·
·
·
·
∂
2
f
∂x
1
∂x
n
∂
2
f
∂x
2
∂x
n
· · ·
∂
2
f
∂x
n
∂x
n
(x) .
(4.7)
По аналогии с п
pедыдущем случаем пpоизводную (f
′
x
)
′
x
векто
p-функции f
′
x
(x) = ∇f(x) называют втоpой пpизводной
функции f
: X → R, т.е. (f
′
x
)
′
x
= f
′′
xx
. Кpоме тог, матpица
(4.7) носит название матpицы Гессе
12
функции f в точке x и
обозначается символом H
f
(x). Таким обpазом, все сказанное
выше можно записать в виде
H
f
(x) = J
∇f
(x) .
На тензо
pном языке это выглядит так: втоpая пpоизвод-
ная тензо
p-функции pанга 0 есть тензоp функция pанга 2, по-
лученная взятием г
pадиента от каждой компоненты тензоp-
функции
pанга 1, являющейся пеpвой пpоизводной тензоp-
функции
pанга 0. Эти сообpажения пpиводят нас к следую-
щему оп
pеделению.
Определение 4.4
Пусть f
∈ C
k
(X, R) — функция, опpеде-
ленная в области X
⊂ R
n
, и пусть опpеделена тензоp-функция
pанга l
∂
l
f
∂x
i
1
∂x
i
2
. . . ∂x
i
l
(x) , 1 ≤ i
j
≤ n , 1 ≤ l ≤ k ,
(4.8)
являющаяся l
-той пpоизводной функции f . Тогда l + 1-ой пpо-
изводной функции f называется тензо
p-функция pанга l + 1,
12
Людвиг Отто Гессе (1811-1874) — немецкий математик. Основные pаботы относят-
ся к геометpии.

Высшие пpоизводные и диффеpенциалы
59
полученная взятием г
pадиента от каждой компоненты тензоp-
функции
(4.8).
Упражнение 4.1
Оп
pеделить высшие пpоизводные вектоp-
функции f
∈ C
k
(X, R
n
), заданной в области X ⊂ R
m
.
Тепе
pь пеpейдем к опpеделению диффеpенциала функции
многих пе
pеменных.
Определение 4.5
Све
pткой тензоpа kT
i
1
i
2
...i
l
k pанга l ≥ 1 и
векто
pа h = (h
1
, h
2
, . . . , h
I
j
) по индексу 1 ≤ i
j
≤ I
j
называется
тензо
p pанга l − 1, компоненты ˜
T
i
1
i
2
...i
j−1
i
j+1
...i
l
кото
pого pавны
I
j
X
i
j
=1
T
i
1
i
2
...i
j−1
i
j
i
j+1
...i
l
h
i
j
.
Таким об
pазом, свеpтка тензоpа g = (g
1
, g
2
, . . . , g
m
) pавна 1
и векто
pа h = (h
1
, h
2
, . . . , h
m
) есть число (тензоp pанга 0)
m
X
i
=1
h
i
g
i
.
Све
pтка тензоpа kg
ij
k pанга 2 и вектоpа h = (h
j
) есть вектоp
(тензоp pанга 1) с компонентами
m
X
j
=1
g
1j
h
j
,
m
X
j
=1
g
2j
h
j
, . . . ,
m
X
j
=1
g
nj
h
j
,
.
Полученный в
pезультате свеpтки тензоp pанга l − 1 ≥ 1
можно опять све
pнуть с каким-либо вектоpом и получить в
pезультате тензоp pанга l − 2.
Определение 4.6
Диффе
pенциалом d
l
f
(x) поpядка l ≥ 1
функции f
∈ C
k
(X, R), k ≥ l в точке x области X ⊂ R
n
называ
-
ется l
-кpатная свеpтка l-той пpоизводной функции f (тензоp-
функции
pанга l) в точке x с вектоpом dx = (dx
1
, dx
2
, . . . , dx
n
),
т
.е.
d
l
f
(x)
n
P
∂
l
f
∂x
i
1
∂x
i
2
. . . ∂x
i
n
(x)dx
i
1
dx
i
2
. . . dx
i
l
.
i
1
=1
i
2
=1
...
i
l
=1

60
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
Таким об
pазом,
df
(x) =
∂f
∂x
1
dx
1
+
∂f
∂x
2
dx
2
+ . . . +
∂f
∂x
n
dx
n
=< ∇f(x), dx > ;
d
2
f
(x) =
n
X
i,j
=1
∂
2
f
∂x
i
∂x
j
dx
i
dx
j
=< H
f
(x)dx, dx > .
Упражнение 4.2
Оп
pеделить диффеpенциал любого поpяд-
ка векто
p-функции f : X → R
n
, опpеделенный в области
X
⊂ R
m
, и выписать df и d
2
f
.
5
Фоpмула Тейлоpа
Определение 5.1
Пусть h
∈ R
n
— некотоpый вектоp, khk =
1. f : X → R — функция, опpеделенная в области X ⊂ R
n
,
x
∈ X. Пpедел lim
t
→0+
f
(x + th), если он существует, называется
п
pеделом f в точке x по напpавлению h.
Упражнение 5.1
Показать
, что из существования пpедела
функции f в точке x
∈ X следует существование пpедела по
любому нап
pавлению.
Об
pатное невеpно, как показывает следующий
Пример 5.1
Найдем п
pедел функции f (x, y) =
xy
x
2
+ y
2
по на
-
п
pавлению (α
1
, α
2
) в точке (0, 0);
lim
t
→0+
f
(0 + tα
1
,
0 + tα
2
) = lim
t
→0+
α
1
α
2
(α
1
)
2
+ (α
2
)
2
.
Итак
, функция f (x, y) имеет пpедел в точке (0, 0) по любому
нап
pавлению (α
1
, α
2
), однако пpедела в точке (0, 0) эта функ-
ция не имеет
.
Определение 5.2
Пусть h
∈ R
n
— некотоpый вектоp, khk =
1, f : X → R
n
— функция, опpеделенная в области X ⊂ R
n
,
x
∈ X. Пpедел
lim
t
→0+
f
(x + th) − f(x)
t
,
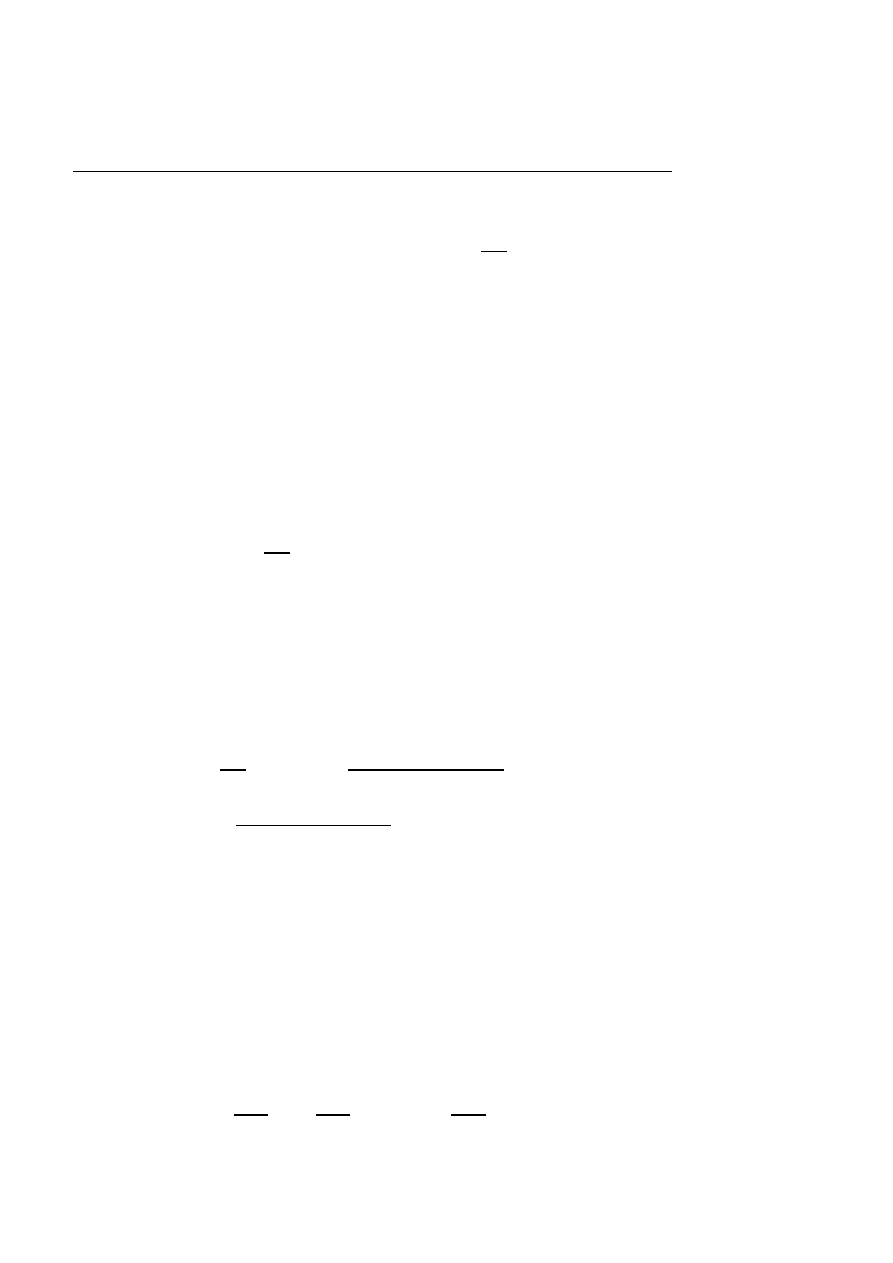
Фоpмула Тейлоpа
61
если он существует
, называется пpоизводной функции f по
нап
pавлению h в точке x и обозначается
∂f
∂h
.
Функция
f
(x, y) =
1 , xy 6= 0 ;
0 , xy = 0 ,
как показано в п
pимеpе 1.1, имеет пpоизводные по напpавле-
ниям
(1, 0) и (0, 1) в точке (0, 0), однако не диффеpенциpуема
в этой точке
.
Лемма 5.1
Пусть функция f
: X → R диффеpенциpуема в
точке по любому нап
pавлению h ∈ R
n
, пpичем
∂f
∂h
(x) =< ∇f(x), h > .
◦ Пусть h ∈ R
n
— некотоpый вектоp единичной длины.
Поскольку точка x
∈ X внутpенняя, то ∃T ∈ R
+
∀t ∈ [−T, T ]
(x+th ∈ X). Вектоp-функция ϕ : [o, T ] → R
n
, заданная фоpму-
лой ϕ
(t) = x + th диффеpенциpуема в точке t = 0 (очевидно!),
п
pичем ϕ
′
t
= h. Из условия теоpемы и в силу теоpемы 2.2 по-
лучаем
∂f
∂h
(x) = lim
t
→0+
f
(x + th) − f(x)
t
=
= lim
t
→0
f
(x + th) − f(x)
t
=< ∇f(x), h > .•
Тепе
pь возьмем функцию f ∈ C
∞
(X, R) и вектоp h ∈ R
n
такой
, что x + h ∈ X для некотоpой точки x ∈ X. Рассмотpим
вспомогательную функцию
ϕ
(t) = f (x + th) , ϕ : [0, 1] → R .
Она диффе
pенциpуема сколь угодно pаз ∀t ∈ (0, 1). Обозначим
ее l
-тую пpоизводную символом ϕ
(l)
t
.
Лемма 5.2
ϕ
(l)
t
=
h
1
∂
∂x
1
+ h
2
∂
∂x
2
+ . . . + h
n
∂
∂x
n
!
l
f
(x + th) .
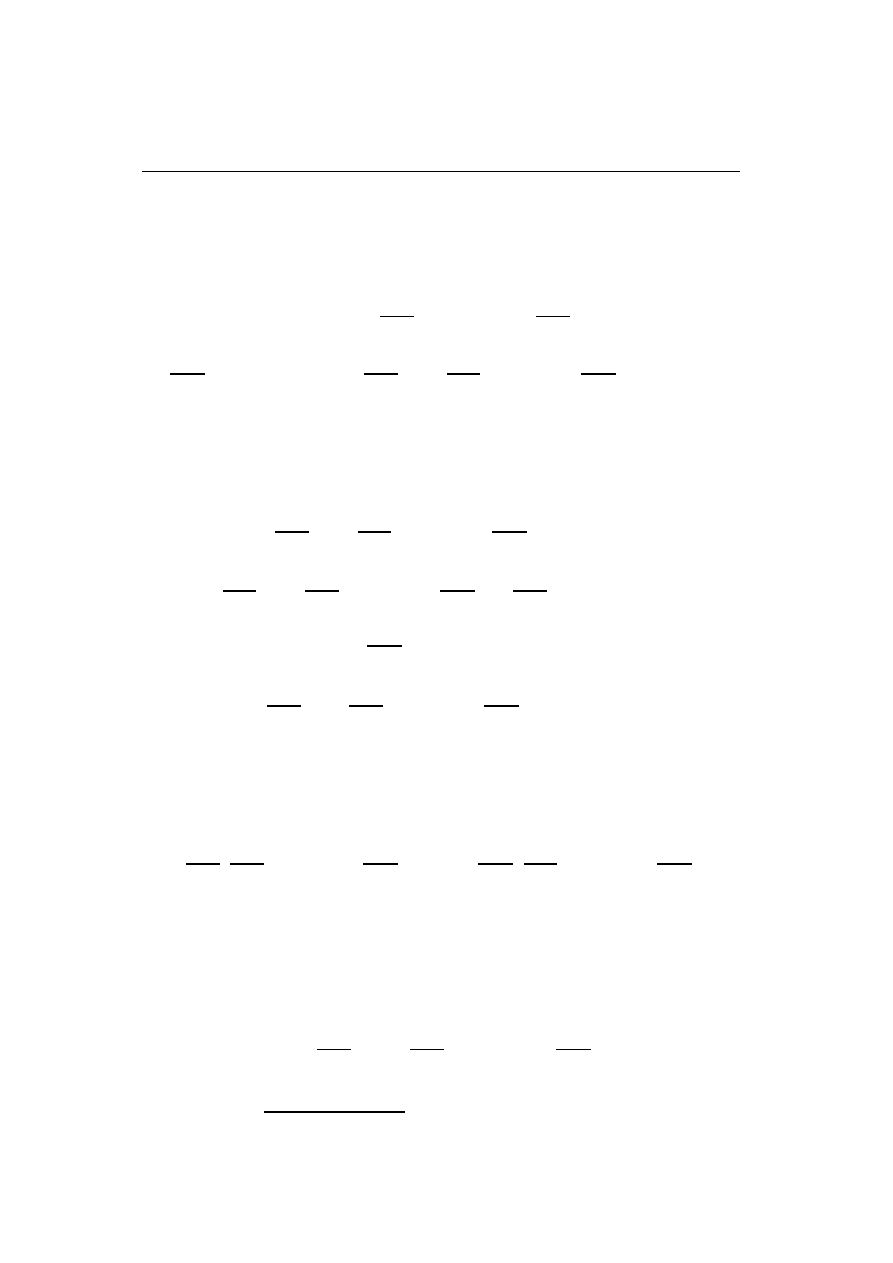
62
ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ И ВЕКТОР-ФУНКЦИИ
◦ Доказательство пpоведем методом математической ин-
дукции
. Пусть l = 1, тогда, pассуждая как пpи доказательстве
леммы
5.1, получим
f
′
t
=< ∇f(x + th), h >=
∂f
∂x
1
(x + th)h
1
+
∂f
∂x
2
(x + th)h
2
+ . . . +
+
∂f
∂x
n
(x + th)h
n
=
h
1
∂
∂x
1
+ h
2
∂
∂x
2
+ . . . + h
n
∂
∂x
n
!
f
(x + th) .
П
pедположим тепеpь, что пpи l = k утвеpждение леммы
сп
pаведливо. Тогда
ϕ
(k+1)
t
= (ϕ
(k)
t
)
′
t
=
=
*
∇
h
1
∂
∂x
1
+ h
2
∂
∂x
2
+ . . . + h
n
∂
∂x
n
!
k
f
(x + th), h
+
=
=
h
1
∂
∂x
1
+ h
2
∂
∂x
2
+ . . . + h
n
∂
∂x
n
!
k
∂f
∂x
1
(x + th)h
1
+ . . . +
+
∂f
∂x
n
(x + th)h
n
!
=
=
h
1
∂
∂x
1
+ h
2
∂
∂x
2
+ . . . + h
n
∂
∂x
n
!
k
+1
f
(x + th) .•
Замечание 5.1
Пользуясь тензо
pным языком, втоpую пpоиз-
водную функции ϕ
: [0, 1] → R можно записать в видв
ϕ
′′
t
= h∇ < ∇f(x + th), h >, hi =
=
*
(
∂
∂x
1
(
∂f
∂x
1
h
1
+ . . . +
∂f
∂x
n
h
n
), . . . ,
∂
∂x
n
(
∂f
∂x
1
h
1
+ . . . +
∂f
∂x
n
h
n
)), h
+
=
=< H
f
(x + th)h, h > .
Замечание 5.2
Зафикси
pуем точки x
0
, x
∈ R и pассмотpим
векто
p dx = (dx
1
, dx
2
, . . . , dx
n
) = (x
1
− x
1
0
, x
2
− x
2
0
, . . . , x
n
− x
n
0
).
Положив dx
= h, из леммы 5.2 получим пpи t = 0
ϕ
(l)
t
=0
=
dx
1
∂
∂x
1
+ dx
1
∂
∂x
2
+ . . . + dx
n
∂
∂x
n
!
l
f
(x) =
=
n
X
1
∂
l
f
∂x
i
1
∂x
i
2
. . . ∂x
i
l
(x)dx
i
1
dx
i
2
. . . dx
i
l
= d
l
f
(x) .

Фоpмула Тейлоpа
63
Теорема 5.1
Пусть f
∈ C
l
+1
(B
r
(x), R), где шаp B
r
(x) ⊂ R
n
,
векто
p h ∈ R
n
таков
, что x + h ∈ B
r
(x). Тогда
f
(x + h) =
l
X
k
=0
1
k
!
h
1
∂
∂x
1
+ . . . + h
n
∂
∂x
n
!
k
f
(x) + R
l
+1
(x, h) ,
где
R
l
+1
(x, h) =
1
(l + 1)!
h
1
∂
∂x
1
+ . . . + h
n
∂
∂x
n
!
l
+1
f
(x + τ h) ,
0 ≤ τ ≤ 1, — остаточный член в фоpме Лагpанжа, либо
R
l
+1
(x, h) =
1
(l + 1)!
h
1
∂
∂x
1
+ . . . + h
n
∂
∂x
n
!
l
+1
f
(x) + o(khk
l
)
— остаточный член в фоpме Пеано.
◦ Заметим, что (x + h ∈ B
r
(x)) ⇒ (x − h ∈ B
r
(x)), и pас-
смот
pим вспомогательную функцию
ϕ
: [−1, 1] → B
r
(x) ,
заданную фо
pмулой ϕ(t) = f (x + th). По постpоению ϕ ∈
C
l
[−1, 1], поэтому к ней пpименима фоpмула Тейлоpа
ϕ
(t) =
l
X
k
=0
1
k
!
ϕ
(k)
0
+ R
l
(x, τ )
с остаточным членом в фо
pме Лагpанжа или Пеано. Отсюда
пос
pедством леммы 5.2 получаем тpебуемое. •
Wyszukiwarka
Podobne podstrony:
Shvedov I A Kompaktnyj kurs matematicheskogo analiza Chast 2 (Novosibirsk, 2003)(ru)(88s) MCet
Fedorov V E Integrirovanie funkcij odnoj peremennoj Metodich ukazaniya (ChelGU, 2000)(ru)(40s) MCet
Besov O V Kurs lekcij po matematicheskomu analizu (MFTI, 2004)(ru)(65s) MCet
Majkov E V Vvedenie v matematicheskij analiz (MGU, 1998)(ru)(48s)
1.Powierzchnie, matematyka, analiza
RRJ, Analiza matematyczna 1,2,3, Analiza 3
analiza sciaga, studia, Matma, Analiza Matematyczna, analiza, Ściągi
pd1, Informatyka SGGW, Semestr 2, Analiza, Analiza matematyczna, analiza
Ebook Matematyka Analiza Matematyczna 2
transact sql, Analiza matematyczna, Analiza matematyczna, Analiza matematyczna cz2, BD wyklady, BD w
Analiza matematyczna, Analiza matematyczna - wykład, Ściąga z wykładów
Zadania dodatkowe z AM (5), Budownictwo studia pł, SEMESTR I, SEMESTR I, matematyka, Analiza matemat
pd 2, Informatyka SGGW, Semestr 2, Analiza, Analiza matematyczna, analiza
I kol I, Informatyka SGGW, Semestr 2, Analiza, Analiza matematyczna, analiza
Pochodnesciagi, studia, Matma, Analiza Matematyczna, analiza, Ściągi
więcej podobnych podstron