Fizyk

a

dla

in»ynieró

w

Zbiór

pra

k

on

troln

y

h

w

semestrze

jesienno-zimo

wym

roku

ak

ademi

kiego

2008/2009

Prof.

dr

hab.

T

adeusz

Lulek

1

PRA

CA

KONTR

OLNA

1

1.

Dane

s¡:

ukªad

nieru

hom

y

O

x, y, z, t,

i

ukªad

ru

hom

y

O

′

x

′

, y

′

, z

′

, t

′

,

p

orusza

j¡y

si

wzgldem

ukªadu

nieru

homego

z

prdk

o±i¡

v =

4

5

c

wzdªu»

wsp

ólnej

osi

x = x

′

;

osie

y

i

y

′

oraz

z

i

z

′

s¡

parami

ró

wnolegªe:

w

h

wili

t = t

′

= 0

osie

obu

ukªadó

w

p

okryw

a

j¡

si;

W

ukªadzie

nieru

hom

ym

sp

o

zyw

a

sfera

o

promieniu

R

i

±ro

dku

w

p

o

z¡tku

ukªadu.

Z

p

o

z¡tku

ukªadu

nieru

homego

wyrzuono

6

kul

(mo»na

je

trakto

w

a¢

jak

punkt

y

materialne)

z

ró

wn

ymi

prdk

o±iami

u =

3

5

c

w

ró

wn

y

h

o

dstpa

h

zasu

T

,

w

kierunk-

a

h

zadan

y

h

przez

tab

el

kula

1

2

3

4

5

6

h

wila

wyrzuenia

0

T1

T2

T3

T4

T5

kierunek

~i

−~i

~j

−~j

~k

−~k

zdarzenie

z

1

z

2

z

3

z

4

z

5

z

6

Oznazm

y

przez

z

i

,

gdzie

i ∈ ˜6 = 1, 2, 3, 4, 5, 6

,

zdarzenie

wyrzuenia

i

-tej

kuli,

za±

przez

y

i

-

zdarzenie

uderzenia

i

-tej

kuli

w

p

o

wierz

hni

sfery

sp

o

zyw

a

j¡ej.

2.

W

yznazy¢

w

arto±i

obu

k

anonizn

y

h

rzuto

w

a«

p

1

: E

A

→ T

,

p

2

: E

A

→ V

zaso-

przestrzeni

Arystotelesa

zadanej

przez

ukªad

nieru

hom

y

dla

zdarze«

z

i

,

y

i

,

i ∈ ˜6

.

3.

Przedyskuto

w

a¢

zagadnienie

ró

wno

zesno±i.

Przy

jaki

h

w

arto±ia

h

parametró

w

R

i

T

niektóre

ze

zdenio

w

an

y

h

zdarze«

mog¡

b

y¢

ró

wno

zesne

(a)

w

zasoprzestrzeni

Galileusza.

(b)

w

zasoprzestrzeni

Mink

o

wskiego

w

ukªadzie

nieru

hom

ym.

()

w

zasoprzestrzeni

Mink

o

wskiego

w

ukªadzie

ru

hom

ym.

(d)

W

yznazy¢

in

terw

aªy

zasoprzestrzenne

∆

z

i

,y

i

, 1 ≤ i ≤ j ≤ 6

i

p

o

da¢

i

h

t

yp

y

w

zale»no±i

o

d

R

i

T.

4.

Ciiem

zasoprzestrzeni

Galileusza

E

G

,

trakto

w

anej

jak

o

wi¡zk

a

wªóknista

(E

G

, T, V, π)

,

gdzie

π : E

G

→ T

,

nazyw

am

y

do

w

olne

o

dwzoro

w

anie

ψ : T → E

G

,

o

wªasno±i

π ◦ ψ = id

T

.

P

o

da¢

kinemat

yzn¡

in

terpretaj

i¢

zadan

y

h

przez:

2

ψ

1

(t) = (t, x

o

),

t ∈ T

ψ

2

(t) = (t, x

o

+ v

o

t),

t ∈ T

ψ

3

(t) = (t, x

o

+ v

o

t +

1

2

gt

2

), t ∈ T

ψ

4

(t) = (t, x

o

cos(ωt)),

t ∈ T

(1)

gdzie

dla

uproszzenia

zapisu

przyjm

ujem

y

,

»e

ru

h

jest

jedno

wymiaro

wy

,

tzn.

V = R

.

Ka»de

z

t

y

h

i¢

okre±la

p

ewien

ukªad

o

dniesienia.

Które

z

ni

h

s¡

ukªadami

inerjaln

ymi?

PRA

CA

KONTR

OLNA

NR

2

1.

P

ok

aza¢,

»e

aªk

a

ogólna

ró

wnania

ru

h

u

Newtona

m¨

x = F

dla

jedno

wymiaro

w

ego

ru

h

u

(a)

jednosta

jnego,

(b)

p

o

d

dziaªaniem

staªej

siªy

F,

()

p

o

d

dziaªaniem

siªy

harmoniznej

F = −kx

ma

o

dp

o

wiednio

p

osta¢:

(a)

x(t) = x

0

+ vt

(b)

x(t) = x

0

+ vt + vt

2

/2m

()

x(t) = x

0

cos(ωt + δ)

Przedyskuto

w

a¢

w

arunki

p

o

z¡tk

o

w

e

w

k

a»ym

przypadku.

2.

Punkt

materialn

y

wyk

on

uje

ru

h

harmonizn

y

opisan

y

w

przypadku

()

zadania

1.

P

o

da¢

mo»liw

e

w

arto±i

(a)

fazy

δ

,

(b)

prdk

o±i

p

o

z¡tk

o

w

ej,

je»eli

wiadomo,

»e

wy

h

ylenie

w

h

wili

t = 0

ró

wna

si

p

oªo

wie

amplitudy

.

3.

Dan

y

jest

ukªad

me

hanizn

y

zw

an

y

w

ahadªem

p

o

dw

ó

jn

ym

pªaskim,

tj.

w

ahadªo

o

dªugo±i

l

1

i

masie

m

1

jest

za

wieszone

z

jednego

k

o«a,

a

na

drugim

k

o«u

za

wieszon

y

jest

p

o

z¡tek

drugiego

w

ahadªa

o

promieniu

l

2

i

masie

m

2

.

Ukªad

zna

jduje

si

w

jednoro

dn

ym

p

olu

przyi¡

gania

Ziemi.

(a)

P

ok

aza¢,

»e

przestrze«

k

ongurayjna

Q

tego

w

ahadªa

jest

toroidem.

(b)

Przedsta

wi¢

przestrze«

k

ongurayjn¡

Q = {(α

1

, α

2

)|0 ≤ α

1

< 2π, 0 ≤ α

2

<

2π}

na

mapie

kw

adratu

o

b

oku

2π

i

przedyskuto

w

a¢

top

ologizne

wªasno±i

brzegu

tego

kw

adratu.

3

PRA

CA

KONTR

OLNA

NR

3

1.

(a)

P

ok

aza¢,

»e

siªy

w

punkta

h

(a),

(b)

i

()

zadania

1

pray

k

on

trolnej

2

s¡

p

oten-

jalne

oraz

wyznazy¢

o

dp

o

wiednie

p

otenjaªy

(w

jedn

ym

wymiarze

przestrzen-

n

ym).

Odp.:

(a) V = const, (b) V = (F/m)x, (c) V = kx

2

/2.

(b)

Sp

orz¡dzi¢

wykresy

zale»no±i

energii

kinet

yznej

T

,

p

otenjalnej

V

oraz

me-

haniznej

E

jak

o

funk

ji

zasu

dla

trze

h

p

o

wy»szy

h

ru

hó

w

i

zin

terpreto

w

a¢

o

dp

o

wiednie

zasady

za

ho

w

ania.

2.

W

yznazy¢

p

o

wierz

hnie

ekwip

otenjalne

oraz

gradien

t

p

otenjaªu

dla

przypadk

ó

w:

(a)

jednoro

dnego

przyi¡

gania

ziemskiego,

V (x, y, z) = −mgz

,

(b)

p

otenjaªu

Coulom

ba,

V (x, y, z) = C/

√

x

2

+ y

2

+ z

2

,

()

tró

jwymiaro

w

ego,

izotrop

o

w

ego

osylatora

harmoniznego,

V (x, y, z)

=

(1/2)k(x

2

+ y

2

+ z

2

).

3.

P

o

dw

ó

jne

w

ahadªo

matemat

yzne

pªaskie

skªada

si

z

w

ahadªa

pierwszego,

zazepi-

onego

w

punk

ie

(0, 0)

(rys.

1),

oraz

w

ahadªa

drugiego,

zazepionego

na

k

o«u

pier-

wszego.

Dªugo±i

w

ahadeª

wynosz¡

o

dp

o

wiednio

l

1

i

l

2

,

a

i

h

masy

-

m

1

i

m

2

.

P

ar

(α

1

, α

2

)

,

0 ≤ α

1

< 2π

,

0 ≤ α

2

< 2π

in

terpretujem

y

jak

o

p

oªo»enie

uogólnione

ukªadu

w

sensie

formalizm

u

Lagrange'a

-

Eulera.

(a)

P

ok

aza¢,

»e

przestrze«

k

ongurayjna

Q

w

ahadªa

jest

toroidem,

sp

orz¡dzi¢

jego

map

w

e

wsp

óªrzdn

y

h

(α

1

, α

2

)

i

przedyskuto

w

a¢

top

ologizne

wªasno±i

brzegó

w

tej

map

y

.

W

sk

aza¢

punkt

y

ró

wno

w

agi

trw

aªej

i

h

wiejnej

(w

jednoro

d-

n

ym

p

olu

przyi¡

gania

ziemskiego

wzdªu»

osi

z).

(b)

P

ok

aza¢,

»e

energia

kinet

yzna

ukªadu

wyraªa

si

wzorem:

T =

1

m

1

+ m

2

l

2
1

˙

α

1

2

+

1
2

m

2

l

2
2

˙

α

2

2

+ m

1

l

1

l

2

˙

α

1

˙

α

2

cos(α

1

− α

2

)

za±

energia

p

otenjalna:

V = −gl

1

(m

1

+ m

2

) cos(α

1

) − gm

2

l

2

cos(α

2

)

P

o

da¢

in

terpretaj

me

hanizn¡

p

oszzególn

y

h

zªonó

w

i

okre±li¢

lagrangian

ukªadu.

4

()

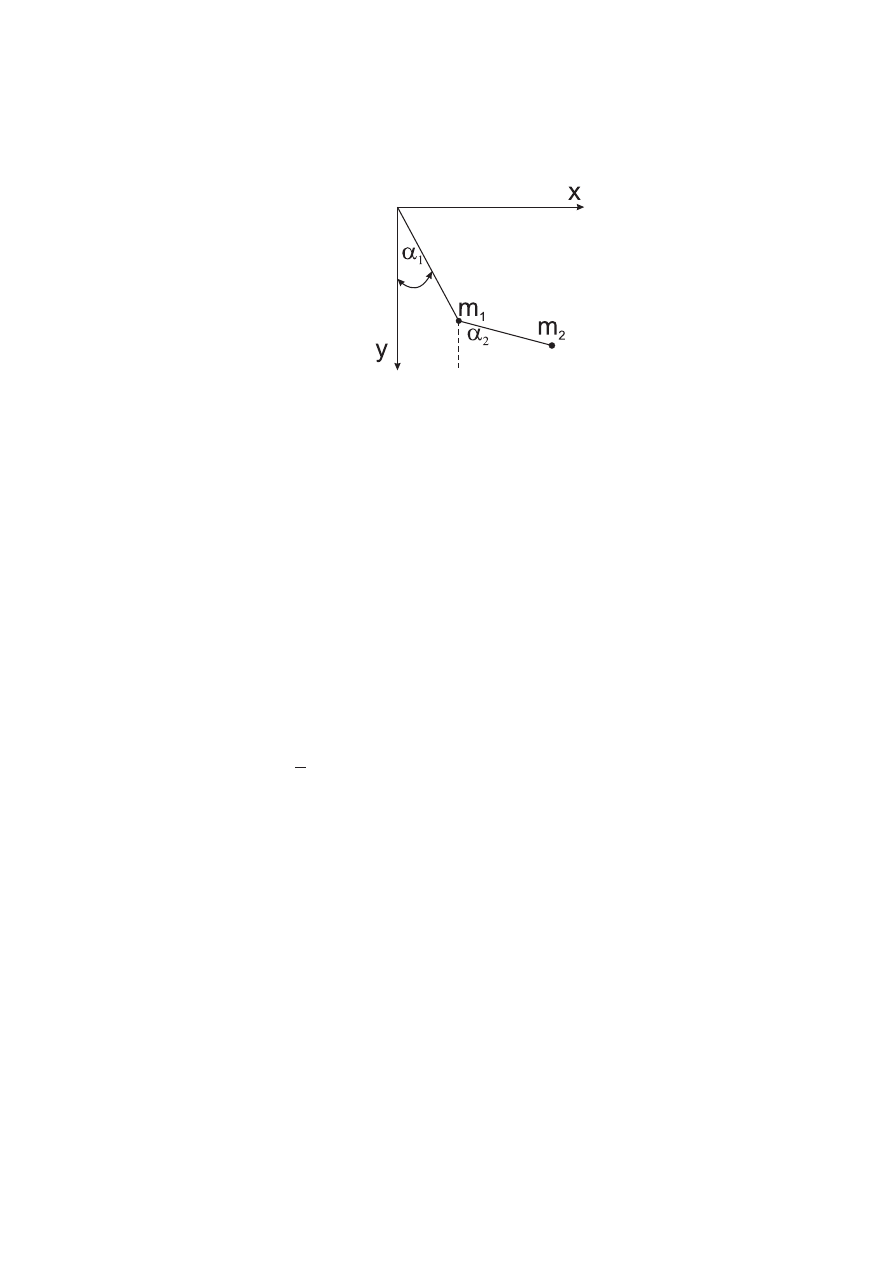
W

yznazy¢

i

zin

terpreto

w

a¢

siªy

i

p

dy

uogólnione

oraz

napisa¢

ukªad

ró

wna«

Lagrangea

-

Eulera.

rys.

1,

W

ahadªo

pªaskie

4.

Caªk

a

ogólna

ró

wnania

ró»nizk

o

w

ego

x + ω

2

x = 0

ma

p

osta¢

x(t) = Acos(ωt + δ)

,

gdzie

A

i

δ

s¡

staªymi

aªk

o

w

ania.

W

yznazy¢

te

staªe

z

w

arunk

ó

w

p

o

z¡tk

o

wy

h

(a)

x(0) = 0

,

˙x(0) = v

0

(b)

x(0) = x

0

,

˙x(0) = 0

5.

Dane

s¡

nastpuj¡e

p

otenjaªy:

(a)

jednoro

dn

y

p

otenjaª

gra

witayjn

y

,

zadan

y

w

e

wsp

óªrzdn

y

h

k

artezja«ski

h

przez

V (x, y, z) = mgz

(b)

p

otenjaª

kulom

b

o

wski,

zadan

y

w

e

wsp

óªrzdn

y

h

sferyzn

y

h

przez

V (r, ϑ, ϕ) =

C

r

()

p

otenjaª

spr»yst

y

,

zadan

y

w

e

wsp

óªrzdn

y

h

sferyzn

y

h

przez

V (r, ϑ, ϕ) = kr

2

.

P

o

da¢

geometryzn

y

opis

p

o

wierz

hni

ekwip

otenjaln

y

h

oraz

wyznazy¢

p

ola

siª

zadan

y

h

przez

k

a»dy

z

t

y

h

p

otenjaªó

w.

W

yznazy¢

w

arto±¢

p

otenjaªu

oraz

w

ektor

siªy

w

punk

ie

~r = a(~i + ~j + ~k)

dla

k

a»dego

przypadku.

PRA

CA

KONTR

OLNA

NR

4

1.

P

o

da¢

geometryzn¡

in

terpretaj

mo

dó

w

normaln

y

h

zadan

y

h

przez

k

a»d¡

k

olumn

tab

eli

W

sp

óªrzdne

symetryzne

wierz

hoªk

ó

w

kw

adratu.

5

(a)

W

sk

aza¢

meto

dy:

translayjne,

rotayjne,

o

ddy

ha

j¡e,

wibrayjne.

(b)

Przedyskuto

w

a¢

stopnie

zwyro

dnienia

o

dp

o

wiedni

h

zsto±i

wªasn

y

h.

2.

Rozwi¡za¢

zagadnienie

wªasne

maierzy

dla

dw

ó

h

przypadk

ó

w

V

1

=










5

2

0

2

2

5

2

0

0

2

5

2

2

0

2

5










V

2

=










7

1

3

1

1

7

1

3

3

1

7

1

1

3

1

7










(2)

(a)

P

ok

aza¢,

»e

specV

1

= (1, 5, 5, 9)

,

specV

2

= (4, 4, 8, 12)

.

(b)

P

ok

aza¢,

»e

do

w

oln

y

w

ektor

wªasn

y

maierzy

,

o

dp

o

wiada

j¡y

zwyro

dniaªej

w

arto±i

wªasnej

λ = 5

dla

maierzy

V

1

,

lub

λ = 4

dla

maierzy

V

2

,

ma

p

osta¢

q = a(e

1

− e

3

) + b(e

2

− e

4

)

,

gdzie

a, b

s¡

do

w

oln

ymi

lizbami

rzezywist

ymi,

za±

e

1

, e

2

, e

3

, e

4

stano

wi¡

baz

ortonormaln¡,

w

której

zadana

jest

maierz

V.

Unormo

w

a¢

ten

w

ektor

wªasn

y

.

()

W

yznazy¢

unormo

w

ane

w

ektory

wªasne,

o

dp

o

wiada

j¡e

w

arto±iom

wªasn

ym

niezwyro

dniaªym.

(d)

Przedsta

wi¢

ró

wnanie

sekularne

w

p

ostai

i.

wyznaznik

o

w

ej,

ii.

wielomian

u

o

d

w

arto±i

wªasnej,

w

p

ostai

rozwinitej

i

sfaktoryzo

w

anej.

(e)

P

o

da¢

in

terpretaj

me

hanizn¡

maierzy

V

i

jej

elemen

tó

w

maierzo

wy

h

w

k

on

tek±ie

zadania

1.

(f

)

W

sk

aza¢

zwi¡zek

w

ektoró

w

wªasn

y

h

maierzy

V

z

mo

dami

normaln

ymi

z

zadania

5.

W

szzególno±i,

dopaso

w

a¢

w

arto±i

lizb

a, b

z

punktu

b)

do

t

y

h

mo

dó

w.

PRA

CA

KONTR

OLNA

NR

5

1.

Stan

kw

an

to

wy

elektron

u

sw

ob

o

dnego

w

szesianie

zadan

y

jest

przez

|φ >=

1

√

3

|2, 1, 0 > +

1

√

2

| − 1, 0, 2 > −

1

√

6

|0, −2, −1 >

(a)

W

yjasni

znazenie

lizb

kw

an

to

wy

h

oraz

amlplitud

pra

wdop

o

dobienst

w

a.

6

(b)

Czy

ten

stan

jest

stanem

wªasn

ym

op

eratora

(a)

ˆ

p

x

,

(b)

ˆ

p

y

,

()

ˆ

p

z

,

(d)

p

2

=

ˆ

p

x

+ ˆ

p

y

+ ˆ

p

z

,

(e)

hamiltonian

u?

Je±li

tak

-

prosz

p

o

da¢

o

dp

o

wiedni¡

w

arto±¢

wªasna,

a

je±li

nie

-

oblizy¢

w

arto±¢

±redni¡

w

t

ym

stanie.

()

Jakie

jest

pra

wdop

o

dobie«st

w

o

znalezienia

n

kw

an

tó

w

p

du,

n = 0, 1, 2, 3 . . .

,

w

kierunku

osi

x, y, z

,

w

t

ym

stanie?

2.

Okresli¢

dziaªanie

grup

y

oktaedryznej

O

h

na

zbiorze

wierz

hoªk

ó

w

szesian

u.

W

yniki

przedsta

wi¢

w

p

ostai

tab

eli,

z

wierszami

n

umero

w

an

ymi

przez

g ∈ O

h

,

z

up

orzad-

k

o

w

aniem

w

edªóug

klas

elemen

to

w

wza

jemnie

sprzezon

y

h,

a

k

olumn

y

-

przez

wierz-

hoªki

A, B, C, D, A

′

, B

′

, C,

′

D,

′

.

Przy

p

omo

y

tej

tab

elki

(a)

p

ok

aza¢,

»e

elemen

t

y

k

a»dej

klasy

ma

j¡

jednak

o

w

¡

struktur

yklo

w

¡,

(b)

p

o

da¢

maierze

reprezen

taji

w

ektoro

w

ej

grup

y

O

h

,

()

sp

orz¡dzi¢

tab

el

prezen

tuj¡a

grup

e

O

h

jak

o

ilo

zyn

p

oªprost

y

O

h

= D

2

h

C

A

3

V

i

zin

terpreto

w

a¢

zynnik

D

2

h

jak

o

grup

e

o

dp

o

wiedzialn¡

za

zmian

znak

ó

w

lizb

kw

an

to

wy

h

|pqr >

stanó

w

elektron

u

sw

ob

o

dnego

w

szesianie,

za±

zynnik

C

A

3

V

jak

o

grup

p

erm

utaji

t

y

h

lizb

kw

an

to

wy

h.

3.

Przedyskuto

w

a¢

zwi¡zek

symetrii

ze

zwyro

dnieniem

na

przykªadzie

elektron

u

sw

ob

o

d-

nego

w

sze±ianie.

(a)

P

o

da¢

mo»liw

e

t

yp

y

stabilizatoró

w

stanó

w

kw

an

to

wy

h

|n

x

n

y

n

z

>

w

grupie

ok-

taedryznej

O

h

.

(b)

Sp

orz¡dzi¢

tab

el,

wi¡»¡a

symetrie

za

stopniem

zwyro

dnienia

p

oziom

u

energii.

()

P

o

da¢

trzy

przykªady

taki

h

szzebli

l

drabin

y

energet

yznej

dla

elektron

u

sw

o-

b

o

dnego

w

szesianie,

gdzie

istniej¡

rozwi¡zania

ró

wnania

diofan

t

yznego

p

2

+ q

2

+ r

2

= l

o

dp

o

wiada

j¡e

dw

óm

ró»n

ym

orbitom

grup

y

oktaedryznej.

7

PRA

CA

KONTR

OLNA

NR

6

1.

(a)

P

o

da¢

relaje

k

om

utaji

dla

kw

an

to

wy

h

op

eratoró

w

skªado

wy

h

momen

tu

p

du.

(b)

P

o

da¢

zagadnienie

wªasne

op

eratoró

w

(~

L)

2

i

L

z

.

Okresli¢

widmo

t

y

h

op

eratoró

w.

P

o

da

wsp

ólne

funk

je

wªasne.

2.

Dane

s¡

nastpujae

dw

a

momen

t

y

p

du:

(a)

j

1

= 1

,

j

2

= 1

,

(b)

j

1

= 1/2

,

j

2

= 2

,

()

j

1

= 1

,

j

2

= 2

.

W

yznazy¢

w

k

a»dym

przypadku

widmo

wypadk

o

w

ego

momen

tu

p

du

J

i

spra

wdzi¢

zwyro

dnienia.

3.

W

yznazy¢

term

y

LS

Russela-Saundersa

nastpuj¡y

h

k

onguraji

elektrono

wy

h:

(1s)

1

,

(2p)

1

,

(2p)

2

,

(3d)

1

,

(3d)

2

,

(3d)

8

,

(3d)

9

i

wsk

aza¢

term

Hunda.

4.

W

yznazy¢

subteln¡

struktur

term

u

4

I

.

P

ok

aza¢,

»e

±ro

dek

ie»k

o±i

tej

struktury

p

okryw

a

si

z

p

oziomem

wyjsio

wym.

Spra

wdzi¢

reguª

in

terw

aªó

w

Landego.

5.

Dane

s¡

nastpuj¡e

pary

(l

1

, l

2

)

momen

tó

w

p

du

(1, 1)

,

(1, 2)

,

(2, 2)

,

(1/2, 1/2)

,

(1/2, 2)

.

(a)

W

ypisa¢

bazy

|l

1

m

1

> |l

2

m

2

>

niesprz»on

y

h

momen

tó

w

p

du

dla

k

a»dej

z

t

y

h

par

i

p

o

da¢

wymiary

o

dp

o

wiedni

h

przestrzeni

kw

an

to

wy

h.

(b)

Sp

orz¡dzi¢

wyk

az

wszystki

h

elemen

tó

w

bazy

|l

1

l

2

LM >

wypadk

o

w

ego

momen

tu

p

du

dla

k

a»dej

z

t

y

h

par

i

p

o

da¢

bilans

wymiaró

w.

6.

W

yznazy¢

nastpuj¡e

lizb

y

niezale»n

y

h

stanó

w

kw

an

to

wy

h

w

teorii

atom

u:

(a)

lizb

t

y

h

stanó

w

jedno

elektrono

wy

h,

dla

który

h

dla

który

h

gªó

wna

lizba

kw

an

to

w

a

n

wynosi

1,

2,

3,

4,

(b)

lizb

stanó

w

jedno

elektrono

wy

h

na

p

o

wªok

a

h

4s

,

4p

,

4d

,

4f

,

()

lizb

stanó

w

ukªadu

zadanego

przez

k

onguraje

elektrono

w

e:

1s

2

, 2p

2

, 2p

3

, 2p

4

, 3d

2

, 3d

3

, 3d

5

, 3d

9

, 3d

10

, 4f

2

, 4f

3

, 4f

7

, 4f

12

.

8

7.

(a)

W

yznazy¢

term

y

Russela-Saundersa

dla

k

onguraji

elektrono

w

ej

3d

3

.

(b)

W

yznazy¢

term

p

o

dsta

w

o

wy

przy

p

omo

y

reguªy

Hunda.

()

W

yznazy¢

subteln¡

struktur

term

u

Hunda

i

spra

wdzi¢

reguª

in

terw

aªó

w

Lan-

dego.

9