Z. Kąkol-Notatki do Wykładu z Fizyki

21-1

Wykład 21

21. Prąd elektryczny i pole magnetyczne

21.1 Prąd elektryczny

Natężenie prądu elektrycznego

t

Q

I

=

(21.1)

Jednostka: 1 amper, 1A.

Gęstość prądu elektrycznego

S

I

j

=

(21.2)

W nieobecności zewnętrznego pola elektrycznego elektrony poruszają się chaotycz-

nie we wszystkich kierunkach. W zewnętrznym polu E uzyskują wypadkową (stałą z

założenia)

prędkość unoszenia

v

u

.

Jeżeli n jest koncentracją elektronów to ilość ładunku Q jaka przepływa przez przewod-

nik o długości l w czasie t = l/

v

u

wynosi

Q = nSle

Tak więc natężenie prądu wynosi

u

u

nSe

l

nSle

t

Q

I

v

v

=

=

=

(21.3)

a gęstość prądu

u

u

ne

S

I

j

v

v

ρ

=

=

=

(21.4)

gdzie

ρ jest gęstością ładunku.

l

S

Z. Kąkol-Notatki do Wykładu z Fizyki

21-2

UMOWA: kierunek prądu = kierunek ruchu ładunków dodatnich.

Przykład 1

Prąd o natężeniu 1A płynie w drucie miedzianym o przekroju 1 mm

2

. Jaka jest średnia

prędkość unoszenia elektronów przewodnictwa ? Masa atomowa miedzi

µ = 63.8 g/mol,

a gęstość

ρ = 8.9 g/cm

3

.

Z równania na natężenie prądu otrzymujemy

nSe

I

u

=

v

Zakładamy, że na jeden atom przypada 1 elektron przewodnictwa (Cu

+1

). Możemy więc

obliczyć koncentrację nośników

µ

ρ

Av

N

n

=

n = 8.4·10

28

atom/m

3

Wstawiając do równania na prędkość otrzymujemy

v

u

= 7.4·10

-5

m/s = 0.074 mm/s

Prądy mogą też płynąć w gazach i cieczach. Lampy jarzeniowe są przykładem wykorzy-
stania przepływu prądu w gazach. W gazach prąd jest wynikiem ruchu nie tylko elektro-
nów ale i jonów dodatnich. Jednak lżejsze elektrony są znacznie szybsze i ich wkład do
prądu jest dominujący. W zderzeniu elektronu z jonem lub atomem gazu energia może
zostać zaabsorbowana przez atom, a następnie wypromieniowana w postaci promienio-
wania elektromagnetycznego w tym również widzialnego.

21.2 Prawo Ohma

Jeżeli do przewodnika przyłożymy różnicę potencjałów V, to przez przewodnik płynie
prąd I. Na początku XIX wieku Ohm zdefiniował

opór przewodnika

jako napięcie po-

dzielone przez natężenie prądu

I

U

I

V

R

=

∆

=

(21.5)

Jest to definicja oporu. Ten stosunek jest stały pod warunkiem, że utrzymuje się stałą
temperaturę.
Jednostką oporu (SI) jest 1 (Ohm) 1

Ω

.

Z. Kąkol-Notatki do Wykładu z Fizyki

21-3

21.2.1 Wyprowadzenie prawa Ohma

Bez pola elektrycznego prędkość ruchu chaotycznego u (nie powoduje przepływu

prądu). Prędkość u jest związana ze średnią drogą swobodną

λ i średnim czasem pomię-

dzy zderzeniami

∆

t zależnością: u =

λ/

∆

t.

Jeżeli przyłożymy napięcie to na każdy elektron będzie działała siła F = eE i po czasie

∆

t każdy elektron osiągnie prędkość unoszenia

v

u

=

∆

u daną II zasadą Newtona

eE

t

u

m

=

∆

∆

Stąd

m

t

eE

u

u

∆

=

=

∆

v

Podstawiając

∆

t =

λ/u otrzymujemy

mu

E

e

u

λ

=

v

(21.6)

Prędkość unoszenia ma ten sam kierunek (przeciwny do E) dla wszystkich elektronów.
Przy każdym zderzeniu elektron traci prędkość unoszenia.
Średnia droga swobodna

λ jest tak mała, że v

u

jest zawsze mniejsza od u.

Obliczamy teraz natężenie prądu wstawiając wyrażenie na

v

u

do wyrażenia (21.3) na

natężenie I.

mu

SE

ne

nSe

I

u

λ

2

=

=

v

Dla elementu przewodnika o długości l (rysunek) obliczymy opór korzystając z faktu, że
napięcie U = El.
Z prawa Ohma

S

ne

mul

I

El

I

U

R

λ

2

=

=

=

(21.7)

R jest proporcjonalny do długości przewodnika i odwrotnie proporcjonalny do przekro-
ju. Zauważmy, że R pozostaje stały tak długo jak długo u jest stałe, a u zależy tylko od
temperatury (patrz wykład 15).
Równanie (21.7) przepiszmy w postaci

S

l

R

ρ

=

(21.8)

Stałą

ρ nazywamy

oporem właściwym

.

Typowa zależność oporu od temperatury dla przewodników metalicznych jest poka-

zana na rysunku na następnej stronie.

Z. Kąkol-Notatki do Wykładu z Fizyki

21-4

Z dobrym przybliżeniem jest to zależność liniowa

ρ ~ T za wyjątkiem temperatur bli-

skich zera bezwzględnego. Wtedy zaczyna odgrywać rolę tzw. opór resztkowy

ρ

0

zależ-

ny w dużym stopniu od czystości metalu. Istnieją jednak metal i stopy, dla których ob-
serwujemy w dostatecznie niskich temperaturach całkowity zanik oporu. Zjawisko to
nosi nazwę

nadprzewodnictwa

. Prądy wzbudzone w stanie nadprzewodzącym utrzymują

się w obwodzie bez zasilania zewnętrznego. Ta możliwość utrzymania stale płynącego
prądu rokuje duże nadzieje na zastosowania techniczne, które znacznie wzrosły po od-
kryciu w 1987 r materiałów przechodzących w stan nadprzewodzący w stosunkowo wy-
sokich temperaturach, około 100 K. Materiały te noszą nazwę wysokotemperaturowych
nadprzewodników a ich odkrywcy Bednorz i Müller zostali wyróżnieni Nagrodą Nobla.

21.3 Straty cieplne

Gdy elektron zderza się z atomem traci nadwyżkę energii, którą uzyskał w polu elek-

trycznym. Ponieważ energia kinetyczna nie wzrasta, cała energia stracona przez elektro-
ny daje

dE

cieplna

= Udq

gdzie dq jest ładunkiem przepływającym(elektronów przewodnictwa).
Dzieląc obie strony przez dt otrzymujemy

UI

t

q

U

t

E

a

ciep

=

=

d

d

d

d

ln

P = UI

(21.8)

przedstawia

straty mocy elektrycznej

.

ρ

0

0

T

ρ

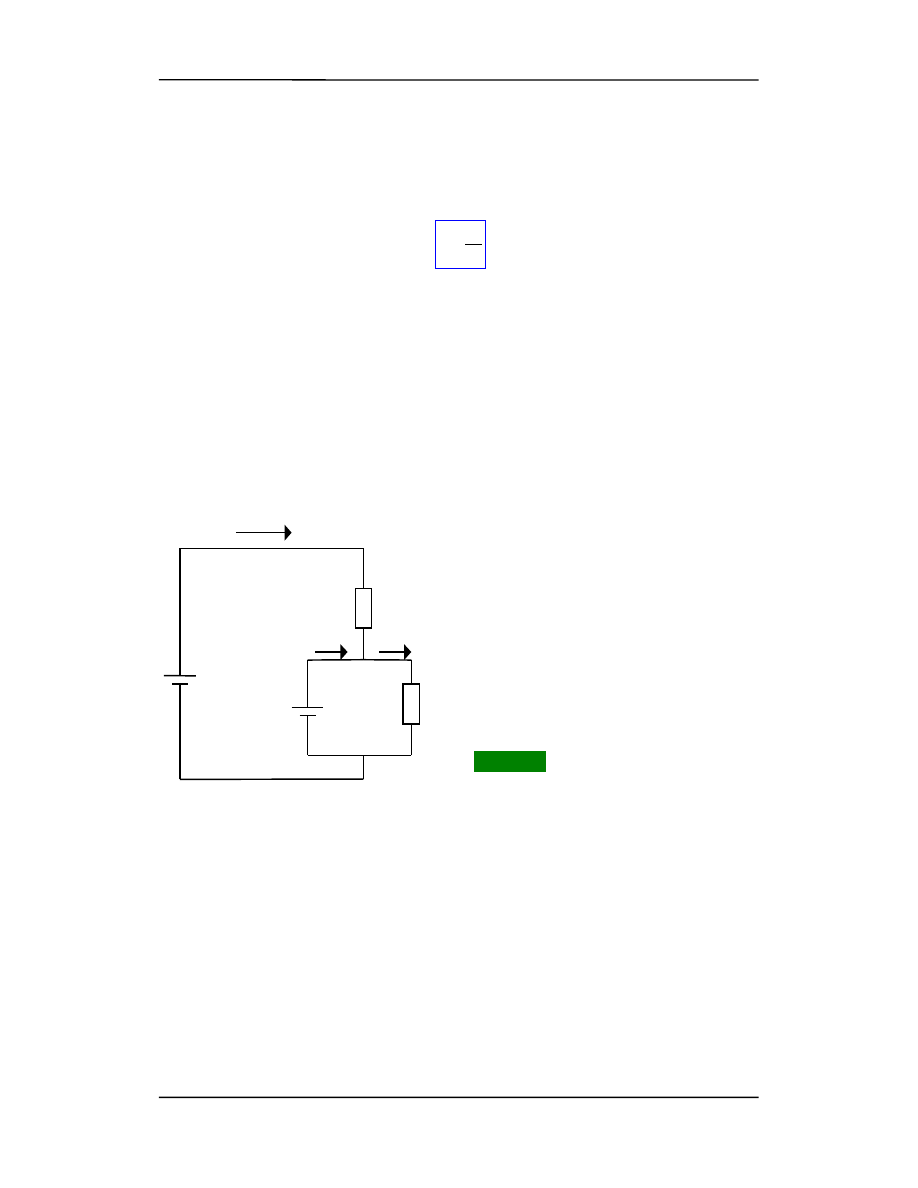
Z. Kąkol-Notatki do Wykładu z Fizyki

21-5

21.3.1 Siła elektromotoryczna

Aby utrzymać prąd potrzeba źródła energii elektrycznej. Np. baterie, generatory. Na-

zywamy je źródłami

siły elektromotorycznej SEM

. W takich źródłach jeden rodzaj ener-

gii jest zamieniany na drugi. SEM oznaczamy

ε i definiujemy

q

W

=

ε

(21.9)

gdzie W jest energią elektryczną przekazywaną ładunkowi q, gdy przechodzi on przez
źródło SEM.

21.4 Obwody prądu stałego

Łączenie oporów:

•

szeregowe (ten sam prąd przez oporniki)

R

z

= R

1

+ R

2

+ .....

•

równoległe (to samo napięcie na opornikach)

1/R

z

= 1/R

1

+ 1/R

2

+ .....

21.4.1 Prawa Kirchoffa

•

Twierdzenie o obwodzie zamkniętym:

algebraiczna suma przyrostów napięć
w dowolnym obwodzie zamkniętym
jest równa zeru

. (Spadek napięcia jest

przyrostem ujemnym napięcia).

•

Twierdzenie o punkcie rozgałęzienia:

algebraiczna suma natężeń prądów
przepływających przez punkt rozgałę-
zienia jest równa zeru

.

Twierdzenie o obwodzie zamkniętym jest
wynikiem prawa zachowania energii, a
twierdzenie o punkcie rozgałęzienia wy-
nika z prawa zachowania ładunku.

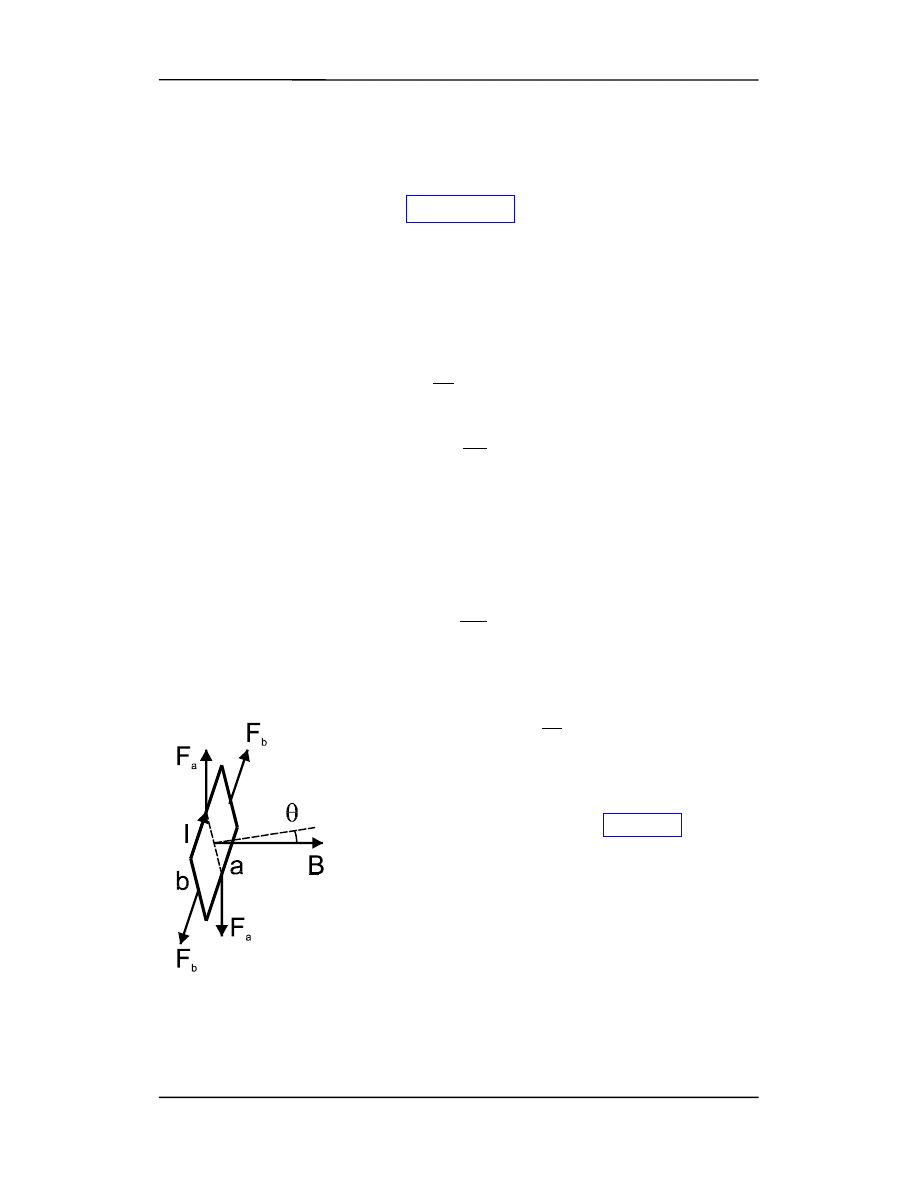
Przykład 2

Regulator napięcia (rysunek na na-

stępnej stronie). Opornik R

1

ma napięcie

określone przez

ε

1

a prąd pobiera z

ε

2

.

W każdej gałęzi obwodu trzeba z osobna przyjąć kierunek prądu i jego natężenie. Praw-
dziwy kierunek rozpoznamy po znaku obliczonego natężenia. Spadek napięcia pojawia
się przy przejściu przez każdy opornik w kierunku zgodnym z prądem. Przyrost napięcia
pojawia się przy przejściu przez źródło od "-" do "+".
Zastosowanie I prawa Kirhoffa do "dużej" pętli daje

ε

2

– I

2

R

2

– I

3

R

1

= 0

a dla "małej" pętli

ε

1

– I

3

R

1

= 0

I

2

R

2

ε

2

ε

1

R

1

I

1

I

3

Z. Kąkol-Notatki do Wykładu z Fizyki

21-6

Po odjęciu stronami otrzymamy

ε

2

–

ε

1

– I

2

R

2

= 0

2

1

2

2

R

I

ε

ε

−

=

Dla węzła

I

1

+ I

2

– I

3

= 0

skąd

2

2

2

1

1

2

1

2

1

1

2

3

1

1

1

R

R

R

R

R

I

I

I

ε

ε

ε

ε

ε

−









+

=

−

−

=

−

=

Zauważmy, że gdy dobrać warunki tak aby

2

2

2

1

1

1

1

R

R

R

ε

ε

=









+

to I

1

= 0 i

ε

1

nie daje żadnego prądu. Taki układ ma ważne zastosowanie praktyczne.

Napięcie

ε

1

może być niskoprądowym ogniwem wzorcowym, mimo że R

1

może pobie-

rać duży prąd (głównie z

ε

2

).

21.5 Pole magnetyczne

Doświadczalnie stwierdzamy, że występuje oddziaływanie:

•

magnesów naturalnych (Fe

3

O

4

)

•

oddziaływanie przewodników z prądem na ładunki w ruchu (kineskop)

•

oddziaływanie przewodników z prądem na siebie

•

Magnesem jest sama Ziemia. Jej działanie na igłę kompasu jest znane od Starożytno-
ści.

Te oddziaływania opisujemy wprowadzając pojęcie

pola magnetycznego

.

21.5.1 Siła magnetyczna

Pole grawitacyjne (natężenie)

m

F

g

graw

=

Pole elektryczne (natężenie)

q

F

E

elekt

=

Pole magnetyczne (indukcja)

v

q

F

B

magn

=

(Siła działa na ładunki w ruchu i jest proporcjonalna do qv).
Jednostką B jest tesla; 1T = N/(Am)

Z. Kąkol-Notatki do Wykładu z Fizyki

21-7

Powyższy wzór jest prawdziwy dla ruchu ładunku prostopadle do B ale siła F

magn

(

siła Lorentza

) zależy od kierunku

v. Ta zależność od kierunku jest zapisana poprzez

równanie wektorowe

B

F

×

=

v

q

magn

(21.10)

gdzie kierunek definiuje się z reguły śruby prawoskrętnej (iloczyn wektorowy).

Zauważmy, że

F

magn

jest zawsze prostopadłe do

v

. Zatem, zgodnie z twierdzeniem

o pracy i energii F

magn

nie może zmienić energii kinetycznej poruszającego się ładunku

i ładunek krąży po okręgu. Stąd

B

q

R

m

v

v

=

2

qB

m

R

v

=

jest promieniem okręgu.

Siła działa na ładunki w ruchu więc działa na cały przewodnik z prądem.

F = ev

u

B

B

nSe

I

e

F

=

W przewodniku o długości l znajduje się nSl elektronów, więc całkowita siła

lB

I

B

nS

I

l

nS

F

=

=

Równanie w ogólnym przypadku ma postać

B

l

F

×

=

I

(21.11)

21.5.2 Działanie pola magnetycznego na obwód z prądem

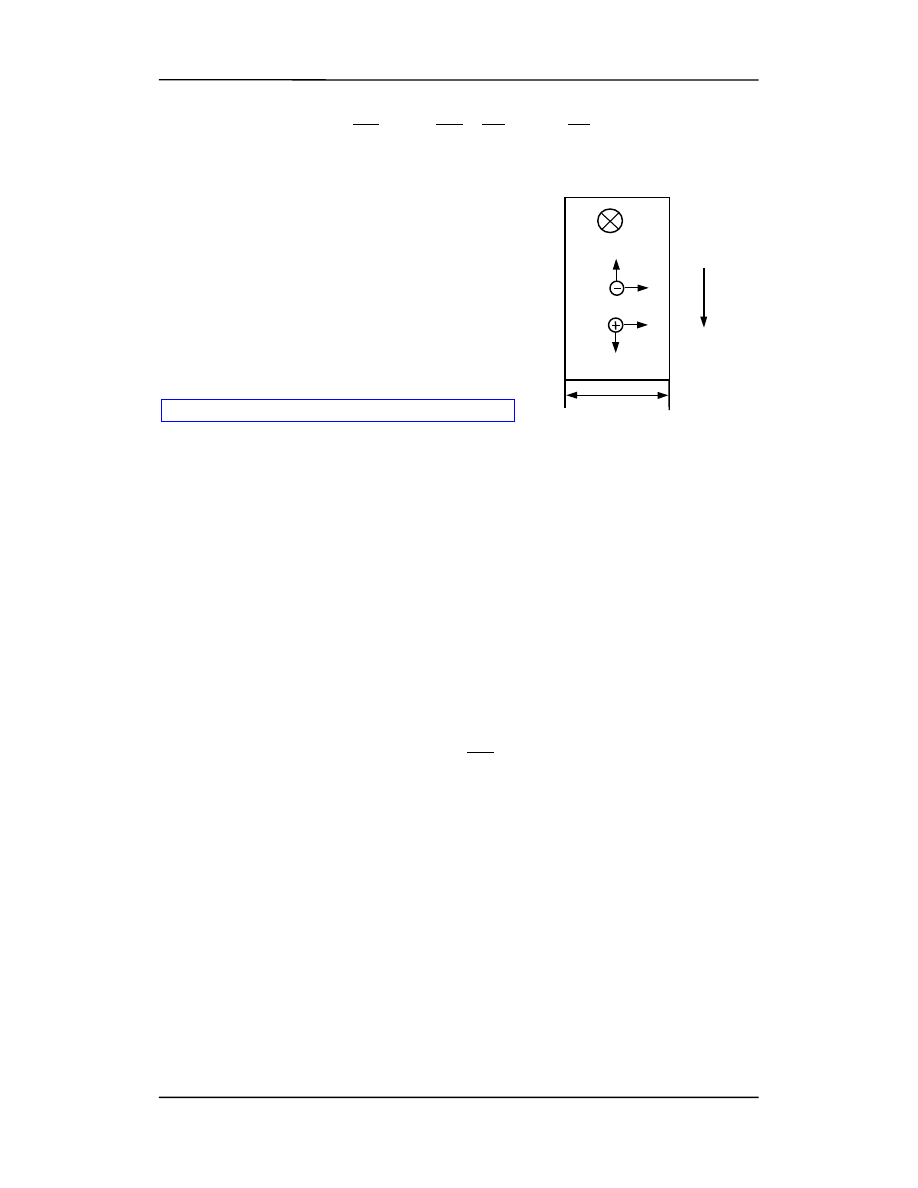
Rozważymy teraz działanie pola magnetycznego na za-

mknięty obwód z prądem.
Prostokątną ramkę o bokach a i b umieszczamy w jednorod-
nym polu magnetycznym o indukcji B. Przez ramkę płynie
prąd o natężeniu I, a normalna do płaszczyzny ramki tworzy

kąt

θ z polem B (rysunek).

Z. Kąkol-Notatki do Wykładu z Fizyki

21-8

Rozpatrujemy siłę działającą na każdy z boków. Siły F

b

działające na odcinki b zno-

szą się wzajemnie. Siły F

a

działające na odcinki a też się znoszą ale tworzą parę sił da-

jącą wypadkowy moment siły

θ

θ

θ

τ

sin

sin

sin

b

F

b

F

b

F

a

a

a

=

+

=

2

2

lub wektorowo (na podstawie definicji iloczynu wektorowego)

b

F

τ

×

=

a

Siła F

a

wynosi

IaB

F

a

=

więc

θ

θ

τ

sin

sin

ISB

IabB

=

=

(21.12)

gdzie S = ab jest powierzchnią ramki. Równanie (21.12) możemy zapisać w postaci
wektorowej

B

S

τ

×

=

I

(21.13)

gdzie S jest wektorem powierzchni.
Wielkość

S

μ I

=

(21.14)

nazywamy

magnetycznym momentem dipolowym

. Pole magnetyczne działa więc na

ramkę z prądem (dipol magnetyczny) momentem skręcającym obracając ją. Położenie
równowagi ramki (dipola magnetycznego) występuje dla

θ = 0 tj. gdy ramka jest usta-

wiona prostopadle do pola B. Przykładem dipola magnetycznego jest igła kompasu, któ-
ra umieszczona w polu magnetycznym obraca się ustawiając zgodnie z polem.

Taką "kołową ramką z prądem" jest również elektron krążący po orbicie w atomie.

Moment dipolowy elektronu krążącego po orbicie o promieniu r wynosi

)

(

2

r

I

e

π

µ

=

Natężenie prądu wytwarzanego przez elektron o ładunku e przebiegający orbitę w czasie
T (okres obiegu) wynosi

r

e

T

e

t

q

I

π

2

v

=

=

=

gdzie

v jest prędkością elektronu. Stąd

Z. Kąkol-Notatki do Wykładu z Fizyki

21-9

L

m

e

r

m

m

e

r

e

r

r

e

e

2

)

(

2

2

)

(

2

2

=

=

=

=

v

v

v π

π

µ

gdzie L = mvr jest momentem pędu elektronu.
Elektron, krążący po orbicie jest więc elementar-
nym dipolem magnetycznym. Własności magne-
tyczne ciał są właśnie określone przez zachowanie
się tych elementarnych dipoli w polu magnetycz-
nym. Własności te omówimy na dalszych wykła-
dach.

Z momentem siły działającym na dipol związa-

na jest tzw.

energia magnetyczna

dipola Można

również pokazać, że ta energia wyraża się wzorem

E

m

= -

µB = - µBcosθ

(21.15)

Zauważmy, że minimum energii odpowiada ustawieniu dipola w kierunku równoległym
do pola magnetycznego B (

θ = 0).

21.5.3 Efekt Halla

Jeżeli płytkę metalu (lub półprzewodnika) umieścimy w polu magnetycznym,

prostopadłym do kierunku przepływu prądu, to na ładunki będzie działała siła odchyla-
jąca powodująca zakrzywienie torów ładunków w kierunku jednej ze ścianek bocznych
płytki. Niezależnie czy prąd jest związany z ruchem ładunków dodatnich czy ujemnych
mamy do czynienia z odchylaniem ładunków w kierunku jednej krawędzi. Przesunięcie
ładunków powoduje powstanie poprzecznego pola elektrycznego Halla E

H

. To pole

przeciwdziała dalszemu przesuwaniu ładunków. Pole Halla jest dane wzorem

d

U

E

xy

H

=

W stanie równowagi odchylające pole magnetyczne jest równoważone przez pole elek-
tryczne

qE

H

+ q(v

u

×

B) = 0

Stąd

E

H

= – v

u

×

B

Wynika stąd, że jeżeli zmierzymy E

H

i B to możemy znaleźć v

u

.

Gdy v

u

i B są prostopadłe to

E

H

= v

u

B

Ponieważ:

v

u

= j/ne

I

y

x

B

v

u

v

u

F

F

d

Z. Kąkol-Notatki do Wykładu z Fizyki

21-10

więc

E

H

= (jB)/(ne)

lub

n = (jB)/(eE

H

)

Możemy wyznaczyć n.
Można też wykorzystać ten efekt do pomiaru pola magnetycznego.