
NASA Technical Memorandum 4644
Shear Buckling Analysis
of a Hat-Stiffened Panel
November 1994
William L. Ko and Raymond H. Jackson

NASA Technical Memorandum 4644
National Aeronautics and
Space Administration
Office of Management
Scientific and Technical
Information Program
1994
William L. Ko and Raymond H. Jackson
Dryden Flight Research Center
Edwards, California
Shear Buckling Analysis
of a Hat-Stiffened Panel
ABSTRACT
A buckling analysis was performed on a hat-stiffened panel subjected to shear loading. Both local
buckling and global buckling were analyzed. The global shear buckling load was found to be several times
higher than the local shear buckling load. The classical shear buckling theory for a flat plate was found to
be useful in predicting the local shear buckling load of the hat-stiffened panel, and the predicted local shear
buckling loads thus obtained compare favorably with the results of finite element analysis.
NOMENCLATURE
cross-sectional area of one corrugation leg,
cross-sectional area of global panel segment bounded by
p,
Fourier coefficient of assumed trial function for
w (x, y),
in.
a
length of global panel, in.
b
horizontal distance between centers of corrugation and curved region
,
in
.
width of rectangular flat plate segment, in.
c
width of global panel, in.
D
flexural rigidity of flat plate,
D
*
flexural stiffness parameter,
transverse shear stiffnesses in
effective bending stiffnesses of equivalent hat-stiffened panel, in-lb
one-half of diagonal region of corrugation leg, in.
modulus of elasticity of hat material,
modulus of elasticity of face sheet material,
lower flat region of hat stiffener, in
.
upper flat region of hat stiffener, in.
shear modulus of hat material,
shear modulus of face sheet material,
distance between middle surfaces of hat top flat region and face sheet,
distance between middle surfaces of hat upper and lower flat regions, in.
A
A
lt
c
in
2
,
=
A
A
A
pt
s
1
2
--- f
1
f
2
–
(
)
t
c
in
2
,
+
+
=
A
mn
b
1
2
--- p
1
2
--- f
1
f
2
+
(
)
–
,
=
b
o
D
E
s
t
s
3
12 1
ν
s
2
–
(
)
------------------------- in-lb
,
=
D
x
D
y
, in-lb
D
Qx
D
Qy
,
xz-, yz-planes, lb/in
D
x
D
y
D
xy
,
,
d
E
c
lb/in
2
E
s
lb/in
2
f
1
f
2
G
c
lb/in
2
G
s
lb/in
2
h
h
h
c
1
2
--- t
c
t
s
+
(
)
in.
,
+
=
h
c

2
distance between middle surface of face sheet and centroid of global panel
segment, in.
moment of inertia, per unit width, of corrugation leg,
moment of inertia, per unit width, of one-half of reinforcing hat taken with
respect to the neutral axis
of the hat stiffened panel,
moment of inertia of corrugation leg of length
l
taken with respect to its neutral
axis
moment of inertia, per unit width, of corrugation flat region
moment of inertia, per unit width, of face sheet with respect to
axis passing
through the centroid of the global panel segment,
moment of inertia, per unit width, of face sheet and corrugation flat region combined,
shear buckling load factor
l
length of corrugation leg,
length of one-half of hat,
m
number of buckle half-waves in x-direction
panel shear load, lb/in
n
number of buckle half-waves in y-direction
p
one half of reinforcing hat pitch, in.
shear buckling load, lb
shear flow in flat panel, lb/in
shear flow in hat, lb/in
radius of circular arc segments of corrugation leg, in.
thickness of reinforcing hat, in.
thickness of face sheet, in.
w
panel out-of-plane displacement, in.
x, y
rectangular Cartesian coordinates, in.
panel twist, 1/in
neutral axis of corrugation leg and face sheet combined
h
o
I
c
1
12
------t
c
3
in
4
/in
,
I
c
η
o
in
4
/in
I
c
*
η
in
4
,
I
f
1
12
------t
c
3
in
4
/in
,
I
s
η
o
I
s
t
s
h
o
2
1
12
------t
s
3
in
4
/in
,
+
=
I
s
′
1
12
------ t
s
t
c
+
(
)
3
in
4
/in
,
k
xy
l
f
2
2d
2 R
θ
in.
,
+
+
=
l
l
l
1
2
--- f
1
f
2
–
(
)
in.
,
+
=
N
xy
Q
cr
q
1
q
c
R
t
c
t
s
∂
2
w
∂
x
∂
y
------------
η
o

3
corrugation angle (angle between the face sheet and the straight diagonal
segment of corrugation leg), rad
Poisson ratio of hat material
Poisson ratio of face sheet material
shear stress,
critical value at buckling
INTRODUCTION
Recently, various hot-structural panel concepts were advanced for applications to hypersonic aircraft
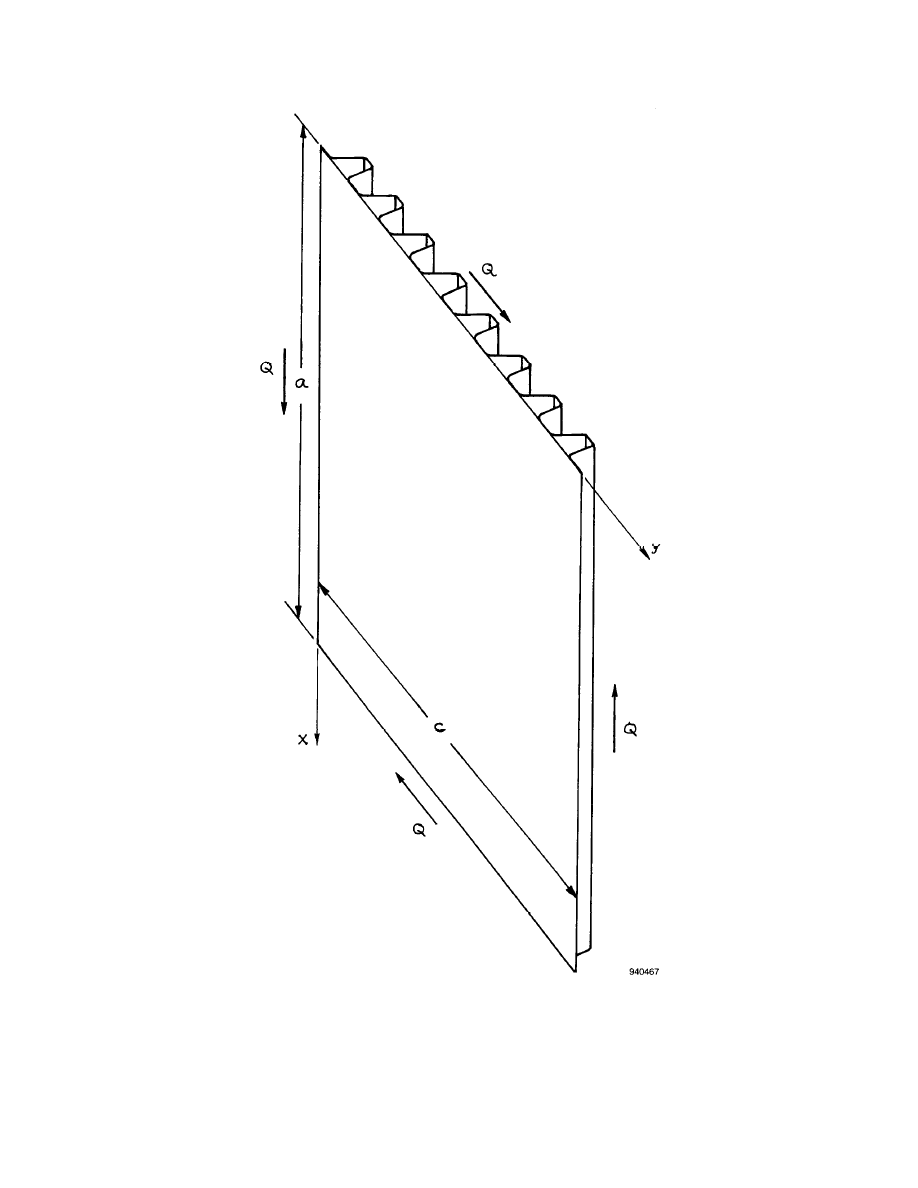
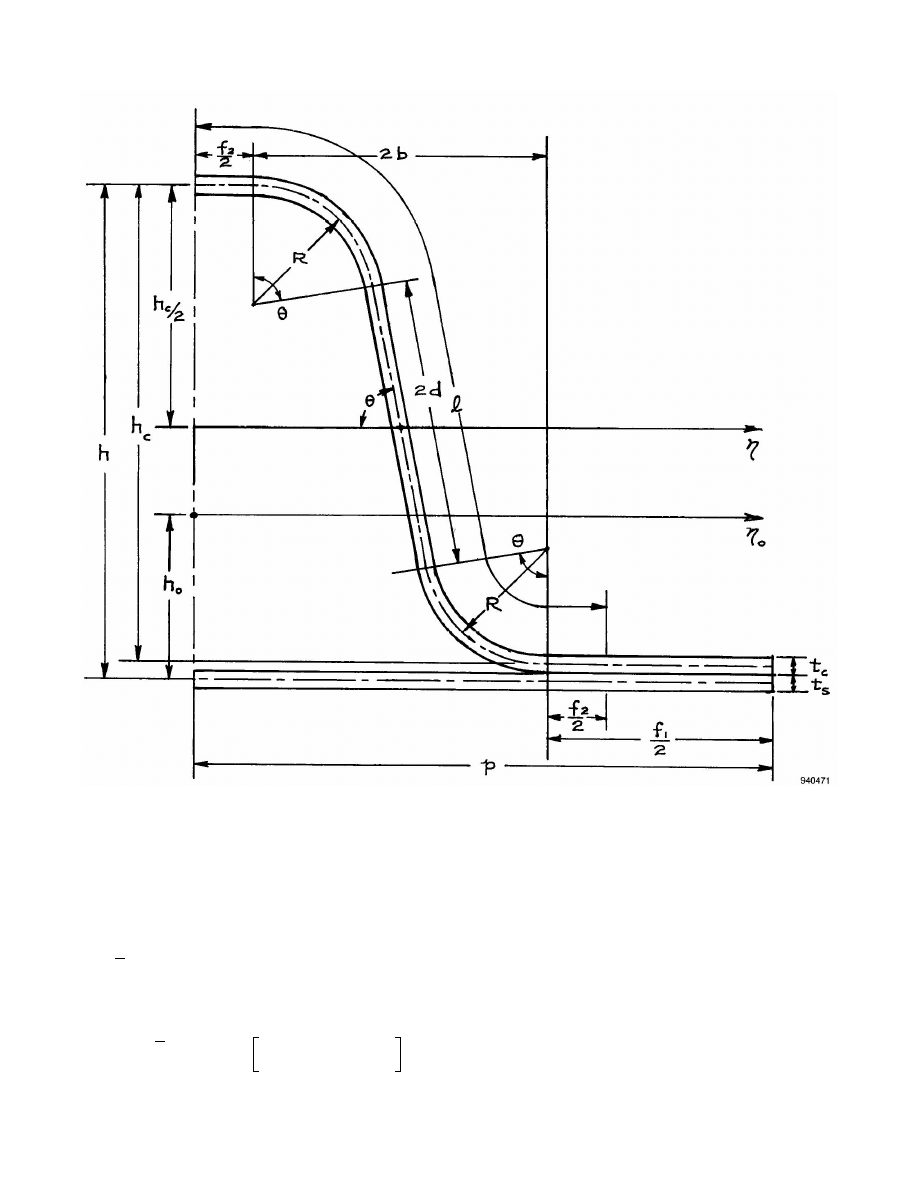
structural panels. Among those panels investigated, the hat-stiffened panel (fig. 1) was found to be an ex-
cellent candidate for potential application to hypersonic aircraft fuselage panels. This type of panel is
equivalent to a corrugated core sandwich panel with one face sheet removed.
Buckling behavior of the hat-stiffened panel under compressive loading in the hat-axial direction, was
investigated by Ko and Jackson recently (ref. 1). They calculated both the local and global (general panel
instability) compressive buckling loads for the panel. The calculated local compressive buckling load was
found to be far lower than the global compressive buckling load, and compared fairly well with the exper-
imental data. To fully understand buckling characteristics of the hat-stiffened panel, the shear buckling be-
havior of this panel needs to be investigated.
This report presents the local and global buckling analyses of the hat-stiffened panel subjected to shear
loading. The predicted shear buckling loads are compared with the finite element shear buckling solutions.
SHEAR BUCKLING ANALYSIS
To analyze the buckling behavior of the complex structure shown in figure 1, two approaches were
taken: (1) local buckling analysis, and (2) global buckling analysis (general panel instability). The follow-
ing sections describe these approaches.
Local Buckling
The purpose of local buckling analysis was to study the buckling behavior of a local weak region of
the panel. This weak region is identified as a rectangular flat plate region bounded by two legs of the re-
inforcing hat located at the center of the global panel (left diagram of fig. 2). The analysis looked at the
buckling behavior of this rectangular flat plate (slender strip). Because the reinforcing hat has high flexural
rigidity, the four edges of the rectangular plate were assumed to be simply supported (right diagram of
fig. 2). From reference 2, the shear buckling stress
in the rectangular flat plate may be written as
(1)
θ
ν
c
ν
s
τ
xy
lb/in
2
( )
cr
τ
xy
(
)
cr
τ
xy
(
)
cr
k
xy
π
2
D
b
o
2
t
s
----------
=
4
Figure 1. Hat-stiffened panel under shear loading.
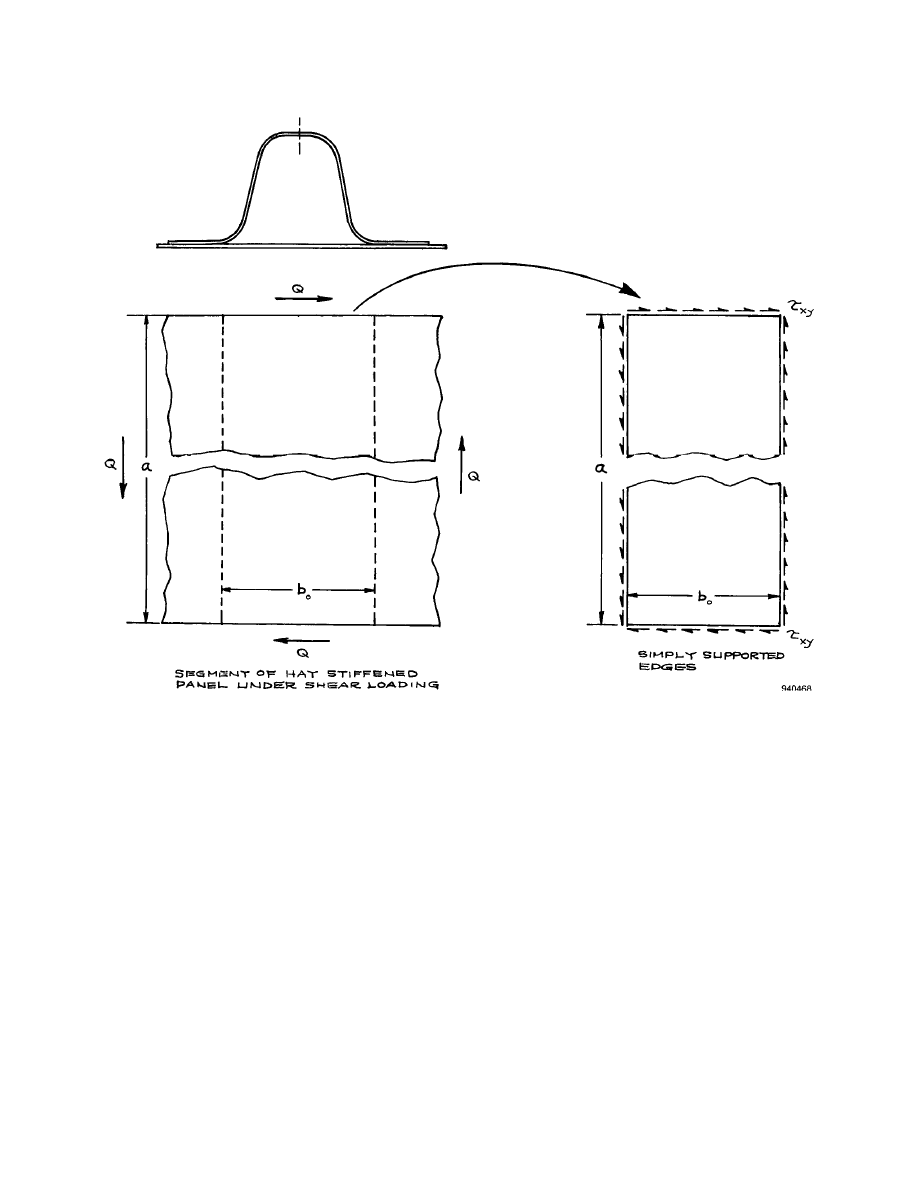
5
Figure 2. Shear buckling of hat-stiffened panel analyzed using a simple model.
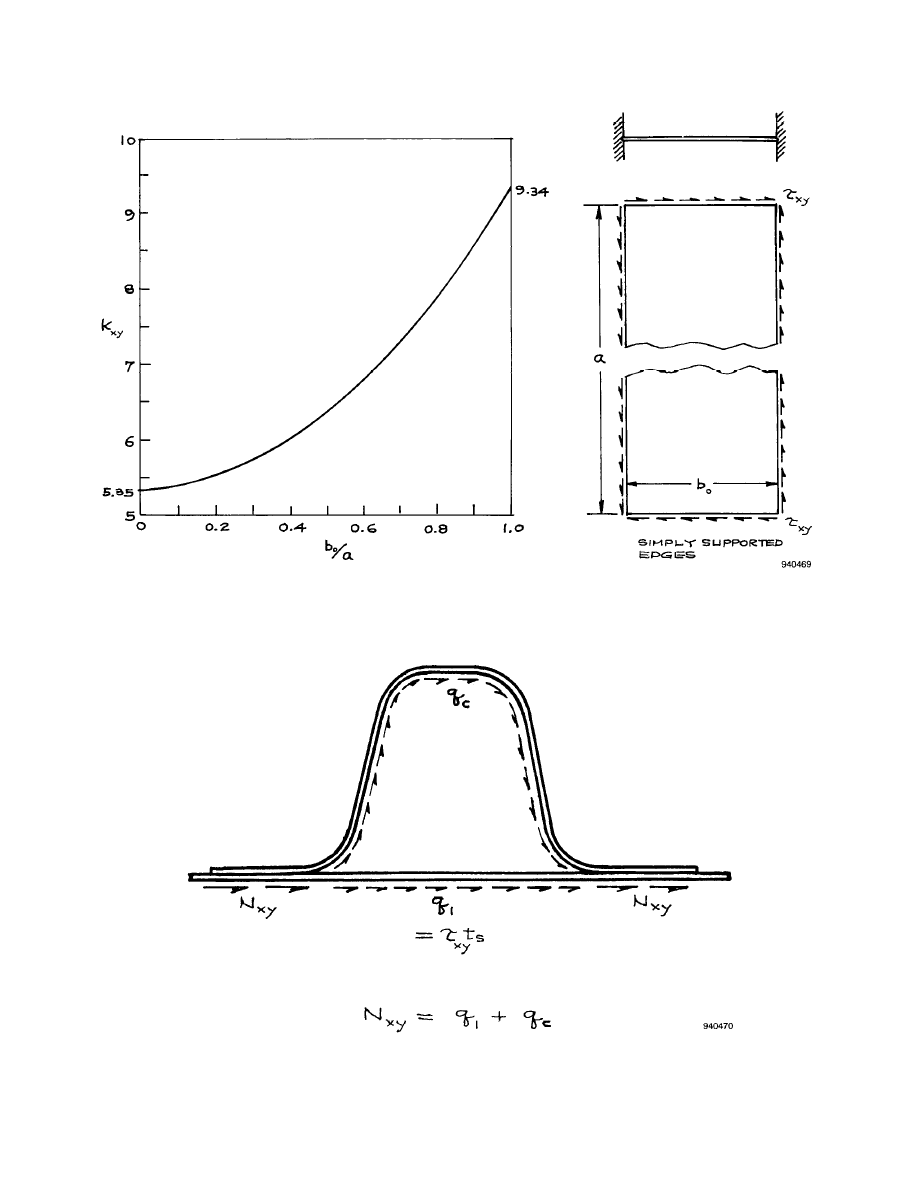
where
is the shear buckling load factor, which is a function of panel aspect ratio
. For
(a
square panel),
; and for
(an infinitely long panel),
. For intermediate val-
ues of
,
may be found from a parabolic curve-fitting equation of the form (ref. 2)
(2)
The curve described by equation (2) is shown on the left in figure 3. The panel shear load
for the hat-
stiffened strip (left diagram of fig. 2) may be written in terms of shear flows (fig. 4) as (ref. 4)
k
xy
b
o
a
-----
b
o
a
-----
1
=
k
xy
9.34
=
b
o
a
-----
0
=
k
xy
5.35
=
b
o
a
----- k
xy
k
xy
5.35
4
b
o
a
-----
2
+
=
N
xy
6
Figure 3. Shear buckling load parameter as a function of panel aspect ratio.
Figure 4. Shear flows in the reinforcing hat and the flat region under the hat.
7
(3)
where
and
are, respectively, the shear flows in the flat panel and the hat, and are given by (ref. 4)
(4)
and
(5)
where
is the panel twist.
From equations (4) and (5), the ratio
may be calculated. Then, from equation (3), the panel shear
buckling load
of the hat-stiffened strip may be calculated as a function of
(eq. (1)).
Global Buckling
In the global buckling analysis (general instability analysis), the complex panel was represented by a
homogeneous anisotropic panel having effective elastic constants. These effective elastic constants must
be calculated first (ref. 3). This analysis is similar to the conventional buckling analysis of a sandwich
panel with one face sheet removed.
By using the small-deflection theory developed for flat sandwich plates (ref. 5) and solving the shear
buckling problem of the hat-stiffened plate using the Rayleigh-Ritz method of minimizing the total poten-
tial energy of a structural system (refs. 5 through 9), the following shear buckling equation is obtained:
(6)
where
(7)
classical thin transverse shear effect terms
plate theory
(8)
N
xy
q
1
q
c
+
=
q
1
q
c
q
1
τ
xy
t
s
2G
s
h
o
t
s
∂
2
w
∂
x
∂
y
------------
=
=
q
c
G
c
t
c
p
l
-------------- h
2h
o
h
c
2 p
------ f
1
f
2
–
(
)
–
–
∂
2
w
∂
x
∂
y
------------
=
∂
2
w
∂
x
∂
y
------------
q
1
/q
c
N
xy
(
)
cr
τ
xy
(
)
cr
M
mn
k
xy
----------- A
mn
δ
mnij
A
ij
j
1
=
∞
∑
i
1
=
∞
∑
+
0
=
M
mn
1
32
------
ab
D
*
--------
a
π
---
2
a
mn
11
a
mn
12
a
mn
23
a
mn
31
a
mn
21
a
mn
33
–
(
)
a
mn
13
a
mn
21
a
mn
32
a
mn
22
a
mn
31
–
(
)
+
a
mn
22
a
mn
33
a
mn
23
a
mn
32
–
------------------------------------------------------------------------------------------------------------------------
+
=
δ
mnij
mnij
m
2
i
2
–
(
)
n
2
j
2
–
(
)
---------------------------------------------
m \ i n \ j
,
=
,
=
m
i = odd,
±
n
j
±
odd
=
;
≡
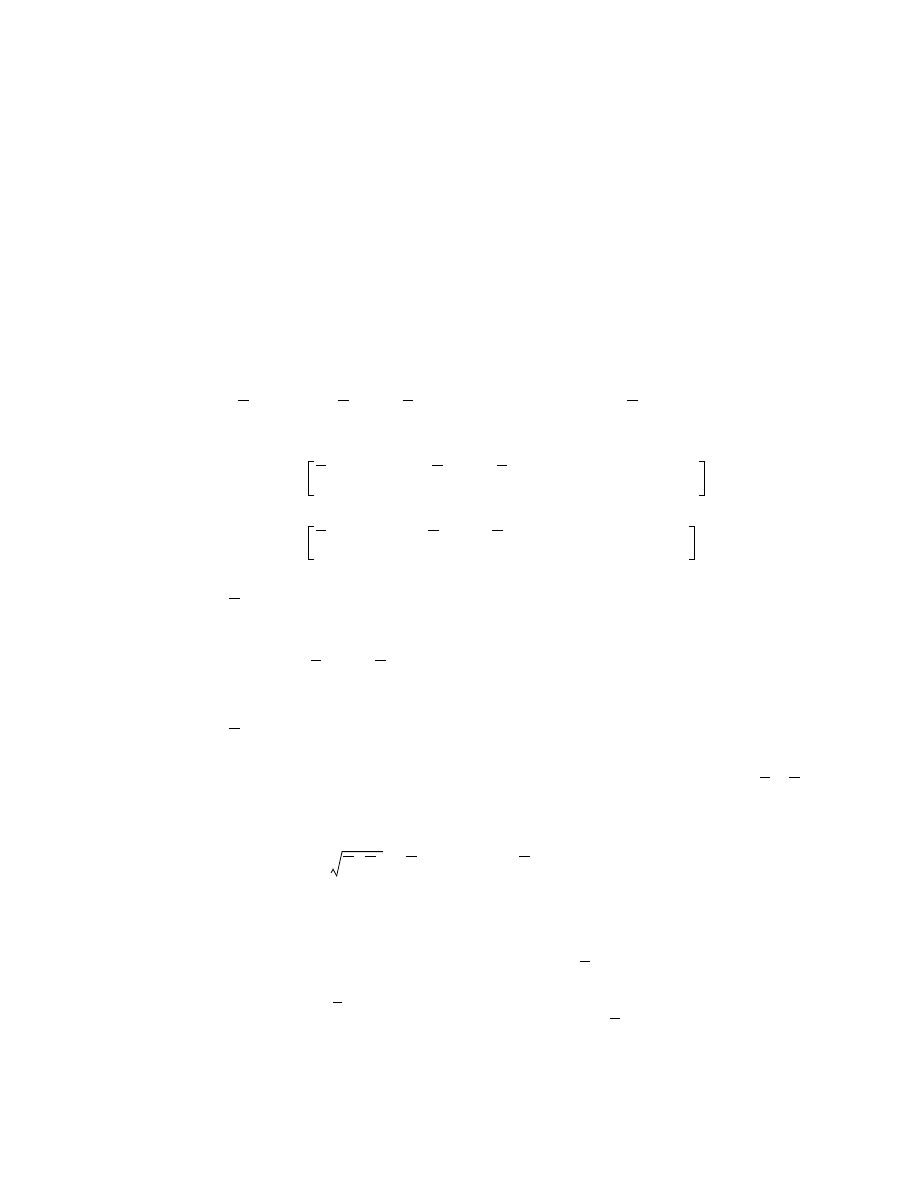
8
and
are the undetermined Fourier coefficients of the assumed out-of-plane displacement w (x, y) of
the plate given by
(9)
Lastly, the shear buckling load factor
appearing in equation (6) and the coefficients of characteristic
equation
= 1, 2, 3) appearing in equation (7) are defined, respectively, as (ref. 7)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
where the flexural stiffness parameter D
*
and the flexural rigidities of the effective panel
are
defined as
(17)
where
(18)
A
mn
w x y
,
(
)
A
mn
m
π
x
a
-----------
n
π
y
c
---------
sin
sin
n=1
∞
∑
m=1
∞
∑
=
k
xy
a
mn
rs
r s
,
(
k
xy
N
xy
(
)
cr
a
2
π
2
D
*
------------------------
=
a
mn
11
D
x
m
π
a
-------
4
D
x
ν
yx
D
y
ν
xy
2D
xy
+
+
(
)
m
π
a
-------
2
n
π
c
------
2
D
y
n
π
c
------
4
+
+
=
a
mn
12
a
mn
21
D
x
m
π
a
-------
3
1
2
--- D
x
ν
yx
D
+
y
ν
xy
2D
xy
+
(
)
m
π
a
-------
n
π
c
------
2
+
–
=
=
a
mn
13
a
mn
31
D
y
n
π
c
------
3
1
2
--- D
x
ν
yx
D
+
y
ν
xy
2D
xy
+
(
)
m
π
a
-------
2
n
π
c
------
+
–
=
=
a
mn
22
D
x
m
π
a
-------
2
D
xy
2
---------
n
π
c
------
+
2
D
Qx
+
=
a
mn
23
a
mn
32
1
2
--- D
x
ν
yx
D
y
ν
xy
D
xy
+
+
(
)
m
π
a
-------
n
π
c
------
=
=
a
mn
33
D
y
n
π
c
------
2
D
xy
2
---------
m
π
a
-------
+
2
D
Qy
+
=
D
x
D
y
,
D
*
D
x
D
y
D
x
,
D
x
1
ν
s
2
–
-------------- D
y
,
D
y
1
ν
s
2
–
--------------
=
=
=
D
x
E
c
I
c
E
s
I
s
D
y
,
+
E
s
I
s
1
E
c
I
c
E
s
I
s
------------
+
1
1
ν
s
2
–
(
)
E
c
I
c
E
s
I
s
------------
+
------------------------------------------
=
=
9
Figure 5. Segment of hat-stiffened flat panel.
where
(19)
and
is the moment of inertia, per unit width, taken with respect to the panel neutral axis
(fig. 5),
and is given by
(20)
I
s
t
s
h
o
2
1
12
------t
s
3
+
=
I
c
η
o
I
c
I
c
*
p
------
A
p
---
1
2
--- h
c
t
c
t
s
+
+
(
)
h
o
–
2
1
24 p
--------- f
1
f
2
–
(
)
t
c
3
f
1
f
2
–
2 p
-----------------t
c
h
o
t
c
t
s
+
2
--------------
–
2
+
+
+
=
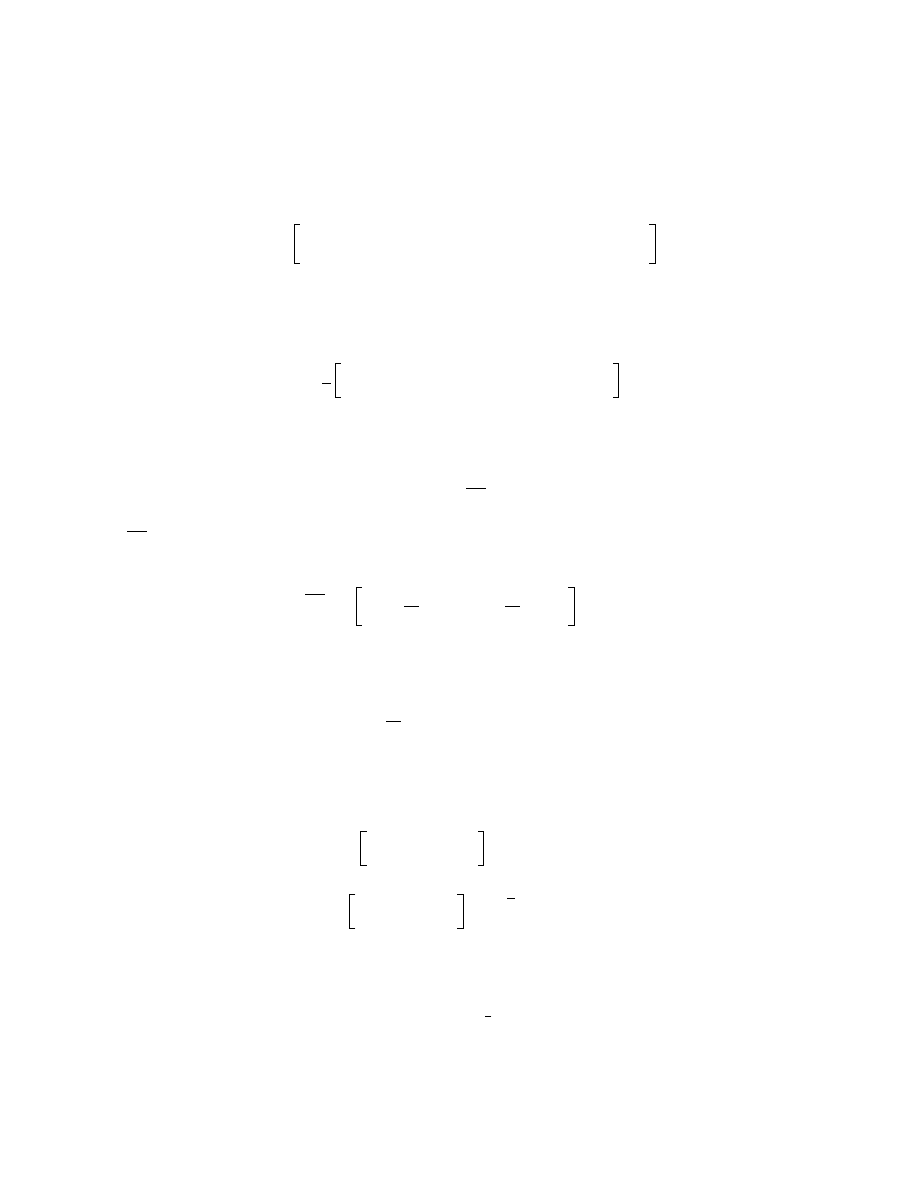
10
where
is the moment of inertia of a corrugation leg of length l, taken with respect to its neutral axis
(fig. 5), and is given by
(21)
and
appearing in equation (19) is the distance between the middle surface of the face sheet and the panel
neutral axis
given by
(22)
The twisting stiffness
appearing in the expressions of
(eqs. (11) through (16)) may be obtained
from reference 4 with slight modification to fit the present problem in the following form:
(23)
where
is the torsional stiffness given by
(24)
where
(25)
and
(26)
(27)
The shear stiffnesses
and
appearing in equations (14) and (16) are given by
(28)
I
c
*
η
I
c
*
h
c
3
t
c
1
4
---
f
2
h
c
----- 1
1
3
---
t
c
2
h
c
2
-----
+
2
3
---
d
3
h
c
3
----- sin
2
θ
1
4
---
t
c
2
d
2
----- cos
2
θ
+
+
=
R
h
c
-----
θ
2
---
R
2
h
c
2
------
θ
1
θ
cos
–
(
)
R
h
c
----- 2
3
R
h
c
-----
–
–
θ
θ
sin
–
(
)
sin
–
+
h
o
η
o
h
o
1
2 A
------- A h
c
t
c
t
s
+
+
(
)
1
2
---t
c
f
1
f
2
–
(
)
t
c
t
s
+
(
)
+
=
D
xy
a
mn
rs
D
xy
2GJ
=
GJ
GJ
G
s
t
s
k
GJ
2
pG
c
t
c
2
A
c
--------------- k
GJ
k
c
–
(
)
2
+
h
2
=
k
GJ
k
c
1
A
c
G
s
t
s
pG
c
t
c
----------------
+
--------------------------
=
k
c
1
2
--- 1
f
1
f
2
–
(
)
h
c
2 ph
----------------------------
–
=
A
c
l
1
2
--- f
1
f
2
–
(
)
+
t
c
l t
c
=
=
D
Qx
D
Qy
D
Qx
G
c
t
c
h
2
pl
---------------- D
Qy
,
Sh
E
c
1
ν
c
2
–
--------------
t
c
h
c
-----
3
=
=
11
where the nondimensional coefficient is defined as
(29)
where the nondimensional parameters
and
are defined as
(30)
(31)
(32)
where
(33)
The shear buckling equation (6) yields a set of homogeneous equations associated with different values of
m and n. This set of equations may be divided into two groups that are independent of each other: one
group in which m
±
n is odd (that is, antisymmetrical buckling), and the other in which m
±
n is even (that
S
S
6
h
c
p
----- D
z
F
t
s
t
c
---
p
h
c
-----
2
+
12
h
h
c
-----
p
h
c
----- D
z
F
2
p
h
c
-----
2
D
z
H
–
h
c
h
----- 6
t
s
t
c
--- D
z
F
D
y
H
D
z
H
2
–
(
)
p
h
c
-----
3
D
y
H
+
+
------------------------------------------------------------------------------------------------------------------------------------------------------------
=
D
z
F
,
D
z
H
,
D
y
H
D
z
F
2
3
---
d
h
c
-----
3
cos
2
θ
2
3
---
I
c
I
f
-----
1
8
---
p
h
c
-----
3
b
h
c
-----
3
–
+
=
R
h
c
----- 2
b
h
c
-----
2
θ
4
Rb
h
c
2
-------
–
1 – cos
θ
(
)
R
h
c
-----
2
θ
θ
sin
θ
cos
–
(
)
+
+
I
c
h
c
2
t
c
--------- 2
d
h
c
-----sin
2
θ
R
h
c
-----
θ
θ
sin
θ
cos
–
(
)
+
+
D
z
H
2
3
---
d
h
c
-----
3
θ
c
sin
os
θ
1
2
---
I
c
I
f
-----
1
4
---
p
h
c
-----
2
b
h
c
-----
2
–
+
=
R
h
c
-----
b
h
c
-----
θ
2
Rb
h
c
2
-------
θ
θ
sin
–
(
)
–
R
h
c
----- 1 – cos
θ
(
)
1
R
h
c
----- 1 – cos
θ
(
)
–
–
+
I
c
h
c
2
t
c
--------- 2
d
h
c
----- sin
θ
θ
R
h
c
-----
+
cos
sin
2
θ
–
D
y
H
2
3
---
d
h
c
-----
3
sin
2
θ
1
2
---
R
h
c
-----
θ
1
2
---
f
h
c
-----
I
c
I
f
-----
+
+
=
R
h
c
-----
2
2
3
R
h
c
-----
–
θ
θ
sin
–
(
)
R
h
c
-----
θ
1
θ
cos
–
(
)
sin
+
–
I
c
h
c
2
t
c
---------
f
h
c
-----
t
c
t
f
----
2
d
h
c
-----cos
2
θ
R
h
c
-----
θ
θ
cos
sin
θ
+
(
)
+
+
+
f
1
2
--- f
1
f
2
+
(
)
b
,
1
2
--- p
1
2
--- f
1
f
2
+
(
)
–
I
c
,
1
12
------t
c
3
I
f
,
1
12
------t
s
3
=
=
=
=

12
is, symmetrical buckling) (refs. 7 and 9). Those equations may be written for as many half-wave numbers
as required for convergence of eigenvalue solutions. For the deflection coefficients
to have values
other than zero, the determinant of the coefficients of the unknown
of the simultaneous homogeneous
equations must vanish. The largest eigenvalue
thus obtained will give the lowest value of
.
Representative 12 12 determinants in terms of the coefficients of homogeneous simultaneous
equations written out from equation (6) for which m
±
n is even and odd are given in the following
(refs. 10 and 11):
For m
±
n = even (symmetrical buckling):
(34)
where the nonzero off-diagonal terms satisfy the conditions m =\ i , n =\ j, m
±
i = odd, and n
±
j = odd.
m=1, n=1
0
0
0
0
0
0
0
m=1, n=3
0
0
0
0
0
0
m=2, n=2
0
0
0
m=3, n=1
0
0
0
0
0
m=1, n=5
0
0
0
0
m=2, n=4
0
0
= 0
m=3, n=3
Symmetry
0
0
0
m=4, n=2
0
m=5, n=1
0
0
m=3, n=5
0
m=4, n=4
m=5, n=3
A
mn
A
mn
1
k
xy
-------
k
xy
×
m n\
,
i j
,
A
11
A
13
A
22
A
31
A
15
A
24
A
33
A
42
A
51
A
35
A
44
A
53
M
11
k
xy
----------
4
9
---
8
45
------
8
45
------
16
225
---------
M
13
k
xy
----------
4
5
---
–
8
7
---
8
25
------
–
16
35
------
M
22
k
xy
----------
4
5
---
–
20
63
-------
–
36
25
------
20
63
------
–
4
7
---
4
7
---
M
31
k
xy
----------
8
25
------
–
8
7
---
16
35
------
M
15
k
xy
----------
40
27
------
–
8
63
------
–
16
27
------
–
M
24
k
xy
----------
72
35
------
–
8
63
------
–
8
3
---
120
147
---------
–
M
33
k
xy
----------
72
35
------
–
144
49
---------
M
42
k
xy
----------
40
27
------
–
120
147
---------
–
8
3
---
M
51
k
xy
----------
16
27
------
–
M
35
k
xy
----------
80
21
------
–
M
44
k
xy
----------
80
21
------
–
M
53
k
xy
----------

13
For m
±
n = odd (antisymmetrical buckling):
(35)
where the nonzero off-diagonal terms satisfy the conditions m =\ i , n =\ j, m
±
i = odd, and n
±
j = odd.
Notice that the diagonal terms in equations (34) and (35) came from the first term of equation (6), and
the series term of equation (6) gives the off-diagonal terms of the matrices. The 12 12 determinant was
found to give sufficiently accurate eigenvalue solutions.
m=1, n=2
0
0
0
0
0
m=2, n=1
0
0
0
0
0
m=1, n=4
0
0
0
0
m=2, n=3
0
0
0
0
m=3, n=2
0
0
0
m=4, n=1
0
0
0
= 0
m=1, n=6
Symmetry
0
0
m=2, n=5
0
0
m=3, n=4
0
m=4, n=3
0
m=5, n=2
m=6, n=1
m n\
,
i j
,
A
12
A
21
A
14
A
23
A
32
A
41
A
16
A
25
A
34
A
43
A
52
A
61
M
12
k
xy
----------
4
9
---
–
4
5
---
8
45
------
–
20
63
------
8
25
------
4
35
------
–
M
21
k
xy
----------
8
45
------
–
4
5
---
4
35
------
–
8
25
------
20
63
------
M
14
k
xy
----------
8
7
---
–
16
225
---------
–
40
27
------
16
35
------
–
8
175
---------
–
M
23
k
xy
----------
36
25
------
–
4
9
---
–
72
35
------
4
7
---
–
M
32
k
xy
----------
8
7
---
–
4
7
---
–
72
35
------
4
9
---
–
M
41
k
xy
----------
8
175
---------
–
16
35
------
–
40
27
------
M
16
k
xy
----------
20
11
------
–
8
45
------
–
36
1225
------------
–
M
25
k
xy
----------
8
3
---
–
100
441
---------
–
M
34
k
xy
----------
144
49
---------
–
8
45
------
–
M
43
k
xy
----------
8
3
---
–
M
52
k
xy
----------
20
11
------
–
M
61
k
xy
----------
×

14
NUMERICAL RESULTS
The titanium hat-stiffened panel has the following material properties and geometries:
Local Buckling
For
and
equation (2) gives
The shear buckling stress
may then be calculated from equation (1) as
(36)
From equations (4) and (5) the ratio of
/
has the value
(37)
Thus, from equation (3), the panel shear buckling load
may be calculated as
(38)
(39)
(40)
which gives the shear buckling load of
=
=
=
=
=
=
=
=
=
=
=
=
=
=
=
E
s
E
c
6.2
10
6
lb/in
2
×
=
G
s
G
c
6.2
10
6
lb/in
2
×
=
ν
s
ν
c
0.31
=
a
24 in.
b
o
1.77 in. (width of rectangular flat strip)
c
24 in.
d
0.3505 in.
f
1
1.12 in.
f
2
0.26 in.
h
h
c
1
2
--- t
c
t
s
+
(
)
+
1.2180 in.
=
h
c
1.1860 in.
p
1.49 in.
R
0.346 in.
t
s
t
c
0.032 in.
=
θ
79.13
°
1.3811 rad
=
a
24 in.
=
b
o
1.77 in.,
=
k
xy
5.37 .
=
τ
xy
(
)
cr
τ
xy
(
)
cr
25 553 lb/in
2
,
=
q
1
q
c
q
1
q
c
-----
3.4727
=
N
xy
(
)
cr
N
xy
(
)
cr
q
1
1
q
c
q
1
-----
+
=
τ
xy
(
)
cr
t
s
1
1
3.4727
----------------
+
=
1 054 lb/in
,
=
Q
cr
25 296 lb.
,
=
15
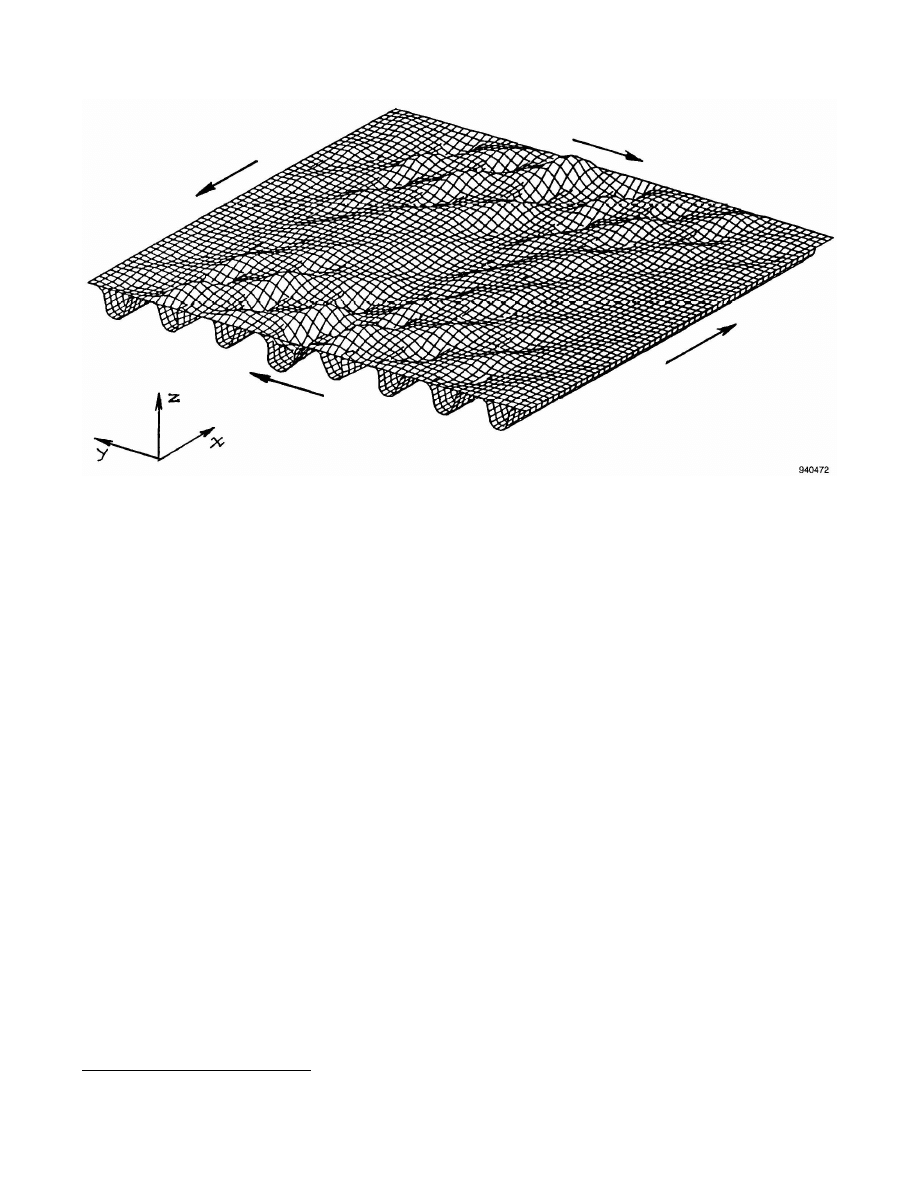
Figure 6. Buckling shape of hat-stiffened panel under shear loading (finite element analysis by
W. Percy, Mc-Donnell-Douglas; full-panel model).
This local shear buckling load prediction is slightly higher than the value
calcu-
lated from finite element buckling analysis carried out by W. Percy of McDonnell-Douglas.* Figure 6
shows the shear buckling shape of the hat-stiffened panel based on Percy’s full-panel finite element model.
Clearly, the panel is under local buckling rather than general instability. The local buckling analysis pre-
dicts a slightly higher value of
because the four edges of the rectangular plate strip analyzed were
assumed to be simply supported. In reality, those four edges are elastically supported.
Global Buckling
To find the order of the determinant (review eqs. (34) and (35)) for converged eigenvalue solutions,
several different orders of the determinants were used for the calculations of
. The eigenvalues were
found to have sufficiently converged beyond order 10. In the actual calculations of
, the orders of the
determinants were taken to be 12, which were shown in equations (34) and (35). The eigenvalue solutions
thus obtained give the following lowest values of
m
±
n = even:
(41)
m
±
n = odd:
(42)
Thus, the square panel will buckle symmetrically. Using
= 1.89, the panel shear buckling load
may be calculated from equation (10) as
*Personal communication with author.
N
xy
(
)
cr
900 lb/in
=
N
xy
(
)
cr
k
xy
k
xy
k
xy
:
k
xy
1.89
=
k
xy
1.93
=
k
xy
N
xy
(
)
cr

16
(43)
which gives the shear buckling load of
this is about four times higher than the local
shear buckling load of
Thus, the panel is unlikely to fail under global buckling.
Summary of Data
The results of the shear buckling analysis of the hat-stiffened panel are summarized in the following
table.
CONCLUSION
The shear buckling behavior of a hat-stiffened panel was analyzed in light of local buckling and global
buckling. The predicted local buckling loads were slightly higher than those predicted using finite element
buckling analysis. The global buckling theory predicted a buckling load about four times higher than was
predicted from local buckling theory. Therefore, the hat-stiffened panel will buckle locally instead of
globally.
REFERENCES
1. Ko, William L. and Raymond H. Jackson, Compressive Buckling Analysis of Hat-Stiffened Panel,
NASA TM-4310, Aug. 1991.
2. Timoshenko, Stephen P. and James M. Gere, Theory of Elastic Stability, McGraw-Hill Book Co., New
York, 1961.
3. Ko, W. L., “Elastic Stability of Superplastically Formed/Diffusion Bonded Orthogonally Corrugated
Core Sandwich Plates,” AIAA 80-0683, presented at the AIAA/ASME/ASCE/AHS/AHC 21st Struc-
tures, Structural Dynamics, and Materials Conference, Seattle, WA, May 12–14, 1980.
4. Libove, Charles and Ralph E. Hubka, Elastic Constants for Corrugated-Core Sandwich Plates,
NACA TN-2289, 1951.
5. Libove, C. and S. B. Batdorf, A General Small-Deflection Theory for Flat Sandwich Plates, NACA
TN-1526, 1948.
6. Bert, Charles W. and K. N. Cho, “Uniaxial Compressive and Shear Buckling in Orthotropic Sandwich
Plates by Improved Theory,” AIAA 86-0977, presented at the AIAA/ASME/ASCE/AHC 27th Struc-
tures, Structural Dynamics, and Materials Conference, San Antonio, TX, May 19–21, 1986.
7. Ko, William L. and Raymond H. Jackson, Combined Compressive and Shear Buckling Analysis of Hy-
personic Aircraft Structural Sandwich Panels, NASA TM-4290. Also AIAA 92-2487-CP, presented
Comparison of shear buckling loads.
,
Case
lb/in
lb
Local buckling
1,054
25,296
Global buckling
4,296
103,107
W. Percy’s finite element
(footnote, p. 15)
900
21,600
N
xy
(
)
cr
4 296 lb/in
,
=
Q
cr
103 107 lb;
,
=
Q
cr
25 296 lb.
,
=
τ
xy
(
)
cr
,
Q
cr

17
at the AIAA/ASME/ASCE/AHS/ASC 33rd Structures, Structural Dynamics, and Materials Confer-
ence, Dallas, TX, Apr. 13–15, 1992.
8. Ko, William L. and Raymond H. Jackson, Combined Load Buckling Behavior of Metal-Matrix Com-
posite Sandwich Panels Under Different Thermal Environments, NASA TM-4321, Sept. 1991.
9. Ko, William L. and Raymond H. Jackson, Compressive and Shear Buckling Analysis of Metal-Matrix
Composite Sandwich Panels Under Different Thermal Environments, NASA TM-4492, June 1993.
Originally prepared for the 7th International Conference on Composite Structures, University of Pais-
ley, Paisley, Scotland, July 1993.
10. Stein, Manuel and John Neff, Buckling Stresses of Simply Supported Rectangular Flat Plates in Shear,
NACA TN-1222, 1947.
11. Batdorf, S. B. and Manuel Stein, Critical Combinations of Shear and Direct Stress for Simply Sup-
ported Rectangular Flat Plates, NACA TN-1223, 1947.
REPORT DOCUMENTATION PAGE
Form Approved
OMB No. 0704-0188
Public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions, searching existing data sources,
gathering and maintaining the data needed, and completing and reviewing the collection of information. Send comments regarding this burden estimate or any other aspect of this col-
lection of information, including suggestions for reducing this burden, to Washington Headquarters Services, Directorate for Information Operations and Reports, 1215 Jefferson Davis
Highway, Suite 1204, Arlington, VA 22202-4302, and to the Office of Management and Budget, Paperwork Reduction Project (0704-0188), Washington, DC 20503.
1. AGENCY USE ONLY (Leave blank)
2. REPORT DATE
3. REPORT TYPE AND DATES COVERED
4. TITLE AND SUBTITLE
5. FUNDING NUMBERS
6. AUTHOR(S)
8. PERFORMING ORGANIZATION
REPORT NUMBER
7. PERFORMING ORGANIZATION NAME(S) AND ADDRESS(ES)
9. SPONSORING/MONITORING AGENCY NAME(S) AND ADDRESS(ES)
10. SPONSORING/MONITORING
AGENCY REPORT NUMBER
11. SUPPLEMENTARY NOTES
12a. DISTRIBUTION/AVAILABILITY STATEMENT
12b. DISTRIBUTION CODE
Unclassified—Unlimited
Subject Category 39
13. ABSTRACT (Maximum 200 words)
14. SUBJECT TERMS
15. NUMBER OF PAGES
16. PRICE CODE
17. SECURITY CLASSIFICATION
OF REPORT
18. SECURITY CLASSIFICATION
OF THIS PAGE
19. SECURITY CLASSIFICATION
OF ABSTRACT
20. LIMITATION OF ABSTRACT
NSN 7540-01-280-5500
Standard Form 298 (Rev. 2-89)
Prescribed by ANSI Std. Z39-18
298-102
Shear Buckling Analysis of a Hat-Stiffened Panel
WU 505-63-40
William L. Ko and Raymond H. Jackson
NASA Dryden Flight Research Center
P.O. Box 273
Edwards, CA 93523-0273
H-2019
National Aeronautics and Space Administration
Washington, DC 20546-0001
NASA TM-4644
A buckling analysis was performed on a hat-stiffened panel subjected to shear loading. Both local
buckling and global buckling were analyzed. The global shear buckling load was found to be several
times higher than the local shear buckling load. The classical shear buckling theory for a flat plate was
found to be useful in predicting the local shear buckling load of the hat-stiffened panel, and the predict-
ed local shear buckling loads thus obtained compare favorably with the results of finite element
analysis.
Hat-stiffened panel; Global buckling; Local buckling; Minimum energy method;
Shear buckling
A03
20
Unclassified
Unclassified
Unclassified
Unlimited
November 1994
Technical Memorandum
Available from the NASA Center for AeroSpace Information, 800 Elkridge Landing Road,
Linthicum Heights, MD 21090; (301)621-0390
Document Outline
- COVER PAGE
- TITLE PAGE
- ABSTRACT
- NOMENCLATURE
- INTRODUCTION
- SHEAR BUCKLING ANALYSIS
- NUMERICAL RESULTS
- CONCLUSION
- REFERENCES
- REPORT DOCUMENT PAGE
Wyszukiwarka
Podobne podstrony:
Elastic Stability of Plates(Plate Buckling Analysis
SEISMIC ANALYSIS OF THE SHEAR WALL DOMINANT BUILDING USING CONTINUOUS-DISCRETE APPROACH
„SAMB” Computer system of static analysis of shear wall structures in tall buildings
Analysis of spatial shear wall structures of variable cross section
Analysis of shear wall structures of variable thickness using continuous connection method
GbpUsd analysis for July 06 Part 1
Decline of Contrastive Analysis Pedagogy
An%20Analysis%20of%20the%20Data%20Obtained%20from%20Ventilat
kurs excel (ebook) statistical analysis with excel X645FGGBVGDMICSVWEIYZHTBW6XRORTATG3KHTA
Lab 2 Visual Analyser oraz kompresje v2
A Contrastive Analysis of Engli Nieznany (3)
05 PRELIMINARY ANALYSES answers
Analysis of soil fertility and its anomalies using an objective model
Pancharatnam A Study on the Computer Aided Acoustic Analysis of an Auditorium (CATT)
Probabilistic slope stability analysis by finite elements
Butterworth Finite element analysis of Structural Steelwork Beam to Column Bolted Connections (2)
więcej podobnych podstron