
KINETYKA POLIMERYZACJI KATIONOWEJ
Reakcje elementarne:
Inicjacja
2 ̇
̇ +
→ ̇
Propagacja
̇ +
̇
̇ +
̇
̇ +
̇
̇ +
̇
Terminacja
̇ + ̇
,
̇ + ̇
,
⎯
+
R’ pierwotny rodnik
M’ rosnący makrorodnik=centrum aktywne
k
d
- stała szybkości inicjatora
k
i
- stała szybkości zainicjowania łańcucha
k
p
- stała szybkości propagacji
k
t
- stała szybkości zakończenia łańcucha
k
t,r
- stała szybkości przez rekombinację
k
t,d
- stała szybkości przez dysproporcjonowanie
k
tr
- stała szybkości przez przeniesienie łańcucha
(transfer)
̇ + ̇ →
Założenie 1- wszystkie reakcje propagacji mają tę samą szybkość kp=const
Ogólnie szybkość reakcji polimeryzacji:
= −
[ ]
=
[ ]
=
[ ][ ̇ ]
Wyznaczenie wartości Kp bezpośrednio na podstawie pomiaru szybkości polimeryzacji oraz stężeń [M’] i
[M] jest bardzo trudne. Z tego powodu w standardowych badaniach kinetycznych korzysta się z innych
równań kinetycznych, w których stężenie centrów aktywnych [M’] wyrażone jest jako funkcja stałej
szybkości reakcji elementarnych, łatwiej mierzonych.
Wyznaczanie [M’] na podstawie badania szybkości inicjowania
Szybkość inicjowania jest zdeterminowana przez szybkość rozpadu(dysocjacji) inicjatora i efektywności
jego działania f(ułamek rodników R’, które rzeczywiście inicjują łańcuch w stosunku do ogólnej liczby
rodników powstającej w czasie dysocjacji).
Szybkość inicjowania:
=
∙
[ ]
Założenie 2- stan stacjonarny lub ustalony:
=
=
− [ ]
=
̇ [ ̇ ]
[ ] =
[ ̇ ]
stąd:
[ ] =
[ ]
= (
∙
[ ]
)
Założenie 3
Szybkość propagacji= całkowitej szybkości zużywania się monomeru M i powstania polimeru P.
Wynika z założenia 3, że średnia długość łańcucha polimerowego jest bardzo duża, czyli że cały M→P
−
=
=
.
files without this message by purchasing novaPDF printer (
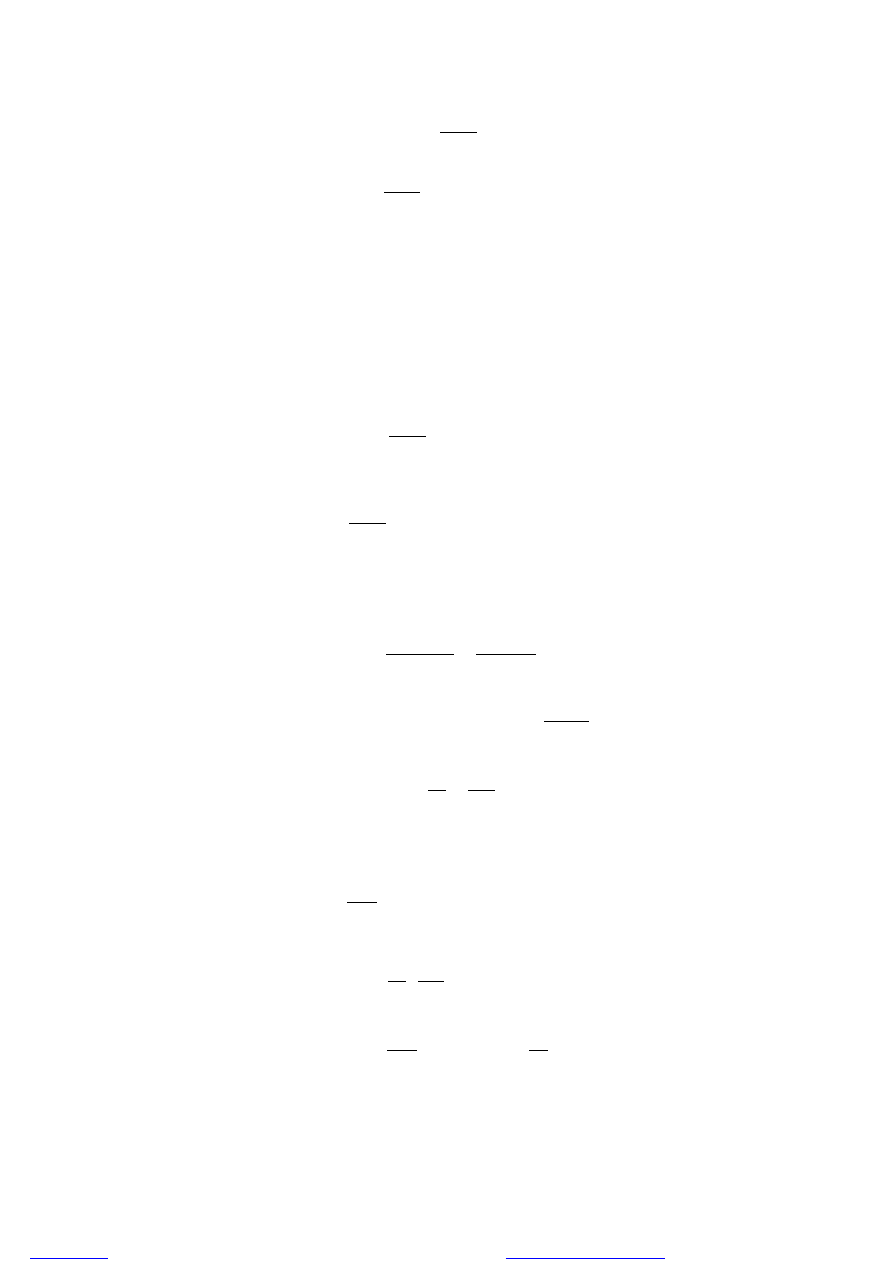
A zatem możemy napisać, że:
=
[ ][ ̇ ]
=
(
[ ]
)
[ ]
=
(
)
[ ]
[ ]
Ostatecznie otrzymujemy:
= [ ][ ]
Obliczanie indywidualnych, absolutnych stałych szybkości kp i kt- jest niemożliwe w warunkach stanu
stacjonarnego;
- potrzebne są specjalne metody pomiaru szybkości polimeryzacji w warunkach stanu niestacjonarnego,
kiedy [M
+
] zmienia się w czasie. Szybkość tych zmian równa jest różnicy między R
i
i R
t
.
[ ̇ ]
=
−
Pamiętając, że w stanie stacjonarnym Ri=Rt, równanie powyższe można przekształcić do postaci
[ ̇ ]
=
([
]
̇
−
̇
)
Ms’- w stanie stacjonarnym
Istotnym parametrem, który wiąże zmiany stężenia rodników ze stopniem konwersji monomeru jest
średni czas życia makrorodnika w stanie stacjonarnym τ
s
=
̇
[ ̇ ]
=
[ ̇ ]
Pamiętając, że szybkość propagacji w stanie ustalonym:
=
[ ] ̇
ą ̇
=
[ ]
otrzymujemy zależność między średnim czasem życia rodnika τ a stałymi szybkości k
p
i k
t
=
=
[ ]
Aby obliczyć τ
s
prowadzi się badania polimeryzacji w stanach niestacjonarnych śledząc wszelkie zmiany
konwersji monomeru w krótkich okresach czasu.
Eksperymentalne oznaczenie w stanie stacjonarnym:
{
=
= (
[ ]
[ ])} ( )
Eksperymentalne oznaczenie w stanie nieustalonym:
=
∙
[ ]
( )
Kombinacja równań (A) i (B) pozwala oznaczyć indywidualne wartości k
p
i k
t
=
=
Znając wartość τ możemy rodzielić k
p
i k
t
files without this message by purchasing novaPDF printer (
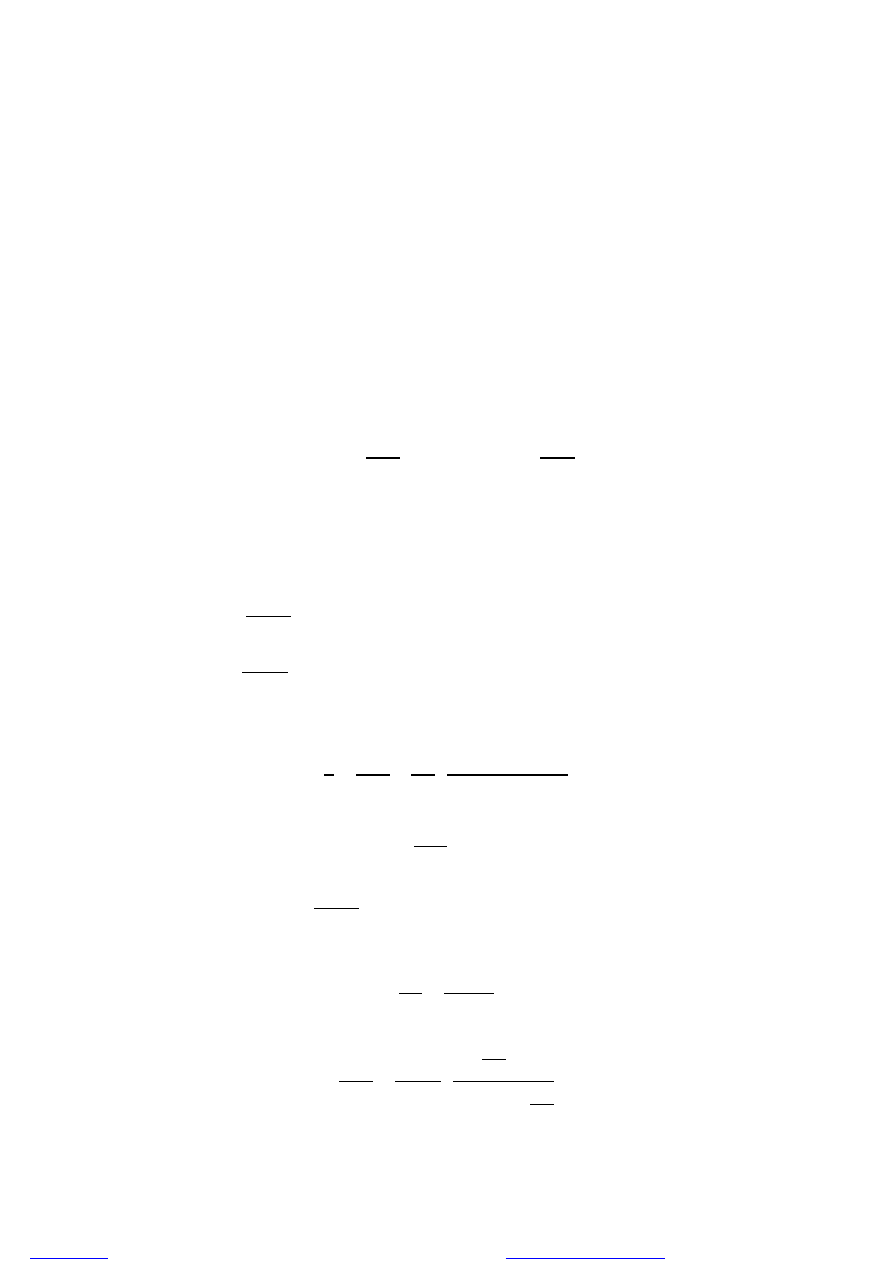
KINETYKA KOPOLIMERYZACJI
Najprostszy przykład kopolimeryzacji statystycznej:
~ +
⎯
̇
~ ̇
~ +
⎯
̇
~ ̇
~ +
⎯
̇
~ ̇
~ +
⎯ ~ ̇
̇
Kopolimery otrzymujemy w reakcji (2) i (3), homopolimery w reakcji (1) i (4)
Współczynniki reaktywności definiujemy jako:
=
=
Ich wyznaczenie dla poszczególnych reakcji kopolimeryzacji pozwala przewidzieć skad kopolimeru dla
określonego stosunku molowego komonomerów.
Wyznaczanie współczynników:
Zakładamy że wychodzimy z danej mieszaniny zawierającej określone stężenie [A] i [B] oraz
makrorodniki [A’] i [B’]. Szybkość zużywania się monomerów:
− [ ]
=
[ ][ ]̇ +
̇
[ ̇ ][ ] = [ ](
[ ̇ ] + ̇
̇
[ ]̇
− [ ]
=
̇ [ ] +
̇ [ ] = [ ](
̇ +
[ ̇ ]
Względne szybkości wbudowywania się każdego z monomerów w łańcuch polimeru określa stosunek:
rów(1):
=
[ ]
[ ]
=
[ ]
[ ]
∙
̇ +
[ ̇ ]
̇ +
[ ̇ ]
Zakładamy stan stacjonarny dla rodników [A’] i równocześnie dla [B’]
[ ̇ ]
=
Zatem w stanie ustalonym:
− [ ]
=
̇ [ ] −
̇ [ ] =
stąd:
rów(2)
[ ]
[ ]
=
[ ]
[ ]
Równanie składu (1) możemy zatem napisać:
[ ]
[ ]
=
[ ][ ̇ ]
[ ][ ̇ ]
∙
[ ̇ ]
[ ̇ ]
+
+
[ ̇ ]
[ ̇ ]
Podstawiając do niego rów(2) otrzymujemy:
files without this message by purchasing novaPDF printer (
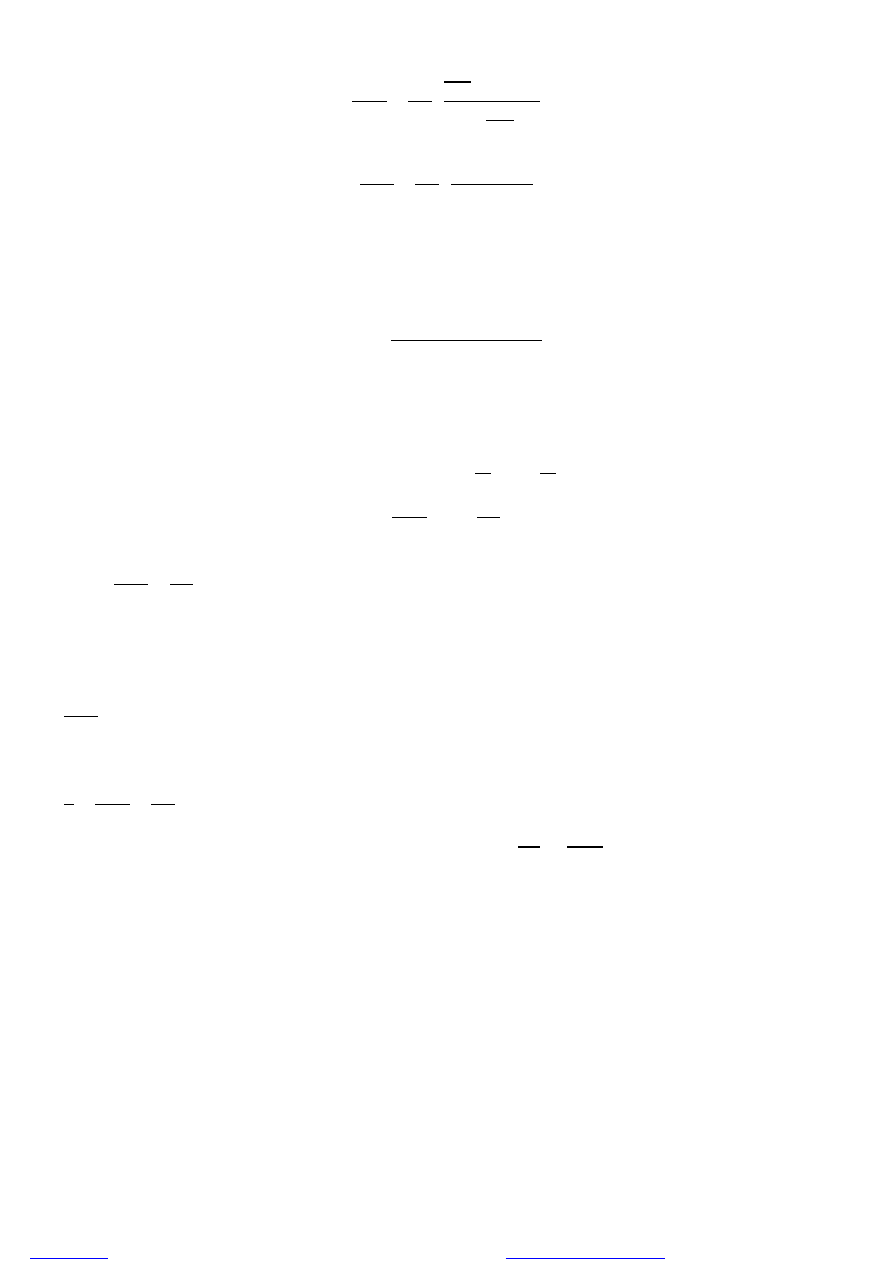
[ ]
[ ]
=
[ ]
[ ]
∙
[ ] + [ ]
[ ] +
[ ]
Ostateczne równanie składu kopolimeru (równanie Mayo-Lewisa):
[ ]
[ ]
=
[ ]
[ ]
∙
[ ] + [ ]
[ ] + [ ]
Często wygodnie jest podawać skład kopolimeru w ułamkach molowych składnika A w kopolimerze:
F
A
i F
B
= uł. molowe A i B w kopolimerze = F
1
i F
2
f
A
i f
B
= uł. molowe monomerów = f
1
i f
2
Równanie skadu można przedstawić w formie udziału ułamka molowego składnika A w kopolimerze:
=
+
+
+
Równanie składu pozwala przeprowadzić klasyfikację kopolimerów statystycznych stosując jako
kryterium iloczyn r
1
*r
2
.
KLASYFIKACJA KOPOLIMERÓW STATYSTYCZNYCH WEDŁUG ILOCZYNU r
1
*r
2
Przypadek 1)
∙
≈
⇒
=
;
=
[ ]
[ ]
=
∙
[ ]
[ ]
=
=
[ ]
[ ]
=
[ ]
[ ]
→
ł
ł
,
Przypadek 2)
∙
< 1 →
ę
a) r
1
=0, r
2
∙
=
[ ]
[ ]
=
= ,
kopolimery naprzemienne np. kopolimer styrenu+ bezwodnik maleinowy
b)
< 1
< 1
=
=
[ ]
[ ]
=
[ ]
[ ]
kopolimery azeotropowe, otrzymujemy azeotrop przy składzie
[ ]
[ ]
=
Przypadek 3)
> 1
jeżeli
≫
≫ tendencja do tworzenia bloków
files without this message by purchasing novaPDF printer (

KINETYKA POLIMERYZACJI JONOWEJ
1. KATIONOWEJ
Jeśli w polimeryzacji kationowej centra aktywne występują w postaci par jonowych to ogólny mechanizm
procesu można przedstawić następującym schematem:
+
↔
inicjowanie
+
→
+
wzrost łańcucha
+
→
+
zakończenie wzrostu łańcucha w reakcji
jednocząsteczkowej
+
+
zakończenie wzrostu łańcucha przez przeniesienie
na monomer
gdzie:
A- kwas Lewisa
RH- kokatalizator
M- monomer
ki, kp, kt, kr – stałe szybkości inicjowania, wzrostu, zakończenia i przeniesienia łańcucha
Szybkość inicjowania można zapisać równaniem:
=
[ ][ ]
[C] – stężenie aktywnego katalizatora
Szybkość polimeryzacji:
=
=
[
][
]
Szybkość terminacji:
=
[
]
W stanie stacjonarnym stężenie kationów jest stałe czyli Ri=Rt, stąd stężenie makrokationów w stanie
stacjonarnym:
=
[ ][ ]
Równanie polimeryzacji kationowej można zatem przedstawić w postaci:
=
[ ][ ]
Jeżeli zakończenie przebiega głównie wg mechanizmu jednocząsteczkowego to kinetyczną długość
łańcucha i stopień polimeryzacji można obliczyć z zależności:
=
=
=
[
][ ]
[
]
=
[ ]
W mechanizmie jednocząsteczkowym stopień polimeryzacji nie zależy od [M]
Jeżeli zakończenie łańcucha ma charakter reakcji dwucząsteczkowej to:
=
=
[
][ ]
[
][ ]
=
=
.
W mechanizmie dwucząsteczkowym stopień polimeryzacji nie zależy od [M] i [C]
2. ANIONOWEJ
Przebieg polimeryzacji anionowej w znacznej mierze zależy od warunków prowadzenia reakcji, dlatego
trudno jest podać ogólną charakterystykę zarówno mechanizmu jak i kinetyki procesu.
Analiza możemy przeprowadzić na przykładzie polimeryzacji z udziałem wolnych jonów:
files without this message by purchasing novaPDF printer (

↔
+
dysocjacja katalizatora
inicjowanie
+
→
zapoczątkowanie wzrostu łańcucha
+
wzrost łańcucha
+
+
→
+
zakończenie łańcucha przez
przeniesienie na rozpuszczalnik
gdzie:
CA – katalizator
M – monomer
RH – rozpuszczalnik
ki, kp, kt – stałe szybkości inicjowania, wzrostu i zakończenia łańcucha
Zakładając, że polimeryzacja przebiega z udziałem wolnych jonów, których reaktywność nie zależy od
długości łańcucha, szybkość inicjowania wyrażamy wzorem:
=
[
][ ]
[A-] stężenie anionów z dysocjacji katalizatora
[M] stężenie monomeru
Szybkość polimeryzacji:
=
=
[
][ ]
Szybkość reakcji zakończenia(terminacji):
=
[
][
]
[M-] stężenie makroanionu AM
n
-
[RH] stężenie rozpuszczalnika przenoszącego łańcuch
W stanie stacjonarnym Ri=Rt, stąd stężenie makroanionów w stanie stacjonarnym:
[
] =
[
][ ]
[
]
Wyrażenie na szybkość polimeryzacji przyjmuje postać:
=
∙
[
][ ]
[
]
Stężenie anionów [A-] można wyliczyć na podstawie znajomości stężenia i stałej dysocjacji katalizatora:
[
] =
[
]
więc:
=
∙ √ ∙
[ ] ∙ { [
]}
[
]
Średni stopień polimeryzacji wprost proporcjonalny do stężenia monomeru, odwrotnie proporcjonalny do
stężenia rozpuszczalnika przenoszącego łańcuch:
=
=
[
][ ]
[ ][
]
=
[ ]
[
]
files without this message by purchasing novaPDF printer (
Wyszukiwarka
Podobne podstrony:
opracowane pytania od Kolonki II(2)
Opracowane pytania technika strzelnicza egz inz, egzamin inzynierski gig
opracowane pytanie od 43, Geodezja i Geoinformatyka UWM, III rok, TiG
Opracowane pytania technika strzelnicza egz inz
opracowane pytania od Kolonki II(2)
pytania z kol od strzelca, Giełdy z farmy
Pytania od Maruchina opracowanie
Lasy - opracowane pytania, 7 sem od Jacka, lasy
strzelectwo opracowane pytania, Wojskowo-lekarski lekarski umed łódź giełdy i materiały I rok, Strze
POPRAWIONE - strzelectwo opracowane pytania, Wojskowo-lekarski lekarski umed łódź giełdy i materiały
pytania od Grzechowiak opracowanie, technologia chemiczna
haran egzamin opracowane pytania
Opracowane pytania BiUD
prawo opracowane pytania egzamin id 3
patomorfologia opracowane pytania opisowe egzamin
1.Rodzaje i geneza gruntów budowlanych, Opracowane pytania na egzamin
opracowane pytania MSI (1), Studia Zarządzanie PWR, Zarządzanie PWR I Stopień, V Semestr, Modelowani
więcej podobnych podstron