2ET-DI-L2

Rzeszów, 16.11.2015 r.

Michał Kucharski
Kinga Łakomy
Łukasz Ślimak
Mateusz Winiarski
Damian Woźniak

SPRAWOZDANIE

Z MEMS I MIKRONAPĘDY

ĆWICZENIE I

,,Sterowanie silnika skokowego

reluktancyjnego’’

I.

Wprowadzenie do ćwiczenia

Celem ćwiczenia jest zapoznanie się z budową silnika skokowego

reluktancyjnego, sposobem sterowania oraz wyznaczeniem jego charakterystyk
dynamicznych. Silnik skokowy reluktancyjny z uwagi na swą budowę
najczęściej zasilany jest unipolarnie. Najprostszym sposobem jego sterowania
jest sterowanie napięciowe. W takim przypadku napięcie zasilające jest
podawane na poszczególne pasma bez żadnych ograniczeń. Jest to przydatne w
zakresie małych częstotliwości pracy. Wraz ze wzrostem częstotliwości
taktowania prądy nie osiągają już wartości ustalonych.

Stosowanie ,,forsowania wzbudzenia” zapobiega zatrzymaniu silnika kiedy

ograniczony zostanie wytworzony moment spowodowany zbyt małym prądem.
Polega ono na zwiększeniu napięic a i dołączeniu rezystancji R

ad

ograniczającej

prąd do wartości znamionowej.

Silniki skokowe wykorzystywane są w precyzyjnych sterowaniach ruchem,

przekształcają one ciąg impulsów na ciąg przesunięć kątowych lub liniowych.

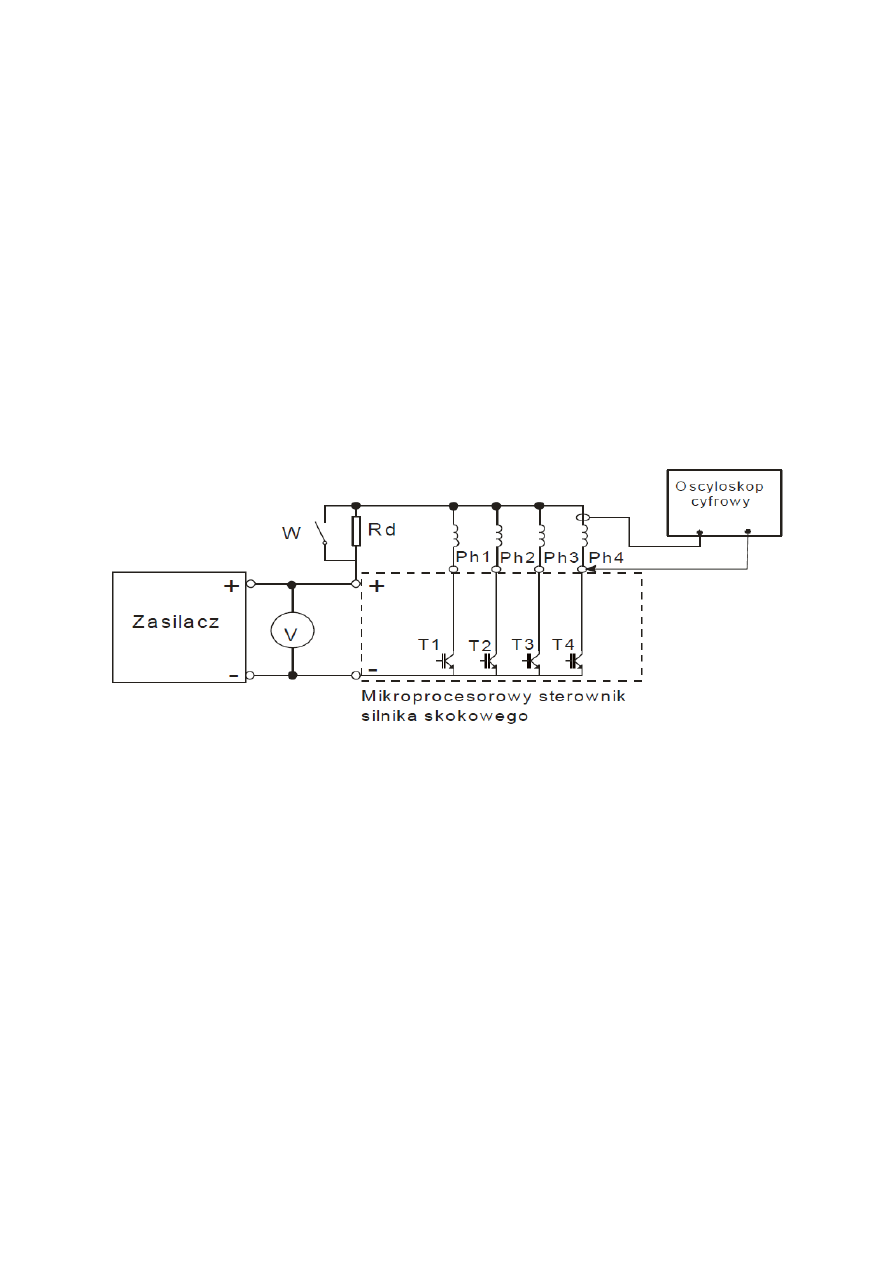
II. Schemat

III. Parametry znamionowe czteropasmowego silnika

skokowego EDS20:

 napięcie znamionowe

= 15 ,

 prąd znamionowy

= 3.7 ,

 pobór mocy

= 120 ,

 skok znamionowy

= 3°,

 moment znamionowy

= 4

,

 maksymalny moment synchronizujący

= 10

,

 moment rozruchowy

= 71

,

 moment bezwładności wirnika

= 53300 ∗ 10

,

 rezystancja pasma

= 3.95 Ω,

 impedancja pasma

= 30.5 Ω,

 częstotliwość graniczna

= 75

.

Układ sterowania silnika zbudowano w oparciu o układ mikroprocesora 8-bitowego.
Umożliwia ona płynną zmianę częstotliwości podawanych impulsów, zmianę kierunku
wirowania oraz komutowanie uzwojeń w sekwencji 1/4, 1/2 i 3/8.

IV. Tabele pomiarowe i obliczenia

Obliczanie momentu obciążenia:

=

× =

, gdzie:

r = 0.1m,

m → masa obciążników [kg],

g ≈ 9.8

m

s

→ przyśpieszenie ziemskie.

Dla:



m = 0.1 kg

T = 0.1 × 9.8 × 0.1 = 0.098



m = 0.3 kg

T = 0.3 × 9.8 × 0.1 = 0.294



m = 0.5 kg

T = 0.5 × 9.8 × 0.1 = 0.49



m = 0.7 kg

T = 0.7 × 9.8 × 0.1 = 0.686



m = 0.9 kg

T = 0.9 × 9.8 × 0.1 = 0.882



m = 1.1 kg

T = 1.1 × 9.8 × 0.1 = 1.078



m = 1.3 kg

T = 1.3 × 9.8 × 0.1 = 1.274

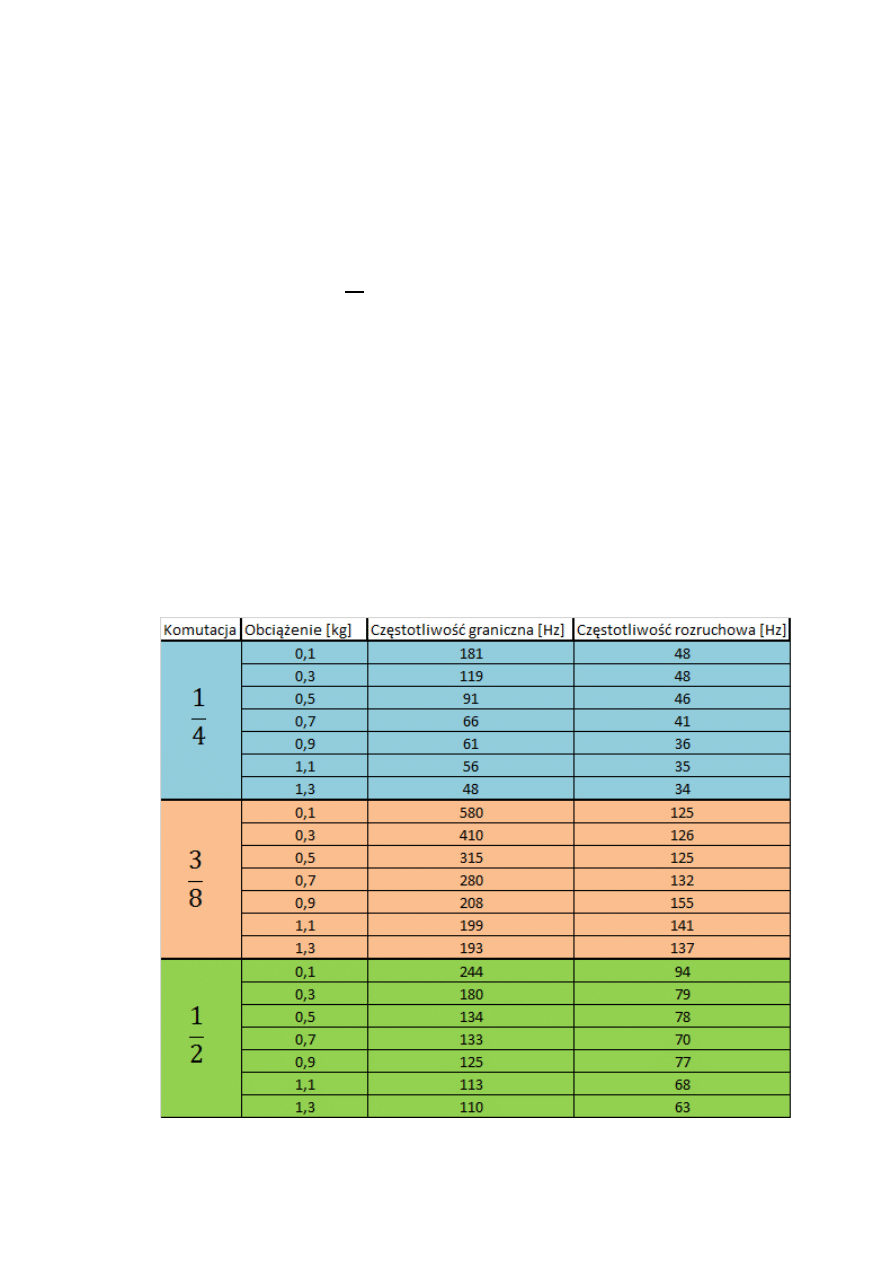
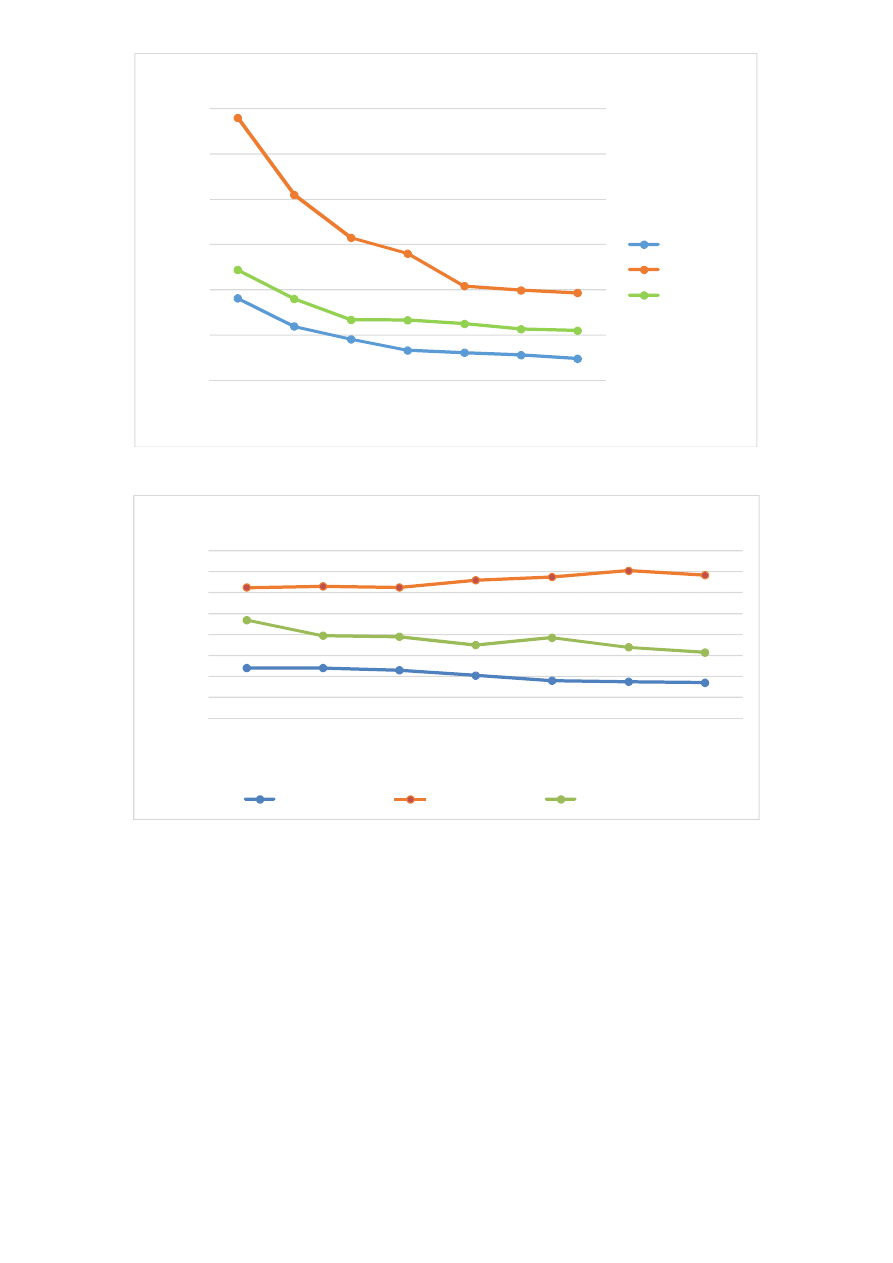
a) Pomiary częstotliwości granicznej

= (

) oraz rozruchowej

= (

) przy

=

:

0

100

200

300

400

500

600

0,098

0,294

0,49

0,686

0,882

1,078

1,274

f

[H

z]

T

L

[Nm]

f

g

= f (T

L

)

Komutacja 1/4

komutacja 3/8

Komutacja 1/2

0

20

40

60

80

100

120

140

160

0,098

0,294

0,49

0,686

0,882

1,078

1,274

f

l

[H

z]

T

L

[Nm]

f

l

= f (T

L

)

Komutacja 1/4

Komutacja 3/8

Komutacja 1/2

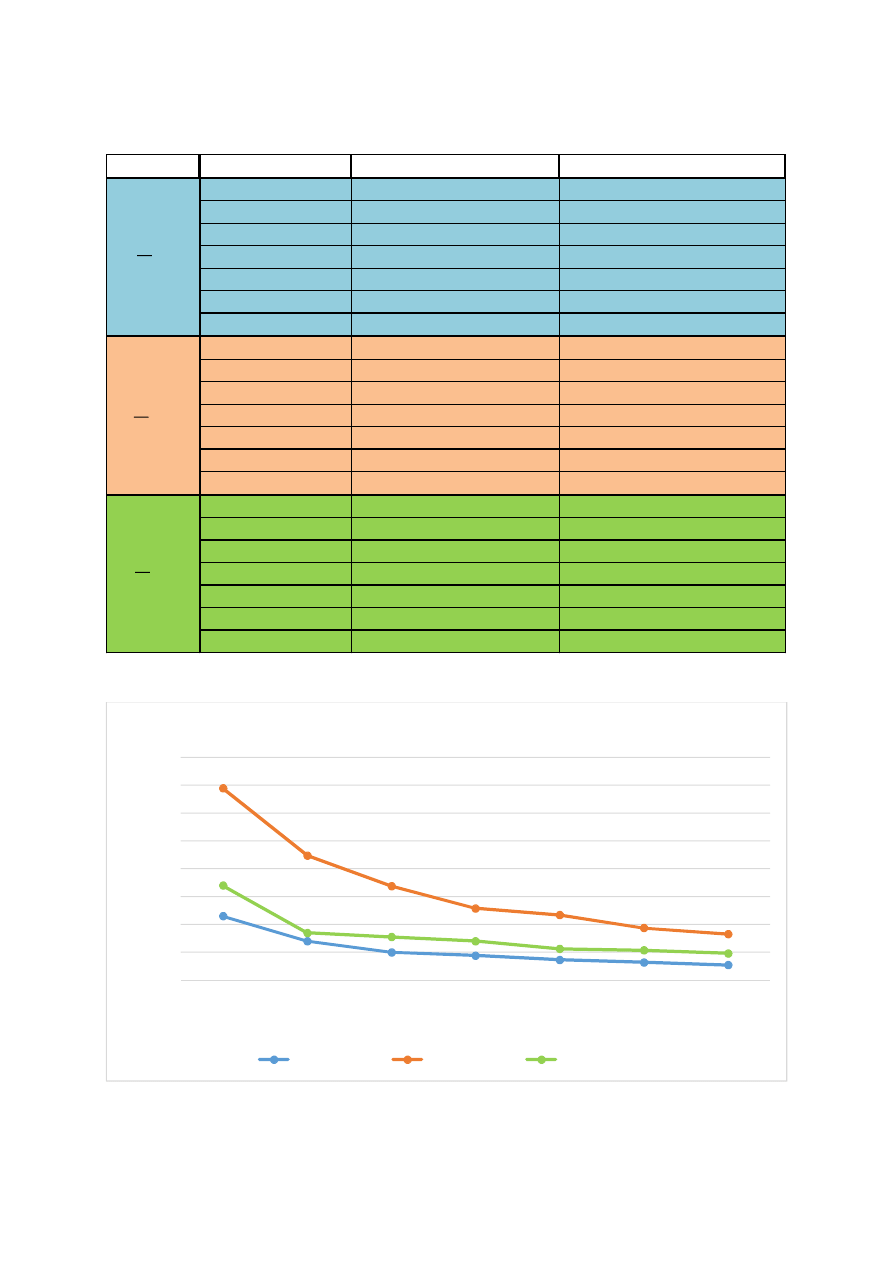
b) Pomiary częstotliwości granicznej

= (

) oraz rozruchowej

= (

) w warunkach forsowania wzbudzenia

=

oraz

≈ Ω:

Komutacja

Obciążenie [kg]

Częstotliwość graniczna [Hz] Częstotliwość rozruchowa [Hz]

0,1

230

49

0,3

140

49

0,5

100

49

0,7

88

46

0,9

73

41

1,1

64

35

1,3

54

34

0,1

689

125

0,3

448

120

0,5

338

117

0,7

258

114

0,9

234

113

1,1

187

107

1,3

165

98

0,1

340

59

0,3

170

59

0,5

155

59

0,7

140

59

0,9

112

57

1,1

107

56

1,3

96

60

1
4

3
8

1
2

0

100

200

300

400

500

600

700

800

0,098

0,294

0,49

0,686

0,882

1,078

1,274

f

g

[H

z]

T

L

[Nm]

f

g

=f(T

L

)

Komutacja 1/4

Komutacja 3/8

Komutacja 1/2

V. Przebiegi czasowe na oscyloskopie w 26 Hz:

a) Dla komutacji 1/4:

0

20

40

60

80

100

120

140

0,098

0,294

0,49

0,686

0,882

1,078

1,274

f

l

[H

z]

T

L

[Nm]

f

l

=f(T

L

)

Komutacja 1/4

Komutacja 3/8

Komutacja 1/2

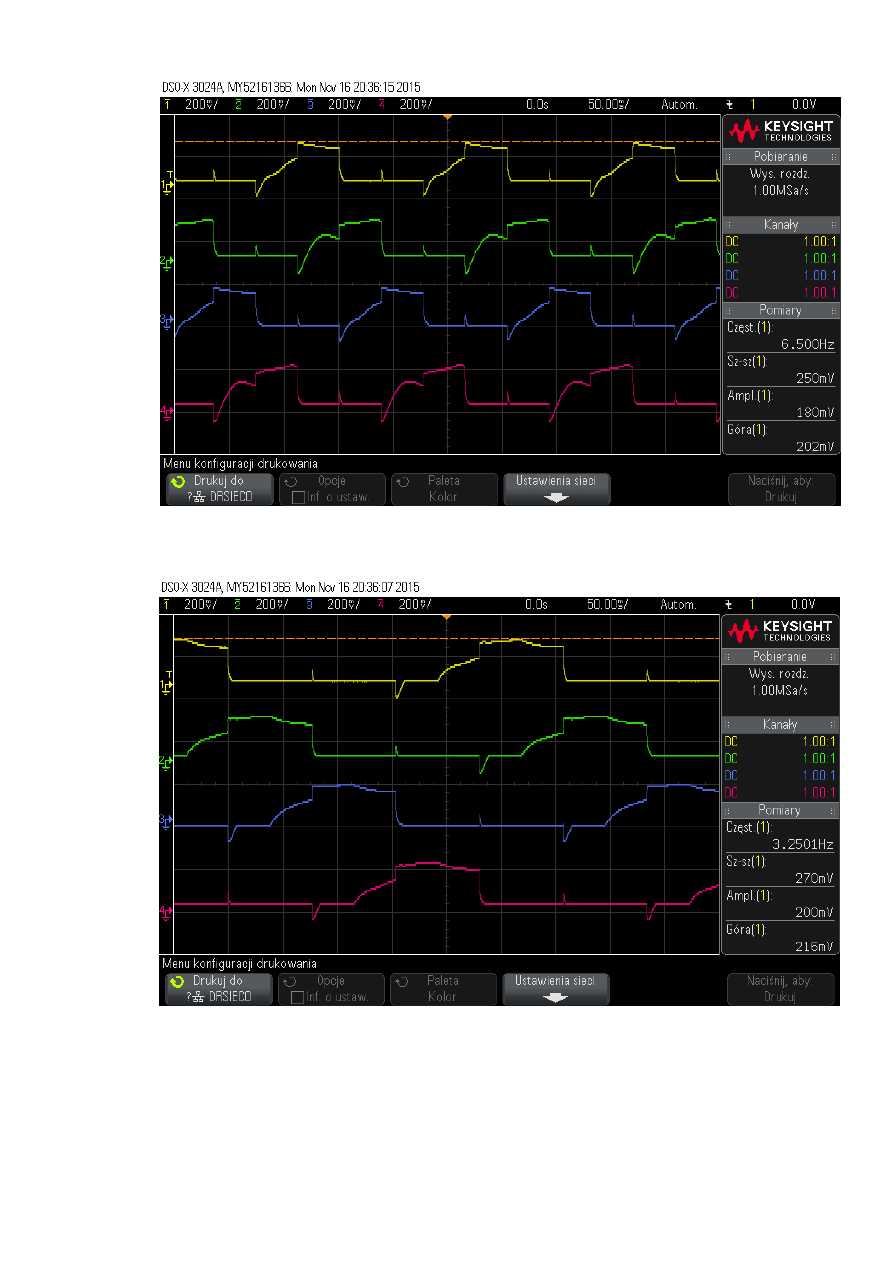
b) Dla komutacji 1/2:

c) Dla komutacji 3/8:

VI. Wnioski:

Częstotliwość graniczna to częstotliwość przy której następuje zatrzymanie
silnika z przymocowanym obciążeniem.

Częstotliwość rozruchowa to częstotliwość przy której następuje ciągła praca
silnika z przymocowanym obciążeniem.

Na podstawie otrzymanych wykresów zauważamy zmiany częstotliwości
granicznych i rozruchowy w zależności od zmian momentu obciążenia silnika.
Mają one duży wpływ na wartości częstotliwości granicznej a mniejszy na
zmianę częstotliwości rozruchowej. Przy komutacji 3/8 częstotliwości osiągają
największe wartości a najmniejsze przy komutacji 1/4.

Przy zwiększeniu wartości napięcia zasilającego do 15 V i jednoczesnym
dołączeniu dodatkowej rezystancji Rd kształt przebiegów jest podobny jak przy
napięciu zasilania 12 V.