XXVII Krajowa Konferencja Elektroniki i Telekomunikacji Studentów

i Młodych Pracowników Nauki, SECON’2004,

WAT, Warszawa, 04 – 05. 11. 2004r.

pchor. Paweł KACZMAREK,

pchor. Hubert STADNIK

– IV rok studiów,

Opiekun naukowy: dr inż. Adam Konrad RUTKOWSKI,
Instytut Radiolokacji, Wydział Elektroniki WAT,
Kaliskiego 2, 00-908 Warszawa

WŁASNOŚCI FAZOWE SPRZĘGACZA ZBLIŻENIOWEGO

1. WPROWADZENIE

Sprzęgacze kierunkowe tworzą obszerną grupę liniowych obwodów wielkiej częstotliwości

wykorzystywanych do kierunkowego rozdziału lub wektorowego sumowania doprowadzonych do nich sygnałów.
Układy takie są zbudowane z dwóch odcinków linii mikrofalowych sprzężonych między sobą otworami lub
szczelinami. Omawiane poniżej sprzęgacze kierunkowe wykonane zostały w technice niesymetrycznej linii
paskowej (NLP). Ich działanie oparte jest na sprzężeniu, jakie występuje między dwiema równoległymi liniami
mikropaskowymi wskutek istnienia pola rozproszenia [4].

łu.

W ogólnym i wyidealizowanym przypadku sprzęgacz kierunkowy jest bezstratnym i odwracalnym

czterowrotnikiem, którego wszystkie wrota są dopasowane, przy czym dwie pary z nich są od siebie odizolowane,
tzn. nie ma pomiędzy nimi przepływu sygna

P

3 -

P

4 -

P

1 +

P

2 -

1

2

3

4

Rys. 1 Zasada pracy sprzęgacza kierunkowego

Doprowadzona do wrót 1 moc P

1+

dzieli się w określonym stosunku między wrota 2 i 4. Stosunek mocy

P1+ do P4- jest parametrem sprzęgacza zwanym sprzężeniem:

−

+

=

4

1

log

10

]

[

P

P

dB

C

(1)

W idealnym sprzęgaczu wrota 3 powinny być izolowane od wrót 1. W rzeczywistych układach we wrotach

tych pojawi się pewna szczątkowa część sygnału wejściowego. Zjawisko to opisuje kolejny parametr zwany
izolacją:

1

XXVII Krajowa Konferencja Elektroniki i Telekomunikacji Studentów

i Młodych Pracowników Nauki, SECON’2004,

WAT, Warszawa, 04 – 05. 11. 2004r.

−

+

=

3

1

log

10

]

[

P

P

dB

I

(2)

W praktyce często wykorzystuje się parametr zwany kierunkowością, który jest miarą jakości sprzęgacza i

określa stosunek mocy we wrotach 3 (izolowanych) do mocy we wrotach 4 (sprzężonych):

]

[

]

[

log

10

]

[

4

3

dB

C

dB

I

P

P

dB

P

−

=

=

−

−

(3)

Podobnie jak wszystkie układy mikrofalowe, sprzęgacze kierunkowe opisuje się również za pomocą

macierzy rozproszenia [S]. Dla czterowrotnika macierz ta posiada cztery wiersze i cztery kolumny.

2.

BUDOWA I ZASADA PRACY SPRZĘGACZA LANGE’A

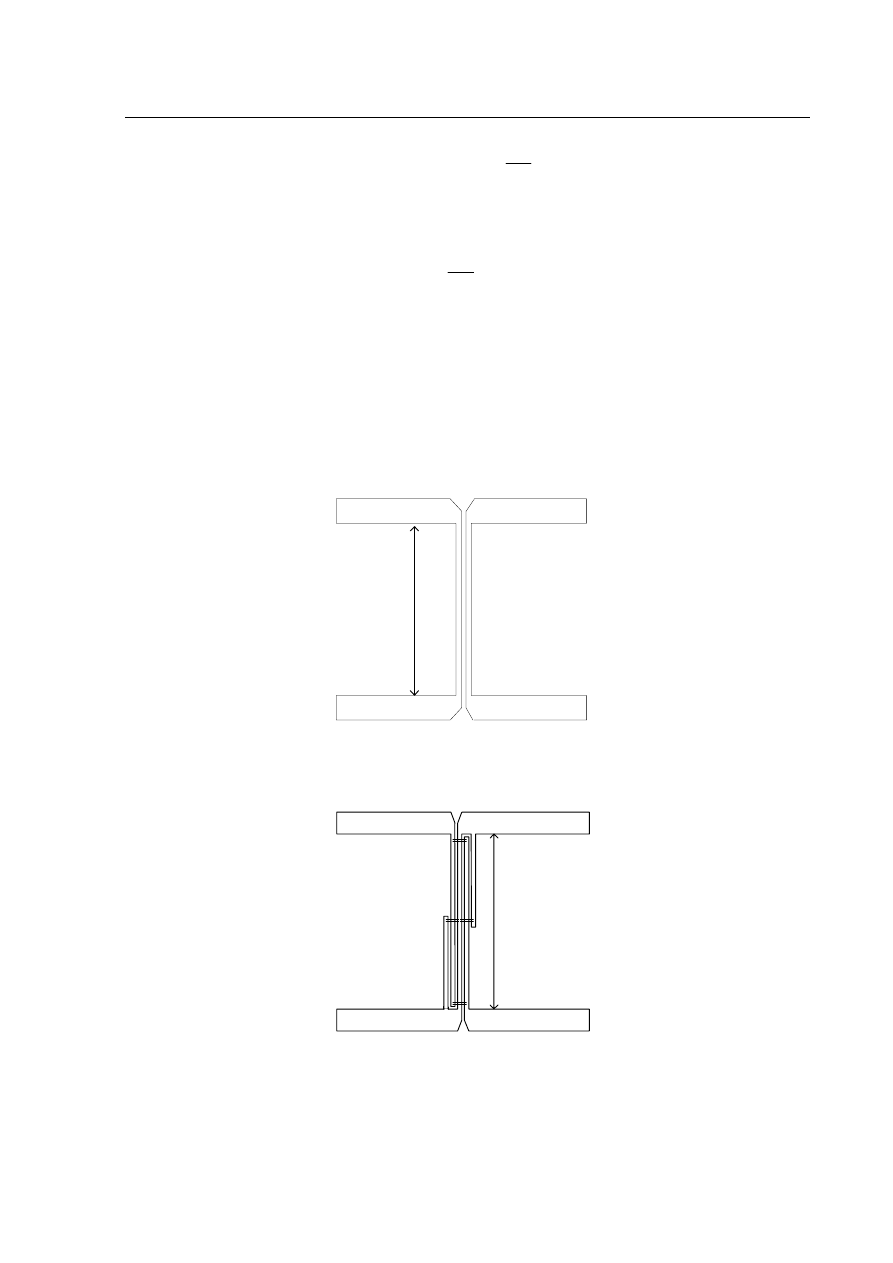
W przedstawionej poniżej podstawowej konfiguracji sprzężonych linii mikropaskowych nie jest

możliwe wykonanie sprzęgacza o sprzężeniu 3dB. Wynika to z faktu, że 3dB sprzężenie wymaga

zrealizowania bardzo wąskiej, nie dającej się wykonać techniką fotolitografii szczeliny między paskami.
W praktycznych rozwiązaniach otrzymuje się sprzężenie na poziomie około 8dB [1].

1

2

4

3

λ/4

Rys. 2 Budowa sprzęgacza zbliżeniowego.

Silniejsze sprzężenie i jednocześnie położenie wrót wzajemnie izolowanych obok siebie uzyskuje

się w sprzęgaczu międzypalczastym Lange’a.

3

2

1

4

λ/4

Rys. 3 Budowa sprzęgacza zbliżeniowego Lange'a.

Na wyjściach sprzęgacza fazy sygnałów różnią się względem siebie o 90°. Jeśli sygnał zostanie

doprowadzony do wrót 1, wówczas wrota 2 będą wrotami bezpośrednimi, wrota 4 – sprzężonymi, a wrota 3 –
izolowanymi. Zaletami tego układu są: małe wymiary, względnie szerokie, łatwe do realizacji szczeliny między
metalowymi paskami struktury oraz szerokie pasmo pracy.

2

XXVII Krajowa Konferencja Elektroniki i Telekomunikacji Studentów

i Młodych Pracowników Nauki, SECON’2004,

WAT, Warszawa, 04 – 05. 11. 2004r.

3. OPIS ANALITYCZNY PARAMETRÓW SPRZĘGACZA

3.1 TRANSMITANCJA S

b

I S

s

Transmitancja S

b

od wrót wejściowych do wrót bezpośrednich (takich, dla których istnieje galwaniczne po-

łączenie z wrotami wejściowymi) sprzęgacza zbliżeniowego określona jest zależnością [2]:

Θ

+

Θ

−

−

=

sin

cos

1

1

2

2

j

k

k

S

b

(4)

gdzie:
k – współczynnik sprzężenia;

Θ – długość elektryczna obszaru sprzężenia wyrażona wzorem:

u

2

π

f

⋅

=

Θ

;

(5)

o

u

f

f

f

=

;

(6)

f

o

– częstotliwość środkowa podstawowego pasma pracy – dla sygnału o tej częstotliwości długość elektryczna

sprzęgacza wynosi 90°.

-540

-440

-340

-240

-140

-40

60

0

1

2

3

4

5

S

b

S

s

f

u

argS [

o

]

6

0

0,2

0,4

0,6

0,8

1

0

1

2

3

4

5

6

k=0.7

k=0.732

k=0.3

|S| [V/V]

f

u

S

s

S

b

n=1

n=3

n=2

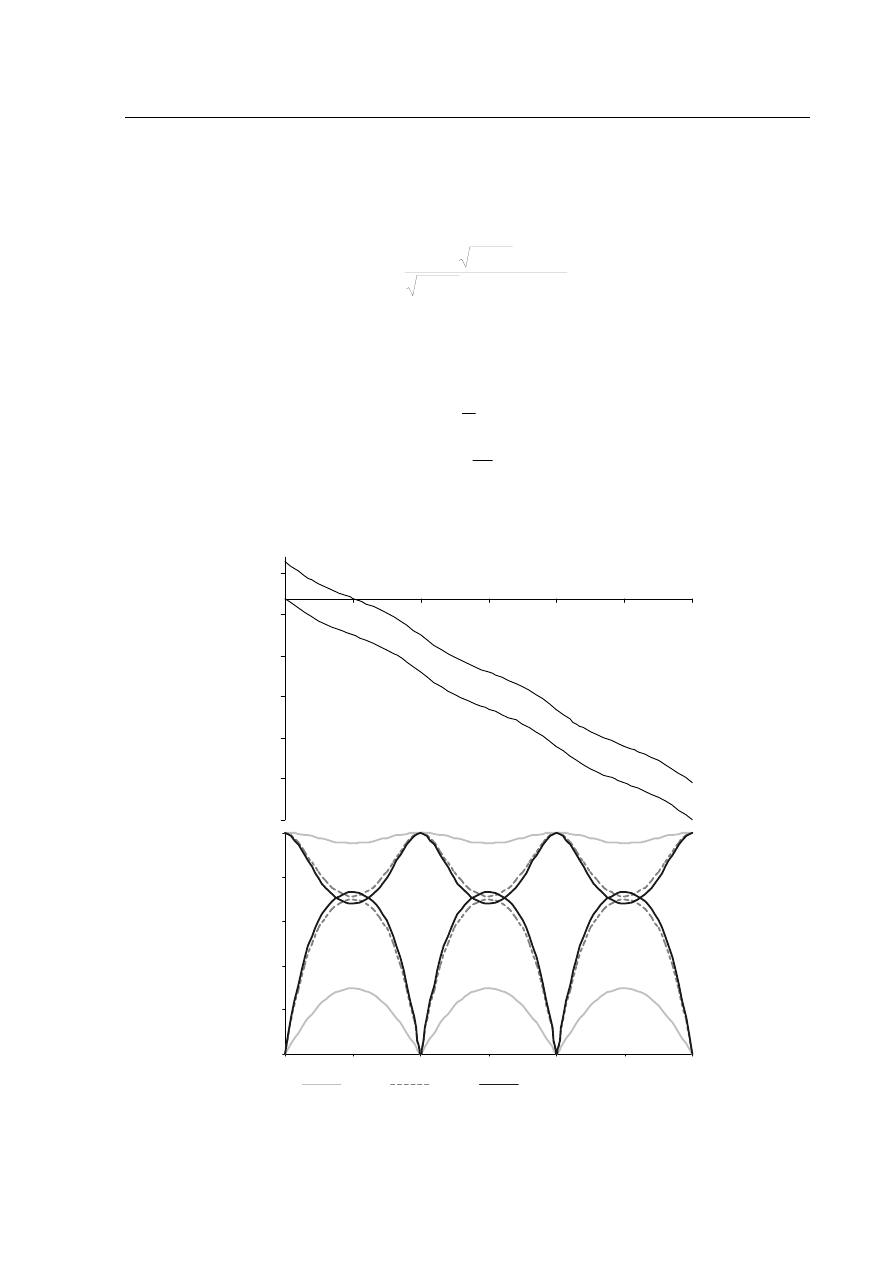
Rys. 4 Przebiegi argumentów transmitancji S

b

i S

s

dla współczynnika k=0,7 i przebiegi modułów transmitancji

dla trzech wartości współczynnika k.

3

XXVII Krajowa Konferencja Elektroniki i Telekomunikacji Studentów

i Młodych Pracowników Nauki, SECON’2004,

WAT, Warszawa, 04 – 05. 11. 2004r.

Przekształcając zależność (4) opisującą S

b

otrzymujemy:

a) moduł transmitancji od wrót wejściowych do wrót bezpośrednich:

Θ

+

Θ

−

−

=

2

2

2

2

sin

cos

)

1

(

1

k

k

S

b

(7)

b) argument transmitancji od wrót wejściowych do wrót bezpośrednich:













−

Θ

−

=

2

1

arg

k

tg

arctg

S

b

(8)

Dla wrót sprzężonych (brak połączenia galwanicznego z wrotami wejściowymi) transmitancję S

s

od wrót

wejściowych opisuje zależność:

Θ

+

Θ

−

Θ

=

sin

cos

1

sin

2

j

k

jk

S

s

(9)

Przekształcając zależność opisującą S

s

otrzymujemy:

a) moduł transmitancji od wrót wejściowych do wrót sprzężonych:

Θ

+

Θ

−

Θ

=

2

2

2

2

2

sin

cos

)

1

(

sin

k

k

S

s

(10)

b) argument transmitancji od wrót wejściowych do wrót sprzężonych:

(

)

Θ

⋅

−

=

ctg

k

arctg

S

s

2

1

arg

(11)

Dla sprzęgacza, którego współczynnik sprzężenia k=0,707 trzydecybelowe pasmo zawiera się w przedzia-

le częstotliwości

∆f=[(2n-1)f

o

-0,68÷(2n-1)f

o

+0,68]GHz, gdzie n=1, 2, 3... – numer podpasma. Oznacza to, że bez-

względna szerokość pasma nie zależy od numeru rozpatrywanego podpasma. Maleje natomiast względna szero-
kość pasma (stosunek bezwzględnej szerokości pasma do częstotliwości środkowej tego pasma) i wynosi
odpowiednio:

δf

1

=1,36;

δf

2

=0,45;

δf

3

=0,27. Można zaobserwować, że w miarę zmniejszania wartości współczyn-

nika sprzężenia, szerokość pasma pracy rośnie. Wzrostowi wartości współczynnika sprzężenia towarzyszy rów-
nież odkształcanie przebiegu argumentu S

s

i S

b

od przebiegu liniowego. Zmiany te są jednak niewielkie i z tego

powodu nie zostały zobrazowane na rys. 4.

3.2 WZGLĘDNE PRZESUNIĘCIE FAZY

Względne przesunięcie fazy układu mikrofalowego jest różnicą argumentu transmitancji

Φ

p

tego układu i

argumentu transmitancji

Φ

lod

tak zwanego toru odniesienia.

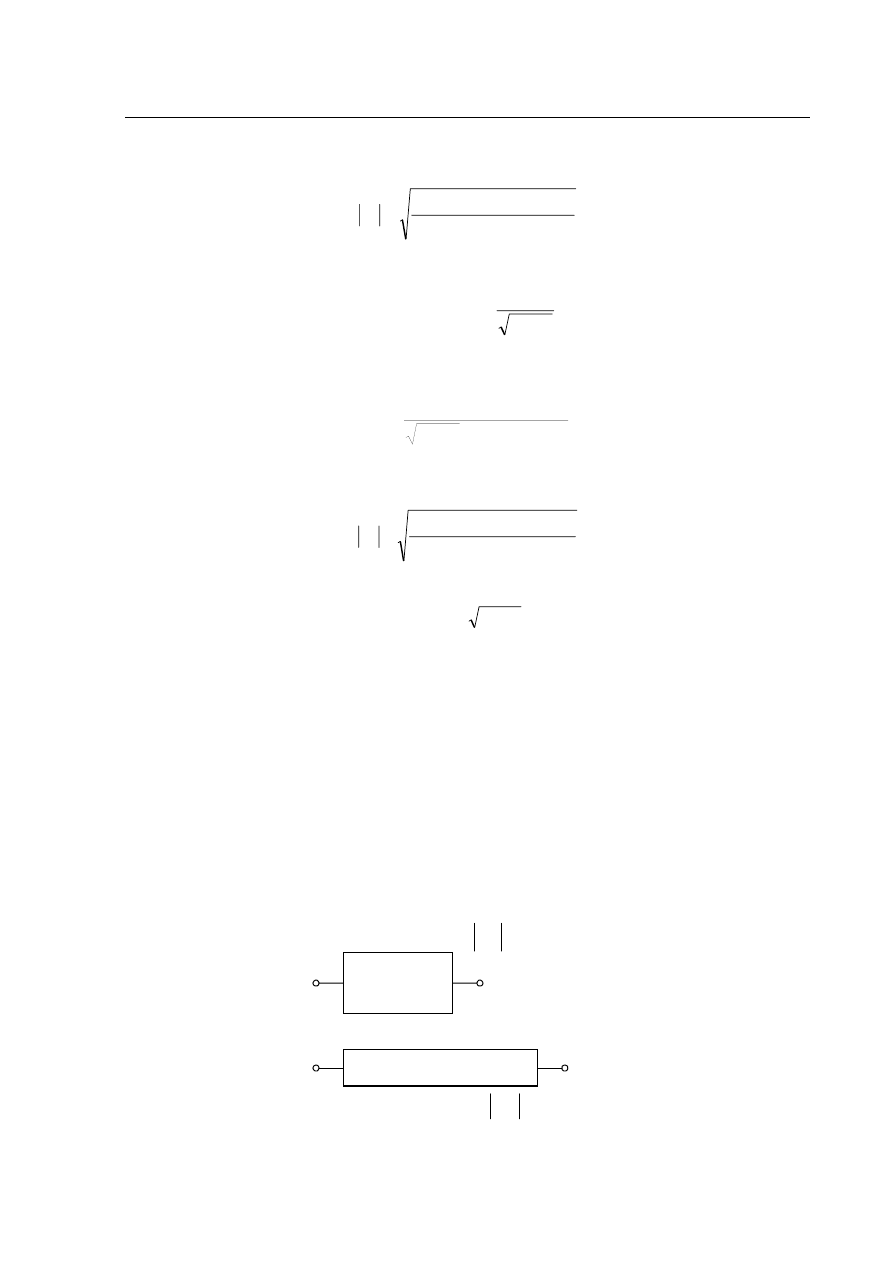
układ

mikrofalowy

linia odniesienia

1

1

2

2

lod

lod

lod

j

e

S

S

Φ

⋅

=

lod

p

w

Φ

−

Φ

=

Φ

p

p

p

j

e

S

S

Φ

⋅

=

Rys. 5 Układ mikrofalowy i linia odniesienia

4

XXVII Krajowa Konferencja Elektroniki i Telekomunikacji Studentów

i Młodych Pracowników Nauki, SECON’2004,

WAT, Warszawa, 04 – 05. 11. 2004r.

Torem odniesienia może być pojedynczy element lub złożony układ mikrofalowy. W przedstawionych roz-

ważaniach za tor odniesienia przyjęto prowadnicę falową z dielektrykiem powietrznym [3].

Licząc pochodną d(argS

b

)/df

u

w punkcie f

u

=1 – otrzymano współczynnik kierunkowy a prostej aproksymu-

jącej przebieg argS

b

. Szukana prosta ma równanie argS

b

=af

u

+b

b

. Współczynnik b

b

obliczono w oparciu o zależ-

ność (8):

a

S

b

fu

b

b

−

=

= )

1

(

arg

(12)

Przesunięcie fazy

φ

b

we wrotach bezpośrednich względem wrót wejściowych wynosi:

(

)















−

−

⋅

−

+

⋅

−

−

=

2

2

1

1

2

2

1

2

2

π

π

π

φ

k

n

f

k

u

b

(13)

Postępując analogicznie dla wrót sprzężonych, prosta ma postać:

(

)















−

⋅

−

+

⋅

−

−

=

2

1

1

2

2

1

2

2

k

n

f

k

u

s

π

π

φ

(14)

Współczynnik kierunkowy jest więc taki sam dla obu powyższych prostych. Iloczyn parametru a i f

u

określa

długość elektryczną linii odniesienia:

(15)

u

lod

f

a

⋅

=

Θ

Przy wykorzystaniu linii o takiej długości elektrycznej, względne przesunięcie fazy sprzęgacza do wrót

wyjściowych w otoczeniu częstotliwości f

u

= f

on

wynosi odpowiednio: dla wrót bezpośrednich:















−

−

−

=

−

=

2

2

1

2

π

π

φ

k

b

b

wbo

(16)

a dla wrót sprzężonych:















−

−

=

−

=

2

1

2

k

b

s

wso

π

φ

(17)

n=1

n=2

n=3

Θ

lod

3ο

=-321,4

o

-200

-150

-100

-50

0

50

100

0

1

2

3

4

5

6

wrota bezpośrednie

wrota sprzężone

Φ

w

[

o

]

k=0.732

Θ

lod2o

=-192,8

o

k=0.7

k=0.3

Θ

lod

1o

=-64,3

o

f

u

Rys. 6 Względne przesunięcie fazy i długość elektryczna linii odniesienia dla trzech wartości k

5

XXVII Krajowa Konferencja Elektroniki i Telekomunikacji Studentów

i Młodych Pracowników Nauki, SECON’2004,

WAT, Warszawa, 04 – 05. 11. 2004r.

W pozostałych częściach pasma podstawowego i wyższych podpasm (częstotliwości, dla których długość

elektryczna sprzęgacza jest nieparzystą całkowitą wielokrotnością 90°) względne przesunięcia fazy wynoszą:

- dla wrót bezpośrednich:

u

lod

b

wb

f

k

k

tg

arctg

S

⋅

−

−













−

Θ

−

=

Θ

−

=

Φ

2

1

1

arg

2

2

π

(18)

- dla wrót sprzężonych:

(

)

u

lod

s

ws

f

k

ctg

k

arctg

S

⋅

−

−

Θ

⋅

−

=

Θ

−

=

Φ

2

1

1

arg

2

2

π

(19)

Przebiegi względnego przesunięcia fazy do obydwu wrót wyjściowych sprzęgacza dla trzech różnych war-

tości współczynnika sprzężenia k przedstawia rysunek 6:

Θ

no

długość elektryczna linii odniesienia dla częstotliwości środkowej pasma o numerze n

Z rysunku 6, przedstawiającego graficzne zobrazowanie zależności (18) i (19), wynika, że wartość współ-

czynnika sprzężenia ma znaczący wpływ na wartość względnego przesunięcia fazy. Dla k=0,3 w środku pasma
podstawowego

Φ

wb

=-4,14°, dla k=0,7

Φ

wb

=-25,72°, a dla k=0,732

Φ

wb

=-28,68°. W kolejnych podpasmach o

numerach n wartość względnego przesunięcia fazy wokół f

u

=f

on

zmienia się zgodnie z zależnością:

(

)

wbo

wbn

n

φ

φ

⋅

−

=

1

2

(20)

W podpasmach wyznaczonych w punkcie 3.1, wartość względnego przesunięcia fazy dla jednego pasma

zmienia się maksymalnie o 9,5°dla k=0,7, a dla k=0,3 zmienia się o 1,79°. Natomiast na krańcach pasma pod-
stawowego i kolejnych podpasm zmiany te dla k=0,7 sięgają 25,7°, a dla k=0,3 wynoszą 4,14°.

Na podstawie zależności opisujących transmitancje S

s

i S

b

, przesunięcie fazy pomiędzy wrotami bezpo-

średnimi a wrotami sprzężonymi sprzęgacza zbliżeniowego wynosi 90° niezależnie od współczynnika sprzężenia
i numeru podpasma.

Długość elektryczną linii odniesienia w środku pasma można opisać równaniem analogicznym do równa-

nia (20) opisującego względne przesunięcie fazy:

(

)

o

lod

lodn

n

1

1

2

Θ

⋅

−

=

Θ

(21)

gdzie:

Θ

lod1o

– długość elektryczna linii odniesienia dla środka pasma podstawowego

Znając częstotliwość środkową pasma podstawowego f

o

można wyznaczyć długość fizyczną szukanej linii

odniesienia z zależności:

c

f

k

l

o

⋅

⋅

−

=

4

1

2

(22)

gdzie: c – prędkość fali elektromagnetycznej w próżni
Długość fizyczna linii odniesienia jest w każdym podpasmie taka sama jak wyznaczona dla pasma podstawowe-
go. Jej długość zależy od wartości współczynnika sprzężenia.

4. WYNIKI

POMIARÓW

Poniżej przedstawiono wyniki pomiarów dwóch rzeczywistych zbliżeniowych sprzęgaczy kierunkowych

Lange’a. Pomiary dokonywane były przy pomocy wektorowego analizatora obwodów HP8720C.
4.1 SPRZĘGACZ SL 0713 NR 3

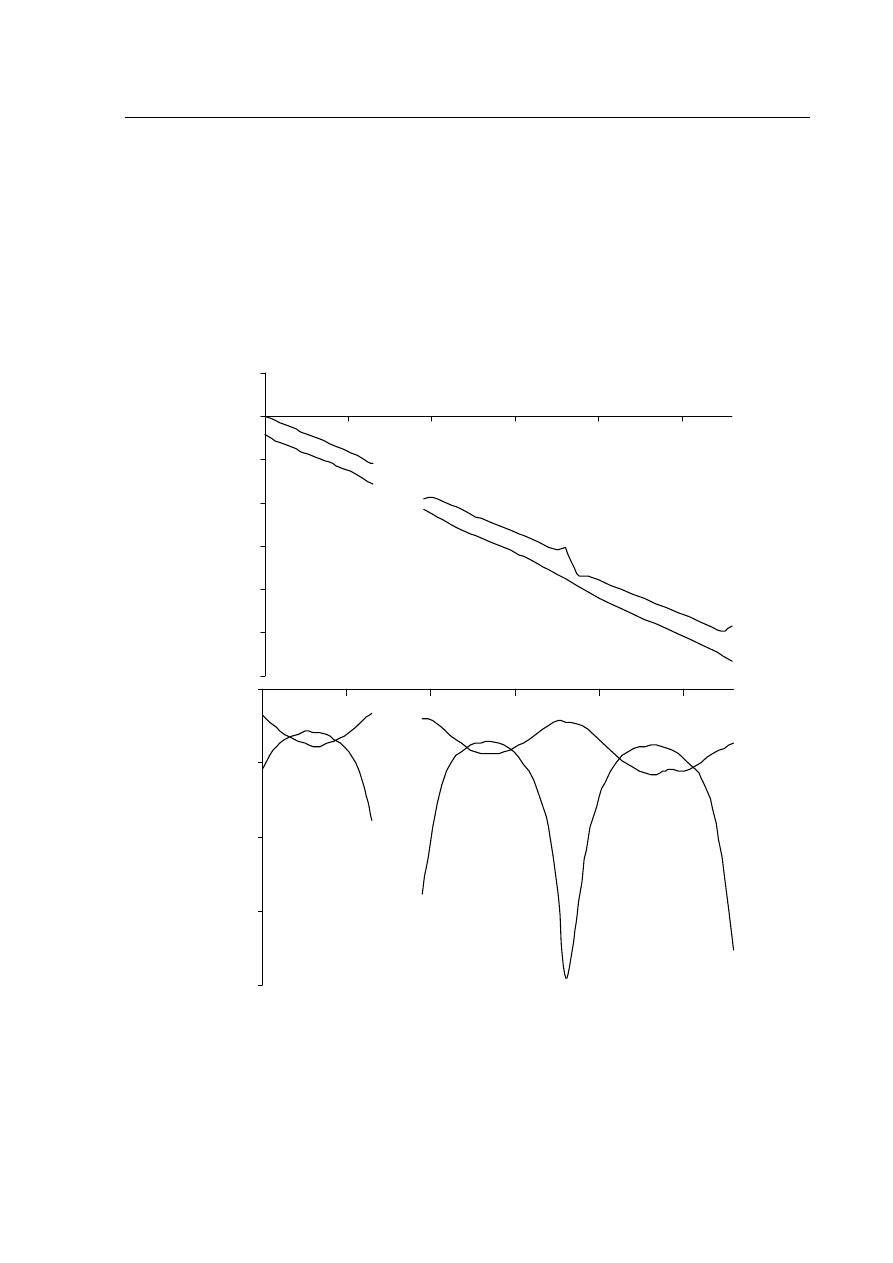
Układ był badany sygnałami o częstotliwości z zakresu: f=(0,4÷6)GHz z wyłączeniem pasma częstotliwo-

ści f=(1,7÷2,3)GHz. Przebiegi modułów i argumentów transmitancji do wrót sprzężonych i bezpośrednich tego
układu w badanym zakresie przedstawia rysunek 7.

6

XXVII Krajowa Konferencja Elektroniki i Telekomunikacji Studentów

i Młodych Pracowników Nauki, SECON’2004,

WAT, Warszawa, 04 – 05. 11. 2004r.

Analizując powyższe przebiegi modułu transmitancji w badanym zakresie można wyróżnić trzy pasma

częstotliwości, w których omawiane wrota układu mają odpowiednio charakter wrót sprzężonych i bezpośrednich.
W paśmie podstawowym współczynnik sprzężenia wynosi k

1

=0,716. W dalszych podpasmach współczynnik ten

wynosi odpowiednio: k

2

=0,661, k

3

=0,649. Spadek wartości tego parametru jest związany ze wzrostem strat

w dielektryku dla wyższych częstotliwości. W paśmie podstawowym pasmo jednodecybelowej zmiany jednego
z modułów transmitancji zawiera się w przedziale częstotliwości

∆f

1

=(0,62÷1,37)GHz. W kolejnych zakresach

pasmo to zawiera się odpowiednio:

∆f

2

=(2,68÷3,45)GHz i

∆f

3

=(4,63÷5,44)GHz. Bezwzględna szerokość wyż-

szych podpasm praktycznie się nie zmienia. Zmianie ulega natomiast względna szerokość tych pasm. Ze wzro-
stem numeru podpasma jego szerokość względna zmniejsza się i dla kolejnych numerów n wynosi:

δf

1

=0,75;

δf

2

=0,25;

δf

3

=0,16.

-1200

-1000

-800

-600

-400

-200

0

200

0,4

1,4

2,4

3,4

4,4

5,4

o

argS [ ]

f [GHz]

S

s

S

b

S

s

S

b

-20

-15

-10

-5

0

0,4

1,4

2,4

3,4

4,4

5,4

f [GHz]

|S| [dB]

S

b

S

b

S

s

S

s

Rys. 7 Przebiegi modułów i argumentów transmitancji sprzęgacza SL 0713 Nr3.

Rozpatrując argumenty transmitancji we wrotach sprzężonych i wrotach bezpośrednich można zauważyć,

że przebiegi te mają podobny charakter. Przesunięte są jednak o pewną, praktycznie niezmienną wartość. Dla
pasma podstawowego, w znacznej jego części, wartość bezwzględna tego przesunięcia, wynosi około 89°, jedy-
nie dla częstotliwości górnych tego pasma rośnie do 92°. Dla pierwszego podpasma różnica ta podlega więk-
szym zmianom, przyjmując wartości od 82° dla częstotliwości dolnych, 93° dla częstotliwości środkowej, oraz do

7

XXVII Krajowa Konferencja Elektroniki i Telekomunikacji Studentów

i Młodych Pracowników Nauki, SECON’2004,

WAT, Warszawa, 04 – 05. 11. 2004r.

115° dla górnych częstotliwości. W drugim podpasmie różnica ta podlega jeszcze większym zmianom. Jej war-
tość dla częstotliwości dolnych wynosi 75°, dla środka podpasma 92°, a dla częstotliwości górnych 118°.
Przebiegi przedstawione na rysunku 8 otrzymano stosując linie odniesienia o następujących długościach (dielek-
tryk powietrzny): dla pasma podstawowego l

lodn1

=137 mm, a w podpasmach 2 i 3 odpowiednio l

lodn2

=135,7mm

i l

lodn3

=135,2mm. Długościom fizycznym odpowiadają następujące długości elektryczne określone dla częstotliwo-

ści środkowych podpasm:

Θ

lodn1

=-169,4°;

Θ

lodn2

=-504,8°;

Θ

lodn3

=-821,1°.

-160

-110

-60

-10

40

90

0

1

2

3

4

5

Φ

wzgl

[

o

]

S

b

S

b

S

b

S

s

S

s

S

s

6

Rys. 8 Względne przesunięcie fazy sprzęgacza SL 0713 Nr3

Z wykresu, przedstawiającego przebiegi względnego przesunięcia fazy badanego sprzęgacza w funkcji

częstotliwości (Rys. 8.) otrzymujemy następujące wyniki dla częstotliwości środkowych pasm: dla wrót bezpo-
średnich:

Φ

wb1

=-26,82°;

Φ

wb2

=-69,26°;

Φ

wb3

=-128,63° i dla wrót sprzężonych:

Φ

ws1

=62,69°;

Φ

ws2

=23,96°;

Φ

wb3

=-

36,82°. Wartość względnego przesunięcia fazy w paśmie nie jest stała. Jeśli szerokość rozpatrywanych pasm
ograniczy się do pasma jednodecybelowego (ze względu na moduł transmitancji), maksymalne zmiany wartości
względnego przesunięcia fazy wynoszą: dla wrót sprzężonych: dla pasma podstawowego ±0,38°, dla pierwszego
podpasma ±1,26°, a dla kolejnego podpasma ±3,14°. Natomiast dla wrót bezpośrednich wartości te wynoszą
odpowiednio: ±0,67°; ±1,91°; ±3,19°.

4.2 SPRZĘGACZ SZ24 NR 2

Układ był badany sygnałami o częstotliwości z zakresu: f=(0,5÷5)GHz. Przebiegi modułów i argumentów

transmitancji tego układu w badanym zakresie przedstawia rysunek 9.
W badanym zakresie częstotliwości można wyróżnić ( ze względu na przebieg modułów transmitancji) dwa trzy-
decybelowe pasma:

∆f

1

=(1,04÷4,2)GHz i

∆f

2

=(7,28÷9,03)GHz. Współczynnik sprzężenia w tych zakresach czę-

stotliwości wynosi odpowiednio: k

1

=0,674 i k

2

=0,536. Bezwzględna szerokość pasma podstawowego wynosi

3,16; a dla podpasma wyższego 1,75. Jest to związane z silniejszym oddziaływaniem dielektryka na parametry
sprzęgacza. Silnej zmianie ulega względna szerokość tych pasm, która zmniejsza się ze wzrostem częstotliwo-
ści:

δf

1

=1,21;

δf

2

=0,21.

Rozpatrując argumenty transmitancji we wrotach sprzężonych i wrotach bezpośrednich można zauważyć,

że w tym sprzęgaczu przebiegi te mają podobny charakter. Przesunięte są one o pewną wartość. Dla pasma
podstawowego wartość bezwzględna tego przesunięcia wynosi około: od 89,9° dla częstotliwości dolnych, 92,2°
dla częstotliwości środkowej oraz do 152° dla częstotliwości górnych tego pasma. W podpasmie dodatkowym
różnica ta podlega większym zmianom, przyjmując wartości od 47° dla częstotliwości dolnych, 100,5° dla często-
tliwości środkowej, do 193° dla górnych częstotliwości.

8

XXVII Krajowa Konferencja Elektroniki i Telekomunikacji Studentów

i Młodych Pracowników Nauki, SECON’2004,

WAT, Warszawa, 04 – 05. 11. 2004r.

-45

-35

-25

-15

-5

0

2

4

6

8

10

|S| [dB]

S

b

S

b

S

s

S

s

f [GHz ]

-1400

-1000

-600

-200

0

2

4

6

8

10

b

S

S

s

S

s

f [GHz]

argS [

o

]

b

S

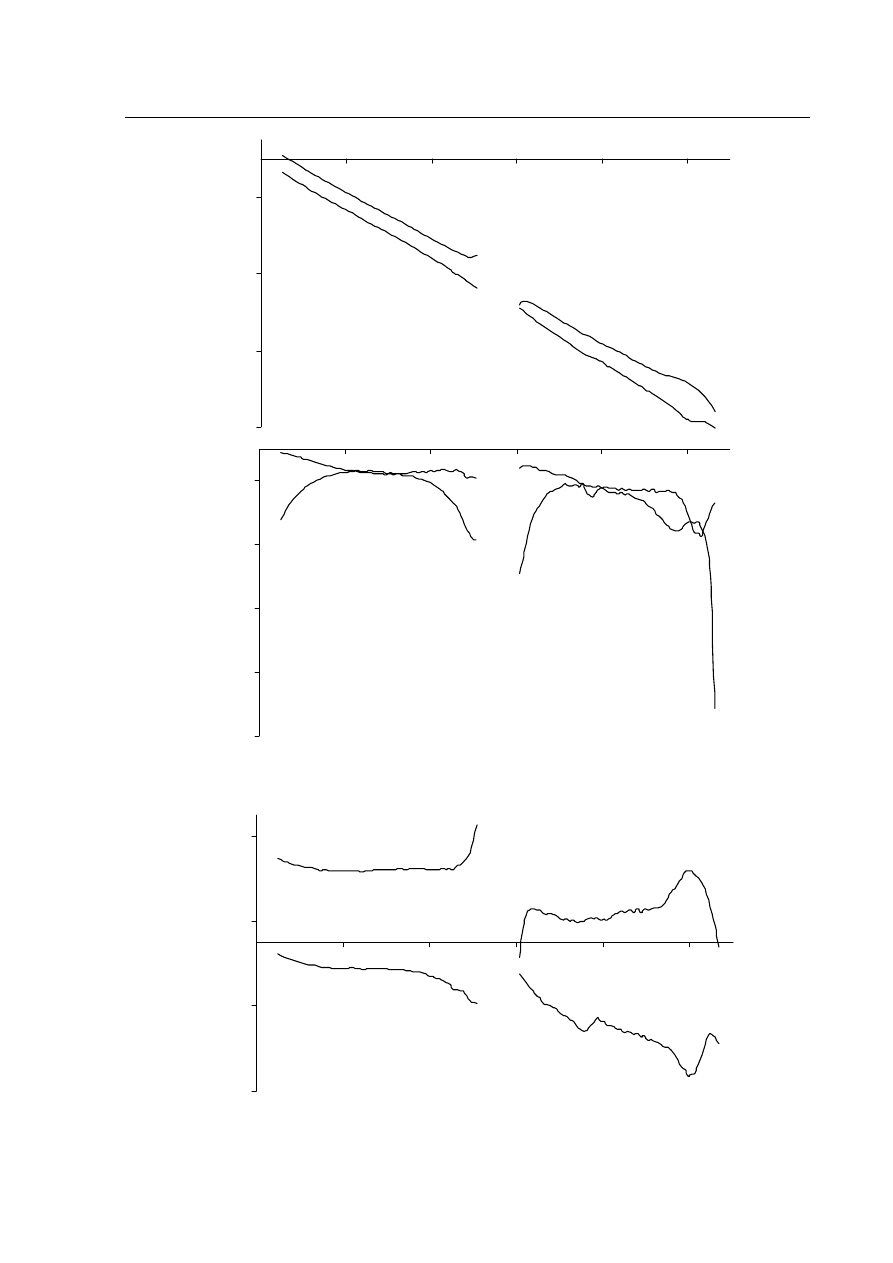
Rys. 9 Przebiegi modułów i argumentów transmitancji sprzęgacza SZ24 Nr2.

-140

-60

20

100

0

2

4

6

8

10

f [GHz]

S

s

S

s

S

b

S

b

Φ

wzgl

[

o

]

Rys. 10 Względne przesunięcie fazy sprzęgacza SZ24 Nr2.

9

XXVII Krajowa Konferencja Elektroniki i Telekomunikacji Studentów

i Młodych Pracowników Nauki, SECON’2004,

WAT, Warszawa, 04 – 05. 11. 2004r.

Prezentowane na rysunku 10 przebiegi otrzymano stosując powietrzne linie odniesienia o następujących

długościach: dla pasma podstawowego l

lodn1

=101,2 mm, a dla podpasma l

lodn2

=102,7 mm. Długościom fizycznym

odpowiadają następujące długości elektryczne (przy częstotliwości środkowej pasma):

Θ

lodn1

=-318,75°;

Θ

lodn2

=-1005,5°.

Z rysunku 10, przedstawiającego przebiegi względnego przesunięcia fazy w funkcji częstotliwości otrzy-

mujemy następujące wyniki na częstotliwościach środkowych pasm: dla wrót bezpośrednich:

Φ

wb1

=-24,8°;

Φ

wb2

=-78,95°; a dla wrót sprzężonych:

Φ

ws1

=67,55° oraz

Φ

ws2

=22,95°. Wartość względnego przesunięcia fazy

w paśmie nie jest stała. Jeśli szerokość rozpatrywanych pasm ograniczy się do pasma trzydecybelowego (ze
względu na moduł transmitancji), maksymalne zmiany wartości względnego przesunięcia fazy wynoszą: dla wrót
sprzężonych: w pasmie podstawowym ±3,45°, w podpasmie dodatkowym ±6,95°; a dla wrót bezpośrednich od-
powiednio: ±9,9°; ±13,45°.

5.

PODSUMOWANIE

Po przeanalizowaniu otrzymanych wyników, stwierdzono istnienie możliwości wykorzystania omawianych

układów również do pracy z sygnałami o częstotliwościach wyższych tzn. takich, przy których długość elektryczna
obszaru sprzężenia kilkakrotnie przekracza wartość 90°. W podpasmach wyższych charakterystyki amplitudowe
wykazują kształty podobne jak w pasmie podstawowym nadal zachowując kwadraturowość sprzęgaczy, ale jed-
nocześnie względne przesunięcia fazy osiągają większe wartości.

Wykorzystywanie badanego sprzęgacza w wyższych podpasmach wiąże się również ze wzrostem strat sy-

gnału we wrotach wyjściowych, wynikających ze wzrostu tłumienia w dielektryku. Należy się też liczyć z zawęże-
niem względnej szerokości pasma pracy i pogorszeniem parametrów takich jak sprzężenie, izolacja i dopasowa-
nie układu. Są to jednak parametry amplitudowe, których wpływ na pracę układu można ograniczyć stosując
układy dopasowujące i wzmacniacze.

Dzięki wykazanym teoretycznie i potwierdzonym eksperymentalnie właściwościom, zbliżeniowe sprzęgacze

kierunkowe mogą być z powodzeniem zastosowane np. jako przesuwniki fazy, sumatory lub jako elementy zło-
żonych systemów antenowych również poza tak zwanym pasmem podstawowym. Wyprowadzone powyżej za-
leżności i sformułowane wnioski są niezbędne do poprawnego projektowania i budowania mikrofalowych syste-
mów pomiarowych, a w tym szybkich systemów namiaru źródeł i analizy struktury wewnętrznej sygnałów wielkiej
częstotliwości.

6.

WYKAZ LITERATURY

[1] Dobrowolski J.: Technika wielkich częstotliwości”, OWPW Warszawa 2001,
[2] Galwas B.: „Miernictwo mikrofalowe”, WKŁ Warszawa 1985,
[3] Rutkowski A.: „Mikrofalowe przesuwniki fazy ze strojnikami równoległymi”, Kwartalnik Elektroniki i Telekomu-

nikacji, 2003, 49, z. 2, s. 201-224,

[4] Litwin R., Suski M.: “Technika mikrofalowa”, WNT Warszawa 1972.

10