1

Teoria masowej obsługi

Podstawowe definicje (1)

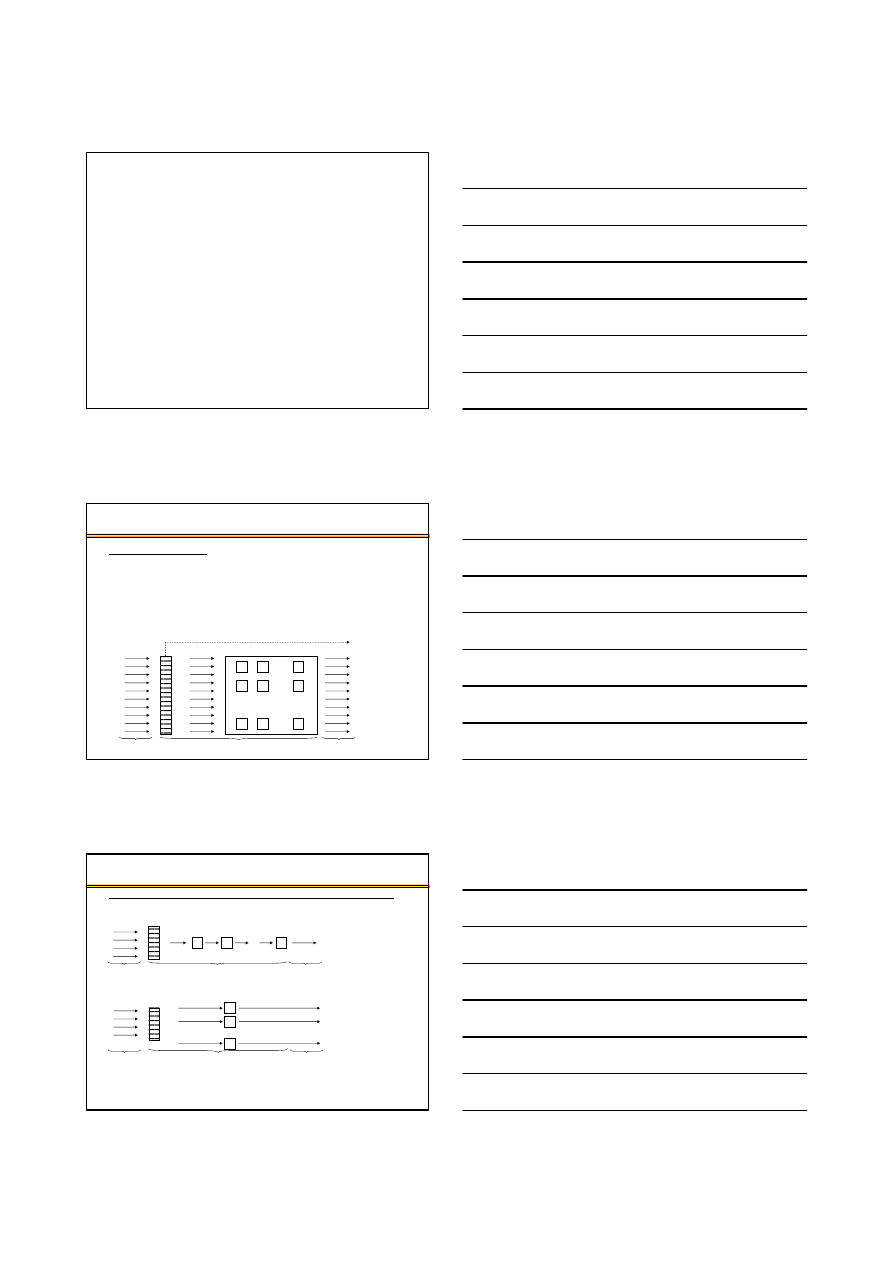
Proces masowej obsługi – proces składaj

ą

cy si

ę

z:

strumie

ń

wchodz

ą

cy (strumie

ń

wej

ś

ciowy, strumie

ń

zgłosze

ń

) –

zgłoszenia nadchodz

ą

ce do systemu;

system obsługi ( kanały obsługi, aparaty obsługi) – zbiór urz

ą

dze

ń

lub

stanowisk

ś

wiadcz

ą

cych obsług

ę

zgłoszenia wraz z kolejk

ą

zgłosze

ń

oczekuj

ą

cych na obsług

ę

;

strumie

ń

wychodz

ą

cy (strumie

ń

wyj

ś

ciowy) – zbiór zgłosze

ń

po

obsłu

ż

eniu oraz zbiór zgłosze

ń

, które zrezygnowały z obsługi.

a

1

a

2

…

a

m

b

1

b

2

…

b

n

…

…

…

c

1

c

2

…

c

k

obsługa

rezygnacja z obsługi

zgłoszenia

strumień

wchodzący

k

o

le

jk

a

system obsługi

strumień

wychodzący

Podstawowe definicje (2)

Klasyfikacja systemów masowej obsługi ze wzgl

ę

du na organizacj

ę

obsługi:

szeregowe (obsługa zgłoszenia w kilku kanałach w

ś

ci

ś

le okre

ś

lonej

kolejno

ś

ci);

równoległe (obsługa w jednym z kilku kanałów realizuj

ą

cych tak

ą

sam

ą

obsług

ę

);

mieszane (obsługa w kolejnych podsystemach szeregowych lub

równoległych).

a

1

b

1

…

c

1

zgłoszenia

strumień

wchodzący

k

o

le

jk

a

system obsługi

strumień

wychodzący

a

1

a

2

…

a

m

…

strumień

wchodzący

k

o

le

jk

a

system obsługi

strumień

wychodzący

zgłoszenia

2

Podstawowe definicje (3)

Klasyfikacja systemów masowej obsługi ze wzgl

ę

du na zachowanie si

ę

zgłoszenia:

ze stratami (zgłoszenie opuszcza po upływie pewnego czasu system

rezygnuj

ą

c z obsługi);

bez strat (zgłoszenie w systemie przebywa do czasu obsłu

ż

enia).

Klasyfikacja systemów masowej obsługi ze wzgl

ę

du na rozmiary i istnienie

kolejki:

systemy z kolejk

ą

ograniczon

ą

lub nieograniczon

ą

;

systemy z kolejk

ą

zabronion

ą

lub niezabronion

ą

.

Podstawowe definicje (4)

Klasyfikacja systemów masowej obsługi ze wzgl

ę

du na organizacj

ę

kolejki

(regulamin kolejki):

FIFO – First In First Out (zgłoszenie stoj

ą

ce na pierwszym miejscu w

kolejce jest obsługiwane jako pierwsze – „kolejka naturalna”);

LIFO – Last In First Out (zgłoszenie stoj

ą

ce na ostatnim miejscu w

kolejce jest obsługiwane jako pierwsze);

SIRO – Selection In Random Order (losowy dobór zgłoszenia do

obsługi);

Obsługa z priorytetem (pierwsze

ń

stwo dla zgłosze

ń

„uprzywilejowanych”).

Charakterystyki liczbowe systemów masowej obsługi (1)

1. Strumie

ń

zgłosze

ń

stopa zgłosze

ń

(liczba zgłosze

ń

napływaj

ą

cych do systemu obsługi w

ustalonej jednostce czasu (

ś

rednio

λ

)

intensywno

ść

zgłosze

ń

(odst

ę

p czasu pomi

ę

dzy kolejnymi zgłoszeniami

(

ś

rednio 1/

λ

)

2. Obsługa

stopa obsługi (liczba zgłosze

ń

obsługiwanych w ustalonej jednostce

czasu (

ś

rednio

µ

)

intensywno

ść

obsługi (czasu obsługi zgłoszenia przez jeden z s

równoległych kanałów obsługi (

ś

rednio 1/

µ

)

3

Charakterystyki liczbowe systemów masowej obsługi (2)

3. Proces obsługi

intensywno

ść

ruchu (stała Erlanga – iloraz

ś

redniej liczby zgłosze

ń

jaka

napływa do systemu w jednostce czasu do

ś

redniej liczby zgłosze

ń

jaka

mo

ż

e by

ć

obsłu

ż

ona w jednostce czasu

):

4. Pozostałe:

liczba zgłosze

ń

w kolejce;

liczba zgłosze

ń

w systemie (ł

ą

cznie w kolejce i obsłudze);

czas oczekiwania w kolejce;

czas pobytu w systemie obsługi (ł

ą

cznie w kolejce i obsłudze);

ρ

λ

µ

=

<

s

1

Charakterystyki liczbowe systemów masowej obsługi (3)

4. Pozostałe (c.d.):

czas przestoju kanału obsługi (w okresie [0,T]);

czas zaj

ę

to

ś

ci kanału obsługi (w okresie [0,T]);

liczba okresów kiedy stanowisko obsługi jest wolne (w przedziale [0,T]).

Modele systemów masowej obsługi (1)

Charakterystyka modeli systemów masowej obsługi:

charakter opisowy;

mo

ż

liwo

ść

wyliczenia podstawowych wielko

ś

ci liczbowych dotycz

ą

cych

procesu masowej obsługi;

modele optymalizacyjne masowej obsługi, jako najcz

ęś

ciej formułowane, w

których poszukuje si

ę

optymalnej liczby kanałów obsługi kieruj

ą

c si

ę

kryterium

najni

ż

szego kosztu całkowitego działania całego systemu (koszt przestoju

stanowiska obsługi w jednostce czasu, koszt utraty zgłoszenia, koszt obsługi
jednego zgłoszenia, itp.).

4

Modele systemów masowej obsługi (2)

Wielko

ś

ci opisuj

ą

ce modele systemów masowej obsługi:

ττττ

1

– czas upływaj

ą

cy mi

ę

dzy dwoma kolejnymi zgłoszeniami;

ττττ

2

– czas obsługi jednego zgłoszenia;

s – liczba równoległych kanałów obsługi;

R – liczebno

ść

obsługiwanej populacji (otoczenia, którego elementy mog

ą

zgłasza

ć

zapotrzebowanie na obsług

ę

);

L – maksymalna liczba miejsc w kolejce.

Modele systemów masowej obsługi (3)

Model masowej obsługi powinien uwzgl

ę

dnia

ć

:

typ rozkładów prawdopodobie

ń

stw zmiennych losowych

ττττ

1

oraz

ττττ

2

;

zale

ż

no

ść

(niezale

ż

no

ść

) zmiennych losowych

ττττ

1

oraz

ττττ

2

;

wielko

ś

ci ograniczaj

ą

ce s, R i L;

dyscyplin

ę

kolejki (kolejno

ść

obsługi).

System kodowania modeli masowej obsługi:

f(

τ

1

) /

f

(

τ

2

) / s (R,L)

Modele systemów masowej obsługi (4)

Oznaczenia rozkładów prawdopodobie

ń

stw zmiennych losowych

ττττ

1

i

ττττ

2

:

D – proces nielosowy (deterministyczny);

M – rozkład wykładniczy lub Poisson’a;

E

n

– rozkład Erlanga n-tego rz

ę

du;

N – rozkład normalny;

GI – ogólny niezale

ż

ny rozkład odst

ę

pu czasu pomi

ę

dzy kolejnymi

zgłoszeniami;

G – ogólny rozkład czasu obsługi.

5

Modele systemów masowej obsługi (5)

Przykład kodowania modeli systemów masowej obsługi:

M / E

4

/ 1 (

∞

, 100)

Model masowej obsługi, w którym czas pomi

ę

dzy kolejnymi zgłoszeniami jest

zmienn

ą

losow

ą

o rozkładzie wykładniczym (b

ą

d

ź

liczba zgłosze

ń

w

jednostce czasu ma rozkład Poissona), czas obsługi jest zmienn

ą

losow

ą

o

rozkładzie Erlanga 4-tego rz

ę

du, model posiada jeden kanał obsługi,

populacja zgłosze

ń

jest nieograniczona, a kolejka nie mo

ż

e przekracza

ć

100

zgłosze

ń

.

Jednokanałowy model masowej obsługi (1)

M / M / 1 (

∞

,

∞

)

Model masowej obsługi, w którym czas pomi

ę

dzy kolejnymi zgłoszeniami jest

zmienn

ą

losow

ą

o rozkładzie wykładniczym (b

ą

d

ź

liczba zgłosze

ń

w

jednostce czasu ma rozkład Poissona), czas obsługi jest zmienn

ą

losow

ą

o

rozkładzie wykładniczym, model posiada jeden kanał obsługi, populacja
zgłosze

ń

jest nieograniczona, a długo

ść

kolejki jest tak

ż

e nieograniczona.

a

1

zgłoszenia

strumień

wchodzący

k

o

le

jk

a

system obsługi

strumień

wychodzący

[M]

[M]

FIFO

Jednokanałowy model masowej obsługi (2)

1. Strumie

ń

zgłosze

ń

odst

ę

p czasu (t) pomi

ę

dzy dwoma kolejnymi zgłoszeniami, który jest zmienn

ą

losow

ą

o tzw. ujemnym rozkładzie wykładniczym:

f(t) = λe

–λt

dla t

≥

0

z warto

ś

ci

ą

oczekiwan

ą

:

E(t) = 1/

λ

oraz

wariancj

ą

:

D

2

(t) = (1/

λ

)

2

lub

6

Jednokanałowy model masowej obsługi (3)

1. Strumie

ń

zgłosze

ń

(c.d)

liczba zgłosze

ń

(n) pojawiaj

ą

ca si

ę

w systemie w jednostce czasu o długo

ś

ci

(T) jest zmienn

ą

losow

ą

o rozkładzie Poissona:

P{n=k} = (λT)

k

e

–λT

/ k!

dla k = 0,1,2,…

z warto

ś

ci

ą

oczekiwan

ą

i wariancj

ą

:

E(n) = D

2

(n) =

λT

Jednokanałowy model masowej obsługi (4)

2. Obsługa jednego zgłoszenia

czasu (t) obsługi zgłoszenia jest zmienn

ą

losow

ą

o ujemnym rozkładzie

wykładniczym:

g(t) = µe

–µt

dla t

≥

0

z warto

ś

ci

ą

oczekiwan

ą

:

E(t) = 1/

µ

oraz

wariancj

ą

:

D

2

(t) = (1/

µ

)

2

Jednokanałowy model masowej obsługi (5)

3. Wybrane charakterystyki liczbowe modelu M / M / 1 (

∞

,

∞

)

λ

– oczekiwana liczba zg

ł

osze

ń

w jednostce czasu

1/µ

– oczekiwany czas obs

ł

ugi jednego zg

ł

oszenia

Intensywno

ść

ruchu (stała Erlanga):

ρ = λ

/

µ

Oczekiwana liczba zgłosze

ń

w systemie (N):

N = ρ / (1 – ρ)

Oczekiwana długo

ść

kolejki (Q):

Q = ρ

2

/ (1 – ρ)

7

Jednokanałowy model masowej obsługi (6)

Oczekiwany czas pobytu w systemie (R):

R = 1 / (µ – λ)

Oczekiwany czas pobytu w kolejce (W):

W = ρ / (µ – λ)

Prawdopodobie

ń

stwo braku zgłosze

ń

w systemie:

P

0

= (1 – ρ)

Prawdopodobie

ń

stwo wyst

ę

powania n zgłosze

ń

w systemie:

P

n

= ρ

n

(1 – ρ)

Jednokanałowy model masowej obsługi (7)

Oczekiwany czas przestoju w przedziale czasu [0,T] (WT):

WT = T / (1 – ρ)

Oczekiwany czas zaj

ę

to

ś

ci w przedziale czasu [0,T] (BT):

BT = T

ρ

Oczekiwana liczba przestojów (przerw w pracy kanału) w przedziale
czasu [0,T] (FPT):

FPT = Tλ(1 – ρ)

Wielokanałowy model masowej obsługi (1)

M / M / s (

∞

,

∞

)

dla s

≥

2

Model masowej obsługi, w którym czas pomi

ę

dzy kolejnymi zgłoszeniami jest

zmienn

ą

losow

ą

o rozkładzie wykładniczym, czas obsługi jest zmienn

ą

losow

ą

o rozkładzie wykładniczym, model posiada s równoległych

jednorodnych kanałów obsługi, populacja zgłosze

ń

jest nieograniczona, a

długo

ść

kolejki jest tak

ż

e nieograniczona.

a

1

a

2

…

a

m

…

strumień

wchodzący

k

o

le

jk

a

system obsługi

strumień

wychodzący

zgłoszenia

[M]

[M]

FIFO

8

Wielokanałowy model masowej obsługi (2)

1. Strumie

ń

zgłosze

ń

odst

ę

p czasu (t) pomi

ę

dzy dwoma kolejnymi zgłoszeniami, który jest zmienn

ą

losow

ą

o tzw. ujemnym rozkładzie wykładniczym:

f(t) = λe

–λt

dla t

≥

0

z warto

ś

ci

ą

oczekiwan

ą

:

E(t) = 1/

λ

oraz

wariancj

ą

:

D

2

(t) = (1/

λ

)

2

lub

Wielokanałowy model masowej obsługi (3)

1. Strumie

ń

zgłosze

ń

(c.d)

liczba zgłosze

ń

(n) pojawiaj

ą

ca si

ę

w systemie w jednostce czasu o długo

ś

ci

(T) jest zmienn

ą

losow

ą

o rozkładzie Poissona:

P{n=k} = (λT)

k

e

–λT

/ k!

dla k = 0,1,2,…

z warto

ś

ci

ą

oczekiwan

ą

i wariancj

ą

:

E(n) = D

2

(n) =

λT

Wielokanałowy model masowej obsługi (4)

2. Obsługa jednego zgłoszenia

czasu (t) obsługi zgłoszenia jest zmienn

ą

losow

ą

o ujemnym rozkładzie

wykładniczym:

g(t) = µe

–µt

dla t

≥

0

z warto

ś

ci

ą

oczekiwan

ą

:

E(t) = 1/

µ

oraz

wariancj

ą

:

D

2

(t) = (1/

µ

)

2

9

Wielokanałowy model masowej obsługi (5)

3. Wybrane charakterystyki liczbowe modelu M / M / s (

∞

,

∞

)

λ

– oczekiwana liczba zg

ł

osze

ń

w jednostce czasu

1/µ

– oczekiwany czas obs

ł

ugi jednego zg

ł

oszenia

Intensywno

ść

ruchu (stała Erlanga):

ρ = λ

/

sµ

Oczekiwana liczba zgłosze

ń

w systemie (N):

N = ρ + P

0

[ρ

s+1

/ (s – ρ

2

)(s – 1)!]

Oczekiwana długo

ść

kolejki (Q):

Q = N – ρ

Wielokanałowy model masowej obsługi (6)

Oczekiwany czas pobytu w systemie (R):

R = N / λ

Oczekiwany czas pobytu w kolejce (W):

W = Q / λ

Prawdopodobie

ń

stwo braku zgłosze

ń

w systemie:

∑

−

=

−

+

=

1

0

0

)

1

(

!

!

1

s

j

s

j

s

s

j

P

ρ

ρ

ρ

Wielokanałowy model masowej obsługi (7)

Prawdopodobie

ń

stwo wyst

ę

powania n

≥

1 zgłosze

ń

w systemie:













>

≤

≤

=

−

s

n

s

s

P

s

n

n

P

P

s

n

n

n

dla

!

1

dla

!

0

0

0

ρ

ρ

10

Jednokanałowy model masowej obsługi – przykład (1)

M / M / 1 (

∞

,

∞

)

a

1

zgłoszenia

strumień

wchodzący

k

o

le

jk

a

system obsługi

strumień

wychodzący

[M]

[M]

FIFO

Gniazdo produkcyjne składa si

ę

z jednego agregatu obsługiwanego przez 1 lub

2 osoby. Przeprowadzono badanie statystyczne i stwierdzono,

ż

e liczba detali

napływaj

ą

ca do gniazda produkcyjnego w ci

ą

gu 1 minuty ma rozkład Poissona

o warto

ś

ci oczekiwanej równej 5 detali na minut

ę

. Czas obsługi jest w ka

ż

dym

przypadku zmienn

ą

losow

ą

o rozkładzie wykładniczym, o warto

ś

ci oczekiwanej

zale

ż

nej od liczby osób obsługuj

ą

cych agregat.

I. 7,5 sek. przy obsłudze 1-osobowej
II. 6,0 sek. przy obsłudze 2-osobowej

Jednokanałowy model masowej obsługi – przykład (2)

Wyznacz podstawowe charakterystyki liczbowe tego systemu w obu
wariantach obsługi.

I. 1/µ = 7,5 sek./detal = 0,125 min./detal

µ = 8 detali/min.

II. 1/µ = 6,0 sek./detal = 0,100 min./detal

µ = 10 detali/min.

I. λ = 5 detali/min.
II. λ = 5 detali/min.

Stała Erlanga (intensywno

ść

ruchu)

→

wykorzystanie gniazda

produkcyjnego:

ρ = λ / µ

I. ρ = 5 / 8 = 0,625 = 62,5%
II. ρ = 5 / 10 = 0,500 = 50,0%

Jednokanałowy model masowej obsługi – przykład (3)

Oczekiwana liczba zgłosze

ń

w systemie (N)

→

detali w gnie

ź

dzie

produkcyjnym:

N

= ρ / (1 – ρ)

I. N = 0,625 / (1 – 0,625) = 1,67
II. N = 0,500 / (1 – 0,500) = 1,00

Oczekiwana długo

ść

kolejki (Q):

Q =

ρ

2

/ (1 –

ρ

)

I. Q = (0,625)

2

/ (1 – 0,625) = 1,04

II. Q = (0,500)

2

/ (1 – 0,500) = 0,50

Oczekiwany czas pobytu w systemie (R)

→

detalu w gnie

ź

dzie

produkcyjnym [min.]:
R = 1 / (

µ

–

λ

)

I. R = 1 / (8 – 5) = 0,33
II. R = 1 / (10 – 5) = 0,20

11

Jednokanałowy model masowej obsługi – przykład (4)

Oczekiwany czas pobytu w kolejce (W) [min.]:
W =

ρ

/ (

µ

–

λ

)

I. W = 0,625 / (8 – 5) = 0,21
II. W = 0,500 / (10 – 5) = 0,10

Prawdopodobie

ń

stwo braku zgłosze

ń

w systemie

→

braku napływu detali

do gniazda produkcyjnego:
P

0

= (1 –

ρ

)

I. P

0

= 1 – 0,625 = 0,375

II. P

0

= 1 – 0,500 = 0,500

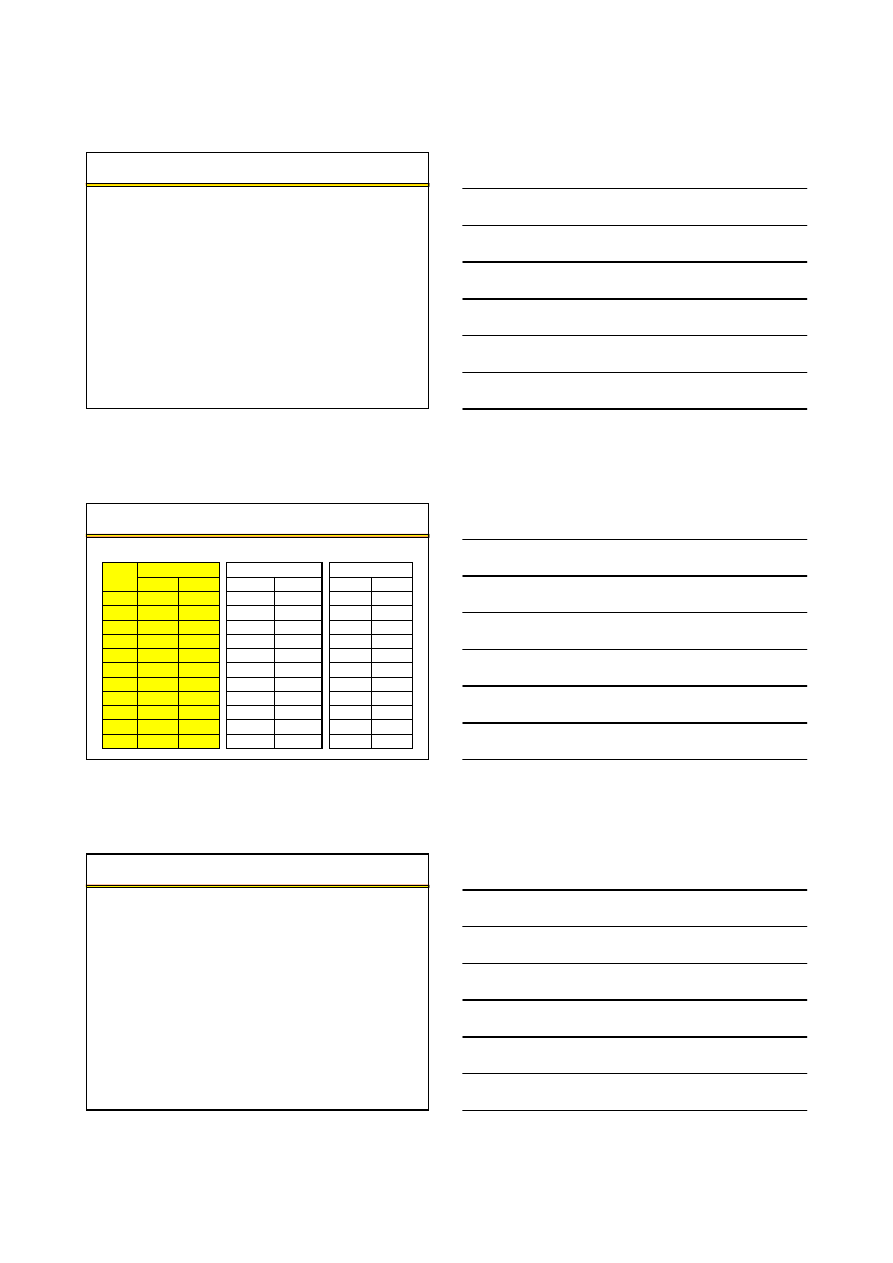
Jednokanałowy model masowej obsługi – przykład (5)

Prawdopodobie

ń

stwo wyst

ę

powania n zgłosze

ń

w systemie:

P

n

=

ρ

n

(1 –

ρ

)

0,999

0,991

0,002

0,015

0,001

0,005

9

0,001

0,004

0,008

0,016

0,031

0,063

0,125

0,250

0,500

1,000

II

1,000

0,994

0,009

0,000

0,003

10

0,998

0,985

0,023

0,002

0,009

8

0,996

0,977

0,037

0,004

0,014

7

0,992

0,963

0,060

0,008

0,022

6

0,984

0,940

0,095

0,016

0,036

5

0,969

0,905

0,153

0,031

0,057

4

0,938

0,847

0,244

0,063

0,092

3

0,875

0,756

0,391

0,125

0,146

2

0,750

0,609

0,625

0,250

0,234

1

0,500

0,375

1,000

0,500

0,375

0

II

I

I

II

I

P{n≤k}

P{n≥k}

P{n=k}

k

Jednokanałowy model masowej obsługi – przykład (6)

Oczekiwany czas przestoju w przedziale czasu [0,T] (WT) [min.]:
WT = T / (1 –

ρ

)

dla T = 8h = 480 min.:
I. WT = 480 / (1 – 0,625) = 180
II. WT = 480 / (1 – 0,500) = 240

Oczekiwany czas zaj

ę

to

ś

ci w przedziale czasu [0,T] (BT)

→

czas pracy [min.]:

BT = T

ρ

dla T = 8h = 480 min.:
I. BT = 480

×

0,625 = 300

II. BT = 480

×

0,500 = 240

Oczekiwana liczba przestojów (przerw w pracy kanału) w przedziale czasu
[0,T] (FPT)

→

liczba detali obrobionych w gnie

ź

dzie produkcyjnym

FPT = T

λ

(1 –

ρ

)

dla T = 8h = 480 min.:
I. FPT = 480

×

5

×

(1–0,625) = 900

II. FPT = 480

×

5

×

(1–0,500) = 1200