Teoria kolejek – systemy

masowej obsługi

Janusz Papliński

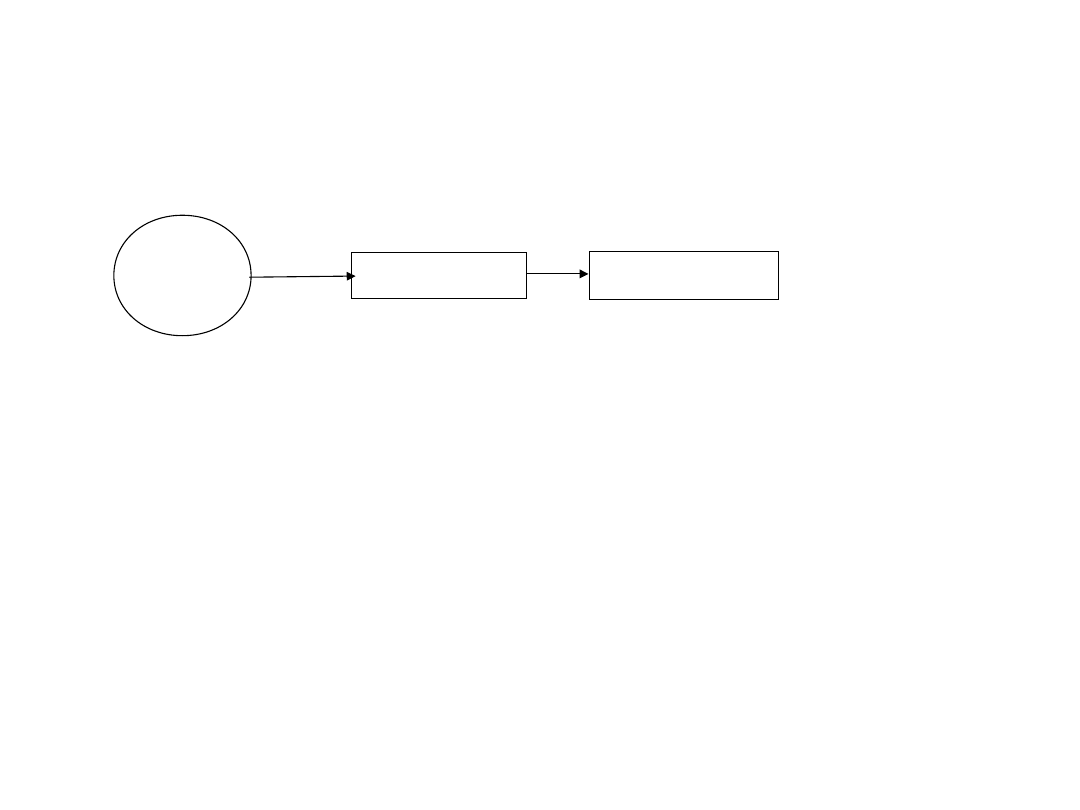
Prosty system obsługi:

Dążymy do takiej organizacji obsługi, która pozwoli na minimalizację
czasu trwania obsługi, a więc czasu straconego, przy jednoczesnej
minimalizacji kosztów funkcjonowania systemu.

Czas oczekiwania jest czasem straconym

Źródło
zadań

kolejka

Stanowisko

obsługi

Strumień
zadań

z

i

Pojęcia podstawowe:

obsługa – czynność pozwalająca zaspokoić określone potrzeby

Zgłoszenie (zadanie) – obiekt/klient/ oczekujący na obsługę,

kolejka – zbiór zgłoszeń oczekujących wg. ustalonych reguł na
obsługę,

regulamin/kolejki lub obsługi/ - zbiór reguł, wg. których zgłoszenia
tworzą kolejkę i są obsługiwane,

aparat obsługi

układ obsługi – zbiór aparatów obsługi łącznie z czynnościami przez
nie wykonywanymi,

System – model obsługi – zbiór, którego elementami są: układ
obsługi, zgłoszenia obsługiwane, oczekujący na obsługę, zgłoszenia do
systemu.

Analiza strumienia zgłoszeń

Zgłoszenia napływają w sposób przypadkowy, nieregularny

Taki proces nazywamy procesem losowym lub stochastycznym. Tu proces
ten określa prawdopodobieństwo tego, że w określonym przedziale czasu
pojawia się w układzie określona liczba zgłoszeń.

Strumień zgłoszeń opisuje funkcja losowa X(t), (t≥0),
czyli dla każdego t≥0 wartość funkcji przedstawia liczbę
zarejestrowanych zgłoszeń, które przybyły do układu w przedziale
czasu[0,t].

Stąd X(t) przyjmuje wartości 0,1,2,…,n.

),

(

}

)

(

{

t

p

n

t

X

P

n





.

0

,...,

2

,

1

,

0





t

n

gdzie

W

dowolnym

momencie

czasu

t

strumień

charakteryzuje

prawdopodobieństwo tego, że układzie znajduje się n zgłoszeń:

- prawdopodobieństwo tego, że w czasie t nadejdzie do

układu obsługi zero zgłoszeń,

Analiza strumienia zgłoszeń

Proces stochastyczny jednorodny - prawdopodobieństwo przybycia
określonej liczby zgłoszeń w przedziale czasu [t

0

, t

0

+t] nie zależy od

momentu t

0

, natomiast jedynie od długości przedziału czasu t.

Tw. 1. Każdy jednorodny proces posiada:

0

)

(

1

lim

0

0











t

t

p

t

Można to zapisać wykorzystując pojęcie nieskończenie małej wartości
wyższego rzędu

:

)

(t



),

(

)

(

1

0

t

t

t

p











gdzie: - parametr procesu zwany intensywnością zgłoszeń,



)

(

0

t

p

- nieskończenie mała wartość wyższego rzędu w porównaniu

z t, tzn. .

)

(t



0

)

(

lim

0





t

t

t



Analiza strumienia zgłoszeń

Procesem o przyrostach niezależnych nazywamy proces
stochastyczny X(t), gdzie t  0 w którym prawdopodobieństwo

wystąpienia n zgłoszeń w przedziale [t

0

, t

0

+t] nie zależy od tego ile

zgłoszeń i w jaki sposób wystąpiło do momentu t

0

.

Strumień jest strumieniem pojedynczym, jeżeli w procesie
stochastycznym X(t), gdzie t  0, brak jest możliwości pojawienia się

więcej niż jednego zgłoszenia w tym samym momencie czasu.

Strumieniem prostym nazywamy strumień spełniający warunki
strumienia jednorodnego, o przyrostach niezależnych i pojedynczy.

Analiza strumienia zgłoszeń

Tw. 2. Jeżeli strumień zgłoszeń spełnia warunki strumienia prostego, to
zmienna losowa określająca:

a/ liczbę zgłoszeń, która przybywa do układu obsługi w czasie t

jest zgodna z rozkładem Poissona o parametrze , postaci:

, n=0,1,2, ...

b/ odstępy czasu między kolejnymi zgłoszeniami są zgodne z

rozkładem wykładniczym o parametrze  a funkcja gęstości jest

postaci:

.

t  0

t

n

n

e

n

t

t

p









!

)

(

)

(

t

e

t

f









)

(

Analiza strumienia zgłoszeń

Tw. 3 Intensywność zgłoszeń strumienia prostego  jest równa:

wartości oczekiwanej zmiennej losowej, jaką jest liczba zgłoszeń n
w przyjętej jednostce czasu, czyli .

)

(

1

n

E





odwrotność wartości oczekiwanej zmiennej losowej, jaką jest odstęp
czasu między poszczególnymi przybyciami, czyli .

)

(

1





E



Przykład 1. Rozkład dzienny przybyć statków do portu w tabeli

poniżej. Wyznaczyć intensywność zgłoszeń statków.

i

n

 
L.
p

 
Liczba statków
przybyłych w
ciągu jednego
dnia i

 

 
Liczba
zaobserwowany
ch
zdarzeń

 

1
2
3
4

 

0
1
2
3

 

223
112

26

4

 

 

 

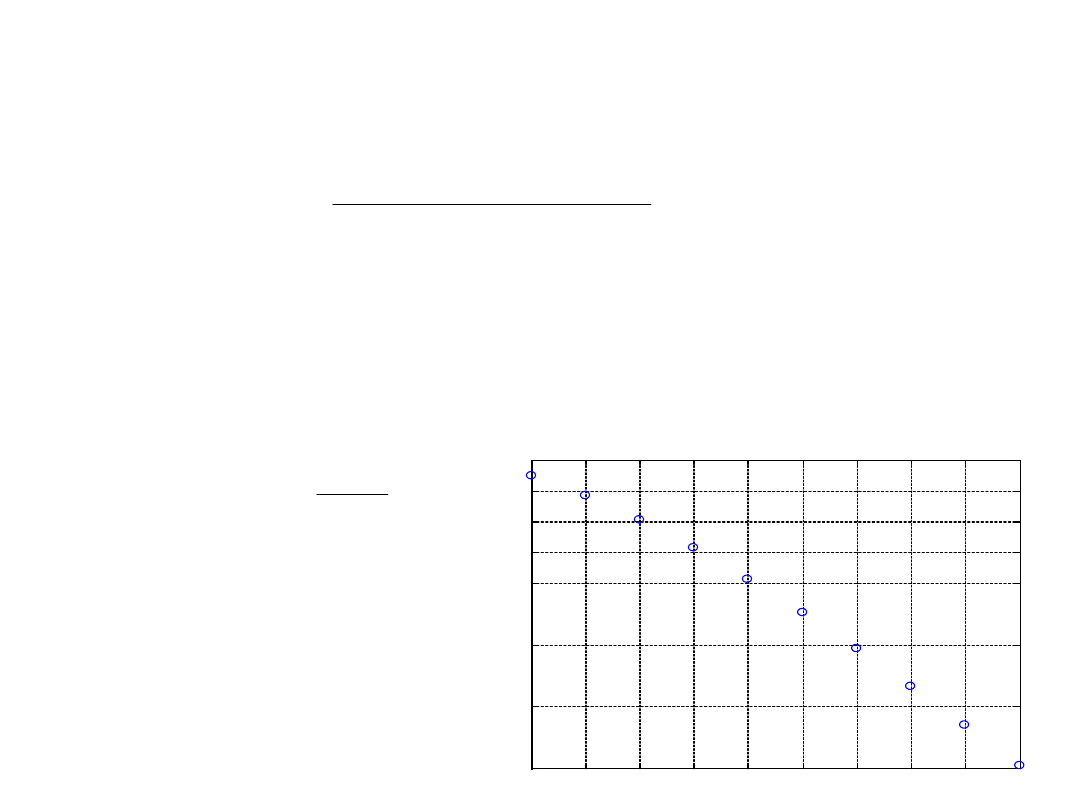
Liczba przybyć statków do portu w ciągu dnia jest równa:

 

.

Jeżeli przyjmiemy, że rozkład przybyć jest zgodny z rozkładem

Poissona, to zgodnie z Tw. 3. .

b/ prawdopodobieństwo wystąpienia i-tej ilości zgłoszeń dla t = 1

/jeden dzień/ ma postać:

dla i=1, 2, 3.

482

,

0

365

4

*

3

26

*

2

112

*

1

223

*

0

)

(

1











n

E

482

,

0





482

,

0

!

482

,

0

)

1

(





e

i

p

i

i

)

(

1

n

E





1

2

3

4

5

6

7

8

9

10

10

-10

10

-8

10

-6

10

-4

10

-3

10

-2

10

-1

10

0

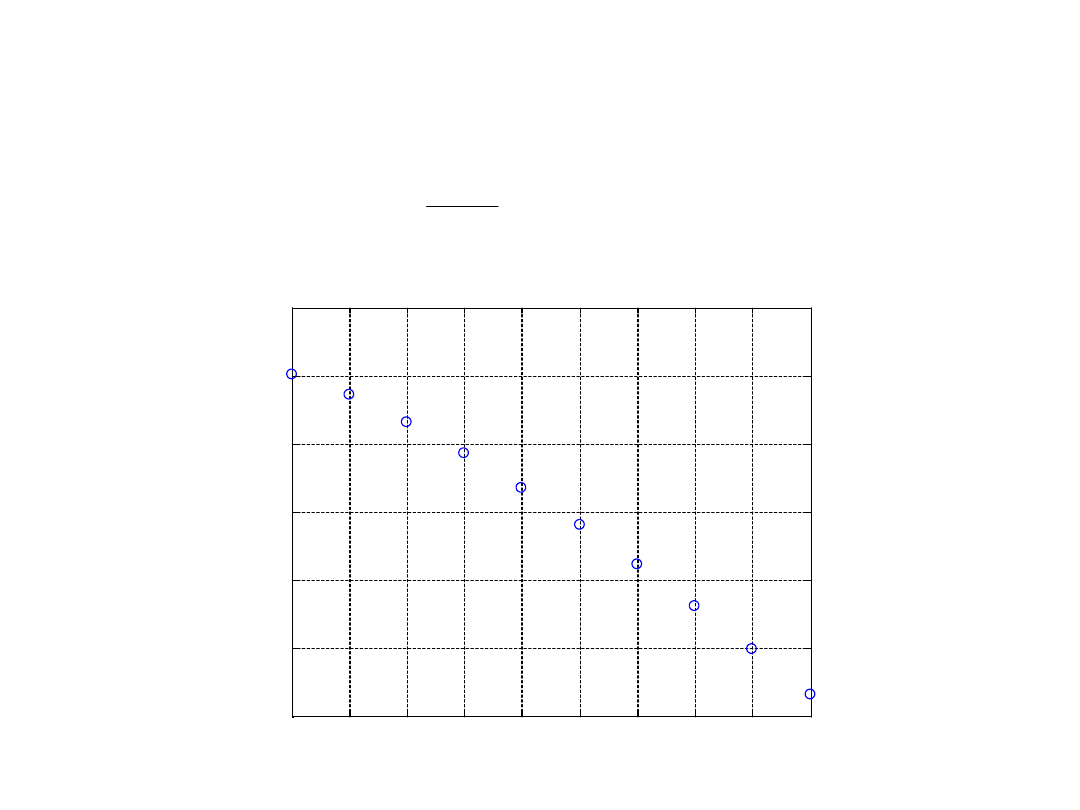
c/ oczekiwana liczba dni z i-tą liczebnością przybyć:

dla i=1, 2, 3.

482

,

0

'

!

482

,

0

365





e

i

n

i

i

1

2

3

4

5

6

7

8

9

10

10

-8

10

-6

10

-4

10

-2

10

0

10

2

10

4

oczekiwana iloœæ statków

oc

ze

ki

w

an

a

ilo

œ

æ

d

ni

Analiza czasu trwania obsługi

Czas trwania obsługi ma rozkład wykładniczy o funkcji gęstości:

gdzie  - intensywność obsługi

i dystrybuancie rozkładu równej:

t

e

T

P

F















1

)

(

)

(

Tw. 4. Intensywność obsługi  jest odwrotnością wartości

oczekiwanej zmiennej losowej, jaką jest czas trwania obsługi
poszczególnych zgłoszeń.











e

f

*

System z jednym stanowiskiem obsługi i nieograniczoną

kolejką

System tworzą:

-

       

jeden aparat obsługi o wykładniczym czasie trwania

obsługi i intensywności ,

-

       

prosty strumień zgłoszeń o intensywności ,

-

       

regulamin obsługi: jeżeli aparat jest zajęty, to zgłoszenia

ustawiają się w kolejce i obsługiwane są w kolejności
przybyć.

Oznaczenia:

E(i) – stan systemu, w którym znajduje się „i” zgłoszeń,

p(t) – prawdopodobieństwo tego, że system w chwili „t”

znajdzie się w stanie E

i

, czyli .

)

(

)

(

i

i

E

p

t

p



System z jednym stanowiskiem obsługi i nieograniczoną

kolejką

System znajduje się w stanie równowagi statycznej wtedy i tylko wtedy
gdy .

n

n

t

p

t

p







)

(

lim

Jeżeli analizowany system masowej obsługi osiągnął stan równowagi
statycznej, to prawdopodobieństwa pojawienia się lub zniknięcia stanu
są takie same:
.

)

(

)

(

)

(

)

(

1

1

1

1























n

n

n

n

n

n

n

n

E

E

P

E

E

P

E

E

P

E

E

P

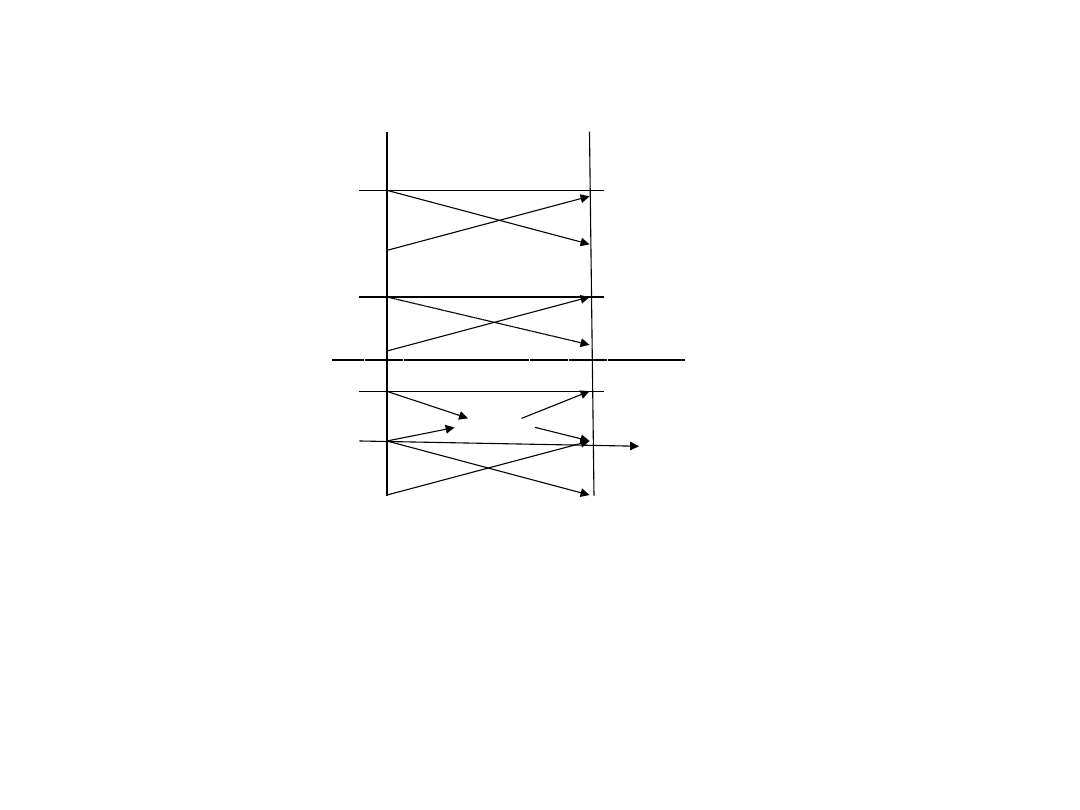
System z jednym stanowiskiem obsługi i nieograniczoną

kolejką

,

1

0

p

p







1

1

2

0

p

p

p

p















……………………………………….

n

n

n

n

p

p

p

p



















1

1

1

1







n

n

p

E

i

i

p

E 





0

0

p

E 

t

0

+∆t

t

0

1

1

p

E 

System z jednym stanowiskiem obsługi i nieograniczoną

kolejką

W wyniku redukcji otrzymujemy:



























































1

),

(

0

0

0

1

1

1

0

0

p

p

p

p

p

p

n

n

n

n

n

n

n

n

Z definicji

0

0



p

stąd

to oznacza, że .

0

1









1







System z jednym stanowiskiem obsługi i nieograniczoną

kolejką

Niech

. Iloraz oznacza intensywność ruchu.

Z tego, że

i definicji q wynika:

q











1





n

n

p

p





I. Prawdopodobieństwo tego, że w systemie znajduje się n zgłoszeń:

)

1

(

q

q

p

n

n





II.

 

Średnia liczba zgłoszeń znajdujących się w systemie

)

(n

E

n

n





q

q

q

q

q

nq

q

q

nq

n

n

n

n

n































1

1

)

1

(

)

1

(

)

1

(

2

0

0

I.

                

III Wariancja liczby zgłoszeń znajdujących się w systemie :

, .





2

0

2

2

0

2

1

)

1

(

)

var(

q

q

q

q

n

n

p

n

n

n

n

n

n

























IV. Średnia liczba zgłoszeń oczekujących w kolejce :

 

gdzie 1-p

0

oznacza, że aparat obsługi jest zajęty.

q

q

q

n

p

n

v











1

)

1

(

2

0

V.

Średni czas przebywania w systemie :

)

1

(

q

q

n

t











System z jednym stanowiskiem obsługi i nieograniczoną

kolejką

System z jednym stanowiskiem obsługi i nieograniczoną

kolejką

VI. Średni czas oczekiwania na obsługę /przebywania w kolejce/ :

)

1

(

2

q

q

v

w











VII. Prawdopodobieństwo, że w systemie znajduje się mniej niż N

zgłoszeń:





N

N

n

n

N

n

n

q

q

q

p

N

n

P

























1

1

)

(

1

0

1

0

System z jednym stanowiskiem obsługi i nieograniczoną

kolejką

)

(

)

(















t

qe

t

P

IX. Prawdopodobieństwo oczekiwania w systemie dłużej niż :

)

(

)

(















t

e

t

P

VIII. Prawdopodobieństwo oczekiwania w kolejce dłużej niż t:

System z ograniczona długością kolejki

Rozpatrzmy system:
-

             

jeden aparat obsługi o wykładniczym czasie trwania obsługi i

intensywności ,

-

             

prosty strumień zgłoszeń o intensywności ,

-

             

regulamin obsługi:

1. jeżeli liczba zgłoszeń osiągnie pewien stan, to następne zgłoszenie

musi zrezygnować z oczekiwania na realizację obsługi,

2. zgłoszenia obsługiwane są wg. kolejności przybyć.

Z analizy systemu wynika, że straty zgłoszeń spowodowane
dotrzymywania regulaminu są tym większe, im większa jest intensywność
ruchu

Przyjmijmy, że kolejka jest ograniczona do N-1 zgłoszeń i każde N-te
zgłoszenie zmuszone jest do opuszczenia systemu

Prawdopodobieństwo odmowy obsługi – rezygnacja oczekiwania na
obsługę:

N

N

N

q

q

q

p

1

1

1









System z ograniczona długością kolejki

System obsługi z nieograniczoną kolejką i n równoległych

kanałów obsługi



n

=

 - średnia liczba zgłoszeń w danym odcinku czasu



n

=n - średnia liczba obsłużonych zadań w danym odcinku czasu