www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´

N Z

M

ATEMATYKI

P

RÓBNY

E

GZAMIN

M

ATURALNY

Z

M

ATEMATYKI

POZIOM PODSTAWOWY

7

MARCA

2012

C

ZAS PRACY

: 170

MINUT

Zadania zamkni˛ete

Z

ADANIE

1

(1

PKT

.)

Liczb˛e

√

32 mo ˙zna przedstawi´c w postaci

A) 8

√

2

B) 12

√

3

C) 4

√

8

D) 4

√

2

Z

ADANIE

2

(1

PKT

.)

Pot˛ega

y
x

5

(gdzie x i y s ˛

a ró ˙zne od zera) jest równa

A)

−

5

·

x
y

B)

x
y

−

5

C)

y

5

x

D)

−

x
y

5

Z

ADANIE

3

(1

PKT

.)

Liczba log

3

1

27

jest równa

A)

−

3

B)

−

1

3

C)

1

3

D) 3

Z

ADANIE

4

(1

PKT

.)

Wyra ˙zenie

||

x

| +

1

|

dla x

<

0 jest równe

A) x

+

1

B) x

−

1

C)

−

x

+

1

D)

−

x

−

1

Z

ADANIE

5

(1

PKT

.)

W pewnym sklepie ceny wszystkich płyt CD obni ˙zono o 20%. Zatem za dwie płyty kupione
w tym sklepie nale ˙zy zapłaci´c mniej o
A) 10%

B) 20%

C) 30%

D) 40%

Z

ADANIE

6

(1

PKT

.)

Wielomian 4x

2

−

100 jest równy

A)

(

2x

−

10

)

2

B)

(

2x

−

10

)(

2x

+

10

)

C) 4

(

x

−

10

)

2

D) 4

(

x

−

10

)(

x

+

10

)

Z

ADANIE

7

(1

PKT

.)

Równanie

x

2

+

36

x

−

6

=

0

A) nie ma rozwi ˛

aza ´n.

B) ma dokładnie jedno rozwi ˛

azanie.

C) ma dokładnie dwa rozwi ˛

azania.

D) ma dokładnie trzy rozwi ˛

azania.

Materiał pobrany z serwisu

www.zadania.info

1

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´

N Z

M

ATEMATYKI

Z

ADANIE

8

(1

PKT

.)

Najwi˛eksz ˛

a liczb ˛

a całkowit ˛

a spełniaj ˛

ac ˛

a nierówno´s´c

(

4

+

x

)

2

< (

x

−

4

)(

x

+

4

)

jest

A)

−

5

B)

−

4

C)

−

3

D)

−

2

Z

ADANIE

9

(1

PKT

.)

Funkcja liniowa f

(

x

) =

1

2

x

−

6

A) jest malej ˛

aca i jej wykres przechodzi przez punkt

(

0, 6

)

B) jest rosn ˛

aca i jej wykres przechodzi przez punkt

(

0, 6

)

C) jest malej ˛

aca i jej wykres przechodzi przez punkt

(

0,

−

6

)

D) jest rosn ˛

aca i jej wykres przechodzi przez punkt

(

0,

−

6

)

Z

ADANIE

10

(1

PKT

.)

Liczby x

1

, x

2

s ˛

a rozwi ˛

azaniami równania 4

(

x

+

2

)(

x

−

6

) =

0. Suma x

2

1

+

x

2

2

jest równa

A) 16

B) 32

C) 40

D) 48

Z

ADANIE

11

(1

PKT

.)

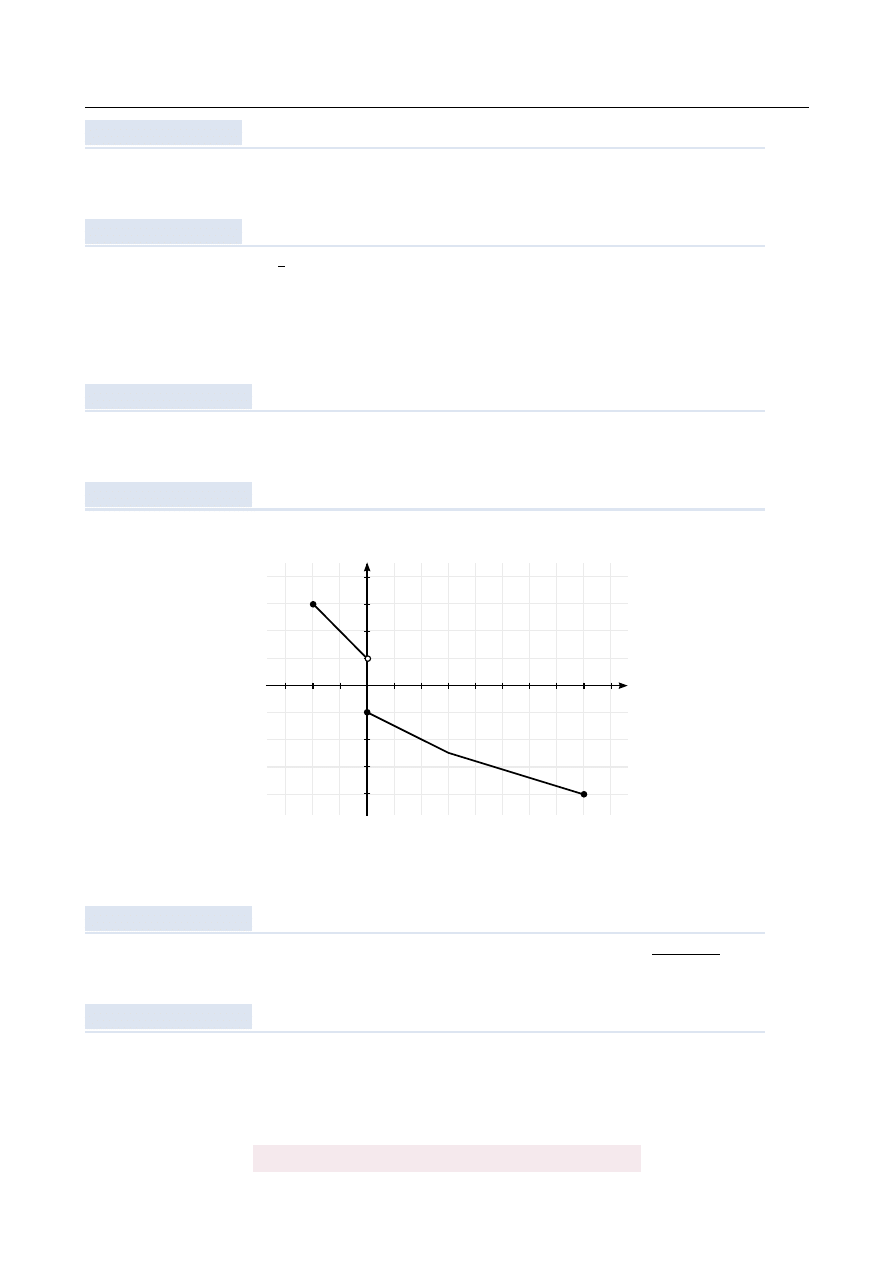
Na rysunku jest przedstawiony wykres funkcji y

=

f

(

x

)

.

x

y

1

2

3

4

5

6

7

8

9

1

2

3

4

-1

-2

-3

-4

-3

-2

-1

Zbiorem warto´sci tej funkcji jest

A)

h−

4, 3

i

B)

h−

4,

−

1

i ∪ h

1, 3

i

C)

h−

4,

−

1

i ∪ (

1, 3

i

D)

h−

5, 6

i

Z

ADANIE

12

(1

PKT

.)

W trójk ˛

acie prostok ˛

atnym dane s ˛

a k ˛

aty ostre: α

=

27

◦

i β

=

63

◦

. Wtedy

cos α

+

sin β

cos α

równa si˛e

A) 1

+

sin 63

◦

B) sin 63

◦

C) 1

D) 2

Z

ADANIE

13

(1

PKT

.)

Ci ˛

ag arytmetyczny

(

a

n

)

jest okre´slony wzorem a

n

= −

2n

+

1 dla n

>

1. Ró ˙znica tego ci ˛

agu

jest równa
A)

−

1

B) 1

C)

−

2

D) 3

Materiał pobrany z serwisu

www.zadania.info

2

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´

N Z

M

ATEMATYKI

Z

ADANIE

14

(1

PKT

.)

W ci ˛

agu geometrycznym

(

a

n

)

dane s ˛

a a

2

=

√

3

2

i a

3

= −

3

2

. Wtedy wyraz a

1

jest równy

A)

−

1

2

B)

1

2

C)

−

√

3

2

D)

√

3

3

Z

ADANIE

15

(1

PKT

.)

Dane s ˛

a punkty A

= (

6, 1

)

i B

= (

3, 3

)

. Współczynnik kierunkowy prostej AB jest równy

A)

−

2

3

B)

−

3

2

C)

3

2

D)

2

3

Z

ADANIE

16

(1

PKT

.)

Pole prostok ˛

ata jest równe 40. Stosunek długo´sci jego boków jest równy 2:5. Dłu ˙zszy bok

tego prostok ˛

ata jest równy

A) 10

B) 8

C) 7

D) 6

Z

ADANIE

17

(1

PKT

.)

Dany jest trójk ˛

at prostok ˛

atny o przyprostok ˛

atnych 5 i 12. Promie ´n okr˛egu opisanego na tym

trójk ˛

acie jest równy

A) 12

B) 8,5

C) 6,5

D) 5

Z

ADANIE

18

(1

PKT

.)

Dane s ˛

a dwa okr˛egi o promieniach 12 i 17. Mniejszy okr ˛

ag przechodzi przez ´srodek wi˛ek-

szego okr˛egu. Odległo´s´c mi˛edzy ´srodkami tych okr˛egów jest równa
A) 5

B) 12

C) 17

D) 29

Z

ADANIE

19

(1

PKT

.)

Sto ˙zek powstał w wyniku obrotu trójk ˛

ata prostok ˛

atnego o przyprostok ˛

atnych 13 i 15 wokół

dłu ˙zszej przyprostok ˛

atnej. Promie ´n podstawy tego sto ˙zka jest równy

A) 15

B) 13

C) 7,5

D) 6,5

Z

ADANIE

20

(1

PKT

.)

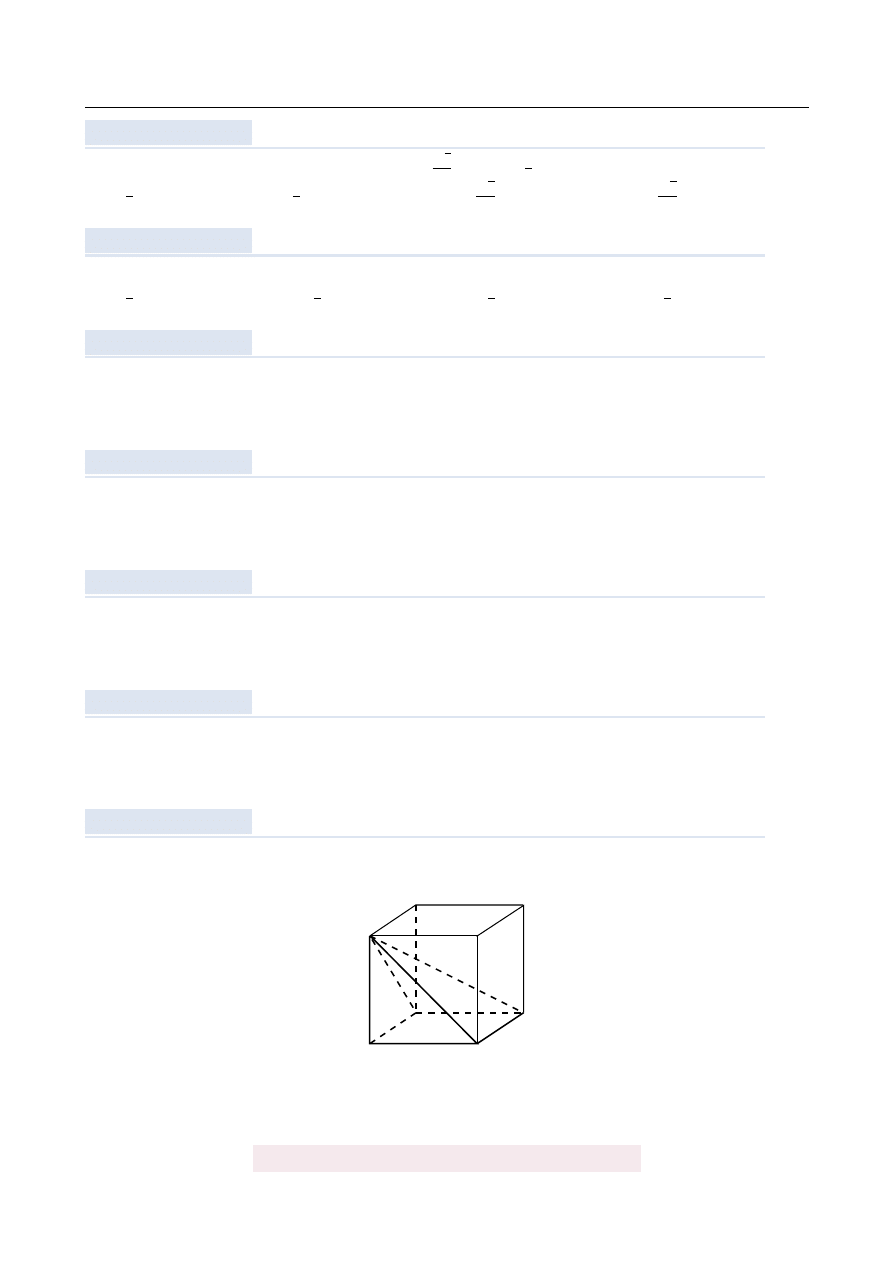
Dany jest sze´scian ABCDEFGH.

A

B

C

D

F

H

E

D

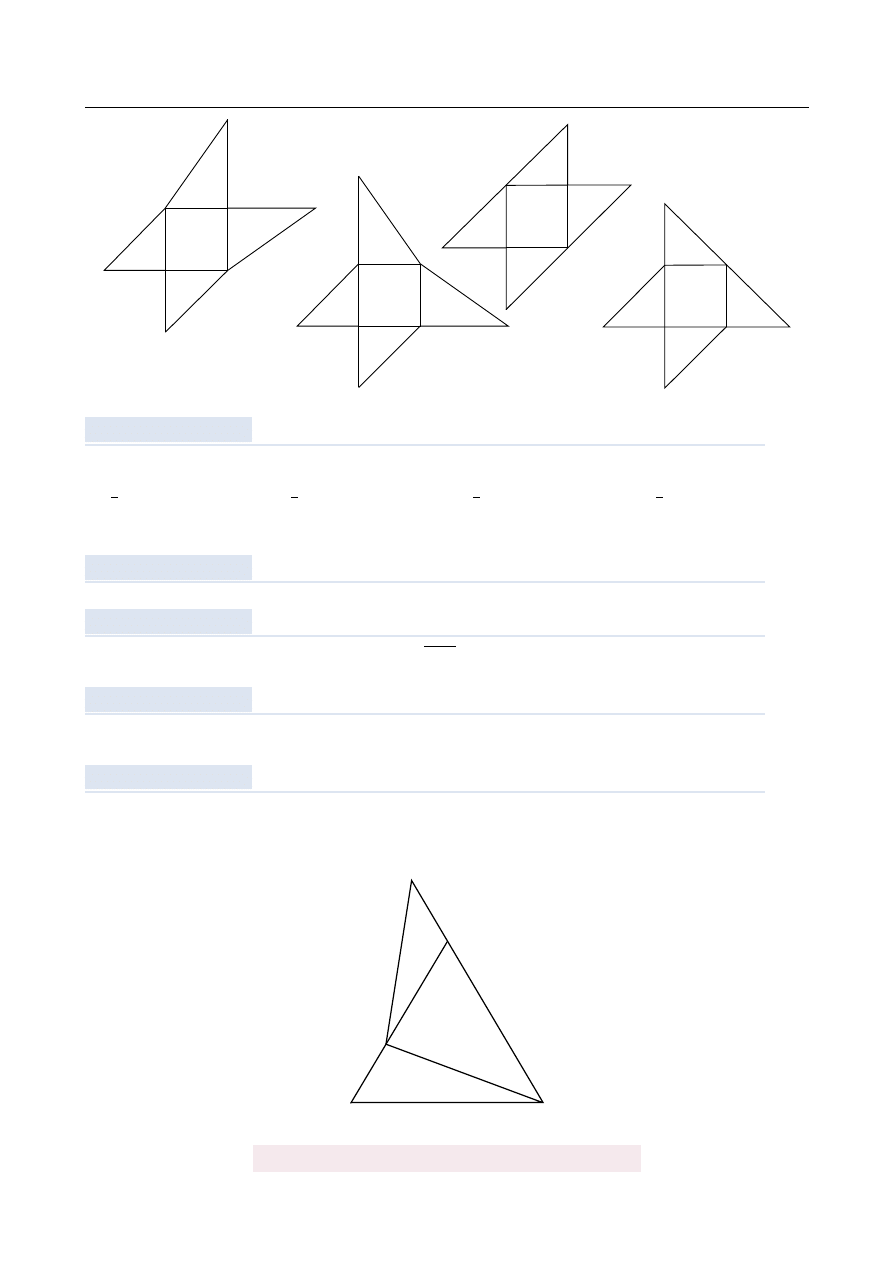
Siatk ˛

a ostrosłupa czworok ˛

atnego ABCDE jest

Materiał pobrany z serwisu

www.zadania.info

3

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´

N Z

M

ATEMATYKI

A)

B)

C)

D)

Z

ADANIE

21

(1

PKT

.)

Je ˙zeli A jest zdarzeniem losowym oraz A

0

jest zdarzeniem przeciwnym do zdarzenia A i

P

(

A

) =

5

·

P

(

A

0

)

, to prawdopodobie ´nstwo zdarzenia A jest równe

A)

4

5

B)

1

5

C)

1

6

D)

5

6

Zadania otwarte

Z

ADANIE

22

(2

PKT

.)

Rozwi ˛

a ˙z nierówno´s´c

−

3x

2

+

3x

+

36

>

0.

Z

ADANIE

23

(2

PKT

.)

Funkcja f jest okre´slona wzorem f

(

x

) =

2x

−

b

x

−

9

dla x

6=

9. Ponadto wiemy, ˙ze f

(

4

) = −

1.

Oblicz współczynnik b.

Z

ADANIE

24

(2

PKT

.)

Podstawy trapezu prostok ˛

atnego maj ˛

a długo´sci 6 i 10 oraz tangens k ˛

ata ostrego jest równy

3. Oblicz pole tego trapezu.

Z

ADANIE

25

(2

PKT

.)

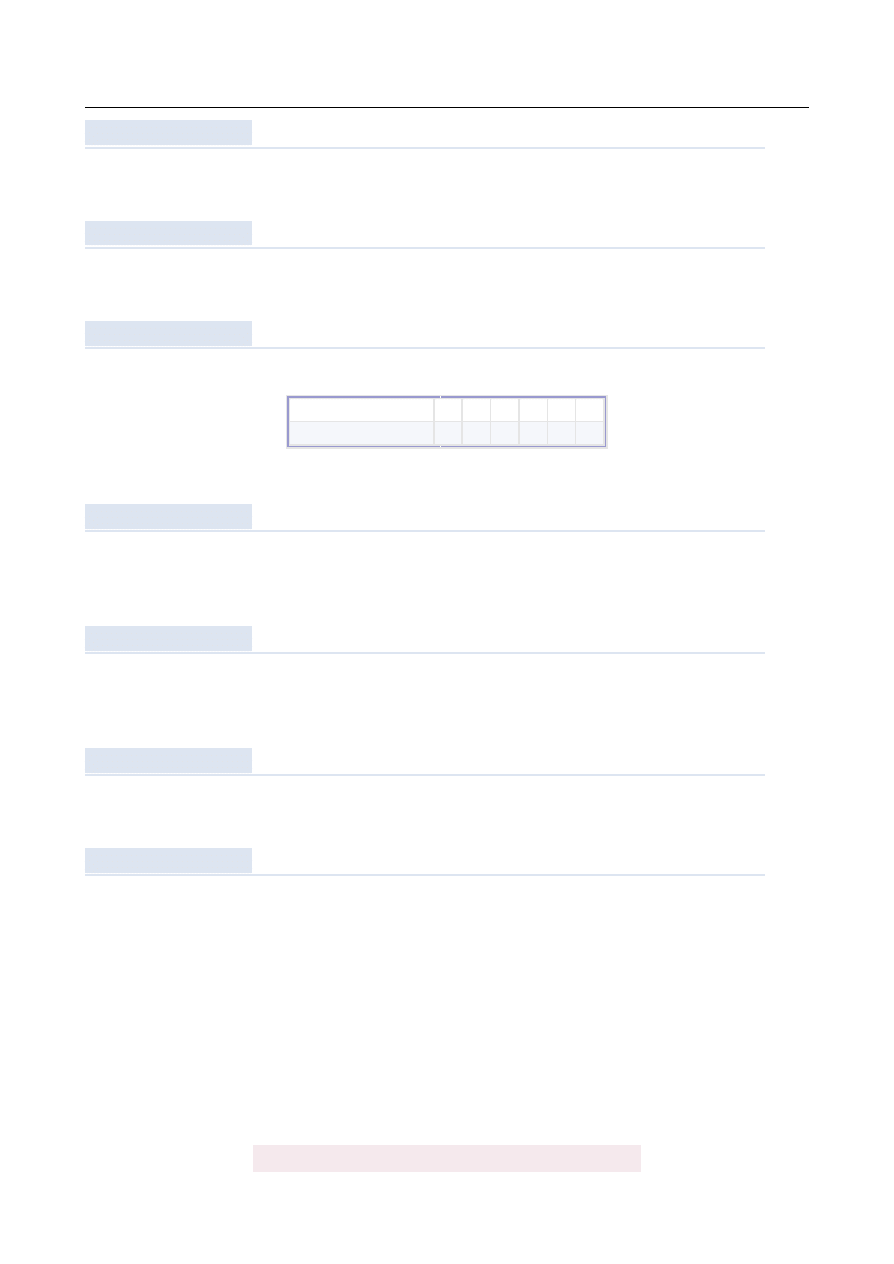
Trójk ˛

at ABC przedstawiony na poni ˙zszym rysunku jest równoboczny, a punkty B, C, N s ˛

a

współliniowe. Na boku AC wybrano punkt M tak, ˙ze

|

AM

| = |

CN

|

. Wyka ˙z, ˙ze

|

BM

| =

|

MN

|

.

A

B

C

M

N

Materiał pobrany z serwisu

www.zadania.info

4

www.zadania.info – N

AJWI ˛

EKSZY

I

NTERNETOWY

Z

BIÓR

Z

ADA ´

N Z

M

ATEMATYKI

Z

ADANIE

26

(2

PKT

.)

Liczby 64, x, 4 s ˛

a odpowiednio pierwszym, drugim i trzecim wyrazem malej ˛

acego ci ˛

agu geo-

metrycznego. Oblicz pi ˛

aty wyraz tego ci ˛

agu.

Z

ADANIE

27

(2

PKT

.)

Uzasadnij, ˙ze dla ka ˙zdej dodatniej liczby całkowitej n liczba 3

n

+

2

−

2

n

+

2

+

3

n

−

2

n

jest wie-

lokrotno´sci ˛

a liczby 10.

Z

ADANIE

28

(2

PKT

.)

Tabela przedstawia wyniki uzyskane na sprawdzianie przez uczniów klasy III.

Oceny

6

5

4

3

2

1

Liczba uczniów

1

2

6

5

9

2

Oblicz ´sredni ˛

a arytmetyczn ˛

a i kwadrat odchylenia standardowego uzyskanych ocen.

Z

ADANIE

29

(2

PKT

.)

Rzucamy dwa razy symetryczn ˛

a sze´scienn ˛

a kostk ˛

a do gry. Oblicz prawdopodobie ´nstwo

zdarzenia A polegaj ˛

acego na tym, ˙ze liczba oczek w drugim rzucie jest o 1 wi˛eksza od liczby

oczek w pierwszym rzucie.

Z

ADANIE

30

(4

PKT

.)

Podstaw ˛

a ostrosłupa ABCDS jest romb ABCD o boku długo´sci 4. K ˛

at ABC rombu ma miar˛e

120

◦

oraz

|

AS

| = |

CS

| =

10 i

|

BS

| = |

DS

|

. Oblicz sinus k ˛

ata nachylenia kraw˛edzi BS do

płaszczyzny podstawy ostrosłupa.

Z

ADANIE

31

(4

PKT

.)

Wyznacz równanie okr˛egu przechodz ˛

acego przez punkt A

= (

2, 1

)

i stycznego do obu osi

układu współrz˛ednych. Rozwa ˙z wszystkie przypadki.

Z

ADANIE

32

(5

PKT

.)

Z dwóch miast A i B, odległych od siebie o 18 kilometrów, wyruszyli naprzeciw siebie dwaj
tury´sci. Pierwszy turysta wyszedł z miasta A o jedn ˛

a godzin˛e wcze´sniej ni ˙z drugi z miasta

B. Oblicz pr˛edko´s´c, z jak ˛

a szedł ka ˙zdy turysta, je ˙zeli wiadomo, ˙ze po spotkaniu pierwszy

turysta szedł do miasta B jeszcze 1,5 godziny, drugi za´s szedł jeszcze 4 godziny do miasta A.

Materiał pobrany z serwisu

www.zadania.info

5