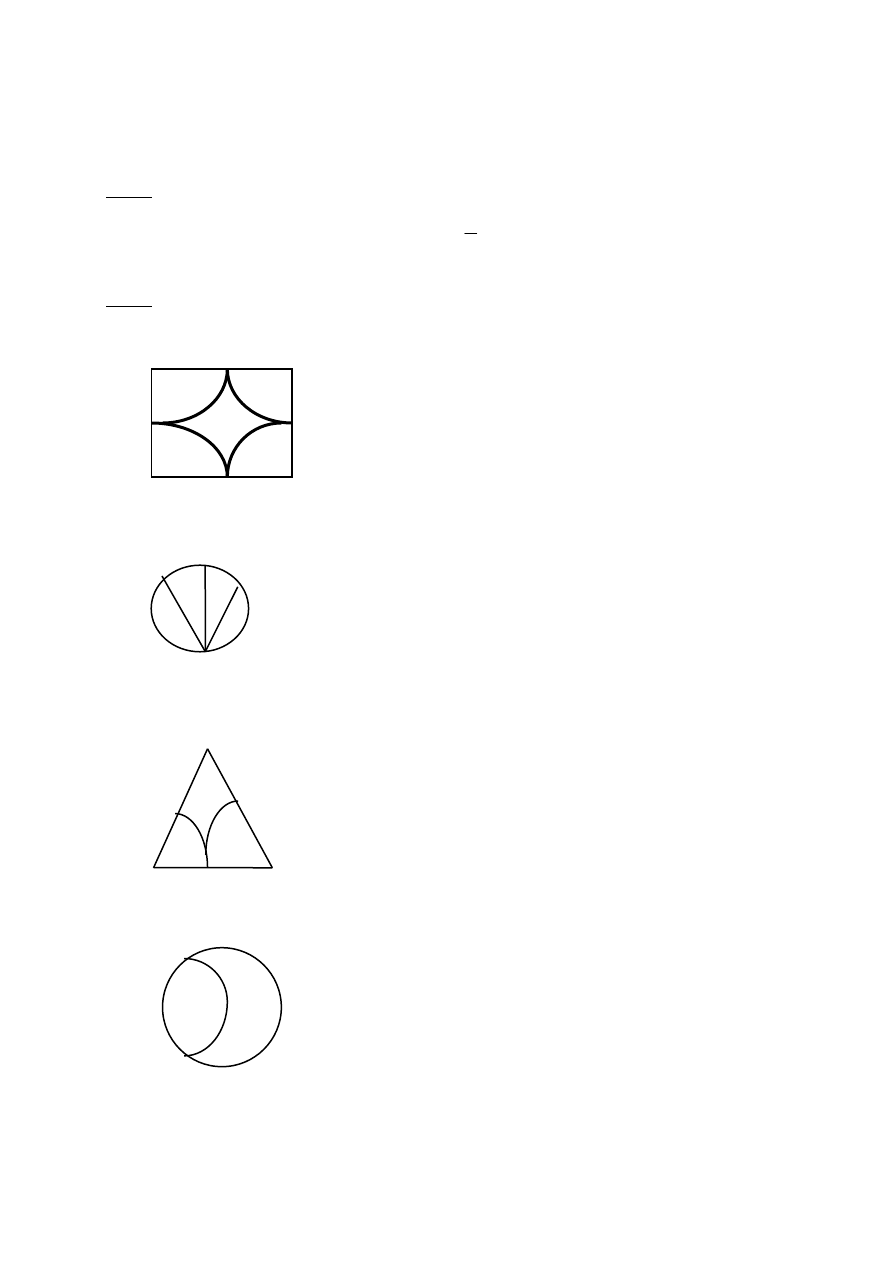
125
Pola figur płaskich
Zad. 1:
Długości boków trójkąta są kolejnymi wyrazami ciągu arytmetycznego. Obwód trójkąta jest
równy 21, a cosinus największego kąta wynosi
−
1
10
. Oblicz długości boków tego trójkąta.
Odp.: 5, 7, 9.
Zad. 2:
Oblicz pole i obwód zacieniowanej figury, wiedząc, Ŝe:
a) bok kwadratu ABCD ma długość k, punkty E, F, G, H są środkami odpowiednich boków
D G C
H F
A E B
(dotyczy to figury HEFG);
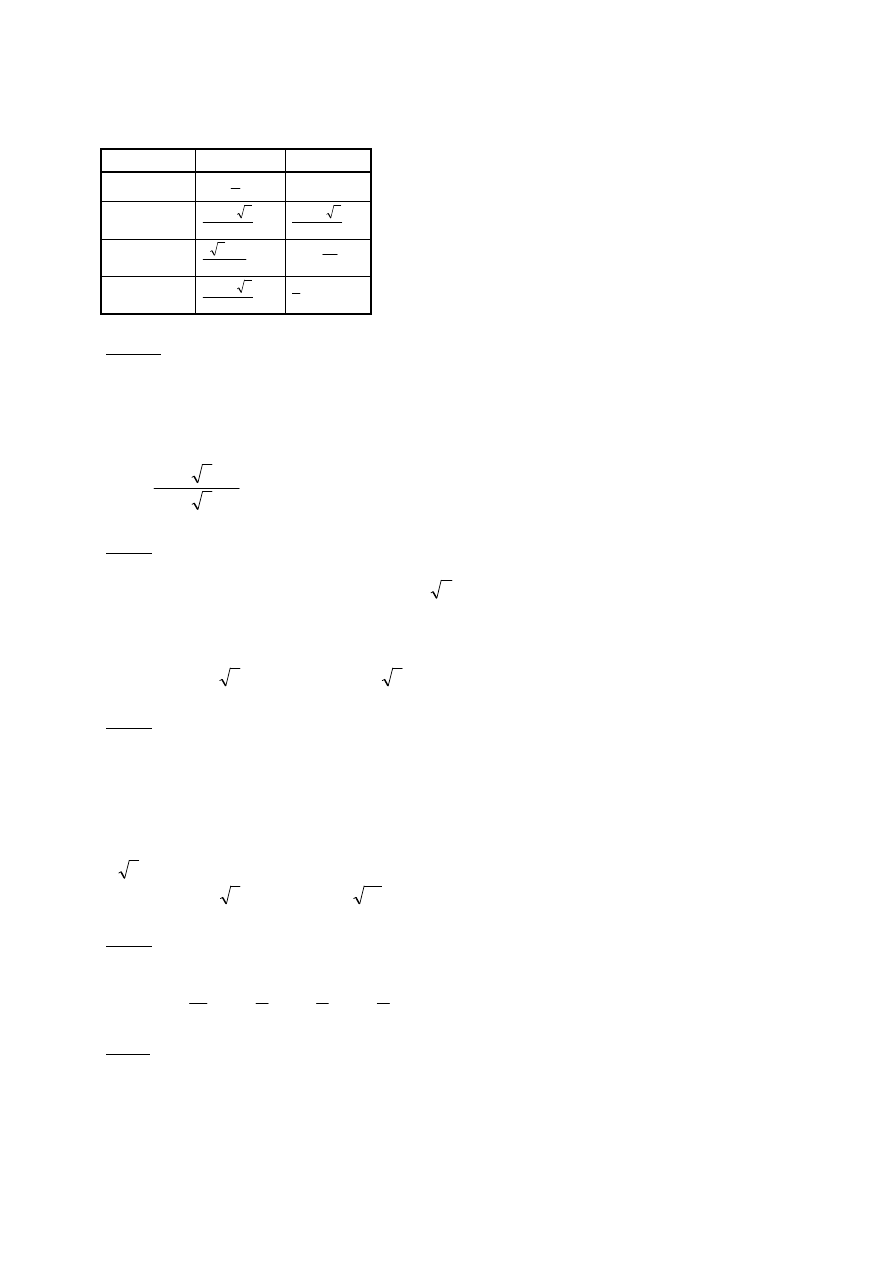
b) promień okręgu wynosi m, punkt O jest środkiem okręgu,
|∠
ABD
|
=
|∠
ABC
|
= 30
°
A
D C
O
B
(dotyczy to figury DBCA);
c) bok trójkąta równobocznego ABC ma długość n, punkty D, E, F są środkami odpowiednich
boków
C
F D
A E B
(dotyczy to figury FEDC);
d) promień okręgu wynosi t, punkt O jest środkiem okręgu
A O
(dotyczy to figury zawierającej punkty A i O).
126
Odp.: Wyniki zestawione są w poniŜszej tabeli:
Podpunkt
Pole
Obwód
a)
( )
2
4
1
k
π
−
k
π
b)
2
3 3
6
2
π +
m
2
6 3
6
π +
m
c)
3 3
12
2
− π
n
(
)
1
2
3
+
π
n
d)
4
3 3
6
2
π −
t
4
3
π
t
Zad. 3*:
W kole o promieniu R poprowadzono trzy równoległe cięciwy w taki sposób, Ŝe zawierają się
w jednym półkolu. Długości tych cięciw są równe odpowiednio długościom boków sześcio-
kąta foremnego, kwadratu i trójkąta równobocznego wpisanych w to koło. Znajdź stosunek
pola tej części koła, która jest zawarta między najkrótszą z tych cięciw i cięciwą średniej dłu-
gości, do pola części zawartej między najdłuŜszą i średnią cięciwą.
Odp.:
π
π
−
+
+
−
3 3
6
3 3
6
.
Zad. 4:
W równoległoboku, w którym jeden z boków jest dwa razy dłuŜszy od drugiego, kąt ostry ma
miarę 60
°
, a dłuŜsza przekątna ma długość
4 7
. Oblicz:
a) pole (obwód) tego równoległoboku;
b) długość krótszej przekątnej;
c) objętość bryły otrzymanej w wyniku obrotu tego równoległoboku wokół dłuŜszego boku.
Odp.: a)
P
=
16 3
(Obw. = 24); b)
4 3
; c) V = 76
π
.
Zad. 5:
W trapezie równoramiennym ABCD dane są długości podstaw:
|
AB
|
= 10 cm,
|
CD
|
= 2 cm.
Oblicz:
a) pole trapezu ABCD, wiedząc, Ŝe moŜna w niego wpisać okrąg;
b) pole trapezu ABCD, wiedząc, Ŝe pole trójkąta ABO, gdzie O jest punktem przecięcia prze-
kątnych trapezu, jest równe 25 cm
2
;
c) miarę kąta między przekątnymi trapezu ABCD, wiedząc, Ŝe przekątne te mają długość
4 3
cm.
Odp.: a)
P
=
12 5
; b)
P
=
+
12
4 13
; c) 120
°
.
Zad. 6:
Ramiona trapezu opisanego na okręgu mają długości 13 cm i 15 cm, a pole trapezu wynosi
168 cm
2
. Oblicz pola czterech trójkątów, na jakie przekątne dzielą trapez.
Odp.: P
P
P
P
1
189
2
2
63
2
3
21
2
4
63
2
=
=
=
=
,
,
,
.
Zad. 7:
a) W okrąg o promieniu 7 wpisano czworokąt ABCD. Oblicz obwód i pole czworokąta, wiedząc,
Ŝ
e
|
AB
|
=
|
BC
|
,
|∠
ADC
|
= 120
°
i stosunek pola trójkąta ABD do pola trójkąta BCD wynosi 2 : 1.
*b) Trójkąt równoboczny XYZ jest wpisany w okrąg. Punkt K naleŜy do krótszego z łuków XY.
Udowodnij, Ŝe
|
XK
|
+
|
YK
|
=
|
ZK
|
.
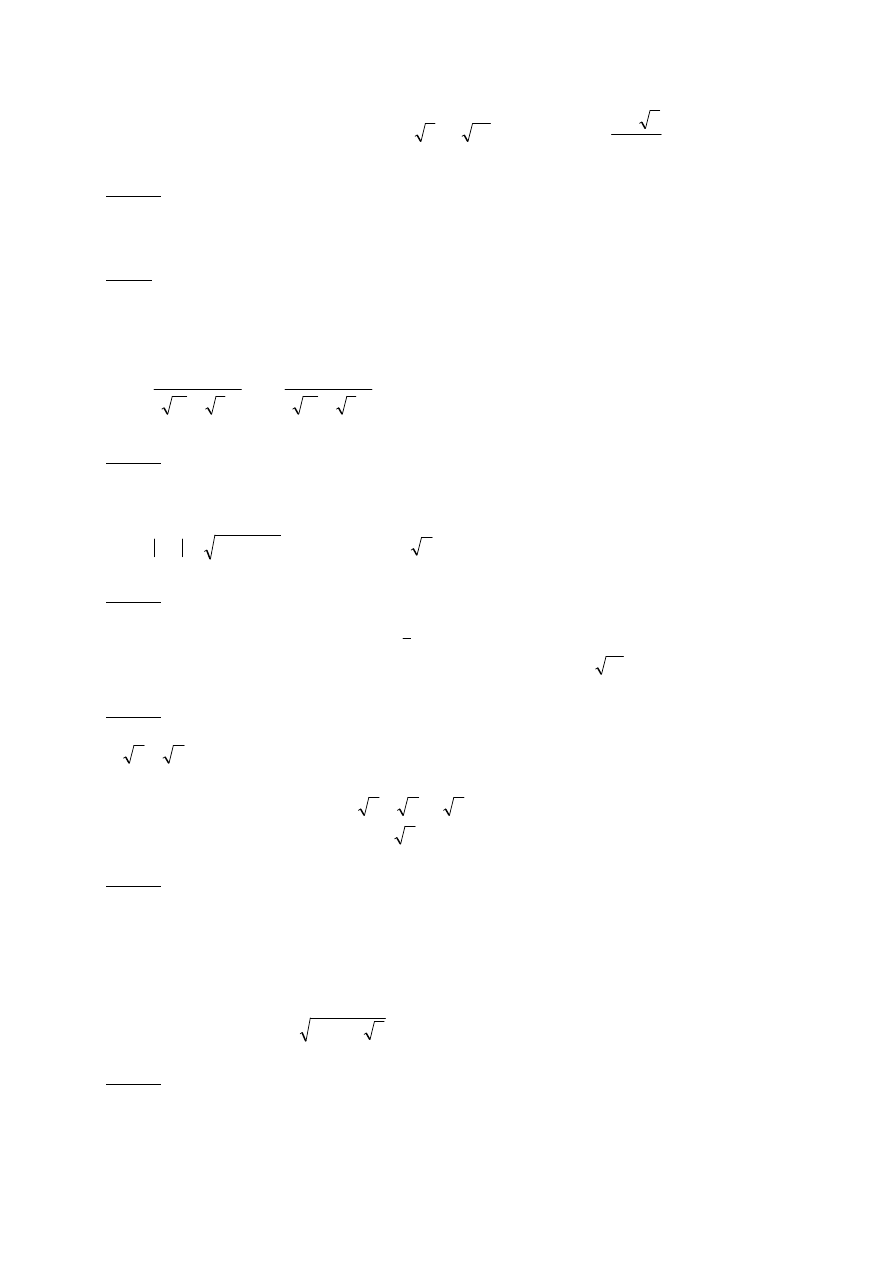
127
Odp.: a) Obwód czworokąta jest równy
14 3
3 21
+
, a pole wynosi
189 3
4
.
Zad. 8*: (profil matematyczno-fizyczny)
WykaŜ, Ŝe jeŜeli boki trójkąta ABC spełniają warunek
|
BC
|
2
=
|
AC
|
2
+
|
AC
|
⋅
|
AB
|
, to jeden z
kątów tego trójkąta jest dwa razy większy od drugiego.
Zad. 9: (profil matematyczno-fizyczny)
Dwa okręgi o promieniach r i R (r < R) są styczne zewnętrznie. Prosta l nie przechodzi przez
punkt wspólny tych okręgów i jest styczna do nich obu. Znajdź promień okręgu stycznego
zewnętrznie do danych okręgów i stycznego do prostej l. RozwaŜ wszystkie moŜliwe przy-
padki.
Odp.:
(
)
(
)
Rr
R
r
Rr
R
r
+
−
2
2
lub
.
Zad. 10: (profil matematyczno-fizyczny)
W trapezie ABCD o podstawach AB i CD dane są długości odcinków
|
BC
|
= q oraz
|
AB
|
=
|
AC
|
=
|
AD
|
= p. Oblicz długość przekątnej BD. Jaki warunek muszą spełniać p i q, aby
zadanie miało rozwiązanie?
Odp.: BD
p
q
=
−
4
2
2
, gdzie 0 < q < p 2 .
Zad. 11:
Długości boków trójkąta są trzema kolejnymi parzystymi liczbami naturalnymi. Cosinus naj-
większego kąta w trójkącie jest równy
−
1
4
. Znajdź długości boków oraz pole tego trójkąta.
Odp.: Boki trójkąta mają długości 4, 6, 8. Pole trójkąta jest równe
3 15
.
Zad. 12:
Miary kątów trójkąta prostokątnego tworzą ciąg arytmetyczny, a obwód trójkąta jest równy
(
)
3
6
2
+
. Oblicz długości boków tego trójkąta oraz objętość bryły otrzymanej w wyniku
obrotu trójkąta wokół krótszej przyprostokątnej.
Odp.: Boki trójkąta mają długości 6 3 2 2 6
,
i
(kąty trójkąta mają miary 30
°
, 60
°
i 90
°
).
Objętość rozwaŜanej bryły jest równa
6 6
π
.
Zad. 13:
W trójkącie ostrokątnym ABC wysokości opuszczone z wierzchołków A, B przecinają się w
punkcie M i mają odpowiednio długości 6 i 8. Miara kąta AMB wynosi 150
°
.
a) Oblicz pole trójkąta ABC.
*b) Oblicz promień okręgu opisanego na trójkącie A
1
B
1
C
, gdzie A
1
, B
1
, oznaczają spodki wy-
sokości trójkąta ABC opuszczonych z wierzchołków A, B.
c) Oblicz objętość bryły otrzymanej w wyniku obrotu trójkąta AA
1
C
wokół prostej AC.
Odp.: a) P = 48; b)
R
=
−
2 75 36 3
; c) V = 108
π
.
Zad. 14:
Długości boków trójkąta prostokątnego są kolejnymi liczbami naturalnymi. W odległości 1,6
cm od wierzchołka kąta prostego poprowadzono prostą równoległą do przeciwprostokątnej,
rozcinającą trójkąt na dwie figury. Oblicz pole oraz długości przekątnych odciętego trapezu.
128
Odp.: P
cm
=
10
3
2
, przekątne mają długość
2 5
145
3
cm i
cm
.
Zad. 15:
Pole trapezu równoramiennego jest równe 39 3
2
cm . Ramię trapezu ma długość 6 3 cm i
tworzy z dłuŜszą podstawą kąt 30
°
. Oblicz obwód i długość przekątnej tego trapezu.
Odp.: Obwód trapezu jest równy
(
)
2 13
6 3
+
cm , a przekątna ma długość 14 cm.
Zad. 16:
W trapezie prostokątnym krótsza przekątna ma długość 8 cm i tworzy z dłuŜszą podstawą
kąt 30
°
. RóŜnica długości podstaw trapezu jest równa 4 cm. Oblicz pole i obwód tego trape-
zu.
Odp.: Pole trapezu jest równe 8 16 3
2
+
cm , a obwód wynosi 8
4 2
8 3
+
+
cm .
Zad. 17:
W trapezie równoramiennym ABCD dane są długości podstaw:
|
AB
|
= 10 cm,
|
CD
|
= 6 cm.
Oblicz:
a) pole trapezu ABCD, wiedząc, Ŝe kąt ostry ma miarę 60
°
;
b) obwód trapezu ABCD, wiedząc, Ŝe trapez jest wpisany w okrąg o średnicy 10 cm;
c) długości przekątnych trapezu ABCD, wiedząc, Ŝe przekątne tworzą kąt 120
°
.
Odp.: a) P
cm
=
16 3
2
; b)
(
)
4 4
5
+
cm ; c) 16 cm lub
16 3
3
cm .
Zad. 18:
W trapezie równoramiennym ABCD dane są długości podstaw:
|
AB
|
= 8 cm,
|
CD
|
= 2 cm.
Oblicz:
a) pole trapezu ABCD, wiedząc, Ŝe jest on opisany na okręgu;
b) obwód trapezu ABCD, wiedząc, Ŝe pole trójkąta ABO, gdzie O jest punktem przecięcia
przekątnych trapezu, jest równe 16 cm
2
;
c) miarę kąta między przekątnymi trapezu ABCD, wiedząc, Ŝe przekątne te mają długość
10 3
3
cm .
Odp.: a) P = 20 cm
2
; b)
(
)
2 5
34
+
cm ; c)
|∠
AOB
|
= 120
°
.
Zad. 19:
O trapezie ABCD wiadomo, Ŝe jest wpisany w okrąg, AB CD,
|
BD
|
= 14,
|∠
BAD
|
= 60
°
i
AB
AD
=
8
5
. Oblicz pole i obwód trapezu oraz promień okręgu.
Odp.: Pole trapezu jest równe
55 3
, obwód wynosi 42. Promień okręgu ma długość
14 3
3
.
Zad. 20:
Na okręgu o promieniu r opisano trapez prostokątny, którego dłuŜsza podstawa ma długość
4r. Znajdź pole tego trapezu oraz stosunek długości jego przekątnych.
Odp.: P
r
=
16
3
2
. Stosunek długości przekątnych wynosi 65 15
:
.
129
Zad. 21*:
Na kole o promieniu R opisano romb, którego dłuŜsza przekątna jest równa 4R. Oblicz pole
tej części rombu, która leŜy poza kołem.
Odp.:
8 3
3
2
−
π
R .
Zad. 22:
Przekątna wychodząca z wierzchołka kąta ostrego rombu ma długość 16 cm. Oblicz pole
tego rombu, wiedząc, Ŝe:
a) kąt ostry ma miarę 60
°
;
b) wysokość rombu ma długość 8 2 cm ;
c) okrąg przechodzący przez trzy wierzchołki rombu dzieli daną przekątną na odcinki długo-
ś
ci 10 cm i 6 cm.
Odp.: a) P
cm
=
128 3
3
2
; b) P = 128 cm
2
; c) P = 64 cm
2
.
Zad. 23:
Obwód równoległoboku jest równy 72 cm. Stosunek długości wysokości równoległoboku
wynosi 5 : 7, a stosunek miar jego kątów wewnętrznych jest równy 1 : 2. Oblicz długości
boków i wysokości tego równoległoboku.
Odp.: Boki równoległoboku mają długości 21 cm i 15 cm, a wysokości
15 3
2
cm i
21 3
2
cm (kąt ostry ma miarę 60
°
).
Zad. 24:
W równoległoboku ABCD boki mają długości:
|
AB
|
= 10,
|
AD
|
= 6. Odległość wierzchołka
D
od prostej BC wynosi 6. Oblicz długości przekątnych i pole tego równoległoboku.
Odp.: AC
BD
=
=
2 58
2 10
,
; P = 36.
Zad. 25*:
W kole o środku O poprowadzono prostopadłe średnice AB i CD oraz cięciwę AM, przecina-
jącą średnicę CD w punkcie K. Jaką miarę powinien mieć kąt BAM, aby w czworokąt OBMK
moŜna było wpisać okrąg?
Odp.:
|∠
BAM
|
= 30
°
.
Zad. 26:
W trójkącie prostokątnym stosunek róŜnicy długości przyprostokątnych do długości przeciw-
prostokątnej jest równy
1
2
.
a) Oblicz sinusy kątów ostrych tego trójkąta.
b) Oblicz stosunek pola trójkąta do pola koła opisanego na tym trójkącie.
c) Wiedząc, Ŝe krótsza przyprostokątna ma długość 2 cm, oblicz promień koła wpisanego w
trójkąt.
Odp.: a)
1
7
4
1
7
4
+
− +
i
; b)
3
4
π
; c)
5
7
3
−
.
130
Zad. 27:
W trójkącie ostrokątnym ABC dane są:
|
AC
|
=
|
BC
|
= b oraz
|∠
ACB
|
=
α
, gdzie
( )
α
π
∈
0
2
;
.
Z wierzchołka B przez środek okręgu opisanego na tym trójkącie poprowadzono prostą, prze-
cinającą bok AC w punkcie D. Oblicz promień okręgu wpisanego w trójkąt ABC oraz długość
odcinka BD.
Odp.:
(
)
( )
r
b
BD
b
=
+
=
sin
sin
,
sin
sin
α
α
α
α
2
1
2
3
2
.
Zad. 28:
W trójkącie równoramiennym stosunek długości ramienia do długości podstawy jest równy
3 : 2. Suma promienia okręgu wpisanego w ten trójkąt i promienia okręgu opisanego na trój-
kącie jest równa 13. Oblicz długości boków tego trójkąta.
Odp.: 8 2 12 2 12 2
,
,
.
Zad. 29:
Na boku BC trójkąta równobocznego ABC obrano taki punkt M, Ŝe pole trójkąta ACM jest
cztery razy mniejsze od pola trójkąta ABM. Oblicz sinusy kątów CAM i MAB.
Odp.: sin
, sin
∠
=
∠
=
CAM
MAB
7
14
2 7
7
.
Zad. 30:
W trójkącie KLM poprowadzono prostą AB równoległą do boku KL tak, Ŝe A
∈
KM, B
∈
LM i
|
AB
|
=
|
AK
|
+
|
BL
|
. Wiedząc, Ŝe
|
KL
|
= c,
|∠
MKL
|
=
α
i
|∠
KLM
|
=
β
, oblicz obwód
trapezu KLBA.
Odp.:
(
)
(
)
3
3
sin
sin
sin
sin
sin
sin
α
β
α β
α
β
α β
+
+
+
+
+
+
.
Zad. 31:
Nierównoległe boki AD i BC trapezu ABCD zawierają się w prostych prostopadłych,
|∠
DAC
|
=
|∠
ABC
|
= 30
°
,
|
AD
|
= 8 cm. Oblicz pole i obwód tego trapezu.
Odp.: Pole trapezu jest równe 64 3
2
cm , a obwód wynosi
(
)
8 5
3
+
cm .
Zad. 32:
Dany jest trapez ABCD, w którym
|∠
DAB
|
=
|∠
CDA
|
= 90
°
i
|
AB
|
>
|
CD
|
.
a) Wiedząc, Ŝe przekątne mają długości 13 i
41
, a róŜnica długości podstaw jest równa 8,
oblicz obwód trapezu ABCD. Czy w ten trapez moŜna wpisać okrąg?
b) Okrąg o promieniu R przechodzi przez punkty A, C, D i przecina odcinki AB i BC w punk-
tach odpowiednio M i N tak, Ŝe
|
AM
|
:
|
AB
|
=
|
CN
|
:
|
CB
|
= 1 : 3. Oblicz pole trapezu ABCD.
c) Przekątne trapezu ABCD przecinają się w punkcie S. Pola trójkątów ABS i DCS są równe
odpowiednio 9 i 4. Oblicz pole trapezu.
Odp.: a) Obwód trapezu jest równy
21
89
+
. W trapez ten nie moŜna wpisać okręgu.
b) P
R
=
4 5
3
2
. c) P = 25.
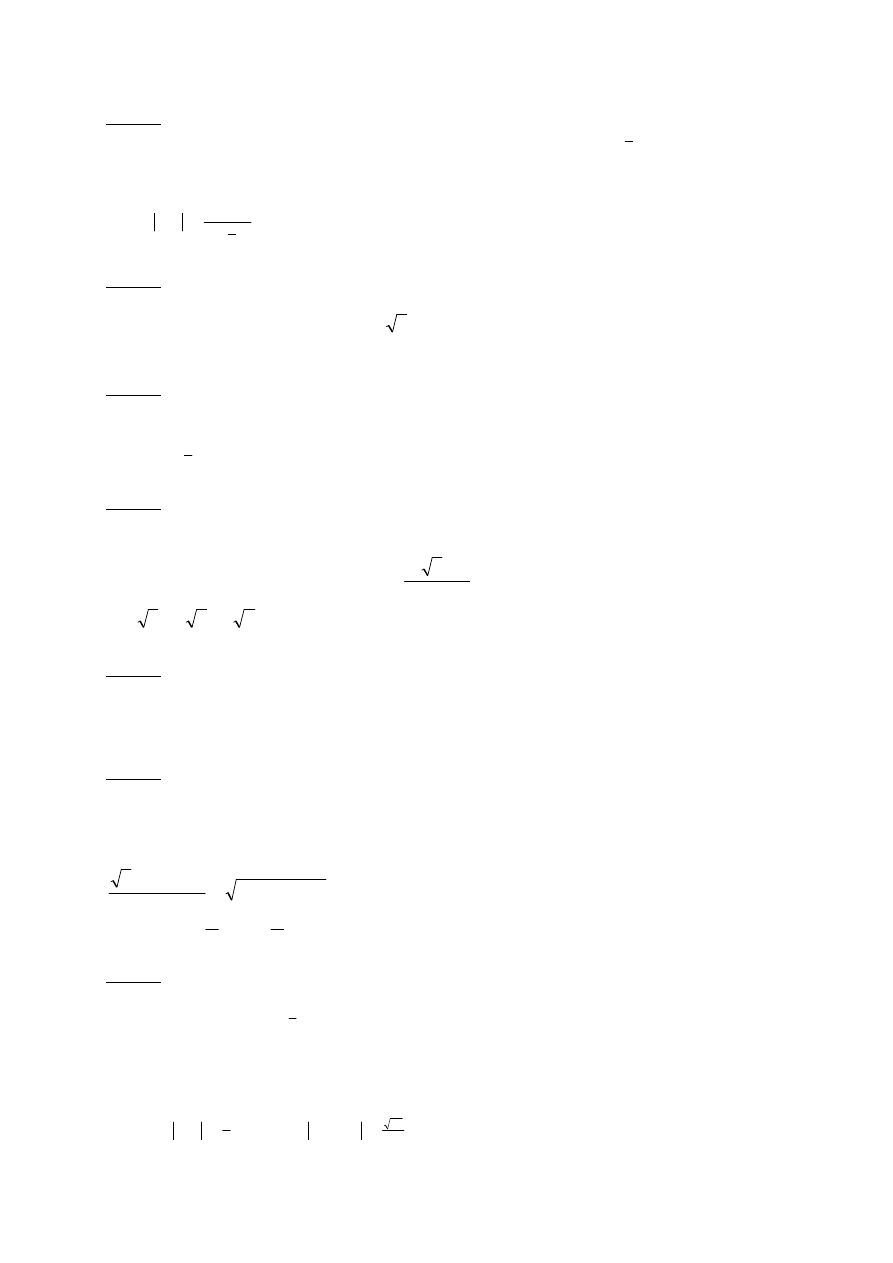
131
Zad. 33: (profil matematyczno-fizyczny)
W trójkącie ABC dane są:
|
AC
|
=
|
BC
|
= b i
|∠
ACB
|
=
α
, gdzie
(
)
α
π
∈
0
2
3
;
. Z wierzchołka B
przez środek okręgu opisanego na tym trójkącie poprowadzono prostą przecinającą prostą AC
w punkcie D. Znajdź długość odcinka BD.
Odp.: BD
b
=
sin
sin
α
α
3
2
.
Zad. 34: (profil matematyczno-fizyczny)
Oblicz długości boków równoległoboku ABCD o obwodzie 26, w którym promień r okręgu
wpisanego w trójkąt ABD ma długość
3
i kąt ABC ma 120
°
.
Odp.: 5 i 8.
Zad. 35: (profil matematyczno-fizyczny)
Nierównoległe boki AD i BC trapezu ABCD zawierają się w prostych prostopadłych. Oblicz
pole tego trapezu, wiedząc, Ŝe
|∠
DAC
|
=
|∠
ABC
|
=
α
,
|
AB
|
= a i
|
AB
|
>
|
CD
|
.
Odp.:
(
)
P
a
tg
tg
=
−
−
1
2
2
2
2
2
2
2
cos
cos
cos
α
α
α α
α
.
Zad. 36: (profil matematyczno-fizyczny)
W okrąg o promieniu R wpisano kwadrat i trójkąt równoboczny, mające wspólny wierzcho-
łek. Oblicz pole i obwód części wspólnej obu figur.
Odp.: Pole rozwaŜanej figury jest równe
11 3
9
4
2
−
R , a obwód wynosi
(
)
R 4 3
2 6
3 2
2
+
−
−
.
Zad. 37:
Długości boków trójkąta prostokątnego o przeciwprostokątnej 30 cm tworzą ciąg arytme-
tyczny. Oblicz promień okręgu wpisanego w ten trójkąt.
Odp.: Promień ma długość 6 (boki trójkąta mają długości 18, 24, 30).
Zad. 38:
a) Długości boków trójkąta prostokątnego są trzema kolejnymi liczbami naturalnymi. Oblicz
objętość i pole powierzchni całkowitej bryły otrzymanej w wyniku obrotu tego trójkąta do-
okoła prostej zawierającej przeciwprostokątną.
*b) WykaŜ, Ŝe w dowolnym trójkącie prawdziwa jest nierówność
(
)
3
2
2
2
2
a
b
c
a
b
c
+ +
>
+
+
, gdzie a, b, c oznaczają długości boków trójkąta.
Odp.: a) V
P
=
=
48
5
84
5
π
π
,
(boki trójkąta mają długości 3, 4, 5).
Zad. 39:
Punkt D leŜy na boku BC trójkąta równobocznego ABC. Stosunek pola trójkąta ADB do pola
trójkąta ADC jest równy
1
3
.
a) Wiedząc, Ŝe bok trójkąta ABC ma długość m, oblicz odległość BD.
b) Znajdź sinus kąta DAB.
c) Uzasadnij, Ŝe suma odległości punktu D od boków AB i AC jest równa wysokości trójkąta
ABC
.
Odp.: a) BD
m
=
1
4
; b)
sin
∠
=
DAB
39
26
.
132
Zad. 40:
Znajdź długość środkowej AD trójkąta ABC, w którym:
|
AB
|
= 10,
|
BC
|
= 6, AC
=
4 5 .
Niech D’ będzie obrazem punktu D w symetrii osiowej względem prostej AB. Uzasadnij, Ŝe
w czworokąt ADBD’ moŜna wpisać okrąg. Oblicz długość tego okręgu.
Odp.:
|
AD
|
= 9. Długość okręgu jest równa
4
3
11
π
.
Zad. 41:
Romb, którego bok ma długość a, kąt ostry zaś ma miarę
α
, podzielono prostymi poprowa-
dzonymi z wierzchołka kąta ostrego na trzy części o równych polach. Oblicz długości odcin-
ków wyciętych z tych prostych przez brzeg rombu.
Odp.: KaŜdy z odcinków ma długość
1
3
13 12
a
+
cos
α
.
Zad. 42:
W trapezie o podstawach a i b (a > b) kąty ostre mają miary 30
°
i 60
°
. Oblicz wysokość, pole
i obwód tego trapezu.
Odp.:
(
)
(
)
h
a
b P
a
b
Obw
a
b
=
−
=
−
=
+
+
−
3
4
3
8
2
2
3
3
2
1
3
2
,
,
.
.
Zad. 43:
Dany jest trapez równoramienny opisany na okręgu.
a) Oblicz długość przekątnej trapezu, wiedząc, Ŝe kąt ostry tego trapezu ma miarę 30
°
, a suma
długości podstaw jest równa 8 cm.
b) Oblicz długości podstaw tego trapezu, wiedząc, Ŝe jego pole jest równe 20 cm
2
, a promień
okręgu wpisanego wynosi 2 cm.
c) Udowodnij, Ŝe kwadrat średnicy okręgu wpisanego w ten trapez jest równy iloczynowi
długości podstaw.
Odp.: a)
2 5
; b) 8 i 2.
Zad. 44:
Promień okręgu wpisanego w trapez równoramienny wynosi
2
, a kąt ostry trapezu ma
miarę 60
°
. Oblicz promień okręgu opisanego na tym trapezie.
Odp.: R
=
2
3
14 .
Zad. 45:
W czworokącie ABCD dane są:
|
AB
|
= 13,
|
BC
|
= 11,
|
CD
|
= 7,
|
AD
|
= 1,
|∠
DAB
|
= 90
°
.
Oblicz pole tego czworokąta oraz długości jego przekątnych.
Odp.: P = 45, BD
AC
=
=
170
170
3
5
,
.
Zad. 46:
Dane jest półkole o średnicy
|
AB
|
= 2r. Okrąg o środku B i promieniu R (R
≥
r) przecina
ś
rednicę AB w punkcie C, a łuk AB w punkcie D.
a) Oblicz sin
|∠
CBD
|
, wiedząc, Ŝe R
r
=
3
2
.
b) Oblicz wysokość trójkąta ABD poprowadzoną z punktu D, wiedząc, Ŝe cos
∠
=
CBD
2
3
.
133
c) Oblicz promień okręgu wpisanego w trójkąt ABD, wiedząc, Ŝe
r
R
=
2
3
.
Odp.: a)
sin
∠
=
CBD
7
4
; b)
4 5
9
r ; c)
(
)
1
4
7
1
−
r .