„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

MINISTERSTWO EDUKACJI

NARODOWEJ

Grażyna Cugowska

Rozpoznawanie elementów maszyn i mechanizmów
812[01].O1.04

Poradnik dla ucznia

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

1

Recenzenci:
mgr inż. Marek Olsza
mgr inż. Robert Wanic



Opracowanie redakcyjne:
mgr inż. Grażyna Cugowska



Konsultacja:
mgr inż. Danuta Pawełczyk












Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej 812[01].O1.04
„Rozpoznawanie elementów maszyn i mechanizmów”, zawartego w modułowym programie
nauczania dla zawodu operator maszyn i urządzeń do obróbki plastycznej.

Wydawca

Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

2

SPIS TRESCI

1.

Wprowadzenie

4

2.

Wymagania wstępne

6

3.

Cele kształcenia

7

4.

Ćwiczenia

8

4.1. Wektory i skalary

8

4.1.1. Materiał nauczania

8

4.1.2. Pytania sprawdzające

12

4.1.3. Ćwiczenia

12

4.1.4. Sprawdzian postępów

14

4.2. Płaski i przestrzenny układ sił

15

4.2.1. Materiał nauczania

15

4.2.2. Pytania sprawdzające

19

4.2.3. Ćwiczenia

19

4.2.4. Sprawdzian postępów

21

4.3. Środek ciężkości

22

4.3.1. Materiał nauczania

22

4.3.2. Pytania sprawdzające

25

4.3.3. Ćwiczenia

25

4.3.4. Sprawdzian postępów

26

4.4. Wytrzymałość materiałów

27

4.4.1. Materiał nauczania

27

4.4.2. Pytania sprawdzające

30

4.4.3. Ćwiczenia

30

4.4.4. Sprawdzian postępów

32

4.5. Ruch obrotowy ciał. Praca, moc, energia i sprawność

33

4.5.1. Materiał nauczania

33

4.5.2. Pytania sprawdzające

36

4.5.3. Ćwiczenia

36

4.5.4. Sprawdzian postępów

37

4.6. Połączenia kształtowe

38

4.6.1. Materiał nauczania

38

4.6.2. Pytania sprawdzające

44

4.6.3. Ćwiczenia

44

4.6.4. Sprawdzian postępów

46

4.7. Osie i wały

47

4.7.1. Materiał nauczania

47

4.7.2. Pytania sprawdzające

50

4.7.3. Ćwiczenia

50

4.7.4. Sprawdzian postępów

51

4.8. Łożyska ślizgowe i toczne

52

4.8.1. Materiał nauczania

52

4.8.2. Pytania sprawdzające

55

4.8.3. Ćwiczenia

55

4.8.4. Sprawdzian postępów

57

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

3

4.9. Sprzęgła i hamulce

58

4.9.1. Materiał nauczania

58

4.9.2. Pytania sprawdzające

63

4.9.3. Ćwiczenia

63

4.9.4. Sprawdzian postępów

64

4.10. Przekładnie mechaniczne

65

4.10.1. Materiał nauczania.

65

4.10.2. Pytania sprawdzające

71

4.10.3. Ćwiczenia

71

4.10.4. Sprawdzian postępów

72

4.11. Mechanizmy

73

4.11.1. Materiał nauczania

73

4.11.2. Pytania sprawdzające

75

4.11.3. Ćwiczenia

75

4.11.4. Sprawdzian postępów.

76

5.

Sprawdzian postępów

77

6.

Literatura

81

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

4

1. WPROWADZENIE

Poradnik będzie Ci pomocny w opanowaniu umiejętności z zakresu rozpoznawania

elementów maszyn i mechanizmów.

W poradniku zamieszczono:

−

wymagania wstępne – wykaz umiejętności, jakie powinieneś mieć już ukształtowane
abyś bez problemów mógł korzystać z poradnika,

−

cele kształcenia – wykaz umiejętności, jakie ukształtujesz podczas pracy z poradnikiem,

−

materiał nauczania – wiadomości ze statyki, dynamiki, wytrzymałości materiałów, zasad
konstruowania połączeń, osi i wałów, łożysk ślizgowych i tocznych, sprzęgieł,
hamulców, przekładni oraz wiadomości dotyczące mechanizmów,

−

zestaw pytań potrzebny do sprawdzenia, czy już opanowałeś materiał nauczania,

−

ć

wiczenia, które pomogą zweryfikować wiadomości teoretyczne oraz ukształtować

umiejętności praktyczne,

−

pytania sprawdzające,

−

sprawdzian osiągnięć – przykładowy zestaw zadań testowych,

−

literaturę uzupełniającą.
W materiale nauczania zostały omówione zagadnienia dotyczące: statyki, dynamiki,

wytrzymałości materiałów oraz części maszyn i mechanizmów.

Informacje zamieszczone w Poradniku mogą zostać rozszerzone w oparciu o literaturę

dodatkową zgodnie z zaleceniami nauczyciela.

Z pytaniami sprawdzającymi możesz zapoznać się:

−

przed przystąpieniem do rozdziału Materiał nauczania, odpowiadając na te pytania
sprawdzisz stan swojej gotowości do wykonywania ćwiczeń,

−

po opanowaniu rozdziału Materiał nauczania, by sprawdzić stan swojej wiedzy, która
będzie Ci potrzebna do wykonywania ćwiczeń.

Z punktu widzenia przyszłej pracy zawodowej ważne jest nabycie przez Ciebie

umiejętności praktycznych w tym umiejętności manualnych. Aby ten cel osiągnąć poradnik
zawiera po każdym rozdziale propozycję ćwiczeń. Podczas wykonywania ćwiczeń zwróć
uwagę na zalecenia nauczyciela dotyczące bezpieczeństwa i higieny pracy.

Po wykonaniu zaplanowanych ćwiczeń, sprawdź poziom swoich postępów wykonując

Sprawdzian postępów. Odpowiedzi Nie wskazują luki w Twojej wiedzy, informują Cię
również, jakich zagadnień jeszcze dobrze nie poznałeś. Oznacza to także powrót do treści,
które nie są dostatecznie opanowane.

Poznanie przez Ciebie wszystkich lub określonej części wiadomości będzie stanowiło dla

nauczyciela podstawę przeprowadzenia sprawdzianu poziomu przyswojonych wiadomości
i ukształtowanych umiejętności. W tym celu nauczyciel może posłużyć się zadaniami
testowymi.

W poradniku jest zamieszczony sprawdzian osiągnięć, który zawiera przykład takiego

testu oraz instrukcję, w której omówiono tok postępowania podczas przeprowadzania
sprawdzianu i przykładową kartę odpowiedzi, w której, w przeznaczonych miejscach wpisz
odpowiedzi na zadania lub zakreśl właściwe odpowiedzi spośród zaproponowanych.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

5

Schemat układu jednostek modułowych

812[02].O1.02

Posługiwanie się dokumentacją

techniczną

812[02].O1.04

Rozpoznawanie elementów maszyn

i mechanizmów

812[02].O1

Techniczne podstawy zawodu

812[02].O1.01

Przestrzeganie przepisów

bezpieczeństwa i higieny pracy, ochrony

przeciwpożarowej i ochrony środowiska

812[02].O1.03

Stosowanie materiałów konstrukcyjnych

i narzędziowych

812[02].O1.05

Analizowanie układów elektrycznych

i automatyki przemysłowej

812[02].O1.06

Stosowanie mechanicznych technik

wytwarzania części maszyn

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

6

2. WYMAGANIA WSTĘPNE

Przystępując do realizacji programu jednostki modułowej powinieneś umieć:

−

przeliczać jednostki,

−

posługiwać się dokumentacją techniczną,

−

rozpoznawać podstawowe elementy maszyn,

−

rozpoznawać materiały konstrukcyjne i narzędziowe,

−

selekcjonować, przechowywać i porządkować informacje,

−

korzystać z różnych źródeł informacji,

−

obsługiwać komputer,

−

współpracować w grupie.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

7

3. CELE KSZTAŁCENIA

W wyniku realizacji programu jednostki modułowej powinieneś umieć:

−

określić warunki równowagi ciała sztywnego,

−

wyjaśnić pojęcia: prędkość obwodowa, prędkość obrotowa, praca mechaniczna, moc,
energia i sprawność,

−

rozróżnić proste przypadki obciążeń elementów konstrukcyjnych,

−

rozróżnić rodzaje naprężeń i odkształceń występujące podczas pracy maszyn i urządzeń,

−

rozróżnić rodzaje połączeń rozłącznych i nierozłącznych,

−

scharakteryzować osie i wały maszynowe,

−

scharakteryzować budowę i rodzaje łożysk tocznych i ślizgowych,

−

dobrać z katalogu na podstawie oznaczenia łożyska toczne,

−

scharakteryzować rodzaje sprzęgieł,

−

sklasyfikować hamulce i określić ich przeznaczenie,

−

sklasyfikować przekładnie mechaniczne,

−

wyjaśnić budowę przekładni zębatych,

−

obliczyć przełożenie przekładni,

−

wyjaśnić budowę i określić zastosowanie mechanizmów,

−

odczytać rysunki zestawieniowe zespołów i podzespołów maszyn, ustalić działanie
i określić elementy składowe,

−

dobrać części maszyn z katalogów,

−

skorzystać z dokumentacji technicznej, PN, katalogów.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

8

4. MATERIAŁ NAUCZANIA

4.1.

Wektory i skalary

4.1.1 Materiał nauczania

Wielkości mechaniczne takie jak siła, praca, czas przyspieszenie i inne można podzielić

na dwie grupy:

−

wielkości skalarowe (bezwymiarowe) – skalary takie jak czas, masa, moc, temperatura
(można jednoznacznie przedstawić za pomocą jednego punktu na przyjętej skali),

−

wielkości wektorowe (kierunkowe) – wektory.

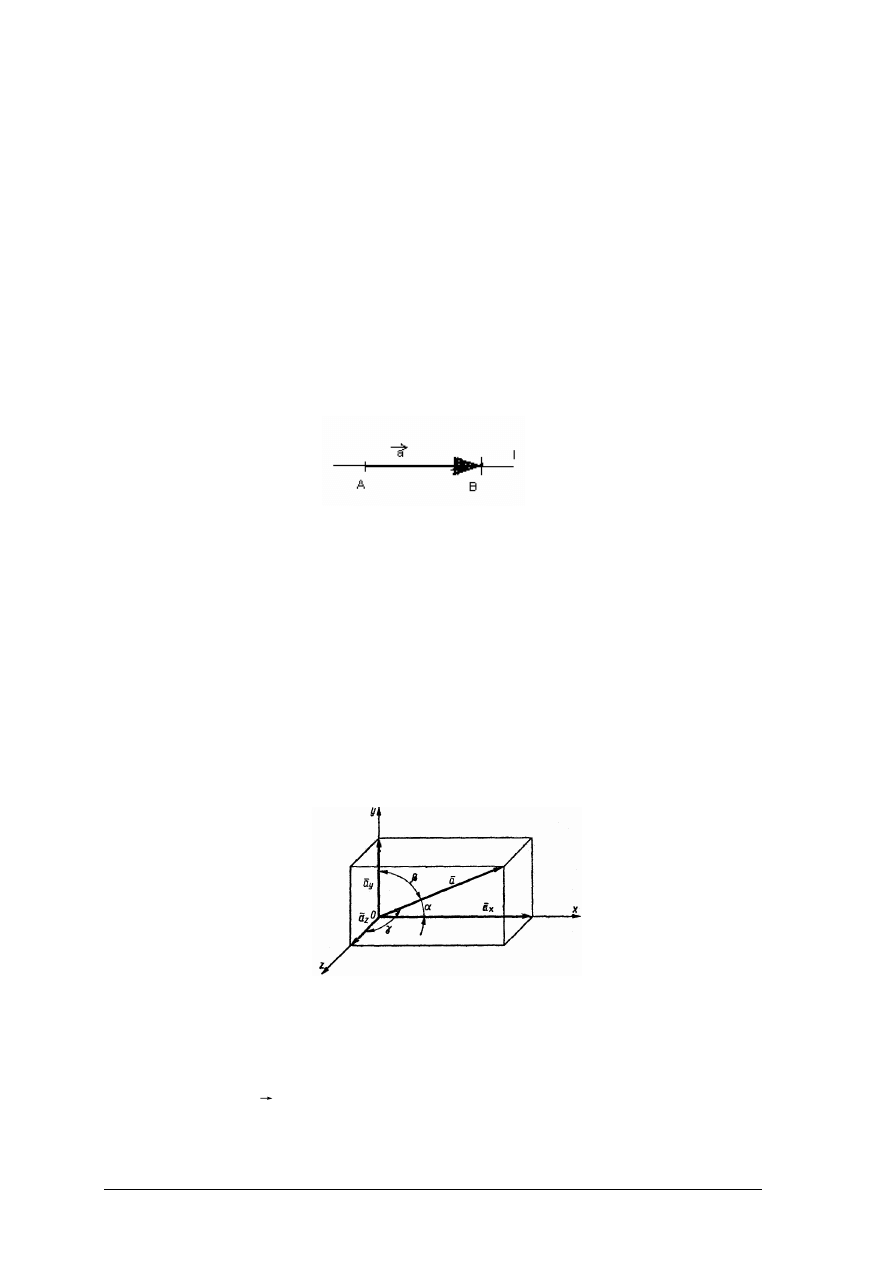
Wektorem nazywamy taką wielkość mechaniczną, którą da się przedstawić za pomocą

usytuowanego w przestrzeni odcinka mającego określony kierunek i zwrot (rys. 1).

Rys. 1. Wektor

l – linia działania wektora
A – początek wektora
B – koniec wektora

Każdy wektor ma trzy zasadnicze cechy:

−

wartość (moduł) – to długość odcinka AB przedstawiającego ten wektor; długość jest
skalarem i można ją określić jedną liczbą,

−

kierunek wektora – to linia jago działania, określana najczęściej przez podanie kąta jakie
ta linia tworzy z przyjętymi osiami współrzędnych,

−

zwrot wektora – to grot umieszczony na końcu wektora.
Nie należy mylić kierunku wektora ze zwrotem. Wszystkie wektory równoległe mają te

same kierunki.

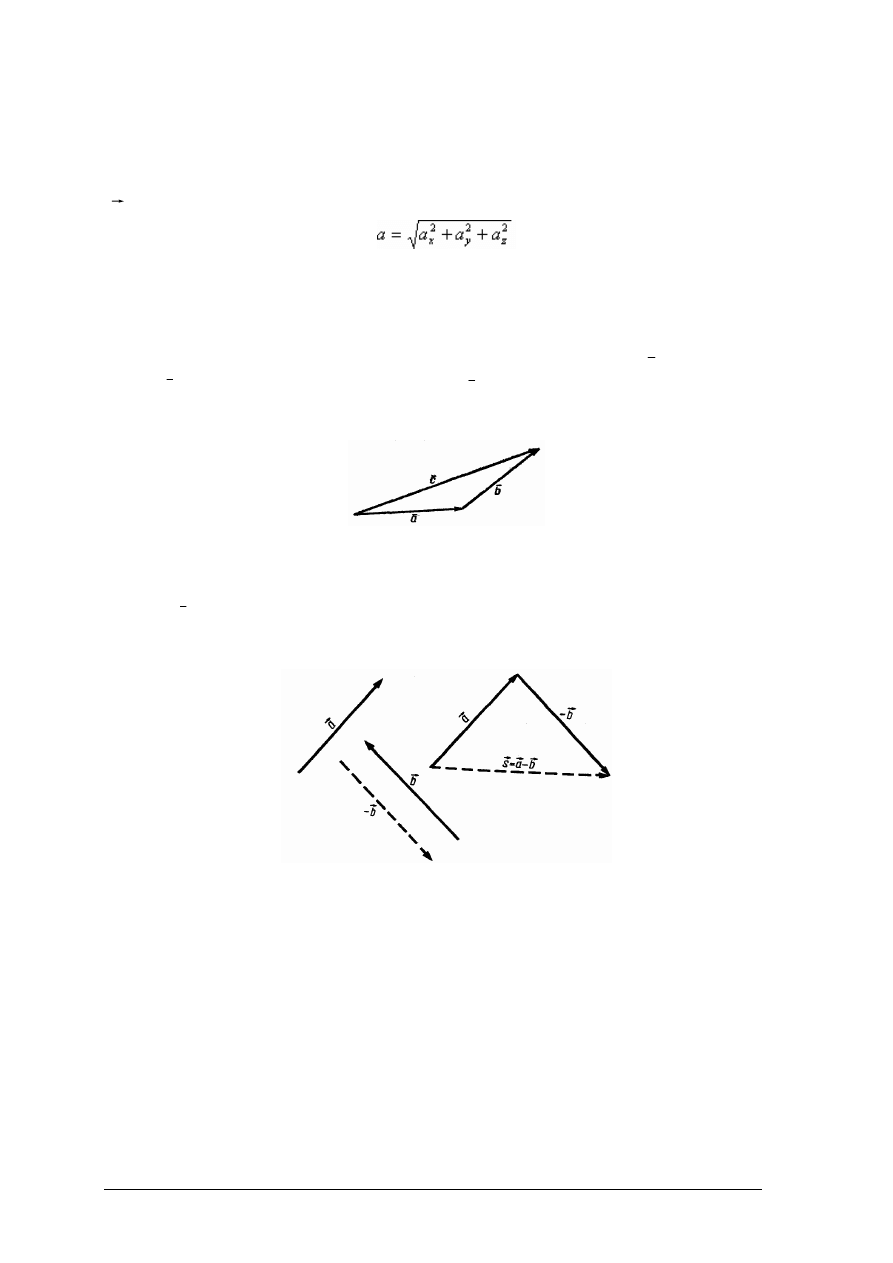
Składowe wektora w układzie współrzędnych prostokątnych (rys. 2)

Rys. 2. Rzut wektora na trzy osie układu współrzędnych prostokątnych [2, s. 9]

Trzy rzuty wektora a na osie x, y, z prostokątnego układu współrzędnych pojmowane

jako wielkości algebraiczne a

x

, a

y

, a

z

, wystarczają do pełnego określenia tego wektora, jako

wektora swobodnego (tj. o dowolnym punkcie początkowym). Oznaczając przez

γ

β

α

,

,

kąty,

jakie tworzy wektor

a

z osiami układu współrzędnych, mamy zależności:

;

cos

α

⋅

=

a

a

x

β

cos

⋅

=

a

a

y

γ

cos

⋅

=

a

a

z

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

9

Kierunek wektora i jego zwrot określają kąty

γ

β

α

,

,

, jakie tworzy on z dodatnimi

kierunkami osi układu współrzędnych. Z powyższych wzorów otrzymuje się wartości
dodatnie lub ujemne, zależnie od tego czy kąty

γ

β

α

,

,

są ostre, czy też rozwarte.

Jeśli mamy dane rzuty wektora na osie współrzędnych, bezwzględną wartość wektora

a

obliczamy według wzoru:

Dodawanie i odejmowanie wektorów

Geometryczne dodawanie wektorów jest uogólnieniem dodawania arytmetycznego

według reguły;

c

b

a

r

r

r

=

+

Regułę tę należy odczytać w następujący sposób: do końca wektora

a

przenosimy drugi

wektor

b

. Sumę geometryczną tych wektorów

c

wyznaczamy łącząc początek pierwszego

wektora z końcem drugiego (rys. 3.).

Rys. 3.

Dodawanie wektorów [2, s. 11]

Geometryczne odejmowanie wektora

b

r

od wektora

a

r

jest równoznaczne dodawaniu

wektora –

b

czyli wektora przeciwnego wektorowi

b

r

(rys. 4);

( )

s

b

a

b

a

r

r

r

r

r

=

−

+

=

−

Rys. 4. Odejmowanie wektorów [10, s. 11]

Siłą nazywamy mechaniczne oddziaływanie jednego ciała na drugie. Oddziaływanie

może być bezpośrednie, gdy zachodzi przy zetknięciu się ciał, lub pośrednie. Siła jest
wielkością wektorową. Jako wektor posiada wartość, kierunek, zwrot i punkt przyłożenia.

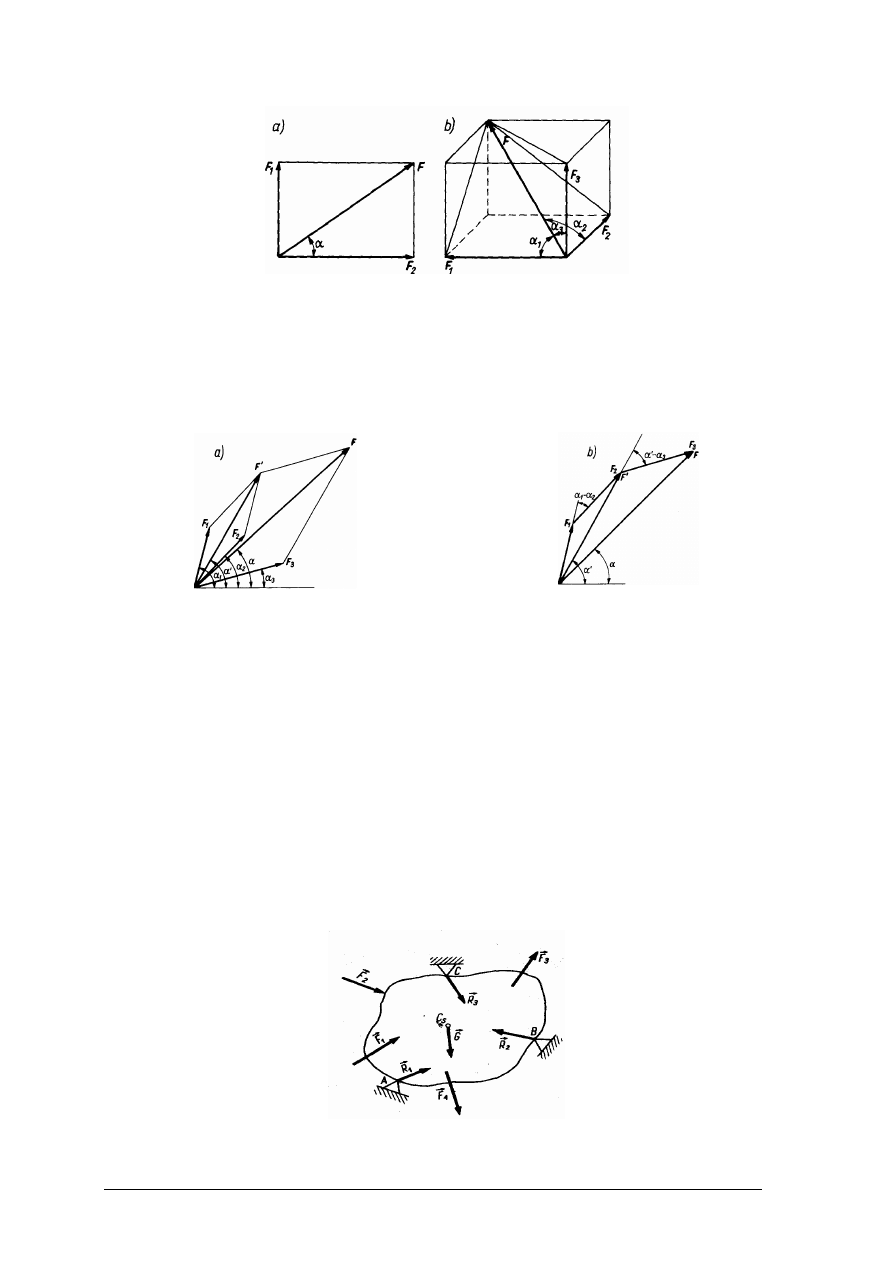
Każdą siłę można w jednoznaczny sposób rozłożyć na dwie siły składowe (na dwa

kierunki), jeżeli siła jest rozpatrywana na płaszczyźnie (rys. 5a), lub na trzy siły składowe,
gdy rozpatrywana siła jest usytuowana przestrzennie (rys. 5b).

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

10

Rys. 5. Rozkład siły F na składowe: a) na płaszczyźnie, b) w przestrzeni [4, s. 8]

Jeżeli siłę można rozłożyć na siły składowe, to wynika z tego, że dwie lub więcej sił

jednocześnie działających na dany element, można również złożyć, tzn. sumować.
Sumowanie sił, tak jak wszystkich innych wielkości wektorowych, polega na dodawaniu
geometrycznym, zgodnie z zasadą równoległoboku (rys. 6a) lub wieloboku (rys. 6b).

Rys. 6. Dodawanie sił: a) zgodnie z zasadą równoległoboku; b) zgodnie z zasadą wieloboku [1, s. 9]

F

1

, F

2

, F

3

– siły składowe, F, F

′

– siły wypadkowe,

α

1

,

α

2

,

α

3

,

α

, – kąty określające kierunki działania

odpowiednich sił

W tym drugim przypadku siłę wypadkową stanowi wektor zamykający wielobok sił

składowych. Wektor wypadkowy łączy, więc początek wektora pierwszego F

1

z końcem

wektora ostatniego F

3

.

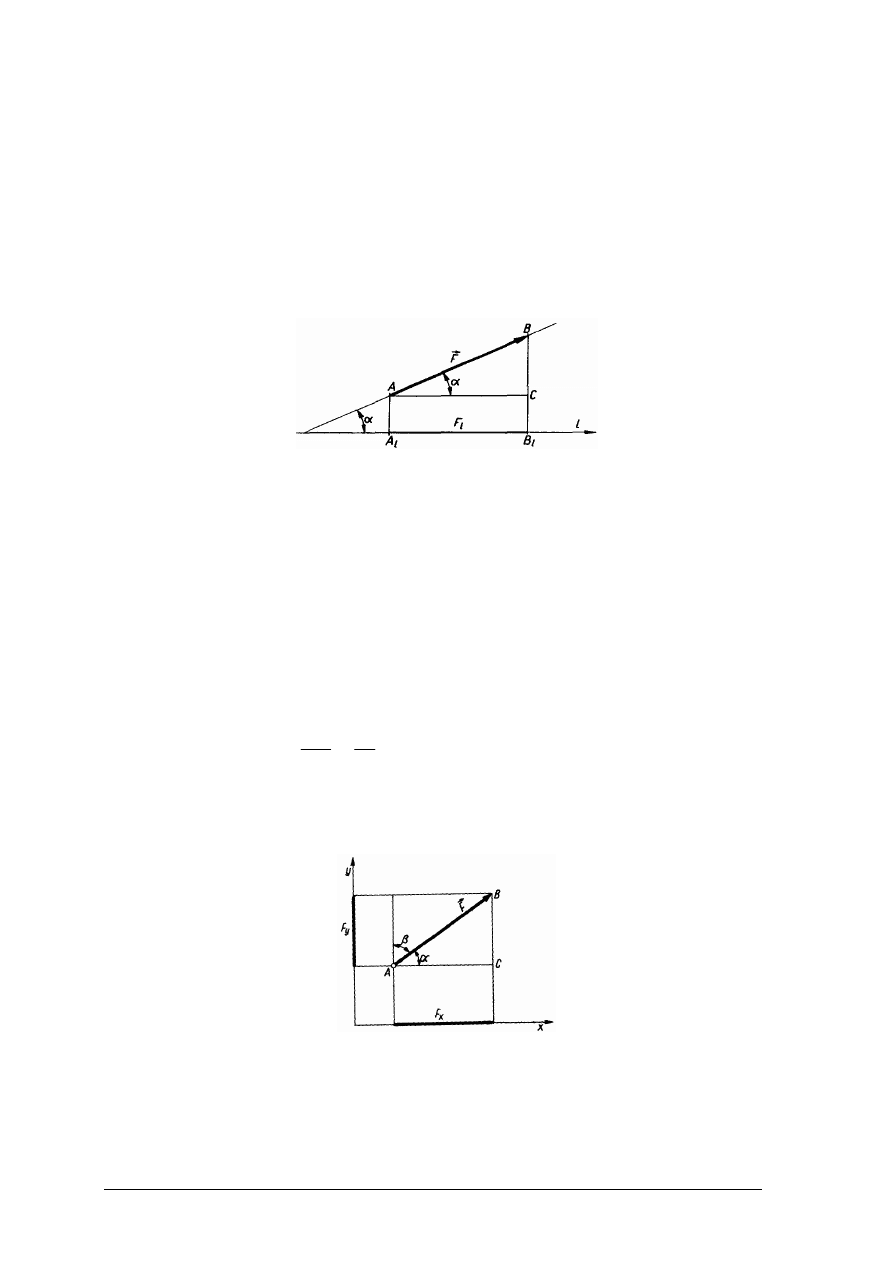
Siły (obciążenia) można podzielić na czynne i bierne. Siły bierne to reakcje, czyli siły,

które są wynikiem oddziaływania więzów (zamocowań, podpór) na element obciążony siłami
czynnymi. Przyjęto, że siły czynne oznacza się symbolem F, a reakcje – symbolem R. Weźmy
pod uwagę ciało o ciężarze ciało G, podparte w trzech miejscach A, B, C i obciążone siłami
F

1

, F

2

, F

3

. W miejscach podparcia wystąpią też pewne siły R

1

, R

2

, R

3

(gdyż w miejscach tych

następuje bezpośrednie działanie ciał na siebie). Wszystkie siły zaznaczone na (rys. 7), a więc
F

1

, F

2

, F

3

, F

4

, G, R

1

, R

2

, R

3

, są siłami zewnętrznymi. Siły F

1

, F

2

, F

3

, F

4

, G – to siły czynne

dążące do wywołania ruchu lub do jego zmiany; Siły R

1

, R

2

, R

3

– to siły reakcyjne (bierne),

które przeciwdziałają działaniu sił zewnętrznych czynnych.

Rys. 7. Podział sił zewnętrznych [10, s. 24]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

11

W statyce będziemy używać jednostek siły w układzie SI. W układzie tym za jednostkę

przyjmujemy siłę, która masie jednego kilograma nadaje przyspieszenie 1 m/s

2

. Ta jednostka

siły nazywa się niuton (symbol N).

W układzie SI siłę ciężkości

G

r

obliczamy z zależności:

g

m

G

⋅

=

[N]

gdzie: g = 9,81 m/s

2

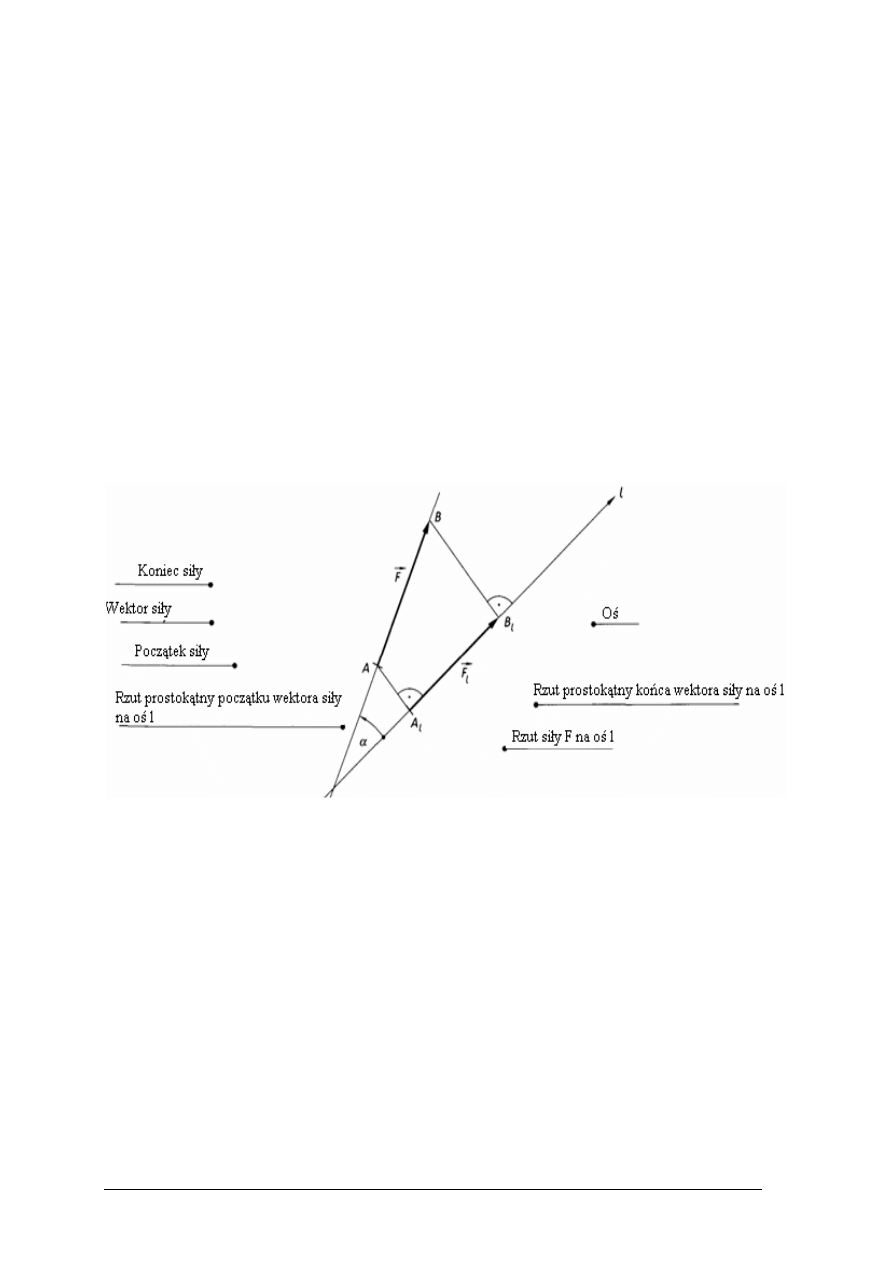
Rzut siły na oś

Rzutem siły na dowolną oś nazywamy odcinek A

1

B

1

, łączący rzut początku i końca danej

siły na tę oś (rys. 8).

Rys. 8. Rzut siły F na prostą [10, s. 37]

Rzut siły przyjmujemy za dodatni, jeżeli kierunek od punktu A

1

do punktu B

1

jest zgodny

z dodatnim zwrotem osi, a za ujemny, jeżeli kierunek od A

1

do B

1

jest przeciwny do zwrotu

osi.

Rzut siły na oś oznaczamy symbolem danej siły z dodaniem u dołu indeksu

wskazującego, na jaką oś rzutujemy siłę, np.:

−

l

F

rzut siły F na oś

l

Przyjmijmy, że kierunek osi

l

tworzy z linią działania siły F kąt

α

(kąt ten będziemy

stale odmierzać w stronę przeciwną do ruchu obrotowego wskazówek zegara). Z trójkąta
ABC (rys. 8) wynika, że:

Rzut siły na oś jest równy iloczynowi wartości tej siły przez cosinus kąta zawartego

pomiędzy osią i linią działania siły.

Rzut siły na osie x, y prostokątnego układu współrzędnych (rys. 9).

Rys. 9. Rzut siły na oś x i y prostokątnego układu współrzędnych [10, s. 39]

F

x

= F

α

cos

⋅

F

y

= F

α

α

α

β

sin

)

90

cos(

,

90

cos,

=

−

−

=

⋅

o

o

zaś

ale

α

cos

⋅

=

F

F

x

α

sin

⋅

=

F

F

y

α

cos

⋅

=

F

F

l

F

F

AB

AC

l

=

=

α

cos

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

12

Dla trójkąta ABC na (rys. 9) słuszny jest następujący związek, wypływający

z twierdzenia Pitagorasa

F

2

=

2

2

y

x

F

F

+

Stąd

2

2

y

x

F

F

F

+

=

Wartość siły jest równa pierwiastkowi kwadratowemu z sumy kwadratów rzutów tej siły

na obie osie układu współrzędnych.

4.1.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Co to jest siła?.

2.

Jakie cechy określają wektor siły?

3.

Jak dzielimy siły zewnętrzne?

4.

Jak nazywa się jednostka siły w układzie SI?

5.

Co to jest rzut siły na oś?

6.

Co nazywamy układem sił?

7.

Ile sił tworzy najprostszy układ sił?

8.

Co oznaczają zapisy:

α

cos

⋅

=

F

F

x

,

α

sin

⋅

=

F

F

y

?

9.

Kiedy rzut siły na dowolną oś jest równy zeru?

10.

Co to jest ciało swobodne i ciało nieswobodne?

11.

Jaki jest układu sił przedstawionego na rysunku poniżej?

4.1.3. Ćwiczenia

Ćwiczenie 1

Rysunek przedstawia graficzny obraz wektora. Rozpoznaj i zaznacz odnośnikami daną

cechę wektora.

Rysunek do ćwiczenia 1

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

13

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

zapoznać się z rysunkiem,

3)

poprowadzić odnoszące,

4)

sprawdzić jakość wykonanej pracy,

5)

zaprezentować wykonane ćwiczenie.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

przybory kreślarskie,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

Ćwiczenie 2

Rysunek przedstawia rzut siły

F

r

na oś

l

. Rozpoznaj i zaznacz odnośnikiem daną

wielkość.

Rysunek do ćwiczenia 2

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

zapoznać się z rysunkiem,

3)

poprowadzić odnoszące,

4)

sprawdzić jakość wykonanej pracy,

5)

zaprezentować wykonane ćwiczenie.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

przybory kreślarskie,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

14

Ćwiczenie 3

Narysuj wektor siły F = 400 N o kierunku poziomym i zwrocie w prawo.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

przyjąć skalę,

2)

narysować wektor,

3)

sprawdzić jakość wykonanej pracy,

4)

zaprezentować wykonane ćwiczenie.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

przybory kreślarskie,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

4.1.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

omówić cechy wektora?

2)

scharakteryzować siłę?

3)

wskazać różnicę pomiędzy siłą wypadkową a siłą równoważącą?

4)

rozłożyć daną siłę na dwie składowe?

5)

znaleźć sumę sił?

6)

wyjaśnić różnice między siłami czynnymi i biernymi (reakcyjnymi)?

7)

omówić różnicę między wielkościami wektorowymi i skalarowymi?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

15

4.2.

Płaski i przestrzenny układ sił

4.2.1. Materiał nauczania

Zbiór dowolnej liczby sił działających na ciało nazywamy układem sił. W zależności od

położenia linii działania sił układy możemy podzielić na dwa rodzaje:

−

płaskie,

−

przestrzenne.
Układ płaski odznacza się tym, że wszystkie siły tworzące ten układ leżą w jednej

płaszczyźnie. Układ ten możemy podzielić na:

−

układ płaski zbieżny – linie działania sił są zbieżne w jednym punkcie,

−

układ płaski równoległy – linie działania sił są do siebie równoległe,

−

układ płaski dowolny – jest zbiorem (w jednej płaszczyźnie) sił o różnych kierunkach
działania.
Układ przestrzenny to zbiór sił mających dowolne kierunki w przestrzeni.
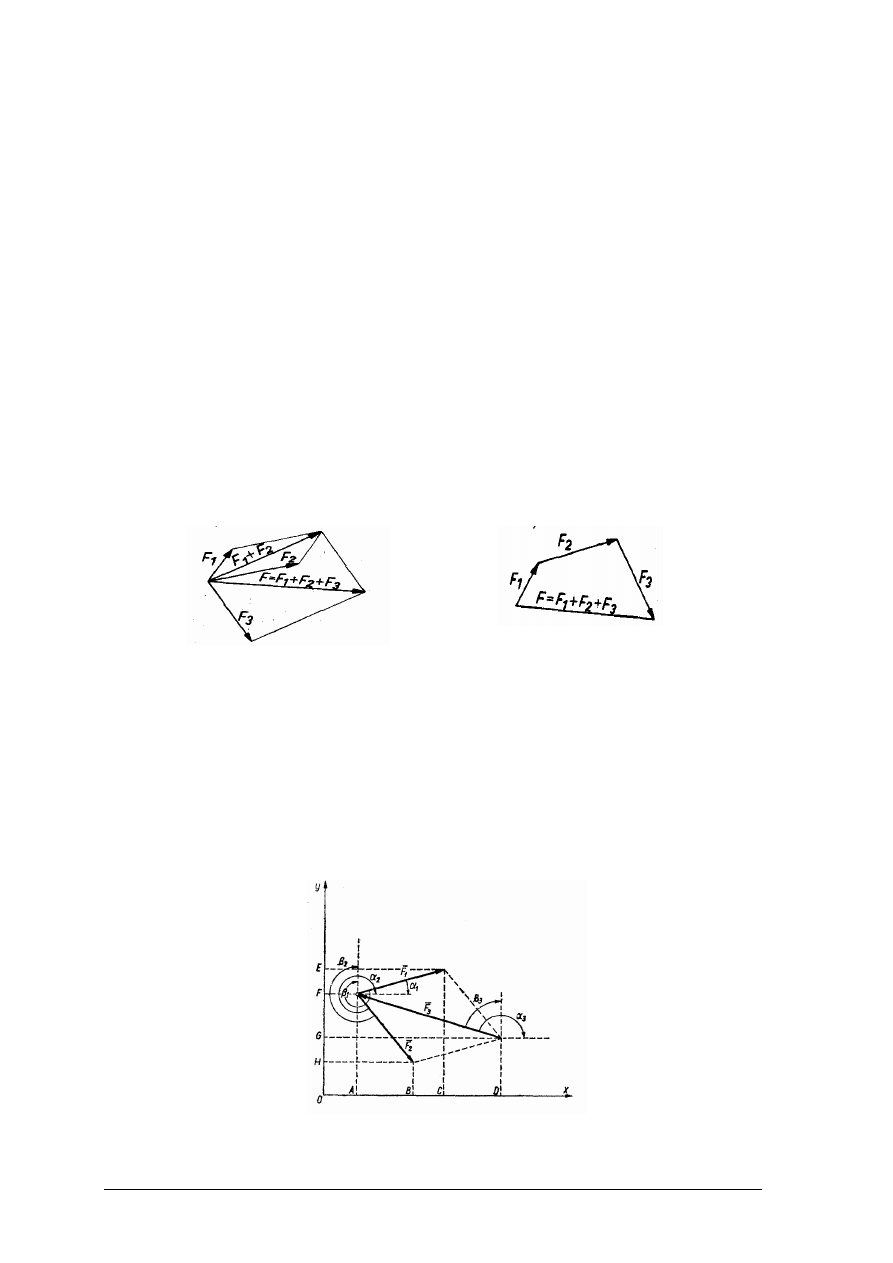
Dany układ sił zbieżnych można zastąpić jedną siłą wypadkową, sumując siły wektorowo

(geometrycznie) na zasadzie równoległoboku (rys. 10a) lub prościej – na zasadzie wieloboku
(rys. 10b).

a)

b)

Rys. 10. Sumowanie trzech sił; a) na zasadzie równoległoboku; b) na zasadzie wieloboku [4, s. 8]

Wektor siły wypadkowej F wektorów F

1

, F

2

, F

3

otrzymujemy przesuwając je równolegle

tak, aby na końcu wektora pierwszego znalazł się początek wektora drugiego, w jego końcu
początek wektora trzeciego itd. oraz łącząc początek wektora pierwszego z końcem wektora
ostatniego. Kolejność dodawania wektorów jest dowolna.

Analityczne warunki równowagi i analityczne składanie sił zbieżnych.
Mamy płaski układ trzech sil zbieżnych (rys. 11), pozostających w równowadze.

Wykonując rzutowanie kolejnych sił na osie układu i dodając algebraicznie te rzuty

otrzymamy:

Rys. 11. Rzut sił zbieżnych [2, s. 16]

3

3

3

2

2

2

1

1

1

cos

cos

cos

α

α

α

⋅

=

=

⋅

=

=

⋅

=

=

⋅

F

F

DA

F

F

AB

F

F

AC

x

x

x

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

16

Warunki te można zapisać w postaci:

Mówimy, że płaski układ sił zbieżnych jest w równowadze, jeśli suma algebraiczna

rzutów wszystkich sił na oś x oraz suma algebraiczna rzutów wszystkich sił na oś y równają
się zeru.

Równowaga dowolnej liczby sił przyłożonych do jednego punktu zachodzi wtedy, gdy

wielobok sił zamyka się, dając R = 0.

Gdyby układ pozostawał w równowadze, musiałby być spełniony warunek

0

...

0

...

3

2

1

3

2

1

=

−

+

+

+

=

−

+

+

+

y

iy

y

y

y

x

ix

x

x

x

W

F

F

F

F

W

F

F

F

F

stąd

iy

y

y

y

y

ix

x

x

x

x

F

F

F

F

W

F

F

F

F

W

.....

....

3

2

1

3

2

1

+

+

+

=

+

+

+

=

Wiemy jednak, że układ nie jest w równowadze. Równowaga byłaby zapewniona,

gdybyśmy do układu przyłożyli dodatkową siłę równoważącą (zgodną, co do kierunku
i wartości z wypadkową

,

W

lecz przeciwnie zwróconą. Mając dane W

x

i W

y

wartość

wypadkowej możemy wyznaczyć ze wzoru:

2

2

y

x

W

W

W

+

=

a jej kierunek i zwrot ze wzorów:

W

W

x

=

α

cos

;

W

W

y

=

β

cos

III zasada dynamiki Newtona mówi, że każdemu działaniu siły czynnej towarzyszy

równe, lecz przeciwnie skierowane siły bierne reakcyjne. Elementy wywołujące reakcje
nazywamy więzami. Ciało, które może wykonywać dowolne ruchy w przestrzeni nazywamy
ciałem swobodnym. Ciało swobodne ma sześć stopni swobody lub inaczej ma możliwość
wykonywania sześciu ruchów składowych: może przesuwać się wzdłuż osi x, y, z (trzy ruchy
składowe przesuwne) oraz może wykonywać rud obrotowe wokół tych osi (trzy ruchy
składowe obrotowe). Wprowadzenie więzów ogranicza liczbę stopni swobody i jest
równoznaczne z wprowadzeniem sił działających na ciała. Siły, którymi więzy oddziałują na
ciało nieswobodne, nazywamy reakcjami więzów.

Więzy dzieli na trzy rodzaje, a mianowicie:

−

więzy ruchome reakcja występuje tu w punkcie styczności podpory z ciałem i ma
kierunek normalny (prostopadły do powierzchni podpierającej) (rys. 12),

Rys.

12. Więzy ruchome [2, s. 124]

−

więzy wiotkie – są to wszelkiego rodzaju cięgna: sznury, liny, łańcuchy; reakcja więzów
wiotkich ma kierunek osi więzów (rys. 13),

0

=

∑

ix

F

0

=

∑

iy

F

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

17

Rys. 13. Więzy wiotkie [10, s. 124]

−

więzy (podpory) stałe – kierunek i wartość reakcji takiej podpory nie są znane; wyznacza
się je z warunków równowagi (rys. 14).

Rys. 14. Więzy stałe [2, s. 14]

Momentem siły F względem punktu (bieguna) 0 nazywamy iloczyn wartości tej siły

przez jej ramię, czyli odległość obranego punktu od linii działania danej siły.

r

F

M

⋅

=

0

Moment uważamy za dodatni, jeżeli siła dąży do obrócenia swego ramienia r dookoła

bieguna 0 w stronę niezgodną z ruchem wskazówek zegara (w lewo). Jeżeli siła dąży do
obrócenia swego r w stronę zgodną z ruchem wskazówek zegara (w prawo), moment
uważamy za ujemny. Moment siły względem punktu jest wektorem, mającym następujące
cechy (rys. 15):

−

wartość liczbową równą iloczynowi

( )

r

F

⋅

wartości siły przez jej ramię,

−

kierunek prostopadły do płaszczyzny wyznaczonej przez linię działania siły i biegun,

−

zwrot momentu przyjmujemy zgodnie z regułą śruby o gwincie prawozwojnym.

Rys. 15. Momenty siły

2

1

F

i

F

[2, s. 52]

Momenty

B

o

M

i

M

są wektorami prostopadłymi do płaszczyzny

β

, w której działają siły

2

1

F

i

F

oraz w której leżą bieguny 0 i B.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

18

Para sił to dwie siły równe, co do wartości kierunku, lecz o przeciwnym zwrocie.

Moment pary sił jest równy iloczynowi wartości siły i ramienia łączącego parę sił (nie zależy
od bieguna 0). Pary sił nie da się zastąpić jedną siłą wypadkową, tylko momentem równym
momentowi pary sił.

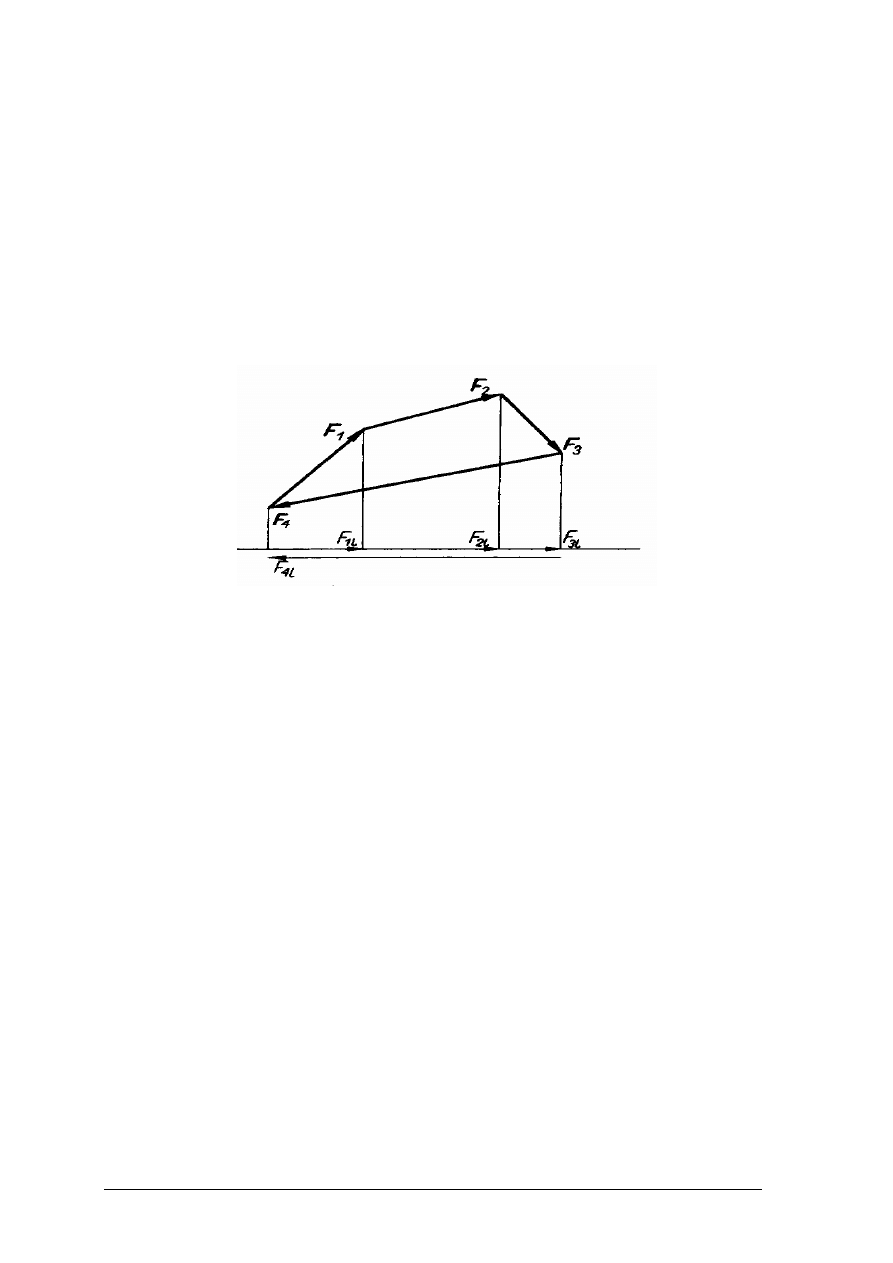
Warunki równowagi obciążeń

Jeżeli ciało znajduje się w równowadze, to zgodnie z podstawową zasadą mechaniki,

wszystkie siły i momenty zewnętrzne działające na to ciało muszą się wzajemnie
równoważyć. Oznacza to, że:

−

suma rzutów sił na dowolną prostą

l

(rys. 16) równa się zeru (wielobok sił tworzy

wówczas układ zamknięty);

0

=

∑

il

F

,

−

suma momentów sił względem dowolnego punktu 0 równa się zeru;

0

0

=

∑

i

M

.

Rys. 16. Wielobok sił: F

1

... F

4

– siły zewnętrzne,

l

l

F

F

4

......

1

⋅

– rzuty sił na prostą

l [2, s. 52]

W praktyce, dla układu płaskiego warunek równowagi przedstawia się najczęściej

w postaci trzech równań:

0

0

0

0

=

=

=

∑

∑

∑

i

iy

ix

M

F

F

w których:

ix

F

– rzut siły F

i

na oś x;

iy

F

– rzut siły Fi na oś y;

0

i

M

– moment siły F względem punktu 0.

Dla układu przestrzennego warunek równowagi wyraża się sześcioma równaniami:

0

0

0

=

=

=

∑

∑

∑

iz

iy

ix

F

F

F

0

0

0

=

=

=

∑

∑

∑

iz

iy

ix

M

M

M

w których:

iz

iy

ix

M

M

M

,

,

– momenty siły względem osi x, y, z.

Powyższe układy równań służą zwykle do obliczania reakcji więzów. Jeżeli liczba

poszukiwanych reakcji jest równa liczbie równań równowagi ciała, to wyznaczenie tych
reakcji nie nastręcza żadnych trudności; mamy wtedy do czynienia z układem statycznie
wyznaczalnym. Gdy zaś liczba niewiadomych reakcji jest większa niż liczba równań
równowagi, czyli gdy zachodzi przypadek statycznie niewyznaczalny, wyznaczenie reakcji
wymaga specjalnych metod.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

19

4.2.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Co to jest ciało swobodne?

2.

Co to jest ciało nieswobodne?

3.

Co to są więzy, podaj rodzaje?

4.

Co charakteryzuje reakcję podpory ruchomej?

5.

Jakie kierunki mają reakcje w poszczególnych rodzajach więzów?

6.

Jakie ruchy dopuszcza, a jakie wyklucza, podpora stała?

4.2.3. Ćwiczenia

Ćwiczenie 1

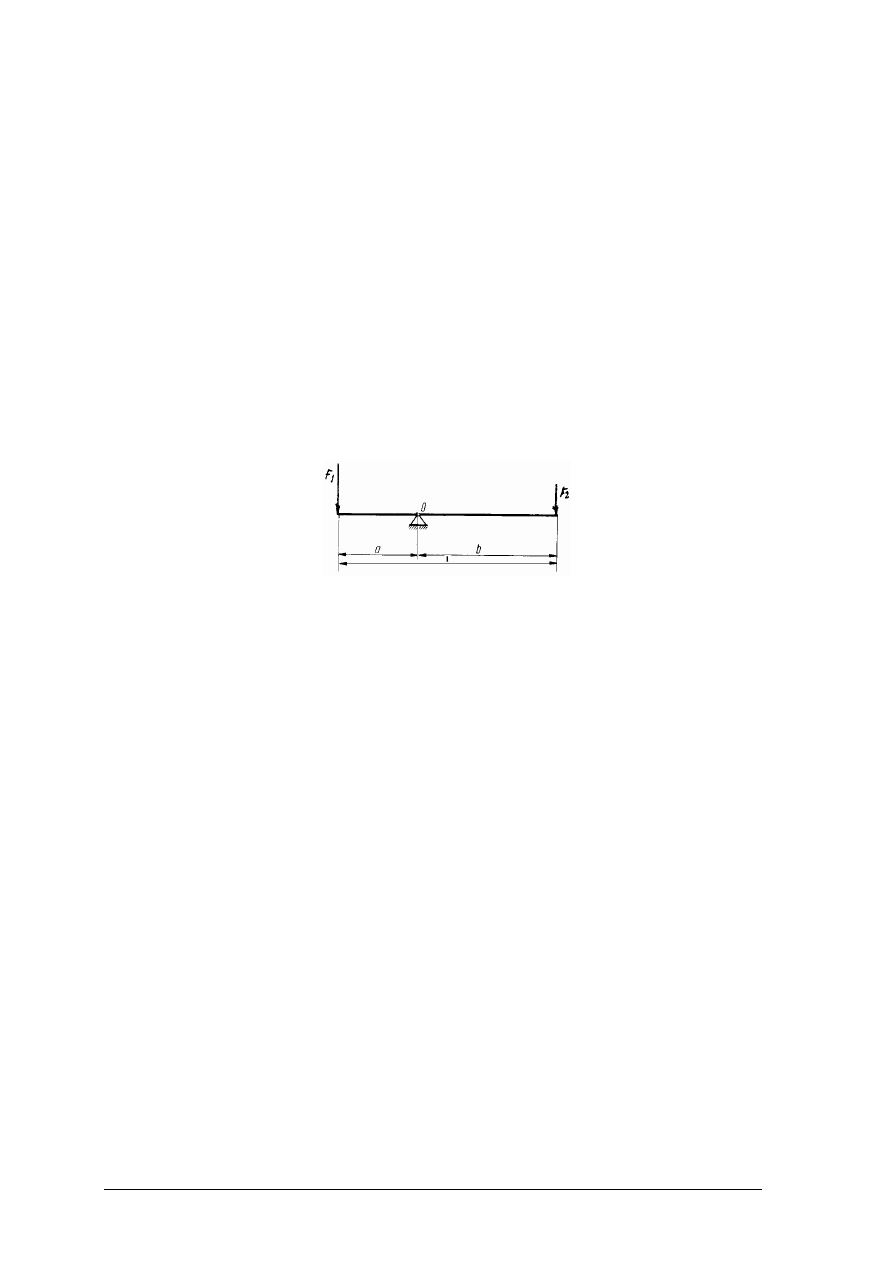
Oblicz, jaką siłę F

2

należy przyłożyć do dźwigni dwustronnej przedstawionej na rysunku

by była w równowadze, jeżeli na jeden koniec w odległości a = 1 m działa siła F

1

= 100 N,

a długość całej dźwigni wynosi l = 5 m?

Rysunek do ćwiczenia 1 [4, s. 24]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

przeanalizować dane do ćwiczenia,

2)

obliczyć długość ramienia b,

3)

obliczyć wartość siły F

2

,

4)

wpisać obliczenia do zeszytu,

5)

sprawdzić jakość wykonanej pracy,

6)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska:

−

zeszyt,

−

przybory do rysowania,

−

kalkulator,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

20

Ćwiczenie 2

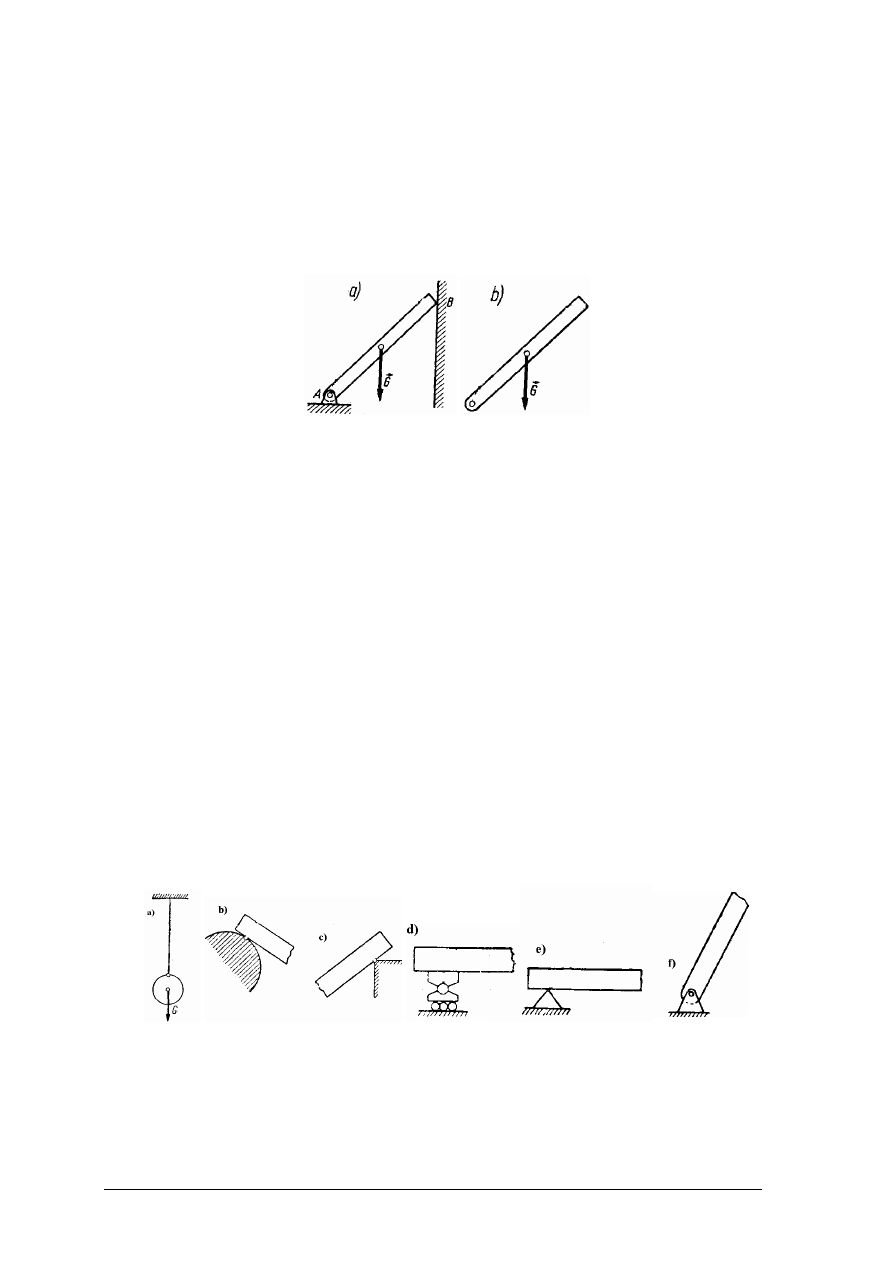
Pręt o ciężarze

G

r

zamocowany przegubowo w punkcie A, drugim zaś końcem

swobodnie opierający się o pionową ścianę.
1.

Jeżeli pod wpływem siły czynnej

G

r

w miejscach podparcia pojawią się siły, to narysuj

i nazwij je.

2.

Określ czy rozważany pręt jest ciałem swobodnym czy nieswobodnym? Udowodnij to.

3.

Określ, czy rozważany pręt może być ciałem swobodnym? Udowodnij to.

Rysunek do ćwiczenia 2 [10, s. 30]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

przeanalizować dane i rysunek do ćwiczenia,

2)

narysować i nazwać siły w podporze A i B,

3)

usunąć więzy,

4)

narysować pręt jako ciało swobodne,

5)

zapisać wnioski,

6)

sprawdzić jakość wykonanej pracy,

7)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska:

−

przybory do rysowania,

−

zeszyt,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

Ćwiczenie 3

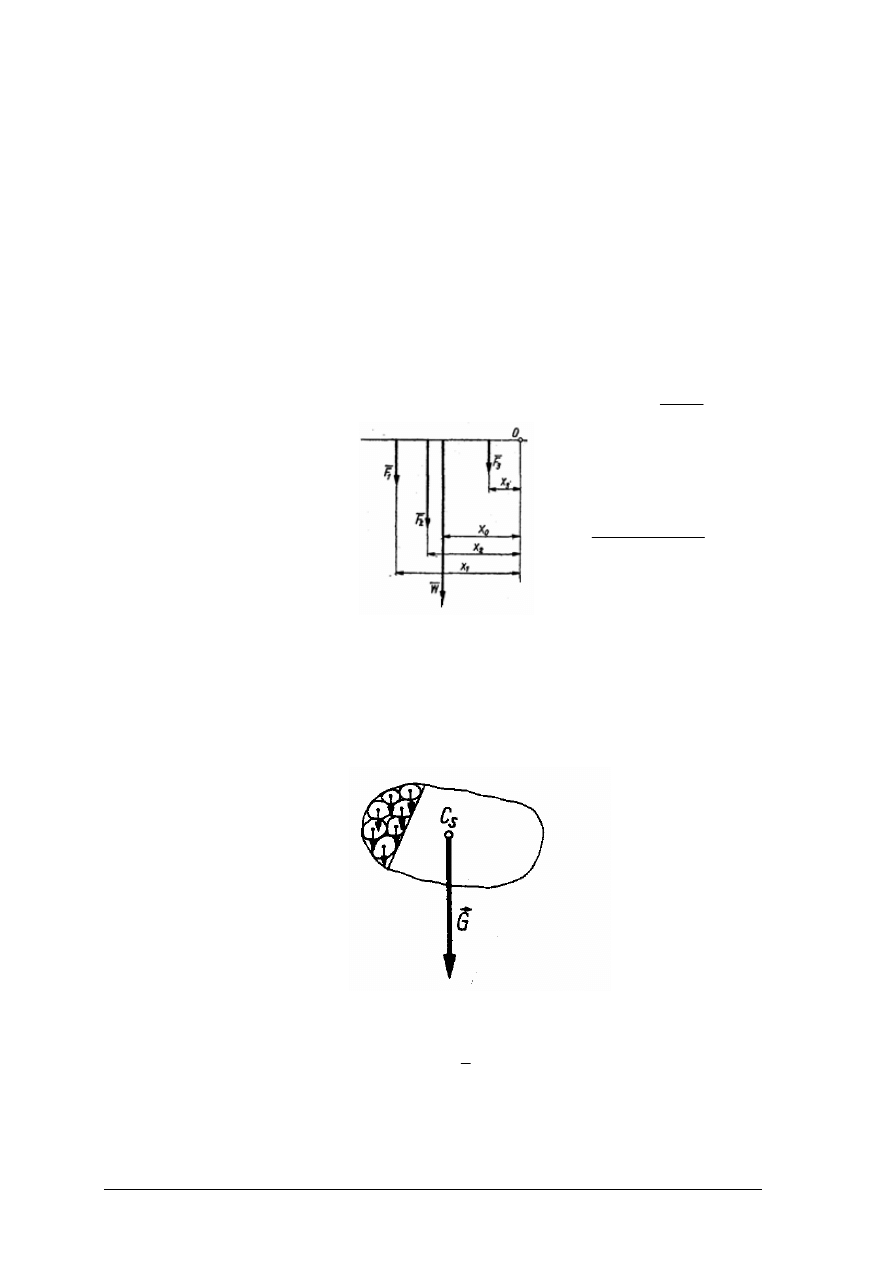
Rysunek przedstawia różne rodzaje więzów. Nazwij, scharakteryzuj i narysuj siły

reakcyjne w tych więzach.

Rysunek do ćwiczenia 3 [6, s. 150]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

21

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

zanalizować przedstawione więzy,

3)

narysować i nazwać siły w poszczególnych więzach,

4)

sprawdzić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

4.2.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

rozróżnić, kiedy ciało jest swobodne a kiedy nieswobodne?

2)

wyjaśnić warunki równowagi dowolnego płaskiego układu sił?

3)

odróżnić kiedy na element działa siła, układ sił, moment?

4)

rozróżnić podpory czyli więzy?

5)

obliczyć siły reakcyjne w podporach?

6)

zastąpić układ sił jedną siłą wypadkową?

7)

określić warunki równowagi dowolnego płaskiego układu sił?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

22

4.3.

Środek ciężkości

4.3.1. Materiał nauczania

Jako szczególny przypadek płaskiego układu sił rozważmy układ sił równoległych.
Położenie linii, na której leży wypadkowa wyznacza się korzystając z twierdzenia, że

moment wypadkowej względem dowolnego punktu 0 równa się sumie momentów sił
składowych względem tego punktu. Ponieważ w przypadku sił równoległych wypadkowa
leży na prostej równoległej do sił składowych, położenie jej określa w zupełności jedna
współrzędna x

0

, prostopadła do kierunku działania sił:

i

i

x

F

x

W

⋅

∑

=

⋅

0

przy czym:

∑

=

i

F

W

Stąd położenie wypadkowej x

0

wyznaczamy z zależności (rys. 17):

∑

∑

⋅

=

i

i

i

F

x

F

x

0

3

3

2

2

1

1

x

F

x

F

x

F

x

W

o

⋅

+

⋅

+

⋅

=

⋅

r

stąd

3

2

1

3

3

2

2

1

1

F

F

F

x

F

x

F

x

F

o

x

+

+

⋅

+

⋅

+

⋅

=

Rys. 17. Wypadkowa sił równoległych [2, s. 25]

Rozpatrzmy figurę płaską, której jest przypisany określony ciężar. Figura ta jest, więc

obciążona układem sił równoległych przyłożonych do wszystkich jej cząstek (elementów).

Wartości sił są proporcjonalne do mas poszczególnych elementów, środkiem ciężkości

będziemy nazywali środek C

s

układu tak rozumianych sił równoległych. Suma sił ciężkości

elementarnych cząstek układu jest ciężarem ciała (rys. 18).

Rys. 18. Ciało o ciężarze G [10, s. 124]

Sumę wszystkich tych sił elementarnych:

G

G

G

G

G

G

i

r

r

s

r

r

=

∑

=

+

+

+

+

....

3

2

1

nazywamy ciężarem ciała, a środek C

s

tych sił nazywamy środkiem ciężkości tego ciała. Tak,

więc środek ciężkości jest to punkt, w którym jest zaczepiona siła przedstawiająca ciężar
ciała.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

23

Zgodnie z właściwością środka sił równoległych środek ciężkości ciała znajduje się

w określonym punkcie C

s

i nie zmienia swego położenia w tym ciele podczas ruchu ciała

(przy założeniu, że mamy do czynienia z ciałem doskonale sztywnym). Położenie środka
ciężkości zależy natomiast od kształtu ciała i od rozłożenia w nim poszczególnych cząstek
materialnych.

Do ciał jednorodnych o prostej formie geometrycznej odnosi się kilka twierdzeń, którymi

będziemy się posługiwać w wyznaczaniu środków ciężkości:

−

jeżeli ciało ma jedną oś symetrii, to środek ciężkości leży na tej osi,

−

jeżeli ciało ma dwie (lub więcej) osie symetrii, to środek ciężkości leży na przecięciu się
tych osi,

−

jeżeli ciało ma środek symetrii, to punkt ten jest równocześnie środkiem ciężkości,

−

ś

rodek ciężkości ciała złożonego z kilku ciał pokrywa się ze środkiem ciężkości punktów

materialnych leżących w środkach poszczególnych ciał składowych, przy czym masy
tych punktów są równe masom poszczególnych ciał składowych.
To ostatnie twierdzenie oraz wzory, określające środek sił równoległych, stosujemy

bardzo często przy określaniu środka ciężkości. Zilustrujemy to na przykładzie określenia
ś

rodka ciężkości linii i powierzchni.

Odciętą i rzędną środka ciężkości wyznaczamy na podstawie wzorów:

∑

∑

⋅

=

∑

∑

⋅

=

i

F

i

y

i

F

y

i

F

i

x

i

F

x

0

0

Dla figur jednorodnych wzory powyższe przyjmują postać:

S

S

y

S

S

x

i

i

i

i

y

x

∑

=

∑

=

⋅

⋅

0

0

gdzie: S – pole figury.
Dla linii:

∑

∑

=

∑

∑

=

⋅

⋅

i

i

i

i

i

i

y

y

l

l

x

l

y

x

0

0

Wiemy z fizyki, że ciała sztywne mogą znajdować się w równowadze: stałej, chwiejnej

lub obojętnej. O rodzaju równowagi danego ciała decyduje położenie jego środka ciężkości.

Każde ciało sztywne podparte (lub zawieszone) pozostaje w spoczynku tylko wówczas,

gdy środek ciężkości i punkt podparcia leżą na jedne pionowej linii prostej. Wówczas,
bowiem siła ciężkości i reakcja podpory działają wzdłuż wspólnej prostej, a zatem wzajemnie
się równoważą.

Rozpatrując równowagę ciał podpartych, będących pod działaniem ich własnego ciężaru,

możemy wyodrębnić trzy rodzaje wspomnianej równowagi.

Pierwszy zachodzi wówczas, gdy, środek ciężkości ciała znajduje się poniżej punktu

podparcia, tak jak obrazuje to rysunek (rys. 19).

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

24

Rys. 19. Równowaga stała [6, s. 188]

W tym wypadku ciężar ciała G i reakcja N podpory wzajemnie się równoważą, gdyż są

równe, co do wielkości, mają zwroty przeciwne i leżą na wspólnej prostej (rys. 19 a).
Ponadto, jeżeli wychylimy nieznacznie ciało z położenia równowagi to siły G i N utworzą
parą sił, której moment powoduje powrót ciała do pierwotnego położenia, taki rodzaj
równowagi nazywamy równowagą stałą.

A zatem równowaga stała zachodzi wówczas, gdy środek ciężkości ciała znajduje się

poniżej punktu podparcia i zajmuje najniższe z możliwych położeń. W równowadze stałej
znajdują się przede wszystkim wszystkie ciała zawieszone na więzach wiotkich. Inny rodzaj
równowagi zachodzi wówczas, gdy środek ciężkości ciała znajduje się powyżej punktu
podparcia.

Rys. 20. Równowaga chwiejna [6, s. 188]

W tym wypadku, kiedy środek ciężkości zajmuje najwyższe położenie (rys. 20), siła

ciężkości G i reakcja N także równoważą się wzajemnie. Jeżeli jednak wychylimy ciało
z położenia równowagi, nawet bardzo nieznacznie, to siły G i N utworzą parę sił, której
moment spowoduje obrót ciała dookoła jego punktu podparcia i ciało do pierwotnego
położenia już nie powróci. Ten rodzaj równowagi nazywamy równowagą chwiejną.

Równowaga chwiejna zachodzi, zatem wówczas, gdy środek ciężkości ciała znajduje się

powyżej punktu podparcia i zajmuje najwyższe możliwe położenie.

Z trzecim rodzajem równowagi mamy do czynienia wówczas, gdy środek ciężkości ciała

pokrywa się z punktem podparcia.

Rys. 21. Równowaga obojętna [6, s. 188]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

25

Przy takim umiejscowieniu środka ciężkości (rys. 21) i punktu podparcia wychylenie

ciała nie powoduje pojawienia się pary sił, co oznacza, że ciało znajduje się w równowadze
przy dowolnym położeniu. Równowagę taką, w czasie, której środek ciężkości ciała pokrywa
się z punktem podparcia, nazywamy równowaga obojętną.

Przykładem takiej równowagi jest, np. równowaga kuli leżącej na poziomej płaszczyźnie,

wałka osadzonego w łożyskach itp. Ciała te, bowiem w każdym położeniu pozostają
w równowadze. Jeżeli ciało ma kilka punktów podparcia, to będzie się ono znajdowało
w stanie równowagi stałej tak długo, dopóki siła ciężkości G i reakcja podpór N będą tworzyć
parę sił, której moment będzie w stanie sprowadzać ciało do pierwotnego położenia.

4.3.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Co nazywamy środkiem ciężkości ciała?

2.

Jakie są twierdzenia dotyczące położenia środka ciężkości?

3.

Jak analitycznie wyznaczyć środek ciężkości figury płaskiej?

4.

Czy w czasie ruchu zmieni się położenie środka ciężkości?

5.

Jak wyznaczyć środek ciężkości linii łamanej?

6.

Co nazywamy punktem podparcia?

4.3.3. Ćwiczenia

Ćwiczenie 1

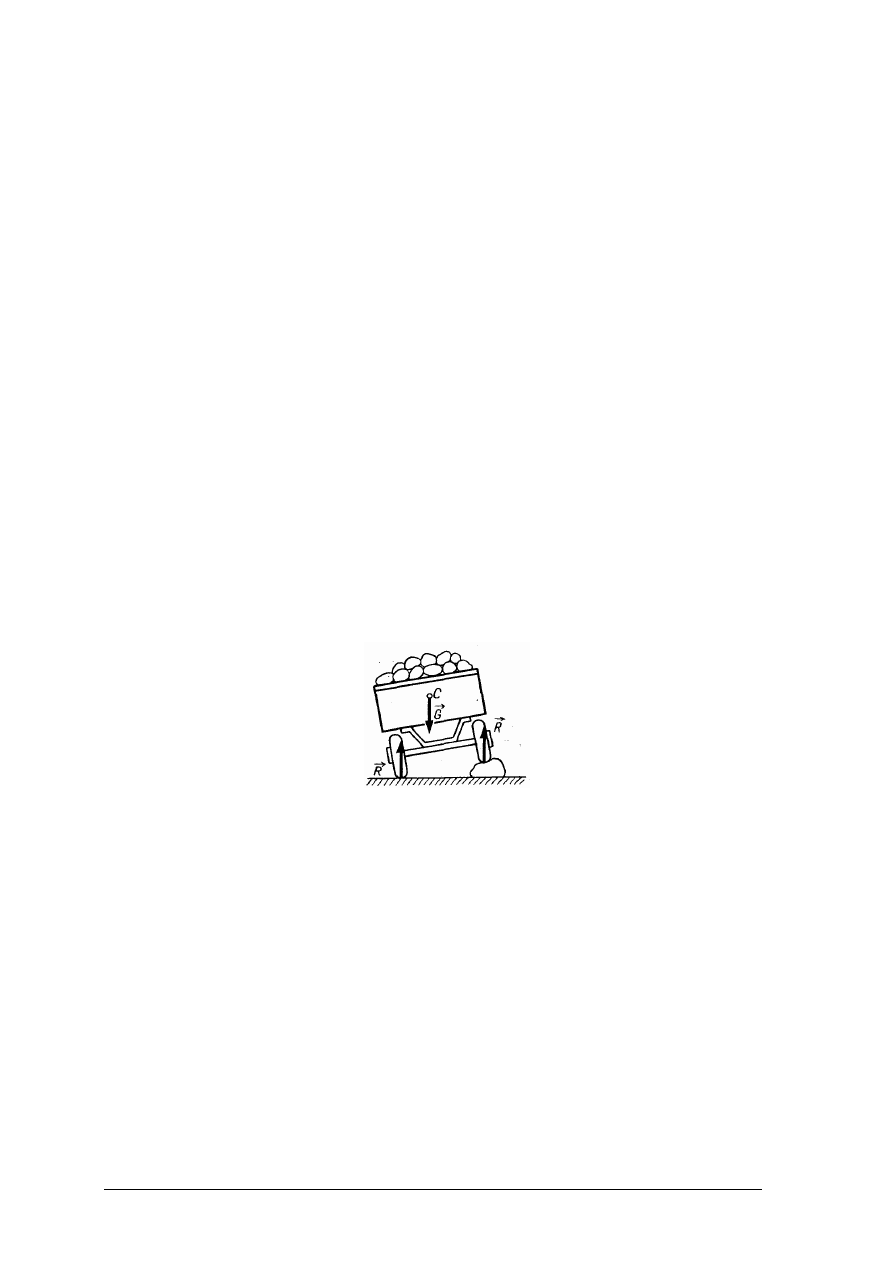
Określ, do jakiego momentu przyczepa ciągnikowa będzie w stanie równowagi, a kiedy

przyczepa przewróci się.

Rysunek do ćwiczenia 1 [6, s. 104]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

omówić stan przyczepy przedstawiony na rysunku,

3)

przeanalizować wszystkie przypadki równowagi ciała,

4)

wskazać kiedy równowaga przyczepy zostanie zachwiana,

5)

zapisać wnioski,

6)

sprawdzić jakość wykonanej pracy,

7)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska:

−

przybory do rysowania,

−

zeszyt,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

26

Ćwiczenie 2

Oblicz współrzędne środka ciężkości kątownika, jeżeli a = 10 cm, b = 20 cm, c = 30 cm.

Rysunek do ćwiczenia 2

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

podzielić figurę na dwa prostokąty,

3)

wskazać położenie środka ciężkości każdego prostokąta,

4)

obliczyć współrzędne środka ciężkości kątownika,

5)

ocenić poprawność wykonanych obliczeń,

6)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska:

−

zeszyt ćwiczeń,

−

przybory,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

4.3.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

określić, kiedy zachodzi równowaga ciała?

2)

scharakteryzować sposoby wyznaczania położenia środka ciężkości?

3)

określić położenie środka ciężkości figury płaskiej?

4)

wyznaczyć w sposób wykreślny położenie środka ciężkości?

5)

określić rolę środka ciężkości w położeniu równowagi ciała
nieswobodnego?

6)

wyjaśnić, od czego zależy położenie środka ciężkości?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

27

4.4.

Wytrzymałość materiałów

4.4.1. Materiał nauczania

Mówiąc o wytrzymałości należy pamiętać o łańcuchu zależności między obciążeniem

naprężeniem a odkształceniem. Nie ma jednego, bez drugiego. Jakie obciążenie takie
naprężenie i tak materiał się odkształca. Jak pojawi się obciążenie to pojawi się naprężenie
i odkształcenie.

Siły zewnętrzne (obciążenia) działające na ciało mogą być:

−

stałe,

−

statyczne,

−

dynamiczne.
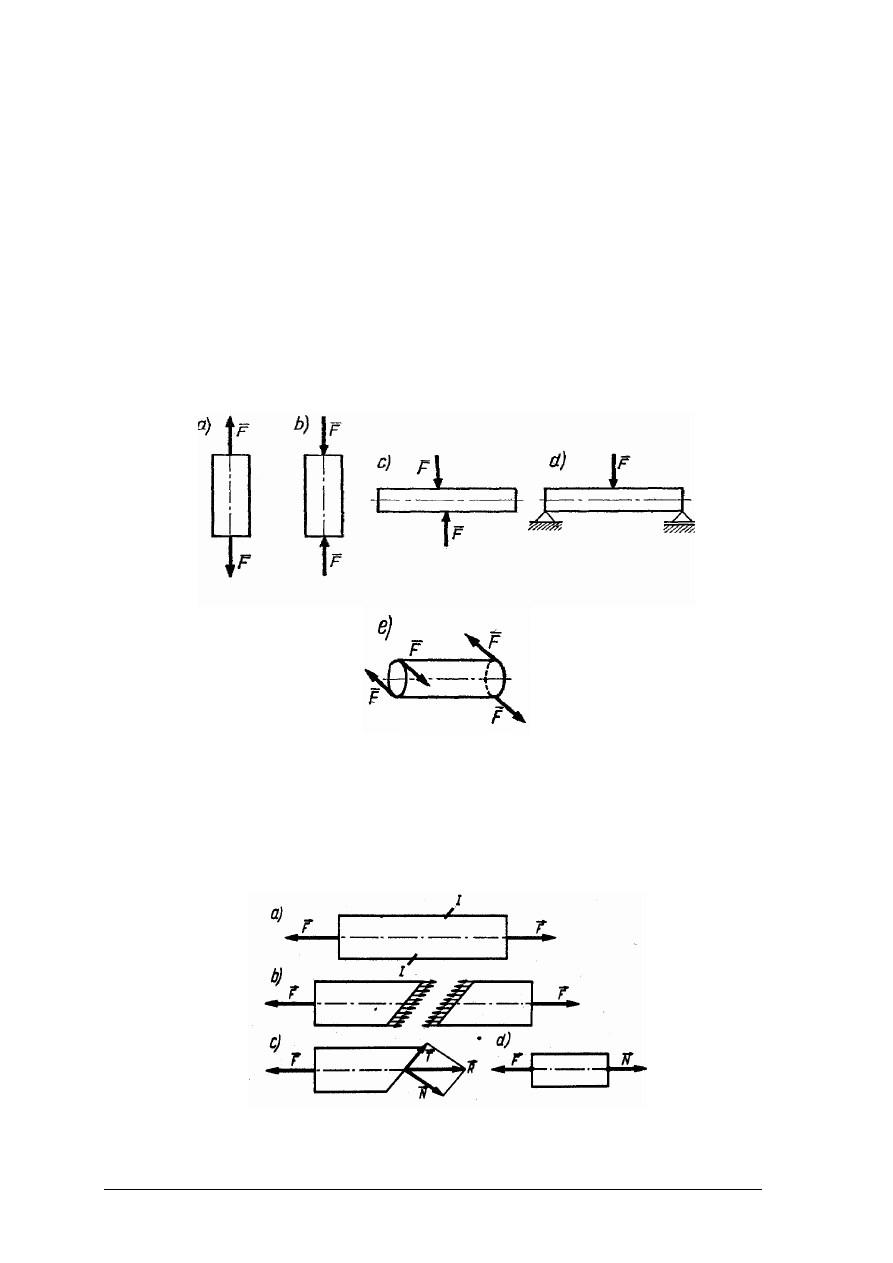
Typowe rodzaje obciążeń części maszyn ilustruje rys. 22.

Rys. 22. Rodzaje obciążeń: a) rozciągające, b) ściskające, c) ścinające, d) zginające, e) skręcające [10, s. 89]

W wielu zagadnieniach technicznych wymienione obciążenia występują jednocześnie –

mówimy wtedy o wytrzymałości złożonej.

Podczas obciążenia elementu konstrukcyjnego siłami zewnętrznymi pojawiają się

wewnątrz elementu (rys. 23) – rozłożone w pewien określony sposób – siły zwane
napięciami.

Rys. 23. Rozkład naprężeń w pręcie rozciąganym [10, s. 172]

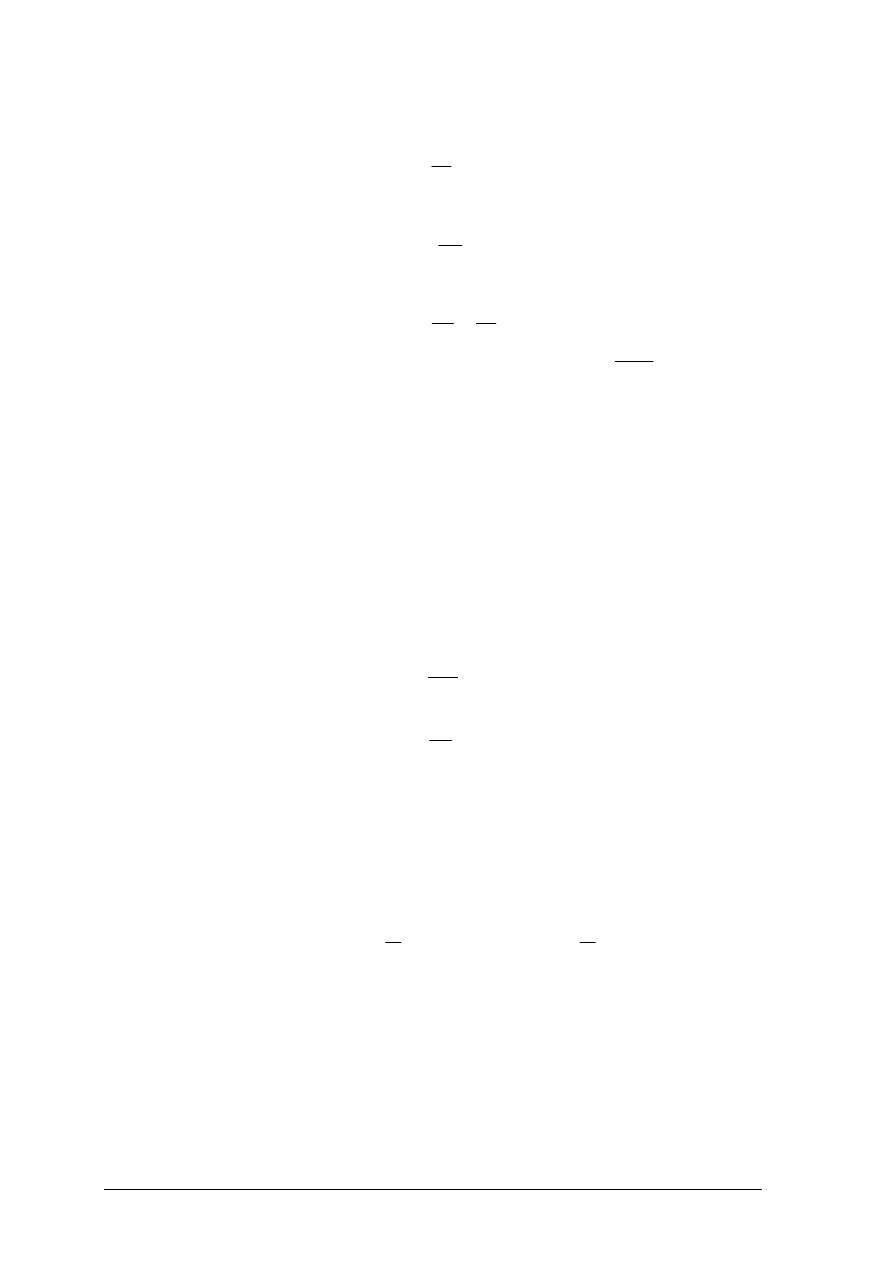
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

28

Stosunek wartości siły N do pola S przekroju nazywamy naprężeniem normalnym

i oznaczamy literką

σ

(sigma):

S

F

=

δ

[Pa]

Stosunek wartości siły T do pola S przekroju nazywamy naprężeniem stycznym

i oznaczamy literką

τ

(tau):

S

F

=

τ

[Pa]

W szczególności dla przekroju prostopadłego do osi pręta będzie N = F i T = 0.

W przekroju tym występuje tylko naprężenie normalne:

S

F

S

N

=

=

δ

W międzynarodowym układzie SI jednostką naprężenia jest [

2

m

N

] niuton na metr

kwadratowy). Jednostkę tę nazywamy paskalem [Pa].

Naprężenia dopuszczalne

Naprężenia, które mogą występować w materiale bez obawy naruszenia warunków

wytrzymałości i sztywności, nazywamy naprężeniami dopuszczalnymi i oznaczamy literą k.

Dla różnych odkształceń dodajemy w indeksie odpowiedni wyróżnik, charakteryzujący

rodzaj odkształcenia, np.: k

r

– naprężenia dopuszczalne na rozciąganie, k

c

– naprężenia

dopuszczalne na ściskanie, k

g

– naprężenia dopuszczalne na zginanie, k

t

– naprężenia

dopuszczalne na ścinanie, k

s

. – naprężenia dopuszczalne na skręcanie.

Aby spełnić te warunki, przyjmujemy z góry współczynnik bezpieczeństwa n o wartości

1,3

÷

12, dzięki któremu otrzymujemy tzw. pewność konstrukcyjną.

Naprężenia dopuszczalne na rozciąganie obliczamy według wzorów:

−

dla materiałów plastycznych:

n

m

R

r

k

=

[MPa]

−

dla materiałów kruchych:

n

e

R

r

k

=

[MPa]

Warunek wytrzymałości jest taki, aby naprężenia rzeczywiste (normalne

σ

lub styczne

τ

)

były zawsze mniejsze, a co najwyżej równe naprężeniom dopuszczalnym:

σ

lub

k

≤

τ

Rozciąganie i ściskanie

Naprężenia rozciągające i ściskające są naprężeniami normalnymi, a różnica między nimi

polega tylko na przeciwnych zwrotach sił. Rzeczywiste naprężenia występujące w elemencie
obliczamy według wzorów:

rozciąganie

S

F

r

=

δ

[Pa] ściskanie

S

F

c

=

δ

[Pa]

Naprężenia te nie mogą przekraczać naprężeń dopuszczalnych, a więc musi być

spełniony warunek wytrzymałości:

r

k

r

≤

δ

i

c

k

c

≤

δ

Ścinanie

Ś

cinanie elementu występuje w wyniku działania dwu sił równoległych o przeciwnych

zwrotach, tworzących parę sił (rys. 24). Ramię działania pary sił jest bardzo małe.

W przypadku gdyby siły te leżały na wspólnej linii działania, nie wystąpiłoby ścinanie,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

29

lecz ściskanie. Rzeczywiste naprężenia występujące w materiale przy ścinaniu obliczamy
według wzoru:

S

F

=

τ

[Pa]

Aby był spełniony warunek wytrzymałości, naprężenia te muszą być mniejsze lub co

najwyżej równe naprężeniom dopuszczalnym na ścinanie:

t

k

≤

τ

.

Rys. 24. Siły występujące przy ścinaniu [10, s. 211]

Naprężenia dopuszczalne na ścinanie są mniejsze od naprężeń dopuszczalnych na

rozciąganie. Przyjmuje się, że k

t

= (0,5

÷

0,8)k

r

.

Zginanie

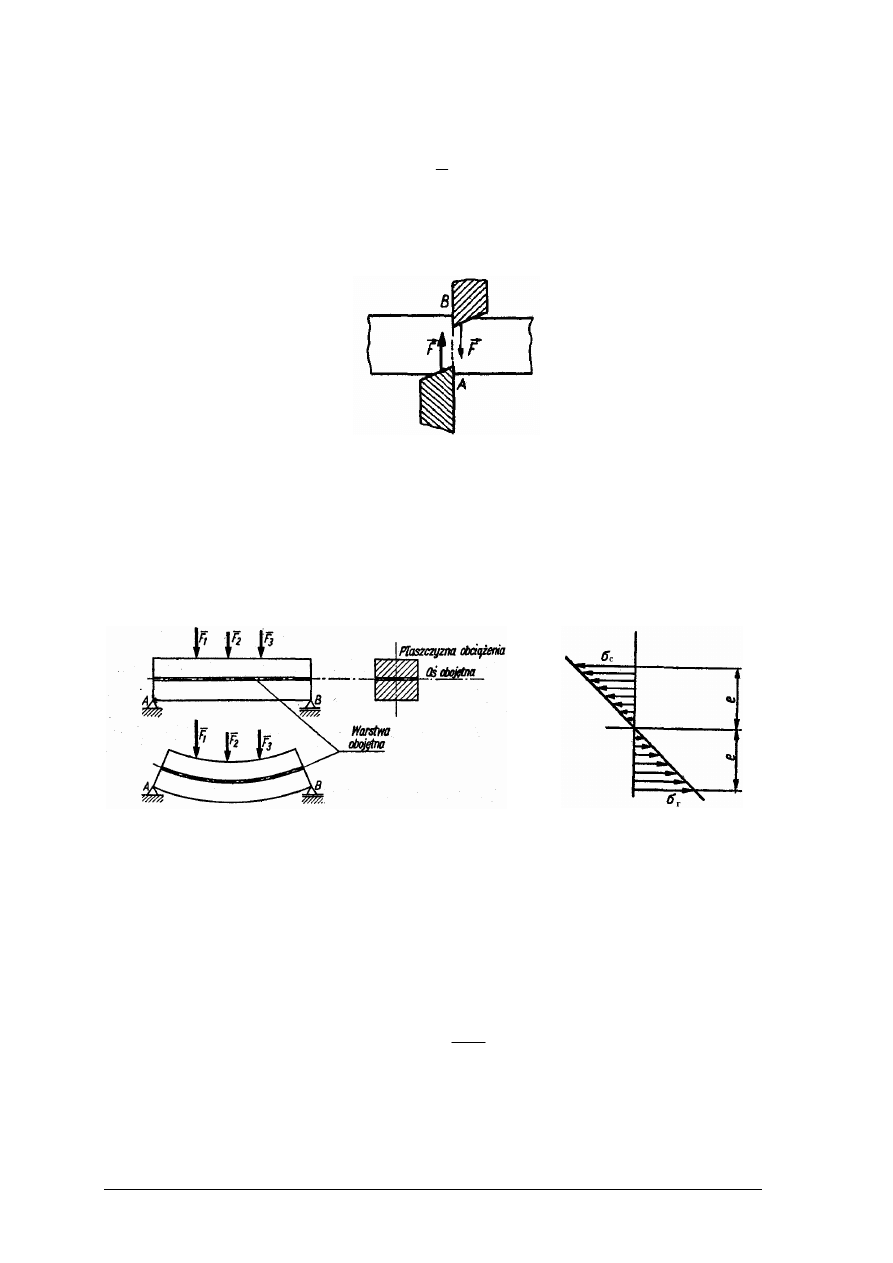
Zginanie najłatwiej można wyjaśnić na przykładzie belki o przekroju prostokątnym,

podpartej na obu końcach, na którą działa obciążenie F (rys. 25).

Rys. 25. Zginane belki [3, s. 142]

Rys. 26. Rozkład naprężeń w belce

[3, s. 142]

Jeżeli wyobrazimy sobie, że materiał belki składa się z włókien ułożonych warstwami, to

podczas zginania ulegają one odkształceniom. Górne włókna (rys. 26) są ściskane

c

σ

, dolne

zaś rozciągane

r

σ

. Mniej więcej w środku belki włókna nie ulegają ściskaniu, ani rozciąganiu

i tworzą tzw. warstwę obojętną (oś x–x na rys. 26), w której ulegają one tylko zgięciu, nie zaś
odkształceniu (skróceniu lub wydłużeniu), jak w pozostałych przypadkach.

Przy obliczeniach naprężeń zginających korzystamy z wzoru:

W

M

g

g

=

σ

w którym:

g

σ

– naprężenia zginające w Pa (w praktyce w MPa),

g

M – moment zginający w N • m,

W – wskaźnik wytrzymałości przekroju na zginanie w m

3

.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

30

Naprężenia zginające zależą od:

−

wartości momentu zginającego Mg; przy takiej samej sile F, lecz różnych długościach
belki wartości

g

σ

są różne,

−

wartości wskaźnika wytrzymałości przekroju na zginanie W; dla tych samych przekrojów
S, lecz różnych ich kształtów i wymiarów wartości

g

σ

są inne.

Aby zginanie było bezpieczne, musi być spełniony warunek wytrzymałości:

g

k

g

≤

σ

Skręcanie

Skręcanie występuje w wyniku przyłożenia pary sił lub siły na ramieniu prostopadle do

osi prętów.

Naprężenie skręcające oblicza się według wzoru:

W

s

M

s

=

τ

gdzie: s

τ

– naprężenie skręcające w Pa,

M

s

– moment skręcający w N • m,

W

s –

wskaźnik wytrzymałości

przekroju na skręcanie w m

3

.

Również w przypadku skręcania musi być spełniony warunek wytrzymałości:

s

s

k

≤

τ

4.4.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonywania ćwiczeń.

1.

Jakie są rodzaje odkształceń w zależności od obciążenia?

2.

Wyjaśnij pojęcie obciążenie, naprężenie, odkształcenie oraz zastanów się czy istnieje
zależność między tymi pojęciami?

3.

Jakiego rodzaju siły zewnętrzne powodują zginanie?

4.

Jaki jest charakter odkształceń i naprężeń przy zginaniu?

5.

Jaki jest rozkład naprężeń w przekroju zginanym?

6.

Jaka jest różnica między naprężeniami rzeczywistymi i dopuszczalnymi i jaka jest
między nimi zależność?

7.

Czym się charakteryzują odkształcenia i naprężenia przy skręcaniu?

4.4.3. Ćwiczenia

Ćwiczenie 1

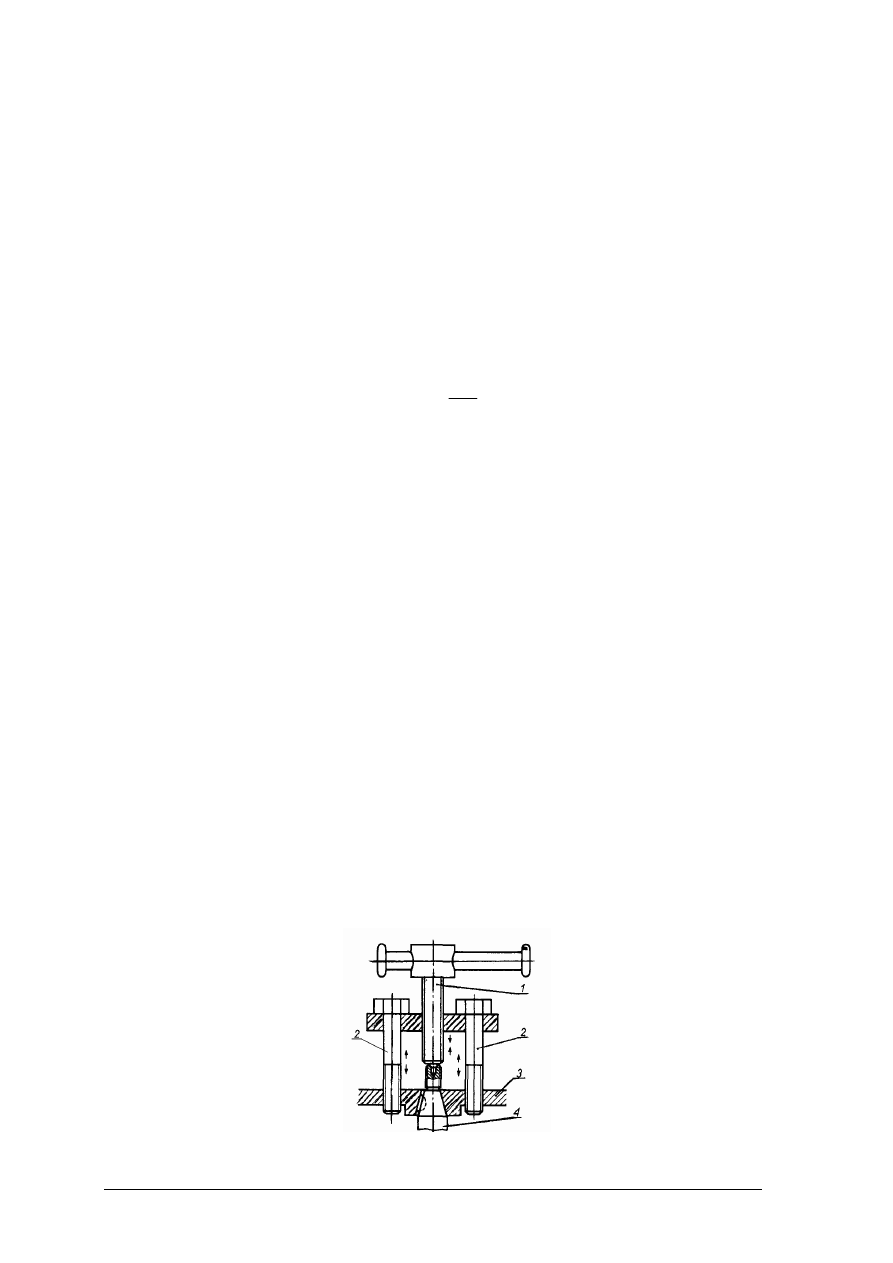
Określ, na jaki rodzaj odkształcenia narażona jest w ściągaczu śruba nr 1, a na jaki śruby

nr 2. Rozpoznaj odkształcenia i podaj warunki wytrzymałości dla tych odkształceń.

Rysunek do ćwiczenia 1: 1– śruba, 2 – śruby, 3 – piasta, 4 – czop [7, s. 22]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

31

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zapoznać się z zasadą działania ściągacza,

2)

odszukać wskazane w ćwiczeniu śruby,

3)

podać odkształcenia tych śrub,

4)

zapisać warunki wytrzymałości dla tych odkształceń,

5)

sprawdzić jakość wykonanej pracy,

6)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

przybory do pisania,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

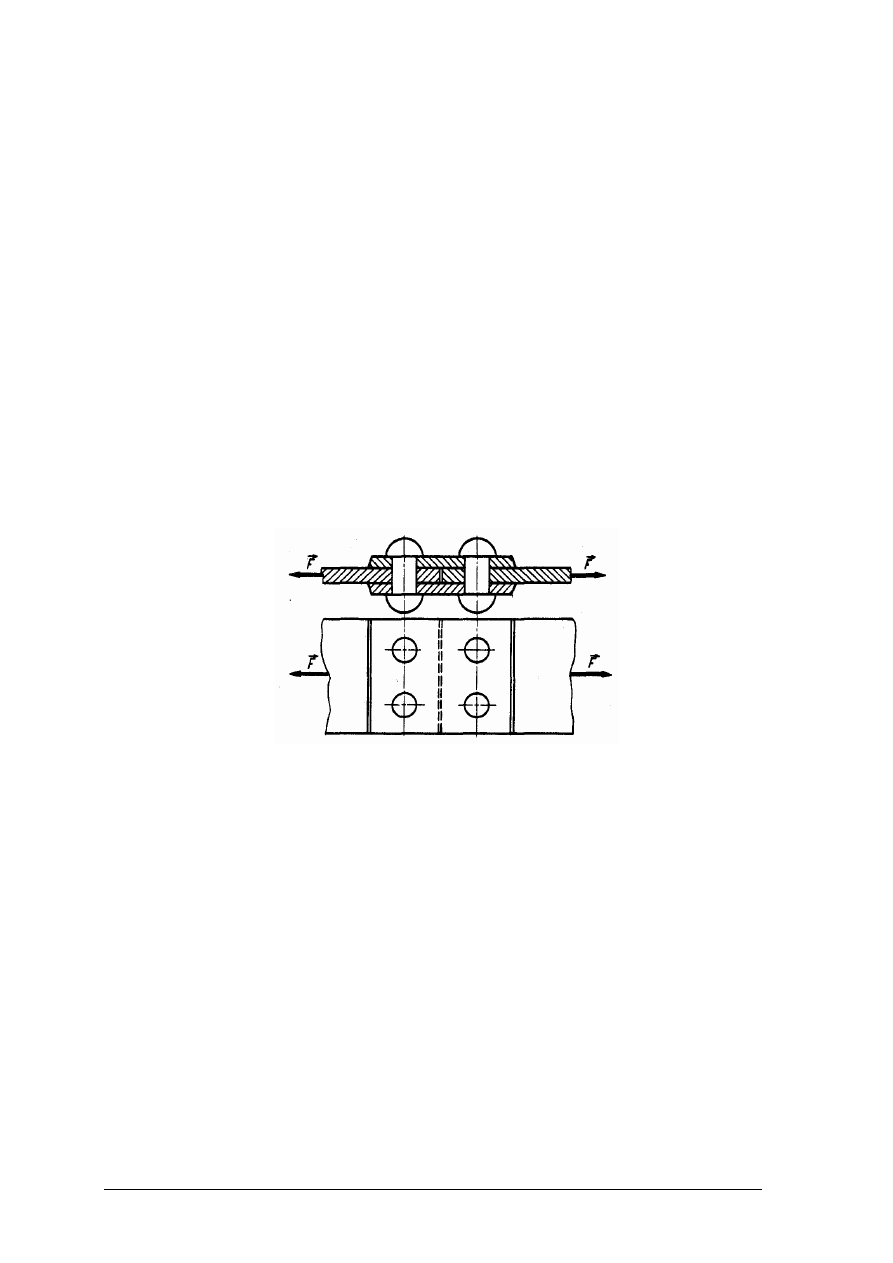
Ćwiczenie 2

Dwa płaskowniki za pomocą dwóch nakładek, są połączone nitami. Płaskowniki

obciążono siłą czynną

F

r

. Rozpoznaj odkształcenie płaskownika i nitów. Zdefiniuj warunki

wytrzymałościowe dla tych odkształceń.

Rysunek do ćwiczenia 2 [2, s. 223]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

przeanalizować rysunek,

3)

podać warunki wytrzymałościowe,

4)

sprawdzić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

przybory do pisania,

−

Poradnik mechanika,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

32

4.4.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

scharakteryzować naprężenie normalne i styczne?

2)

wyjaśnić pojęcie warunku wytrzymałości?

3)

podać naprężenie występujące przy ścinaniu?

4)

dobrać naprężenie dopuszczalne dla danego materiału?

5)

wyjaśnić, jak należy wygiąć rurę ze szwem?

6)

wyjaśnić różnicę między odkształceniami sprężystymi a plastycznymi?

7)

podać odkształcenia występujące w wałach i w osiach?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

33

4.5.

Ruch obrotowy ciał. Praca, moc, energia i sprawność

4.5.1. Materiał nauczania

Jeżeli wszystkie punkty ciała sztywnego zakreślają okręgi, których wspólny środek leży

w osi obrotu, i droga mierzona po łukach stanowiących tory tych punktów jest stała w czasie,
to ruch taki nazywamy ruchem obrotowym jednostajnym. Gdy ciało porusza się takim
ruchem, jego kąt obrotu w jednostce czasu zachowuje stałą wartość. Stałą wartość ma, zatem
także jego prędkość kątowa w, określana wzorem:

t

α

ω

=

[ s

1 ]

Kąt

α

jest określany w mierze łukowej, tzn. w radianach (liczba bezwymiarowa), dlatego

prędkość jest wyrażana w l/s.

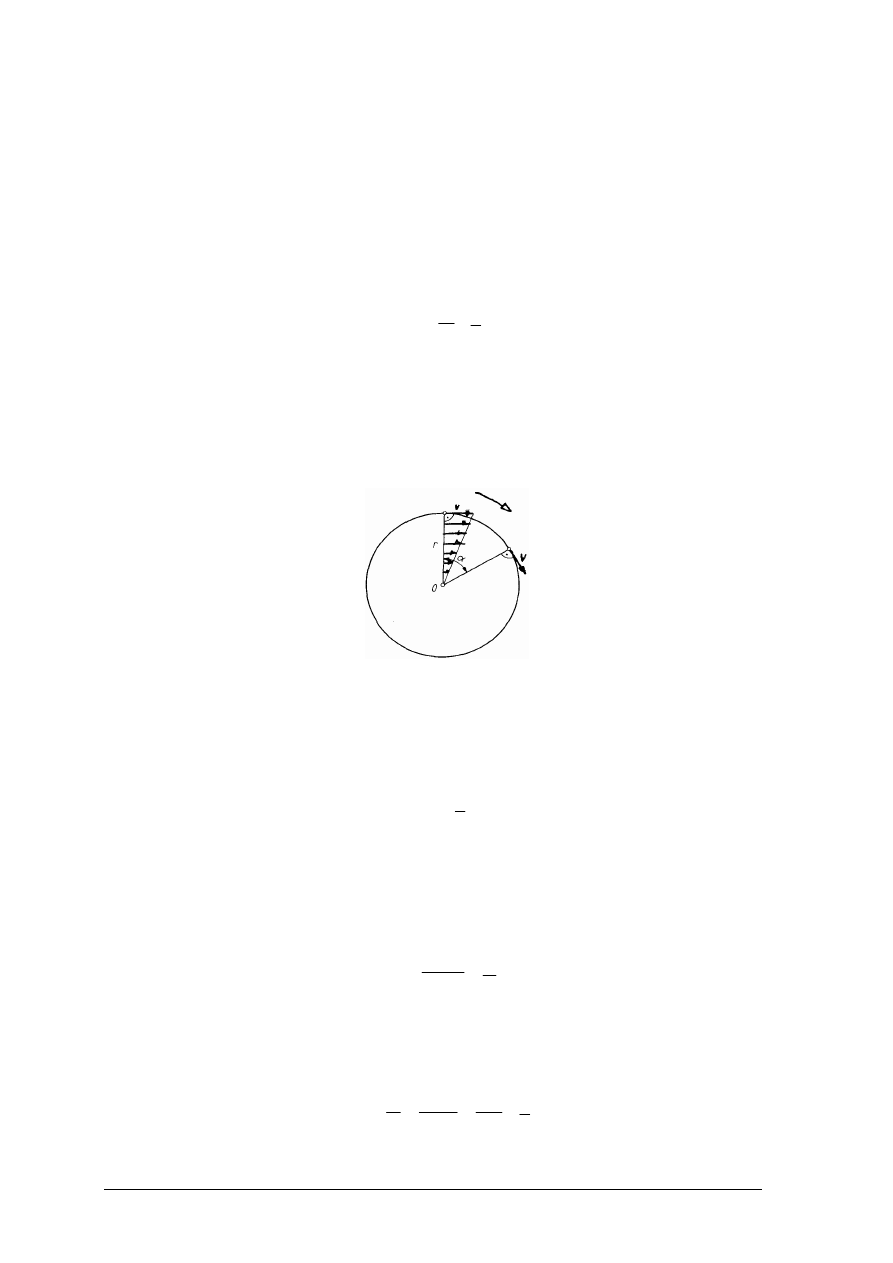
Prędkość obwodowa

υ

punktu leżącego na danym okręgu o promieniu r w ruchu

obrotowym jednostajnym jest również stała. W miarę zbliżania się tych punktów do osi
obrotu prędkość ta proporcjonalnie zmniejsza się, by w punkcie 0 osiągnąć wartość równą
zeru (rys. 26).

Rys. 26. Ruch ciała po okręgu [1, s. 11]

Stąd wniosek, że prędkość obwodowa punktów leżących najdalej od osi obrotu 0 jest

największa, w osi obrotu zaś punkt jest nieruchomy.

Zgodnie z definicją prędkość obwodową wyraża się wzorem, w którym s jest drogą

przebytą przez punkt:

t

s

=

ϑ

Po wykonaniu jednego pełnego obrotu będzie ona obwodem okręgu o promieniu r, czyli:

d

r

s

⋅

=

⋅

⋅

=

π

π

2

Po uwzgl

ę

dnieniu liczby pełnych obrotów n wykonywanych przez jeden punkt

w jednostce czasu, np. w ci

ą

gu minuty (n w obr/min), pr

ę

dko

ść

obwodowa wyniesie:

n

s

⋅

=

υ

Ostatecznie gdy wyrazimy

υ

w m/s, wzór przyjmie posta

ć

:

60

n

d

⋅

⋅

=

π

υ

[ ]

s

m

gdzie:
d = r –

ś

rednica okr

ę

gu w m,

n – pr

ę

dko

ść

obrotowa w obr/min.

Mi

ę

dzy pr

ę

dko

ś

ci

ą

k

ą

tow

ą

ω

wyra

ż

on

ą

w 1/s a pr

ę

dko

ś

ci

ą

obrotow

ą

ν

obr/min zale

ż

no

ść

jest nast

ę

puj

ą

ca:

30

60

2

n

n

t

⋅

=

⋅

⋅

=

=

π

π

α

ω

[

s

1

]

Poniewa

ż

drog

ę

punktu poruszaj

ą

cego si

ę

po luku mo

ż

na wyrazi

ć

wzorem

r

s

⋅

=

α

, zatem

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

34

t

r

t

s

α

υ

⋅

=

=

Skoro

t

α

ω

=

wzór na prędkość obwodową przybierze postać:

ω

υ

⋅

=

r

W technice ruch obrotowy jednostajny występuje bardzo często – np. w obrabiarkach,

silnikach: elektrycznych, spalinowych, parowych. Prędkość obwodową w tych przypadkach
oblicza się według nieco innego wzoru, a mianowicie:

1000

n

d

⋅

⋅

=

π

υ













min

m

gdzie: d – średnica okręgu w mm,

n – prędkość obrotowa w obr/mm.

Praca

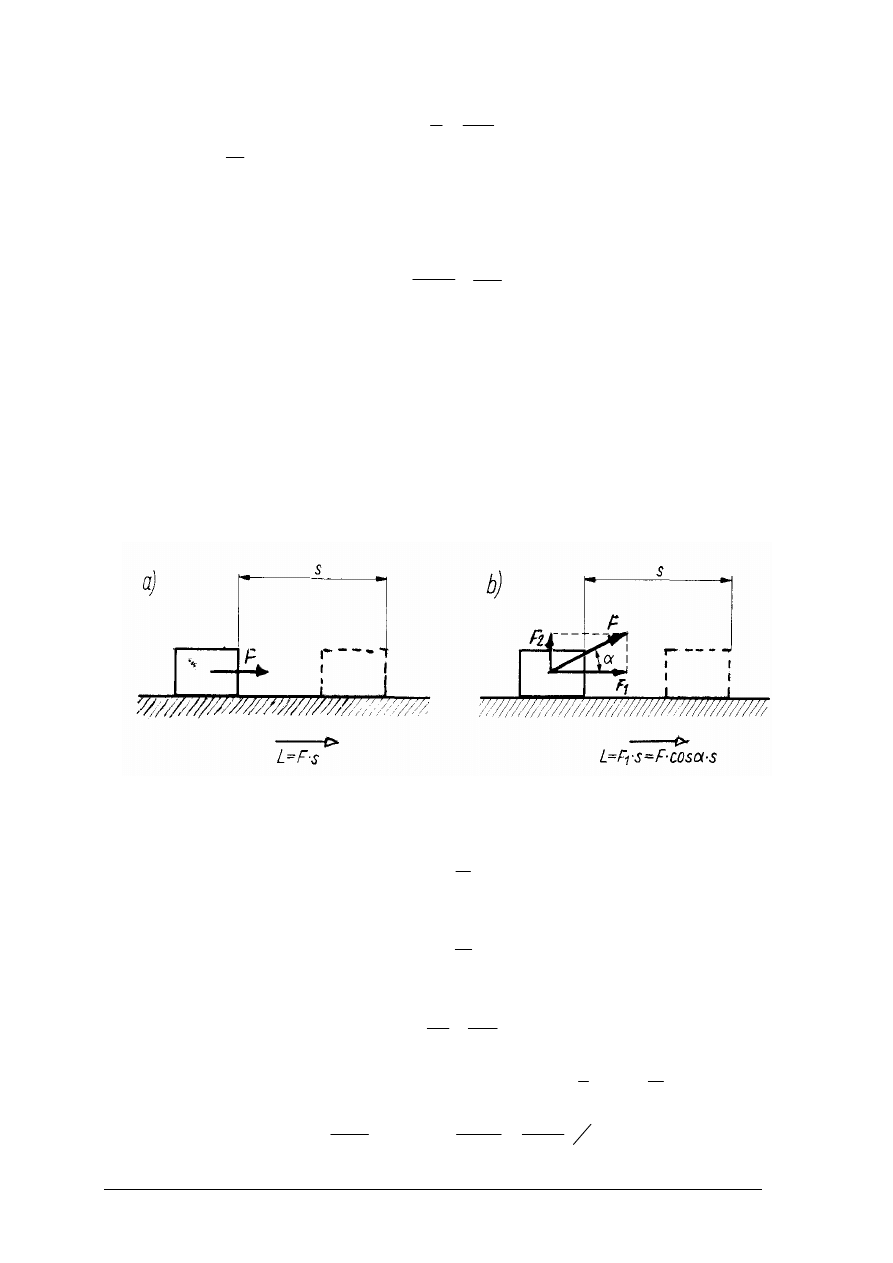
Praca jest iloczynem siły F i drogi przebytej w kierunku działania tej siły.

s

F

L

⋅

=

Jednostką pracy jest dżul (1 J).
1 dżul to praca, jaką siła 1 niutona wykonuje na drodze 1 m. Warunkiem wykonania

pracy jest zgodność kierunku działania siły F lub jej składowej z kierunkiem przesunięcia
(rys. 27).

Rys. 27. Kierunek działania siły i przesunięcia a wykonanie pracy [1, s. 16]

Moc to stosunek pracy L do czasu t, w jakim została ona wykonana:

t

L

P

=

Jednostką mocy jest wat (1 W).
1 wat to moc urządzenia wykonującego pracę 1 dżula w ciągu 1 sekundy:

s

J

W

1

1

1

=

W ruchu obrotowym moc obliczamy według wzoru:

t

s

F

t

M

P

⋅

=

=

Jeżeli moc P będzie wyrażona w kW, siła F w N, a stosunek

t

s =

ϑ

w s

m , to

1000

ϑ

⋅

=

F

P

gdzie

s

m

n

r

n

d

30

60

⋅

⋅

=

⋅

⋅

=

π

π

υ

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

35

stąd:

kW

n

M

n

r

F

P

9554,1

1000

30

⋅

=

⋅

⋅

⋅

⋅

=

π

gdzie: M– moment siły w ruchu obrotowym (M = F · r) [Nm]

n – prędkość obrotowa w obr/min.

Z zależności tej możemy obliczyć moment obrotowy:

m

N

n

P

M

⋅

=

1

,

9554

Nagromadzon

ą

w jakim

ś

ciele prac

ę

nazywamy energi

ą

i dlatego mierzymy j

ą

takimi

samymi jednostkami. Energia wyst

ę

puje w ró

ż

nych postaciach. Rozró

ż

nia si

ę

energi

ę

:

mechaniczn

ą

, elektryczn

ą

, chemiczn

ą

, ciepln

ą

, j

ą

drow

ą

itd.

Energia jest niezniszczalna, zmienia jedynie swoj

ą

posta

ć

, np. z elektrycznej na

mechaniczn

ą

, z cieplnej na elektryczn

ą

. Energia mechaniczna jest sum

ą

nagromadzonej

energii potencjalnej i kinetycznej danego ciała:

E = E

p

+ E

k

Energi

ę

potencjaln

ą

E

p

ma ciało o masie m podniesione na wysoko

ść

h:

h

g

m

p

E

⋅

⋅

=

[J]

gdzie: m – masa ciała w kg,

g – przyspieszenie ziemskie (g=9,81 m/s

2

).

Energi

ę

kinetyczn

ą

E

k

ma ciało o masie m poruszaj

ą

ce si

ę

z pr

ę

dko

ś

ci

ą

υ

:

2

2

υ

⋅

=

m

k

E

[J]

Do wykorzystania energii w celu przetworzenia jej na prac

ę

słu

żą

maszyny robocze, a do

zmiany postaci energii – silniki. Niecała jednak energia dostarczana do urz

ą

dzenia jest

efektywnie wykorzystywana, gdy

ż

ka

ż

da maszyna lub silnik po wprawieniu w ruch musi

pokona

ć

pewne opory, na co jest zu

ż

ywana cz

ęść

energii.

Tak, wi

ę

c aby uzyska

ć

zało

ż

on

ą

warto

ść

energii z okre

ś

lonego urz

ą

dzenia, musimy

dostarczy

ć

jej wi

ę

cej, przewiduj

ą

c straty energii w wyniku ruchu urz

ą

dzenia. W tym celu

posługujemy si

ę

współczynnikiem zwanym sprawno

ś

ci

ą

.

Sprawno

ś

ci

ą

η

(eta) maszyny lub urz

ą

dzenia nazywamy stosunek pracy lub energii

u

ż

ytecznej (L

u

, E

u

) do pracy lub energii wło

ż

onej (L

w

, E

w

):

Sprawno

ść

jest wielko

ś

ci

ą

niemianowan

ą

lub wyra

ż

an

ą

w procentach (gdy warto

ść

współczynnika pomno

ż

ymy przez 100%). Sprawno

ść

jest zawsze mniejsza od 1 lub 100%,

gdy

ż

praca lub energia u

ż

yteczna jest zawsze mniejsz

ą

od wło

ż

onej. Gdyby osi

ą

gn

ę

ła warto

ść

równ

ą

1, powstałaby maszyna idealna, tzw. perpetuum mobile, o której człowiek ci

ą

gle

marzy, lecz nie jest w stanie jej zbudowa

ć

(raz wprowadzona w ruch maszyna taka

pracowałaby niesko

ń

czenie długo bez dostarczania energii).

Je

ż

eli urz

ą

dzenie składa si

ę

z wielu mechanizmów współpracuj

ą

cych ze sob

ą

, mo

ż

na

rozpatrywa

ć

osobno sprawno

ść

ka

ż

dego z nich, a ogólna sprawno

ść

urz

ą

dzania wynosi

wówczas:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

36

4.5.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonywania ćwiczeń.

1.

Co nazywamy pracą mechaniczną?

2.

Jakie są jednostki pracy w układzie SI?

3.

Co to jest moc i jakim wzorem można ją wyrazić?

4.

Co to jest energia kinetyczna i w jakich jednostkach się ją wyraża?

5.

Co to jest energia potencjalna i od czego zależy jej wielkość?

6.

O czym mówi zasada zachowania energii mechanicznej?

4.5.3. Ćwiczenia

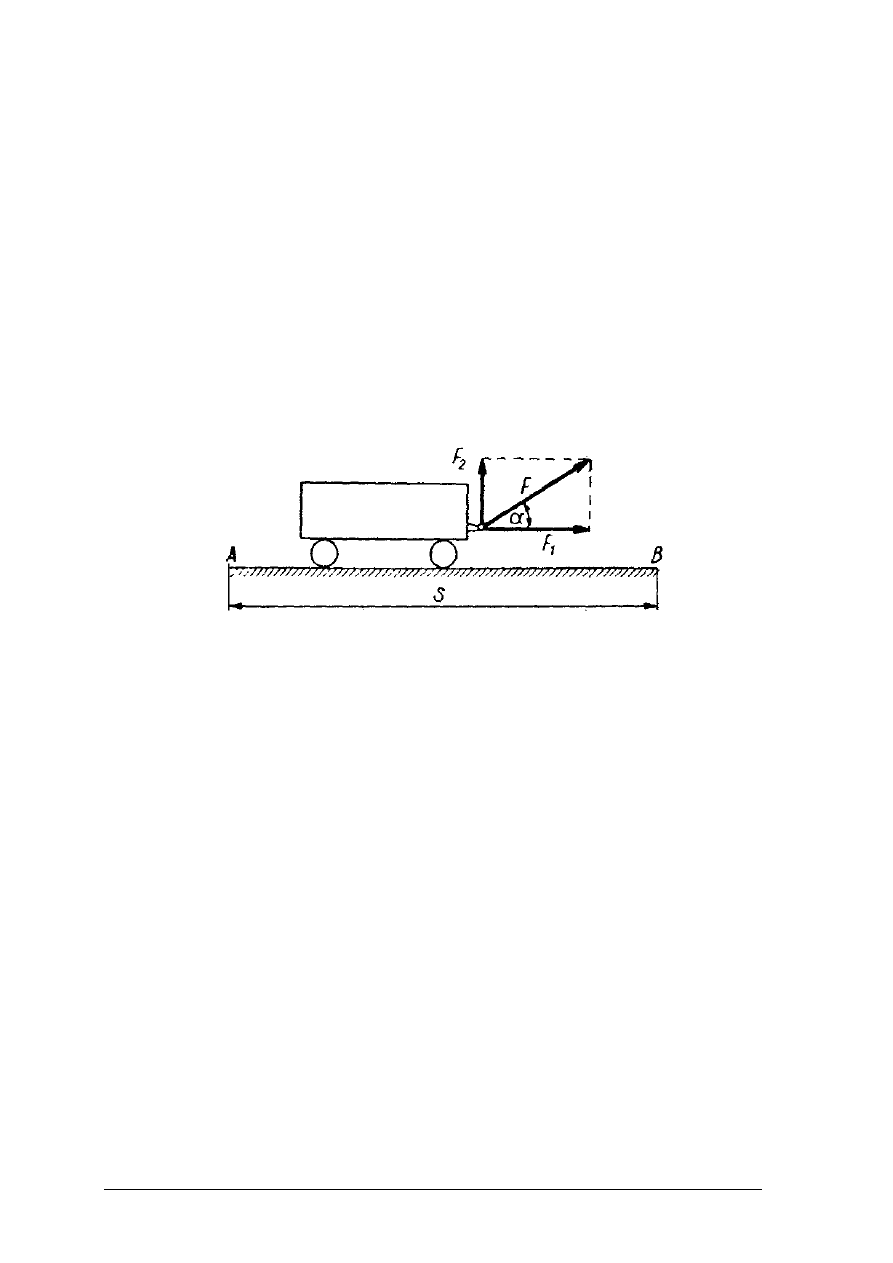
Ćwiczenie 1

Oblicz, jaką pracę wykona ciągnik, aby przetransportować przyczepę po drodze poziomej

na odległość 2 km, jeżeli opór, jaki stawia przyczepa w czasie ruchu, wynosi 20 N.

Rysunek do ćwiczenia 1 [8, s. 223]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

przeanalizować rysunek,

2)

obliczyć pracę,

3)

podać jednostkę pracy w układzie SI,

4)

sprawdzić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

przybory do pisania,

−

kalkulator,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

Ćwiczenie 2

Ciało o ciężarze G = 5 N spadając z pewnej wysokości wykonało pracę L = 30 Nm.

Obliczyć, na jakiej wysokości znajdowało się ciało.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

przeanalizować dane do ćwiczenia,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

37

2)

obliczyć wysokość,

3)

ustalić jednostkę wysokości w układzie SI,

4)

sprawdzić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

przybory do rysowania, pisania i kalkulator,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

Ćwiczenie 3

Oblicz, jakiej mocy silnik powinien być zastosowany do napędu dźwigu, który musi

podnieść ciężar Q = 150 N na wysokość h = 6 m w ciągu czasu t = 30 sek. Sprawność dźwigu
wynosi η = 0,8.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

obliczyć sprawność dźwigu,

3)

obliczyć moc silnika,

4)

sprawdzić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

przybory do pisania,

−

kalkulator,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

4.5.4. Sprawdzian postępów według wzorca

Czy potrafisz:

Tak

Nie

1)

odróżnić silnik od maszyny roboczej?

2)

obliczyć sprawność maszyny składającej się z szeregu mechanizmów?

3)

podać czynniki wpływające na wielkość energii kinetycznej i energii

potencjalnej?

4)

dokonać podziału energii mechanicznej?

5)

obliczyć energię kinetyczną ciała o masie m poruszającego się

z prędkością

υ

?

6)

zinterpretować zasadę zachowania energii mechanicznej?

7)

określić zależność między prędkością obrotową a prędkością kątową?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

38

4.6.

Połączenia kształtowe

4.6.1. Materiał nauczania

Połączenia raz wykonane, które nie mogą być rozłączone bez zniszczenia elementów

łączonych lub łączników, nazywamy nierozłącznymi.

Połączenia, które mogą być wielokrotnie łączone i rozłączane, nazywamy rozłącznymi.
Połączenia kształtowe należą do spoczynkowych połączeń rozłącznych. Zależnie od

rodzaju powierzchni styku lub rodzaju łączników mamy połączenia kształtowe:

−

bezpośrednie: wielowypustowe,

−

pośrednie: wpustowe, kolkowe, sworzniowe, klinowe.

Połączenia wpustowe

Połączenia wpustowe należą do pośrednich połączeń kształtowych i znajdują powszechne

zastosowanie przy przenoszeniu momentu obrotowego między wałem i osadzonym na nim
kołem zębatym, kołem pasowym itp. Odznaczają się prostotą i niezawodnością konstrukcji,
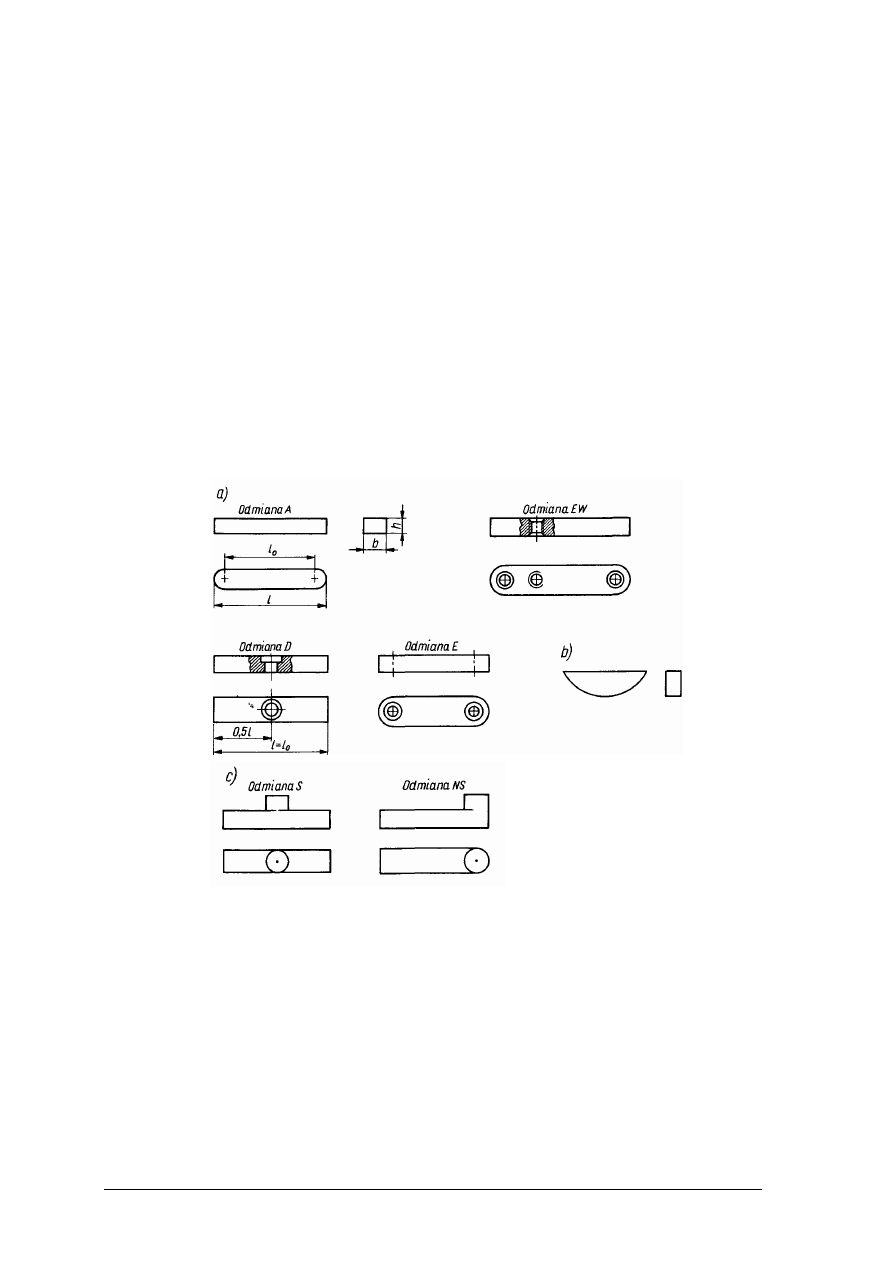
wygodnym montażem i demontażem, niskimi kosztami. Rodzaje wpustów (rys. 28).

Rys. 28. Rodzaje wpustów: a) pryzmatyczne – zaokrąglone pełne (A), ścięte jednootworowe (D), zaokrąglone

dwuotworowe (E), zaokrąglone dwuotworowe wyciskowe (EW); b) czółenkowe; c) czopkowe
symetryczne (S) i niesymetryczne (NS) [8, s. 93]

Podczas pracy połączeń wpustowych występują naciski na boczne powierzchnie

wpustów, dlatego dla uniknięcia niepożądanych luzów osadza się je ciasno, stosując
pasowania N9/h9 lub P9/h9. W połączeniach ruchowych (przesuwnych) należy zapewnić
swobodne przesuwanie kół wzdłuż wału, dlatego pasowania ciasne stosuje się tylko do
osadzania wpustu w czopie wału, natomiast rowek w piaście kola wykonuje się w tolerancji
D10, otrzymując pasowanie luźne D10/h9.

Dla ułatwienia montażu połączeń wpustowych suma wysokości obu rowków powinna

być większa od wysokości wpustu o 0,2÷0,4 mm.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

39

Wał i osadzone na nim elementy powinny być dokładnie osiowane, tzn. powinny mieć

wspólną oś obrotu. Jest to niezbędne dla uniknięcia występowania sił odśrodkowych podczas
ruchu obrotowego, czyli tzw. „bicia”. Ponieważ wpusty nie zapewniają osiowania, należy
stosować dość ciasne pasowanie czopa z otworem w piaście, np. H7/j6 w połączeniach
spoczynkowych i H7/f7 w połączeniach przesuwnych.

Dobór i obliczanie wpustów. Wymiary poprzeczne wpustów pryzmatycznych (b x h) są

dobierane, w zależności od średnicy czopa wału. W przypadkach technicznie uzasadnionych
(np. dla wałów drążonych) dopuszcza się stosowanie wpustów o mniejszych przekrojach niż
podane w tablicy ogólnej. Ponieważ wymiary przekroju wpustów dobiera się według norm
w zależności od średnicy czopa wału, zatem obliczanie wpustów polega tylko na ustaleniu ich
długości. Całkowitą długość wpustu zaokrągla się do wartości podanych w normie; dla
wpustów zaokrąglonych l = l

0

+b, przy czym szerokość piasty kola współpracującego

powinna być co najmniej równa czynnej długości dobranego wpustu.

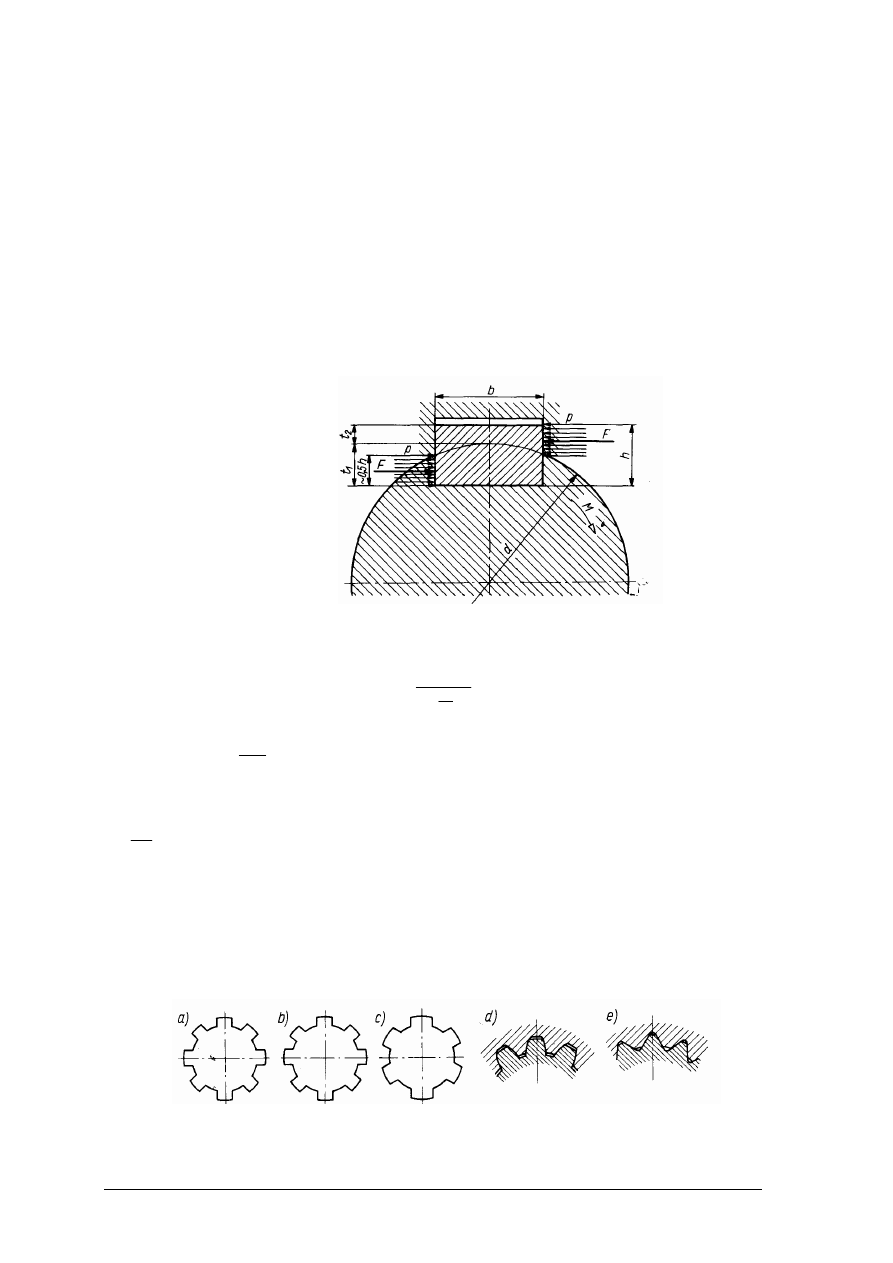
Rys. 29. Obciążenie wpustu [8, s. 95]

Wpusty oblicza się z warunku na naciski powierzchniowe (rys. 29) według wzoru:

0

0

2

k

n

h

l

F

p

≤

⋅

⋅

=

w którym:

F – siła (

d

M

F

2

=

),

0

l

– czynna długość wpustu,

N – liczba wpustów,

2

h

– przybliżona wartość wysokości powierzchni wpustu narażonej na naciski,

k

0

– naciski dopuszczalne.

Połączenia wielowypustowe

Połączenia wielowypustowe należą do najczęściej stosowanych połączeń kształtowych.

Są to połączenia bezpośrednie; na czopie wału są wykonane występy (wypusty),
współpracujące z odpowiednimi rowkami w piaście. Podstawowe rodzaje znormalizowanych
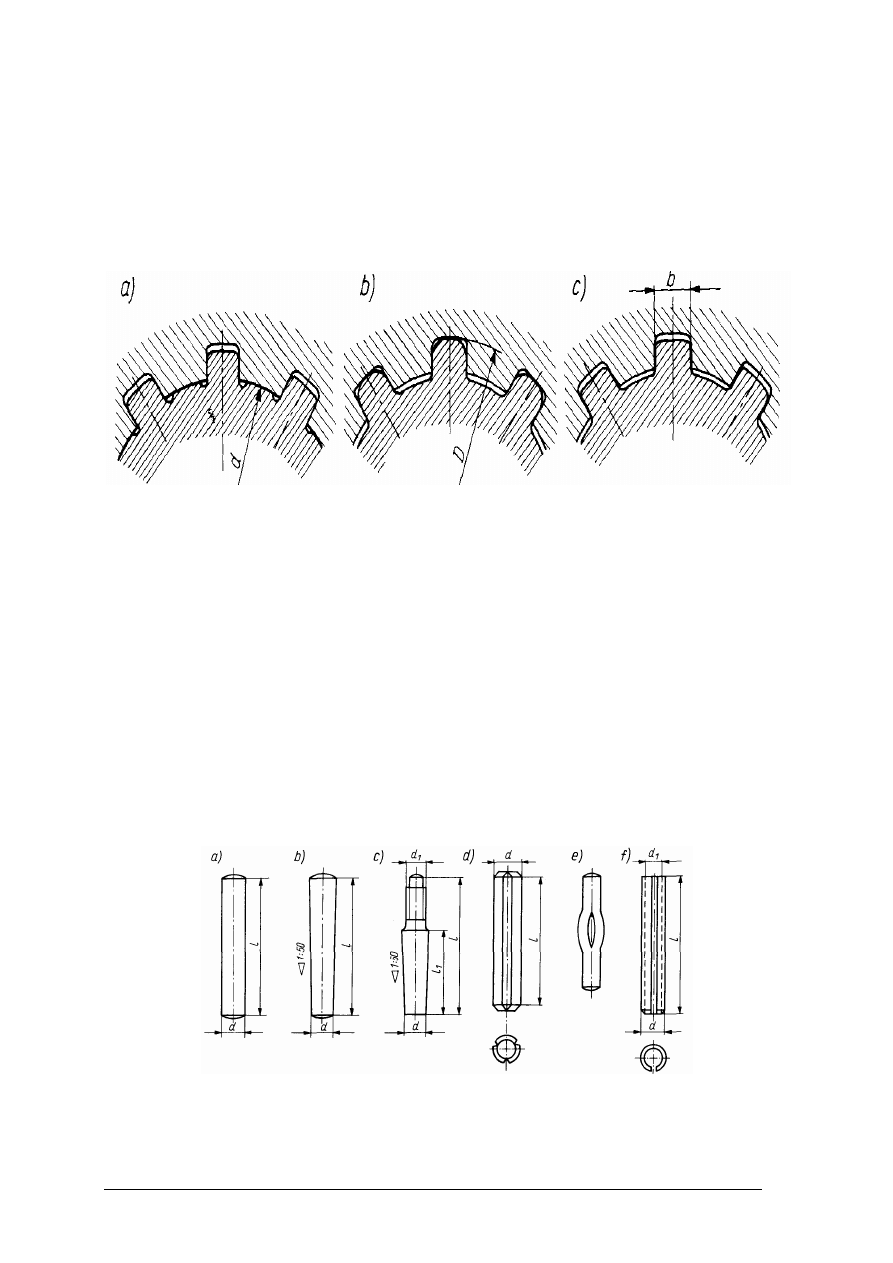
połączeń wielowypustowych o różnych kształtach wypustów podano na (rys. 30).

Rys. 30. Połączenia wielowypustowe: ogólnego przeznaczenia: a) lekkie, b) średnie; c) do obrabiarek,

d) zębate ewolwentowe, e) wielokarbowe [8, s. 98]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

40

Połączenia wielowypustowe umożliwiają uzyskanie dokładnego osiowania, zmniejszenie

nacisków jednostkowych (lub stosowanie większych obciążeń) w porównaniu z połączeniami
wpustowymi oraz zmniejszenie oporów tarcia przy przesuwaniu elementów w połączeniach
ruchowych. W połączeniach wielowypustowych równoległych występują 3 rodzaje osiowań
na wewnętrznej średnicy d, na zewnętrznej średnicy D oraz na bokach wypustów b. Wybór
rodzaju osiowania jest uzależniony od warunków pracy, twardości powierzchni styku oraz od
wymaganej dokładności połączenia (rys. 31).

Rys. 31. Rodzaje osiowań w połączeniach wielowypustowych: a) na wewnętrznej średnicy czopa d,

b) na zewnętrznej średnicy wypustów D, c) na bocznych powierzchniach wypustów [8, s. 98]

Osiowanie na wewnętrznej średnicy d jest stosowane w połączeniach dokładnych, przy

wypustach utwardzonych – głównie w produkcji małoseryjnej.

Osiowanie na zewnętrznej średnicy D stosuje się w połączeniach spoczynkowych

i średnio dokładnych połączeniach ruchowych, przy wypustach miękkich (nie utwardzonych).

Najmniej dokładne jest osiowanie na bokach wypustów. Stosuje się je w celu

zmniejszenia do minimum luzu obwodowego.

Dobór pasowań uzależnia się od charakteru połączenia i rodzaju osiowania. Zalety te

powodują, że połączenia wielowypustowe znajdują bardzo szerokie zastosowanie w wielu
gałęziach przemysłu.

Połączenia kołkowe i sworzniowe

Połączenia kołkowe. Kołki są to elementy w kształcie walca lub stożka o dość dużej

długości w stosunku do ich średnicy; najczęściej

d

l

d

20

2

≤

≤

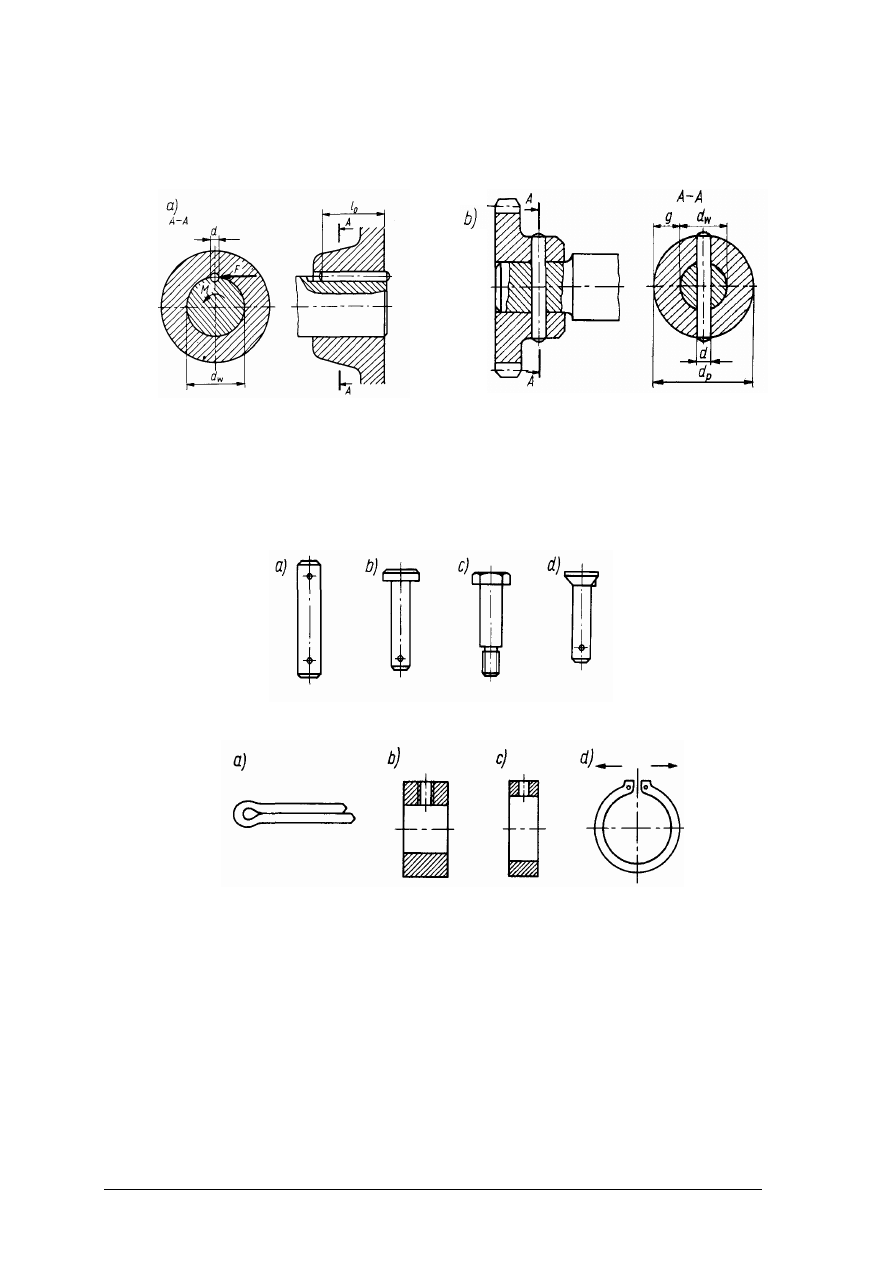
(rys. 32).

Rys. 32. Rodzaje kołków: a) walcowy, b) stożkowy, c) stożkowy z czopem gwintowanym,

d, e) karbowy, f) rozcięty [8, s. 101]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

41

Zadaniem kołka jest łączenie elementów maszyn lub ustalenie ich wzajemnego

położenia.
W zależności od kierunku działania sił na kołek połączenie kołkowe dzieli się na połączenie
wzdłużne i połączenie poprzeczne (rys. 33).

Rys. 33. Połączenia kołkowe: a) wzdłużne, b) poprzeczne [1, s. 67]

Odmianą kołka są sworznie (rys. 34) mające kształt walca o średnicy większej niż kołki

walcowe. Połączenia sworzniowe przenoszą większe obciążenia niż połączenia kołkowe oraz
zawsze są zabezpieczone przed przesuwaniem się wzdłuż ich osi za pomocą podkładek,
zawleczek, pierścieni lub kołków (rys. 35).

Rys. 34. Rodzaje sworzni: a) bez łba, b) z dużym łbem, c) z czopem gwintowanym, d) noskowy [8, s. 103]

Rys. 35. Zabezpieczenia sworzni: a) zawleczka; b) pierścień osadczy ciężki, c) kołkowy lub

zawleczkowy, d) sprężynujący [6, s. 103]

Połączenia sworzniowe są stosowane przede wszystkim w połączeniach ruchowych.

Zależnie od przewidywanych warunków pracy i wymagań konstrukcyjnych, sworznie mogą
być pasowane ciasno w obu częściach łączonych i obliczane są z warunku na ścinanie lub też
luźno i wtedy obliczane są na zginanie.

Połączenia klinowe

Połączenia klinowe są zaliczane do połączeń rozłącznych spoczynkowych. Klin jest

elementem, którego powierzchnie robocze (płaskie lub walcowe) są zbieżne względem siebie,
tworząc niewielki kąt rozwarcia

α

. W zależności od kształtu rozróżnia się kliny dwustronne

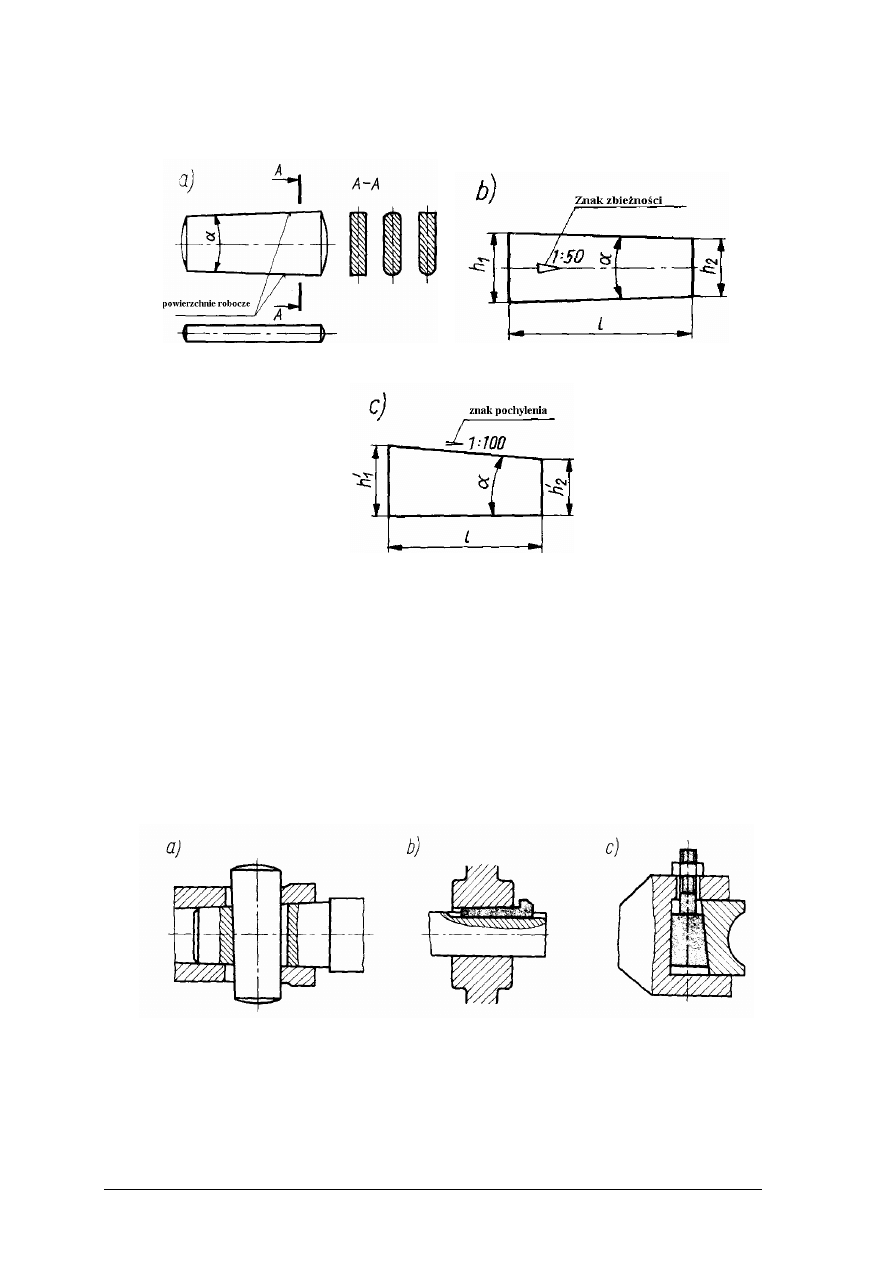
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

42

i jednostronne (rys. 36). Kliny jednostronne często są zakończone tzw. noskiem w celu
ułatwienia demontażu połączenia.

Rys. 36. a) klin, b) klin dwustronny symetryczny, c) klin jednostronny [1, s. 65]

Rozróżnia się:

−

połączenia klinowe poprzeczne (rys. 37a), w których oś kima jest prostopadła do osi
łączonych elementów; połączenia takie są stosowane do łączenia wałów i tulei przy
wstępnym napięciu łączonych elementów,

−

połączenia klinowe wzdłużne (rys. 37b), o osi kima usytuowanej równolegle względem
osi łączonych elementów; połączenia takie są stosowane – podobnie jak wpusty – do
łączenia wałów z piastami kół pasowych, zębatych itp.
Stosuje się także połączenia klinowe nastawne (rys. 37c), umożliwiające regulację

wzajemnego położenia kojarzonych elementów oraz utrzymanie stałego napięcia
w połączeniu mimo zużywania się tych elementów.

Rys. 37. Połączenia klinowe: a) poprzeczne, b) wzdłużne, c) nastawne [1,s.66]

Połączenia gwintowe – powszechnie stosowane w budowie maszyn – należą do połączeń

rozłącznych. Powstają przez skojarzenie części zewnętrznej (nakrętki) z częścią wewnętrzną
(śrubą), które współpracują ze sobą powierzchniami śrubowymi. Gwint powstaje przez
nacięcie bruzd (rowków) o określonym kształcie wzdłuż linii śrubowej.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

43

Linię śrubową otrzymuje się przez nawinięcie na walcu o średnicy D trójkąta

prostokątnego o podstawie

π

d i wysokości P.

Do gwintów powszechnie stosowanych należą gwinty trójkątne: metryczne i rurowe

walcowe oraz trapezowe: symetryczne i niesymetryczne. Ponadto gwinty dzieli się na:

−

zwykłe, drobne (drobnozwojne) i grube (grubozwojne),

−

jednokrotne (pojedyncze) wielokrotne (dwukrotne, trzykrotne itd.),

−

prawe i lewe.
Łączniki gwintowe mogą być znormalizowane lub wykonane jako specjalne. Dzieli się je

na: śruby, wkręty i nakrętki.

Ś

ruby mają odpowiednio ukształtowany łeb pasujący do klucza maszynowego. Wymiary

łbów są uzależnione od wielkości gwintów.

Wkręty różnią się od śrub tym, że mają łby z naciętym rowkiem, służącym do

przykręcania ich wkrętakiem.

Na skutek wstrząsów i drgań, przenoszonych przez niektóre łączniki gwintowe, istnieje

możliwość ich luzowania. W celu wyeliminowania tego zjawiska łączniki powinny być
ustalane za pomocą podkładek sprężystych, zawleczek itp. Łączniki gwintowe można także
zabezpieczyć przed odkręceniem przez punktowanie trzpienia śruby lub wkręta za pomocą
punktaka. Dotyczy to zwłaszcza połączeń ruchowych.

Połączenia nitowe są zaliczane do połączeń spoczynkowych. Połączenie blach lub

kształtowników za pomocą nitów polega na skojarzeniu otworów wykonanych
w wymienionych elementach o średnicy nieco większej niż średnica trzonu nitu. Po włożeniu
nitów w otwory następuje ich zamykanie (ręcznie lub maszynowo), dzięki któremu uzyskuje
się odpowiednie ukształtowanie zakuwki.

Na nity stosuje się na ogół materiał tego samego rodzaju jak łączone części, np. części

stalowe łączy się nitami stalowymi, a w przypadku łączenia różnych materiałów – taki jak
materiał o większej odkształcalności. Średnicę d nitu dobiera się w zależności od grubości
blachy, najczęściej przyjmuje się

g

d

2

≈

; gdzie: g – grubo

ść

blachy;

Długo

ść

nitu ustalamy ze wzoru:

l = s + l

0

gdzie: s– ł

ą

czna grubo

ść

ł

ą

czonych elementów,

0

l

– naddatek na sp

ę

cznienie nitu w otworze oraz na wykonanie zakuwki.

Orientacyjnie przyj

ąć

mo

ż

na:

d

l

)

8

,

1

3

,

1

(

0

÷

=

Nitowanie odbywa si

ę

na zimno lub na gor

ą

co. Na zimno zakuwa si

ę

łby z metali

nie

ż

elaznych oraz stalowe o

ś

rednicy do 9 mm.

Ś

rednica otworu pod takie nity jest wi

ę

ksza

od

ś

rednicy trzonu nitu od 0,2 do 0,5 mm. Nity o

ś

rednicy trzonu d

n

>9 mm zamyka si

ę

na

gor

ą

co.

Ś

rednica otworu nitowego jest wi

ę

ksza od

ś

rednicy trzonu d

n

o 1 mm, dla ułatwienia

wło

ż

enia we

ń

rozgrzanego nitu.

Rozró

ż

nia si

ę

:

−

nity normalne z łbami: kulistym, płaskim, soczewkowym, grzybkowym i trapezowym,

−

nity specjalne.
Poł

ą

czenia nitowe dzieli si

ę

na:

−

mocne,

−

mocno – szczelne,

−

szczelne,

−

specjalne.
Poł

ą

czenia nitowe zapewniaj

ą

du

żą

elastyczno

ść

konstrukcji stalowych – dlatego stosuje

si

ę

je cz

ę

sto w elementach budowlanych, mostach, samolotach i odpowiedzialnych w

ę

złach

konstrukcyjnych statków.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

44

Wytrzymałość połączeń nitowych oblicza się sprawdzając naprężenia ścinające trzon,

według wzoru:

gdzie:
n – liczba nitów,

4

2

d

S

⋅

=

π

– przekrój poprzeczny nitu,

m – liczba ścinanych przekrojów w jednym nicie.

4.6.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Do jakiego rodzaju połączeń zaliczamy połączenia wielowypustowe?

2.

Jak dobiera się wpust?

3.

Jakie są rodzaje wielowypustów?

4.

Jaka jest różnica między sworzniem a kołkiem?

5.

Jakie rodzaj osiowań stosowany jest w połączeniach dokładnych?

6.

Kiedy stosuje się wpusty pryzmatyczne zaokrąglone?

4.6.3. Ćwiczenia

Ćwiczenie 1

Połączenie wpustowe ma przenieść moment obrotowy M = 500 Nm. Średnica wału

wykonanego ze stali 35 wynosi 45 mm. Przyjmując połączenie spoczynkowe i warunki pracy
ś

rednie oraz materiał oprawy stal St7 i wpustu pryzmatycznego St6, dobierz wymiary wpustu.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

sprawdzić wytrzymałość wpustu z warunku wytrzymałościowego,

3)

dobrać wpust,

4)

sprawdzić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

normy,

−

Poradnik mechanika,

−

foliogram,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

t

m

S

n

F

k

≤

=

⋅

⋅

τ

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

45

Ćwiczenie 2

Przedstaw, wszystkie znane, sposoby zabezpieczania sworzni przed przesunięciem

wzdłużnym. Uzasadnij ich zastosowanie.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

zapoznać się z normą dotyczącą sworzni,

3)

przedstawić sposoby zabezpieczeń sworzni,

4)

sprawdzić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

normy,

−

Poradnik mechanika,

−

sworzeń,

−

zabezpieczenia: podkładki, zawleczki, pierścienie,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

Ćwiczenie 3

W tablicy rysunkowej podaje się oznaczenia: śrub i wkrętów. Rozpoznaj oznaczenia

i objaśnij na przykładach:

Przykład oznaczeń:

−

ś

ruba

Ms

M

70

25

,

1

12

×

×

,

−

wkręt

25

6

×

M

.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zgromadzić normy dotyczące łączników gwintowych,

2)

zapoznać się oznaczeniami,

3)

podać z czego się składa oznaczenie i co oznacza,

4)

sprawdzić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

foliogramy,

−

normy,

−

Poradnik mechanika,

−

zeszyt,

−

przybory do pisania,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

46

4.6.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

dobrać wymiary wpustu b x h?

2)

scharakteryzować połączenie wielowypustowe?

3)

określić na jakie odkształcenie narażony jest sworzeń pasowany
ciasno?

4)

dobrać odpowiednie zabezpieczenie sworzni?

5)

wskazać różnicę między kołkiem a sworzniem?

6)

scharakteryzować połączenia klinowe?

7)

wskazać różnicę między połączeniem wpustowym
a wielowypustowym?

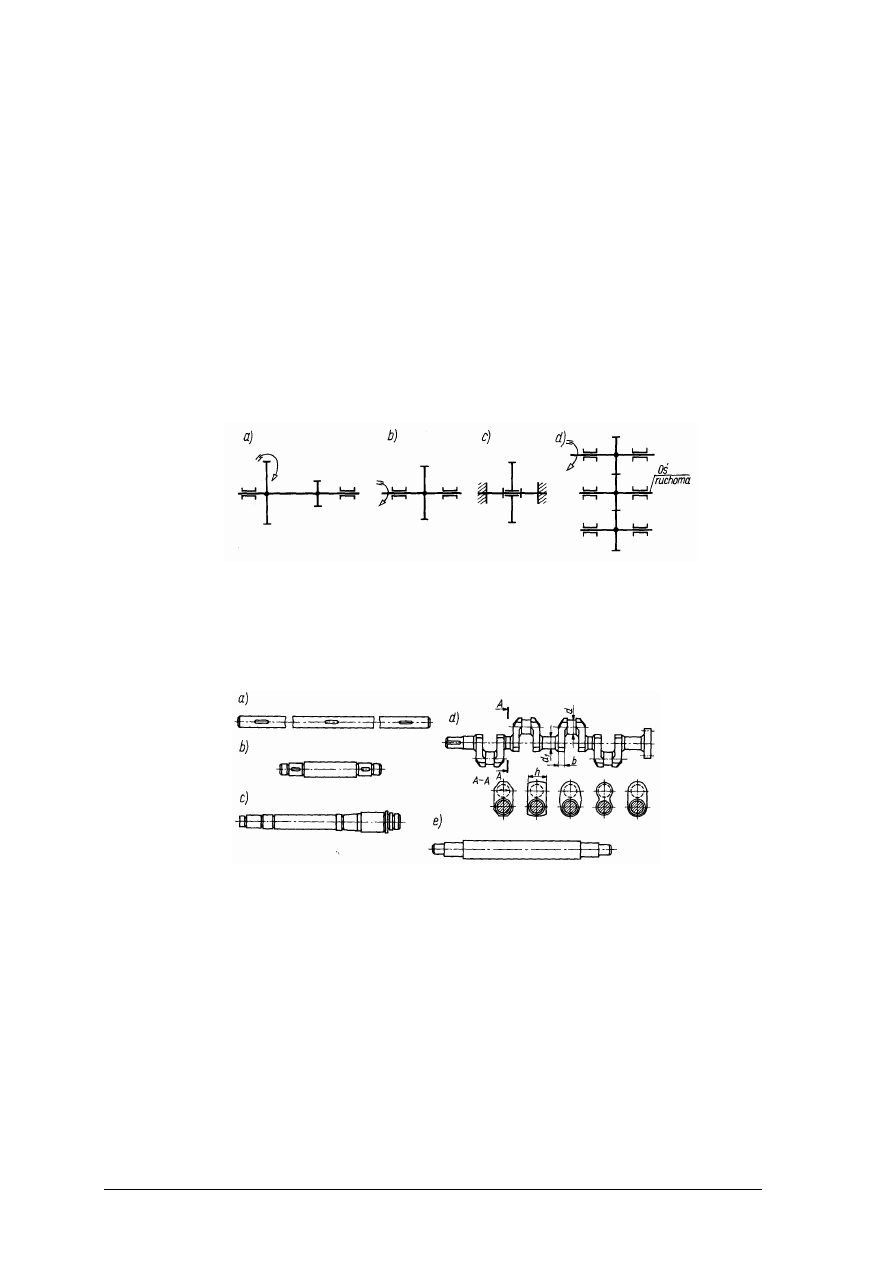
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

47

4.7.

Osie i wały

4.7.1. Materiał nauczania

Osią lub wałem nazywa się element maszyny podparty w łożyskach i podtrzymujący

osadzone na nim części maszyn, które wykonują ruchy obrotowe (np. koła zębate, pasowe)
lub wahadłowe (np. koło zębate współpracujące z zębatką). Głównym zadaniem walu jest
przenoszenie momentu obrotowego, zatem wał wykonuje zawsze ruch obrotowy. W związku
z tym wał jest narażony jednocześnie na skręcanie oraz – pod wpływem sił poprzecznych – na
zginanie (rys. 38a, b). W niektórych przypadkach wał może być narażony tylko na skręcanie.

Oś nie przenosi momentu obrotowego i jest narażona tylko na zginanie. Oś może być

nieruchoma (rys. 38c), utwierdzona w miejscach podparcia, lub ruchoma(wykonująca ruch
obrotowy), osadzona w łożyskach (rys. 38d). Oś nieruchomą mocuje się w podporach za
pomocą połączeń wpustowych, gwintowych itp.

Rys. 38. Schematy: a, b) wału, c) osi nieruchomej, d) osi ruchomej [8, s. 190]

Osie i wały sztywne są to pręty o przekroju okrągłym albo (znacznie rzadziej)

sześciokątnym lub innym. Rozróżnia się osie i wały (rys. 39.) gładkie o prawie niezmiennym
przekroju na całej długości oraz kształtowe o zmiennych przekrojach, dostosowanych do
obciążenia i funkcji osi lub wału.

Rys. 39. Rodzaje wałów i osi: a) wał gładki pędniany, b, c) wały schodkowe, d) wał wykorbiony,

e) oś nieruchoma [8, s. 191]

Obciążenia osi i wałów

Podstawą obliczania wytrzymałości osi lub wału jest wyznaczenie wszystkich sił

i momentów działających na wał (oś). Rozróżnia się obciążenia:

−

zmienne co do wartości i kierunku, wywołujące naprężenia zmienne,

−

stałe (statyczne), wywołujące w osiach nieruchomych naprężenia stałe, a w osiach
ruchomych i wałach – naprężenia zmienne,

−

zmieniające swoje położenie (w płaszczyźnie prostopadłej do osi wału) wraz z obrotem
wału – np. siły odśrodkowe, które wywołują naprężenia stałe.

Osie nieruchome oblicza się na wytrzymałość statyczną, a osie ruchome i wały – na

wytrzymałość zmęczeniową tzn. dokonanie (drogą obliczeń) takiego wyboru kształtu,

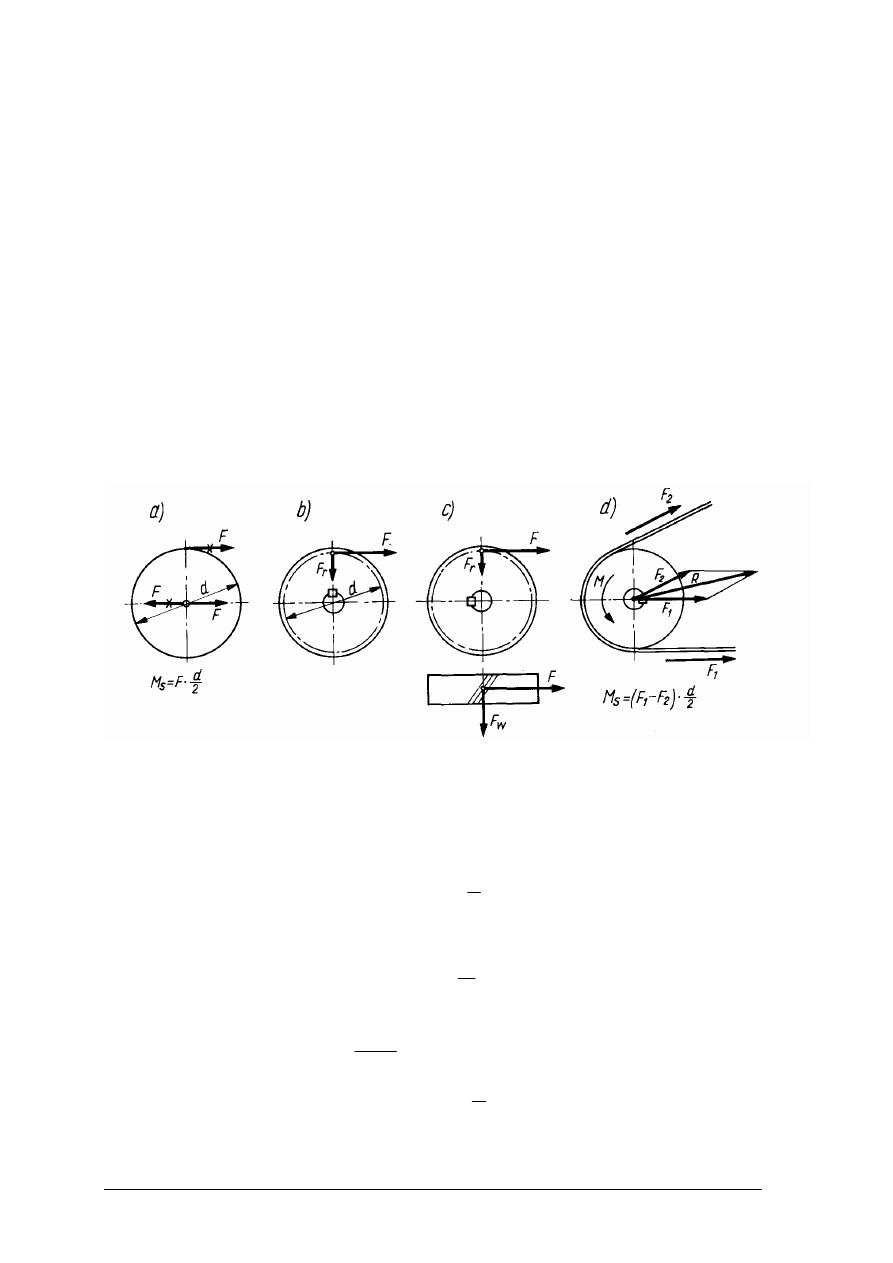
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

48

wymiarów i rodzaju materiału części, aby mogła ona — z uwzględnieniem odpowiedniego
współczynnika bezpieczeństwa — pracować bez obawy uszkodzenia w określonych
warunkach obciążeniowych.

Projektowanie osi i wałów obejmuje:

−

obliczenia wstępne, umożliwiające ustalenie kształtu i przybliżonych wymiarów osi lub
wału. Obliczenia te wykonuje się w zasadzie na wytrzymałość statyczną, uwzględniając
jednak wpływ zmienności obciążeń przez przyjęcie odpowiednich naprężeń
dopuszczalnych (np. kgj, kgo),

−

obliczenia

dokładne

(sprawdzające),

uwzględniające

czynniki

decydujące

o wytrzymałości zmęczeniowej (m.in. działanie karbów) oraz sztywność giętną i skrętną
wału.

Ruch obrotowy wału (osi ruchomej) jest wywołany siłami działającymi na obwodzie

elementu napędzającego osadzonego na wale (koła zębatego, pasowego itp.) i jest
przekazywany np. na inne wały za pośrednictwem kół napędzanych. Dla ustalenia wpływu
działania siły obwodowej F na wał, w jego osi zaczepia się tzw. układ zerowy sił, tj. dwie siły
F, których suma jest równa zeru (rys. 40a). Z otrzymanego układu sił wynika, że wał jest
obciążony momentem skręcającym (równym momentowi obrotowemu) oraz siłą F,
wywołującą zginanie wału.

Rys. 40. Przykłady obciążenia wałów i osi [8, s. 193]

Na (rys. 40b, c, d) podano przykłady obciążenia wałów i osi. Przy wstępnym obliczaniu

wałów uwzględnia się tylko wartość siły obwodowej F (pomijając wpływ pozostałych
obciążeń), wyznaczaną z wzoru na moment obrotowy:

2

d

F

M

⋅

=

Warto

ść

momentu obrotowego oblicza si

ę

z zale

ż

no

ś

ci:

ω

P

M

=

(gdy P – moc w [W],

ω

– w [rad/s], to moment M jest wyra

ż

ony w [N m]).

Podstawiaj

ą

c P w [kW] oraz

60

2

n

⋅

=

π

ω

, otrzymuje si

ę

:

n

P

P

9550

≈

gdzie: M – w [Nm], n – w [obr/min].

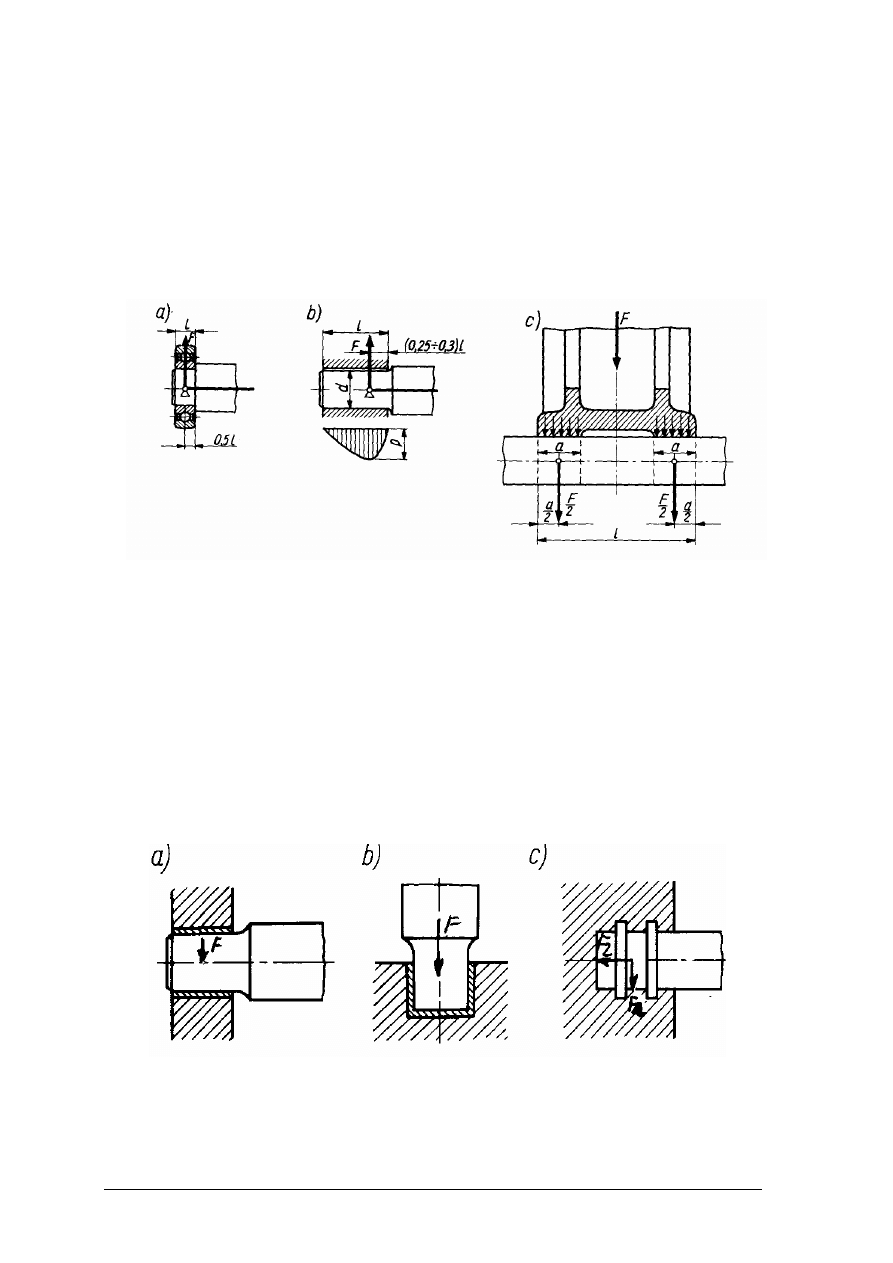
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

49

W obliczeniach osi i wałów z reguły pomija się ciężar wału (osi) i osadzonych na nim

części.

Zarówno siły zewnętrzne, jak i reakcje w łożyskach obciążają wały (osie) w różny

sposób, zależnie od kształtu piasty kola i rodzaju łożyska. Przykłady wyznaczania punktu
zaczepienia reakcji oraz wyznaczanie punktów zaczepienia obciążenia, przenoszonego na wał
przez części na nim osadzone, podano na (rys. 41). Przy wstępnych obliczeniach wału
wymiary czopów i osadzonych na nich elementów nie są znane. Przyjmuje się wówczas, że
obciążenie czopów stanowią siły skupione, zaczepione w środku długości piasty koła lub
w środku długości łożyska.

Rys. 41. Wyznaczanie reakcji w czopach wałów w przypadku: a) łożyska tocznego, b) łożyska

ś

lizgowego, c) kół pasowych [8, s. 194]

Czopami nazywa się odcinki osi lub wału, których powierzchnie stykają się ze

współpracującymi elementarni: łożyskami, kołami zębatymi itd. Rozróżnia się czopy ruchowe
i czopy spoczynkowe. Czopy ruchowe współpracują z panewkami łożysk ślizgowych,
z kołami przesuwnymi lub obracającymi się względem nieruchomej osi itp., natomiast czopy
spoczynkowe współpracują z elementami osadzonymi na stałe względem wału i obracającymi
się wraz z nim. Kształty czopów (rys. 41) ustała się w zależności od wartości i kierunku
reakcji w podporach oraz od wymagań konstrukcyjno-technologicznych.

Ś

rednice czopów są znormalizowane. Doboru ich można dokonać na podstawie normy

lub poradników, w których są podane wzory do obliczeń wytrzymałościowych. Z uwagi na
trudne warunki pracy czopów muszą być one dokładnie wykonane –niekiedy jest wymagane
utwardzenie materiału czopa.

Rys. 42. Rodzaje czopów: a) poprzeczny, b) wzdłużny, c) poprzeczno-wzdłużny [1, s. 75]

Dobór materiałów zależy od przeznaczenia wałów oraz ich wymaganej sztywności

i wytrzymałości. Własności wybranego materiału decydują o wymiarach wału i pośrednio:
łożysk, części osadzonych na wale, wielkości urządzenia, a także o jego sprawności.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

50

4.7.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Jaka jest różnica między osią a wałem?

2.

Z jakimi częściami maszyn współpracują czopy ruchome?

3.

Na jakiej podstawie dobiera się czopy?

4.

Jak jest różnica w obliczaniu osi ruchomych i wałów a osi nieruchomych?

5.

Czy w obliczeniach osi i wałów uwzględnia się ich ciężar i ciężar części osadzonych na
nich?

6.

Kiedy stosujemy wały drążone?

4.7.3. Ćwiczenia

Ćwiczenie 1

Na rysunku wciągarki numerem 1 oznaczono wał czy oś? Rozpoznaj i opisz dany

element.

Rysunek do ćwiczenia 1 [1, s. 124]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

zanalizować działanie wciągarki,

3)

rozpoznać i opisać część,

4)

ocenić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

Poradnik mechanika,

−

foliogramy,

−

zeszyt, przybory do pisania,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

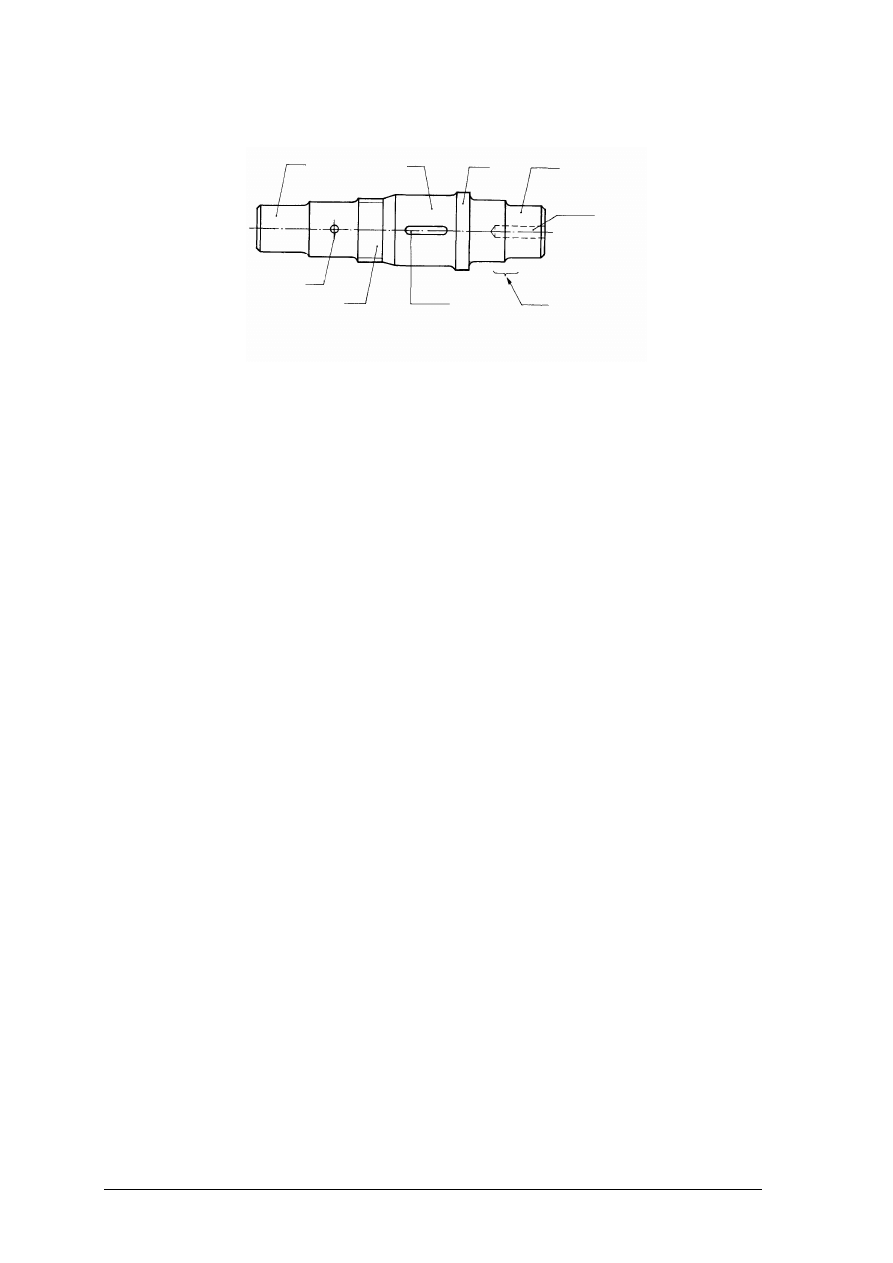
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

51

Ćwiczenie 2

Rysunek przedstawia wał. Odczytaj, zdefiniuj i opisz części wału wskazane na rysunku.

Rysunek do ćwiczenia 2 [1, s. 82]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

przeanalizować rysunek,

3)

rozpoznać i opisać części wału,

4)

wpisać nazwy części w odpowiednie miejsce,

5)

zaprezentować wykonane ćwiczenie.

Wyposażenie stanowiska pracy:

−

Poradnik mechanika,

−

zeszyty,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

4.7.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

scharakteryzować czopy?

2)

odróżnić wał od osi?

3)

omówić kryteria doboru czopu?

4)

scharakteryzować materiały na wały i osie?

5)

uzasadnić kiedy zastosujemy wał drążony?

6)

określić zadania wału i osi?

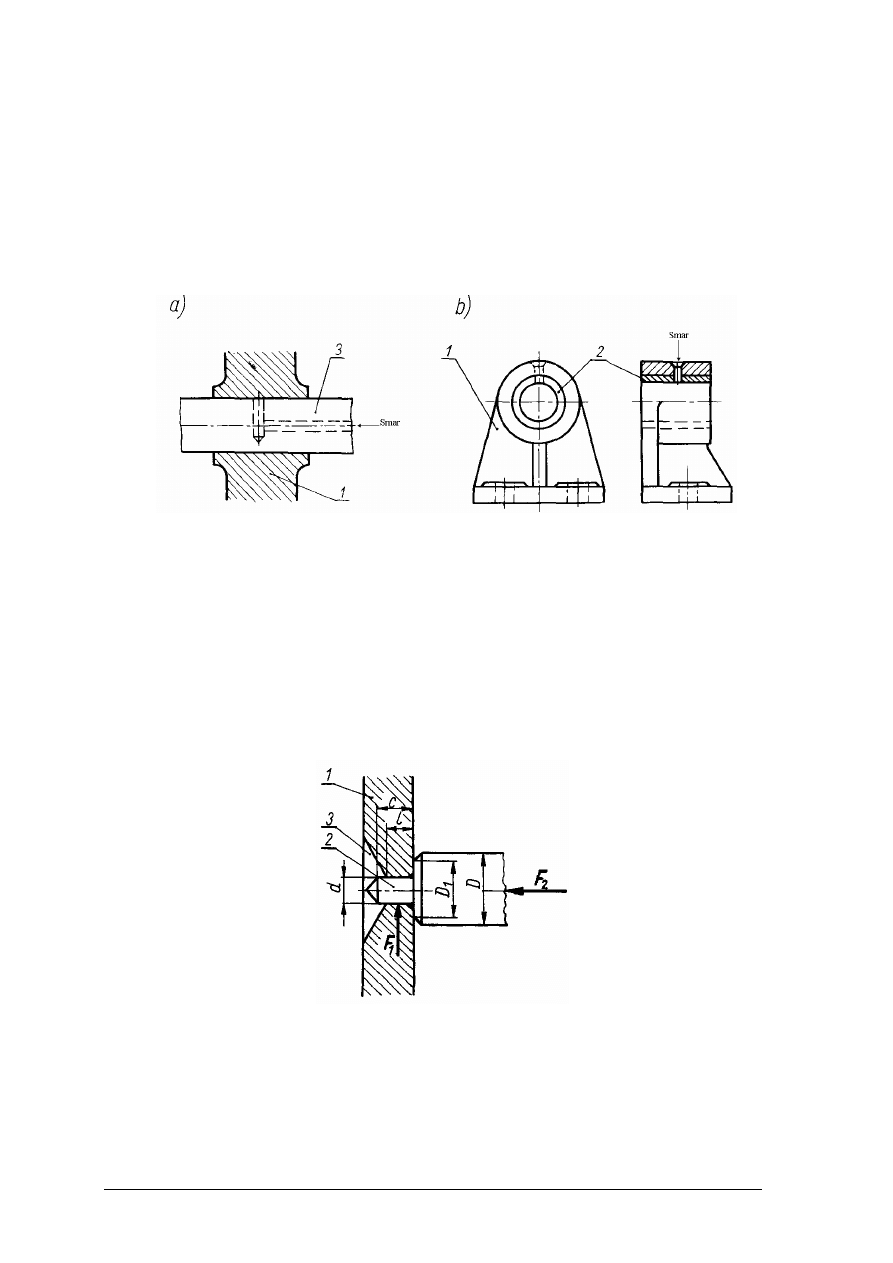
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

52

4.8.

Łożyska ślizgowe i toczne

4.8.1. Materiał nauczania

Zadania ułożyskowania to zapewnienie ruchu obrotowego współpracujących elementów,

przy możliwie małych oporach ruchu, oraz przeniesienie sił obciążających te elementy.

W zależności od rodzaju występującego w nich tarcia łożyska dzielimy na: ślizgowe

(tarcie ślizgowe), toczne (tarcie toczne), sprężyste (tarcie wewnętrzne).

Rys. 43. Łożyska ślizgowe poprzeczne niedzielone: a) bezpośrednio wykonane w korpusie maszyny,

b) z tuleją (panwią), 1 – korpus, 2 – tuleja, 3 – czop walu [2, s. 76]

Łożysko ślizgowe (rys. 43) tworzy zwykle tulejka wciśnięta w korpus maszyny.

Łożyskiem może być także otwór wykonany bezpośrednio w korpusie, jednak rozwiązanie
takie jest stosowane rzadko. Tuleje zwane też panwiami, mogą być jednolite lub dzielone:
łożyska ślizgowe niedzielone i dzielone. Smarowanie łożyska wywiera korzystny wpływ na
warunki jego pracy.

Znacznie korzystniejsze są warunki pracy ułożyskowania, gdy wałek jest podparty nie

w jednym, lecz w dwóch punktach. Przykładem może być osadzenie wałka w dwóch
łożyskach walcowych typu zegarowego (rys. 44).

Rys. 44. Łożysko walcowe typu zegarowego [4, s. 70]: 1 – płyta łożyskowa, 2 – czop, 3 – zagłębienie smarowe

Gdy szkielet mechanizmu jest wykonany z materiału nie nadającego się na panewkę lub

gdy obciążenia są duże, niecelowe jest wykonanie otworów łożyskowych bezpośrednio
w szkielecie. Stosuje się wówczas łożyskowanie wałka w panewkach wykonanych
z odpowiednich materiałów i zamocowanych w szkielecie przez (rys. 45): zalanie,
zanitowanie, przykręcenie, wtłoczenie.

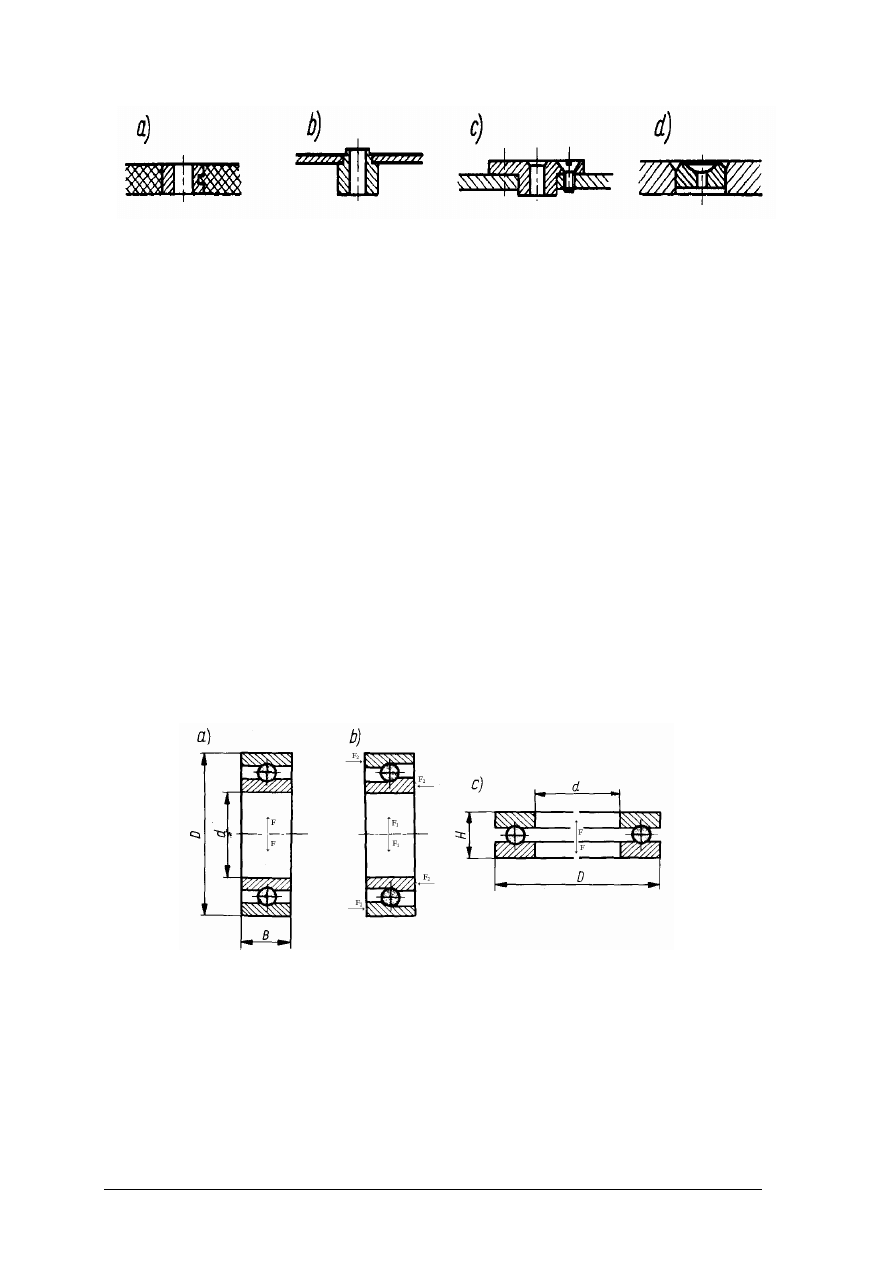
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

53

Rys. 45. Panewki i ich zamocowanie: a) przez zalanie, b) przez zanitowanie, c) przez przykręcenie,

d) przez wtłoczenie [4, s. 71]

Dobór materiałów czopa i panewki powinien zapewnić małe tarcie, małą zużywalność

i dostatecznie dużą obciążalność łożyska. Panewki mineralne charakteryzują się dużą
odpornością na zużycie. Łożyska z panewkami metalowymi wymagają smarowania,
z panewkami zaś z tworzyw sztucznych mogą pracować również bez użycia smaru, przy
małych oporach ruchu i niewielkiej zużywalności.

Smarowanie ma na celu przedłużenie trwałości łożysk. Dotyczy to zwłaszcza łożysk

ś

lizgowych, które wymagają smarowania ciągłego.

Do smarowania łożysk ślizgowych używa się smarów stałych lub ciekłych, tzw. olejów.

Oleje zwane maszynowymi służą do smarowania łożysk bardzo obciążonych. W przypadku
obciążeń mniejszych są stosowane tzw. oleje wrzecionowe. Rozróżniamy trzy podstawowe
sposoby smarowania: dopływowe, obiegowe i pod ciśnieniem.

Do zalet łożysk ślizgowych zaliczamy: małe wymiary promieniowe, łatwy montaż

i demontaż, przenoszenie dużych obciążeń a także przy obciążeniach udarowych, gdy
konieczne jest, aby łożyska tłumiły drgania wałów, przy dużych prędkościach obrotowych.
Ponadto wykonanie łożyska z odpowiedniego materiału umożliwia zastosowanie go
w mechanizmie pracującym w środowisku korozyjnym.

Wadami łożysk ślizgowych są wysokie koszty eksploatacji z uwagi na stosowanie

drogich stopów łożyskowych oraz duże zużycie smarów (nie dotyczy to łożysk z tworzyw
sztucznych), znaczne opory ruchu i duże wymiary osiowe.

W budowie maszyn znacznie częściej są stosowane łożyska toczne. W zależności od

kierunku przenoszenia obciążeń rozróżniamy łożyska wzdłużne i poprzeczne (rys. 46).

Rys. 45. Łożyska toczne: a) poprzeczne

α

= 0°, b) poprzeczne 0°<

α

<45°, c) wzdłużne

α

= 90° [1, s. 78]

Łożysko toczne składa się z pierścienia zewnętrznego o średnicy D, pierścienia

wewnętrznego o średnicy d, elementów tocznych osadzonych w koszyczku ustalającym
odległość między nimi. Pierścienie – zewnętrzny i wewnętrzny – mają odpowiednio
ukształtowane rowki, zwane bieżniami, po których poruszają się elementy toczne.

W zależności od kształtu elementów tocznych łożyska dzieli się na kulkowe

i wałeczkowe. Wałeczki mogą mieć kształt walcowy, igiełkowy, stożkowy, baryłkowy, i stąd
wynika dalszy podział łożysk tocznych. Elementy toczne mogą być usytuowane w jednym
lub kilku rzędach i dlatego rozróżnia się łożyska jednorzędowe i wielorzędowe.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

54

Wymiary łożysk są znormalizowane w celu zapewnienia ich zamienności. Są one ujęte

w odpowiednich normach krajowych i międzynarodowych oraz katalogach wytwórni.
W zależności od wartości wymiaru D przy zachowaniu stałych wymiarów d, b lub H
rozróżnia się łożyska: lekkie, średnie i ciężkie.

Czynniki decydujące o doborze łożyska można podzielić na dwie podstawowe grupy.

Jedną z nich stanowi wybór typ łożyska, uzależniony od konstrukcji i przeznaczenia maszyny,
warunków pracy łożyska, warunków montażu i obsługi itp. Wybór odpowiedniego typu
łożyska w tym zakresie zależy od konstruktora maszyn.

Drugą grupę stanowią czynniki decydujące o wymiarach łożyska. Należą do nich:

wartość obciążenia, przy którym łożysko przepracuje określony okres bez zniszczenia, oraz
maksymalna prędkość obrotowa dla danego łożyska. Obciążenie łożyska okre1a się w czasie
ruchu (nośność ruchowa) tj. w przypadku, gdy pierścienie obracają się względem siebie
z prędkością obrotową n> 10 obr/min, oraz w czasie spoczynku (nośność spoczynkowa)
tj. przy n ≤10 obr/min.

Za trwałość łożyska przy danym obciążeniu przyjmuje się czas pracy łożyska do chwili

wystąpienia pierwszych oznak zniszczenia łożyska, którymi są rysy i mikropęknięcia na
powierzchniach tocznych.

Nośność ruchowa podana w katalogu dla poszczególnych łożysk jest wyznaczana przy

założeniu niewielkiej trwałości (1 mln obrotów określa trwałość odpowiadającą 500
godzinom pracy przy n = 33 l/3 obr/min), natomiast w rzeczywistości przeważnie jest
wymagane uzyskanie znacznie większej trwałości, przy stosowanych większych prędkościach
obrotowych.

W związku z tym przy doborze łożysk należy przyjmować łożysko o odpowiednio

wyższej nośności C, co pozwoli na uzyskanie żądanej trwałości łożyska przy obciążeniu
rzeczywistym niższym od nośności. Zależność między żądaną trwałością, nośnością ruchową
i rzeczywistym obciążeniem łożyska określa wzór:

p

F

C

L













=

gdzie:
L – trwałość łożyska w mln obrotów,
C – nośność ruchowa (według katalogu),
F – obciążenie równoważne,
p – wykładnik potęgowy: dla łożysk kulkowych p = 3, dla łożysk wałeczkowych

p = 10/3.

Warunkiem prawidłowej pracy łożysk tocznych jest ich odpowiednie osadzenie na czopie

osi lub wału oraz w korpusie. Zasada montażu jest następująca: przy ruchomym czopie
łożysko musi być na nim osadzone ciasno (tolerancja wymiaru czopa k5, k6) i bez wcisku
w korpusie maszyny (tolerancja otworu H7, H8), a przy ruchomym korpusie łożysko należy
osadzać ciasno w otworze korpusu (tolerancja średnicy otworu N7, M7) i bez wcisku na
czopie (tolerancja średnicy czopa h6, h7).

Normalizacja łożysk tocznych wymaga ujednolicenia zasad ich oznaczania. Omówione

poniżej zasady są powszechnie obowiązujące w Polsce, natomiast producenci zagraniczni
stosują odrębne zasady oznaczeń – o czym należy pamiętać przy korzystaniu z katalogów
innych producentów niż fabryki krajowe.

Podstawą systemu oznaczania łożysk tocznych jest ich podział według głównych cech

konstrukcyjnych. Każde łożysko jest oznaczone symbolem cyfrowym lub literowo-cyfrowym,
w którym wyróżnia się:

−

oznaczenie serii (w tym odmiany średnicowej,

−

oznaczenie wymiaru średnicy otworu (d) łożyska,

−

inne informacje.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

55

Ostatni dwie cyfry symbolu cyfrowego określają średnicę d otworu łożyska: 00 – oznacza

d = 10 mm, 01–12 mm, 02–15 mm oraz 03–17 mm, wyższe liczby (04÷96) mnoży się przez
5, otrzymując w wyniku średnicę otworu łożyska. Przy d ≥500 mm wymiar otworu podaje się
bezpośrednio za kreską ułamkową (po znaku serii), np. 60/500. Dla średnic d < 10 mm,
stosowanych w łożyskach kulkowych zwykłych i wahliwych, wymiar ten podaje się
pojedynczą cyfrą, równą średnicy otworu; dla d = 7 mm oznaczenie jest np. 607.

Pozostała część symbolu – przed cyframi określającymi średnicę d – określa serię

łożyska oraz podstawowe cechy konstrukcyjne, w tym głównie odmianę średnicową.
Symbolem odmiany średnicowej jest cyfra bezpośrednio poprzedzająca wymiar łożyska (dla
łożysk o d ≥10 mm jest to trzecia cyfra od końca, dla łożysk o d < 10 mm – druga od końca
symbolu).

Symbol literowy podany przed numerem serii, określa ich główne cechy konstrukcyjne.
Oznaczenia literowe umieszczone na końcu oznaczenia (po cyfrach) określają różne

szczegóły konstrukcyjne, np.:

w łożyskach kulkowych zwykłych:
Z (2Z) – jedna (dwie) blaszka ochronna;
RS (2RS) jedna (dwie) uszczelka gumowa;
w łożyskach kulkowych skośnych jednorzędowych:
C, A, B – kąt działania α= 15°, 25°, 40°;
w łożyskach kulkowych wahliwych oraz baryłkowych:
K – łożysko z otworem stożkowym (zbieżność otworu 1: 12);
w łożyskach wa1cowych jednorzędowych:
E – łożysko o wyższej nośności przy tych samych wymiarach.
Objaśnienia wszystkich symboli stosowanych przy oznaczaniu łożysk tocznych są

podane w normach.

4.8.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Jakie są zadania łożysk?

2.

Jakie zadanie w łożysku tocznym pełni koszyczek?

3.

Jakie są wady i zalety łożysk tocznych?

4.

Kiedy stosujemy łożyska ślizgowe a kiedy toczne?

5.

Kiedy stosujemy łożyska ślizgowe dzielone?

6.

Jakich smarów używamy do smarowania łożysk ślizgowych?

4.8.3. Ćwiczenia

Ćwiczenie 1

Odczytaj, na rysunku, części składowe łożyska tocznego i określ ich zadania.

Przedstawione łożysko toczne narysuj w uproszczeniu zgodnie z PN.

Rysunek do ćwiczenia 1

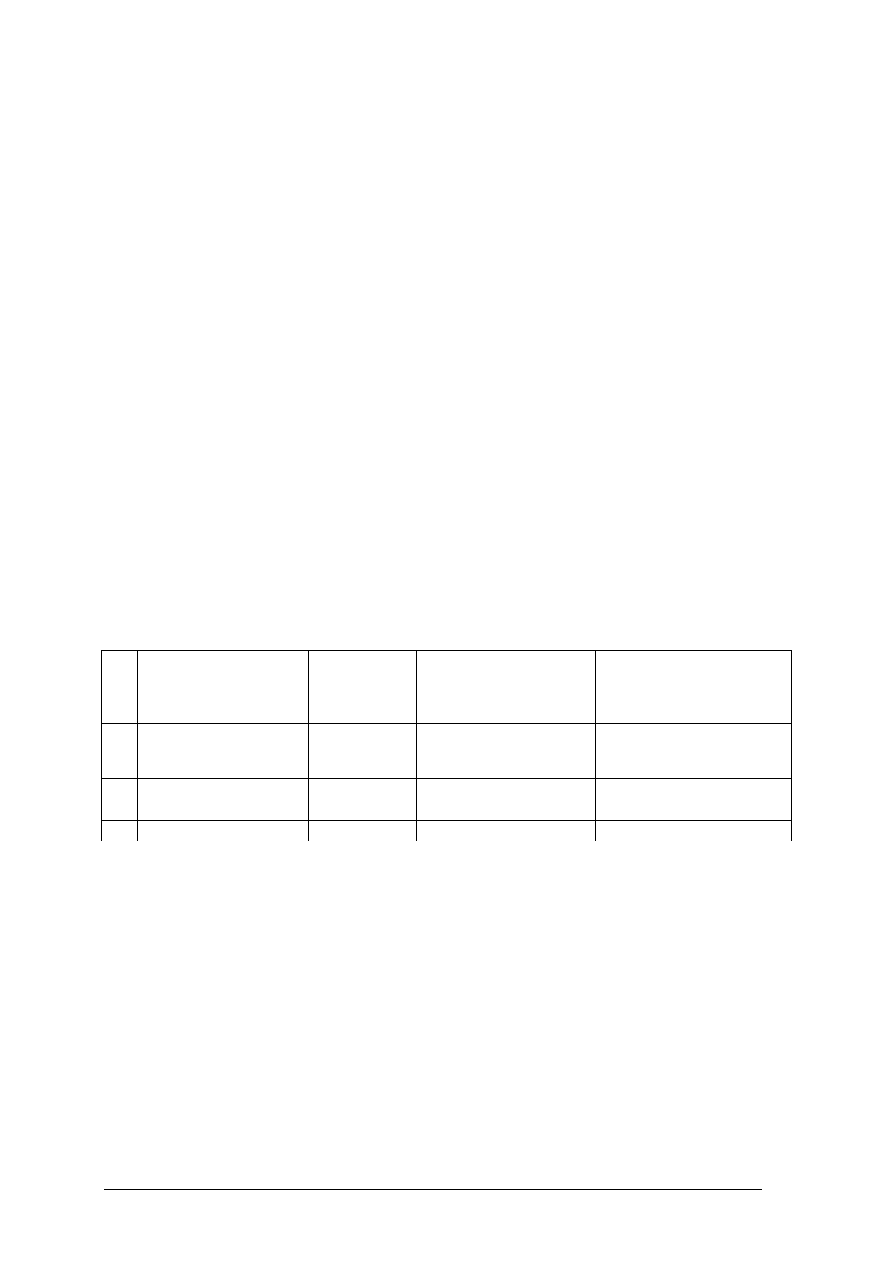
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

56

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

zapoznać się z normami,

3)

nazwać i omówić części składowe łożyska,

4)

narysować łożysko w uproszczeniu,

5)

ocenić jakość wykonanej pracy,

6)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

PN – 81/M–01135– zasady rysowania łożysk,

−

przybory do rysowania,

−

zeszyt,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

Ćwiczenie 2

Wykonaj demontaż urządzenia mechanicznego, a następnie dokonaj analizy konstrukcji

mechanizmu.

Aby wykonać ćwiczenie, powinieneś:

1)

przygotować zestaw narzędzi do demontażu,

2)

zdemontować urządzenie, zwracając uwagę by nie spowodować uszkodzenia,

3)

przeanalizować konstrukcję mechaniczną urządzenia,

4)

zamieścić wyniki analizy w tabeli, zgodnie z poniższym przykładem,

Lp.

Nazwa

części/mechanizmu

Funkcja

Czy część/mechanizm

można naprawiać?

Sposób naprawy

1.

Łożyska

Podtrzymują
wał

Nie

Wymianie podlega cały

wał

2.

5)

zmontować urządzenie,

6)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

różnorodne urządzenia elektroniczne do demontażu,

−

literatura wskazana przez nauczyciela.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

57

4.8.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

określić zadania łożysk?

2)

uzasadnić kiedy stosujemy łożyska ślizgowe?

3)

określić kryteria doboru łożysk?

4)

określić wady i zalety łożysk ślizgowych?

5)

uzasadnić dlaczego łożyska są smarowane?

6)

uzasadnić kiedy stosujemy łożyska toczne?

7)

sklasyfikować łożyska?

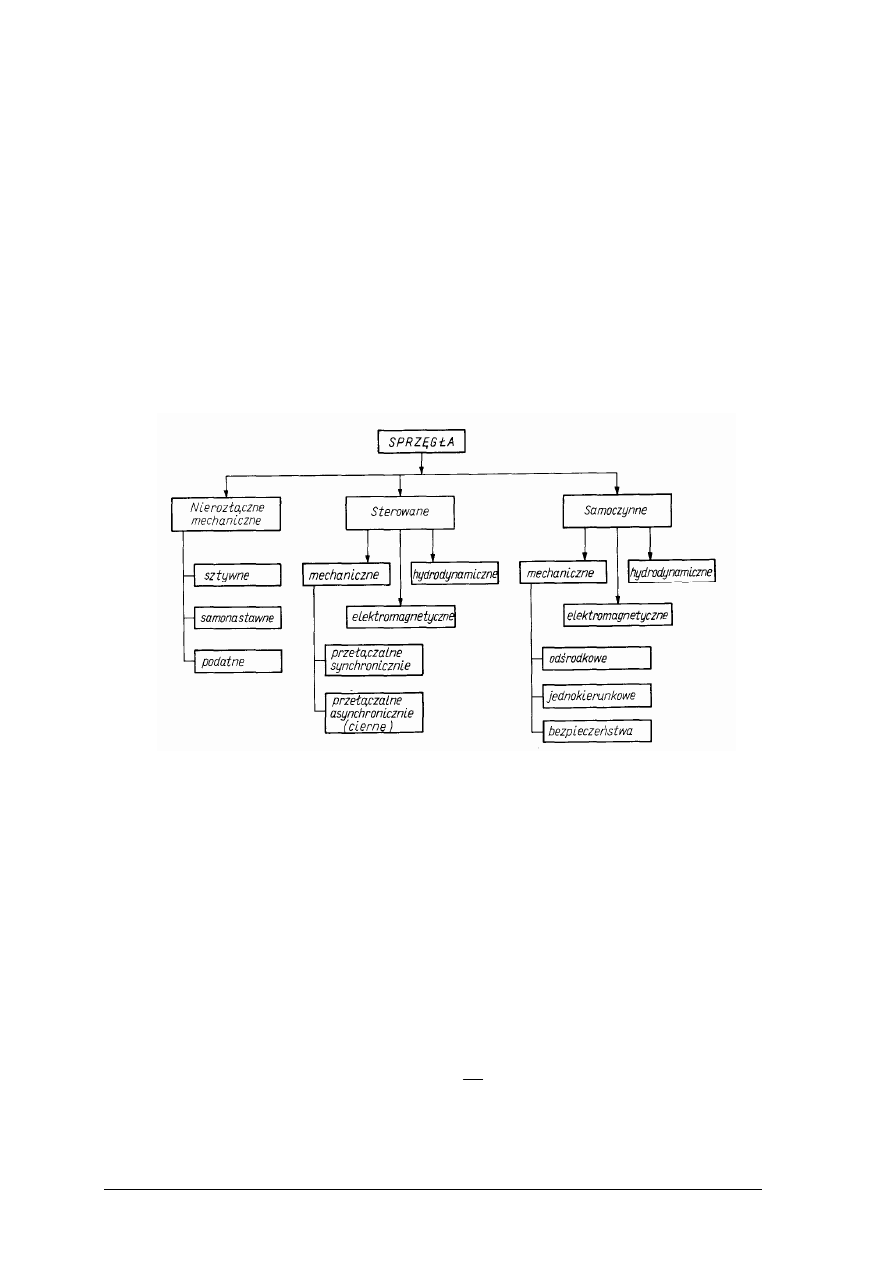
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

58

4.9.

Sprzęgła i hamulce

4.9.1. Materiał nauczania

Sprzęgła to zespoły, których zadaniem jest trwałe lub okresowe łączenie wałków,

umożliwiające przeniesienie napędu. Sprzęgła mogą spełniać również dodatkowe zadania,
jak: kompensować niedokładność wzajemnego położenia łączonych wałków, zapewniać
napęd tylko w jednym kierunku, zabezpieczać elementy napędzane przed przeciążeniem,
łagodzić gwałtowne włączanie napędu itd.

W zależności od konstrukcji i zadań, sprzęgła mechaniczne (rys. 47) dzielimy na

−

nierozłączne (stałe),

−

sterowane, które dają się rozłączyć podczas ruch wału,

−

samoczynne, w których połączenie lub rozłączenie wałów następuje samoczynnie
w skutek zmian parametrów pracy.

Rys. 47. Podział sprzęgieł według cech funkcjonalno-konstrukcyjnych [8, s. 365]

Podejmując decyzję o wyborze odpowiedniego sprzęgła należy opierać się na Polskich

Normach oraz na katalogach wytwórni, a dobór sprzęgieł lub projektowanie nowych
konstrukcji należy poprzedzać dokładną analizą żądanych ich cech i parametrów.

Normalizacja i zasady doboru sprzęgieł

Sprzęgła są zespołami, które ze względu na szerokie zastosowanie najczęściej są

produkowane niezależnie od maszyn i urządzeń. Wiele sprzęgieł podlega normalizacji
i wówczas parametry ich budowy są podane w Polskich Normach. Niektóre rodzaje sprzęgieł
są stosowane w węższym zakresie i wówczas są produkowane według rozwiązań ustalanych
przez zakłady wytwórcze w uzgodnieniu z odbiorcami. Zakres parametrów produkowanych
sprzęgieł jest wtedy podawany w katalogach zakładowych lub branżowych.
Podstawowym parametrem charakteryzującym pracę sprzęgła jest przenoszony moment
obrotowy, zależny od przenoszonej mocy i prędkości obrotowej według znanego wzoru

n

P

M

9550

=

[Nm]

gdzie:
P – moc [kW],
N – prędkość obrotowa[obr/min].

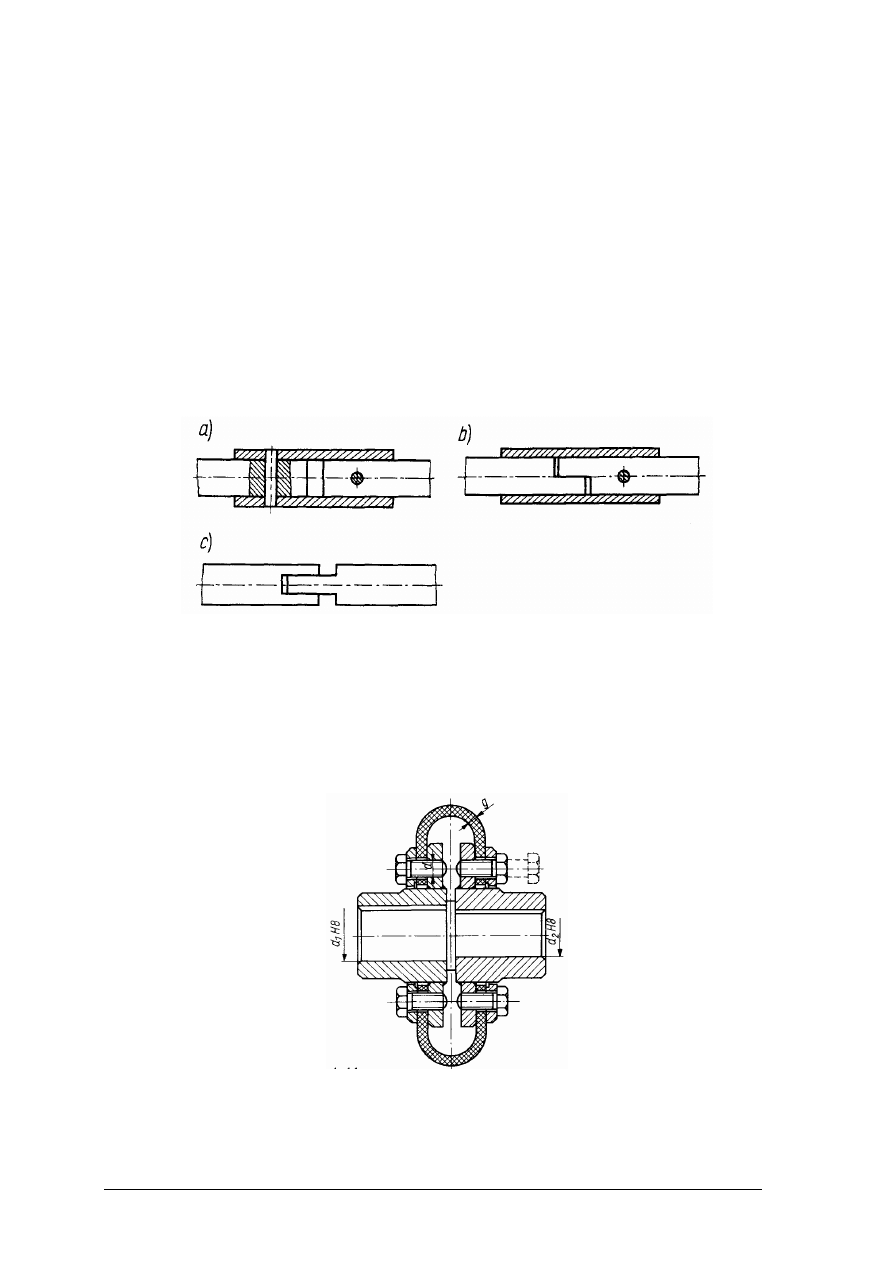
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

59

W celu zastosowania właściwego sprzęgła należy na podstawie zadań, jakie ma ono

spełniać, określić rodzaj sprzęgła i jeśli będzie to sprzęgło znormalizowane dobrać z katalogu
odpowiednią jego wielkość, zależną od przenoszonego momentu. W czasie pracy sprzęgło
może podlegać chwilowym przeciążeniom. Ponieważ nie wszystkie przyczyny przeciążeń
mogą być przewidywane w czasie projektowania, uwzględnia się je w postaci współczynnika
przeciążenia K, ustalanego doświadczalnie. Moment obrotowy maksymalny wynosi wówczas

M

max

=

M

K

⋅

Dobór sprzęgieł z norm i katalogów dokonuje się w zasadzie na podstawie M

max

, należy

jednak zawsze dokładnie zapoznać się z zaleceniami podanymi w normie, ponieważ dla
niektórych konstrukcji normy dopuszczają nawet 2÷5-krotne chwilowe przekroczenie
momentu nominalnego (M

nom

).

Sprzęgła nierozłączne odznaczają się prostą budową. Sprzęgła sztywne (rys. 48) łączą

wały w jednolitą całość, uniemożliwiają przesunięcie jednego wału względem drugiego.
Dlatego wały te muszą być dokładnie współosiowe.

Rys. 47. Sprzęgła sztywne: a) tulejowe; b) tulejowe wysuwne; c) płetwowe wysuwne [7, s. 145]

Sprzęgła podatne (rys. 49) to sprzęgła z łącznikiem sprężystym, który kompensuje

drgania walów i niewielkie błędy ich położenia. Sprzęgłami podatnymi można, zatem łączyć
wały o pewnej niewspółosiowości. Łącznikami sprężystymi są w nich elementy z gumy,
skóry, sprężyny itp. Rozróżniamy sprzęgła podatne: tulejkowe (rys. 50), sprężynowe,
oponowe.

Rys. 49. Sprzęgło kabłąkowe (oponowe) [6, s. 375]

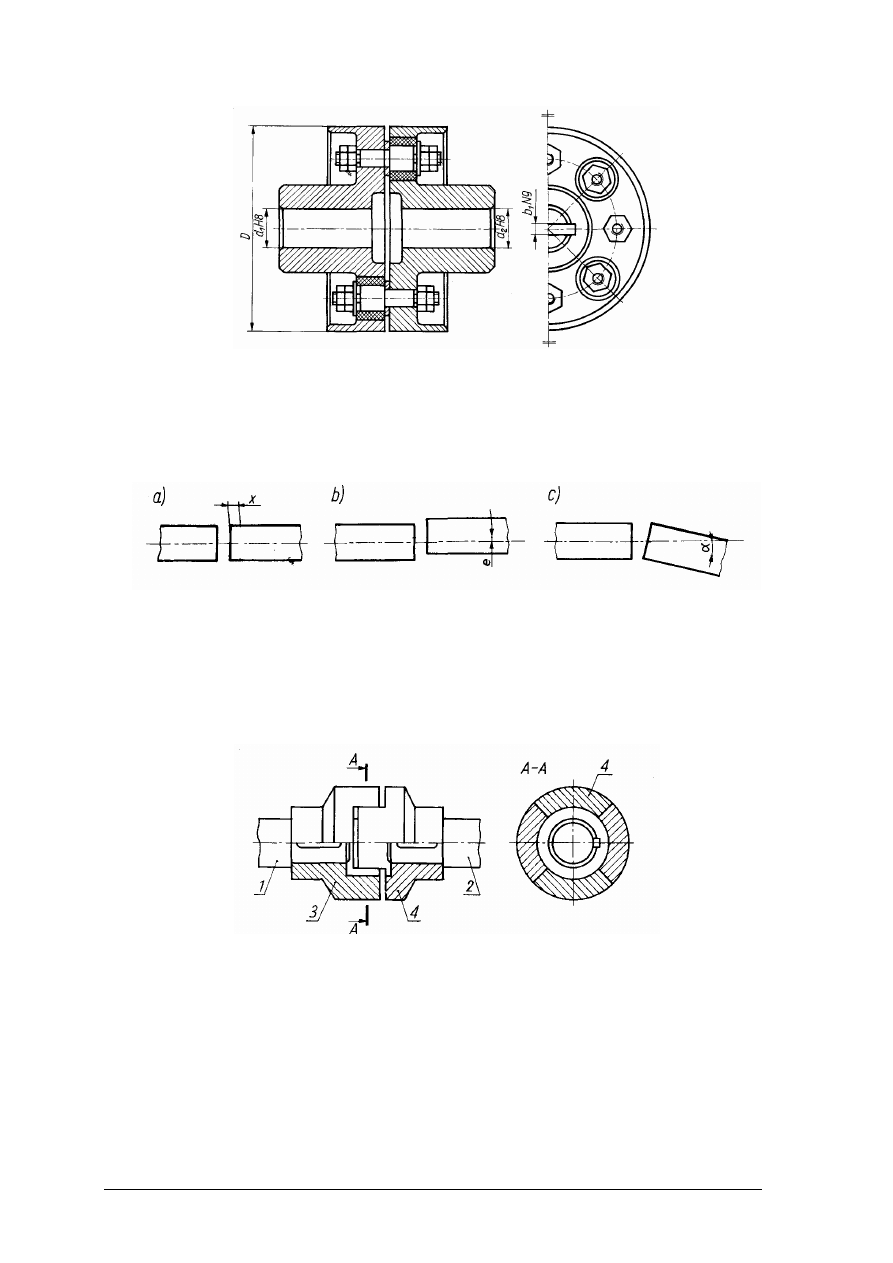
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

60

Rys. 50. Sprzęgło wkładkowe tulejkowe [8, s. 375]

Sprzęgła samonastawne łączą wały, których osie nie pokrywają się. W zależności od

charakteru przesunięcia osi wałów sprzęgła te mogą być odpowiednio – osiowe, promieniowe
i kątowe (rys. 51).

Rys. 51. Przesunięcia osi walów: a) osiowe, b) promieniowe, c) kątowe [1, s. 84]

Sprzęgłem osiowym (wysuwnym), kompensującym przesunięcie osiowe, jest sprzęgło

kłowe (rys. 52). Połączenie wałów (w stanie spoczynku) następuje przez wsunięcie kłów
tarczy przesuwnej 4, osadzonej na wale biernym (napędzanym) 2 w odpowiednie rowki tarczy
stałej 3, osadzonej na wale czynnym (napędzającym) 1.

Rys. 52. Sprzęgło kłowe: 1 – wał czynny (napędzający), 2 – wał bierny (napędzany),

3 – tarcza stała, 4 – tarcza przesuwna [1, s. 84]

Niewspółosiowość wałków łączonych przez sprzęgło wynika zwykle z niedokładności

wykonawczych i montażowych. Zazwyczaj jest ona nieznaczna i do jej kompensacji mogą
służyć sprzęgła przedstawione na (rys. 53).

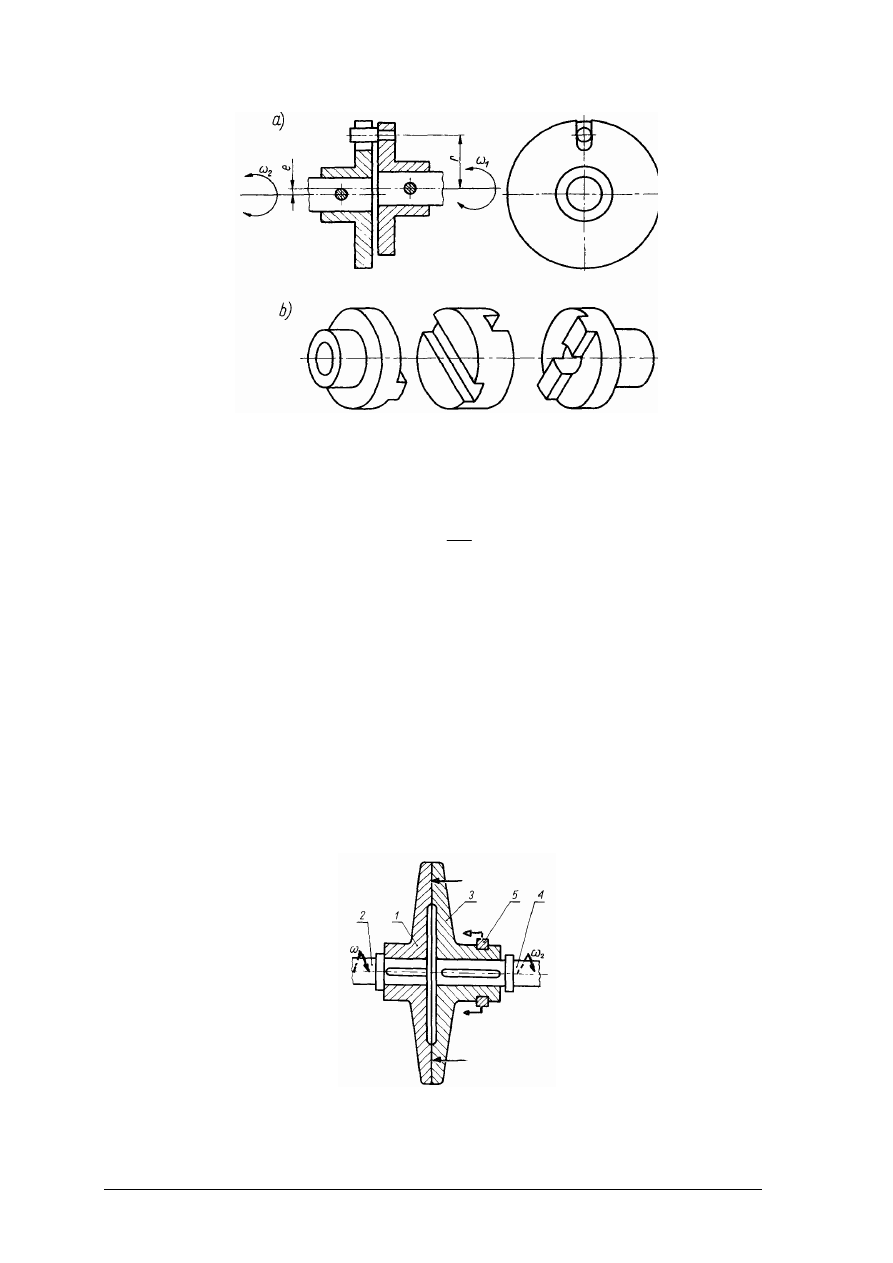
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

61

Rys. 53. Sprzęgła do łączenia wałków niewspółosiowych: a) tarczowe; b) Oldhama [4, s. 82]

Sprzęgło tarczowe ma prostą konstrukcję, lecz jego wadą jest zmienne, w granicach

jednego obrotu, przełożenie (przełożenie to stosunek prędkości kątowej wałka
napędzającego – czynnego do napędzanego – biernego:

2

1

ω

ω

=

i

Przyczyną tego jest nieuniknione – ze względów wykonawczych – przesunięcie (e)

względem siebie osi wałka czynnego i osi wałka biernego.

Wady tej jest pozbawione sprzęgło Oldhama (rys. 53 b), w którym przełożenie jest stałe

niezależne od wartości niewspółosiowości wałków, dzięki wzajemnie prostopadłemu
usytuowaniu płetw i wycięć elementów sprzęgła.

Coraz powszechniejsze zastosowanie w budowie maszyn znajdują sprzęgła cierne.

Rozróżniamy sprzęgła cierne: tarczowe płaskie i stożkowe oraz wielopłytkowe. Mogą one
być sterowane mechanicznie, elektromagnetycznie, pneumatycznie i hydraulicznie. Sprzęgło
cierne tarczowe (rys. 54) składa się z dwóch tarcz, z których jedna 1 jest osadzona
nieruchomo na wale czynnym (napędzającym) 2, druga 3 zaś przesuwa się wzdłuż wpustu na
wale biernym (napędzanym) 4 za pomocą pierścienia 5, stanowiącego część mechanizmu
włączającego. Z chwilą zetknięcia się powierzchni tarcz następuje wskutek tarcia łagodne
przeniesienie momentu obrotowego z wału czynnego na bierny.

Rys. 54. Sprzęgło cierne tarczowe; budowa i zasada działania [1, s. 87]

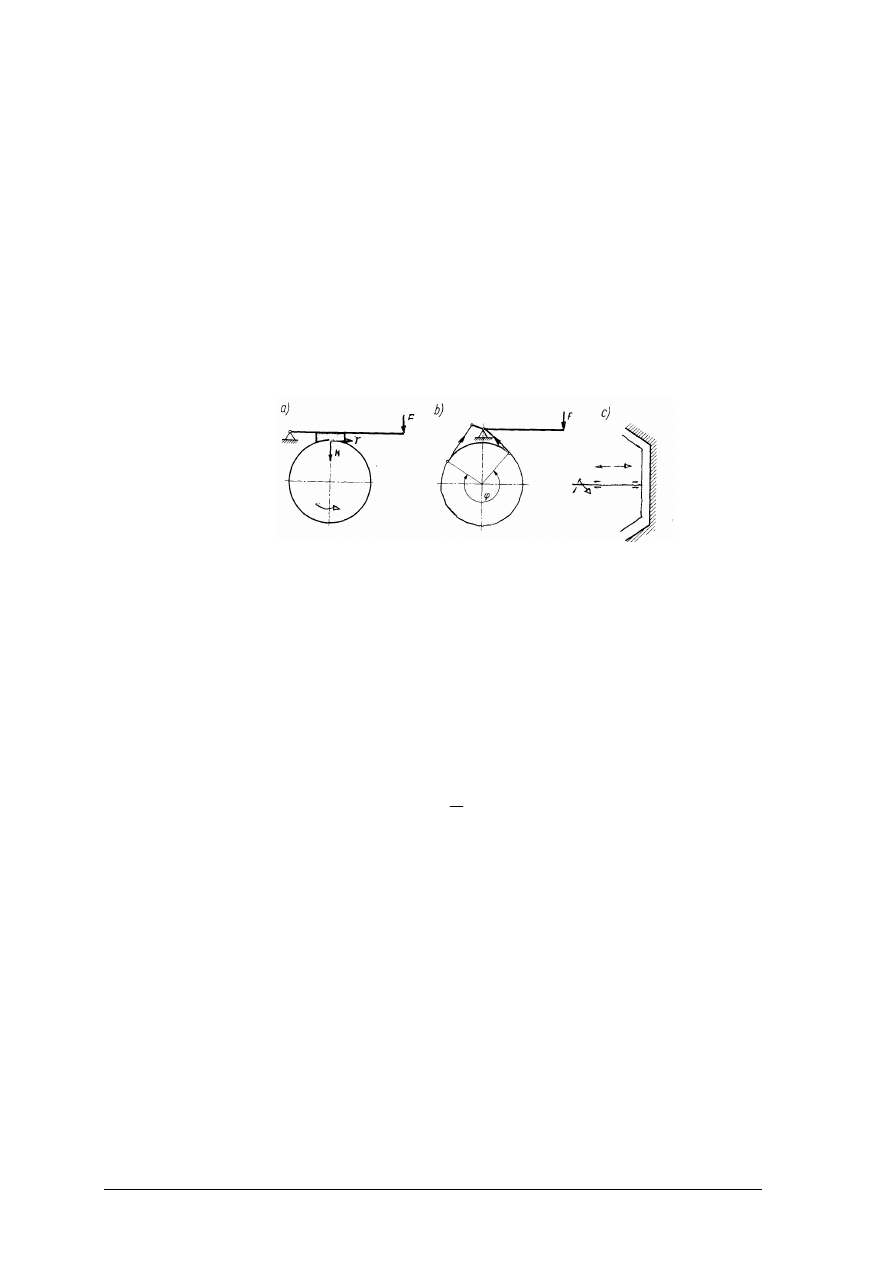
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

62

Sprzęgła tarczowe (rys. 54) są powszechnie stosowane w układach przeniesienia napędu

pojazdów samochodowych. Sprzęgło tarczowe jest włączone, gdy kierowca nie naciska nogą
pedału. W chwili naciśnięcia na pedał następuje odsunięcie tarczy ciernej. Dzięki temu, mimo
ż

e wał korbowy nadal się obraca, nie następuje przeniesienie napędu na wałek sprzęgłowy

skrzyni biegów.

Hamulce służą do zmniejszania prędkości obrotowej i zatrzymywania obracających się

części maszyn. Hamulce stanowią odmianę sprzęgieł ciernych. Ich budowa jest prostsza niż
sprzęgieł, ponieważ jeden człon zawsze pozostaje w spoczynku. Powierzchnie cierne
hamulców mogą być płaskie, walcowe lub stożkowe. Składają się one z dwu zasadniczych
części – jednej w postaci tarczy (lub bębna), która obraca się wraz z walem, i drugiej –
nieruchomej. Wskutek dociśnięcia nieruchomej (nie obracającej się) części do części
ruchomej hamulca powstają siły tarcia, które powodują zmniejszenie prędkości lub
zatrzymanie obracających się elementów maszyny. Najważniejsze rodzaje hamulców
ciernych przedstawiono schematycznie na rysunku 55.

Rys. 55. Schematy hamulców: a) jednoklockowego, b) cięgnowego, c) talerzowego [1, s. 90]

Hamulce klockowe (rys. 55a) mogą być jedno – lub dwuklockowe. Podstawowym ich

elementem jest klocek drewniany lub żeliwny, który jest dociskany do tarczy za pomocą
dźwigni – ręcznie lub mechanicznie. W hamulcach cięgnowych (rys. 55b) zasadniczym
elementem jest taśma stalowa opasująca bęben. Skuteczność hamowania zależy od kąta
opasania

ϕ

który wynosi zwykle 250+270°. W hamulcach talerzowych (rys. 55 c) hamowanie

następuje po dociśnięciu talerza do nieruchomej osłony. Siła docisku elementów hamujących
może być wywoływana przez ciężar, sprężynę, pole elektromagnetyczne lub ciśnienie płynu –
cieczy albo gazu.

Moment hamujący od pojedynczego elementu hamującego wynosi:

2

d

t

F

h

M

⋅

=

[N m]

przy czym: F

t

– siła tarcia w N, d –

ś

rednica b

ę

bna hamulcowego w m.

Wymiary klocka hamulcowego dobiera si

ę

z warunku na nacisk powierzchniowy.

Wymiary powierzchni ciernych hamulców musz

ą

by

ć

tak du

ż

e, aby warto

ść

nacisków

wyst

ę

puj

ą

cych podczas hamowania nie była wi

ę

ksza od dopuszczalnej. Przekroczenie tej

warto

ś

ci grozi bowiem szybkim zu

ż

yciem powierzchni ciernych. Wydzielaj

ą

ce si

ę

ciepło

mo

ż

e, oprócz przyspieszenia zu

ż

ycia, zmniejszy

ć

współczynnik tarcia, a tym samym –

skuteczno

ść

hamowania. W urz

ą

dzeniach nap

ę

dzanych silnikami elektrycznymi efekt

hamowania mo

ż

na uzyska

ć

wykorzystuj

ą

c silnik jako hamulec. Silnik obci

ąż

amy wtedy po

wył

ą

czeniu jak pr

ą

dnic

ę

lub przeł

ą

czamy zasilanie na przeciwny kierunek nap

ę

du.

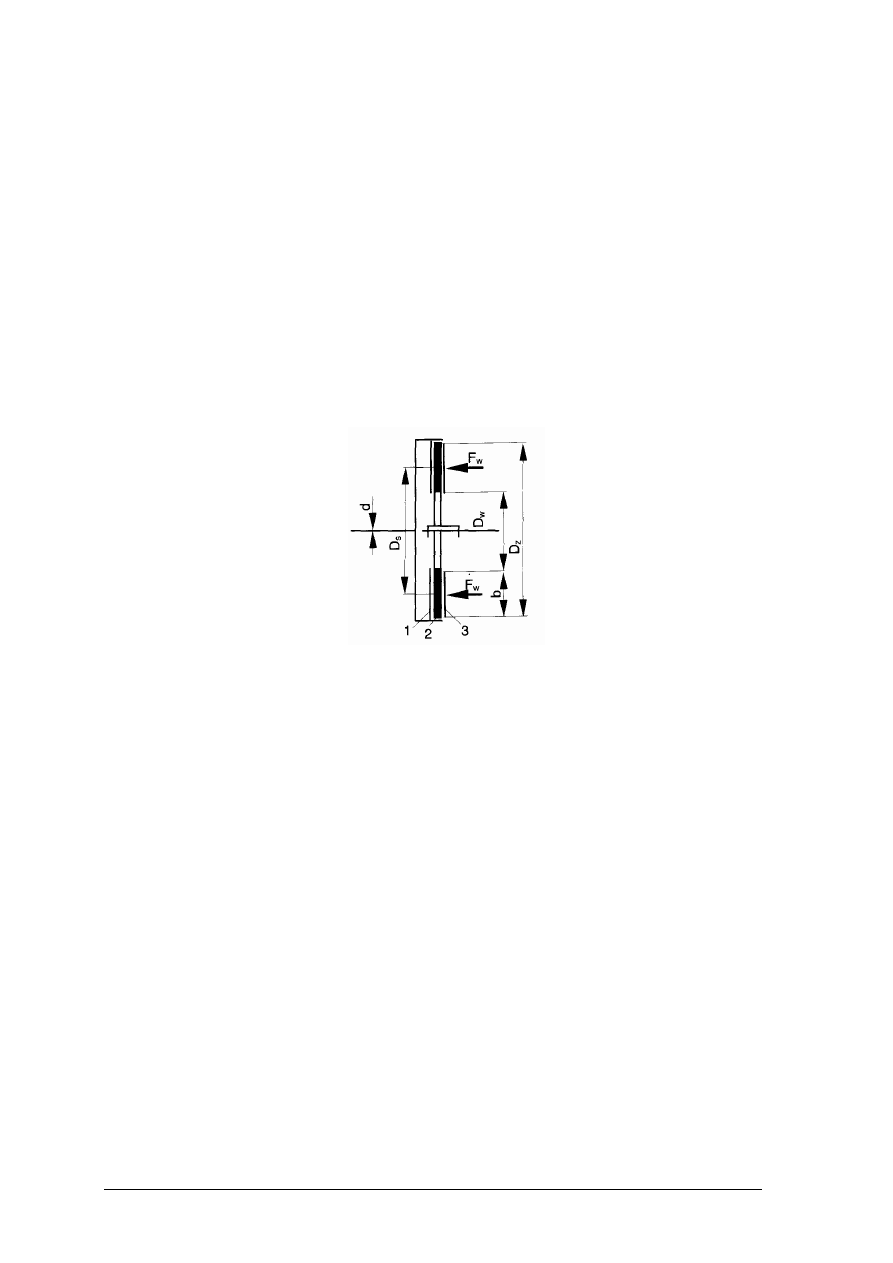
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

63

4.9.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Do czego służy sprzęgło?

2.

Jaka jest różnica między sprzęgłem ciernym a hamulcem?

3.

Określić zasady doboru sprzęgieł?

4.

Kiedy stosujemy sprzęgła nierozłączne?

5.

Jakie sprzęgła zapewniają przemieszczanie osi wałów?

6.

Jakie zastosowanie mają sprzęgła samoczynne?

4.9.3. Ćwiczenia

Ćwiczenie 1

Odczytaj, na rysunku, części składowe sprzęgła ciernego i określ ich zadanie.

Rysunek do ćwiczenia 1 [10, s. 76]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

przeanalizować schemat sprzęgła,

2)

wyjaśnić budowę i zasadę działania sprzęgła,

3)

rozpoznać wskazane części i określić ich zadanie,

4)

ocenić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

przybory do pisania,

−

normy,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

64

Ćwiczenie 2

Odczytaj, z rysunku, rodzaj sprzęgła, jego budowę i określ zadania.

Rysunek do ćwiczenia 2 [8, s. 390]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

dokonać analizy działania sprzęgła,

3)

nazwać i opisać części składowe sprzęgła,

4)

ocenić jakość wykonanej pracy,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

przybory do pisania,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

4.9.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

sklasyfikować sprzęgła?

2)

scharakteryzować materiały na okładziny cierne?

3)

wyjaśnić budowę sprzęgła Oldhama?

4)

scharakteryzować hamulec klockowy?

5)

określić parametry charakteryzujące sprzęgła?

6)

wskazać różnicę między hamulcem a sprzęgłem ciernym?

7)

scharakteryzować sprzęgło tulejowe?

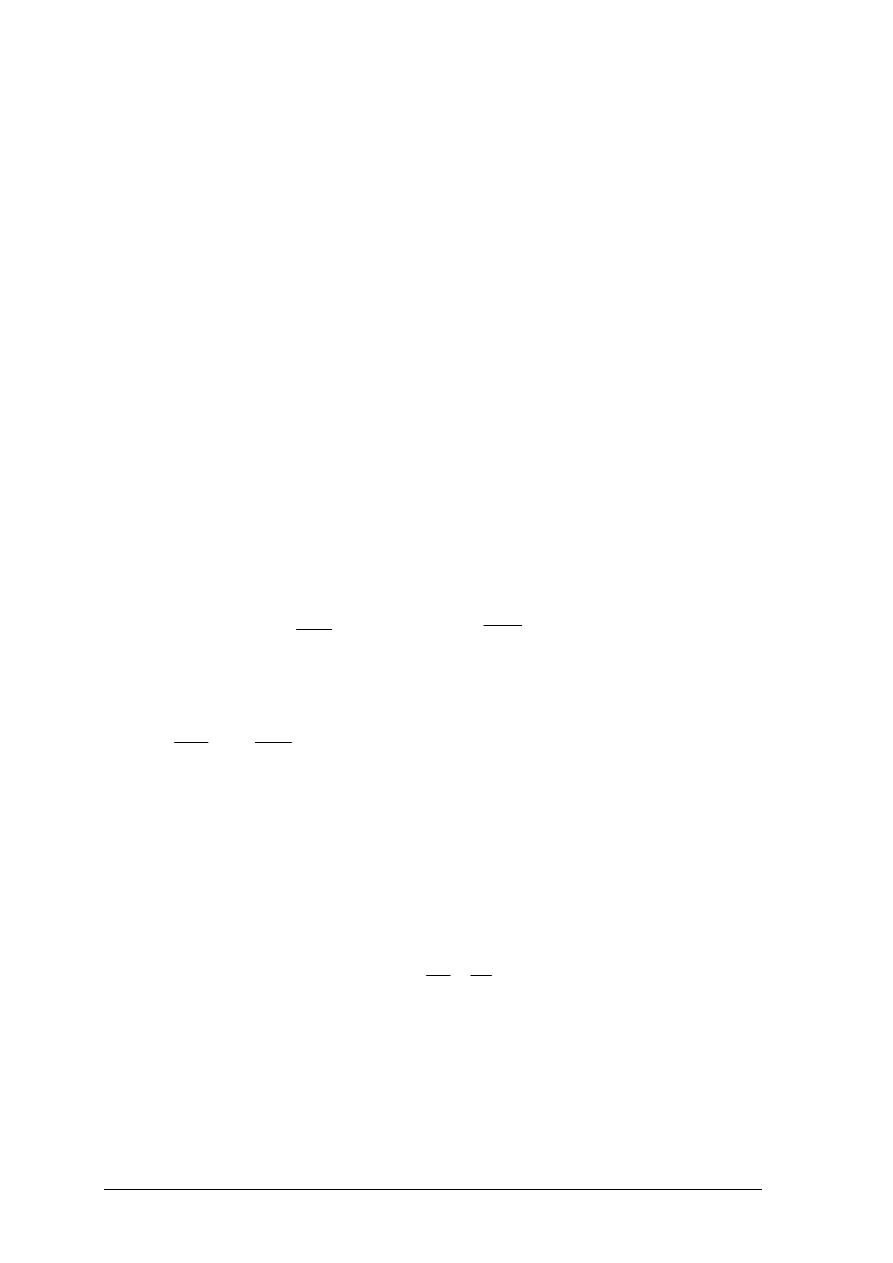
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

65

30

1

1

n

⋅

=

π

ω

4.10. Przekładnie mechaniczne

4.10.1. Materiał nauczania

Napęd mechaniczny służący do przenoszenia ruchu obrotowego z wału czynnego

(napędzającego) na wał bierny (napędzany) nazywa się przekładnią mechaniczną.

Podstawowym zadaniem przekładni mechanicznej jest przeniesienie energii z wału

czynnego na wał bierny, a ponadto dokonanie zmiany wartości momentu obrotowego,
prędkości i sił.

Potrzebę stosowania przekładni można uzasadnić następująco:

−

w większości maszyn roboczych są potrzebne duże momenty obrotowe, co – przy
określonej mocy – wymaga stosowania małych prędkości obrotowych, a tymczasem
silniki budowane są na ogół jako wysokoobrotowe,

−

stosowanie silników o małej prędkości obrotowej jest ekonomicznie nieuzasadnione,
gdyż są one większe, cięższe i droższe,

−

zakres regulacji prędkości obrotowych, niezbędnych w maszynach roboczych, jest
najczęściej niemożliwy do osiągnięcia przez zmianę prędkości obrotowej silnika.
Ponadto istnieje wiele czynników, które nie pozwalają na bezpośrednie połączenie silnika

z maszyną roboczą, np. względy konstrukcyjne, bezpieczeństwo pracy, gabaryty silnika,
wygoda obsługi itd.

Podstawowe cechy użytkowe przekładni mechanicznych. Ruch obrotowy kół przekładni

można scharakteryzować przez podanie prędkości: kątowej

ω

, obrotowej n lub obwodowej

υ

danego koła. Relacje między wymienionymi prędkościami określają zależności:

[rad/s],

w których:

ω

1,2

– prędkości kątowe wyrażone w [rad/s],

n

1,2

– prędkości obrotowe w [obr/min];

60

1

1

1

n

D

⋅

⋅

=

π

υ

60

2

2

2

n

D

⋅

⋅

=

π

υ

[m/s],

przy czym:

υ

1,2

– prędkości liniowe wyrażone w [m/s],

D

1,2

– średnice w[ m].

Przełożenie

Podstawową cechą każdej przekładni jest jej przełożenie. Przełożeniem kinematycznym

przekładni nazywa się stosunek prędkości kątowej koła czynnego do prędkości kątowej koła
biernego. Przełożenie kinematyczne można również określić jako stosunek prędkości
obrotowych:

2

1

2

1

n

n

i

=

=

ω

ω

W zależności od wartości przełożenia rozróżnia się następujące rodzaje przekładni:

−

reduktory (przekładnie zwalniające, i> 1), w których prędkość kątowa koła biernego jest
mniejsza od prędkości kątowej koła czynnego,

−

multiplikatory (przekładnie przyspieszające, i < 1), w których prędkość kątowa koła
biernego jest większa od prędkości kątowej koła czynnego.
Jak wynika z wyjaśnień podanych w ogólnej charakterystyce, najczęściej są stosowane

reduktory.

30

2

2

n

⋅

=

π

ω

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

66

Stosowanie przełożeń różnych od jedności wymaga dobrania odpowiednich wymiarów

kół. W celu ich ustalenia należy rozpatrzeć współpracę dwóch kół ciernych, toczących się po
sobie bez poślizgu. Prędkości obwodowe obu kół są w tym przypadku jednakowe (

2

1

ν

ν

=

).

Podstawiając otrzymuje się:

a po przekształceniu

Poślizgi kół lub cięgna na kole powodują zmianę wartości przełożenia kinematycznego.

W przekładniach zębatych wartość przełożenia może być wyrażona stosunkiem średnic
podziałowych (odpowiadających omówionym średnicom kół ciernych) lub stosunkiem liczby
zębów:

Przełożenie to nazywa się przełożeniem geometrycznym. Jest ono stałe dla danej

przekładni. Przełożenie kinematyczne różni się nieznacznie od geometrycznego, m.in. ze
względu na poślizgi kół lub pasów, wskutek błędów wykonawczych i podatności zębów oraz
innych czynników. W przekładniach złożonych wielostopniowych, składających się z kilku
przekładni pojedynczych ustawionych szeregowo, przełożenie całkowite jest iloczynem
przełożeń na kolejnych stopniach:

W napędach maszyn są również stosowane przekładnie cierne o zmiennym przełożeniu,

za pomocą których uzyskuje się zmianę przełożenia w sposób ciągły (bezstopniowo).
Zakresem regulacji przełożenia (rozpiętością przełożenia) nazywa się wówczas stosunek
największych i najmniejszych prędkości obrotowych lub przełożeń:

Moment obrotowy

Kolejną wielkością charakterystyczną dla przekładni mechanicznych jest przenoszony

moment obrotowy. Wartość momentu obrotowego na każdym wale i kole oblicza się
z zależności:

n

P

M

9550

=

[N · m]

w którym:
M – w N m, P – w kW oraz n – w obr/min.
Z analizy wynika m.in., że stosując silnik wysokoobrotowy uzyskuje się na jego wale

niewielki moment, a tym samym niewielkie siły obwodowe. Pozwała to na zmniejszenie
wymiarów silnika, a pośrednio również na zmniejszenie wymiarów przekładni.

Moc i sprawność



gdzie:

P

2

– moc na wale biernym,

P

1

– moc na wale czynnym.

Sprawność pojedynczych przekładni mechanicznych jest wysoka (0,95÷0,99).

1

2

P

P

=

η

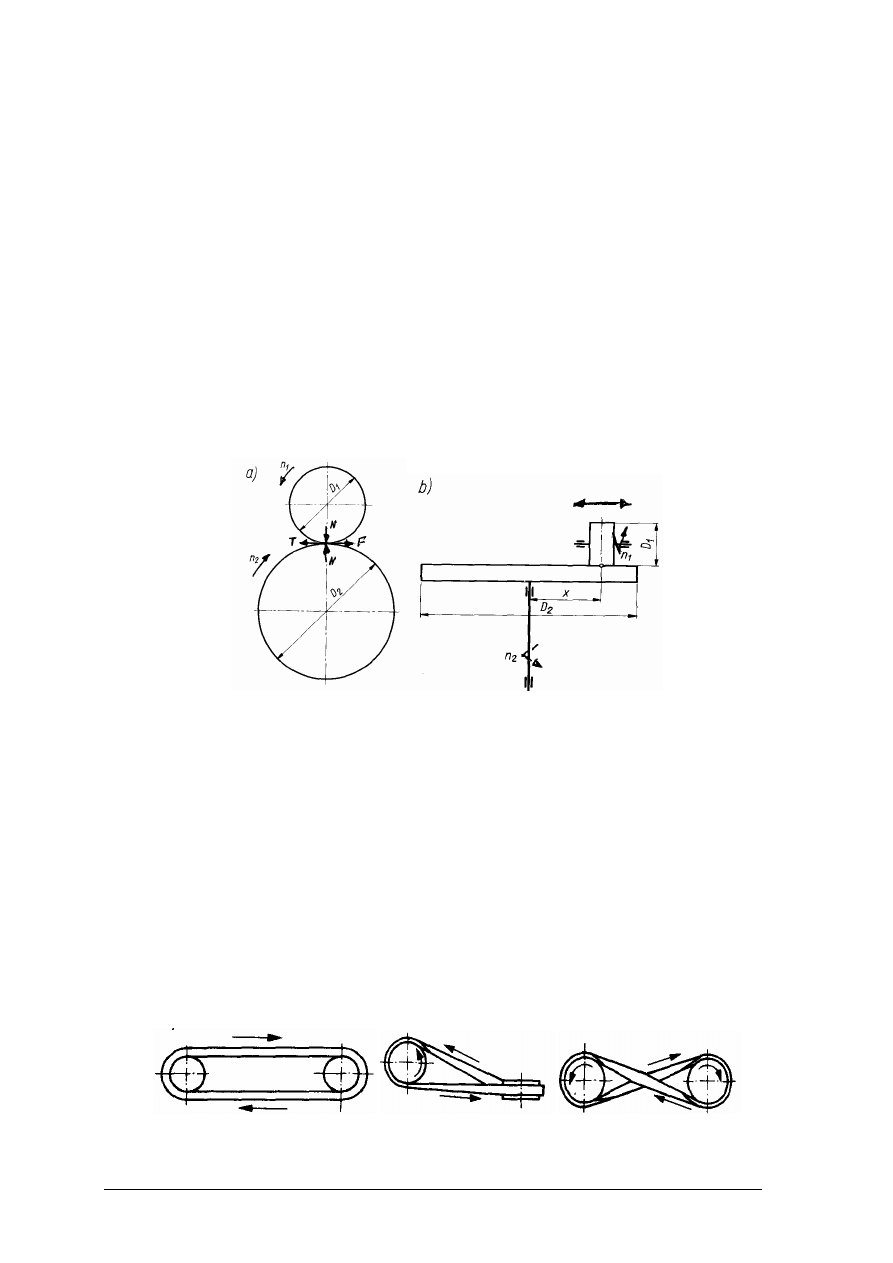
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

67

Dzięki przekładni mechanicznej w zależności od potrzeb można dobierać prędkość

obrotową. Przekładnie mechanicznie zmniejszające prędkość obrotową silnika nazywamy
reduktorami, a zwiększające multiplikatorami.

Rozróżniamy trzy podstawowe rodzaje przekładni mechanicznych: cierne, cięgnowe

(pasowe, łańcuchowe) i zębate.

W przekładniach ciernych przenoszenie ruchu obrotowego z wału czynnego na bierny

następuje dzięki siłom tarcia, które powstają wskutek dociskania do siebie kół ciernych
o gładkiej powierzchni. Aby możliwe było przenoszenie dużych obciążeń, kola te,
a przynajmniej ich stykające się części (powierzchnie), powinny być wykonane z materiałów
charakteryzujących się dużym współczynnikiem tarcia tocznego i dużą odpornością na
ś

cieranie. Najodpowiedniejszym materiałem jest stal. Często stosuje się ponadto żeliwo,

gumę, niektóre tworzywa sztuczne.

Rozróżniamy przekładnie cierne o stałym i zmiennym przełożeniu (rys. 56). Te ostatnie

są stosowane częściej (np. w prasach ciernych do tłoczenia metali); sprawność (stosunek
mocy przenoszonej przez wał bierny do mocy przenoszonej przez wał czynny przekładni) ich
jest duża i wynosi 0,85÷0,90.

Rys. 56. Przekładnie cierne: a) o stałym przełożeniu, b) o zmiennym przełożeniu [1, s. 92]

W przekładni ciernej o zmiennym przełożeniu koło napędzające poruszające się ze stałą

prędkością n

1

zmienia swoje położenie x od wartości do 0,5 D

2

, powodując w sposób

bezstopniowy zmianę wartości prędkości obrotowej koła napędzanego n

2

.

Spośród wad przekładni ciernych należy wymienić szybkie zużywanie się

współpracujących elementów na skutek wywierania dużych nacisków oraz poślizg
powodujący brak stabilności przełożenia.

Przekładnie pasowe zaliczamy do przekładni cięgnowych. Cięgnem przenoszącym

moment obrotowy jest pas. Zastosowanie pasa umożliwia przekazywanie ruchu na większe
odległości.

Rozróżniamy przekładnie pasowe (rys. 57): otwarte, skrzyżowane i półotwarte.

W przekładni otwartej kierunek obrotów kola biernego jest taki sam jak koła czynnego,
natomiast w przekładni skrzyżowanej odwrotny. W przekładni półotwartej przeniesienie
napędu następuje w dwóch prostopadłych do siebie płaszczyznach.

Rys. 57. Rodzaje przekładni pasowych: otwarta półskrzyżowana skrzyżowana [8, s. 338]

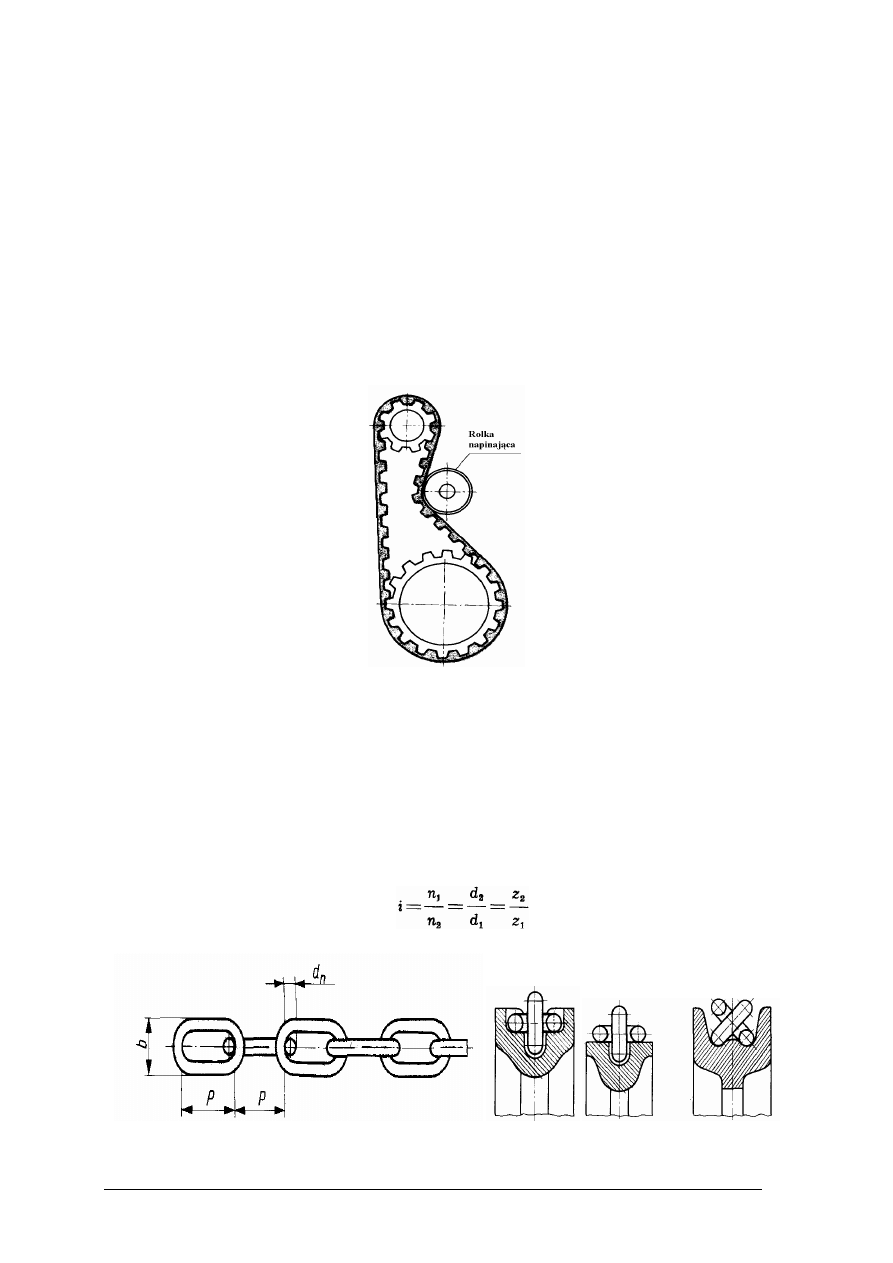
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

68

Pasy stosowane w przekładniach mogą być: płaskie i klinowe. Wykonuje się je z tkanin

kordowych, linek poliamidowych lub zawulkanizowanych w gumie. Dawniej pasy
wykonywano ze skóry. Koła pasowe wykonuje się ze stali, żeliwa, staliwa lub tworzyw
sztucznych.

Największe zastosowanie w napędach (zwłaszcza obrabiarek) znajdują przekładnie

z pasem klinowym o liczbie pasów od 2 do 10 (zatem o takiej samej liczbie rowków). Stosuje
się je przy stosunkowo małych odległościach osi wałów czynnego i biernego. Do
przekazywania napędu na większe odległości nadal używa się pasów płaskich. Pasy płaskie są
łączone za pomocą specjalnych złączy.

Odrębną grupę przekładni pasowych stanowią przekładnie z pasem zębatym (rys. 58),

w których nie występuje poślizg, charakterystyczny dla opisanych przekładni z pasami
płaskimi i klinowymi. Są one stosowane coraz częściej, zwłaszcza w pojazdach
samochodowych.

Rys. 58. Przekładnia pasowa z pasem zębatym [1, s. 94]

Zaletami przekładni pasowych są: prosta i tania konstrukcja, dowolna dokładność

rozstawu osi kół, płynność ruchu; wadami: duże wymiary, zmienność przełożenia, szybkie
zużywanie się pasów, duże naciski na wały i łożyska.

Przekładnie łańcuchowe podobnie jak pasowe należą do przekładni cięgnowych. Cięgno

stanowi łańcuch spoczywający na kole łańcuchowym w odpowiednio ukształtowanych
gniazdach. Dzięki temu uniemożliwiony jest poślizg łańcucha względem koła.

Warunkiem pracy przekładni łańcuchowych jest jednakowa podziałka P łańcucha i koła.

Przełożenie przekładni łańcuchowej obliczamy według wzoru:

Łańcuchy dzielimy na: pierścieniowe (rys. 59), drabinkowe i zębate.

Rys. 59. Łańcuch pierścieniowy i wieńce kół i krążków do łańcuchów pierścieniowych [1, s. 99]

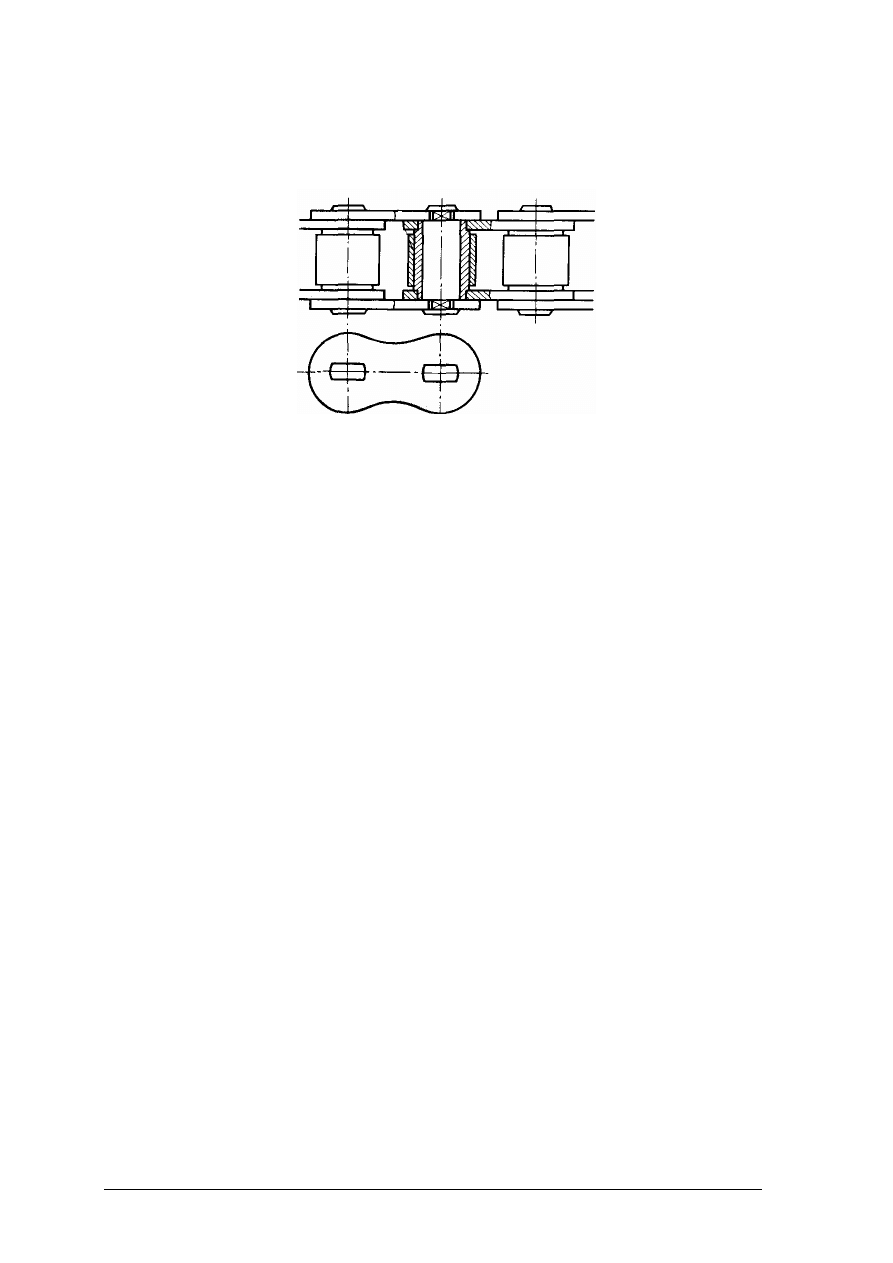
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

69

Łańcuchy pierścieniowe stosuje się w urządzeniach dźwigowych przy małych

prędkościach podnoszenia. Najbardziej obciążane mogą być przekładnie z łańcuchem
tulejowym lub widełkowym, gdyż powierzchnie ich styku z kołem są największe.

Rys. 60. Łańcuch tulejkowy [1, s. 99]

Zaletami przekładni łańcuchowych (rys. 60) są: małe naciski na wały i łożyska,

możliwość przenoszenia dużych obciążeń ,stałe przełożenie, wysoka sprawność (0,97÷0,98),
wadami : konieczność regulacji zwisu łańcucha, nieprzydatność do pracy przy nagłych
nawrotach ,duży hałas, konieczność smarowania i wysoki koszt wykonania.

Przekładnie zębate znajdują największe zastosowanie w budowie maszyn, ponieważ

odznaczają się dużą sprawnością 0,99, mogą przenosić duże moce do 20 000 kW, cechuje je
duża zwartość konstrukcji i stałe przełożenie, przenoszą moment obrotowy na niewielkie
odległości.

Ze względu na kształt koła zębatego dzieli się na: walcowe stożkowe i płaskie (zębatki).

W zależności od kształtu zębów rozróżniamy kola z zębami prostymi, skośnymi, łukowymi
i daszkowymi. Koła zębate o zębach skośnych i łukowych są stosowane tam, gdzie
wymagana jest większa cichobieżność i bardziej równomierna praca. Umożliwiają one
przenoszenie większych momentów obrotowych i mocy. Powodują jednak większe
obciążenia osiowe łożysk. Wadę tę eliminują kola o zębach daszkowych, lecz montaż łożysk
jest wówczas utrudniony.

Zespół kół współpracujących ze sobą tworzy przekładnię zębatą. Przekładnia

jednostopniowa składa się z dwóch kół, wielostopniowa zaś z większej ich liczby.
Ze względu na położenie osi kół przekładnie (rys. 61) dzieli się na: równolegle, kątowe
i wichrowate.

W zależności od sposobu zazębiania mówimy o przekładniach zewnętrznych

i wewnętrznych.

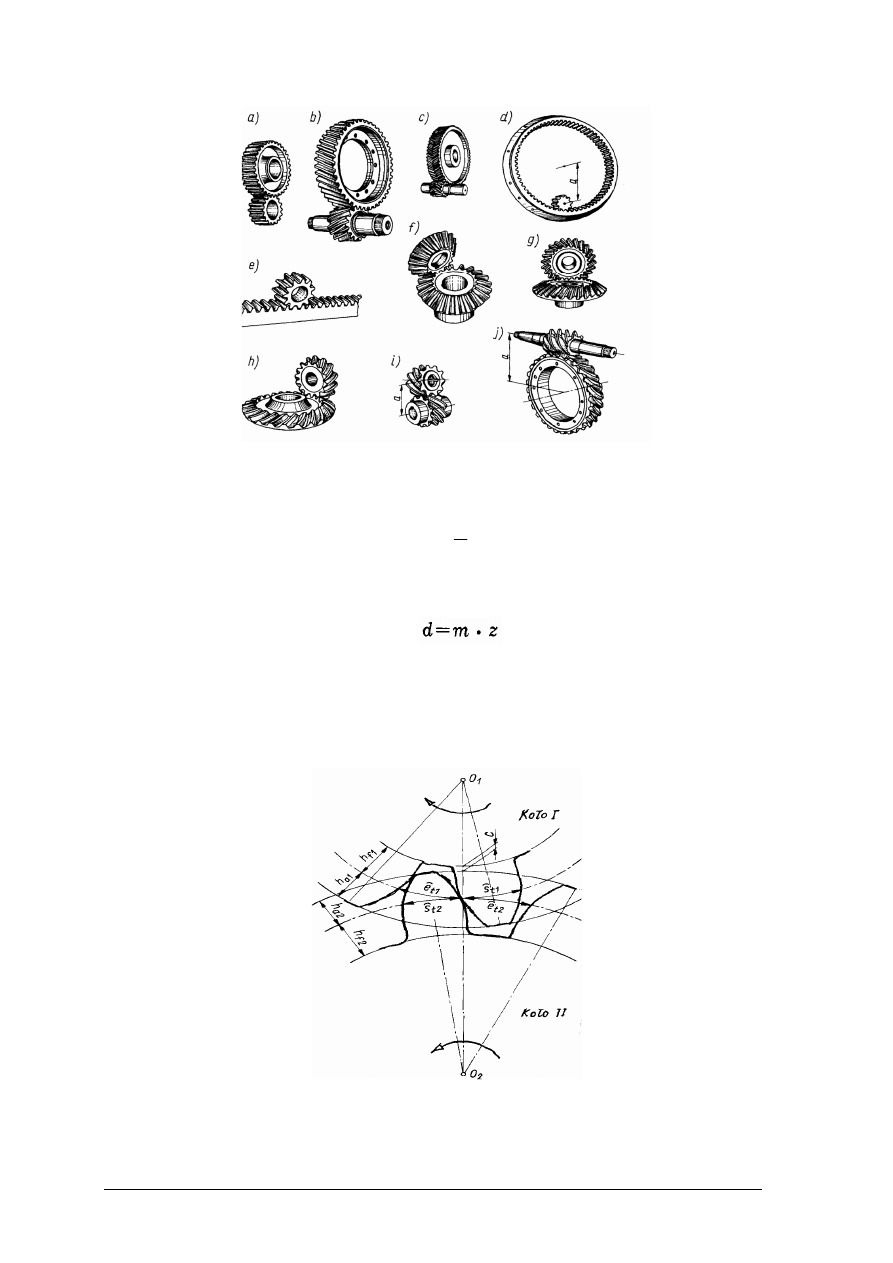
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

70

Rys. 61. Przekładnie zębate: a÷d) walcowe, e) zębatkowa, f÷h) stożkowe, i) śrubowa, j) ślimakowa [8, s. 256]

Wielkość m, zwana modułem, jest podstawowym parametrem kola zębatego.

z

d

m

=

Z powyższego równania wynika, że moduł mieści się w średnicy podziałowej d tyle razy,

ile wynosi liczba zębów z. Zatem średnica podziałowa wynosi

Wartości modułów są znormalizowane i objęte ciągiem liczbowym: 1; 1,25; 1,5; 2; 2,5;

3; 4; 5; 6; 8; 10 itd.

Warunkiem współpracy dwóch kół zębatych jest taki sam zarys ich zębów oraz ich

jednakowy moduł. Ponadto między zębami musi być zachowany luz obwodowy
j

t

i wierzchołkowy c. Zarys zębów jest najczęściej ewolwentowy.

Rys. 62. Zazębienie kół zębatych [1, s. 105]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

71

Pozostałe wielkości charakteryzujące koła zębate oblicza się według następujących

wzorów:

−

wysokość głowy zęba h

a

= m

−

wysokość stopy zęba

h

f

= 1,2 m

−

wysokość całkowita zęba h = m + 1,2 m = 2,2 m

−

ś

rednice wierzchołków i średnice stóp:

d

a

= d + 2h

a

=m (z+2)

d

f

= d – 2h

f

= m (z–2,4)

−

odległość osi współpracujących kół:
a = 0,5 (d

1

+ d

2

)

4.10.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Jaka jest różnica między przekładnią łańcuchową a przekładnią pasową?

2.

Jakie znasz rodzaje kół i przekładni zębatej?

3.

Kiedy stosujemy przekładnie ślimakowe?

4.

W jaki sposób można uzyskać w przekładni pasowej różne kierunki obrotu koła
czynnego koła biernego?

5.

W jaki sposób oblicza się przełożenie przekładni zębatej, prostej i wielostopniowej?

6.

Jaka jest różnica między przekładnią pasową z paskiem zwykłym a paskiem klinowym?

7.

Jakie dwa koła zębate mogą z sobą współpracować?

4.10.3. Ćwiczenia

Ćwiczenie 1

Oblicz prędkość obrotową n

2

wału biernego oraz średnicę koła D

2

w przekładni ciernej

o stałym przełożeniu i = 4 : 1 i średnicy koła D

1

= 40 mm, jeżeli prędkość obrotowa wału

czynnego n

1

wynosi 1600 obr/min.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

przeanalizować dane do ćwiczenia,

2)

podać zależność na przełożenie dla przekładni ciernej o stałym przełożeniu,

3)

obliczyć prędkość obrotową wału biernego,

4)

obliczyć średnicę koła D

2,

5)

sprawdzić jakość wykonanej pracy,

6)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

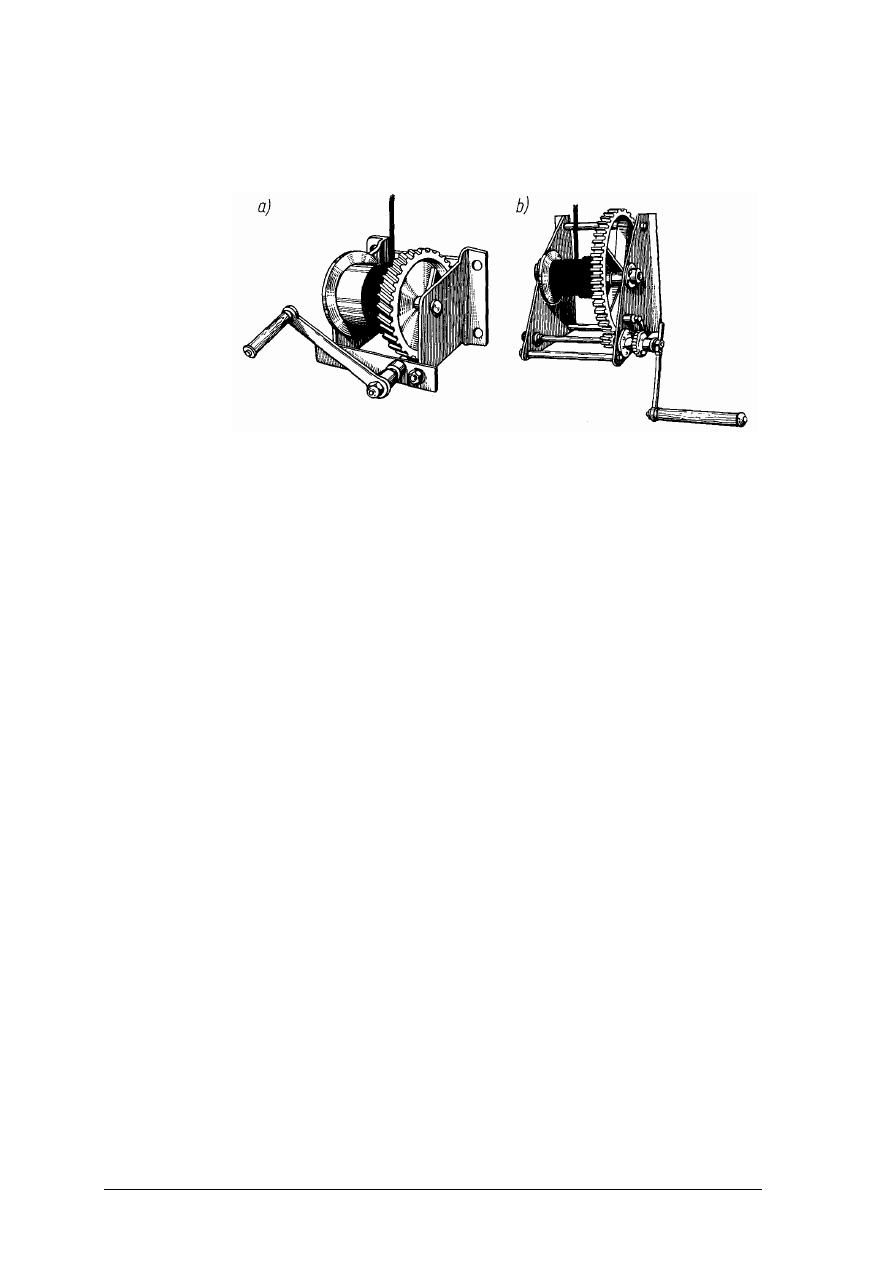
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

72

Ćwiczenie 2

Określ, rodzaj przekładni jaki zastosowano we wciągarkach przedstawionych na rysunku

a) i b). Przedstaw budowę oraz wady i zalety tych przekładni.

Rysunek do ćwiczenia 2 [4, s. 124]

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy,

2)

dokonać analizy budowy i działania wciągarek,

3)

scharakteryzować przekładnie,

4)

określić wady i zalety przekładni,

5)

zaprezentować wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

4.10.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

sklasyfikować przekładnie pasowe?

2)

określić parametry przekładni zębatej?

3)

określić różnicę między przekładnią cięgnową pasową a przekładnią
cięgnową łańcuchową?

4)

obliczyć przełożenie przekładni prostej i wielostopniowej?

5)

wskazać

różnicę

między

przekładniami

przyspieszającymi

a zwalniającymi?

6)

określić zastosowanie przekładni ciernych?

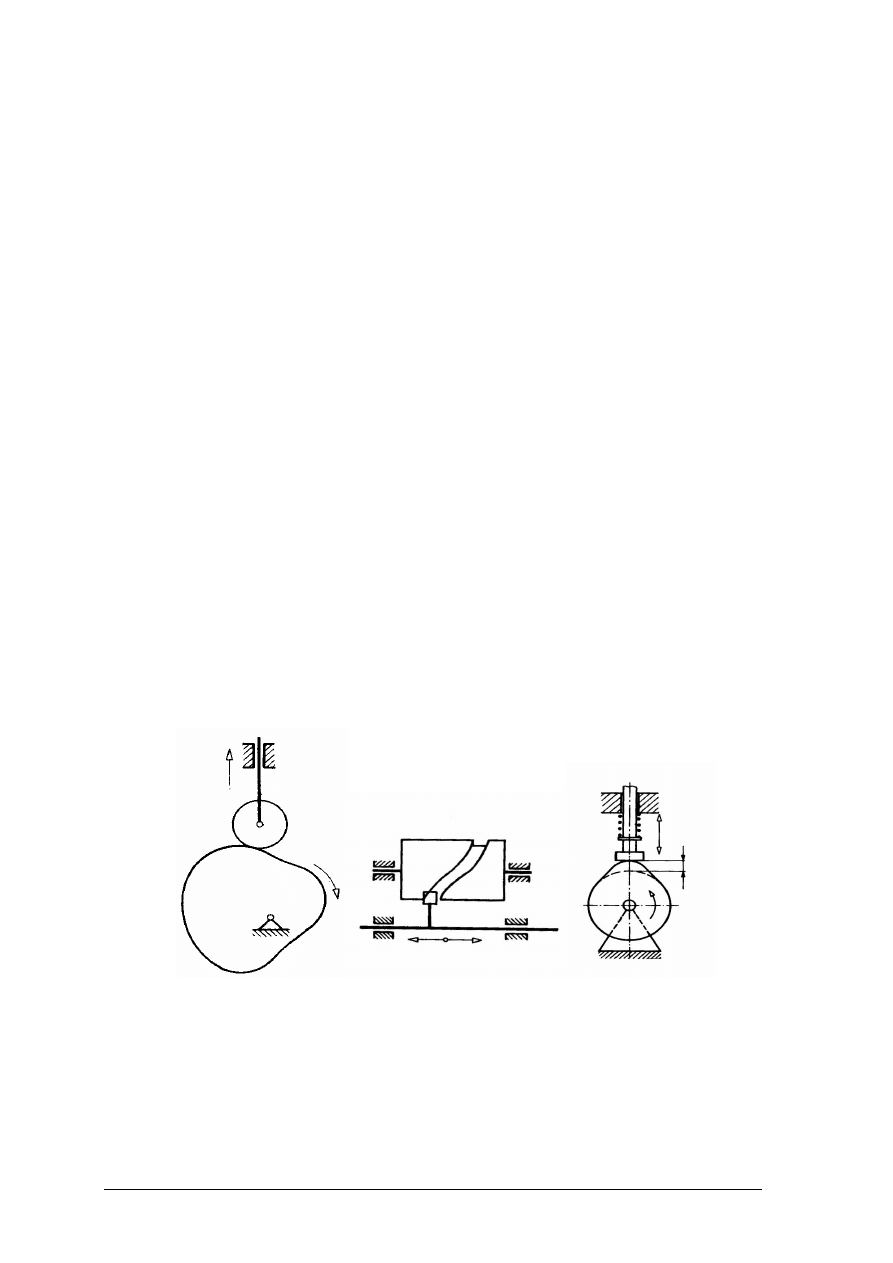
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

73

4.11. Mechanizmy

4.11.1. Materiał nauczania

Mechanizmem nazywa się zespół części maszynowych połączonych ze sobą ruchowo

tak, aby ruch jednej z nich powodował ściśle określone ruchy użyteczne pozostałych części
danego zespołu. W każdej maszynie można wyodrębnić mechanizmy:

−

napędzające,

−

wykonawcze,

−

przekaźnikowe.
Poszczególne części mechanizmu nazywa się członami (ogniwami).
W każdym mechanizmie można wyodrębnić: człon czynny (napędzający), człon bierny

(napędzany) oraz podstawę, którą stanowi człon nieruchomy lub człon, względem którego
określa się ruchy innych członów.

Człon bierny jest napędzany przez człon czynny bezpośrednio lub za pomocą członów

pomocniczych, zwanych łącznikami. Członami mechanizmu mogą być elementy sztywne
(np. dźwignie, tłoki, wały, korby itd.) lub odkształcalne (sprężyny, cięgna: pasy, łańcuchy,
itd.). W niektórych mechanizmach rolę członu odgrywają również ciała ciekłe lub gazowe,
zamknięte w cylindrze lub przewodach.

Mechanizm krzywkowy

Mechanizm krzywkowy (rys. 63) umożliwia otrzymanie dowolnego ruchu elementu

napędzanego. Ruch ten zależy głównie od rodzaju ruchu krzywki i jej kształtu. Mechanizm
krzywkowy składa się z krzywki i popychacza. Kształt krzywki ustała się w zależności od
programu pracy mechanizmu krzywkowego, na który składa się:

−

rodzaj ruchu krzywki,

−

rodzaj ruchu popychacza,

−

sposób przekazywania ruchu.

Rys. 63. Schemat mechanizmu krzywkowego [8, s. 412]

Elementem napędzającym mechanizmu (członem czynnym) jest zwykle krzywka,

a członem napędzanym (biernym) – popychacz. Warunkiem koniecznym dla uzyskania
prawidłowej pracy mechanizmu jest nieprzerwany styk powierzchni roboczej krzywki
z popychaczem.

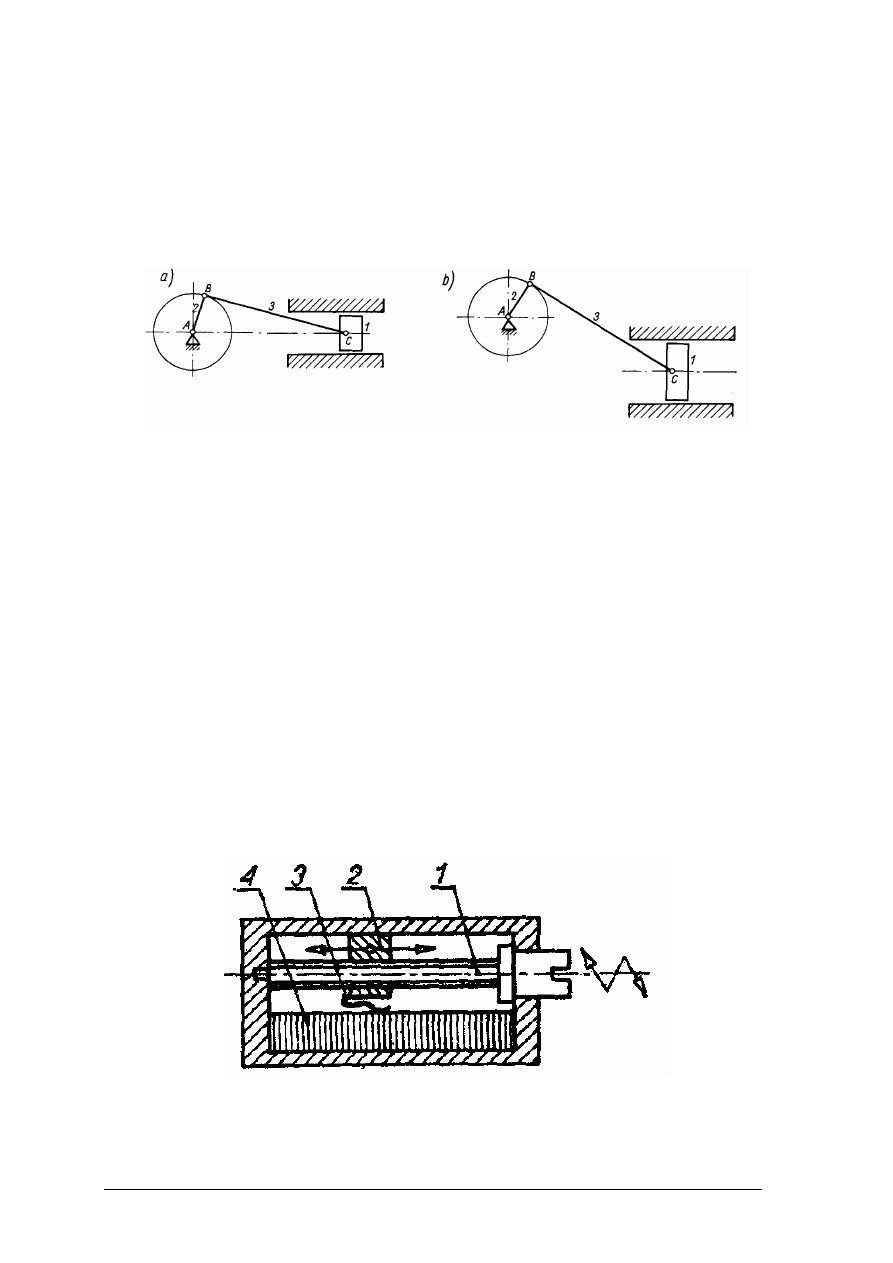
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

74

Mechanizm korbowy

Mechanizm korbowo-tłokowy służy do zamiany ruchu obrotowego wału wykorbionego

na ruch postępowo-zwrotny tłoka. Wartość przesunięcia tłoka zależy od wykorbienia wału.

Mechanizm korbowy składa się w zasadzie z dwóch członów: korby i korbowodu oraz

trzech węzłów: A. B. C. Ruch obrotowy korby wywołuje ruch prostoliniowy (postępowo-
zwrotny) wodzika 1, który jest umieszczony w węźle C i przesuwa się w prowadnicach.

Rys. 64. Schematy mechanizmów korbowych: a) symetrycznego, b) niesymetrycznego

Mechanizm korbowy może być symetryczny (gdy oś prowadnicy wodzika przechodzi

przez oś obrotu korby (rys. 64a) lub niesymetryczny gdy osie te nie pokrywają się (rys. 64b).

Podczas montażu układu korbowo-tłokowego należy spełnić następujące warunki:

−

montaż musi być bardzo staranny ze względu na ciężkie warunki pracy mechanizmu,

−

wartości luzów montażowych muszą być zgodne z podanymi w instrukcji montażu,

−

osie łożysk głównych i czopów wału wykorbionego muszą zachować współosiowość,

−

osie czopów głównych i korbowych muszą zachować równoległość,

−

wał wykorbiony powinien być wyrównoważony dynamicznie (przed montażem).
Mechanizmy korbowo-tłokowe mają zastosowanie w silnikach spalinowych, sprężarkach

i pompach tłokowych. W prasach korbowych są stosowane tylko mechanizmy korbowe.

Mechanizmy śrubowe

Mechanizmy śrubowe służą do zmiany ruchu obrotowego nakrętki (lub śruby) na ruch

prostoliniowy śruby (lub nakrętki). Rzadziej (gdy gwint nie jest samohamowny) można
zamieniać ruch prostoliniowy na obrotowy. Są one stosowane wówczas, gdy zachodzi
konieczność uzyskania powolnego, precyzyjnego ruchu prostoliniowego lub do wywołania
dużej siły (podnośnik, prasa śrubowa). Na rys. 65 przedstawiono mechanizm śrubowy napędu
ś

lizgacza w potencjometrze wieloobrotowym.

Rys. 65

.

Mechanizm śrubowy napędu ślizgacza w potencjometrze wieloobrotowym: 1 – śruba,

2 – nakrętka, 3 – szczotka, 4 – element rezystancyjny

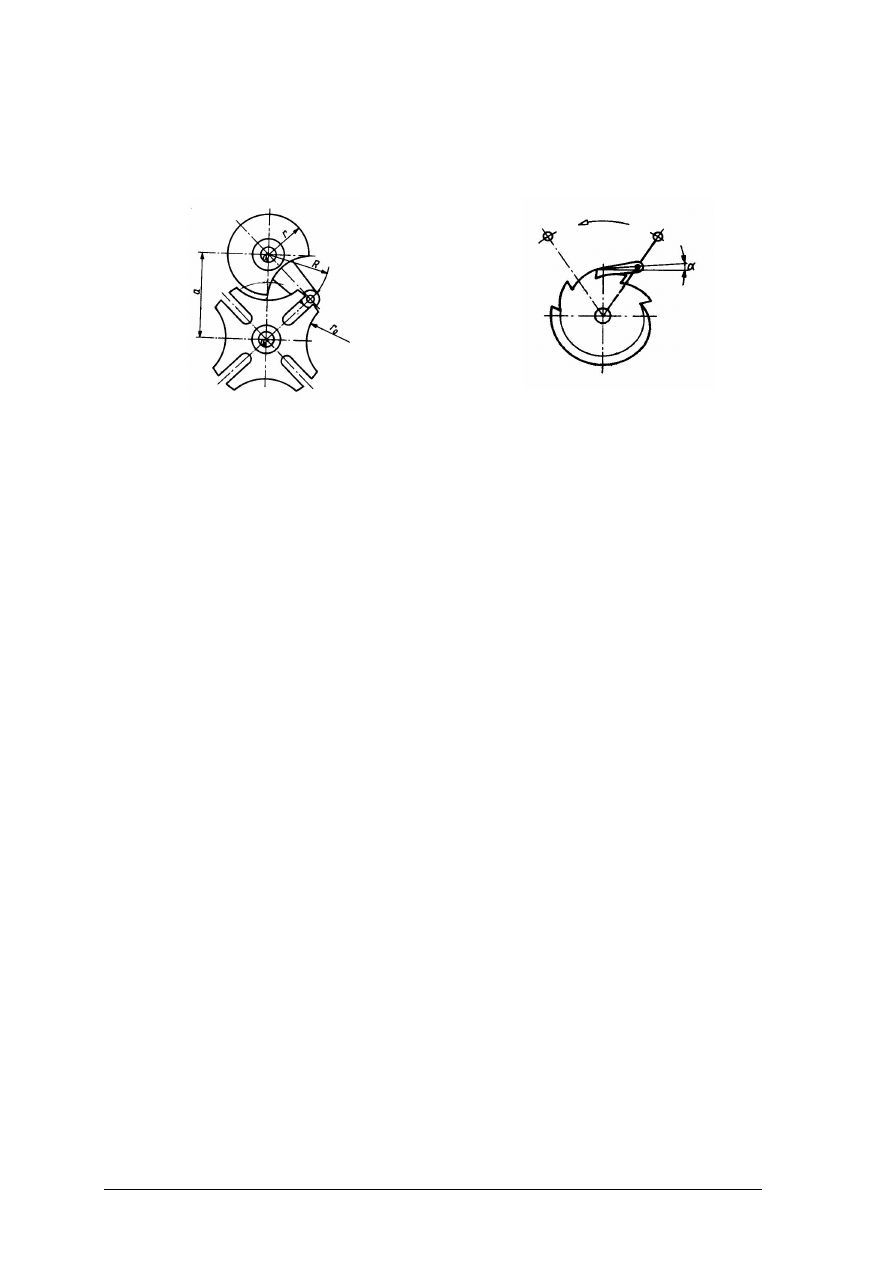
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

75

Mechanizmy do otrzymywania ruchu przerywanego mają za zadanie w zależności od

konstrukcji: uzyskanie ruchu przerywanego jednokierunkowego, przenoszenie ruchu
obrotowego w sposób nieciągły, przenoszenie ruchu prostoliniowego w sposób nieciągły.

Przykłady takich mechanizmów przedstawiają rysunki 66, 67.

Rys. 66. Krzyż maltański [7, s. 395]

Rys. 67. Mechanizm zapadkowy [7, s. 394]

4.11.2. Pytania sprawdzające

Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.

1.

Co to jest para kinematyczna?

2.

Jakie mechanizmy wchodzą w skład każdej maszyny?

3.

Jaka jest różnica między maszyną roboczą a silnikiem?

4.

Od czego zależy kształt krzywki w mechanizmie krzywkowym?

5.

Z czego składa się mechanizm?

6.

Do czego służy mechanizm śrubowy?

4.11.3. Ćwiczenia

Ćwiczenie 1

Mechanizmy ruchu postępowo-zwrotnego wymagają dokładnej obróbki elementów

i dokładnego montażu ze względu na powstające podczas ruchu tarcie, które może zakłócić
pracę układu. Określ, jakie zadanie pełnią w nich prowadnice. Wyjaśnij dlaczego
w konstrukcjach prowadnic metale coraz częściej są zastępowane innym materiałem. Podaj,
jakie to materiały i czym się charakteryzują?

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

zorganizować stanowisko pracy do wykonania ćwiczenia,

2)

dokonać analizy budowy mechanizmów,

3)

opisać zadania prowadnic,

4)

wybrać materiał,

5)

omówić ćwiczenie.

Wyposażenie stanowiska pracy:

−

zeszyt,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

76

Ćwiczenie 2

Na podstawie dokumentacji techniczno-ruchowej urządzenia określ, jakie zastosowano

w nim elementy maszyn oraz rodzaje połączeń.

Sposób wykonania ćwiczenia

Aby wykonać ćwiczenie, powinieneś:

1)

szczegółowo przeanalizować dokumentację techniczną urządzenia,

2)

określić rodzaje zastosowanych połączeń i mechanizmów,

3)

zapisać wyniki analizy konstrukcji urządzenia w tabeli:

Połączenia i mechanizmy

Rodzaj i krótki opis

1 Połączenia nierozłączne

2 Połączenia rozłączne

3 Łożyska

4 Sprzęgła

5 Hamulce

6 Przekładnie mechaniczne
7 Inne mechanizmy

4) przedstawić wyniki ćwiczenia.

Wyposażenie stanowiska pracy:

−

dokumentacja techniczno-ruchowa urządzenia,

−

literatura zgodna z punktem 6 Poradnika dla ucznia.

4.11.4. Sprawdzian postępów

Czy potrafisz:

Tak

Nie

1)

rozpoznać mechanizmu krzywkowe?

2)

sklasyfikować mechanizmy?

3)

opisać części składowe mechanizmu śrubowego?

4)

scharakteryzować mechanizm korbowy?

5)

określić zadania prowadnic?

6)

scharakteryzować

mechanizmy

do

otrzymywania

ruchu

przerywanego?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

77

5. SPRAWDZIAN OSIĄGNIĘĆ

INSTRUKCJA DLA UCZNIA

1.

Przeczytaj uważnie instrukcję.

2.

Podpisz imieniem i nazwiskiem kartę odpowiedzi.

3.

Zapoznaj się z zestawem zadań testowych.

4.

Test zawiera 20 zadań. Zadania są wielokrotnego wyboru i tylko jedna odpowiedź jest
prawidłowa.

5.

Udzielaj odpowiedzi tylko na załączonej karcie odpowiedzi:

6.

Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania.

7.

Kiedy udzielenie odpowiedzi będzie Ci sprawiało trudność, wtedy odłóż jego
rozwiązanie na później i wróć do niego, gdy zostanie Ci wolny czas.

8.

Czas trwania testu – 45 minut.

9.

Maksymalna liczba punktów, jaką można osiągnąć za poprawne rozwiązanie testu
wynosi 20 pkt.

Powodzenia!

ZESTAW ZADAŃ TESTOWYCH

1.

Do wielkości skalarowych (bezkierunkowych) należą
a)

prędkość, naprężenie.

b)

masa, moc.

c)

siła, przyspieszenie,

d)

ciśnienie, moment siły.

2.

Suma sił od wypadkowej różni się
a)

kierunkiem.

b)

zwrotem.

c)

wartością.

d)

punktem zaczepienia.

3.

Kierunek siły reakcji więzów jest znany w przypadku
a)

utwierdzenia.

b)

łożysk stałych.

c)

przegubów.

d)

więzów wiotkich.

4.

Aby z ciała nieswobodnego uczynić ciało swobodne, należy
a)

usunąć więzy ograniczające ruch ciała.

b)

zastąpić więzy siłami reakcji tych więzów.

c)

podpory stałe zastąpić podporami ruchomymi.

d)

siły reakcji więzów zastąpić naciskami na więzy.

5.

Płaski zbieżny układ sił charakteryzuje się tym, że
a)

linie działania sił są do siebie równoległe.

b)

siły mają zgodny kierunek, ale różne zwroty.

c)

linie działania sił przechodzą przez jeden punkt.

d)

siły działają wzdłuż jednej prostej.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

78

6.

Linia działania siły F tworzy z osią x kąt ostry α. Rzut siły F na oś x przedstawia
wyrażenie
a)

F cos α.

b)

F sin α.

c)

F/ cos α.

d)

F/ sin α.

7.

Moment siły F ma największą wartość bezwzględną względem punktu
a)

I.

b)

II.

c)

III.

d)

IV.

8.

Połączenie sworzniowe podlega w szczególności obciążeniom
a)

rozciągającym.

b)

skręcającym.

c)

ś

cinającym.

d)

ś

ciskającym.

9. Wał to element maszyny, który jest

a)

skręcany.

b)

skręcany i zginany.

c)

zginany.

d)

rozciągany.

10. Oś to element maszyny, która jest

a)

rozciągana.

b)

zginana i skręcana.

c)

skręcana.

d)

zginana.

11. Przekładnię nazywamy wichrowatą, której osie wałów

a)

nie są równoległe i nie przecinają się.

b)

są równoległe.

c)

przecinają się.

d)

są równoległe i przecinają się.

12. Zastosowanie przekładni zębatej o zębach skośnych powoduje

a)

głośną pracę.

b)

zwiększenie przełożenia.

c)

cichą pracę.

d)

zmniejszenie przełożenia.

13. Czopami nazywamy

a)

wały o dużej sztywności skrętnej.

b)

krótkie osie lub wały.

c)

osie lub wały bez powierzchni oporowych.

d)

odcinki wału lub osi, których powierzchnie stykają się ze współpracującymi
elementami.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

79

14. Koszyczek w łożysku tocznym służy do

a)

zapewnienia równomiernego rozmieszczenia elementów tocznych.

b)

zapewnienia zmniejszenia tarcia w łożysku.

c)

zabezpieczenia elementów tocznych przed wypadnięciem.

d)

zabezpieczenia elementów tocznych przed uszkodzeniem.

15. Wymiary poprzeczne wpustów pryzmatycznych (b x h) są dobierane w zależności od

a)

rodzaju połączenia (spoczynkowe, ruchowe).

b)

ś

rednicy czopa wału.

c)

ś

rednicy piasty koła.

d)

rodzaju pasowania wpustu w rowek czopa.

16. W przekroju poprzecznym belki obciążonej momentem zginającym występuje naprężenie

a)

normalne rozłożone równomiernie w przekroju.

b)

styczne rozłożone równomiernie w przekroju.

c)

normalne rozłożone nierównomiernie w przekroju.

d)

styczne rozłożone równomiernie w przekroju.

17. W przekroju poprzecznym skręcanego wałka występuje naprężenie styczne, które ma

wartość
a)

zero na obwodzie przekroju.

b)

maksymalną w środku przekroju.

c)

maksymalną na obwodzie przekroju.

d)

jednakową w całym przekroju.

18.

Moment siły względem punktu ma wartość 50 Nm. Wartość siły wynosi 200 N jeśli
odległość linii działania siły od punktu jest
a)

4 m.

b)

2 m.

c)

1 m.

d)

0,25 m.

19.

Dla belki zginanej będzie spełniony warunek wytrzymałości, jeżeli

a)

naprężenie belki nie przekroczy naprężenia dopuszczalnego.

b)

ugięcie belki nie przekroczy wysokości przekroju belki.

c)

naprężenie belki nie przekroczy granicy plastyczności.

d)

strzałka ugięcia nie przekroczy dopuszczalnej wartości ugięcia.

20.

Pręt metalowy utwierdzony jest z jednej strony, a z drugiej strony obciążony jest parą sił
w płaszczyźnie prostopadłej do osi pręta. Moment skręcający pręt ma wartość

a)

maksymalną w połowie pręta.

b)

jednakową na całej długości pręta.

c)

maksymalną w miejscu przyłożenia pary sił.

d)

maksymalną w miejscu utwierdzenia pręta.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

80

KARTA ODPOWIEDZI

Imię i nazwisko ................................................................................................

Rozpoznawanie elementów maszyn i mechanizmów

Zakreśl poprawną odpowiedź.

Nr

zadania

Odpowiedź

Punkty

1

a

b

c

d

2

a

b

c

d

3

a

b

c

d

4

a

b

c

d

5

a

b

c

d

6

a

b

c

d

7

a

b

c

d

8

a

b

c

d

9

a

b

c

d

10

a

b

c

d

11

a

b

c

d

12

a

b

c

d

13

a

b

c

d

14

a

b

c

d

15

a

b

c

d

16

a

b

c

d

17

a

b

c

d

18

a

b

c

d

19

a

b

c

d

20

a

b

c

d

Razem:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”

81

6. LITERATURA

1.

Bożenko L.: Maszynoznawstwo. WSiP, Warszawa 1994

2.

Krajewski B.: Mechanika techniczna. WSiP, Warszawa 1979

3.

Malik B.: Podstawy konstrukcji maszyn. PWN, Warszawa 2000

4.

Oleksiak W., Paprocki K.: Podstawy konstrukcji mechanicznych. WSiP, Warszawa 1996

5.

Osiński Z., Bajon W., Szuski T.: Podstawy konstrukcji maszyn. PWN, 1986

6.

Pszczółkowski T.: Mechanika techniczna. PWN, 1973

7.

Ptyński A.: Podstawy technologii i konstrukcji mechanicznych. WSiP, Warszawa 1998

8.

Rutkowski A.: Części maszyn. WSiP, Warszawa 1986

9.

Rutkowski A. Stępniewska A.: Zbiór zadań z części maszyn. WSiP, Warszawa1987

10.

Siuta W.: Mechanika techniczna. WSiP, Warszawa 2003