
Spis treści
Symbole i oznaczenia.
5
Wstęp.
7
1
Modele algorytmiczne — warunek dopóki.
9
2
Indukcja i dowodzenie jednoczesne.
15
3
Definicje rekurencyjne.
21
4
Ciągi rekurencyjne.
25
5
Przeliczanie.
31
6
Modele kombinatoryczne.
35
6.1
Inne problemy kombinatoryczne. . . . . . . . . . . . . . . . . . . . . . . .
39
7
Funkcje tworzące.
43
8
Grafy.
47
9
Izomorfizmy grafów.
51
10 Własności grafów.
55
10.1 Drogi a krawędzie. Drogi wewnątrz grafu. . . . . . . . . . . . . . . . . . .
56
11 Zasada włączania - wyłączania.
61
12 Zasada Dirichleta.
63
12.1 Teoretyczne podstawy metody. . . . . . . . . . . . . . . . . . . . . . . . .
63
12.2 Zastosowanie metody modelowania w zadaniach. . . . . . . . . . . . . . .
65
13 Równania rekurencyjne.
69
13.0.1 Renumeracja i przesunięcie o stałą wyrazów ciągu geometrycznego.
70
13.1 Modelowanie rekurencyjne z wykorzystaniem liczb Fibonacciego. . . . . .
71
13.1.1 Definicja i własności ciągu liczb Fibonacciego. . . . . . . . . . . . .
71
13.1.2 Wzór Bineta. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
72
13.2 Inne własności ciągu liczb Fibonacciego. . . . . . . . . . . . . . . . . . . .
74
3

SPIS TREŚCI
13.2.1 Przykłady zadań rozwiązanych metodą modelowania rekurencyjne-
go z wykorzystaniem liczb Fibonacciego. . . . . . . . . . . . . . . .
75
13.3 Metoda modelowania rekurencyjnego w zadaniach. . . . . . . . . . . . . .
77
13.3.1 Zadania z kombinatoryki. . . . . . . . . . . . . . . . . . . . . . . .
77
13.3.2 Zadania z rachunku prawdopodobieństwa. . . . . . . . . . . . . . .
79
13.3.3 Zadania algebraiczne.
. . . . . . . . . . . . . . . . . . . . . . . . .
87
14 Modelowanie okrężne.
91
15 Zadania.
95
15.1 Zadania do rozdziałów. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
15.1.1 Rozdziały 1–2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
95
15.1.2 Rozdziały 3–4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
100
15.1.3 Rozdział 4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
101
15.1.4 Rozdziały 5–6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
104
15.1.5 Rozdziały 7–9. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
111
15.1.6 Rozdział 14. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
115
15.2 Zestawy kolokwialne. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
116
15.2.1 Zestaw 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
116
15.2.2 Zestaw 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
117
15.2.3 Zestaw 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
119
4

Symbole i oznaczenia.
i ∈ 1, n ⇔ i ∈ {1, 2, . . . , n}
a | b – a dzieli b
bxc – część całkowita z liczby x
µ(A), |A| – moc (miara) zbioru A
n
k
– symbol Newtona
C
k
n
– kombinacja bez powtórzeń
e
C
k
n
– kombinacja z powtórzeniami
V
k
n
– wariacja bez powtórzeń
e
V
k
n
– wariacja z powtórzeniami
C
k
n
– liczba kombinacji bez powtórzeń
e
C
k
n
– liczba kombinacji z powtórzeniami
V
k
n
– liczba wariacji bez powtórzeń
e
V
k
n
– liczba wariacji z powtórzeniami
P
n
– liczba permutacji
e
P
n
1
,n
2
,...,n
p
– liczba permutacji z powtórzeniami
(A | B) – zdarzenie A pod warunkiem zajścia zdarzenia B.
5

Symbole i oznaczenia.
6

Wstęp.
Elementy matematyki dyskretnej dla finansistów adresowane są przede wszystkim do osób
o elementarnym przygotowaniu z analizy matematycznej, algebry i podstaw matematyki.
Mogą to być studenci matematyki finansowej, ekonometrii czy tez ekonomiści specjalizu-
jący się w inżynierii finansowej, teorii ryzyka lub teorii inwestycji.
Taki wybór adresatów przesądził o nietypowym układzie podręcznika. Nie zawiera on
rozbudowanej dla potrzeb informatyków teorii grafów i sieci. Natomiast większy ciężar
kładziony jest na konstrukcje dotyczące modelowania matematycznego, w tym: kombi-
natorycznego, rekurencyjnego, szufladkowego, przeliczeniowego i okrężnego. Dość silnie
są podkreślone także zastosowania i problemy z zakresu rachunku prawdopodobieństwa.
Taki układ został przyjęty ze względu na potrzeby praktyki.
W zagadnieniach inżynierii i matematyki finansowej wyjściowymi badanymi obiektami
są ciągi i szeregi, na przykład ciągi Fibonacciego wykorzystywane w teorii fal Elliota, a
więc obiekty charakterystyczne dla matematyki dyskretnej. Jednakże relacje między nimi
wymagają odpowiedniego do potrzeb opracowania modeli, hierarchizacji, strukturalizacji,
badania n-tych stanów, na przykład przez przeliczanie lub sumowanie. Dotyczy to zarów-
no konstrukcji deterministycznych jak i losowych. Dlatego dość istotnym wydaje się być
aspekt konstruowania modeli probabilistycznych — fundamentalnych dla analizy z zakre-
su finansów — oczywiście ograniczono się tu przede wszystkim do prawdopodobieństwa
klasycznego w oparciu o konstrukcje przestrzeni dyskretnych.
W niektórych problemach istotne jest także wyznaczanie granic analizowanych ciągów
i szeregów. Jednakże narzucające się tutaj naturalne przejście do metod analizy matema-
tycznej nie wydaje się niezbędne. Techniki badania granic (np. ciągów rekurencyjnych)
są typowym elementem wykładu analizy matematycznej i nie zostały szerzej włączone do
niniejszego podręcznika.
Zasygnalizowane tu zostały jedynie niektóre bardziej zaawansowane techniki modelo-
wania kombinatorycznego, bez rozwinięcia metod analizy kombinatorycznej.
Konstrukcją spinającą, którą przyjąłem dla „przyjaznego” przejścia do metod anali-
tycznych, jest badanie funkcji tworzących. Są to swoiste generatory, które w oparciu o
źródłowe ciągi pozwalają na zastosowanie technik analizy funkcji do zintergowanych wiel-
kości pomocniczych, jakimi są właśnie funkcje tworzące. Również to podejście zawiera
elementy modelowania okrężnego, szczególnie wtedy, gdy poszukujemy pewnych charak-
terystyk parametrycznych badanego modelu, na przykład chcemy wyznaczyć wartości
przeciętne czy miarę zmienności danego skwantyfikowanego procesu. Dlatego ostatni roz-
dział części teoretycznej w zasadzie mógłby być traktowany jako dotatek. Jednakże, ze
względu na jego szczególną rolę, został ujęty jako zamykający wykład.
Do podręcznika dołączone są także przykładowe zadania w układzie uporządkowanym
stosownie do kolejnych działów wykładu oraz zestawy zadań kolokwialnych.
7

Wstęp.
Zarówno konstrukcja merytoryczna podręcznika jak i dobór zadań oparte są o wiele ist-
niejących podręczników i zbiorów. Przykładowo, struktura merytoryczna analizowanych
problemów wybrane przykłady i techniki dowodzenia w rozdziałach: 1, 2, 7, 8, 9 były
wzorowane na klasycznej monografii [1]. Jednakże wiele problemów i zadań ma charakter
autorski. Dotyczy to również ogólnej koncepcji i formalizacji modelowania matematycz-
nego.
8

Rozdział 1
Modele algorytmiczne —
warunek dopóki. ([1])
Wykłady dotyczą ciągów: zdań logicznych, kroków algorytmu, wartości elementów. Chce-
my, by przechodząc od elementu ciągu do następnego, zawsze przy zachowaniu założeń
otrzymać poprawne wyniki.
Zaczniemy od analizy modułu algorytmu dopóki, dopóki zachodzi w którym jest po-
wtarzany zdefiniowany krok tak długo jak zachodzi wyrózniony warunek dopóki.
Twierdzenie 1.1 ∀m ∈ N
0
∀n ∈ N ∃q ∈ N
0
∃r ∈ 0, n − 1
m = qn + r
Dowód. Udowodnimy to twierdzenie, wykorzystując pętlę dopóki, wyznaczając warto-
ści q i r.
Konstrukcja werbalna algorytmu:
1. Dla ustalonych m i n zgadujemy parę wartości q i r, takich że zachodzi m = qn + r.
2. Poprawiamy krok po kroku te wartości zachowując prawdziwość warunku m =
qn + r, kończąc poprawianie gry r ∈ 0, n − 1
Konstrukcję można rozpocząć przyjmując na przykład q = 0 i r = m. O ile m > n
to para (q, r) nie spełnia założenia r ∈ 0, n − 1, natomiast już w tej konstrukcji, na
początku równość m = qn + r pozostaje prawdziwa i będzie taka, gdy zwiększymy q o 1
i zmniejszymy r o n. Powtarzając tę procedurę qn + r = (q + 1)n + (r − n) powinniśmy
otrzymać r ∈ 0, n − 1.
2
Algorytm dzielenia (całkowitoliczbowego).
Wejście { Dane: m ∈ N
0
n ∈ N }
Wyjście { Wyniki: q ∈ N
0
r ∈ 0, n − 1 takie, że qn + r = m }
Wygodniej zapisać q, r ∈ N
0
qn + r = m ∧ r < n.
Początek inicjujący algorytm:
q:=0
r:=m
Zasadnicza część, pętla:
9

ROZDZIAŁ 1. Modele algorytmiczne — warunek dopóki.
DOPÓKI r>=n WYKONUJ
q:=q+1
r:=r-n
KONIEC
Rysunek 1.1: Schemat blokowy algorytmu.
Ogólna postać pętli, dopóki g wykonuj S:
Sprawdź, czy warunek g jest prawdziwy. Jeśli g jest prawdziwy, to wykonaj komplet
instrukcji opisany przez S i wróć do sprawdzenia g, w przeciwnym przypadku przejdź do
nowej instrukcji za pętlą.
Zdefiniujmy kilka pojęć:
Warunek g jest zdaniem w sensie logiki, nazywamy go warunkiem dozoru pętli.
S jest ciągiem kroków nazywanym treścią pętli. S może zmieniać wartość logiczną g
(tzw. pętle warunkowe formalnie zawierają warunek — na przykład wartość liczby
kroków).
Wykonanie kroków S w pętli nazywamy przebiegiem pętli lub iteracją. Pętla kończy
się, gdy warunek dozoru g nie jest spełniony i kontynuacja działania następuje poza
pętlą.
DOPÓKI A niepusty WYKONUJ
wybierz x z A
usun x z A
A może być na przykład zbiorem krawędzi grafu, czy wierzchołków sympleksu. Jeśli
A < ℵ
0
to wykonywanie pętli się zakończy po odrzuceniu wszystkich wierzchołków, jeśli
A jest co najmniej przeliczalny, to wykonywanie pętli się nie zakończy.
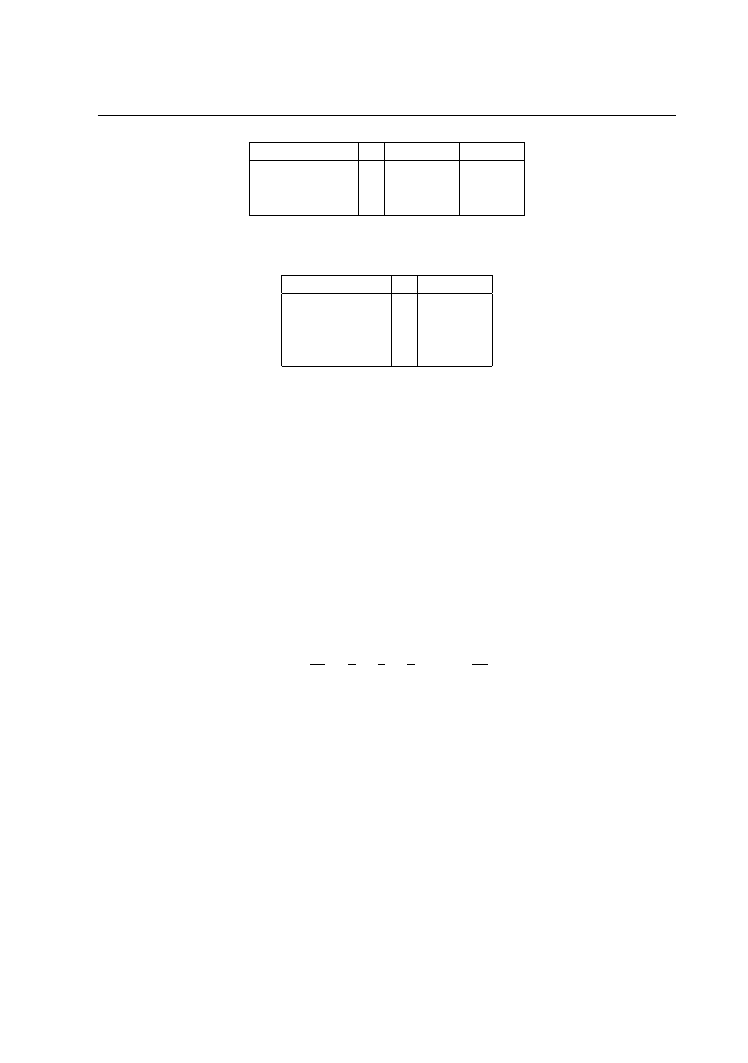
W tabeli zobrazujemy wyniki kolejnych pętli dla dzielenia m = 28 n = 9. Algorytm nie
wchodzi w pętlę dopóki po raz czwarty bo warunek dozoru nie jest spełniony po trzecim
przebiegu.
Nasuwają się następujące pytania:
10

numer iteracji
q
r
r n
0
0
28
prawda
1
1
19
prawda
2
2
10
prawda
3
3
1
fałsz
Tabela 1.1:
1. Czy algorytm zatrzyma się po jakimś czasie?
2. Czy kiedy już się zatrzyma, to otrzymane wyniki są poprawne?
Na pytanie pierwsze odpowiedź brzmi tak, gdyż początek był trywialny (0, m). W każdym
przebiegu pętli wykonujemy q = q + 1, r = r − n w skończonym czasie, czyli wystarczy
wykazać, że algorytm wykona skończenie wiele przebiegów. Kluczowe są zmiany r: m, m−
n, m−2n, . . . na początku r = m 0, ponieważ każdy niepusty podzbiór liczb naturalnych
ma element najmniejszy, to malejące ciągi lizb naturalnych muszą być skończone. Stąd
po k wykonaniach pętli (dla q > k) mamy m − kn = r < n (wybieramy najmniejsze k o
tej własności).
Czyli algorytm zatrzymuje się, co jednakże z poprawnością wyników?
Definicja 1.1.1 Zdanie p jest niezmiennikiem pętli dopóki g, wykonuj S wtedy gdy, speł-
nia ono warunek: jeśli zdania g i q są prawdziwe, zanim wykonamy S, to zdanie p będzie
prawdziwe po wykonaniu S.
Twierdzenie 1.2 Załóżmy, że p jest niezmiennikiem pętli dopóki g, wykonuj S oraz,
że zdanie p jest prawdziwe, kiedy wchodzimy w pętle. Wówczas zdanie p jest prawdziwe po
każdej iteracji pętli. Jeśli pętla kończy się, to po jej zakończeniu zdanie p jest prawdziwe,
a zdanie g fałszywe.
Dowód. Uzasadniajmy nie wprost, p jest prawdziwe na początku. Niech p będzie fałszy-
we po n-tej iteracji po raz pierwszy. Czyli n 1 i zdanie p było prawdziwe po zakończeniu
n − 1 przebiegu (początek to iteracja o numerze 0) zdanie g również było prawdziwe, gdyż
wykonaliśmy n-tą iterację. Ponieważ p jest niezmiennikiem pętli, to musi być prawdziwe.
Sprzeczność.
2
W dowodzie rozpatrywaliśmy zbiór: A = { n ∈ N: zdanie p jest fałszywe po n-tym
przebiegu }. Z założenia zbiór A jest niepusty i ma element najmniejszy, co daje sprzecz-
ność.
Rozważmy następujący algorytm dzielenia:
{ Dane: m ∈ N
0
n ∈ N }
{ Wyniki: q ∈ N
0
r ∈ N
0
takie, że qn + r = m oraz r ∈ 0, n − 1 }
POCZĄTEK
q:=0
r:=m
{qn+r=m oraz r>=0}
DOPÓKI r>=n WYKONUJ
q=:q+1
11

ROZDZIAŁ 1. Modele algorytmiczne — warunek dopóki.
r=:r-n
KONIEC
Stwierdzenie 1.2.1 qn + r = m i r 0 jest niezmiennikiem pętli
Dowód. Warunek jest prawdziwy przed wejściem w pętle dopóki z doboru q i r. Po-
nadto, jeśli qn + r = m i r n i po wykonaniu treści pętli dostajemy q
0
i r
0
takie,
że
q
0
n + r
0
= (q + 1)n + (r − n) = qn + r = m
oraz r‘ = r − n 0 Czyli stwierdzenie to pozostaje prawdziwe po wykonaniu pętli. Tak
więc
1. Pętla kończy się.
2. Z twierdzenia 1.2 po zakończeniu pętli zdania m = qn + r oraz r 0 są prawdziwe,
a zdanie r n jest fałszywe czyli r < n.
Koniec dowodu.
2
Przykład. Rozważmy procedure wyliczania wartości n!!.
Wzór
0!! = 1!! = 1
n!! = (n − 2)!!n
{ Dane: n ∈ N
0
}
{ Wyniki: s ∈ N taka, że s = „silnia silnia”= n!! }
POCZĄTEK
s:=1 {s:=m!!}
JEŚLI 2 dzieli n TO m:=1
W PRZECIWNYM PRZYPADKU m:=0
DOPÓKI m<n-1 WYKONUJ
m:=m+2
s:=sm
KONIEC
Planowanym niezmiennikiem pętli jest s = m!!. Jeśli s = m!! na początku pętli dopóki,
to:
s
nowe
= s
stare
m
nowe
= m!!(m + 2) = (m + 2)!! = (m
nowe
)!!
Co było wymagane na końcu pętli. Pętla kończy się, gdy m = n.
Uwaga. W powyższym algorytmie obliczyliśmy oprócz n!! także (n − 2)!!, (n − 4)!!,
. . . .
Możemy zmodyfikować porządek mnożenia, unikając trudniejszego sformułowania wa-
runku początkowego:
{ Dane: n ∈ N
0
}
{ Wyniki: p ∈ N takie, że p = n!! }
12

POCZĄTEK
p:=1
m:=n
{m!!p=n!!}
DOPÓKI m>1 WYKONUJ
p:=pm
m:=m-2
Sprawdzenie niezmiennika pętli: na początku jest on prawdziwy i jest m!!p = n!! więc:
m
nowe
!!p
nowe
= (m − 2)!!pm = m!!p = n!!
Warunek dozoru pętli powoduje, że pętla kończy się gdy m = 3 lub m = 2 (o ile n > 1).
Jeśli zaś n ∈ {0, 1}, to n!! = 1 = m!!p dla wszystkich n ∈ N
0
. Powyższy algorytm oblicza
w trakcie działania wyrażenia postaci n, n(n − 2), n(n − 2)(n − 4), . . . .
Uwaga. W algorytmie dzielenia występowała zmienna zwiększająca się o 1 w każdym
przebiegu pętli. Nie było jednak wiadome, ile przebiegów wykonamy. W poprzednim algo-
rytmie m przyjmowało wartości 0, 2, 4, . . . , n lub 1, 3, 5, . . . , n w tej kolejności, wiadome
było kiedy algorytm się zatrzyma. Tego typu przewidywalne zwiększanie o 1, 2 lub inną
ustaloną liczbę można opisać przy pomocy następującej notacji:
Definicja 1.2.1 Instrukcja algorytmiczna: dla k od m do n z krokiem r wykonuj S, powo-
duje podstawienie liczb m, m+r, m+2r, . . . , n zamiast k, w takiej kolejności i wykonanie
S za każdym razem (o ile krok jest tak dobrany że m + qr = n).
Fragment algorytmu,
s:=1
DLA k OD 1 DO n WYKONAJ
s:=sk
daje wynik s = n!. Używając pętli dopóki możemy to zapisać:
k=m
DOPÓKI k=<n WYKONUJ
{S} k=k+1
Uwaga. Fragment S nie może zmieniać wartości k.
Przykład. Pętla dopóki.
k:=1
DOPÓKI k=<4 WYKONUJ
k:=k^2
wypisz} k
k:=k+1
KONIEC
Przykład. Pętla ze stałym krokiem (bezwarunkowa).
POCZĄTEK
DLA k OD 1 DO 4 WYKONUJ
k:=k*k
wypisz k
KONIEC
13
ROZDZIAŁ 1. Modele algorytmiczne — warunek dopóki.
numer iteracji
k
wypisz k
k ¬ 4
0
1
-
-
1
2
1
prawda
2
5
4
fałsz
Tabela 1.2:
numer iteracji
k
wypisz k
0
1
1
1
2
4
2
3
9
3
4
16
Tabela 1.3:
Przykład. Algorytm obliczania sumy.
n
X
k=m
a
k
= a
m
+ a
m+1
+ . . . + a
n
n ∈ N
Algorytm:
s:=0
DLA k OD m DO n WYKONUJ
s:=s+a(k)
Na przykład
n
X
k=1
1
k
2
=
1
1
+
1
4
+
1
9
+ . . . +
1
n
2
Uwaga. Nie zawsze da się prosto zastosować pętle bezwarunkowe. Trzeba znać liczbę
przebiegów pętli.
14

Rozdział 2
Indukcja i dowodzenie
jednoczesne. ([1], [4])
Omówimy tutaj konsekwencje twierdzenia 1.2 o niezmiennikach pętli, w konstrukcji in-
dukcyjnej (poprawność wynika z dobrego uporządkowania zbioru N).
Przykład. Wykażmy, że 14 | 37
700
− 37
100
i znajdźmy wynik dzielenia (liczbę ponad
1000-cyfrową). Z nieparzystości 37 mamy 2 | 37
700
− 37
100
wystarczy wykazać, że 7 |
37
700
− 37
100
, lecz jeżeli q = 3
100
to 7 | q
7
− q i zamiast liczyć możemy spróbować
wykazać, że ∀n ∈ N 7 | n
7
− n (sprawdzamy doświadczalnie dla małych q ∈ N),
7 | 1
7
− 1 = 0
7 | 2
7
− 2 = 126
7 | 3
7
− 3 = 2184
7 | 4
7
− 4 = 16380
..
.
7 | 15
7
− 15 = 170859360
Konstruujemy pętlę, która ma sprawdzić czy n
7
−n jest podzielne przez 7 dla n ∈ 1, 37
100
.
POCZĄTEK
n:=1
DOPÓKI n<37^100 WYKONUJ
JEŚLI n^7-n jest podzielne przez 7 TO
n:=n+1
KONIEC
Niezmiennikiem pętli jest: n
7
−n podzielne przez 7. Pętla sprawdza, czy warunek zachodzi
i jeżeli jest prawdziwy, to przechodzi do następnego n. Sprawdziliśmy, że 7 | 1
7
− 1, stąd
na początku wchodząc w pętlę przewidywany niezmiennik jest prawdziwy. Twierdzimy,
że algorytm się kończy (dla n = 37
100
) oraz, że podane zdanie jest niezmiennikiem pętli.
Rozważmy k-ty przebieg pętli k < 37
100
. Jeśli 7 - k
7
− k to nie nastąpi wykonanie
treści pętli, algorytm nie zatrzyma się. Jeśli zaś 7 | k
7
− k, to z treści pętli k ⇒ k + 1,
algorytm sprawdza warunek dozoru k + 1 < 37
100
i następnie warunek podzielności dla
15

ROZDZIAŁ 2. Indukcja i dowodzenie jednoczesne.
k + 1. Wystarczy pokazać, że w każdej iteracji zdanie warunkowe jest prawdziwe. Zapewni
to wykonanie i zatrzymanie algorytmu. Czy 7 | (k + 1)
7
− (k + 1)?
(k + 1)
7
− (k + 1) =
k
7
+ 7k
6
+ 21k
5
+ 35k
4
+ 35k
3
+ 21k
2
+ 7k + 1 − k − 1 =
k
7
− k + 7k(k
5
+ 3k
4
+ 5k
3
+ 5k
2
+ 3k + 1)
Stąd algorytm możemy uprościć, nie musi sprawdzać zdania warunkowego, podzielność
jest zagwarantowana. Czyli w iteracji zwiększamy jedynie n o 1 aż dla n = 37
100
pętla
kończy się. W początkowej wersji algorytm musiałby sprawdzać podzielność dla wszyst-
kich liczb 1
7
−1, 2
7
−2, 3
7
−3, . . . , (37
100
−1)
7
−(37
100
−1). Jednakże jedyną liczbą, którą
należało sprawdzić była 1
7
− 1. Dla wszystkich pozostałych wykazaliśmy algebraicznie,
że o ile 7 | k
7
− k ⇒ 7 | (k + 1)
7
− (k + 1) i nie było potrzeby wykonywania w praktyce
naszego algorytmu, posłużył on jedynie do wykazania, że 7 | 37
700
− 37
100
.
Analogicznie możemy pokazać, że ∀n ∈ N 7 | n
7
− n stosując powyższe rozumowanie
do nie kończącej się pętli.
n:=1
DOPÓKI n>=1 WYKONUJ
JEŚLI 7 dzieli n^7-n TO
n:=n+1
Uogólnijmy to rozumowanie. Weźmy skończony ciąg zdań:
p(m), p(m + 1), . . . , p(n) gdzie p(k), k ∈
hm, ni
m < n
m, n ∈ N. W przykładzie
powyżej, było to 7 | k
7
− k dla k ∈ 1, 37
100
.
Ponadto wiemy że:
1. Zdanie p(m) jest prawdziwe.
2. Zdanie p(k + 1) jest prawdziwe jeżeli zdanie p(k) jest prawdziwe i k ∈ m, n − 1
Wówczas wszystkie zdania p(k), k ∈ m, n są prawdziwe. Uzasadnienie możemy zrealizować
przy pomocy pętli:
k:=m
{zdanie p(k) jest prawdziwe}
DOPÓKI k należy do <m,n-1> WYKONUJ
JEŚLI p(k) jest prawdziwe TO
k:=k+1
Z 2 wynika, że zdanie p(k) jest prawdziwe, jest niezmiennikiem pętli i pętla kończy się
dla k=n. Czyli zachodzi p(k) ⇒ p(k + 1), stąd p(k) jest prawdziwe na końcu każdego
przebiegu pętli. Z dobrego uporządkowania N wynika, że jeśli kiedykolwiek zdanie p(k)
będzie fałszywe, to musi istnieć najmniejsze i dla którego jest nieprawdziwe. Lecz z 1 i 2
otrzymujemy, że i /
∈ m, n.
Tą techniką wykazaliśmy:
Twierdzenie 2.1 Zasada skończonej indukcji matematycznej. Niech p(k), k ∈ m, n bę-
dzie skończonym ciągiem zdań. Jeśli
1. zdanie p(m) jest prawdziwe oraz
16
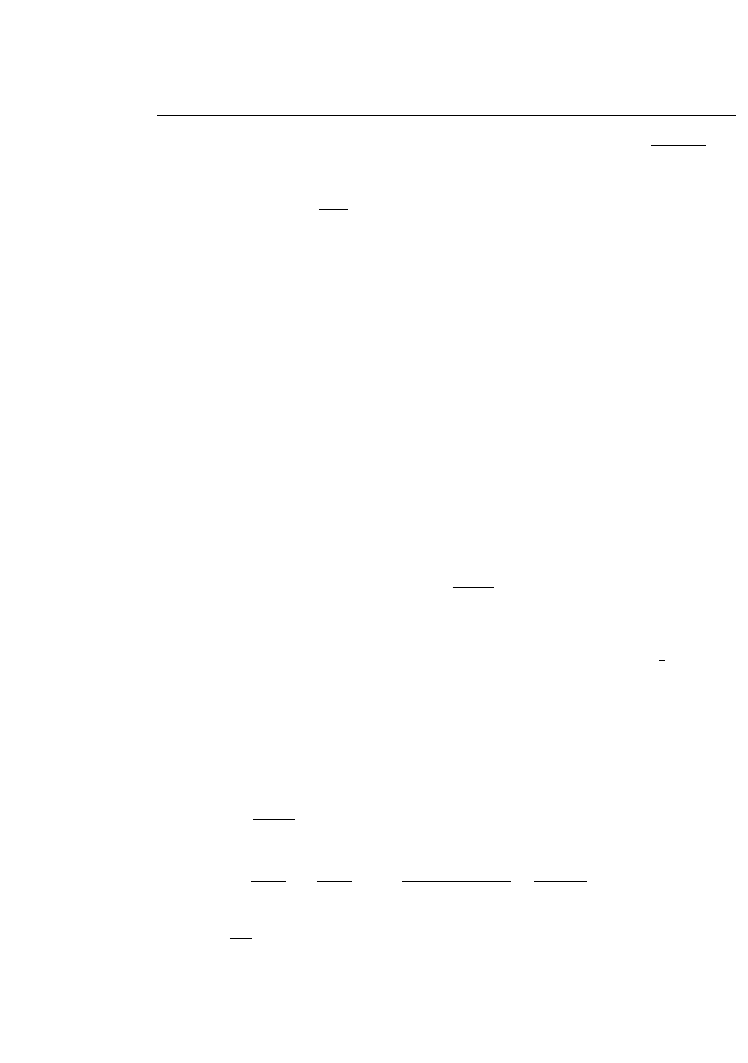
2. zdanie p(k + 1) jest prawdziwe, jeżeli zdanie p(k) jest prawdziwe, k ∈ m, n − 1.
To wszystkie zdania są prawdziwe.
Zastępując warunek k ∈ m, n warunkiem k ∈ N ∧ k m mamy
Twierdzenie 2.2 Zasada indukcji matematycznej. Niech p(m), p(m + 1), . . . , będzie
ciągiem zdań. Jeżeli
1. zdanie p(m) jest prawdziwe oraz
2. zdanie p(k + 1) jest prawdziwe jeżeli zdanie p(k) jest prawdziwe k m, k ∈ N to
∀k ∈ N;
k m zdania p(k) są prawdziwe.
Definicja 2.2.1 Punkt pierwszy w każdej z postaci zasady indukcji jest warunkiem po-
czątkowym.
Definicja 2.2.2 Punkt drugi nazywamy krokiem indukcyjnym.
Jeśli wykażemy oba punkty to mamy zakończony dowód indukcyjny.
W dowodach indukcyjnych nie dowodzimy bezpośrednio prawdziwości zdania p(k +
1). Dowodzimy implikacji p(k) ⇒ p(k + 1) jeżeli teraz p(k) jest prawdziwe, to z reguły
odrywania p(k+1) jest prawdziwe. Czyli w pewnym sensie dowodzimy nieskończenie wielu
twierdzeń, p(1), p(1) ⇒ p(2), p(2) ⇒ p(3), . . . . W technice dowodu nie musimy wykonywać
pętli. Pętla została wykorzystana do dowodu (2.2) zasady indukcji matematycznej. Mamy
tylko sprawdzić oba warunki.
Przykład. Udowodnić indukcyjnie, że
P
1
i
1
i
2
...i
k
= n gdzie sumowanie przebiega po
wszystkich niepustych (różnych) podzbiorach {i
1
, i
2
, . . . , i
k
} zbioru {1, 2, . . . , n}, (i
1
<
i
2
< . . . < i
k
).
Dowód. Indukcja względem n.
Warunek 1. Dla n = 1 tylko {1} 6= ∅, {1} ⊂ {1} odpowiada mu suma
P
1
1
= 1.
Warunek 2. Załóżmy, że twierdzenie jest prawdziwe dla pewnej liczby n 1. Każdy
niepusty pozdbiór zbioru {1, 2, . . . , n, n + 1} jest:
suma mnogościową {n + 1} i niepustego podzbioru zbioru {1, 2, . . . , n}
zbiorem jednoelementowym {n + 1}
podzbiorem zbioru {1, 2, . . . , n}
Stąd suma
P
1
i
1
i
2
...i
k
brana po wszystkich niepustych podzbiorach zbioru {1 , 2, . . ., n,
n + 1}, wynosi
1
n + 1
n +
1
1 + n
+ n =
n + 1 + n(n + 1)
n + 1
=
(n + 1)
2
n + 1
= n + 1
Gdyż w pierwszym składniku korzystamy z założenia indukcyjnego i wyłączamy wspól-
nyczynnik
1
n+1
2
Przykład. Złe użycie indukcji. ∀n 2
2 | n.
Warunek 1 Sprawdzamy dla n = 2 :
2 | 2.
Warunek 2.
2 | 2, 2 | 3, . . . , 2 | (k − 1), 2 | k
k 2
17

ROZDZIAŁ 2. Indukcja i dowodzenie jednoczesne.
Stąd 2 | (k + 1) bo 2 | (k − 1) ⇒ (k − 1) = c2, c ∈ N
0
⇒ k + 1 = 2 + (k − 1) =
2(c + 1) ⇒ c
1
= c + 1
∃c
1
∈ N k + 1 = 2c
1
.
Przykład. Ciąg (x
n
) jest określony wzorem:
x
1
= c
c ∈ N
x
n+1
= cx
n
+
p(c
2
− 1)(x
2
n
− 1)
n ∈ N
Wykażemy, że ∀n
x
n
∈ N.
Sprawdzamy dla pierwszych dwóch wyrazów warunek 1.
x
1
= c
x
2
= 2c
2
− 1 ∈ N
Zakładamy, że (warunek 2)
∀k ∈ 1, n
x
k
∈ N ⇒ x
n+1
∈ N
x
n+1
− cx
n
=
p
(c
2
− 1)(x
2
n
− 1)
czyli
(x
n+1
− cx
n
)
2
= (c
2
− 1)(x
2
n
− 1)
(2.1)
analogicznie renumerując
n − 1 → n
(x
n
− cx
n−1
)
2
= (c
2
− 1)(x
2
n−1
− 1)
x
2
n
− 2cx
n
x
n−1
+ c
2
x
2
n−1
= c
2
x
2
n−1
− c
2
− x
2
n−1
+ 1
x
2
n
+ c
2
− 1 = 2cx
n
x
n−1
− x
2
n−1
c
2
x
2
n
− x
2
n
− c
2
+ 1 = c
2
x
2
n
− 2cx
n
x
n−1
+ x
2
n−1
(c
2
− 1)(x
2
n
− 1) = (cx
n
− x
n−1
)
2
(2.2)
Porównując 2.1 i 2.2 mamy (x
n+1
−cx
n
)
2
= (cx
n
−x
n−1
)
2
z definicji ciągu x
n+1
cx
n
ponadto c ∈ N oraz (x
n
) jest niemalejący to cx
n
x
n−1
stąd mamy x
n+1
− cx
n
=
cx
n
− x
n−1
⇒ x
n+1
= 2cx
n
− x
n−1
∈ N.
Zapiszmy dotychczas poznaną zasadę indukcji matematycznej (twierdzenie 2.2) ina-
czej.
Stwierdzenie 2.2.1 Niech m ∈ Z oraz p(n) niech będzie ciągiem zdań dla n ∈ Z, n m.
Jeśli
1. zdanie p(m) jest prawdziwe oraz
2. dla k > m zdanie p(k) jest prawdziwe, jeśli zdanie p(k − 1) jest prawdziwe
To zdanie p(n) jest prawdziwe dla każdego n ∈ Z, n m.
Twierdzenie 2.3 Druga zasada indukcji matematycznej. Niech n ∈ Z oraz niech p(n)
będzie ciągiem zdań zdefiniowanych na zbiorze {n ∈ Z n m} jeśli
1. zdanie p(m) jest prawdziwe oraz
2. dla k > m zdanie p(k) jest prawdziwe, jeśli wszystkie zdania p(m), . . . , p(k − 1) są
prawdziwe.
To zdanie p(n) jest prawdziwe ∀n ∈ Z n m.
18
Sprawdzenie warunku 2.
Mamy
k =m + 1
p(m) ⇒ p(m + 1)
k =m + 2
p(m) ∧ p(m + 1) ⇒ p(m + 2)
..
.
..
.
Uwaga. Zasady indukcji matematycznej używamy gdy prawdziwość zdań w (warunku
2) wynika z poprzednich, lecz nie bezpośrednio poprzedzających zdań.
Stwierdzenie 2.3.1 Każda liczba całkowita n 2 może być zapisana jako iloczyn liczb
pierwszych, przy czym jeśli n ∈ P to iloczyn traktujemy jako n, czyli tę liczbę.
Dowód. Zauważmy, że do wykazania że 2
132049
można tak zapisać (jako iloczyn 2 . . . 2
| {z }
132049
),
nie potrzebujemy korzystać z liczby poprzedniej czyli 2
132049
−1 która jest liczba pierwszą i
ma 39751 cyfr. Czyli pierwsza zasada indukcji (twierdzenie 2.2) nie będzie tu bezpośrednio
przydatna.
Warunek 1. Bierzemy p(2), jest to liczba pierwsza, czyli „iloczyn” z definicji.
Warunek 2. Bierzemy k 2 i zakładamy, że zdanie p(n) jest prawdziwe dla wszystkich
n ∈ 2, k − 1. Mamy wykazać, że p(k) jest prawdziwe jeśli k ∈ P, to jest to prawda. Jeśli
k /
∈ P, to k = ij gdzie i, j ∈ N − {1} czyli 2 ¬ i < k oraz 2 ¬ j < k, lecz p(i) i p(j)
są z założenia (twierdzenie 2.2) zdaniami prawdziwymi czyli i i j są iloczynami liczb
pierwszych, więc ij jest również iloczynem liczb pierwszych.
2
Uwaga. Konstrukcja egzystencjalna dowodu nie wymaga stałego kroku (różnego od
jeden) dlatego nie jest konieczne sprawdzanie w warunku 1 innych zdań niż p(2).
Uwaga. Są sytuacje, gdy ogólny dowód kroku indukcyjnego nie funkcjonuje dla skoń-
czenie wielu początkowych wartości k. Te wartości muszą być wówczas sprawdzane od-
dzielnie, czyli włączamy je w konstrukcję warunku drugiego. To uogólnienie można sfor-
mułować następująco:
Twierdzenie 2.4 Druga zasada indukcji matematycznej. Niech m ∈ Z, niech p(n) będzie
ciągiem zdań zdefiniowanych dla n ∈ Z, n m niech l ∈ N
0
. Jeśli
1. wszystkie zdania p(m), . . . , p(m + l) są prawdziwe oraz
2. dla k > m + l zdanie p(k) jest prawdziwe, jeśli wszystkie zdania p(m), . . . , p(k − 1)
są prawdziwe
To zdanie p(n) jest prawdziwe dla każdego n ∈ Z, n m.
Poprzednią wersję pierwszej zasady otrzymujemy dla l = 0, jeśli zaś l > 0 to renumeracja
ciągu sprowadza sformułowanie do poprzedniej postaci drugiej zasady.
Uwaga. Obie wersje zasady indukcji matematycznej można sformułować dla ciągów
skończonych jako zasady skończonej indukcji matematycznej.
Twierdzenie 2.5 Wykażemy równoważność obu postaci zasady indukcji matematycznej
w wersji nieskończonej.
19

ROZDZIAŁ 2. Indukcja i dowodzenie jednoczesne.
Dowód. Z drugiej wynika pierwsza, bo jeśli zachodzi p(m) ∧ . . . ∧ p(k − 1) to zachodzi
p(k − 1). Z pierwszej wynika druga. Udowodnimy przez zaprzeczenie.
1. Warunek 1. p(m), . . . , p(m + l) są prawdziwe.
2. Warunek 2. Dla k > m+l zdanie p(k) jest prawdziwe, jeśli zdania p(m), . . . , p(k −1)
są prawdziwe i zdanie p(n) jest fałszywe dla pewnego n m.
Konstruujemy zbiór S = {n ∈ Z n m oraz zdanie p(n) jest fałszywe } 6= ∅ Na mocy
zasady dobrego uporządkowania, zbiór S ma element najmniejszy n
0
z warunku 1: n
0
>
m + l. Ponieważ p(n) jest prawdziwe dla n ∈ m, n
0
, to p(n
0
) jest prawdziwe na mocy
pierwszej postaci, to n
0
/
∈ S sprzeczność. Więc p(n) jest prawdziwe dla n m.
2
20

Rozdział 3
Definicje rekurencyjne. ([1], [2],
[5], [10], [11])
Definicja 3.0.1 Mówimy że model ma konstrukcję rekurencyjną, jeżeli:
1. Określony jest pewien skończony zbiór obiektów modelu (zwykle jeden lub kilka pierw-
szych obiektów).
2. Pozostałe obiekty są zdefiniowane za pomocą poprzednich.
Wzór definiujący obiekt nazywamy: wzorem, równaniem lub zależnością rekurencyjną.
Punkt 1 to warunek zawierający początek lub krok początkowy definicji, a punkt 2
definiuje następne obiekty jako reguła rekurencyjna.
Przykład. Badamy ciąg s(n) =
P
n
k=0
1
k!
1. s(0) = 1
2. s(n + 1) = s(n) +
1
(n+1)!
Gdzie z kolei ciąg n! = s(n) jest zdefiniowany rekurencyjnie dla n ∈ N
0
.
1. s(0) = 1
2. s(n + 1) = (n + 1)s(n)
Wygodę stosowania definicji rekurencyjnej bez ciągłego obliczania na przykład n! daje
konstrukcja:
Q(0)
=
1
Q(n + 1)
=
n + 1
Q(n)
Kilka początkowych wartości umieściliśmy w tabeli 3.1.
Uwaga. Nie znamy wzoru ogólnego! Wyrazy, na przykład Q(55) istnieją, chyba, że
któryś krok wymaga czynności niedozwolonej matematycznie. Dla dowodu skorzystajmy
z zasady dobrego uporządkowania N.
S = {n ∈ N Q(n) = 0 ∨ Q(n) nie jest określony}
21

ROZDZIAŁ 3. Definicje rekurencyjne.
n = 0
Q(1) =
1
1
= 1
n = 1
Q(2) =
2
1
= 2
n = 2
Q(3) =
3
2
n = 3
Q(4) =
8
3
Tabela 3.1:
Pokażemy, że S = ∅. W przeciwnym przypadku, istniałby najmniejszy element m ∈ S.
Z warunku 1 Mamy m 6= 0, to m − 1 ∈ N
0
, Q(m − 1) 6= 0 i Q(m − 1) jest określona. Z
warunku 2 mamy Q(m) =
m
Q(m−1)
6= 0 czyli m /
∈ S ⇒ S = ∅ (przez sprzeczność), czyli
Q(n) jest dobrze określona dla n ∈ N
0
.
Uwaga. W powyższym dowodzie korzystaliśmy z faktu, że Q(n + 1) zależy tylko od
Q(n). Jeżeli konstrukcja zależy od innych niż tylko poprzedzający wyrazów, to dowód
można poprawić modyfikując warunek 1, również z zasady dobrego uporządkowania albo
z rozszerzonej wersji zasady indukcji matematycznej (twierdzenie 2.4).
Uwaga. Istnieją konstrukcje rekurencyjne bardziej efektywne, gdy nie trzeba wyliczać
wszystkich wyrazów poprzednich, a tylko niektóre.
Przykład.
T (1)
=
1
T (n)
=
2T
j
n
2
k
dla
n 2
Wówczas
T (99) = 2T
j
99
2
k
= 2T (49) =
2 · 2T (24) = 2
3
T (12) = 2
4
T (6) = 2
5
T (3) =
2
6
T
j
3
2
k
= 2
6
T (1) = 2
6
Potrzebne są wartości T (49), T (24), T (12), T (6), T (3), nie ma potrzeby obliczać innych.
Przykład. Ciąg Fibonacciego.
F (0)
=
F (1) = 1
F (n)
=
F (n − 1) + F (n − 2)
dla
n ∈ N, n 2
Oczywiście wzór rekurencyjny nie ma sensu dla n = 1 stąd F (1) musi być zdefiniowane
w warunku 1. Początkowe wyrazy ciągu podajemy w tabeli 3.2.
Przykład. Jak zdefiniować ciąg 1, 1, 1, 2, 2, 2, 3, 3, 3, . . .
Q(0) = Q(1) = Q(2) = 1
Q(n) = Q(n − 3) + 1
n 3
22
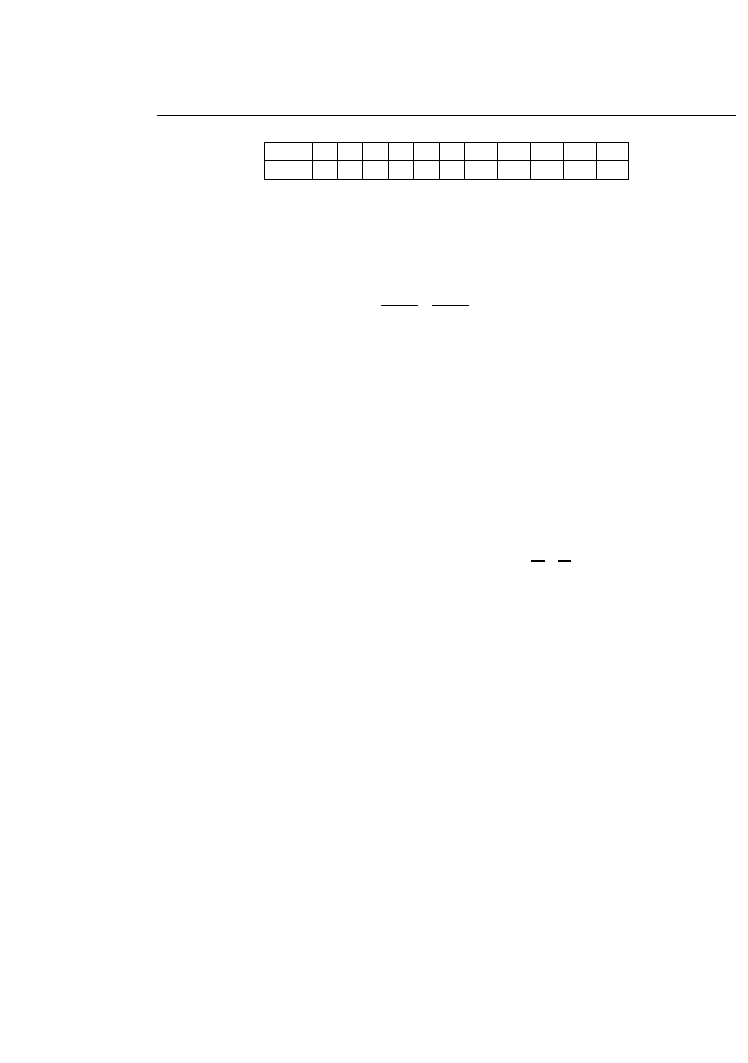
n
0
1
2
3
4
5
6
7
8
9
10
F(n)
1
1
2
3
5
8
13
21
34
55
89
Tabela 3.2: Wartości ciągu Fibonacciego.
Przykład. Niech ω = {a, b}, będzie alfabetem złożonym z dwóch liter. Niech s
n
oznacza
liczbę słów długości n, w których nie występują kolejne dwie litery a, a. Oznaczmy przez
A
n
zbiór słów zawartych w ω
n
=
n
z
}|
{
ω × ω × . . . × ω nie zawierających dwóch kolejnych liter
a: A
0
= ∅, A
1
= ω, A
2
= ω
2
− {(a, a)}. Przyjmujemy długość 0 słowa pustego. Liczba
słów o długości zero to s
0
= 1 (założenie), s
1
= 2, s
2
= 3, aby przeliczyć liczbę słów
spełniających warunek, czyli wyznaczyć s
n
załóżmy, że n 2 i przyjmujemy konstrukcje
rekurencyjną przy pomocy słów krótszych. Jeżeli słowo należące do A
n
kończy się literą
b, to może je poprzedzać dowolna litera, czyli dowolne słowo z A
n−1
. Jeśli jest to a, to
musi ją poprzedzać b czyli słowo z A
n−2
a po nim b. Stąd:
s
n
= s
n−1
+ s
n−2
oraz
s
0
= 1
s
1
= 2
Łatwo zauważyć, że s
n
= F (n + 1), n ∈ N. Można także, przerachować słowa zawierające
powtórzenia a. Jest ich 2
n
− F (n + 1), z czego 2
n
=
2 · . . . · 2
|
{z
}
n możliwości wyboru
to liczba wszystkch
słów o długości n.
23

ROZDZIAŁ 3. Definicje rekurencyjne.
24

Rozdział 4
Ciągi rekurencyjne. ([1], [3], [5],
[6], [7], [10], [11], [13], [17], [21])
Definicja 4.0.2 Ciąg (a
n
) nazywamy ciągiem rekurencyjnym rzędu k, jeżeli istnieje licz-
ba naturalna k i liczby rzeczywiste (lub zespolone), γ
1
, γ
2
, . . ., γ
k
, takie, że poczynając od
pewnej wartości m wskaźnika n, dla wszystkich następnych wartości wskaźnika n, zachodzi
związek
a
n+k
= γ
1
a
n+k−1
+ γ
2
a
n+k−2
+ . . . + γ
k
u
n
(4.1)
Powyższy związek nazywamy równaniem rekurencyjnym rzędu k.
Tak więc ciąg rekurencyjny ma tę własność, że poczynając od pewnego miejsca każ-
dy jego wyraz wyraża się przy pomocy wzoru 4.1 przez stale tę samą ilość k wyrazów
poprzedzających.
Rozważmy ciąg rekurencyjny zdefiniowany następująco:
a
0
= c
0
a
1
= c
1
c
0
, c
1
∈ R (lub innego ciała liczbowego)
a
n+2
= αa
n+1
+ βa
n
n ∈ N
0
Definiujemy równanie charakterystyczne dla tego ciągu w postaci:
x
2
= αx + β
lub
x
2
− αx − β = 0
(4.2)
Zbadajmy najpierw przypadki szczególne:
1.
β = 0
α 6= 0
=⇒
a
0
= c
0
a
1
= c
1
a
n+1
= αa
n
n ∈ N to
a
2
= αa
1
a
3
= αa
2
= α
2
a
1
i przez indukcję
a
n+1
= α
n
a
1
= α
n
c
1
jeżeli
c
1
= αc
0
to
a
n
= α
n
c
0
25

ROZDZIAŁ 4. Ciągi rekurencyjne.
2.
α = 0 ∧ β 6= 0
=⇒
a
0
= c
0
a
1
= c
1
a
n+2
= βa
n
a
2
= βa
0
= βc
0
a
3
= βa
1
= βc
1
a
4
= β
2
c
0
i przez indukcję
a
2n
= β
n
c
0
n ∈ N
0
a
2n+1
= β
n
c
1
Weźmy α, β 6= 0, stąd możemy postawić hipotezę, że rozwiązania mogą przyjąć postać
wzoru ogólnego a
n
= bq
n
, z b jako stałą lub kombinacji liniowej takich wyrażeń. Ponadto,
w takiej sytuacji określmy q:
q
n+2
= αq
n+1
+ βq
n
/ : q
n
q 6= 0
czyli
q
2
− αq − β = 0
Czyli q jest rozwiązaniem równania charakterystycznego. Załóżmy że q ∈ R.
Twierdzenie 4.1 Przyjmijmy zależność rekurencyjną w postaci:
a
n+2
= αa
n+1
+ βa
n
n ∈ N
0
a
0
= c
0
, a
1
= c
1
(4.3)
Dla której równanie charakterystyczne ma postać:
x
2
− αx − β = 0
α, β 6= 0
(4.4)
Jeśli równanie charakterystyczne ma dwa różne pierwiastki q
1
6= q
2
to
a
n
= k
1
q
n
1
+ k
2
q
n
2
(4.5)
Wartości stałych wyznaczamy z układu liniowego
c
0
= k
1
+ k
2
c
1
= k
1
q
1
+ k
2
q
2
Jeżeli istnieje jeden podwójny pierwiastek q to
a
n
= k
1
q
n
+ k
2
nq
n
(4.6)
i k
1
, k
2
wyznaczamy z układu
c
0
= k
1
c
1
= k
1
q + k
2
q ⇒ k
2
= −c
0
+
c
1
q
26

Dowód 4.5. Układ
c
0
= k
1
+ k
2
c
1
= k
1
q
1
+ k
2
q
2
ma zawsze rozwiązanie ponieważ q
1
6= q
2
. Zależność rekurencyjna to a
n+2
= αa
n+1
+ βa
n
.
Wystarczy pokazać, że ciąg zdefiniowany w punkcie 4.5 spełnia tę zależność. Ponieważ
q
2
i
= αq
i
+ β
i = 1, 2
to
q
n+2
i
= αq
n+1
i
+ βq
n
i
i = 1, 2
Gdyż q
i
spełniały równanie charakterystyczne 4.2, sprawdzamy kombinacje liniową (in-
dukcja)
αa
n+1
+ βa
n
=
α(k
1
q
n+1
1
+ k
2
q
n+1
2
) + β(k
1
q
n
1
+ k
2
q
n
2
) =
k
1
(αq
n+1
1
+ βq
n
1
) + k
2
(αq
n+1
2
+ βq
n
2
) =
k
1
q
n+2
1
+ k
2
q
n+2
2
= a
n+2
n ∈ N
0
2
Dowód 4.6. Równanie charakterystyczne ma postać:
(x − q)
2
= 0
x
2
− 2qx + q
2
= x
2
− αx − β ⇒ α = 2q
β = −q
2
Równanie rekurencyjne przyjmuje postać:
a
n+2
= 2qa
n+1
− q
2
a
n
n ∈ N
a
0
= c
0
= k
1
a
1
= c
1
= (k
1
+ k
2
)q
q 6= 0
to
k
1
= c
0
k
2
= −c
0
+
c
1
q
Wystarczy pokazać, że dowolny ciąg określony wzorem 4.6 spełnia zależność
a
n+2
= 2qa
n+1
− q
2
a
n
lecz
2qa
n+1
− q
2
a
n
=
2q(k
1
q
n+1
+ k
2
(n + 1)q
n+1
) − q
2
(k
1
q
n
+ k
2
nq
n
) =
k
1
(2q
n+2
− q
n+2
) + k
2
(2(n + 1)q
n+2
− nq
n+2
) =
k
1
q
n+2
+ k
2
(n + 2)q
n+2
= a
n+2
n ∈ N
0
2
Uwaga. Dowód jest również prawdziwy dla q
1
, q
2
/
∈ R, (∈ C−R), lecz o ile α, β, c
0
, c
1
∈
R to ∀n ∈ N
0
a
n
∈ R.
27
ROZDZIAŁ 4. Ciągi rekurencyjne.
Przykład. Niech a
n+2
= a
n+1
+ 2a
n
, a
0
= a
1
= 3
n ∈ N
0
. Równanie charaktery-
styczne x
2
− x − 2 = 0 ma pierwiastki: q
1
= 2, q
2
= −1, stosujemy punkt 4.5 twierdzenia
4.1 i:
a
n
= k
1
2
n
+ k
2
(−1)
n
a
0
= 3 = k
1
+ k
2
a
1
= 3 = 2k
1
− k
2
⇒ k
1
= 2
k
2
= 1
czyli
a
n
= 2 · 2
n
+ (−1)
n
= 2
n+1
+ (−1)
n
n ∈ N
0
Przykład. Ciąg Fibonacciego.
a
0
= a
1
= c
0
= c
1
= 1
a
n+2
= a
n+1
+ a
n
n ∈ N
0
czyli α = β = 1, to równanie charakterystyczne x
2
− x − 1 ma dwa pierwiastki
q
1
=
1 +
√
5
2
q
2
=
1 −
√
5
2
Stosujemy punkt 4.5 twierdzenia 4.1 skąd:
a
n
= k
1
1 +
√
5
2
n
+ k
2
1 −
√
5
2
n
n ∈ N
0
lub dla wygody k
1
q
n
1
+ k
2
q
n
2
. Wyznaczmy k
1
, k
2
:
1 = k
1
+ k
2
1 = k
1
1 +
√
5
2
+ k
2
1 −
√
5
2
=
k
1
+ k
2
2
+
√
5
2
(k
1
− k
2
) =
1
2
+
√
5
2
(k
1
− k
2
)
otrzymujemy więc
k
1
+ k
2
= 1
k
1
− k
2
=
1
√
5
2k
1
= 1 +
1
√
5
⇒ k
1
=
5 +
√
5
10
k
2
= 1 −
1 +
√
5
2
√
5
=
5 −
√
5
10
stosując twierdzenie 4.1 punkt 4.5 mamy:
a
n
= k
1
q
n
1
+ k
2
q
n
2
=
a
√
5
q
n
1
−
q
2
√
5
q
n
2
=
1
√
5
(q
n+1
1
− q
n+1
2
)
to
F (n) =
1
√
5
"
1 +
√
5
2
n+1
−
1 −
√
5
2
n+1
#
∈ N
0
28

Łatwo zauważyć przez oszacowanie
√
5 − 1
2
<
2
3
⇒ ∀n
1
√
5
1 −
√
5
2
n+1
<
1
2
to
F (n) ∼
=
$
1
√
5
(
1 +
√
5
2
)
n+1
+
1
2
%
dla dużych n
Przykład.
mamy ciąg
(a
n
):
a
0
= 1
a
1
= −3
a
n+2
= 6a
n+1
− 9a
n
n ∈ N
0
równanie charakterystyczne:
x
2
− 6x + 9 = 0 ⇒ α = −6
β = 9
Mamy podwójny pierwiastek q = 3 stąd z punktu 4.6 z twierdzenia 4.1 wynika:
a
n
= k
1
3
n
+ k
2
n3
n
n ∈ N
0
dla n = 0, 1 odpowiednio 1 = k
1
, −3 = 3k
1
+ 3k
2
, k
2
= −2 czyli
a
n
= 3
n
− 2n3
n
= 3
n
(1 − 2n)
n ∈ N
0
Wiele algorytmów wykorzystuje sortowanie, podział pliku (zbioru) na części, wykona-
nie działań w podczęściach a następnie agregowanie wyników. Wyliczając jednostkowe,
porównywalne operacje potrzebne do wykonania algorytmu przy zadanej wielkości n zbio-
ru mamy układ:
2 | n ⇒ Q(n) = 2Q
n
2
+ R(n)
R(n) – działania agregujące wyniki.
Twierdzenie 4.2 Niech a
n
będzie ciągiem spełniającym zależność rekurencyjną:
a
2n
= 2a
n
+ r(n)
n ∈ N
(4.7)
wówczas:
a
2
k
= 2
k
"
a
1
+
1
2
k−1
X
m=0
r(2
m
)
2
m
#
k ∈ N
0
(4.8)
Uwaga. Gdy a
2
n
= 2a
n
+ a + bn gdzie a, b stałe, to:
a
2
k
= 2
k
a
1
+ (2
k
− 1)a +
b
2
2
k
k
zaś dla n = 2
k
mamy (szczególna postać):
a
n
= na
1
+ (n − 1)a +
b
2
n log
2
n
Dowód. Sprawdzamy warunek 1.
k = 0
a
0
2
= a
1
= 2
0
a
1
bo
k − 1 < 0 ⇒
k−1
X
m=0
(. . .) = 0
29
ROZDZIAŁ 4. Ciągi rekurencyjne.
Warunek 2.
a
2
k
= 2
k
"
a
1
+
1
2
k−1
X
m=0
r(2
m
)
2
m
#
dla k ∈ N
0
mamy:
a
2
k+1
= a
2·2
k
= 2a
2
k
+ r(2
k
) =
jest to zależność rekurencyjna i z założenia 2 wynika, że
= 2
k+1
"
a
1
+
1
2
k−1
X
m=0
r(2
m
)
2
m
#
+ r(2
k
) =
2
k+1
"
a
1
+
1
2
k−1
X
m=0
r(2
m
)
2
m
+
1
2 · 2
k
r(2
k
)
#
=
2
k+1
"
a
1
+
1
2
k
X
m=0
r(2
m
)
2
m
#
W szczególnym przypadku, gdy f (n) = a + bn można podstawić ten wynik, lub bezpo-
średnio sprawdzić że:
a
2
k
= 2
k
a
1
+ (2
k
− 1)a +
b
2
k2
k
k ∈ N
0
2
Uwaga, wzór z twierdzenia 4.2 nie podaje wszystkich wyrazów ciągu. Jednakże na
przykład, dla monotonicznych ciągów pozwala na oszacowania wielkości a
n
.
30
Rozdział 5
Przeliczanie. ([1], [4], [6], [7],
[10], [11], [18], [19], [20], [21])
Bedziemy rozważać modele przeliczające zbiory skończone
X = µ(X) < ∞. Konstrukcja
modelu polega na dobraniu takiej wzajemnie jednoznacznej funkcji f : X → Y , że Y jest
zbiorem o znanej strukturze kombinatorycznej, to znaczy znamy µ(Y ).
Definicja 5.0.1 Modelowanie zastępujące zbiór X o skomplikowanej strukturze, zbiorem
o zdefiniowanej strukturze, realizowane w sposób wzajemnie jednoznaczny (nawet dla zbio-
rów o większej mocy) nazywamy modelowaniem wzajemnie jednoznacznym lub przelicze-
niowym (dla zbiorów skończonych).
Ograniczmy się do zbiorów skończonych X = {x
1
, x
2
, . . . , x
n
}. Zbiorowi X odpowiada
wówczas zbiór indeksów I
X
= {1, 2, . . . n}. W niektórych przypadkach, gdy nie powoduje
to kłopotów interpretacyjnych (X ⇔ I
X
) utożsamia się powyższe zbiory.
Definicja 5.0.2 Niech I
n
= {1, 2, . . . , n} = 1, n, zbiór {i
1
, i
2
, . . . , i
k
} składający się z do-
wolnych elementów zbioru I
n
nazywamy ciągiem k-elementów zbioru I
n
(lub k-tką zbioru
I
n
). Analogicznie dla zbioru X, µ(X) = n.
Możemy w k-tkach wprowadzić rozróżnienie ze względu na to, czy ma znaczenie kolejność
elementów k-tki, oraz czy mogą powtarzać się elementy w k-tce. Oznaczamy:
C
k
n
= { zbiór nieuporządkowanych k-tek bez powtórzeń }
k ∈ 0, n
e
C
k
n
= { zbiór nieuporządkowanych k-tek z powtórzeniami }
k ∈ N
V
k
n
= { zbiór uporządkowanych k-tek bez powtórzeń }
k ∈ 0, n
e
V
k
n
= { zbiór uporządkowanych k-tek z powtórzeniami }
k ∈ N
Elementy zbiorów
C
k
n
i e
C
k
n
nazywamy kombinacjami z n elementów po k, odpowiednio bez
i z powtórzeniami. Elementy zbiorów
V
k
n
i e
V
k
n
nazywamy wariacjami, z n elementów po k
odpowiednio bez i z powtórzeniami.
Dla k = n zbiór
V
n
n
=
P
n
nazywamy zbiorem permutacji n elementów, gdzie przez per-
mutację rozumiemy konkretne ustawienie (ciąg uporządkowany n elementowy). Operacja
permutowania polega na przestawieniu elementów permutacji.
31

ROZDZIAŁ 5. Przeliczanie.
Dla przedstawienia liczebności elementów wyżej wymienionych zbiorów wprowadzamy
oznaczenia:
µ(
C
k
n
) = C
k
n
µ(e
C
k
n
) = e
C
k
n
µ(
V
k
n
) = V
k
n
µ(e
V
k
n
) = e
V
k
n
µ(
P
n
) = P
n
Indukcyjnie łatwo dowodzimy:
Twierdzenie 5.1
P
n
= n!
(5.1)
e
V
k
n
= n
k
(5.2)
V
k
n
=
n!
(n − k)!
= n(n − 1)(n − 2) · . . . · (n − k + 1)
(5.3)
Twierdzenie 5.2
C
k
n
=
n
k
=
n!
k!(n − k)!
(5.4)
e
C
k
n
=
n + k − 1
k
(5.5)
Dowód 5.4. Otrzymujemy natychmiast z twierdzenia 5.1 punkt 5.3 utożsamiając per-
mutację k-elementów (nie rozróżniamy kolejności)
C
k
n
=
V
k
n
P
k
=
n
k
2
Dowód 5.5. Niech X = {a
1
, a
2
, . . ., a
n
}, a
i
6= a
j
, i 6= j, i, j ∈ 1, n. Uzupełniamy
zbiór X o k − 1 nowych elementów a
n+1
, a
n+2
, . . ., a
n+k−1
tworzymy zbiór X
∗
= {a
1
,
a
2
, . . ., a
n
, a
n+1
, . . ., a
n+k−1
}, a
i
6= a
j
, i 6= j, i, j ∈ 1, n + k − 1. Wybieramy dowolny
k-elementowy ciąg uporządkowany {a
i
1
, a
i
2
, . . ., a
i
k
} z powtórzeniami elementów zbioru
X, gdzie i
1
i
2
. . . i
k
. Temu ciągowi (czyli k-tce) przyporządkowujemy następujący
ciąg k elementowy (k-tkę): {a
i
1
+0
, a
i
2
+1
, a
i
3
+2
, . . ., a
i
k
+k−1
}.
Ta konstrukcja tworzy funkcję wzajemnie jednoznaczną pomiędzy zbiorem wszystkich
k-tek z powtórzeniami utworzonych z elementów zbioru X a zbiorem wszystkich k-tek
bez powtórzeń utworzonych z elementów zbioru X
∗
, czyli
e
C
k
n
= C
k
n+k−1
2
Przykład.
n = 2
X = {a, b}
k = 3 to do X
∗
dodajemy zbiór {c, d}
(a, a, a) → (a, b, c)
(a, a, b) → (a, b, d)
(a, b, b) → (a, c, d)
(b, b, b) → (b, c, d)
32

Twierdzenie 5.3 Niech ∀
i ∈ 1, k A
i
=
a
i
1
, a
i
1
, . . . , a
i
n
, n
i
∈ N. Zbiór k-tek upo-
rządkowanych postaci
a
1
i
1
, a
2
i
2
,. . ., a
k
i
k
gdzie a
1
i
1
∈ A
1
, a
2
i
2
∈ A
2
,. . . , a
k
i
k
∈ A
k
jest
iloczynem kartezjańskim A
1
× A
2
× . . . × A
k
= ×
k
i=1
A
i
wówczas µ(A
1
× A
2
× . . . × A
k
) =
n
1
n
2
· . . . · n
k
=
Q
k
i=1
n
i
Dowód. Dowód metodą indukcji względem k. Z definicji k = 1, µ(A
1
) = n
1
. Dla k = 2
tworzymy macierz jak w poniższej tabeli. Stąd mamy µ(A
1
× A
2
) = n
1
n
2
. Analogicznie
A
2
A
1
a
1
1
a
1
2
a
1
3
. . .
a
1
n
1
a
2
1
(a
1
1
, a
2
1
)
(a
1
2
, a
2
1
)
(a
1
3
, a
2
1
)
. . .
(a
1
n
1
, a
2
1
)
a
2
2
(a
1
1
, a
2
2
)
(a
1
2
, a
2
2
)
(a
1
3
, a
2
2
)
. . .
(a
1
n
1
, a
2
2
)
..
.
..
.
..
.
..
.
. .
.
..
.
a
2
n
2
(a
1
1
, a
2
n
2
)
(a
1
2
, a
2
n
2
)
(a
1
3
, a
2
n
2
)
. . .
(a
1
n
1
, a
2
n
2
)
Tabela 5.1:
zwiększając wymiar produktu kartezjańskiego z k do k +1, mając A
∗
1
= A
1
×A
2
×. . .×A
k
,
A
∗
2
= A
1
× A
2
× . . . × A
k
× A
k+1
i zachowując konstrukcję tablicy jak dla k = 2
µ(A
∗
1
× A
∗
2
) = (n
1
n
2
· . . . · n
k
)n
k+1
=
k+1
Y
i=1
n
i
2Wniosek z twierdzenia 5.3:
µ(A
k
) = µ(A × A × . . . × A
|
{z
}
k
) = n
k
co daje konstrukcję twierdzenia 5.1 punkt 5.2.
Twierdzenie 5.4 Niech A
∗
=
n
a
1
1
, a
1
2
, . . ., a
1
n
1
, a
2
1
, a
2
2
, . . ., a
2
n
2
, . . ., a
p
1
, a
p
2
, . . ., a
p
n
p
o
,
gdzie
P
p
i=1
n
i
= n. Tworzymy zbiór wszystkich permutacji elementów zbioru A
∗
, przy
czym traktujemy elementy a
i
1
, a
i
2
,. . ., a
i
n
i
jako nierozróżnialne dla i ∈ 1, p. Otrzymane
ciągi nazywamy permutacjami z powtórzeniami o długości n, utworzonymi z elementów
zbioru A =
a
1
, a
2
,. . ., a
p
} w których element a
i
powtarza się n
i
razy. Oznaczamy zbiór
tych permutacji przez e
P
n
1
,n
2
,...,n
p
n
. Wówczas
µ(e
P
n
1
,n
2
,...,n
p
n
) = e
P
n
1
,n
2
,...,n
p
n
=
n!
n
1
!n
2
! · . . . · n
p
!
(5.6)
Dowód. Element a
1
możemy umieścić na C
n
1
n
różnych sposobów na n
1
ze wszystkich
n miejsc permutacji. Niezależnie od tego, każdemu z tych sposobów odpowiada C
n
2
n−n
1
różnych sposobów na jakie można wybrać n
2
z pozostałych n − n
1
miejsc, w których
umieszczamy element a
2
, i konstruujemy tak dalej aż do p-tego kroku, gdy a
p
umieszczamy
na C
n
p
n−n
1
−n
2
−...−n
p−1
= C
n
p
n
p
= 1 sposobów na pozostałych n − n
1
− n
2
− . . . − n
p−1
= n
p
33

ROZDZIAŁ 5. Przeliczanie.
miejscach, stąd:
µ( e
P
n
1
n
2
·...·n
p
n
) =
n!
n
1
!(n − n
1
)!
·
(n − n
1
)!
n
2
!(n − n
1
− n
2
)!
·
·
(n − n
1
− n
2
)!
n
3
!(n − n
1
− n
2
− n
3
)!
· . . . ·
(n − n
1
− . . . − n
p−1
)!
n
p
!0!
=
n!
n
1
!n
2
! · . . . · n
p
!
2
Przykład. Rozmieszczamy kule w szufladach.
1. Ułożono k nierozróżnialnych kul w n rozróżnialnych szufladach. Obliczyć liczbę
sposobów rozmieszczenia, gdy każda z szuflad może zawierać co najwyżej jedną
kulę.
(model Fermiego-Diraca)
C
k
n
2. Rozmieszczono k nierozróżnialnych kul w n rozróżnialnych szufladach. Obliczyć licz-
bę sposobów rozmieszczenia, gdy nie ma ograniczenia na liczbę kul w szufladzie
(model Bosego-Einsteina)
C
k
n+k−1
= e
C
k
n
3. Rozmieszczamy k rozróżnialnych kul w n rozróżnialnych szufladach. Oblicz liczbę
sposobów rozmieszczenia, jeżeli nie ma ograniczenia na liczbę kul, które mogą się
znaleźć w jednej szufladzie.
(model Maxwella-Boltzmanna)
e
V
k
n
4. Rozmieszczamy k rozróżnialnych kul w n rozróżnialnych szufladach. Oblicz liczbę
sposobów rozmieszczenia, jeśli jedna szuflada może zawierać co najwyżej jedną kulę.
V
k
n
Przykład. Udowodnić w oparciu o wzajemnie jednoznaczne modelowanie przeliczenio-
we, że
1.
n
k
=
n
n−k
2.
n
k
=
n−1
k−1
+
n−1
k
3. V
k
n
= V
k
n−1
+ kV
k−1
n−1
4. e
C
k
n
= e
C
k
n−1
+ e
C
k−1
n−1
+ . . . + e
C
1
n−1
+ e
C
1
n−1
5. e
V
k
n
= n e
V
k−1
n
34
Rozdział 6
Modele kombinatoryczne. ([1],
[2], [4], [5], [6], [9], [24])
W tym rozdziale zajmiemy się symetrycznym błądzeniem przypadkowym, fluktuacjami
przy rzutach monetą oraz modelami kombinatorycznymi.
Przykład. Rozważmy n kolejnych rzutów idealną monetą. Gracz „Grzegorz” w każdym
rzucie (doświadczeniu) wygrywa lub przegrywa kolejną jednostkową stawkę. Ciąg {s
1
, s
2
,
. . ., s
n
} reprezentuje łącznie zyski lub straty Grzegorza, na przykład nadwyżki orłów
nad reszkami. Jeśli s
n
= 0 zachodzi remis, s
n
= 1 wygrana a s
n
= −1 przegrana. Dla
uproszczenia przyjmujemy, że Grzegorz ma przewagę jeżeli s
n
> 0 lub s
n
= 0 ∧ s
n−1
> 0.
Pytanie na intuicję. Czy w długim ciągu rzutów Grzegorz powinien prowadzić przez
około połowę ciągu, a jego przeciwnik Gaweł przez pozostałą część czyli również przez
mniej więcej połowę.?
Definicja 6.0.1 Niech x ∈ N, y ∈ Z. Drogą {s
1
, s
2
, . . ., s
x
} od punktu (0, 0) do (x, y)
nazywamy łamaną, której wierzchołki mają odcięte w 1, x i rzędne s
i
, s
i
∈ Z s
0
= 0,
s
n
= y oraz s
i
− s
i−1
= ε = ±1, i ∈ 1, x.
Rysunek 6.1: Elementy łamanej.
Jeśli p spośród ε
i
, i ∈ 1, x jest równe 1, zaś q równych −1 to
x = p + q
y = p − q
⇒ p =
x + y
2
(gdy
2 | x + y)
q =
x − y
2
(6.1)
Dowolny punkt (x, y) można połączyć drogą wychodzącą z (0, 0) wtedy i tylko wtedy gdy
x,y spełniają powyższe równanie.
Drogi można przeliczyć jednoznacznie, wybierając miejsca w ciągu (1, 1, −1, −1, 1,
−1, . . .) z ε = 1 lub ε = −1 czyli odpowiednio p miejsc z 1 albo q miejsc z −1 w ciągu
35

ROZDZIAŁ 6. Modele kombinatoryczne.
p + q = x miejsc. Przyjmując L(x, y) = 0 gdy x, y nie spełnia warunków 6.1 to różnych
wyborów dróg mamy:
L(x, y) =
p + q
p
=
p + q
q
=
x
x+y
2
=
x
x−y
2
Wówczas istnieje dokładnie L(x, y) różnych dróg z (0, 0) do (x, y).
Poprzez translację wynika, że liczba dróg wiodących z punktu kratowego (x
0
, y
0
) do
punktu (x, y), 0 < x
0
< x, |y
0
| ¬ x
0
, |y| ¬ x, 2 | x
0
+ y
0
, 2 | x + y, jest równa liczbie
dróg z początku układu współrzędnych (0, 0) do punktu (x − x
0
, y − y
0
) czyli jest równa
L(x − x
0
, y − y
0
).
Lemat 6.0.1 (Zasada odbicia) Niech punkty kratowe A(x
0
, y
0
), B(x, y), 0 < x
0
<
x, y
0
> 0, y > 0 i A
0
= (x
0
, −y
0
) punkt symetryczny względem osi odciętych do A.
Wówczas liczba dróg z A do B, które dotykają lub przecinają oś odciętych jest równa
liczbie wszystkich dróg wiodących z punktu A
0
do B.
Rysunek 6.2: Model zasady odbicia.
Dowód. Budujemy relację wzajemnie jednoznaczną. Każdej drodze z A do B która
dotyka lub przecina oś odciętych przyporządkowujemy drogę z A
0
do B w taki sposób że,
jeżeli droga z A do B dochodzi po raz pierwszy do osi odciętych w punkcie C, to konstru-
ujemy element drogi A
0
C jako odbicie symetryczne AC względem osi odciętych. Pozostała
część drogi pozostawiamy bez zmian. Czyli mamy model wzajemnie jednoznaczny.
2
Możemy definiować:
Drogi dodatnie – wierzchołki leżą nad osią odciętych.
Drogi nieujemne – wierzchołki nie leża pod osią odciętych.
Drogi ujemne – wierzchołki leżą pod osią odciętych.
Drogi niedodatnie – wierzchołki nie leża nad osią odciętych.
Lemat 6.0.2 Liczba dróg dodatnich łączących początek układu współrzędnych (0, 0) z
punktem (x, y), 0 < y ¬ x jest równa
y
x
L(x, y) gdzie L(x, y) oznacza liczbę wszystkich
dróg z (0, 0) do (x, y).
Dowód. Dla wszystkich dróg dodatnich po wierzchołku (0, 0) następuje punkt (1, 1)
dlatego też szukana liczba dróg jest równa liczbie dróg dodatnich wiodących z (1, 1) do
(x, y), ta zaś jest równa różnicy między liczbą wszystkich dróg z (1, 1) do (x, y) a liczbą
36
Rysunek 6.3: Ilustracja dowodu.
wszystkich tych dróg z (1, 1) do (x, y) które dotykają lub przecinają oś odciętych. Odjem-
nik z zasady odbicia (lemat 6.0.1) można zastąpić przez liczbę wszystkich dróg wiodących
z A
0
do B(x, y), czyli razem liczba dróg dodatnich wynosi:
L(x − 1, y − 1) − L(x − 1, y − 1 + 2) =
x − 1
x+y
2
− 1
−
x − 1
x+y
2
=
x
x+y
2
x+y
2
−
x−y
2
x
=
y
x
L(x, y)
2Z symetrii wynika ponadto, że liczba dróg ujemnych wiodących do punktu (x, −y), y > 0
wynosi
y
x
L(x, y).
Przykład. Problem balotowania (tzw. twierdzenie o głosowaniu) J. Bertrand (1881).
Jeśli dwaj kandydaci R i S otrzymali w wyborach odpowiednio r i s głosów r > s to jaka
jest szansa na to, że przy zliczaniu głosów kandydat R będzie cały czas wyprzedzał pod
względem liczby głosów kandydata S.
Problem sprowadza się do obliczenia liczby dróg dodatnich z (0, 0) do punktu (r +
s, r − s), gdzie r + s to suma głosów a r − s przewaga R nad S. Na podstawie lematu 6.0.2
znamy liczbę dróg dodatnich która wynosi
r−s
r+s
L(r + s, r − s). Stąd szanse stałej przewagi
kandydata R nad S przy zliczaniu głosów są ilorazem tej liczby przez liczbę wszystkich
dróg L(r + s, r − s) i wynoszą
r−s
r+s
.
Przykład. Dwaj równorzędni gracze w grze bez remisów grają mecz złożony z 10 partii.
Mecz zakończył się zwycięstwem gracza A w stosunku 6 : 4. Jakie są szanse, że zwycięzca
prowadził po każdej partii? Stosując lemat 6.0.2 i poprzedni przykład mamy
6−4
6+4
= 0,2
Rozważmy problem dualny do lematu 6.0.2. Rozpatrujemy wszystkie drogi z (0, 0)
do (x, y) które posiadają tę własność, że rzędne wszystkich wierzchołków pośrednich są
mniejsze od y. Nazywamy je drogami osiągającymi po raz pierwszy poziom y w chwili x
lub drogami pierwszego osiągnięcia y.
Lemat 6.0.3 Liczba dróg wychodzących z początku układu współrzędnych (0, 0) i osiąga-
jących po raz pierwszy poziom y > 0 w chwili x jest równa
y
x
L(x, y).
Dowód. Rozpatrzmy relację równoważności między zbiorami dróg spełniających za-
łożenia lematu i dróg dualnych. Drogą dualną do {s
1
, s
2
, . . ., s
x
= y}, s
i
< y, i ∈
1, x − 1 nazywamy drogę odwróconego porządku, przesuniętą do punktu (0, 0) czyli s
∗
0
,
s
∗
1
= s
x
− s
x−1
, . . . , s
∗
i
= s
x
− s
x−i
, . . . , s
∗
x
= s
x
oczywiście s
∗
i
> 0 dla i ∈ 1, x inaczej
s
∗
1
= ε
x
, s
∗
2
= ε
x
+ ε
x−1
, s
∗
3
= ε
x
+ ε
x−1
+ ε
x−2
, . . . , to stosownie do lematu 6.0.2 dla
dróg dodatnich mamy liczbę dróg dualnych (odwróconych) wynoszącą
y
x
L(x, y). Stąd z
37

ROZDZIAŁ 6. Modele kombinatoryczne.
wzajemnej jednoznaczności liczba dróg osiągających po raz pierwszy poziom y > 0 wynosi
y
x
L(x, y).
2
Lemat 6.0.3 dotyczy dróg, których wierzchołek jest najwyższy (geometrycznie). Droga
i dualna do niej łączą te same punkty i powstają w wyniku obrotu o 180
◦
jedna z drugiej
(względem „środka łamanej”).
Rysunek 6.4: Droga i dualna do niej.
Wniosek. Uwzględniając symetrie, liczba wszystkich dróg które osiągną po raz pierw-
szy poziom −y, y > 0 jest równa
y
x
L(x, y).
Lemat 6.0.4 Liczba dróg dodatnich wychodzących z punktu (0, 0) i kończących się w
punktach o odciętej x > 1 jest równa:
(
x−1
x
2
dla
2 | x
x−1
x−1
2
dla
2 - x
(6.2)
Dowód. Szukamy liczby wszystkich dróg dodatnich prowadzących z (0, 0) do zbioru
B = {(x, y):
y > 0}, wszystkie te drogi zawierają punkt (1, 1). Liczba dróg z (1, 1) do B
jest równa:
(
P
x
y=2
L(x − 1, y − 1)
dla
2 | x
P
x
y=1
L(x − 1, y − 1)
dla
2 - x
Zaś liczba dróg z (1, −1) do B wynosi:
(
P
x−2
y=2
L(x − 1, y + 1)
dla
2 | x
P
x−2
y=1
L(x − 1, y + 1)
dla
2 - x
Na podstawie lematu 6.0.1 znamy liczbę dróg dodatnich z (0, 0) do B:
(
P
x
y=2
L(x − 1, y − 1) −
P
x−2
y=2
L(x − 1, y + 1)
P
x
y=1
L(x − 1, y − 1) −
P
x−2
y=1
L(x − 1, y + 1)
=
=
(
L(x − 1, 1) +
P
x
y=4
L(x − 1, y − 1) −
P
x−2
y=2
L(x − 1, y + 1)
L(x − 1, 0) +
P
x
y=3
L(x − 1, y − 1) −
P
x−2
y=1
L(x − 1, y + 1)
=
=
(
L(x − 1, 1)
L(x − 1, 0)
=
(
x−1
x
2
dla
2 | x
x−1
x−1
2
dla
2 - x
2
38
6.1. Inne problemy kombinatoryczne.
Wniosek. Ogólna liczba dróg dodatnich i ujemnych wychodzących z początku układu
współrzędnych i kończących się w punktach o odciętej x > 1 jest równa:
(
2
2n−1
n
= 2
2n
n
dla
x = 2n
2
2n
n
dla
x = 2n + 1
6.1
Inne problemy kombinatoryczne.
([18])
Niech w będzie wielomianem jednej zmiennej, wówczas h(w) jest z definicji jego współ-
czynnikiem przy zmiennej w pierwszej potędze. Na przykład w(x) = c
0
+ c
1
x + . . . + c
n
x
n
to h(w) = c
1
.
Istotną rolę odgrywać będzie następujące twierdzenie,
Twierdzenie 6.1 Niech a ∈ R i k ∈ N. Wtedy
h
x + a
k
!
=
(−1)
a+k+1
k
(
k−1
a
)
a ∈ 0, k − 1
a
k
P
k−1
j=0
1
a−j
a /
∈ 0, k − 1
(6.3)
Dowód. Z definicji symbolu Newtona mamy
x + a
k
=
1
k!
[x + a][x + (a − 1)] · . . . · [x + (a − k + 1)]
(6.4)
Oznaczmy kolejne czynniki w iloczynie 6.4 przez: (x + a
1
)(x + a
2
) · . . . · (x + a
k
). Po
wykonaniu mnożenia otrzymamy wielomian, którego współczynnik przy x jest sumą k
czynników w postaci a
1
· . . . · a
j−1
· . . . · a
k
. Rozważmy dwa przypadki:
1. Niech jedna z liczb a
1
, . . ., a
k
, na przykład a
j
, jest zerem. Wtedy wszystkie iloczyny
zawierające czynnik a
j
są równe 0 i współczynnik przy x redukuje się do jednego
iloczynu a
1
· . . . · a
j−1
· a
j+1
· . . . · a
k
. W szczególnoście dla rozważanego wielomianu
x+a
k
, przy podstawieniu
x + a = x + a
1
, x + (a − 1) = x + a
2
, . . . , x + (a − k + 1) = x + a
k
oraz założeniu, że a ∈ 0, k − 1 otrzymujemy:
c
1
=
1
k!
a(a − 1) · . . . · 2 · 1 · (−1) · . . . · (a − k + 1) =
1
k!
a!(k − a − 1)!(−1)
a−k+1
=
(−1)
a−k+1
k!
a!(k−a−1)!
=
(−1)
a−k+1
k
k−1
a
=
(−1)
a+k+1
k
k−1
a
2. Niech każda z liczb a
1
, . . . , a
k
jest różna od 0. Wspomnianą wcześniej sumę iloczy-
nów możemy w tym przypadku przekształcić następująco
k
X
j=1
a
1
· . . . · a
j−1
· a
j+1
· . . . · a
k
=
k
X
j=1
a
1
· . . . · a
j−1
· a
j+1
· . . . · a
k
a
j
= a
1
· . . . · a
k
k
X
j=1
1
a
j
39
ROZDZIAŁ 6. Modele kombinatoryczne.
Stad dla naszego wielomianu
x+a
k
mamy:
c
1
=
1
k!
a(a − 1) · . . . · (a − k + 1)
k
X
j=1
1
a − j + 1
=
1
k!
a(a − 1) · . . . · (a − k + 1)
k−1
X
j=0
1
a − j
To kończy dowód twierdzenia.
2
Z powyższego twierdzenia wynika, że h przyporządkowuje wyrażeniu kombinatorycz-
nemu również wyrażenie komobinatoryczne.
Przykład.
1.
h
x
2
=
(−1)
0+2+1
2
2−1
0
= −
1
2
2.
h
x + 1
4
=
(−1)
1+4+1
4
4−1
1
= −
1
12
Przykład. Zastosujemy przekształcenie h dla kilku tożsamości kombinatorycznych.
n
X
k=1
n
k
x
k
=
x + n
k
− 1
n ∈ N x ∈ R
Zajmiemy się lewą stroną równości:
h
n
X
k=1
n
k
n
k
=
n
X
k=1
n
k
h
n
k
=
n
X
k=1
n
k
(−1)
k+1
k
k−1
0
=
n
X
k=1
n
k
(−1)
k+1
k
W konsekwencji otrzymalismy nową tożsamość kombinatoryczną:
n
X
k=1
(−1)
k+1
k
n
k
=
n
X
k=1
1
k
n ∈ N
n
X
k=1
x + k
k
=
x + n + 1
n
− 1,
n ∈ N,
x ∈ R
Stosując twierdzenie dla lewej strony równości otrzymujemy:
h
n
X
k=1
x + k
k
=
n
X
k=1
h
x + k
k
=
n
X
k=1
k
k
k−1
X
j=0
1
k − j
=
n
X
k=1
k
X
j=1
1
j
i
40

6.1. Inne problemy kombinatoryczne.
Podobnie przekształcamy stronę prawą:
h
x + n + 1
n
− 1
= h
x + n + 1
n
− h(1) =
n + 1
n
n−1
X
j=0
1
n + 1 − j
= (n + 1)
n+1
X
j=2
1
j
n ∈ N
Stąd otrzymujemy nową tożsamość
n
X
k=1
k
X
j=1
1
j
= (n + 1)
n+1
X
j=2
1
j
n ∈ N
(6.5)
Przykład. Zastosowanie tożsamości 6.5. Dla n = 5 nowo wyprowadzona równość przyj-
muje postać:
5
X
k=1
k
X
j=1
1
j
= 6
6
X
j=2
1
j
a stąd
1 +
1 +
1
2
+
1 +
1
2
+
1
3
+
1 +
1
2
+
1
3
+
1
4
+
1 +
1
2
+
1
3
+
1
4
+
1
5
= 6
1
2
+
1
3
+
1
4
+
1
5
+
1
6
41

ROZDZIAŁ 6. Modele kombinatoryczne.
42

Rozdział 7
Funkcje tworzące. ([2], [5], [6],
[7])
Definicja 7.0.1 Jeżeli A(s) =
P
∞
n=0
a
n
s
n
, a
n
∈ R; n ∈ N
0
, jest zbieżny dla |s| < s
0
to
funkcję A(s) nazywamy funkcją tworzącą ciągu {a
n
}
Wniosek. Jeżeli ciąg (a
n
) jest ograniczony, to powyższy szereg jest zbieżny co najmniej
dla |s| < 1.
Przykłady.
1. a
1
= 1
n ∈ N
⇒ A(s) =
1
1−s
2. a
0
= a
1
= 0
a
n
= 1
n 2 ⇒ A(s) =
s
2
1−s
3. a
n
=
1
n!
n ∈ N
⇒ A(s) = e
s
4. Dla ustalonego k ∈ N, n ∈ 0, k
a
n
=
k
n
⇒ A(s) = (1 + s)
k
5. Jeżeli f oznacza liczbę oczek wyrzuconą przy rzucie symetryczną kostką do gry, to
rozkład prawdopodobieństwa zmiennej losowej f ma funkcję tworzącą:
s + s
2
+ . . . + s
6
6
=
s
6
1 − s
6
1 − s
Niech f będzie zmienną losową o która przyjmuje wartości nieujemne i całkowite.
Oznaczymy:
P (f = n) = p
n
P (f > n) = q
n
n ∈ N
0
To wówczas:
q
n
= p
n+1
+ p
n+2
+ . . . =
∞
X
k=n+1
p
k
n 0
43

ROZDZIAŁ 7. Funkcje tworzące.
Funkcje tworzące ciągów (p
n
) i q
n
są następujące:
P (s) =
∞
X
n=0
p
n
s
n
Q(s) =
∞
X
n=0
q
n
s
n
Jednakże P (1) = 1, stąd szereg P (s) jest zbieżny bezwzględnie co najmniej dla |s| ¬ 1.
Współczynniki w Q
s
są ograniczone, stąd Q(s) jest zbieżny co najmniej dla |s| < 1.
Lemat 7.0.1 Dla −1 < s < 1 zachodzi wzór:
Q(s) =
1 − P (s)
1 − s
(7.1)
Dowód. W szeregu (1 − s)Q(s) współczynnik przy s
n
wynosi:
q
n
− q
n−1
= −p
n
n 1
q
0
= p
1
+ p
2
+ . . . = 1 − p
0
n = 0
i stąd:
(1 − s)Q(s) = 1 − P (s)
2
Badając pochodną:
P
0
(s) =
∞
X
n=0
np
n
s
n−1
zbieżne dla
|s| < 1
(7.2)
Dla s=1 P
0
(1) =
P
∞
n=1
np
n
= E(f ). Jeżeli istnieje ta wartość oczekiwana to P
0
(s) jest
ciągła dla |s| ¬ 1. Jeżeli dla s → 1 P
0
(s) → ∞ to mówimy, że f ma nieskończoną wartość
oczekiwaną P
0
(1) = E(f ) = ∞.
Twierdzenie 7.1 Wartość oczekiwana zmiennej losowej f o wartościach całkowitych
nieujemnych wyraża się wzorem:
E(f ) =
n=1
X
∞
np
n
=
∞
X
n=0
q
n
= P
0
(1) = Q(1)
(7.3)
Dowód. Stosując do równania 7.1 twierdzenie o wartości średniej mamy:
Q(s) = P
0
(ϑ)
s < ϑ < 1
Q(s) % E(f )
s → 1
Stąd wynika wzór 7.3.
2
Przyjmijmy dla uproszczenia następującą definicję wariancji:
Definicja 7.1.1
D
2
(f ) = E(f
2
) − E
2
(f ) = E
h
(f − E(f ))
2
i
44

Różniczkując równanie 7.2 po s mamy:
P
0
(1) =
∞
X
n=1
n(n − 1)p
n
= E[f (f − 1)] = E(f
2
) − E(f )
(7.4)
Wyliczjąc z równania 7.1, 1 − P (s) = (1 − s)Q(s) i różniczkując, mamy:
P
0
(s) = Q(s) − (1 − s)Q
0
(s)
P
00
(s) = 2Q
0
(s) − (1 − s)Q
00
(s)
P
00
(1) = 2Q
0
(1)
Dla wyliczenia wariancji wystarczy dodać E(f ) − E
2
(f ), czyli z zależności 7.3 i 7.4
otrzymujemy:
D
2
(f ) = P
00
(1) + P
0
(1) − P
02
(1) = 2Q
0
(1) + Q(1) − Q
2
(1)
W przypadku nieskończonej wariancji P
00
(s) → ∞ dla s → 1.
Twierdzenie 7.2 Jeżeli niezależne zmienne losowe f
1
i f
2
mają funkcje tworzące od-
powienio P
1
(s) i P
2
(s), to zmienna losowa f = f
1
+ f
2
ma funkcję tworząca P (s) =
P
1
(s) · P
2
(s).
Dowód. Niech P (f
1
= n) = p
n
i P (f
2
= n) =
e
p
n
i n ∈ N, stąd
P
1
(s) =
∞
X
n=0
p
n
s
n
P
2
(s) =
∞
X
n=0
e
p
n
s
n
Zdarzenie (f
1
= j, f
2
= k) ma prawdopodobieństwo p
j
e
p
k
. Zdarzenie f = n jest sumą
zdarzeń rozłącznych.
n
[
t=0
(f
1
= t, f
2
= n − t)
Stąd, prawdopodobieństwo
c
n
= P (f = n) =
n
X
t=0
p
t
e
p
n−t
(7.5)
Mnożąc wyraz po wyrazie P
1
P
2
i łącząc składniki przy jednakowych potęgach otrzymu-
jemy współczynnik c
n
przy s
n
w rozwinięciu P
1
(s)P
2
(s) dany wzorem 7.5. Czyli:
P (s) =
∞
X
n=0
c
s
s
n
= P
1
(s)P
2
(s)
2
Definicja 7.2.1 Kompozycja. Niech (a
n
), (b
n
) są ciągami, ciąg (c
n
) = (a
n
) · (b
n
) zdefi-
niowany wzorem 7.5 nazywamy kompozycją ciągów (a
n
) i (b
n
).
Wniosek. Kompozycja jest operacją łączną i przemienną.
Wniosek. Jeżeli zmienne f
1
, . . ., f
m
, mają jednakowy rozkład prawdopodobieństwa
(p
n
) wówczas rozkład zmiennej f =
P
m
i=1
f
i
oznaczamy (p
n
)
m
∗
:
(p
n
)
m
∗
= (p
n
)
(m−1)
∗
· (p
n
)
45

ROZDZIAŁ 7. Funkcje tworzące.
Przykład. Rozkład dwumianowy.
b(k, n, p) =
n
k
p
k
q
n−k
Funkcja tworząca:
P (s) =
n
X
k=0
n
k
(ps)
k
q
n−k
= (q + ps)
n
Z faktu, że funkcja tworząca rozkładu dwumianowego jest n-tą potęgą q+ps wynika, że
(b(k,n,p)) jest rozkładem sumy f = f
1
+ . . . + f
n
gdzie n to liczba niezależnych zmiennych
losowych o wspólnej tworzącej q + ps, każda ze zmiennych f
j
przyjmuje wartość 0 z
prawdopodobieństwem q oraz 1 z prawdopodobieństwem p. Stąd otrzymujemy:
Wniosek. Własność multiplikatywności:
(b(k, n, p)) = (b(k, 1, p))
n
∗
E(f ) = np
D
2
(f ) = npq
46

Rozdział 8
Grafy. ([1], [5], [8])
Definicja 8.0.2 Graf skierowany G składa się ze zbiorów W (G) i E(G) gdzie W (G) 6= ∅
oznacza zbiór wierzchołków grafu G, zaś E(G) zbiór krawędzi grafu G i funkcji δ. Ponadto
δ:E(G) −→ W (G) tak że, jeśli e ∈ E(G) czyli jest krawędzią grafu G, to δ(e) = (w
p
, w
k
),
gdzie w
p
nazywamy początkiem krawędzi grafu, zaś w
k
końcem krawędzi grafu. Mówimy też
że krawędź e wiedzie od w
p
do w
k
. Można dla uproszczenia przyjąć że, |W (G)|, |E(G)| <
∞.
Definicja 8.0.3 Wykres grafu skierowanego G, składa się z punktów odwzorowujących
wierzchołki W (G) oraz strzałek odwzorowujących skierowane krawędzie E(G), czyli wio-
dących od w
p
do w
k
.
Rysunek 8.1: Graf skierowany.
Uwaga. Nie ma krawędzi wielokrotnych! Funkcja δ:E(G) → W
2
(G) jest funkcja róż-
nowartościową.
47
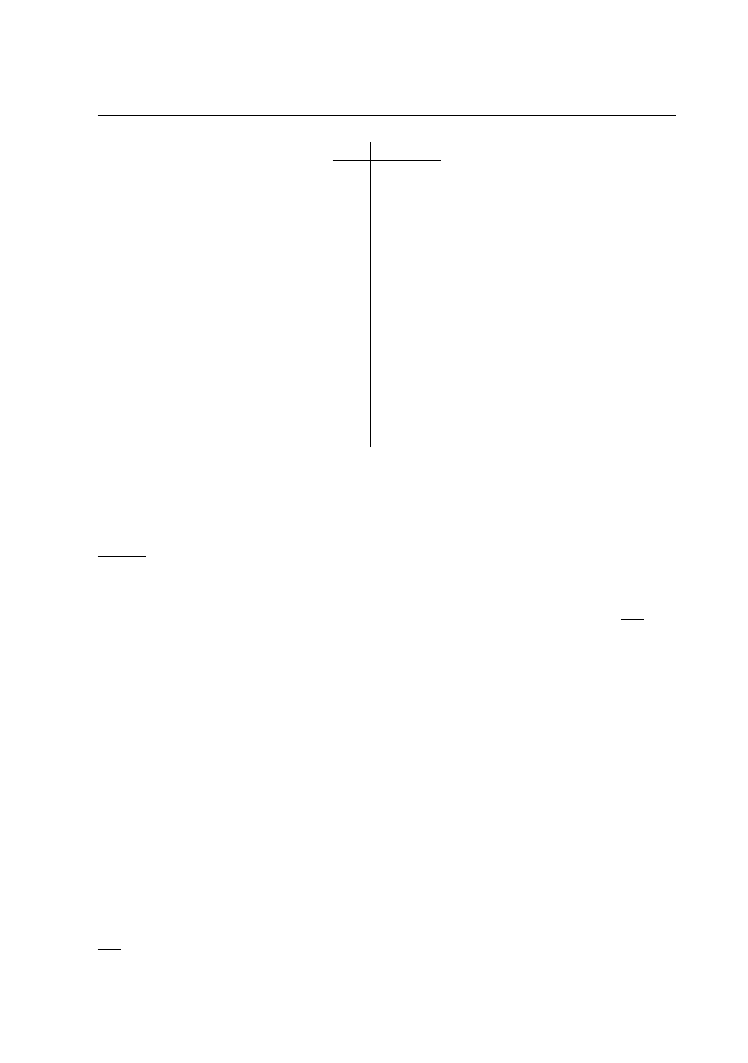
ROZDZIAŁ 8. Grafy.
E
δ(E)
e
1
(w
1
, w
2
)
e
2
(w
1
, w
3
)
e
3
(w
1
, w
4
)
e
4
(w
1
, w
5
)
e
5
(w
1
, w
6
)
e
6
(w
1
, w
7
)
e
7
(w
2
, w
3
)
e
8
(w
3
, w
4
)
e
9
(w
4
, w
5
)
e
10
(w
5
, w
6
)
e
11
(w
6
, w
7
)
e
12
(w
7
, w
8
)
e
13
(w
4
, w
2
)
e
14
(w
2
, w
6
)
e
15
(w
6
, w
4
)
e
16
(w
6
, w
6
)
Tabela 8.1:
Definicja 8.0.4 Drogą w grafie skierowanym nazywamy uporządkowany ciąg krawędzi
(e
1
, e
2
, . . ., e
n
) taki, że jeśli δ(e
i
) = (w
i
, w
i+1
), to wtedy δ(e
i+1
) = (w
i+1
, w
i+2
) i ∈
1, n − 1, gdzie e
i
∈ E(G), w
i
∈ W (G), wówczas długość drogi określamy jako n gdy
wiedzie ona od wierzchołka w
1
do w
n+1
.
Drogę nazywamy zamkniętą, gdy w
1
= w
n+1
. Drogę zamkniętą długości n 1 z wierz-
chołkami (w
1
, w
2
, . . ., w
n
, w
1
) nazywamy cyklem jeśli w
i
6= w
j
dla i 6= j, i, j ∈ 1, n
Definicja 8.0.5 W grafie G wierzchołki x, y nazywamy sąsiednimi w sensie y sąsiaduje
z x, wtedy gdy istnieje e ∈ E(G) takie, że δ(e) = (x, y).
Definicja 8.0.6 R
S
⊂ W
2
(G) nazywamy relacją sąsiedztwa wtedy i tylko wtedy, gdy
∀
(x, y) ∈ R
S
y jest wierzchołkiem sąsiednim do x.
Uwaga. R
S
nie musi być ani zwrotna (wszystkie pętle) ani symetryczna.
Uwaga. Różne grafy skierowane mogą mieć tą samą relację sąsiedztwa.
Uwaga. Jeżeli grafy skierowane nie posiadają krawędzi wielokrotnych, to istnieje funk-
cja wzajemnie jednoznaczna przekształcająca grafy skierowane na relacje sąsiedztwa.
Definicja 8.0.7 Graf nieskierowany składa się z W (G) i E(G) oraz funkcji δ:E(G) −→
W
2
(G). Przy czym W (G) to zbiór wierzchołków, a E(G) zbiór krawędzi. Jeśli e
i
6= e
j
i
δ(e
i
) = δ(e
j
) to e
i
i e
j
nazywamy krawędziami wielokrotnymi.
Wykres grafu składa się z punktów odwzorowujących wierzchołki W (G) i łuków odwzo-
rowujących krawędzie E(G).
Drogę nazywamy prostą, jeżeli wszystkie jej krawędzie są różne. e
i
6= e
j
, i 6= j i, j ∈
1, n.
Uwaga. W drodze prostej mogą wystąpić wielokrotne wierzchołki.
Graf nie zawierający cykli w sensie teoriomnogościowym nazywamy grafem acyklicz-
nym.
48
Definicja 8.0.8 Podgrafem G
1
(W
1
,E
1
,δ
1
) grafu G (W ,E,δ) nazywamy taki graf, że
W (G
1
) ⊂ W (G), E(G
1
) ⊂ E(G) δ |
E(G)
≡ δ
1
.
Drogę nazywamy acykliczną, gdy podgraf składający się z wierzchołków W i krawędzi E
tej drogi jest acykliczny.
Przykład. Droga e
1
e
1
z ciągiem wierzchołków jest droga zamkniętą i nie jest drogą
Rysunek 8.2: Graf G
1
.
prostą. Nie jest także cyklem. Graf G
1
jest acykliczny.
Przykład. Droga e
1
e
3
e
4
e
2
o długości 4 jest drogą zamkniętą i jest drogą prostą. Graf
Rysunek 8.3: Graf G
2
.
G
2
zawiera dwa cykle.
Twierdzenie 8.1 Każda droga zamknięta e
1
e
2
. . . e
n
o długości większej niż 3, taka że
w
i
6= w
j
, i 6= j i, j ∈ 1, n jest cyklem.
Dowód. Rozważmy drogę zamkniętą. Wystarczy wykazać, że e
i
6= e
j
dla i 6= j, lecz
kiedy w
i
= w
j
, to droga e
1
e
2
. . . e
n−1
jest drogą prostą, czyli e
i
6= e
j
dla i 6= j i, j ∈
1, n − 1 ponadto δ(e
n
) = {w
n
, w
1
} oraz δ(e
j
) = {w
i
, w
i+1
} i ∈ 1, n − 1 to e
n
6= e
i
,
i ∈ 1, n − 1. Stąd droga e
1
e
2
. . . e
n
jest drogą prostą.
2
Twierdzenie 8.2 Droga e
1
e
2
. . . e
n
o wierzchołkach w
1
w
2
. . . w
n+1
jest prosta i acyklicz-
na, wtedy i tylko wtedy, gdy w
i
6= w
j
i 6= j, i, j ∈ 1, n + 1.
Dowód. ⇐ Rozważmy drogę która ma wszystkie wierzchołki różne, analogicznie jak w
dowodzie twierdzenia 8.1. Jest to droga prosta. W cyklu, jeden z wierzchołków musi być
początkiem jednej i końcem innej krawędzi, więc musi się powtórzyć. Jeśli wierzchołki się
nie powtarzają, są różne, to droga jest acykliczna.
⇒ Załóżmy przez zaprzeczenie, że w ciągu wierzchołków w
1
w
2
. . . w
n
w
n+1
występują
powtórzenia, na przykład w
i
= w
j
dla i < j i, j ∈ 1, n + 1. Z zasady dobrego upo-
rządkowania, istnieje minimalne j spełniające ten warunek. Wówczas ciąg wierzchołków
w
1
w
2
. . . w
j−1
spełnia warunek w
k
6= w
l
k 6= l k, l ∈ i, j − 1. Stąd droga w
i
w
i+1
. . . w
j−1
w
i
jest cyklem, co daje sprzeczność bo droga w
1
. . . w
n+1
była acykliczna.
2
Twierdzenie 8.3 Jeśli w, v ∈ W (G); w 6= v i istnieje w grafie G droga wiodąca z w do
v, to istnieje w tym grafie acykliczna droga wiodąca z w do v.
49

ROZDZIAŁ 8. Grafy.
Dowód. Ze zbioru wszystkich dróg wiodących z w do v w grafie G, wybieramy naj-
krótszą drogę o długości którą oznaczamy n i ciąg jej wierzchołków w
1
w
2
. . . w
n+1
; gdzie
w
1
= w a w
n+1
= v. Gdyby wierzchołki w
i
6= w
j
i 6= j i, j ∈ 1, n + 1 to droga byłaby pro-
sta i acykliczna z konstrukcji, gdyby zaś ∃i < j w
i
= w
j
i, j ∈ 1, n + 1 to droga wiodąca
od w
i
do w
j
w
i
w
i+1
. . . w
j
jest zamknięta. Konstruujemy drogę w
1
w
2
. . . w
i
w
j+1
. . . w
n+1
która wiedzie z w do v i jej długość jest mniejsza od n, co daje sprzeczność i wierzchołki
są różne.
2
Wniosek. Jeśli e ∈ E(G) i e jest krawędzią w zamkniętej drodze prostej w grafie G, to
istnieje cykl do którego należy ta krawędź.
Dowód. Jeśli e
1
jest pętlą mamy przypadek trywialny. Jeśli nie, to weźmy δ(e
1
) =
{w, v} w 6= v i rozważmy graf G
1
z krawędziami E(G) − {e
1
}, który jest podgrafem
grafu G. Z zamkniętości drogi w grafie G, w grafie G
1
istnieje droga wiodąca z w do v. Z
twierdzenia 8.3 wynika, że istnieje prosta droga acykliczna wiodąca z w do v. Zawierająca
oczywiście e
1
. Połączenie wierzchołków końcowych tej drogi krawędzią e
1
, tworzy cykl
zawierający wierzchołki w i v.
2
50

Rozdział 9
Izomorfizmy grafów. ([1])
Twierdzenie 9.1 Jeżeli w 6= v ∈ W (G), gdzie G jest grafem acylkicznym, to istnieje co
najwyżej jedna droga prosta w G wiodąca z w do v.
Dowód. Zaprzeczymy tezie twierdzenia. Niech istnieje para wierzchołków w, v ∈ W (G)
połączona co najmniej dwiema drogami prostymi z w do v. Przy czym można przyjąć,
że jedna z takich dróg jest najkrótsza dla wszystkich par (w, v) spełniających warunek
posiadania co najmniej dwóch różnych dróg prostych. Wtedy albo zbiór wspólnych wierz-
chołków tych dróg składa się jedynie z {w, v} i wówczas mamy sprzeczność z acyklicznością
grafu G, gdyż droga w . . . v . . . w złożona z tych dwóch dróg jest cyklem, lub te dwie drogi
mają poza {w, v} jeszcze co najmniej jeden wspólny wierzchołek. Oznaczmy go ω ∈ W (G),
wówczas możemy skonstruować dwie różne drogi proste wiodące z w do ω lub z ω do v,
co daje sprzeczność z minimum długości drogi z w do v.
2
Przykład. Droga w
5
w
2
w
6
w
4
w
5
będąca połączeniem (sumą) dróg w
5
w
2
, w
2
w
5
jest cy-
Rysunek 9.1:
klem. Podobną konstrukcję otrzymujemy dla drogi w
2
w
3
w
1
w
2
, która wiedzie z w
2
do
w
2
, utworzonej jako suma dróg z w
2
do w
1
i z w
1
do w
2
. Drogi w
3
w
2
w
6
w
5
w
2
w
1
oraz
w
3
w
2
w
6
w
4
w
2
w
1
są proste i wiodą z w
3
do w
1
. Łącząc części tych dróg, jednej z w
6
do w
2
a drugiej z w
2
do w
6
, można utworzyć cykl w
6
w
5
w
2
w
4
w
6
.
51

ROZDZIAŁ 9. Izomorfizmy grafów.
Definicja 9.1.1 Izomorfizm grafów bez krawędzi wielokrotnych. Mówimy, że grafy G i Q
są izomorficzne jeżeli istnieje wzajemnie jednoznaczne przekształcenie
H:W (G) → W (Q)
takie, że {w, v} jest krawędzią grafu G, wtedy i tylko wtedy, gdy {
H(w), H(v)} jest kra-
wędzią grafu Q. Przekształcenie
H nazywamy izomorfizmem grafów G i Q, zapisujemy
G ' Q jeżeli G jest izomorficzny z Q. Oczywiście Q jest wtedy izomorficzny z G. Izomor-
fizmem jest
H
−1
.
Dla grafów z krawędziami wielokrotnymi zakładamy, że istnieją wzajemnie jednoznaczne
przekształcenia
H:W (G) → W (Q) i Γ:E(G) → E(Q) takie, że dla dowolnej krawędzi
e ∈ E(G), łączy ona wierzchołki w, v ∈ W (G) wtedy i tylko wtedy, gdy odpowiednia
krawędź Γ(e) łączy wierzchołki
H(w) i H(v). Czyli modele ikonograficzne dwóch grafów
izomorficznych pokrywają się z dokładnością do oznaczeń.
Przykład. Izomorfizm G i Q.
H(x
i
) = y
i
; i ∈ 1, 11.
Rysunek 9.2: Grafy G i Q.
Uwaga. Identyfikacja grafów wymaga przeliczenia ich wierzchołków i krawędzi. Dwa
grafy izomorficzne posiadają identyczną liczbą wierzchołków i krawędzi.
Niezmienniki izomorfizmu grafów to na przykład:
• liczba wierzchołków
• liczba krawędzi
• liczba pętli
• liczba dróg prostych o przyjętej długości
• liczba punktów wielokrotnych
Definicja 9.1.2 Stopniem wierzchołka w ∈ W (G) nazywamy sumę liczby różnych kra-
wędzi {v, w} v 6= w (dla grafów o skończonej liczbie wierzchołków) oraz podwojonej liczby
pętli o wierzchołku w. Oznaczamy ten stopień deg(W ).
Liczbę wierzchołków stopnia n ∈ N
0
w grafie G oznaczamy D
n
(G). Jest to również nie-
zmiennik izomorfizmu
H.
Wniosek. Ciąg liczb wierzchołków (D
i
(G))
i∈0,n
max
jest niezmiennikiem izomorfizmu
H.
Przykład. Dla grafu G
1
mamy (D
i
(G
1
)) = (0, 0, 3, 4), (D
i
(G
2
)) = (0, 3, 0, 4 ,3) przy
i ∈ 0, n
max
.
52

Rysunek 9.3: Graf G
1
.
Rysunek 9.4: Graf G
2
.
53

ROZDZIAŁ 9. Izomorfizmy grafów.
54

Rozdział 10
Własności grafów. ([2], [4], [5],
[8])
Graf nazywamy regularnym jeżeli wszystkie jego wierzchołki posiadają identyczny stopień.
Rysunek 10.1: Grafy regularne.
Graf nazywamy pełnym, jeżeli wszystkie jego wierzchołki są połączone ze wszystkimi
innymi oraz nie posiadają pętli i krawędzi wielokrotnych, oznaczamy je
G
n
.
Uwaga. W grafie pełnym posiadającym n wierzchołków każdy wierzchołek ma stopnień
(n − 1). Grafy pełne o tej samej liczbie wierzchołków są ze sobą izomorficzne.
Uwaga. Graf pełny
G
n
zawiera
n
m
grafów izomorficznych z
G
m
, m ¬ n. Grafy te
powstają przez wybór różnych m wierzchołków z n możliwych i wszystkich krawędzi je
łączących.
Uwaga. Dowolny graf bez pętli i krawędzi wielokrotnych posiadający n wierzchołków
jest izomorficzny z podgrafem grafu
G
n
.
Twierdzenie 10.1 Suma stopni wierzchołków grafu jest równa podwojonej liczbie jego
55

ROZDZIAŁ 10. Własności grafów.
Rysunek 10.2: Grafy pełne.
Rysunek 10.3: Grafy regularne niepełne.
krawędzi. Czyli:
X
w∈W (G)
deg(w) = 2|E(G)| = 2
X
e∈E(G)
1
(10.1)
ponadto,
n
max
X
i=0
iD
i
(G) = 2|E(G)|
(10.2)
Dowód 10.1. Wszystkie krawędzie nie będące pętlami łączą dwa wierzchołki, czyli
uwzględnienie takiej krawędzi zwiększa sumę stopni wierzchołków o 2. Z definicji 9.1.2
stopnia wierzchołka otrzymujemy to również dla pętli.
2
Dowód 10.2. Sumując stopnie wszystkich wierzchołków łatwo zauważyć, że wszystkie
wierzchołki stopnia i dają wkład iD
i
(G), gdyż tyle krawędzi lub krawędzi i podwojoną
liczbę pętli dokłada jeden wierzchołek.
2
10.1
Drogi a krawędzie. Drogi wewnątrz grafu.
Przykład. Problem mostów Królewieckich.
Czy można skonstruować drogę tak by po
każdym moście przejść tylko raz i powrócić do punktu wyjścia? Inaczej, czy istnieje droga
zamknięta w tym grafie, przechodząca przez każdą krawędź dokładnie jeden raz?
Drogę tego typu określa się jako cykl Eulera w grafie G. Drogą Eulera w grafie G,
nazywamy drogę prostą zawierającą wszystkie krawędzie grafu G.
Twierdzenie 10.2 Wszystkie wierzchołki grafu który zawiera cykl Eulera są stopnia pa-
rzystego.
56

10.1. Drogi a krawędzie. Drogi wewnątrz grafu.
Rysunek 10.4: Mosty w Królewcu.
Rysunek 10.5: Graf odpowiadający połączeniom mostów.
Dowód. Przebiegając drogę wychodzącą z ustalonego wierzchołka, eliminujemy kra-
wędzie dochodzącą i wychodzącą z kolejnych osiąganych po drodze wierzchołków lub też
eliminując pętle. Każda krawędź ma być osiągana tylko raz i zostaje wyeliminowana po-
nieważ droga jest cyklem więc nie pozostanie żadna krawędź i po eliminacji zostają same
wierzchołki. Tak więc, mają one stopień 0. Każde przejście przez wierzchołek odpowia-
da zmniejszeniu jego stopnia o 2 (lub wielokrotność, jeśli eliminujemy pętle), stąd na
początku wszystkie wierzchołki musiały mieć parzystość stopnia deg(w
k
) = (0 + 2n
k
),
w
k
∈ W (G).
2
Wniosek. Graf G posiadający drogę Eulera ma wszystkie wierzchołki stopnia parzy-
stego, albo dokładnie dwa z nich są stopnia nieparzystego.
Dowód. Niech droga Eulera dla grafu G rozpoczyna się w wierzchołku w i kończy w
wierzchołku v, wówczas:
• w = v i z twierdzenia 10.2 droga jest cyklem Eulera, to stopień wszystkich wierz-
chołków jest parzysty.
• w 6= v to konstruujemy krawędź e wiodącą z w do v. Wówczas nadgraf G
0
= G ∪
{e} posiada cykl Eulera będący sumą drogi Eulera i krawędzi e. Stąd wszystkie
wierzchołki grafu G
0
są stopnia parzystego, więc jedynie w, v dla grafu G są stopnia
nieparzystego.
2
Przykład. Graf G
1
nie posiada cyklu Eulera gdyż 2 - deg(w
2
), deg(w
4
), natomiast
57

ROZDZIAŁ 10. Własności grafów.
Rysunek 10.6: Graf G
1
.
droga e
4
e
5
e
1
e
6
e
2
e
7
e
3
e
8
e
9
jest drogą Eulera.
Rysunek 10.7: Graf G
2
.
Graf G
2
jest sumą dwóch rozłącznych podgrafów które posiadają cykle Eulera.
Definicja 10.2.1 Graf G nazywamy spójnym, gdy dla dowolnej pary w, v ∈ W (G) w 6= v
istnieje droga wiodąca z w do v w tym grafie.
Definicja 10.2.2 Każdy maksymalny spójny podgraf grafu G nazywamy składową grafu
G.
Uwaga. Składowa z zadanym wierzchołkiem w zawiera wszystkie drogi (w tym wierz-
chołki i krawędzie) zaczynające się w wierzchołku w.
Przykład. Graf G
3
ma dwie składowe.
Twierdzenie 10.3 (Euler) Dowolny skończony spójny graf, którego wszystkie wierz-
chołki są stopnia parzystego posiada cykl Eulera.
Dowód. Niech G będzie skończonym grafem spójnym który posiada wszystkie wierz-
chołki stopnia parzystego. Jeżeli W (G) = {w
1
} to przebiegamy wszystkie pętle (jeżeli
są); niech więc |W (G) > 1|, ze spójności G mamy ∀i w
i
∈ W (G), deg(w
i
) = 2n
i
2
konstruujemy w
1
w
2
. . . w
n
jako ciąg drogi o maksymalnej długości która nie powtarza
żadnej krawędzi. Z założenia o skończoności ciągu |E(G)| < ∞ to istnieje co najmniej
58

10.1. Drogi a krawędzie. Drogi wewnątrz grafu.
jedna taka droga. Tworzymy ciąg podgrafów eliminując po kolei krawędzie tej drogi jeżeli
w zbiorze {w
2
, . . ., w
n−1
} wystąpił wierzchołek w
n
, to każde jego przekroczenie wiąże
się z eliminacją dwóch krawędzi, czyli zmniejsza stopień wierzchołka w
n
w odpowiednim
podgrafie o 2. Eliminując ostatnią krawędź wiodącą od w
n−1
do w
n
zmniejszymy stopień
wierzchołka w
n
o 1. Gdyby w
n
6= w
1
to stopień w
n
byłby nieparzysty, czyli istniałaby kra-
wędź wychodząca z w
n
, co jest sprzeczne z maksymalnością długości dróg, stąd w
n
= w
1
.
Gdyby najdłuższa droga nie przechodziła przez wszystkie wierzchołki grafu G, to ze spój-
ności grafu G istnieje krawędź e nie zawarta w drodze wiodącej od w
1
do w
n
łączącą jakiś
wierzchołek w
i
∈ {w
1
, . . ., w
n
} z w
p
6∈ {w
1
, . . ., w
n
}. Teraz najdłuższa droga wiodąca
z w
i
z w
i
do w
i
ma długość n (istnieje bo w
1
= w
n
), może być przedłużona poprzez do-
łączenie początkowej krawędzi e, co zwiększa długość maksymalnej drogi, co oczywiście
jest sprzeczne z założeniem. Analogicznie, do najdłuższej drogi możemy zawsze dołączyć
krawędź e pominiętą w jej konstrukcji, gdyż musi łączyć wierzchołki zawarte w tej drodze,
(w
i
, w
j
) co znów daje sprzeczność z maksymalnością długości drogi.
2
Wniosek. Jeżeli graf G jest skończony, spójny i posiada dokładnie dwa wierzchołki
stopnia nieparzystego, to posiada drogę Eulera.
Dowód. Jeżeli w 6= v, w, v ∈ W (G), 2 - deg(w), 2 - deg(v) to konstruujemy krawędź
łączącą w z v. Wówczas nadgraf G
0
= G ∪ {e} cechuje się parzystością wszystkich wierz-
chołków, stąd z twierdzenia 10.3 posiada cykl Eulera. Po eliminacji krawędzi e z cyklu
Eulera, pozostaje droga Eulera zawarta w grafie G.
2
Definicja 10.3.1 Drzewem nazywamy dowolny acykliczny i spójny graf.
Rysunek 10.8: Drzewa.
Definicja 10.3.2 Podgraf T G nazywamy drzewem spinającym grafu G, jeśli W (T ) =
W (G).
Liśćmi nazywamy wierzchołki stopnia 1 w drzewie. Na rysunku 10.9 są to dla T
1
: w
1
,
w
2
, w
3
, w T
2
: w
1
, w
5
, w T
3
: w
1
, w
3
, w
5
.
59

ROZDZIAŁ 10. Własności grafów.
Rysunek 10.9: Drzewa spinające.
60

Rozdział 11
Zasada włączania - wyłączania.
([1], [5])
Podane tu twierdzenie będzie szczególnym przypadkiem ogólniejszego twierdzenia mate-
matyki dyskretnej zwanego Zasadą włączania - wyłączania. Zasada ta, jako swoisty ogólny
model matematyczny, zostanie następnie zaaplikowana na gruncie rachunku prawdopo-
dobieństwa do wzoru na obliczanie prawdopodobieństwa sumy zdarzeń, a w dalszej części
do rozwiązania konkretnego problemu z rachunku prawdopodobieństwa.
Twierdzenie 11.1 Dla dowolnych zbiorów A
1
, A
2
, . . . , A
n
zachodzi:
|A
1
∪ . . . ∪ A
n
| =
n
X
r=1
(−1)
r+1
X
1¬i
1
<...<i
r
¬n
|A
i
1
∩ . . . ∩ A
i
r
| =
n
X
i=1
|A
i
| −
X
1¬i
1
<i
2
¬n
|A
i
1
∪ A
i
2
| +
X
1¬i
1
<i
2
<i
3
¬n
|A
i
1
∪ A
i
2
∪ A
i
3
|+
. . . + (−1)
n+1
|A
1
∪ . . . ∪ A
n
|
(11.1)
W oparciu o zasadę włączania - wyłączania łatwo udowodnić poniższe twierdzenie ra-
chunku prawdopodobieństwa.
Twierdzenie 11.2 (Wzór Poincare’go) Prawdopodobieństwo zajścia jednego ze zda-
rzeń A
1
, A
2
, . . . , A
n
, A
i
∈ Ω, wynosi:
P (A
1
∪ . . . ∪ A
n
) =
n
X
r=1
(−1)
r+1
X
1¬i
i
<...<i
r
¬n
P (A
i
1
∩ . . . ∩ A
i
r
) =
n
X
i=1
P (A
i
) −
X
1¬i
1
<i
2
¬n
P (A
i
1
∩ A
i
2
)+
X
1¬i
1
<i
2
<i
3
¬n
P (A
i
1
∩ A
i
2
∩ A
i
3
) + . . . + (−1)
n+1
P (A
1
∪ . . . ∪ A
n
)
(11.2)
Rozważmy teraz następujące zdanie: Do pociągu złożonego z n wagonów wsiada N
pasażerów (n ¬ N ). Wyznaczyć prawdopodobieństwo zdarzenia że żaden wagon nie będzie
pusty.
61

ROZDZIAŁ 11. Zasada włączania - wyłączania.
Rozwiązanie. Za przestrzeń zdarzeń elementarnych Ω weźmy zbiór wszystkich N -
wyrazowych wariacji z powtórzeniami zbioru n-elementowego. Zatem |Ω| = n
N
. Niech
zdarzenie B polega na tym, że żaden wagon nie będzie pusty. Niech A
i
gdzie 1 ¬ i ¬ n,
będzie zdarzeniem polegającym na tym, że wagon o numerze i będzie pusty. Oznaczmy
ponadto zdarzenie A jako sumę zdarzeń A
i
, czyli A = A
1
∪ . . . ∪ A
n
. Zdarzenie A polega
więc na tym, że po zajęciu miejsc przez pasażerów w pociągu pozostaną puste wago-
ny. Interesujące nas w zadaniu zdarzenie B jest zdarzeniem przeciwnym do zdarzenia A,
zatem |B| = |Ω| − |A|. Z zasady włączania-wyłączania obliczymy moc zbioru zdarzeń
elementarnych sprzyjających zdarzeniu A:
|A| = |A
1
∪ . . . ∪ A
n
| =
n
X
r=1
(−1)
r+1
X
1¬i
1
<...<i
n
¬n
|A
i
1
∩ . . . ∩ A
i
r
| =
n
X
r=1
(−1)
r+1
n
r
(n − r)
N
Wobec tego:
|B| = n
N
−
n
X
r=1
(−1)
r+1
n
r
(n − r)
N
=
n
N
+
n
X
r=1
(−1)
r
n
r
(n − r)
N
=
n
X
r=0
(−1)
r+1
n
r
(n − r)
N
Ostatecznie:
P (B) =
|B|
|Ω|
=
P
n
r=0
(−1)
r+1 n
r
(n − r)
N
n
N
=
n
X
r=0
(−1)
r+1
n
r
(
n − r
n
)
N
(11.3)
62

Rozdział 12
Zasada Dirichleta. ([12], [15],
[22], [23])
W tym rozdziale przedstawię twierdzenie nazywane zasadą szufladkową Dirichleta. Ma
ono charakter kombinatoryczny i przy bardzo prostym sformułowaniu prowadzi do cieka-
wych i niebanalnych wniosków, ułatwia rozwiązywanie wielu trudnych zadań. Sformuło-
waną przez siebie zasadę szufladkową, Dirichlet z powodzeniem stosował w rozważaniach
dotyczących przybliżeń diofanycznych (tzn. przybliżania liczb niewymiernych liczbami
wymiernymi). Prawdopodobnie po raz pierwszy użył tej zasady w dowodzie twierdzenia
z 1842 roku:
∀a ∈ R ∀n ∈ N
h
n > 1 ⇒ ∃p ∈ Z∃q ∈ N
q ¬
n ∧ |pa − q| <
1
n
i
(12.1)
12.1
Teoretyczne podstawy metody.
Zasada szufladkowa Dirichleta bywa często istotnym elementem wielu zaawansowanych
rozumowań w różnych dziedzinach matematyki. Formalnie wiąże się ona z pojęciem mocy
zbioru (liczby kardynalnej) i zbioru skończonego w sensie Dedekinda.
Twierdzenie 12.1 (zasada szufladkowa) Jeżeli |X| > n oraz X = X
1
∪ X
2
∪ . . . ∪ X
n
,
to dla pewnego i ∈ {1 , 2, . . ., n} jest |X
i
| > 1.
Dowód. Dowód zostanie przeprowadzony metodą indukcji matematycznej. Dla n = 1
twierdzenie jest prawdziwe. Zakładamy jego prawdziwość dla pewnej liczby naturalnej
k > 1:
X = X
1
∪ X
2
∪ . . . ∪ X
k
i
|X| > k ⇒ ∃i ¬ k
|X
i
| > 2
Pokażemy teraz, że jest ono prawdziwe dla liczby k + 1, czyli:
X = X
1
∪ X
2
∪ . . . ∪ X
k+1
i
|X| > k + 1 ⇒ ∃i ¬ k + 1
|X
i
| > 2
Jeżeli X
k+1
= ∅, to twierdzenie jest prawdziwe na mocy przyjętego założenia. Jeżeli
X
k+1
= 1, to zbiór X
1
∪ X
2
∪ . . . ∪ X
k
ma więcej niż k elementów i na mocy założenia
indukcyjnego jest |X
i
| 2 dla pewnego i ¬ k. Jeżeli w końcu |X
k+1
| 2, to teza
jest spełniona dla i = k + 1. Zatem na mocy indukcji matematycznej twierdzenie jest
prawdziwe dla wszystkich liczb naturalnych.
2
Uogólnieniem zasady szufladkowej Dirichleta jest
63

ROZDZIAŁ 12. Zasada Dirichleta.
Twierdzenie 12.2 (zasada podziałowa) Niech q
1
, q
2
, . . . , q
n
będzie ciągiem liczb na-
turalnych. Jeśli X = X
1
∪ X
2
∪ . . . ∪ X
n
oraz |X| (
P
n
i=1
q
i
) − n + 1, to |X
i
| q
i
dla
pewnego i ∈ {1 , . . ., n}.
Inne sformułowanie zasady szufladkowej używa pojęcia funkcji:
Twierdzenie 12.3 Jeżeli A i B są zbiorami skończonymi, takimi że |A| > |B| (liczba
elementów zbioru A jest większa od liczby elementów zbioru B), zaś f :A → B jest funkcją
przekształcającą zbiór A w zbiór B, wtedy istnieją takie różne elementy a, b ∈ A, że
f (a) = f (b).
W tym ujęciu zasada szufladkowa wyraża więc fakt, że nie istnieje funkcja różnowarto-
ściowa (wariacja bez powtórzeń) ze zbioru o większej liczbie elementów. Szufladami stają
się tutaj tzw. warstwice funkcji f , czyli przeciwobrazy jednoelementowych podzbiorów
zbioru A.
W języku potocznym zasadę szufladkową formułuje się następująco:
Twierdzenie 12.4 Jeżeli rozmieścimy n kul w m szufladach, przy czym n > m to w
pewnej szufladzie znajdą się co najmniej dwie kule.
W postaci ogólniejszej zasada szufladkowa mówi, że:
Twierdzenie 12.5 Jeżeli rozmieścimy n kul w m szufladach, przy czym n > km dla
pewnej liczby naturalnej k, to w pewnej szufladzie znajdzie się co najmniej k + 1 kul.
Czasem łatwiejsza w użyciu jest następująca wersja tejże zasady:
Twierdzenie 12.6 Jeżeli rozmieścimy km+1 kul w m szufladach, to w pewnej szufladzie
znajdzie się co najmniej k + 1 kul.
Stąd na mocy tej zasady stwierdzamy na przykład, że:
• jeżeli z 3 samochodów wysiadło 10 osób, to pewnym samochodem przyjechały co
najmniej 4 osoby;
• wśród 13 liczb naturalnych jest co najmniej 7 jednakowej parzystości oraz co naj-
mniej dwie, których różnica jest podzielna przez 12;
• w klasie 25-osobowej znajdziemy co najmniej troje uczniów urodzonych w tym sa-
mym w tym samym miejscu, itd.
Podane przykłady pokazują, jak prosta jest sama zasada szufladkowa Dirichleta, ale
jak dalej zostanie pokazane może ona mieć nietrywialne zastosowania w matematyce.
W matematyce formułuje się także „nieskończoną” postać zasady szufladkowej:
Twierdzenie 12.7 Jeśli rozmieścimy nieskończenie wiele kul w skończonej ilości szuflad,
to w pewnej szufladzie znajdzie się nieskończenie wiele kul.
Na gruncie arytmetyki liczb naturalnych można zasadzie Dirichleta nadać czysto arytme-
tyczne sformułowanie:
Twierdzenie 12.8 Funkcja o wartościach mniejszych od k, dla k argumentów, musi mieć
co najmniej dwie wartości jednakowe, tzn.
∀n ¬ k
h
F (n) < k ⇒ ∃ l, m ¬ k
l 6= m ∧ F (m) = F (l)
i
(12.2)
64

12.2. Zastosowanie metody modelowania w zadaniach.
Kontrapozycja powyższego arytmetycznego sformułowania zasady Dirichleta ma postać:
∀x, y ¬ k
F (x) = F (y) ⇒ x = y
⇒ ∃x ¬ k F (x) k
(12.3)
Tak sformułowane twierdzenie o szufladkowaniu przez kontrapozycję opisuje pewną wła-
sność funkcji wzajemnie jednoznacznych.
W arytmetyce teoretycznej udowadnia się nim następujące metatwierdzenie:
Twierdzenie 12.9 Zasada szufladkowa Dirichleta i kontrapozycja zasady Dirichleta są
równoważne zasadzie indukcji.
Oczywiście wszystkie podane wyżej sformułowania zasady szufladkowej są równoważne,
co służy jej wszechstronnym zastosowaniom i aplikacjom.
Na koniec zauważmy jeszcze, że terminologia polska nie jest jednolita: zasadę szu-
fladkową (niem. Dirichletsche Schubfachprinzip) nazywa się także zasadą pudełkową; w
literaturze angielskiej bywa ona nazywana pigeon hole principle (tzn. zasadą gniazd go-
łębich), mówi się tam bowiem o rozmieszczeniu n gołębi w k gniazdach.
12.2
Zastosowanie metody modelowania w zadaniach.
Można powiedzieć, że zasada szufladkowa jest „wytrychem” załatwiającym wiele tech-
nicznych kłopotów przy rozwiązywaniu zadań. Podobny schemat rozmieszczania kul w
szufladach przyjeliśmy w modelowaniu kombonatorycznym. Jednocześnie jednak przy roz-
wiązywaniu zadań, w których moglibyśmy zastosować tę zasadę, najtrudniej jest stwier-
dzić czym w zadaniu są „kule”, a czym „szuflady”. Należy przy tym uzmysłowić sobie, w
jaki sposób będziemy rozmieszczać kule w szufladach. Inaczej mówiąc należy zdefiniować
zbiory A i B oraz funkcję f :A → B w taki sposób, by równość f (a) = f (b) (występująca
w twierdzeniu 12.3) dawała rozwiązanie zadania. W ten sposób dokonujemy transformacji
od modelu logicznego do modelu matematycznego. Transformacje tę nazywamy właśnie
modelowaniem.
W zadaniach o podzielności liczb rolę kul spełniać mogą reszty z dzielenia liczb na-
turalnych przez ustaloną liczbę p. Rolę szuflad spełniają wówczas liczby 1, 2, . . ., p − 1.
Zasada Dirichleta przybiera wtedy następującą postać:
Twierdzenie 12.10 Jeśli zbiór M zawiera p − 1 różnych liczb naturalnych, które nie są
podzielne przez p i różnica dowolnych dwóch spośród tych liczb nie jest podzielna przez p,
to zbiór reszt z dzielenia przez p liczb zbioru M jest równy {1 , 2, . . ., p − 1}.
W niektórych (na ogól trudnych) zadaniach, zasadę Dirichleta stosuje się kilkakrotnie,
wyodrębniając najpierw grupę obiektów, które spełniają tylko część żądanych warunków,
a następnie wybierając z tej grupy obiekt spełniający wszystkie warunki.
Zauważmy jednak, że dowody oparte o zasadę Dirichleta mają w pewnym sensie cha-
rakter egzystencjalny, gdyż nie wskazują obiektów, których istnienia się dowodzi. Jest to
charakterystyczna cecha dla zastosowań tejże zasady.
W niniejszym podrozdziale zaprezentuję atrakcyjność i możliwości, jakie daje metoda
modelowania matematycznego oparta o zasadę szufladkową Dirichleta w zastosowaniach
dydaktycznych. Dokonam tego przedstawiając konkretne problemy zadaniowe i ich roz-
wiązania.
Przykład. Wykazać że w Warszawie mieszkają dwie osoby, mające tę samą liczbę
włosów na głowie.
65

ROZDZIAŁ 12. Zasada Dirichleta.
Rozwiązanie. Liczba włosów na głowie człowieka nie przekracza 1000000. Ponumeruj-
my szuflady liczbami od 0 do 1000000 (jest ich 1000001) i przyporządkujmy każdemu
mieszkańcowi Warszawy tę szufladę, której numer wskazuje liczbę włosów na jego głowie.
Ponieważ Warszawa liczy ponad 1000000 mieszkańców, więc na mocy zasady Dirichleta
przynajmniej dwie osoby spośród nich mają tę samą liczbę włosów na głowie.
Przykład. W sali znajduje się k osób, k 2. Udowodnić, że co najmniej dwie z tych
osób mają wśród obecnych tę samą liczbę znajomych. Przyjmujemy, że jeżeli osoba A zna
osobę B, to również B zna A.
Rozwiązanie. Niech f (A) będzie liczbą osób na sali, które zna osoba A. Oczywiście
0 ¬ f (A) ¬ k − 1. Nie jest jednak możliwe, by funkcja f przyjmowała zarówno wartość
0, jak i k − 1. Byłaby bowiem osoba X, nie mająca znajomych na sali (f (X) = 0) i osoba
Y , znająca wszystkie pozostałe osoby (f (Y ) = k − 1), a więc i osobę X. Sprzeczność.
Zatem funkcja f przeprowadza k-elementowy zbiór X w zbiór (k − 1)-elementowy {0 , 1,
. . ., k − 2} lub {1 , 2, . . ., k − 1}. Nie jest więc ona różnowartościowa, tzn. istnieją dwie
osoby K i L, dla których f (K) = f (L), czyli mające tę samą liczbę znajomych w sali.
Przykład. Okrągły stół udekorowano proporczykami n różnych krajów w taki sposób,
że przy każdym nakryciu umieszczono jeden proporczyk. Przy stole siedzi n ambasadorów
z tych krajów, przy czym żaden z nich nie siedzi przy proporczyku swego kraju. Wykazać,
że można stół obrócić o taki kąt, że po obrocie co najmniej dwóch ambasadorów będzie
siedziało przy właściwym proporczyku.
Rozwiązanie. Istnieje n − 1 obrotów stołu, po których wzajemne położenie proporczy-
ków i ambasadorów zmieni się. Każdemu ambasadorowi przyporządkowujemy ten obrót,
po którym znajdzie się on przy proporczyku swojego kraju. Ambasadorów utożsamiamy
z kulami, natomiast obroty z szufladami. Zgodnie z zasadą Dirichleta istnieje przynaj-
mniej jeden taki obrót, po którym dwóch (a może nawet więcej) posłów znajdzie się przy
właściwych proporczykach.
Przykład. Dany jest zbiór złożony z dziesięciu liczb naturalnych dwucyfrowych w
rozwinięciu dziesiętnym. Dowieść, że w tym zbiorze istnieją dwa niepuste podzbiory takie,
że sumy liczb obu podzbiorów są równe.
Rozwiązanie. Przyporządkowujemy elementowi a
k
liczbę naturalną będącą maksymal-
ną długością ciągu rosnącego, jaki można utworzyć bez zmiany kolejności elementów a
1
,
. . ., a
k
. Jeśli jakiemuś elementowi przyporządkowaliśmy liczbę większą od 10, to zadanie
jest rozwiązane. Jeśli nie, to podzielmy ciąg a
1
, a
2
, . . ., a
101
na 10 podciągów, zaliczając
do i-tego podciągu te liczby, którym przyporządkowano i. Podciągi traktujemy jako „szu-
flady” (mamy więc 10 szuflad), natomiast elementy i-tego podciągu jako kule wrzucone
do i-tej szuflady. Problem sprowadza się do rozmieszczenia 101 kul w 10 szufladach. Na
mocy uogólnionej zasady szufladkowej pewien podciąg (szuflada) ma więc co najmniej 11
elementów.
Przykład. Danych jest 11 liczb rzeczywistych. Udowodnić, że co najmniej dwie spo-
śród nich mają rozwinięcia dziesiętne pokrywające się w nieskończonej ilości miejsc po
przecinku. (Jeśli liczba ma skończone rozwinięcie dziesiętne, to uzupełniamy je zerami.)
Rozwiązanie. Przypuśćmy dla dowodu nie wprost, że każda para rozważanych liczb
pokrywa się na skończonej ilości miejsc po przecinku. Par tych liczb jest również skończenie
wiele
11
2
= 55. Zatem dla dostatecznie dużej liczby naturalnej n, na n-tym miejscu
po przecinku żadna para nie może się pokrywać. To jednak jest niemożliwe, liczb (kul)
mamy 11, cyfr (szuflad) 10, więc, na mocy zasady szufladkowej Dirichleta, pewne dwie
liczby pokrywają się na n-tym miejscu po przecinku. Uzyskana sprzeczność dowodzi tezy
zadania.
66

12.2. Zastosowanie metody modelowania w zadaniach.
Przykład. Wykazać, że w trójkącie równobocznym o boku 4, nie można umieścić 17
punktów tak, by odległość dwóch z nich była większa niż 1.
Rozwiązanie. Wykorzystujemy następującą własność trójkąta, odległość dowolnych
dwóch punktów leżących w trójkącie, nie przekracza długości jego największego boku.
Każdy bok naszego trójkąta dzielimy na cztery odcinki równej długości. Przez punkty
podziału prowadzimy proste równoległe do boków trójkąta. W ten sposób uzyskujemy
podział wyjściowego trójkąta na 16 trójkątów o boku 1. Gdy rozmieścimy w nich 17
punktów, to zgodnie z zasada szufladkową dwa z nich znajdą się w tym samym trójkącie
o boku 1, a więc ich odległość będzie nie większa niż 1.
Rysunek 12.1: Podział trójkąta.
Przykład. Udowodnić, że w dowolnym 2n-kącie wypukłym istnieje przekątna nierów-
noległa do żadnego z boków tego wielokąta.
Rozwiązanie. Ilość przekątnych dowolnego s-kąta wypukłego wynosi
1
2
s(s − 3). Przy-
puśćmy dla dowodu nie wprost, że każda spośród
1
2
2n(2n − 3) = n(2n − 3) przekątnych
danego 2n-kąta jest równoległa do pewnego z jego boków. Ponieważ:
n(2n − 3)
2n
= n −
3
2
> n − 2
więc na mocy zasady szufladkowej Dirichleta istnieje bok, do którego jest równoległych
co najmniej n − 1 przekątnych. Stąd wynika, że dany wielokąt ma co najmniej 2n + 1
wierzchołków. Uzyskana sprzeczność dowodzi tezy zadania.
Przykład. Na płaszczyźnie danych jest 5 punktów kratowych (są to punkty o współ-
rzędnych całkowitych). Wykazać, że środek jednego z odcinków łączących te punkty jest
też punktem kratowym.
Rozwiązanie. Korzystając z liter p (od: parzysty) i n (od: nieparzysty) tworzymy cztery
szufladki: (p, p), (p, n), (n, n) i (n, p) i przydzielamy do nich dane punkty w zależności od
parzystości ich współrzędnych. Zasada Dirichleta gwarantuje, że dwa z tych punktów
znajdą się w jednej szufladce. Oczywiście środek odcinka łączącego te dwa punkty jest
punktem kratowym.
Przykład. Udowodnić, że w zbiorze n + 1 liczb całkowitych istnieją dwie, których
różnica jest podzielna przez n.
Rozwiązanie. Skorzystamy z twierdzenia o dzieleniu z resztą mówiącego, że jeżeli a i
b są liczbami całkowitymi i b 6= 0, to istnieją liczby całkowite q i r (i są one wyznaczone
przez liczby a i b jednoznacznie), spełniające warunki:
a = bq + r
∧
0 ¬ r < |b|
67

ROZDZIAŁ 12. Zasada Dirichleta.
Liczbę r nazywamy resztą z dzielenia a przez b. Niech liczbami, o których mowa w
zadaniu, będą a
1
, a
2
, . . . , a
n+1
. Niech r
i
będzie resztą z dzielenia liczby a
i
przez n, zatem
r
i
jest liczbą ze zbioru 0, 1, . . . , n − 1. Umieśćmy w jednej szufladzie te spośród liczb a
1
,
a
2
, . . . , a
n+1
, które dają tę samą resztę przy dzieleniu przez n. Ponieważ liczb jest n + 1,
a możliwych reszt (szuflad) tylko n, zatem dwie liczby znajdą się w tej samej szufladzie.
Oznacza to, że istnieją różne liczby i oraz j, dla których a
i
= nq
i
+ r, a
j
= nq
j
+ r.
Odejmując stronami te równości otrzymujemy równość a
i
− a
j
= n(q
i
− q
j
), więc różnica
liczb a
i
oraz a
j
jest podzielna przez n, co kończy dowód.
Przykład. Zbiór M składa się z 1874 różnych liczb naturalnych. Pokazać, że można
wybrać a, b, c ∈ M takie, że a(b − c) dzieli się przez 1874.
Rozwiązanie. Jeśli któraś z liczb na przykład a ∈ M dzieli się przez 1874, to b i
c można wybrać dowolnie. Jeśli nie ma takiej liczby, to na podstawie zasady Dirichleta
wnioskujemy, że istnieją co najmniej dwie liczby b, c ∈ M , których reszty z dzielenia przez
1874 są takie same. Wówczas b − c dzieli się przez 1874, natomiast liczbę a można wybrać
dowolnie.
68

Rozdział 13
Równania rekurencyjne. ([1],
[5], [10], [18], [23])
Podana zostanie obecnie inna niż w rozdziale 4 metoda wyznaczenia wzorów bezpośrednio
określających n-ty wyraz ciągu określonego zależnością rekurencyjną:
u
n
= au
n−1
+ bu
n−2
dla
n ∈ N
(13.1)
Ciąg takiej postaci nazywamy uogólnionym ciągiem Fibonacciego. Przyjmujemy, że b 6= 0,
gdyż w przeciwnym razie ciąg (u
n
) jest ciągiem geometrycznym. Współczynniki a i b
występujące w zależności rekurencyjnej 13.1 wyznaczają wielomian
f (x) = x
2
− ax − b
który nazywamy wielomianem charakterystycznym równania rekurencyjnego (13.1).
Twierdzenie 13.1 Ciąg (t
n
) dla t 6= 0 spełnia zależność rekurencyjną 13.1 wtedy i tylko
wtedy, gdy t jest pierwiastkiem wielomianu charakterystycznego.
Ciąg (nt
n
) dla t 6= 0 spełnia zależność rekurencyjną 13.1 wtedy i tylko wtedy, gdy t
jest dwukrotnym pierwiastkiem wielomianu charakterystycznego.
Jeśli t
1
, t
2
są różnymi pierwiastkami wielomianu charakterystycznego, to rozwiązaniem
zależności rekurencyjnej 13.1 jest ciąg (u
n
) określony
u
n
= c
1
t
n
1
+ c
2
T
n
2
(13.2)
gdzie c
1
, c
2
są ustalonymi liczbami.
Jeśli t jest dwukrotnym pierwiastkiem wielomianu charakterystycznego, to rozwiąza-
niem zależności rekurencyjnej 13.1 jest ciąg (u
n
) określony
u
n
= c
1
t
n
+ c
2
nt
n
(13.3)
gdzie c
1
,c
2
są ustalonymi liczbami.
Dowód. Jeśli ciąg (t
n
) spełnia zależność 13.1, to mamy:
t
n
= at
n−1
+ bt
n−2
dla
n = 2, 3, . . .
69

ROZDZIAŁ 13. Równania rekurencyjne.
skąd oczywiście wynika t
2
= at + b, więc t jest pierwiastkiem wielomianu x
2
− ax − b. Jeśli
t jest pierwiastkiem tego wielomianu, to t
2
= at + b, więc
t
n
= at
n−1
+ bt
n−2
dla
n = 2, 3, . . .
Jeśli ciąg (nt
n
) spełnia zależność 13.1, to mamy:
nt
n
= a(n − 1)t
n−1
+ b(n − 2)t
n−2
więc
t
n−2
[n(t
2
− at − b) + at + 2b] = 0
dla
n = 2, 3, . . .
Wynika stąd, że t
2
− at − b = 0 oraz at + 2b = 0, a to znaczy, że t = −
2b
a
spełnia
równanie t
2
−at−b = 0, to zaś pociąga za sobą, że a
2
+4b = 0. Liczba t jest więc pierwiast-
kiem dwukrotnym wielomianu charakterystycznego. Przeprowadzone rachunki dowodzą
jednocześnie, że jeśli t jest pierwiastkiem dwukrotnym wielomianu charakterystycznego,
to ciąg (nt
n
) spełnia zależność 13.1.
Jeśli ciągi (t
n
1
) i (t
n
2
) albo odpowiednio (t
n
) i (nt
n
) spełniają zależność 13.1, to oczy-
wiście przy każdych stałych c
1
, c
2
, odpowiednio ciągi
(c
1
t
n
1
+ c
2
t
n
2
)
i
(c
1
t
n
+ c
2
nt
n
)
spełniają zależność 13.1. Ponieważ ciąg określony rekurencyjnie ma konkretne wyrazy u
1
,
u
2
, więc stałe c
1
, c
2
(dla równania 13.2) są jednoznacznie wyznaczone przez zależności:
u
1
= c
1
t
1
+ c
2
t
2
u
2
= c
1
t
2
1
+ c
2
t
2
2
albo (dla 13.3)
u
1
= c
1
t
1
+ c
2
t
2
u
2
= c
1
t
2
+ c
2
t
2
Dowód twierdzenia został w ten sposób zakończony.
2
Przykłady w dalszej części pracy zilustrują sposób wykorzystania wielomianu charak-
terystycznego przy znajdowaniu wzoru ogólnego ciągów zadanych rekurencyjnie. Trzeba
jednocześnie w tym miejscu podkreślić, że taka umiejętność niejednokrotnie decyduje o
sukcesie przy rozwiązywaniu zadania techniką modelowania rekurencyjnego.
13.0.1
Renumeracja i przesunięcie o stałą wyrazów ciągu geome-
trycznego.
Przykład. Często występujący przypadek renumeracji który sprawia niekiedy kłopoty w
rozwiązaniu zadania to sytuacja, gdy dana jest zależność:
a
n+2
= qa
n
,
gdzie
q 6= 0
q 6= 1
oraz jest zadana wartość a
n
0
6= 0 dla pewnego n
0
∈ N. Oczywiście w ogólnym przypadku
nie można zapisać:
a
n+1
= a
n
√
q
dla
n ∈ N
70

13.1. Modelowanie rekurencyjne z wykorzystaniem liczb Fibonacciego.
Mamy natomiast:
a
n
0
+2(p+1)
= qa
n
0
+2p
gdzie
p ∈ N
Z powyższego otrzymujemy wzór na (n
0
+ 2p)-ty wyraz ciągu geometrycznego:
a
n
0
+2p
= a
n
0
q
p
p ∈ N
Przykład. Kolejny przypadek dotyczy przesunięcia o stałą wyrazów ciągu geometrycz-
nego. Na wejściu dana jest zależność:
a
n+1
= qa
n
+ c
q 6= 0
q 6= 1
c 6= 0
a
1
6= 0
n ∈ N
Wystarczy wówczas dokonać następującego podstawienia:
b
n
= a
n
+
c
q − 1
b
1
= a
1
+
c
q − 1
n ∈ N;
by zadanie sprowadziło się do wyznaczenia n-tego wyrazu ciągu geometrycznego b
n+1
=
qb
n
przy danym b
1
i n ∈ N.
13.1
Modelowanie rekurencyjne z wykorzystaniem
liczb Fibonacciego. ([1], [13])
13.1.1
Definicja i własności ciągu liczb Fibonacciego.
Oryginalne zadanie, które Fibonacci rozważał dotyczyło rozmnażania się królików. Cho-
dziło mianowicie o określenie, ile par królików będzie liczyła po 12 miesiącach populacja
zaczęta przez jedną parę, przy założeniu, że po urodzeniu każda para królików dojrzewa
przez pierwszy miesiąc, a począwszy od drugiego wydaje na świat co miesiąc potomstwo
(przyjmuje się przy tym, że każda para jednorazowo płodzi jedną parę królicząt). Przy
tych założeniach rozumowanie Fibonacciego przebiegało następująco. Ponieważ pierwsza
para w pierwszym miesiącu daje jako potomstwo jedną parę, więc w tym miesiącu będą
dwie pary; z nich jedna para, a mianowicie pierwsza, rodzi również w następnym miesią-
cu, więc w drugim miesiącu będą trzy pary. Z nich w następnym miesiącu będą dawały
potomstwo dwie pary, a więc w trzecim rodzą się jeszcze dwie pary królików i w tym
miesiącu bedzie pięć par królików. Dalej analogiczny wywód ciągnie się aż do dwunastego
miesiąca, aby po kilku dodawaniach dojść do liczby 377, będącej końcowym wynikiem.
Idea wywodu daje się streścić następująco. W pierwszym miesiącu mamy dwie pary,
w drugim trzy. Chcąc uzyskać liczbę par królików w miesiącu n + 2 powinniśmy do ich
liczby z miesiąca n + 1 dodać te, które istniały w miesiącu n i wydały właśnie na świat
kolejne (być może pierwsze) młode.
Zakładamy, zgodnie z tradycją oznaczania liczb Fibonacciego a niezgodnie z orygina-
łem, że zarówno pierwsza jak i druga liczba Fibonacciego są jedynkami (tak jak gdyby w
zerowym miesiącu macierzysta para powstawała, a w następnym jeszcze dojrzewała).
Definiujemy ciąg Fibonacciego następująco:
F
0
= 1
F
1
= 1
F
n
= F
n−1
+ F
n−2
n 2
Kolejne liczby uzyskane bezpośrednio z definicji, są wypisane w tabeli 13.1.
Jak widzimy definicja rekurencyjna pozwala wyznaczyć kolejne wyrazy ciągu, choć
niestety w celu obliczenia tą metodą któregoś wyrazu ciągu trzeba obliczyć wszystkie
71

ROZDZIAŁ 13. Równania rekurencyjne.
F
0
F
1
F
2
F
3
F
4
F
5
F
6
F
7
F
8
F
9
F
10
. . .
1
1
2
3
5
8
13
21
34
55
89
. . .
Tabela 13.1: Liczby Fibonacciego.
wyrazy poprzednie. Znalezienie jawnego wzoru na wyrazy ciągu Fibonacciego nie jest
najłatwiejsze. Wzór na n-ty wyraz ciągu Fibonacciego został udowodniony dopiero w
XIX wieku (a więc ponad 600 lat po Fibonaccim) przez J.Bineta. Trudno uwierzyć bez
dowodu, że ten skomplikowany wzór daje w wyniku dla każdego n liczby naturalne.
13.1.2
Wzór Bineta.
Twierdzenie 13.2 (wzór Bineta)
F
n
=
√
5
5
1 +
√
5
2
n
−
1 −
√
5
2
n
!
n = 0, 1, 2, . . .
(13.4)
Przedstawię teraz dwie metody wyprowadzenia ogólnego wzoru ciągu Fibonacciego.
Jednocześnie w ten sposób zostaną zaprezentowane dwie podstawowe metody wyzna-
czania wyrazu ogólnego dowolnego ciągu określonego zależnością rekurencyjną. Metoda
pierwsza, akademicka, wykorzystuje pojęcie funkcji tworzącej i własności szeregów po-
tęgowych, z tego też względu nie kandyduje do wykorzystania w liceum. Metoda druga
bazuje na wielomianie charakterystycznym równania rekurencyjnego, który z zosatał już
w podręczniku zdefiniowany i wykorzystany
Metoda I.
Dowód. Określmy funkcję F jako sumę szeregu potęgowego o wspólczynnikach F
n
, czyli
funkcję tworzącą ciągu liczb Fibonacciego (F
n
).
F (t) = F
0
+ F
1
t + F
2
t
2
+ . . . =
∞
X
n=0
F
n
t
n
Znajdziemy teraz jawny wzór na funkcję F . Zauważmy, że:
F (t) − t − 1 =
∞
X
n=2
F
n
t
n
=
∞
X
n=0
F
n+2
t
n+2
=
∞
X
n=0
(F
n
+ F
n+1
)t
n+2
=
t
2
∞
X
n=0
F
n
t
n
+ t
∞
X
n=0
F
n+1
t
n+1
= t
2
F (t) + t(F (t) − 1)
Tak więc funkcja F spełnia równanie:
F (t) − t − 1 = t
2
F (t) + t(F (t) − 1)
Jedyną taką funkcją jest (jak łatwo obliczyć):
F (t) =
1
1 − t − t
2
72
13.1. Modelowanie rekurencyjne z wykorzystaniem liczb Fibonacciego.
Aby znaleźć współczynniki rozwinięcia funkcji F , zapiszemy ją inaczej. Pierwiastkami
trójmianu t
2
+ t − 1 są liczby:
t
1
=
−1 −
√
5
2
t
2
=
−1 +
√
5
2
Tak więc
F (t) = −
√
5
5
1
t
2
·
1
1 −
t
t
2
−
1
t
1
·
1
1 −
t
t
1
!
Teraz korzystając ze wzoru na sumę szeregu geometrycznego, otrzymujemy:
F (t) = −
√
5
5
1
t
2
·
∞
X
n=0
t
t
2
n
−
1
t
1
·
∞
X
n=0
t
t
1
n
!
=
∞
X
n=0
t
n
√
5
5
·
t
n+1
1
− t
n+1
2
t
n+1
1
t
n+1
2
Wzór ten ma sens dla |t| < min(|t
1
|, |t
2
|). Z jednoznaczności rozwinięcia funkcji w szereg
potęgowy mamy:
F
n
=
√
5
5
·
(1 +
√
5)
n+1
− (1 −
√
5)
n+1
2
n+1
=
√
5
5
1 +
√
5
2
n+1
−
1 −
√
5
2
n+1
!
n = 0, 1, 2, . . .
Koniec dowodu.
2
Metoda II.
Dowód. Przypomnijmy definicję rekurencyjną ciągu Fibonacciego:
F
0
= F
1
= 1
(13.5)
F
n+2
= F
n+1
+ F
n
n > 1
(13.6)
Zależności 13.6 odpowiada wielomian charakterystyczny:
f (x) = x
2
− x − 1
Pierwiastki tego wielomianu wynoszą x
1
=
1−
√
5
2
, x
2
=
1+
√
5
2
, więc z 13.5 otrzymujemy,
że
F
n
= c
1
x
n
1
+ c
2
x
n
2
= c
1
1 −
√
5
2
n
+ c
2
1 +
√
5
2
n
gdzie liczby c
1
, c
2
spełniają zależności:
c
1
+ c
2
= 1
c
1
·
1 −
√
5
2
+ c
2
·
1 +
√
5
2
= 1
Rozwiązując ten układ równań otrzymujemy: c
1
=
5−
√
5
10
, c
2
=
5+
√
5
10
. Zatem
F
n
=
5 −
√
5
10
1 −
√
5
2
n
+
5 +
√
5
10
1 +
√
5
2
n
73

ROZDZIAŁ 13. Równania rekurencyjne.
Po przekształceniach dostajemy
F
n
=
√
5(
√
5 − 1)
2 · 5
1 −
√
5
2
n
+
√
5(
√
5 + 1)
2 · 5
1 +
√
5
2
n
=
√
5
5
1 −
√
5
2
n+1
−
1 +
√
5
2
n+1
!
Koniec dowodu.
2
13.2
Inne własności ciągu liczb Fibonacciego.
Dla dowolnych liczb naturalnych zachodzą związki:
F
n+2
− 1 = F
0
+ F
1
+ F
2
+ . . . + F
n
F
2n
= F
1
+ F
3
+ . . . + F
2n−1
F
2n+1
− 1 = F
0
+ F
2
+ F
4
+ . . . + F
2n
F
2m−1
− 1 = F
0
− F
1
+ F
2
− F
3
+ F
4
+ . . . + (−1)
n
F
n
F
n
+ F
n+1
= F
2
0
+ F
2
1
+ F
2
2
+ . . . + F
2
n
F
n+m
= F
n−1
F
m−1
+ F
n
F
m
m, n 1
F
2n
= F
2
n+1
− F
2
n−1
F
2
n
= F
n−1
F
n+1
+ (−1)
n+1
F
4
n
= 1 + F
n−2
F
n−1
F
n+1
F
n+2
n 2
F
2
2n
= F
0
F
1
+ F
1
F
2
+ F
2
F
3
+ . . . + F
2n−1
F
2n
F
n+1
= F
m
F
n−m
+ F
m+1
F
n−m+1
n m 0
F
2n+1
= F
2
n
+ F
2
n+1
n 0
F
2n
= F
2
n+1
− F
2
n−1
n 1
F
3n
= F
3
n
+ F
3
n+1
− F
3
n−1
n 1
F
n−1
F
n+1
− F
2
n
= (−1)
n
n 1
F
n+4
− (n + 3) = nF
1
+ (n − 1)F
2
+ . . . + 2F
n−1
+ F
n
nF
n+2
− F
n+3
+ 2 = F
1
+ 2F
2
+ . . . + nF
n
n | m ⇒ F
n
| F
m
NWD(F
n
, F
n+1
) = 1
NWD(F
m
, F
n
) = F
NWD(m,n)
n−1
X
k=0
n
k
F
n−k
= F
2n
n
X
k=0
F
k+2
F
k+1
F
k+3
=
F
3
F
1
F
2
−
F
n+4
F
n+2
F
n+3
74

13.2. Inne własności ciągu liczb Fibonacciego.
13.2.1
Przykłady zadań rozwiązanych metodą modelowania re-
kurencyjnego z wykorzystaniem liczb Fibonacciego.
Zauważmy, że Fibonacci zamiast podać wynik zadania, podał jedynie sposób, w jaki
można do niego dojść. Czy można uznać to zadanie za rozwiązane?
Jeżeli mamy ochotę odrzucić tego typu „algorytmiczne” rozwiązania, to zdajmy so-
bie sprawę, że w wielu przypadkach trudno jest inaczej rozwiązać problem, niż w taki
rekurencyjny sposób w jaki zrobił to Fibonacci. Przykładowo rozważymy kilka takich
problemów.
Przykład. Ile pra-pra-. . . -pra (n-razy) dziadków i babć ma pszczeli truteń?
Rozwiązanie. Trzeba oczywiście wiedzieć, że u pszczół trutnie mają tylko matkę –
królową, powstają bez udziału ojca, podczas gdy królowe mają już dwoje rodziców – inną
królową i trutnia.
Rysunek 13.1: Drzewo genealogiczne trutnia.
Niech T
n
oznacza liczbę n-praprzodków. Widzimy już, że na poziomie pierwszych pra-
dziadków truteń ma dwie prababcie i jednego pradziadka, łącznie troje. Piętro wyżej – na
poziomie drugich pradziadków – pięcioro, trzy prababcie i dwóch prapradziadków. Ogól-
nie na poziomie n-tych dziadków ma dokładnie T
n−1
n-prababć oraz T
n−2
n-pradziadków,
łącznie więc ma:
T
n
= T
n−1
+ T
n−2
n 2
n-praprzodków. Otrzymaliśmy zatem identyczne równanie rekurencyjne, określające zde-
finiowany wyżej ciąg Fibonacciego. Pozostaje określić warunki początkowe, T
0
= 2 (przyj-
mujemy dziadków za 0-pradziadków), T
1
= 3 i jasne jest, że ogólnie zachodzi po prostu:
T
n
= F
n+2
n 0
Przykład. Elfy skacząc po schodach czasami przeskakują po dwa schodki. Na ile spo-
sobów może elf wskoczyć na n schodów?
Rozwiązanie. Tym razem od razu poddamy się i zaczniemy rozumowanie rekurencyjne.
Oznaczmy przez E
n
liczbę sposobów za pomocą których elf może wskoczyć na n schodów.
Przyjmujemy, że E
0
= 1 i zauważamy ponadto, że E
1
= 1 oraz E
2
= 2. Aby wskoczyć na
75

ROZDZIAŁ 13. Równania rekurencyjne.
n-ty schodek, elf musi to zrobić ze schodka n − 1 lub n − 2. W związku z tym mamy:
E
n
= E
n+1
+ E
n−2
n 3
W ten sposób dostajemy oczywistą odpowiedź, że szukana liczba sposobów wynosi:
E
n
= F
n
n 1
Przykład. Ile jest eleganckich sposobów posadzenia łącznie n pań i panów na podłużnej
ławie? Eleganckich, czyli takich, aby żadne dwie panie nie siedziały obok siebie (interesują
nas jedynie różne wzajemne rozmieszczenia pań i panów, czyli interesuje nas tylko, które
miejsca są zajęte przez panie a które przez panów).
Rozwiązanie. Widać, że jeżeli mamy do dyspozycji samych panów, to możemy ich
posadzić na jeden sposób. Jedną panią z n − 1 panami można posadzić na n sposobów.
Z dwiema już będzie trochę kłopotu. Z trzema – tym bardziej. Łatwo zauważyć, że pań
nie może być więcej niż [
n
2
]. Rekurencja ze względu na liczbę pań przy ustalonym n
jest trudna do wyprowadzenia. Zastanówmy się jednak, czy nie dałoby się przeprowadzić
rozumowania rekurencyjnego ze względu na n?
Oznaczmy przez S
n
liczbę takich n-posadzeń, że żadne dwie panie nie siedzą obok
siebie i załóżmy, że znamy S
k
dla wszystkich k < n. Przeliczając wszystkie n-posadzenia
musimy zdecydować, czy na n-tym miejscu będzie siedziała pani, czy też pan. Jeżeli pani,
to na n − 1 miejscu musi siedzieć pan, a na pierwszych n − 2 miejscach możemy posadzić
dowolny z S
n−2
układów. Jeżeli pan, to ze względu na to, że pan na n-tym miejscu nie
czyni żadnego kłopotu, widzimy, że na pierwszych n − 1 miejscach możemy użyć dowolny
z S
n
układów. Łącznie, oczywiście, uzyskujemy:
S
1
= 2
S
2
= 3
S
n
= S
n−1
+ S
n−2
n > 2
więc szukana liczba usadzeń pań i panów na ławie wynosi:
S
n
= F
n+2
Przykład. Wyznaczyć liczbę takich podzbiorów zbioru {1 , 2, . . ., n}, które nie zawie-
rają dwóch kolejnych liczb.
Rozwiązanie. Dla n = 1 są dwa takie podzbiory: ∅, {1}. Dla n = 2 są trzy takie
podzbiory: ∅, {1}, {2}. Przypuśćmy, że n 2. Każdy podzbiór zbioru {1 , 2, . . ., n + 1}
nie zawierający dwóch kolejnych liczb, do którego nie należy liczba n + 1 jest podzbiorem
żądanej postaci zbioru {1 , 2, . . ., n}. Każdy podzbiór zbioru {1 , 2, . . ., n + 1} nie zawie-
rający dwóch kolejnych liczb do którego należy liczba n + 1 jest podzbiorem postaci {k
1
,
k
2
, . . ., k
m
, n + 1}, przy czym liczby k
1
, k
2
, . . . , k
m
są mniejsze od n i nie ma wśród nich
dwóch kolejnych.
Jeśli więc a
n
jest liczbą omawianych podzbiorów zbioru {1, 2, . . . n}, to dla n 2 jest
a
n+1
= a
n
+ a
n−1
. Ciąg (a
n
) spełnia więc warunki:
a
1
= 2
a
2
= 3
a
n
= a
n−1
+ a
n−2
n > 2
Jest to ciąg Fibonacciego. Wystarczy tylko zauważyć, że:
a
n
= F
n+1
n 1
aby otrzymać dający natychmiastowe rozwiązane model rekurencyjny.
Oczywiście nie każde rozumowanie rekurencyjne daje w wyniku liczby Fibonacciego.
Wystarczy zmienić każde z tych zadań (np. dopuścić aby elfy skakały także po trzy schod-
ki, albo rozważyć usadzenia przy okrągłym stole), aby nie tylko warunki początkowe, ale
i same równania otrzymać w innej postaci.
76

13.3. Metoda modelowania rekurencyjnego w zadaniach.
13.3
Metoda modelowania rekurencyjnego
w zadaniach.
13.3.1
Zadania z kombinatoryki.
W rozdziale 4 zostały już przedstawione pewne zadania z kombinatoryki, przy rozwią-
zywaniu których efektywnie wykorzystywano modele rekurencyjne związane z ciągiem
Fibonacciego. Poniżej przedstawione zostaną inne przykłady zadań kombinatorycznych,
które można łatwo rozwiązać konstruując odpowiednie modele rekurencyjne.
Przykład. W tańcu ludowym tancerze stoją w dwóch rzędach naprzeciw siebie, w
jednym rzędzie n dziewcząt, w drugim n chłopców. Każdy z tancerzy podaje lewą rękę
osobie stojącej naprzeciw siebie lub sąsiadowi z lewej strony lub osobie stojącej naprzeciw
sąsiada z lewej strony. Analogiczna reguła dotyczy prawej ręki. Nikt nie podaje ręki tej
samej osobie. Wyznaczyć liczbę możliwych układów rąk.
Rozwiązanie. Oznaczmy liczbę możliwych układów rąk przez u
n
. Przypuśćmy, że ob-
serwujemy tancerzy stojąc za rzędem chłopców. Numerujemy chłopców kolejnymi liczbami
naturalnymi zaczynając od lewej strony: c
1
, c
2
, . . . , c
n
; dziewczynce stojącej naprzeciw
chłopca c
i
przypisujemy symbol d
i
. Tancerze są ustawieni tak jak na rysunku 13.2.
Z warunku zadania wynika, że chłopiec c
1
podaje lewą rękę dziewczynce d
1
, chłopiec
c
n
podaje prawą rękę dziewczynce d
n
. Ponieważ nikt nie podaje obu rąk tej samej osobie,
więc przy n = 1 nie można spełnić warunków zadania, zatem u
1
= 0. Dla n = 2 możliwe
są dwa układy rąk przedstawione schematycznie na rysunku 13.3, albo c
1
podaje prawą
rękę c
2
a d
1
lewą rękę a
2
albo c
1
podaje prawą rękę d
2
, zaś c
2
lewą rękę d
1
. Wobec tego
u
2
= 2.
Każdy z tych dwóch układów rąk można na dwa sposoby przedłużyć dołączając trze-
cią parę. Trzeba w tym celu rozłączyć prawą rękę chłopca c
2
i lewą rękę dziewczynki d
2
.
Następnie chłopiec c
2
może podać swą prawą rękę albo dziewczynce d
3
albo chłopcu c
3
.
Po dokonaniu tego wyboru przez chłopca c
2
układ pozostałych rąk jest już jednoznacz-
nie wyznaczony. Mamy więc możliwe cztery układy rąk przedstawione schematycznie na
rysunku 13.4. Zatem u
3
= 4.
Zbudujemy teraz model rekurencyjny danego w zadaniu problemu. Polegać to bę-
dzie na ustaleniu zależności rekurencyjnej określającej wyrazy u
n
w zależności od dwóch
poprzednich.
Przypuśćmy, że n > 3. Rozważmy dowolny układ rąk tancerzy i zwróćmy szczególną
uwagę na trzy ostatnie pary. Możliwe są przypadki przedstawione na rysunku 13.5.
W przypadkach a) i b) układ rąk tancerzy d
1
, . . . , d
n−2
, c
1
, . . . , c
n−2
jest dowolnym
układem dla n − 2 par, zatem liczba układów postaci a) wynosi u
n−2
i liczba układów
postaci b) jest równa u
n−2
. W czterech pozostałych przypadkach rozważane układy po-
Rysunek 13.2: Ustawienie tancerzy.
77

ROZDZIAŁ 13. Równania rekurencyjne.
Rysunek 13.3: Układy rąk dla dwóch par.
Rysunek 13.4: Układy rąk dla trzech par.
Rysunek 13.5:
wstały z układu dla n − 1 par (d
1
, c
1
), . . . , (d
n−1
, c
n−1
) przez rozłączenie prawej ręki
chłopca c
n−1
i lewej ręki dziewczynki d
n−1
. Jeśli przy tym c
n−1
podał prawą rękę chłop-
cu c
n
, to mamy przypadki c) i e), jeśli zaś c
n−1
podał prawą rękę dziewczynce d
n
, to
78

13.3. Metoda modelowania rekurencyjnego w zadaniach.
otrzymujemy przypadki d) i f).
Stwierdziliśmy w ten sposób, że każdy układ rąk dla n par tancerzy można otrzymać
albo z układu rąk dla n − 2 par, albo z układu rąk dla n − 1 par, przy czym z każdego
układu rąk dla n − 2 par albo n − 1 par można otrzymać dwa różne układy rąk dla n par.
Wobec tego:
u
n
= 2u
n−1
+ 2u
n−2
n 3
Ciąg (u
n
) ma (na podstawie twierdzenia 4.1) wielomian charakterystyczny:
f (x) = x
x
− 2x − 2
którego pierwiastkami są liczby x
1
= 1 +
√
3 oraz x
2
= 1 −
√
3. Zatem
u
n
= c
1
x
n
1
+ c
2
x
n
2
= c
1
(1 +
√
3)
n
+ c
2
(1 −
√
3)
n
gdzie liczby c
1
, c
2
obliczymy podstawiając n = 1, 2. Otrzymamy układ:
c
1
(1 +
√
3) + c
2
(1 −
√
3) = 0
c
1
(1 +
√
3)
2
+ c
2
(1 −
√
3)
2
= 2
Po jego rozwiązaniu, dostajemy c
1
=
3−
√
3
6
, c
2
=
3+
√
3
6
. Ostatecznie więc liczba moż-
liwych układów rąk dna n par wynosi:
u
n
=
3 −
√
3
6
(1 +
√
3)
n
+
3 +
√
3
6
(1 −
√
3)
n
n 1
13.3.2
Zadania z rachunku prawdopodobieństwa.
Przykład. Gracz rzuca monetą. Jeśli wypadnie reszka, to wygrywa on 1 zł, a jeśli orzeł -
to traci 1 zł. Na początku gry gracz ma n złotych. Gra kończy się, gdy gracz wygra z góry
ustaloną sumę a zł albo też przegra wszystkie pieniądze. Jakie jest prawdopodobieństwo
zrujnowania się gracza? (Problem ruiny gracza.)
Rozwiązanie. Oznaczmy przez p(n) prawdopodobieństwo zrujnowania się gracza, jeśli
na początku gry ma on n złotych. Zauważmy, że wówczas p(n + 1) oznacza prawdopodo-
bieństwo zrujnowania się tego gracza przy założeniu, że wygrał on przy pierwszym rzucie,
ma on wtedy bowiem n + 1 zł. Natomiast p(n − 1) oznacza prawdopodobieństwo zrujno-
wania się tego gracza przy założeniu, że przegrał on przy pierwszym rzucie, ma on wtedy
n − 1 zł.
Dla potrzeb konstrukcji prawdopodobieństwa warunkowego i całkowitego oznaczmy
przez B
1
, B
2
prawdopodobieństwa odpowiednio wygranej i przegranej gracza przy pierw-
szym rzucie, a przez A prawdopodobieństwo zrujnowania się gracza. Wtedy:
P (B
1
) = P (B
2
) =
1
2
P (A | B
1
) = p(n + 1)
P (A | B
2
) = p(n − 1)
Uwzględniając wzór na prawdopodobieństwo całkowite,
P (A) = P (A | B
1
)P (B
1
) + P (A | B
2
)P (B
2
)
79
ROZDZIAŁ 13. Równania rekurencyjne.
otrzymujemy równanie:
p(n) =
1
2
p(n + 1) +
1
2
p(n − 1)
0 ¬ n ¬ a
Przekształcając powyższe równanie otrzymujemy następującą postać modelu rekurencyj-
nego:
p(n + 1) = 2p(n) − p(n − 1)
0 ¬ n ¬ a
Powyższej zależności rekurencyjnej odpowiada wielomian charakterystyczny, o postaci:
f (x) = x
2
− 2x + 1 = (x − 1)
2
Ponieważ pierwiastkiem dwukrotnym tego wielomianu jest liczba x
0
, więc, (na mocy twier-
dzenia 4.1):
p(n) = c
1
x
n
0
+ c
2
nx
n
0
= c
1
+ c
2
n
Stałe c
1
, c
2
wyznaczamy z warunków zadania:
p(0) = c
1
= 1
p(a) = c
1
+ c
2
a = 0
Skąd otrzymujemy c
1
= 1, c
2
= −
1
a
.
W rezultacie szukane prawdopodobieństwo zrujnowania się gracza wynosi:
p(n) = 1 −
n
a
a n 0
Przykład. W pewnej rodzinie mąż i żona zawarli następującą umowę: jeżeli któregoś
dnia zmywa naczynia żona, to następnego dnia zmywa naczynia mąż. Jeżeli natomiast
pewnego dnia zmywa naczynia mąż, to o tym, kto zmywa następnego dnia, decyduje
losowanie za pomocą rzutu monetą. Obliczyć prawdopodobieństwo zdarzenia, że setne-
go dnia trwania umowy będzie zmywał mąż. Przyjmujemy, że pierwszego dnia trwania
umowy rzucono monetą.
Rozwiązanie. Niech p
n
oznacza prawdopodobieństwo zdarzenia, że n-tego dnia trwania
umowy zmywa naczynia mąż. Wobec tego z warunków zadania mamy p
1
=
1
2
. Zauważmy,
że jeżeli n-tego dnia naczynia zmywa mąż, to możliwe są dwa rozłączne przypadki:
1. (n-1)-szego dnia zmywał mąż. Prawdopodobieństwo tego zdarzenia wynosi
1
2
p
n−1
.
2. (n-1)-szego dnia zmywała żona. Prawdopodobieństwo tego zdarzenia jest równe 1 −
p
n−1
.
Uwzględniając konstrukcję prawdopodobieństwa całkowitego mamy więc:
p
n
=
1
2
p
n−1
+ (1 − p
n−1
)
n 2
Po uproszczeniu otrzymujemy następującą relację uwarunkowania rekurencyjnego:
p
n
= −
1
2
p
n−1
+ 1
n 2
80

13.3. Metoda modelowania rekurencyjnego w zadaniach.
Wykorzystamy teraz metodę przesunięcia o stałą wyrazów ciągu geometrycznego. W tym
celu dokonamy podstawienia:
q
n
= p
n
+
1
−
1
2
− 1
= p
n
−
2
3
n 1
Otrzymujemy wtedy:
q
1
= p
1
−
2
3
= −
1
6
oraz
q
n
= −
1
2
q
n−1
n 2
Z powyższych zależności dostajemy:
p
n
−
2
3
= −
1
6
−
1
2
n−1
n 2
Przekształcając powyższą zależność i podstawiając n = 100, znajdujemy szukane praw-
dopodobieństwo:
p
100
= −
1
6
−
1
2
99
+
2
3
=
1
3 · 2
100
+
2
3
=
1
3
1
2
100
+ 2
Przykład. Jakie jest prawdopodobieństwo otrzymania parzystej liczby sukcesów w
schemacie n prób Bernoulliego, w którym prawdopodobieństwo sukcesu w pojedyńczej
próbie wynosi p.
Rozwiązanie. Oznaczmy przez p
k
prawdopodobieństwo uzyskania parzystej liczby suk-
cesów po przeprowadzeniu pierwszych k doświadczeń. Zauważamy, że p
1
= 1 − p. Przed
przeprowadzeniem k-tego doświadczenia możliwe są dwie hipotezy:
1. W pierwszych k − 1 doświadczeniach uzyskano parzystą liczbę sukcesów.
2. W pierwszych k − 1 doświadczeniach uzyskano nieparzystą liczbę sukcesów.
Prawdopodobieństwa tych hipotez są równe odpowiednio p
k−1
i 1 − p
k−1
. Uwzględnia-
jąc konstrukcję prawdopodobieństwa całkowitego, uzyskujemy w ten sposób następującą
postać modelu rekurencyjnego:
p
k
= p
k−1
(1 − p) + (1 − p
k−1
)p
k 2
po uproszczeniu zaś:
p
k
= p + p
k−1
(1 − 2p)
k 2
Aby dokonać przesunięcia o stałą wyrazów wyżej określonego ciągu rekurencyjnego, do-
konamy podstawienia:
q
k
= p
k
+
p
1 − 2p − 1
=
1
2
p
k
k 2
Otrzymujemy stąd:
q
k
= q
k−1
(1 − 2p)
k 2
q
1
=
1
2
− p
Z powyższych zależności można już wyznaczyć postać wzoru na poszukiwane prawdopo-
dobieństwo:
p
k
−
1
2
= q
k
=
1
2
− p
(1 − 2p)
k−1
k 2
81

ROZDZIAŁ 13. Równania rekurencyjne.
Po przekształceniach otrzymujemy:
p
n
=
1
2
(1 + (1 − 2p)
n
)
n 1
Przykład. W urnie znajdują się 3 kule, oznaczone odpowiednio cyframi: 0, 1, 2. Wycią-
gamy w sposób losowy jedną kule, a następnie ją zwracamy. Jakie jest prawdopodobień-
stwo, że w wyniku n (n ∈ N) losowań suma liczb odpowiadających cyfrom oznaczającym
losowanie kule jest liczbą nieparzystą?
Rozwiązanie. Oznaczmy przez a
i
dla i = 1, 2, 3, . . ., n liczby odpowiadające cyfrom
oznaczającym kule przy i-tym losowaniu. Niech S
n
oznacza sumę liczb a
i
po n losowa-
niach. Szukamy więc prawdopodobieństwa tego, że S
n
jest liczbą nieparzystą. Nie zaj-
mując się historią wcześniejszych wyników niż (n − 1)-sza wartość sumy S
n−1
, wystarczy
zauważyć następującą relację uwarunkowania rekurencyjnego:
1. Jeżeli S
n−1
jest liczbą parzystą, to w n-tym losowaniu należy koniecznie wyciągnąć
kulę oznaczoną cyfrą 1, czyli musi być a
n
= 1.
2. Jeżeli S
n−1
jest liczbą nieparzystą, to w n-tym losowaniu należy koniecznie wycią-
gnąć kulę oznaczoną cyframi 0 lub 2, czyli musi być a
n
= 0 lub a
n
= 2.
Przechodząc od modelu strukturalnego do matematycznego, przy oznaczeniu:
P (S
k
= 1, 3, . . . , 2k − 1) = p
k
k 1
oraz uwzględniając konstrukcję prawdopodobieństwa całkowitego, niezależność zdarzeń
losowania kuli oraz wzór na prawdopodobieństwo dopełnienia (p
0
k
= 1 − p
k
) otrzymamy
następującą postać modelu rekurencyjnego:
p
k
=
2
1
3
1
p
k−1
+
1
1
3
1
(1 − p
k−1
) =
1
3
+
1
3
p
k−1
k 2
Z analizy pojedyńczego losowania mamy:
p
1
=
1
3
W tym zadaniu model rekurencyjny sprowadza się do konstrukcji przesunięcia o stałą
wyrazów ciągu geometrycznego. Dokonując podstawienia
q
k
= p
k
+
1
3
1
3
− 1
= p
k
−
1
2
k 2
do otrzymanych wcześniej zależności rekurencyjnych otrzymamy:
q
k
=
1
3
q
k−1
k 2
oraz
q
1
= −
1
6
Ostatecznie:
p
n
−
1
2
= −
1
6
1
3
n−1
n 1
Stąd szukane prawdopodobieństwo wynosi:
p
n
=
1
2
1 −
1
3
n
n 1
82
13.3. Metoda modelowania rekurencyjnego w zadaniach.
Przykład. Urna zawiera jedną białą i jedną czarną kulę. Losujemy kolejno po jednej
kuli ze zwracaniem dopóty, dopóki liczba wylosowanych kul jednego koloru nie będzie o
k większa od liczby wylosowanych kul drugiego koloru. Jakie jest prawdopodobieństwo,
że wykonamy:
1. 2n losowań, jeśli k = 2
2. n losowań, jeśli k = 3
Rozwiązanie 1. Zauważamy, że gra może zakończyć się tylko po parzystej liczbie loso-
wań. Niech p
k
będzie prawdopodobieństwem, że gra nie zakończy się po (2k)-tym losowa-
niu. Przyjmujemy p
0
= 1. Otrzymujemy wtedy następujący model rekurencyjny:
p
k+1
=
1
2
p
k
k = 0, 1, 2, . . . , n − 1
p
n−1
=
1
2
n−1
· p
0
=
1
2
n−1
Szukane prawdopodobieństwo wynosi:
p
n
=
1
2
p
n−1
=
1
2
n
n 1
Rozwiązanie 2. Na początku należy zauważyć, że liczba n może być tylko nieparzysta.
Niech p
k
będzie prawdopodobieństwem, że gra nie zakończy się po (2k+1)-szym losowaniu.
Dostajemy wtedy następującą relację uwarunkowania rekurencyjnego:
p
k
= p
k−1
1 −
1
2
·
1
2
=
3
4
p
k−1
k = 0, 1, . . . ,
1
2
(n − 3)
a więc
p
k
=
3
4
k
k = 0, 1, . . . ,
1
2
(n − 3)
szukane prawdopodobieństwo wynosi:
p
n
=
1
4
p
(n−3)/2
=
1
4
3
4
(n−3)/2
n 3
Przykład. Rzucamy n-krotnie monetą i wynik zapisujemy w postaci ciągu (a
1
, a
2
, . . .,
a
n
), gdzie a
i
= 1 lub a
i
= 2 w zależności od tego, czy w i-tym rzucie wypadł orzeł,
czy reszka. Przyjmujemy, b
j
= a
1
+ a
2
+ . . . + a
j
dla j = 1, 2, . . . , n. Niech p(n) będzie
prawdopodobieństwem tego, że w ciągu (b
1
, b
2
, . . . , b
n
) wystąpi liczba n. Wyznaczyć p(n).
Rozwiązanie. Bezpośrednio stwierdzamy, że p(1) =
1
2
, p(2) =
1
4
. Przypuśćmy, że n 3.
Zauważamy, że b
i
j dla każdego j. Liczba n może wystąpić w ciągu (b
1
, b
2
, . . ., b
n
) w
następujących dwóch przypadkach:
1. Pewien wyraz tego ciągu równy jest n − 1, np. b
k
= n − 1
k ¬ n − 1 i ponadto
a
k+1
= 1.
2. Pewien wyraz tego ciągu równy jest n − 2, np. b
r
= n − 2
r ¬ n − 2 i ponadto
a
r+1
= 2.
83

ROZDZIAŁ 13. Równania rekurencyjne.
Prawdopodobieństwo dla wymienionych tu przypadków wynosi odpowiednio
1
2
p(n − 1)
oraz
1
2
p(n − 2), przy czym przypadki te nie mogą wystąpić jednocześnie. Wobec tego,
uwzględniając konstrukcję prawdopodobieństwa całkowitego, dostajemy następującą po-
stać modelu rekurencyjnego:
p(n) = p(n − 1) ·
1
2
+ p(n − 2) ·
1
2
Otrzymaliśmy zależność rekurencyjną, której odpowiada (zgodnie z twierdzeniem 4.1)
wielomian charakterystyczny:
f (x) = x
2
−
1
2
x −
1
2
Pierwiastkami tego wielomianu są liczby x
1
= 1, x
2
= −
1
2
, zatem rozwiązaniem naszej
zależności rekurencyjnej jest ciąg postaci:
p(n) = c
1
x
n
1
+ c
2
x
n
2
= c
1
+ c
2
−
1
2
n
Ponieważ p(1) =
1
2
i p(2) =
1
4
, więc stałe c
1
, c
2
otrzymamy rozwiązując układ:
c
1
+ c
2
−
1
2
=
1
2
c
1
+ c
2
−
1
2
2
=
1
4
Dostajemy stąd c
1
=
1
3
, c
2
= −
1
3
. Ostatecznie więc:
p(n) =
1
3
−
1
3
−
1
2
n
n = 1, 2, 3, . . .
Przykład. Wypisujemy kolejno wyrazy ciągu (n
1
, n
2
, . . ., n
k
), gdzie n
1
= 1000, zaś n
j
dla j > 1 jest liczbą całkowitą wybraną losowo z przedziału h0, n
j−1
− 1i (wybór każdej
liczby z tego przedziału jest jednakowo prawdopodobny). Kończymy wypisywanie, gdy
wybrana liczba jest zerem, tzn. n
k−1
6= 0, n
k
= 0. Długość k, ciągu (n
1
, n
2
, . . . , n
k
) jest
zmienną losową. Udowodnić, że wartość oczekiwana tej zmiennej losowej jest większa od
7.
Rozwiązanie. Dla danej liczby całkowitej nieujemnej n rozważmy zbiór A
n
wszystkich
ciągów (n
1
, n
2
, . . ., n
k
), w których n
1
= n, zaś n
j
dla j > 1 jest liczbą całkowitą
wybraną losowo z przedziału h0, n
j−1
− 1i a n
k
= 0. Każdej liczbie całkowitej k ∈ h0, ni
przypisujemy prawdopodobieństwo tego, że losowo wybrany ciąg z rozważanego zbioru
ma dokładnie k wyrazów. Otrzymujemy w ten sposób zmienną losową X
n
.
Oznaczmy przez E
n
wartość oczekiwaną tej zmiennej losowej. Oczywiście E
0
= 1,
gdyż dla n = 0 istnieje tylko jeden ciąg mający długość 1, którego jedynym wyrazem jest
0.
Niech n będzie liczbą naturalną. Przypuśćmy, że wyznaczyliśmy wartości oczekiwane
E
m
dla wszystkich m < n. Rozważmy ciągi (n
1
, n
2
, . . ., n
k
), w których n
1
= n. Możliwe
są dwa następujące zdarzenia:
1. n
2
= n − 1. Prawdopodobieństwo tego zdarzenia wynosi
1
n
. Rozważmy ciąg (n
2
,
. . ., n
k
) należący do zbioru A
n−1
. Wartość oczekiwana długości tego ciągu wynosi
E
n−1
, więc wartość oczekiwana długości ciągu (n
1
, n
2
, . . ., n
k
) należącego do A
n
i
mającego o jeden wyraz więcej wynosi E
n−1
+ 1.
84

13.3. Metoda modelowania rekurencyjnego w zadaniach.
2. n
2
< n − 1. Prawdopodobieństwo tego zdarzenia wynosi
n−1
n
. W tym przypadku
wartość oczekiwana długości ciągu (n
1
, n
2
, . . ., n
k
) należącego do A
n
jest dokładnie
taka, jak wartość oczekiwana długości ciągu (m
1
, m
2
, . . ., m
k
) należącego do A
n−1
,
w którym m
1
= n − 1. Ta wartość oczekiwana wynosi E
n−1
.
Tak więc, uwzględniając konstrukcję prawdopodobieństwa całkowitego, otrzymujemy mo-
del rekurencyjny postaci:
E
n
=
1
n
(E
n−1
+ 1) +
n − 1
n
E
n−1
= E
n−1
+
1
n
Ponieważ E
0
= 1, więc:
E
1
= 1 +
1
1
E
2
= 2 +
1
2
..
.
E
n
= 2 +
1
2
+
1
3
+ . . . +
1
n
Interesująca nas wartość oczekiwana
E
1000
= 2 +
1
2
+
1
3
+ . . . +
1
1000
= 2 +
1
2
+
1
3
+
1
4
+
1
5
+ . . . +
1
8
+
1
9
+ . . . +
1
16
+ +
1
17
+ . . . +
1
32
+
1
33
+ . . . +
1
64
+
1
65
+ . . . +
1
128
+
1
129
+ . . . +
1
256
+
1
257
+ . . . +
1
512
+
1
513
+ . . . +
1
1024
−
1
1001
+ . . . +
1
1024
Liczba w ostatnim nawiasie jest mniejsza od
24
1000
, natomiast każda z liczb w poprzed-
nich nawiasach (których jest osiem) jest większa od
1
2
, gdyż w (k − 1)-szym nawiasie jest
liczba
1
2
k
+ 1
+
1
2
k
+ 2
+ . . . +
1
2
k+1
;
k = 2, 3, . . . , 9
będącą sumą 2
k
składników, z których wszystkie są większe od (tylko ostatni jest równy)
1
2
k+1
. Wobec tego:
E
1000
> 2 +
1
2
+
1
3
+
1
4
+ 8 ·
1
2
−
24
1000
= 6 +
3178
3000
> 7
Przykład. Rzucamy cztery razy sześcienną kostką do gry. Jakie jest prawdopodobień-
stwo, że suma wypadających oczek jest podzielna przez dwa.
Rozwiązanie. Rozwiązując zadanie metodą modelowania rekurencyjnego sprawą naj-
istotniejszą jest przedstawienie relacji kolejnych zdarzeń. W powyższym zadaniu dotyczy
to zdarzeń polegających na rzucie kostką. Rozpatrując k-ty wynik rzutu kostką należy
zwrócić uwagę na istniejącą w zadaniu zależność rekurenvcyjną:
• jeśli S
n−1
jest liczbą nieparzystą, więc aby suma wylosowanych oczek była podzielna
przez dwa należy wylosować kostkę z numerem nieparzystym
85

ROZDZIAŁ 13. Równania rekurencyjne.
• jeśli S
n−1
jest liczbą parzystą, więc aby suma wylosowanych oczek była podzielna
przez dwa należy wylosować kostkę z numerem parzystym.
Zatem można zapisać zbiór zdarzeń sprzyjających w postaci
A = {ε = (a
1
, a
2
, . . . , a
n
) : (S
n−1
= 1, 3, . . . , 6n − 1
a
n
= 1, 3, 5)∨
(S
n−1
= 2, 4, . . . , 6n
a
n
= 2, 4, 6)}
Oznaczmy
P (S
k
= 2, 4, . . . , 6n) = p
k
k ∈ N
Na podstawie definicji prawdopodobieństwa, uwzględniając niezależność zdarzeń rzutu
kostką oraz wzór na prawdopodobieństwo dopełnienia (prawdopoodbiwństwo całkowite)
możemy skonstruować model rekurencyjny w celu obliczenia szukanego prawdopodobień-
stwa:
p
k
= p
k−1
3
1
6
1
+ (1 − p
k−1
)
3
1
6
1
co bezpośrednio daje nam wynik
p
k
=
1
2
Przykład. Dla losowo wybranej permutacji f = (f
1
, . . . , f
n
) zbioru {1, . . . , n} oznacz-
my przez X(f ) największą liczbę k ¬ n taką, że f
i
< f
i+1
dla każdego i < k. Udowodnić,
że wartość oczekiwana zmiennej losowej X wynosi
P
n
k=1
1
k!
.
Rozwiązanie. Opiszmy przestrzeń probabilistyczną, czyli przestrzeń zdarzeń elemen-
tarnych, którą stanowią ciągi n-elementowe o wyrazach rosnących:
Ω =
f = (f
1
, . . . , f
n
) : f
i
∈ {1, . . . , n},
i = 1, . . . , n
n ∈ N
Oznaczmy zmienną losową przez Z
i
. Wartość zmiennej losowej Z
1
jest to długość n-
elementowego ciągu o wyrazach rosnących. Oczywiście E(Z
1
) = 1. Przy rozwiązywaniu
zadania bardzo pomocnym okaże się poniższy lemat (13.2.1). Dla zmiennej losowej Z
przyjmującej wartości ze skończonego zbioru udowodnimy własność wynikającą z linio-
wości operacji obliczania zmiennej losowej
Lemat 13.2.1 Jeżeli
Z =
(
X
z prawdopodobieństwem
p
Y
z prawdopodobieństwem
(1 − p)
to
E(Z) = E(X)p + E(Y )(1 − p)
Dowód. Oznaczmy
Z
l
=
(
X
l
l = 1, . . . , n
Y
l
l = n + 1, . . . , n + m
p
l
=
(
p
0
l
l = 1, . . . , n
p
00
l−n
l = n + 1, . . . , n + m
gdzie P (Z = Z
l
) = p
l
, dla l = 1, . . . , n + m. Oczywiście
n
X
l=1
p
0
l
= p
oraz
n+m
X
l=n+1
p
00
l
= 1 − p
(13.7)
86
13.3. Metoda modelowania rekurencyjnego w zadaniach.
Opierając się na poniższych założeniach, obliczymy teraz wartość oczekiwaną zmiennej
losowej Z:
E(Z) =
n+m
X
l=1
Z
l
p
l
=
n
X
l=1
X
l
p
0
l
+
n+m
X
l=n+1
Y
l−n
p
00
l−n
=
n
X
l=1
X
l
p
0
l
+
m
X
k=1
Y
k
p
00
k
=
n
X
l=1
X
l
p
0
l
p
p +
m
X
k=1
Y
k
p
00
k
1 − p
(1 − p) = E(X)p + E(Y )(1 − p)
gdyż z 13.7 wynika, że
n
X
l=1
p
0
l
p
=
m
X
k=1
p
0
k
1 − p
= 1
Co kończy dowód lematu.
2
Znajdziemy teraz zależność rekurencyjną między wartościami oczekiwanymi E(Z
n−1
)
i E(Z
n
). Niech n jest dowolną liczbą naturalną taką, że n 2. Weźmy dowolną permutację
f = (f
1
, . . . , f
n
) zbioru {1, 2, . . . , n}. Po odrzuceniu ostatniego wyrazu f
n
, otrzymujemy
permutację f
0
= (f
1
, . . . , f
n−1
) zbioru {1, 2, . . . , n − 1}. Dołączając z powrotem wyraz f
n
,
rozpatrujemy dwa przypadki
1. Jeśli do permutacji f
0
dołączamy ostatni wyraz ze zbioru {1, 2, . . . , n}, a więc jeśli
f
n
= n, wówczas długość ciągu rosnącego zwiększy się o jeden. Prawdopodobieństwo
takiego zdarzenia wynosi
1
n!
.
2. Jeśli do permutacji f
0
dołączamy dowolny wyraz ze zbioru {1, 2, . . . , n − 1}, a więc
długość ciągu rosnącego pozostaje nie zmieniona. Prawdopodobieństwo takiego zda-
rzenia można wyznaczyć korzystając ze wzoru na prawdopodobieństwo dopełnienia.
Zatem wynosi ono: 1 −
1
n!
Z warunków 1 i 2 otrzymujemy
Z
n
=
(
Z
n−1
+ 1
z prawdopodobieństwem
1
n!
Z
n−1
z prawdopodobieństwem
1 −
1
n!
Z powyższego zapisu oraz lematu wynika poszukiwana zależność rekurencyjna:
E(Z
n
) = (E(Z
n−1
) + 1)
1
n!
+ E(Z
n−1
)
1 −
1
n!
= E(Z
n−1
) +
1
n!
Na podstawie indukcji oraz warunku początkowego: E(Z
1
) = 1 wynika dany do udowod-
nienia w zadaniu wzór
E(Z
n
) =
n
X
k=1
1
k!
13.3.3
Zadania algebraiczne.
Przykład. Wyznaczyć największą wartość wyrażenia m
2
+ n
2
, gdzie m i n są takimi
liczbami całkowitymi, że 1 m 2000, 1 n 2000 oraz (n
2
− mn − m
2
)
2
= 1.
Rozwiązanie.
Lemat 13.2.2 Liczby naturalne k ¬ r spełniają równanie (x
2
− xy − y
2
) = 1 wtedy i
tylko wtedy, gdy liczby k + r, r spełniają to równanie.
87

ROZDZIAŁ 13. Równania rekurencyjne.
Dowód. Ponieważ
[(k + r)
2
− (k + r)r − r
2
]
2
= (k
2
+ 2kr + r
2
− kr − r
2
− r
2
)
2
=
(k
2
+ kr − r
2
)
2
= (r
2
− kr − k
2
)
2
wobec tego (r
2
− kr − k
2
)
2
= 1 wtedy i tylko wtedy, gdy:
((k + r)
2
) − (k + r)r − r
2
)
2
= 1
Koniec dowodu.
2
Ponieważ para liczb (1, 1) spełnia równanie (x
2
− xy − y
2
)
2
= 1, więc z powyższego
lematu wynika, że równanie to spełnia każda para kolejnych wyrazów ciągu określonego
w następujący sposób:
a
1
= a
2
= 1
a
k
= a
k−2
+ a
k−1
k 3
Jest to ciąg Fibonacciego. Wystarczy udowodnić teraz, że żadna para liczb natural-
nych, które nie są kolejnymi wyrazami ciągu Fibonacciego, nie spełnia danego w zadaniu
równania.
Przypuśćmy, że dla liczb naturalnych m ¬ n jest (n
2
− mn − m
2
) = 1, przy czym
m, n nie są kolejnymi wyrazami ciągu Fibonacciego oraz n jest najmniejszą liczbą o tej
własności, tzn. każda para liczb naturalnych r ¬ s spełniających warunki (s
2
−rs−r
2
)
2
=
1 oraz s < n jest parą kolejnych wyrazów ciągu Fibonacciego. Zauważmy, że liczby m,
n − m spełniają dane równanie:
(m
2
− m(n − m) − (n − m)
2
)
2
= (m
2
− mn + m
2
− n
2
+ 2mn − m
2
)
2
=
(m
2
− mn − n
2
)
2
= (n
2
− mn − m
2
)
2
= 1
Jest przy tym m < n, gdyby bowiem było m = n, to musiałoby być m = n = 1 i
liczby te byłyby kolejnymi wyrazami ciągu Fibonacciego. Udowodniliśmy w ten sposób,
że wszystkimi rozwiązaniami danego równania w liczbach naturalnych są pary kolejnych
wyrazów ciągu liczb Fibonacciego. Aby wyznaczyć największą wartość wyrażenia m
2
+ n
2
dla m ¬ n spełniających warunki zadania, należy wyznaczyć największy wyraz ciągu
Fibonacciego nie przekraczający 2000. Wypisując kolejne wyrazy tego ciągu:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, . . .
stwierdzamy, że szukaną wartością jest:
987
2
+ 1597
2
= 3514478
Przykład. Znaleźć rozwiązanie równania a
2
+ b
2
+ c
2
= 3abc w liczbach naturalnych
a, b, c nie większych od n.
Rozwiązanie. Zauważmy na początku, że rozwiązaniem danego równania są liczby:
(1, 1, 1), (2, 1, 1), (5, 2, 1), (13, 5, 1), . . . , itd. Pokażemy teraz (co łatwo zauważyć), że jeśli
trójka liczb naturalnych (a, b, c) (gdzie a > b > c) stanowi rozwiązanie danego równania,
to rozwiązaniem tego równania jest trójka liczb postaci:
(3ab − c, a, b)
przy czym 3ab − c > 3a − c > a.
88

13.3. Metoda modelowania rekurencyjnego w zadaniach.
Przekształcając lewą stronę danego równania i korzystając z założenia:
(3ab − c)
2
+ a
2
+ b
2
= 9a
2
b
2
− 6abc + c
2
+ a
2
+ b
2
=
9a
2
b
2
− 6abc + 3abc = 9a
2
b
2
− 3abc = 3(3ab − c)ab
otrzymujemy prawą stronę równania, co należało pokazać.
Rozważmy teraz ciąg (b
n
) określony w następujący sposób:
b
1
= b
2
= 1
b
k+2
= 3b
k+1
− b
k
k 1
Udowodnimy indukcyjnie, że każda z trójek
(b
k+1
, b
k
, 1)
k 1
spełnia dane równanie. (1, 1, 1) jest rozwiązaniem. Załóżmy, że (b
k+1
, b
k
, 1) jest rozwiąza-
niem, a więc
b
2
k+1
+ b
2
k
+ 1
2
= 3b
k+1
b
k
Pokażemy, że (b
k+2
, b
k+1
, 1) jest rozwiązaniem, czyli:
b
2
k+2
+ b
2
k+1
+ 1
2
= 3b
k+2
b
k+1
W tym celu przekształćmy lewą stronę równości tezy:
L = b
2
k+2
+ b
2
k+1
+ 1
2
= (3b
k+1
− b
k
)
2
+ b
2
k+1
+ 1 =
9b
2
k+1
− 6b
k+1
b
k
+ b
2
k
+ b
2
k+1
+ 1 = 9b
2
k+1
− 6b
k+1
b
k
+ 3b
k+1
b
k
=
9b
2
k+1
− 3b
k+1
b
k
Przekształćmy teraz prawą stronę równości tezy:
P = 3b
k+2
b
k+1
= 3(3b
k+1
− b
k
) = 9b
2
k+1
− 3b
k+1
b
k
Zatem L = P .
Na mocy zasady indukcji każda trójka (b
k+1
, b
k
, 1) dla k 1 spełnia dane równanie.
Na podstawie przeprowadzonego wyżej rozumowania stwierdzamy ponadto, że trójka
(3b
k
b
k+1
− 1, b
k+1
)
k 1
jest rozwiązaniem danego równania. Wszystkie trzy liczby występujące w tej trójce są nie
mniejsze niż k, bo (b
k
) jest rosnącym ciągiem liczb naturalnych.
Znajdziemy teraz wyraz ogólny ciągu (b
k
). Zależności rekurencyjnej występującej w
definicji tego ciągu odpowiada wielomian charakterystyczny:
f (x) = x
2
− 3x + 1
którego pierwiastkami są liczby x
1
=
3−
√
5
2
, x
2
=
3+
√
5
2
. Otrzymujemy zatem (na podsta-
wie metody podanej w rozdziale 4)
b
k
= c
1
x
k
1
+ c
2
x
k
2
= c
1
3 −
√
5
2
k
+ c
2
3 +
√
5
2
k
k 1
89

ROZDZIAŁ 13. Równania rekurencyjne.
Ponieważ b
1
= 1, b
2
= 1, więc stałe c
1
, c
2
spełniają zależności:
c
1
3 −
√
5
2
+ c
2
3 +
√
5
2
= 1
c
1
3 −
√
5
2
2
+ c
2
3 +
√
5
2
2
= 2
Rozwiązując powyższy układ otrzymujemy, że c
1
=
5+
√
5
10
, c
2
=
5−
√
5
10
. Ostatecznie dosta-
jemy następujący wzór ogólny ciągu (b
k
):
b
k
=
5 +
√
5
10
3 −
√
5
2
k
+
5 −
√
5
10
3 +
√
5
2
k
k 1
Rozwiązaniem danego w zadaniu równania w liczbach naturalnych większych od n są
trójki liczb postaci:
(3b
k
b
k+1
− 1, b
k+1
, b
k
)
k > n
90

Rozdział 14
Modelowanie okrężne. ([14],
[18])
Twierdzenie 14.1
b
n+1
2
c
X
k=1
n
2k − 1
2
n−(2k−1)
=
1
2
(3
n
− 1)
(14.1)
Dla n = 1 mamy L = P = 1, potraktujmy 14.1 jako założenie indukcyjne i udowodnimy
b
n
2
c+1
X
k=1
n + 1
2k − 1
2
n+1−(2k−1)
=
1
2
(3
n+1
− 1)
(14.2)
Dowód.
L =
b
n
2
c
X
k=1
n
2k − 1
2
n+1−(2k−1)
+
b
n
2
c
X
k=1
n
2(k − 1)
2
n−2(k−1)
+
n + 1
2b
n
2
c + 1
2
n−2[
n
2
]
lecz
b
n
2
c
X
k=1
n
2(k − 1)
2
n−2(k−1)
=
b
n
2
c−1
X
k=0
n
2k
2
n−2k
=
b
n
2
c
X
k=0
n
2k
2
n−2k
−
n
2b
n
2
c
2
n−2[
n
2
]
=
1
2
(3
n
+ 1) −
n
2b
n
2
c
2
n−2[
n
2
]
także
b
n
2
c
X
k=1
n
2k − 1
2
n+1−(2k−1)
= 2
b
n+1
2
c
X
k=1
n
2k − 1
2
n−(2k−1)
−
1
2
[1 + (−1)
n−1
]
!
=
2(3
n
− 1) − [1 + (−1)
n−1
]
91
ROZDZIAŁ 14. Modelowanie okrężne.
oraz
n + 1
2b
n
2
c + 1
2
n−2[
n
2
]
−
n
2b
n
2
c
2
n−2[
n
2
]
=
2
n−2b
n
2
c
n + 1
2[
n
2
] + 1
− 1
n
2[
n
2
]
!
= [1 + (−1)
n−1
]
L = 2
b
n
2
c
X
k=1
n
2k − 1
2
n−(2k−1)
+
b
n
2
c
X
k=0
n
2k
2
n−2k
−
n
2b
n
2
c
2
n−2[
n
2
]
+
n + 1
2b
n
2
c + 1
2
n−2b
n
2
c
mamy, że
b
n
2
c
X
k=0
n
2k
2
n−2k
=
1
2
(3
n
+ 1)
oraz
−
n
2b
n
2
c
2
n−2[
n
2
]
+
n + 1
2b
n
2
c + 1
2
n−2[
n
2
]
=
n
2b
n
2
c
2
n−2[
n
2
]
"
n + 1
2[
n
2
] + 1
− 1
#
=
n
2b
n
2
c
2
n−2b
n
2
c
"
n − 2b
n
2
c
2b
n
2
c + 1
#
Tak więc dla n-parzystego mamy
L = 2 ·
1
2
(3
n
− 1) +
1
2
(3
n
+ 1) − 1 + 1 =
1
2
(3
n+1
− 1)
a dla n-nieparzystego
L = 2
"
b
n+1
2
c
X
k=1
n
2k − 1
2
n−(2k−1)
− 1
#
+
1
2
(3
n
+ 1) − 2n + 2(n + 1) =
1
2
(3
n+1
− 1)
b
n+1
2
c
X
k=1
n
2k − 1
2
n−2(k−1)
=
b
n
2
c
X
k=1
n
2k − 1
2
n−(2k−1)
+
1
2
(1 − 1
n−1
)
Wystarczy pokazać, że
p
X
k=1
"
2p
2k − 1
+ 2
2p
2k − 2
#
2
2p−(2k−1)
+
p
X
k=2
2p
2k − 3
2
2p−(2k−1)
+
+
1
2(2p + 2)
=
p
X
k=0
2p
2k
2
2(p−k)
+ 2
p
X
k=1
2p
2k − 1
2
2(p−k)
+
+
p
X
k=1
2p
2k − 2
2
2(p−k)
92
Podstawiamy a =
P
p
k=1
2p
2k−1
, b = P
p
k=0
2p
2k
2
2(p−k)
, a = b−1 z założenia indukcyjnego.
p
X
k=1
2p
2k − 2
2
2[p−(k−1)]
=
p−1
X
k=0
2p
2k
2
2(p−k)
=
p
X
k=0
2p
2k
2
2(p−k)
− 1 = b − 1
p
X
k=2
2p
2k − 3
2
2p−(2k−1)
=
1
2
2
p
X
k=2
2p
2k − 3
2
2p−(2k−3)
=
1
2
2
"
p
X
k=1
2p
2k − 1
2
2p−(2k−1)
− 4p
#
L = a + b − 1 +
1
4
(a − 4p) + p + 1 = a + b +
1
4
a
P = b + a +
1
4
(b − 1)
1
4
p
X
k=1
2p
2(k − 1)
2
2[p−(k−1)]
=
1
4
p−1
X
k=0
2p
2k
2
2[p−k]
=
1
4
"
n
X
k=0
2p
2k
2
2(p−k)
− 1
#
czyli
L = 2 ·
1
2
(3
n
− 1) − [1 + (−1)
n−1
] +
1
2
(3
n
+ 1) + [1 + (−1)
n−1
] =
1
2
(3
n+1
− 1)
2
Trudniejsze relacje pomocnicze:
b
n+1
2
c
X
k=1
n
2k − 1
2
n−(2k−1)
=
b
n
2
c
X
k=1
n
2k − 1
2
n−(2k−1)
+
1
2
[1 + (−1)
n−1
]
n
2b
n
2
c
=
j
n
2
k
(1 + (−1)
n+1
) + 1
Stwierdzenie 14.1.1 Powyższy wynik można uzyskać znacznie prościej stosując metodę
modelowania okrężnego.
W przypadku pierwszym wystarczy rozwiązać następujące zadanie. Losujemy n-krotnie
ze zwracaniem kule z urny, w której znajdują się 3 kule oznaczone cyframi 0, 1, 2. Tworzy-
my sumy wylosowanych liczb odpowiadających cyfrom znaczącym kule. Ile jest różnych
układów różnych układów losowań, przy których uzyskana suma jest liczbą nieparzystą?
93

ROZDZIAŁ 14. Modelowanie okrężne.
Rysunek 14.1: Modelowanie okrężne. T – transformacja, R – procedura rozwiązania pro-
blemu, T
−1
transformacja odwrotna, P – problem, P
0
– problem po transformacji, W
0
–
wynik w postaci transformowanej, W – poszukiwany wynik.
Lewa strona twierdzenia 14.1 przedstawia model kombinatoryczny problemu. Podczas
gdy z prawej strony mamy model ciągu rekurencyjnego. Ustalamy model kombinatoryczny
rozłącznych zdarzeń polegający na wypadnieciu różnej nieparzystej liczby jedynek, w spo-
sób niezależny rozmieszczając je w ciągu n-elementowym, w dowolny sposób zmieniając
pozostałe elementy wybrane ze zbioru {0, 2}. Czyli mnożymy kombinacje k nieparzystych
elementów wybranych spośród n przez wariacje z powtórzeniami (n − k)-elementowe o
dwóch wartościach i sumujemy otrzymane iloczyny po wszystkich nieparzystych k takich,
że k ¬ n. Model rekurencyjny, czyli prawą stronę wzoru, uzyskujemy spostrzegając, że
nieparzystość sumy po n-tym losowaniu otrzymamy przy wyciągnięciu „1” – gdy po n − 1
losowaniach suma była parzysta; oraz przy wyciągnięcu „0” lub „2” gdy odpowiadająca
suma była nieparzysta. Zauważmy tu, że efektywność i wyjściowa elegancja modelu re-
kurencyjnego w stosunku do kombinatorycznego, wynika z ukrytego porządku liniowego
następstw zdarzeń. Ilość układów nie zależy od techniki przeliczania (rodzaju modelu),
to lewa strona twierdzenia 14.1 jest równa prawej stronie.
94
Rozdział 15
Zadania. ([1], [4], [7], [10], [11],
[19], [21])
15.1
Zadania do rozdziałów.
15.1.1
Rozdziały 1–2.
Zadanie 1. Przeprowadzić dowody indukcyjne następujących twierdzeń i zależności.
1. Dla każdego n ∈ N ilość wszystkich podzbiorów zbioru n-elementowego jest równa
2
n
.
2. p | n
p
− n gdzie p jest liczbą pierwszą, n ∈ N.
3. (1 + a)
n
1 + na
a > −1
a ∈ R (nierówność Bernoulliego)
4. 2
n
> n
5. 13 | 6
n+2
+ 7
2n+1
6. n! > 2
n
n 4
7. n!
√
n
n
8.
n
k
+
n
k−1
=
n+1
k
n > 1 n k > 1
9. ∀n ∈ N i f orallk ¬ n ilość wszystkich k-elementowych kombinacji zbioru n-
elementowego jest równa
n
k
.
10. 1
2
+ 2
2
+ . . . + n
2
=
n(n+1)(2n+1)
6
11. sin α + sin 2α + . . . + sin nα =
cos
1
2
α−cos(n+
1
2
)α
2 sin
1
2
α
12. 2
n
> n
2
n > 4
13. (a + b)
n
=
P
n
k=0
n
k
a
n−k
b
k
14. Jeżeli suma cyfr w liczbie b jest podzielna przez 9 to 9 | b.
95
ROZDZIAŁ 15. Zadania.
15. 6 | 10
n
− 4
16. 9 | n
3
+ (n + 1)
3
+ (n + 2)
3
Zadanie 2. Znaleźć granice ciągów określonych rekurencyjnie.
1.
(
a
1
=
√
2
a
n+1
=
√
2a
n
∀n
2.
(
a
1
= sin 1
◦
a
n+1
= sin a
n
3.
(
a
1
=
√
3
a
n+1
=
√
3 + a
n
Zadanie 3. Określamy ciąg za pomocą wzoru rekurencyjnego:
1.
(
a
1
= 6
a
1
= 18
a
n+2
= 2a
n+1
+ 8a
n
− 18
Dowieść za pomocą indukcji, że a
n
= 4
n
+ 2
2.
(
a
0
a
1
= 1
a
n+2
= a
n
+ a
n+1
Ciąg Fibonacciego.
Wykazać, że a
n
=
1
√
5
h
1+
√
5
2
n
−
1−
√
5
2
n
i
.
Zadanie 4. Przedział ha, bi dzielmy punktem x
1
na połowę. Otrzymaną prawą połowę
dzielimy punktem x
2
na połowy. Z punktami x
n
; n > 2 postępujemy analogicznie. Wykaż,
że lim
n→∞
x
n
= 6.
Zadanie 5. Wypisz pięć pierwszych wartości x dla każdego z następujących fragmentów
algorytmów:
1. x:=0
DOPÓKI 0=<x WYKONUJ
x:=2x+3
2. x:=1
DOPÓKI x>=0 WYKONUJ
x:=2x+3
3. x:=1
DOPÓKI x>=0 WYKONUJ
x:=2x-1
Zadanie 6. Znajdź liczbę całkowitą b taką, że ostatnią wypisaną liczbą będzie 6.
1. n:=0
DOPÓKI n<b WYKONUJ
wypisz n
n:=n+1
96

15.1. Zadania do rozdziałów.
2. n:=0
DOPÓKI n<0 WYKONUJ
n:=n+1
wypisz n
Zadanie 7. Pokaż, że podane warunki są niezmiennikami pętli:
1. DOPÓKI 1=<n WYKONUJ
m:=m+1
n:=n+1
(
2 | m + n
2 - m + n
2. DOPÓKI 1=<m WYKONUJ
m:=2m
n:=3n
(
n
2
m
3
2m
6
< n
Zadanie 8. Rozważmy pętlę:
DOPÓKI j>=n WYKONUJ
i:=i+2
j:=j+1
i, j ∈ Z. Czy poniższe warunki są niezmiennikami pętli?
1. i < j
2
n = 1
2. i < j
2
n = 0
3. i =< j
2
n = 0
4. i >= j
2
n = 0
Zadanie 9. Rozważmy pętlę:
DOPÓKI k>=1 WYKONUJ
k:=2k
Sprawdź czy poniższe warunki są niezmiennikami pętli:
1. k
2
≡ 1 mod 3
2. k
2
≡ 1 mod 4
Zadanie 10. Dla jakich wartości liczby całkowitej b, każdy z następujących algorytmów
zakończy działanie?
1. k:=b
DOPÓKI k<5 WYKONUJ
k:=2k-1
97

ROZDZIAŁ 15. Zadania.
2. k:=b
DOPÓKI k<>5 WYKONUJ
k:=2k-1
3. k:=b
DOPÓKI k<5 WYKONUJ
k:=2k+1
Zadanie 11. Czy dwa poniższe algorytmy dają ten sam wynik?
1. m:=1
n:=1
DOPÓKI 1=<m=<3 WYKONUJ
m:=2m
n:=n+1
wypisz m
2. m:=1
n:=1
DOPÓKI 1=<m=<3 i 1=<n=<3 WYKONUJ
m:=2m
n:=n+1
wypisz m
Zadanie 12. Dla poniższej pętli sprawdź:
DOPÓKI 1=<I WYKONUJ
S:=S+2I+1
I:=I+1
1. Że, warunek S = I
2
jest niezmiennikiem pętli.
2. Że, warunek S = I
2
+ 1 też jest niezmiennikiem tej pętli.
3. Jaka będzie siedemdziesiąta trzecia liczba wypisana przez ten algorytm? Odpowiedź
uzasadnij.
Zadanie 13. Które z nastepujących zbiorów liczb całkowitych mają najmniejszy ele-
ment na podstawie zasady dobrego uporządkowania? Odpowiedź uzasadnij.
1. P = Z
+
2. Z
3. {n ∈ N n
2
17}
4. {n ∈ N n
2
< 0}
5. {n ∈ Z n
2
> 17}
6. {n ∈ N n! > 80}
Zadanie 14. Czy warunek 5
k
< k! jest niezmiennikiem następującej pętli?
98

15.1. Zadania do rozdziałów.
DOPÓKI 4=<k WYKONUJ
k:=k+1
Czy na tej podstawie można wywnioskować, że 5
k
< k! ∀k 4?
Zadanie 15. Oto algorytm który rozkłada liczbę całkowitą n na iloczyn liczby niepa-
rzystej i potęgi 2.
m:=n
k:=0
DOPÓKI m jest parzyste WYKONUJ
m:=m/2
k:=k+1
Pokazać, że warunek m2
k
= n jest niezmiennikiem pętli.
Zadanie 16. Udowodnij, że
4 + 10 + 16 + . . . + (6n − 2) = n(3n + 1)
n ∈ N
Zadanie 17. Udowodnij, że:
1. 10 | 37
100
− 37
20
2. 10 | 37
20
− 37
4
3. 10 | 37
500
− 37
4
4. 10 | 37
4
− 1
5. 10 | 37
500
− 1
6. 7 | 11
n
− 4
n
7. 16 | 5
n
− 4n − 1
8. 8 | 5
n+1
+ 2 · 3
n
+ 1
9. 73 | 8
n+2
+ 9
2n+1
Zadanie 18. Udowodnij, że:
1
1 · 5
+
1
5 · 9
+
1
9 · 13
+ . . . +
1
(4n − 3)(4n + 1)
=
n
4n + 1
∀n ∈ N
Zadanie 19. Pokaż przez indukcję, że jeśli s
0
= a oraz s
n
= 2s
n−1
+ b ∀n ∈ N, to
s
n
= 2
n
a + (2
n
− 1)b ∀n ∈ N.
Zadanie 20. Pokaż, że warunek
P
k
i=0
2
i
= 2
k+1
− 1 jest niezmiennikiem pętli w algo-
rytmie:
k:=0
DOPÓKI 0=<k WYKONUJ
JESLI suma od i=0 do k po 2^i=2^(k+1) TO
k:=k+1
Zadanie 21. Udowodnij, że:
99
ROZDZIAŁ 15. Zadania.
1.
P
n
i=1
1
√
i
√
n
2.
P
n
i=1
1
√
i
¬ 2
√
n − 1
Zadanie 22. Udowodnij, następujące zależności:
1. | sin nx| ¬ n| sin x|
x ∈ R ∧ n ∈ N
2. 1
3
+ 2
3
+ . . . + n
3
= (1 + 2 + 3 + . . . + n)
2
15.1.2
Rozdziały 3–4.
Zadanie 23. Udowodnić, że następujące zależności rekurencyjne mają wzór jawny.
1.
b
0
= 1
b
1
= 2
b
2
= 4
b
n
= b
n−1
+ b
n−2
+ 2b
n−3
2.
s
0
= a
s
n
= 2s
n−1
+ b
Zadanie 24. Definiujemy ciąg:
(
a
0
= a
1
= a
2
= 1
a
n
= a
n−1
+ a
n−2
+ a
n−3
n 3
Udowodnij, że wszystkie a
n
¬ 2
n−1
∀n ∈ N
Zadanie 25. Udowodnić następujące nierówności:
1. (1 + a)
n
1 + na +
n(n−1)
2
a
2
a 0
n 0
2.
n
√
n ¬ 1 +
q
2
n
3. 2 ¬ (1 +
1
n
)
n
¬ n + 1
n 1
4. (x
2
+ x + 1) | ((x + 1)
2n+1
+ x
n+2
)
5. n!
√
n
n
6. n! <
n+1
2
n
Zadanie 26. Ciąg liczb (a
n
) jest określony następująco:
(
a
1
= a
2
= 1
a
n
=
a
2
n−1
+2
a
n−2
Wykazać, że wszystkie wyrazy tego ciągu są liczbami całkowitymi.
Zadanie 27. Niech ciąg (c
n
) będzie określony następująco:
(
c
1
=
a
2
c
n+1
=
a+c
2
n
2
a ∈ (0, 1i
Pokazać, że wszystkie wyrazy ciągu (b
n
), gdzie b
n
= 1 −
√
1 − a − c
n
są dodatnie.
100

15.1. Zadania do rozdziałów.
15.1.3
Rozdział 4.
Zadanie 28. Definiujemy rekurencyjnie s
0
= 1 i s
n+1
=
2
s
n
. Wypisz pięć pierwszych
wyrazów ciągu i wyznacz jego zbiór wartości.
Zadanie 29. Definiujemy rekurencyjnie SEQ(0) = 0 i SEQ(n + 1) =
1
1+SEQ
n ∈ N.
Oblicz SEQ(n) dla n = 1, 2, 3, 4 oraz 6.
Zadanie 30. Weźmy ciąg SEQ: (1, 3, 9, 27, 81, . . .). Podaj wzór na n-ty wyraz ciągu
SEQ(n) gdzie SEQ(0) = 1 oraz jego definicję rekurencyjną.
Zadanie 31. Podaj definicję rekurencyjną ciągu 2, 2
2
, 2
2
2
, . . ., czyli ciągu 2, 4, 16, 256,
. . ..
Zadanie 32. Czy następująca definicja jest definicją rekuencyjną ciągu SEQ? Odpo-
wiedź uzasadnij.
(
SEQ(0) = 1
SEQ(n + 1) =
SEQ(n)
(100−n)
Zadanie 33. Oblicz:
1. SEQ = 9 gdzie
(
SEQ(0) = 1
SEQ(n + 1) =
n+1
SEQ(n)
l
n ∈ N
2. F IB(11) gdzie
(
FIB(0) = FIB(1) = 1
FIB(n) = FIB(n − 1) + FIB(n − 2)
n 2
Zadanie 34. Niech Σ = {a, b, c} – alfabet i niech s
n
oznacza liczbę słów długości n które
nie mają kolejnych liter a. Oblicz s
0
, s
1
, s
2
, znajdź wzór rekurencyjny na s
n
i następnie
oblicz s
3
i s
4
.
Zadanie 35. Niech Σ = {a, b} – alfabet dwuliterowy i niech s
k
oznacza liczbę słów
długości n, w których jest parzysta liczba liter a. Oblicz s
0
, s
1
, s
2
, s
3
i znajdź wzór
rekurencyjny na s
n
.
Zadanie 36. Niech Σ = {a, b} i niech s
n
oznacza liczbę słów długości nnie zawierających
ciągu ab. Oblicz s
0
, s
1
, s
2
oraz znajdź wzór na s
n
.
Zadanie 37. Weźmy ciąg SEQ(0) = 1, SEQ(1) = 0 SEQ(n) = SEQ(n − 2) n 2.
Wypisz pieć wyrazów tego ciągu, określ zbiór jego wartości.
Zadanie 38. a
0
= a
1
= 1
a
n
= a
n+1
+ 2a
n−2
n 2. Obliczyć a
6
i udowodnić, że
a
n
∀n ∈ N są nieparzyste.
Zadanie 39. Udowodnij, że ciąg macierzy M
1
, M
2
określony wzorami
M
1
=
1 1
1
0
M
2
=
2 1
1
1
M
n
=
FIB(n)
FIB(n − 1)
FIB(n − 1)
FIB(n − 2)
n 2
spełnia zależność M
n+1
= M
1
· M
n
.
Zadanie 40. Definiujemy rekurencyjnie ciąg za pomocą wzoru b
0
= b
1
= 1 b
n
=
2b
n−1
+ b
n−2
n 2. Oblicz b
5
metodą iteracyjną oraz udowodnij, że wszystkie wyrazy
tego ciągu są nieparzyste.
Zadanie 41. SEQ(0) = 1 i niech SEQ(n) =
P
n−1
i=0
SEQ(i)
n 1. Okazuje się, że jest
to znany prosty ciąg. Jaki?
101

ROZDZIAŁ 15. Zadania.
Zadanie 42. Definiujemy rekurencyjnie ciąg wzorem a
0
= 0, a
1
= 1, a
2
= 2 a
n
=
a
n−1
− a
n−2
+ a
n−3
n 3. Wypisz pięć pierwszych wyrazów tego ciągu. Jaki jest zbiór
wartości tego ciągu?
Zadanie 43. Proces przydzielania n dzieci do n miejsc w klasie może być podzielony
na dwie fazy:
1. Wybór dziecka na pierwsze miejsce.
2. Przydzielenie pozostałych n − 1 dzieci do n − 1 miejsc.
Niech A(n) będzie liczbą różnych usadzeń n dzieci na n miejscach. Napisz definicję reku-
rencyjną ciągu A. Oblicz rekurencyjnie A(6). Czy ciąg A wydaje ci się znajomy.
Zadanie 44. Weźmy pod uwagę proces przydzielania 2n dzieci do n wagoników kolejki,
tak by w każdym wagoniku była dwójka dzieci. Najpierw wybieramy dwoje dzieci do
pierwszego wagonika na C
2
2n
=
2n(2n−1)
2
sposobów. Następnie przydzielamy pozostałe
dzieci do n−1 wagoników. Niech B(n) będzie liczbą sposobów, na które można przydzielić
2n dzieci do n wagoników. Napisz definicję rekurencyjną B(n). Oblicz rekurencyjnie B(3)
oraz metodą iteracyjną B(5). Podaj wzor ogólny na B(n).
Zadanie 45. Weźmy ciągi określone wzorami
1.
FOO(0) = 1
FOO(1) = 1
FOO(n) =
10FOO(n − 1) + 100
FOO(n − 2)
n 2
2.
GOO(0) = 1
GOO(1) = 2
GOO(n) =
10GOO(n − 1) + 100
GOO(n − 2)
n 2
Zadanie 46. Niech (a
1
, a
2
, . . .) będzie ciągiem liczb rzeczywistych. Podaj definicję re-
kurencyjną ciągu suma(n) =
P
n
j=1
a
j
, n 1. Zmień twoją definicję rekurencyjną ciągu
suma(n), zaczynając od n = 0. Co to jest „suma pusta”?
Zadanie 47. Niech (A
1
, A
2
, . . .) będzie ciągiem podzbiorów pewnego zbioru S.
1. Podaj definicję rekurencyjną dla
S
n
j=1
A
j
. Jak zdefiniować sumę pustą?
2. Podaj definicję rekurencyjną dla
T
n
j=1
A
j
. Jak zdefiniować puste przecięcie?
Zadanie 48. Udowodnij, że jeśli s
n
= as
n−1
dla n 1 i a 6= 0, to s
n
= a
n
s
0
dla n ∈ N.
Zadanie 49. Sprawdź, że ciąg s
n
dany wzorem
1. s
n
= 2
n+1
+ (−1)
n
spełnia warunki s
0
= s
1
= 3 s
n
= s
n−1
+ 2s
n−2
.
2. s
n
= 3
n
− 2n3
n
spełnia warunki s
0
= 1, s
1
= −3 s
n
= 6s
n−1
Zadanie 50. Podaj wzór jawny na s
n
, gdzie
1. s
0
= 3
s
n
= −2s
n−1
n 1
2. s
n
= 4s
n−2
s
0
= s
1
= 1
3. s
n
= s
n−1
+ 2s
n−2
s
0
= 3
s
1
= 6
4. s
n
= s
n−1
+ 2s
n−2
s
0
= 3
s
1
= −3
5. s
n
= s
n−1
+ s
n−2
s
0
= 1
s
1
= 2
102
15.1. Zadania do rozdziałów.
6. s
n
= s
n−1
+ s
n−2
s
0
= 2
s
1
= 1
n 2. Oblicz s
n
dla n = 2, 3, 4, 5, 6.
7. s
n
= −s
n−1
+ 6s
n−2
s
0
= 2
s
1
= 1
n 2
8. s
n
= 5s
n−1
s
0
= 2
n 1
9. s
n
= 4s
n−1
− 4s
n−2
s
0
= 1
s
1
= 8
n 2
Zadanie 51. W każdym z następujących przypadków podaj wzór jawny na s
s
m
.
1. s
2
n
= 3s
n
+ 3
s
1
= 1
2. s
2
n
= 2s
n
s
1
= 3
3. s
2
n
= 2s
n
+ 5n
s
1
= 0
4. s
2n
= 2s
n
+ 3 + 5n
s
1
= 2
5. s
2n
= 2s
n
− 7
s
1
= 1
Zadanie 52. Przypuścmy, że ciąg (s
n
) spełnia zależność rekurencyjną s
2
n
= 2s
n
+ n
2
.
Podaj wzór na s
2
m
oraz uzasadnij, że jest on poprawny.
Zadanie 53. Jeśli s
n
będzie ciągiem rekurencyjnym spełniającym zależność rekuren-
cyjną postaci
s
2
n
= 2s
n
+ f (n)
n ∈ N
to wtedy
s
2
m
= 2
m
h
s
1
+
1
2
m−1
X
j=0
f (2
i
)
2
i
i
. Sprawdź tą zależność dla f (n) = A + Bn.
Zadanie 54. Definiujemy rekurencyjnie ciąg (a
n
) wzorami
a
0
= 1
a
1
= 2
a
n
=
a
n−1
a
n−2
n 2
oraz (b
n
)
a
0
= 1
a
1
= 2
a
n
=
a
n−1
−1
a
n−2
n 2
Oblicz kilka pierwszych wyrazów tych ciągow oraz zgadnij ich wzory ogólne na tej pod-
stawie. Udowodnij je.
Zadanie 55. Definiujemy rekurencyjnie ciąg (a
n
)
a
0
= 1
a
1
= 2
a
2
= 3
a
n
= a
n−2
+ 2a
n−3
n 3
Oblicz a
n
dla n = 3, 4, 5, 6, 7. Udowodnij, że a
n
>
3
2
n
n 1.
103
ROZDZIAŁ 15. Zadania.
Zadanie 56. Definiujemy rekurencyjnie ciąg a
n
a
0
= 1
a
1
= 3
a
2
= 5
a
n
= 3a
n−2
+ 2a
n−3
n 3
Oblicz a
n
dla n = 3, 4, 5, 6, 7. Udowodnij, że a
n
> 2
n
dla n 1, a
n
< 2
n+1
dla n 1
oraz, że a
n
= 2a
n−1
+ (−1)
n−1
n 1.
Zadanie 57. Definiujemy rekurencyjnie ciąg a
n
(
a
0
= a
1
= a
2
= 1
a
n
= a
n−1
+ a
n−3
n 3
Oblicz a
n
dla n = 3, 4, 5, 6. Udowodnij, że a
n
> (
√
2)
n−2
dla n 2 oraz, że a
n
< (
3
2
)
n−1
dla n 1.
Zadanie 58. Definiujemy rekurencyjnie ciąg SEQ(n) za pomocą wzorów
(
SEQ(0) = 0
SEQ(1) = 1
SEQ(n) =
1
n
SEQ(n − 1) +
n−1
n
SEQ(n − 2)
n 2
Udowodnij, że 0 SEQ(n) 1 dla n ∈ N.
Zadanie 59. Rozważmy ciąg Fibonacciego
FIB(0) = FIB(1) = 1FIB(n) = FIB(n − 1) + FIB(n − 2)
n 2
Udowodnij, że FIB(n) = 1 +
P
n−2
k=0
FIB(k) dla n 2.
15.1.4
Rozdziały 5–6.
Zadanie 60. Ile różnych wyników można otrzymać przy rzucaniu dwoma kostkami do gry,
jeśli
1. kostki są rozróżnialne
2. kostki są nierozróżnialne
3. rozróżniamy wyniki w zależności od sumy wyrzuconych oczek
Zadanie 61. Ile liczb 4-cyfrowych można utworzyć z cyfr 1, 2, 3, 4 tak aby żadna cyfra
w liczbie nie powtarzała się a ile takich w których dopuszczalne są powtórzenia
Zadanie 62. Ile liczb czterocyfrowych można utworzyć z cyfr 0, 1, 2, 3, tak aby żadna
cyfra w liczbie nie powtarzała się?
Zadanie 63. W urnie znajduje się n kul ponumerowanych i m kul bez numerów. Ku-
le wyjmujemy z urny jedną po drugiej i układamy w rząd. Ile jest różnych rezultatów
ciągnienia przy założeniu, że kule nienumerowane są nierozróżnialne?
Zadanie 64. Na 4 różne posady zgłosiło się 20 kandydatów. Na ile sposobów można
obsadzić te posady?
Zadanie 65. Ile różnych słów pięcioliterowych można utworzyć z 24 liter przy założeniu,
że każda litera może występować w słowie dokładnie jeden raz? Ile ich jest jeśli mogą
występować powtórzenia?
104

15.1. Zadania do rozdziałów.
Zadanie 66. Ile można utworzyć liczb trzycyfrowych z cyfr 1, 2, 3, 4, 5?
Zadanie 67. Ile istnieje liczb trzycyfrowych?
Zadanie 68. Ile słów można utworzyć z 18 spółgłosek i 6 samogłosek, jeżeli każde słowo
składa się z 2 samogłosek i 3 spółgłosek oraz samogłoski zajmują 2 i 4 miejsce?
Zadanie 69. Iloma sposobami można z 18 osób utworzyć 3 drużyny sześcioosobowe?
Zadanie 70. Ile prostych można utworzyć z n punktów przestrzeni jeśli wiadomo, że m
punktów leży w jednej płaszczyźnie, a poza tym żadne 4 nie leżą w jednej płaszczyźnie.
Zadanie 71. W kwiaciarni są trzy gatunki kwiatów. Ile różnych bukietów można utwo-
rzyć z 10 kwiatów.
Zadanie 72. W skład 5-osobowej komisji wchodzą przedstawiciele 10 narodów. Iloma
sposobami można taką komisję utworzyć przy założeniu, że komisja nie może składać się
wyłącznie z przedstawicieli jednego narodu.
Zadanie 73. Każdą krawędź sześcianu podzielono na n równych części i przez każdy
punkt podziału poprowadzono płaszczyznę prostopadłą do tej krawędzi. Ile prostopadlo-
ścianów powstaje w wyniku tego podziału?
Zadanie 74. Na sali mamy n osób. Na ile sposobów można wymienić uscisk dłoni?
Zadanie 75. Pewna grupa studencka składa się z 212 mężczyzn i 16 kobiet. Ile da się
z nich utworzyć komisji składających się z
1. 7 osób
2. 3 mężczyzn i 4 kobiet
3. 7 kobiet lub 7 mężczyzn
Zadanie 76. Ile można utworzyć komisji składających się z 4 osób wybranych z 9
osobowej grupy? A ile przy założeniu, że są dwie osoby, które nie chcą być w tej samej
komisji?
Zadanie 77. Niech S = {a, b, c, d} T = {1, 2, 3, 4, 5, 7}.
1. Ile jest funkcji różnowartościowych z T w S?
2. Ile jest funkcji różnowartościowych z S w T ?
3. Ile jest funkcji z S w T ?
Zadanie 78. Niech P = {1, 2, 3, . . . , 9}, Q = {A, B, C, D, E}
1. Ile jest czteroelementowych podzbiorów zbioru P ?
2. Ile jest permutacji zbioru Q.
3. Ile jest numerów rejestracyjnych składających się z trzech liter ze zbioru Q i nastę-
pujących po nich dwóch cyfr ze zbioru P ? Powtórzenia są dozwolone.
Zadanie 79. Niech Ω będzie zbiorem uporządkowanych n-tek z powtórzeniami złożo-
nych z cyfr 1, 2, 3. Wyznaczyć liczbę elementów Ω, które:
1. rozpoczynają się od 1
2. zawierają dokładnie k+2 jedynek, przy czym rozpoczynają się i kończą 1, a n k+2.
3. zawierają dokładnie k dwójek n k
105

ROZDZIAŁ 15. Zadania.
4. są złożone z k
1
jedynek, k
2
dwójek, k
3
trójek, gdzie k
1
+ k
2
+ k
3
= n.
Zadanie 80. W n różnych komórkach rozmieszczono k rozróżnialnych cząstek b
1
, . . . , b
k
,
przy czym k n i komórka może zawierać nie więcej niż 1 cząstkę. Obliczyć liczbę
wszystkich sposobów rozmieszczenia przy których
1. w komórce a
1
znajduje się cząstka b
1
2. w komórkach a
1
, a
2
znajdują się cząstki b
1
, b
2
Zadanie 81. Numer telefoniczny, może się rozpoczynać od każdej z cyfr 0, 1, 2, . . ., 9.
Obliczyć liczbę sześciocyfrowych numerów telefonów, w których wszystkie cyfry są:
1. różne
2. nieparzyste
Zadanie 82. Spośród n osób należy wybrać r osób. Następnie z r osób należy wybrać k
członków zarządu. Pozostali utworzą komisję rewizyjną. Na ile sposobów można wybrać
zarząd i komisję rewizyjną. Czy liczba wyborów będzie taka sama gdy najpierw wybierze
się k członków zarządu a z pozostałych n − k osób wybierze się r − k członków komisju
rewizyjnej?
Zadanie 83. Ile dzielników ma liczba 2 · 3 · 5 · 7 · 11.
Zadanie 84.
1. Wyjaśnij, dlaczego wsród dowolnych czterech liczb całkowitych dwie muszą przy-
stawać
mod 3.
2. Udowodnij, że jeśli a
1
, . . . , a
p+1
są całkowite, to dwie muszą przystawać
mod p.
Zadanie 85. Przypuścmy, że 73 kulki zostały umieszczone w ośmiu pudełkach. Wykaż,
że
1. jedno z pudełek zawiera co najmniej 10 kulek
2. jeśli dwa pudełka są puste, to jakieś pudełko zawiera co najmniej 13 kule
Zadanie 86. Niech B będzie dwunastoelementowym podzbiorem zbioru {1, 2, . . . , 6} ×
{1, 2, . . . , 6}.
1. Wykaż, że B zawiera dwie różne pary uporządkowane, mające różne sumy elemen-
tów, poprzednika i następnika.
2. Ile razy można rzucić parą kostek bez dwukrotnego otrzymania tej samej liczby
oczek?
Zadanie 87. Worek zawiera 50 szklanych kulek w 4 różnych kolorach.
1. Wyjaśnij dlaczego jest co najmniej 13 kulek tego samego koloru.
2. Jeśli czerwonych kulek jest dokładnie 8, to wyjaśnij dlaczego jest co najmniej 14
kulek tego samego koloru
106

15.1. Zadania do rozdziałów.
Zadanie 88. Niech A będzie dziesięcioelementowym podzbiorem zbioru {1, 2, 3, . . . , 50}.
Wykazać, że A ma dwa różne czteroelementowe podzbiory, których sumy elementów są
równe.
Zadanie 89. Niech A będzie podzbiorem zbioru {1, 2, 3, . . . , 149, 150} złożonym z 25
liczb. Wykaż, że istnieją dwie rozłączne pary elementów zbioru A, mające te równe sumy.
Zadanie 90. Weźmy 9 nieujemnych liczb rzeczywistych a
1
, a
2
, . . . , a
9
, których suma
jest równa 90.
1. Pokazać, że wśród tych liczb muszą istnieć trzy takie, których suma równa się co
najmniej 30.
2. Pokażemy, że wśród tych liczb muszą istnieć cztery takie, których suma równa się
co najmniej 40
Zadanie 91. Urna zawiera M czarnych i N − M białych kul (M < N ). Dokonujemy
wyboru losowej próbki bez zwracania o liczności n (n < N , n < N − M ). Obliczyć
prawdopodobieństwo tego, że próbka zwiera dokładnie k czarnych kul (k ¬ n, k ¬ M )
Zadanie 92. Cyfry 1, 2, 3, 4, 5 zapisane są na 5 kartkach. Wybierzmy losowo jedną po
drugiej trzy kartki i zapisujemy umieszczone na nich cyfry w kolejności losowania. Obliczyć
prawdopodobieństwo, że otrzymana w ten sposób liczba będzie parzysta.
Zadanie 93. Zamek cyfrowy zawiera 5 dysków osadzonych na wspólnej osi. Każdy
z nich jest podzielony na 6 sektorów oznaczonych różnymi literami. Zamek otwiera się
tylko wtedy, gdy każdy dysk zajmie pewną określoną pozycję względem korpusu zamka.
Obliczyć prawdopodobieństwo otwarcia zamka po ustawieniu losowo wybranej kombinacji
liter na dyskach.
Zadanie 94. Obliczyć prawdopodobieństwo, że numer losowo wybranej obligacji nie
zawiera jednakowych cyfr, jeśli numer ten może być dowolną liczbą pięciocyfrową, poczy-
nając od 00001.
Zadanie 95. Grupa składająca się z 2n siada w sposób losowy wokół okrągłego stołu.
Obliczyć prawdopodobieństwo, że dwie z góry ustalone osoby
1. usiądą obok siebie
2. nie będą sąsiadować ze sobą
Zadanie 96. W pudełku znajduje się pięć jednakowych klocków, przy czym trzy z nich
są pomalowane. Losowo wyciągnięto dwa klocki. Znaleźć prawdopodobieństwo tego, że
wśród wyciągnietych dwóch klocków jest
1. jeden pomalowany
2. dwa pomalowane
3. co najmniej jeden pomalowany
Zadanie 97. W magazynie znajduje się 15 kineskopów, w tym 10 jest wyprodukowanych
przez zakłady X. Znaleźć prawdopodobieństwo tego, że wśród losowo wybranych pięciu
kineskopów będą trzy kineskopy produkcji X.
Zadanie 98. Wykręcając numer telefonu abonent zapomniał ostatnie trzy cyfry. Pamię-
tając tylko, że te cyfry są różne wykręcił je na chybił trafił. Znaleźć prawdopodobieństwo
tego, że znalazł właściwy numer.
Zadanie 99. Pomyślano dwucyfrową liczbę, której cyfry są różne. Znaleźć prawdopo-
dobieństwo tego, że okaże się równa pomyślanej liczbie
107

ROZDZIAŁ 15. Zadania.
1. przypadkowa liczba dwucyfrowa
2. przypadkowa liczba dwucyfrowa, której cyfry są różne
Zadanie 100. Przy przewożeniu skrzyni zawierającej 21 detali standardowych i 10
niestandardowych, zgubiono jeden z nich, nie wiadomo który. Ze skrzyni po przewiezieniu
wyciągnięto losowo jeden detal standardowy. Znaleźć prawdopobieństwo tego, że zgubiono
detal standardowy, oraz tego że zgubiono detal niestandardowy.
Zadanie 101. W kolejce po bilety w cenie 10 zł ustawiło się n + m osób z których n
ma tylko dziesięciozłotówki, a m tylko dwudziestozłotówki (m ¬ n + 1). Wszyscy kupują
po jednym bilecie. Przed rozpoczęciem sprzedaży w kasie nie było pieniędzy. Jakie jest
prawdopodobieństwo, że nikt z kolejki nie będzie musiał czekać na resztę?
Zadanie 102. Obliczyć ile jest liczb całkowitych w zbiorze S = {1, 2, 3, . . . , 2000}, które
są podzielne przez 9, 11, 13 lub 15.
Zadanie 103. Wybieramy losowo liczbę ze zbioru T = {1000, 1001, . . . , 9999}. Znaleźć
prawdopobieństwo tego, że wśród cyfr wylosowanej liczby co najmniej raz występuje 0,
co najmniej raz 1 oraz co najmniej raz 2 (na przykład 1072 lub 2101).
Zadanie 104. Wśród 200 osób 150 uprawia pływanie lub jogging lub jedno i drugie.
Jeśli 85 osób uprawia pływanie a 60 pływanie i jogging to ile uprawia jogging?
Zadanie 105. Niech S = {100, 101, 102, . . . , 999}, a więc |S| = 900.
1. Ile jest liczb ze zbioru S ma co najmnie jedną cyfrę równą 3 lub 7?
2. Ile liczb ze zbioru S ma co najmniej jedną z cyfr równą 3 i co najmnie jedną z cyfr
równą 7?
Zadanie 106. Wybieramy losowo liczbę całkowitą ze zbioru {1, 2, 3, . . . , 1000}. Ile wy-
nosi prawdopodobieństwo, że jest ona podzielna przez 4, 5 lub 6?
Zadanie 107. Wybieramy losowo liczbe całkowitą ze zbioru {1, 2, 3, . . . , 1000}. Ile wy-
nosi prawdopodobieństwo, że liczba ta jest
1. podzielna przez 7
2. podzielna przez 11
3. niepodzielna przez 7 lub 11
4. podzielna przez 7 lub 11, a także przez obie te liczby
Zadanie 108. Ile jest sposobów rozmieszczenia pięciu kul w czterech pudełkach?
Zadanie 109. Na ile sposobów dziesięć identycznych czerwonych kulek można umieścić
w pięciu rozróżnialnych torbach?
Zadanie 110. Ile jest liczb ze zbioru {1, 2, 3, . . . , 1000} ma tę własność, że suma cyfr
wynosi 7?
Zadanie 111. Na ile sposobów można wybrać 10 monet mając nieograniczony zapas
jednogroszówek, pięciogroszówek, dziesięciogroszówek i pięćdziesięciogroszówek?
Zadanie 112. Pewien inwestor ma 7 przekazów gotówkowych po 1200 zł każdy, które
chce przesłać pocztą trzem fundacjom emerytalnym (powierniczym).
1. na ile sposobów może zainwestować swoje pieniądze?
2. na ile sposobów może zainwestować swoje pieniądze zakładając, że każdy fundusz
wymaga wpłaty co najmniej 1000 zł.
108

15.1. Zadania do rozdziałów.
Zadanie 113. Dwanaście identycznych listów ma zostać wrzuconych do czterech róż-
nych skrzynek pocztowych. Policz
1. na ile różnych sposobów można to zrobić?
2. na ile różnych sposobów można to zrobić, jeśli do każdej ze skrzynek muszą trafić
co najmniej dwa listy?
Zadanie 114. Ile można otrzymać różnych mieszanek po 10 cukierków, jeśli mamy do
dyspozycji cztery rodzaje cukierków w nieograniczonych ilościach?
Zadanie 115. Na ile sposobów można rozmieścić 14 przedmiotów w 3 pudełkach
1. tak by w jednym z pudełek znalazło się co najmniej 8 przedmiotów?
2. tak ,by w żadnym z pudełek nie znalazło się więcej niż 7 przedmiotów?
Zadanie 116. W związku z wzajemną jednoznacznością między ciągami złożonymi z
pięciu zer i trzech jedynek, a rozmieszczniem pięciu przedmiotów w czterech pudełkach
1. Znajdź rozmieszcznienia, które odpowiadają następującym ciągom:
10101000
01001001
10000011
11100000
2. Znajdź ciągi, które odpowiadają następującym rozmieszczeniom:
|0|0|0|00|
|00| |0|00|
|00000| | | | |
Zadanie 117. Podać model kombinatoryczny prowadzący do dowódu równości
n + 1
r
=
n
r − 1
+
n
r
1 ¬ r ¬ n
Zadanie 118. Dla dowolnych a, b ∈ R oraz n ∈ N mamy
(a + b)
n
=
n
X
r=0
n
r
a
r
b
n−r
Znajdź rozwinięcią następujących wyrażeń:
1. (x + 2y)
4
2. (x − y)
6
3. (3x + 1)
4
4. (x + 2)
5
109
ROZDZIAŁ 15. Zadania.
Rysunek 15.1: Grafy.
e
a
b
c
d
e
f
g
γ(e)
(x, w)
(w, x)
(x, x)
(w, z)
(w, y)
(w, z)
(z, y)
Tabela 15.1: Wartości funkcji γ.
Rysunek 15.2: Graf skierowany.
110

15.1. Zadania do rozdziałów.
15.1.5
Rozdziały 7–9.
Zadanie 119. Podaj tabelę funkcji p dla każdego z grafów z rysunku 15.1.
Zadanie 120. Zrób rysunek grafu skierowanego G, w którym zbiorem wierzchołków
jest V (G) = {w, x, y, z}, a zbiorem krawędzi E(G) = {a, b, c, d, e, f , g}, a funkcją γ
podaną w tabeli 15.1.
Zadanie 121. Które z podanych ciągów wierzchołków opisują drogi w grafie skierowa-
nym przedstawionym na rysunku 15.2.
1. zywvwt
2. vstx
3. xzyvs
Zadanie 122. Weźmy graf skierowany przedstawiony na rysunku 15.3. Opisz drogę
acykliczną
1. od x do y
2. od v do w
3. od z do v
Rysunek 15.3: Graf.
Zadanie 123. Podaj przykład grafu skierowanego o wierchołkach x, y, z w którym są
cykle jeden z wierzchołkami x i y a drugi z y i z, ale nie ma cyklu mającego wierzchołki
x i z.
Zadanie 124. Które z następujących ciągów wierzchołków odpowiadają drogom w gra-
fie z rysunku 15.4.
1. zxw
2. wwxz
3. zxwyywz
4. yyww
111

ROZDZIAŁ 15. Zadania.
Rysunek 15.4: Graf.
Podaj długość każdej drogi. Które z nich są drogami zamkniętymi? Wypisz krawędzie
wielokrotne, ile jest pętli w tym grafie?
Zadanie 125. Podaj relację sąsiedztwa A dla grafu z rysunku 15.4?
Zadanie 126. Dla grafu przedstawionego na rysunku 15.5 podaj przykład każdej z
następujących dróg. Sprawdź czy podałeś ciąg krawędzi i ciąg wierzchołków.
Rysunek 15.5: Graf.
1. droga długości 3 od y do w
2. droga długości 4 od v do y
Zadanie 127. Mamy daną macierz sąsiedztwa grafu skierowanego
1.
0
1
0
0
1
0
0
0
1
2
0
0
3
0
0
1
2.
0
1
0
1
0
0
0
1
1
1
0
0
0
1
1
1
Jakie informacje o grafie zawarte są w tych macierzach sąsiedztwa?
Zadanie 128. Dla grafu przedstawionego na rysunku 15.6 podaj ciąg wierzchołków
najkrótszej drogi łączącej następujące pary wierzchołków i podaj jej długość.
112

15.1. Zadania do rozdziałów.
Rysunek 15.6: Graf.
1. s i v
2. u i y
Zadanie 129.
1. Zrób rysunek pięciu grafów regularnych o 4 wierzchołkach, z którch każdy ma stopień
równy dwa.
2. Zrób rysunek wszystkich grafów regularnych o pięciu wierzchołkach, z których każdy
ma stopień równy trzy.
Zadanie 130. Które pary grafów z rysunku 15.7 są izomorficzne? Uzasadnij odpowiedź
opisując izomorfizm lub wyjaśniając dlaczego nie istnieje.
Rysunek 15.7: Grafy.
Zadanie 131. Które z następujących ciągów są ciągami liczb wierzchołków kolejnych
stopni grafów? W każdym przypadku narysuj graf o danym ciągu liczb wierzchołków
kolejnych stopni tego grafu, albo wyjaśnij dlaczego taki graf nie istnieje.
113

ROZDZIAŁ 15. Zadania.
1. (1, 1, 0, 3, 1, 0, 0, . . .)
2. (0, 0, 1, 2, 1, 0, 0, . . .)
Zadanie 132. Zbadać spójność oraz podać liczbę składowych grafów z rysunku 15.8.
Rysunek 15.8: Grafy.
Zadanie 133. Który z grafów przedstawionych na rysunku 15.9 ma cykle Eulera?
Rysunek 15.9: Grafy.
Zadanie 134. Czy grafy przedstawione na rysunku 15.10 mają drogę Eulera?
Rysunek 15.10: Grafy.
Zadanie 135. Znaleźć wzór na s
2
m
1.
s
1
= 1
s
2n
= 2s
n
+ 3
R(n) = 3
2.
s
1
s
2n
= 2s
n
114

15.1. Zadania do rozdziałów.
3.
s
1
= 0
s
2n
= 2s
n
+ 5n
4.
s
1
= 2
s
2n
= 2s
n
+ 3 + 5n
5.
s
1
s
2n
= 2s
n
− 7
6.
s
1
= 3
s
2n
= 2s
n
− n
7.
s
1
= 0
s
2n
= 2s
n
+ 5 − 7n
Zadanie 136. Wyprowadzić wzór na s
2
m
dla R(n) = n
3
.
15.1.6
Rozdział 14.
Zadanie 137. Zmienna losowa X ma funkcję zadaną wzorem
1. g(s) =
1
4
(1 + s)
2
2. g(s) =
s(1−s
6
)
6(1−s)
3. g(s) =
s
2−s
Wyznaczyć rozkład zmiennej losowej oraz E(X) i D
2
(X).
Zadanie 138. Weźmy X
1
, X
2
niezależne zmienne losowe o rozkładzie Poissona z λ
1
,λ
2
>
0. Korzystając z funkcji tworzących znaleźć rozkład Y = X
1
+ X
2
.
Zadanie 139. Dana jest funkcja tworząca f (s) rozkładu zmiennej losowej X. Policzyć
funkcje tworzące rozkładów
1. Y = X + 1
2. Y = 2X
Zadanie 140. Dana jest funkcja tworząca f (s) rozkładu zmiennej losowej X. Policzyć
funkcje tworzące dla
1. P ({ε : X(ε) ¬ n})
2. P ({ε : X(ε) n})
3. P ({ε : X(ε) < n})
4. P ({ε : X(ε) > n + 1})
5. P ({ε : X(ε) = 2n})
115

ROZDZIAŁ 15. Zadania.
15.2
Zestawy kolokwialne.
15.2.1
Zestaw 1.
Wersja I.
1. Udowodnić, że (x
2
+ x + 1) | ((x + 1)
2n+1
+ x
n+2
) dla n ∈ N.
2. Sprawdzić czy podane niżej warunki są niezmiennikami pętli
DOPÓKI 1=<m WYKONUJ
m:=2m
n:=3n
(a) n
2
m
3
(b) 2m
6
< n
4
3. Niech Σ = {a, b, c} i niech A(n) będzie zbiorem słów w Σ
n
, w których występuje
parzysta liczba elementów a oraz niech s
n
oznacza liczbę słów w A(n)
(a) podaj wartość s
0
, s
1
, s
2
(b) znajdź wzór rekurencyjny na s
n
(c) oblicz s
3
, s
4
, s
5
4. Znaleźć zbiór ogólny ciągu s
n
i s
2
n
mając dane
(a) s
n
= 5s
n−1
+ 7s
n−2
s
0
= 1
s
1
= 2
(b) s
n
= 2s
n
+ n
3
s
1
= 5
Wersja II.
1. Udowodnić, że n! <
n+1
2
n
dla n 2.
2. Sprawdzić czy podane niżej warunki są niezmiennikami pętli
DOPÓKI 1=<k WYKONUJ
k:=2k
(a) k
2
≡ 1( mod 3)
(b) k
2
≡
mod 4
3. Niech Σ = {0, 1} i niech A(n) będzie zbiorem ciągów w Σ
n
, w których dwie jedynki
nie stoją obok siebie oraz niech s
n
oznacza liczbę ciągów w A(n)
(a) podaj wartość s
0
, s
1
, s
2
(b) znajdź wzór rekurencyjny na s
n
(c) oblicz s
3
, s
4
, s
5
4. Znaleźć wzór ogólny ciągu s
n
i s
2
n
mając dane
(a) s
n
= 4s
n−1
+ 2s
n−2
s
0
= 0
s
1
= 5
(b) s
2n
= 2s
n
+ n
4
s
1
= 8
116

15.2. Zestawy kolokwialne.
Wersja III
1. Udowodnić, że (
n
3
)
n
¬ n! ¬ (
n
2
)
n
dla n 6.
2. Sprawdzić czy warunek
P
k
i=0
2
i
= 2
k+1
− 1 jest niezmiennikiem pętli
DOPÓKI k>=0 WYKONUJ
JEŚLI suma od 0 do k po 2^i = 2^(k+1)-1 TO k:=k+1
3. Wyznaczyć ciąg s
n
określony rekurencyjnie, oznaczający liczbę takich podziałów
podzbiorów zbioru {1, 2, . . . , n}, które nie zawierają dwóch kolejnych liczb
(a) podaj wartość s
0
, s
1
, s
2
(b) oblicz s
3
, s
4
, s
5
4. Znaleźć wzór ogólny ciągu s
n
i s
2
n
mając dane
(a) s
n
= 5s
n−1
+ 6s
n−2
s
0
= 5
s
1
= 8
(b) s
2n
= 2s
n
+ An
2
+ Bn + Cs
1
= 2
A, B, C ∈ R
15.2.2
Zestaw 2.
Wersja I.
1. Spośród n osób należy wybrać r osób. Następnie z r osób należy wybrać k członków
zarządu. Pozostali utworzą komisję rewizyjną. Na ile sposobów można wybrać zarząd
i komisję rewizyjną? Czy liczba wyborów będzie taka sama, gdy najpierw wybierze
się k członków zarządu, a z pozostałych n − k osób wybierze się r − k członków
komisji rewizyjnej?
2. W urnie znajduje sie n białych i m czarnych kul m < n. Wyjmujemy kolejno bez
zwracania kule z urny. Niech M (k) i N (k) oznaczają odpowiednio liczbę kul czarnych
i białych wyjętych w pierwszych k losowaniach. Obliczyć prawdopodobieństwo, że
dla wszystkich k = 1, 2, . . . , n + m będzie
(a) M (k) < N (k)
(b) M (k) ¬ N (k)
3. Ile jest liczb całkowitych od 1 do 5000, które są podzielne przez 9, 11, 13 i 15.
4. Dany jest zbiór złożony z 10 liczb naturalnych dwucyfrowych w rozwinięciu dzie-
siętnym. Dowieść, że w tym zbiorze istnieją dwa niepuste podzbiory takie, że sumy
liczb obu podzbiorów są równe.
5. Dwanaście identycznych listów ma zostać wrzuconych do czterech różnych skrzynek
pocztowych.
(a) Na ile sposobów można to zrobić?
(b) Na ile sposobów można to zrobić, jeśli do każdej ze skrzynek muszą trafić
przynajmniej dwa listy?
117

ROZDZIAŁ 15. Zadania.
Wersja II.
1. Liczby 1, 2, . . . , n ustawiono przypadkowo, oblicz prawdopodobieństwo, że
(a) liczby 1 i 2
(b) liczby 1, 2 i 3
występują w sąsiedztwie i w wyżej wymienionej kolejności.
2. W urnie znajduje się n białych i m czarnych kul m < n. Wyjmujemy kolejno bez
zwracania kule z urny. Niech M (k) i N (k) oznaczają odpowiednio liczbę kul czarnych
i białych wyjętych w pierwszych k losowaniach. Obliczyć prawdopodobieństwo, że
dla wszystkich k = 1, 2, . . . , n + m będzie
(a) M (k) < N (k)
(b) M (k) ¬ N (k)
3. Ile jest liczb całkowitych od 1 do 3000, które są podzielne przez 9, 11, 13 i 15?
4. Dany jest zbiór złożony z 10 liczb naturalnych dwucyfrowych w rozwinięciu dzie-
siętnym. Dowieść, że w tym zbiorze istnieją dwa niepuste podzbiory takie, że sumy
liczb obu podzbiorów są równe.
5. Siedemnaście identycznych kul ma być włożonych do pięciu różnych szuflad
(a) Na ile sposobów można to zrobić?
(b) Na ile sposobów można to zrobić, jeśli do każdej szuflady muszą trafić co naj-
mniej dwie kule?
Wersja III.
1. Z n par obuwia wybrano losowo 2r butów (2r < n). Obliczyć prawdopodobieństwo,
że wśród wybranych butów
(a) nie ma ani jednej pary.
(b) są dokładnie dwie pary.
2. Na każdym przystanku k = 1, 2, . . . , n + m stoi jedna osoba. Na wszystkich przy-
stankach jest n + m osób w tym n chłopców i m dziewcząt gdzie m < n. W trakcie
trwania kursu nikt nie wychodzi z autobusu. Oblicz prawdopodobieństwo, że
(a) w autobusie po przejechaniu k-tego przystanku k = 1, 2, . . . , n + m będzie
mniej dziewcząt niż chłopców dla każdego k?
(b) w autobusie będzie nie więcej dziewcząt niż chłopców dla każdego k.
3. Ile jest liczb całkowitych od 1 do 7000, które są podzielne przez 9, 11, 13 i 15?
4. Na płaszczyźnie danych jest pięć punktów kratowych (są to punkty o wspołrzędnych
całkowitych). Wykazać, że środek jednego z odcinków łączących te punkty jest też
punktem kratowym.
5. Na ile sposobów można rozmieścić 14 przedmiotów w 3 pudełkach, tak aby
(a) w jednym z pudełek znalazłoby się co najmniej 8 przedmiotów?
(b) w żadnym z pudełek nie znalazłoby się więcej niż 7 przedmiotów?
118

15.2. Zestawy kolokwialne.
Wersja IV.
1. Z n par obuwia wybrano losowo 2r butów (2r < n). Obliczyć prawdopodobieństwo,
że wśród wybranych butów
(a) jest dokładnie jedna para?
(b) są dokładnie trzy pary?
2. Na każdym przystanku k = 1, 2, . . . , n + m stoi jedna osoba. Na wszystkich przy-
stankach jest n + m osób w tym n chłopców i m dziewcząt gdzie m < n. W trakcie
trwania kursu nikt nie wychodzi z autobusu. Oblicz prawdopodobieństwo, że
(a) w autobusie po przejechaniu k-tego przystanku k = 1, 2, . . . , n + m będzie
mniej dziewcząt niż chłopców dla każdego k?
(b) w autobusie będzie nie więcej dziewcząt niż chłopców dla każdego k.
3. Ile jest liczb całkowitych od 1 do 4000, które są podzielne przez 9, 11, 13 i 15?
4. Wykazać, że w trójkącie równobocznym o boku 4 nie można umieścić 17 punktów,
tak by odległość dwóch z nich była większa od jedynki.
5. Dwanaście identycznych listów ma zostać wrzuconych do czterech różnych skrzynek
pocztowych.
(a) na ile sposobów można to zrobić?
(b) na ile sposobów można to zrobić, jeśli do każdej ze skrzynek muszą trafić co
najmniej dwa listy?
15.2.3
Zestaw 3.
Wersja I.
1. Niech Σ = {0, 1} i niech A(n) będzie zbiorem ciągów w Σ
n
, w których dwie jedynki
nie stoją obok siebie oraz niech s
n
oznacza liczbę ciągów w A(n)
(a) podaj wartość s
0
, s
1
, s
2
(b) znajdź wzór rekurencyjny na s
n
(c) oblicz s
3
, s
4
, s
5
2. Sprawdzić czy podane warunki są niezmiennikami pętli
DOPÓKI j>=n WYKONUJ
i:=i+2
j:=j+2
(a) i < j
2
dla n = 1
(b) i ¬ j
2
dla n = 0
3. Dwanaście identycznych książek – nowości wydawniczych ma trafić do 4 różnych
bibliotek w pewnym mieście. Na ile sposobów można to zrobić? Jak zmieni się licz-
ba tych sposobów przydzialania, gdy każda biblioteka wymaga co najmniej dwóch
książek?
119

ROZDZIAŁ 15. Zadania.
4. Niech A będzie pewnym ustalonym dziesięcioelementowym podzbiorem zbioru {1,
2, . . ., 50}. Pokazać, że zbiór A ma dwa różne pięcioelementowe podzbiory takie, że
sumy wszystkich elementów każdego z nich są równe.
5. Jeśli dwaj kandydaci P i Q otrzymali w wyborach p i q głosów, p > q. Jaka jest
szansa na to, że przy zliczaniu głosów kandydat P będzie cały czas wyprzedzał bądź
dorównywał pod względem liczby głosów kandydatowi Q?
Wersja II.
1. Niech Σ = {a, b, c} i niech A(n) będzie zbiorem słów w Σ
n
, w których występuje
parzysta liczba elementów a oraz niech s
n
oznacza liczbę słów w A(n)
(a) podaj wartość s
0
, s
1
, s
2
(b) znajdź wzór rekurencyjny na s
n
(c) oblicz s
3
, s
4
, s
5
2. Sprawdzić czy podane warunki są niezmiennikami pętli
DOPÓKI j>=n WYKONUJ
i:=i+2
j:=j+2
(a) i < j
2
dla n = 1
(b) i ¬ j
2
dla n = 0
3. Piętnaście identycznych kul ma trafić do trzech różnych szuflad. Na ile sposobów
można to zrobić? Jak zmieni się liczba tych sposobów przydzielania, gdy do każdej
szuflady muszą trafić co najmniej trzy kule?
4. Nich A będzie pewnym ustalonym 25-elementowym podzbiorem zbioru {1 , 2 , . . .,
150}. Pokazać, że zbiór A ma dwa różne dwuelementowe podzbiory takie, że sumy
wszystkich elementów każdego z nich są równe.
5. Jeśli dwaj kandydaci P i Q otrzymali w wyborach p + 1 i q głosów, p > q. Jaka
jest szansa na to, że przy zliczaniu głosów kandydat P będzie cały czas wyprzedzał
bądź dorównywał pod względem liczby głosów kandydatowi Q?
120

Spis literatury
[1] Ross K. A., Wright R.B., Matematyka dyskretna, PWN, Warszawa 2000.
[2] Graham R. L., Knuth D., Patashnik O., Matematyka konkretna, PWN, Warszawa
2001.
[3] Weron A., Weron R., Inżynieria finansowa, WNT, Warszawa 2001.
[4] Jeśmianowicz L., Łoś J., Zbiór zadań z algebry, PWN, Warszawa 1976.
[5] Lipski W., Marek W., Analiza kombinatoryczna, PWN, Warszawa 1986.
[6] Feller W., Wstęp do rachunku prawdopodobieństwa, PWN, Warszawa 1981.
[7] Stojanow J., Zbiór zadań z rachunku prawdopodobieństwa, PWN, Warszawa 1982.
[8] Deo N., Teoria grafów i jej zastosowania w technice i informatyce, PWN, Warszawa
1980.
[9] Plucińska A., Pluciński E., Zadania z rachunku prawdopodobieństwa i statystyki ma-
tematycznej : dla studentów politechnik, PWN, Warszawa 1976.
[10] Browkin J., Zadania z olimpiad matematycznych V-VI, WSiP, Warszawa 1983.
[11] Bryński M., Olimipiady matematyczne VII, WSiP, Warszawa 1995
[12] Chełmiński K., Pompe W., Zasada szufladkowa Dirichleta, Delta, nr 12, 1994.
[13] Chrząstowski P., Liczby Fibonacciego, Delta, nr 2, 1992.
[14] Łukasiewicz G., Szafrański N., O metodzie okrężnej, Delta, nr 5, 1989.
[15] Mąkowski A., Iwaniec T., Zasada szufladkowa Dirichleta. Geometria okręgów i sfer,
WSiP, Warszawa 1980.
[16] Rutkowski J., O pewnym hokus-pokus w kombinatoryce, Delta, nr 2, 1988.
[17] Ryll J., Ciągi rekurencyjne a szeregi potęgowe, Delta, nr 5, 1985.
[18] Starczyk-Podhalicz D., Marczak M., Modelowanie matematyczne w nauczaniu ma-
tematyki na poziomie szkoły średniej, Politechnika Radomska, Prace naukowo-
pedagogiczne, nr 4, 1998.
[19] Strasiewicz S., Zadania z olimpiad matematycznych tom I-IV, PZWS, Warszawa
1956, 1961, 1967, 1972.
121

SPIS LITERATURY
[20] Traczyk T., Modele matematyczne i jak z nich korzystać, Delta, nr 7, 1978.
[21] Pawłowski H., Zadania z olimpiad matemayczynych z całego świata, Oficyna Wy-
dawnicza TUTOR, Toruń 1997.
[22] Żołądek M., Zasada szufladkowa Dirichleta w mechanice, Delta, nr 3, 1998.
[23] Makarec A., Wybrane metody modelowania matematycznego w problemach zadanio-
wych matematyki szkoły średniej, praca magisterska, promotor Marczak M., Uniwer-
sytet w Białymstoku, Białystok 2000.
[24] Ryba A., Marczak M., Wpływ wykorzystania technologii informacyjnej i metod mo-
delowania w rozwiązywaniu problemów na aktywność i motywację do nauki uczniów,
Rocznik Edukacji Alternatywnej, Łódź 2001.
122
Wyszukiwarka
Podobne podstrony:
J Jaworski Z Palka J Szymański Matematyka dyskretna dla informatyków
Matematyka Dyskretna dla informatyków Wojciech Kordecki
Elementy matematyki finansowej 2014
Hordi wzór zaliczenia, Matematyka dla ambitnych, matematyka dyskretna
4 ELEMENTY MATEMATYKI FINANSOWEJ
Hordi Ćw1, Matematyka dla ambitnych, matematyka dyskretna
Elementy matematyki finansowej, Różne Dokumenty, MARKETING EKONOMIA ZARZĄDZANIE
rozwiązania zadań, studia AGH, ZiIP, Magister, Elementy Matematyki Finansowej
Hordi Ćw2, Matematyka dla ambitnych, matematyka dyskretna
Elementy matematyki finansowej dodatkowe zadania
Program zajęć terapii pedagogicznej z elementami?ukacji matematycznej dla uczniów w młodszym wieku s
Elementy matematyki finansowej 2014
matematyka dyskretna w 2 id 283 Nieznany
Denisjuk A Matematyka Dyskretna
ANOVA hierarch odp folia Word2003, Elementy matematyki wyższej
więcej podobnych podstron